Comparative Study of Machine Learning for Predicting Compressive Strength in Oyster Shell Cementitious Composites
Highlights
- Superplasticizer and cement had the strongest Pearson correlations with compressive strength.
- Random forest achieved the highest performance among the base models, with R2 = 0.8411.
- LightGBM was identified as the optimal model, effectively capturing nonlinear patterns in the data.
- Ensemble models accurately predict compressive strength of oyster shell cementitious composites.
- Insights into the relative importance and directional influence of input variables are provided.
- Reliable evaluation of the structural performance of composites incorporating waste oyster shells.
Abstract
1. Introduction
2. Experimental Program
2.1. Experimental Process
2.2. Datasets
3. Research Method
3.1. Correlation Analysis
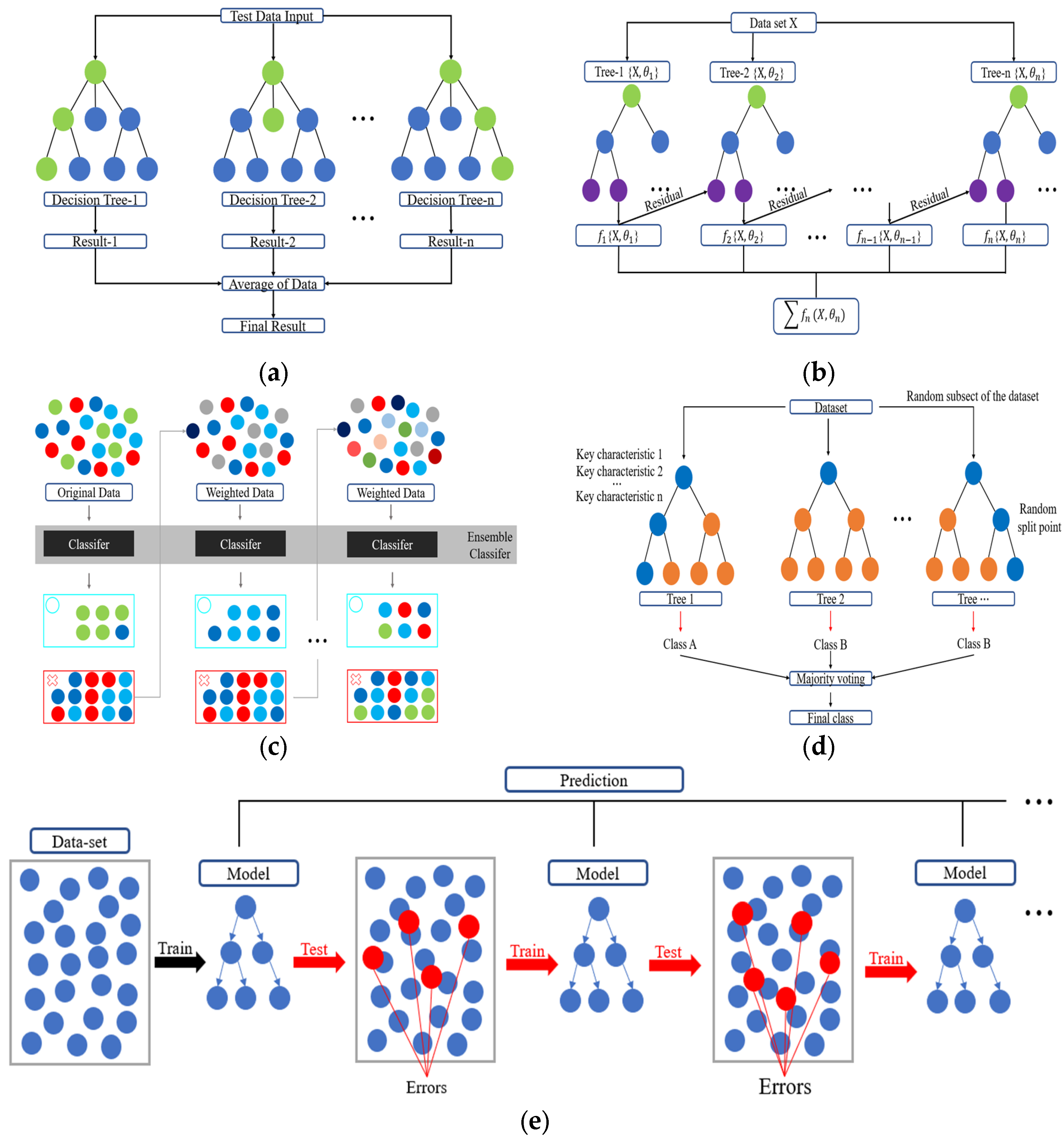
3.2. Background on Machine Learning Algorithms
3.3. Performance Metrics
4. Results and Discussion
4.1. Algorithm Performance Comparison and Optimal Model Selection
4.2. Detailed Analysis of Ensemble Models
5. Conclusions
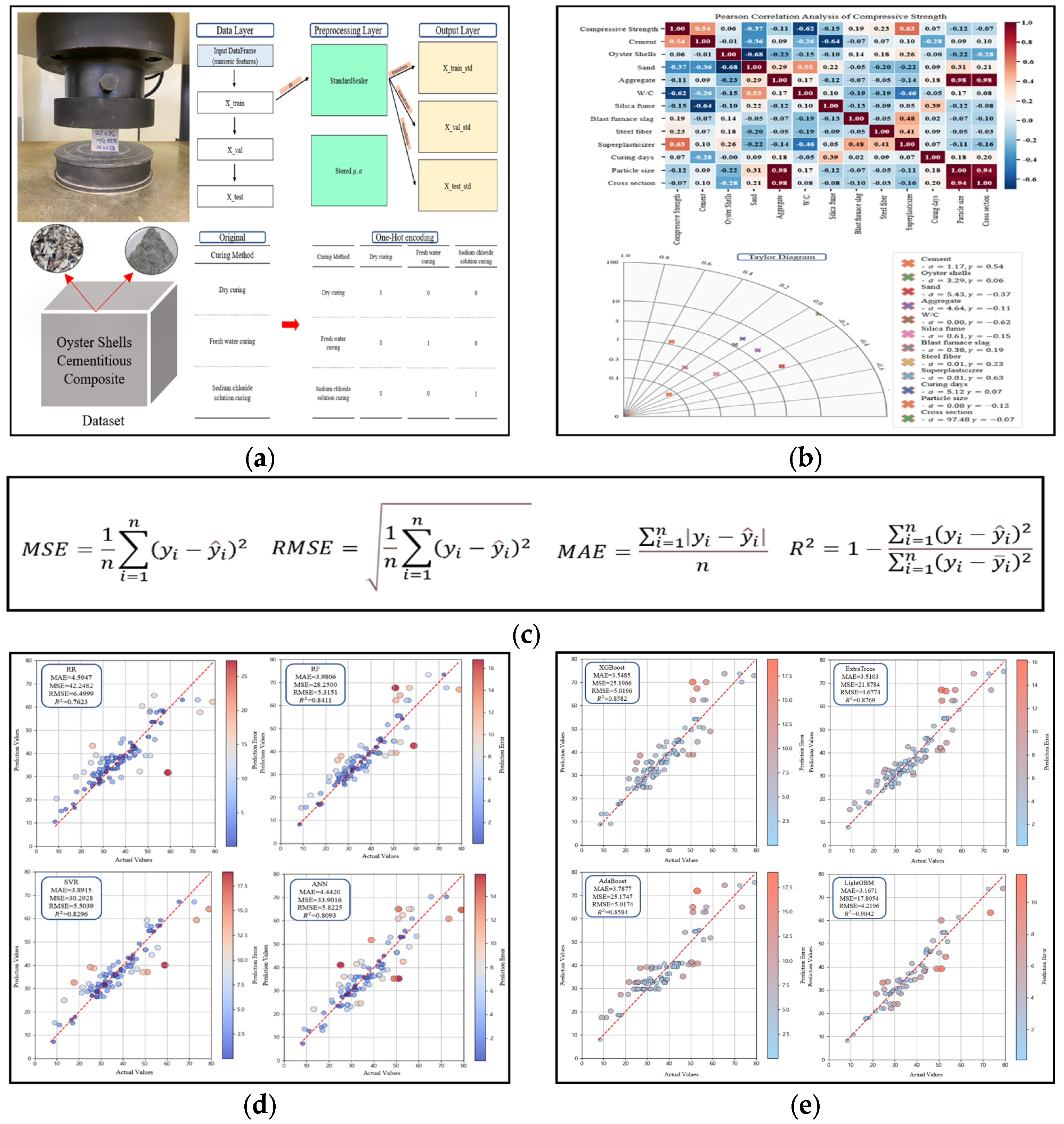
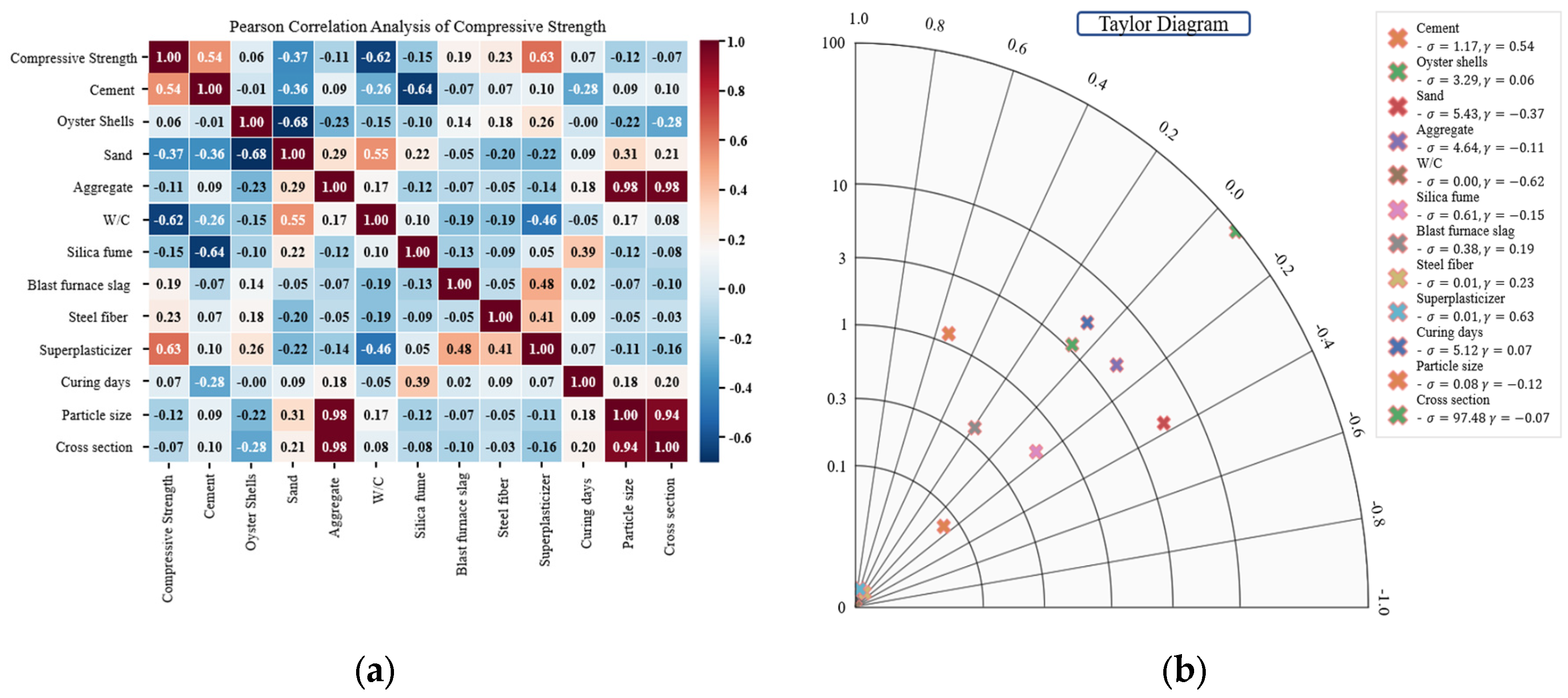
- Pearson correlation analysis revealed that superplasticizer (0.63) and cement (0.54) exhibited the strongest positive correlations with compressive strength. In contrast, W/C (−0.62), sand (−0.37), and silica fume (−0.15) showed negative correlations. The strongest negative correlation (−0.68) was found between oyster shells and sand, confirming the substitutive relationship between these two materials. These trends were consistent with the Taylor diagram.
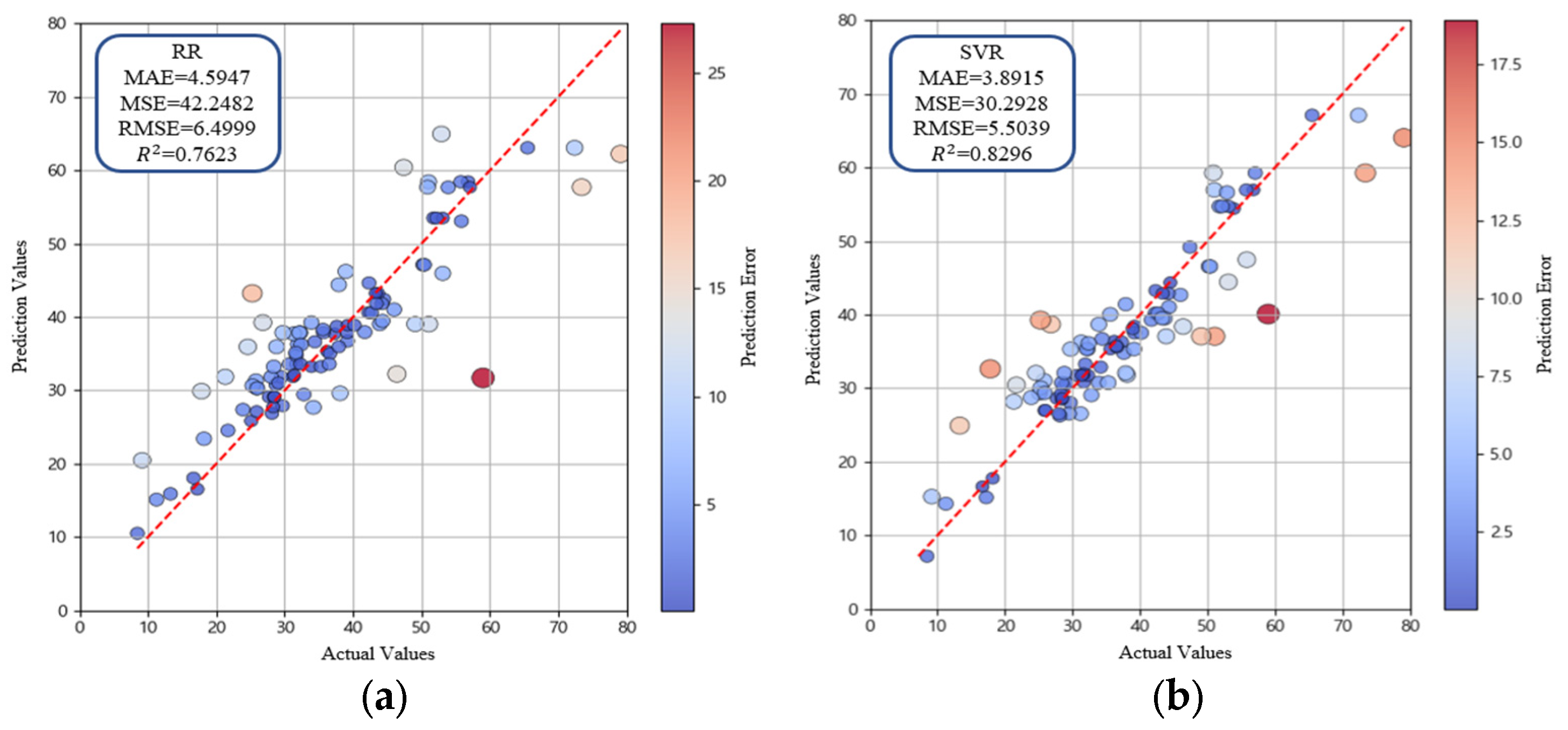
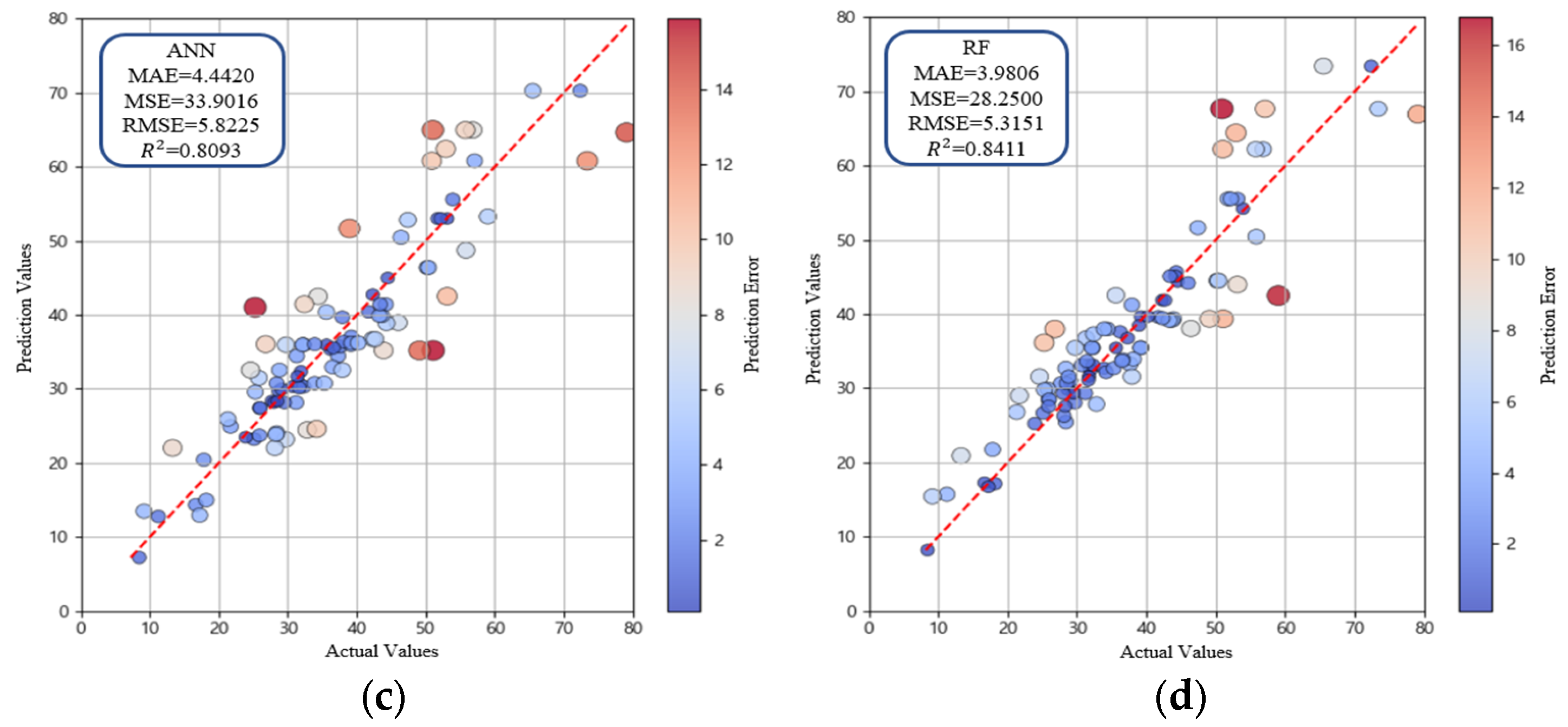
- In the comparison of predictive algorithms, RR showed the lowest performance with R2 = 0.7623. SVR (R2 = 0.8296) and ANN (R2 = 0.8093) partially captured nonlinear patterns, resulting in improved accuracy relative to RR. RF achieved the highest performance among the base models with R2 = 0.8411, showing the effectiveness of the model in reducing variance and mitigating overfitting. Accordingly, ensemble modeling was identified as the most suitable approach.
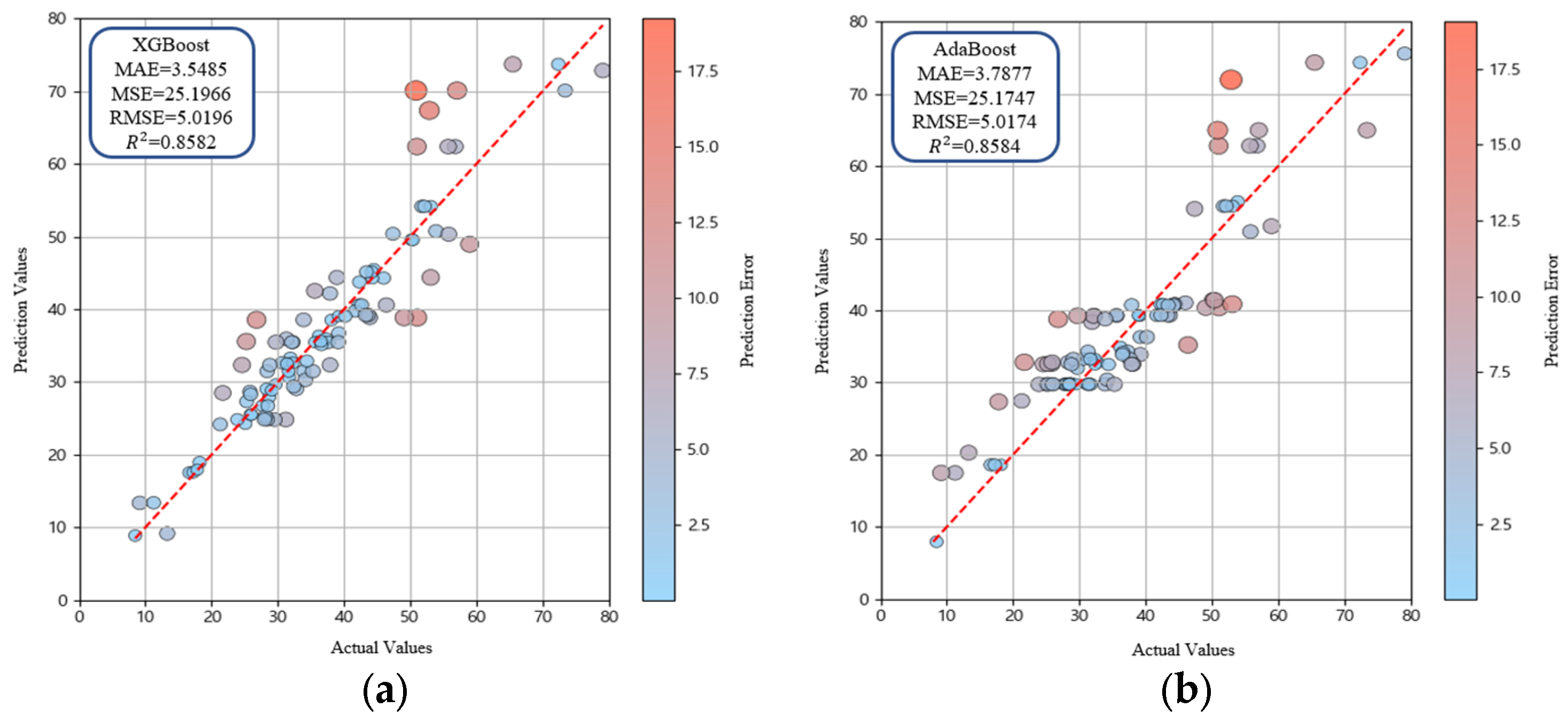
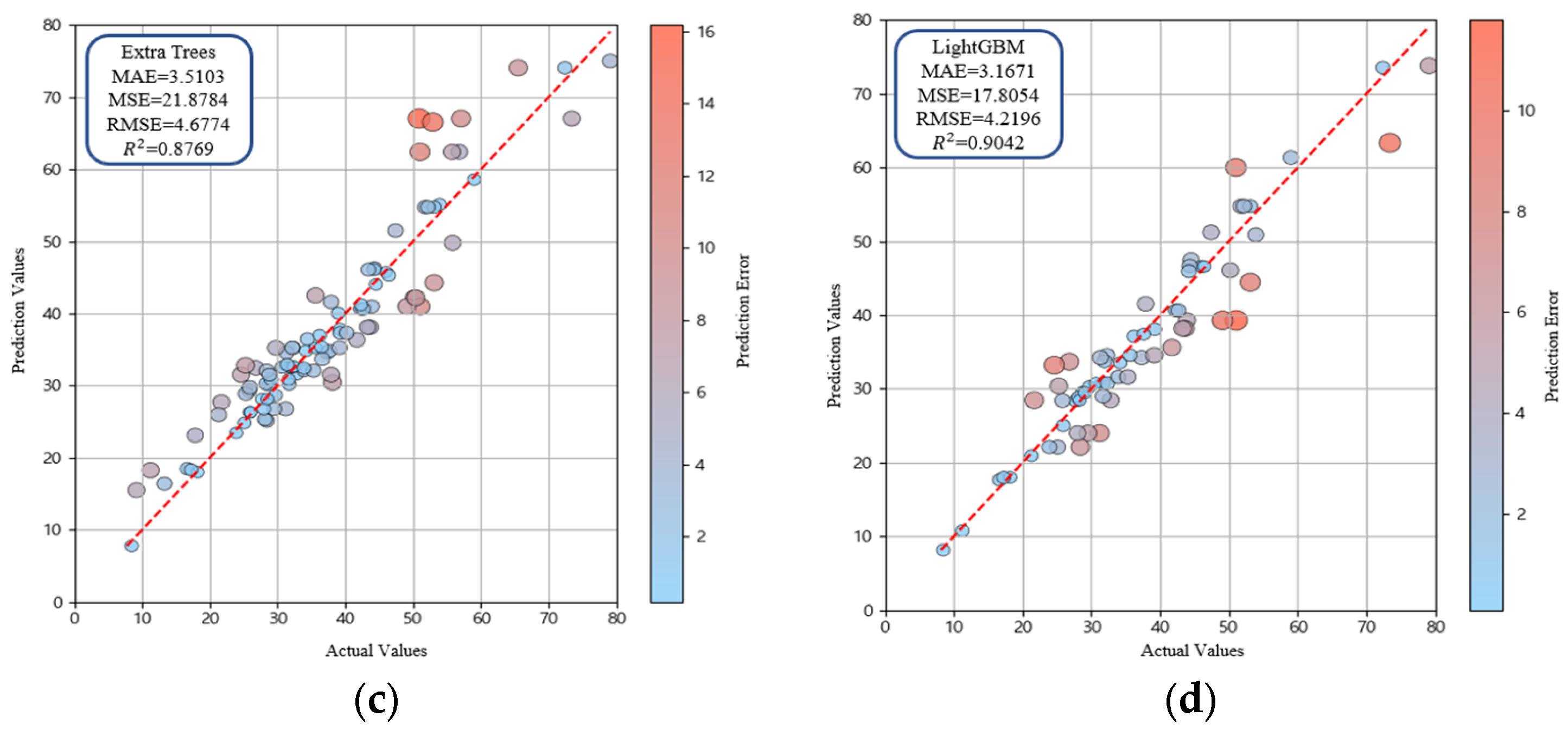
- Further ensemble analysis excluded RF and focused on XGBoost, AdaBoost, Extra Trees, and LightGBM. Hyperparameter tuning was performed using GridSearchCV. LightGBM achieved the highest predictive accuracy with MAE = 3.1671, MSE = 17.8056, RMSE = 4.2196, and R2 = 0.9042, confirming the superiority of the LightGBM model among the four models. Extra Trees produced stable performance by reducing variance through randomized splitting criteria, while XGBoost and AdaBoost improved accuracy using boosting techniques but showed lower performance compared with LightGBM. Overall, LightGBM was identified as the optimal detailed model, effectively capturing nonlinear patterns in the data.
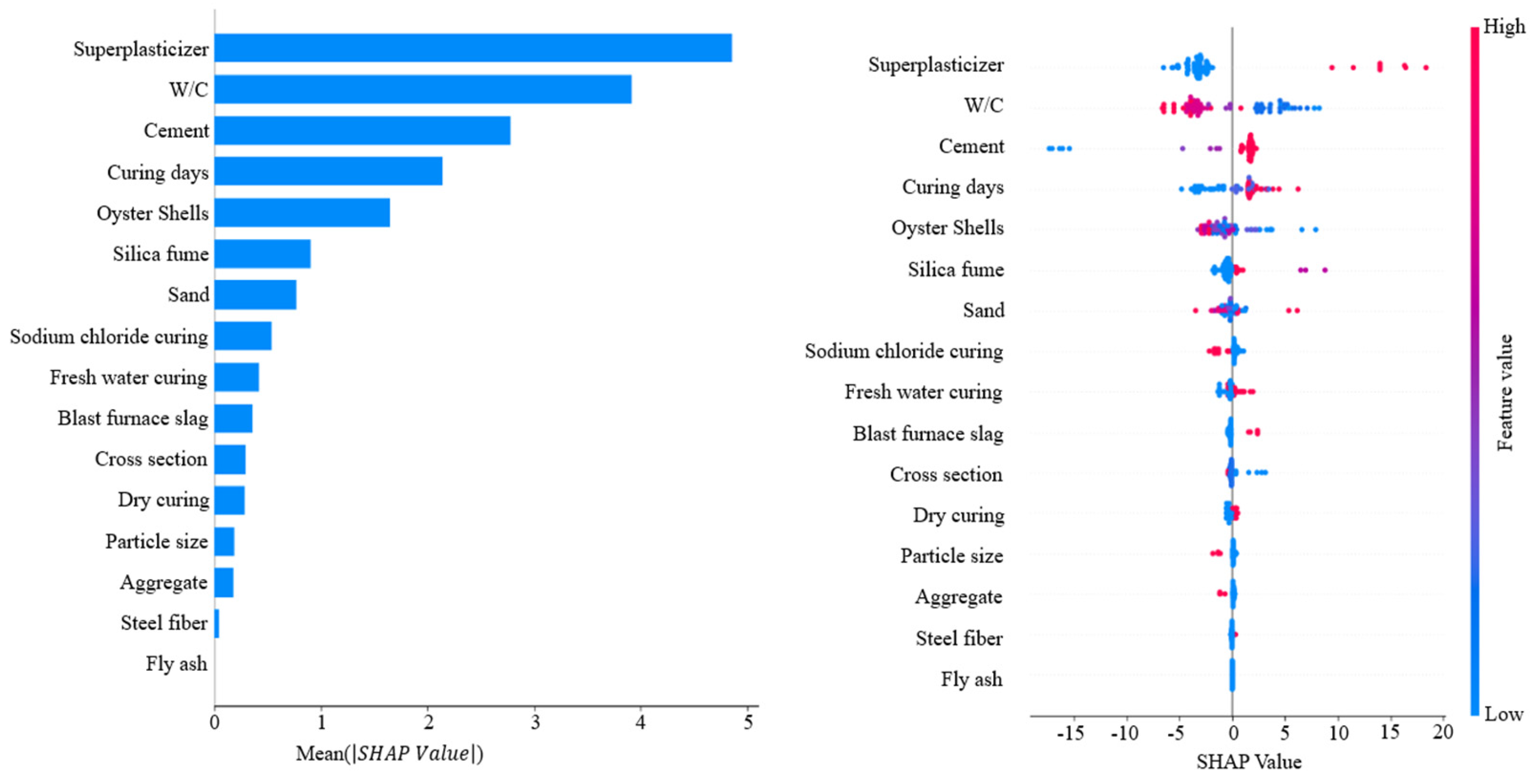
- SHAP analysis confirmed that superplasticizer and W/C were the most influential variables while cement and curing days also contributed significantly. Oyster shells showed moderate influence and could function as a substitute material because negative correlation with sand was observed. Distribution plots indicated that superplasticizer and cement generally had positive SHAP values whereas W/C showed negative SHAP values. Curing days exhibited positive SHAP values, which confirms strength improvement with extended curing. These results indicate that oyster shell cementitious composites can maintain compressive strength and serve as sustainable construction materials when waste oyster shells are incorporated with appropriate admixtures.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| W/C | water-to-cement ratio |
| SF | Silica fume |
| BFS | Blast furnace slag |
| RR | Ridge recession |
| SVR | Support vector regression |
| ANN | Artificial neural network |
| RF | Random forest |
| MAE | Mean Absolute Error |
| MSE | Mean Squared Error |
| RMSE | Root Mean Squared Error |
| XGBoost | eXtreme Gradient Boosting |
| AdaBoost | Adaptive Boosting |
| LightGBM | Light Gradient Boosting Machine |
References
- Yoon, H.; Park, S.; Lee, K.; Park, J. Oyster shell as substitute for aggregate in mortar. Waste Manag. Res. 2004, 22, 158–170. [Google Scholar] [CrossRef]
- Kim, J.H.; Yoo, S.H. Public perspective on the environmental impacts of sea sand mining: Evidence from a choice experiment in South Korea. Resour. Policy 2020, 69, 101811. [Google Scholar] [CrossRef]
- Jung, U.I.; Kim, B.J. Characteristics of mortar containing oyster shell as fine aggregate. Materials 2022, 15, 7301. [Google Scholar] [CrossRef]
- Korea Ministry of Oceans and Fisheries. Reducement of Environmental Pollution Caused by Marine Waste. Press Release. 3 February 2021. Available online: https://www.mof.go.kr (accessed on 15 August 2025).
- Government of The Republic of Korea. Marine Waste and Marine Polluted Sediment Management Act (Act No. 18065); Government of The Republic of Korea: Seoul, Republic of Korea, 2021. [Google Scholar]
- Kim, M.O.; Lee, M.K. Strength and microstructural changes in cementitious composites containing waste oyster shell powder. Buildings 2023, 13, 3078. [Google Scholar] [CrossRef]
- Ruslan, H.N.; Muthusamy, K.; Syed Mohsin, S.M.S.; Jose, R.; Omar, R. Oyster shell waste as a concrete ingredient: A review. Mater. Today Proc. 2022, 48, 713–719. [Google Scholar] [CrossRef]
- Kwon, S.J.; Wang, X.Y. A hydration-based integrated model to evaluate properties development and sustainability of oyster shell powder–cement binary composites. Buildings 2024, 14, 1578. [Google Scholar] [CrossRef]
- Bellei, P.; Torres, I.; Solstad, R.; Flores-Colen, I. Potential use of oyster shell waste in the composition of construction composites: A review. Buildings 2023, 13, 1546. [Google Scholar] [CrossRef]
- Oh, S.E.; Chung, S.Y.; Kim, K.; Han, S.H. Comparative analysis of the effects of waste shell aggregates on the material properties of cement mortars. Constr. Build. Mater. 2024, 412, 134887. [Google Scholar] [CrossRef]
- Seo, J.H.; Park, S.M.; Yang, B.J.; Jang, J.G. Calcined oyster shell powder as an expansive additive in cement mortar. Materials 2019, 12, 1322. [Google Scholar] [CrossRef]
- Kuo, W.T.; Wang, H.Y.; Shu, C.Y.; Su, D.S. Engineering properties of controlled low-strength materials containing waste oyster shells. Constr. Build. Mater. 2013, 46, 128–133. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, X.; Wang, L.; Yin, Z.; Da, B.; Chen, D. Effect of waste oyster shell powder content on properties of cement-metakaolin mortar. Case Stud. Constr. Mater. 2022, 16, e01088. [Google Scholar] [CrossRef]
- Chen, D.; Pan, T.; Yu, X.; Liao, Y.; Zhao, H. Properties of hardened mortars containing crushed waste oyster shells. Environ. Eng. Sci. 2019, 36, 1079–1088. [Google Scholar] [CrossRef]
- Kim, J.; Cha, I.; Jo, B.; Lee, H. Evaluation of compressive strength of eco-friendly cementitious composites incorporating waste oyster shells under sodium chloride solution exposure. Case Stud. Constr. Mater. 2025, 23, e04944. [Google Scholar] [CrossRef]
- Hong, Y.M.; Choudhury, S.R. The substitution effect of the fine aggregate in concrete with oyster shell. Materials 2024, 17, 6148. [Google Scholar] [CrossRef]
- Luo, K.; Zhang, M.; Jiang, Q.; Wang, S.; Zhuo, X. Evaluation of using oyster shell as a complete replacement for aggregate to make eco-friendly concrete. J. Build. Eng. 2024, 84, 108587. [Google Scholar] [CrossRef]
- Lin, Y.; Ren, Y.; Ge, T.; Al-Ajamee, M.; Xu, Y.; Mohamed, A.A.M.S.; Ma, L.; Zhang, H. Effects of waste oyster shell replacing fine aggregate on the dynamic mechanical characteristics of concrete. Sci. Rep. 2024, 14, 19800. [Google Scholar] [CrossRef]
- Cha, I.; Kim, J.; Lee, H. Enhancing compressive strength in cementitious composites through effective use of wasted oyster shells and admixtures. Buildings 2023, 13, 2787. [Google Scholar] [CrossRef]
- Yang, E.I.; Kim, M.Y.; Park, H.G.; Yi, S.T. Effect of partial replacement of sand with dry oyster shell on the long-term performance of concrete. Constr. Build. Mater. 2010, 24, 758–765. [Google Scholar] [CrossRef]
- Yoon, G.L.; Kim, B.T.; Kim, B.O.; Han, S.H. Chemical–mechanical characteristics of crushed oyster-shell. Waste Manag. 2003, 23, 825–834. [Google Scholar] [CrossRef]
- Altuncı, Y.T. A comprehensive study on the estimation of concrete compressive strength using machine learning models. Buildings 2024, 14, 3851. [Google Scholar] [CrossRef]
- Baghabra Al-Amoudi, O.S.B.; Al-Kutti, W.A.; Ahmad, S.; Maslehuddin, M. Correlation between compressive strength and certain durability indices of plain and blended cement concretes. Cem. Concr. Compos. 2009, 31, 672–676. [Google Scholar] [CrossRef]
- Marchewka, A.; Ziolkowski, P.; García Galán, S. Real-time prediction of early concrete compressive strength using AI and hydration monitoring. Sci. Rep. 2025, 15, 15463. [Google Scholar] [CrossRef] [PubMed]
- Sah, A.K.; Hong, Y.M. Performance comparison of machine learning models for concrete compressive strength prediction. Materials 2024, 17, 2075. [Google Scholar] [CrossRef] [PubMed]
- Shaaban, M.; Amin, M.; Selim, S.; Riad, I.M. Machine learning approaches for forecasting compressive strength of high-strength concrete. Sci. Rep. 2025, 15, 25567. [Google Scholar] [CrossRef] [PubMed]
- Mustapha, I.B.; Abdulkareem, M.; Jassam, T.M.; AlAteah, A.H.; Al-Sodani, K.A.A.; Al-Tholaia, M.M.H.; Nabus, H.; Alih, S.C.; Abdulkareem, Z.; Ganiyu, A. Comparative analysis of gradient-boosting ensembles for estimation of compressive strength of quaternary blend concrete. Int. J. Concr. Struct. Mater. 2024, 18, 20. [Google Scholar] [CrossRef]
- Qing, S.; Li, C. Data-driven prediction on critical mechanical properties of engineered cementitious composites based on machine learning. Sci. Rep. 2024, 14, 15322. [Google Scholar] [CrossRef]
- Uddin, M.N.; Shanmugasundaram, N.; Praveenkumar, S.; Li, L.Z. Prediction of compressive strength and tensile strain of engineered cementitious composite using machine learning. Int. J. Mech. Mater. Des. 2024, 20, 671–716. [Google Scholar] [CrossRef]
- Al-Shamasneh, A.R.; Mahmoodzadeh, A.; Karim, F.K.; Saidani, T.; Alghamdi, A.; Alnahas, J.; Sulaiman, M. Application of machine learning techniques to predict the compressive strength of steel fiber reinforced concrete. Sci. Rep. 2025, 15, 30674. [Google Scholar] [CrossRef]
- Sobuz, M.H.R.; Aditto, F.S.; Datta, S.D.; Kabbo, M.K.I.; Jabin, J.A.; Hasan, N.M.S.; Khan, M.M.H.; Rahman, S.M.A.; Raazi, M.; Zaman, A.A.U. High-strength self-compacting concrete production incorporating supplementary cementitious materials: Experimental evaluations and machine learning modelling. Int. J. Concr. Struct. Mater. 2024, 18, 67. [Google Scholar] [CrossRef]
- Singh, R.; Tipu, R.K.; Mir, A.A.; Patel, M. Predictive modelling of flexural strength in recycled aggregate-based concrete: A comprehensive approach with machine learning and global sensitivity analysis. Iran. J. Sci. Technol. Trans. Civ. Eng. 2024, 49, 1089–1114. [Google Scholar] [CrossRef]
- Haruna, S.I.; Zhu, H.; Ibrahim, Y.E.; Yang, J.; Farouk, A.I.B.; Shao, J.; Adamu, M.; Ahmed, O.S. Sustainable polyurethane-based polymer concrete: Mechanical and non-destructive properties with machine learning technique. Int. J. Concr. Struct. Mater. 2025, 19, 62. [Google Scholar] [CrossRef]
- Han, S.; Heo, T.; Yeum, C.M.; Kim, K.; Choi, J.; Tia, M. Machine learning approach to rapidly evaluate curling of concrete pavement. Int. J. Concr. Struct. Mater. 2024, 18, 71. [Google Scholar] [CrossRef]
- Lai, B.L.; Bao, R.L.; Zheng, X.F.; Vasdravellis, G.; Mensinger, M. Machine-learning assisted analysis on the seismic performance of steel reinforced concrete composite columns. Structures 2024, 68, 107065. [Google Scholar] [CrossRef]
- Megahed, K.; Mahmoud, N.S.; Abd-Rabou, S.E.M. Application of machine learning models in the capacity prediction of RCFST columns. Sci. Rep. 2023, 13, 20878. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Cao, J.; Pan, K.; Zeng, J.J. Prediction of shear capacity of RC columns and discussion on shear contribution via the explainable machine learning. Structures 2024, 69, 107562. [Google Scholar] [CrossRef]
- Cui, R.; Yang, H.; Li, J.; Xiao, Y.; Yao, G.; Yu, Y. Machine learning-based prediction of compressive strength in circular FRP-confined concrete columns. Front. Mater. 2024, 11, 1408670. [Google Scholar] [CrossRef]
- Yeh, I.C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- DeRousseau, M.A.; Laftchiev, E.; Kasprzyk, J.R.; Rajagopalan, B.; Srubar, W.V., III. A comparison of machine learning methods for predicting the compressive strength of field-placed concrete. Constr. Build. Mater. 2019, 228, 116661. [Google Scholar] [CrossRef]
- Jia, J.F.; Chen, X.Z.; Bai, Y.L.; Li, Y.L.; Wang, Z.H. An interpretable ensemble learning method to predict the compressive strength of concrete. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 46, pp. 201–213. [Google Scholar] [CrossRef]
- Nguyen-Sy, T.; Wakim, J.; To, Q.D.; Vu, M.N.; Nguyen, T.D.; Nguyen, T.T. Predicting the compressive strength of concrete from its compositions and age using the extreme gradient boosting method. Constr. Build. Mater. 2020, 260, 119757. [Google Scholar] [CrossRef]
- Yu, Y.; Li, W.; Li, J.; Nguyen, T.N. A novel optimised self-learning method for compressive strength prediction of high performance concrete. Constr. Build. Mater. 2018, 184, 229–247. [Google Scholar] [CrossRef]
- Feng, D.C.; Liu, Z.T.; Wang, X.D.; Chen, Y.; Chang, J.Q.; Wei, D.F.; Jiang, Z.M. Machine learning-based compressive strength prediction for concrete: An adaptive boosting approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Inqiad, W.B.; Siddique, M.S.; Alarifi, S.S.; Butt, M.J.; Najeh, T.; Gamil, Y. Comparative analysis of various machine learning algorithms to predict 28-day compressive strength of Self-compacting concrete. Heliyon 2023, 9, e22036. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Kang, J.; Liu, W.; Su, J.; Li, M. Research on prediction of compressive strength of fly ash and slag mixed concrete based on machine learning. PLoS ONE 2022, 17, e0279293. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Zhong, Y.; Liao, G.; Ding, Q.; Zhang, T.; Li, X. Prediction of compressive strength of concrete specimens based on interpretable machine learning. Materials 2024, 17, 3661. [Google Scholar] [CrossRef] [PubMed]
- Abdelsattar, D.M.; Owais, M.; Fahmy, M.F.M.; Osman, R.; Nafadi, M.K. Optimizing pozzolanic concrete mixtures using machine learning and global sensitivity analysis techniques. Int. J. Concr. Struct. Mater. 2025, 19, 77. [Google Scholar] [CrossRef]
- Saeheaw, T. Interpretable machine learning framework for non-destructive concrete strength prediction with physics-consistent feature analysis. Buildings 2025, 15, 2601. [Google Scholar] [CrossRef]
- Gazi, M.U.; Hasan, M.T.; Debnath, P. Few-shot meta-learning for concrete strength prediction: A model-agnostic approach with SHAP analysis. AI Civ. Eng. 2025, 4, 20. [Google Scholar] [CrossRef]
- Vargas, J.F.; Oviedo, A.I.; Ortega, N.A.; Orozco, E.; Gómez, A.; Londoño, J.M. Machine-learning-based predictive models for compressive strength, flexural strength, and slump of concrete. Appl. Sci. 2024, 14, 4426. [Google Scholar] [CrossRef]
- ASTM A820/A820M-22; Standard Specification for Steel Fibers for Fiber-Reinforced. Concrete Communications; ASTM International: West Conshohocken, PA, USA, 2021.
- ASTM C989; Standard Specification for Slag Cement for Use in Concrete and Mortars. Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM C1240-20; Standard Specification for Silica Fume Used in Cementitious Mixtures. ASTM International: West Conshohocken, PA, USA, 2020.
- ASTM C494; Standard Specification for Chemical Admixtures for Concrete. ASTM International: West Conshohocken, PA, USA, 2019.
- ASTM C109; Standard Test Method for Compressive Strength of Hydraulic Cement Mortars (Using 2-In, or [50-mm] Cube Specimens). Annual Book of ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2016.
- Liao, Y.; Shi, H.; Zhang, S.; Da, B.; Chen, D. Particle size effect of oyster shell on mortar: Experimental investigation and modeling. Materials 2021, 14, 6813. [Google Scholar] [CrossRef]
- Chen, D.; Zhang, P.; Pan, T.; Liao, Y.; Zhao, H. Evaluation of the eco-friendly crushed waste oyster shell mortars containing supplementary cementitious materials. J. Clean. Prod. 2019, 237, 117811. [Google Scholar] [CrossRef]
- Pinto Dabés Guimarães, A.C.; Nouailletas, O.; Perlot, C.; Grégoire, D. Granular skeleton optimisation and the influence of the cement paste content in bio-based oyster shell mortar with 100% aggregate replacement. Sustainability 2024, 16, 2297. [Google Scholar] [CrossRef]
- Yehia, S.A.; Fayed, S.; Zakaria, M.H.; Shahin, R.I. Prediction of RC T-Beams Shear Strength based on machine learning. Int. J. Concr. Struct. Mater. 2024, 18, 52. [Google Scholar] [CrossRef]
- Tran, N.; Van Tran, M.; Tran, P.; Nguyen, A.K.; Nguyen, C.Q. Eco-friendly 3D-printed concrete using steel slag aggregate: Buildability, printability and mechanical properties. Int. J. Concr. Struct. Mater. 2024, 18, 66. [Google Scholar] [CrossRef]
- Zalhaf, N.M. Application of artificial neural network for prediction of concrete–high-performance concrete interfacial bond strength after exposure to elevated temperature. Int. J. Concr. Struct. Mater. 2025, 19, 31. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Adeli, H. Neural networks in civil engineering: 1989–2000. Comput. Aid. Civ. Infrastruct. Eng. 2001, 16, 126–142. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A comparative analysis of gradient boosting algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Cao, Y.; Miao, Q.G.; Liu, J.C.; Gao, L. Advance and prospects of AdaBoost algorithm. Acta Autom. Sin. 2013, 39, 745–758. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Zhang, J.; Mucs, D.; Norinder, U.; Svensson, F. LightGBM: An effective and scalable algorithm for prediction of chemical toxicity–application to the Tox21 and mutagenicity data sets. J. Chem. Inf. Model. 2019, 59, 4150–4158. [Google Scholar] [CrossRef] [PubMed]
- Yan, H.J.; Xie, N. Optimized machine learning algorithms for predicting the punching shear resistance of flat slabs with transverse reinforcement. Int. J. Concr. Struct. Mater. 2024, 18, 76. [Google Scholar] [CrossRef]
- Yoon, J.; Yonis, A.; Park, S.; Rajabipour, F.; Pyo, S. Prediction of the R 3 test-based reactivity of supplementary cementitious materials: A machine learning approach utilizing physical and chemical properties. Int. J. Concr. Struct. Mater. 2024, 18, 75. [Google Scholar] [CrossRef]
- Kim, J.; Lee, D. Comparative study on hyperparameter tuning for predicting concrete compressive strength. Buildings 2025, 15, 2173. [Google Scholar] [CrossRef]
- Ghafari, S.; Nejad, F.M.; Sheikh-Akbari, A.; Kazemi, H. Automating the determination of low-temperature fracture resistance curves of normal and rubberized asphalt concrete in single-edge notched beam tests using convolutional neural networks. Constr. Build. Mater. 2024, 428, 136376. [Google Scholar] [CrossRef]
- Park, W.Y.; Moon, J. Machine learning based reactivity prediction of fly ash type F produced from South Korea. Int. J. Concr. Struct. Mater. 2023, 17, 58. [Google Scholar] [CrossRef]
- Al Adnan, M.; Babur, M.; Farooq, F.; Shahid, M.; Ahmed, Z.; Das, P. Prediction of split tensile strength of fiber-reinforced recycled aggregate concrete utilizing machine learning models with SHAP analysis. Hybrid Adv. 2025, 11, 100507. [Google Scholar] [CrossRef]
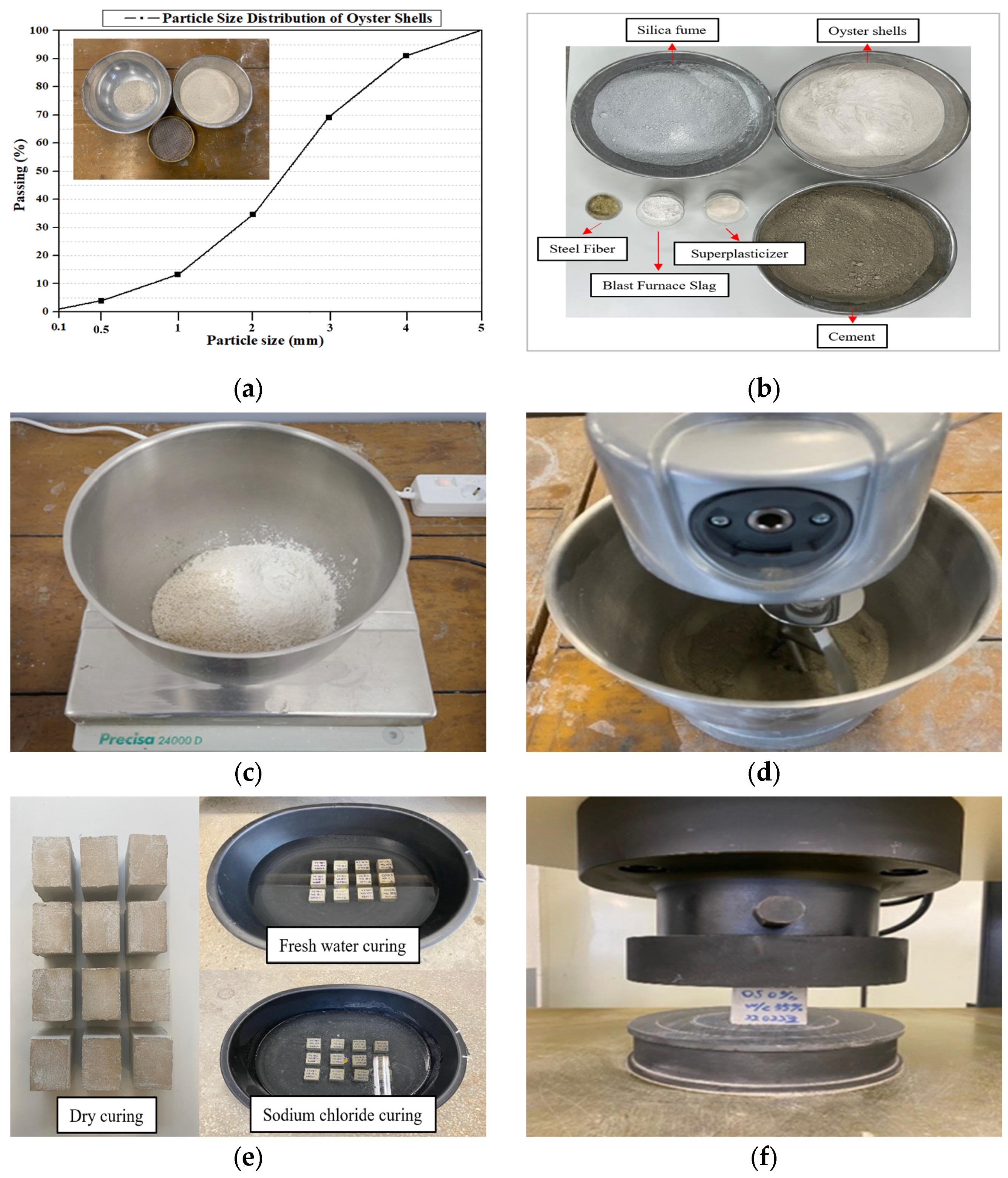


| Variables | Unit | Range of Data |
|---|---|---|
| Cement | % | 25–100 |
| Oyster Shell | 0–227 | |
| Sand | 0–300 | |
| Aggregate | 0–267 | |
| Silica fume | 0–25 | |
| Blast furnace slag | 0–40 | |
| Steel fiber | 0–1 | |
| Fly ash | 0–40 | |
| Superplasticizer | 0–0.5 | |
| W/C | - | 0.3–0.5 |
| Curing day | days | 3–365 |
| Particle size | 0.15–5 | |
| Cross-section | 1600–7854 | |
| Curing Type | - | Dry curing |
| Fresh water curing | ||
| Sodium chloride curing |
| Index | Data Count | Reference |
|---|---|---|
| 190–213 | 24 | [19] |
| 214–222 | 9 | [57] |
| 223–234 | 12 | [58] |
| 235–238 | 4 | [14] |
| 239–248 | 10 | [11] |
| 249–288 | 40 | [6] |
| 310–327 | 18 | [59] |
| 328–336 | 9 | [8] |
| Machine Learning Model | MAE | MSE | RMSE | |
|---|---|---|---|---|
| RR | 4.5947 | 42.2482 | 6.4999 | 0.7623 |
| SVR | 3.8915 | 30.2928 | 5.5039 | 0.8296 |
| ANN | 4.4420 | 33.9016 | 5.8225 | 0.8093 |
| RF | 3.9806 | 28.2500 | 5.3151 | 0.8411 |
| XGBoost | colsample_bytree | 0.7 |
| learning_rate | 0.1 | |
| max_depth | 3 | |
| n_estimators | 200 | |
| Subsample | 0.7 | |
| Adaboost | max_depth | 6 |
| learning_rate | 0.1 | |
| n_estimators | 200 | |
| Extra Trees | Bootstrap | False |
| max_depth | 10 | |
| max_features | 0.8 | |
| min_samples_leaf | 1 | |
| min_samples_split | 2 | |
| n_estimators | 500 | |
| LightGBM | colsample_bytree | 0.8 |
| learning_rate | 0.05 | |
| max_depth | −1 | |
| min_child_samples | 10 | |
| num_leaves | 31 | |
| reg_lambda | 1.0 | |
| Subsample | 0.8 |
| Machine Learning Model | MAE | MSE | RMSE | |
|---|---|---|---|---|
| XGBoost | 3.5485 | 25.1966 | 5.0196 | 0.8582 |
| Adaboost | 3.7877 | 25.1747 | 5.0174 | 0.8584 |
| Extra Trees | 3.5103 | 21.8784 | 4.6774 | 0.8769 |
| LightGBM | 3.1671 | 17.8054 | 4.2196 | 0.9042 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Jang, W.; Kang, S.; Kim, D.; Lee, H. Comparative Study of Machine Learning for Predicting Compressive Strength in Oyster Shell Cementitious Composites. Materials 2025, 18, 5314. https://doi.org/10.3390/ma18235314
Kim J, Jang W, Kang S, Kim D, Lee H. Comparative Study of Machine Learning for Predicting Compressive Strength in Oyster Shell Cementitious Composites. Materials. 2025; 18(23):5314. https://doi.org/10.3390/ma18235314
Chicago/Turabian StyleKim, Jinwoong, Woosik Jang, Sunho Kang, Dongwook Kim, and Heeyoung Lee. 2025. "Comparative Study of Machine Learning for Predicting Compressive Strength in Oyster Shell Cementitious Composites" Materials 18, no. 23: 5314. https://doi.org/10.3390/ma18235314
APA StyleKim, J., Jang, W., Kang, S., Kim, D., & Lee, H. (2025). Comparative Study of Machine Learning for Predicting Compressive Strength in Oyster Shell Cementitious Composites. Materials, 18(23), 5314. https://doi.org/10.3390/ma18235314









