Effects of Extrinsic Magnetized GaAs in One-Dimensional Ternary Photonic Crystals
Abstract
1. Introduction
2. Methodology and Formulation
3. Numerical Results and Discussion
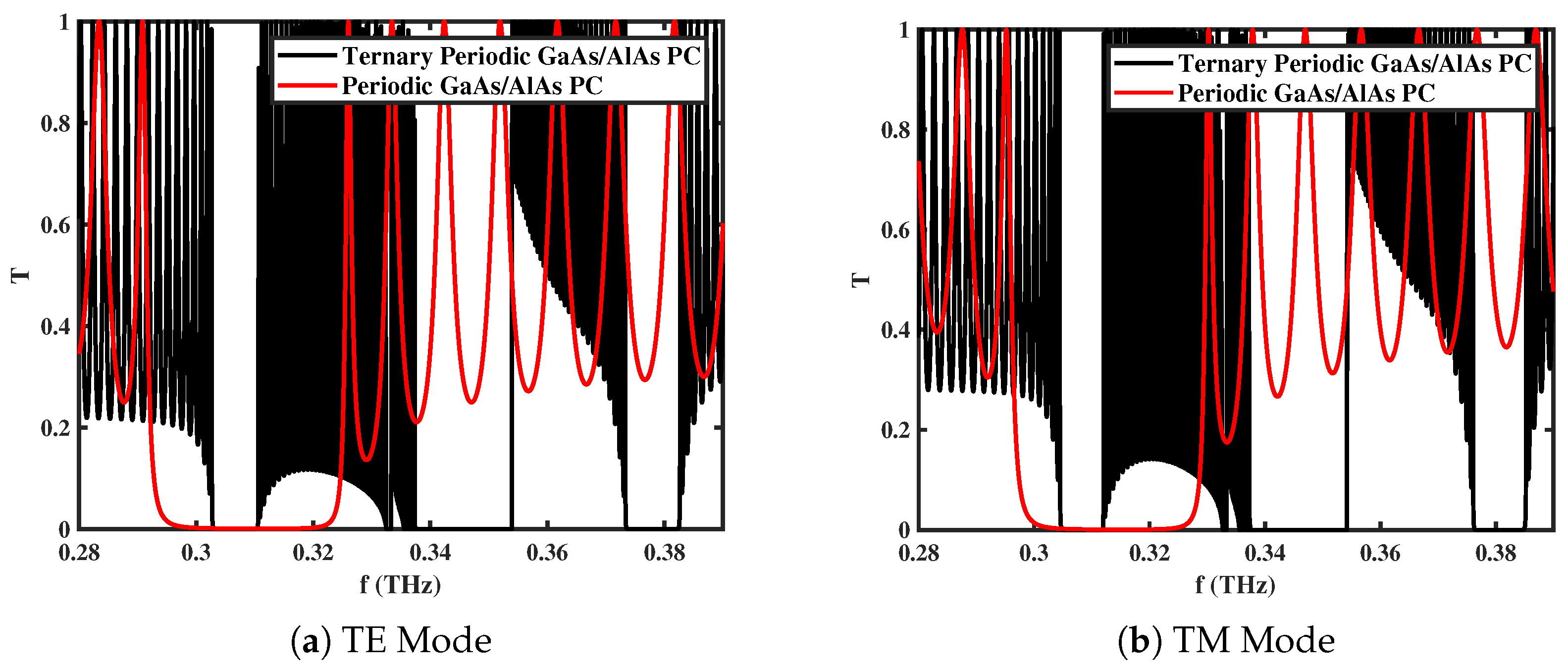
3.1. Transmission Spectra with and Without Ternary Layer
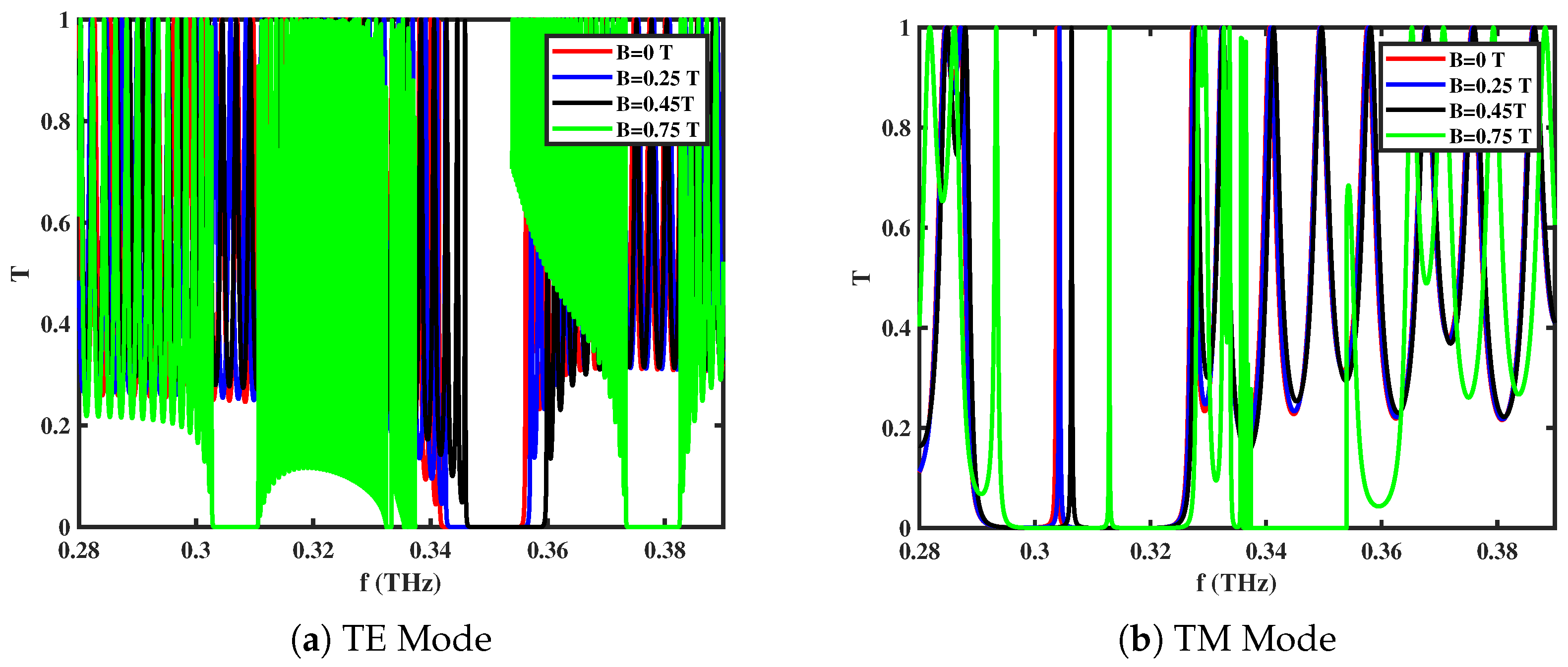
3.2. Effect of External Magnetic Field (B)
3.3. Effect of Electron Density ()
3.4. Effect of Incident Angle ()
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Meade, R.D.; Winn, J. Appendix D. In Photonic Crystals-Molding the Flow of Light; Princeton University Press: Princeton, NJ, USA, 1997. [Google Scholar]
- Soukoulis, C.M. Photonic band gap materials: The “semiconductors” of the future. Phys. Scr. 1996, 1996, 146. [Google Scholar] [CrossRef]
- Elsayed, H.A.; Aly, A.H. Terahertz frequency superconductor-nanocomposite photonic band gap. Int. J. Mod. Phys. B 2018, 32, 1850056. [Google Scholar] [CrossRef]
- Gong, Q.; Hu, X. Photonic Crystals: Principles and Applications; Jenny Stanford Publishing: Singapore, 2014. [Google Scholar]
- Vakhrushev, A. Theoretical Foundations and Application of Photonic Crystals; BoD–Books on Demand: Norderstedt, Germany, 2018. [Google Scholar]
- Shaban, S.M.; Mehaney, A.; Aly, A.H. Determination of 1-propanol, ethanol, and methanol concentrations in water based on a one-dimensional phoxonic crystal sensor. Appl. Opt. 2020, 59, 3878–3885. [Google Scholar] [CrossRef]
- Natesan, A.; Govindasamy, K.P.; Gopal, T.R.; Dhasarathan, V.; Aly, A.H. Tricore photonic crystal fibre based refractive index sensor for glucose detection. IET Optoelectron. 2018, 13, 118–123. [Google Scholar] [CrossRef]
- Amiri, I.S.; Paul, B.K.; Ahmed, K.; Aly, A.H.; Zakaria, R.; Yupapin, P.; Vigneswaran, D. Tri-core photonic crystal fiber based refractive index dual sensor for salinity and temperature detection. Microw. Opt. Technol. Lett. 2019, 61, 847–852. [Google Scholar] [CrossRef]
- Nouman, W.M.; Abd El-Ghany, S.E.S.; Sallam, S.M.; Dawood, A.F.B.; Aly, A.H. Biophotonic sensor for rapid detection of brain lesions using 1D photonic crystal. Opt. Quantum Electron. 2020, 52, 287. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Aly, A.H. Theoretical study of a tunable low-temperature photonic crystal sensor using dielectric-superconductor nanocomposite layers. J. Supercond. Nov. Magn. 2020, 33, 2983–2990. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Aly, A.H. Modeling of a biosensor using Tamm resonance excited by graphene. Appl. Opt. 2021, 60, 1411–1419. [Google Scholar] [CrossRef]
- Rahimi, F.; Vahdani, M.R.K. Effects of external magnetic fields on the confined states and optical properties of conical quantum dot nanowire. J. Magn. Magn. Mater. 2024, 591, 171660. [Google Scholar] [CrossRef]
- Awad, M.; Aly, A.H. Experimental and theoretical studies of hybrid multifunctional TiO2/TiN/TiO2. Ceram. Int. 2019, 45, 19036–19043. [Google Scholar] [CrossRef]
- Bazian, M. Photonic crystal add–drop filter: A review on principles and applications. Photonic Netw. Commun. 2021, 41, 57–77. [Google Scholar] [CrossRef]
- Guo, S.; Hu, C.; Zhang, H. Unidirectional ultrabroadband and wide-angle absorption in graphene-embedded photonic crystals with the cascading structure comprising the Octonacci sequence. J. Opt. Soc. Am. B 2020, 37, 2678–2687. [Google Scholar] [CrossRef]
- Biswal, A.; Kumar, R.; Nayak, C.; Samiappan, D. n-GaAs based extrinsic Dodecanacci photonic quasicrystal. Phys. B Condens. Matter 2020, 595, 412340. [Google Scholar] [CrossRef]
- Biswal, A.; Kumar, R.; Nayak, C.; Samiappan, D. Photonic transmission spectra in an extrinsic semiconductor based Gaussian random multilayer. Opt. Mater. 2020, 102, 109799. [Google Scholar] [CrossRef]
- Arregui, G.; Lanzillotti-Kimura, N.D.; Sotomayor-Torres, C.M.; García, P.D. Anderson photon-phonon colocalization in certain random superlattices. Phys. Rev. Lett. 2019, 122, 043903. [Google Scholar] [CrossRef]
- Torres-Torres, C.; García-Beltrán, G. Optical Nonlinearities in Nanostructured Systems; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Ilegems, M.; Pearson, G. Infrared Reflection Spectra of Ga1−xAlx As Mixed Crystals. Phys. Rev. B 1970, 1, 1576. [Google Scholar] [CrossRef]
- Abadla, M.M.; Tabaza, N.A.; Tabaza, W.; Ramanujam, N.; Wilson, K.J.; Vigneswaran, D.; Taya, S.A. Properties of ternary photonic crystal consisting of dielectric/plasma/dielectric as a lattice period. Optik 2019, 185, 784–793. [Google Scholar] [CrossRef]
- Vincenti, M.; De Ceglia, D.; Grande, M.; D’Orazio, A.; Scalora, M. Nonlinear control of absorption in one-dimensional photonic crystal with graphene-based defect. Opt. Lett. 2013, 38, 3550–3553. [Google Scholar] [CrossRef]
- Kumar, N.; Suthar, B.; Rostami, A. Novel optical behaviors of metamaterial and polymer-based ternary photonic crystal with lossless and lossy features. Opt. Commun. 2023, 529, 129073. [Google Scholar] [CrossRef]
- Minden, H. Some Optical Properties of Aluminum Arsenide. Appl. Phys. Lett. 1970, 17, 358–360. [Google Scholar] [CrossRef]
- Biswal, A.; Kumar, R.; Nayak, C.; Dhanalakshmi, S. Photonic bandgap characteristics of GaAs/AlAs-based one-dimensional quasi-periodic photonic crystal. Optik 2021, 234, 166597. [Google Scholar] [CrossRef]
- Chen, X.; Xiong, S. Optical properties of GaAs/AlAs superlattices with randomly distributed layer thicknesses. Phys. Rev. B 1993, 47, 7146. [Google Scholar] [CrossRef]
- Adachi, S. GaAs and Related Materials: Bulk Semiconducting and Superlattice Properties; World Scientific: Singapore, 1994. [Google Scholar]
- El-Khozondar, H.J.; Mahalakshmi, P.; El-Khozondar, R.J.; Ramanujam, N.; Amiri, I.; Yupapin, P. Design of one dimensional refractive index sensor using ternary photonic crystal waveguide for plasma blood samples applications. Phys. E Low-Dimens. Syst. Nanostruct. 2019, 111, 29–36. [Google Scholar] [CrossRef]
- Aly, A.H.; Sayed, F.A. THz cutoff frequency and multifunction Ti2Ba2Ca2Cu3O10/GaAs photonic bandgap materials. Int. J. Mod. Phys. B 2020, 34, 2050091. [Google Scholar] [CrossRef]
- Barati, M.; Aghajamali, A. Near-infrared tunable narrow filter properties in a 1D photonic crystal containing semiconductor metamaterial photonic quantum-well defect. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 79, 20–25. [Google Scholar] [CrossRef]
- Mekis, A.; Fan, S.; Joannopoulos, J. Bound states in photonic crystal waveguides and waveguide bends. Phys. Rev. B 1998, 58, 4809. [Google Scholar] [CrossRef]
- Bertolotti, J.; Gottardo, S.; Wiersma, D.S.; Ghulinyan, M.; Pavesi, L. Optical necklace states in Anderson localized 1D systems. Phys. Rev. Lett. 2005, 94, 113903. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.-F.; Liu, S.-B.; Kong, X.-K.; Zou, L.; Li, C.-Z.; Qing, W.-s. Enhancement of omnidirectional photonic band gaps in one-dimensional dielectric plasma photonic crystals with a matching layer. Phys. Plasmas 2012, 19, 022103. [Google Scholar] [CrossRef]
- Biswal, A.; Kumar, R.; Nayak, C.; Dhanalakshmi, S.; Behera, H.; Lyubchanskii, I. Analysis of transmission spectra in one-dimensional ternary photonic crystals with complex unit cell. Optik 2022, 261, 169169. [Google Scholar] [CrossRef]
- Kumar, N.; Kaliramna, S.; Singh, M. Design of cold plasma based ternary photonic crystal for microwave applications. Silicon 2022, 14, 6933–6944. [Google Scholar] [CrossRef]
- Dadoenkova, N.N.; Dadoenkova, Y.S.; Panyaev, I.S.; Sannikov, D.G.; Lyubchanskii, I.L. One-dimensional dielectric bi-periodic photonic structures based on ternary photonic crystals. J. Appl. Phys. 2018, 123, 043101. [Google Scholar] [CrossRef]
- Zaky, Z.A.; Sharma, A.; Alamri, S.; Saleh, N.; Aly, A.H. Detection of fat concentration in milk using ternary photonic crystal. Silicon 2022, 14, 6063–6073. [Google Scholar] [CrossRef]
- Taya, S.A.; Sharma, A.; Doghmosh, N.; Colak, I. Detection of water concentration in ethanol solution using a ternary photonic crystal-based sensor. Mater. Chem. Phys. 2022, 279, 125772. [Google Scholar] [CrossRef]
- Molaei-Yeznabad, A.; Bahador, H. Refractive Index-Based Optimized Ternary Photonic Crystal Biosensor for Ultra Precise Detection of Cancer Cells. Sens. Imaging 2025, 26, 36. [Google Scholar] [CrossRef]
- Hughes, S.; Ramunno, L.; Young, J.F.; Sipe, J. Extrinsic Optical Scattering Loss in Photonic Crystal Waveguides: Role of Fabrication Disorder and Photon Group Velocity. Phys. Rev. Lett. 2005, 94, 033903. [Google Scholar] [CrossRef] [PubMed]
- King, T.C.; Wang, C.C.; Kuo, W.K.; Wu, C.J. Analysis of effective plasma frequency in a magnetized extrinsic photonic crystal. IEEE Photon. J. 2013, 5, 2700706. [Google Scholar] [CrossRef]
- King, T.C.; Yang, C.C.; Hsieh, P.H.; Chang, T.W.; Wu, C.J. Analysis of tunable photonic band structure in an extrinsic plasma photonic crystal. Phys. E Low-Dimens. Syst. Nanostruct. 2015, 67, 7–11. [Google Scholar] [CrossRef]
- Daher, M.G.; Taya, S.A.; Colak, I.; Vigneswaran, D.; Olaimat, M.M.; Patel, S.K.; Ramahi, O.M.; Almawgani, A.H. Design of a nano-sensor for cancer cell detection based on a ternary photonic crystal with high sensitivity and low detection limit. Chin. J. Phys. 2022, 77, 1168–1181. [Google Scholar] [CrossRef]
- Taya, S. Ternary photonic crystal with left-handed material layer for refractometric application. Opto-Electron. Rev. 2018, 26, 236–241. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; Wiley Online Library: Hoboken, NJ, USA, 1988; Volume 95. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Chu, C.; Ohkawa, T. Transverse Electromagnetic Waves with ‖. Phys. Rev. Lett. 1982, 48, 837. [Google Scholar] [CrossRef]
- Aghajamali, A.; Zare, A.; Wu, C.J. Analysis of defect mode in a one-dimensional symmetric double-negative photonic crystal containing magnetized cold plasma defect. Appl. Opt. 2015, 54, 8602–8606. [Google Scholar] [CrossRef] [PubMed]




| Parameters | Values |
|---|---|
| External magnetic field (B) | T |
| Electron concentration () | cm−3 |
| Static permittivity () | |
| Angle of incident () | |
| Electron mass () | kg |
| Effective mass of electron () | 0.066 m |
| Vacuum permittivity () | C2N−1m−2 |
| Spacial periodicity (N) | 30 |
| GaAs () | 60 m |
| AlAs () | 100 m |
| Magnetized GaAs ( ) | 110 m |
| Plasma frequency ( | 0.707 THz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Biswal, A.; Behera, H.; Hsu, T.-W. Effects of Extrinsic Magnetized GaAs in One-Dimensional Ternary Photonic Crystals. Materials 2025, 18, 5293. https://doi.org/10.3390/ma18235293
Biswal A, Behera H, Hsu T-W. Effects of Extrinsic Magnetized GaAs in One-Dimensional Ternary Photonic Crystals. Materials. 2025; 18(23):5293. https://doi.org/10.3390/ma18235293
Chicago/Turabian StyleBiswal, Amita, Harekrushna Behera, and Tai-Wen Hsu. 2025. "Effects of Extrinsic Magnetized GaAs in One-Dimensional Ternary Photonic Crystals" Materials 18, no. 23: 5293. https://doi.org/10.3390/ma18235293
APA StyleBiswal, A., Behera, H., & Hsu, T.-W. (2025). Effects of Extrinsic Magnetized GaAs in One-Dimensional Ternary Photonic Crystals. Materials, 18(23), 5293. https://doi.org/10.3390/ma18235293








