Calculation Simulation of Equivalent Thermomechanical Properties of Dispersion Nuclear Fuel
Abstract
1. Introduction
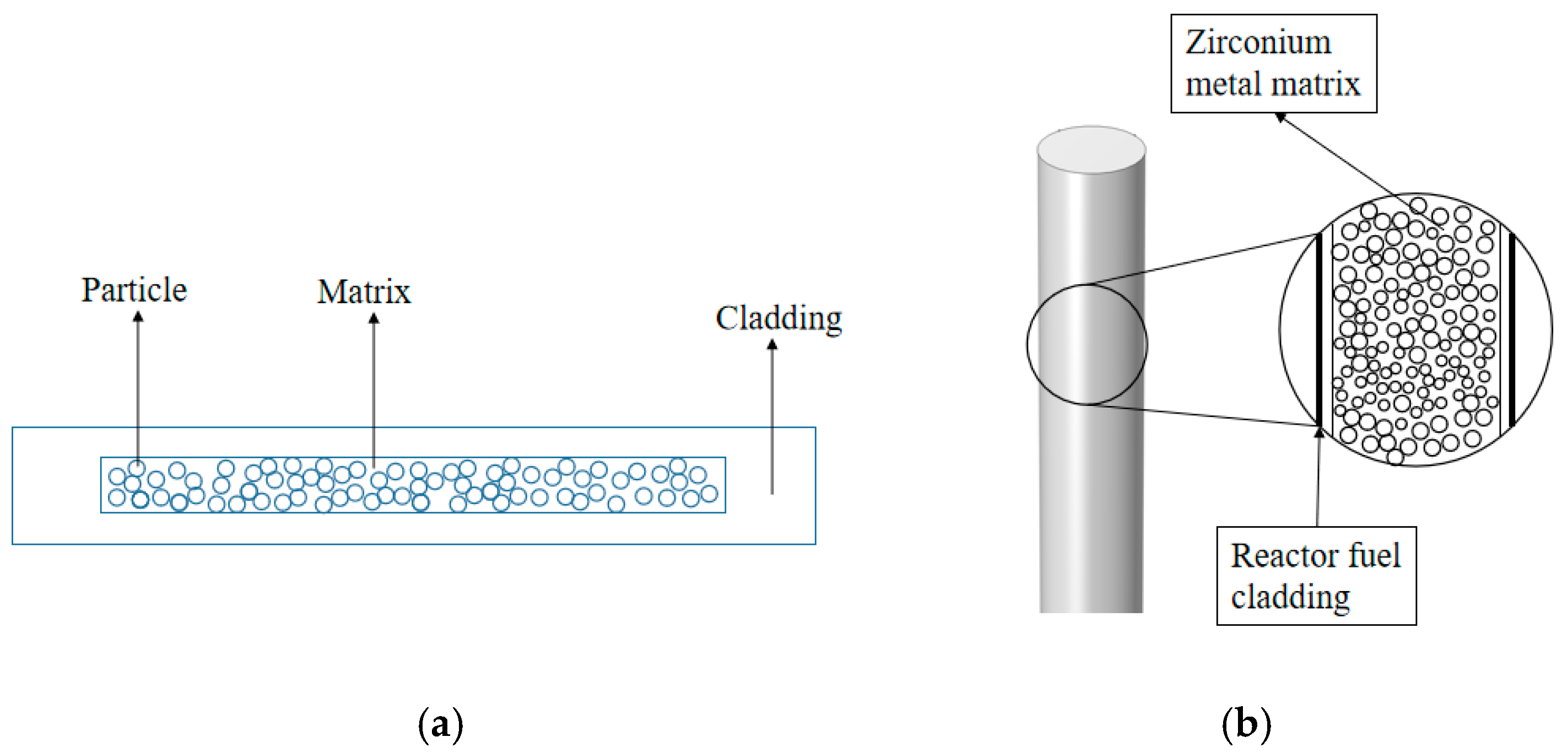
2. Physical Model and Material Properties
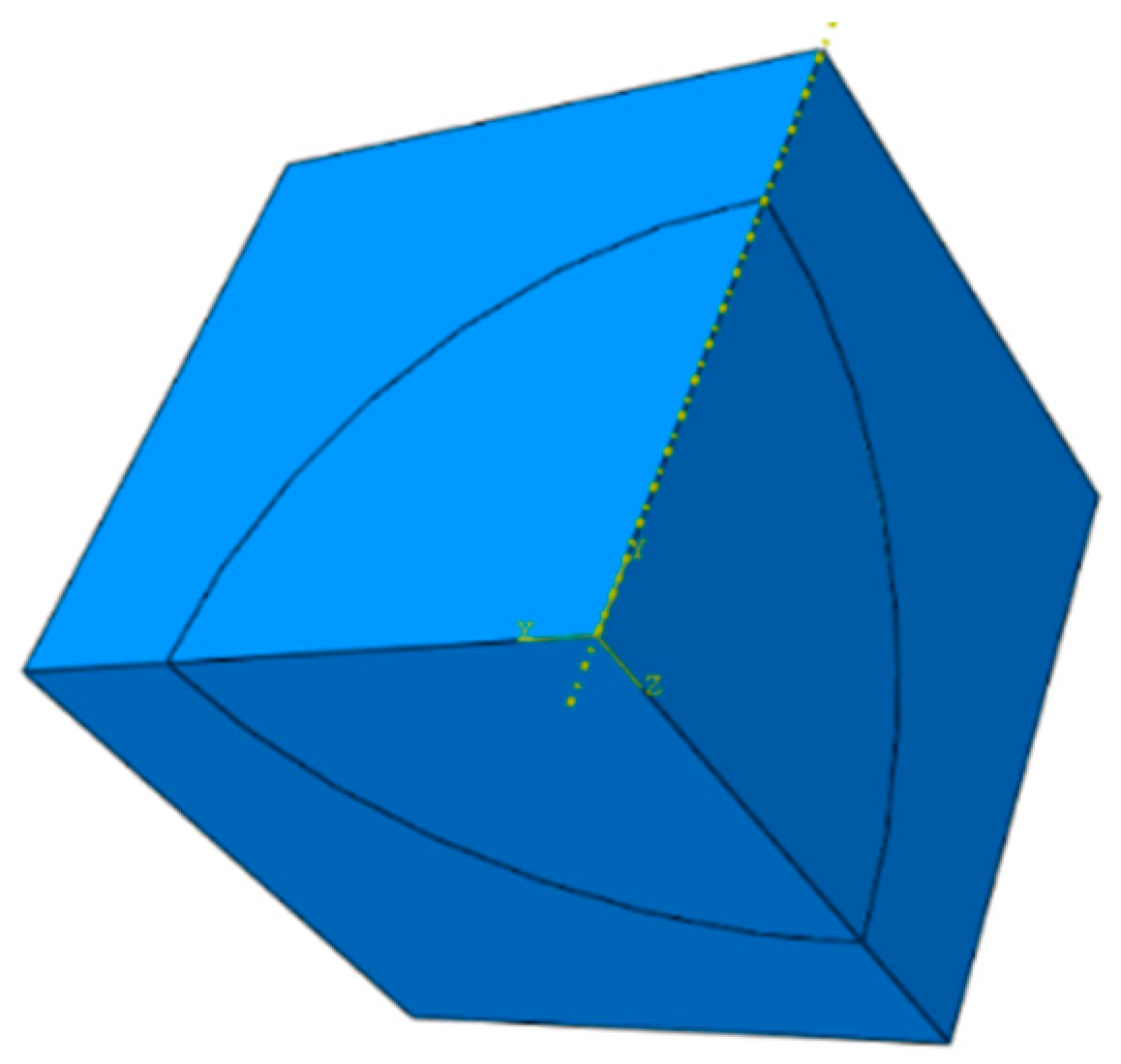
2.1. Finite Element Modeling Methods
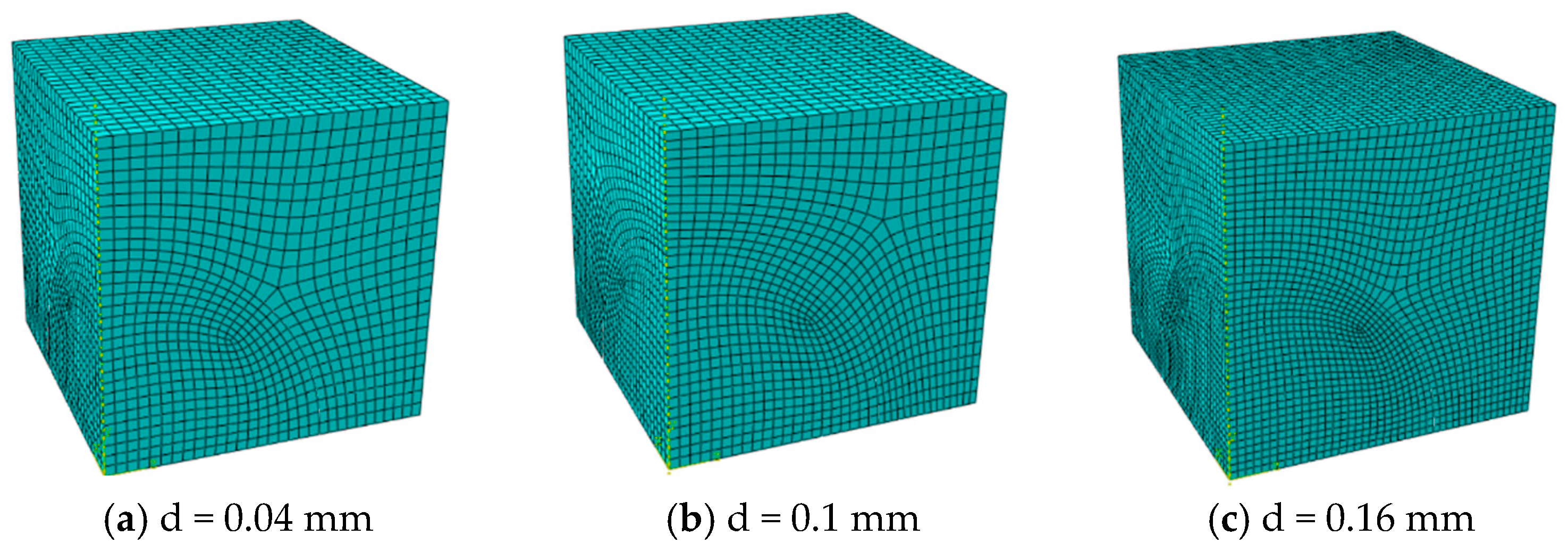
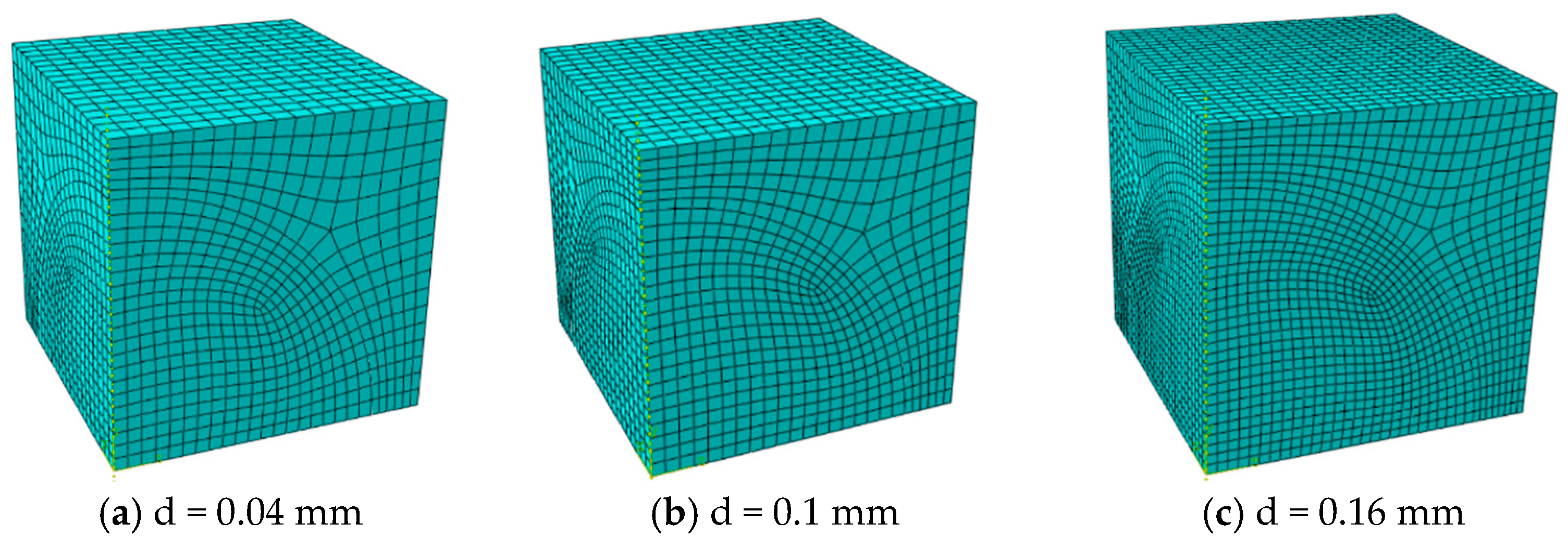
2.2. Finite Element Mesh
2.3. Numerical Simulation Methods
2.4. Material Properties
2.5. The Boundary Conditions
2.5.1. Boundary Conditions of Equivalent Elastic Properties
2.5.2. Boundary Conditions of Equivalent Coefficient of Thermal Expansion
2.6. Data Post-Processing
3. Model Verification
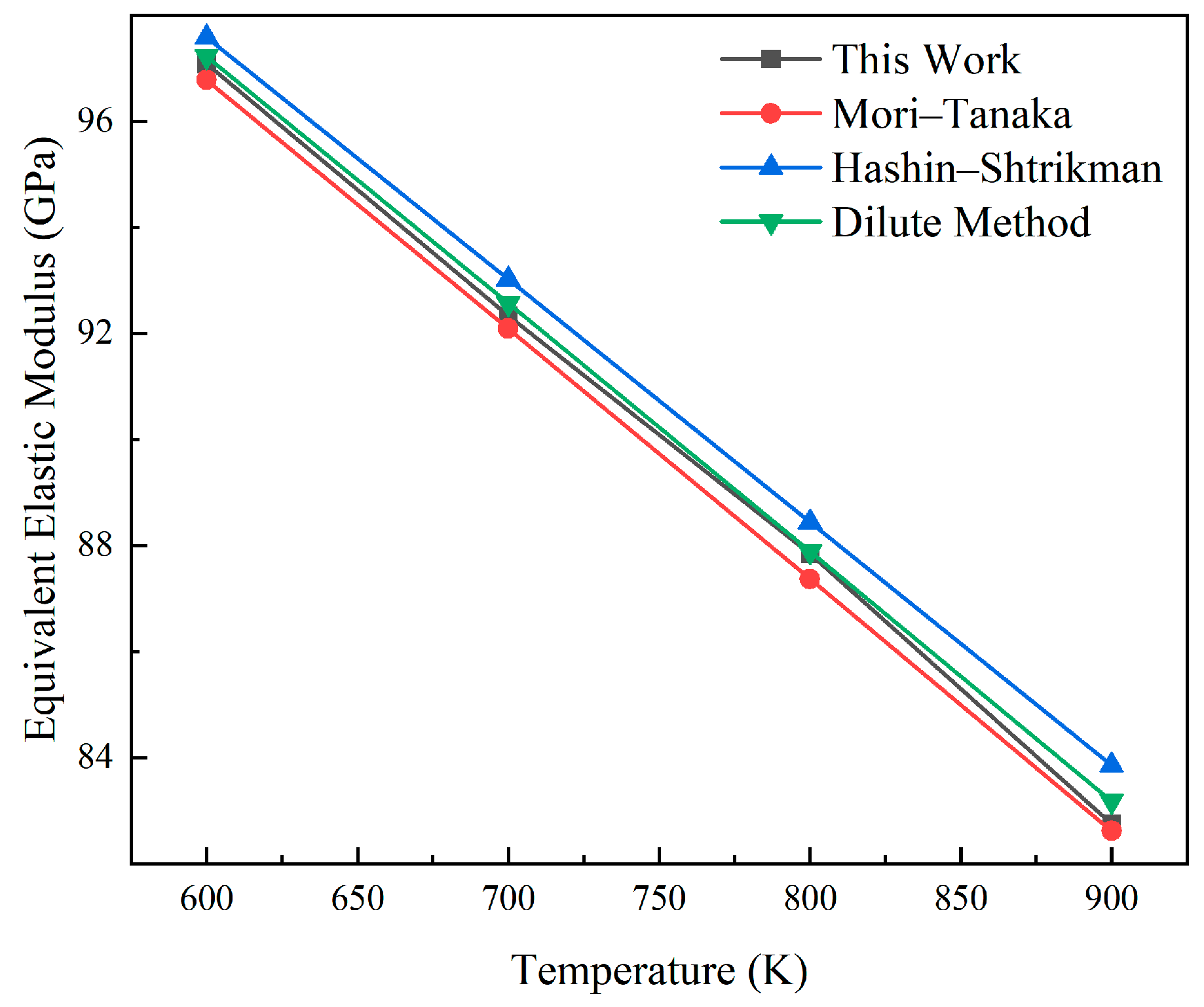
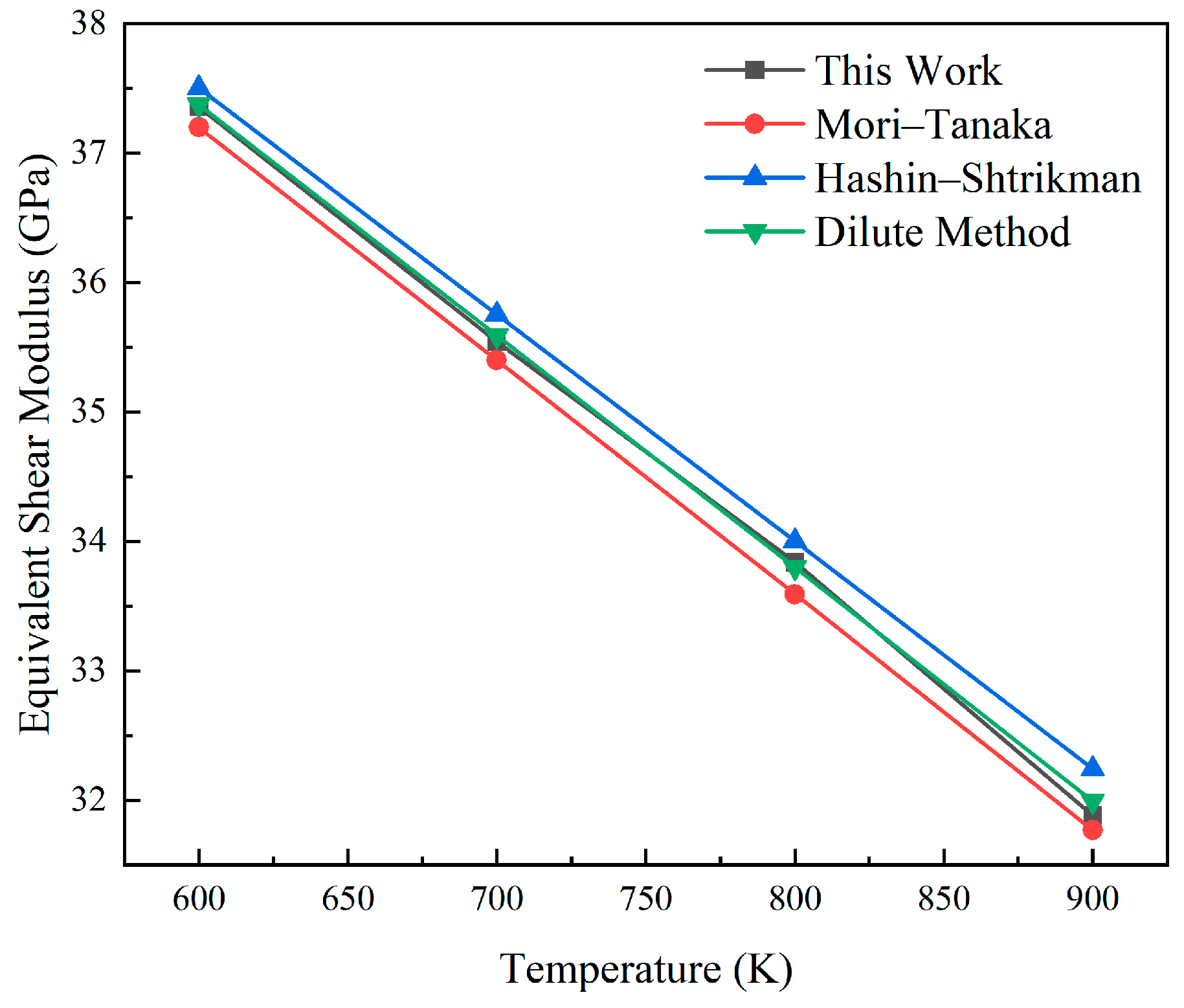
3.1. Verification of Elastic Constitutive Model
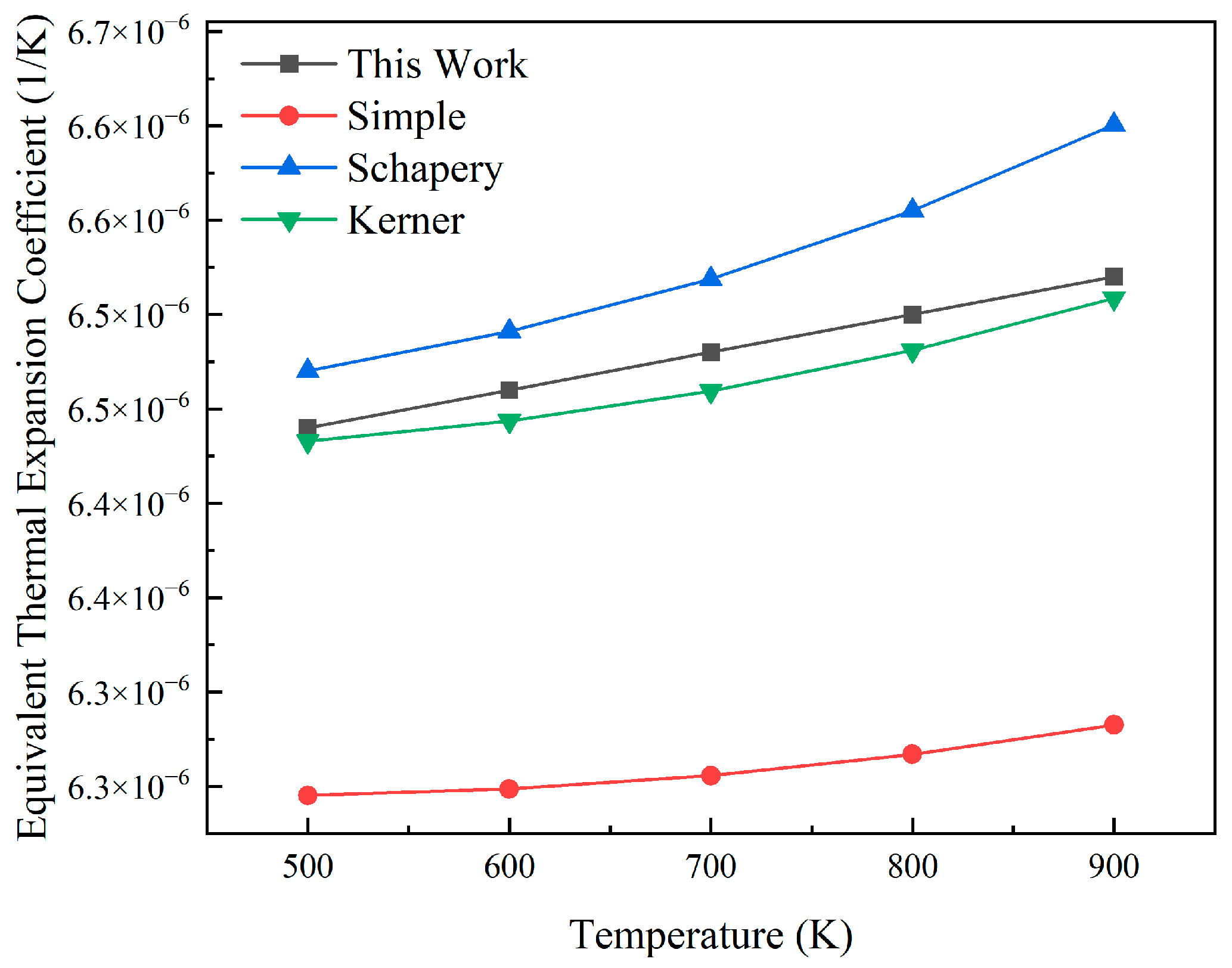
3.2. Verification of Thermal Expansion Model
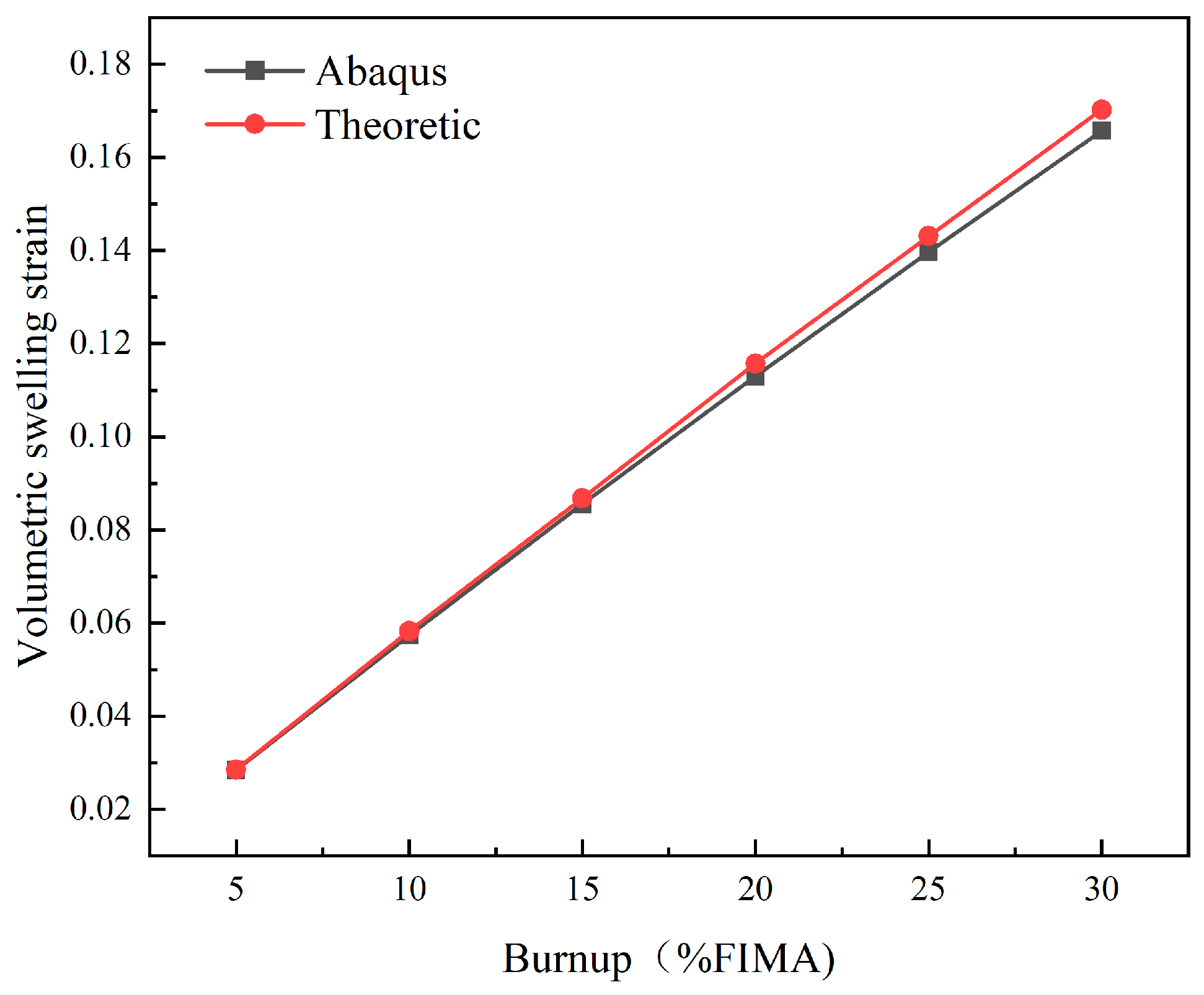
3.3. Verification of Irradiation Swelling of the Pellet
4. Analysis of Numerical Results
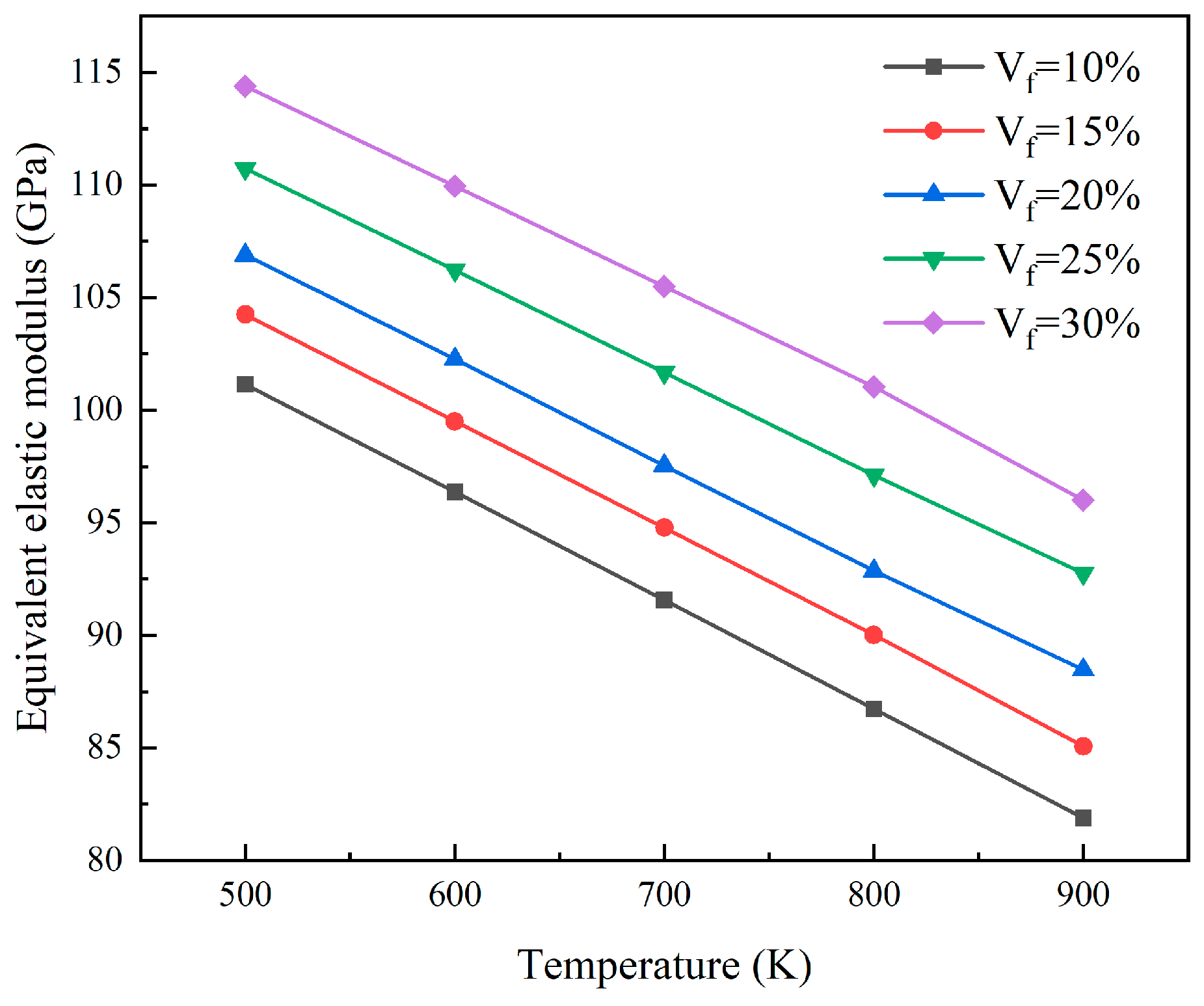
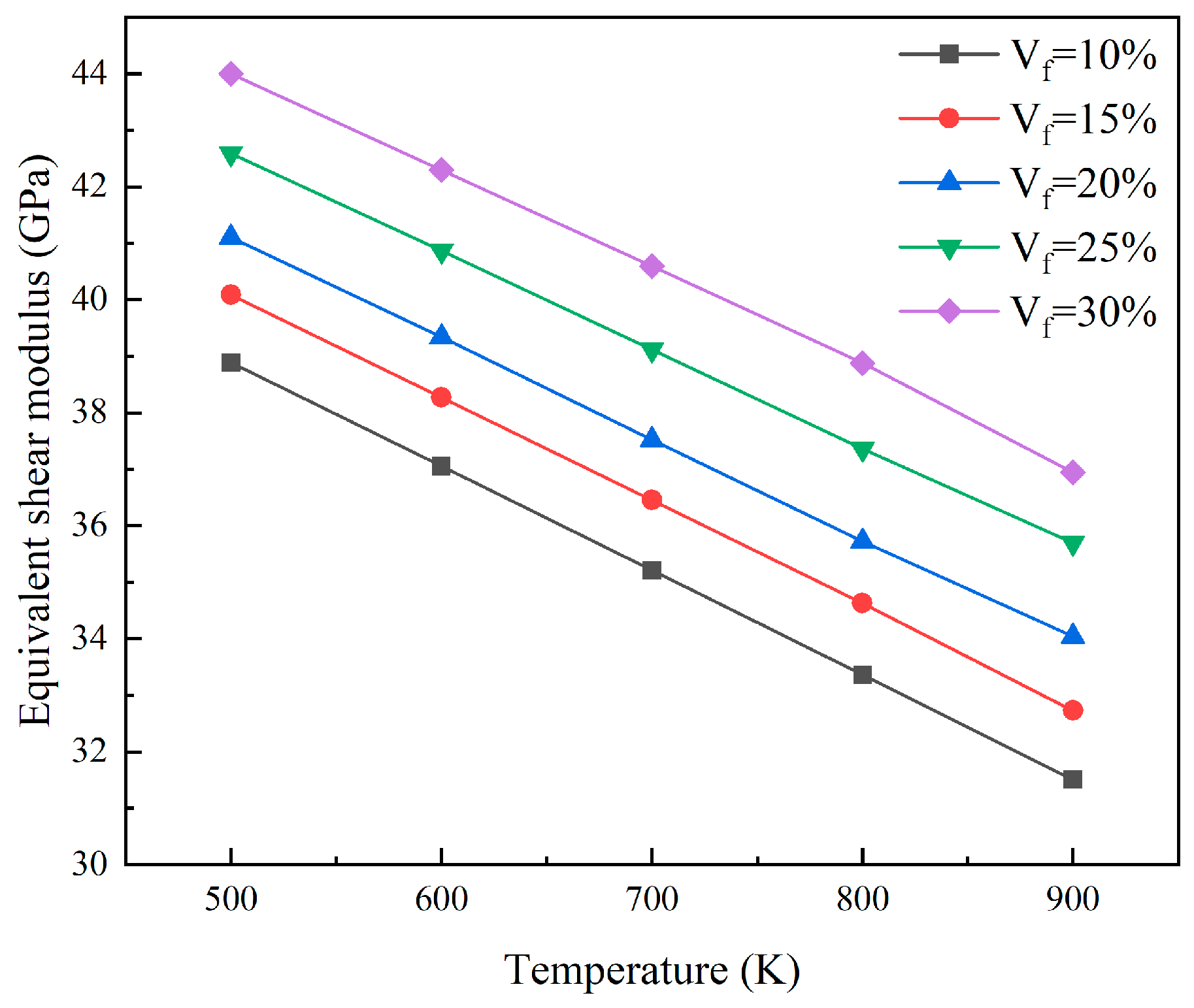
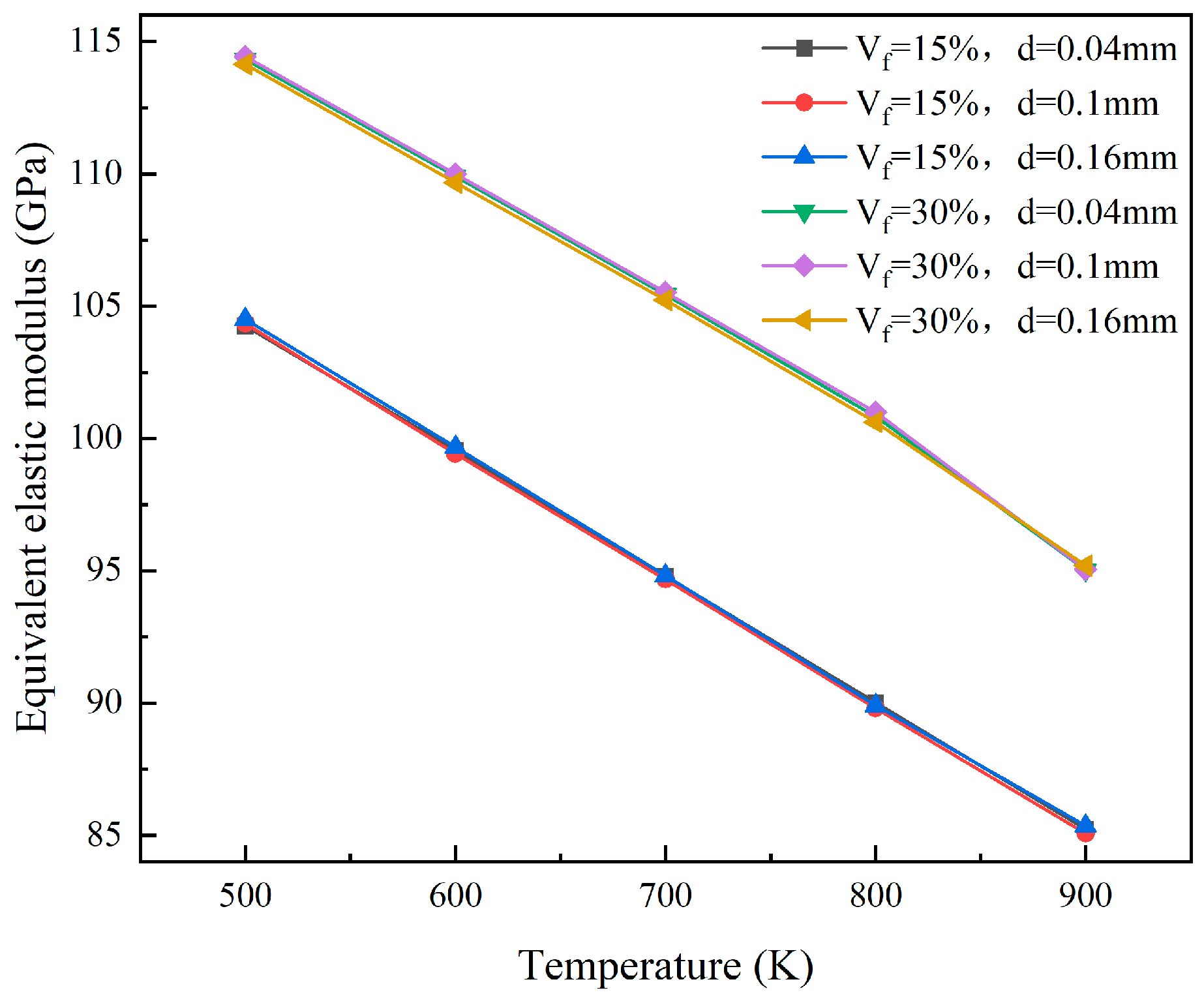
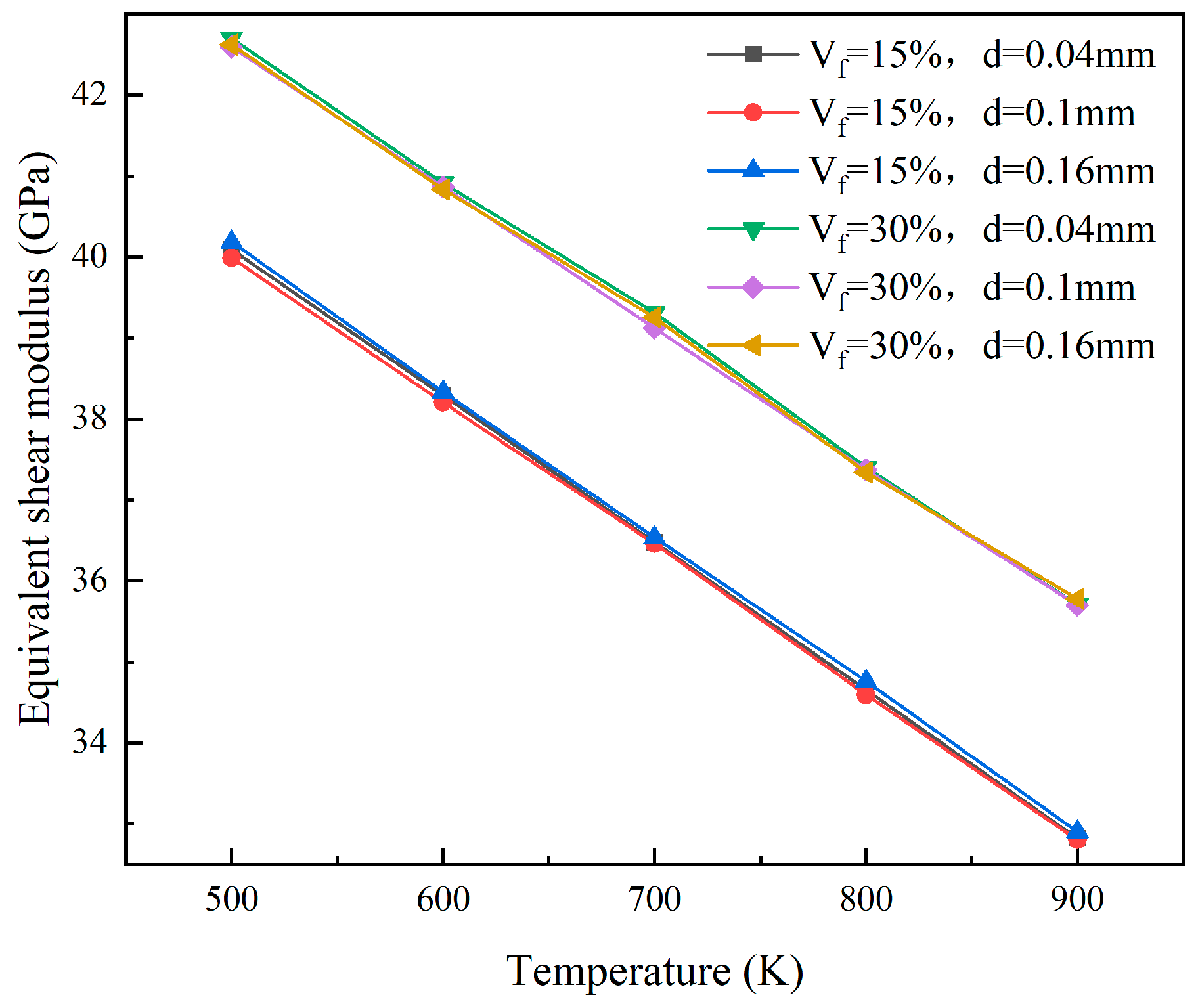
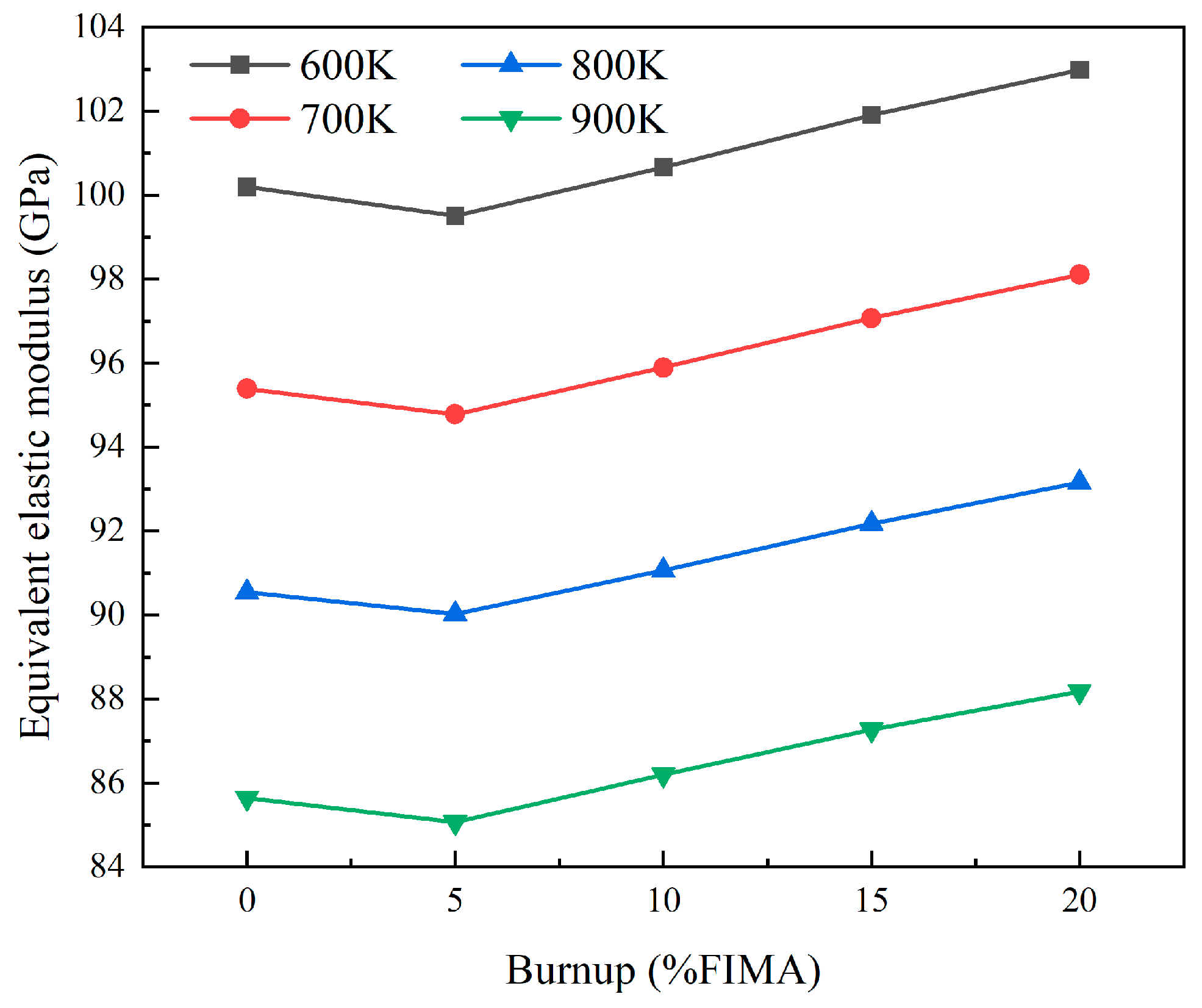
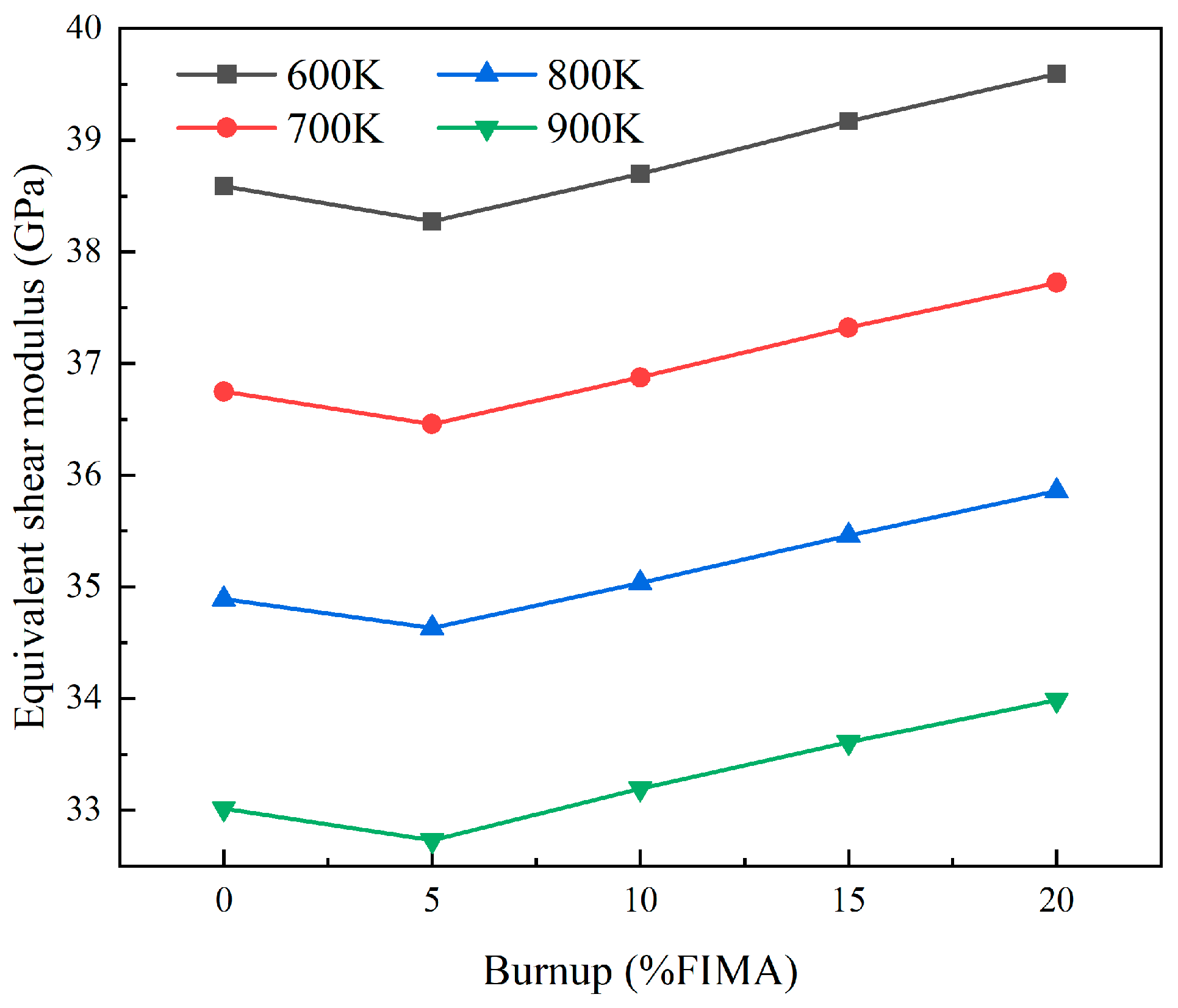
4.1. Equivalent Elastic Model for Dispersion Fuels
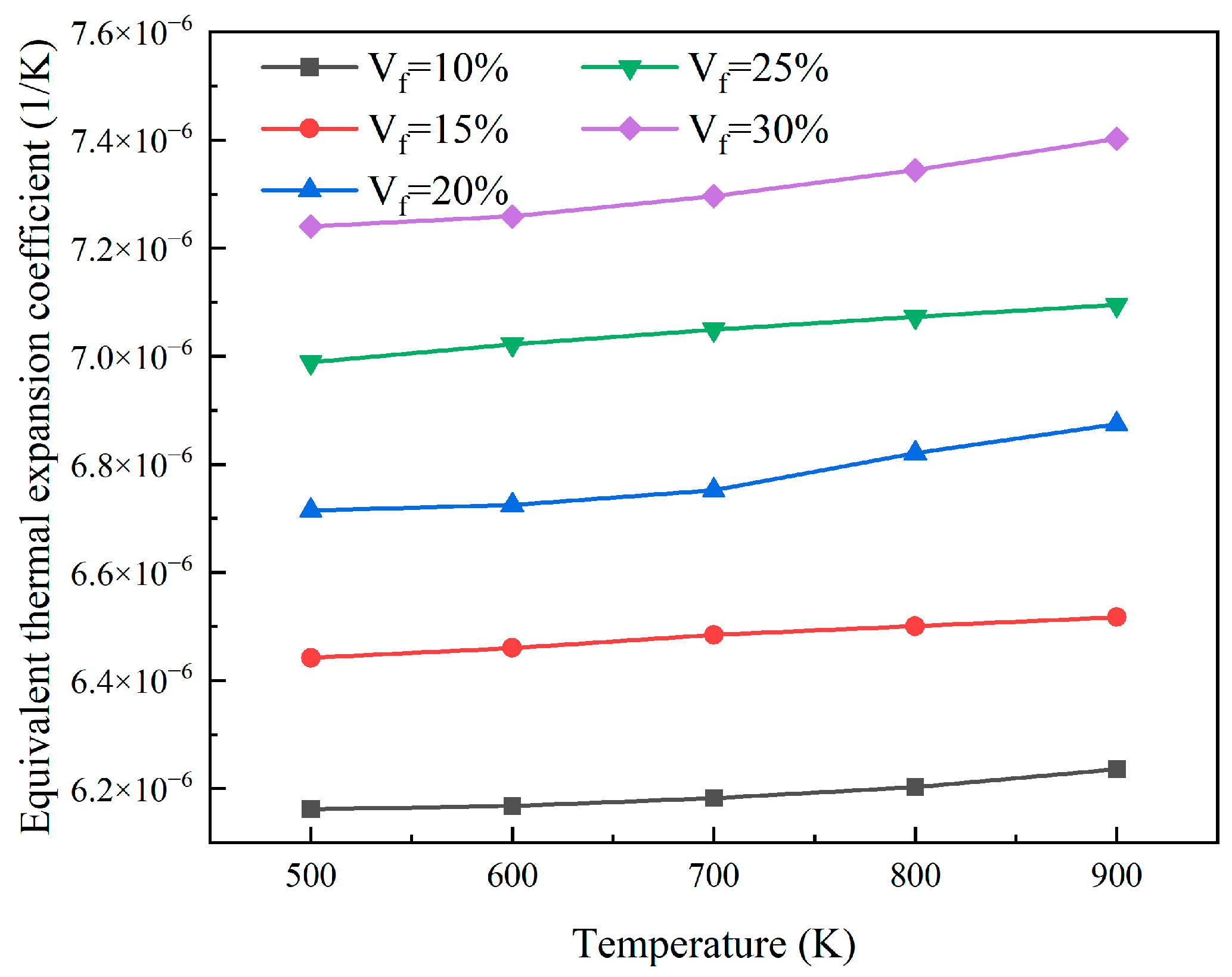
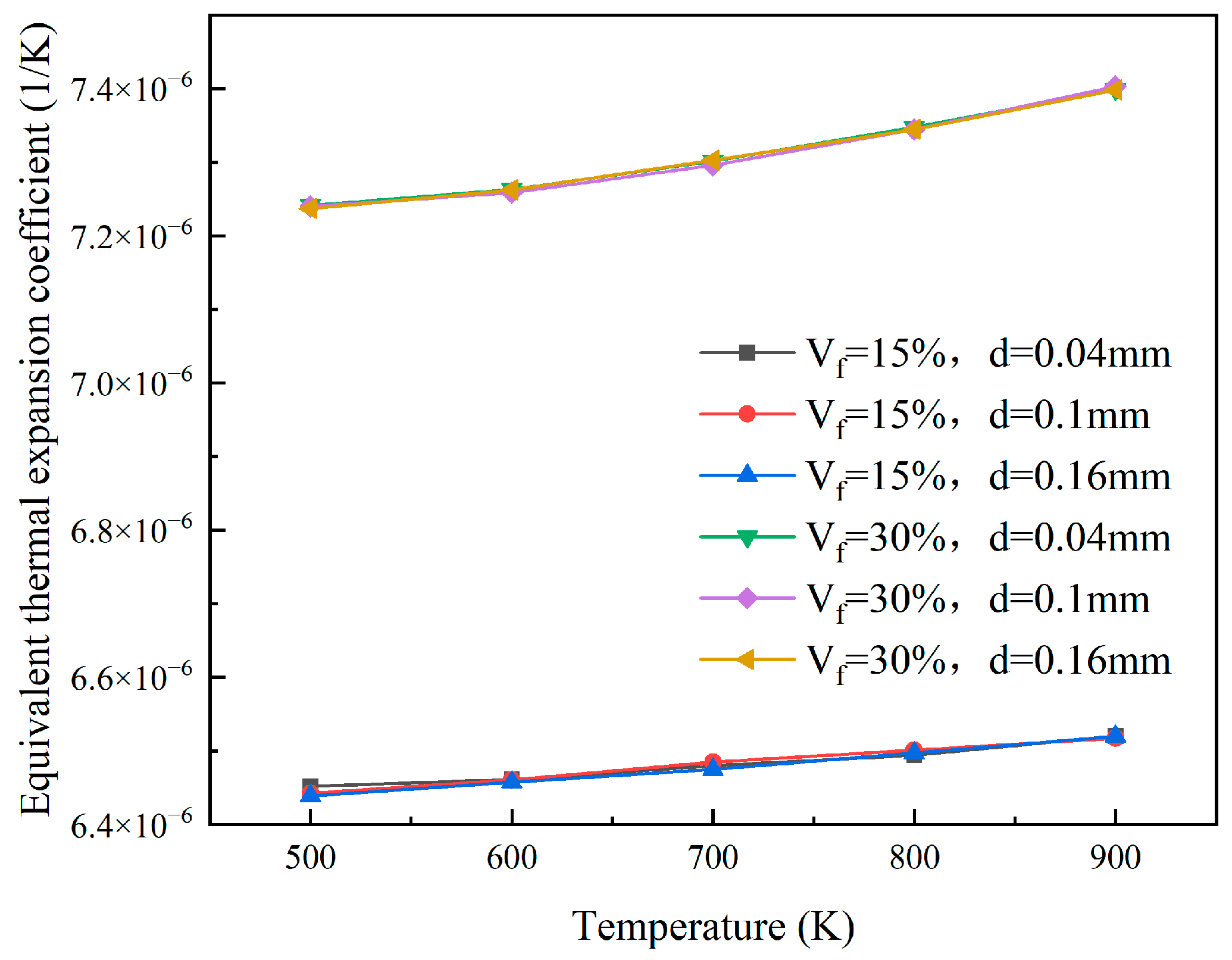
4.2. Equivalent Coefficient of Thermal Expansion of Dispersion Fuels
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Weber, C.E. Progress on dispersion elements. In Proceedings of the International Conference on the Peaceful use of Atomic Energy, Geneva, Switzerland, 8–20 August 1955. [Google Scholar]
- McDeavitt, S.M.; Downar, T.J.; Solomon, A.A.; Revankar, S.T.; Hash, M.C.; Hebden, A.S. Thoria-based cermet nuclear fuel: Cermet fabrication and behavior estimates. In Proceedings of the International Conference on Nuclear Engineering, Arlington, VA, USA, 14–18 April 2002; Volume 35987, pp. 59–67. [Google Scholar] [CrossRef]
- Leenaers, A.; Van Renterghem, W.; Van den Berghe, S. High burn-up structure of U(Mo) dispersion fuel. J. Nucl. Mater. 2016, 476, 218–230. [Google Scholar] [CrossRef]
- Ding, S.; Gong, X.; Zhao, Y.; Cui, Y.; Huo, Y.; Wei, Z. Key mechanical problems in dispersion nuclear fuels during their burning evolution process. Chin. Q. Mech. 2018, 39, 1–21. [Google Scholar] [CrossRef]
- Dai, X.; Cao, X.; Yu, S.; Zhu, C. Conceptual core design of an innovative small PWR utilizing fully ceramic microencapsulated fuel. Prog. Nucl. Energy 2014, 75, 63–71. [Google Scholar] [CrossRef]
- Duyn, L.B.V. Evaluation of the Mechanical Behavior of a Metal-Matrix Dispersion Fuel for Plutonium Burning. Master’s Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2003. [Google Scholar]
- Lombardi, C.; Luzzi, L.; Padovani, E.; Vettraino, F. Thoria and inert matrix fuels for a sustainable nuclear power. Prog. Nucl. Energy 2008, 50, 944–953. [Google Scholar] [CrossRef]
- Sun, R.; Gui, M.; Wang, J.; Chen, R.; Zhang, K.; Tian, W.; Qiu, S.; Su, G.H. SACOS-PLATE: A new thermal-hydraulic subchannel analysis code for plate type fuel assemblies. Ann. Nucl. Energy 2024, 204, 110517. [Google Scholar] [CrossRef]
- Xiang, F.; He, Y.; Niu, Y.; Deng, C.; Wu, Y.; Wang, K.; Tian, W.; Su, G.; Qiu, S. A new method to simulate dispersion plate-type fuel assembly in a multi-physics coupled way. Ann. Nucl. Energy 2022, 166, 108734. [Google Scholar] [CrossRef]
- Yue, Z.; He, Y.; Xiang, F.; Wu, Y.; Zhang, J.; Tian, W.; Su, G.; Qiu, S. Coupled neutronics, thermal-hydraulics, and fuel performance analysis of dispersion plate-type fuel assembly in a cohesive way. Nucl. Eng. Des. 2023, 413, 112548. [Google Scholar] [CrossRef]
- Weber, C.E.; Hisrsch, H. Dispersion type fuel elements. In Proceedings of the International Conference on the Peaceful use of Atomic Energy, Geneva, Switzerland, 8–20 August 1956. [Google Scholar]
- White, D.W.; Beard, A.P.; Willis, A.H. Irradiation behaviour of dispersion fuels. In Proceedings of the Paris Fuel Element Conference, Paris, France, 18–23 November 1957. [Google Scholar]
- Kim, Y.S.; Hofman, G.L. Fission product induced swelling of U–Mo alloy fuel. J. Nucl. Mater. 2011, 419, 291–301. [Google Scholar] [CrossRef]
- Yoo, J.; Oka, Y.; Ishiwatari, Y.; Liu, J. Thermo-mechanical analysis of supercritical pressure light water-cooled fast reactor fuel rod by FEMAXI-6 code. Ann. Nucl. Energy 2006, 33, 1379–1390. [Google Scholar] [CrossRef]
- Kim, Y.S.; Hofman, G.L.; Cheon, J.S.; Robinson, A.B.; Wachs, D.M. Fission induced swelling and creep of U–Mo alloy fuel. J. Nucl. Mater. 2013, 437, 37–46. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Jian, X.; Ding, G.; Cai, Y.; Yan, F.; Ding, S.; Li, Y. A novel multi-scale model of equivalent irradiation creep rate for U-10Mo/Zr dispersion fuels during irradiation. Prog. Nucl. Energy 2025, 187, 105857. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, J.; Jian, X.; Yan, F.; Ding, S.; Li, Y. Effects of Matrix Creep Properties on Effective Irradiation Swelling of U-10Mo/Zr Dispersion Nuclear Fuels. Front. Energy Res. 2022, 10, 851747. [Google Scholar] [CrossRef]
- Li, Y.; Ding, G.; Xie, Z.; Zhang, J.; Jian, X.; Ding, S.; Li, Y. Models for effective elastic constants of irradiated U-10Mo fuels with distributed fission gas bubbles. J. Nucl. Mater. 2023, 579, 154359. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Wei, H.; Zhang, J.; Tang, C.; Lu, C.; Huang, C.; Ding, S.; Li, Y. Modelling of effective irradiation swelling for inert matrix fuels. Nucl. Eng. Technol. 2021, 53, 2616–2628. [Google Scholar] [CrossRef]
- Schneider, C.; Fayette, L.; Zacharie-Aubrun, I.; Blay, T.; Sercombe, J.; Favergeon, J.; Chevalier, S. Study of the hardness and Young’s modulus at the fuel-cladding interface of a high-burnup PWR fuel rod by nanoindentation measurements. J. Nucl. Mater. 2022, 560, 153511. [Google Scholar] [CrossRef]
- Terrani, K.A.; Balooch, M.; Burns, J.R.; Smith, Q.B. Young’s modulus evaluation of high burnup structure in UO2 with nanometer resolution. J. Nucl. Mater. 2018, 508, 33–39. [Google Scholar] [CrossRef]
- Dong, Y.; Cao, X.; Peng, X.; Lv, J.; Li, Q. In-pile heat conduction model of the dispersion nuclear fuel plate with particle agglomeration. Part II: Predicting the effective thermal conductivity under the in-pile thermal transfer pattern based on a deep neural network. J. Nucl. Mater. 2025, 607, 155692. [Google Scholar] [CrossRef]
- Huang, Z.; Dong, Y.; Liu, Q.; Hao, X.; Zuo, H.; Li, Q. Effective thermal conductivity prediction of dispersion nuclear fuel elements based on deep learning and property-oriented inverse design. Nucl. Eng. Des. 2025, 434, 113918. [Google Scholar] [CrossRef]
- Dong, Y.; Huang, Z.; Peng, X.; Lv, J.; Li, Q. In-pile heat conduction model of the dispersion nuclear fuel plate with particle agglomeration. Part I: Numerical method and analysis of influencing factors. J. Nucl. Mater. 2025, 607, 155613. [Google Scholar] [CrossRef]
- Gong, X.; Ding, S.; Zhao, Y.; Huo, Y.; Zhang, L.; Li, Y. Effects of irradiation hardening and creep on the thermo-mechanical behaviors in inert matrix fuel elements. Mech. Mater. 2013, 65, 110–123. [Google Scholar] [CrossRef]
- Gong, X.; Jiang, Y.; Ding, S.; Huo, Y.; Wang, C.; Yang, L. Simulation of the in-pile behaviors evolution in nuclear fuel rods with the irradiation damage effects. Acta Mech. Solida Sin. 2014, 27, 551–567. [Google Scholar] [CrossRef]
- Pontedeiro, A.C.; Cotta, R.M.; Su, J. Improved lumped model for thermal analysis of high burn-up nuclear fuel rods. Prog. Nucl. Energy 2008, 50, 767–773. [Google Scholar] [CrossRef]
- Ding, S.; Jiang, X.; Huo, Y.; Lin, A. Reliability analysis of dispersion nuclear fuel elements. J. Nucl. Mater. 2008, 374, 453–460. [Google Scholar] [CrossRef]
- Williamson, R.L. Enhancing the ABAQUS thermomechanics code to simulate multipellet steady and transient LWR fuel rod behavior. J. Nucl. Mater. 2011, 415, 74–83. [Google Scholar] [CrossRef]
- Ding, S.; Wang, Q.; Huo, Y. Mechanical behaviors of the dispersion nuclear fuel plates induced by fuel particle swelling and thermal effect II: Effects of variations of the fuel particle diameters. J. Nucl. Mater. 2010, 397, 80–91. [Google Scholar] [CrossRef]
- Zhang, C.; Wu, Y.; Liu, S.; Chen, P.; Li, W.; Deng, C.; Zhang, J.; Su, G.; Qiu, S.; Wu, J. Multidimensional multiphysics modeling of TRISO particle fuel with SiC/ZrC coating using modified fission gas release model. Ann. Nucl. Energy 2020, 145, 107599. [Google Scholar] [CrossRef]
- Wei, H.; Zhang, J.; Zhang, Y.; Li, L.; Ding, S.; Ren, Q. Modeling of irradiation-induced thermo-mechanical coupling and multi-scale behavior in a fully ceramic-microencapsulated fuel pellet. J. Nucl. Mater. 2021, 544, 152673. [Google Scholar] [CrossRef]
- Cai, M.; Cong, T.; Gu, H. Multiphysics fuel performance modeling of dispersed TRISO-coated particle fuel plate under long-time normal condition and accident conditions. Nucl. Eng. Des. 2023, 415, 112725. [Google Scholar] [CrossRef]
- Berger, H.; Kari, S.; Gabbert, U.; Rodríguez-Ramos, R.; Bravo-Castillero, J.; Guinovart-Díaz, R. A comprehensive numerical homogenisation technique for calculating effective coefficients of uniaxial piezoelectric fibre composites. Mater. Sci. Eng. A 2005, 412, 53–60. [Google Scholar] [CrossRef]
- Spino, J.; Cobos-Sabate, J.; Rousseau, F. Room-temperature microindentation behaviour of LWR-fuels, part 1: Fuel microhardness. J. Nucl. Mater. 2003, 322, 204–216. [Google Scholar] [CrossRef]
- MacDonald, P.E.; Thompson, L.B. MATPRO-09. A Handbook of Materials Properties for Use in the Analysis of Light Water Reactor Fuel Rod Behavior; Idaho National Engineering Lab: Idaho Falls, ID, USA, 1976. [Google Scholar]
- Van Uffelen, P.; Pastore, G.; Di Marcello, V.; Luzzi, L. Multiscale modelling for the fission gas behaviour in the transuranus code. Nucl. Eng. Technol. 2011, 43, 477–488. [Google Scholar] [CrossRef]
- Suzuki, M.; Udagawa, Y.; Nagase, F.; Saitou, H. Input/Output Manual of Light Water Reactor Fuel Analysis Code FEMAXI-7 and Its Related Codes; Japan Atomic Energy Agency: Ibaraki, Japan, 2013. [Google Scholar]
- Laux, D.; Baron, D.; Despaux, G.; Kellerbauer, A.I.; Kinoshita, M. Determination of high burn-up nuclear fuel elastic properties with acoustic microscopy. J. Nucl. Mater. 2012, 420, 94–100. [Google Scholar] [CrossRef]
- Shen, Y.L. Thermal expansion of metal–ceramic composites: A three-dimensional analysis. Mater. Sci. Eng. A 1998, 252, 269–275. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion, and related problems. Proc. R. Soc. A Math. Phys. Eng. Sci. 1957, 241, 376–396. [Google Scholar] [CrossRef]
- Eshelby, J.D. The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. A Math. Phys. Eng. Sci. 1959, 252, 561–569. [Google Scholar] [CrossRef]
- Clyne, T.W.; Withers, P.J. An Introduction to Metal Matrix Composites; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Nemat-Nasser, S.; Hori, M.; Achenbach, J.D. Micromechanics: Overall Properties of Heterogeneous Materials; North-Holland: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Mura, T. Micromechanics of Defects in Solids, 2nd ed.; Springer: Dordrecht, The Netherlands, 1987. [Google Scholar]
- Kezhi, H.; Yonggang, H. Constitutive Relationship of Solids; Tsinghua University Press: Beijing, China, 1999. [Google Scholar]
- Mori, T.; Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Benveniste, Y. A new approach to the application of Mori-Tanaka’s theory in composite materials. Mech. Mater. 1987, 6, 147–157. [Google Scholar] [CrossRef]
- Weng, G.J. Elastic properties of reinforced solids, with special reference to isotropic ones containing spherical inclusions. Int. J. Eng. Sci. 1984, 22, 845–856. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Suzuki, M.; Udagawa, Y.; Saitou, H. Light Water Reactor Fuel Analysis Code FEMAXI-7; Model and Structure; Japan Atomic Energy Agency: Ibaraki, Japan, 2011. [Google Scholar]
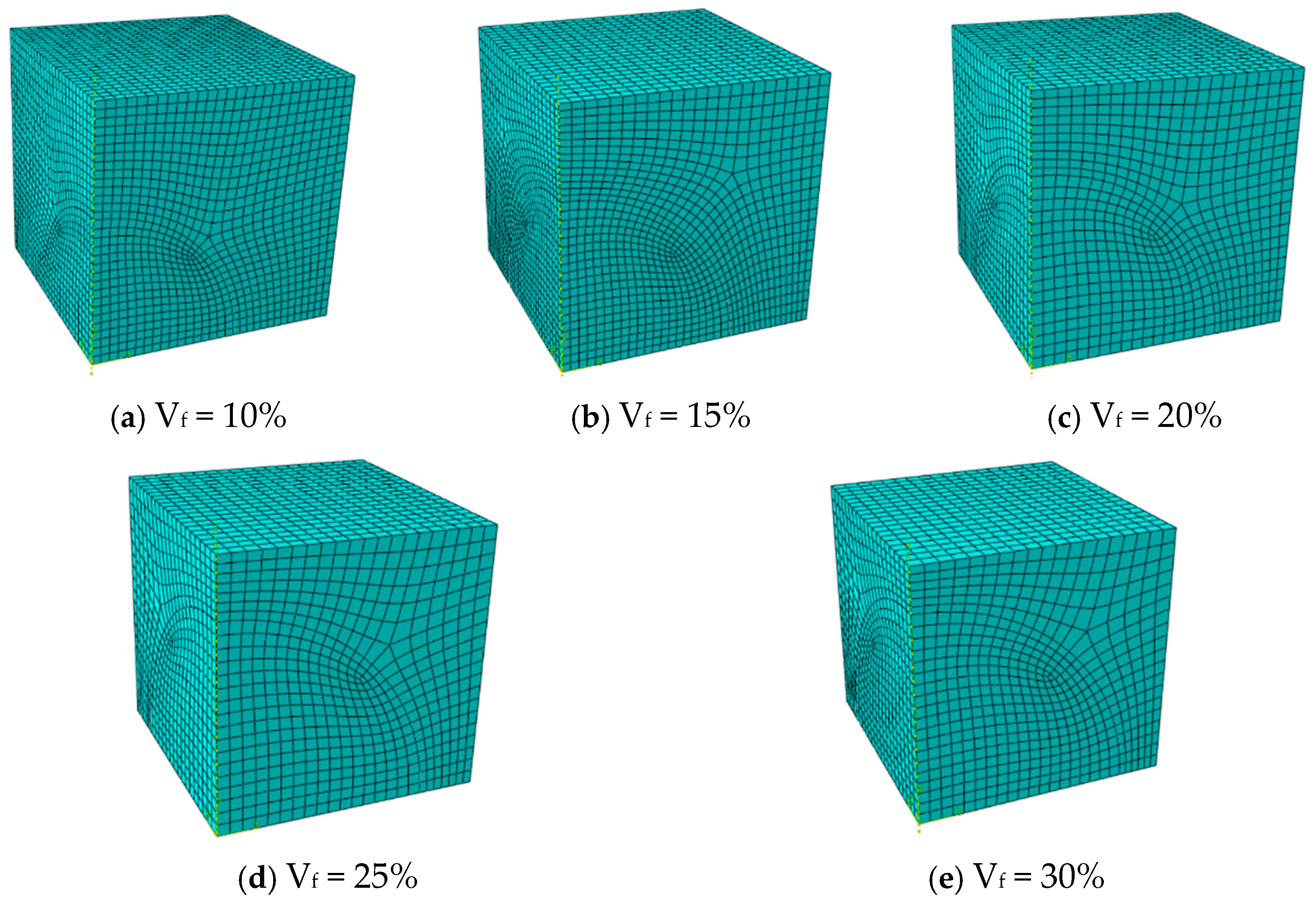
| Volume Fraction | Elements | Nodes |
|---|---|---|
| 10% | 21,755 | 24,795 |
| 15% | 20,604 | 23,584 |
| 20% | 15,896 | 18,468 |
| 25% | 13,183 | 15,449 |
| 30% | 10,072 | 12,104 |
| Fuel Particle Diameter (mm) | Volume Fraction | Elements | Nodes |
|---|---|---|---|
| 0.04 | 15% | 15,872 | 18,362 |
| 0.1 | 20,604 | 23,584 | |
| 0.16 | 48,224 | 53,496 | |
| 0.04 | 30% | 8465 | 10,153 |
| 0.1 | 10,072 | 12,104 | |
| 0.16 | 24,697 | 28,179 |
| Method | Formula | Variable Description |
|---|---|---|
| Dilute method [46] | —Equivalent bulk modulus; —Equivalent shear modulus; —Particle bulk modulus; —Particle shear modulus; —Particle Poisson’s ratio; —Particle volume percentage; —Matrix bulk modulus; —Matrix shear modulus; —Matrix volume percentage; —Matrix Poisson’s ratio | |
| Mori–Tanaka model [47,48,49] | ||
| Hashin–Shtrikman model [50] |
| Method | Formula | Variable Description |
|---|---|---|
| Simple model | —Equivalent thermal expansion coefficient; —Particle thermal expansion coefficient; —Matrix thermal expansion coefficient; —Bulk modulus calculated by Hashin–Shtrikman model | |
| Kerner model | ||
| Schapery model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Cong, T.; Zhang, J. Calculation Simulation of Equivalent Thermomechanical Properties of Dispersion Nuclear Fuel. Materials 2025, 18, 5266. https://doi.org/10.3390/ma18235266
Yu H, Cong T, Zhang J. Calculation Simulation of Equivalent Thermomechanical Properties of Dispersion Nuclear Fuel. Materials. 2025; 18(23):5266. https://doi.org/10.3390/ma18235266
Chicago/Turabian StyleYu, Haoqi, Tenglong Cong, and Jie Zhang. 2025. "Calculation Simulation of Equivalent Thermomechanical Properties of Dispersion Nuclear Fuel" Materials 18, no. 23: 5266. https://doi.org/10.3390/ma18235266
APA StyleYu, H., Cong, T., & Zhang, J. (2025). Calculation Simulation of Equivalent Thermomechanical Properties of Dispersion Nuclear Fuel. Materials, 18(23), 5266. https://doi.org/10.3390/ma18235266




