Lateral Resistance of Modular CFS Shear Wall Connected with Rectangular Steel Tubes and Its Contribution to Frame Structures
Abstract
1. Introduction
2. Fine Model of the Modular CFS Shear Wall with Self-Tapping Screw Connection Details
2.1. Test Introduction
2.2. Test Results
2.3. Establishment of Fine Model
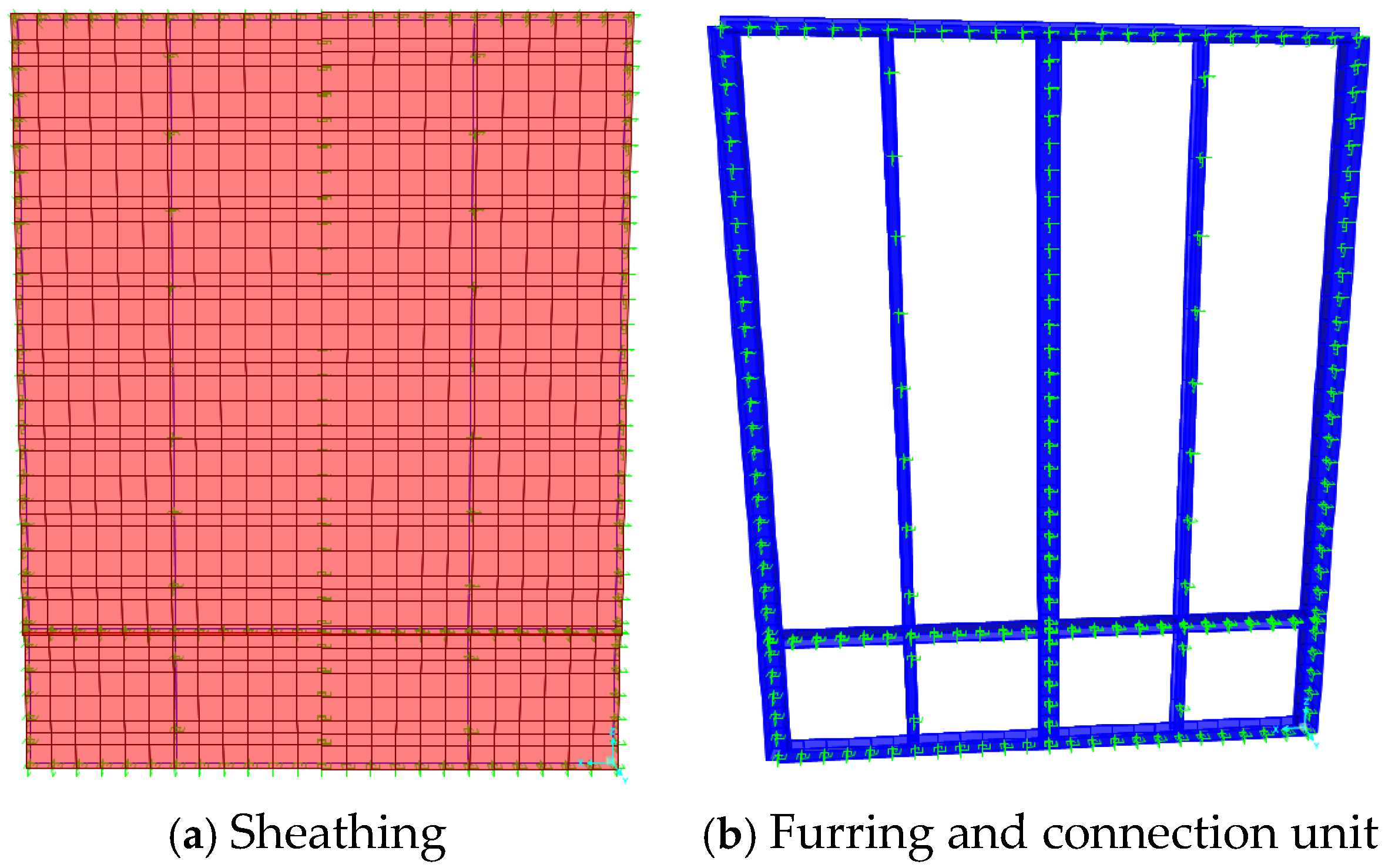
2.3.1. Simulation of CFS Studs and Sheathing
2.3.2. Simulation of Self-Tapping Screws
2.3.3. Boundary Conditions and Loading
2.4. Comparison of Results Obtained from the Fine Model and Test
2.4.1. Comparison of Deformation of the Modular Wall
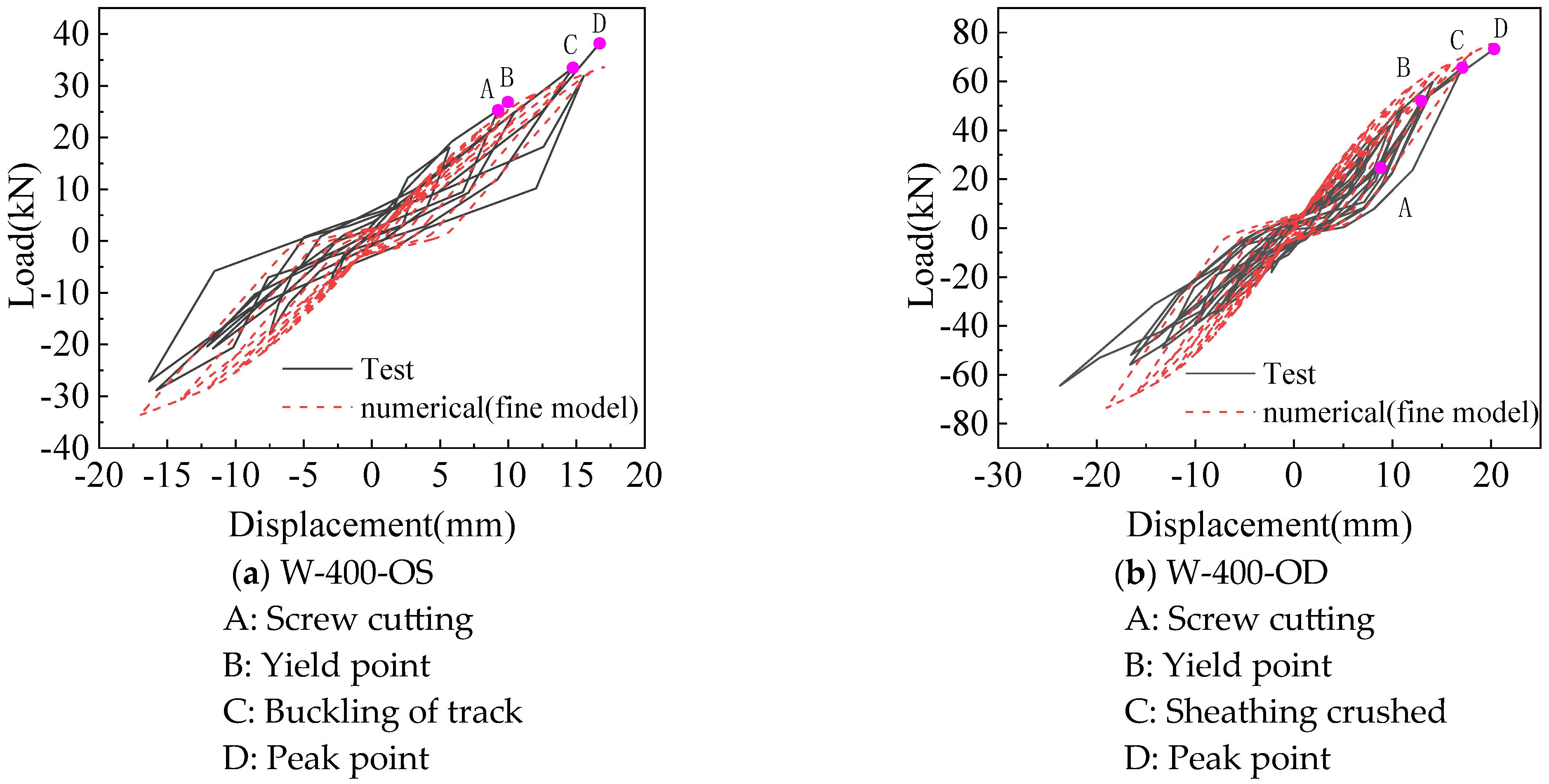
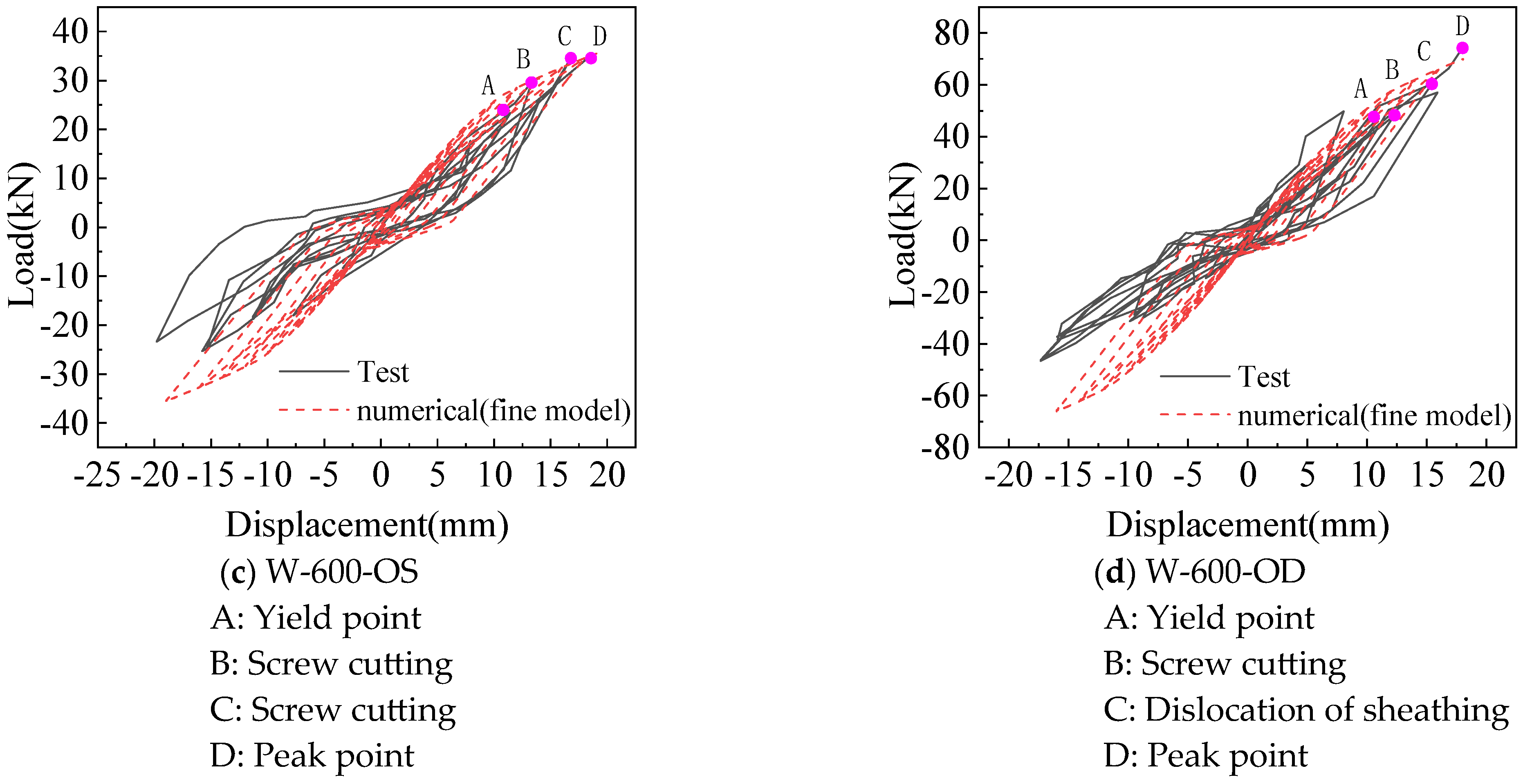
2.4.2. Comparison of Hysteretic Curve and Skeleton Curve from the Fine Model Analysis
2.4.3. Comparison of the Performance Indices Between Test and Fine Model
3. Simplified Model of the Modular CFS Shear Wall Using Equivalent Spring Method
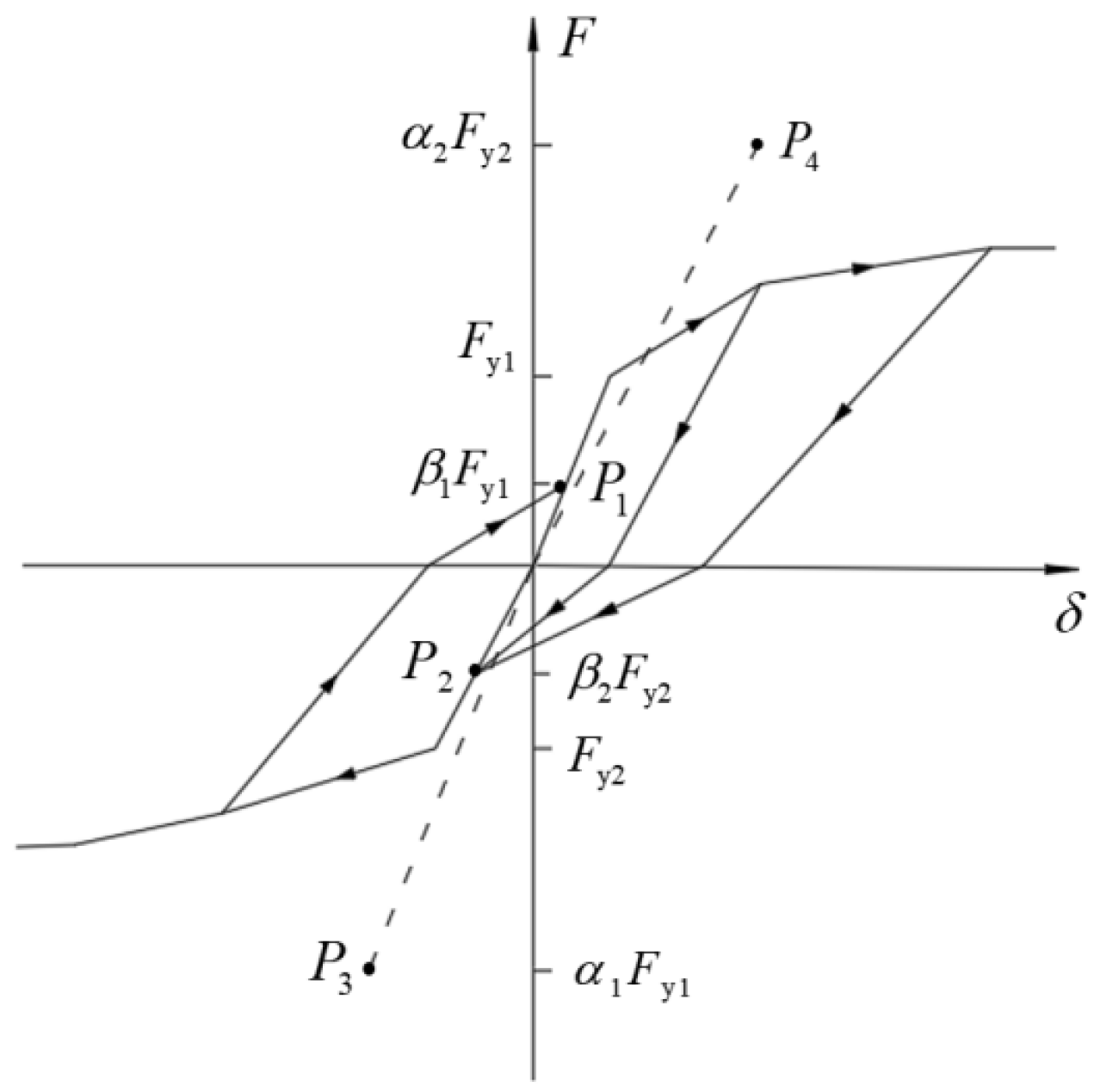
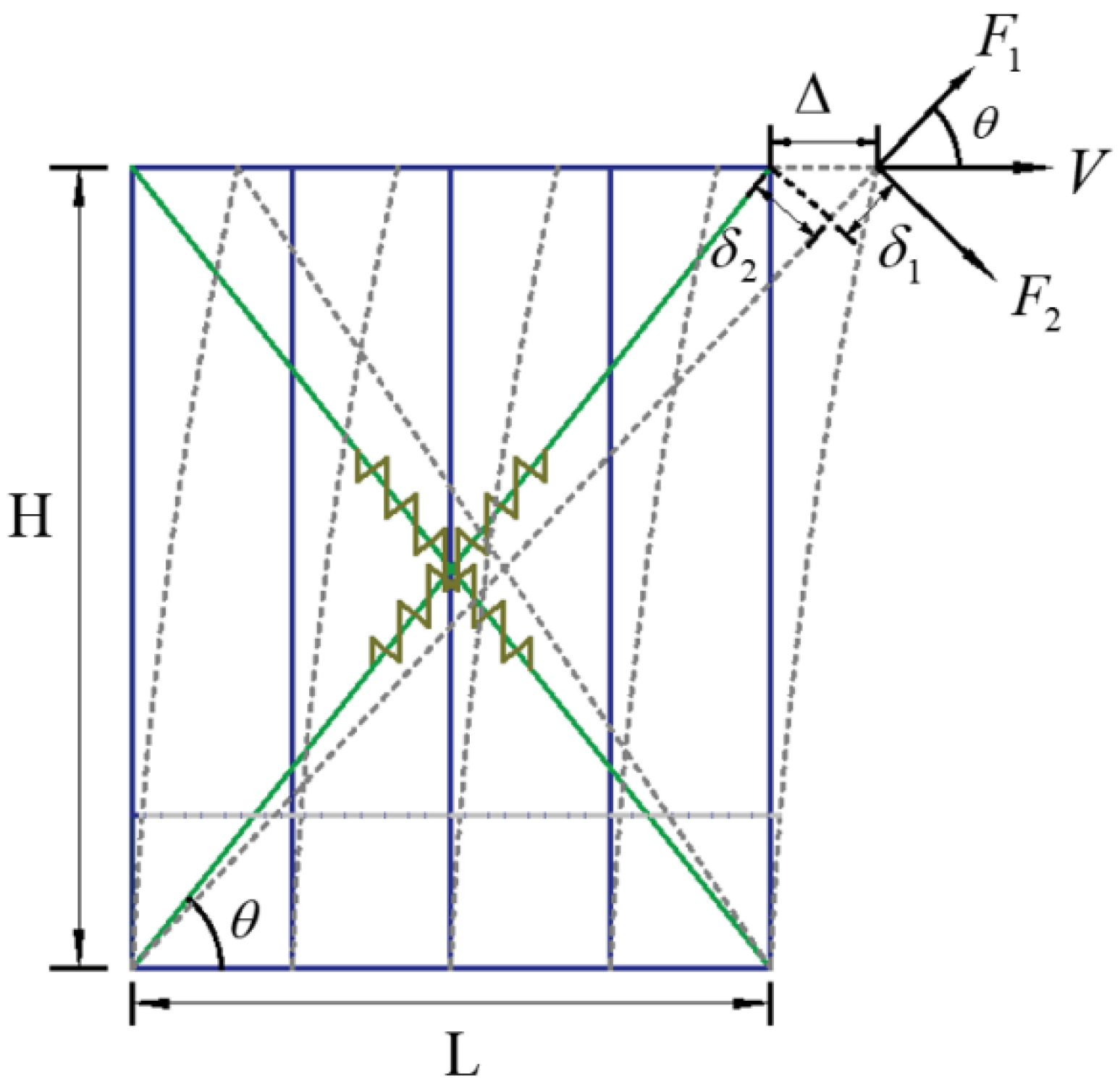
3.1. Equivalent Spring Method and Establishment of Simplified Model
3.2. Comparison of Results Obtained from Simplified Model and Test
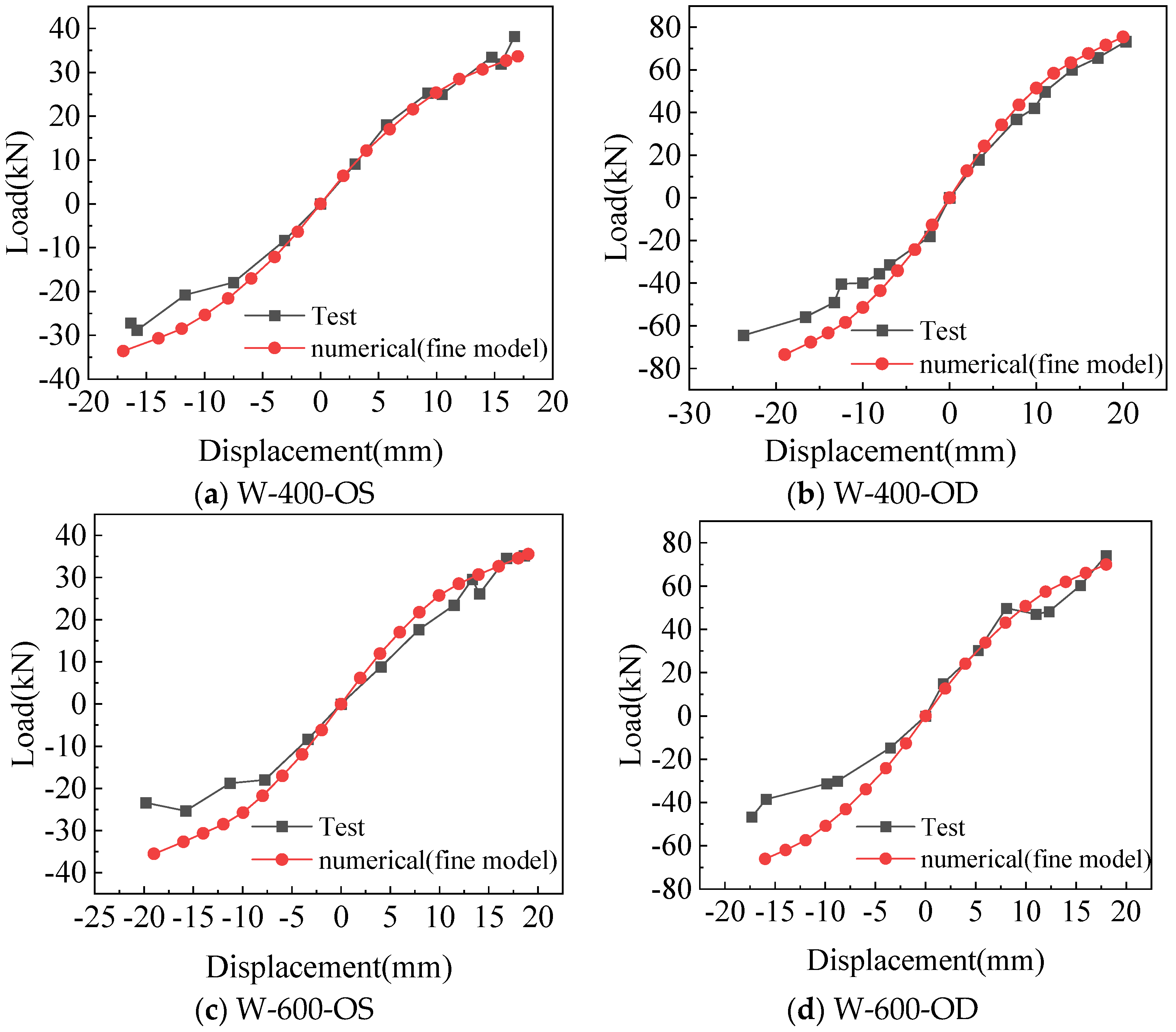
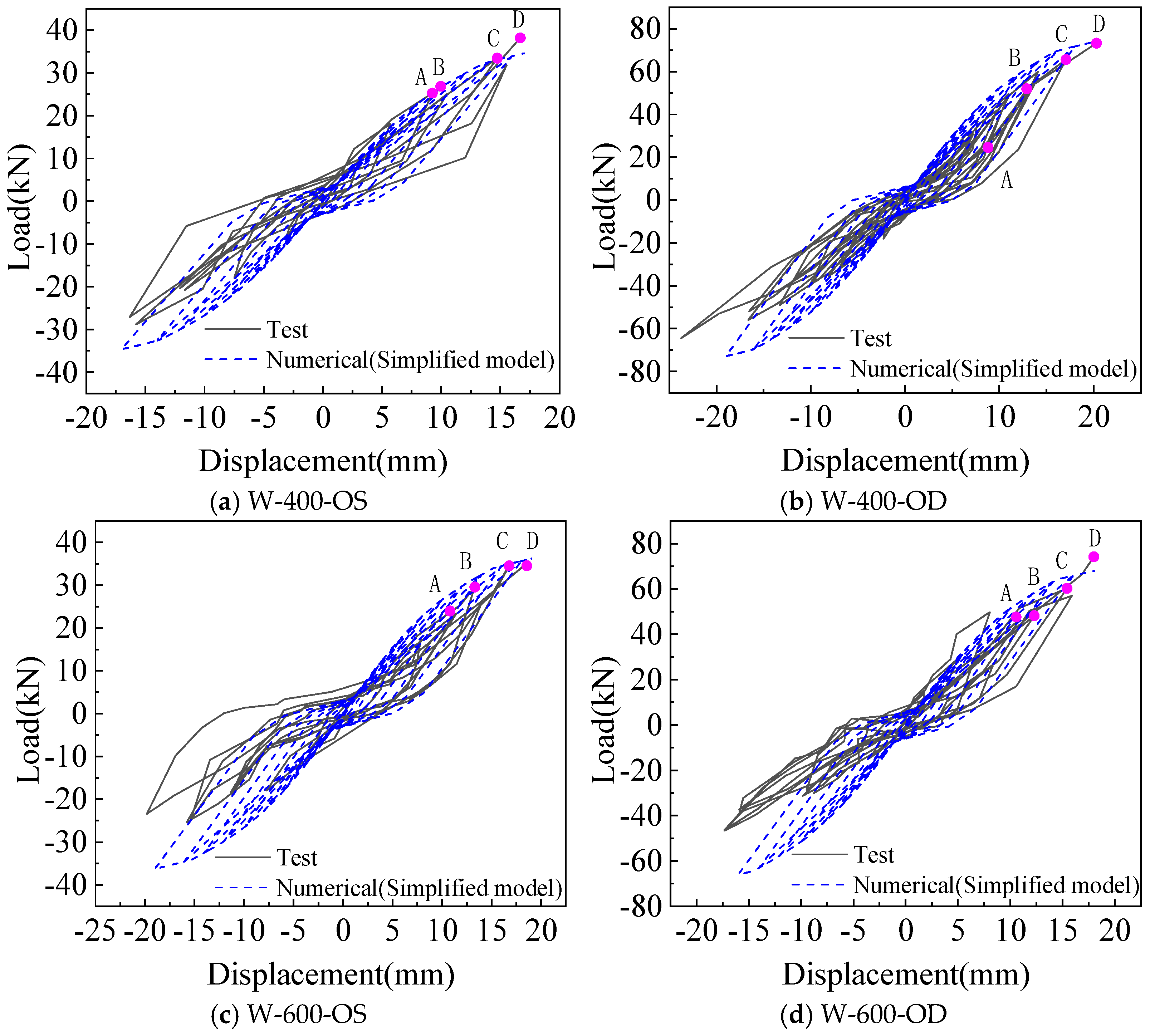
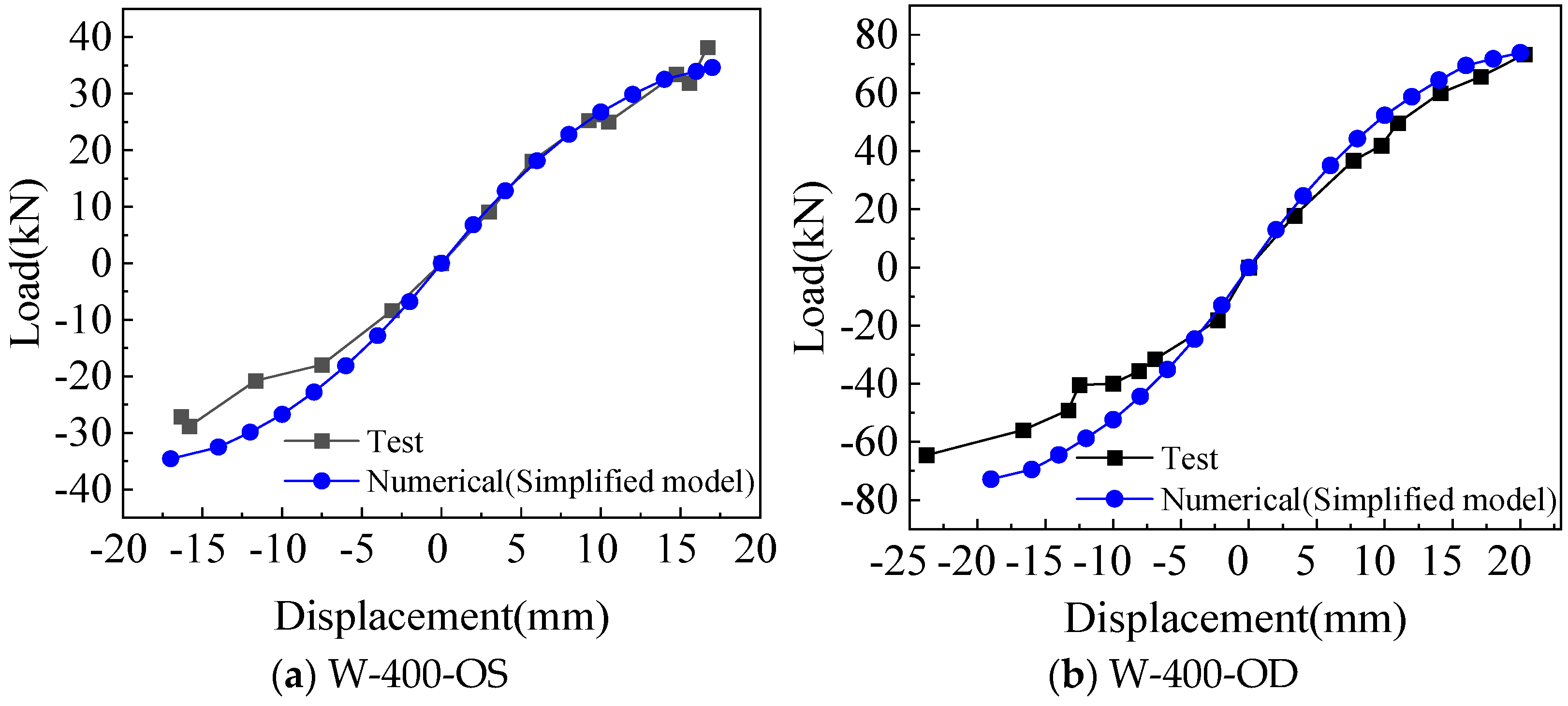
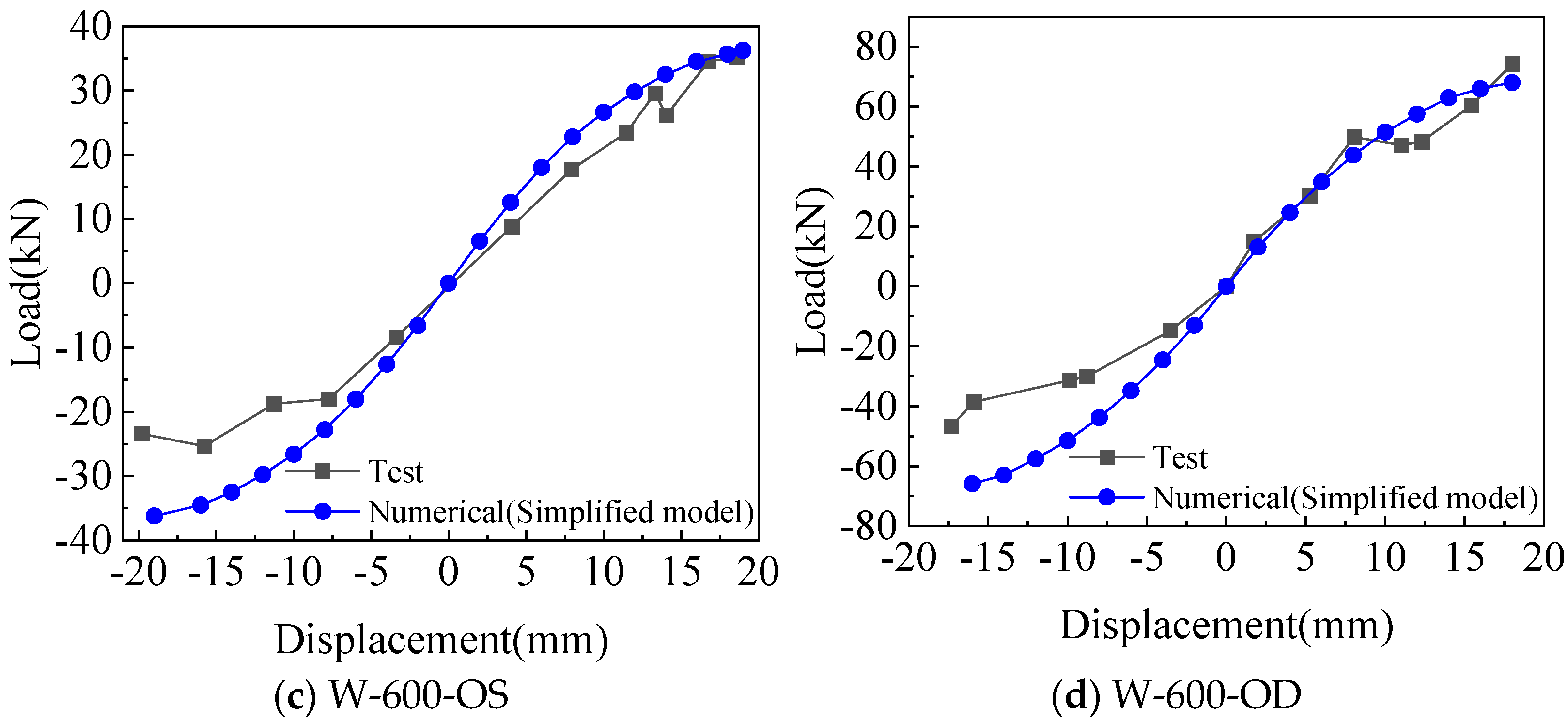
3.2.1. Comparison of Hysteretic Curve and Skeleton Curve from the Simplified Model Analysis
3.2.2. Comparison of the Performance Indices Between Test and Simplified Model
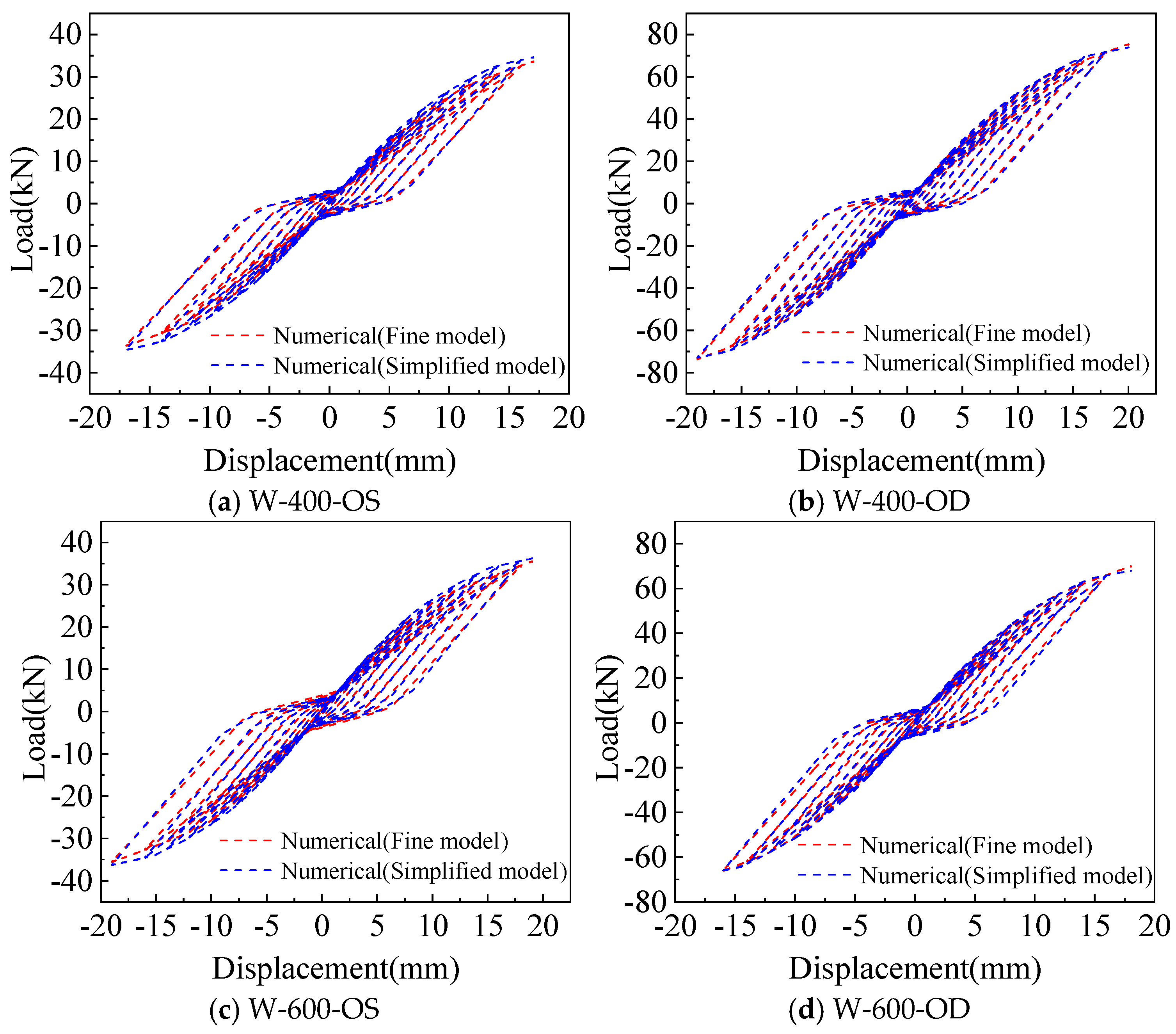
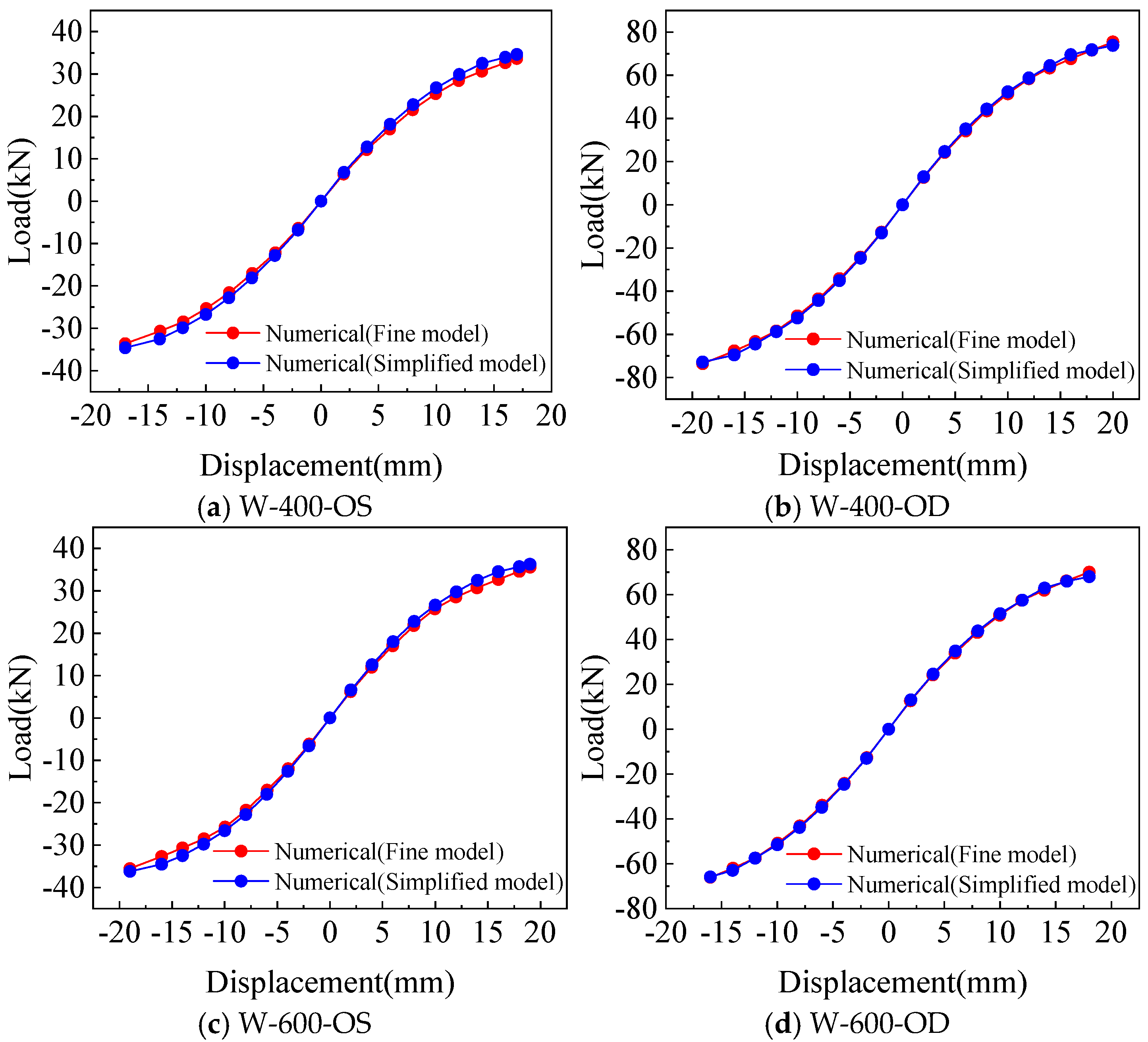
3.3. Comparison of the Results Between the Fine Model and the Simplified Model Analysis
4. Seismic Response Analysis of Multi-Story Building Structures Based on the Collaborative Work of Modular Walls and Frames
4.1. Establishment of Multi-Story Building Model
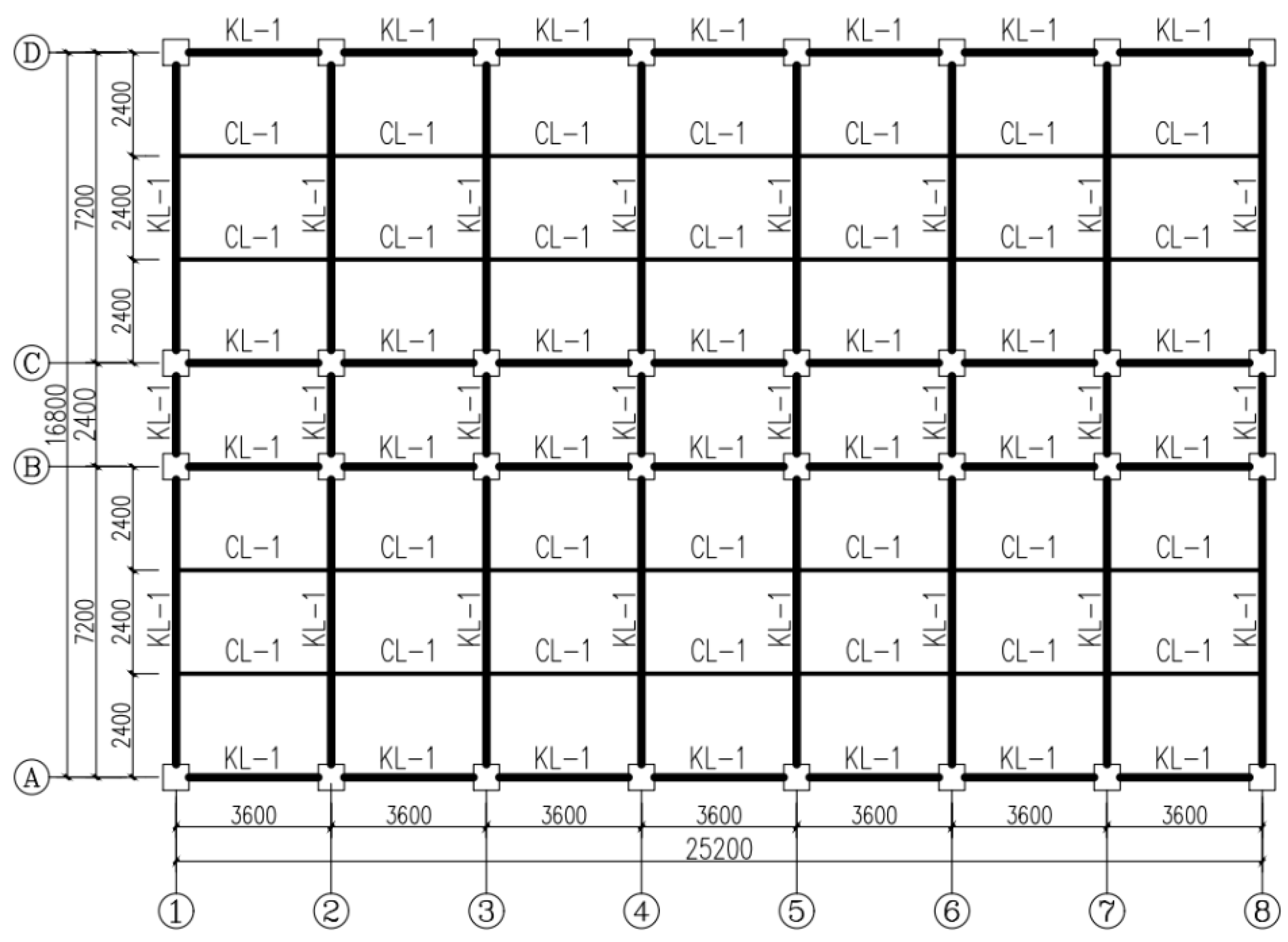
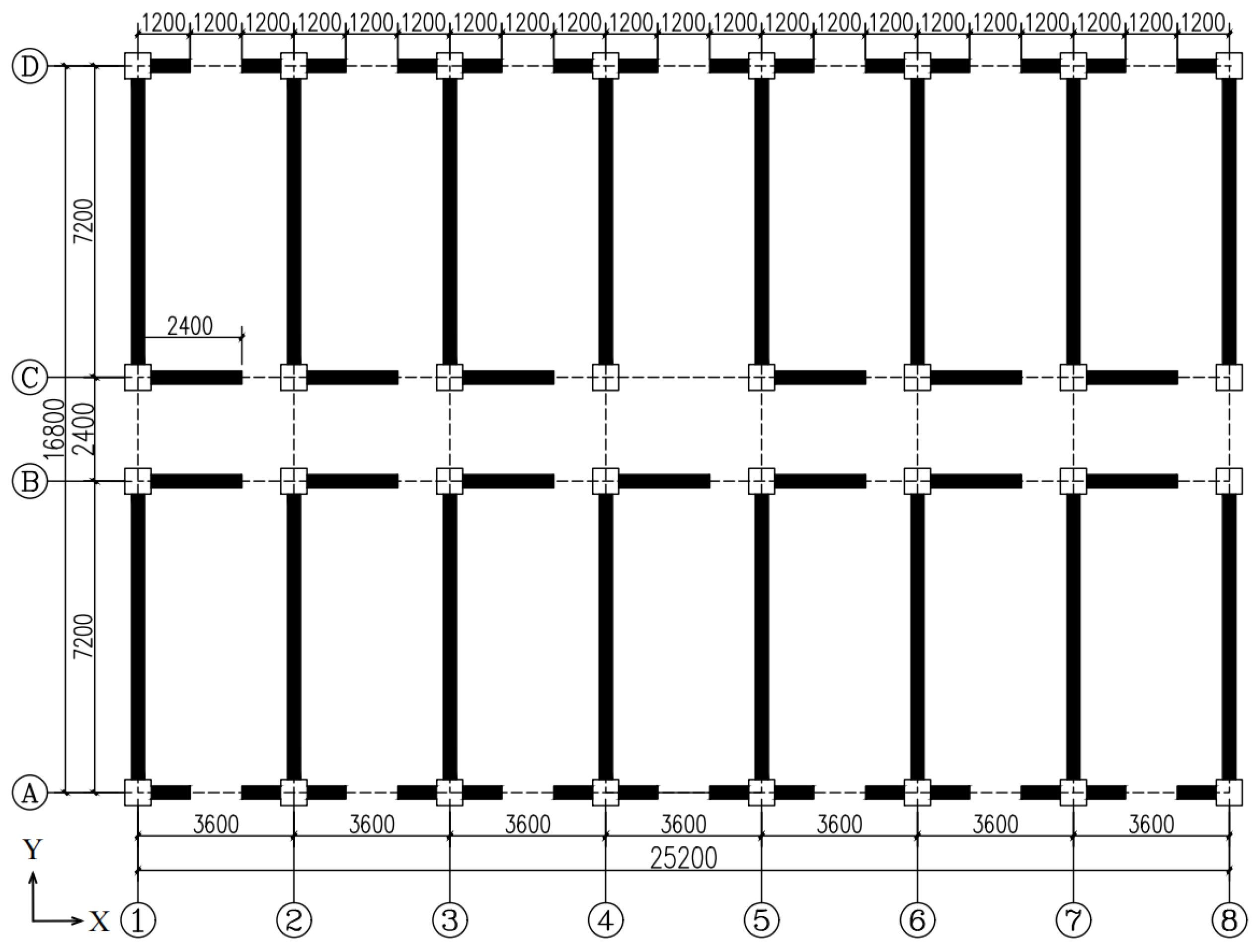
4.1.1. Engineering Background and General Introduction
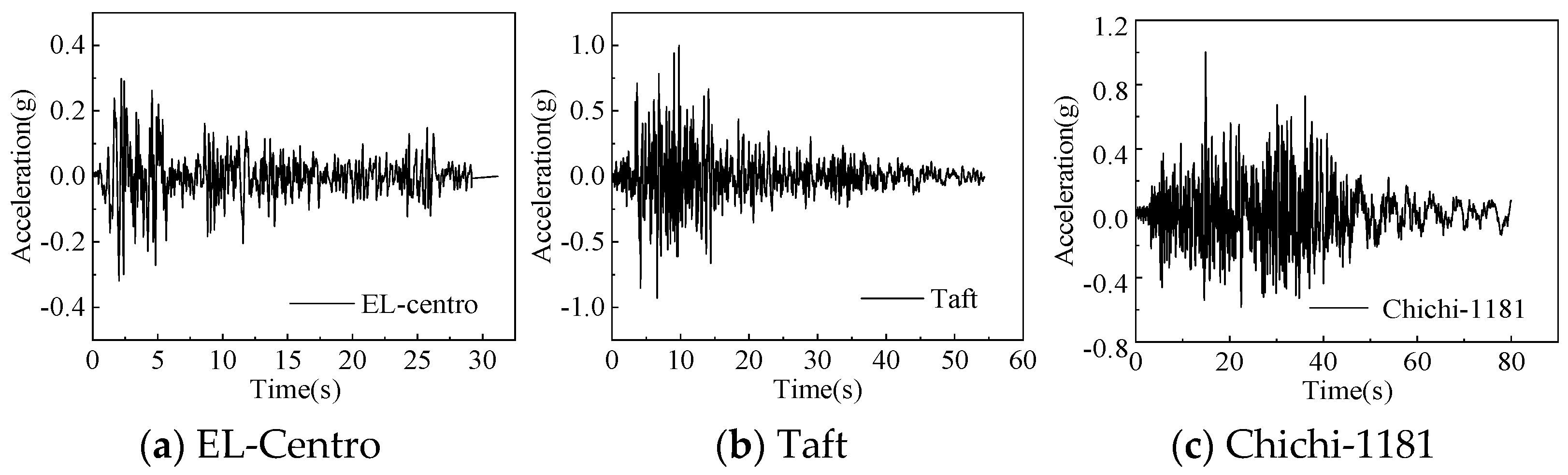
4.1.2. Establishment of Models and Selection of Parameters
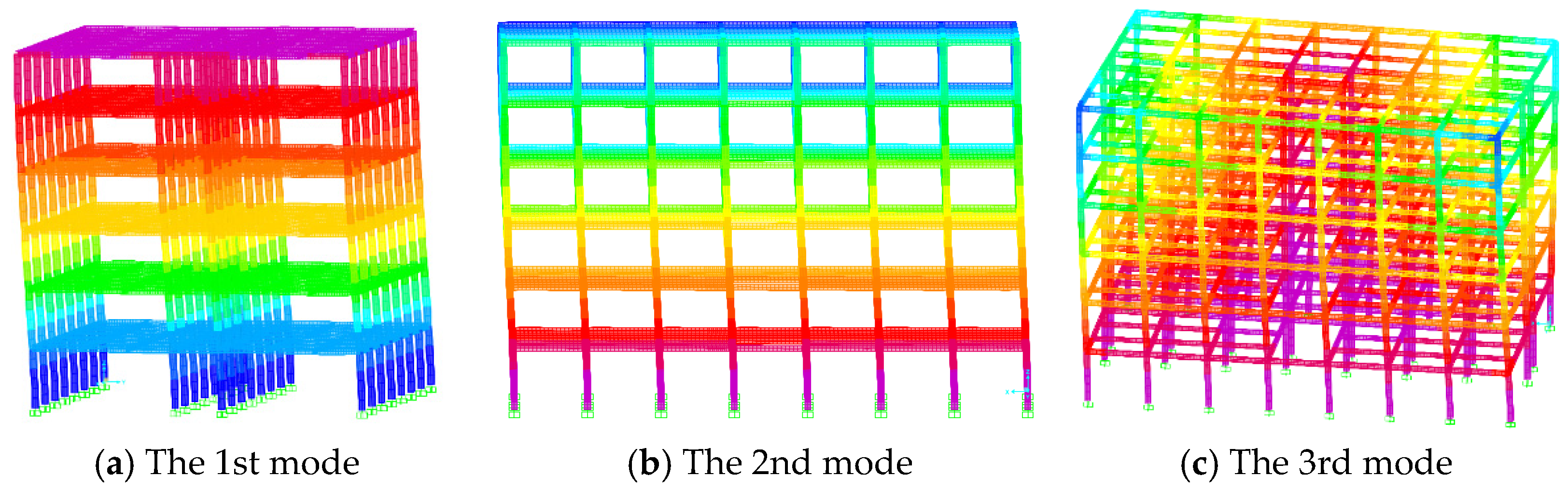
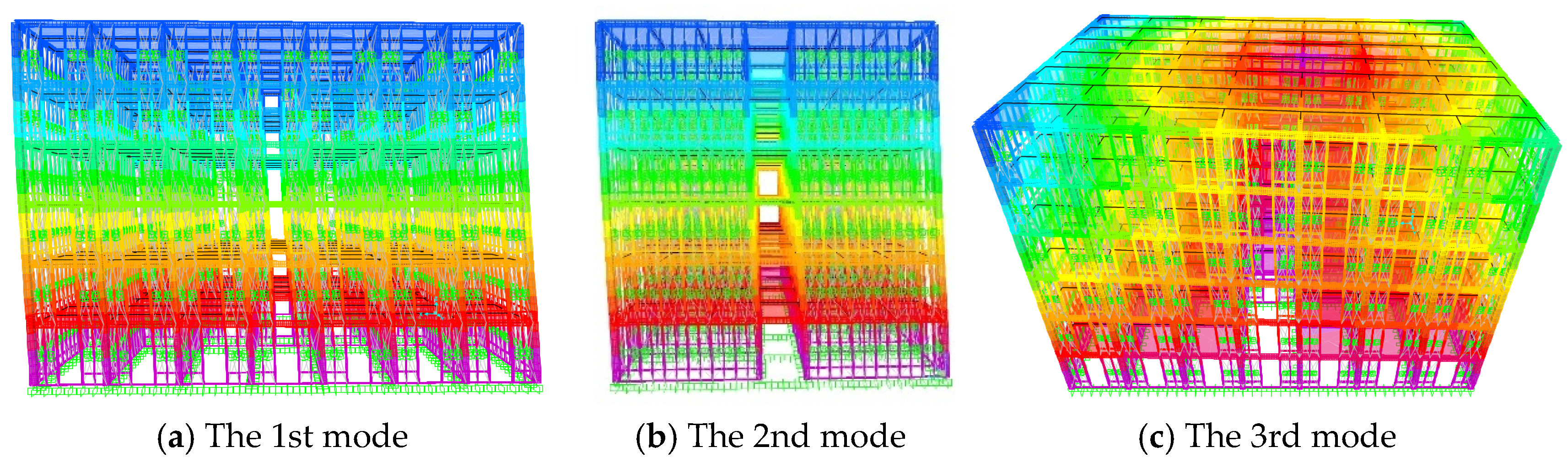
4.2. Modal Analysis of the Building Models
4.3. Comparison of Seismic Response of the Frame Buildings with and Without Infilled Wall
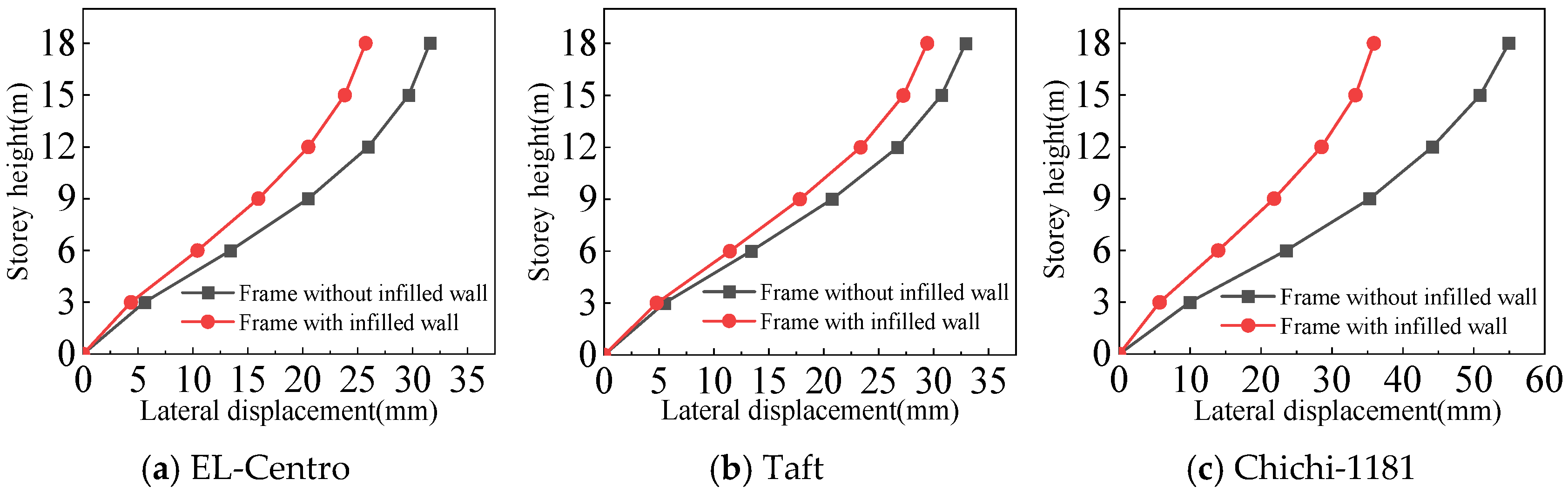
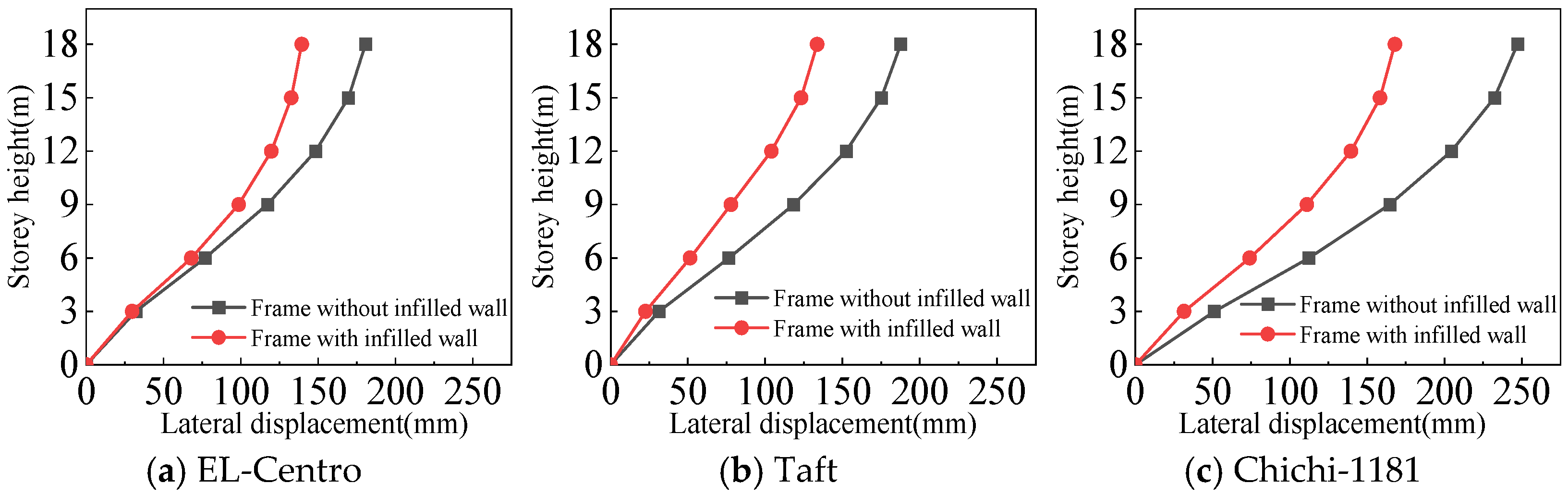
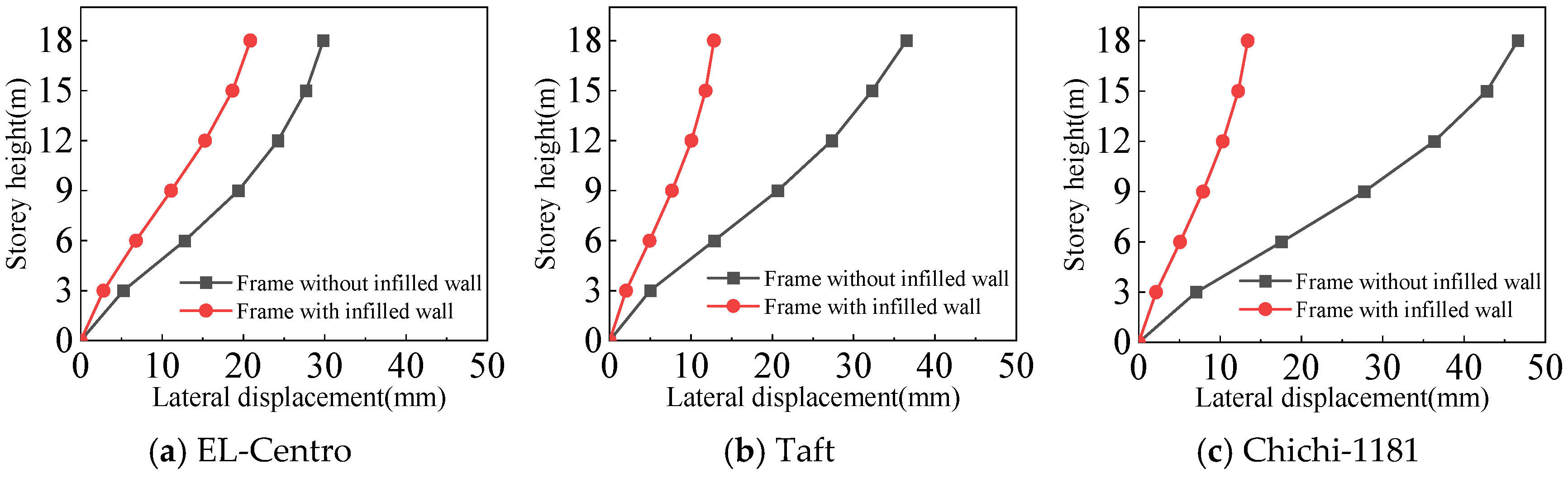
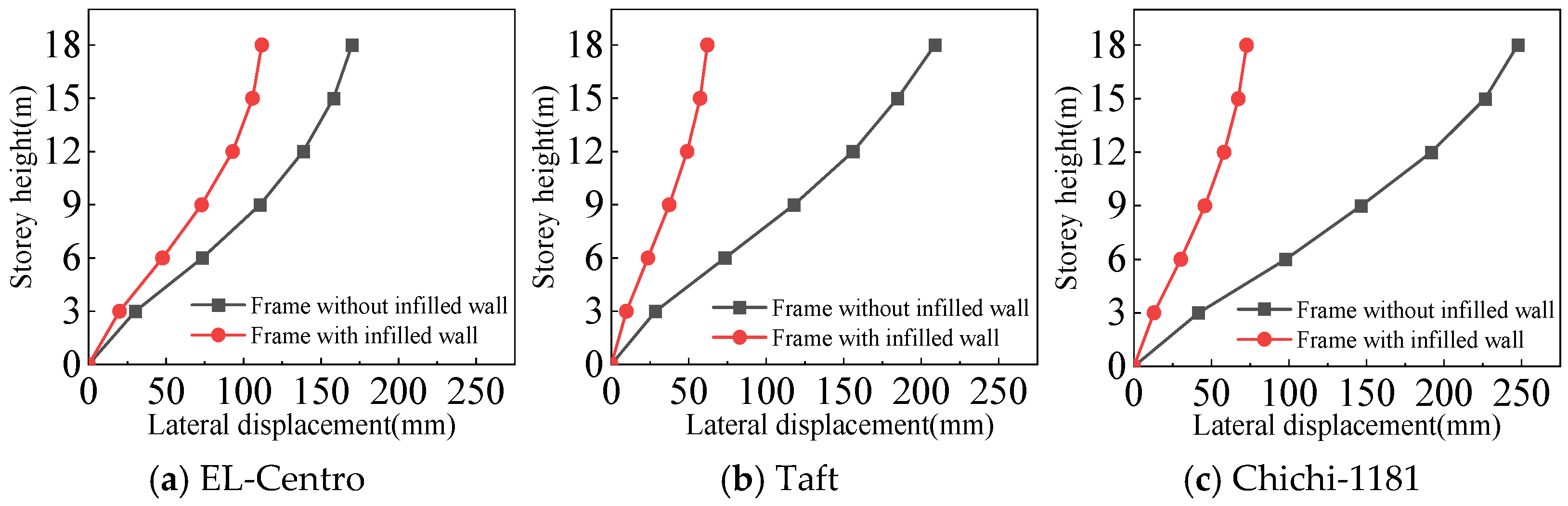
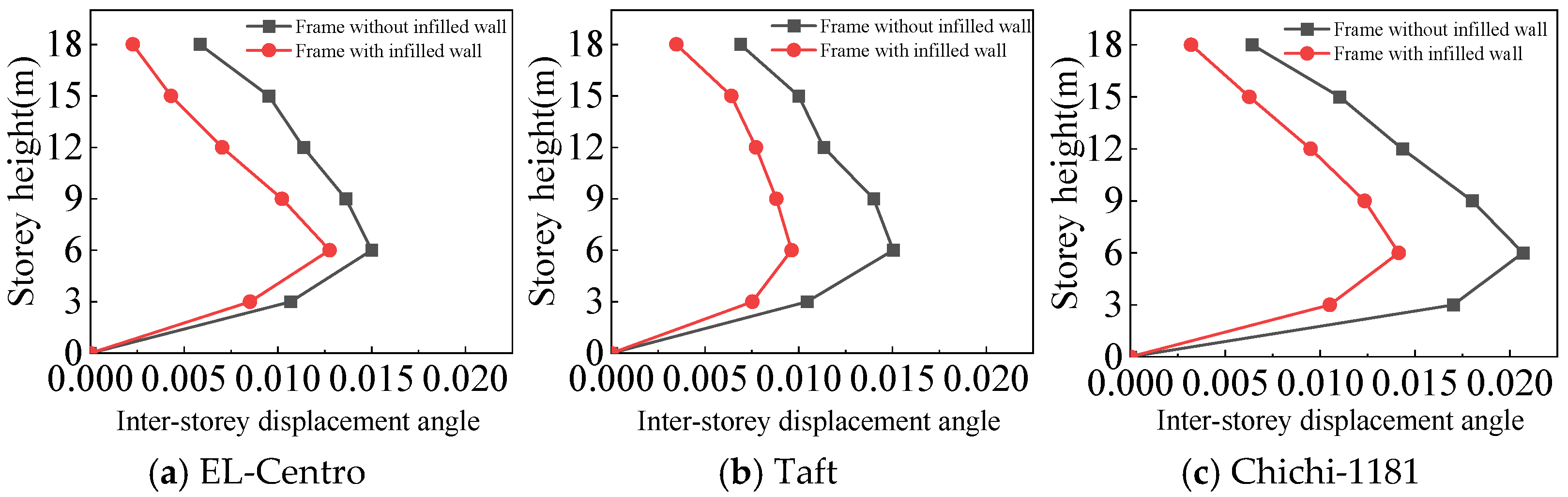
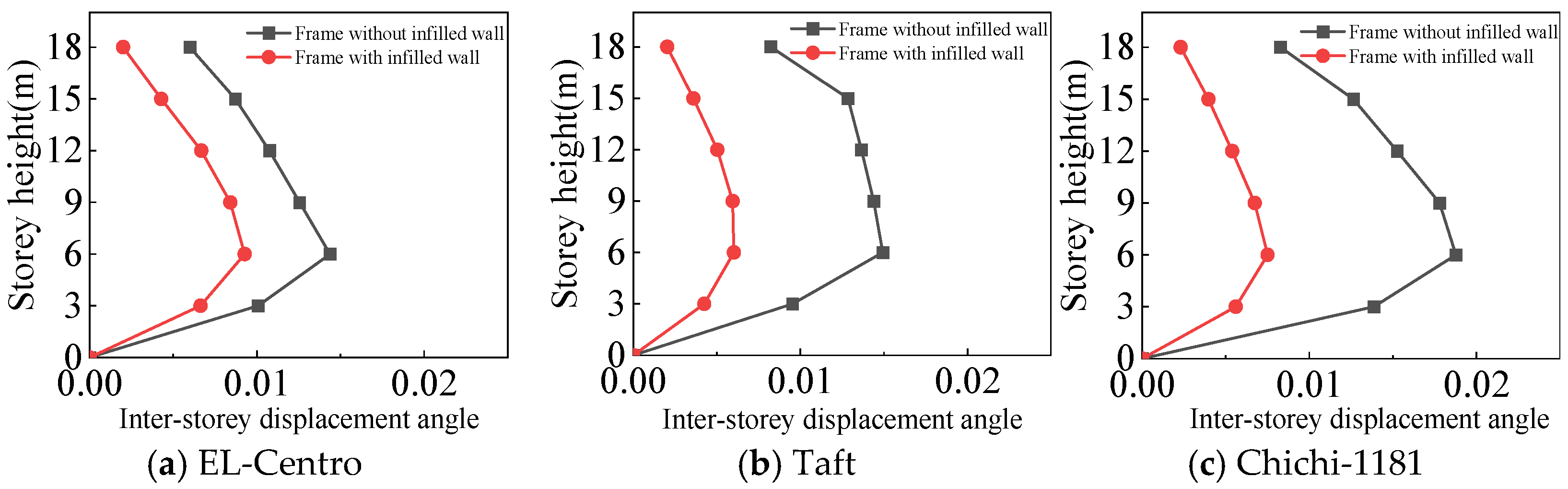
4.3.1. Lateral Displacement of the Structures
- (1)
- For the frame with infilled wall, because the doors and windows are set in the X-direction, the stiffness of the X-direction of the model is lower. The lateral displacement of the top floor in the X-direction is greater than that in the Y-direction under frequent and rare earthquakes. This corresponds to the fact that the X-direction translational natural vibration period from the structural modal analysis is greater than that in the Y-direction.
- (2)
- Both the frame with infilled wall and frame without infilled wall show shear-type deformation under all three seismic wave time history analyses. Horizontal lateral displacement increases with increasing earthquake intensity for both frames. In the same situation, the lateral displacement of each floor of the frame with infilled wall is always smaller than that of the frame without infilled wall. Comparisons show that the maximum lateral displacements of the top floor of the frame with infilled wall are 11–71% lower than those of the frame without infilled wall, which indicates that the infilled wall increases the horizontal lateral stiffness of the structure.
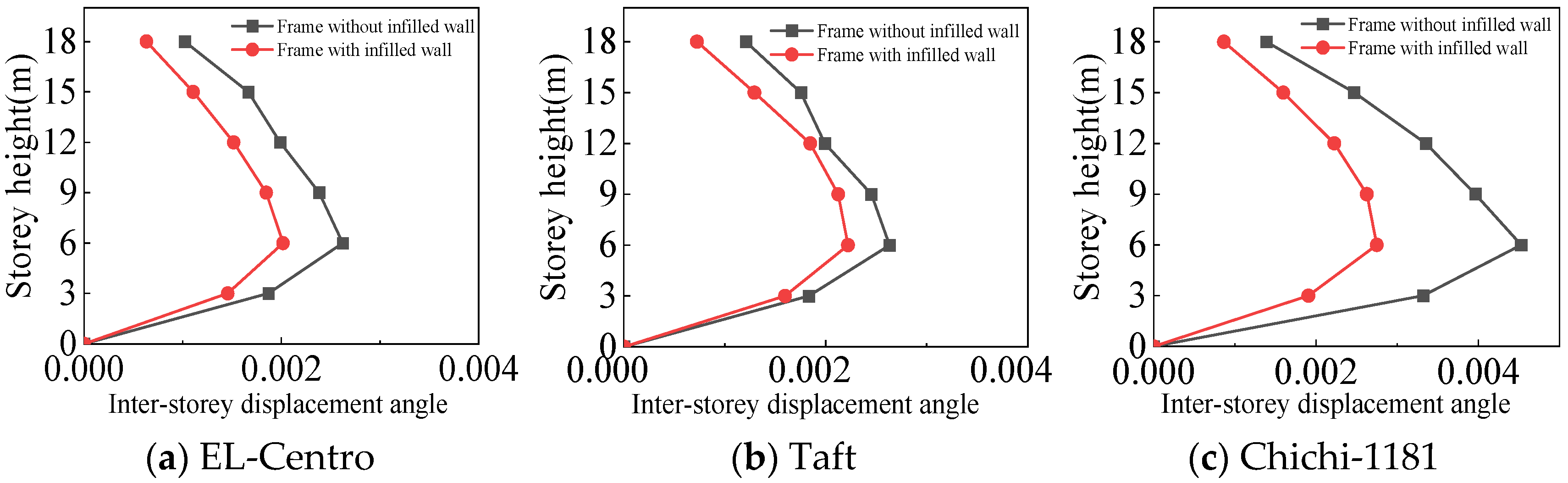
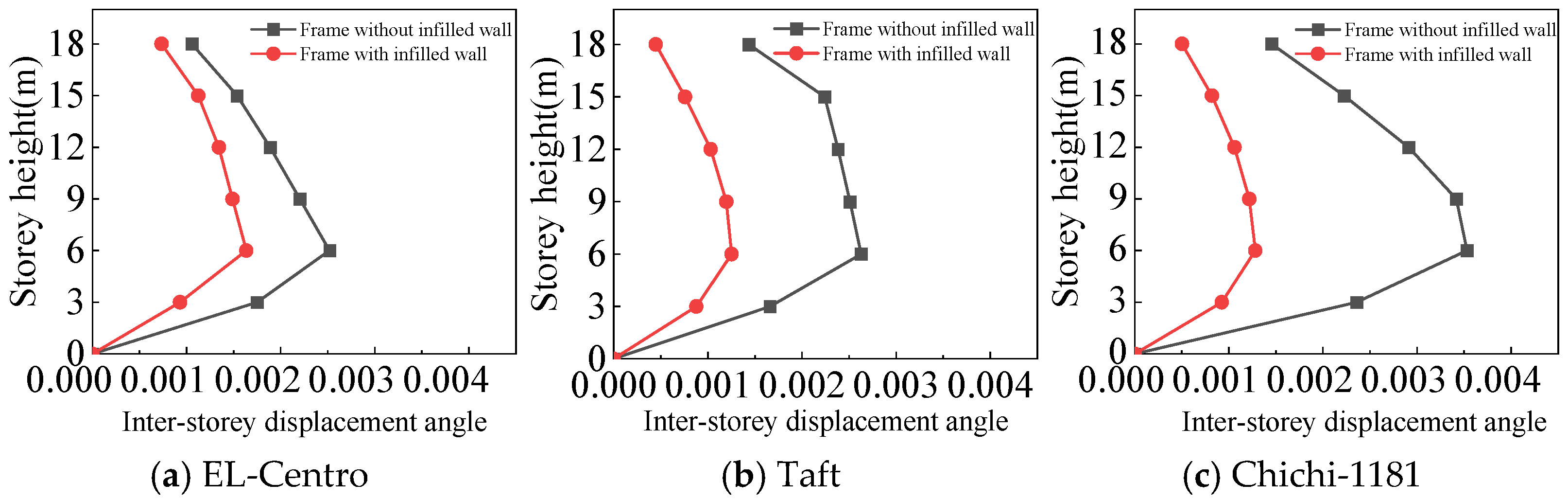
4.3.2. Inter-Story Displacement Angle
- (1)
- The maximum inter-story displacement angle occurs in the second floor for both frames under frequent and rare earthquakes. This indicates that the second floor is the weak floor for both frames.
- (2)
- The inter-story displacement angle of the frame with infilled wall under the same situation is smaller than that of the frame without infilled wall. The maximum inter-story displacement angle of the frame with infilled wall is 15–67% lower than that of the frame without infilled wall.
- (3)
- The code for the seismic design of buildings [31] stipulates that the elastic inter-story displacement angle limit for multi-story structures under frequent earthquakes is 1/250, and under rare earthquakes it is 1/50. The maximum inter-story displacement angle of the frame with infilled wall is 1/364 under frequent earthquakes, and the maximum inter-story displacement angle of the frame with infilled wall is 1/71 under rare earthquakes, which satisfies the requirements of the code for the seismic design of buildings [31].
4.3.3. Base Shear
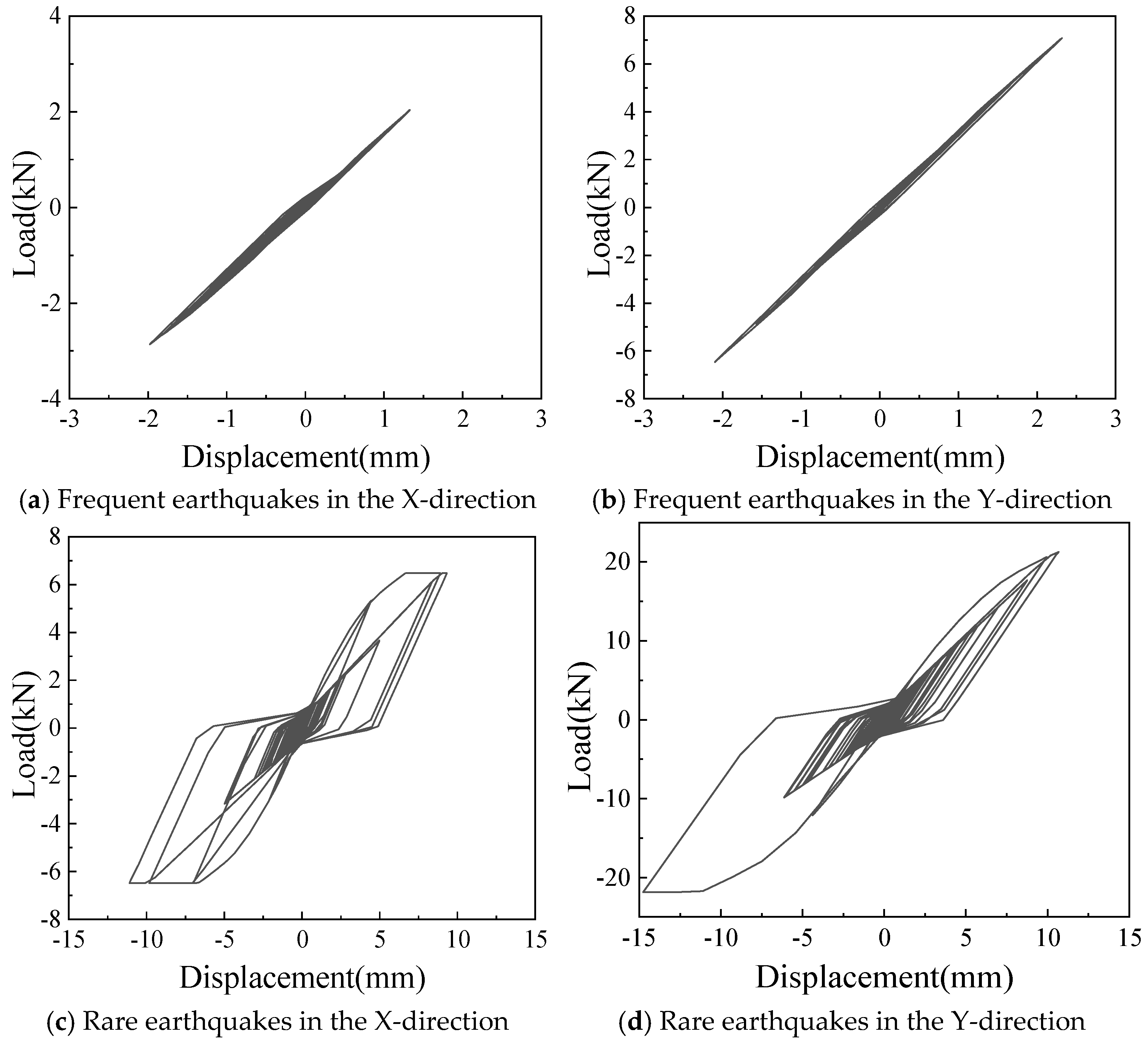
4.3.4. Performance Analysis of Wall Components
5. Conclusions
- (1)
- Both the fine model with screw connection details and the simplified model using the equivalent spring method established in this paper can well simulate the deformation of the modular CFS shear wall under lateral low cyclic loading, reflecting the same characteristics of the pinch effect. The yield and peak load, as well as yield and peak displacement, calculated by the two models are in good agreement with the test. Although the calculation accuracy of the simplified model is slightly lower than that of the fine model, it greatly simplifies the calculation and is more suitable for the subsequent analysis of multi-story building structures.
- (2)
- Both the frame with infilled wall and frame without infilled wall show shear-type deformation under the same horizontal seismic force. It is shown that the maximum lateral displacements of the top floor of the six-story frame with infilled wall are 11–71% lower than those of the frame without infilled wall, and the maximum inter-story displacement angles were reduced by 15–67%, which indicates that the infilled wall effectively increases the horizontal lateral stiffness of the structure.
- (3)
- Under frequent earthquake conditions, both of the frames with and without infilled walls are in the elastic state, while under rare earthquake conditions, the modular CFS shear wall is in the plastic state and participates plastic energy dissipation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFS | Cold-formed steel |
| OSB | Oriented strand board |
| RCFS | Reinforced cold-formed steel |
References
- Shi, Y.; Luo, Z.Q.; Xu, Y.P.; Zou, Y.X.; Xu, L.; Ma, Q.T. Experimental study on the seismic behavior of high-performance cold-formed steel plate shear walls. Eng. Struct. 2022, 251, 113552. [Google Scholar] [CrossRef]
- Pan, C.L.; Shan, M.Y. Monotonic shear tests of cold formed steel wall frames with sheathing. Thin-Walled Struct. 2011, 49, 363–370. [Google Scholar] [CrossRef]
- Baran, E.; Alica, C. Behavior of cold-formed steel wall panels under monotonic horizontal loading. J. Constr. Steel Res. 2012, 79, 1–8. [Google Scholar] [CrossRef]
- Yu, C. Shear resistance of cold-formed steel framed shear walls with 0.686 mm, 0.762 mm, and 0.838 mm steel sheet sheathing. Eng. Struct. 2010, 32, 1522–1529. [Google Scholar] [CrossRef]
- Yu, C.; Chen, Y.J. Detailing recommendations for 1.83 m wide cold-formed steel shear walls with steel sheathing. J. Constr. Steel Res. 2011, 67, 93–101. [Google Scholar] [CrossRef]
- Jiang, L.Q.; Zhang, X.S.; Hu, Y.; Liu, R.Q.; Jiang, L.Z. Experimental study of novel wrapped CFRP-strengthened CFS-to-sheathing screw connections. Thin-Walled Struct. 2023, 192, 111161. [Google Scholar] [CrossRef]
- Yu, C.; Tian, Y.; Yan, W.M.; Zhang, W.Y. Novel energy dissipation bracing designed for corrugated sheet-sheathed cold-formed steel shear wall. J. Struct. Eng. 2021, 147, 04021171. [Google Scholar] [CrossRef]
- Yao, X.M.; Zou, Y.X.; Zhou, Z.M.; Hou, S.Q.; Zhou, X.H.; Shi, Y.; Xiang, Y.; Guan, Y. Experimental study on the shear behavior of cold-formed steel clamped thin steel plate shear walls and screw connections. Eng. Struct. 2025, 338, 120550. [Google Scholar] [CrossRef]
- Ye, J.H.; Jiang, L.Q.; Wang, X.X. Seismic Failure Mechanism of Reinforced Cold-Formed Steel Shear Wall System Based on Structural Vulnerability Analysis. Appl. Sci. 2017, 7, 182. [Google Scholar] [CrossRef]
- Usefi, N.; Sharafi, P.; Ronagh, H. Numerical models for lateral behaviour analysis of cold-formed steel framed walls: State of the art, evaluation and challenges. Thin-Walled Struct. 2019, 138, 252–285. [Google Scholar] [CrossRef]
- Fiorino, L.; Shakeel, S.; Macillo, V.; Landolfo, R. Behaviour factor (q) evaluation the CFS braced structures according to FEMA P695. J. Constr. Steel Res. 2017, 138, 324–339. [Google Scholar] [CrossRef]
- Fiorino, L.; Shakeel, S.; Macillo, V.; Landolfo, R. Seismic response of CFS shear walls sheathed with nailed gypsum panels: Numerical modelling. Thin-Walled Struct. 2018, 122, 359–370. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Mahdavian, M.; Yu, C. Lateral strength and deflection of cold-formed steel shear walls using corrugated sheathing. J. Constr. Steel Res. 2018, 148, 399–408. [Google Scholar] [CrossRef]
- Kechidi, S.; Bourahla, N. Deteriorating hysteresis model for cold-formed steel shear wall panel based on its physical and mechanical characteristics. Thin-Walled Struct. 2016, 98, 421–430. [Google Scholar] [CrossRef]
- Kechidi, S.; Macedo, L.; Castro, J.M.; Bourahla, N. Seismic risk assessment of cold-formed steel shear wall systems. J. Constr. Steel Res. 2017, 138, 565–579. [Google Scholar] [CrossRef]
- Kechidi, S.; Bourahla, N.; Castro, J.M. Seismic design procedure for cold-formed steel sheathed shear wall frames: Proposal and evaluation. J. Constr. Steel Res. 2017, 128, 219–232. [Google Scholar] [CrossRef]
- Ashok, J.; Jayachandran, S.A. Cold formed steel shear wall racking analysis through a mechanistic approach: Cfs-rama. Adv. Steel Constr. 2022, 18, 648–657. [Google Scholar]
- Wang, X.; Wang, W.; Li, Y.C. Cyclic performance of K-braced cold-formed steel shear walls with concrete-filled steel-tubular struts. J. Constr. Steel Res. 2020, 173, 106249. [Google Scholar]
- Xie, Z.Q.; Fan, Y.; Zhang, W.Y.; Lei, X.Y.; Su, M.N.; Zhou, D.X.; Zhang, X.D. Seismic performance of hybrid-connection CFS shear walls with self-piercing rivet and self-tapping screw. Thin-Walled Struct. 2024, 204, 112228. [Google Scholar] [CrossRef]
- Wu, J.C.; Rogers, C.A. Cold-formed steel centre-sheathed (mid-ply) shear walls of intermediate resistance. Thin-Walled Struct. 2023, 188, 110834. [Google Scholar] [CrossRef]
- Bao, W.; Jiang, J.; Shao, Y.S.; Liu, Y. Experimental study of the lateral performance of a steel stud wall with a semi-rigid connected frame. Eng. Struct. 2019, 183, 677–689. [Google Scholar] [CrossRef]
- Zhang, W.Y.; Lan, X.; Mahdavian, M.; Yu, C. Seismic performance cold-Formed steel framed shear walls using in-Frame corrugated steel sheathing. Adv. Struct. Eng. 2023, 26, 1988–2005. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Shi, Y.Z.; Cao, W.L.; Dong, H.Y.; Bian, J.L. Seismic behavior of lightweight steel frame with thin-walled steel skeleton-lightweight concrete wall. J. Constr. Steel Res. 2024, 222, 109003. [Google Scholar] [CrossRef]
- Wang, W.Q.; Wang, J.F.; Zhao, P.; Cheng, J.; Guo, L.; Hu, P.F. Seismic performance investigation on assembled steel frame structure with LEM-filled CFS shear wall. Structures 2025, 79, 109554. [Google Scholar] [CrossRef]
- Hu, P.; Liu, Y.; Wang, J.; Wang, W.; Pan, G. Experimental Investigation and Numerical Analyses on Cyclic Behavior of the Prefabricated Concrete Frame Infilled with CFS-CLPM Composite Walls. Buildings 2022, 12, 1991. [Google Scholar] [CrossRef]
- Wu, F.W.; Li, Y.Q. Large-scale shaking table tests of a six-story floor-by-floor assembled CFS frame-framing shear wall structure. Eng. Struct. 2023, 293, 116608. [Google Scholar] [CrossRef]
- Wu, H.H.; Tu, T.T.; Lu, S.; Yan, F.; Zhou, T.H. A novel modular CFS composite frame-wall structure: Experimental investigation and numerical analysis. J. Constr. Steel Res. 2024, 218, 108702. [Google Scholar] [CrossRef]
- Hu, M. Investigation on the Lateral Resistance of New-Type Prefabricated Steel Framed Composite Wall. Master’s Thesis, Central South University, Changsha, China, 2021. (In Chinese). [Google Scholar]
- Wang, L.P.; Wu, X.Y.; Hu, M. Analysis of lateral resistance performance of a novel prefabricated cold-formed thin-walled steel framed wall. J. Southeast Univ. 2024, 54, 135–141. (In Chinese) [Google Scholar]
- Li, Y.Q.; Ma, R.K.; Shen, Z.Y. Numerical simulation on dynamic behavior of a cold formed steel framing building test model. In Proceedings of the 22nd International Specialty Conference on Cold-Formed Steel Structures, St. Louis, MO, USA, 5–6 November 2014. [Google Scholar]
- GB/T 50011-2010; Code for Seismic Design of Buildings. China Construction Industry Press: Beijing, China, 2010.

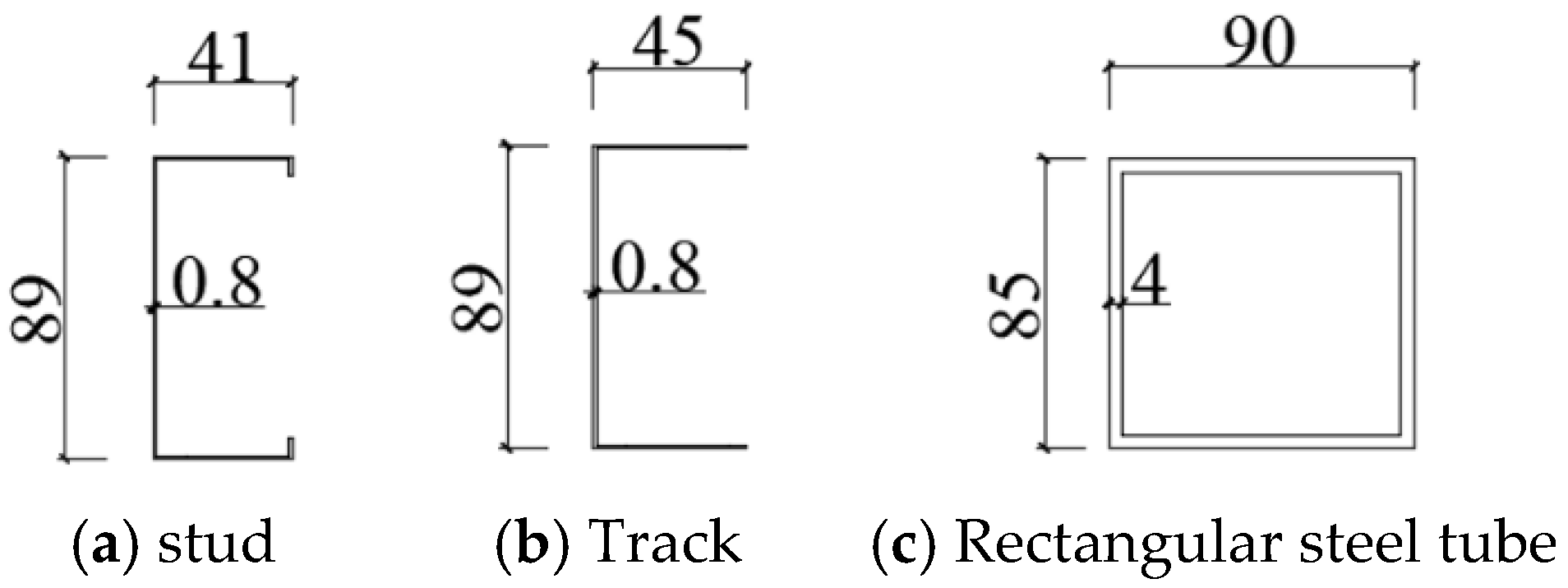


| Specimen Number | Sheathing Materials | Number of Sheathing | Sheathing Thickness (mm) | Keel Spacing (mm) |
|---|---|---|---|---|
| W-400-OS | OSB | 1 | 11 | 400 |
| W-600-OS | OSB | 1 | 11 | 600 |
| W-400-OD | OSB | 2 | 11 | 400 |
| W-600-OD | OSB | 2 | 11 | 600 |
| Specimen Number | Yield Point | Peak Point | Ductility Factor | ||
|---|---|---|---|---|---|
| Py (kN) | Δy (mm) | Pmax (kN) | Δmax (mm) | μ | |
| W-400-OS | 32.83 | 15.07 | 38.19 | 16.70 | 1.11 |
| W-400-OD | 65.36 | 16.92 | 73.30 | 20.30 | 1.20 |
| W-600-OS | 34.02 | 16.40 | 35.17 | 18.58 | 1.13 |
| W-600-OD | 61.89 | 15.72 | 74.20 | 18.03 | 1.15 |
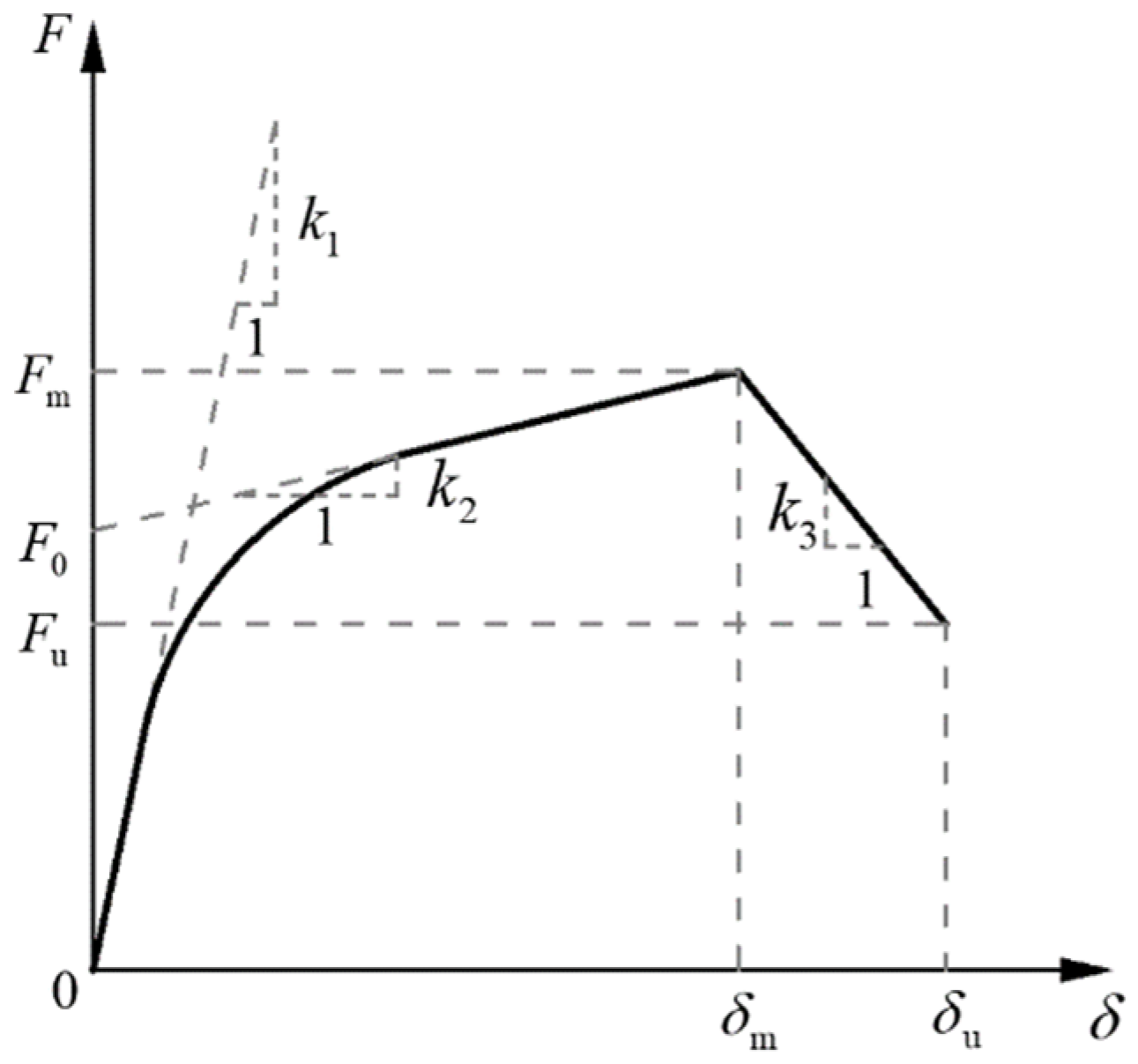
| Control Parameters | K1 (kN/mm2) | K2 (kN/mm2) | K3 (kN/mm2) | F0 (kN) | δm (mm) | δu (mm) |
|---|---|---|---|---|---|---|
| selection value | 1.869 | 0.098 | −0.125 | 1.224 | 6.6 | 18.6 |
| Specimen | Item | Yield Point | Peak Point | Ductility Factor | ||
|---|---|---|---|---|---|---|
| Py (kN) | Δy (mm) | Pmax (kN) | Δmax (mm) | μ | ||
| W-400-OS | Test | 32.83 | 15.07 | 38.19 | 16.70 | 1.11 |
| Fine model | 29.82 | 13.19 | 33.66 | 17.13 | 1.29 | |
| Ratio | 0.91 | 0.88 | 0.88 | 1.03 | 1.16 | |
| W-400-OD | Test | 65.36 | 16.92 | 73.30 | 20.30 | 1.20 |
| Fine model | 66.30 | 15.34 | 75.44 | 20.02 | 1.30 | |
| Ratio | 1.01 | 0.91 | 1.03 | 0.99 | 1.08 | |
| W-600-OS | Test | 34.02 | 16.40 | 35.17 | 18.58 | 1.13 |
| Fine model | 31.10 | 14.38 | 35.56 | 19.12 | 1.32 | |
| Ratio | 0.91 | 0.88 | 1.01 | 1.03 | 1.17 | |
| W-600-OD | Test | 61.89 | 15.72 | 74.20 | 18.03 | 1.15 |
| Fine model | 61.86 | 13.92 | 69.97 | 18.31 | 1.29 | |
| Ratio | 1.00 | 0.89 | 0.94 | 1.02 | 1.12 |
| Specimen Number | Item | Yield Point | Peak Point | Ductility Factor | ||
|---|---|---|---|---|---|---|
| Py (kN) | Δy (mm) | Pmax (kN) | Δmax (mm) | μ | ||
| W-400-OS | Test | 32.83 | 15.07 | 38.19 | 16.70 | 1.11 |
| Simplified model | 30.90 | 12.77 | 34.63 | 17.00 | 1.33 | |
| Ratio | 0.94 | 0.85 | 0.91 | 1.02 | 1.20 | |
| W-400-OD | Test | 65.36 | 16.92 | 73.30 | 20.30 | 1.20 |
| Simplified model | 65.71 | 14.51 | 73.89 | 20.01 | 1.38 | |
| Ratio | 1.01 | 0.86 | 1.01 | 0.99 | 1.15 | |
| W-600-OS | Test | 34.02 | 16.40 | 35.17 | 18.58 | 1.13 |
| Simplified model | 32.24 | 13.83 | 36.26 | 19.23 | 1.37 | |
| Ratio | 0.95 | 0.84 | 1.03 | 1.03 | 1.21 | |
| W-600-OD | Test | 61.89 | 15.72 | 74.20 | 18.03 | 1.15 |
| Simplified model | 60.65 | 13.17 | 67.98 | 18.12 | 1.37 | |
| Ratio | 0.98 | 0.84 | 0.92 | 1.00 | 1.19 |
| Model | Mode | Natural Vibration Period (s) | Vibration Mode |
|---|---|---|---|
| Frame without infilled wall | No. 1 | 1.254 | Y |
| No. 2 | 1.139 | X | |
| No. 3 | 1.086 | RotZ | |
| Frame with infilled wall | No. 1 | 0.867 | X |
| No. 2 | 0.541 | Y | |
| No. 3 | 0.530 | RotZ |
| Seismic Wave | Direction | Types | Lateral Displacement (mm) | ||
|---|---|---|---|---|---|
| Frame Without Infilled Wall | Frame with Infilled Wall | Reduction Ratio | |||
| EL-Centro | X | Frequently | 31.57 | 25.73 | 18% |
| X | Rarely | 180.57 | 139.40 | 23% | |
| Y | Frequently | 29.83 | 20.86 | 30% | |
| Y | Rarely | 170.03 | 111.80 | 34% | |
| Taft | X | Frequently | 32.91 | 29.41 | 11% |
| X | Rarely | 187.65 | 133.60 | 29% | |
| Y | Frequently | 36.49 | 12.83 | 65% | |
| Y | Rarely | 208.90 | 62.05 | 70% | |
| Chichi-1181 | X | Frequently | 54.94 | 35.92 | 35% |
| X | Rarely | 247.32 | 167.90 | 32% | |
| Y | Frequently | 46.62 | 13.39 | 71% | |
| Y | Rarely | 247.57 | 72.65 | 71% | |
| Seismic Wave | Direction | Types of Earthquake | Inter-Story Displacement Angle | ||
|---|---|---|---|---|---|
| Frame Without Infilled Wall | Frame with Infilled Wall | Reduction Ratio | |||
| EL-Centro | X | Frequent | 1/381 | 1/495 | 23% |
| X | Rare | 1/66 | 1/78 | 15% | |
| Y | Frequent | 1/397 | 1/613 | 35% | |
| Y | Rare | 1/70 | 1/108 | 35% | |
| Taft | X | Frequent | 1/380 | 1/450 | 16% |
| X | Rare | 1/67 | 1/104 | 36% | |
| Y | Frequent | 1/381 | 1/799 | 52% | |
| Y | Rare | 1/67 | 1/166 | 60% | |
| Chichi-1181 | X | Frequent | 1/251 | 1/364 | 31% |
| X | Rare | 1/58 | 1/71 | 18% | |
| Y | Frequent | 1/258 | 1/781 | 67% | |
| Y | Rare | 1/53 | 1/133 | 60% | |
| Seismic Wave | Direction | Types of Earthquake | Base Shear (KN) | ||
|---|---|---|---|---|---|
| Frame Without Infilled Wall | Frame with Infilled Wall | Ratio | |||
| EL-Centro | X | Frequent | 1339.20 | 1923.87 | +44% |
| X | Rare | 7622.47 | 8461.52 | +11% | |
| Y | Frequent | 1192.75 | 2202.11 | +85% | |
| Y | Rare | 6759.51 | 10,026.35 | +48% | |
| Taft | X | Frequent | 1379.20 | 1951.27 | +41% |
| X | Rare | 7855.26 | 7764.40 | −1% | |
| Y | Frequent | 1090.74 | 2393.56 | +119% | |
| Y | Rare | 6188.23 | 9867.01 | +59% | |
| Chichi-1181 | X | Frequent | 2484.19 | 2318.96 | −7% |
| X | Rare | 9884.89 | 9354.02 | −5% | |
| Y | Frequent | 1615.33 | 2476.07 | +53% | |
| Y | Rare | 8562.47 | 11,587.39 | +35% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, Y.; Mei, J.; Wu, X.; Wang, L. Lateral Resistance of Modular CFS Shear Wall Connected with Rectangular Steel Tubes and Its Contribution to Frame Structures. Materials 2025, 18, 5257. https://doi.org/10.3390/ma18235257
Kang Y, Mei J, Wu X, Wang L. Lateral Resistance of Modular CFS Shear Wall Connected with Rectangular Steel Tubes and Its Contribution to Frame Structures. Materials. 2025; 18(23):5257. https://doi.org/10.3390/ma18235257
Chicago/Turabian StyleKang, Yanbo, Jiyuan Mei, Xinyu Wu, and Liping Wang. 2025. "Lateral Resistance of Modular CFS Shear Wall Connected with Rectangular Steel Tubes and Its Contribution to Frame Structures" Materials 18, no. 23: 5257. https://doi.org/10.3390/ma18235257
APA StyleKang, Y., Mei, J., Wu, X., & Wang, L. (2025). Lateral Resistance of Modular CFS Shear Wall Connected with Rectangular Steel Tubes and Its Contribution to Frame Structures. Materials, 18(23), 5257. https://doi.org/10.3390/ma18235257





