Influence of Surface Roughness on the Mechanical Behavior of Granular Material Under Triaxial Shear: A DEM Study
Abstract
1. Introduction
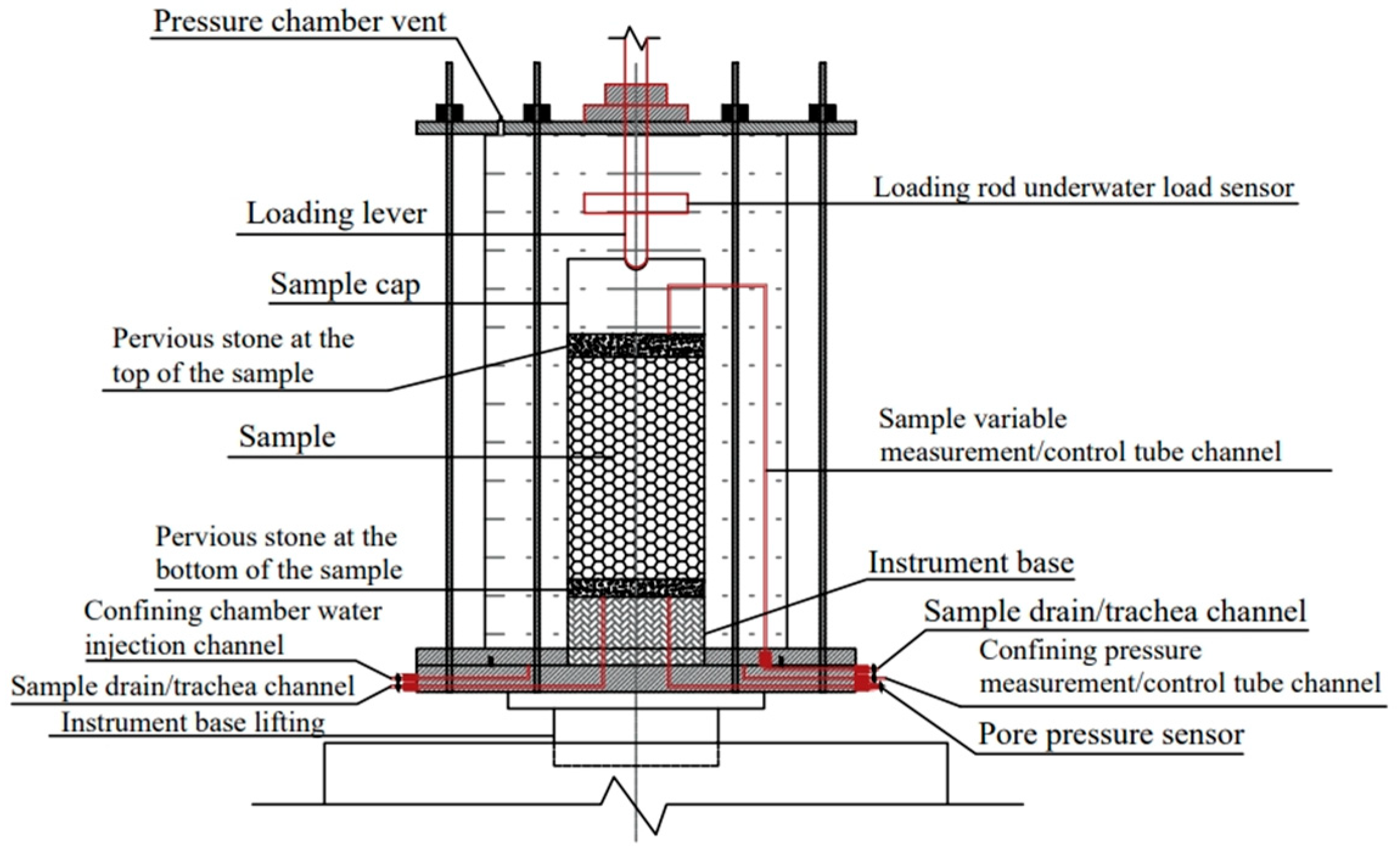
2. Experiment Test
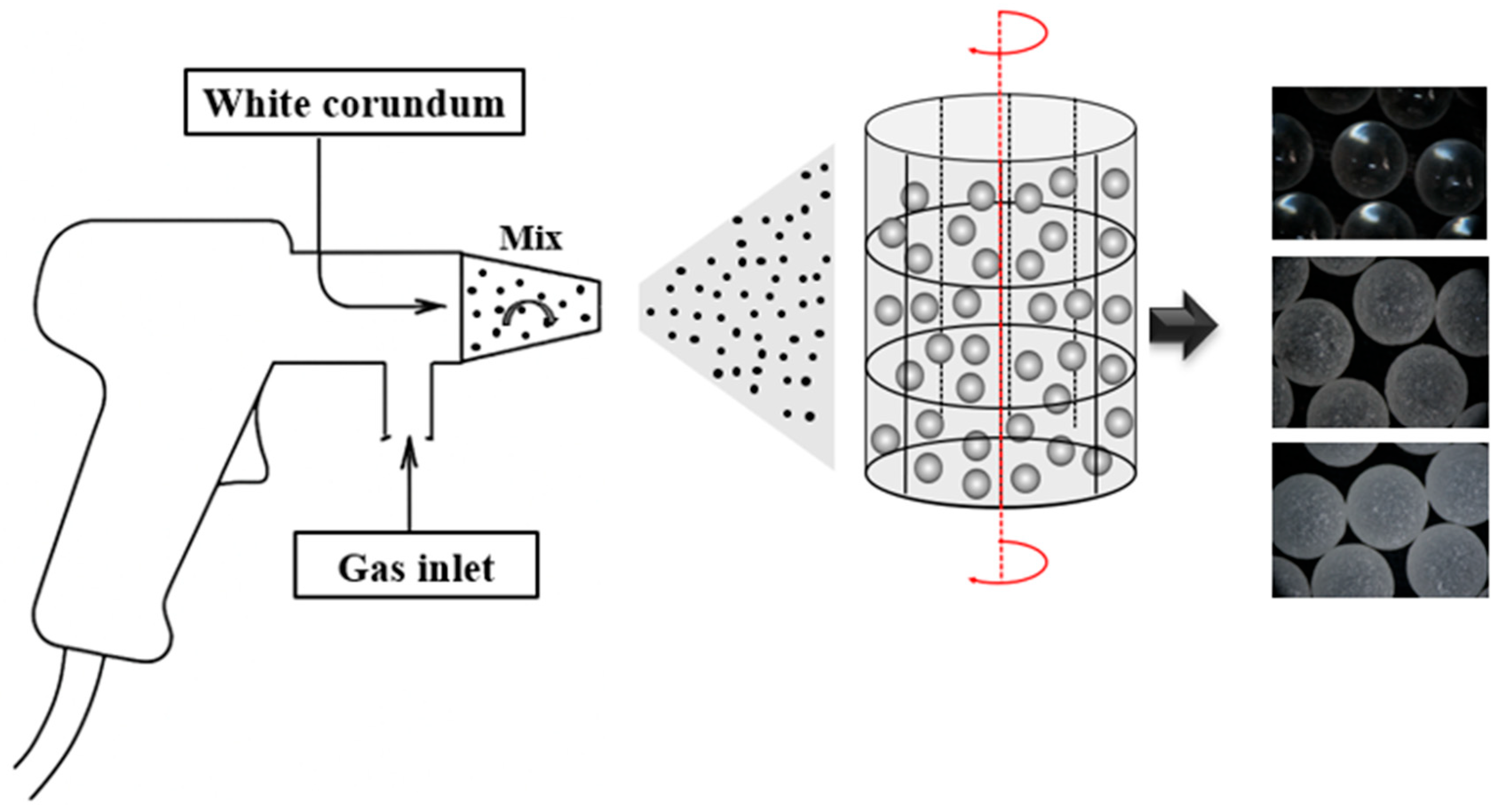
2.1. Materials
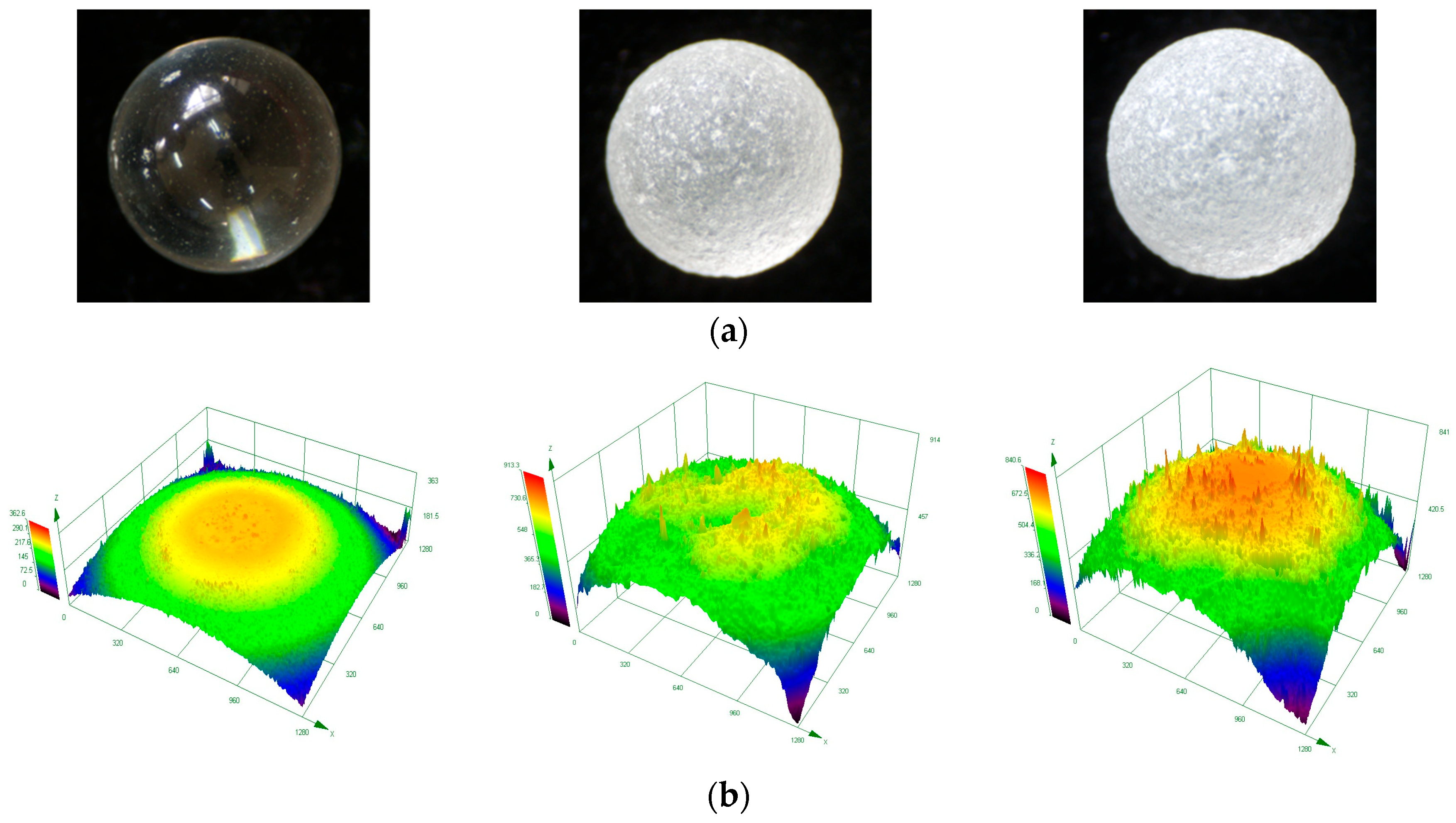
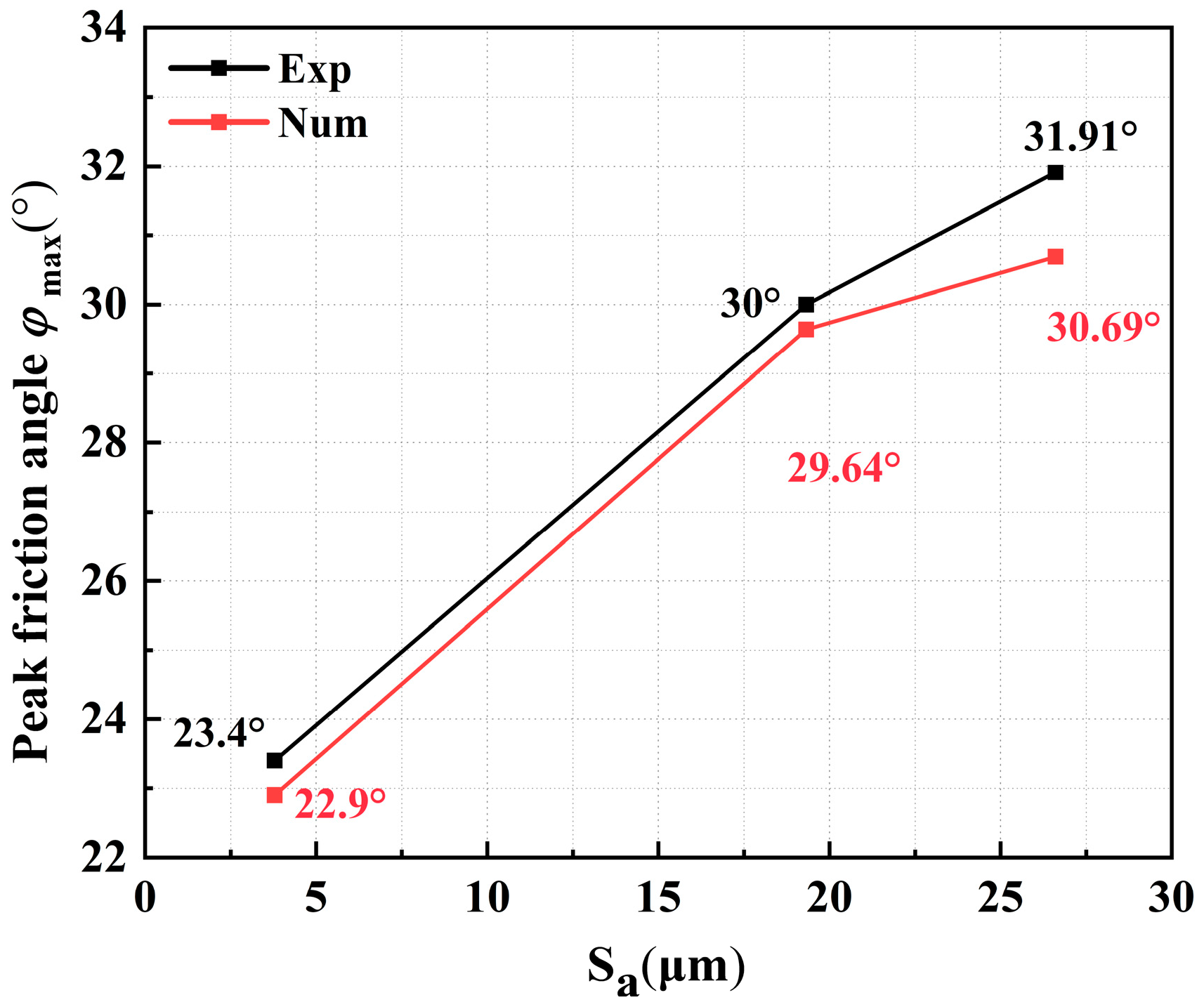
2.2. Characterization of Roughness
2.3. Test Program
- (1)
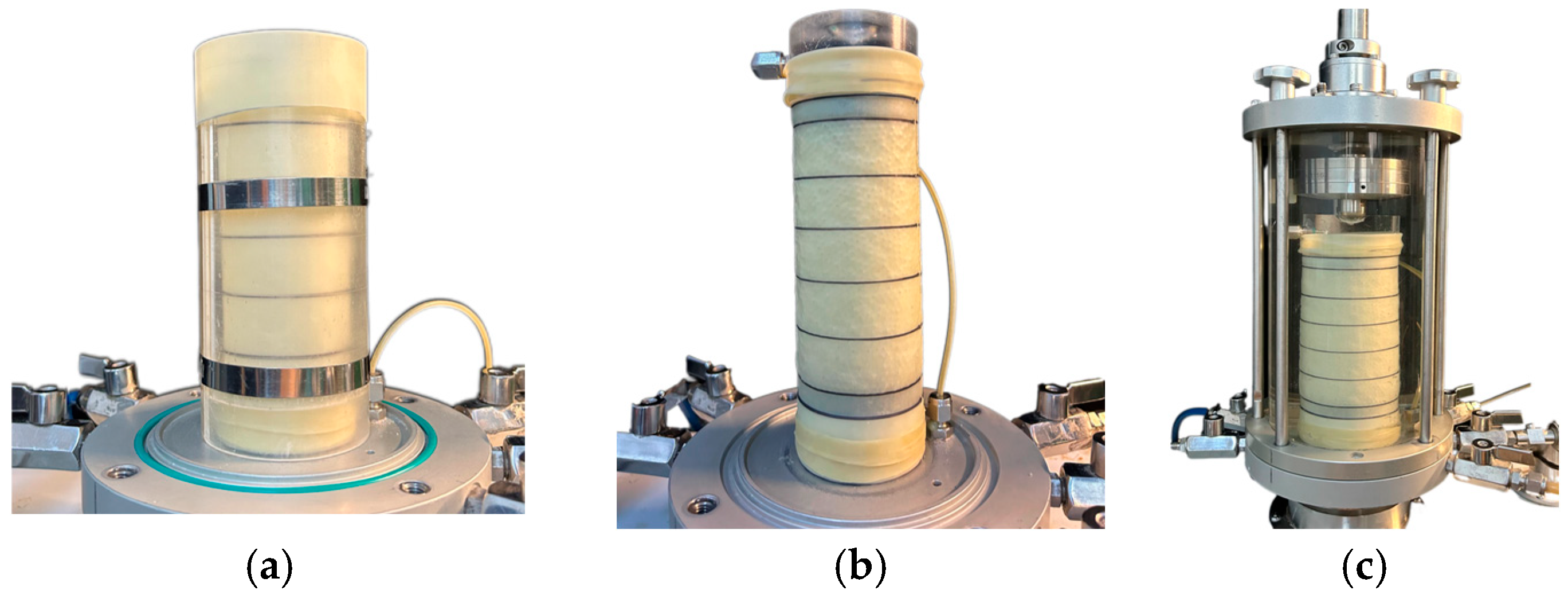
- A 0.5 mm-thick rubber membrane was placed inside the customized membrane-holding cylinder. Then, a vacuum pump was used to extract air from the suction port, causing the membrane to adhere to the cylinder wall. A permeable stone was positioned at the bottom as illustrated in Figure 4a.
- (2)
- The layered compaction method was employed to ensure sample density uniformity. The total sample mass, calculated based on the target void ratio, was divided into five equal portions. Each portion was sequentially placed into the rubber membrane. The surface of each layer was trimmed flush with scale marks on the membrane-holding cylinder using a scraper, following a “Z”-shaped path.
- (3)
- A negative pressure of 10 kPa was applied to the sample interior to maintain its cylindrical shape and prevent collapse after the membrane-holding cylinder was removed as shown in Figure 4b.
- (4)
- Finally, the pressure chamber was assembled, and the securing bolts were tightened to complete the experimental preparation as shown in Figure 4c.
3. DEM Simulation
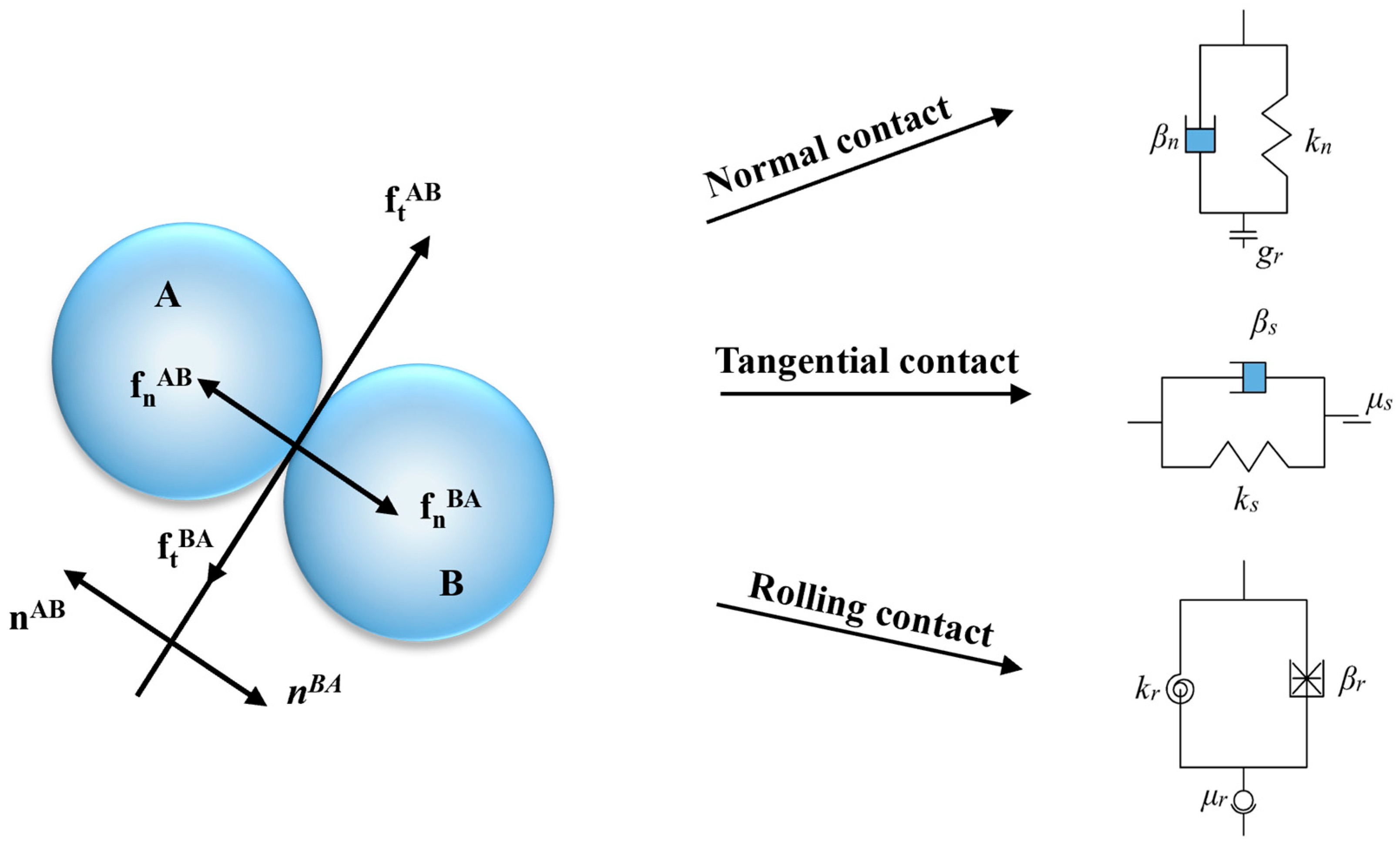
3.1. Contact Model
3.2. Parameters in DEM
3.3. Test Program in DEM
- (1)
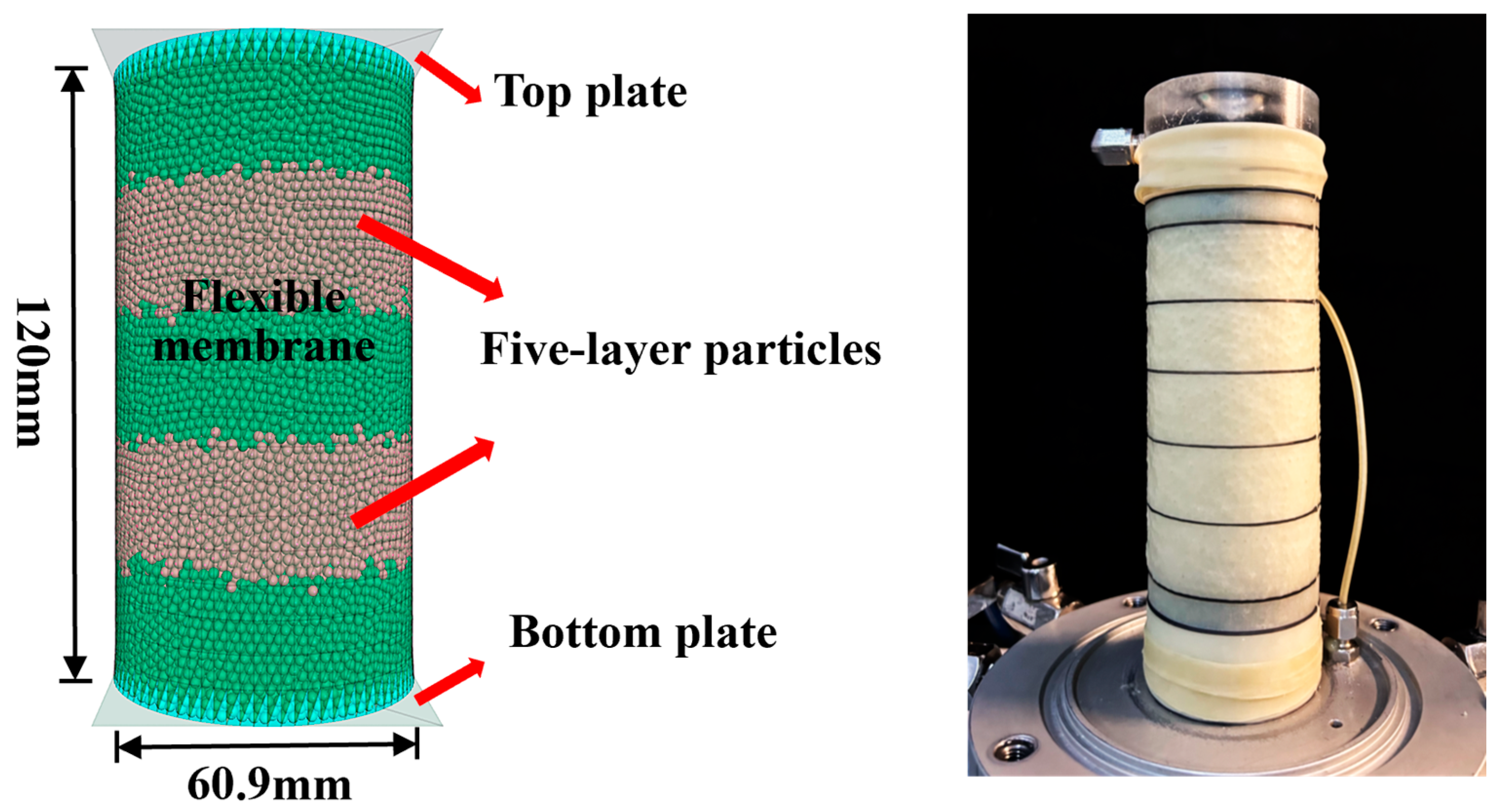
- In the sample generation, the multilayer compaction method was used to generate 53,704 particles within cylindrical rigid boundaries. The sample height was divided into five equal layers. Particles were deposited under gravity. The bottom wall was fixed for each layer, while the top wall position was dynamically adjusted. Interparticle damping and friction were utilized to dissipate residual unbalanced forces below the threshold (set to 1 × 10−3) until sample generation was completed.
- (2)
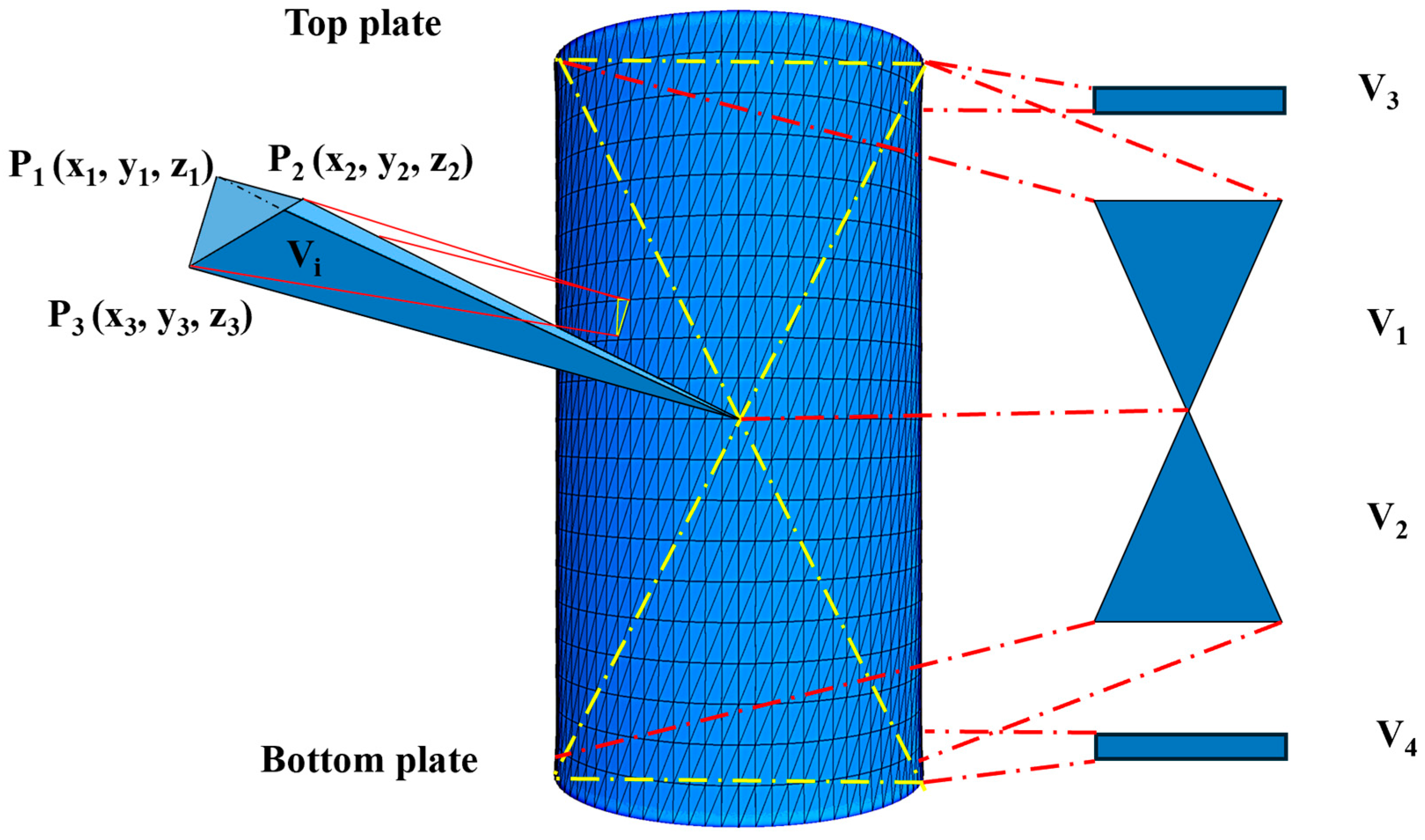
- The rigid wall elements in DEM were replaced with shell elements. The membrane was divided into 81 nodes in the circumferential direction and 20 segments of equal height along the axial direction to balance computational efficiency and membrane flexibility.
- (3)
- The simulation entered the isotropic consolidation.
- (4)
- In the shearing stage, three confining pressures (100 kPa, 200 kPa, and 300 kPa) and the shearing rate (0.24 mm/min) were similarly applied. The test was terminated when the axial strain reached 15%.
4. Results and Discussion
4.1. Calibration of Parameters
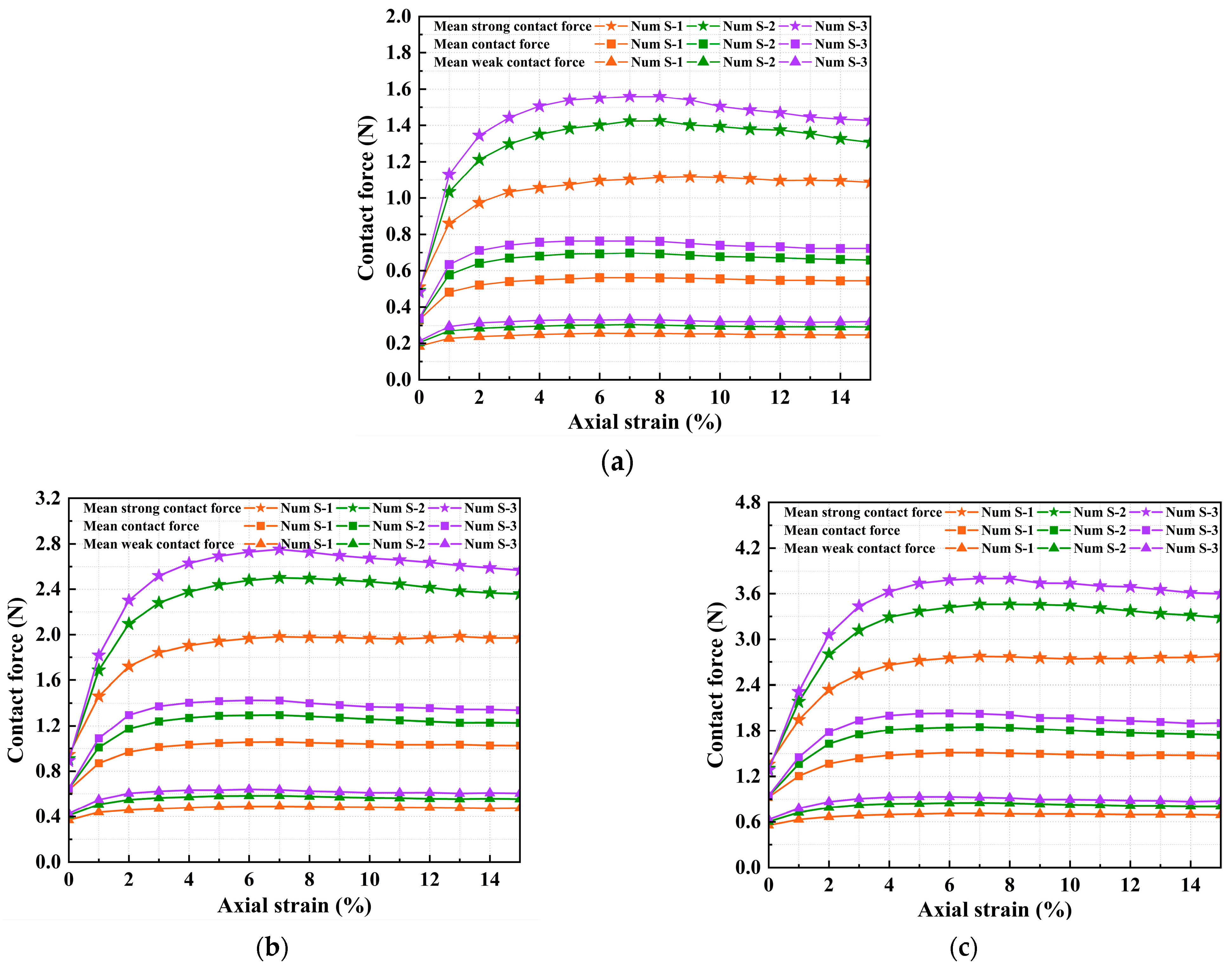
4.2. Influence of the Interparticle Friction Coefficients on Contact Forces
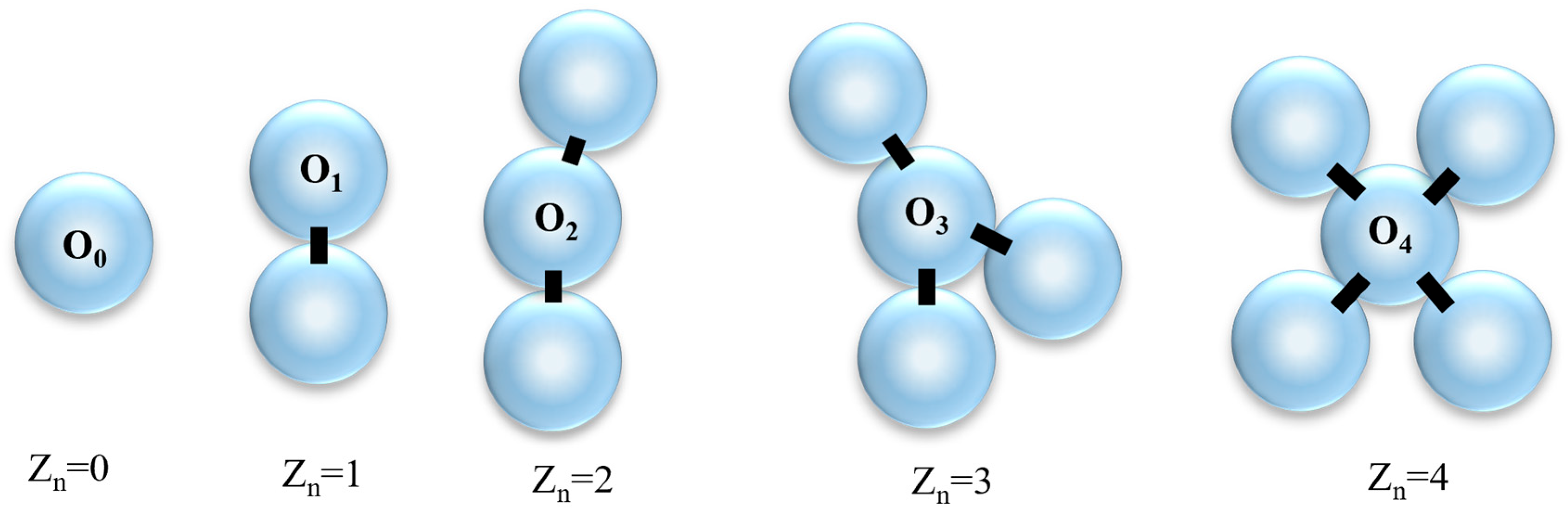
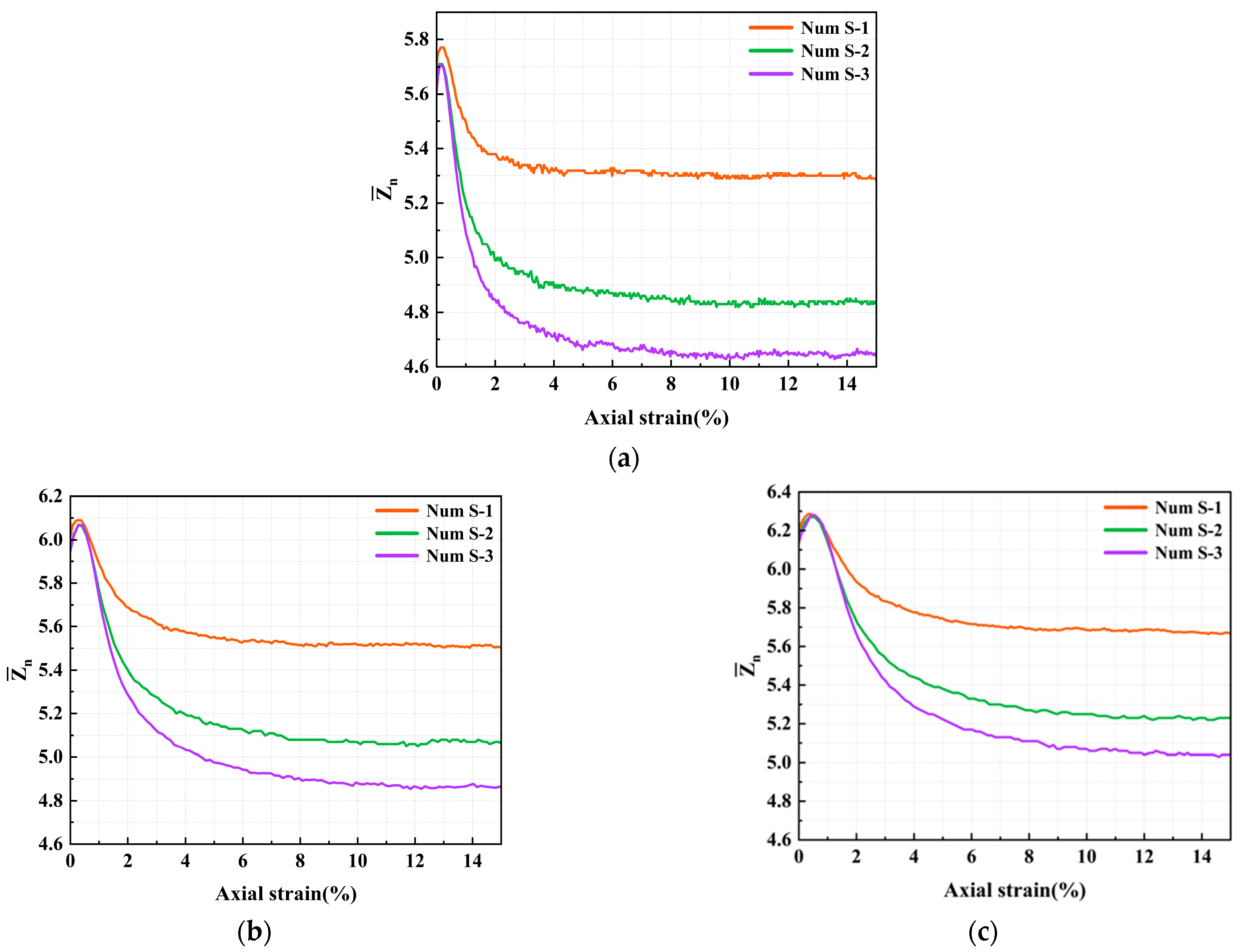
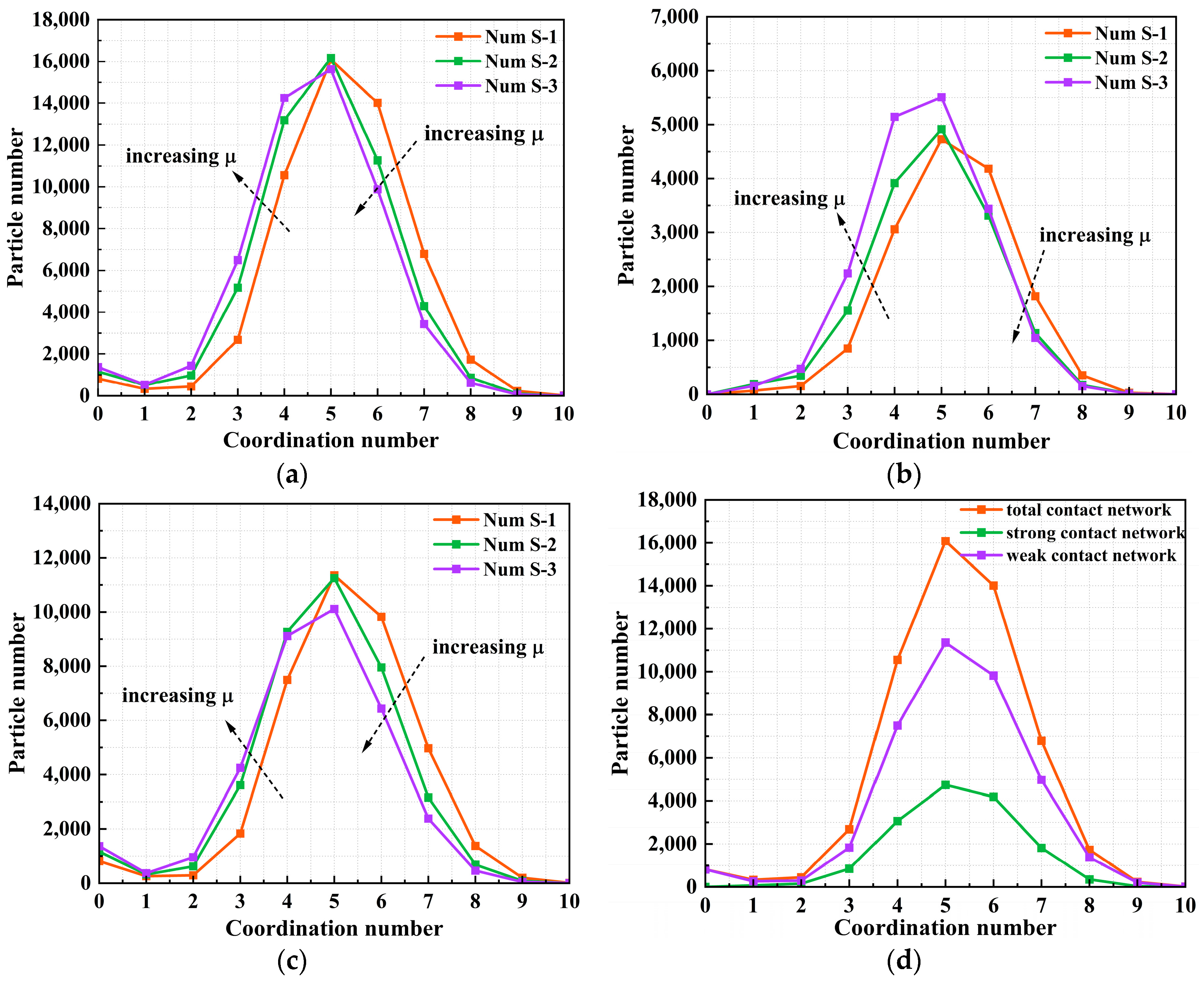
4.3. Influence of the Interparticle Friction Coefficients on the Coordination Number
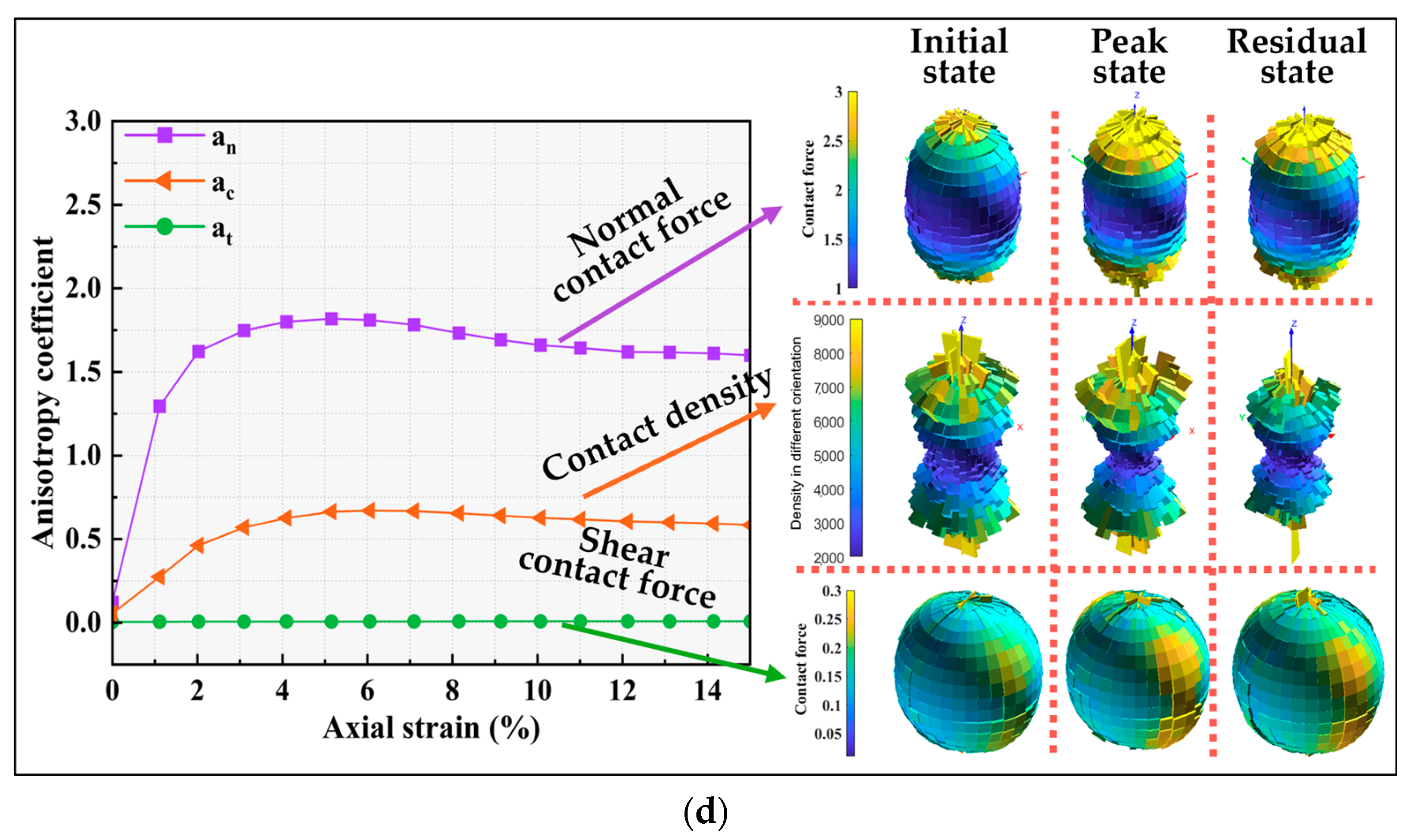
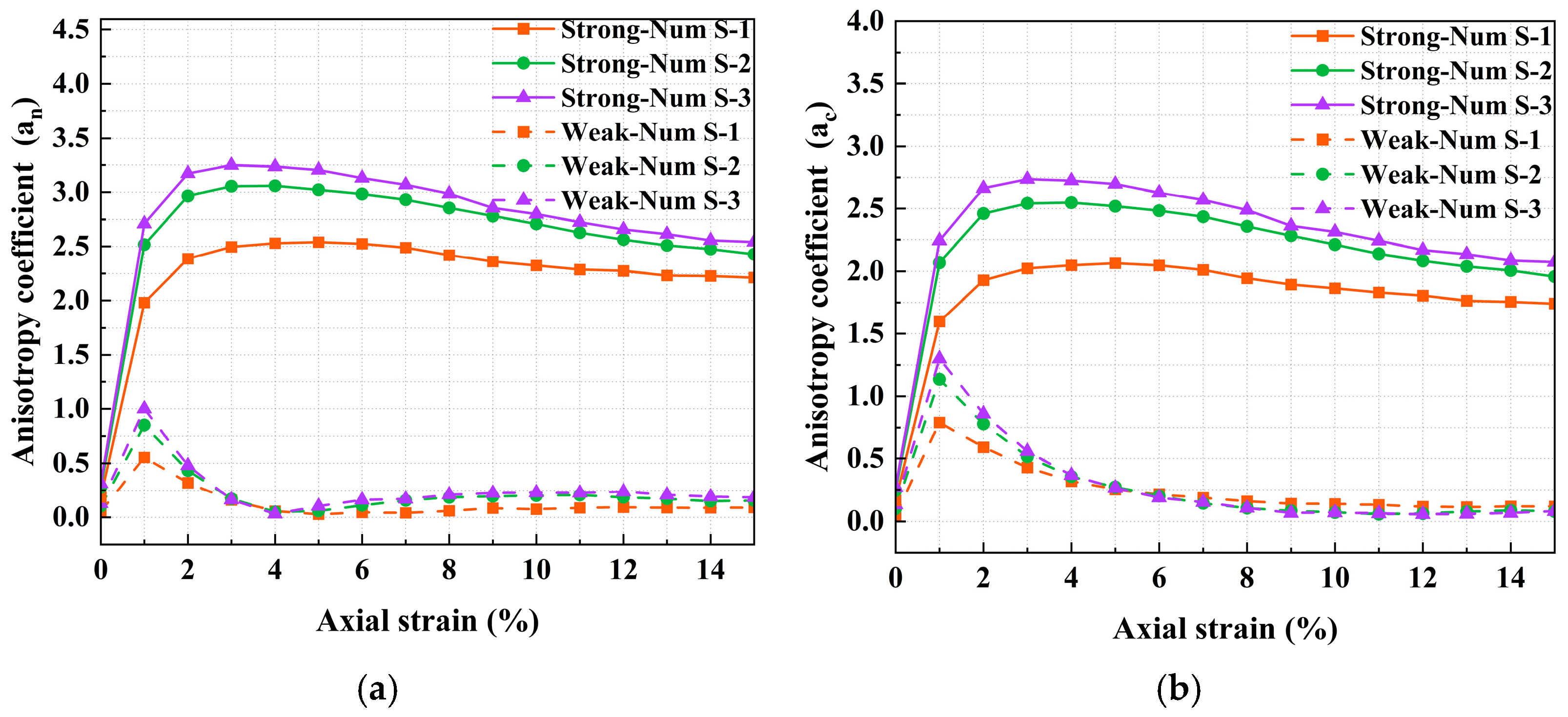
4.4. Influence of the Interparticle Friction Coefficients on Fabric Anisotropy
5. Conclusions
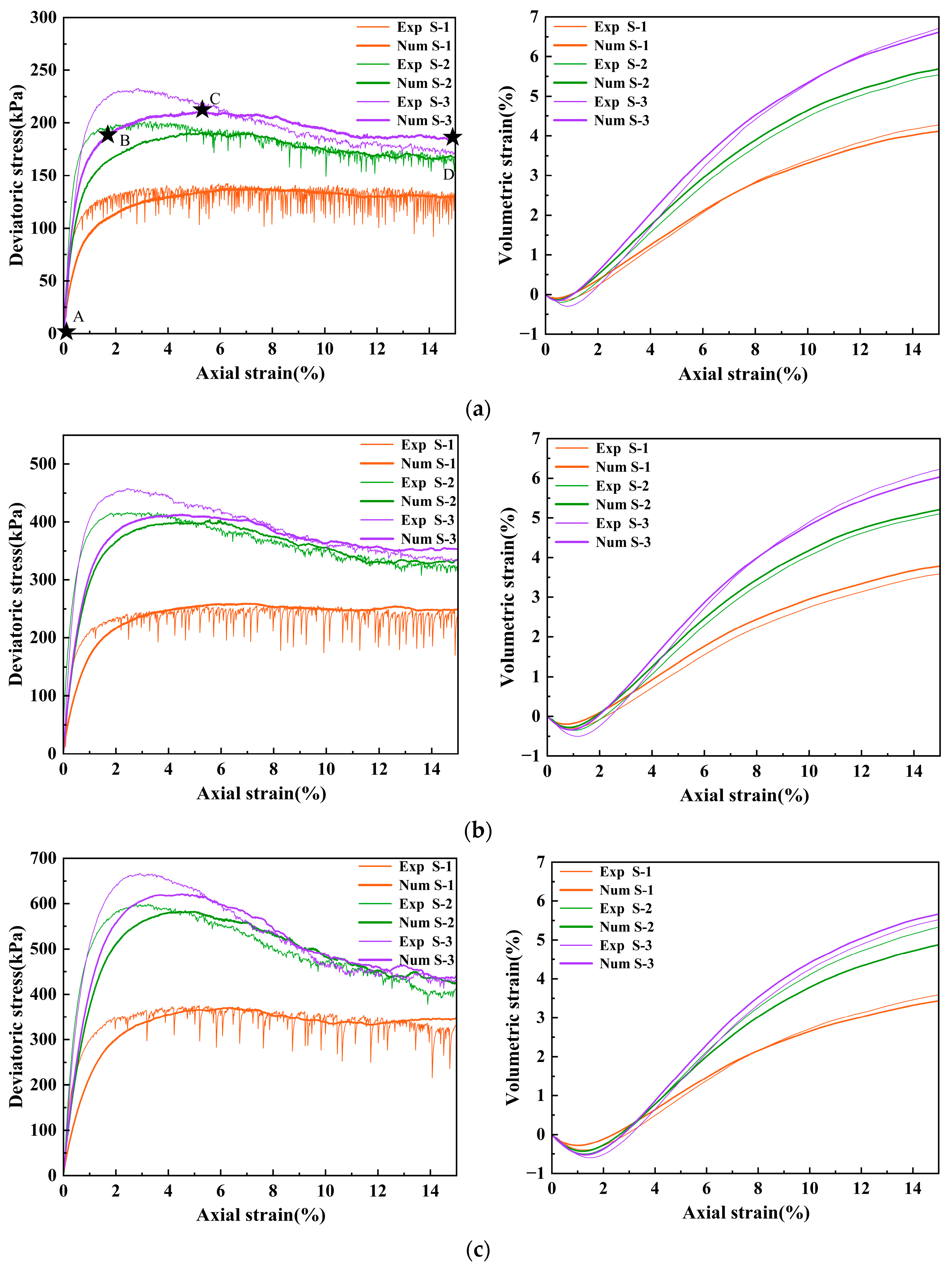
- Through a comparison of experimental and numerical results, we calibrated the model parameters against stress–strain curves, volumetric strain, and strength data. An increase in the interparticle friction coefficient significantly enhances the shear strength of the specimens.
- During shearing, the contact force network evolves from an initially uniform distribution to a directional distribution. In this process, strong force chains intensify and orient themselves preferentially in the axial direction. A higher interparticle friction coefficient markedly enhances all contact forces, with the strong force network showing the most pronounced increase. This force drives a more intensive fabric reorganization, which in turn optimizes the pathways for stress transmission This ultimately leads to the enhancement of the macroscopic shear strength.
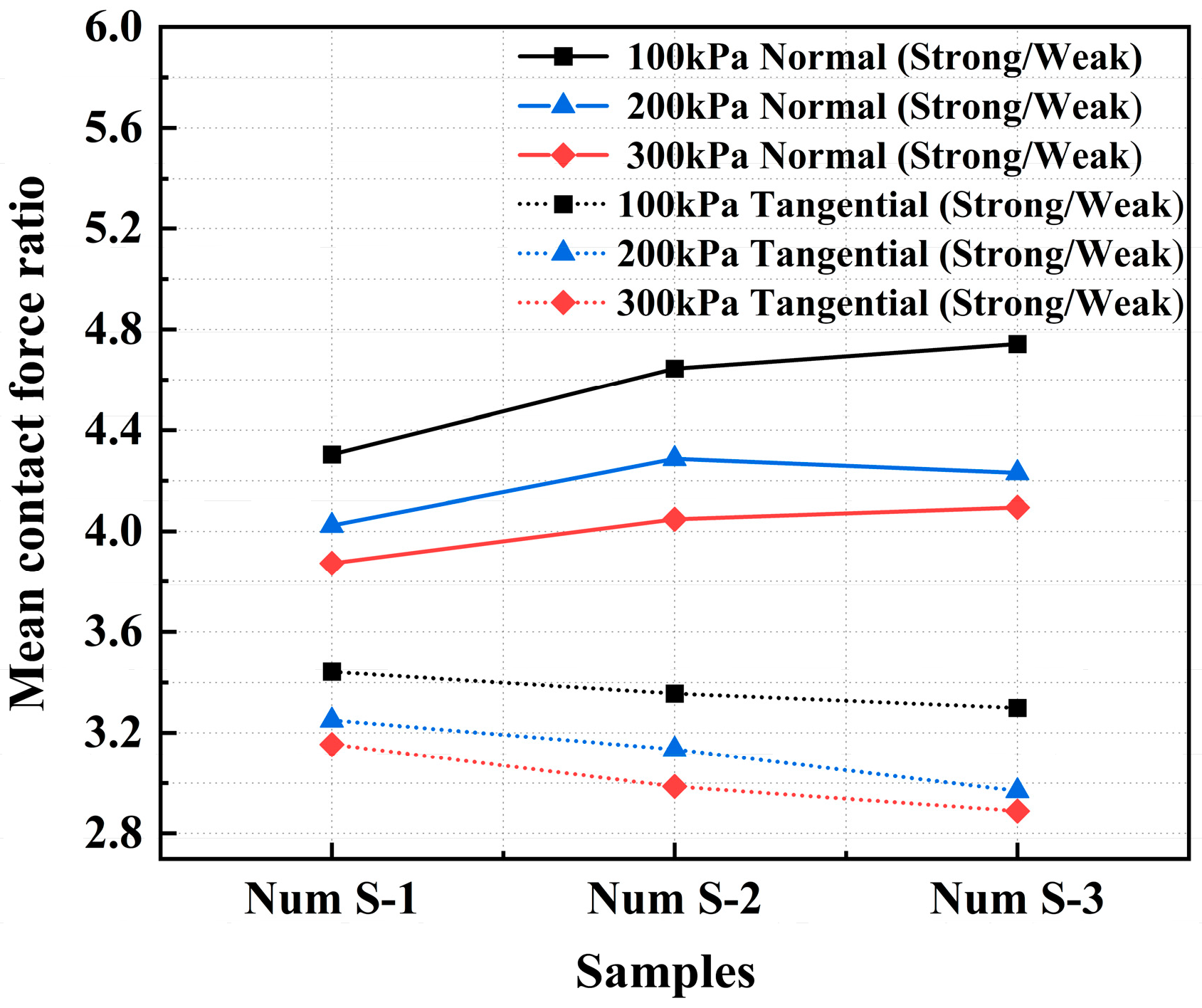
- The strong contact network acts as the primary backbone for stress transmission, while the weak contact network maintains structural stability. Under high interparticle friction coefficients, force chains become concentrated due to a reduction in the coordination number. Each contact exhibits stronger tangential friction, which increases the resistance of force chains to breakage under shearing. Strong contact networks enhance shear strength by effectively transmitting shear stress. Interparticle friction controls coordination numbers and mechanical behavior by influencing contact states and the structure of force chains.
- The contact and force transmission between particles exhibit significant anisotropic characteristics. Mechanical anisotropy develops earlier than geometric anisotropy. Samples with higher interparticle friction coefficient exhibit greater shear strength and anisotropy. Particularly, the anisotropy parameter of normal contact forces is most prominent, and the changes in their spatial distribution are more pronounced. The anisotropy of the normal contact forces within the strong contact network contributes more significantly to the overall mechanical anisotropy.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, C.; Sun, Q.; Zhang, G. Multiscale properties of dense granular materials. Eng. Comput. 2015, 32, 956–972. [Google Scholar] [CrossRef]
- Chen, M.; Wu, G.; Gan, B.; Jiang, W.-H.; Zhou, J.-W. Physical and compaction properties of granular materials with artificial grading behind the particle size distributions. Adv. Mater. Sci. Eng. 2018, 2018, 8093571. [Google Scholar] [CrossRef]
- Tripathi, P.; Lee, S.J. Particle geometry space: An integrated characterization of particle shape, surface area, volume, specific surface, and size distribution. arXiv 2025. [Google Scholar] [CrossRef]
- Fang, Y.; Li, B. Multiscale problems and analysis of soil mechanics. Mech. Mater. 2016, 103, 55–67. [Google Scholar] [CrossRef]
- Reardon, R.; Humire, F.; Ahmed, S.S.; Ziotopoulou, K.; Martinez, A.; DeJong, J.T. Effect of gradation on the strength and stress-dilatancy of coarse-grained soils: A comparison of monotonic direct simple shear and triaxial tests. Geo-Congress 2022, 2022, 226–236. [Google Scholar] [CrossRef]
- Shu, S.; Zhang, F.; Wang, D.; Ge, B.; Jiang, Y. Dynamic behavior and characteristics of geogrid-reinforced sand under cyclic loading. Soil Dyn Earthq. Eng. 2024, 180, 108630. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y. Liquefaction characteristics of gravelly soil under cyclic loading with constant strain amplitude by experimental and numerical investigations. Soil. Dyn. Earthq. Eng. 2017, 92, 388–396. [Google Scholar] [CrossRef]
- Cho, G.; Dodds, J.; Santamarina, J.C. Particle shape effects on packing density, stiffness, and strength: Natural and crushed sands. J. Geotech. Geoenviron. Eng. 2006, 132, 591–602. [Google Scholar] [CrossRef]
- Xu, W.; Li, X.; Yang, W.; Jia, H. Triaxial test on glass beads simulating coarse-grained soil. Res. Cold Arid. Reg. 2022, 14, 274–280. [Google Scholar] [CrossRef]
- Wu, K.; Abriak, N.; Becquart, F.; Pizette, P.; Remond, S.; Liu, S. Shear mechanical behavior of model materials samples by experimental triaxial tests: Case study of 4 mm diameter glass beads. Granul. Matter 2017, 19, 65. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Gong, J.; Cheng, L.; Liu, M.; Jiang, J.; Ou, X. The effect of particle shape on the collapse characteristics of granular columns via the DEM. Adv. Powder Technol. 2024, 35, 104283. [Google Scholar] [CrossRef]
- Xu, M.Q.; Guo, N.; Yang, Z.X. Particle shape effects on the shear behaviors of granular assemblies: Irregularity and elongation. Granul. Matter 2021, 23, 25. [Google Scholar] [CrossRef]
- Wu, M.; Zhou, F.; Wang, J. DEM modeling of mini-triaxial test on soil-rock mixture considering particle shape effect. Comput. Geotech. 2023, 153, 105110. [Google Scholar] [CrossRef]
- Wu, M.; Wu, F.; Wang, J. Particle shape effect on the shear banding in DEM-simulated sands. Granul. Matter 2022, 24, 48. [Google Scholar] [CrossRef]
- Shen, Z.; Li, X.; Yi, X.; Wang, Z.; Gao, H. DEM simulation of microscopic structure and macroscopic mechanical behavior of clay in oedometer and triaxial compression tests. Comput. Geotech. 2024, 173, 106544. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, P.; Yin, Z.; Wang, R. Micromechanical investigation of the particle size effect on the shear strength of uncrushable granular materials. Acta Geotech. 2022, 17, 4277–4296. [Google Scholar] [CrossRef]
- Jiang, M.D.; Yang, Z.X.; Barreto, D.; Xie, Y.H. The influence of particle-size distribution on critical state behavior of spherical and non-spherical particle assemblies. Granul. Matter 2018, 20, 80. [Google Scholar] [CrossRef]
- Gong, J.; Zou, J.; Zhao, L.; Li, L.; Nie, Z. New insights into the effect of interparticle friction on the critical state friction angle of granular materials. Comput. Geotech. 2019, 113, 103105. [Google Scholar] [CrossRef]
- Antony, S.J.; Kruyt, N.P. Role of interparticle friction and particle-scale elasticity in the shear-strength mechanism of three-dimensional granular media. Phys. Rev. E 2009, 79, 031308. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Pizette, P.; Becquart, F.; Rémond, S.; Abriak, N.; Xu, W.; Liu, S. Experimental and numerical study of cylindrical triaxial test on mono-sized glass beads under quasi-static loading condition. Adv. Powder Technol. 2017, 28, 155–166. [Google Scholar] [CrossRef]
- Miao, M.; Liu, F.; Yin, Y.; Tang, Y.; Zhong, L. The influence of surface roughness on the shear mechanical behavior of 2 mm spherical particle materials. Granul. Matter 2024, 27, 17. [Google Scholar] [CrossRef]
- Miao, M.; Liu, F.; Yin, Y.; Tang, Y. The effect of surface roughness and particle size on the shear characteristics of spherical particle materials. Powder Technol. 2025, 459, 121017. [Google Scholar] [CrossRef]
- Yin, Y.; Liu, F.; Miao, M.; Yuan, Z.; Tang, Y. Effect of surface roughness on the liquid bridge between two rigid spheres. Powder Technol. 2025, 449, 120377. [Google Scholar] [CrossRef]
- GB/T 33523.2-2017; SAC: Geometrical Product Specifications (GPS)—Surface Texture:AREAL—Part 2: Terms, Definitions and Surface Texture Parameters. China Planning Press: Beijing, China, 2017.
- Jiang, M.; Shen, Z.; Wang, J. A novel three-dimensional contact model for granulates incorporating rolling and twisting resistances. Comput. Geotech. 2015, 65, 147–163. [Google Scholar] [CrossRef]
- Ai, J.; Chen, J.; Rotter, J.M.; Ooi, J.Y. Assessment of rolling resistance models in discrete element simulations. Powder Technol. 2011, 206, 269–282. [Google Scholar] [CrossRef]
- Group, I.C. PFC 6.0: Particle Flow Code User’s Guide; Itasca Consulting Group, Inc.: Minneapolis, MN, USA, 2018. [Google Scholar]
- Nguyen, D.; Chen, Y.; Martinez, A. A DEM sensitivity study on the effects of contact parameters on triaxial response for the development of a calibration method. Comput. Geotech. 2025, 184, 107241. [Google Scholar] [CrossRef]
- Ling, D.; Hu, T.; Wang, J.; Wang, X.; Shi, C.; Tang, Y. Numerical study on the shear strength of granular materials under the low confining pressure. Soils Found. 2024, 64, 101447. [Google Scholar] [CrossRef]
- Sazzad, M.M. Micro-scale behavior of granular materials during cyclic loading. Particuology 2014, 16, 132–141. [Google Scholar] [CrossRef]
- Ma, G.; Zhou, W.; Chang, X.; Ng, T.-T.; Yang, L.-F. Formation of shear bands in crushable and irregularly shaped granular materials and the associated microstructural evolution. Powder Technol. 2016, 301, 118–130. [Google Scholar] [CrossRef]
- Dondi, G.; Simone, A.; Vignali, V.; Manganelli, G. Numerical and experimental study of granular mixes for asphalts. Powder Technol. 2012, 232, 31–40. [Google Scholar] [CrossRef]
- Wang, X.; Xu, C.; Liang, K.; Iqbal, K. Mechanical characteristics and microstructure of saturated sand under monotonic and cyclic loading conditions. Soil Dyn. Earthq. Eng. 2024, 176, 108283. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Chen, S.; Xu, C.-S. Biaxial compression test and application considering interparticle rolling resistance and particle shape effects. Soil Dyn. Earthq. Eng. 2020, 139, 106394. [Google Scholar] [CrossRef]
- Shi, D.; Niu, J.; Zhang, J.; Chao, Z.; Fowmes, G. Effects of particle breakage on the mechanical characteristics of geogrid-reinforced granular soils under triaxial shear: A DEM investigation. Geomech. Energy Environ. 2023, 34, 100446. [Google Scholar] [CrossRef]
- Wu, M.; Fan, Y.; Wang, J.; Yin, Z.-Y. Modeling a flexible membrane for triaxial tests with coupled FDM–DEM: Considering realistic particle shape effects. Int. J. Geomech. 2024, 24, 04024155. [Google Scholar] [CrossRef]
- Wu, K.; Sun, W.; Liu, S.; Zhang, X. Study of shear behavior of granular materials by 3D DEM simulation of the triaxial test in the membrane boundary condition. Adv. Powder Technol. 2021, 32, 1145–1156. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, J.; Wu, M. DEM simulation of particle crushing in a triaxial test considering the influence of particle morphology and coordination number. Comput. Geotech. 2022, 148, 104769. [Google Scholar] [CrossRef]
- Wu, W.; Ma, G.; Zhou, W.; Wang, D.; Chang, X. Force transmission and anisotropic characteristics of sheared granular materials with rolling resistance. Granul. Matter 2019, 21, 88. [Google Scholar] [CrossRef]
- Barreto, D.; O’Sullivan, C. The influence of inter-particle friction and the intermediate stress ratio on soil response under generalised stress conditions. Granul. Matter 2012, 14, 505–521. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, J. The signature of shear-induced anisotropy in granular media. Comput. Geotech. 2013, 47, 1–15. [Google Scholar] [CrossRef]
- Zhao, J.; Guo, N. Rotational resistance and shear-induced anisotropy in granular media. Acta Mech. Solida Sin. 2014, 27, 1–14. [Google Scholar] [CrossRef]
- Liu, J.; Wu, X.; Jiang, J.; Ding, Z.; Lü, C.; Shi, X. A network-based investigation on the strong contact system of granular materials under isotropic and deviatoric stress states. Comput. Geotech. 2023, 153, 105077. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, W.; Ma, G.; Yang, S.; Chang, X. Strong contacts, connectivity and fabric anisotropy in granular materials: A 3D perspective. Powder Technol. 2020, 366, 747–760. [Google Scholar] [CrossRef]
- Yang, S.; Zhou, W.; Ma, G.; Liu, J.; Qi, T. Mechanism of inter-particle friction effect on 3D mechanical response of granular materials. Chin. J. Geotech. Eng. 2020, 42, 1885–1893. [Google Scholar]
- Liu, J.; Zhou, W.; Ma, G.; Li, Y.; Liu, Q. Contact fabric characteristics of granular materials under three dimensional stress paths. Chin. J. Theor. Appl. Mech. 2019, 51, 26–35. [Google Scholar] [CrossRef]
- Fan, M.; Su, D.; Chen, X. Systematic investigation into the role of particle multi-level morphology in determining the shear behavior of granular materials via DEM simulation. Comput. Geotech. 2024, 170, 106298. [Google Scholar] [CrossRef]
| Parameters | Value | Unit |
|---|---|---|
| Density | 2.5 | g/cm3 |
| Poisson’s ratio | 0.2 | - |
| Young’s modulus | 71 | GPa |
| Specific gravity Gs | 2.5 | g/cm3 |
| Samples | Roughness Index | ||
|---|---|---|---|
| Sa (μm) | Sq (μm) | Sz (μm) | |
| S-1 | 3.19 | 5.17 | 251.52 |
| S-2 | 16.91 | 28.12 | 739.94 |
| S-3 | 24.88 | 52.63 | 839.75 |
| 2D/3D | μs | μr | kn (N/m2) | ks (N/m2) | k* | Damping Coefficient | Literature |
|---|---|---|---|---|---|---|---|
| 3D | 0–1 | - | - | - | 4/3 | 0.7 | [19] |
| 3D | 0.15 | 0.01 | - | - | - | 0.8 | [21] |
| 2D | 0.8 | 0.2 | - | - | - | 0.3 | [27] |
| 3D | 0.5 | - | 4 × 105 | 4 × 105 | 1.0 | 0.7 | [30] |
| 2D | 0.5 | - | 1 × 108 | 1 × 108 | 1.0 | 0.05 | [31] |
| 2D | 0.6 | - | 4.5 × 1012 | 1.875 × 1012 | - | - | [32] |
| 3D | 0.42 | - | 1 × 107 | 1 × 107 | - | - | [33] |
| 3D | 0.15 | 0.5 | - | - | 1.5 | 0.7 | [34] |
| 2D | 0.5 | 0, 0.1, 0.3, 0.5 | 1.2 × 106 | 1 × 106 | - | - | [35] |
| Parameters | Value | Unit |
|---|---|---|
| Sample size (Φ × H) | 120 × 60.9 | mm |
| Void ratio (e) | 0.61 | - |
| Damping coefficient (d) | 0.7 | - |
| Shear Rate (v) | 0.04 | mm/min |
| Ball-Ball effective modulus (E*) | 1 × 108 | N/mm2 |
| Ball-Facet effective modulus (E*) | 1 × 108 | N/mm2 |
| Stiffness ratio (k*) | 1.5 | - |
| Sliding friction coefficient (μs) | 0.1, 0.2, 0.3, 0.4, 0.5 | - |
| Rolling friction coefficient (μr) | 0.01, 0.015, 0.02, 0.025, 0.03 | - |
| Shell density/(ρm) | 0.93 | g/cm3 |
| Flexible membrane thickness | 0.5 | mm |
| Poisson’s ratio (ν) | 0.2 | - |
| Samples | μs | μr |
|---|---|---|
| Num S-1 | 0.15 | 0.015 |
| Num S-2 | 0.3 | 0.02 |
| Num S-3 | 0.4 | 0.025 |
| Samples | σ3 (kPa) | Exp. | Num. | Relative Error |
|---|---|---|---|---|
| S-1 | 100 | 142.44 | 138.11 | 3% |
| 200 | 255.86 | 259.37 | 1.4% | |
| 300 | 375.34 | 370.48 | 1.3% | |
| S-2 | 100 | 201.2 | 190.84 | 5.2% |
| 200 | 416.47 | 403.71 | 3.1% | |
| 300 | 599.44 | 582.42 | 2.8% | |
| S-3 | 100 | 232.84 | 212.38 | 8.8% |
| 200 | 457.75 | 413.03 | 9.8% | |
| 300 | 667.26 | 620.64 | 6.9% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Y.; Liu, F.; Miao, M.; Yin, Y. Influence of Surface Roughness on the Mechanical Behavior of Granular Material Under Triaxial Shear: A DEM Study. Materials 2025, 18, 5251. https://doi.org/10.3390/ma18225251
Tang Y, Liu F, Miao M, Yin Y. Influence of Surface Roughness on the Mechanical Behavior of Granular Material Under Triaxial Shear: A DEM Study. Materials. 2025; 18(22):5251. https://doi.org/10.3390/ma18225251
Chicago/Turabian StyleTang, Yuqing, Fengyin Liu, Meng Miao, and Yu Yin. 2025. "Influence of Surface Roughness on the Mechanical Behavior of Granular Material Under Triaxial Shear: A DEM Study" Materials 18, no. 22: 5251. https://doi.org/10.3390/ma18225251
APA StyleTang, Y., Liu, F., Miao, M., & Yin, Y. (2025). Influence of Surface Roughness on the Mechanical Behavior of Granular Material Under Triaxial Shear: A DEM Study. Materials, 18(22), 5251. https://doi.org/10.3390/ma18225251






