Quantitative Depth Estimation in Lock-In Thermography: Modeling and Correction of Lateral Heat Conduction Effects
Abstract
1. Introduction
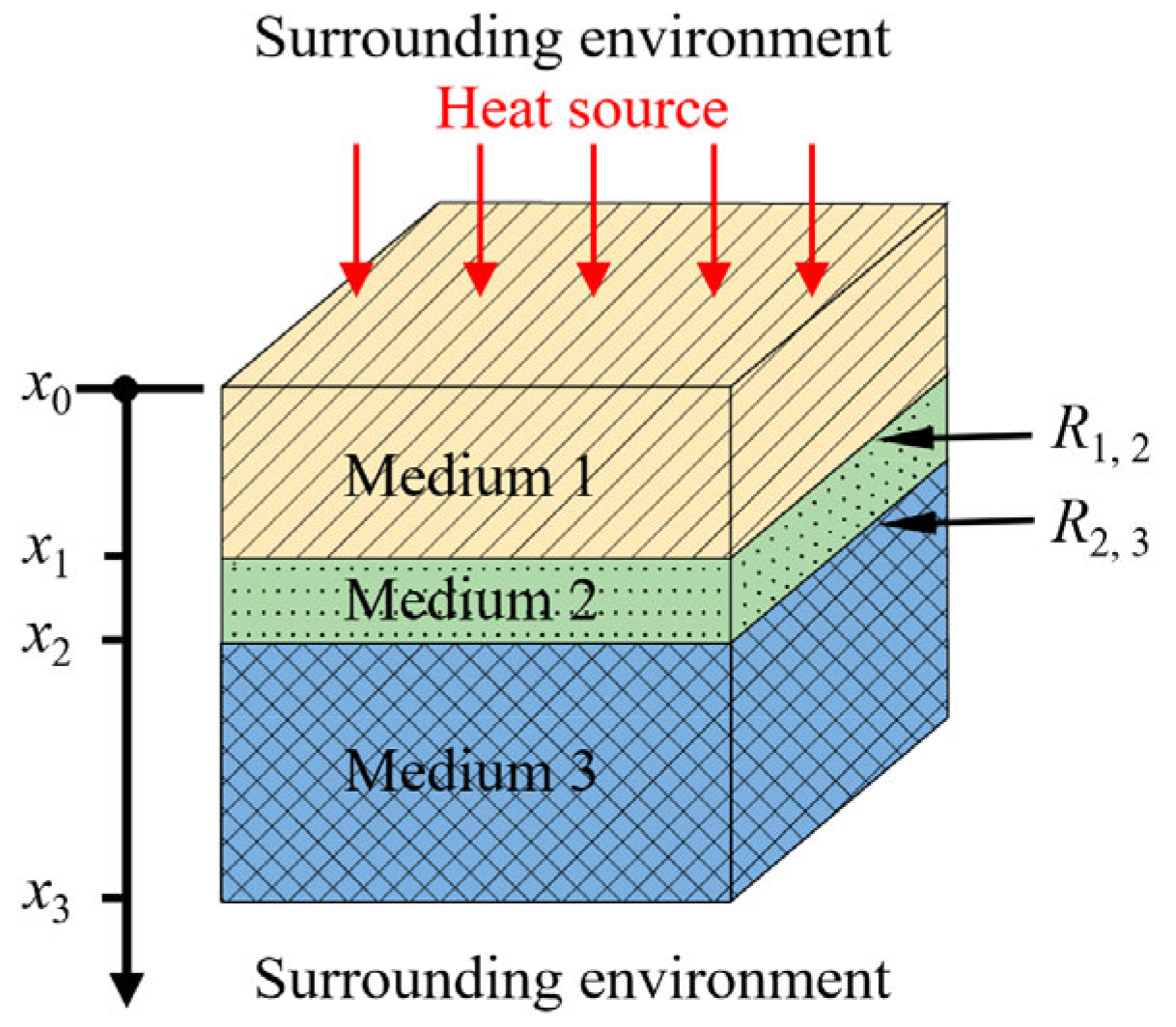
2. Theory
3. Methods
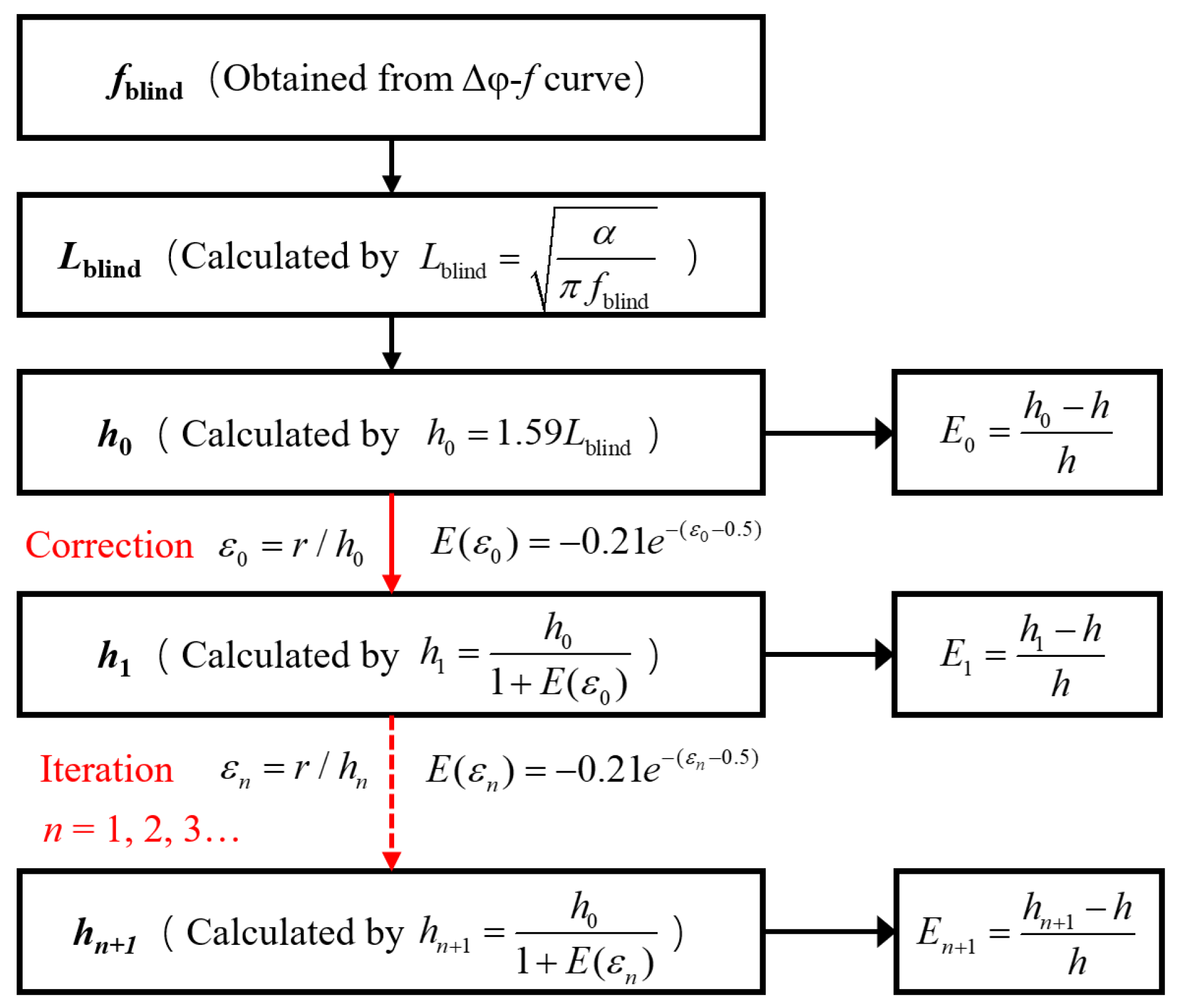
3.1. Theoretical Analysis of Defect Depth Prediction Methods
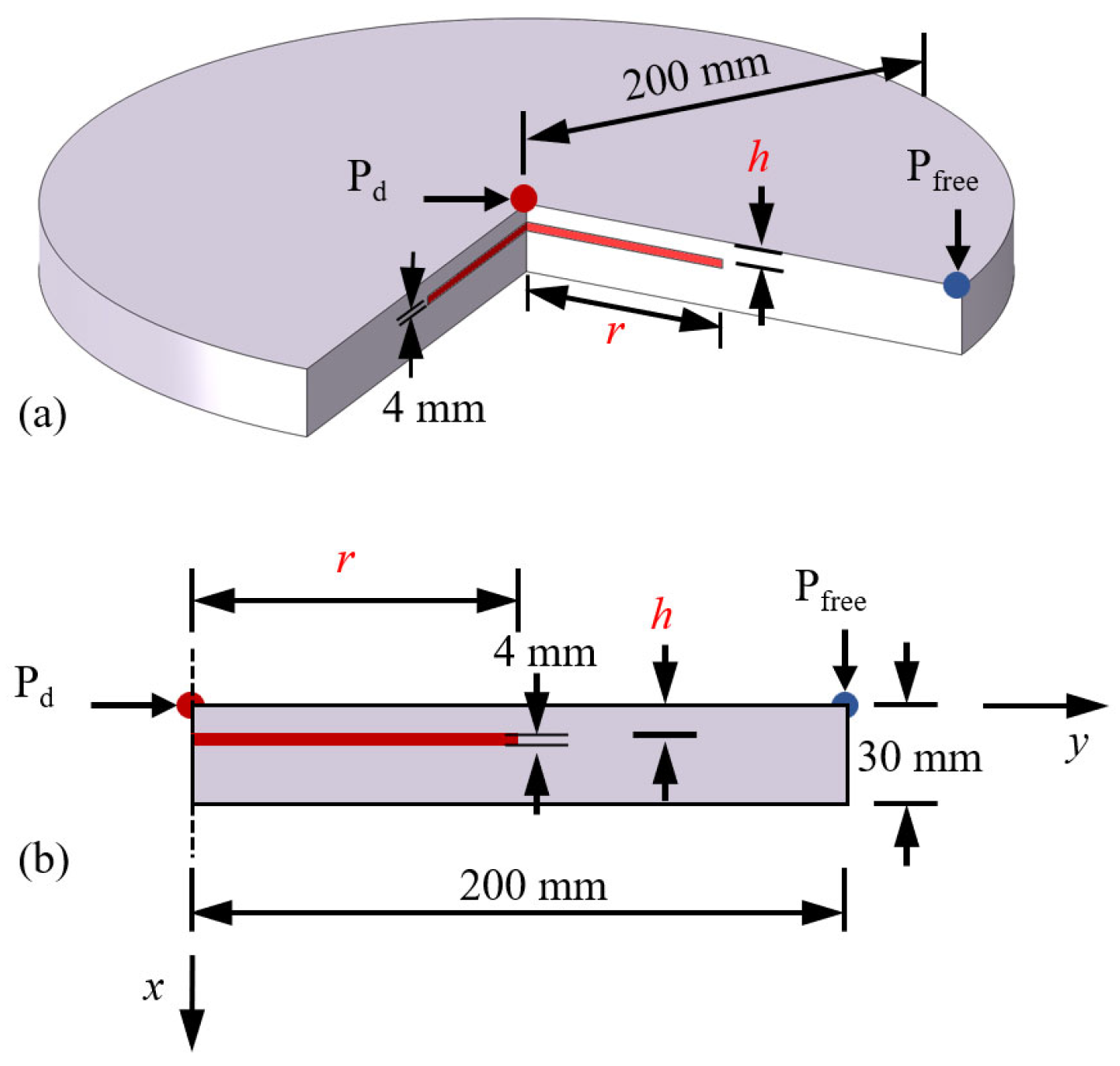
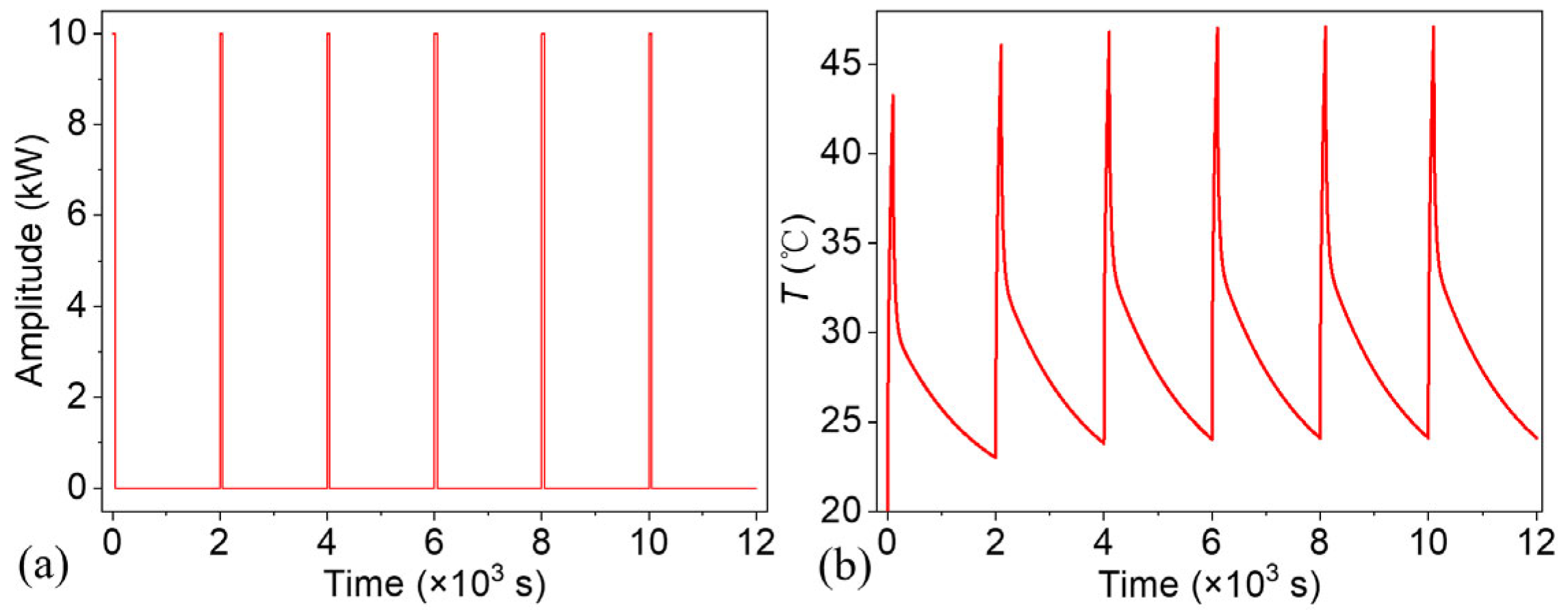
3.2. Finite Element Simulations for Thermal Response
4. Results and Discussion
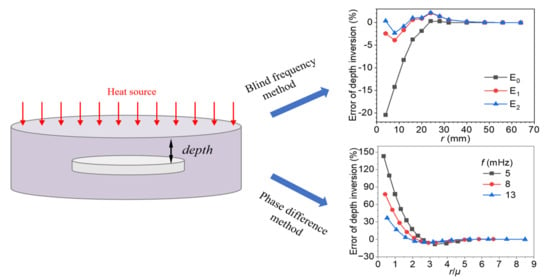
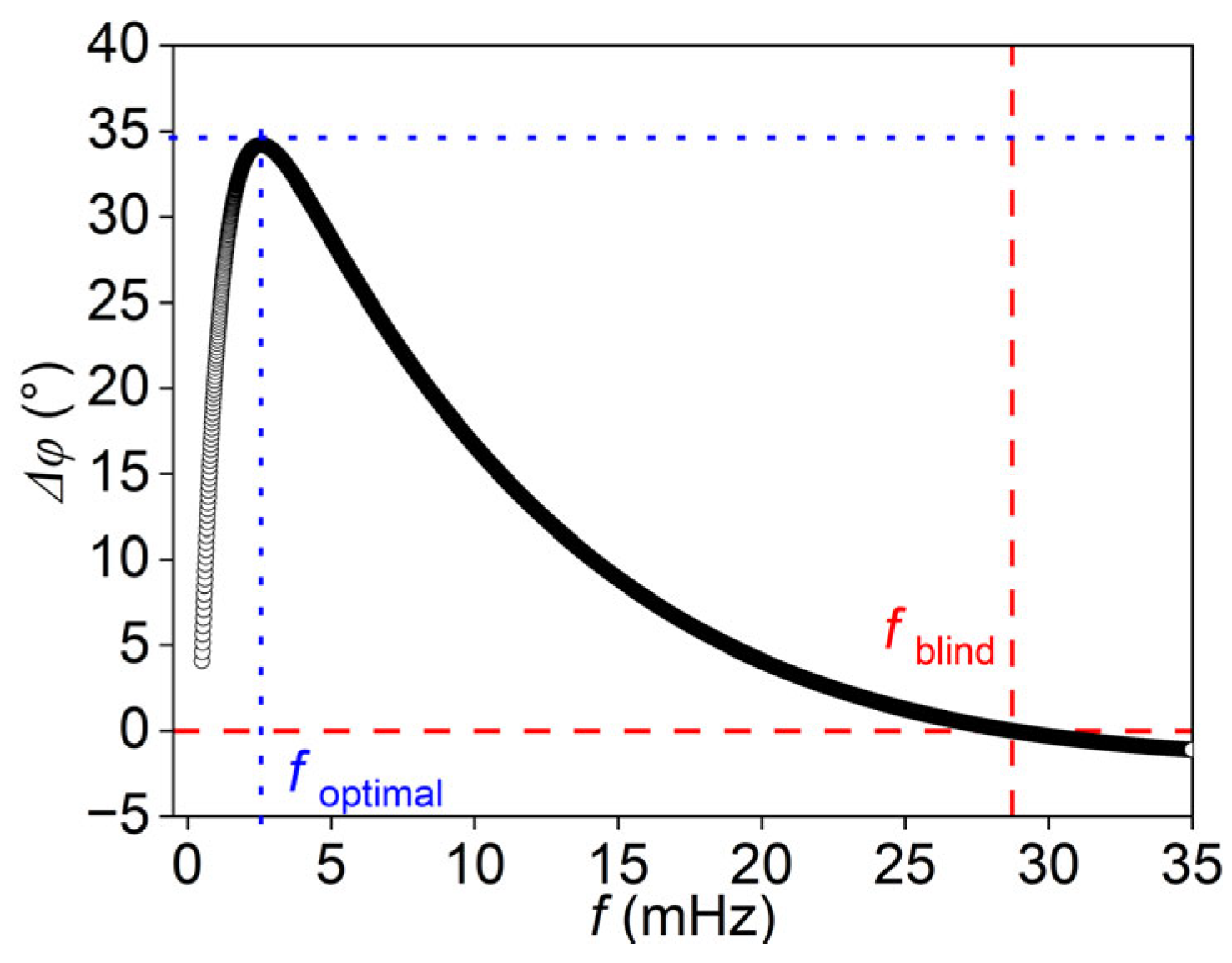
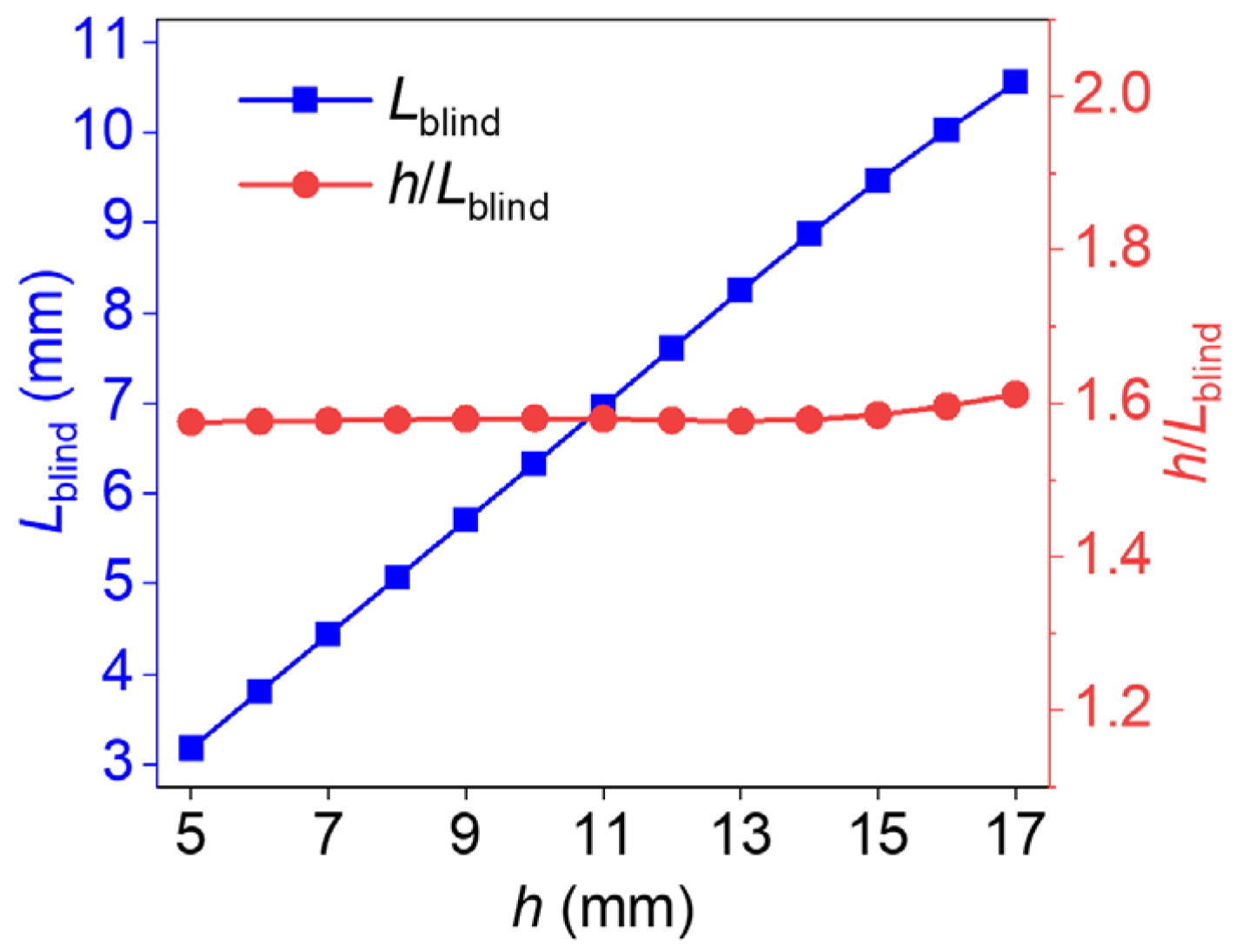
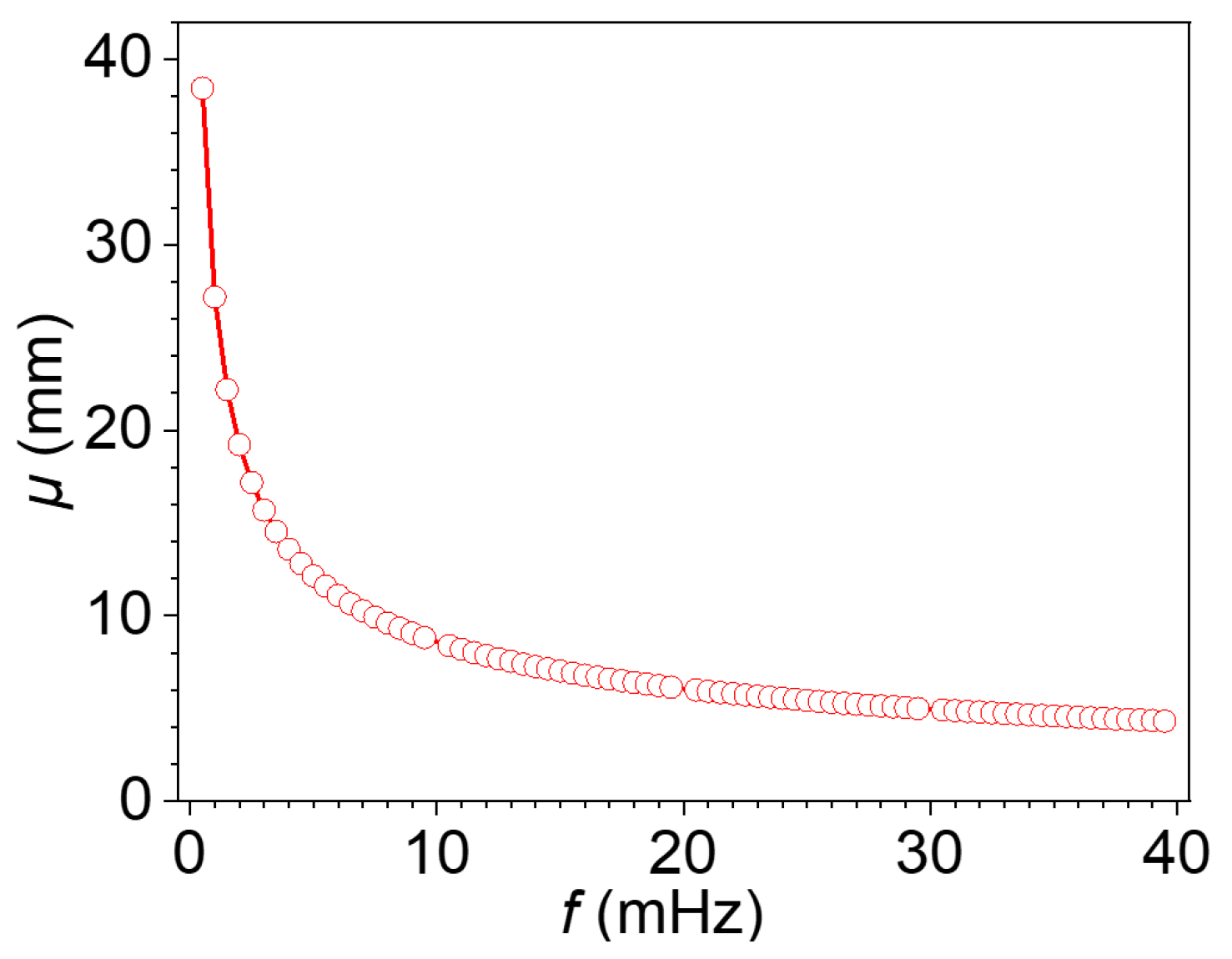
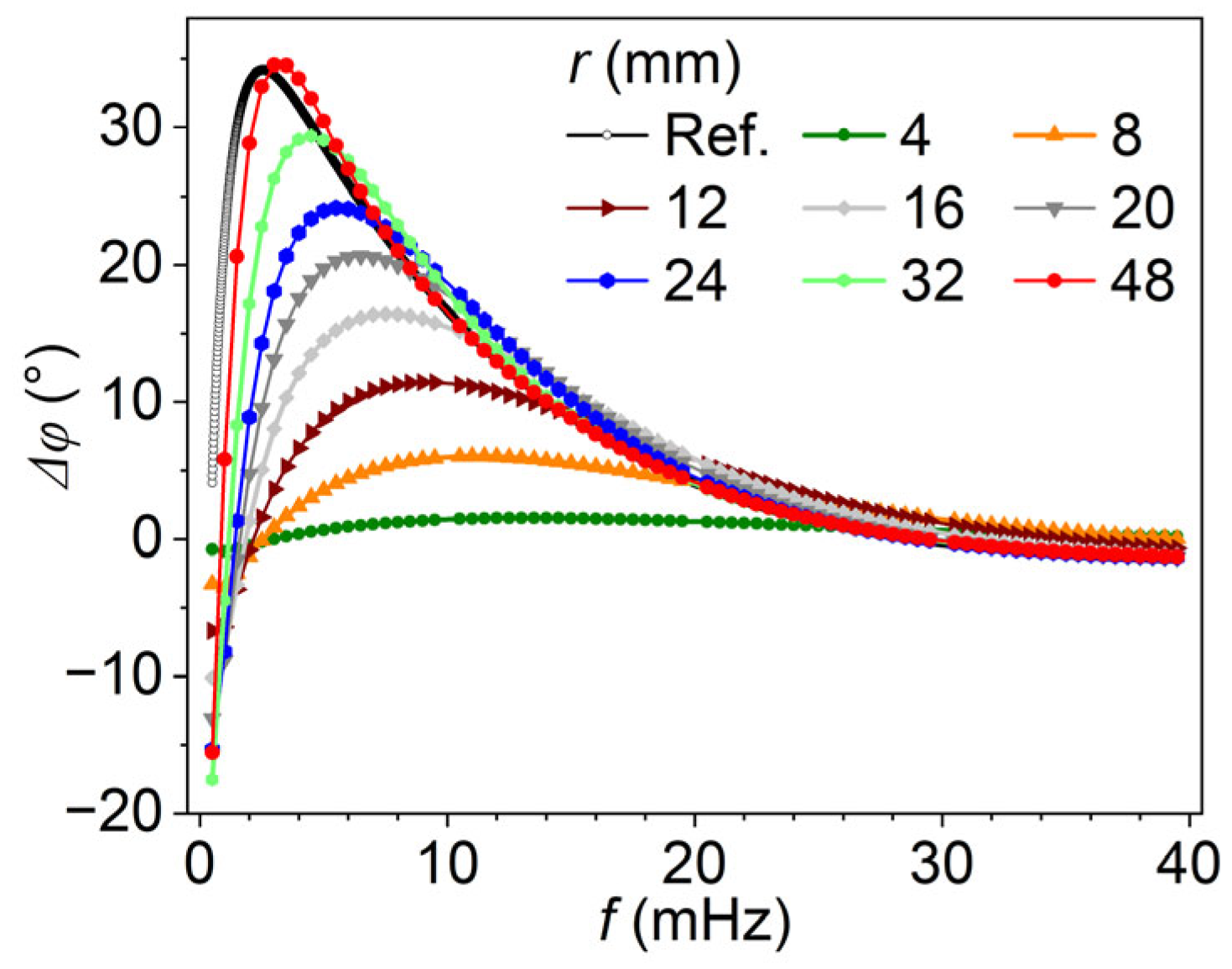
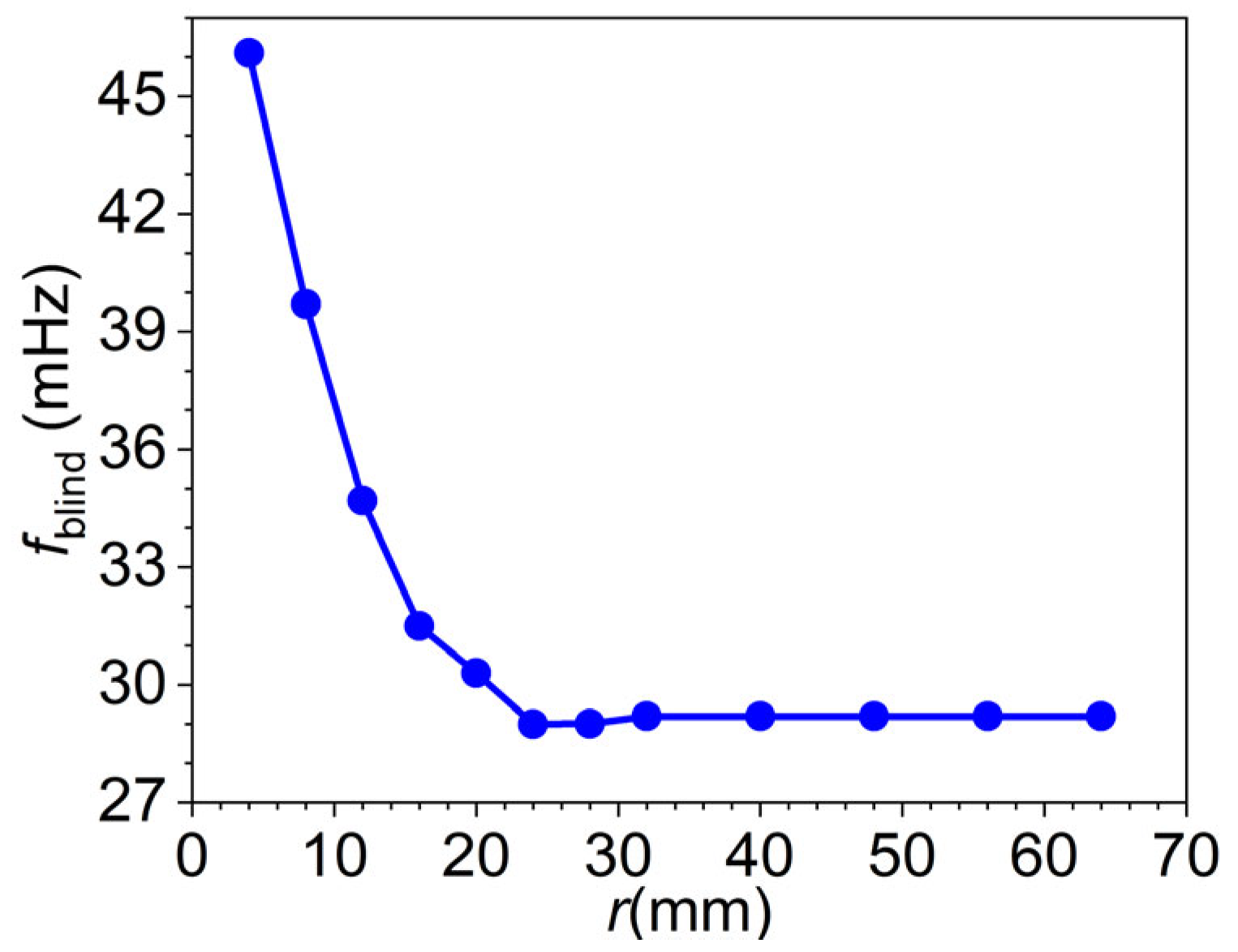
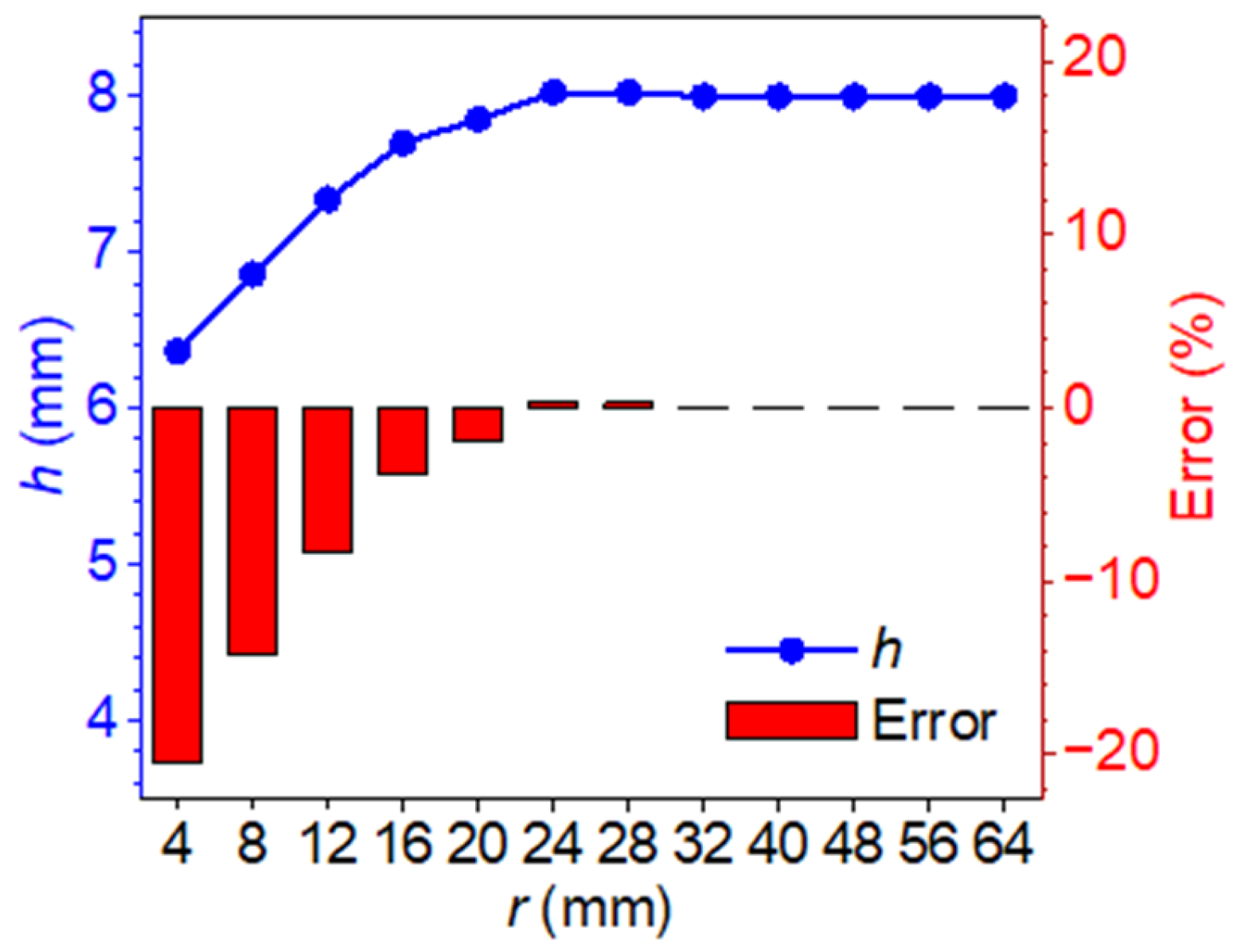
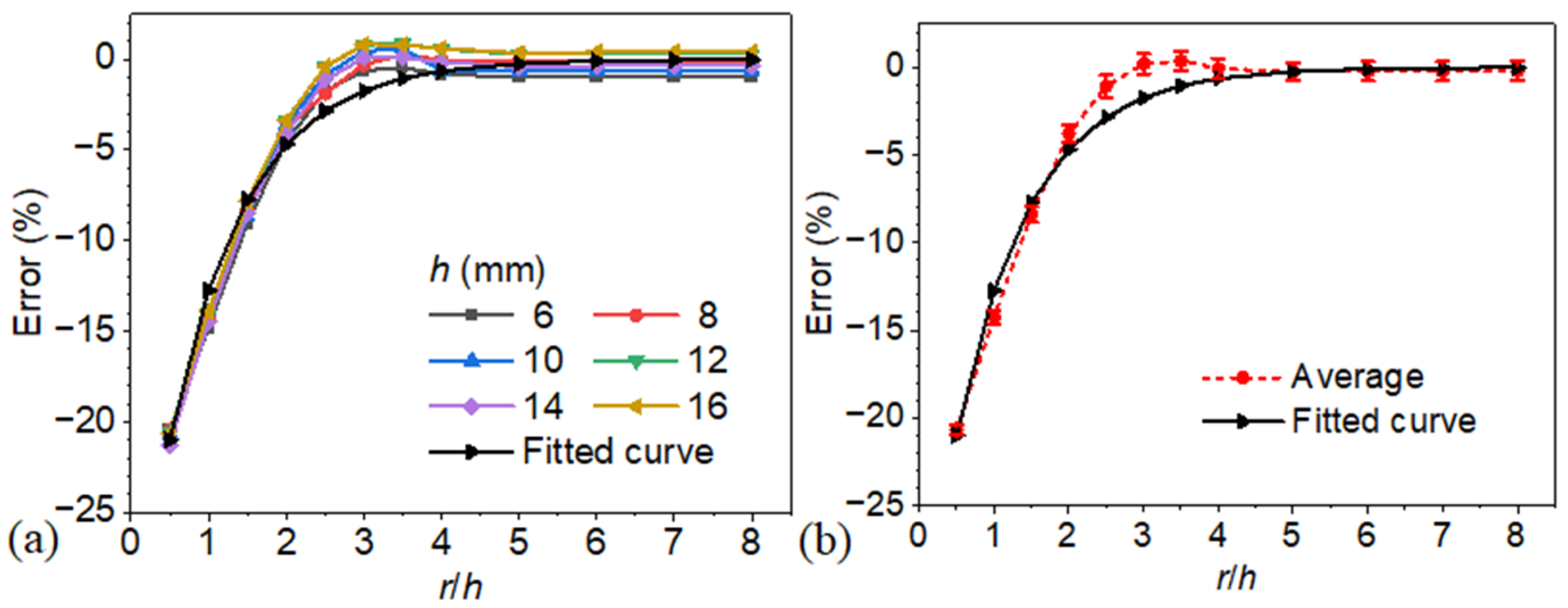
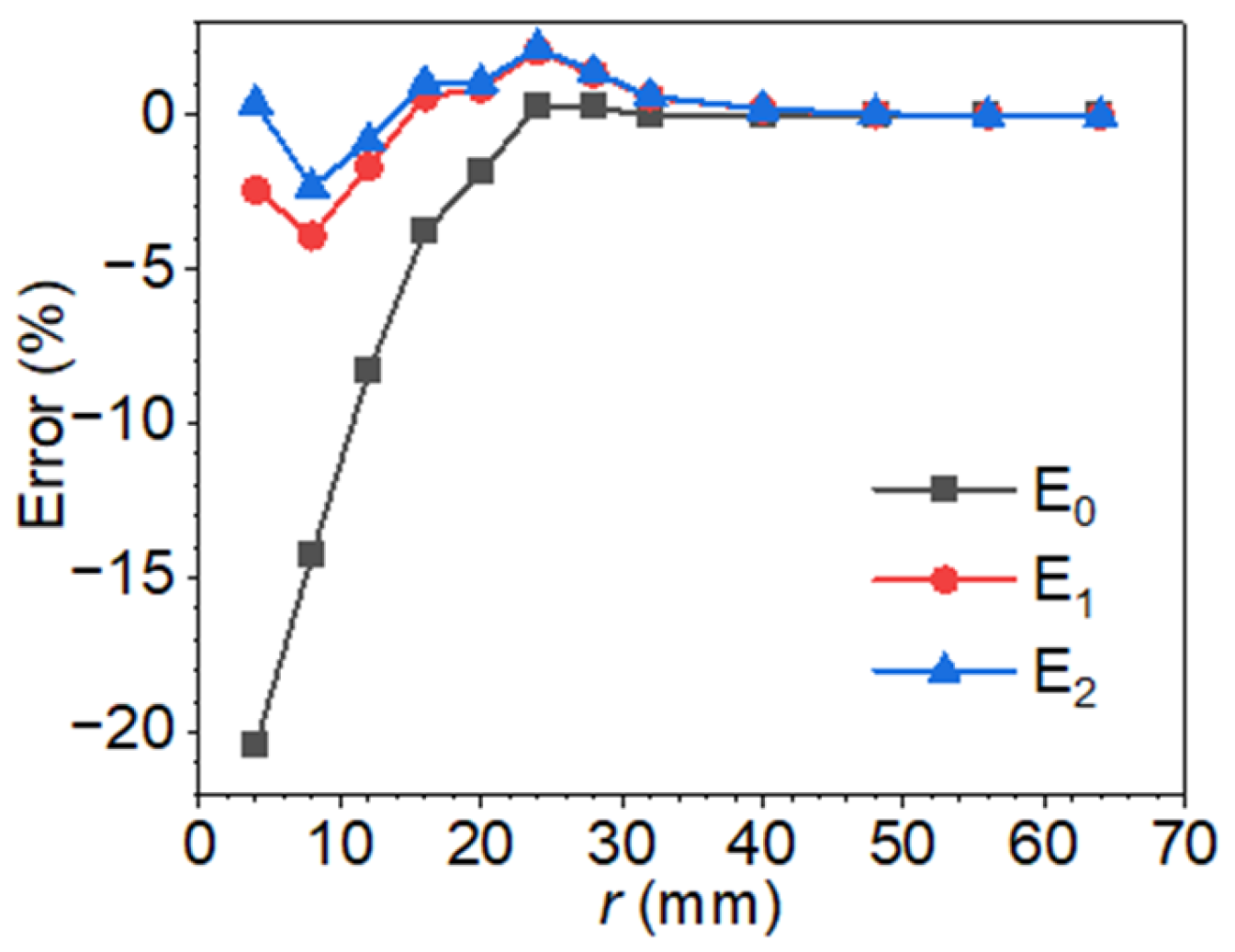
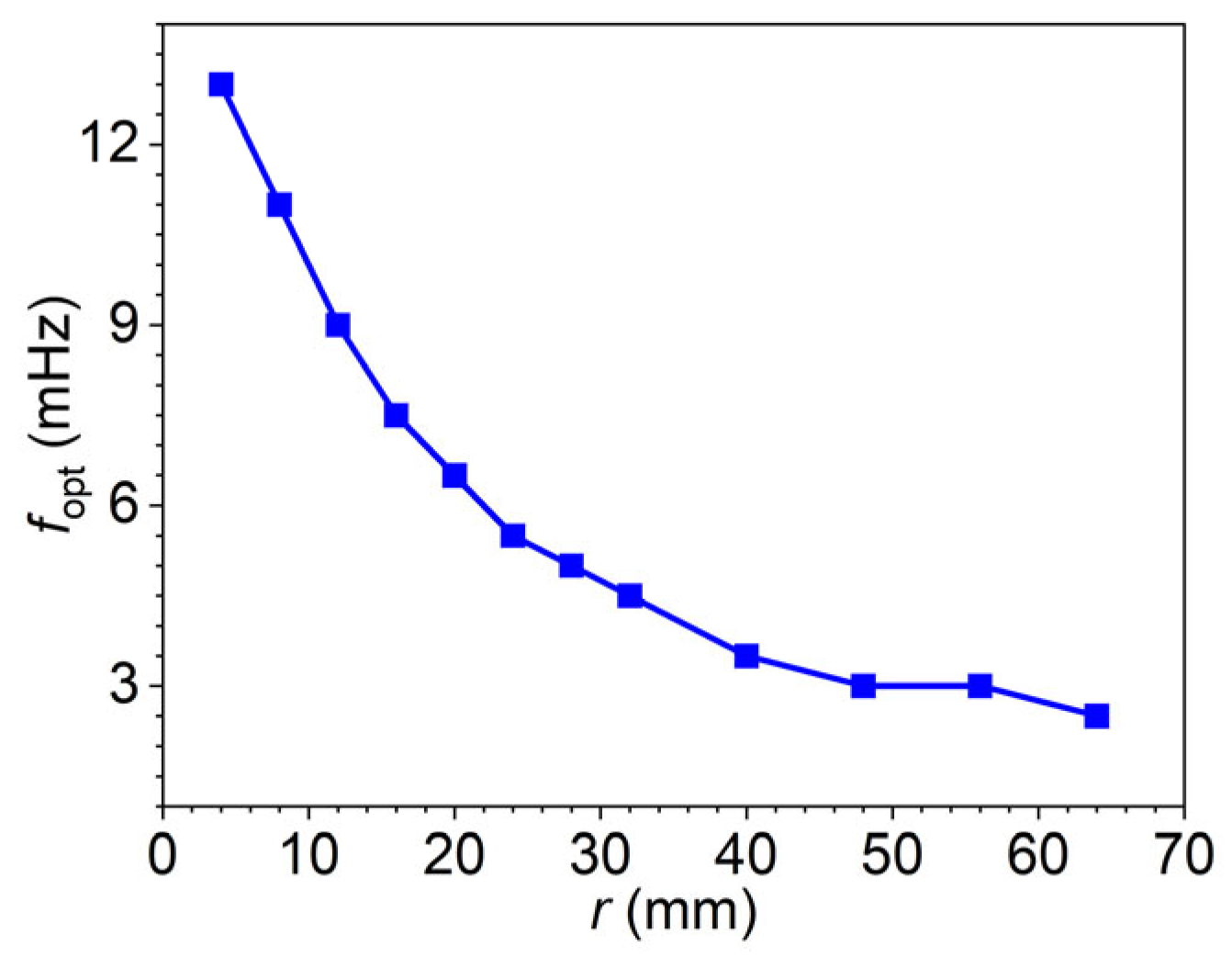
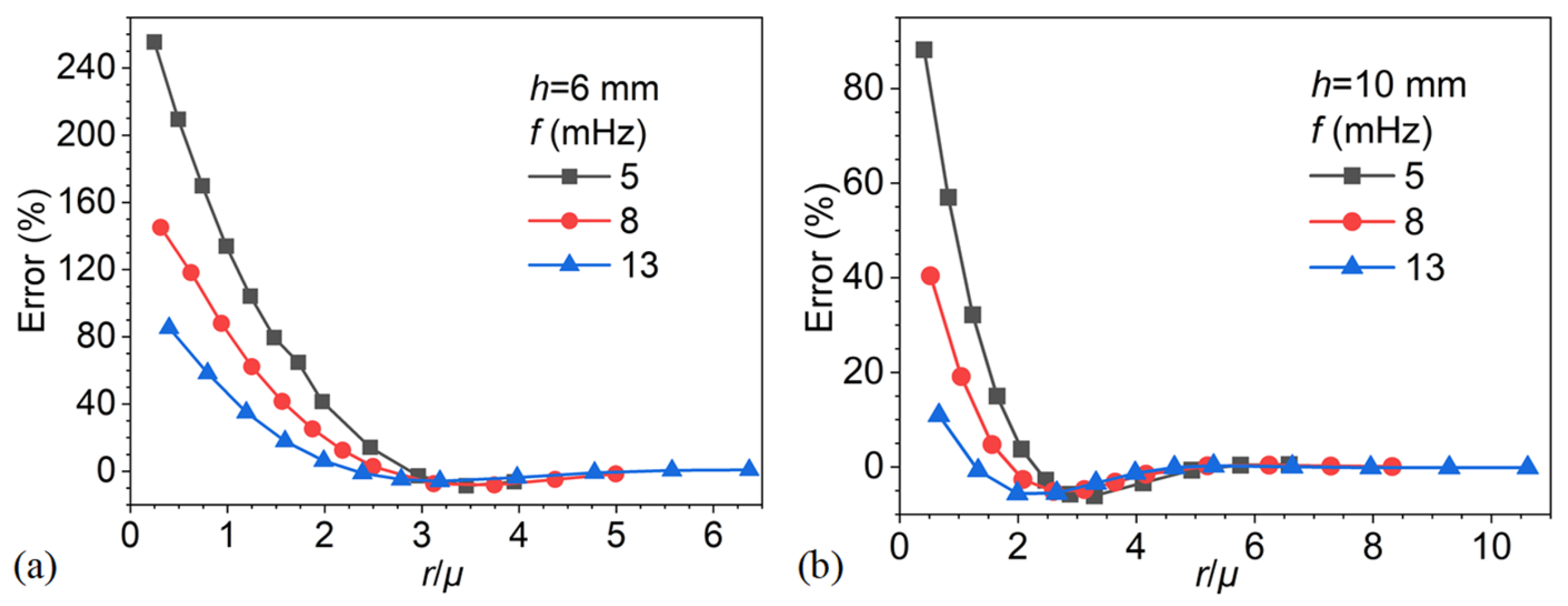
4.1. Analysis of the Effect of Radius on the Blind Frequency Method
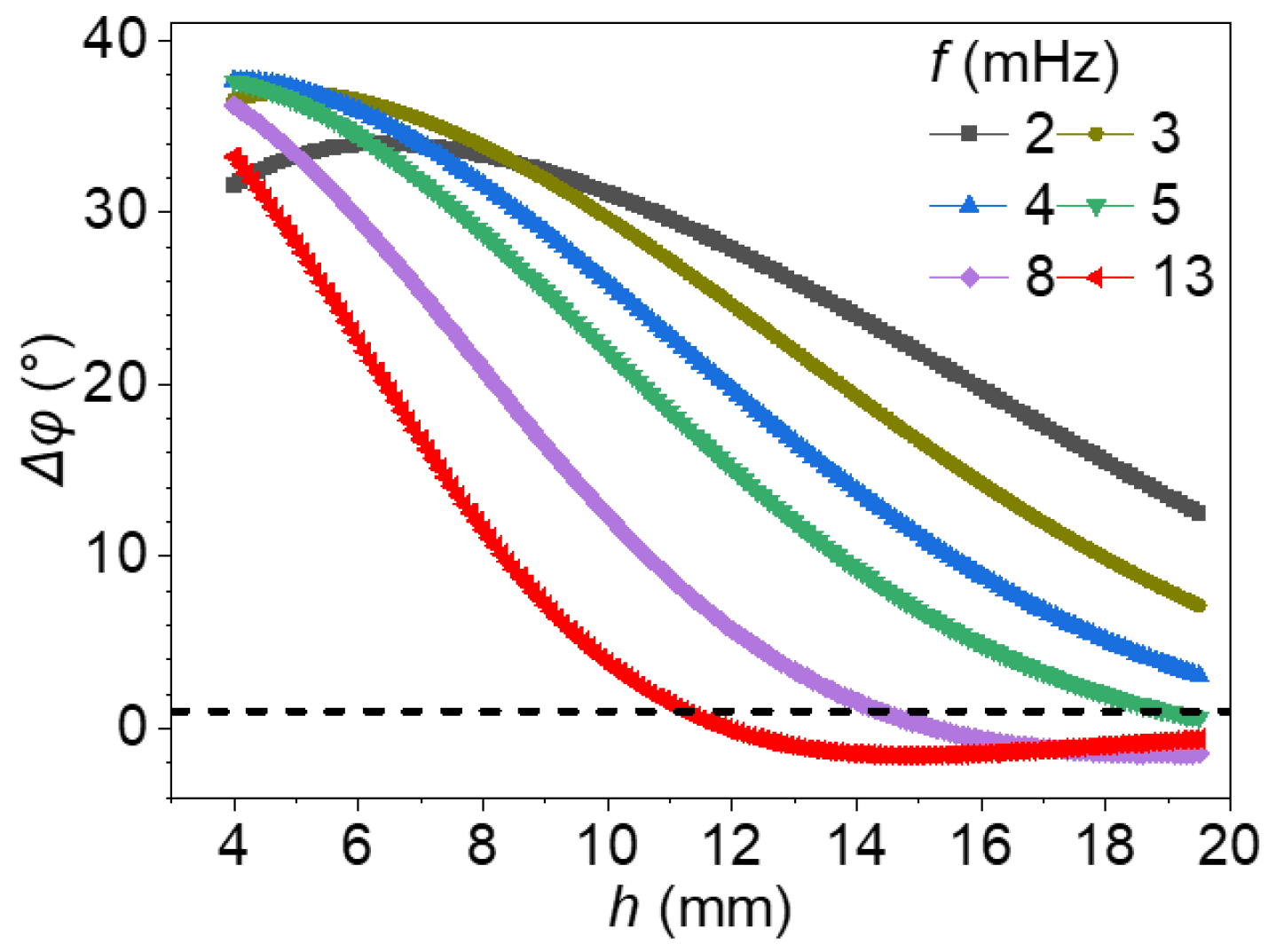
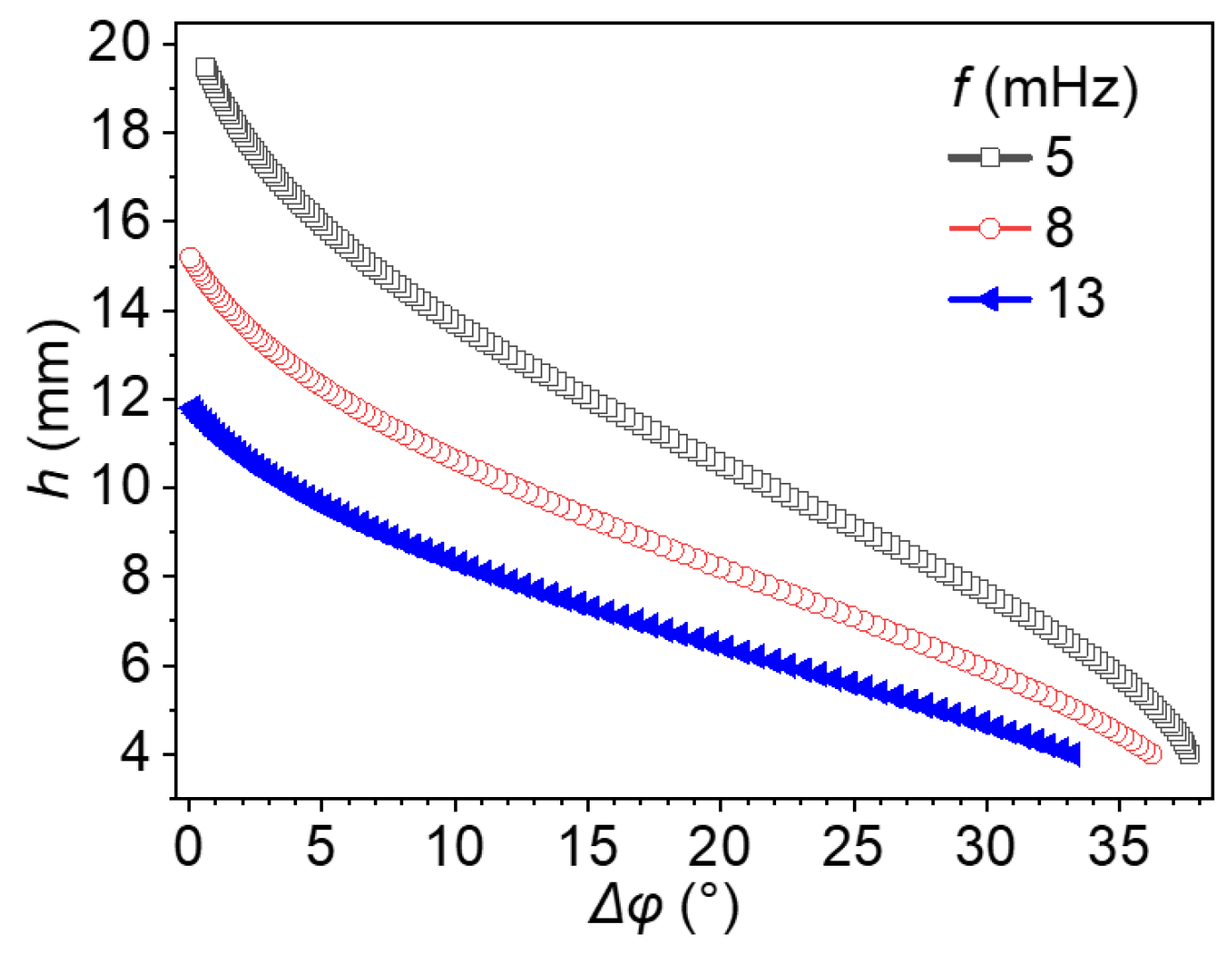
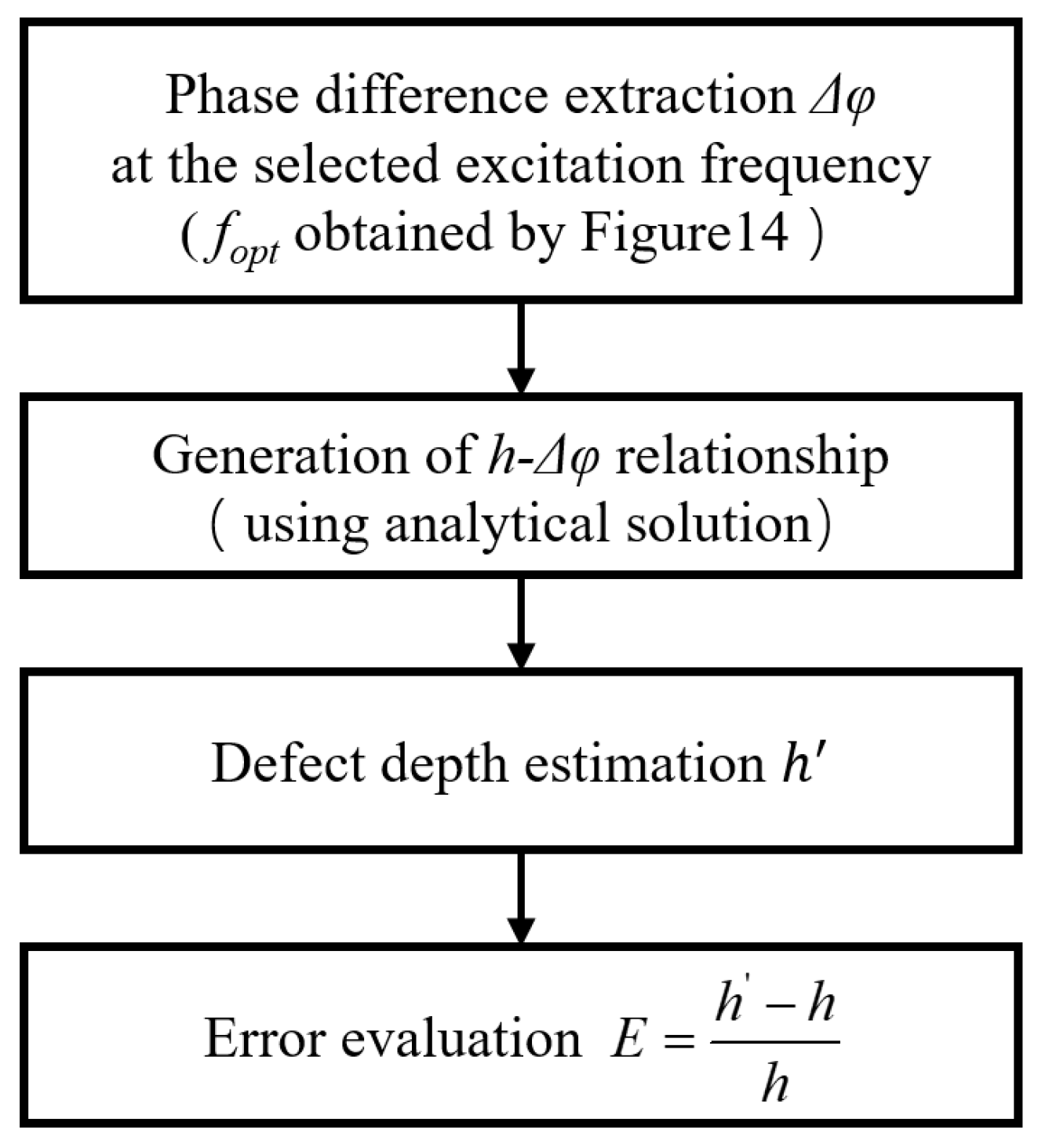
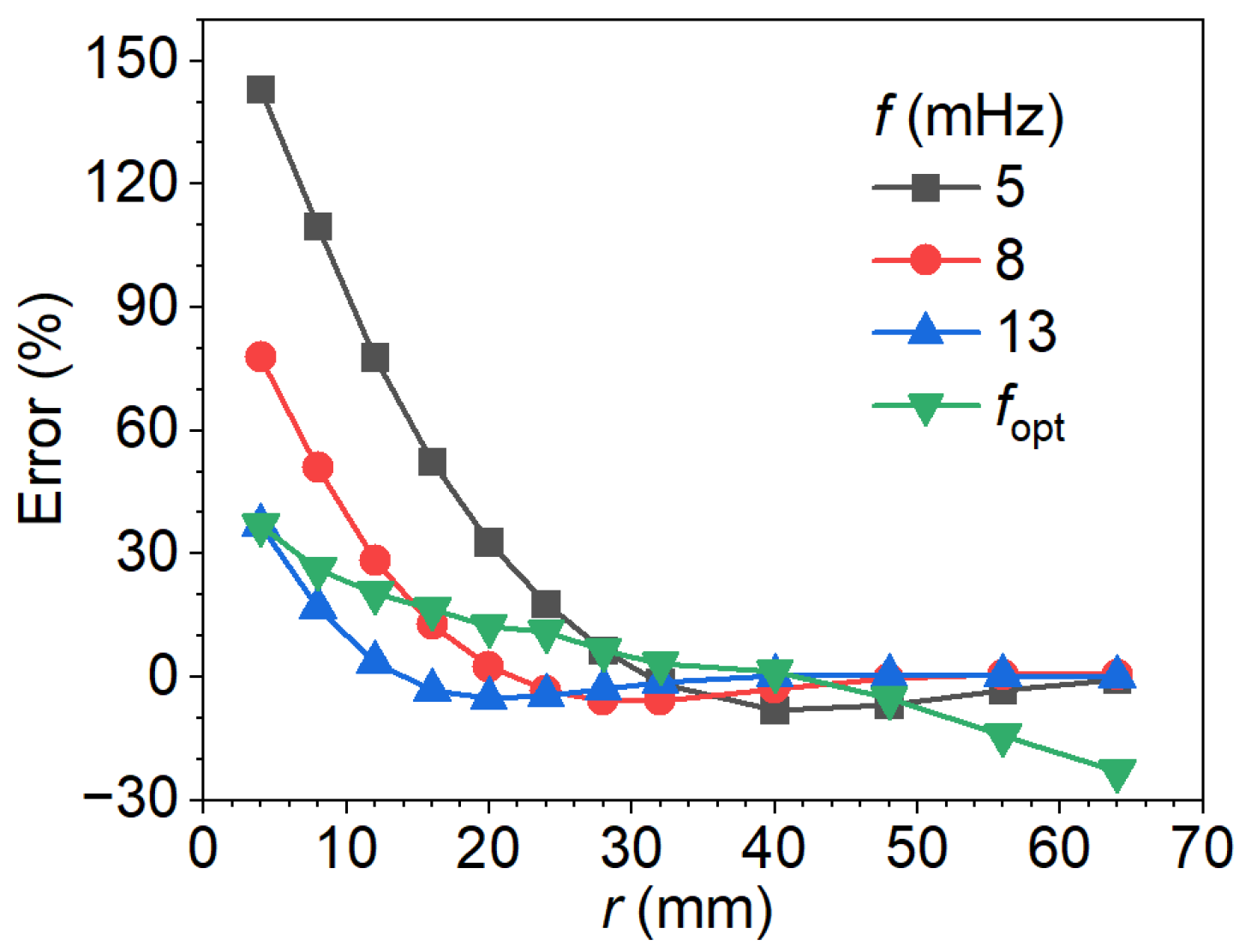
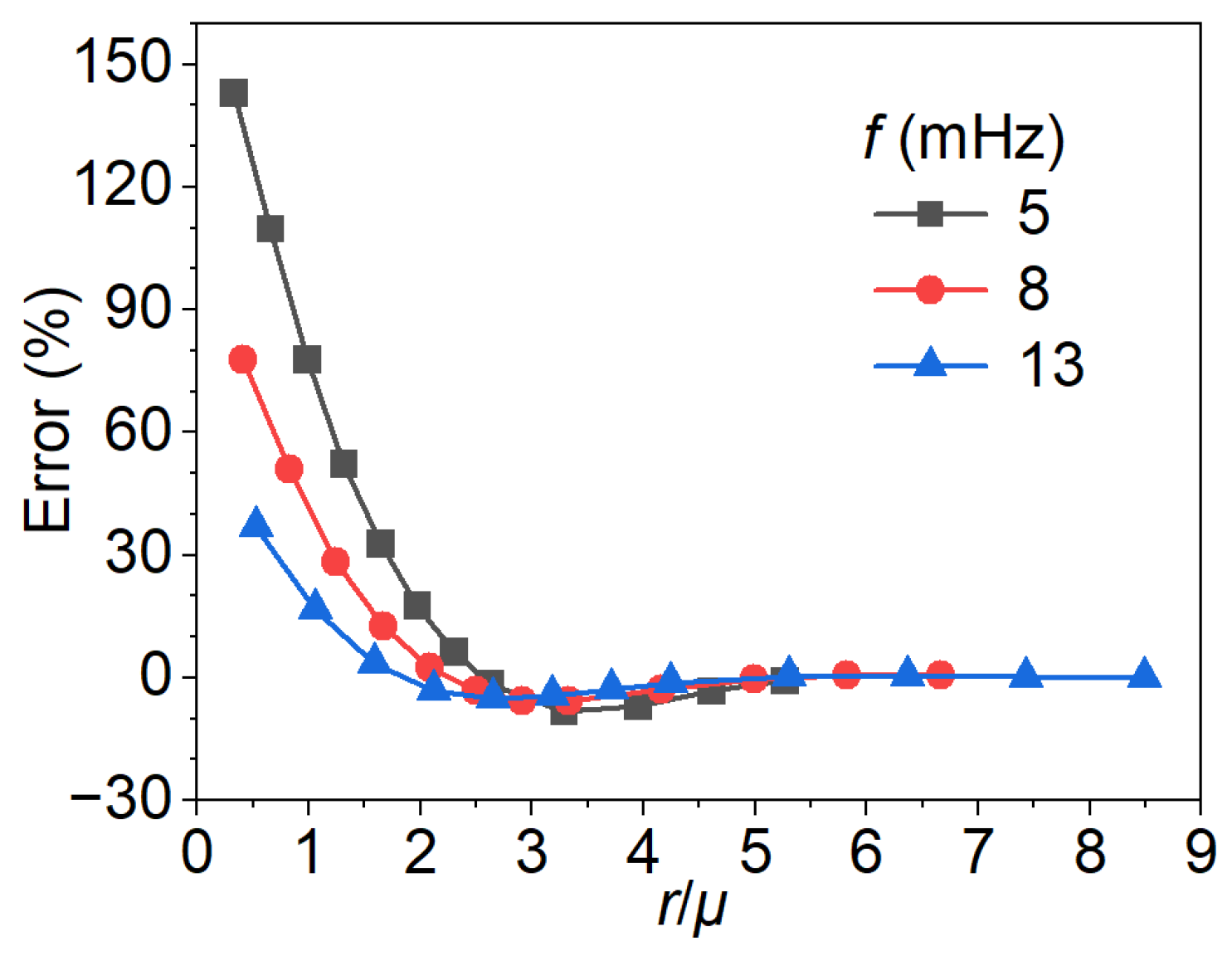
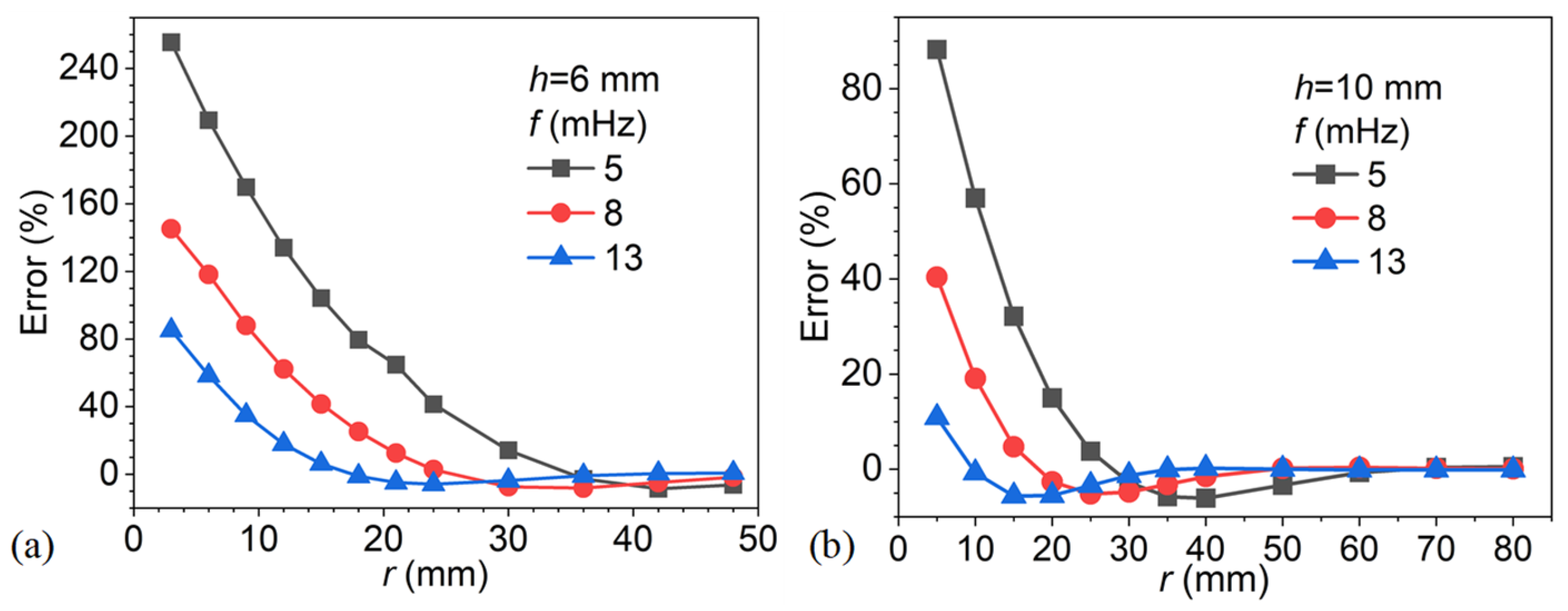
4.2. Analysis of the Effect of Radius on the Phase Difference Method
4.3. Limitations and Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| NDT | Nondestructive testing |
| IRT | Infrared thermography |
| LIT | Lock-in thermography |
| 1D | One-dimensional |
| 3D | Three-dimensional |
| Temperature measurement point in the defect-free region | |
| Temperature measurement point above the defect center |
References
- Bardis, K.; Avdelidis, N.P.; Ibarra-Castanedo, C.; Maldague, X.P.; Fernandes, H. Advanced diagnostics of aircraft structures using automated non-invasive imaging techniques: A comprehensive review. Appl. Sci. 2025, 15, 3584. [Google Scholar] [CrossRef]
- Tai, J.L.; Sultan, M.T.H.; Łukaszewicz, A.; Józwik, J.; Oksiuta, Z.; Shahar, F.S. Recent trends in non-destructive testing approaches for composite materials: A review of successful implementations. Materials 2025, 18, 3146. [Google Scholar] [CrossRef]
- Zhu, J.; Mao, Z.; Wu, D.; Zhou, J.; Jiao, D.; Shi, W.; Zhu, W.; Liu, Z. Progress and trends in non-destructive testing for thermal barrier coatings based on infrared thermography: A review. J. Nondestruct. Eval. 2022, 41, 49. [Google Scholar] [CrossRef]
- Honarvar, F.; Varvani-Farahani, A. A review of ultrasonic testing applications in additive manufacturing: Defect evaluation, material characterization, and process control. Ultrasonics 2020, 108, 106227. [Google Scholar] [CrossRef] [PubMed]
- Monu, M.C.; Chekotu, J.C.; Brabazon, D. Eddy current testing and monitoring in metal additive manufacturing: A review. J. Manuf. Process. 2025, 134, 558–588. [Google Scholar] [CrossRef]
- Wang, D.; Ban, H.; Jiang, P. Three-dimensional (3D) tensor-based methodology for characterizing 3D anisotropic thermal conductivity tensor. Int. J. Heat Mass Transf. 2025, 242, 126886. [Google Scholar] [CrossRef]
- Wang, D.; Ban, H.; Jiang, P. Spatially resolved lock-in micro-thermography (SR-LIT): A tensor analysis-enhanced method for anisotropic thermal characterization. Appl. Phys. Rev. 2024, 11, 021407. [Google Scholar] [CrossRef]
- Wang, D.; Ban, H. Infrared radiometry based steady-state method for thermal conductivity measurement. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2021; P V011T11A075. [Google Scholar]
- Song, Z.; Zhang, L.; Wang, D.; Tan, S.; Ban, H. Thermal diffusivity measurement of microscale slabs by rear-surface detection thermoreflectance technique. Rev. Sci. Instrum. 2021, 92, 034903. [Google Scholar] [CrossRef]
- Tran, Q.H.; Dang, Q.M.; Pham, X.T.; Truong, T.C.; Nguyen, T.X.; Huh, J. Passive infrared thermography technique for concrete structures health investigation: Case studies. Asian J. Civ. Eng. 2023, 24, 1323–1331. [Google Scholar] [CrossRef]
- Pozzer, S.; Omidi, Z.; El Refai, A.; López, F.; Ibarra-Castanedo, C.; Maldague, X. Passive infrared thermography for subsurface delamination detection in concrete infrastructure: Capabilities. Constr. Build. Mater. 2024, 419, 135542. [Google Scholar] [CrossRef]
- Doshvarpassand, S.; Wu, C.; Wang, X. An overview of corrosion defect characterization using active infrared thermography. Infrared Phys. Technol. 2019, 96, 366–389. [Google Scholar] [CrossRef]
- Ciampa, F.; Mahmoodi, P.; Pinto, F.; Meo, M. Recent advances in active infrared thermography for non-destructive testing of aerospace components. Sensors 2018, 18, 609. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Zhang, S.; Luo, Y.; Ding, L.; Zhang, D. Accurate depth determination of defects in composite materials using pulsed thermography. Compos. Struct. 2021, 267, 113846. [Google Scholar] [CrossRef]
- Qu, Z.; Jiang, P.; Zhang, W.X. Development and application of infrared thermography non-destructive testing techniques. Sensors 2020, 20, 3851. [Google Scholar] [CrossRef]
- Chung, Y.; Lee, S.; Kim, W. Latest advances in common signal processing of pulsed thermography for enhanced detectability: A review. Appl. Sci. 2021, 11, 12168. [Google Scholar] [CrossRef]
- Lema, D.G.; Pedrayes, O.D.; Usamentiaga, R.; Garcia, D.F. Improved detection of subsurface defects through active thermography and ensembling techniques. Qual. Eng. 2023, 35, 669–685. [Google Scholar] [CrossRef]
- Elizalde, J.S.G.; Chiou, Y.-S. Improving the detectability and confirmation of hidden surface corrosion on metal sheets using active infrared thermography. J. Build. Eng. 2023, 66, 105931. [Google Scholar] [CrossRef]
- Wang, F.; Liu, J.; Dong, B.; Liu, G.; Chen, M.; Wang, Y. Optimization of thermal-wave radar thermography by transverse heat flow suppression technique for accurate defect detection of CFRP laminates. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Wei, Q.; Huang, J.; Zhu, J.; Zhuo, L.; Li, C. Experimental investigation on detection of coating debonds in thermal barrier coatings using vibrothermography with a piezoceramic actuator. NDT E Int. 2023, 137, 102859. [Google Scholar] [CrossRef]
- Tao, N.; Wang, L.; Wu, Z.; Wang, C.; Ma, Y.; Zhang, C.; Sun, J.-G. Analysis of step-heating thermography methods for defect depth prediction. NDT E Int. 2023, 135, 102800. [Google Scholar] [CrossRef]
- Oswald-Tranta, B. Inductive thermography–review of a non-destructive inspection technique for surface crack detection. Quant. InfraRed Thermogr. J. 2025, 22, 1–25. [Google Scholar] [CrossRef]
- Li, R.; Wang, F.; Yin, P.; Yang, F.; Zhao, J.; Yue, Z.; Liu, L.; Sfarra, S.; Vesala, G.; Yue, H. A review of ultrasonic infrared thermography in non-destructive testing and evaluation (NDT&E): Physical principles, theory, and data processing. Infrared Phys. Technol. 2025, 150, 105961. [Google Scholar]
- Wang, F.; Liu, J.; Mohummad, O.; Wang, Y. Research on debonding defects in thermal barrier coatings structure by thermal-wave radar imaging (TWRI). Int. J. Thermophys. 2018, 39, 71. [Google Scholar] [CrossRef]
- Almond, D.P.; Patel, P. Photothermal Science and Techniques; Chapman & Hall: London, UK, 1996. [Google Scholar]
- Sapieta, M.; Dekýš, V.; Kopas, P.; Jakubovičová, L.; Šavrnoch, Z. The impact of excitation periods on the outcome of lock-in thermography. Materials 2023, 16, 2763. [Google Scholar] [CrossRef]
- Sagarduy-Marcos, D.; Rodríguez-Aseguinolaza, J. Dimensionless numerical sensitivity analysis of narrow cracks by means of infrared lock-in thermography. Int. J. Therm. Sci. 2024, 200, 108935. [Google Scholar] [CrossRef]
- Pérez-Arbulu, J.; Ciria, J.C.; Mendioroz, A.; Celorrio, R.; Salazar, A. Characterization of semi-infinite inhomogeneous delaminations using lock-in thermography. NDT E Int. 2025, 155, 103417. [Google Scholar] [CrossRef]
- Sekhar Yadav, G.C.; Ghali, V.; Subhani, S. Time-Frequency Based Thermal Imaging: An Effective Tool for Quantitative Analysis. Russ. J. Nondestruct. Test. 2023, 59, 1165–1176. [Google Scholar] [CrossRef]
- Yang, R.; He, Y. Optically and non-optically excited thermography for composites: A review. Infrared Phys. Technol. 2016, 75, 26–50. [Google Scholar] [CrossRef]
- Delanthabettu, S.; Menaka, M.; Venkatraman, B.; Raj, B. Defect depth quantification using lock-in thermography. Quant. InfraRed Thermogr. J. 2015, 12, 37–52. [Google Scholar] [CrossRef]
- Ekanayake, S.; Gurram, S.; Schmitt, R.H. Depth determination of defects in CFRP-structures using lock-in thermography. Compos. Part B Eng. 2018, 147, 128–134. [Google Scholar] [CrossRef]
- Zhuo, L.; Xu, Y.; Zhu, J.; Li, C.; Liu, C.; Yi, F. Quantitative evaluation of interfacial defect size and pattern by solving a 3D inverse problem based on step heating thermography. Exp. Mech. 2024, 64, 245–259. [Google Scholar] [CrossRef]
- Salazar, A.; Sagarduy-Marcos, D.; Rodríguez-Aseguinolaza, J.; Mendioroz, A.; Ciria, J.; Celorrio, R. Resolution of multiple semi-infinite delaminations using lock-in infrared thermography. NDT E Int. 2024, 146, 103156. [Google Scholar] [CrossRef]
- D’Accardi, E.; Palumbo, D.; Galietti, U. A comparison among different ways to investigate composite materials with lock-in thermography: The multi-frequency approach. Materials 2021, 14, 2525. [Google Scholar] [CrossRef]
- Wang, H.; Li, W.; Dong, L.; Cai, D.; Wang, H.; Liu, H. Interface debonding defect detection of thermal barrier coatings with laser lock-in thermography based on edge sharpness optimization. Infrared Phys. Technol. 2025, 146, 105744. [Google Scholar] [CrossRef]
- Mulaveesala, R.; Tuli, S. Theory of frequency modulated thermal wave imaging for nondestructive subsurface defect detection. Appl. Phys. Lett. 2006, 89, 191913. [Google Scholar] [CrossRef]
- Subhani, S.; Suresh, B.; Ghali, V. Quantitative subsurface analysis using frequency modulated thermal wave imaging. Infrared Phys. Technol. 2018, 88, 41–47. [Google Scholar] [CrossRef]
- Wang, H.; Chen, H.; He, Y.; Chen, P.; Gong, Z.; Song, M.; Wang, Y.; Giron-Palomares, B. Research on CFRP small-gap defect detection by joint scanning laser thermography based on restored pseudo heat flux. In IEEE Transactions on Instrumentation and Measurement; IEEE: New York, NY, USA, 2025; Early Access. [Google Scholar]
- Zhuo, L.; Yang, X.; Zhu, J.; Huang, Z.; Chao, J.; Xie, W. Size determination of interior defects by reconstruction of subsurface virtual heat flux for step heating thermography. NDT E Int. 2023, 133, 102734. [Google Scholar] [CrossRef]
- Wang, F.; Sheng, J.; Sfarra, S.; Zhou, Y.; Xu, L.; Liu, L.; Chen, M.; Yue, H.; Liu, J. Multimode infrared thermal-wave imaging in non-destructive testing and evaluation (NDT&E): Physical principles, modulated waveform, and excitation heat source. Infrared Phys. Technol. 2023, 135, 104993. [Google Scholar]
- Wang, H.; Hou, Y.; He, Y.; Wen, C.; Giron-Palomares, B.; Duan, Y.; Gao, B.; Vavilov, V.P.; Wang, Y. A Physical-constrained decomposition method of infrared thermography: Pseudo restored heat flux approach based on Ensemble Bayesian Variance Tensor Fraction. IEEE Trans. Ind. Inform. 2023, 20, 3413–3424. [Google Scholar] [CrossRef]
- Zhao, H.; Zhou, Z.; Fan, J.; Li, G.; Sun, G. Application of lock-in thermography for the inspection of disbonds in titanium alloy honeycomb sandwich structure. Infrared Phys. Technol. 2017, 81, 69–78. [Google Scholar] [CrossRef]
- Luo, Z.; Wang, H.; Huang, Y.; Shen, P.; Zheng, E.; Zhang, H. Nondestructive detection of CFRP subsurface defects using transient lock-in thermography. J. Therm. Anal. Calorim. 2024, 150, 8229–8239. [Google Scholar] [CrossRef]
- Ma, B.; Ma, X.; Wang, T.; Zhang, L. Enhancing defect detection in solid materials using low-duty cycle square wave lock-in thermography: A time-efficient and quantitative approach. Eng. Res. Express 2024, 6, 025422. [Google Scholar] [CrossRef]
- Wallbrink, C.; Wade, S.; Jones, R. The effect of size on the quantitative estimation of defect depth in steel structures using lock-in thermography. J. Appl. Phys. 2007, 101, 104907. [Google Scholar] [CrossRef]
- Chatterjee, K.; Tuli, S. Prediction of blind frequency in lock-in thermography using electro-thermal model based numerical simulation. J. Appl. Phys. 2013, 114, 174905. [Google Scholar] [CrossRef]
- Ranjit, S.; Kang, K.; Kim, W. Investigation of lock-in infrared thermography for evaluation of subsurface defects size and depth. Int. J. Precis. Eng. Manuf. 2015, 16, 2255–2264. [Google Scholar] [CrossRef]
- Laureti, S.; Bison, P.; Ferrarini, G.; Zito, R.; Ricci, M. Simultaneous Multi-frequency lock-in Thermography: A new flexible and effective Active Thermography scheme. NDT E Int. 2024, 146, 103144. [Google Scholar] [CrossRef]
- Zhuo, L.; Xu, Y.; Zhu, J.; Chen, H.; Yang, Q. Depth estimation of internal defects from a sensitive frequency using thermal wave radar. NDT E Int. 2025, 154, 103367. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L. Detection of pavement cracks by deep learning models of transformer and UNet. IEEE Trans. Intell. Transp. Syst. 2024, 25, 15791–15808. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, L. A generative adversarial network approach for removing motion blur in the automatic detection of pavement cracks. Comput.-Aided Civ. Infrastruct. Eng. 2024, 39, 3412–3434. [Google Scholar] [CrossRef]
- Jibril, M.U.; Gao, B.; Woo, W.L.; Tian, G.; Khan, N.A.; Zakariyya, R.S.; Muhammad, A.J. Physics-aware state space network with uncertainty quantification for automated defect detection in infrared NDT thermography. NDT E Int. 2025, 158, 103586. [Google Scholar] [CrossRef]
- Ma, B.; Liu, C.; Sun, S.; Zhang, L. Phase-Based Thermal Wave Analysis for Lateral Characterization of Subsurface Defects in Solid Materials via Modeling and Simulation. Materials 2025, 18, 3753. [Google Scholar] [CrossRef] [PubMed]
| Material | Thermal Diffusivity (mm2/s) | Thermal Conductivity (W/(m·K)) | Specific Heat Capacity (J/(kg·K)) | Density (kg/m3) |
|---|---|---|---|---|
| Titanium | 2.32 | 7 | 678 | 4450 |
| Air | 22.24 | 0.026 | 1007 | 1.161 |
| Defect Depth h (mm) | Radii r (mm) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| r/h | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 5 | 6 | 7 | 8 | |
| 6 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 30 | 36 | 42 | 48 | |
| 8 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 40 | 48 | 56 | 64 | |
| 10 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 50 | 60 | 70 | 80 | |
| 12 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 60 | 72 | 84 | 96 | |
| 14 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 70 | 84 | 98 | 112 | |
| 16 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 80 | 96 | 112 | 128 | |
| Radius-to -Depth Ratio | Depth 6 mm | Depth 8 mm | Depth 10 mm | Depth 12 mm | Depth 14 mm | Depth 16 mm | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Radii (mm) | fblind (mHz) | Error (%) | Radii (mm) | fblind (mHz) | Error (%) | Radii (mm) | fblind (mHz) | Error (%) | Radii (mm) | fblind (mHz) | Error (%) | Radii (mm) | fblind (mHz) | Error (%) | Radii (mm) | fblind (mHz) | Error (%) | |
| 0.5 | 3 | 82.1 | −20.47 | 4 | 46.1 | −20.45 | 5 | 29.7 | −20.71 | 6 | 20.5 | −20.53 | 7 | 15.1 | −21.27 | 8 | 11.7 | −20.68 |
| 1.0 | 6 | 71.5 | −14.83 | 8 | 39.7 | −14.28 | 10 | 25.2 | −13.93 | 12 | 17.5 | −14.00 | 14 | 12.8 | −14.51 | 16 | 9.9 | −13.87 |
| 1.5 | 9 | 62.7 | −9.05 | 12 | 34.7 | −8.31 | 15 | 22.4 | −8.70 | 18 | 15.3 | −7.97 | 21 | 11.2 | −8.50 | 24 | 8.7 | −7.82 |
| 2.0 | 12 | 56.9 | −4.53 | 16 | 31.5 | −3.77 | 20 | 20.1 | −3.62 | 24 | 13.9 | −3.35 | 28 | 10.2 | −4.08 | 32 | 7.9 | −3.36 |
| 2.5 | 15 | 53.7 | −1.73 | 20 | 30.3 | −1.88 | 25 | 19.0 | −0.87 | 30 | 13.1 | −0.40 | 35 | 9.6 | −1.13 | 40 | 7.5 | −0.39 |
| 3.0 | 18 | 52.5 | −0.61 | 24 | 29.0 | −0.30 | 30 | 18.5 | 0.46 | 36 | 12.8 | 0.80 | 42 | 9.4 | 0.08 | 48 | 7.3 | 0.83 |
| 3.5 | 21 | 52.4 | −0.47 | 28 | 29.0 | 0.28 | 35 | 18.5 | 0.59 | 42 | 12.7 | 0.88 | 49 | 9.4 | 0.09 | 56 | 7.3 | 0.81 |
| 4.0 | 24 | 52.7 | −0.80 | 32 | 29.2 | −0.05 | 40 | 18.9 | −0.61 | 48 | 12.8 | 0.57 | 56 | 9.4 | −0.14 | 64 | 7.4 | 0.61 |
| 5.0 | 30 | 52.9 | −0.99 | 40 | 29.2 | −0.05 | 50 | 18.9 | −0.61 | 60 | 12.9 | 0.29 | 70 | 9.5 | −0.40 | 80 | 7.4 | 0.35 |
| 6.0 | 36 | 52.9 | −0.99 | 48 | 29.2 | −0.05 | 60 | 18.9 | −0.61 | 72 | 12.9 | 0.29 | 84 | 9.5 | −0.35 | 96 | 7.4 | 0.40 |
| 7.0 | 42 | 52.9 | −0.99 | 56 | 29.2 | −0.05 | 70 | 18.9 | −0.61 | 84 | 12.9 | 0.29 | 98 | 9.5 | −0.35 | 112 | 7.4 | 0.40 |
| 8.0 | 48 | 52.9 | −0.99 | 64 | 29.2 | −0.05 | 80 | 18.9 | −0.61 | 96 | 12.9 | 0.29 | 112 | 9.5 | −0.35 | 128 | 7.4 | 0.40 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, B.; Sun, S.; Zhang, L. Quantitative Depth Estimation in Lock-In Thermography: Modeling and Correction of Lateral Heat Conduction Effects. Materials 2025, 18, 5247. https://doi.org/10.3390/ma18225247
Ma B, Sun S, Zhang L. Quantitative Depth Estimation in Lock-In Thermography: Modeling and Correction of Lateral Heat Conduction Effects. Materials. 2025; 18(22):5247. https://doi.org/10.3390/ma18225247
Chicago/Turabian StyleMa, Botao, Shupeng Sun, and Lin Zhang. 2025. "Quantitative Depth Estimation in Lock-In Thermography: Modeling and Correction of Lateral Heat Conduction Effects" Materials 18, no. 22: 5247. https://doi.org/10.3390/ma18225247
APA StyleMa, B., Sun, S., & Zhang, L. (2025). Quantitative Depth Estimation in Lock-In Thermography: Modeling and Correction of Lateral Heat Conduction Effects. Materials, 18(22), 5247. https://doi.org/10.3390/ma18225247