Numerical Analysis of Cross-Laminated Timber Panels Under Three-Point Bending Using Laminate Theory
Abstract
1. Introduction
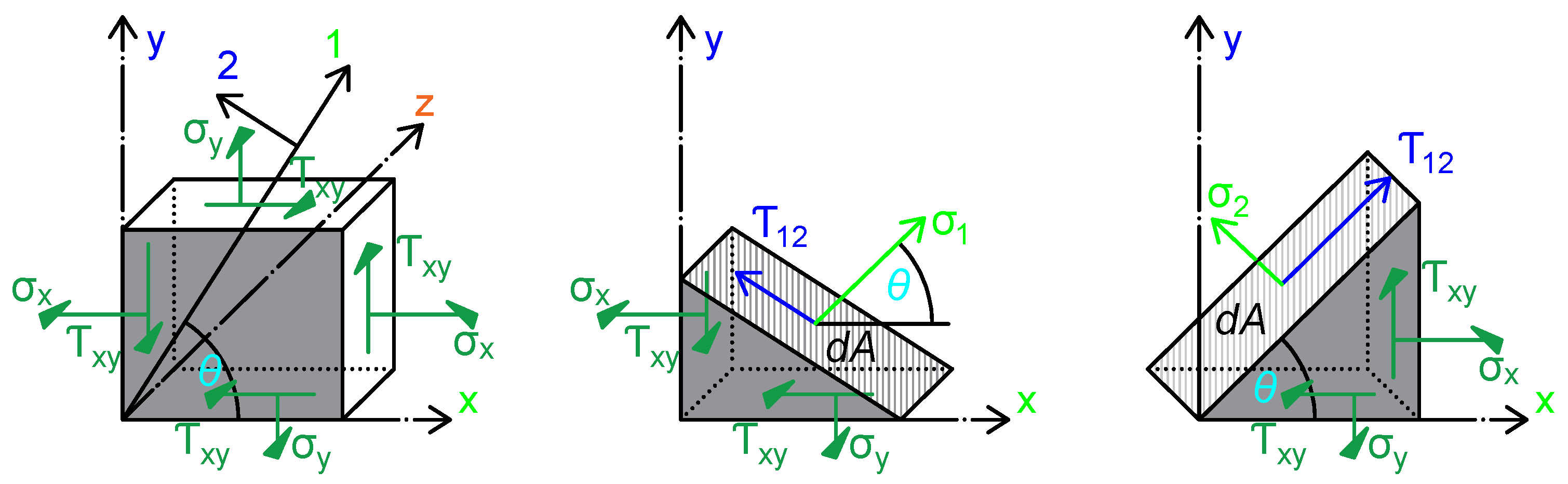
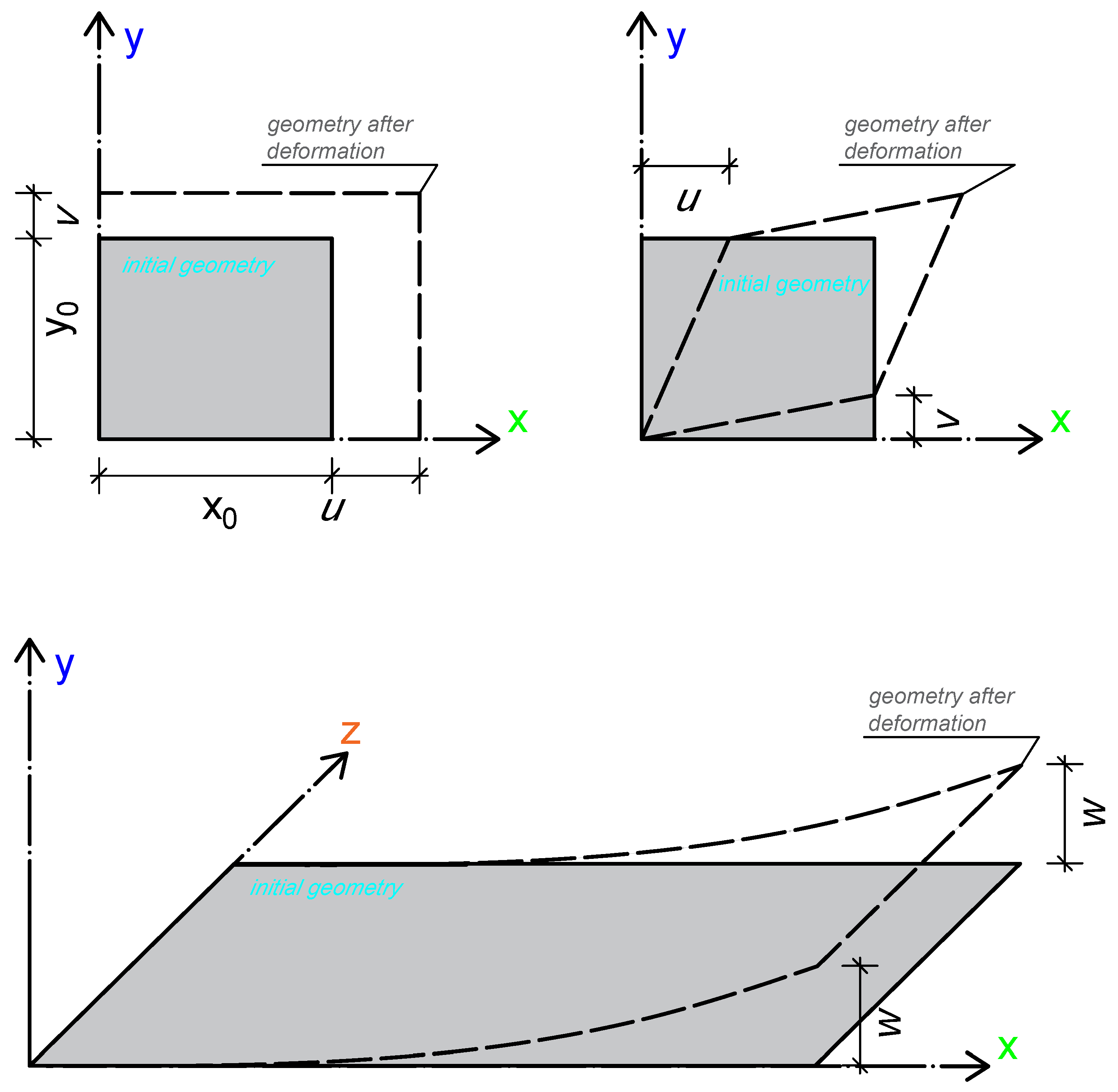
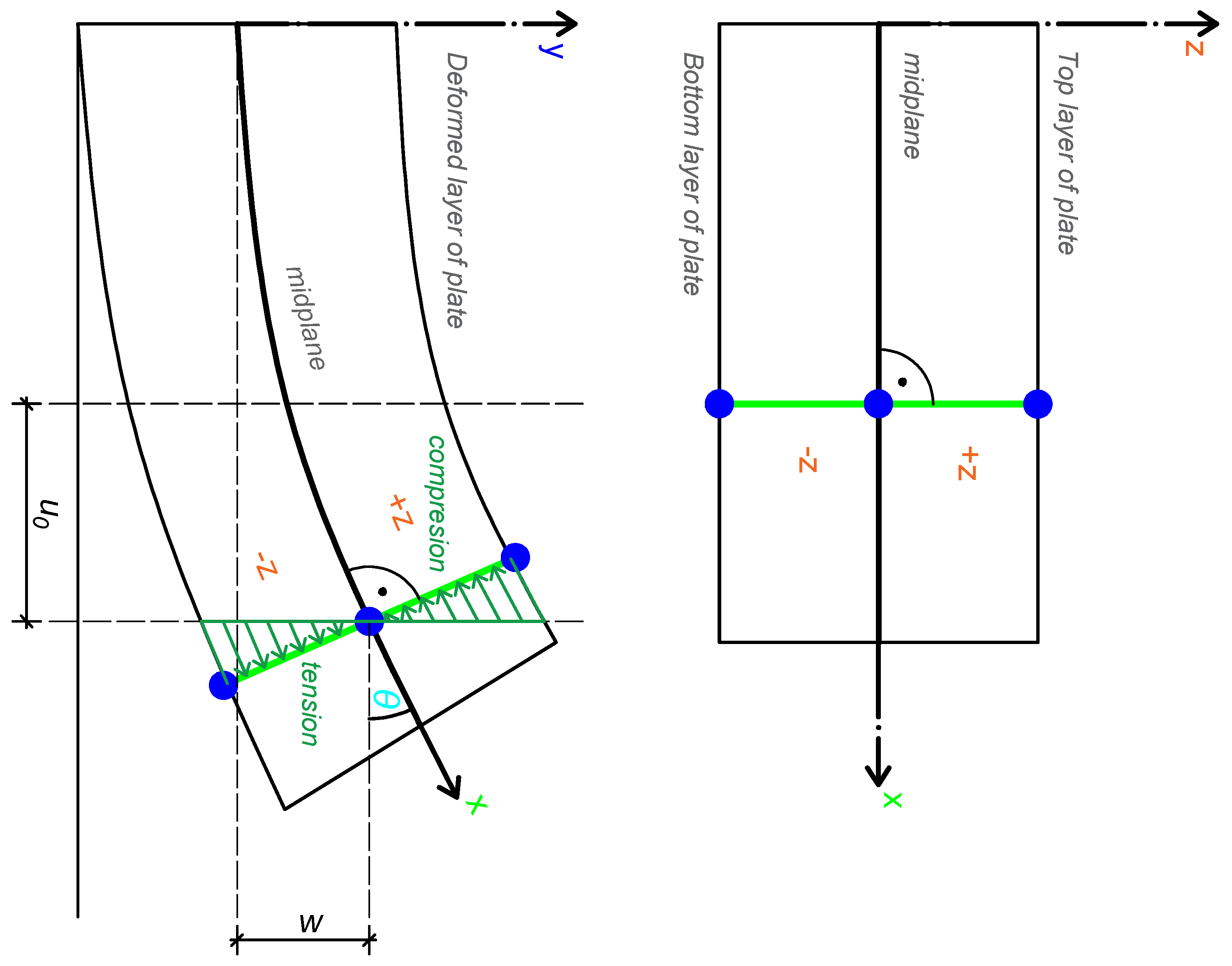
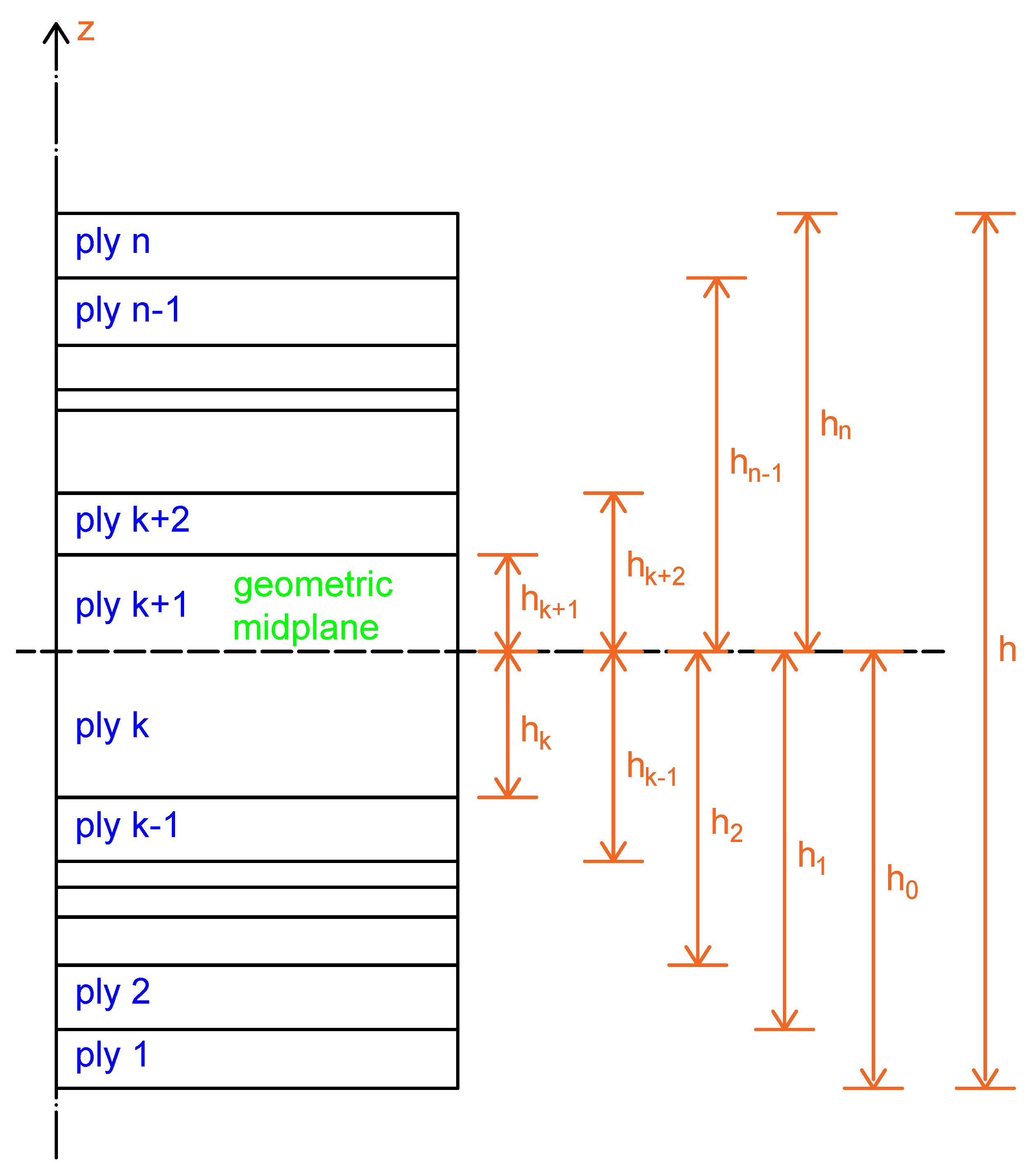
2. The Kirchhoff Plate Theory
2.1. Assumptions for Orthotropic Materials Based on Hooke’s Law
2.2. Mechanical Properties of Laminated Composites
2.3. Engineering Constants Define the Plane Properties of the Laminate
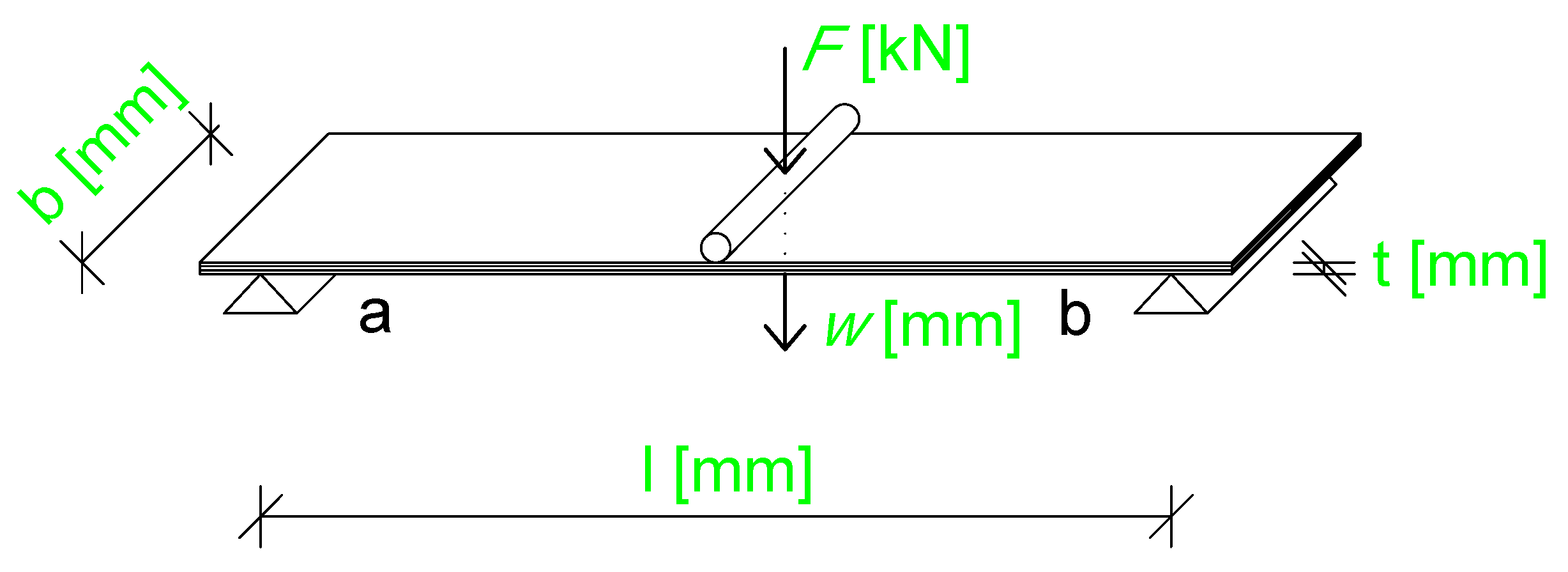
3. Implementation of Plate Theory in Three-Point-Bending
3.1. Application of Kirchhoff Plate Theory Based on Implementing and Defining Differential Relations
3.1.1. Geometry and Meshing
3.1.2. Material Properties
3.1.3. Stiffness Matrices
3.1.4. Global A, B Matrices
3.1.5. Loading
3.1.6. Solution Strategy
4. Materials and Methods
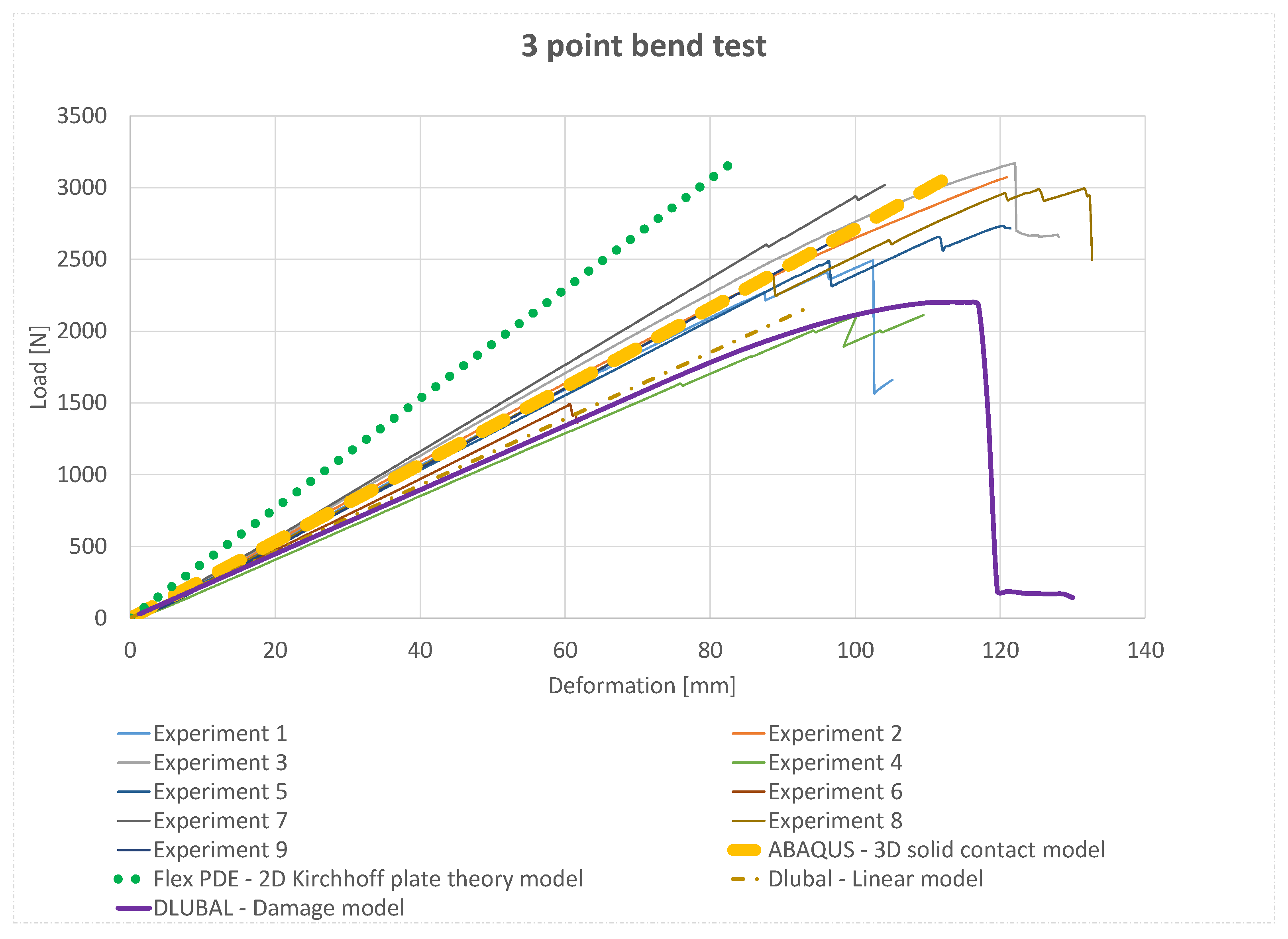
5. Results and Discussion
6. Conclusions
- The proposed methodology provides accurate predictions of load–deflection behaviour, showing strong agreement with laboratory experiments and 3D Abaqus simulations.
- The modular formulation of stiffness matrices (A, B, and D) enables flexible application to both symmetrical and unsymmetrical laminate configurations while explicitly accounting for coupling effects.
- Comparisons with commercial software, literature-based damage models and cohesive zone simulations confirm the robustness and versatility of the developed framework.
- The approach demonstrates computational efficiency while capturing the essential anisotropic and multilayered nature of laminated boards.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Spera, L.; Sciomenta, M.; Bedon, C.; Fragiacomo, M. Out-of-Plane Strengthening of Existing Timber Floors with Cross Laminated Timber Panels Made of Short Supply Chain Beech. Buildings 2024, 14, 749. [Google Scholar] [CrossRef]
- Schickhofer, G.; Brandner, R.; Bauer, H. Introduction to CLT, product properties, strength classes. In Cross Laminated Timber—A Competitive Wood Product for Visionary and Fire Safe Buildings; KTH Royal Institute of Technology: Stockholm, Sweden, 2016. [Google Scholar]
- EN 1991-1-1: Eurocode 1; Actions on Structures—Part 1-1: General Actions—Densities, Self-Weight, Imposed Loads for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2002.
- EN 1998-1: Eurocode 8; Design of Structures for Earthquake Resistance—Art 1: General Rules, Seismic Actions and Rules for Buildings. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- Foster, R.M.; Smith, A.J.; Bodiguel, J.W.D. Cross-laminated timber (CLT): From research to standards. Struct. Eng. Int. 2016, 26, 262–267. [Google Scholar]
- Huang, Z.; Bian, Y.; Ni, C. A rolling shear analysis-based method for determining the apparent stiffness and bending capacity of CLT panel under out-of-plane load. J. Wood Sci. 2024, 70, 8. [Google Scholar] [CrossRef]
- Yang, S.; Lee, H.; Choi, G.; Kang, S. Mechanical properties of ply-lam cross-laminated timbers fabricated with lumber and plywood. Eur. J. Wood Wood Prod. 2024, 82, 189–202. [Google Scholar] [CrossRef]
- Nakagawa, M.; Hiramatsu, Y.; Shindo, K.; Ohki, F.; Miyatake, A. Bending performance of sugi cross-laminated timber (CLT) composed of different thickness laminae. J. Wood Sci. 2025, 71, 22. [Google Scholar] [CrossRef]
- Dinwoodie, J.; Huang, Z.; Bian, Y.; Ni, C. Dynamic and quasi-static evaluation of stiffness properties of CLT: Longitudinal MoE and effective rolling shear modulus. Eur. J. Wood Wood Prod. 2025, 83, 16. [Google Scholar] [CrossRef]
- Tako, D.; Denouwe, D.D.; Messan, A.; Bouchaïr, A. Experimental and numerical investigation of timber connections under shear. Int. J. Adhes. Adhes. 2019, 93, 102445. [Google Scholar] [CrossRef]
- Smith, J.; Doe, J. Numerical analysis of cross-laminated timber panels under bending loads. Appl. Sci. 2022, 12, 1701. [Google Scholar] [CrossRef]
- Kamperidou, V.; Vasileiou, V. Bending Capacity of Middle Joints of Upholstered Furniture Frames. Drv. Ind. 2012, 63, 255–261. [Google Scholar] [CrossRef]
- Nettles, A.T. Basic Mechanics of Laminated Composite Plates; NASA Technical Memorandum NASA TM-109177; NASA Langley Research Center: Huntsville, AL, USA, 1994. [Google Scholar]
- Forest Products Laboratory. Wood Handbook: Wood as an Engineering Material; General Technical Report FPL-GTR-190; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2010. [Google Scholar]
- GmbH, D.S. RFEM 6.10. 2024. Available online: https://www.dlubal.com (accessed on 9 November 2025).
- Sandhaas, C.; Sarnaghi, A.K.; van de Kuilen, J.W. Numerical modelling of timber and timber joints: Computational aspects. Wood Sci. Technol. 2020, 54, 31–61. [Google Scholar] [CrossRef]
- Maimí, P.; Camanho, P.P.; Mayugo, J.; Dávila, C. A continuum damage model for composite laminates: Part I–Constitutive model. Mech. Mater. 2007, 39, 897–908. [Google Scholar] [CrossRef]
- Maimí, P.; Camanho, P.P.; Mayugo, J.A.; Dávila, C.G. A Thermodynamically Consistent Damage Model for Advanced Composites; Technical report; Cranfield University: Wharley End, UK, 2006. [Google Scholar]
- Matzenmiller, A.; Lubliner, J.; Taylor, R.L. A constitutive model for anisotropic damage in fiber-composites. Mech. Mater. 1995, 20, 125–152. [Google Scholar] [CrossRef]
- Gustafsson, P.J. Fracture energy of wood in tension perpendicular to grain. Wood Sci. Technol. 2005, 39, 673–688. [Google Scholar]
- Eberhardsteiner, J.; Duschlbauer, D.; Hofstetter, K.; Serrano, E.; Stepinac, M. Experimental determination and numerical validation of cohesive laws for spruce rolling shear. Eng. Fract. Mech. 2012, 96, 281–295. [Google Scholar]
- Babjak, J.; Sedliacik, J.; Dulova, N. Mechanika Kompozitných Materiálov a Ich Aplikácie; Fakulta Výrobných Technológií, Technická Univerzita v Košiciach: Košice, Slovakia, 2008. [Google Scholar]
- ASTM International. Standard Test Methods of Static Tests of Lumber in Structural Sizes; Number D198 in ASTM Standard; ASTM International: West Conshohocken, PA, USA, 2016. [Google Scholar]
- European Committee for Standardization (CEN). Timber—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties; Number EN 408:2010 in European Standard; CEN: Brussels, Belgium, 2010. [Google Scholar]
- Brandner, R.; Flatscher, G.; Ringhofer, A.; Schickhofer, G.; Thiel, A. Cross laminated timber (CLT): Overview and development. Eur. J. Wood Wood Prod. 2016, 74, 331–351. [Google Scholar] [CrossRef]
- Blass, H.J.; Sandhaas, C. Chapter: Rolling shear in CLT elements. In Timber Engineering—Principles for Design; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
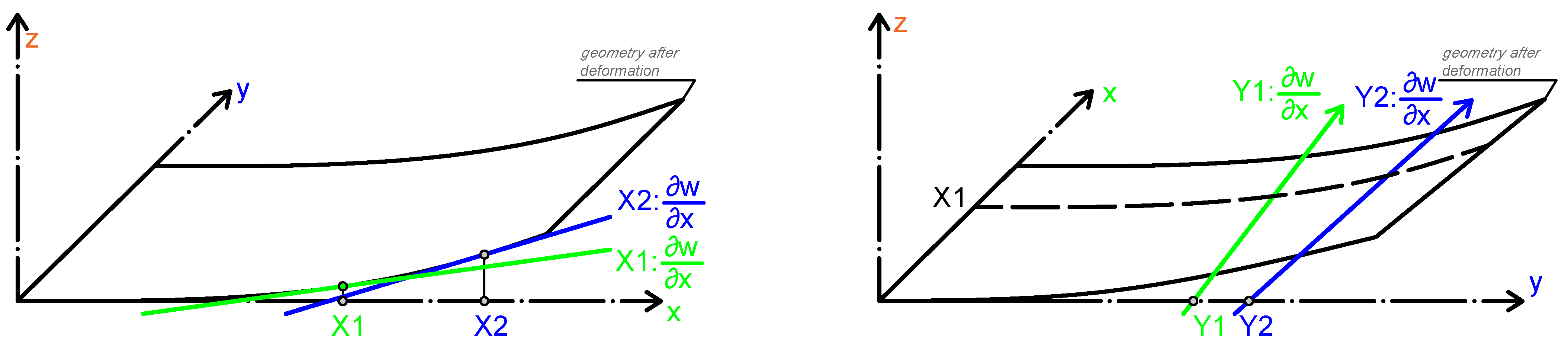



| Linear Elastic Properties | Symbol | Value |
|---|---|---|
| Wood Young’s modulus | 10 GPa | |
| Wood Young’s modulus | 0.33 GPa | |
| Wood Shear modulus | 0.63 GPa | |
| Wood Poisson’s ratio | 0.35 | |
| Polyurethane Young’s modulus | 22 GPa | |
| Polyurethane Shear modulus | 0.25 GPa | |
| Polyurethane Poisson’s ratio | 0.44 |
| Property | Symbol | Value |
|---|---|---|
| Linear elastic properties | ||
| Longitudinal Young’s modulus | 9.6 GPa | |
| Radial Young’s modulus | 1.3 GPa | |
| Shear modulus (L-R) | 0.68 GPa | |
| Shear modulus (L-T) | 0.60 GPa | |
| Poisson’s ratio (L-R) | 0.35 | |
| Poisson’s ratio (L-T) | 0.33 | |
| Strengthproperties | ||
| Tensile strength (parallel to grain) | 33 MPa | |
| Tensile strength (perpendicular to grain) | 3.5 MPa | |
| Compressive strength (parallel to grain) | 37 MPa | |
| Compressive strength (perpendicular to grain) | 4.0 MPa | |
| Shear strength | 6.9 MPa | |
| Non-linear(fracture energy) properties | ||
| Fracture energy (tension, parallel to grain) | 4 N/mm | |
| Fracture energy (tension, perpendicular to grain) | 2 N/mm | |
| Fracture energy (shear) | 1.2 N/mm | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bošanský, M.; Trcala, M. Numerical Analysis of Cross-Laminated Timber Panels Under Three-Point Bending Using Laminate Theory. Materials 2025, 18, 5232. https://doi.org/10.3390/ma18225232
Bošanský M, Trcala M. Numerical Analysis of Cross-Laminated Timber Panels Under Three-Point Bending Using Laminate Theory. Materials. 2025; 18(22):5232. https://doi.org/10.3390/ma18225232
Chicago/Turabian StyleBošanský, Michal, and Miroslav Trcala. 2025. "Numerical Analysis of Cross-Laminated Timber Panels Under Three-Point Bending Using Laminate Theory" Materials 18, no. 22: 5232. https://doi.org/10.3390/ma18225232
APA StyleBošanský, M., & Trcala, M. (2025). Numerical Analysis of Cross-Laminated Timber Panels Under Three-Point Bending Using Laminate Theory. Materials, 18(22), 5232. https://doi.org/10.3390/ma18225232







