Thin Wall Milling at a Maximized Axial Depth of Cut
Abstract
1. Introduction
2. Materials and Methods
3. Results
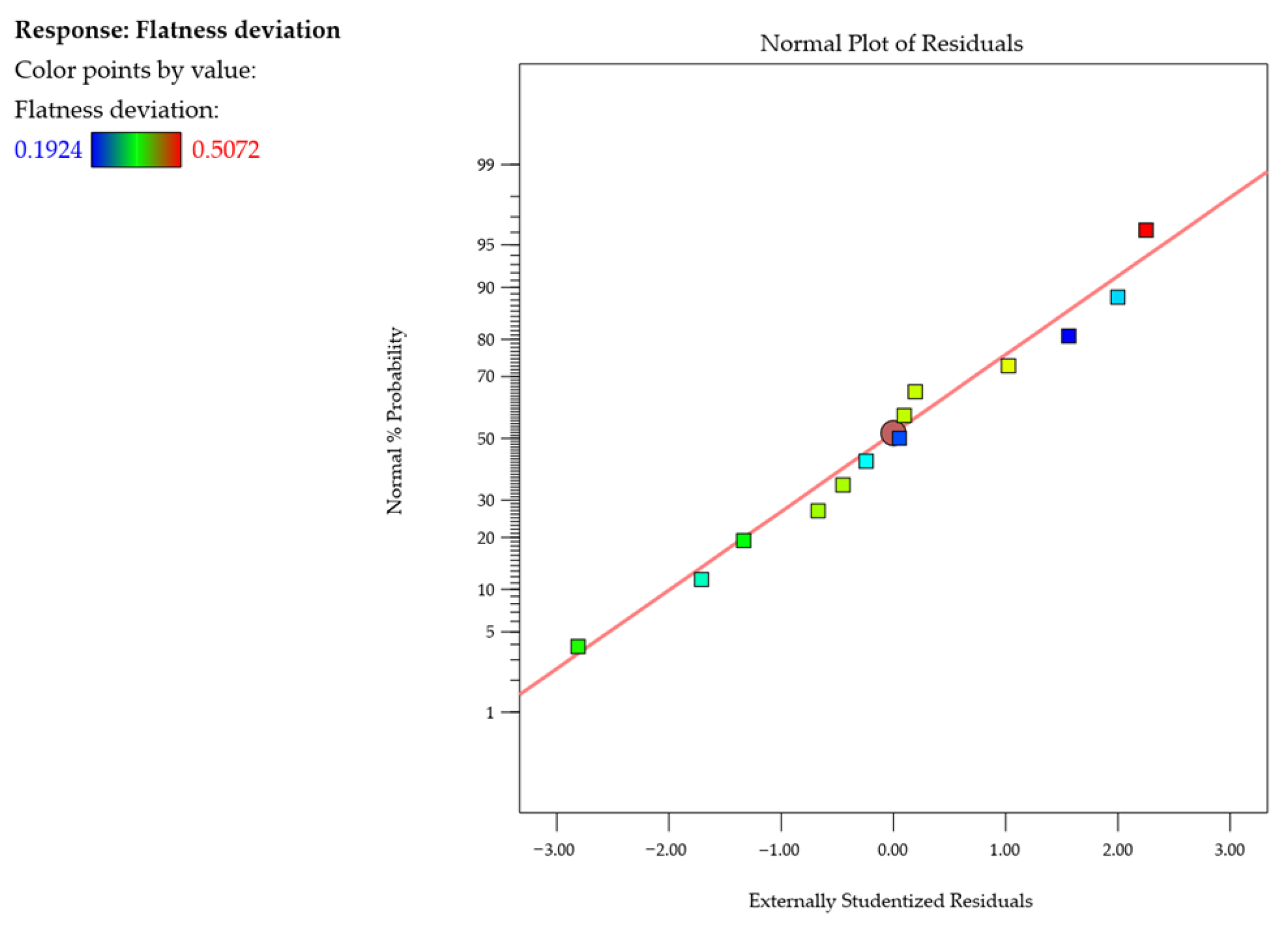
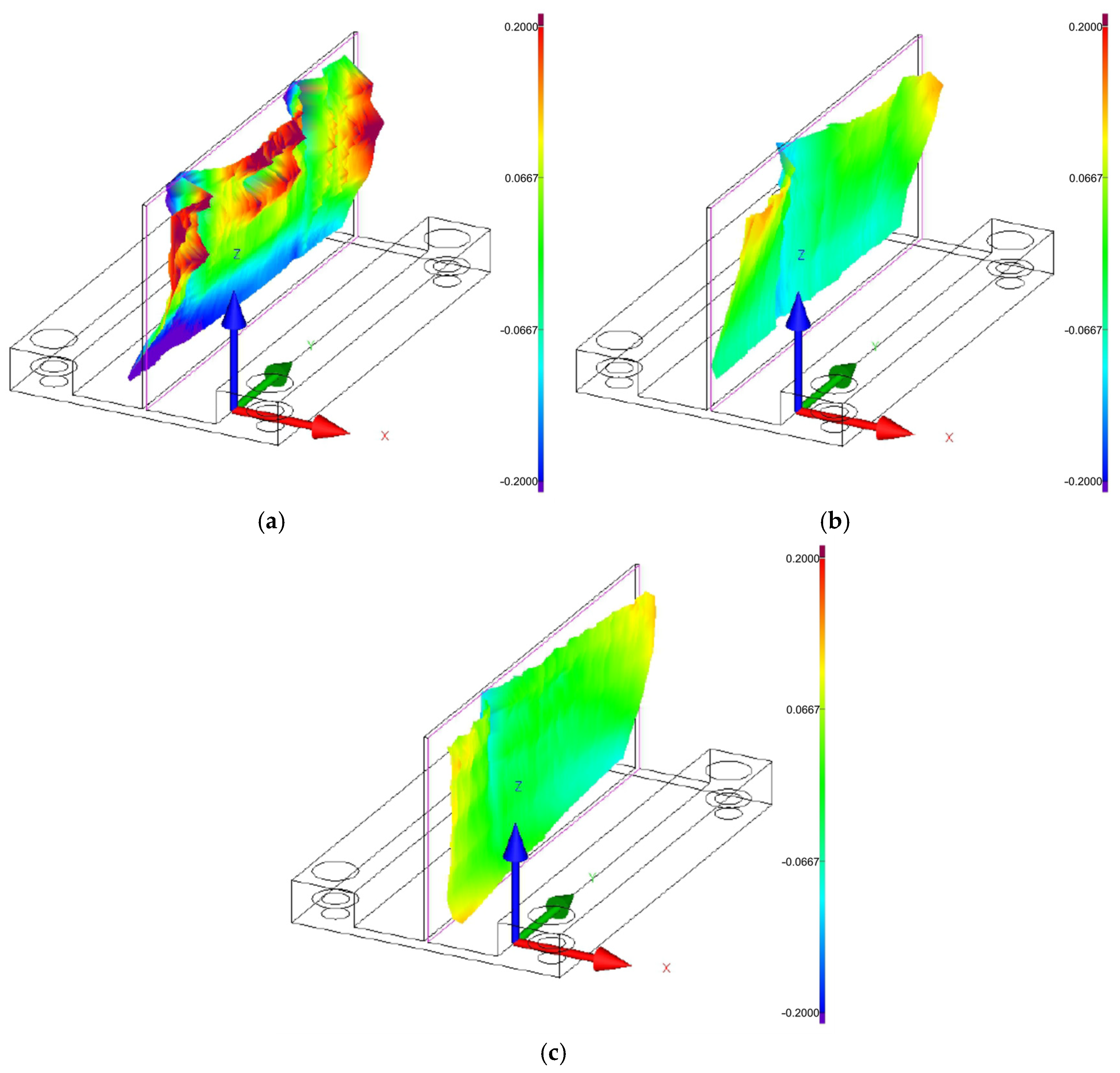
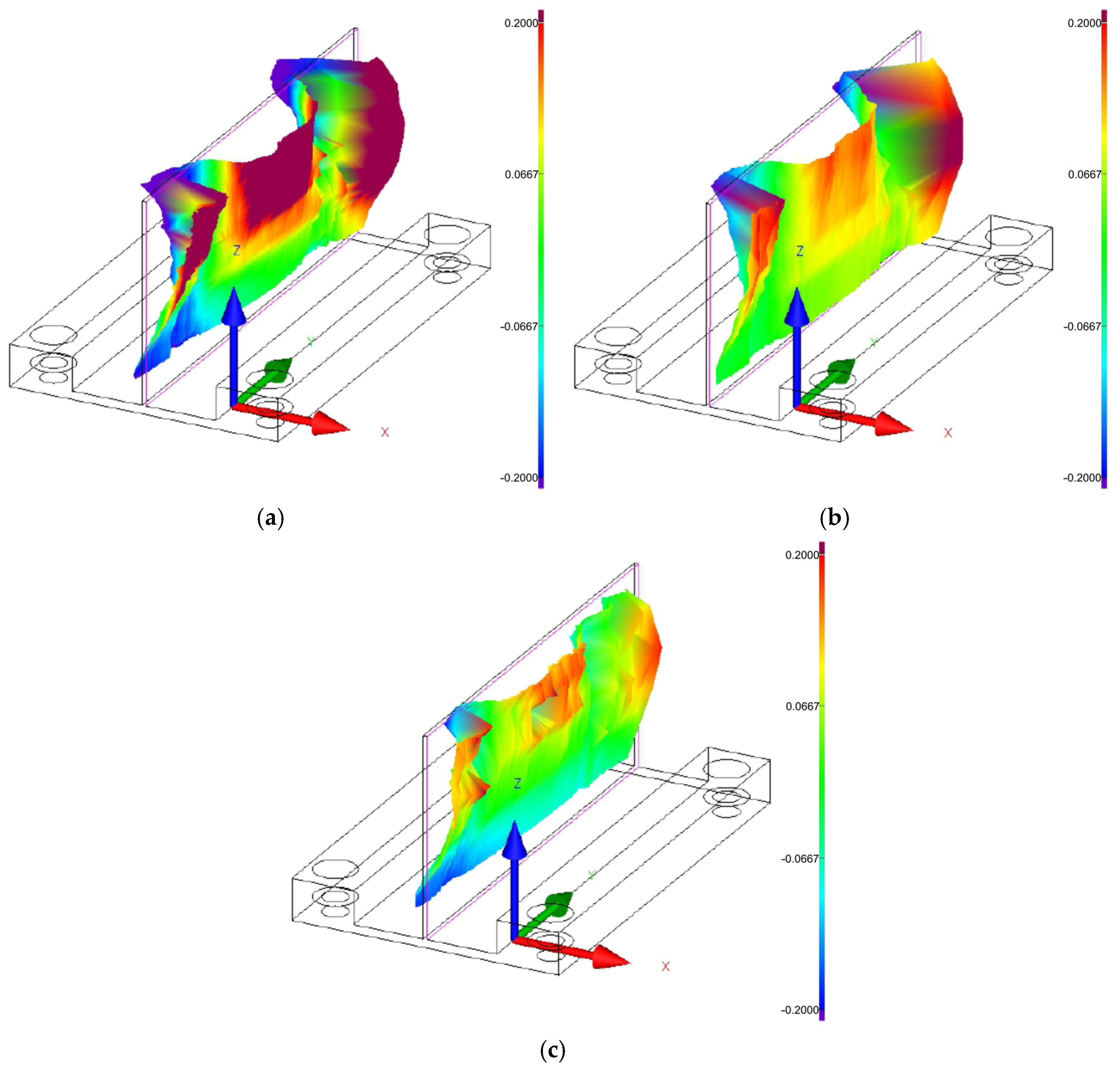
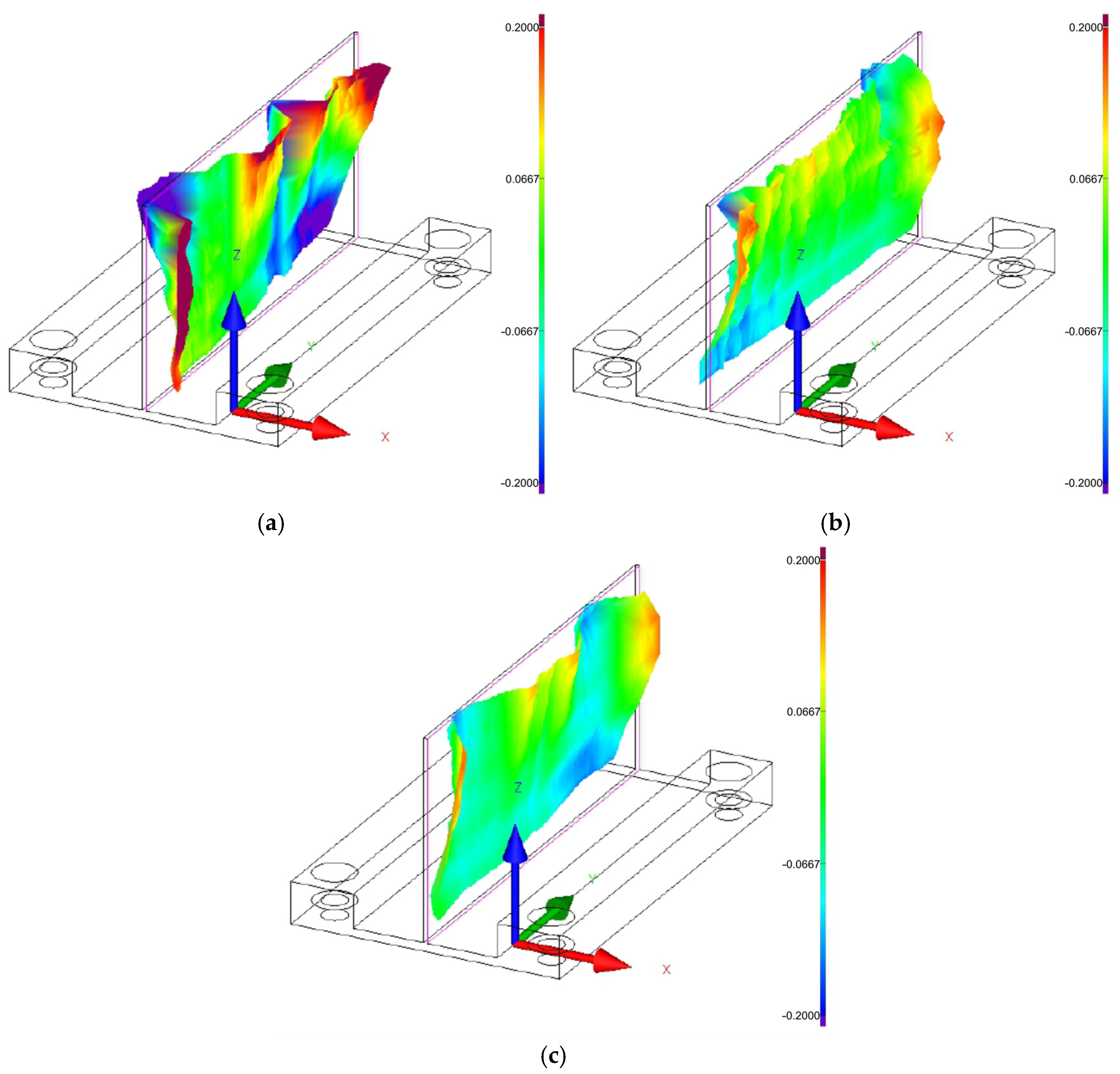
3.1. Flatness Deviation
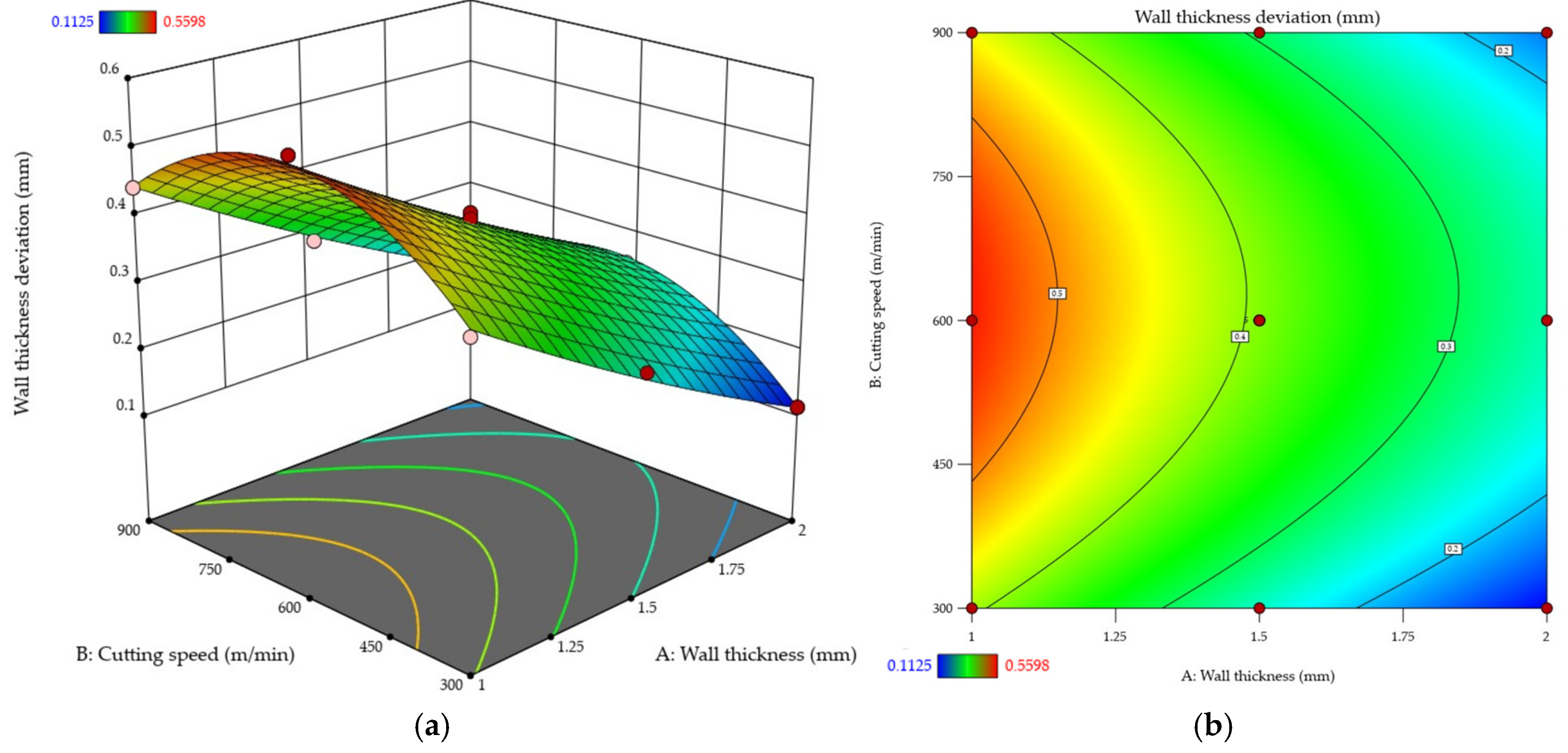
3.2. Wall Thickness Deviation
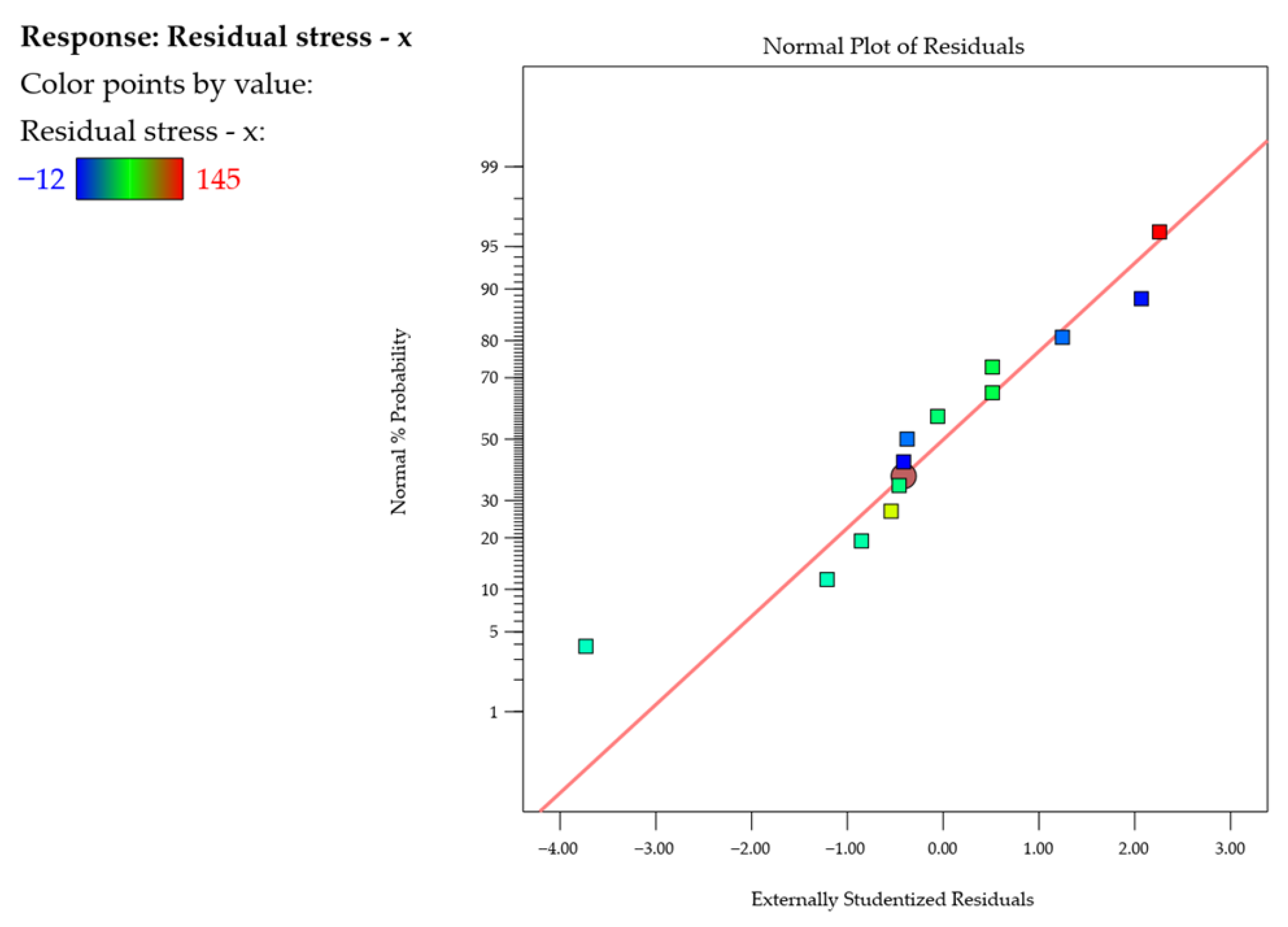
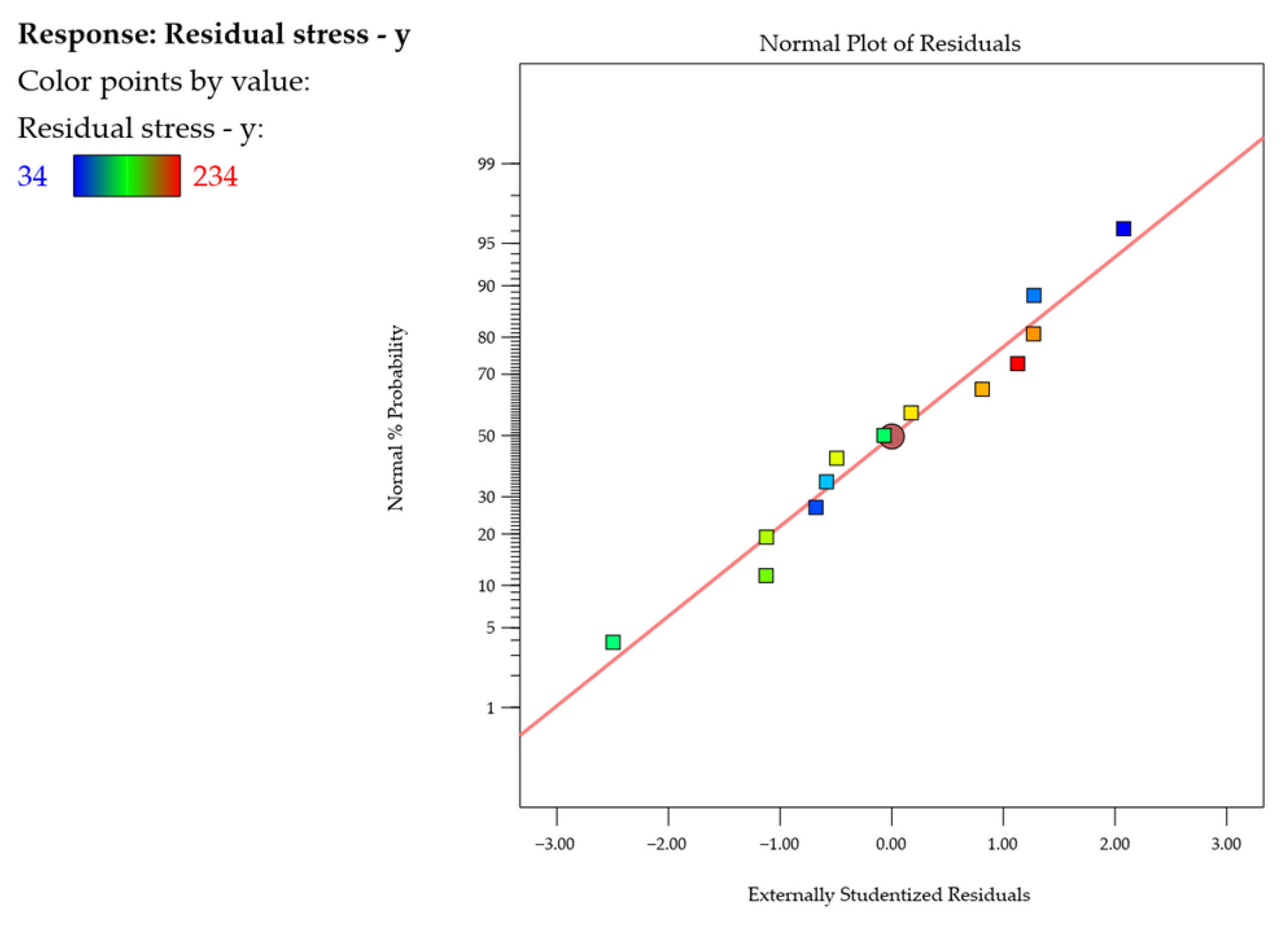
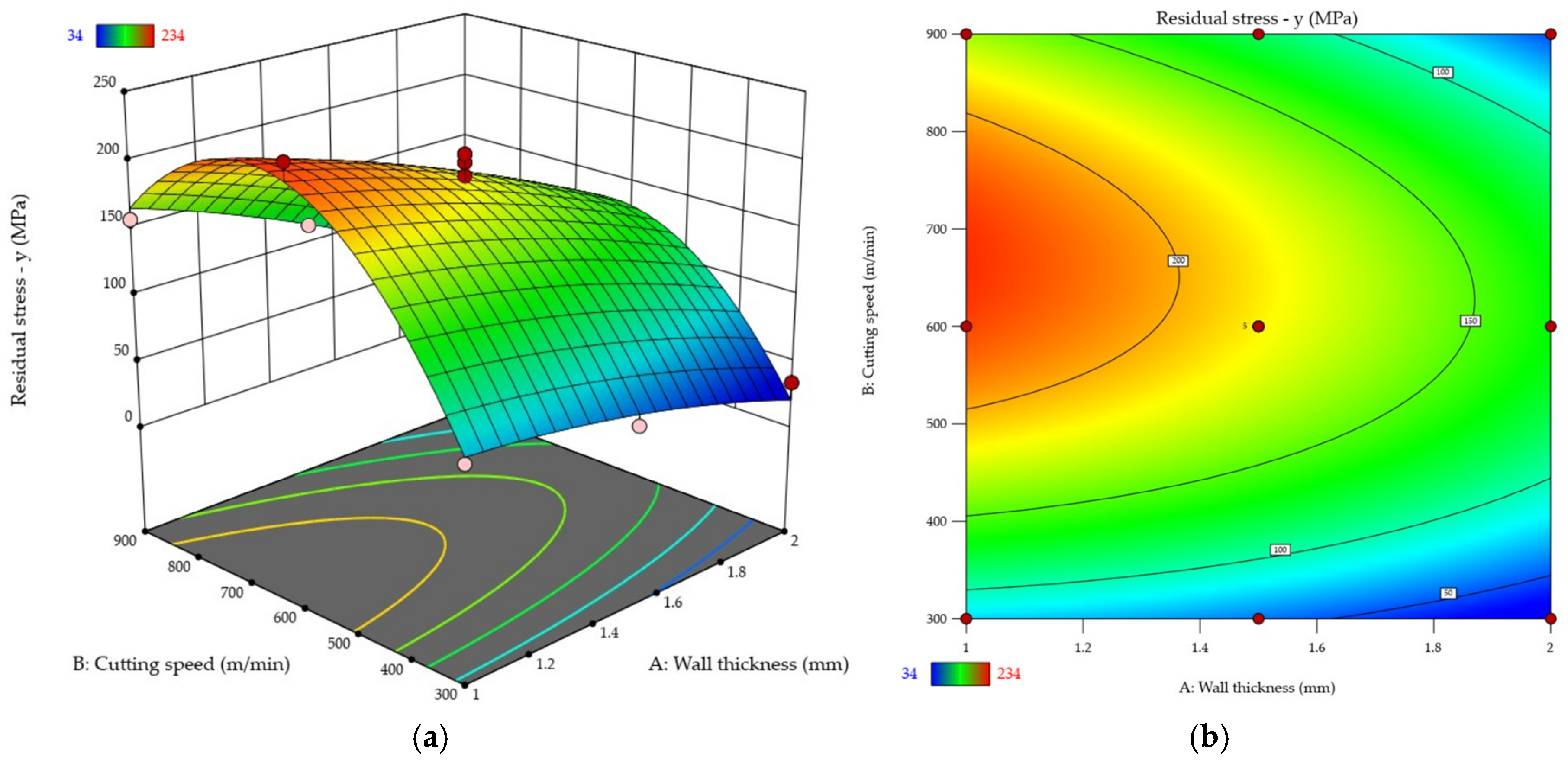
3.3. Residual Stress
4. Discussion
5. Conclusions
- Although thin wall milling at a maximum axial depth of cut is feasible, it largely depends on wall thickness. For the wall thickness t = 1 mm, one could observe the formation of considerable post-machining deformation, while the wall thickness t ≥ 1.5 mm, with the height of 48 mm, made it possible to achieve the required shape and dimensional accuracy.
- Cutting speed has a significant impact on the post-machining deformation of a thin wall and residual stress. For each tested wall thickness, the dependent variables reached the maximum values when the cutting speed was about vc ≈ 600 m/min, followed by their decrease. For the cutting speed vc = 900 m/min, the post-machining deformation of the wall decreased (compared to vc = 600 m/min); nevertheless, it was still higher than the distortion obtained at vc = 300 m/min.
- The examination of the thin-walled part revealed the predominance of tensile stress on the surface, its values being higher in the direction y rather than along x . The highest residual stress occurred at vc ≈ 600 m/min, which probably results from thermal interactions, whereas at vc = 300 m/min and the wall thickness t ≥ 1.5 mm, the compressive stress prevailed (in x direction), which was probably connected with the dominant impact of the cutting edge. In contrast, an increase in the wall thickness caused a decrease in the residual stress.
- The response surface regression models showed a very good fit to the experimental results (R2 > 0.96), which confirms that they can be used for predicting the post-machining deformation of thin walls and residual stress under similar machining conditions.
- The results of this study have a practical application in industry, particularly the aerospace branch, demonstrating that the optimization of milling performed at a maximum axial depth of cut should include selecting the appropriate cutting speed and wall thickness already in the part design stage. The results can serve as a basis for developing technological guidelines for machining parts made of aluminum alloys.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Run | Actual Variable 1: Wall Thickness A [mm] | Coded Variable 1: Wall Thickness A [-] | Actual Variable 1: Cutting Speed B [m/min] | Coded Variable 1: Cutting Speed B [-] | Response 1: Flatness Deviation fd [mm] | Response 2: Wall Deviation Δt [mm] | Response 3: Residual Stress—x σx [MPa] | Response 4: Residual Stress—y σy [MPa] |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | −1 | 300 | −1 | 0.2912 | 0.3984 | 37 | 72 |
| 2 | 1.5 | 0 | 300 | −1 | 0.2116 | 0.2586 | −9 | 49 |
| 3 | 1.5 | 0 | 600 | 0 | 0.4208 | 0.3752 | 55 | 199 |
| 4 | 1 | −1 | 900 | +1 | 0.3470 | 0.4425 | 99 | 157 |
| 5 | 2 | +1 | 600 | 0 | 0.3596 | 0.2515 | 47 | 111 |
| 6 | 1.5 | 0 | 600 | 0 | 0.4096 | 0.3952 | 55 | 189 |
| 7 | 1.5 | 0 | 900 | +1 | 0.2732 | 0.2857 | 6 | 115 |
| 8 | 1 | −1 | 600 | 0 | 0.5072 | 0.5598 | 145 | 234 |
| 9 | 2 | +1 | 300 | −1 | 0.1924 | 0.1125 | −12 | 34 |
| 10 | 1.5 | 0 | 600 | 0 | 0.4109 | 0.4060 | 41 | 205 |
| 11 | 2 | +1 | 900 | +1 | 0.2590 | 0.1745 | 5 | 58 |
| 12 | 1.5 | 0 | 600 | 0 | 0.3998 | 0.3871 | 49 | 178 |
| 13 | 1.5 | 0 | 600 | 0 | 0.4025 | 0.3971 | 38 | 169 |
References
- Kurpiel, S.; Cudok, B.; Zagórski, K.; Cieślik, J.; Skrzypkowski, K.; Brostow, W. Influence of Tools and Cutting Strategy on Milling Conditions and Quality of Horizontal Thin-Wall Structures of Titanium Alloy Ti6Al4V. Sensors 2023, 23, 9905. [Google Scholar] [CrossRef]
- Wang, L.; Yue, C.; Ma, W.; Liu, X.; Li, C.; Liang, S.Y. Prediction of Residual Stress and Deflection in Multi-Process Milling of Large Thin-Walled Components with Initial Bulk Residual Stress. Meas. J. Int. Meas. Confed. 2025, 247, 116814. [Google Scholar] [CrossRef]
- Li, W.; Wang, L.; Yu, G. Force-Induced Deformation Prediction and Flexible Error Compensation Strategy in Flank Milling of Thin-Walled Parts. J. Mater. Process. Technol. 2021, 297, 117258. [Google Scholar] [CrossRef]
- Cheng, D.J.; Xu, F.; Xu, S.H.; Zhang, C.Y.; Zhang, S.W.; Kim, S.J. Minimization of Surface Roughness and Machining Deformation in Milling of Al Alloy Thin-Walled Parts. Int. J. Precis. Eng. Manuf. 2020, 21, 1597–1613. [Google Scholar] [CrossRef]
- Bałon, P.; Rejman, E.; Świątoniowski, A.; Kiełbasa, B.; Smusz, R.; Szostak, J.; Cieślik, J.; Kowalski, Ł. Thin-Walled Integral Constructions in Aircraft Industry. Procedia Manuf. 2020, 47, 498–504. [Google Scholar] [CrossRef]
- Del Sol, I.; Rivero, A.; de Lacalle, L.N.L.; Gamez, A.J. Thin-Wall Machining of Light Alloys: A Review of Models and Industrial Approaches. Materials 2019, 12, 2012. [Google Scholar] [CrossRef] [PubMed]
- Anh, N.T.; Tung, T.T. Methodical Approach to Fixture Design in the Milling of Thin-Walled Mechanical Components. Results Eng. 2025, 27, 106518. [Google Scholar] [CrossRef]
- Yiyang, Z.; Jian, M.; Gang, L.; Man, Z. A Review on Error Generation and Control in Efficient Precision Machining of Thin-Walled Parts. Int. J. Adv. Manuf. Technol. 2024, 133, 2083–2101. [Google Scholar] [CrossRef]
- Weber, D.; Kirsch, B.; D’Elia, C.R.; Linke, B.S.; Hill, M.R.; Aurich, J.C. Simulation-Based Investigation of the Distortion of Milled Thin-Walled Aluminum Structural Parts Due to Residual Stresses. In Proceedings of the 3rd Conference on Physical Modeling for Virtual Manufacturing Systems and Processes, Pacific Grove, CA, USA, 19–23 June 2023; Springer International Publishing: Berlin/Heidelberg, Germany, 2023; pp. 149–169. [Google Scholar]
- Korpysa, J.; Habrat, W. Dimensional Accuracy after Precision Milling of Magnesium Alloys Using Coated and Uncoated Cutting Tools. Materials 2024, 17, 5578. [Google Scholar] [CrossRef]
- Li, Y.; Liu, C.; Hao, X.; Gao, J.X.; Maropoulos, P.G. Responsive Fixture Design Using Dynamic Product Inspection and Monitoring Technologies for the Precision Machining of Large-Scale Aerospace Parts. CIRP Ann. Manuf. Technol. 2015, 64, 173–176. [Google Scholar] [CrossRef]
- Bałon, P.; Rejman, E.; Smusz, R.; Szostak, J.; Kiełbasa, B. High Speed Milling in Thin-Walled Aircraft Structures. Appl. Comput. Sci. 2018, 14, 82–95. [Google Scholar] [CrossRef]
- Fang, Z.; Qian, S.; Wang, C.; Wu, J.; Shen, B. Milling Deformation Prediction for Thin-Walled Components Based on Fusion Model. Int. J. Adv. Manuf. Technol. 2024, 135, 3437–3449. [Google Scholar] [CrossRef]
- Cerutti, X.; Mocellin, K. Influence of the Machining Sequence on the Residual Stress Redistribution and Machining Quality: Analysis and Improvement Using Numerical Simulations. Int. J. Adv. Manuf. Technol. 2016, 83, 489–503. [Google Scholar] [CrossRef]
- Hussain, A.; Lazoglu, I. Distortion in Milling of Structural Parts. CIRP Ann. Manuf. Technol. 2019, 68, 105–108. [Google Scholar] [CrossRef]
- Ciecieląg, K. Evaluation of Machinability Indicators in Milling of Thin-Walled Composite Structures. Adv. Sci. Technol. Res. J. 2024, 18, 202–212. [Google Scholar] [CrossRef]
- Czyżycki, J.; Marciniak-Podsadna, L.; Twardowski, P. Classification of Deflections of Thin-Walled Elements Made of EN AW-7075A Aluminum Alloy during Milling. Adv. Sci. Technol. Res. J. 2023, 17, 301–314. [Google Scholar] [CrossRef]
- Chuchala, D.; Dobrzynski, M.; Pimenov, D.Y.; Orlowski, K.A.; Krolczyk, G.; Giasin, K. Surface Roughness Evaluation in Thin EN AW-6086-T6 Alloy Plates after Face Milling Process with Different Strategies. Materials 2021, 14, 3036. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Yue, C.; Xu, Y.; Liu, X.; Wang, L.; Hu, D. Simulation Study on Multi-Process Milling Deformation of Frame Thin-Walled Parts Considering Initial Residual Stress. Int. J. Adv. Manuf. Technol. 2025, 136, 5553–5568. [Google Scholar] [CrossRef]
- Yang, Y.; Li, M.; Li, K.R. Comparison and Analysis of Main Effect Elements of Machining Distortion for Aluminum Alloy and Titanium Alloy Aircraft Monolithic Component. Int. J. Adv. Manuf. Technol. 2014, 70, 1803–1811. [Google Scholar] [CrossRef]
- Lukic, D.; Cep, R.; Vukman, J.; Antic, A.; Djurdjev, M.; Milosevic, M. Multi-Criteria Selection of the Optimal Parameters for High-Speed Machining of Aluminum Alloy AL7075 Thin-Walled Parts. Metals 2020, 10, 1570. [Google Scholar] [CrossRef]
- Li, Z.; Zeng, Z.; Yang, Y.; Ouyang, Z.; Ding, P.; Sun, J.; Zhu, S. Research Progress in Machining Technology of Aerospace Thin-Walled Components. J. Manuf. Process. 2024, 119, 463–482. [Google Scholar] [CrossRef]
- Jiang, X.; Wang, Y.; Ding, Z.; Li, H. An Approach to Predict the Distortion of Thin-Walled Parts Affected by Residual Stress during the Milling Process. Int. J. Adv. Manuf. Technol. 2017, 93, 4203–4216. [Google Scholar] [CrossRef]
- Zhang, S.; Shi, H.; Qi, J.; Sha, Z.; Ma, F. Prediction of Residual Stress in Milling Large or Medium-Sized Thin-Walled Parts Based on Equivalent Loads. J. Manuf. Process. 2025, 151, 282–297. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Z.; Zhang, D.; Luo, M. Milling Distortion Prediction for Thin-Walled Component Based on the Average MIRS in Specimen Machining. Int. J. Adv. Manuf. Technol. 2020, 111, 3379–3392. [Google Scholar] [CrossRef]
- Weber, D.; Kirsch, B.; Chighizola, C.R.; D’Elia, C.R.; Linke, B.S.; Hill, M.R.; Aurich, J.C. Analysis of Machining-Induced Residual Stresses of Milled Aluminum Workpieces, Their Repeatability, and Their Resulting Distortion. Int. J. Adv. Manuf. Technol. 2021, 115, 1089–1110. [Google Scholar] [CrossRef]
- Zawada-Michałowska, M.; Pieśko, P.; Mrówka-Nowotnik, G.; Nowotnik, A.; Legutko, S. Effect of the Technological Parameters of Milling on Residual Stress in the Surface Layer of Thin-Walled Plates. Materials 2024, 17, 1193. [Google Scholar] [CrossRef] [PubMed]
- Chighizola, C.R.; D’Elia, C.R.; Jonsson, J.E.; Weber, D.; Kirsch, B.; Aurich, J.C.; Linke, B.S.; Hill, M.R. The Effect of Bulk Residual Stress on Milling-Induced Residual Stress and Distortion. Exp. Mech. 2022, 62, 1437–1459. [Google Scholar] [CrossRef]
- Huang, X.; Sun, J.; Li, J. Effect of Initial Residual Stress and Machining-Induced Residual Stress on the Deformation of Aluminium Alloy Plate. Stroj. Vestn. J. Mech. Eng. 2015, 61, 131–137. [Google Scholar] [CrossRef]
- Akhtar, W.; Lazoglu, I.; Liang, S.Y. Prediction and Control of Residual Stress-Based Distortions in the Machining of Aerospace Parts: A Review. J. Manuf. Process. 2022, 76, 106–122. [Google Scholar] [CrossRef]
- Masoudi, S.; Amini, S.; Saeidi, E.; Eslami-Chalander, H. Effect of Machining-Induced Residual Stress on the Distortion of Thin-Walled Parts. Int. J. Adv. Manuf. Technol. 2015, 76, 597–608. [Google Scholar] [CrossRef]
- Cerutti, X.; Mocellin, K. Parallel Finite Element Tool to Predict Distortion Induced by Initial Residual Stresses during Machining of Aeronautical Parts. Int. J. Mater. Form. 2015, 8, 255–268. [Google Scholar] [CrossRef]
- Kuczmaszewski, J.; Łogin, W.; Pieśko, P.; Zagórski, I. State of Residual Stresses after the Process of Milling Selected Aluminium Alloys. Adv. Sci. Technol. Res. J. 2018, 12, 63–73. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, Y.; Zhou, J.; Zhan, K.; Ding, Z.; Liang, S.Y. Residual Stress Generation and Evaluation in Milling: A Review. Int. J. Adv. Manuf. Technol. 2023, 126, 3783–3812. [Google Scholar] [CrossRef]
- Yue, Q.; He, Y.; Li, Y.; Tian, S. Investigation on Effects of Single- and Multiple-Pass Strategies on Residual Stress in Machining Ti-6Al-4V Alloy. J. Manuf. Process. 2022, 77, 272–281. [Google Scholar] [CrossRef]
- Zheng, Y.; Tian, Y.; Ma, J.; Zhang, F.; Cui, X.; Ren, L. Residual Stress Formation Mechanism Considering Cutting Energy in Milling of 7075 Aluminum Alloy. Int. J. Adv. Manuf. Technol. 2024, 131, 3039–3055. [Google Scholar] [CrossRef]
- Aijun, T.; Zhanqiang, L. Deformations of Thin-Walled Plate Due to Static End Milling Force. J. Mater. Process. Technol. 2008, 206, 345–351. [Google Scholar] [CrossRef]
- Tunc, L.T.; Gulmez, D.A. Tool Path Strategies for Efficient Milling of Thin-Wall Features. J. Manuf. Mater. Process. 2024, 8, 169. [Google Scholar] [CrossRef]
- Lassila, A.A.; Svensson, D.; Wang, W.; Andersson, T. Numerical Evaluation of Cutting Strategies for Thin-Walled Parts. Sci. Rep. 2024, 14, 1459. [Google Scholar] [CrossRef]
- Wang, J.; Ibaraki, S.; Matsubara, A. A Cutting Sequence Optimization Algorithm to Reduce the Workpiece Deformation in Thin-Wall Machining. Precis. Eng. 2017, 50, 506–514. [Google Scholar] [CrossRef]
- Elhendawy, G.A.; El-Taybany, Y. Evaluation of Different Milling Strategies on the Performance of Aluminium Thin-Walled Parts. Int. J. Mach. Mach. Mater. 2024, 26, 85–96. [Google Scholar] [CrossRef]
- Agarwal, A.; Desai, K.A. Tool and Workpiece Deflection Induced Flatness Errors in Milling of Thin-Walled Components. Procedia CIRP 2020, 93, 1411–1416. [Google Scholar] [CrossRef]
- Zhang, S.; Bi, Q.; Ji, Y.; Wang, Y. Real-Time Thickness Compensation in Mirror Milling Based on Modified Smith Predictor and Disturbance Observer. Int. J. Mach. Tools Manuf. 2019, 144, 103427. [Google Scholar] [CrossRef]
- Soori, M. Deformation Error Compensation in 5-Axis Milling Operations of Turbine Blades. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 289. [Google Scholar] [CrossRef]
- Gao, H.; Li, X.; Wu, Q.; Lin, M.; Zhang, Y. Effects of Residual Stress and Equivalent Bending Stiffness on the Dimensional Stability of the Thin-Walled Parts. Int. J. Adv. Manuf. Technol. 2022, 119, 4907–4924. [Google Scholar] [CrossRef]
- Liu, C.; Sun, J.; Li, Y.; Li, J. Investigation on the Milling Performance of Titanium Alloy Thin-Walled Part with Air Jet Assistance. Int. J. Adv. Manuf. Technol. 2018, 95, 2865–2874. [Google Scholar] [CrossRef]
- Tan, Z.; Wang, Y.; Xu, K. Stress Deformation Simulation for Optimizing Milling Thin-Walled Ti-6Al-4 V Titanium Alloy Parts. Int. J. Interact. Des. Manuf. 2024, 18, 265–273. [Google Scholar] [CrossRef]
- Wu, D.; Wang, H.; Peng, J.; Zhang, K.; Yu, J.; Zheng, X.; Chen, Y. Machining Fixture for Adaptive CNC Machining Process of Near-Net-Shaped Jet Engine Blade. Chin. J. Aeronaut. 2020, 33, 1311–1328. [Google Scholar] [CrossRef]
- Gu, H.; Qin, Y.; Chen, Y. The Frame Thin-Walled Parts’ Optimization Method about Processing Technology and Tool Path Parameters. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 657. [Google Scholar] [CrossRef]
- Bałon, P.; Rejman, E.; Smusz, R.; Szostak, J.; Kiełbasa, B. Implementation of High Speed Machining in Thin-Walled Aircraft Integral Elements. Open Eng. 2018, 8, 162–169. [Google Scholar] [CrossRef]
- Zawada-Michałowska, M.; Kuczmaszewski, J.; Legutko, S.; Pieśko, P. Techniques for Thin-Walled Element Milling with Respect to Minimising Post-Machining Deformations. Materials 2020, 13, 4723. [Google Scholar] [CrossRef] [PubMed]
- ISCAR LTD. Manufacturer of Metalworking Tools. Available online: https://www.iscar.com/en-hq/home (accessed on 1 September 2025).
- Kyocera SGS Solid Carbide Tools. Available online: https://www.kyocera-sgstool.com/ (accessed on 1 September 2025).
- Seco Tools. Available online: https://www.secotools.com/ (accessed on 1 September 2025).
- Li, Z.; Yan, Q.; Tang, K. Multi-Pass Adaptive Tool Path Generation for Flank Milling of Thin-Walled Workpieces Based on the Deflection Constraints. J. Manuf. Process. 2021, 68, 690–705. [Google Scholar] [CrossRef]
- Rai, J.K.; Xirouchakis, P. Finite Element Method Based Machining Simulation Environment for Analyzing Part Errors Induced during Milling of Thin-Walled Components. Int. J. Mach. Tools Manuf. 2008, 48, 629–643. [Google Scholar] [CrossRef]
- Singh, A. Experimental Investigations on Surface Integrity in Thin Structure Machining of Aluminum 6061-T6. J. Mater. Eng. Perform. 2025, 34, 1959–1973. [Google Scholar] [CrossRef]
- Zawada-Michałowska, M. The Application of an Optical Measurement System to Investigate Strains in a Thin-Walled Element During Milling. In Proceedings of the 2025 IEEE 12th International Workshop on Metrology for AeroSpace (MetroAeroSpace), Naples, Italy, 18–20 June 2025; pp. 639–643. [Google Scholar]
- Gang, L. Study on Deformation of Titanium Thin-Walled Part in Milling Process. J. Mater. Process. Technol. 2009, 209, 2788–2793. [Google Scholar] [CrossRef]
- Si-meng, L.; Xiao-dong, S.; Xiao-bo, G.; Dou, W. Simulation of the Deformation Caused by the Machining Cutting Force on Thin-Walled Deep Cavity Parts. Int. J. Adv. Manuf. Technol. 2017, 92, 3503–3517. [Google Scholar] [CrossRef]
- Rajewski, J.; Dobrzyńska-Inger, A. Application of Response Surface Methodology (RSM) for the Optimization of Chromium(III) Synergistic Extraction by Supported Liquid Membrane. Membranes 2021, 11, 854. [Google Scholar] [CrossRef] [PubMed]
- Behera, S.K.; Meena, H.; Chakraborty, S.; Meikap, B.C. Application of Response Surface Methodology (RSM) for Optimization of Leaching Parameters for Ash Reduction from Low-Grade Coal. Int. J. Min. Sci. Technol. 2018, 28, 621–629. [Google Scholar] [CrossRef]
- AMS4050K Standard; Aluminum Alloy, Plate 6.2Zn-2.3Cu-2.2Mg-0.12Zr (7050-T7451) Solution Heat Treated, Stress Relieved, and Overaged. SAE International: Warrendale, PA, USA, 2021.
- AMAG ROLLING. Manufacturer’s Inspection Certificate of 7050 T7451, Nr 89320442; AMAG ROLLING: Ranshofen, Austria, 2024. [Google Scholar]
- Li, X.; Ni, J.; Liu, X.; Yue, C.; Yang, S.; Ji, X.; Liang, S.Y.; Wang, L. Chatter-Free Milling of Aerospace Thin-Walled Parts. J. Mater. Process. Technol. 2025, 341, 118903. [Google Scholar] [CrossRef]
- Wu, G.; Li, G.; Pan, W.; Raja, I.; Wang, X.; Ding, S. A State-of-Art Review on Chatter and Geometric Errors in Thin-Wall Machining Processes. J. Manuf. Process. 2021, 68, 454–480. [Google Scholar] [CrossRef]
- Feng, J.; Hou, N.; Jian, Z.; Sun, Z.; Zhang, J. An Efficient Method to Predict the Chatter Stability of Titanium Alloy Thin-Walled Workpieces during High-Speed Milling by Considering Varying Dynamic Parameters. Int. J. Adv. Manuf. Technol. 2020, 106, 5407–5420. [Google Scholar] [CrossRef]
- Zhao, P.; Lin, B.; Zhou, J.; Lv, B.; Li, J.; Zhang, J.; Wang, L.; Sui, T. Review of Grinding Temperature Theory and Measurement for the Needs of the Times: Promoting the Development of Advanced Manufacturing. J. Mater. Process. Technol. 2025, 337, 118744. [Google Scholar] [CrossRef]
- Chen, Z.; Qian, L.; Cui, R.; Liu, J.; Zhang, Q. Machining-Induced Residual Stress Analysis and Multi-Objective Optimization for Milling Process of Mg–Li Alloy. Measurement 2022, 204, 112127. [Google Scholar] [CrossRef]
- Jiang, X.; Kong, X.; He, S.; Wu, K. Modeling the Superposition of Residual Stresses Induced by Cutting Force and Heat during the Milling of Thin-Walled Parts. J. Manuf. Process. 2021, 68, 356–370. [Google Scholar] [CrossRef]
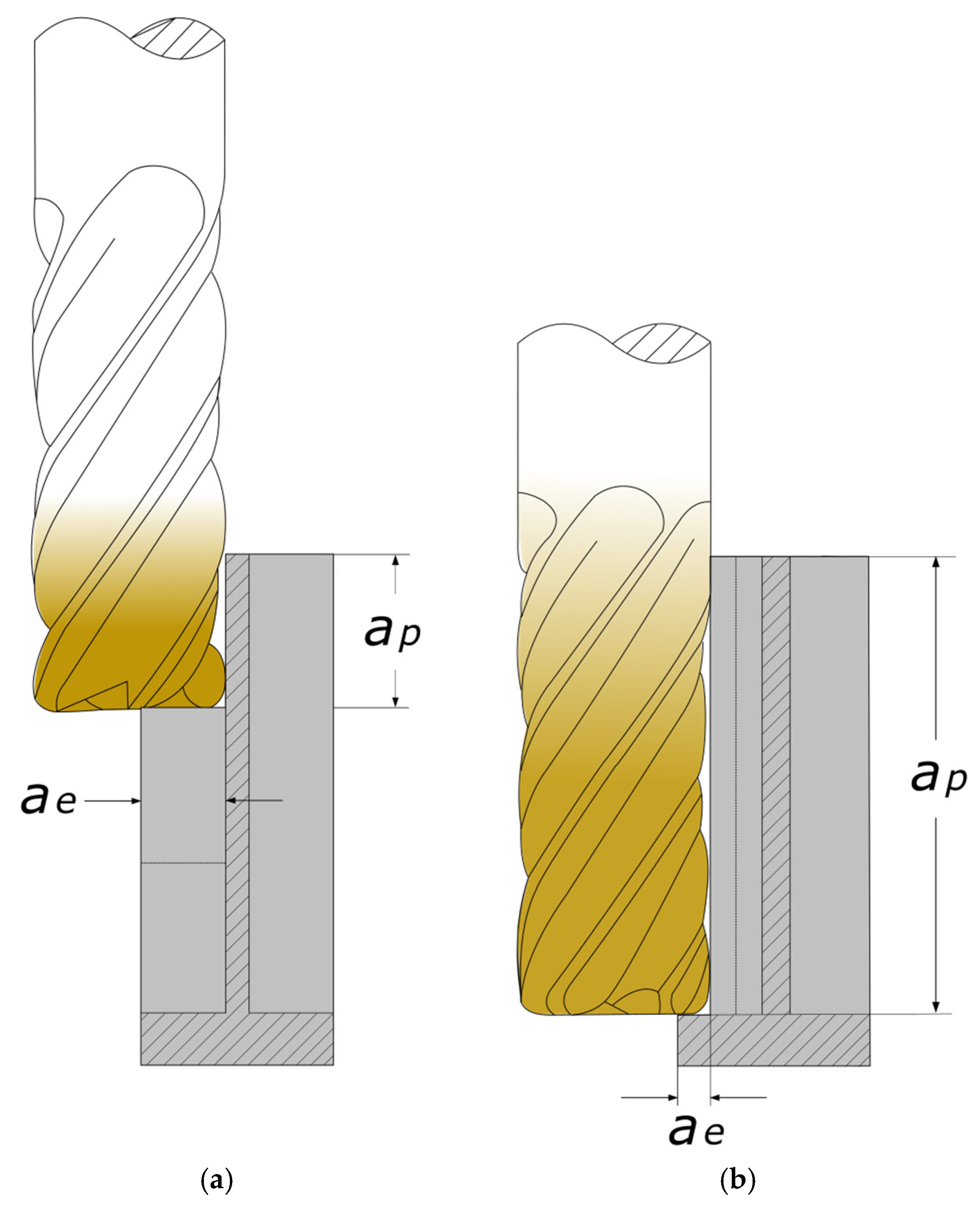


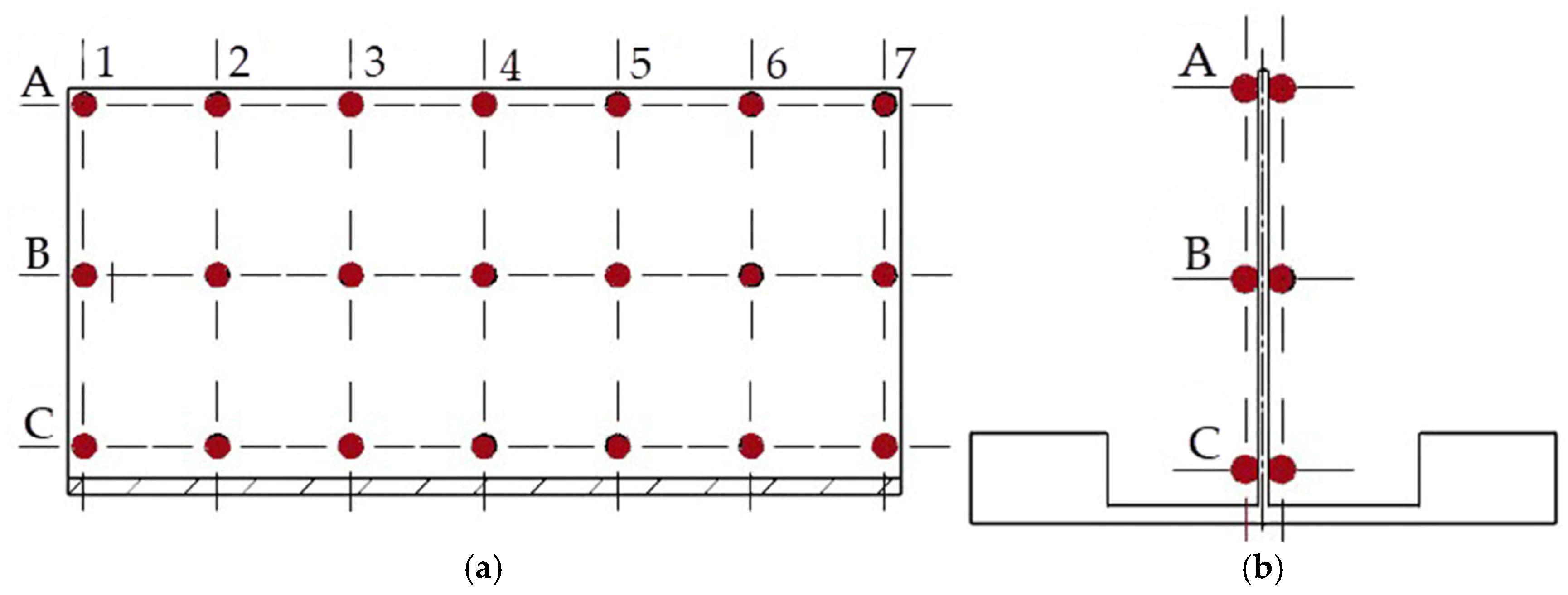



| Material | Machining Parameters | Method of Minimizing Post-Machining Deformation | Reference |
|---|---|---|---|
| Aluminum alloy EN AC-46000 | Numerical machining parameters:
| Suitable machining strategy selection; in this study, the waterline strategy (machining is performed on one side of the wall first and then on the other) yields better machining results than the side-by-side strategy (machining is performed on both sides of the wall, once on one side and once on the other). It is also recommended to use a cutting tool with a bigger diameter. | [39] |
| Aluminum alloy A5052 (denoted according to JIS) | Dry up-cut machining parameters:
| Cutting tool path optimization and material removal in a strictly defined sequence of machining passes via the application of an appropriate machining sequence for material blocks along the wall. | [40] |
| Aluminum alloy 5083 | Machining parameters:
| Use of a parallel spiral tool path to produce the best machining effects in terms of manufacturing quality of a thin-walled element. | [41] |
| Aluminum alloy 6061-T6 | Machining parameters:
| Machining parameters optimization, i.e., axial depth of cut and radial depth of cut (milling width). | [42] |
| Aluminum alloy 6061 | Machining parameters:
Tool parameters:
| Use of mirror milling, wherein the opposite side of the machined wall is supported. A system for online measurement of wall thickness is devised. | [43] |
| Aluminum alloy 7075 | Machining parameters:
| Tool path compensation in a virtual environment after the use of the proposed simulation methodology to predict the post-machining deformation of thin-walled elements. | [44] |
| Aluminum alloy 7075 and titanium alloy Ti6Al4V | 9 standard thin-walled structures with different geometries were analyzed, and the machining effects of their manufacture were determined for the following variants:
| Use of a suitable technological process for milling a thin-walled component with stiffening ribs in the first operation and then leaving it for 96 h, or performing a combination of heat treatment and vibratory treatment for residual stress relaxation, followed by another milling operation to remove the stiffening ribs. In addition, topological optimization of the arrangement of stiffening ribs is proposed. | [45] |
| Titanium alloy Ti6Al4V | Machining parameters:
| Airflow applied on the opposite side of the wall relative to the machined surface for additional reinforcement. | [46] |
| Titanium alloy Ti6Al4V | Machining parameters:
| Machining parameters optimization, including rotational speed, axial depth of cut, radial depth of cut (milling width), and feed rate. | [47] |
| Titanium alloy Ti6Al4V | Machining parameters:
| Special clamping solution for machining thin-walled parts is proposed, with critical components of the clamp made of polyetheretherketone (PEEK-GF30). | [48] |
| Titanium alloy (unspecified) | Numerical down-cut machining parameters:
| Tool path optimization and the use of a ring-cutting tool path for both cutting force and machining time reduction, leading to higher productivity. It is suggested that the workpiece be removed from the clamp after roughing to release residual stress and then reclamped for finishing. | [49] |
| Independent Variables | Codes | Levels of Coded Variables | ||
|---|---|---|---|---|
| Low | Medium | High | ||
| −1 | 0 | +1 | ||
| Wall thickness t [mm] | A | 1 | 1.5 | 2 |
| Cutting speed vc [m/min] | B | 300 | 600 | 900 |
| Chemical Composition [%] | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Si | Fe | Cu | Mn | Mg | Cr | Zn | Ti | Zr | Others | Others Total | Al |
| 0.05 | 0.07 | 2.20 | 0.01 | 2.10 | 0.01 | 6.30 | 0.03 | 0.10 | 0.01 | 0.03 | The rest |
| Cutting Parameters | Roughing | Finishing |
|---|---|---|
| Cutting speed vc [m/min] | 900 | 300, 600, 900 |
| Feed per tooth fz [mm/tooth] | 0.05 | 0.025 |
| Axial depth of cut ap [mm] | 5 and 3 (for the final tool pass) | 48 |
| Radial depth of cut (milling width) ae [mm] | 8.9 and 10.4 (for a wall thickness of 1 mm) | 0.2 |
| 8.65 and 10.4 (for a wall thickness of 1.5 mm) | ||
| 8.4 and 10.4 (for a wall thickness of 2 mm) |
| Technical Parameters | 44985 | 44748 |
|---|---|---|
| Cutting diameter [mm] | 16 | 12 |
| Shank diameter [mm] | 16 | 12 |
| Length of cut [mm] | 35 | 48 |
| Overall length [mm] | 108 | 100 |
| Helix angle [°] | Variable | 41 |
| Number of flutes [-] | 3 | 4 |
| Coating | TiB2 | TiB2 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 0.1011 | 5 | 0.0202 | 112.15 | <0.0001 | significant |
| A-Wall thickness | 0.0186 | 1 | 0.0186 | 103.42 | <0.0001 | |
| B-Cutting speed | 0.0053 | 1 | 0.0053 | 29.63 | 0.0010 | |
| AB | 0.0000 | 1 | 0.0000 | 0.1618 | 0.6995 | |
| A2 | 0.0019 | 1 | 0.0019 | 10.39 | 0.0146 | |
| B2 | 0.0729 | 1 | 0.0729 | 404.50 | <0.0001 | |
| Residual | 0.0013 | 7 | 0.0002 | |||
| Lack of Fit | 0.0010 | 3 | 0.0003 | 4.90 | 0.0793 | not significant |
| Pure Error | 0.0003 | 4 | 0.0001 | |||
| Cor Total | 0.1023 | 12 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 0.1718 | 5 | 0.0344 | 218.61 | <0.0001 | significant |
| A-Wall thickness | 0.1239 | 1 | 0.1239 | 788.46 | <0.0001 | |
| B-Cutting speed | 0.0030 | 1 | 0.0030 | 18.82 | 0.0034 | |
| AB | 0.0001 | 1 | 0.0001 | 0.5098 | 0.4984 | |
| A2 | 0.0004 | 1 | 0.0004 | 2.42 | 0.1635 | |
| B2 | 0.0409 | 1 | 0.0409 | 260.57 | <0.0001 | |
| Residual | 0.0011 | 7 | 0.0002 | |||
| Lack of Fit | 0.0006 | 3 | 0.0002 | 1.39 | 0.3674 | not significant |
| Pure Error | 0.0005 | 4 | 0.0001 | |||
| Cor Total | 0.1729 | 12 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 21,656.93 | 5 | 4331.39 | 36.56 | <0.0001 | significant |
| A-Wall thickness | 9680.17 | 1 | 9680.17 | 81.70 | <0.0001 | |
| B-Cutting speed | 1472.67 | 1 | 1472.67 | 12.43 | 0.0097 | |
| AB | 506.25 | 1 | 506.25 | 4.27 | 0.0776 | |
| A2 | 4717.25 | 1 | 4717.25 | 39.81 | 0.0004 | |
| B2 | 8714.75 | 1 | 8714.75 | 73.55 | <0.0001 | |
| Residual | 829.38 | 7 | 118.48 | |||
| Lack of Fit | 582.18 | 3 | 194.06 | 3.14 | 0.1490 | not significant |
| Pure Error | 247.20 | 4 | 61.80 | |||
| Cor Total | 22,486.31 | 12 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value | |
|---|---|---|---|---|---|---|
| Model | 51,619.14 | 5 | 10,323.83 | 35.48 | <0.0001 | significant |
| A-Wall thickness | 11,266.67 | 1 | 11,266.67 | 38.73 | 0.0004 | |
| B-Cutting speed | 5104.17 | 1 | 5104.17 | 17.54 | 0.0041 | |
| AB | 930.25 | 1 | 930.25 | 3.20 | 0.1169 | |
| A2 | 216.91 | 1 | 216.91 | 0.7456 | 0.4165 | |
| B2 | 27,267.79 | 1 | 27,267.79 | 93.72 | <0.0001 | |
| Residual | 2036.55 | 7 | 290.94 | |||
| Lack of Fit | 1164.55 | 3 | 388.18 | 1.78 | 0.2899 | not significant |
| Pure Error | 872.00 | 4 | 218.00 | |||
| Cor Total | 53,655.69 | 12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zawada-Michałowska, M. Thin Wall Milling at a Maximized Axial Depth of Cut. Materials 2025, 18, 5219. https://doi.org/10.3390/ma18225219
Zawada-Michałowska M. Thin Wall Milling at a Maximized Axial Depth of Cut. Materials. 2025; 18(22):5219. https://doi.org/10.3390/ma18225219
Chicago/Turabian StyleZawada-Michałowska, Magdalena. 2025. "Thin Wall Milling at a Maximized Axial Depth of Cut" Materials 18, no. 22: 5219. https://doi.org/10.3390/ma18225219
APA StyleZawada-Michałowska, M. (2025). Thin Wall Milling at a Maximized Axial Depth of Cut. Materials, 18(22), 5219. https://doi.org/10.3390/ma18225219






