Bi3+-Related Multimode Emission in Garnet: A First-Principles Study
Abstract
1. Introduction
2. Computation Details
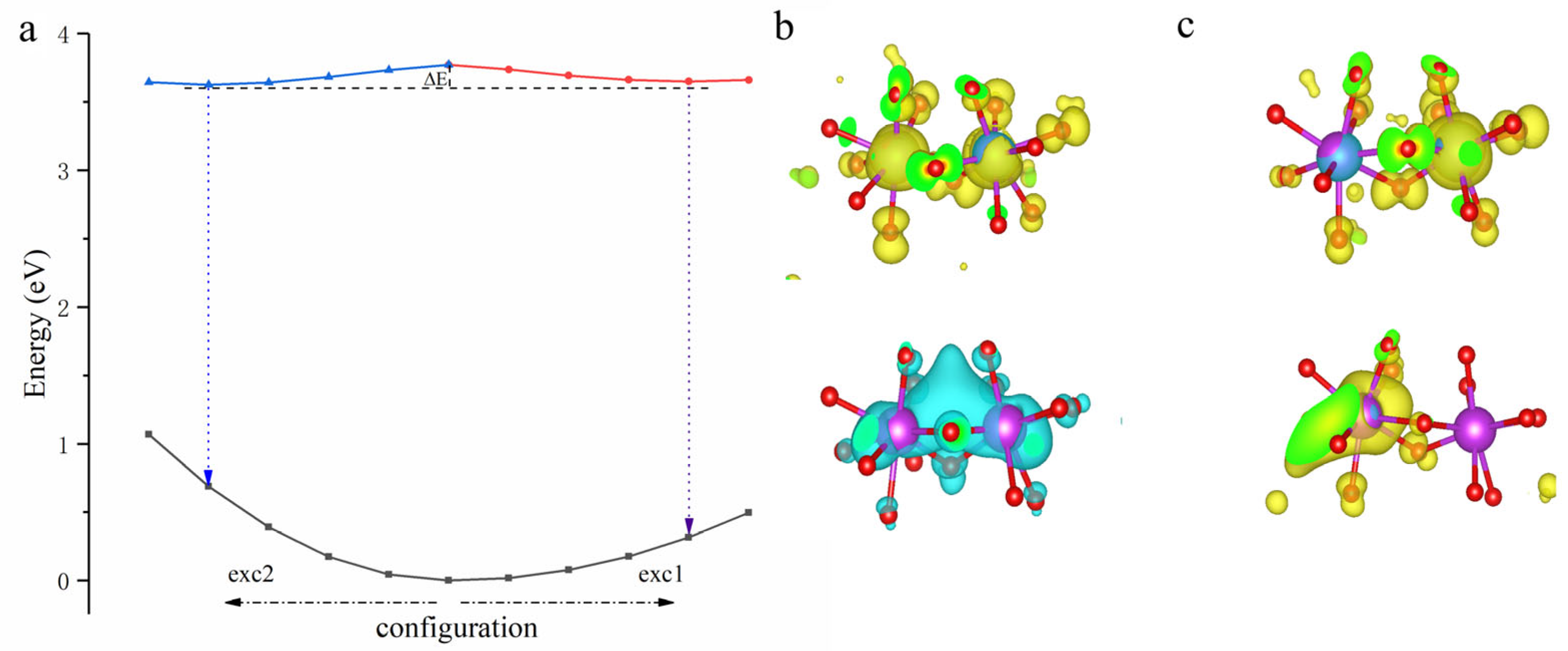
3. Results
| Calculated | Experimental [41,42] | |||||
|---|---|---|---|---|---|---|
| a | α | volume | a | α | volume | |
| YAG | 10.385 | 109.471 | 862.203 | 10.396 [41] | 109.471 | 864.951 |
| YGG | 10.631 | 109.471 | 924.878 | 10.692 [42] | 109.471 | 940.797 |
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
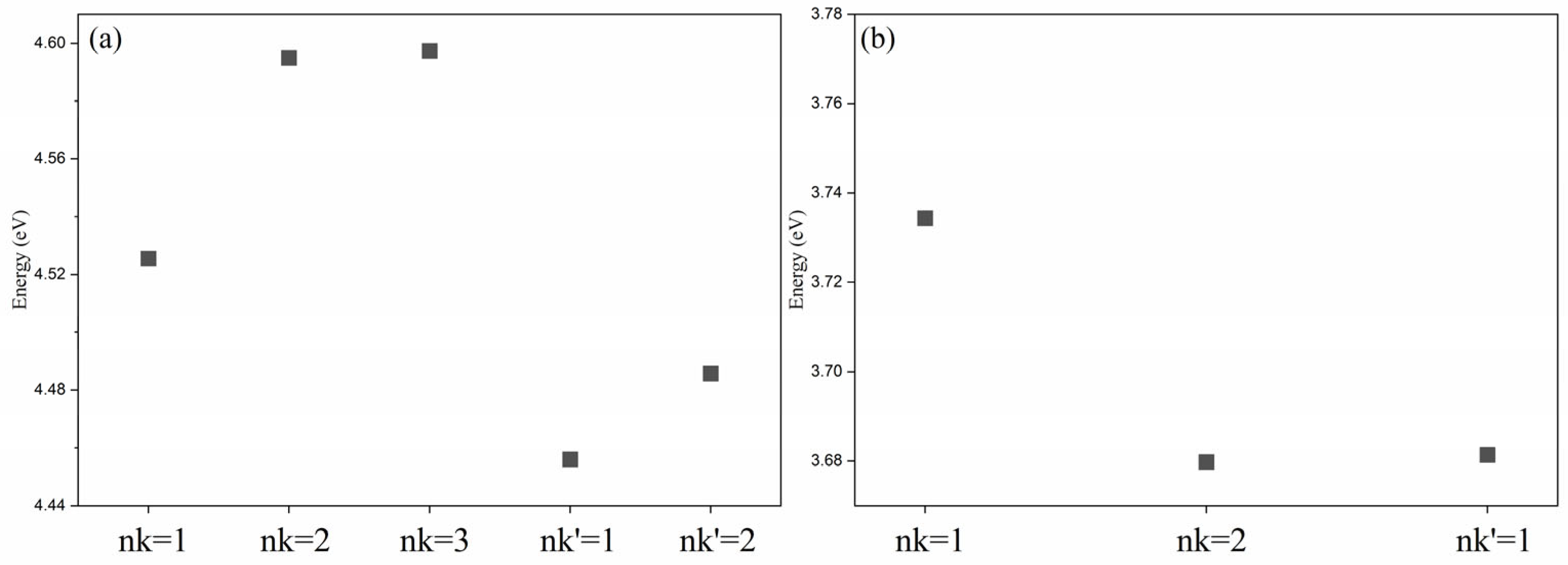
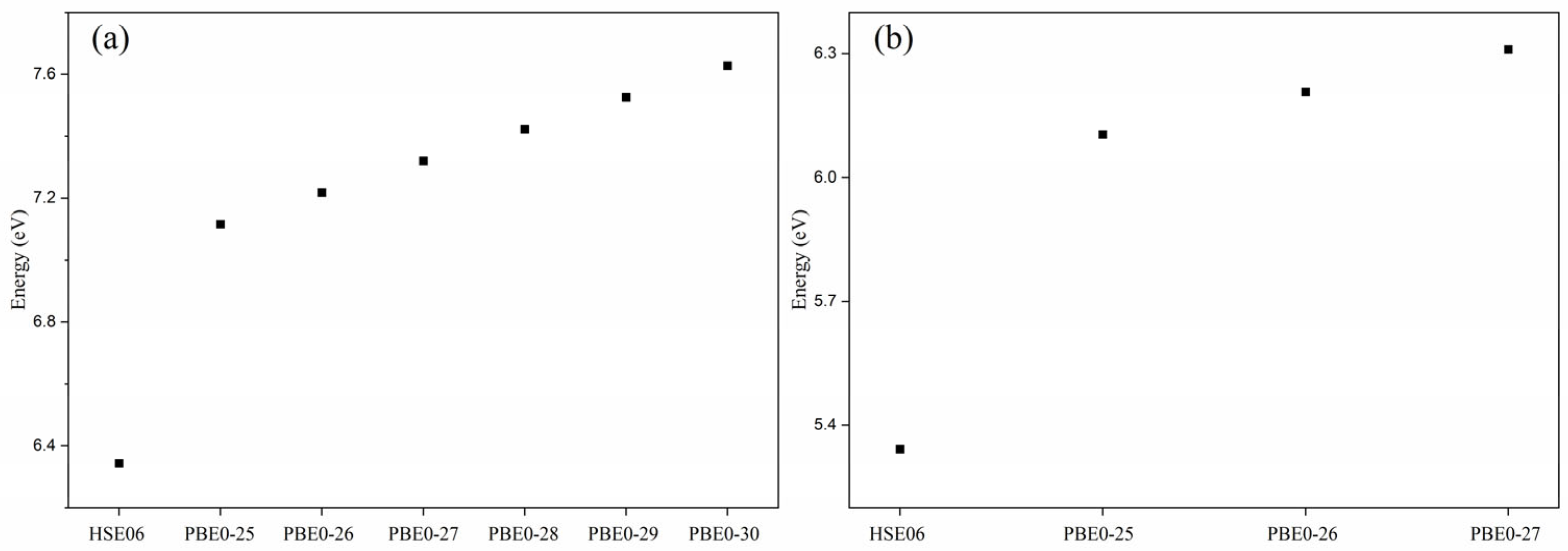
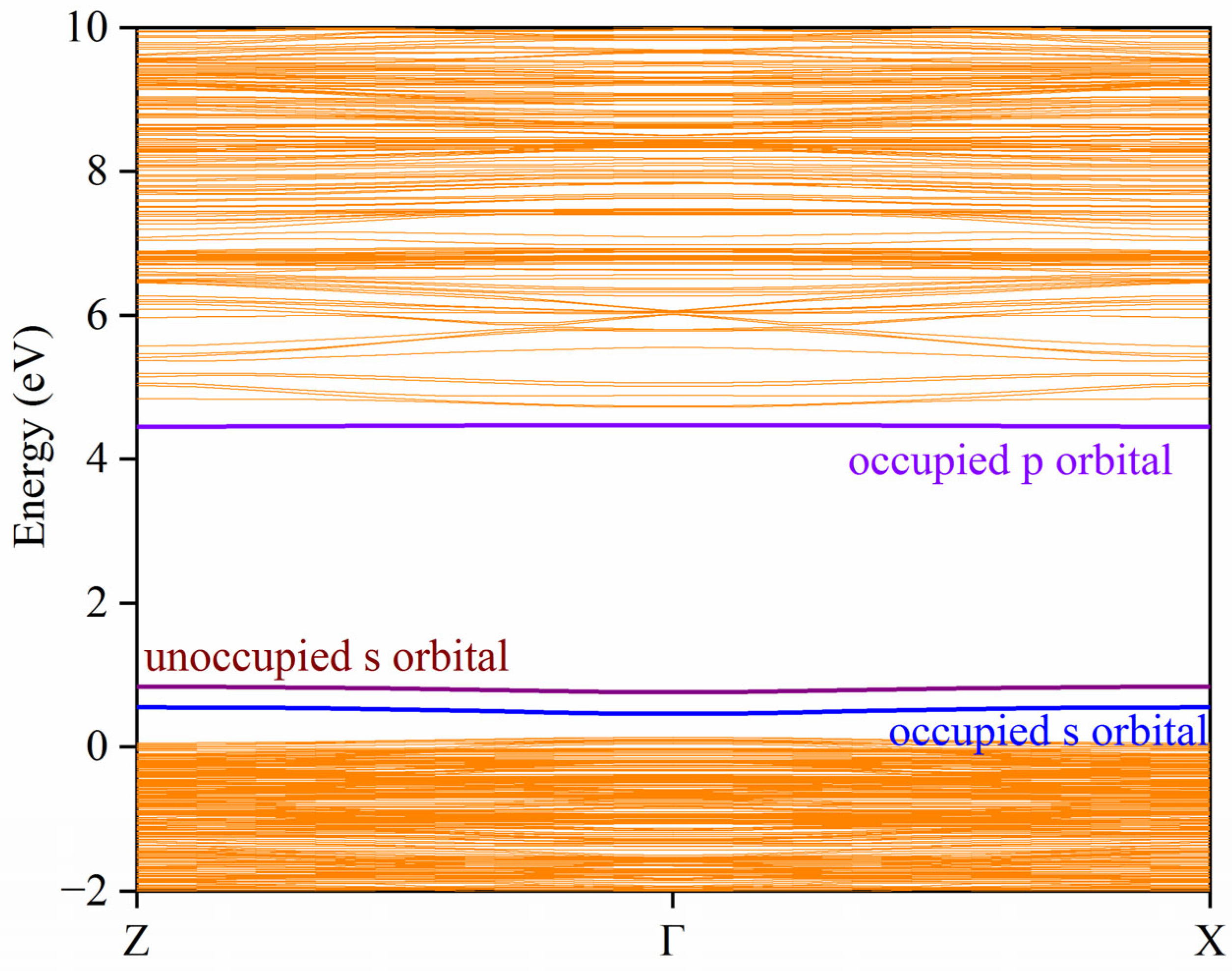
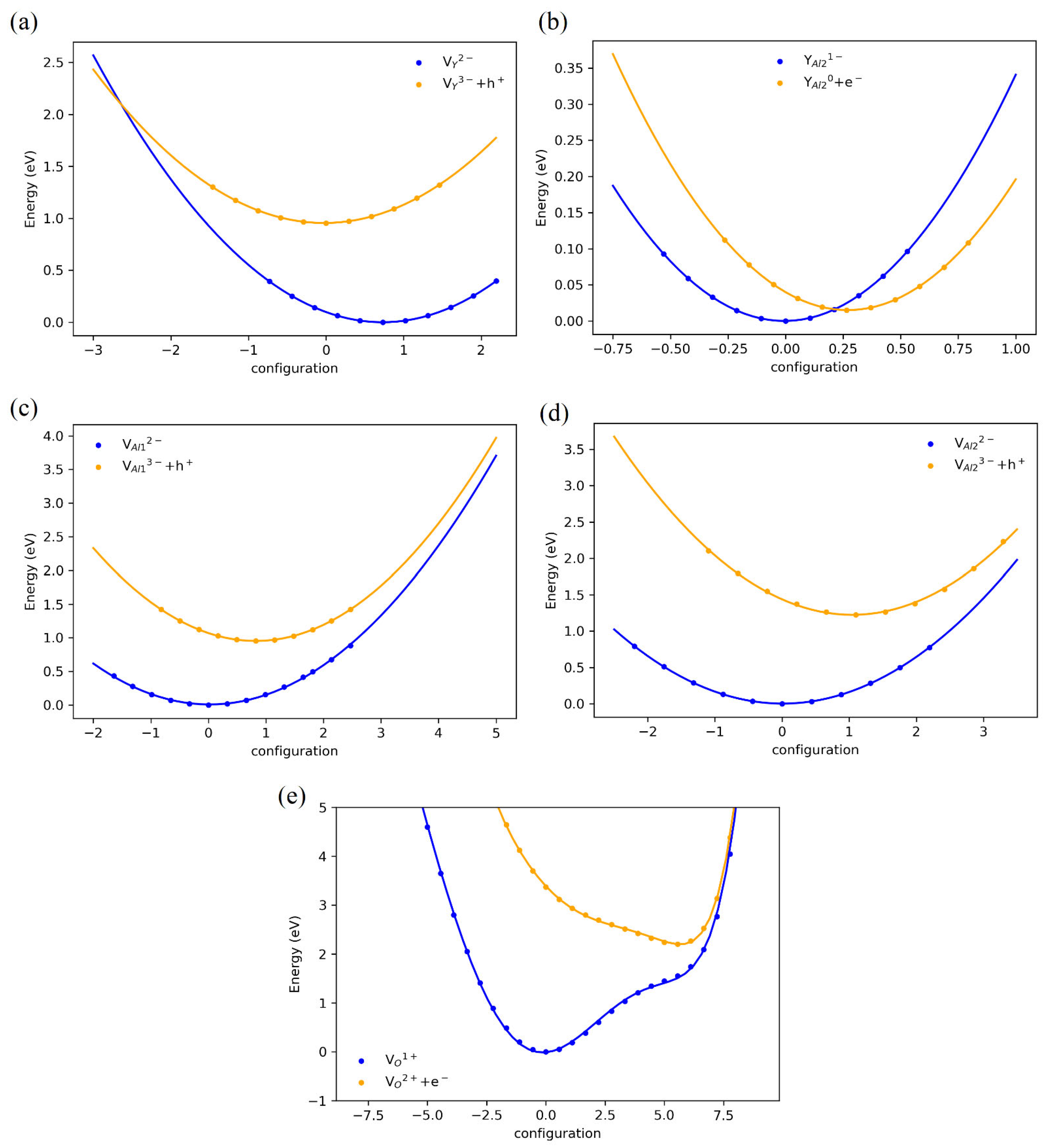
References
- Sasvári, J.; Werner, P.-E.; Fægri, K., Jr.; Haaland, A.; Schilling, B.E.R.; Seip, R.; Taugbøl, K. Structural studies of gadolinium gallium garnet. Acta Chem. Scand. 1983, 37, 203–206. [Google Scholar] [CrossRef][Green Version]
- Song, Z.; Wen, Z.; Chen, F.; Chen, M.; Suescun, L.; Liu, Q. Polyhedron Distortion and Site-Specific Rigidity in Garnet-Type Compounds. Cryst. Growth Des. 2024, 24, 2226–2234. [Google Scholar] [CrossRef]
- Chaika, M.; Tomala, R.; Vovk, O.; Nizhankovskyi, S.; Mancardi, G.; Strek, W. Upconversion luminescence in Cr3+:YAG single crystal under infrared excitation. J. Lumin. 2020, 226, 117467. [Google Scholar] [CrossRef]
- Shiba, T.; Ho, K.; Ma, X.; Cho, Y.W.; Chen, C.-Y.; Kim, D.M. Effect of Er,Cr:YSGG Laser Irradiation on the Surface Modification and Cell Adhesion on Titanium Discs: An In Vitro Study. Materials 2024, 17, 4899. [Google Scholar] [CrossRef]
- Tsai, M.-J.; Wu, L.-F. Multi-Objective Optimization of Nd: YAG Laser Drilling of Optical-Grade Acrylic Plate Using Taguchi-Based Grey Relational Analysis. Materials 2022, 15, 8998. [Google Scholar] [CrossRef]
- Gulyaeva, K.N.; Trofimov, A.N.; Zamoryanskaya, M.V. A study of cathodoluminescent characteristics of YAG:Nd3+. Opt. Spectrosc. 2013, 114, 709–712. [Google Scholar] [CrossRef]
- Sao, S.; Sharma, R.; Brahme, N.; Bisen, D.P.; Thakkar, K.; Richhariya, T.; Tiwari, K.; Verma, A.; Dubey, K. Luminescence Studies of Polycrystalline Eu3+-Doped Gadolinium Gallium Garnet Phosphor. J. Electron. Mater. 2025, 54, 2952–2965. [Google Scholar] [CrossRef]
- Ha, H.; Yang, S.; Park, S. Photoluminescence Spectra Correlations with Structural Distortion in Eu3+- and Ce3+-Doped Y3Al5-2x(Mg,Ge)xO12 (x = 0, 1, 2) Garnet Phosphors. Materials 2024, 17, 2445. [Google Scholar] [CrossRef] [PubMed]
- Bachmann, V.; Ronda, C.; Meijerink, A. Temperature Quenching of Yellow Ce3+ Luminescence in YAG:Ce. Chem. Mater. 2009, 21, 2077–2084. [Google Scholar] [CrossRef]
- Xia, Z.; Meijerink, A. Ce3+-Doped garnet phosphors: Composition modification, luminescence properties and applications. Chem. Soc. Rev. 2017, 46, 275–299. [Google Scholar] [CrossRef]
- Feng, Z.; Lou, B.; Yin, M.; Yeung, Y.Y.; Sun, H.T.; Duan, C.K. First-Principles Study of Bi3+-Related Luminescence and Electron and Hole Traps in (Y/Lu/La)PO4. Inorg. Chem. 2021, 60, 4434–4446. [Google Scholar] [CrossRef]
- Lou, B.; Wen, J.; Cai, J.; Yeung, Y.Y.; Yin, M.; Duan, C.K. First-principles study of Bi3+-related luminescence and traps in the perovskites CaMO3(M=Zr,Sn,Ti). Phys. Rev. B 2021, 103, 075109. [Google Scholar] [CrossRef]
- Lou, B.; Wen, J.; Ning, L.; Yin, M.; Ma, C.G.; Duan, C.K. Understanding the defect levels and photoluminescence in a series of bismuth-doped perovskite oxides: First-principles study. Phys. Rev. B 2021, 104, 115101. [Google Scholar] [CrossRef]
- Liu, J.; Liang, Y.; Yan, S.; Chen, D.; Miao, S.; Wang, W. Narrowband ultraviolet-B persistent luminescence from (Y,Gd)3Ga5O12:Bi3+ phosphors for optical tagging application. Dalton Trans. 2021, 50, 15413–15421. [Google Scholar] [CrossRef]
- Ding, J.; Li, Y.; Zhou, X.; Yuan, W.; Zhang, W.; Ye, S.; Zhou, J.; Chen, M.; Wu, Q. A novel Bi3+-Activated garnet phosphor with site-selected excitations and high temperature sensitivity. Ceram. Int. 2022, 48, 23784–23792. [Google Scholar] [CrossRef]
- Babin, V.; Gorbenko, V.; Krasnikov, A.; Makhov, A.; Nikl, M.; Zazubovich, S.; Zorenko, Y. Photoluminescence of Lu3Al5O12:Bi and Y3Al5O12:Bi single crystalline films. Radiat. Meas. 2010, 45, 331–335. [Google Scholar] [CrossRef]
- Liu, D.X.; Zhang, Z.H.; Wang, L.L. The downconversion luminescence properties of Y3Al5O12: Bi3+/Sm3+ phosphors with tunable emissions. J. Lumin. 2022, 243, 118617. [Google Scholar] [CrossRef]
- Kumar, K.S.; Lou, C.; Manohari, A.G.; Cao, H.; Pribat, D. Broadband down-conversion of near-infrared emission in Bi3+-Yb3+ co-doped Y3Al5O12 phosphors. Optik 2018, 157, 492–496. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Zhu, T.; Huo, X.; Wang, Y.; Suo, H.; Li, L.; Li, P. Achieving multicolour and multimodal luminescence in Ca3Al2Ge3O12:Bi3+/Ln3+(Ln = Tb, Eu, Sm, and Dy) persistent phosphors for multiple applications. J. Mater. Chem. C 2023, 11, 8892–8902. [Google Scholar] [CrossRef]
- Liu, J.; Liang, Y.; Yan, S.; Chen, D.; Miao, S.; Wang, W.; Bi, J. Sunlight-activated long persistent luminescence in the ultraviolet-B spectral region from Bi3+-doped garnet phosphors for covert optical tagging. J. Mater. Chem. C 2021, 9, 9692–9701. [Google Scholar] [CrossRef]
- Dong, L.P.; Zhang, L.; Jia, Y.C.; Shao, B.Q.; Zhao, S.; You, H.P. Luminescence properties and energy transfer of novel Bi3+ and Mn2+-co-activated Y3Ga5O12 single-component white light-emitting phosphor. J. Mater. Chem. C 2020, 8, 12231–12239. [Google Scholar] [CrossRef]
- Zorenko, Y.; Gorbenko, V.; Voznyak, T.; Vistovsky, V.; Nedilko, S.; Nikl, M. Luminescence of ions in single crystalline films. Radiat. Meas. 2007, 42, 882–886. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758. [Google Scholar] [CrossRef]
- Bergerhoff, G.; Hundt, R.; Sievers, R.; Brown, I.D. The inorganic crystal structure data base. J. Chem. Inf. Comput. Sci. 1983, 23, 66–69. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- He, J.G.; Franchini, C. Screened hybrid functional applied to 3d0→3d8 transition-metal perovskites LaMO3 (M = Sc-Cu): Influence of the exchange mixing parameter on the structural, electronic, and magnetic properties. Phys. Rev. B 2012, 86, 235117. [Google Scholar] [CrossRef]
- Wang, V.; Xu, N.; Liu, J.C.; Tang, G.; Geng, W.T. VASPKIT: A user-friendly interface facilitating high-throughput computing and analysis using VASP code. Comput. Phys. Commun. 2021, 267, 108033. [Google Scholar] [CrossRef]
- Shi, H.; Han, D.; Chen, S.; Du, M.H. Impact of metal ns2 lone pair on luminescence quantum efficiency in low-dimensional halide perovskites. Phys. Rev. Mater. 2019, 3, 034604. [Google Scholar] [CrossRef]
- Freysoldt, C.; Grabowski, B.; Hickel, T.; Neugebauer, J.; Kresse, G.; Janotti, A.; Van de Walle, C.G. First-principles calculations for point defects in solids. Rev. Mod. Phys. 2014, 86, 253–305. [Google Scholar] [CrossRef]
- Lany, S.; Zunger, A. Assessment of correction methods for the band-gap problem and for finite-size effects in supercell defect calculations: Case studies for ZnO and GaAs. Phys. Rev. B 2008, 78, 235104. [Google Scholar] [CrossRef]
- Tomiki, T.; Ganaha, Y.; Shikenbaru, T.; Futemma, T.; Yuri, M.; Aiura, Y.; Fukutani, H.; Kato, H.; Tamashiro, J.; Miyahara, T.; et al. Optical Spectra of Y3Al5O12(YAG) Single Crystals in the Vacuum Ultraviolet Region. II. J. Phys. Soc. Jpn. 1993, 62, 1388–1400. [Google Scholar] [CrossRef]
- Sirdeshmukh, D.B.; Sirdeshmukh, L.; Subhadra, K.G. Microand Macro-Properties of Solids; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Yi, Z.; Liu, P.; Xu, Y. Multimode Dynamic Photoluminescence of Bi3+-Activated ZnGa2O4 for Optical Information Encryption. Inorg. Chem. 2023, 62, 9671–9678. [Google Scholar] [CrossRef]
- Zhang, S.; Hu, Y.; Chen, R.; Wang, X.; Wang, Z. Photoluminescence and persistent luminescence in Bi3+-doped Zn2GeO4 phosphors. Opt. Mater. 2014, 36, 1830–1835. [Google Scholar] [CrossRef]
- Yousif, A.; Som, S.; Kumar, V.; Swart, H.C. Comparison and analysis of Eu3+ luminescence in Y3Al5O12 and Y3Ga5O12 hosts material for red lighting phosphor. Mater. Chem. Phys. 2015, 166, 167–175. [Google Scholar] [CrossRef]
- Yousif, A.; Kumar, V.; Ahmed, H.A.A.S.; Som, S.; Noto, L.L.; Ntwaeaborwa, O.M.; Swart, H.C. Effect of Ga3+ Doping on the Photoluminescence Properties of Y3Al5-xGaxO12:Bi3+ Phosphor. ECS J. Solid State Sci. Technol. 2014, 3, R222. [Google Scholar] [CrossRef]
- Ueda, J.; Tanabe, S.; Nakanishi, T. Analysis of Ce3+ luminescence quenching in solid solutions between Y3Al5O12 and Y3Ga5O12 by temperature dependence of photoconductivity measurement. J. Appl. Phys. 2011, 110, 053102. [Google Scholar] [CrossRef]
- Almessiere, M.A.; Ahmed, N.M.; Massoudi, I.; Al-Otaibi, A.L.; Al-shehri, A.A.; Shafouri, M.A. Study of the structural and luminescent properties of Ce3+ and Eu3+ co-doped YAG synthesized by solid state reaction. Optik 2018, 158, 152–163. [Google Scholar] [CrossRef]
- Verma, A.; Malhan, N.; Ganguli, A.K. Preparation, structure and characterization of nanocrystalline-Nd:Y3Ga5O12. Mater. Lett. 2012, 81, 242–244. [Google Scholar] [CrossRef]
- Dorenbos, P. Modeling the chemical shift of lanthanide 4f electron binding energies. Phys. Rev. B 2012, 85, 165107. [Google Scholar] [CrossRef]
- Chen, Q.L.; Jing, W.G.; Yeung, Y.Y.; Yin, M.; Duan, C.K. Mechanisms of bismuth-activated near-infrared photoluminescence—A first-principles study on the MXCl3 series. Phys. Chem. Chem. Phys. 2021, 23, 17420–17429. [Google Scholar] [CrossRef]
- Chen, Q.; Lou, B.; Jing, W.; Yin, M.; Yeung, Y.-Y.; Su, L.; Duan, C.-K. First principles study on low valence states photoluminescence in Bi-doped M2B5O9Cl crystals. J. Alloys Compd. C 2021, 863, 158704. [Google Scholar] [CrossRef]
- Feng, Z.Y.; Lou, B.B.; Chen, Q.L.; Yin, M.; Ma, C.-G.; Duan, C.-K. Self-Activated and Bismuth-Related Photoluminescence in Rare-Earth Vanadate, Niobate, and Tantalate Series—A First-Principles Study. Inorg. Chem. 2021, 60, 16614–16625. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Duan, C.-K.; Tanner, P.A.; Ma, C.-G.; Yin, M. Rationalizing the Photoluminescence of Bi3+ and Sb3+ in Double Perovskite Halide Crystals. J. Phys. Chem. C 2021, 125, 26670–26678. [Google Scholar] [CrossRef]
- Chen, Q.; Feng, Z.; Liu, M.; Lou, B.; Ma, C.G.; Duan, C.K. The photoluminescence of isolated and paired Bi3+ ions in layered LnOCl crystals: A first-principles study. Phys. Chem. Chem. Phys. 2022, 24, 14064–14071. [Google Scholar] [CrossRef]
- Alkauskas, A.; Yan, Q.; Van de Walle, C.G. First-principles theory of nonradiative carrier capture via multiphonon emission. Phys. Rev. B 2014, 90, 075202. [Google Scholar] [CrossRef]
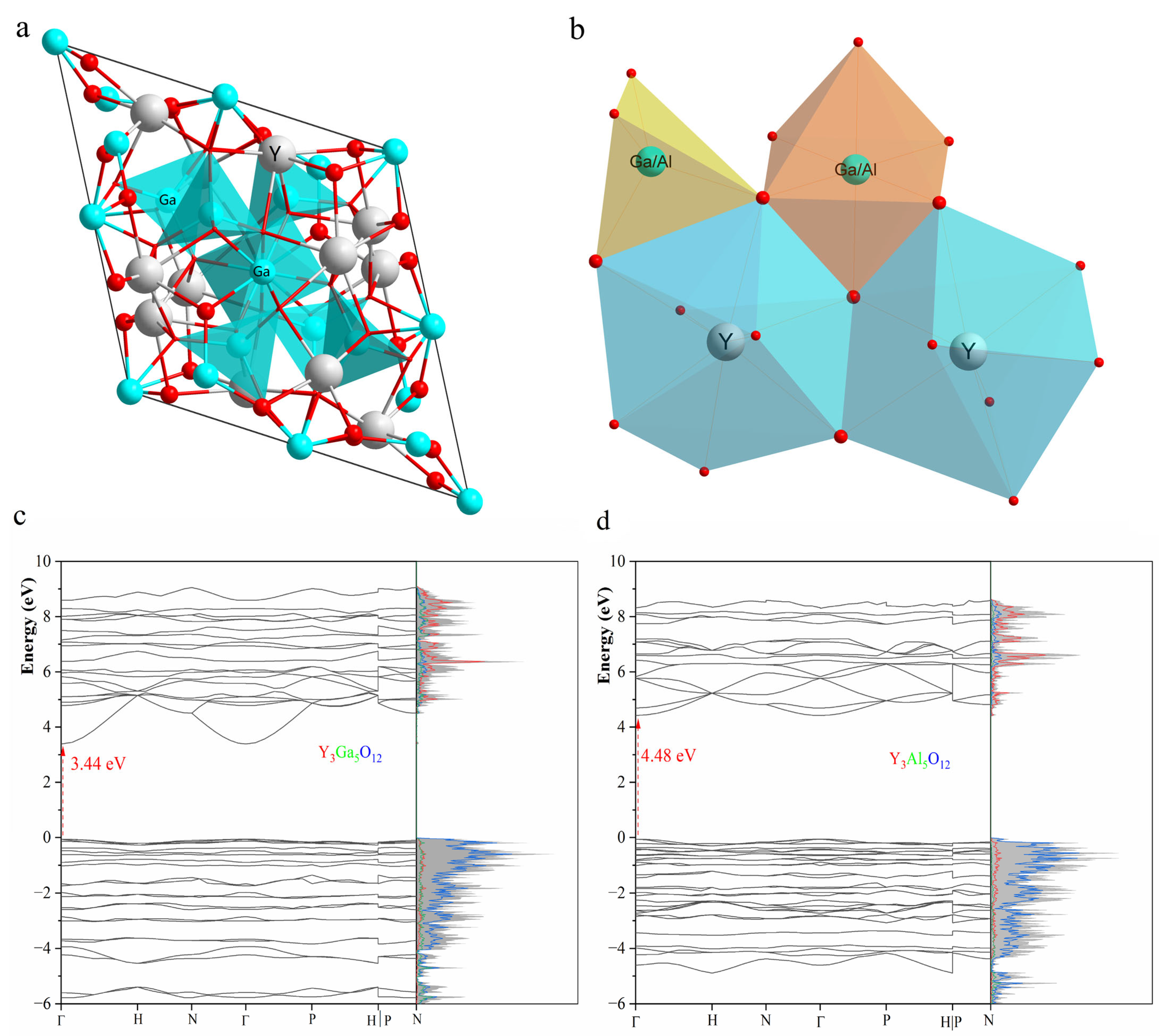
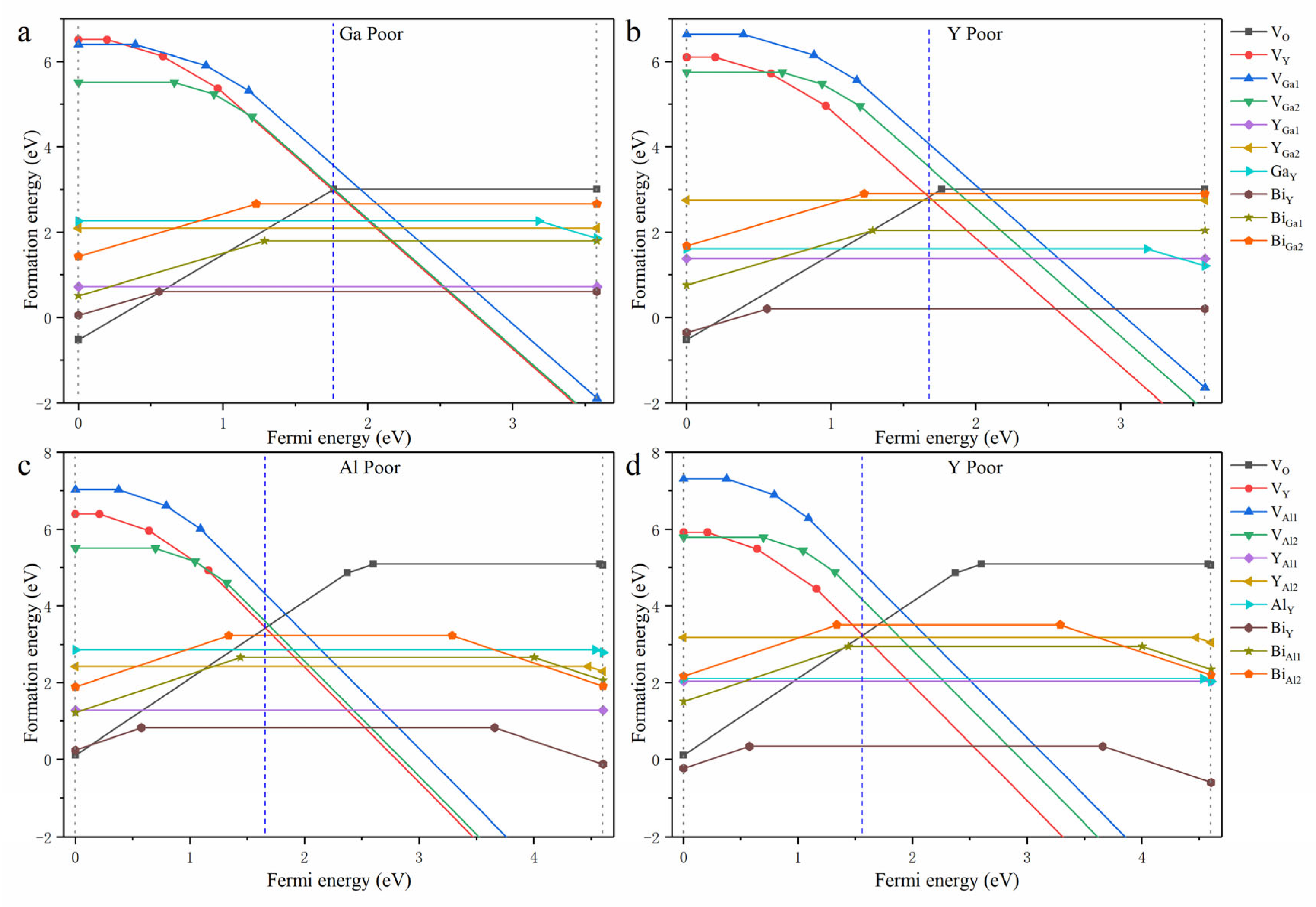
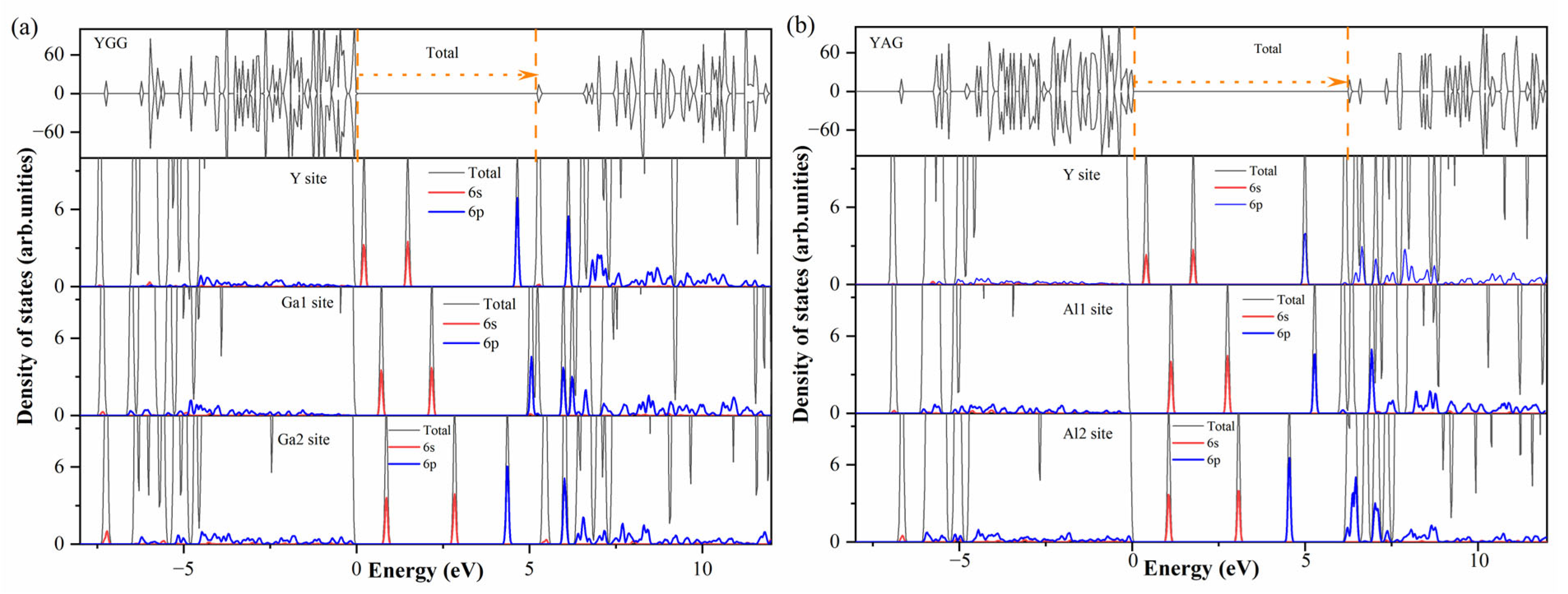

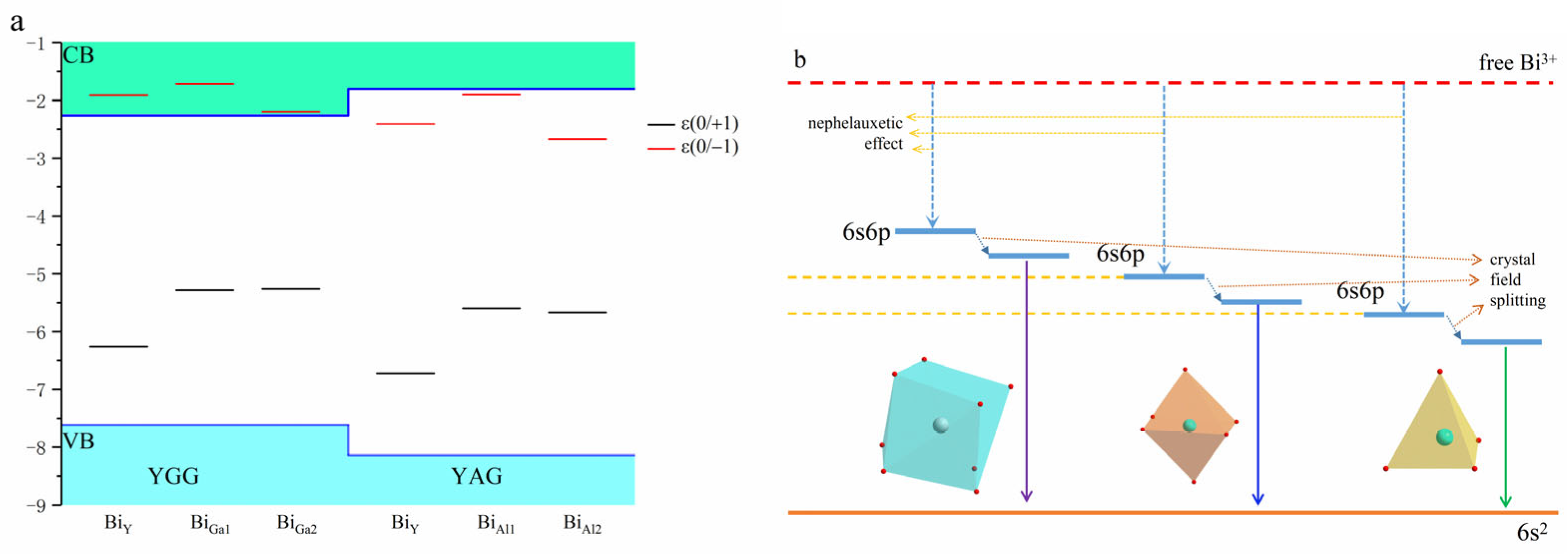
| YGG | YAG | ||||||
|---|---|---|---|---|---|---|---|
| Bi3+Y | Bi3+Ga1 | Bi3+Ga2 | Bi3+Y | Bi3+Ga1 | Bi3+Ga2 | ||
| A band | ex | 4.35 | 3.58 | 2.82 | 4.41 | 3.77 | 2.88 |
| em | 4.08 | 3.47 | 2.71 | 4.22 | 3.64 | 2.67 | |
| MMCT | ex | 4.32 | 3.55 | 3.46 | 5.24 | 4.42 | 4.35 |
| em | 3.63 | 2.46 | 2.52 | 4.58 | 3.21 | 3.34 | |
| exp | ex | 4.29 [20], 3.75 [21], 3.54 [21] | 4.43 [16] | ||||
| em | 3.32 [21], 2.92 [21], 2.61 [21], 2.53 [21], 3.96 [20] | 4.07 [16], 2.63 [16], 2.95 [17] | |||||
| Original | Bi3+-O | Bi3+*-O | Bi4+-O | ||
|---|---|---|---|---|---|
| YGG | Y | 2.3782 | 2.4454 | 2.4906 | 2.3784 |
| Ga1 | 1.9967 | 2.2730 | 2.2721 | 2.1852 | |
| Ga2 | 1.8510 | 2.1491 | 2.1570 | 2.0698 | |
| YAG | Y | 2.3661 | 2.4328 | 2.4533 | 2.3704 |
| Al1 | 1.9239 | 2.2616 | 2.2602 | 2.1724 | |
| Al2 | 1.7728 | 2.1392 | 2.1441 | 2.0602 |
| Pair Distance (Å) | Ebinding (eV) | Em1 | Em2 | |
|---|---|---|---|---|
| YGG | 3.787 | −0.013 | 3.1 | 2.8 |
| YAG | 3.698 | −0.019 | 3.3 | 2.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, B.; Liu, Q.; Chi, F.; Lou, B. Bi3+-Related Multimode Emission in Garnet: A First-Principles Study. Materials 2025, 18, 5082. https://doi.org/10.3390/ma18225082
Jiang B, Liu Q, Chi F, Lou B. Bi3+-Related Multimode Emission in Garnet: A First-Principles Study. Materials. 2025; 18(22):5082. https://doi.org/10.3390/ma18225082
Chicago/Turabian StyleJiang, Bin, Qing Liu, Fengfeng Chi, and Bibo Lou. 2025. "Bi3+-Related Multimode Emission in Garnet: A First-Principles Study" Materials 18, no. 22: 5082. https://doi.org/10.3390/ma18225082
APA StyleJiang, B., Liu, Q., Chi, F., & Lou, B. (2025). Bi3+-Related Multimode Emission in Garnet: A First-Principles Study. Materials, 18(22), 5082. https://doi.org/10.3390/ma18225082





