Identification of Ultra-Short Laser Parameters for a 3D Model of a Thin Metal Film Using the Lattice Boltzmann Method
Abstract
1. Introduction
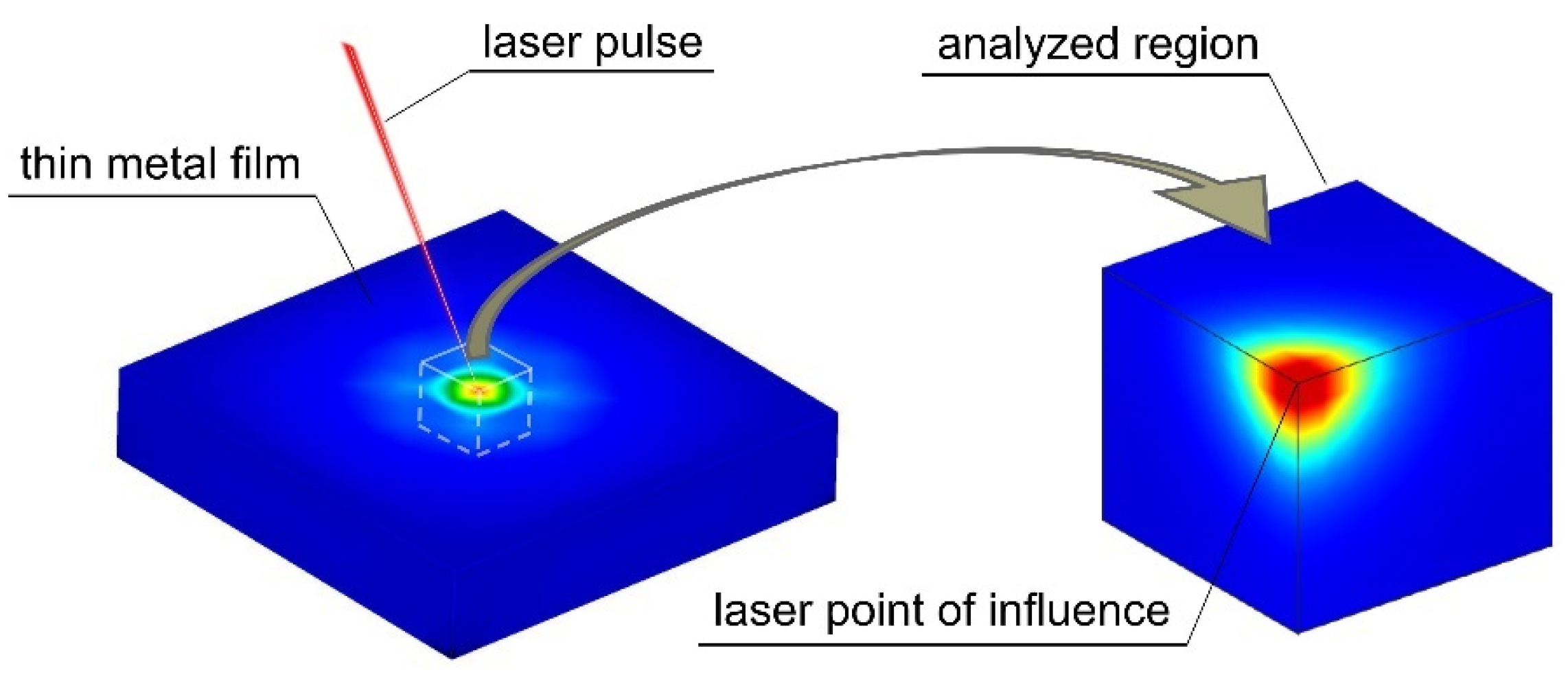
2. Formulation of the Problem
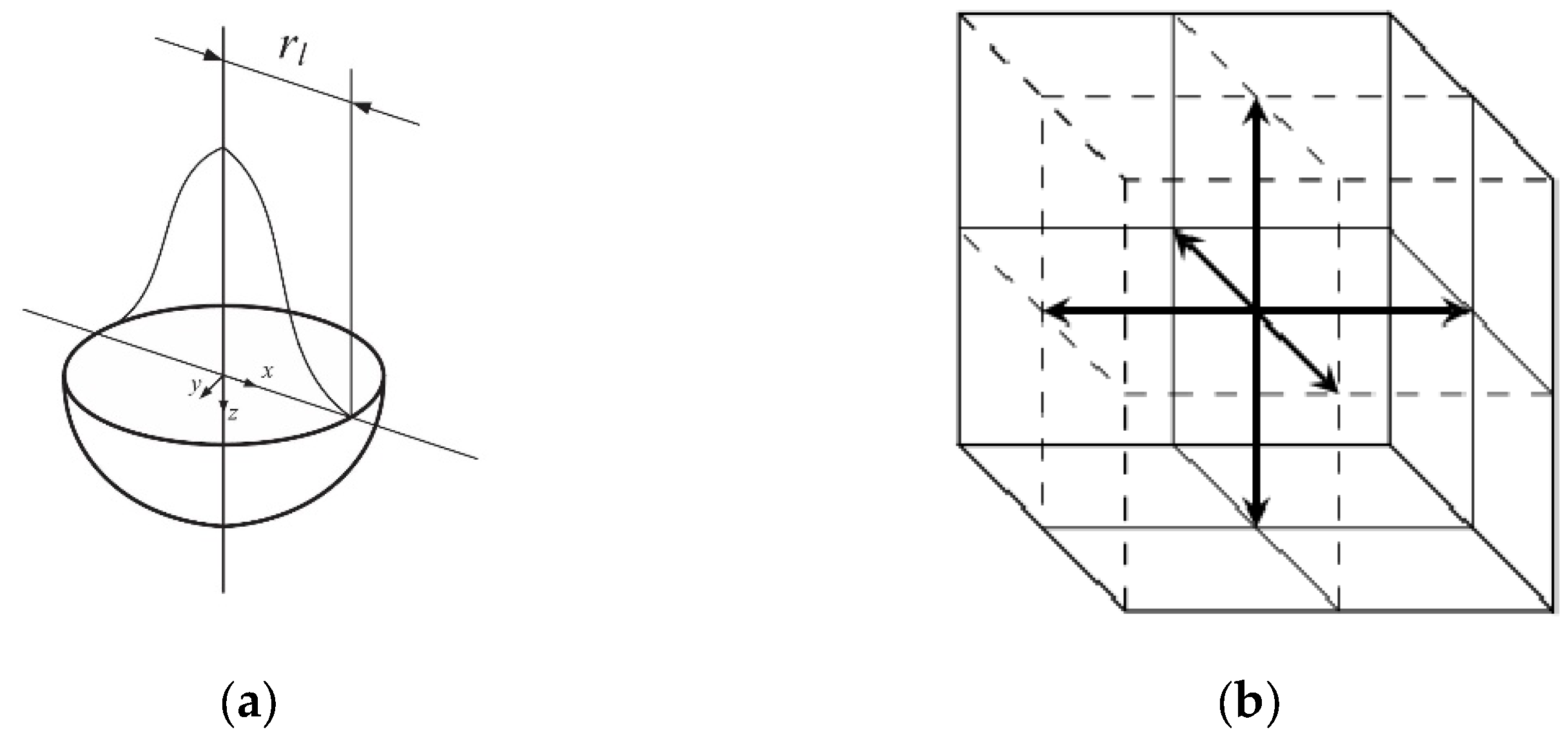
2.1. Heat Flow in Metals by Means of the Boltzmann Transport Equations
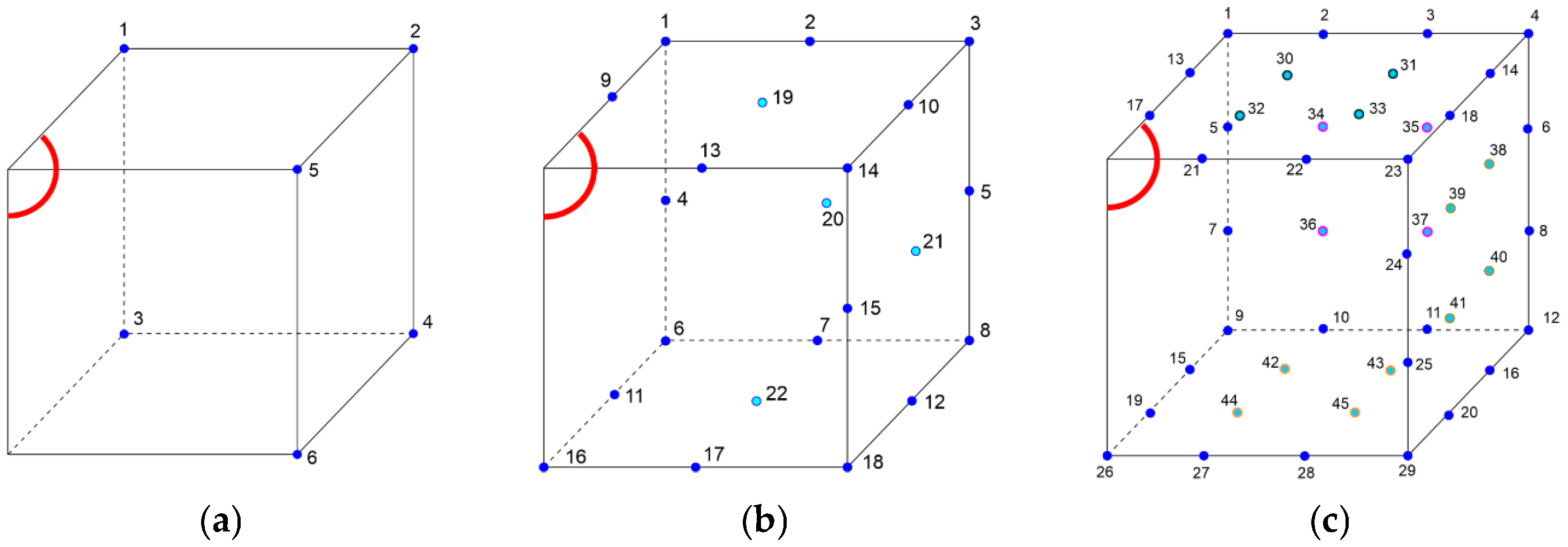
2.2. Implementation of the Identification Problem
- Variant 1: simultaneous identification of rl and β
- Variant 2: simultaneous identification of rl and P.
3. Identification Algorithms
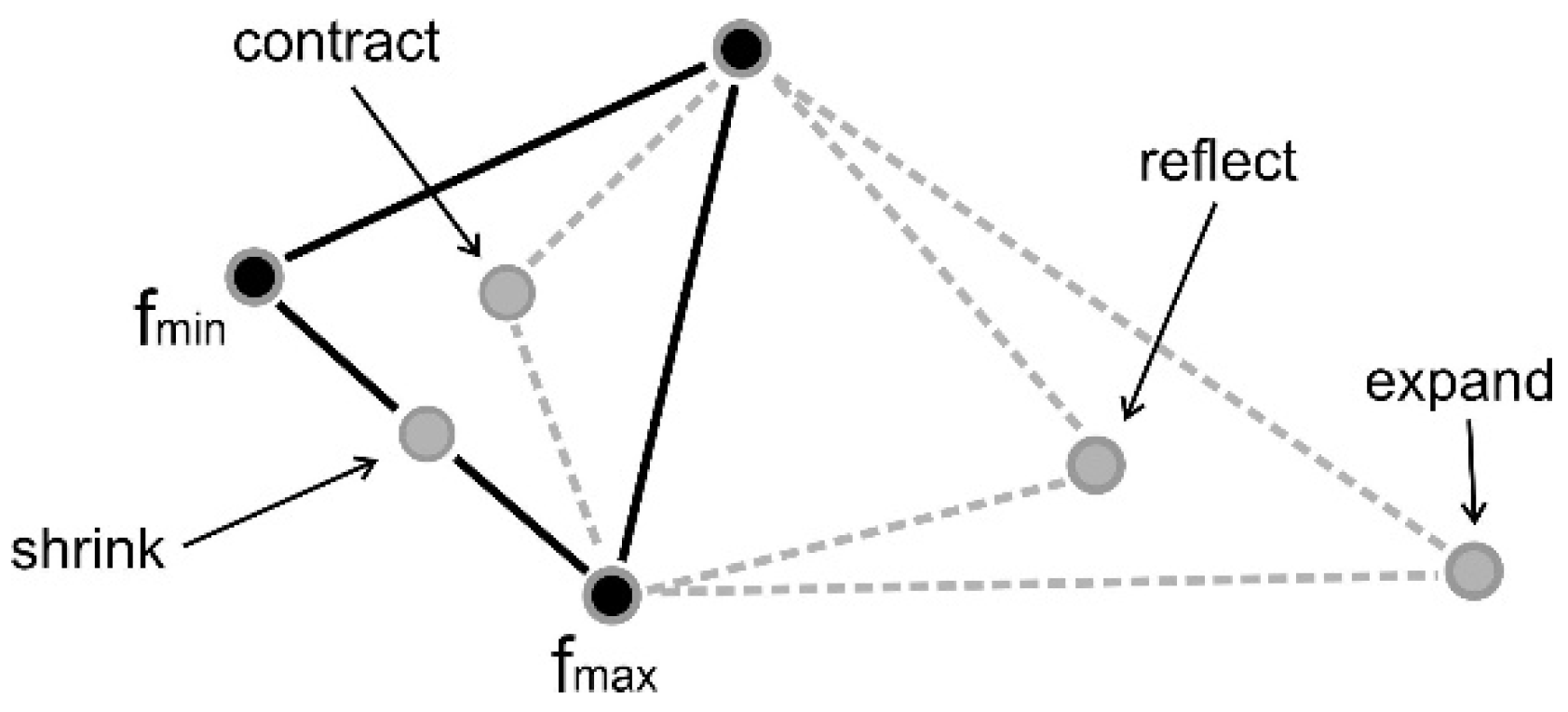
3.1. Evolutionary Algorithm
3.2. Nelder-Mead Algorithm
3.3. Monte Carlo Method
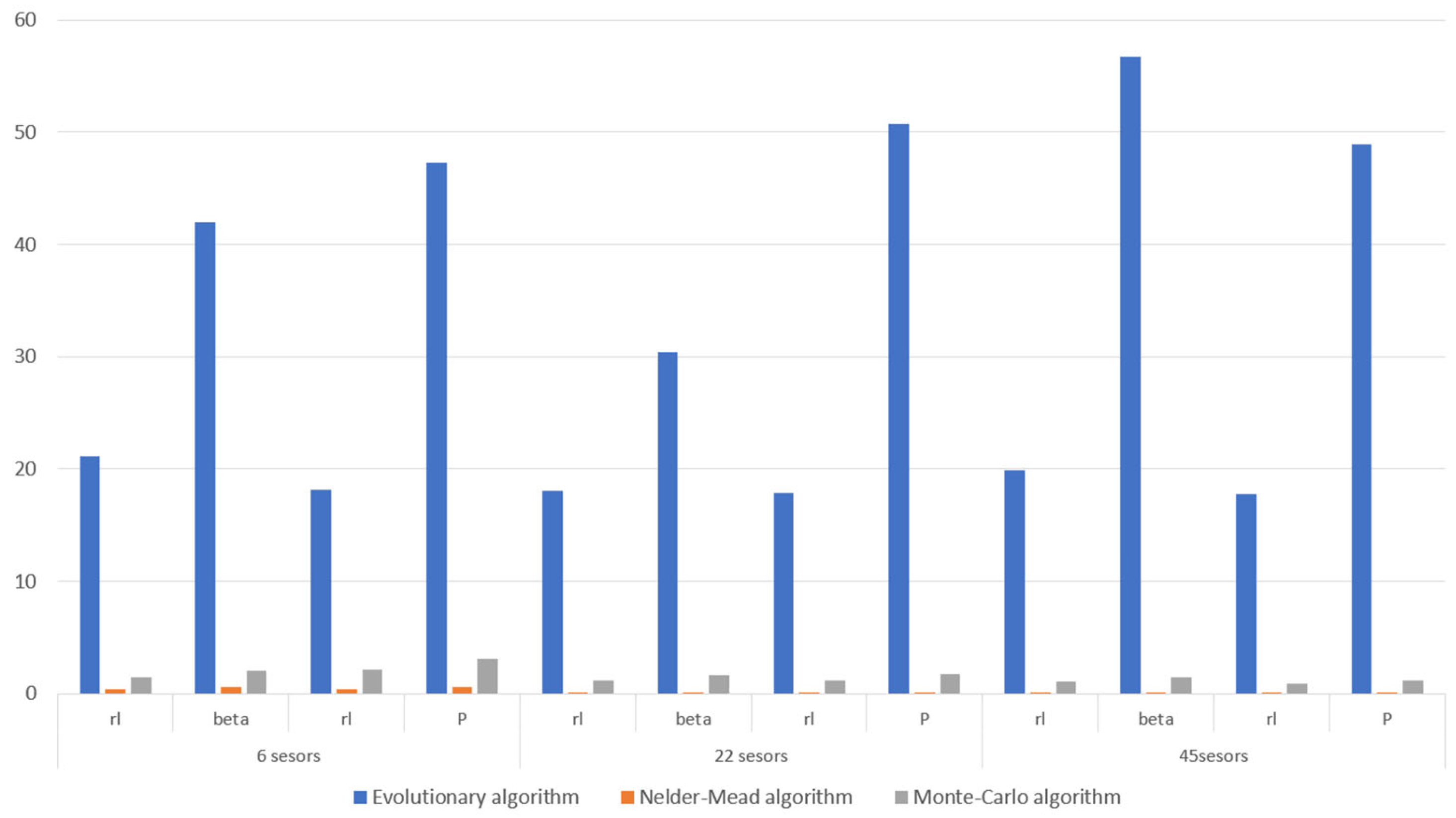
4. Results of the Identification Tasks
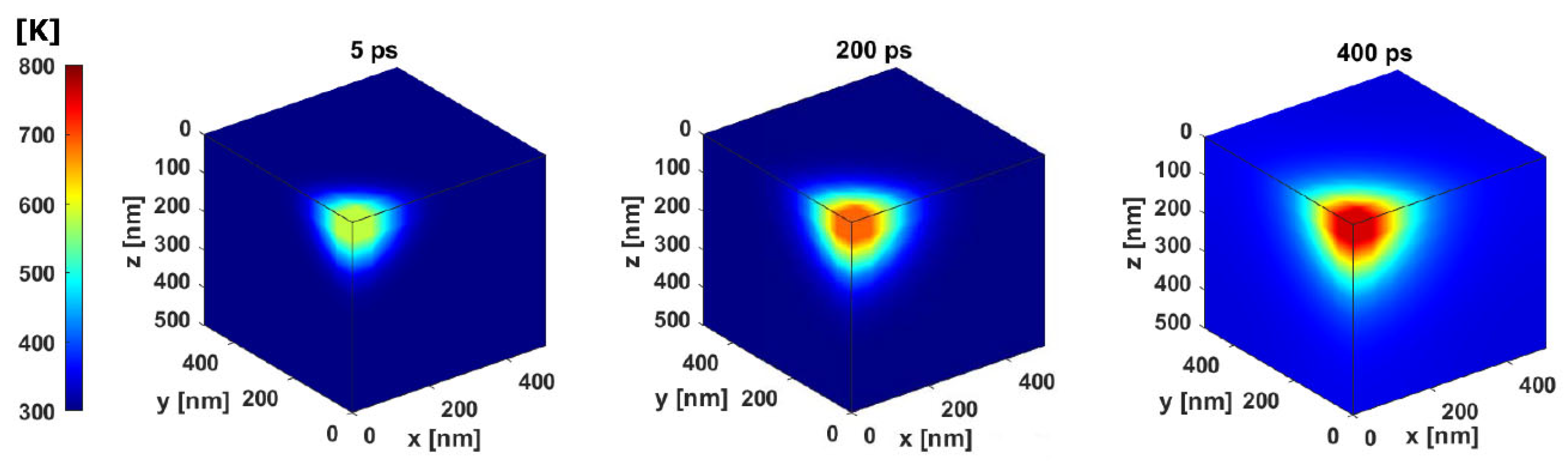
4.1. Identification for Unnoisy Data
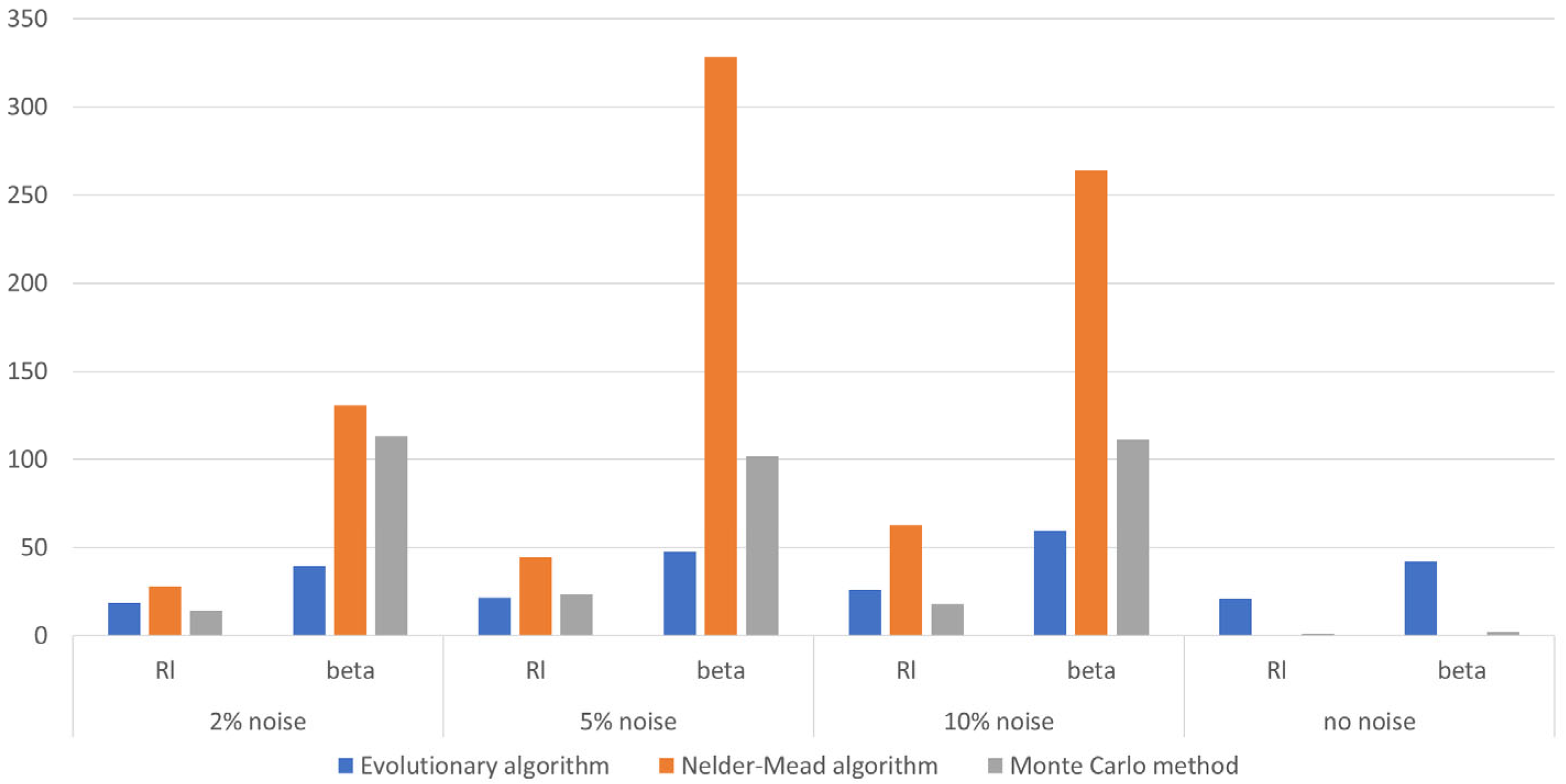
4.2. Identification for Data with Noise
5. Discussion
6. Concluding Remarks
- The common feature of evolutionary algorithms, which is to assure an appropriate balance between exploration and exploitation of the feasible solution space, unfortunately did not yield satisfactory results in this case. The reason for this is the very high density of peaks with local minima, which is significantly higher than when using other numerical methods, such as FEM, BEM or FDM.
- Good and satisfactory results were obtained using the Nelder-Mead algorithm, in which the solution obtained usually depends on the selected starting point. In this case, sharp peaks did not prevent a satisfactory solution from being obtained for the creeping simplex method. The correct search direction was observed even for completely different starting points.
- Interesting results were also obtained for measurement data that included Gaussian noise at different levels. The most resilient algorithm for noisy data was determined to be the evolutionary algorithm. It seems that the results in this case could be improved by using the previously mentioned Morozov’s discrepancy principle. The implementation of this principle to such a metaheuristic algorithm requires further research and is also worth considering.
- A remarkable phenomenon observed concerning the unusual nature of the identification function, unusual for numerical methods, can be additionally used in another way. The problem presented in this paper can also certainly be used as a test function (i.e., a benchmark) to evaluate the quality of optimization algorithms. Despite the fact that the use of the Monte Carlo method and Nelder-Mead algorithm with a multi-start allowed us to obtain significantly better results compared with EA (for data with no noise), none of the optimization algorithms should be used without a deeper study of a problem such as this one. For a small number of parameters, it is possible to visualize at least a fragment of the identification function domain. However, this should be undertaken with a sufficiently high resolution to circumvent any loss of information relating to local drastic changes in the function. In the authors’ opinion, the identification task for non-noisy data could be a good example of a new test function for other metaheuristic algorithms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations/Nomenclature
| Nomenclature | |
| Roman symbols | |
| distribution function | |
| velocity vector | |
| carrier generation coefficient | |
| energy density | |
| source function | |
| source function associated with laser irradiation | |
| Boltzmann constant | |
| electron density | |
| reduced Planck constant | |
| coupling coefficient | |
| power of the stationary laser pulse | |
| radius of the laser beam | |
| identification functional | |
| vector of the identification parameters | |
| computed temperatures in sensors | |
| postulated temperatures in sensors | |
| Greek symbols | |
| laser beam absorptivity | |
| Fermi energy | |
| phonon density | |
| relaxation time | |
| ΘD | Debye temperature |
| Subscripts | |
| e | electrons |
| ph | phonons |
| i | index of sensor point |
| j | index of time interval |
| Superscripts | |
| 0 | in the equilibrium state |
| Abbreviations | |
| LBM | Lattice Boltzmann Method |
| BTE | Boltzmann transport equations |
| DPLE | Dual phase lag equation |
| D3Q7 | Numerical implementation of the three-dimensional model using LBM |
| BVP | Boundary Value Problem |
| EA | Evolutionary Algorithm |
| ER | Relative error |
| MR | Mean error |
References
- Kotsedi, L.; Furlan, V.; Bharadwaj, V.; Kaviyarasu, K.; Sotillo, B.; Mtshali, C.B.; Matinise, N.; Demir, A.G.; Previtali, B.; Ramponi, R.; et al. Chromium oxide formation on nanosecond and femtosecond laser irradiated thin chromium films. Opt. Mater. 2019, 95, 109206. [Google Scholar] [CrossRef]
- Udaya Kumar, G.; Suresh, S.; Sujith Kumar, C.S.; Back, S.; Kang, B.; Lee, H.J. A review on the role of laser textured surfaces on boiling heat transfer. Appl. Therm. Eng. 2020, 174, 115274. [Google Scholar] [CrossRef]
- Wang, C.; Matthies, H.G. Non-probabilistic interval process model and method for uncertainty analysis of transient heat transfer problem. Int. J. Therm. Sci. 2019, 144, 147–157. [Google Scholar] [CrossRef]
- Mansoor, S.B.; Yilbas, B.S. Phonon transport in a curved aluminum thin film due to laser short pulse irradiation. Opt. Laser Technol. 2018, 101, 107–115. [Google Scholar] [CrossRef]
- Murat Tunç, K.M.; Erdem Günay, M.; Bayata, F. Analysis of the thermalization dynamics of two-layer thin films irradiated by femtosecond laser. Optik 2020, 208, 164137. [Google Scholar] [CrossRef]
- Peters, D.W.; El-Kady, I.; Kemme, S.A. Extraordinary Optical Transmission Through Patterned Subwavelength Apertures; SAND2004-6435; Sandia National Laboratories: Albuquerque, NM, USA; Livermore, CA, USA, 2004. [Google Scholar]
- Fathima, R.; Mujeeb, A. Nonlinear optical investigations of laser generated gold, silver and gold-silver alloy nanoparticles and optical limiting applications. J. Alloys Compd. 2021, 858, 157667. [Google Scholar] [CrossRef]
- Maillet, D. A review of the models using the Cattaneo and Vernotte hyperbolic heat equation and their experimental validation. Int. J. Therm. Sci. 2019, 139, 424–432. [Google Scholar] [CrossRef]
- Deng, D.; Jiang, Y.; Liang, D. High-order finite difference method for a second order dual-phase-lagging models of microscale heat transfer. Appl. Math. Comput. 2017, 309, 31–48. [Google Scholar] [CrossRef]
- Smith, A.N.; Norris, P.M. Microscale Heat Transfer. In Heat Transfer Handbook; Rohsenow, W.M., Hartnett, J.P., Cho, Y.I., Eds.; McGraw-Hill: New York, NY, USA, 1997; pp. 18.1–18.61. [Google Scholar]
- Nasri, F.; Ben Aissa, M.F.; Belmabrouk, H. Effect of second-order temperature jump in Metal-Oxide-Semiconductor Field Effect Transistor with Dual-Phase-Lag model. Microelectron. J. 2015, 46, 67–74. [Google Scholar] [CrossRef]
- Majchrzak, E.; Mochnacki, B. Modelling of thin metal film heating using the dual-phase lag equation with temperature-dependent parameters. Int. J. Heat Mass Transf. 2023, 209, 124088. [Google Scholar] [CrossRef]
- Lee, H.L.; Chen, W.L.; Chang, W.J.; Yang, Y. Estimation of energy absorption rate and temperature distributions in short-pulse laser heating of metals with a dual-phase-lag model. Appl. Therm. Eng. 2014, 65, 352–360. [Google Scholar] [CrossRef]
- Askarizadeh, H.; Ahmadikia, H. Analytical analysis of the dual-phase-lag model of bioheat transfer equation during transient heating of skin tissue. Heat Mass Transf. 2014, 50, 1673–1684. [Google Scholar] [CrossRef]
- Kumar, M.; Kaur, H.; Upadhyay, S.; Singh, S.; Rai, K.N. Mathematical modelling and simulation of three phase lag bio-heat transfer model during cancer treatment. Int. J. Therm. Sci. 2023, 184, 108002. [Google Scholar] [CrossRef]
- Jasinski, M.; Majchrzak, E.; Turchan, L. Numerical analysis of the interactions between laser and soft tissues using generalized dual-phase lag equation. Appl. Math. Model. 2016, 40, 750–762. [Google Scholar] [CrossRef]
- Kovács, R. Heat equations beyond Fourier: From heat waves to thermal metamaterials. Phys. Rep. 2024, 1048, 1–75. [Google Scholar] [CrossRef]
- Pisipati, S.; Geer, J.; Sammakia, B.; Murray, B.T. A novel alternate approach for multiscale thermal transport using diffusion in the Boltzmann Transport Equation. Int. J. Heat Mass Transf. 2011, 54, 3406–3411. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, X. Mesoscopic simulation of molten pool heat transfer and fluid flow with moving annular laser via lattice Boltzmann method. Appl. Therm. Eng. 2022, 215, 118947. [Google Scholar] [CrossRef]
- Shen, J.; Zhang, X. Analysis of dual-phase-lag heat conduction in a two-dimensional slab heated by a moving annular laser pulse. Appl. Math. Model. 2022, 105, 160–178. [Google Scholar] [CrossRef]
- Saurav, S.; Mazumder, S. Extraction of thermal conductivity using phonon Boltzmann Transport Equation based simulation of frequency domain thermo-reflectance experiments. Int. J. Heat Mass Transf. 2023, 204, 123871. [Google Scholar] [CrossRef]
- Hu, B.; Bao, W.; Chen, G.; Wang, Z.; Tang, D. Boltzmann transport equation simulation of phonon transport across GaN/AlN interface. Comput. Mater. Sci. 2023, 230, 112485. [Google Scholar] [CrossRef]
- Zahiri, S.; Zuo, J.; Shen, Y.; Bao, H. Numerical investigation of ballistic-diffusive heat transfer through a constriction with the Boltzmann transport equation. Appl. Therm. Eng. 2018, 141, 126–133. [Google Scholar] [CrossRef]
- Paruch, M.; Piasecka-Belkhayat, A.; Korczak, A. Identification of the ultra-short laser parameters during irradiation of thin metal films using the interval lattice Boltzmann method and evolutionary algorithm. Adv. Eng. Softw. 2023, 180, 103456. [Google Scholar] [CrossRef]
- Kirch, A. An Introduction to the Mathematical Theory of Inverse Problems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Marthaler, D.E. An Overview of Mathematical Methods for Numerical Optimization. In Numerical Methods for Metamaterial Design; Diest, K., Ed.; Springer: Cham, Switzerland, 2013; pp. 31–53. [Google Scholar]
- Martí, R. Multi-Start Methods. In Handbook of Metaheuristics; Glover, F., Kochenberger, G.A., Eds.; Springer: Boston, MA, USA, 2003; pp. 355–368. [Google Scholar]
- Michalewicz, Z. Genetic Algorithms + Data Structures = Evolution Programs, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Gujarathi, A.M.; Babu, B.V. Evolutionary Computation Techniques and Applications, 1st ed.; Apple Academic Press: New York, NY, USA, 2016. [Google Scholar]
- Zhang, L.; Li, L.; Ju, H.; Zhu, B. Inverse identification of interfacial heat transfer coefficient between the casting and metal mold using neural network. Energy Convers. Manag. 2010, 51, 1898–1904. [Google Scholar] [CrossRef]
- Wen, S.; Zhang, J.; Liu, S.; Liu, J. Numerical simulation investigation of heat exchangers for active chilled beams based on neural networks and a genetic algorithm. Appl. Energy 2025, 378, 124818. [Google Scholar] [CrossRef]
- Masrouri, M.; Tahsini, A.M. A comparative experimental study on inverse identification of an industrial heat gun using deep learning and two inverse heat transfer techniques. J. Therm. Anal. Calorim. 2023, 148, 9597–9608. [Google Scholar] [CrossRef]
- Blackwell, B.; Beck, J.V. A technique for uncertainty analysis for inverse heat conduction problems. Int. J. Heat Mass Transf. 2010, 53, 753–759. [Google Scholar] [CrossRef]
- Hamila, R.; Chaabane, R.; Askri, F.; Jemni, A.; Nasrallah, S.B. Lattice Boltzmann method for heat transfer problems with variable thermal conductivity. Int. J. Heat Technol. 2017, 35, 313–324. [Google Scholar] [CrossRef]
- Piasecka-Belkhayat, A.; Korczak, A. Modeling of thermal processes proceeding in a thin gold film using the lattice Boltzmann method with interval source function. AIP Conf. Proc. 2018, 1922, 060006. [Google Scholar]
- Wilde, D.; Nidhan, S.; Pham, H.T.; Foysi, H.; Reith, D.; Sarkar, S. Stratified Taylor–Green vortex by lattice Boltzmann methods: Influence of stencils, forcing schemes, and collision models. Comput. Fluids 2023, 256, 105838. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, Y.; Rani Kasinathan, A.; Imani Shahabad, S.; Ali, U.; Mahmoodkhani, Y.; Toyserkani, E. 3-Dimensional heat transfer modeling for laser powder-bed fusion additive manufacturing with volumetric heat sources based on varied thermal conductivity and absorptivity. Opt. Laser Technol. 2019, 109, 297–312. [Google Scholar] [CrossRef]
- Zhang, J.; Chen, G.; Bi, J. Analytical inversion solutions for temperature dependent surface absorptivity of metal film irradiated by laser. Optik 2017, 130, 1173–1182. [Google Scholar] [CrossRef]
- Burczyński, T.; Kuś, W.; Beluch, W.; Długosz, A.; Poteralski, A.; Szczepanik, M. Intelligent Computing in Optimal Design. Solid Mech. Its Appl. 2020, 261, 1–18. [Google Scholar]
- Długosz, A.; Pokorska, I.; Jaskulski, R.; Glinicki, M.A. Evolutionary identification method for determining thermophysical parameters of hardening concrete. Arch. Civ. Mech. Eng. 2021, 21, 35. [Google Scholar] [CrossRef]
- Beluch, W.; Burczyński, T. Two-scale identification of composites’ material constants by means of computational intelligence methods. Arch. Civ. Mech. Eng. 2014, 14, 636–646. [Google Scholar] [CrossRef]
- Długosz, A.; Schlieter, T. Evolutionary identification of microstructure parameters in the thermoelastic porous material. J. Theor. Appl. Mech. 2020, 58, 373–384. [Google Scholar] [CrossRef]
- Ali, A.F.; Hassanien, A.E.; Snášel, V. The Nelder-Mead Simplex Method with Variables Partitioning for Solving Large Scale Optimization Problems. In Innovations in Bio-Inspired Computing and Applications; Abraham, A., Krömer, P., Snášel, V., Eds.; Springer: Cham, Switzerland, 2014; pp. 271–284. [Google Scholar]
- Surjanovic, S.; Bingham, D. Virtual Library of Simulation Experiments: Test Functions and Datasets. 2013. Available online: http://www.sfu.ca/~ssurjano (accessed on 7 October 2025).
- Shonkwiler, R.W.; Lefton, L. Monte Carlo optimization. In An Introduction to Parallel and Vector Scientific Computation; Cambridge University Press: Cambridge, UK, 2006; pp. 244–264. [Google Scholar]
- Bhatnagar, S.; Prasad, H.; Prashanth, L. Kiefer-Wolfowitz Algorithm. In Stochastic Recursive Algorithms for Optimization; Springer: London, UK, 2013; pp. 31–39. [Google Scholar]
- Kuś, W.; Dziatkiewicz, J. Multicriteria identification of parameters in microscale heat transfer. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 587–597. [Google Scholar] [CrossRef]
- Dziatkiewicz, J.; Kuś, W.; Majchrzak, E.; Burczyński, T.; Turchan, Ł. Bioinspired identification of parameters in microscale heat transfer. Int. J. Multiscale Comput. Eng. 2014, 12, 79–89. [Google Scholar] [CrossRef]
- Pillonetto, G.; Chen, T.; Chiuso, A.; De Nicolao, G.; Ljung, L. Regularized System Identification: Learning Dynamic Models from Data; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Zhao, Z.; Meng, Z. A modified Tikhonov regularization method for a backward heat equation. Inverse Probl. Sci. Eng. 2011, 19, 1175–1182. [Google Scholar] [CrossRef]
- Gall, D. Electron mean free path in elemental metals. J. Appl. Phys. 2016, 119, 085101. [Google Scholar] [CrossRef]
- Escobar, R.A.; Ghai, S.S.; Jhon, M.S.; Amon, C.H. Multi-length and time scale thermal transport using the lattice Boltzmann method with application to electronics cooling. Int. J. Heat Mass Transf. 2006, 49, 97–107. [Google Scholar] [CrossRef]
- Escobar, R.A.; Amon, C.H. Thin film phonon heat conduction by the dispersion lattice Boltzmann Method. J. Heat Transf. 2008, 130, 092402. [Google Scholar] [CrossRef]






| Parameter | Value |
|---|---|
| Lattice steps | Δx = Δy = Δz = 50 nm |
| Time step | Δt = 0.01 ps |
| Number of time steps | 400 |
| Relaxation time for electrons | τe = 0.04 ps |
| Relaxation time for phonons | τph = 0.8 ps |
| Debye temperature | QD = 170 K |
| Fermi energy | εF = 5.53 eV |
| Coupling coefficient | G = 2.3 × 1016 W/m3 K |
| Boltzmann constant | kb = 1.38065 × 10−23 J/K |
| Initial temperature | T0 = 300 K |
| Best | Worst | Median | MR | ER < 5% | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | ER | Value | ER | Value | ER | ||||
| 6 sensors | rl | 96.613 | 3.387 | 64.423 | 35.577 | 124.353 | 24.353 | 21.181 | 0 |
| β | 0.421 | 5.196 | 0.979 | 144.816 | 0.302 | 24.393 | 41.964 | ||
| rl | 99.669 | 0.331 | 62.124 | 37.876 | 111.921 | 11.921 | 18.145 | 2 | |
| P | 0.904 | 0.479 | 2.471 | 174.531 | 0.773 | 14.118 | 47.239 | ||
| 22 sensors | rl | 100.881 | 0.881 | 72.133 | 27.867 | 123.790 | 23.790 | 18.024 | 3 |
| β | 0.395 | 1.267 | 0.727 | 98.745 | 0.302 | 24.482 | 30.432 | ||
| rl | 100.002 | 0.002 | 62.307 | 37.692 | 120.726 | 20.726 | 17.835 | 5 | |
| P | 0.900 | 0.0002 | 2.459 | 173.249 | 0.701 | 22.161 | 50.788 | ||
| 45 sensors | rl | 103.761 | 3.761 | 64.362 | 35.638 | 84.806 | 15.194 | 19.892 | 1 |
| β | 0.380 | 4.885 | 0.982 | 145.380 | 0.519 | 29.657 | 56.718 | ||
| rl | 99.361 | 0.639 | 62.458 | 37.542 | 85.693 | 14.306 | 17.773 | 2 | |
| P | 0.908 | 0.901 | 2.427 | 169.716 | 1.146 | 27.289 | 48.896 | ||
| Test No. | f(x) | rl | β | ER(rl) | ER(β) | ΣER | |
|---|---|---|---|---|---|---|---|
| 1 | −2.156 | 138.912 | 0.269 | 38.912 | 33.049 | 71.961 | |
| 2 | −0.653 | 64.512 | 0.975 | 35.489 | 143.826 | 179.315 | |
| 3 | −0.301 | 78.540 | 0.602 | 21.460 | 50.429 | 71.889 | |
| 4 | −3.491 | 147.181 | 0.253 | 47.181 | 36.865 | 84.046 | |
| 5 | −0.025 | 94.481 | 0.435 | 5.5195 | 8.797 | 14.3172 | |
| 6 | −0.286 | 79.190 | 0.592 | 20.810 | 47.966 | 68.776 | |
| 7 | −0.707 | 124.353 | 0.302 | 24.353 | 24.393 | 48.745 | ← median |
| … | … | … | … | … | … | … | |
| 24 | −0.656 | 64.423 | 0.979 | 35.577 | 144.815 | 180.393 | ← worst |
| … | … | … | … | … | … | … | |
| 27 | −0.01 | 96.613 | 0.421 | 3.387 | 5.195 | 8.583 | ← best |
| 28 | −0.587 | 67.144 | 0.869 | 32.856 | 117.327 | 150.183 | |
| 29 | −0.658 | 123.607 | 0.304 | 23.607 | 23.862 | 47.468 | |
| 30 | −0.021 | 104.709 | 0.375 | 4.709 | 6.237 | 10.946 |
| Best | Worst | Median | MR | ER < 5% | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | ER | Value | ER | Value | ER | ||||
| 6 sensors | rl | 100.027 | 0.027 | 100.704 | 0.704 | 99.561 | 0.439 | 0.413 | 30 |
| β | 0.399 | 0.028 | 0.396 | 1.0017 | 0.402 | 0.633 | 0.593 | ||
| rl | 100.068 | 0.068 | 100.723 | 0.723 | 100.432 | 0.432 | 0.417 | 30 | |
| P | 0.899 | 0.096 | 0.891 | 1.0271 | 0.894 | 0.6248 | 0.596 | ||
| 22 sensors | rl | 100.001 | 0.001 | 99.884 | 0.1162 | 99.951 | 0.0488 | 0.0513 | 30 |
| β | 0.399 | 0.001 | 0.401 | 0.1683 | 0.4003 | 0.07 | 0.0737 | ||
| rl | 99.999 | 0.0009 | 100.127 | 0.127 | 99.9718 | 0.0282 | 0.0418 | 30 | |
| P | 0.899 | 0.0016 | 0.898 | 0.1856 | 0.900 | 0.043 | 0.0609 | ||
| 45 sensors | rl | 100.000 | 0.0 | 100.034 | 0.034 | 100.018 | 0.018 | 0.0173 | 30 |
| β | 0.3999 | 0.001 | 0.3998 | 0.0475 | 0.3998 | 0.0255 | 0.0242 | ||
| rl | 99.999 | 0.0004 | 100.028 | 0.028 | 99.985 | 0.0147 | 0.0137 | 30 | |
| P | 0.900 | 0.0016 | 0.8996 | 0.0398 | 0.9002 | 0.0192 | 0.0194 | ||
| Best | Worst | Median | MR | ER < 5% | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | ER | Value | ER | Value | ER | ||||
| 6 sensors | rl | 99.933 | 0.067 | 103.872 | 3.872 | 100.965 | 0.965 | 1.422 | 29 |
| β | 0.400 | 0.101 | 0.379 | 5.208 | 0.394 | 1.368 | 2.008 | ||
| rl | 99.960 | 0.04 | 95.176 | 4.823 | 97.987 | 2.012 | 2.103 | 26 | |
| P | 0.900 | 0.053 | 0.968 | 7.556 | 0.926 | 2.985 | 3.064 | ||
| 22 sensors | rl | 100.093 | 0.093 | 97.171 | 2.829 | 100.958 | 0.958 | 1.159 | 30 |
| β | 0.399 | 0.169 | 0.417 | 4.284 | 0.394 | 1.361 | 1.677 | ||
| rl | 100.026 | 0.026 | 95.754 | 4.246 | 99.0337 | 0.966 | 1.196 | 29 | |
| P | 0.8997 | 0.03 | 0.960 | 6.697 | 0.9128 | 1.428 | 1.756 | ||
| 45 sensors | rl | 100.043 | 0.043 | 96.786 | 3.214 | 100.824 | 0.824 | 1.050 | 30 |
| β | 0.400193 | 0.048 | 0.4189 | 4.709 | 0.396 | 1.111 | 1.494 | ||
| rl | 100.039 | 0.039 | 97.156 | 2.844 | 100.477 | 0.477 | 0.866 | 30 | |
| P | 0.900322 | 0.036 | 0.938 | 4.177 | 0.894 | 0.7101 | 1.214 | ||
| Best | Worst | Median | MR | ER < 5% | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | ER | Value | ER | Value | ER | ||||
| 2% noise | rl | 98.695 | 1.305 | 65.006 | 34.994 | 83.749 | 16.251 | 18.648 | 4 |
| β | 0.412 | 2.916 | 0.956 | 139.024 | 0.531 | 32.737 | 39.668 | ||
| 5% noise | rl | 101.368 | 1.368 | 64.595 | 35.405 | 80.345 | 19.655 | 21.470 | 2 |
| β | 0.400 | 0.012 | 0.964 | 141.095 | 0.579 | 44.641 | 47.754 | ||
| 10% noise | rl | 97.241 | 2.759 | 65.707 | 34.293 | 140.037 | 40.037 | 26.086 | 1 |
| β | 0.405 | 1.337 | 0.935 | 133.685 | 0.264 | 33.984 | 59.467 | ||
| Best | Worst | Median | MR | ER < 5% | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | ER | Value | ER | Value | ER | ||||
| 2% noise | rl | 98.892 | 1.108 | 50.274 | 49.726 | 130.964 | 30.964 | 28.112 | 3 |
| β | 0.405 | 1.260 | 2.756 | 589.078 | 0.283 | 29.158 | 130.818 | ||
| 5% noise | rl | 116.948 | 16.948 | 50.007 | 49.993 | 60.491 | 39.509 | 44.593 | 0 |
| β | 0.323 | 19.187 | 2.850 | 612.428 | 1.180 | 194.880 | 328.211 | ||
| 10% noise | rl | 110.498 | 10.498 | 50.086 | 49.914 | 207.147 | 107.147 | 62.771 | 0 |
| β | 0.356 | 11.096 | 2.958 | 639.613 | 0.185 | 53.766 | 263.865 | ||
| Best | Worst | Median | MR | ER < 5% | |||||
|---|---|---|---|---|---|---|---|---|---|
| Value | ER | Value | ER | Value | ER | ||||
| 2% noise | rl | 147.995 | 47.995 | 92.998 | 7.002 | 95.800 | 4.200 | 14.084 | 0 |
| β | 0.562 | 40.623 | 0.998 | 149.515 | 0.953 | 138.264 | 113.369 | ||
| 5% noise | rl | 145.305 | 45.305 | 93.177 | 6.823 | 94.049 | 5.951 | 23.149 | 0 |
| β | 0.569 | 42.134 | 0.999 | 149.843 | 0.975 | 143.765 | 102.008 | ||
| 10% noise | rl | 136.910 | 36.910 | 91.142 | 8.858 | 92.791 | 7.209 | 18.114 | 0 |
| β | 0.389 | 2.751 | 0.997 | 149.299 | 0.980 | 145.085 | 111.328 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Długosz, A.; Korczak, A. Identification of Ultra-Short Laser Parameters for a 3D Model of a Thin Metal Film Using the Lattice Boltzmann Method. Materials 2025, 18, 5079. https://doi.org/10.3390/ma18225079
Długosz A, Korczak A. Identification of Ultra-Short Laser Parameters for a 3D Model of a Thin Metal Film Using the Lattice Boltzmann Method. Materials. 2025; 18(22):5079. https://doi.org/10.3390/ma18225079
Chicago/Turabian StyleDługosz, Adam, and Anna Korczak. 2025. "Identification of Ultra-Short Laser Parameters for a 3D Model of a Thin Metal Film Using the Lattice Boltzmann Method" Materials 18, no. 22: 5079. https://doi.org/10.3390/ma18225079
APA StyleDługosz, A., & Korczak, A. (2025). Identification of Ultra-Short Laser Parameters for a 3D Model of a Thin Metal Film Using the Lattice Boltzmann Method. Materials, 18(22), 5079. https://doi.org/10.3390/ma18225079







