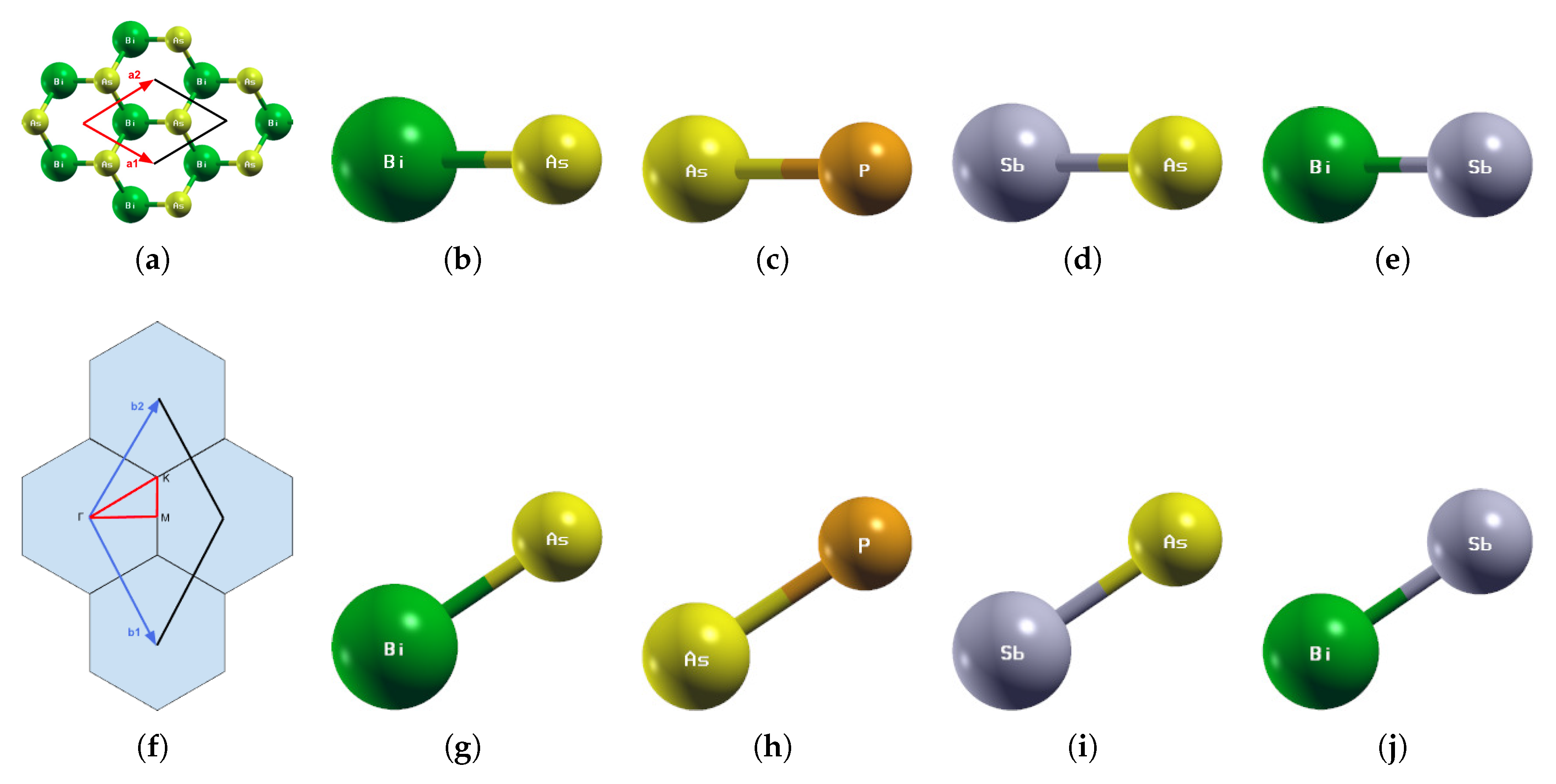
Figure 1.
(a) The primitive vectors and (f) the brillouin zone of BiAs. Displayed here are the top (b–e) and side (g–j) views of a 1 × 1 × 1 supercell of the optimized atomic structures of (b,g) BiAs, (c,h) AsP, (d,i) SbAs, and (e,j) BiSb. Each atom is labeled with its atomic symbol. The green, yellow, orange, and gray atoms represent Bi, As, P, and Sb, respectively.
Figure 1.
(a) The primitive vectors and (f) the brillouin zone of BiAs. Displayed here are the top (b–e) and side (g–j) views of a 1 × 1 × 1 supercell of the optimized atomic structures of (b,g) BiAs, (c,h) AsP, (d,i) SbAs, and (e,j) BiSb. Each atom is labeled with its atomic symbol. The green, yellow, orange, and gray atoms represent Bi, As, P, and Sb, respectively.
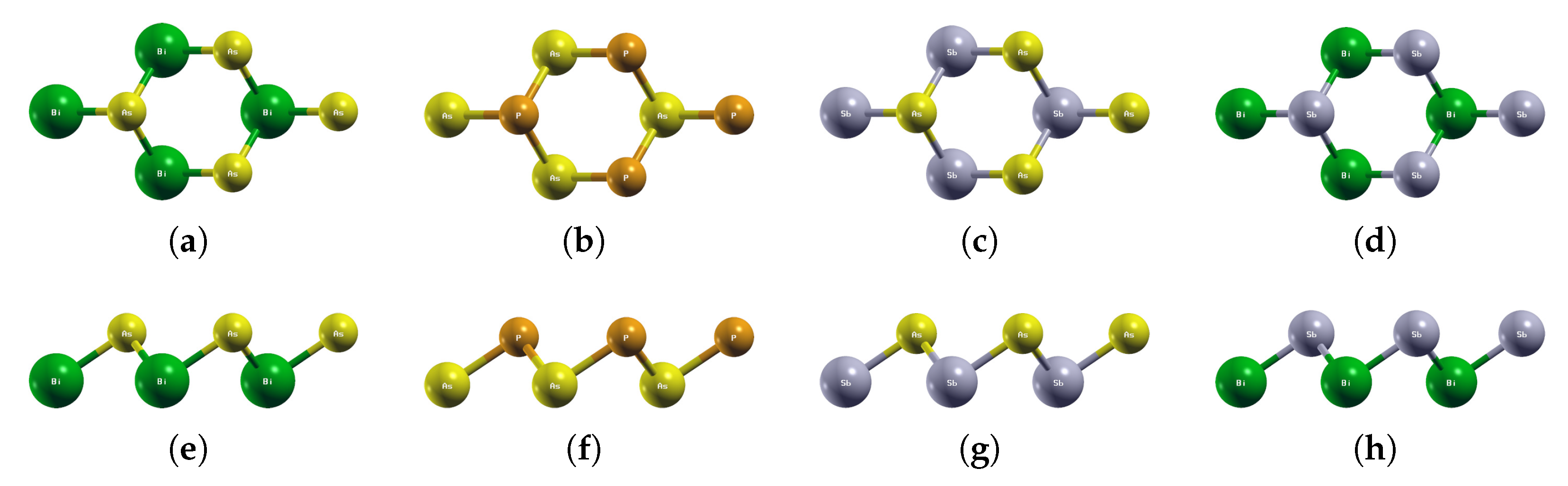
Figure 2.
Optimized atomic structures of BiAs, AsP, SbAs, and BiSb. Displayed here are the (a–d) top and (e–h) side views of a 2 × 2 × 1 supercell of (a,e) BiAs; (b,f) AsP; (c,g) SbAs; (d,h) BiSb. Each atom is labeled with its atomic symbol. The green, yellow, orange, and gray atoms represent Bi, As, P, and Sb, respectively.
Figure 2.
Optimized atomic structures of BiAs, AsP, SbAs, and BiSb. Displayed here are the (a–d) top and (e–h) side views of a 2 × 2 × 1 supercell of (a,e) BiAs; (b,f) AsP; (c,g) SbAs; (d,h) BiSb. Each atom is labeled with its atomic symbol. The green, yellow, orange, and gray atoms represent Bi, As, P, and Sb, respectively.
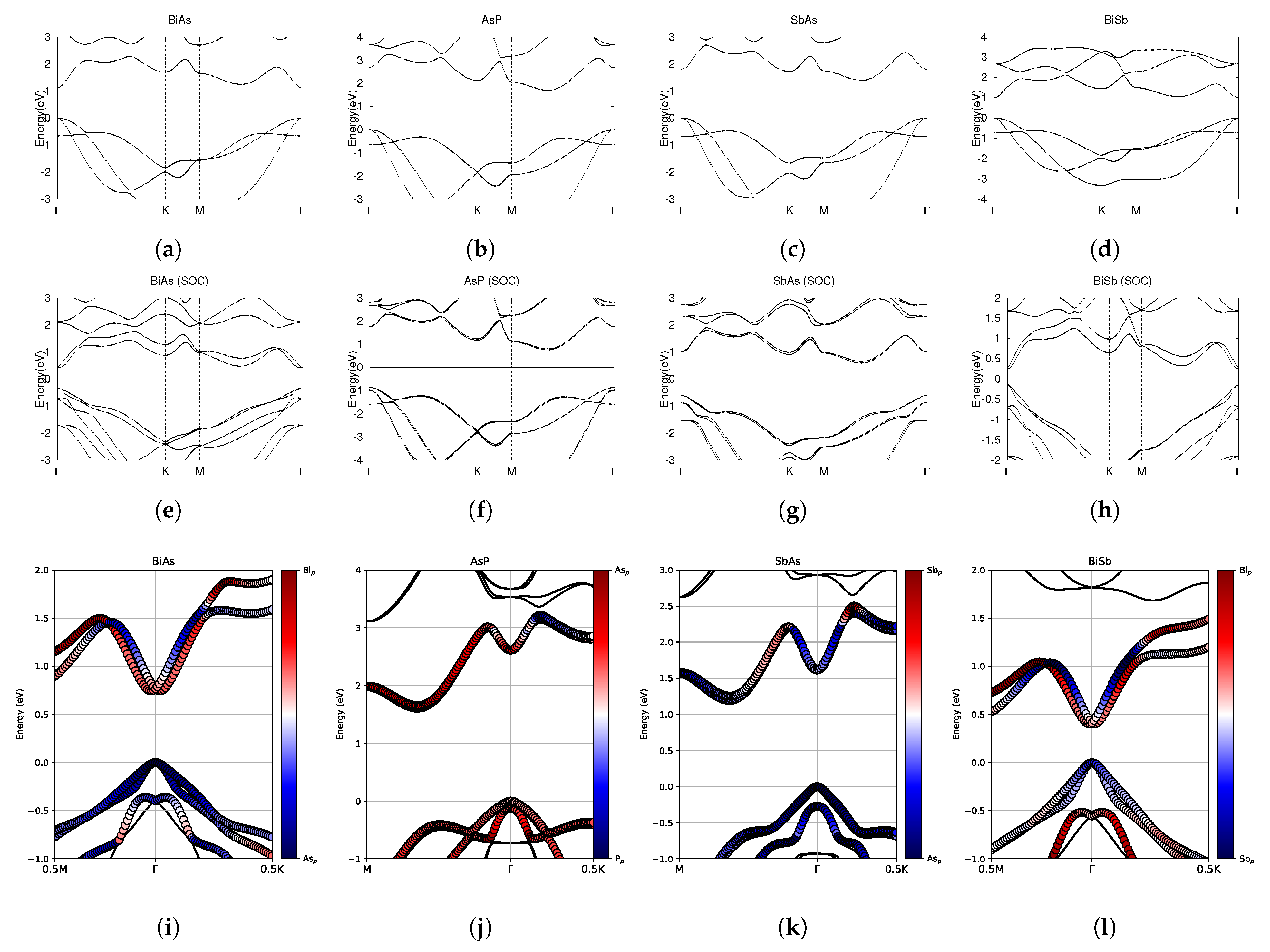
Figure 3.
Electronic band structures of pure monolayers BiAs, AsP, SbAs, and BiSb. (a–d) The top row displays the bands without SOC. (e–h) The middle row displays the bands with SOC. (i–l) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
Figure 3.
Electronic band structures of pure monolayers BiAs, AsP, SbAs, and BiSb. (a–d) The top row displays the bands without SOC. (e–h) The middle row displays the bands with SOC. (i–l) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
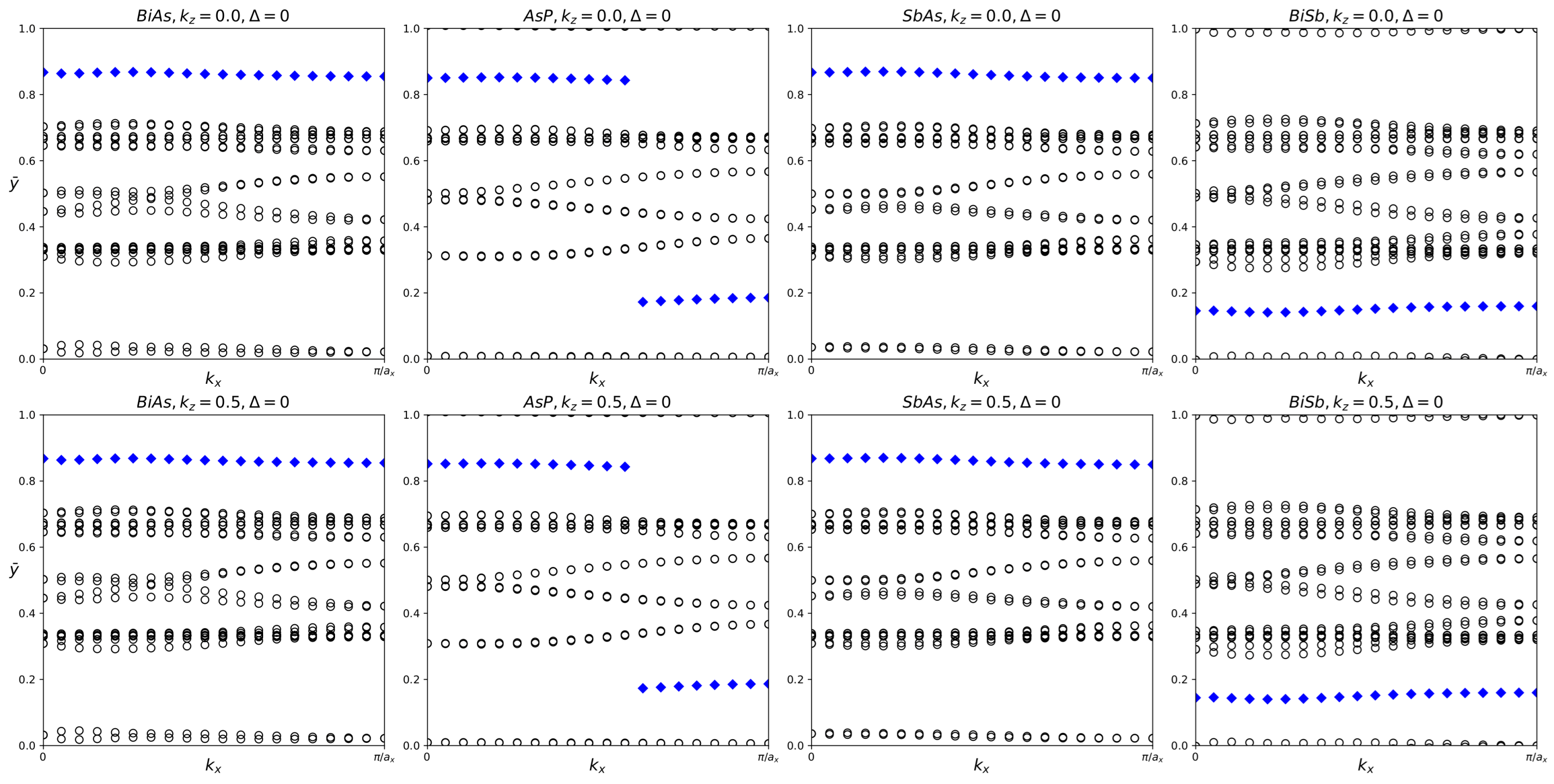
Figure 4.
Hybrid Wannier charge centers for pure BiAs, AsP, SbAs, and BiSb monolayers. The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
Figure 4.
Hybrid Wannier charge centers for pure BiAs, AsP, SbAs, and BiSb monolayers. The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
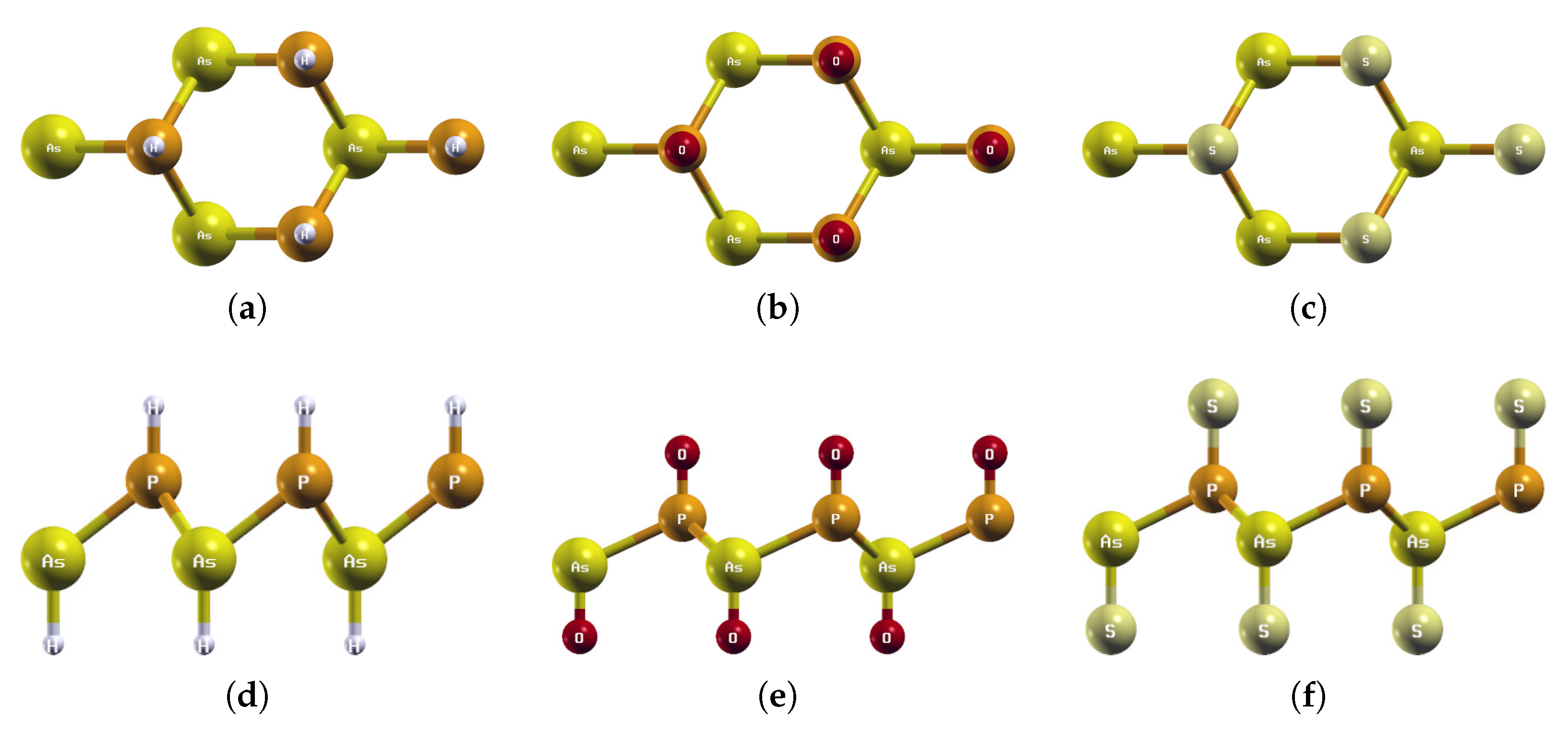
Figure 5.
Optimized atomic structures of BiAsX2 (X = H, O, S). Displayed here are the (a–c) top and (d–f) side views of a 2 × 2 × 1 supercell of (a,d) BiAsH2; (b,e) BiAsO2; (c,f) BiAsS2. Each atom is labeled with its atomic symbol. The green, yellow, white, red, and grayish-yellow atoms represent Bi, As, H, O, and S, respectively.
Figure 5.
Optimized atomic structures of BiAsX2 (X = H, O, S). Displayed here are the (a–c) top and (d–f) side views of a 2 × 2 × 1 supercell of (a,d) BiAsH2; (b,e) BiAsO2; (c,f) BiAsS2. Each atom is labeled with its atomic symbol. The green, yellow, white, red, and grayish-yellow atoms represent Bi, As, H, O, and S, respectively.
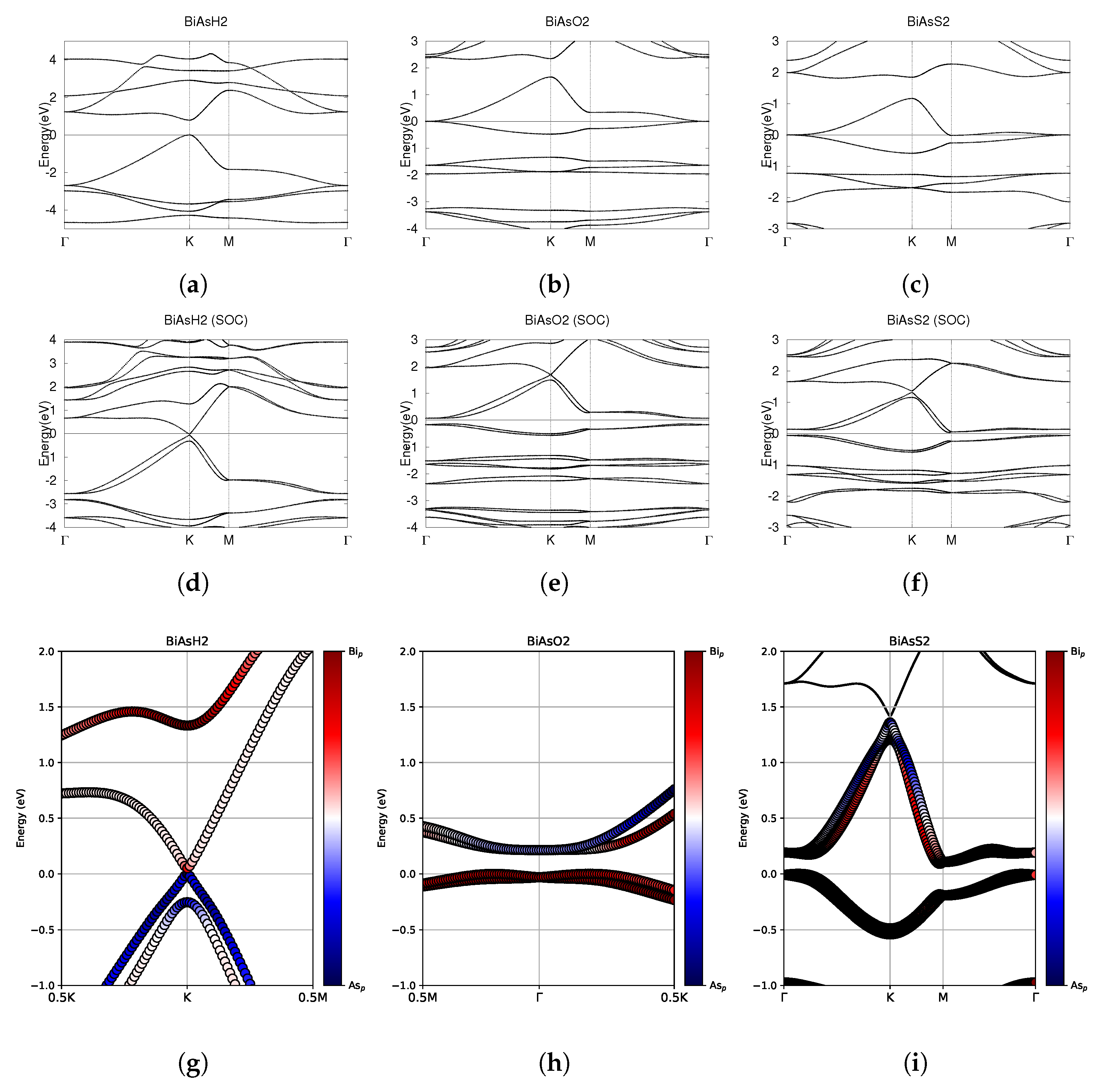
Figure 6.
Electronic band structures of functionalized monolayers BiAsH2, BiAsO2, and BiAsS2. (a–c) The top row displays the bands without SOC. (d–f) The middle row displays the bands with SOC. (g–i) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
Figure 6.
Electronic band structures of functionalized monolayers BiAsH2, BiAsO2, and BiAsS2. (a–c) The top row displays the bands without SOC. (d–f) The middle row displays the bands with SOC. (g–i) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
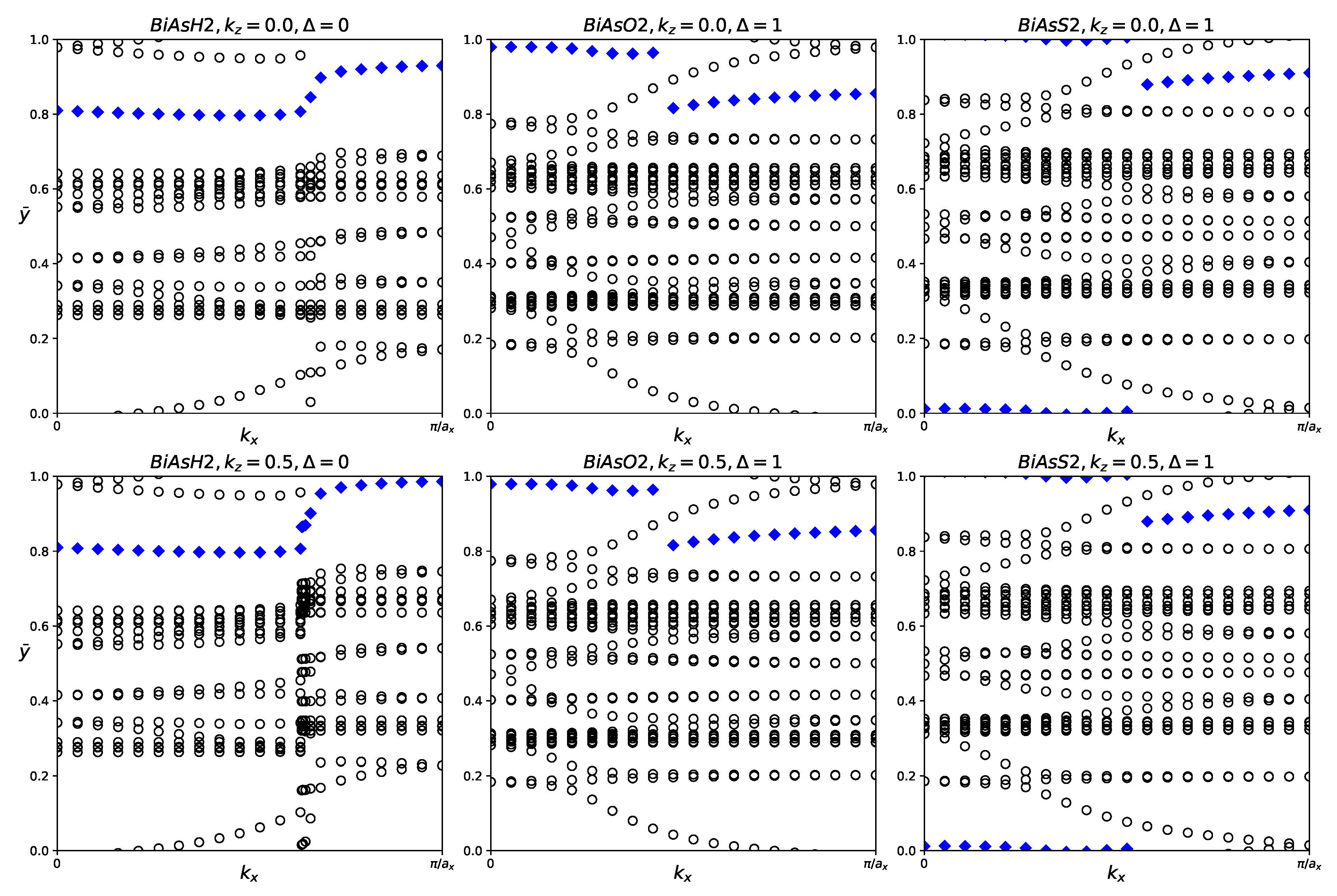
Figure 7.
Hybrid Wannier charge centers for functionalized BiAsX2 monolayers (X = H, O, S). The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
Figure 7.
Hybrid Wannier charge centers for functionalized BiAsX2 monolayers (X = H, O, S). The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
Figure 8.
Optimized atomic structures of AsPX2 (X = H, O, S). Displayed here are the (a–c) top and (d–f) side views of a 2 × 2 × 1 supercell of (a,d) AsPH2; (b,e) AsPO2; (c,f) AsPS2. Each atom is labeled with its atomic symbol. The yellow, orange, white, red, and grayish-yellow atoms represent As, P, H, O, and S, respectively.
Figure 8.
Optimized atomic structures of AsPX2 (X = H, O, S). Displayed here are the (a–c) top and (d–f) side views of a 2 × 2 × 1 supercell of (a,d) AsPH2; (b,e) AsPO2; (c,f) AsPS2. Each atom is labeled with its atomic symbol. The yellow, orange, white, red, and grayish-yellow atoms represent As, P, H, O, and S, respectively.
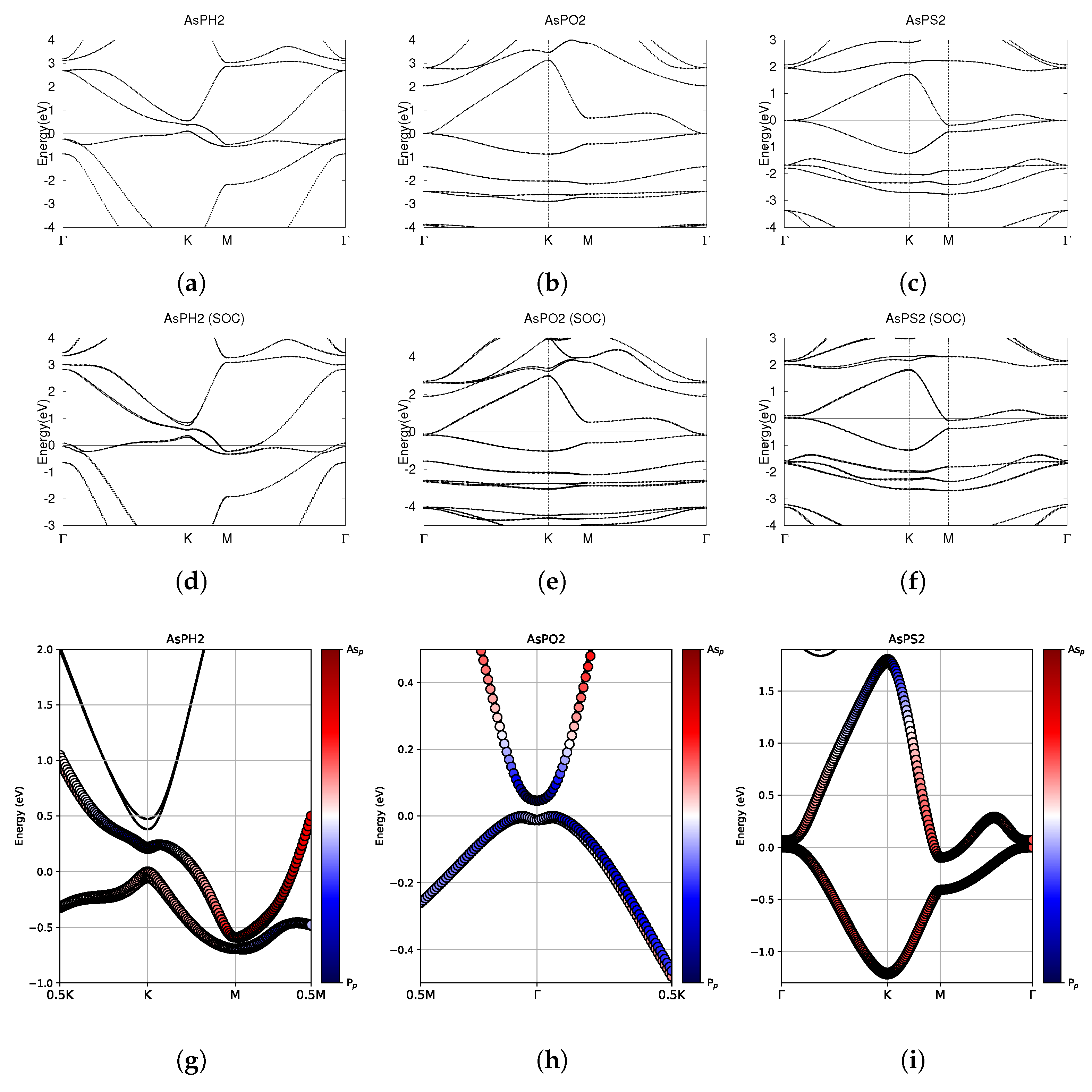
Figure 9.
Electronic band structures of functionalized monolayers AsPH2, AsPO2, and AsPS2. (a–c) The top row displays the bands without SOC. (d–f) The middle row displays the bands with SOC. (g–i) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
Figure 9.
Electronic band structures of functionalized monolayers AsPH2, AsPO2, and AsPS2. (a–c) The top row displays the bands without SOC. (d–f) The middle row displays the bands with SOC. (g–i) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
Figure 10.
Hybrid Wannier charge centers for functionalized AsPX2 monolayers (X = H, O, S). The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
Figure 10.
Hybrid Wannier charge centers for functionalized AsPX2 monolayers (X = H, O, S). The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
Figure 11.
Optimized atomic structures of SbAsX2 (X = H, O, S). Displayed here are the (a–c) top and (d–f) side views of a 2 × 2 × 1 supercell of (a,d) SbAsH2; (b,e) SbAsO2; (c,f) SbAsS2. Each atom is labeled with its atomic symbol. The gray, yellow, white, red, and grayish-yellow atoms represent Sb, As, H, O, and S, respectively.
Figure 11.
Optimized atomic structures of SbAsX2 (X = H, O, S). Displayed here are the (a–c) top and (d–f) side views of a 2 × 2 × 1 supercell of (a,d) SbAsH2; (b,e) SbAsO2; (c,f) SbAsS2. Each atom is labeled with its atomic symbol. The gray, yellow, white, red, and grayish-yellow atoms represent Sb, As, H, O, and S, respectively.
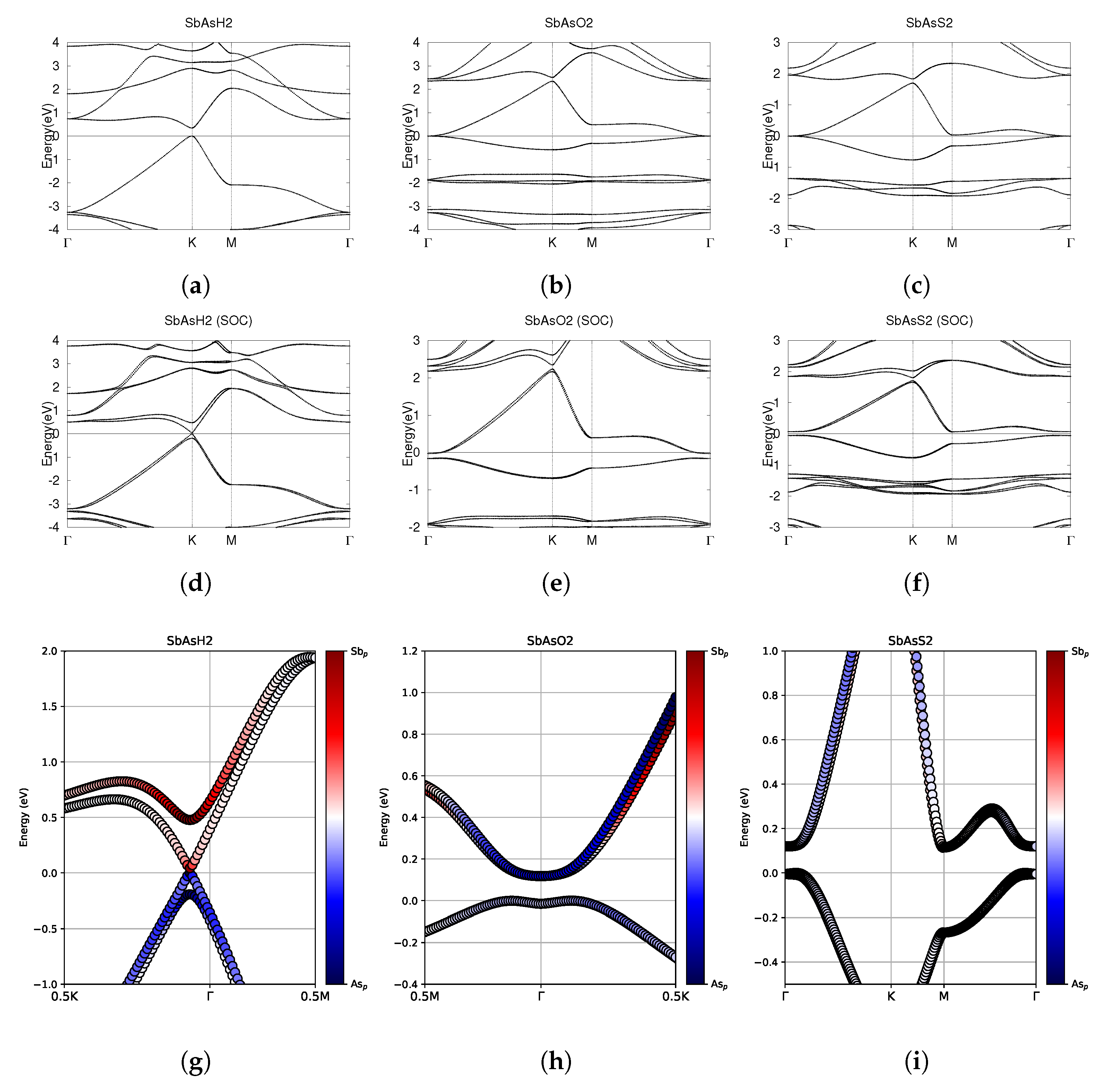
Figure 12.
Electronic band structures of functionalized monolayers SbAsH2, SbAsO2, and SbAsS2. (a–c) The top row displays the bands without SOC. (d–f) The middle row displays the bands with SOC. (g–i) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
Figure 12.
Electronic band structures of functionalized monolayers SbAsH2, SbAsO2, and SbAsS2. (a–c) The top row displays the bands without SOC. (d–f) The middle row displays the bands with SOC. (g–i) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
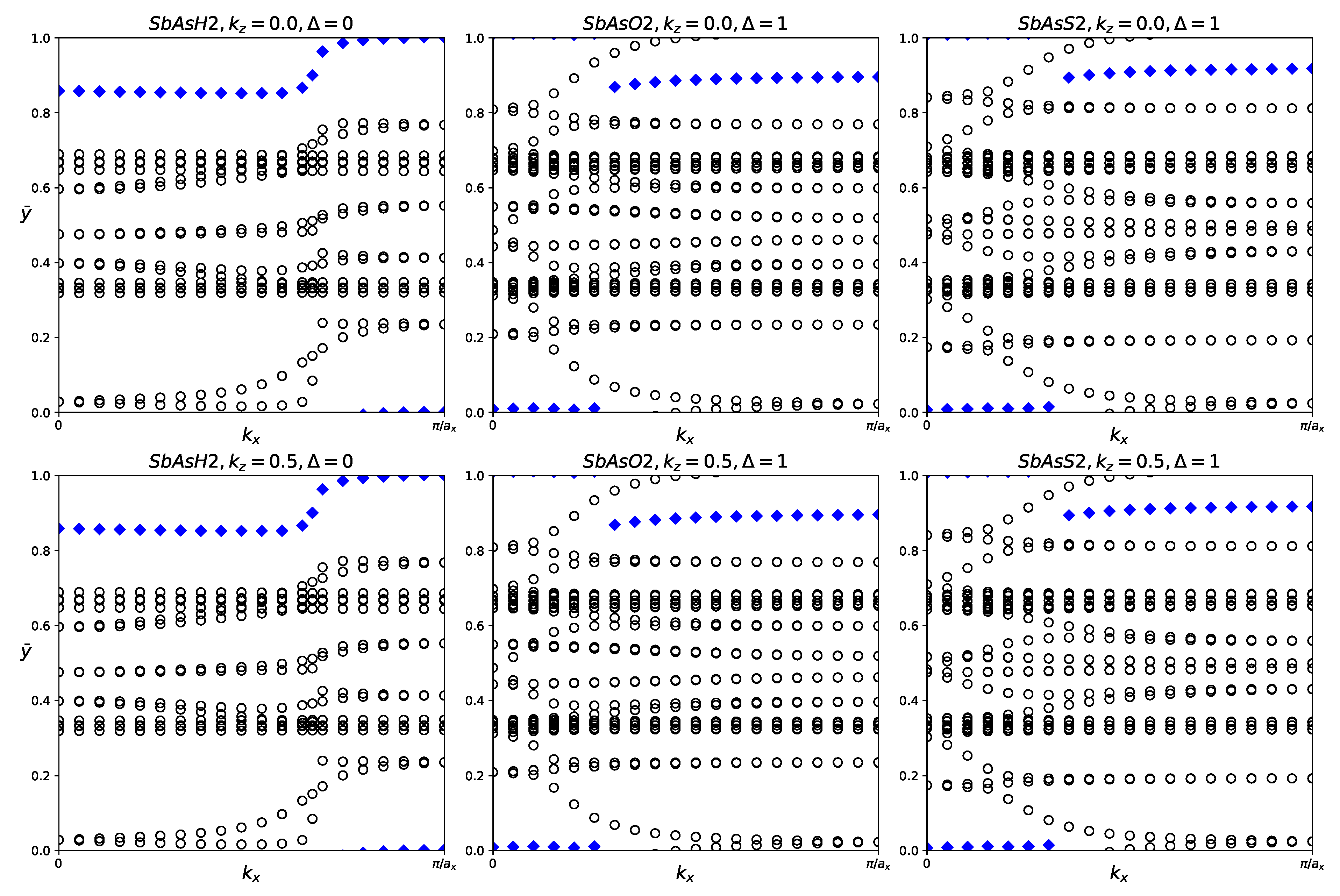
Figure 13.
Hybrid Wannier charge centers for functionalized SbAsX2 monolayers (X = H, O, S). The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
Figure 13.
Hybrid Wannier charge centers for functionalized SbAsX2 monolayers (X = H, O, S). The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
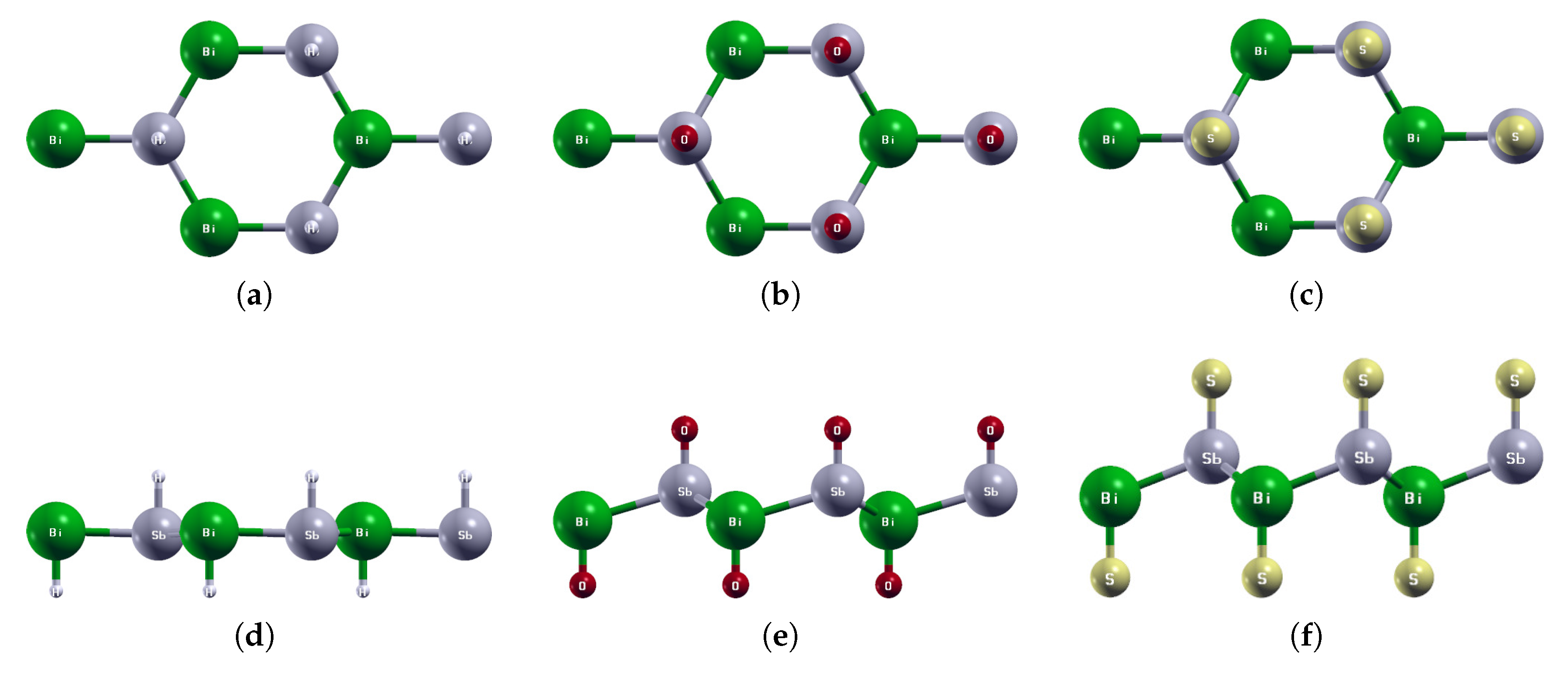
Figure 14.
Optimized atomic structures of BiSbX2 (X = H, O, S). Displayed here are the (a–c) top and (d–f) side views of a 2 × 2 × 1 supercell of (a,d) BiSbH2; (b,e) BiSbO2; (c,f) BiSbS2. Each atom is labeled with its atomic symbol. The green, gray, white, red, and grayish-yellow atoms represent Bi, Sb, H, O, and S, respectively.
Figure 14.
Optimized atomic structures of BiSbX2 (X = H, O, S). Displayed here are the (a–c) top and (d–f) side views of a 2 × 2 × 1 supercell of (a,d) BiSbH2; (b,e) BiSbO2; (c,f) BiSbS2. Each atom is labeled with its atomic symbol. The green, gray, white, red, and grayish-yellow atoms represent Bi, Sb, H, O, and S, respectively.
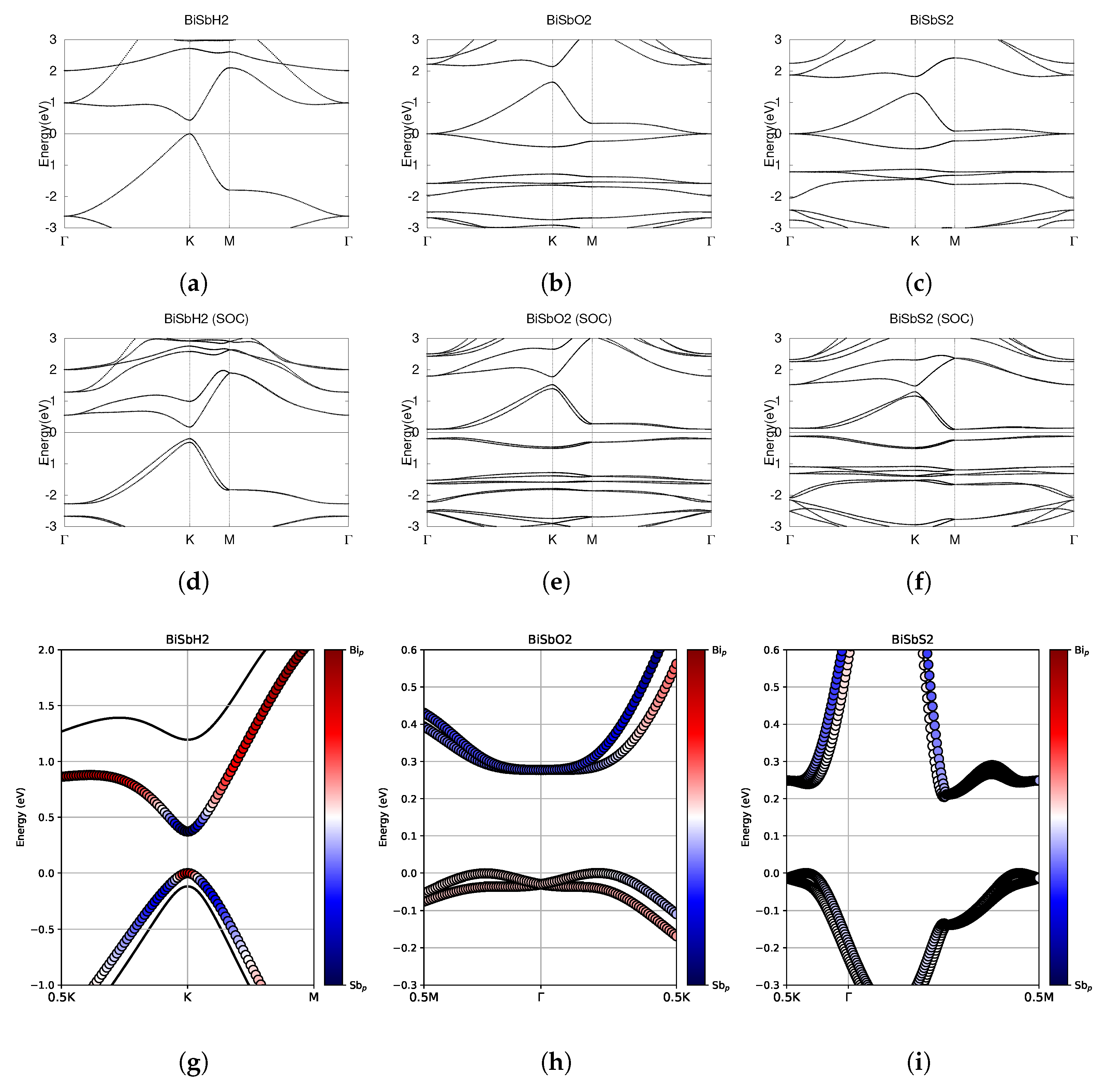
Figure 15.
Electronic band structures of functionalized monolayers BiSbH2, BiSbO2, and BiSbS2. (a–c) The top row displays the bands without SOC. (d–f) The middle row displays the bands with SOC. (g–i) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
Figure 15.
Electronic band structures of functionalized monolayers BiSbH2, BiSbO2, and BiSbS2. (a–c) The top row displays the bands without SOC. (d–f) The middle row displays the bands with SOC. (g–i) The bottom row shows the fatbands, with SOC. The fermi energy level position from the DFT calculation is set to 0.
Figure 16.
Hybrid Wannier charge centers for functionalized BiSbX2 monolayers (X = H, O, S). The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
Figure 16.
Hybrid Wannier charge centers for functionalized BiSbX2 monolayers (X = H, O, S). The open circles represent hybrid Wannier charge centers. The first row is at the surface kz = 0. The second row is at the surface kz = 0.5. The indicates the Z2 invariant—0 represents trivial topology, while 1 represents nontrivial topology.
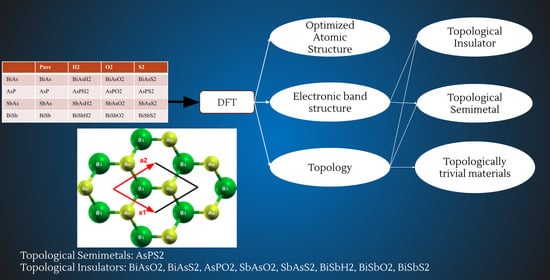
Table 1.
Electron configurations and radius cutoffs in angstroms of the atoms used in current calculations.
Table 1.
Electron configurations and radius cutoffs in angstroms of the atoms used in current calculations.
| Element | Electron Configuration | Radius Cutoff (Å) |
|---|
| P | [Ne]3s23p3 | 1.01 |
| As | [Ar]4s23d104p3 | 1.11 |
| Sb | [Kr]5s24d105p³3 | 1.27 |
| Bi | [Xe]6s24f145d106p3 | 1.28 |
| H | 1s1 | 0.53 |
| O | [He]2s22p4 | 0.75 |
| S | [Ne]3s23p4 | 1.01 |
Table 2.
Converged kinetic energy cutoff, k-point grid, and vacuum height for each structure.
Table 2.
Converged kinetic energy cutoff, k-point grid, and vacuum height for each structure.
| Structure | Kinetic Energy Cutoff (Ha) | k-Point Grid | Vacuum Height (Å) |
|---|
| BiAs | 21 | 10 × 10 × 1 | 17 |
| BiAsH2 | 21 | 8 × 8 × 1 | 19 |
| BiAsO2 | 21 | 8 × 8 × 1 | 21 |
| BiAsS2 | 21 | 8 × 8 × 1 | 25 |
| AsP | 14 | 10 × 10 × 1 | 13 |
| AsPH2 | 21 | 10 × 10 × 1 | 22 |
| AsPO2 | 21 | 8 × 8 × 1 | 19 |
| AsPS2 | 21 | 10 × 10 × 1 | 24 |
| SbAs | 14 | 10 × 10 × 1 | 15 |
| SbAsH2 | 21 | 10 × 10 × 1 | 19 |
| SbAsO2 | 21 | 8 × 8 × 1 | 20 |
| SbAsS2 | 21 | 8 × 8 × 1 | 25 |
| BiSb | 21 | 10 × 10 × 1 | 18 |
| BiSbH2 | 21 | 8 × 8 × 1 | 19 |
| BiSbO2 | 21 | 6 × 6 × 1 | 20 |
| BiSbS2 | 21 | 8 × 8 × 1 | 25 |
Table 3.
Current and previous other calculations of BiAs, AsP, SbAs, BiSb. a (Å) is the lattice constant; h (Å) is the buckling height; Eg (eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
Table 3.
Current and previous other calculations of BiAs, AsP, SbAs, BiSb. a (Å) is the lattice constant; h (Å) is the buckling height; Eg (eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
| Materials | BiAs | AsP | SbAs | BiSb |
|---|
| Properties | Current | Other | Current | Other | Current | Other | Current | Other |
|---|
| a (Å) | 3.98 | 3.982 [45], 4.00 [28,31] | 3.48 | 3.45 [46], 3.46 [31] | 3.86 | 3.87 [24], 3.86 [31,35] | 4.23 | 4.255 [47], 4.24 [28,31,48] |
| h (Å) | 1.56 | 1.532 [45], 1.56 [28,31] | 1.34 | 1.33 [46], 1.32 [31] | 1.52 | 1.52 [24,35], 1.51 [31] | 1.69 | 1.69 [28,31,47,48] |
| Eg (eV) | 1.12 | | 1.70 | 1.82 [46] | 1.39 | 1.47 [35] | 1.00 | 0.95 [47], 0.96 [48] |
| (eV) | 0.75 | 0.70 [45] | 1.61 | | 1.20 | 1.27 [35] | 0.40 | 0.37 [47], 0.36 [48] |
| Z2 | 0 | | 0 | | 0 | | 0 | |
Table 4.
The calculated lattice parameters and band gaps of BiAsX2 (X = H, O, S). a (Å) is the lattice constant; d (Å) is the bond length between the two subscripted atoms; h (Å) is the buckling height; Eg (eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
Table 4.
The calculated lattice parameters and band gaps of BiAsX2 (X = H, O, S). a (Å) is the lattice constant; d (Å) is the bond length between the two subscripted atoms; h (Å) is the buckling height; Eg (eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
| System | a (Å) | (Å) | (Å) | (Å) | h (Å) | Eg (eV) | (eV) | Z2 |
|---|
| BiAsH2 | 5.05 | 2.92 | 1.81 | 1.54 | 0.04 | 0.79 | 0.05 | 0 |
| BiAsO2 | 4.99 | 3.03 | 1.93 | 1.65 | 0.96 | 0 | 0.21 | 1 |
| BiAsS2 | 4.78 | 2.99 | 2.33 | 2.06 | 1.15 | 0 | 0.09 | 1 |
Table 5.
The calculated lattice parameters and band gaps of AsPX2 (X = H, O, S). a (Å) is the lattice constant; d (Å) is the bond length between the two subscripted atoms; h (Å) is the buckling height; Eg (eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
Table 5.
The calculated lattice parameters and band gaps of AsPX2 (X = H, O, S). a (Å) is the lattice constant; d (Å) is the bond length between the two subscripted atoms; h (Å) is the buckling height; Eg (eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
| System | a (Å) | (Å) | (Å) | (Å) | h (Å) | Eg (eV) | (eV) | Z2 |
|---|
| AsPH2 | 3.44 | 2.52 | 1.69 | 1.48 | 1.54 | 0 | 0 | 0 |
| AsPO2 | 4.08 | 2.60 | 1.64 | 1.49 | 1.09 | 0 | 0.05 | 1 |
| AsPS2 | 4.02 | 2.59 | 2.04 | 1.92 | 1.15 | 0 | 0 | 1 |
Table 6.
The calculated lattice parameters and band gaps of SbAsX2 (X = H, O, S). a(Å) is the lattice constant; d(Å) is the bond length between the two subscripted atoms; h(Å) is the buckling height; Eg(eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
Table 6.
The calculated lattice parameters and band gaps of SbAsX2 (X = H, O, S). a(Å) is the lattice constant; d(Å) is the bond length between the two subscripted atoms; h(Å) is the buckling height; Eg(eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
| System | a (Å) | (Å) | (Å) | (Å) | h (Å) | Eg (eV) | (eV) | Z2 |
|---|
| SbAsH2 | 4.93 | 2.85 | 1.73 | 1.53 | 0.06 | 0.35 | 0.04 | 0 |
| SbAsO2 | 4.74 | 2.93 | 1.83 | 1.64 | 1.05 | 0 | 0.12 | 1 |
| SbAsS2 | 4.53 | 2.88 | 2.23 | 2.05 | 1.20 | 0 | 0.11 | 1 |
Table 7.
The calculated lattice parameters and band gaps of BiSbX2 (X = H, O, S). a(Å) is the lattice constant; d(Å) is the bond length between the two subscripted atoms; h(Å) is the buckling height; Eg(eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
Table 7.
The calculated lattice parameters and band gaps of BiSbX2 (X = H, O, S). a(Å) is the lattice constant; d(Å) is the bond length between the two subscripted atoms; h(Å) is the buckling height; Eg(eV) and (eV) are the band gaps calculated without and with SOC, respectively. Z2 is the topological invariant. 1 represents nontrivial topology, 0 indicates trivial topology.
| System | a (Å) | (Å) | (Å) | (Å) | h (Å) | Eg (eV) | (eV) | Z2 |
|---|
| BiSbH2 | 5.36 | 3.10 | 1.81 | 1.73 | 0.08 | 0.43 | 0.37 | 1 |
| BiSbO2 | 5.32 | 3.20 | 1.94 | 1.84 | 0.91 | 0 | 0.28 | 1 |
| BiSbS2 | 5.07 | 3.15 | 2.34 | 2.25 | 1.16 | 0 | 0.20 | 1 |