Analysis of the Dual-Functional Broadband Properties of an Asymmetric Piezoelectric Metamaterial Beam for Simultaneous Vibration Reduction and Energy Harvesting
Abstract
1. Introduction
2. Theoretical Analysis
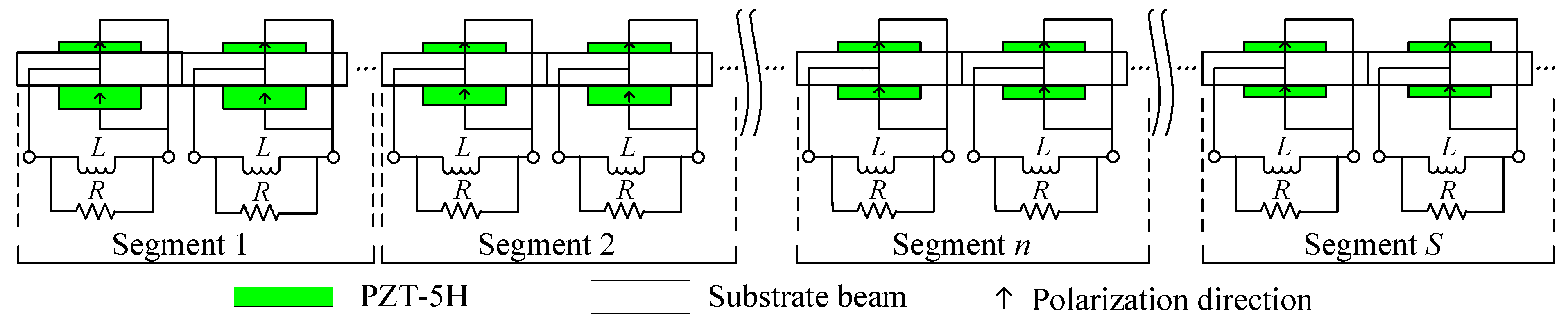
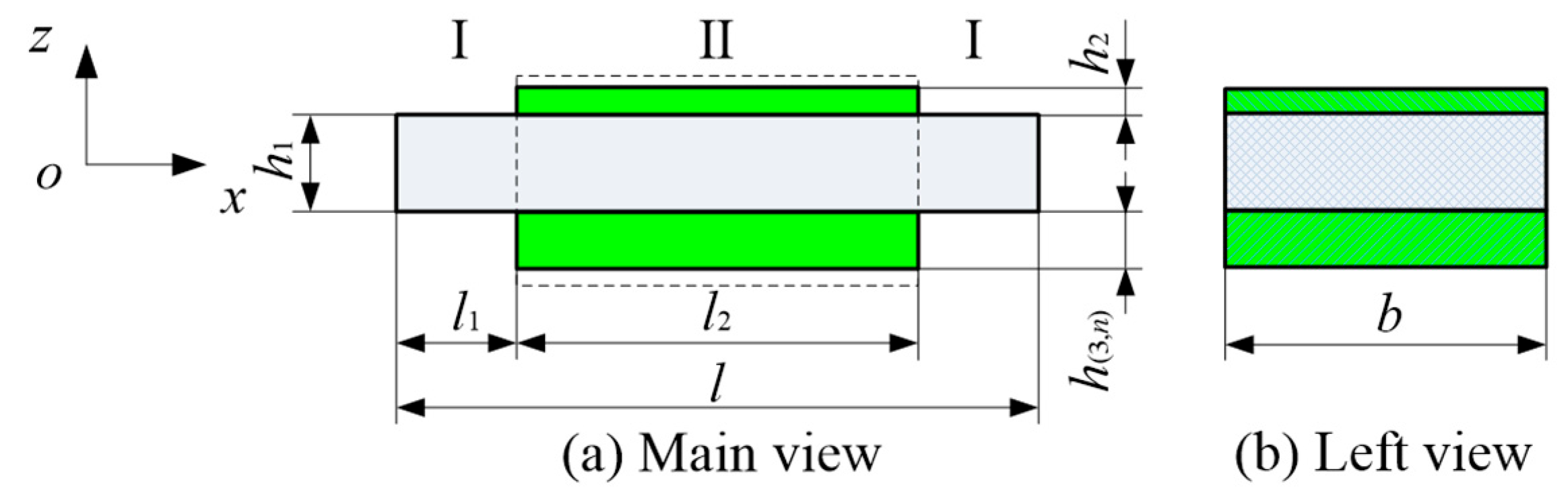
2.1. Structure Model
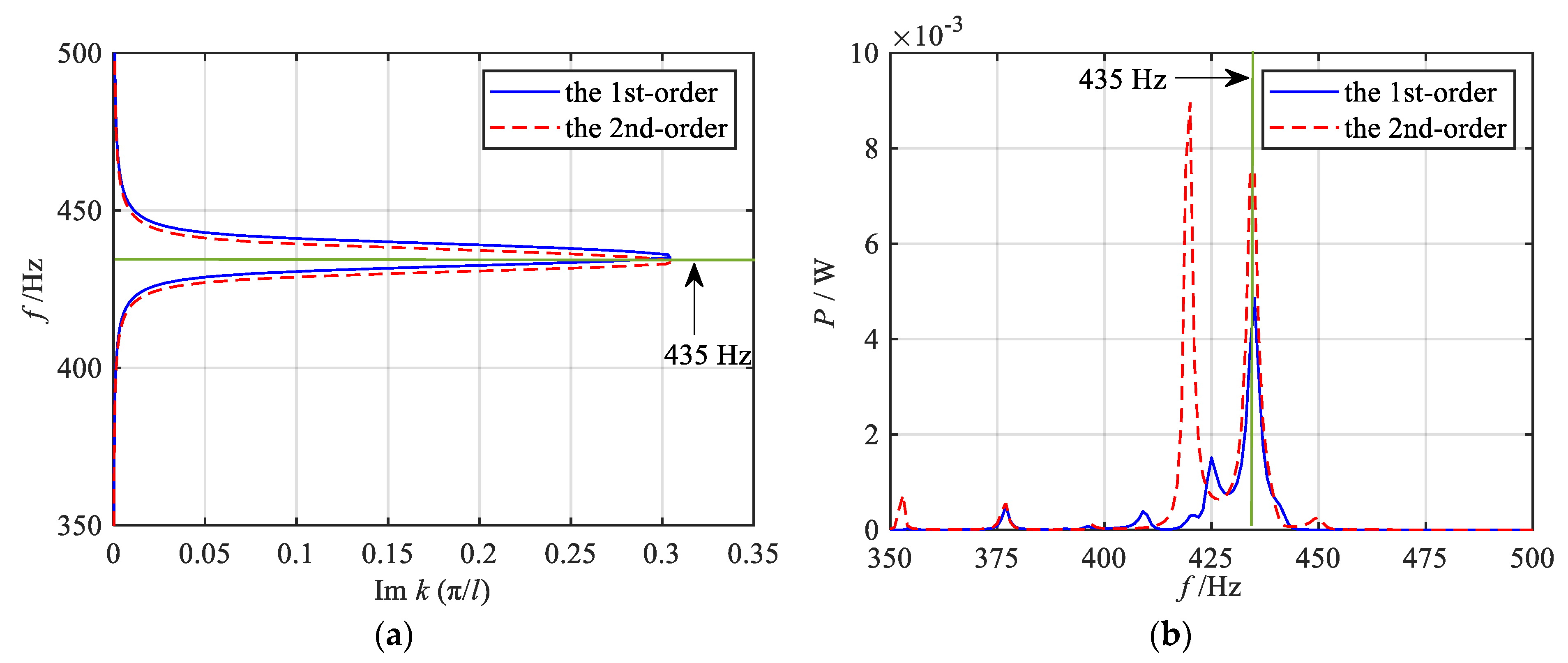
2.2. The Propagation and Energy Harvesting Mechanism of Bending-Dominated Wave
2.3. Vibration Reduction Performance Analysis
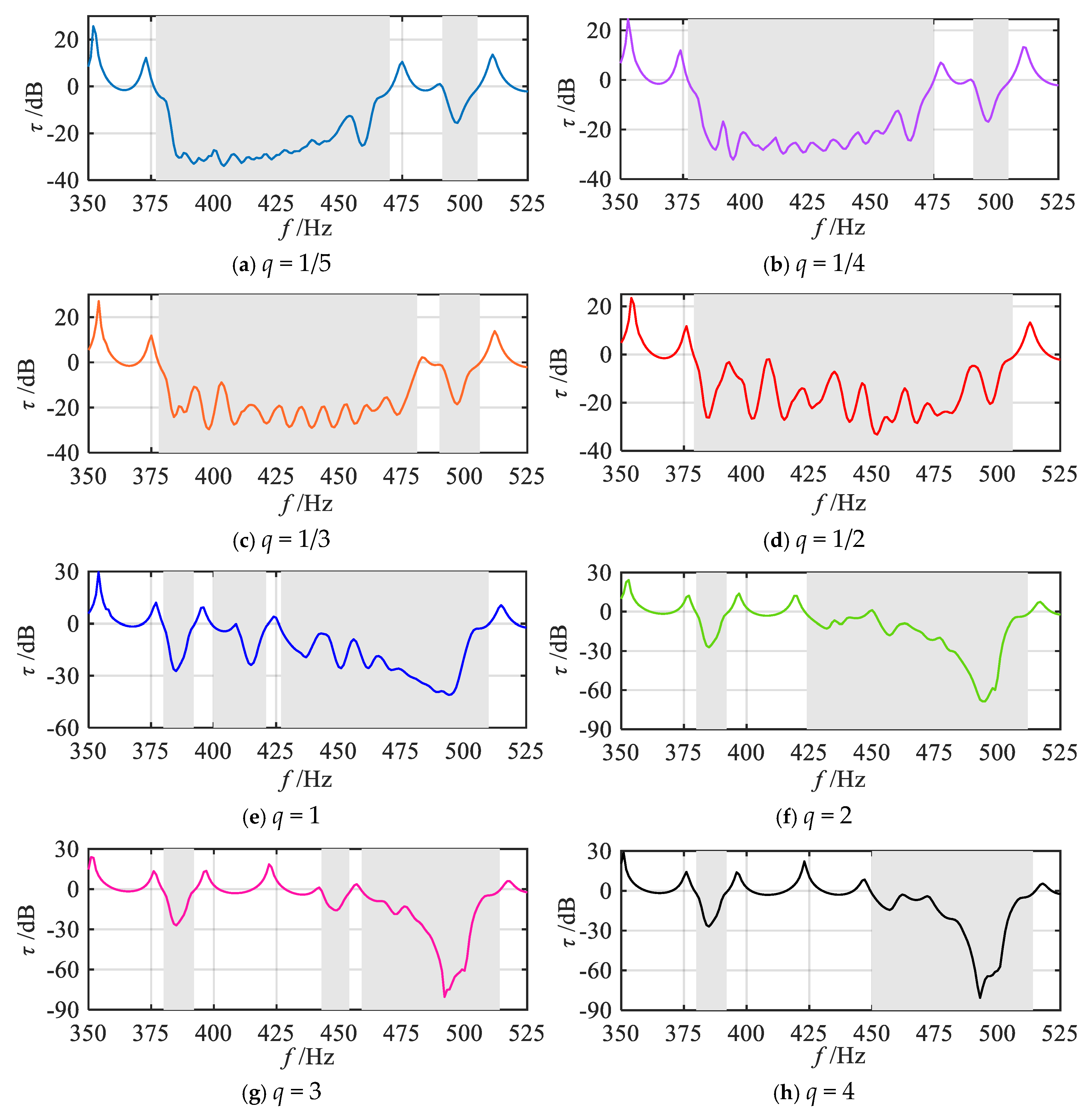
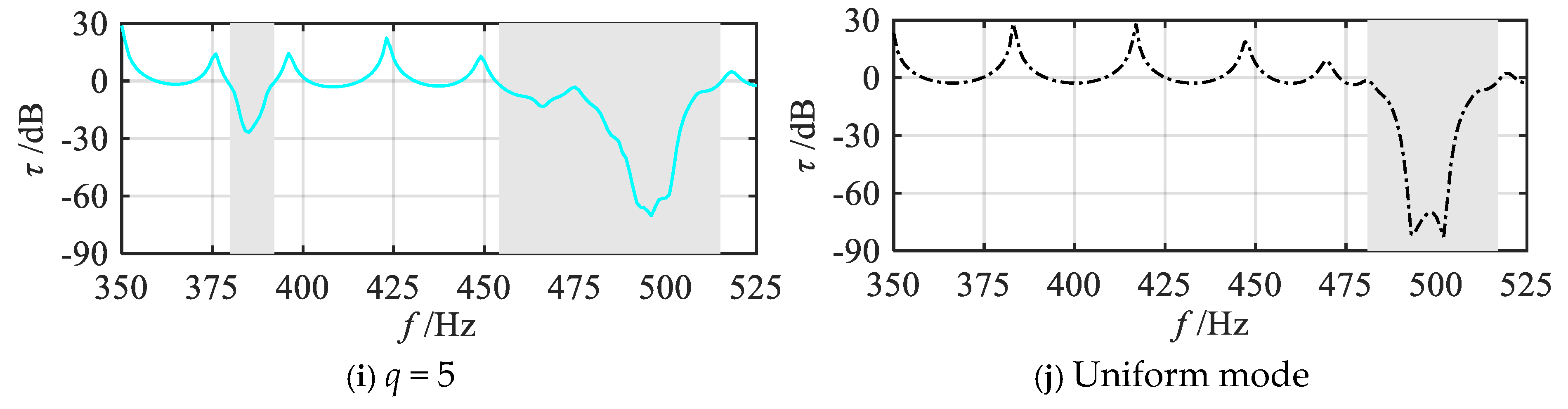
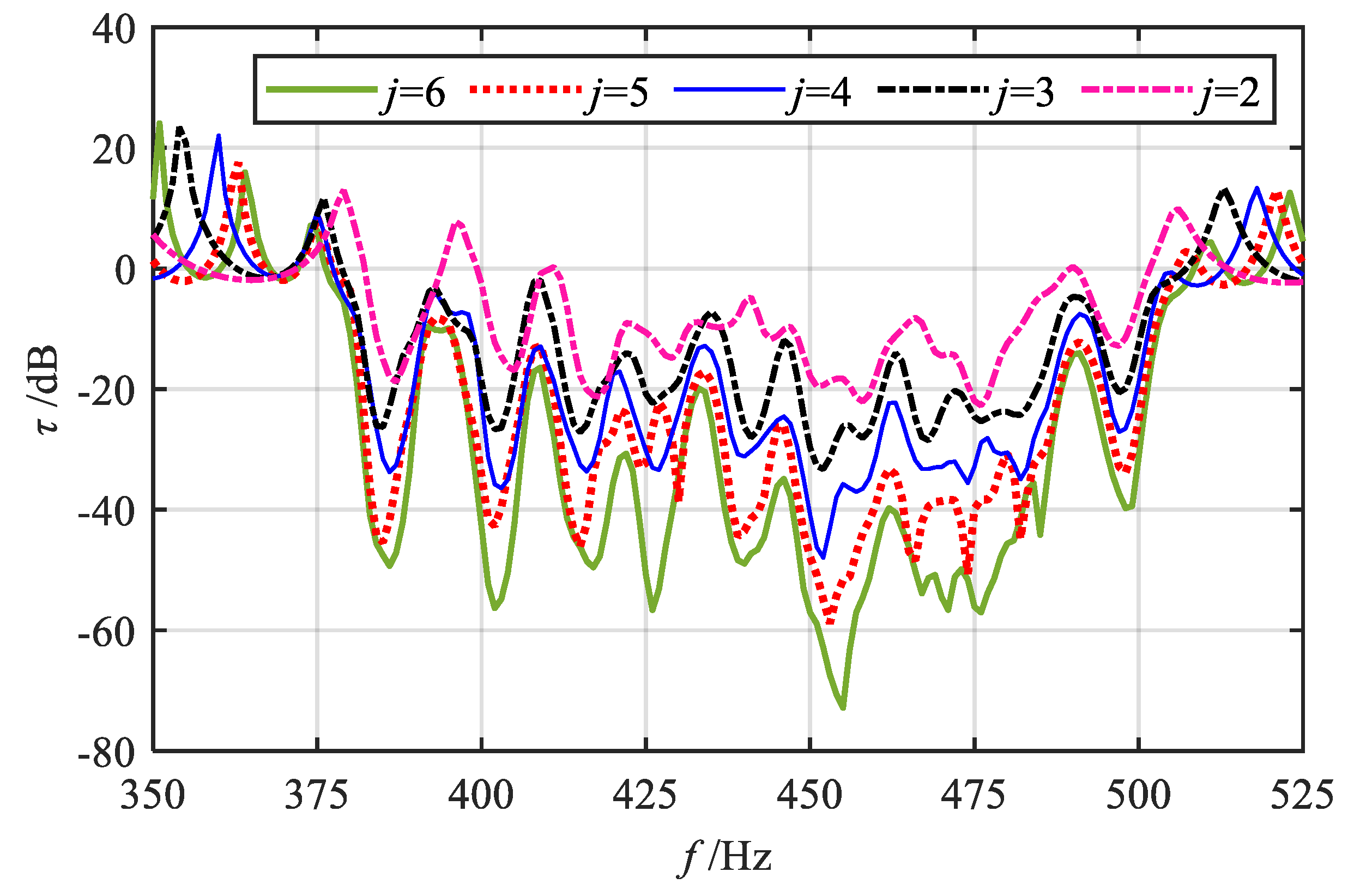
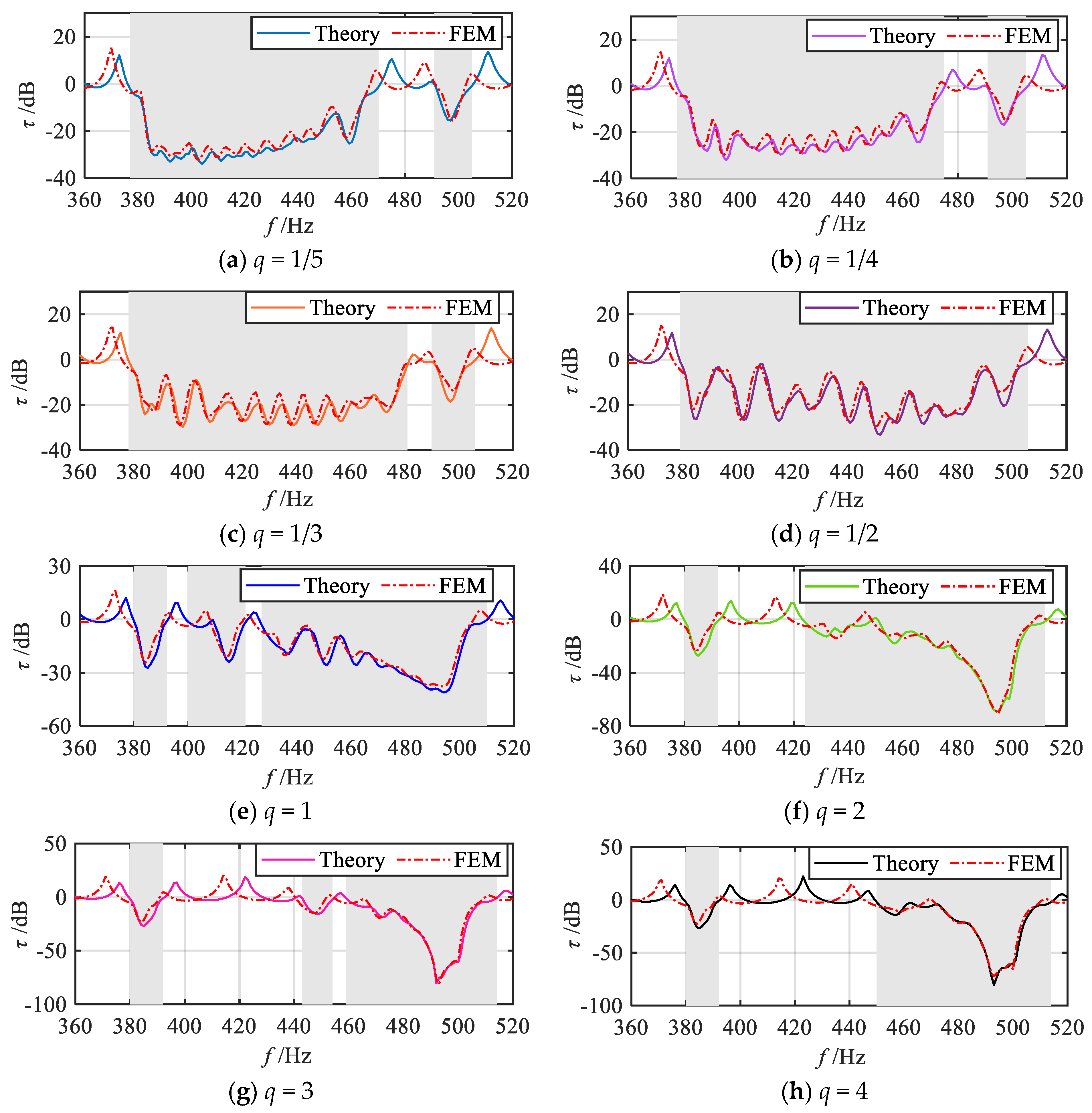
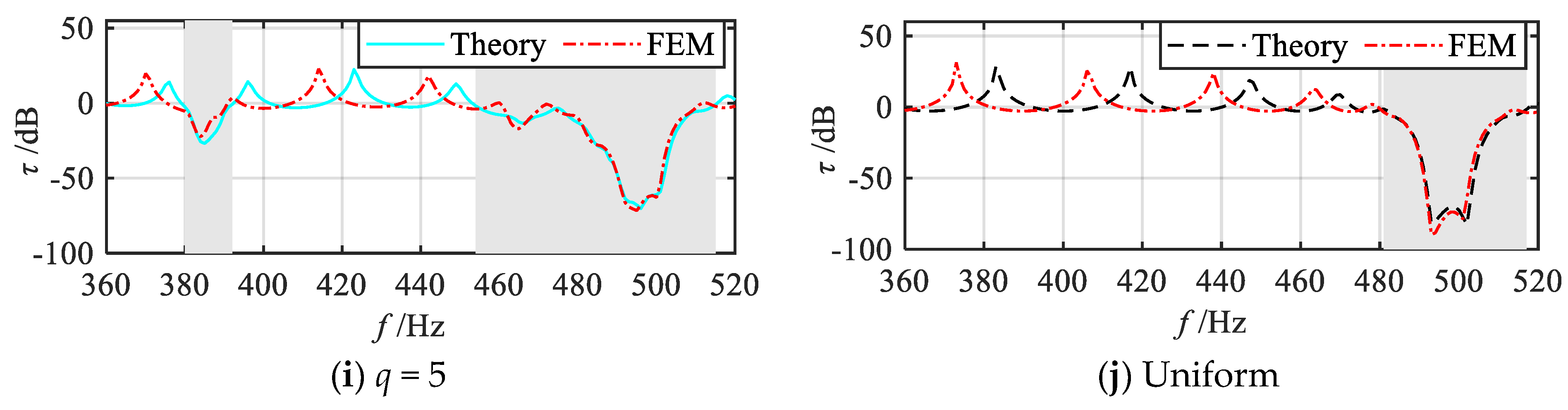
2.3.1. Evaluation Criteria and Vibration Reduction Properties of Various Gradient Modes
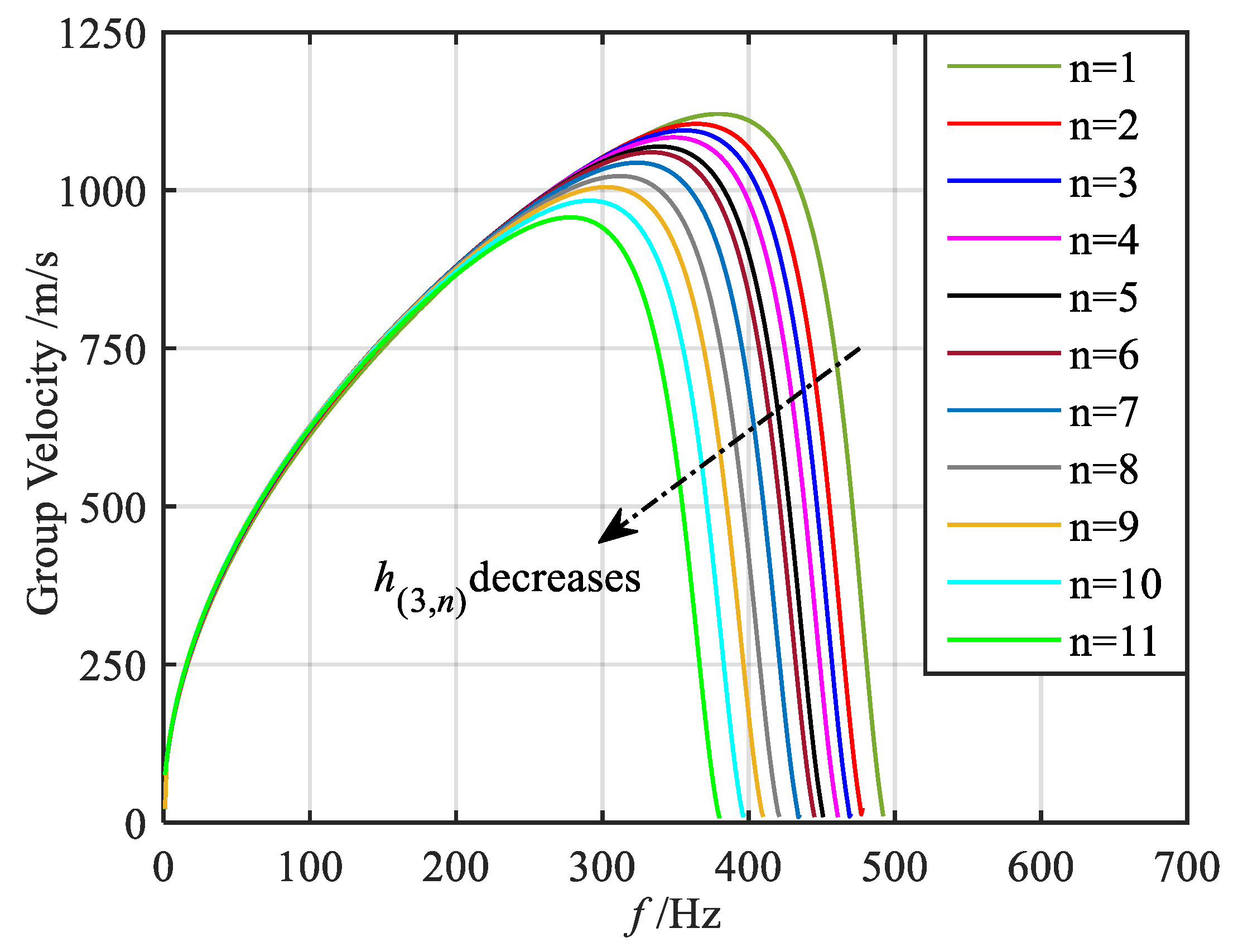
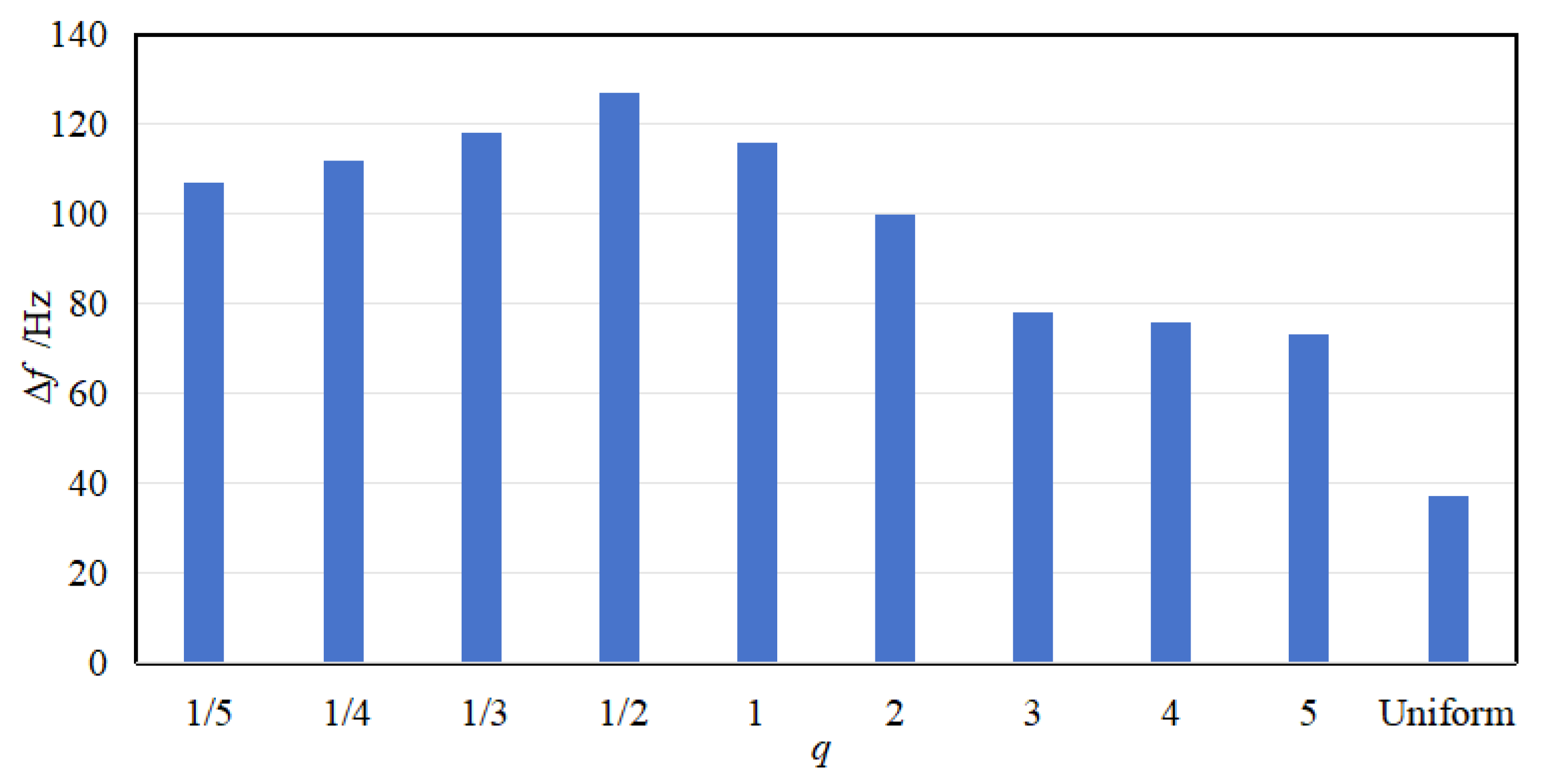
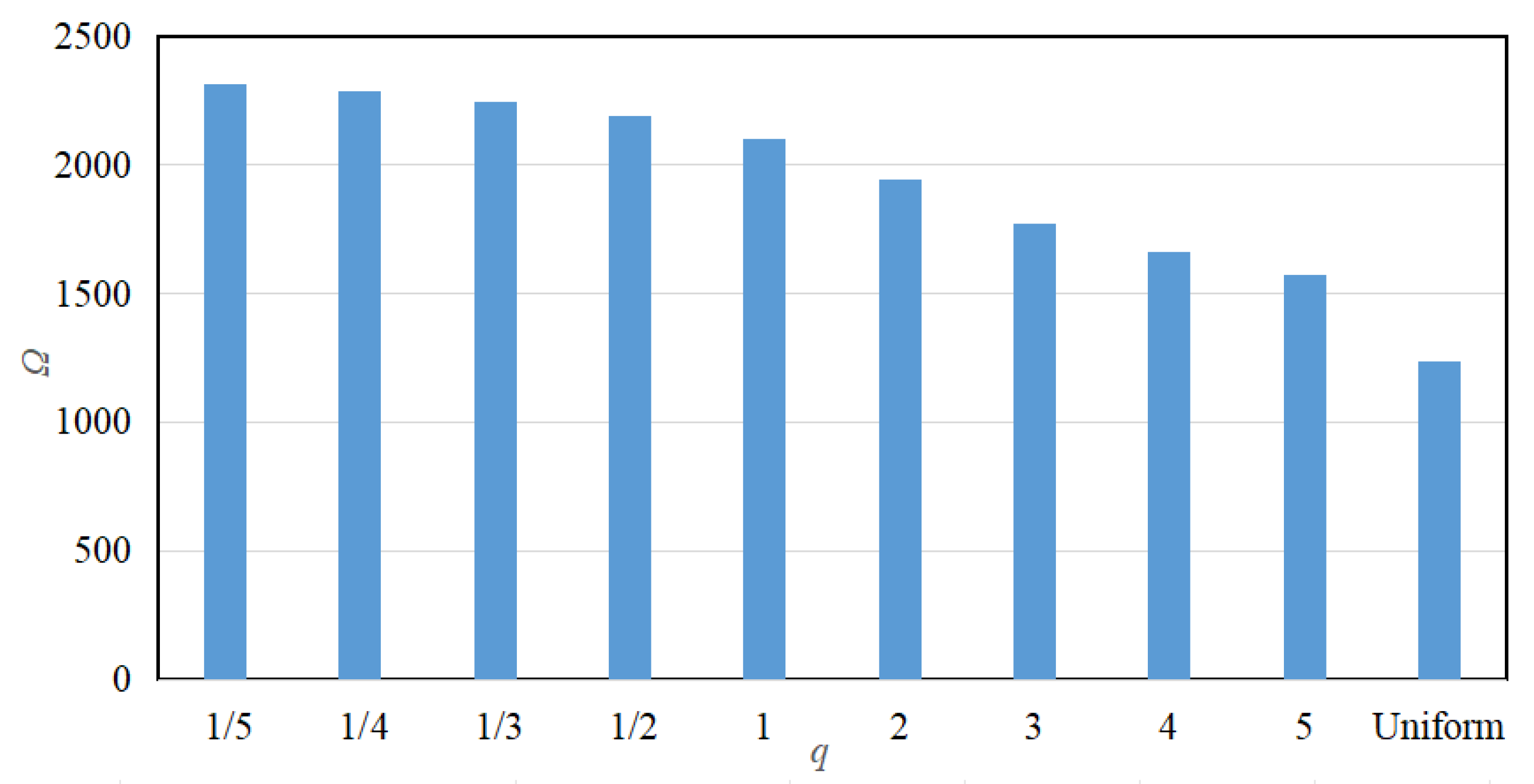
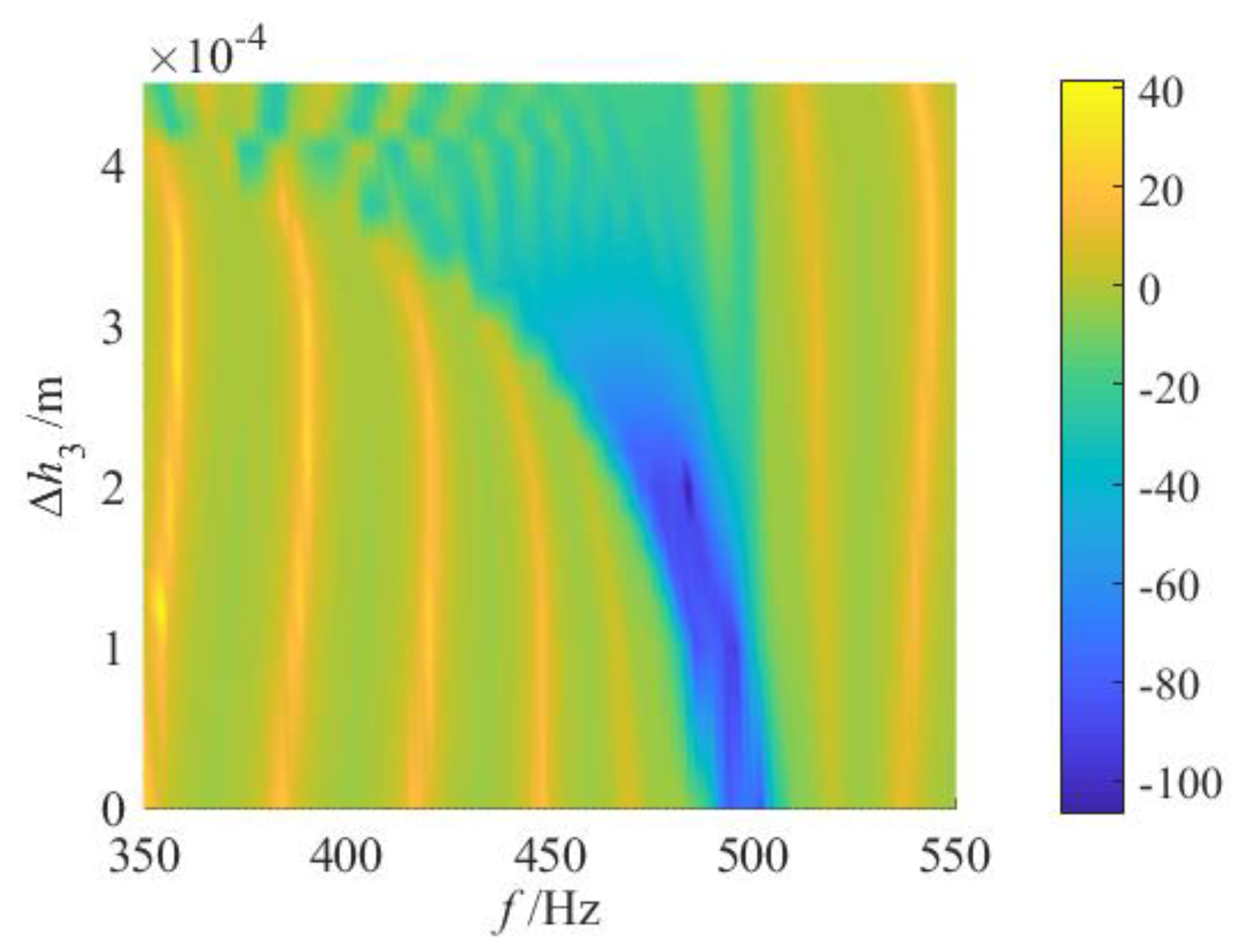
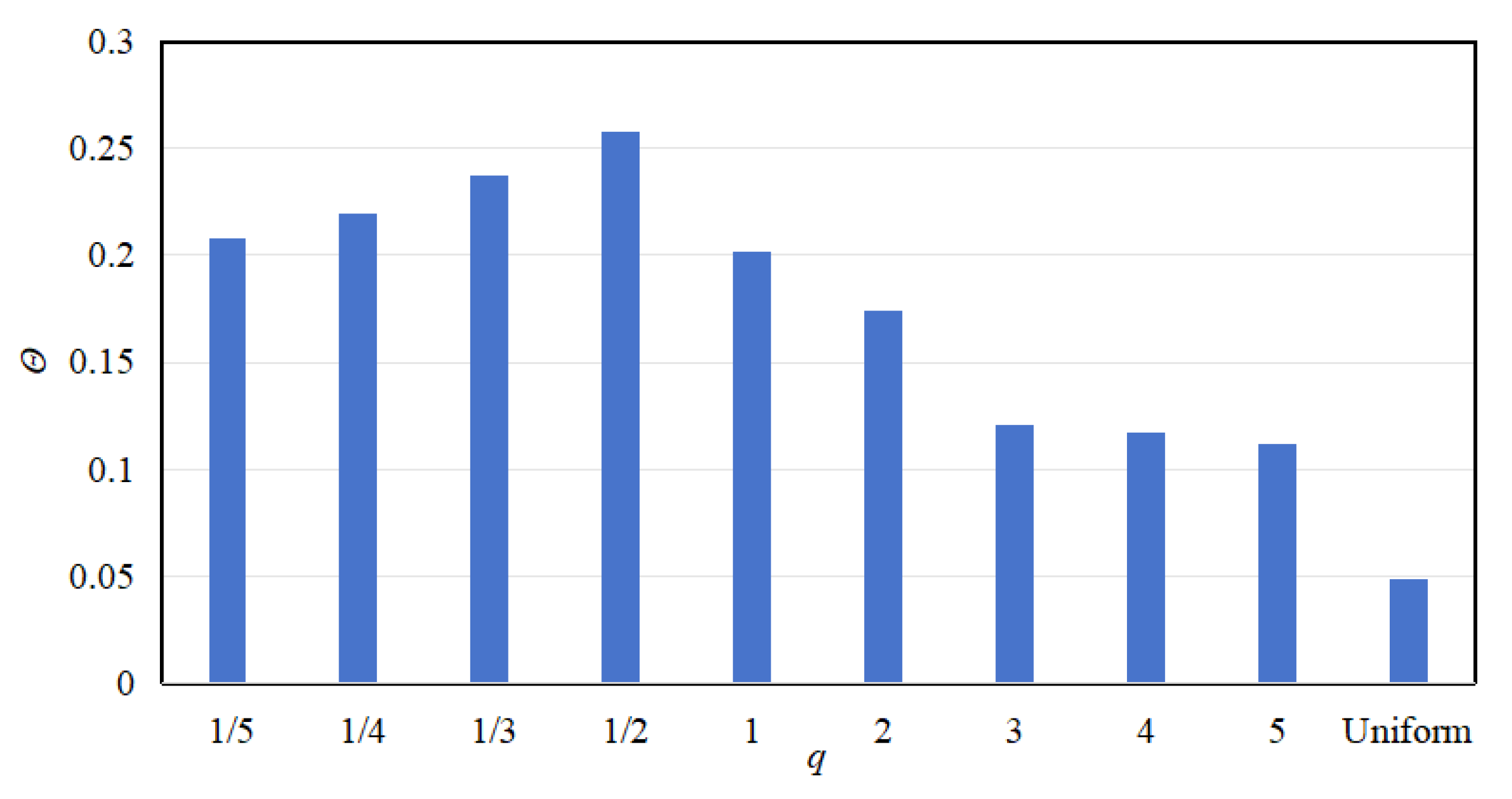
2.3.2. Effects of the Grading Parameters on Vibration Reduction
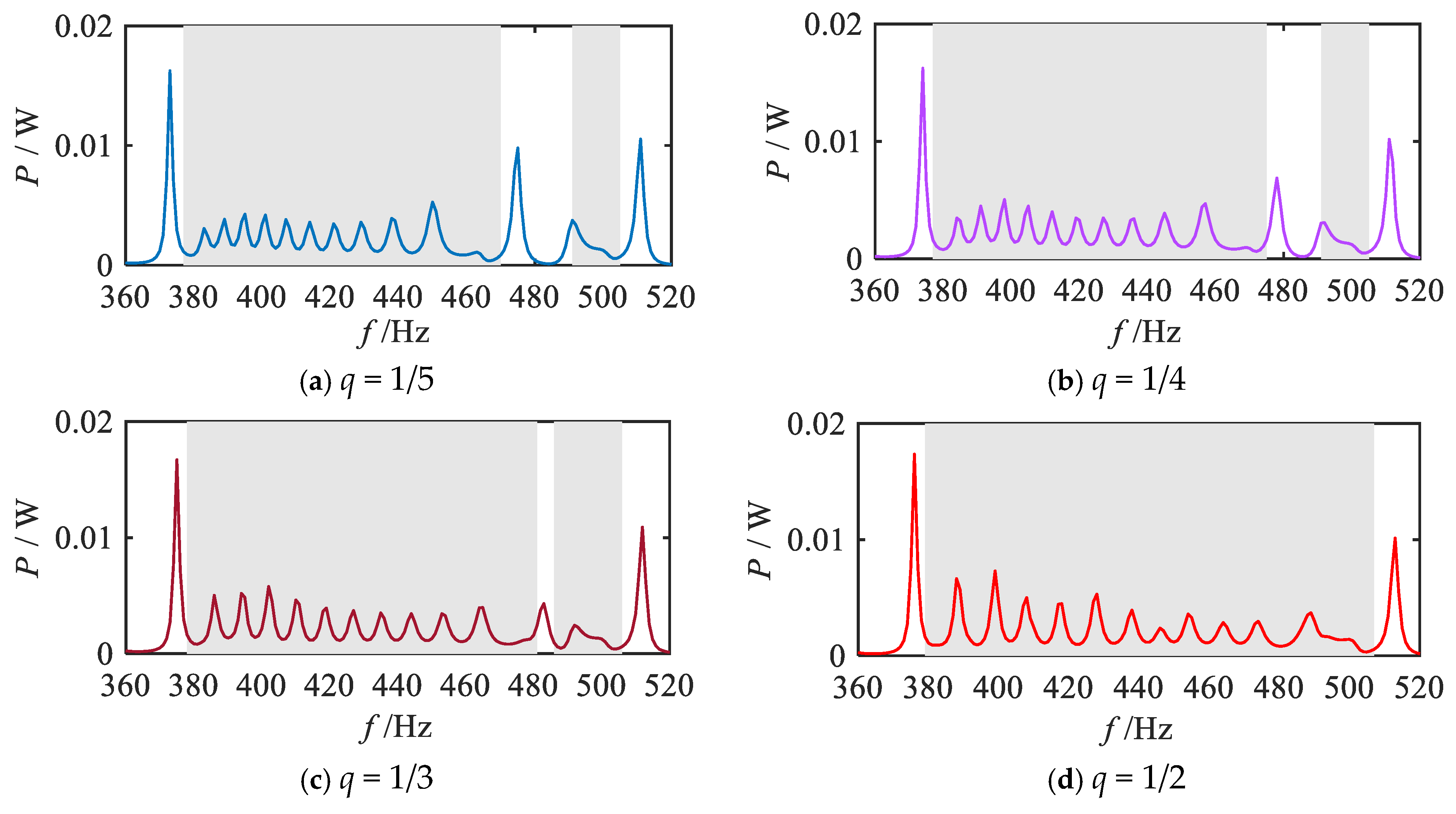
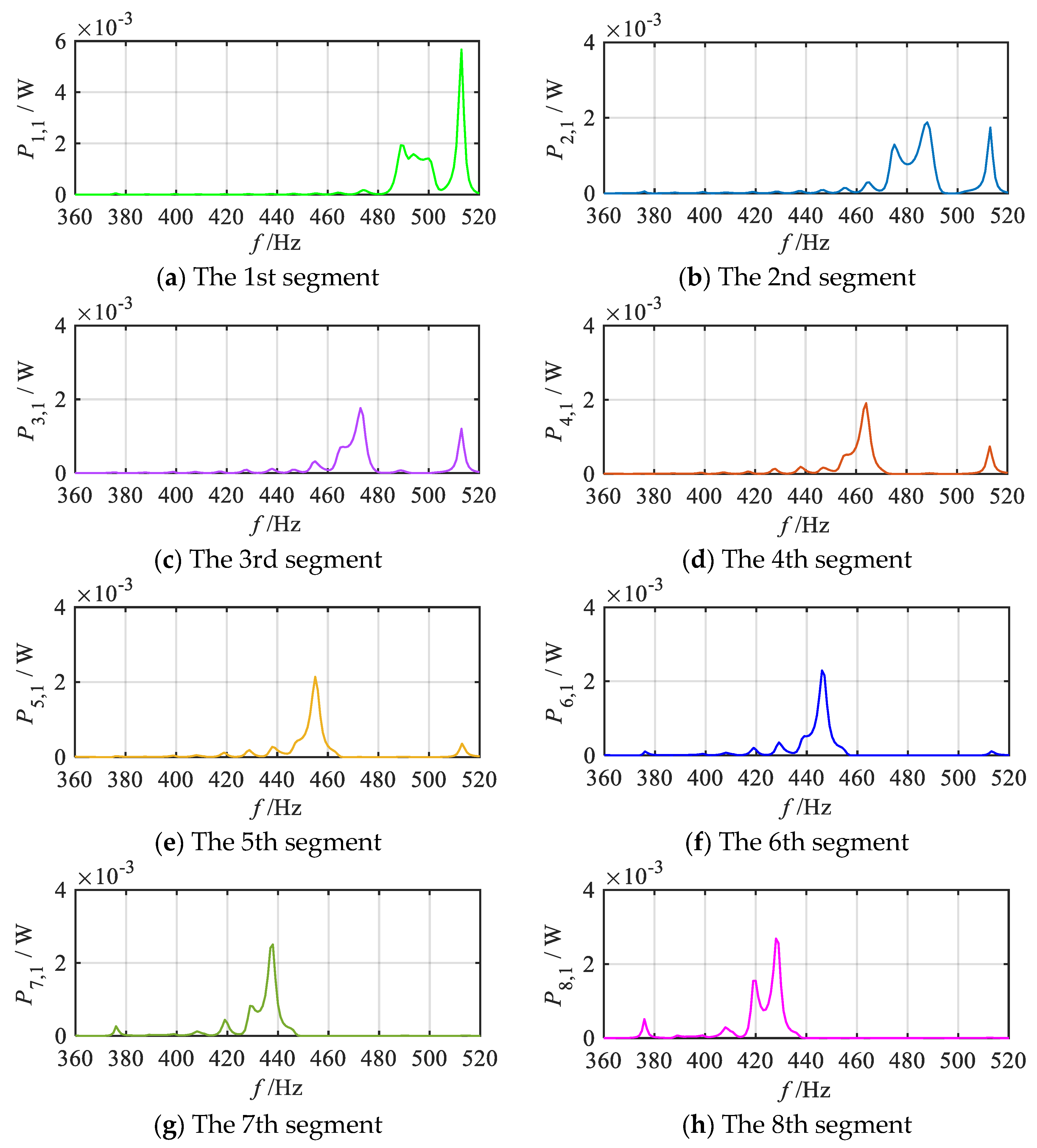
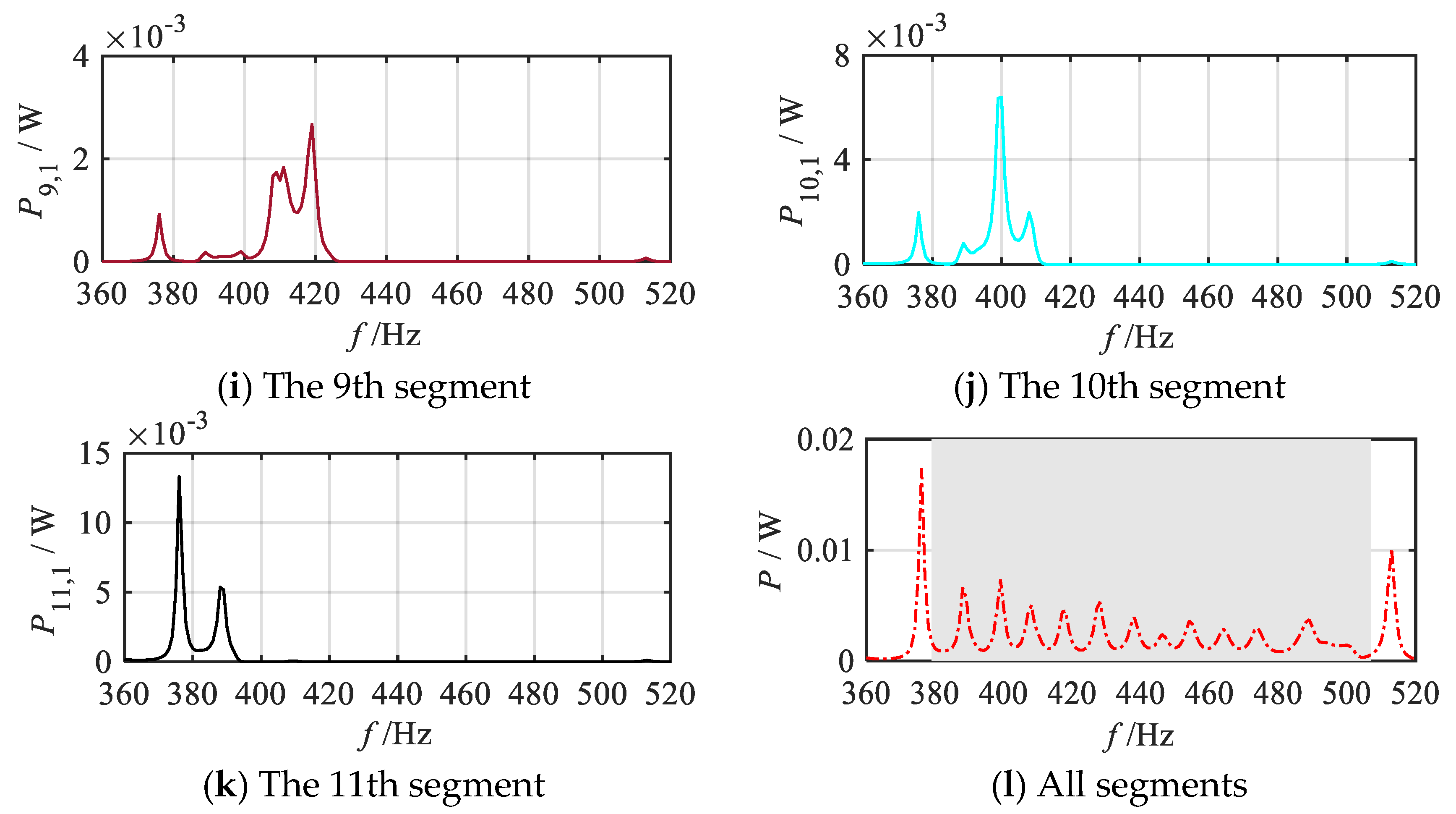
2.4. Energy Harvesting Performance Analysis
3. Finite Element Method
4. Conclusions
- (1)
- In the gradient mode metamaterial beam, the propagation of the bending waves leads to spatial frequency division and enhanced wavefield energy, enabling each segment to efficiently capture bending wave energy at its corresponding resonant frequency, thereby significantly improving energy conversion efficiency.
- (2)
- Compared with the uniform mode metamaterial beam, the dual-functional properties bandwidth of the gradient mode metamaterial beam is significantly improved with the same electrical parameters, and the drawback of the existing graded method, which needs to use a large inductance element to realize the low frequency, is also avoided. The gradient mode and the variation range of graded thickness have a significant effect on the dual-functional performance, and optimal performance can be achieved by appropriately selecting these parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, Y.B.; Popa, B.I.; Zigoneanu, L.; Cummer, S.A. Measurement of a broadband negative index with space-coiling acoustic metamaterials. Phys. Rev. Lett. 2013, 110, 175501. [Google Scholar] [CrossRef]
- Chen, H.J.; Zhai, S.L.; Ding, C.L.; Luo, C.R.; Zhao, X.P. Acoustic metamaterial with negative mass density in water. J. Appl. Phys. 2015, 118, 094901. [Google Scholar] [CrossRef]
- Liu, Y.H.; Yang, J.; Yi, X.S.; Guo, W.J.; Feng, Q.S.; Chronopoulos, D. Enhanced vibration suppression using diatomic acoustic metamaterial with negative stiffness mechanism. Eng. Struct. 2022, 271, 114939. [Google Scholar] [CrossRef]
- Thorp, O.; Ruzzene, M.; Baz, A. Attenuation and localization of wave propagation in rods with periodic shunted piezoelectric patches. Smart Mater. Struct. 2001, 10, 979–989. [Google Scholar] [CrossRef]
- Ren, H.; Zhao, D.; Dong, L.; Liu, S.G.; Yang, J.S.; Zhao, T.Y.; Fan, Y.L. Deep learning accelerates reverse design of magnetorheological elastomer. Compos. Sci. Technol. 2025, 265, 111148. [Google Scholar] [CrossRef]
- Kim, H.G.; Jeon, O.; Wang, S. A numerical and experimental study on an interconnected metamaterial for flexural vibration control based on modal strain energy. Appl. Sci. 2021, 11, 4530. [Google Scholar] [CrossRef]
- Muhammad, S.; Wang, S.; Li, F.M.; Zhang, C.Z. Bandgap enhancement of periodic nonuniform metamaterial beams with inertial amplification mechanisms. J. Vib. Control 2020, 26, 1309–1318. [Google Scholar] [CrossRef]
- Bae, M.H.; Choi, W.; Ha, J.M.; Seung, H.M. Development of L-shaped ultrasonic waveguide using elastic metamaterial. J. Korean Soc. Nondestruct. Test. 2022, 42, 284–292. [Google Scholar] [CrossRef]
- Casadei, F.; Delpero, T.; Bergamini, A.; Ermanni, P.; Ruzzene, M. Piezoelectric resonator arrays for tunable acoustic waveguides and metamaterials. J. Appl. Phys. 2012, 112, 064902. [Google Scholar] [CrossRef]
- Zareei, A.; Darabi, A.; Leamy, M.J.; Alam, M.R. Continuous profile flexural GRIN lens: Focusing and harvesting flexural waves. Appl. Phys. Lett. 2018, 112, 023901. [Google Scholar] [CrossRef]
- Tol, S.; Degertekin, F.L.; Erturk, A. Gradient-index phononic crystal lens-based enhancement of elastic wave energy harvesting. Appl. Phys. Lett. 2016, 109, 063902. [Google Scholar] [CrossRef]
- Hu, G.B.; Tang, L.H.; Liang, J.R.; Lan, C.B.; Das, R. Acoustic-elastic metamaterials and phononic crystals for energy harvesting: A review. Smart Mater. Struct. 2021, 30, 085025. [Google Scholar] [CrossRef]
- Mir, F.; Mandal, D.; Banerjee, S. Metamaterials for acoustic noise filtering and energy harvesting. Sensors 2023, 23, 4227. [Google Scholar] [CrossRef]
- Gonella, S.; To, A.C.; Liu, W.K. Interplay between phononic bandgaps and piezoelectric microstructures for energy harvesting. J. Mech. Phys. Solids 2009, 57, 621–633. [Google Scholar] [CrossRef]
- Hu, G.B.; Tang, L.H.; Banerjee, A.; Das, R. Metastructure with piezoelectric element for simultaneous vibration suppression and energy harvesting. J. Vib. Acoust. 2017, 139, 011012. [Google Scholar] [CrossRef]
- Chen, J.S.; Su, W.J.; Cheng, Y.; Li, W.C.; Lin, C.Y. A metamaterial structure capable of wave attenuation and concurrent energy harvesting. J. Intell. Mater. Syst. Struct. 2019, 30, 2973–2981. [Google Scholar] [CrossRef]
- Li, Y.; Baker, E.; Reissman, T.; Sun, C.; Liu, W.K. Design of mechanical metamaterials for simultaneous vibration isolation and energy harvesting. Appl. Phys. Lett. 2017, 111, 251903. [Google Scholar] [CrossRef]
- Anigbogu, W.; Bardaweel, H. A metamaterial-inspired structure for simultaneous vibration attenuation and energy harvesting. Shock Vib. 2020, 2020, 4063025. [Google Scholar] [CrossRef]
- Hu, G.B.; Tang, L.H.; Das, R. Internally coupled metamaterial beam for simultaneous vibration suppression and low frequency energy harvesting. J. Appl. Phys. 2018, 123, 055107. [Google Scholar] [CrossRef]
- Khattak, M.M.; Sugino, C.; Erturk, A. Concurrent vibration attenuation and low-power electricity generation in a locally resonant metastructure. J. Intell. Mater. Syst. Struct. 2022, 33, 1990–1999. [Google Scholar] [CrossRef]
- Zhao, B.; Thomsen, H.R.; De Ponti, J.M.; Riva, E.; Van Damme, B.; Bergamini, A.; Chatzi, E.; Colombi, A. A graded metamaterial for broadband and high-capability piezoelectric energy harvesting. Energy Convers. Manag. 2022, 269, 116056. [Google Scholar] [CrossRef]
- Schimidt, C.S.; De Sousa, V.C.; De Marqui, C. Piezoelectric energy harvesting in graded elastic metastructures using continuous and segmented electrodes. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 329. [Google Scholar] [CrossRef]
- Zhang, L.W.; Bai, Z.H.; Chen, Y.F. Multi-objective design and optimization of stretching-dominated plate-based mechanical metamaterials for simultaneous vibration insulation and energy absorption. Mech. Adv. Mater. Struct. 2024, 31, 2759–2771. [Google Scholar] [CrossRef]
- Hyun, J.; Jung, J.; Park, J.; Choi, W.; Kim, M. Simultaneous low-frequency vibration isolation and energy harvesting via attachable metamaterials. Nano Converg. 2024, 11, 38. [Google Scholar] [CrossRef]
- Cao, D.X.; Guo, X.Y.; Hu, W.H. A novel low-frequency broadband piezoelectric energy harvester combined with a negative stiffness vibration isolator. J. Intell. Mater. Syst. Struct. 2019, 30, 1105–1114. [Google Scholar] [CrossRef]
- Zhang, Y.W.; Su, C.; Ni, Z.Y.; Zang, J.; Chen, L.Q. A multifunctional lattice sandwich structure with energy harvesting and nonlinear vibration control. Compos. Struct. 2019, 221, 110875. [Google Scholar] [CrossRef]
- Bukhari, M.; Barry, O. Simultaneous energy harvesting and vibration control in a nonlinear metastructure: A spectro-spatial analysis. J. Sound Vib. 2020, 473, 115215. [Google Scholar] [CrossRef]
- Lu, Z.Q.; Zhao, L.; Ding, H.; Chen, L.Q. A dual-functional metamaterial for integrated vibration isolation and energy harvesting. J. Sound Vib. 2021, 509, 116251. [Google Scholar] [CrossRef]
- Chaurha, A.; Malaji, P.V.; Mukhopadhyay, T. Dual functionality of vibration attenuation and energy harvesting: Effect of gradation on non-linear multi-resonator metastructures. Eur. Phys. J. Spec. Top. 2022, 231, 1403–1413. [Google Scholar] [CrossRef]
- Xu, C.; Chen, S.; Wang, C.H.; Yang, Y.W.; Zhao, L.Y. Amplitude-robust metastructure with combined bistable and monostable mechanisms for simultaneously enhanced vibration suppression and energy harvesting. Appl. Phys. Lett. 2023, 122, 151701. [Google Scholar] [CrossRef]
- Zhao, L.; Lu, Z.Q.; Ding, H.; Chen, L.Q. A viscoelastic metamaterial beam for integrated vibration isolation and energy harvesting. Appl. Math. Mech. 2024, 45, 1243–1260. [Google Scholar] [CrossRef]
- Banerjee, P.; Balaji, P.S.; Murugan, S. A dual-function compliant metastructure based on quasi-zero-stiffness for combined vibration isolation and vibration energy harvesting. Int. J. Dyn. Control 2025, 13, 135. [Google Scholar] [CrossRef]
- Thorp, O.; Ruzzene, M.; Baz, A. Attenuation of wave propagation in fluid-loaded shells with periodic shunted piezoelectric rings. Smart Mater. Struct. 2005, 14, 594–604. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M.; Cunefare, K. Vibration and wave propagation control of plates with periodic arrays of shunted piezoelectric patches. J. Intell. Mater. Syst. Struct. 2009, 20, 979–990. [Google Scholar] [CrossRef]
- Casadei, F.; Ruzzene, M.; Dozio, L.; Cunefare, K.A. Broadband vibration control through periodic arrays of resonant shunts: Experimental investigation on plates. Smart Mater. Struct. 2010, 19, 015002. [Google Scholar] [CrossRef]
- Chen, S.B.; Wen, J.H.; Wang, G.; Yu, D.L.; Wen, X.S. Improved modeling of rods with periodic arrays of shunted piezoelectric patches. J. Intell. Mater. Syst. Struct. 2012, 23, 1613–1621. [Google Scholar] [CrossRef]
- Sugino, C.; Ruzzene, M.; Erturk, A. An analytical framework for locally resonant piezoelectric metamaterial plates. Int. J. Solids Struct. 2020, 182, 281–294. [Google Scholar] [CrossRef]
- Junyi, L.; Balint, D.S. Optimal shunt parameters for maximising wave attenuation with periodic piezoelectric patches. J. Intell. Mater. Syst. Struct. 2017, 28, 108–123. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, J.H.; Xiao, Y.; Wang, G.; Wen, X.S. Sound transmission loss of metamaterial thin plates with periodic subwavelength arrays of shunted piezoelectric patches. J. Sound Vib. 2015, 343, 104–120. [Google Scholar] [CrossRef]
- Sugino, C.; Ruzzene, M.; Erturk, A. Merging mechanical and electromechanical bandgaps in locally resonant metamaterials and metastructures. J. Mech. Phys. Solids 2018, 116, 323–333. [Google Scholar] [CrossRef]
- Li, X.P.; Chen, Y.Y.; Hu, G.K.; Huang, G.L. A self-adaptive metamaterial beam with digitally controlled resonators for subwavelength broadband flexural wave attenuation. Smart Mater. Struct. 2018, 27, 045015. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Hu, G.K.; Huang, G.L. An adaptive metamaterial beam with hybrid shunting circuits for extremely broadband control of flexural waves. Smart Mater. Struct. 2016, 25, 105036. [Google Scholar] [CrossRef]
- Yi, K.J.; Collet, M. Broadening low-frequency bandgaps in locally resonant piezoelectric metamaterials by negative capacitance. J. Sound Vib. 2021, 493, 115837. [Google Scholar] [CrossRef]
- Sugino, C.; Guillot, V.; Erturk, A. Multifunctional energy harvesting locally resonant metastructures. In Proceedings of the ASME Conference on Smart Materials, Adaptive Structures and Intelligent Systems (SMASIS 2017), Snowbird, UT, USA, 18–20 September 2017; p. V001T07A014. [Google Scholar]
- Sugino, C.; Erturk, A. Analysis of multifunctional piezoelectric metastructures for low-frequency bandgap formation and energy harvesting. J. Phys. D Appl. Phys. 2018, 51, 215103. [Google Scholar] [CrossRef]
- Sugino, C.; Erturk, A. Graded multifunctional piezoelectric metastructures for wideband vibration attenuation and energy harvesting. Smart Mater. Struct. 2021, 30, 015029. [Google Scholar]
- Santini, J.; Sugino, C.; Riva, E.; Erturk, A. Harnessing rainbow trapping via hybrid electromechanical metastructures for enhanced energy harvesting and vibration attenuation. Smart Mater. Struct. 2022, 132, 064903. [Google Scholar] [CrossRef]
- Lin, Z.; Al Ba’ba’a, H.; Tol, S. Piezoelectric metastructures for simultaneous broadband energy harvesting and vibration suppression of traveling waves. Smart Mater. Struct. 2021, 30, 075037. [Google Scholar] [CrossRef]
- Wang, X.G.; Wang, L.; Shu, H.S.; Zhang, L. Research on dual-functional properties of an improved piezoelectric metamaterial beam for simultaneous vibration suppression and energy harvesting. Appl. Phys. A-Mater. Sci. Process. 2022, 128, 906. [Google Scholar] [CrossRef]
- Wang, X.G.; Wang, L.; Shu, H.S. Research on dual-functional properties of an asymmetric piezoelectric metamaterial beam for simultaneous vibration reduction and power generation. J. Vib. Eng. Technol. 2023, 12, 3069–3085. [Google Scholar] [CrossRef]
- Jian, Y.P.; Tang, L.H.; Hu, G.B.; Li, Z.Y.; Aw, K.C. Design of graded piezoelectric metamaterial beam with spatial variation of electrodes. Int. J. Mech. Sci. 2022, 218, 107068. [Google Scholar] [CrossRef]
- Jian, Y.P.; Hu, G.B.; Tang, L.H.; Tang, W.; Abdi, M.; Aw, K.C. Analytical and experimental study of a metamaterial beam with grading piezoelectric transducers for vibration attenuation band widening. Eng. Struct. 2023, 275, 115091. [Google Scholar] [CrossRef]
- Liu, Y.J.; Han, C.Y.; Liu, D.Y. Broadband vibration suppression of graded/disorder piezoelectric metamaterials. Mech. Adv. Mater. Struct. 2023, 30, 710–723. [Google Scholar] [CrossRef]
- Chen, S.B.; Wang, G. Wave propagation in beams with anti-symmetric piezoelectric shunting arrays. Chin. Phys. B 2016, 25, 034301. [Google Scholar] [CrossRef]
- Tsakmakidis, K.L.; Boardman, A.D.; Hess, O. ‘Trapped rainbow’ storage of light in metamaterials. Nature 2007, 450, 397–401. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Huang, Y.; Zhou, W.J.; Yang, Z.B. Metamaterial beam for flexural wave resonance rainbow trapping and piezoelectric energy harvesting. J. Appl. Phys. 2021, 129, 064505. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.B.; Zhang, H.; Bi, X.Y.; Hu, N.; Zhang, C.Z. Rainbow zigzag metamaterial beams as broadband vibration isolators for beam-like structures. J. Sound Vib. 2022, 530, 116945. [Google Scholar] [CrossRef]
- De Ponti, J.M.; Colombi, A.; Ardito, R.; Braghin, F.; Corigliano, A.; Craster, R.V. Graded elastic metasurface for enhanced energy harvesting. Int. J. Mech. Sci. 2020, 22, 013013. [Google Scholar] [CrossRef]




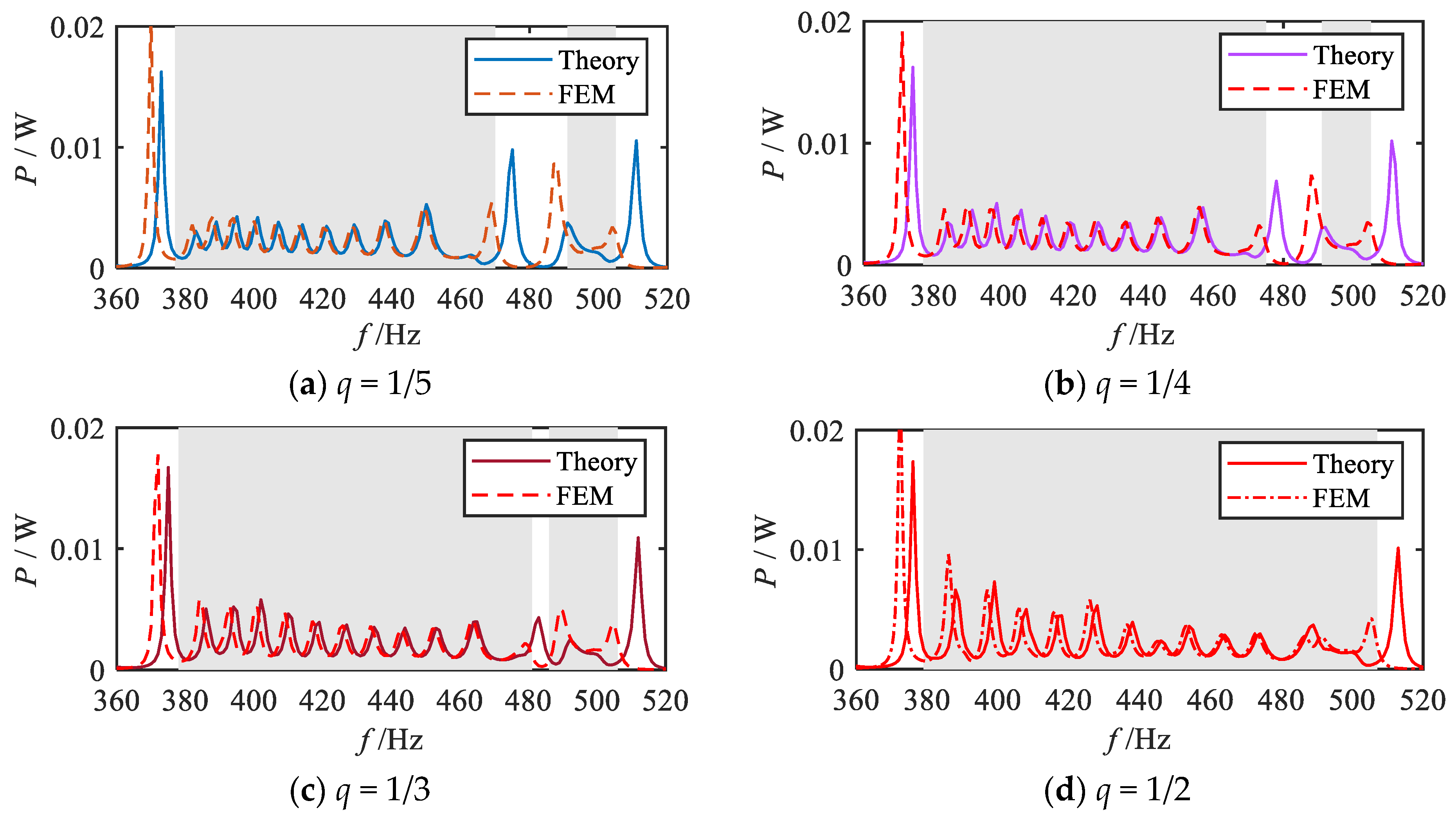
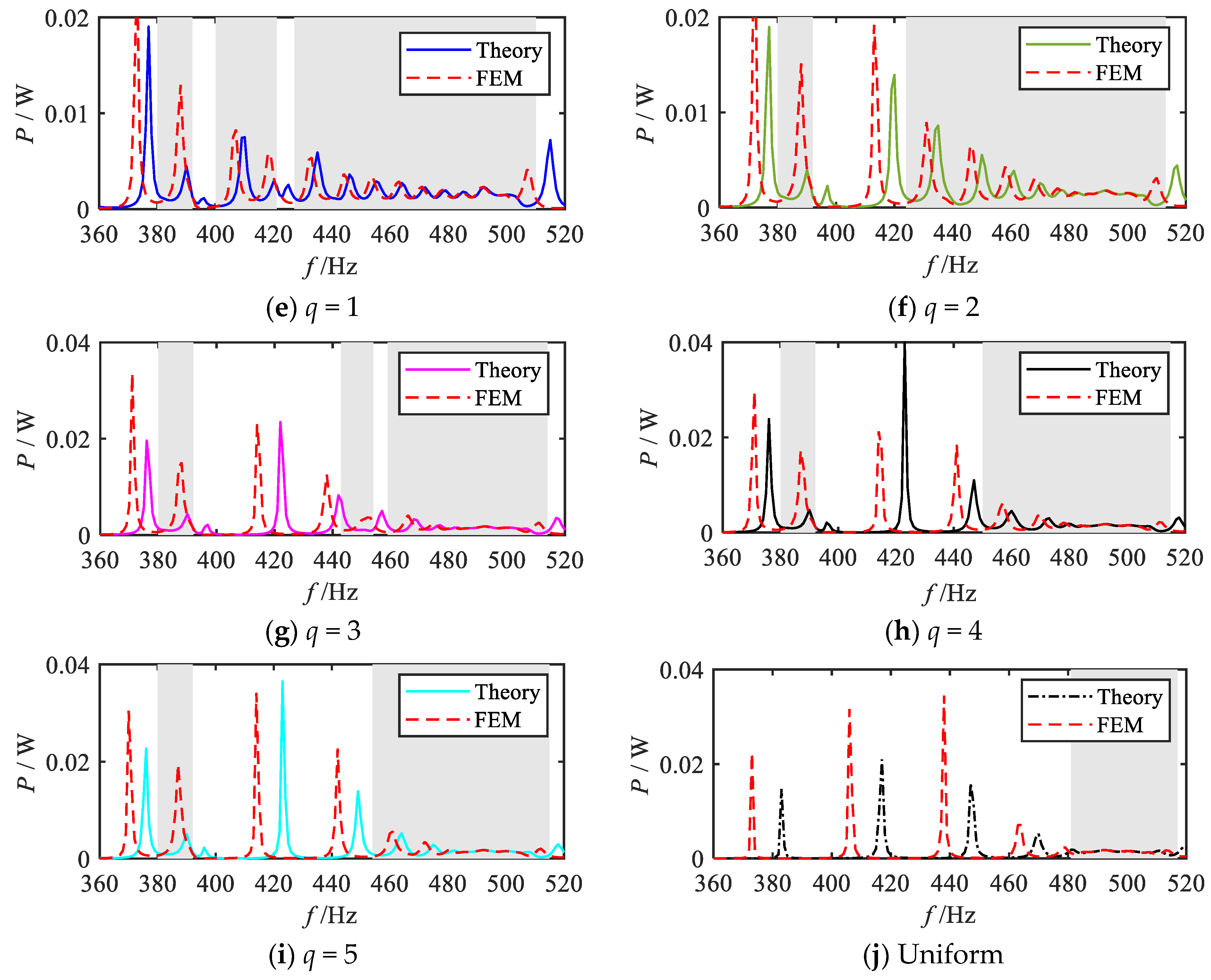

| Items | Parameters | Values | Units |
|---|---|---|---|
| PMMA | 1142 | kg/m3 | |
| E1 | 2.0 | GPa | |
| b | 20 | mm | |
| 5 | mm | ||
| 65 | mm | ||
| 10 | mm | ||
| j | 3 | ||
| S | 11 | ||
| PZT-5H | 7500 | kg/m3 | |
| 1.65 × 10−11 | m3/N | ||
| 3.01 × 10−8 | F/m | ||
| −2.74 × 10−10 | C/m2 | ||
| 45 | mm | ||
| 0.1 | mm | ||
| 0.5 | mm | ||
| 0.4 | mm | ||
| Circuit | L | 0.33 | H |
| R | 100 | kΩ |
| Item | Gradient Mode |
|---|---|
| Spatial dimension | 2D |
| Physical field | Solid Mechanics-Piezoelectric Devices-Circuits |
| Research type | Frequency domain analysis |
| S | 11 |
| j | 3 |
| q | 1/5, 1/4, 1/3, 1/2, 1, 2, 3, 4, 5, uniform |
| Loading method | The acceleration amplitude of the left-hand end face is 10 g |
| Polarization direction | Vertical upward |
| Piezoelectric bimorph connection type | Parallel connection |
| Circuits | L-R parallel connection |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xie, Q.; Wang, L.; Shu, H.; Wang, H. Analysis of the Dual-Functional Broadband Properties of an Asymmetric Piezoelectric Metamaterial Beam for Simultaneous Vibration Reduction and Energy Harvesting. Materials 2025, 18, 5003. https://doi.org/10.3390/ma18215003
Wang X, Xie Q, Wang L, Shu H, Wang H. Analysis of the Dual-Functional Broadband Properties of an Asymmetric Piezoelectric Metamaterial Beam for Simultaneous Vibration Reduction and Energy Harvesting. Materials. 2025; 18(21):5003. https://doi.org/10.3390/ma18215003
Chicago/Turabian StyleWang, Xingguo, Qiuju Xie, Lan Wang, Haisheng Shu, and Hongyan Wang. 2025. "Analysis of the Dual-Functional Broadband Properties of an Asymmetric Piezoelectric Metamaterial Beam for Simultaneous Vibration Reduction and Energy Harvesting" Materials 18, no. 21: 5003. https://doi.org/10.3390/ma18215003
APA StyleWang, X., Xie, Q., Wang, L., Shu, H., & Wang, H. (2025). Analysis of the Dual-Functional Broadband Properties of an Asymmetric Piezoelectric Metamaterial Beam for Simultaneous Vibration Reduction and Energy Harvesting. Materials, 18(21), 5003. https://doi.org/10.3390/ma18215003





