Analysis of Thermally Induced Residual Stress in Resistance Welded PC/CF Composite to Aluminum
Abstract
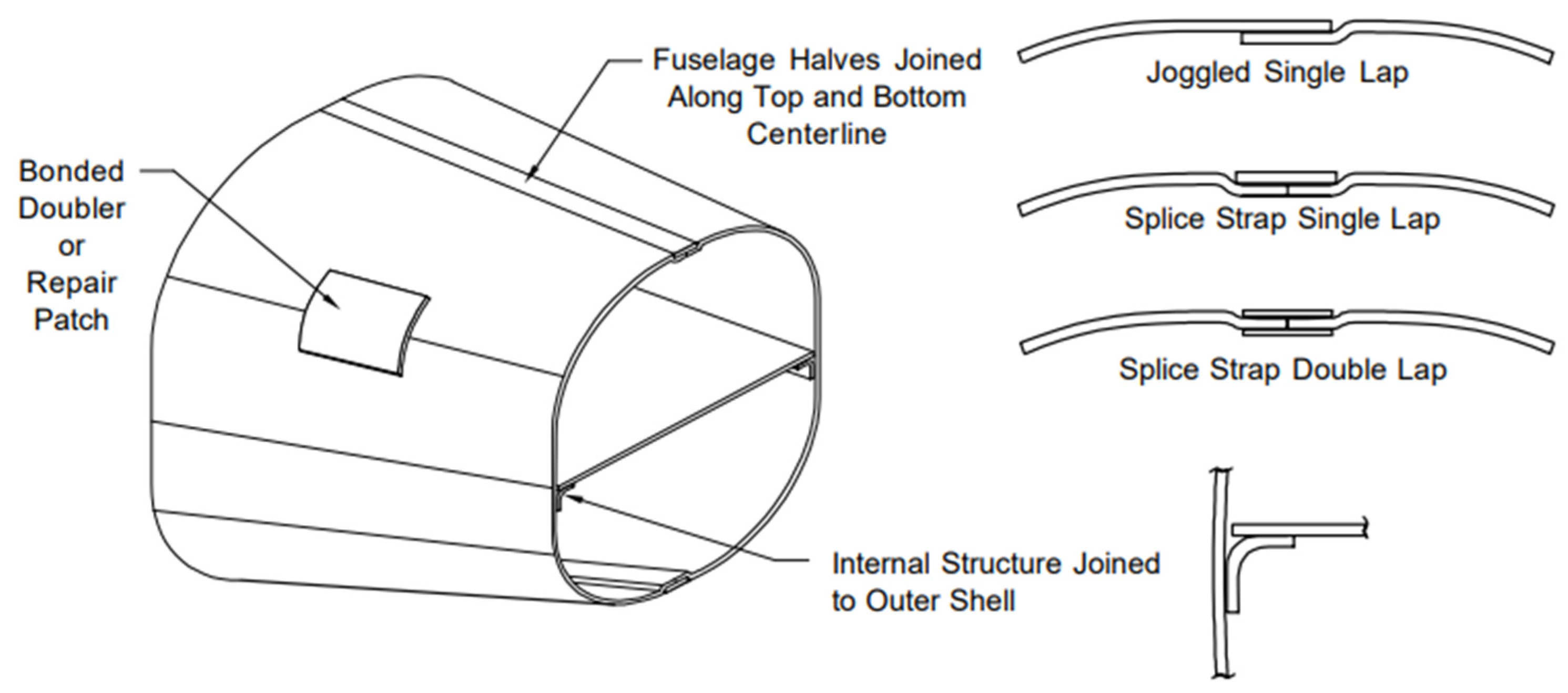
1. Introduction
2. The Experiment
2.1. Materials and Specimens
2.2. Surface Preparation
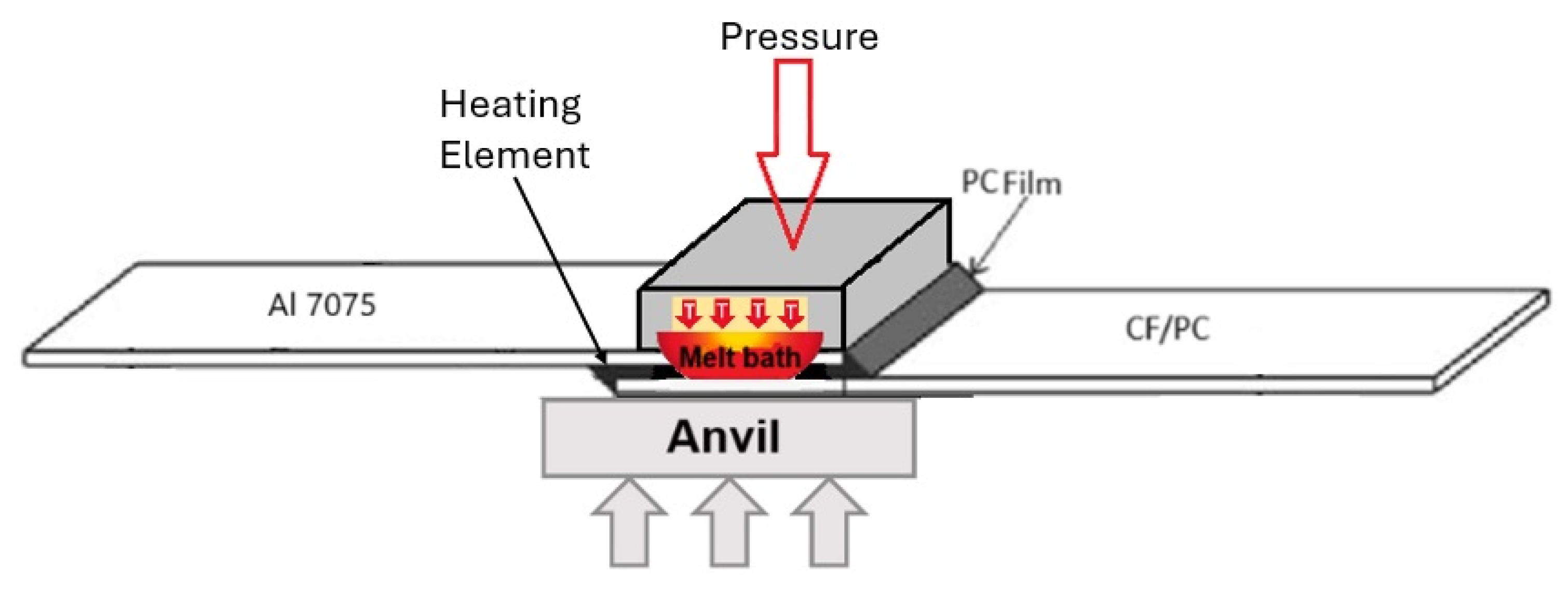
2.3. Resistance Welding Carbon Fibre Reinforced Polycarbonate with Aluminum
2.3.1. Introduction to Resistance Welding of Thermoplastic Composites
- A worktable serving as an anvil where the bonding process is performed.
- Copper electrical connectors to supply power to the welding machine.
- An aluminum clamp, onto which the press applies force.
- A steel mesh to ensure uniform heating.
- Glass fabric coated with polyimide film, serving as an insulator.

- Surface Preparation: Aluminum requires proper preparation to ensure good adhesion with molten polycarbonate. This includes mechanical grinding and cleaning of the surface to remove oxides and contaminants [7].
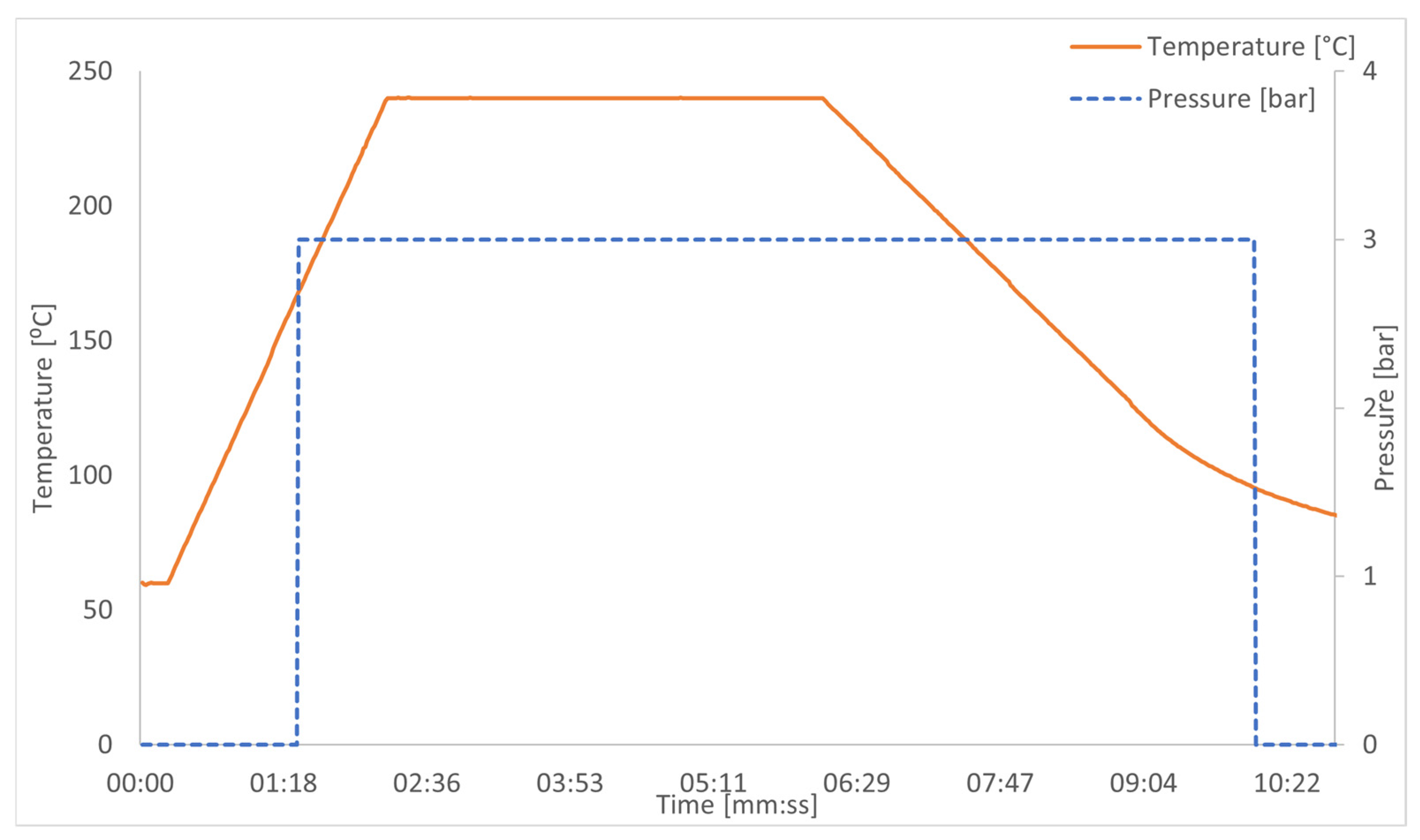
- Setting Welding Parameters: For PC-aluminum joints, it is recommended to set the temperature in the range of 220–260 °C. Exceeding this temperature may lead to polycarbonate degradation, reducing joint strength. Optimal heating time is usually 120–200 s, depending on material thickness and applied pressure, which should be approximately 0.2–0.5 MPa (Figure 6) [7].
- Welding: During heating, electric current flows through the resistive heating element, quickly heating the surfaces of polycarbonate and aluminum. The high temperature causes the polycarbonate to melt, bonding with the aluminum surface and forming a durable connection [7].
2.3.2. The Welding Process
- Welding Temperature: 220–260 °C
- Heating Time: 120–200 s
- Pressure: 0.2–0.5 MPa

2.3.3. Welded Parts
3. Nondestructive Testing Using Thermography
3.1. Thermography Testing Using the C-CheckIR
3.1.1. The Description of the Equipment
3.1.2. Testing Procedure
3.2. Sample Preparation
3.3. Results
4. Analytical Considerations of the Residual Stress in a Joint
4.1. Normal Stress
4.2. Results and Conclusions
5. Numerical Model

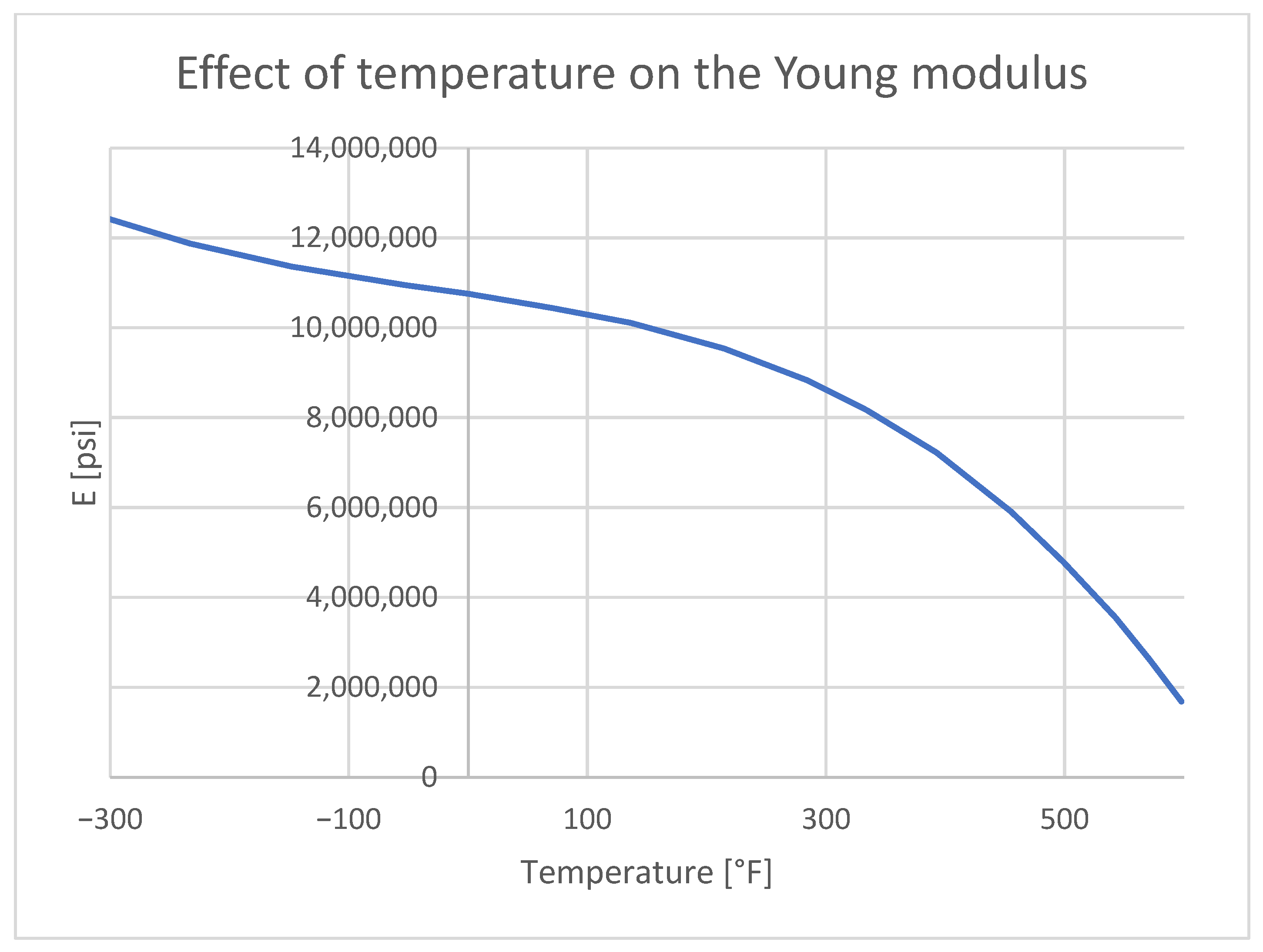
5.1. Thermal Distribution
5.2. Deformation
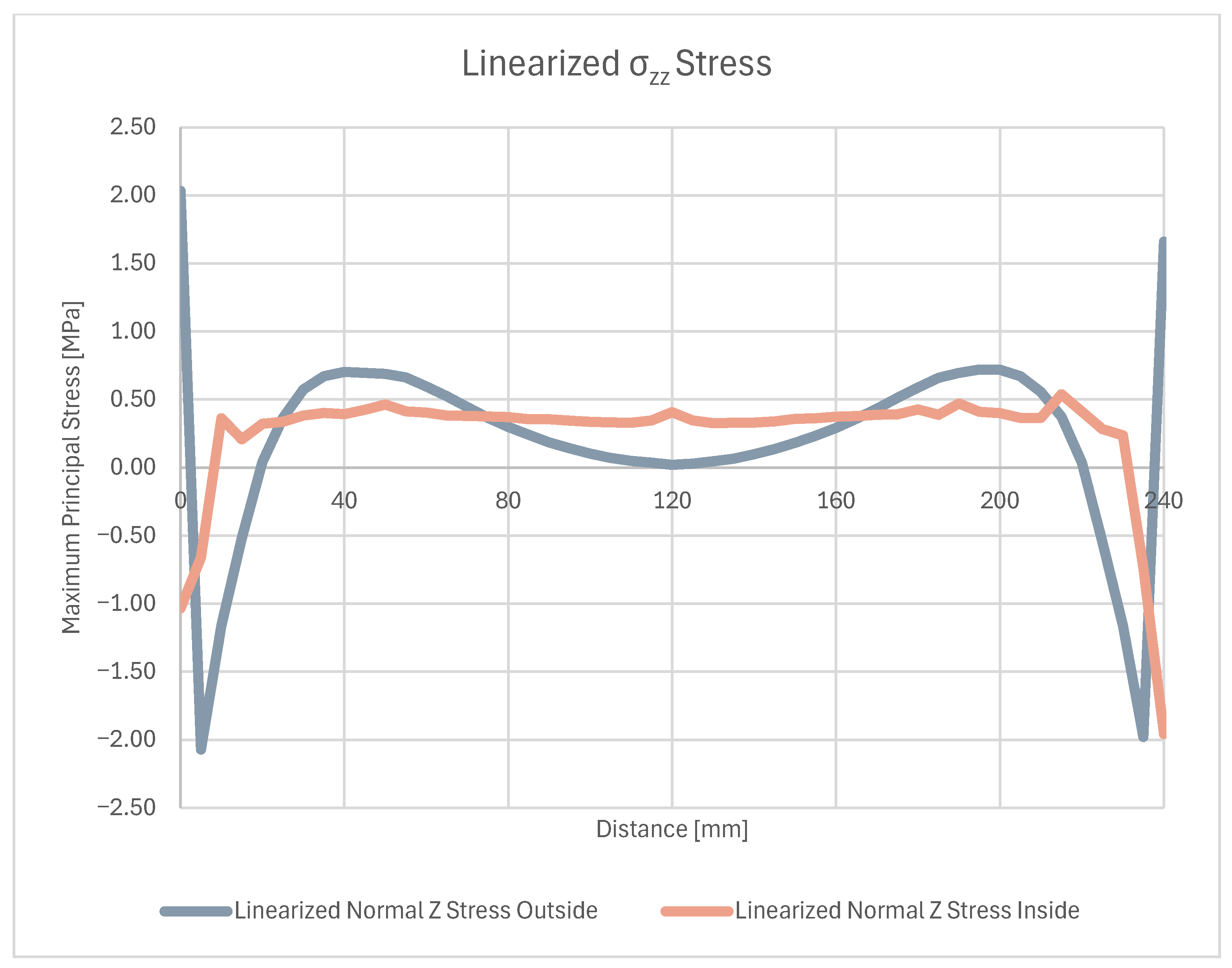
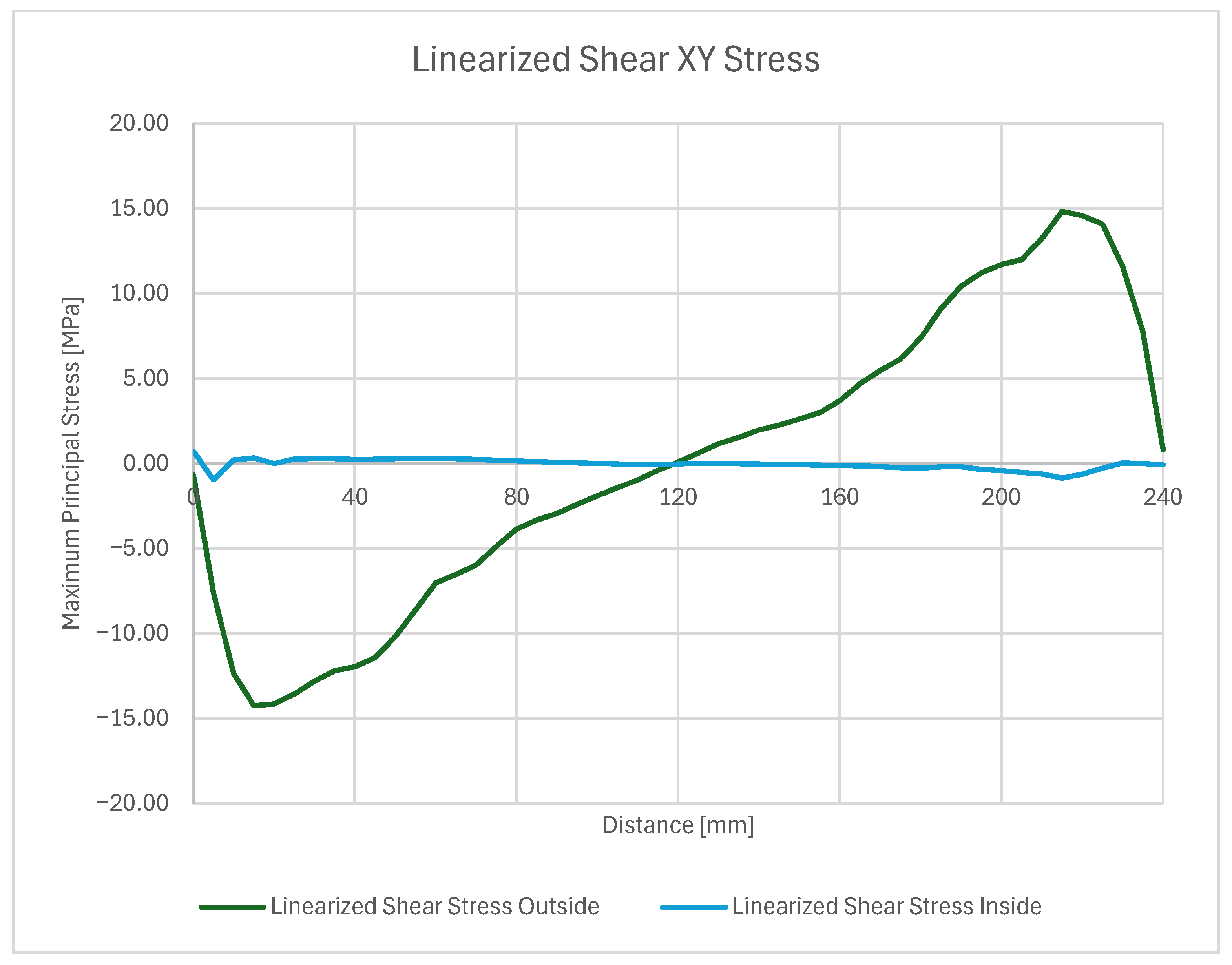
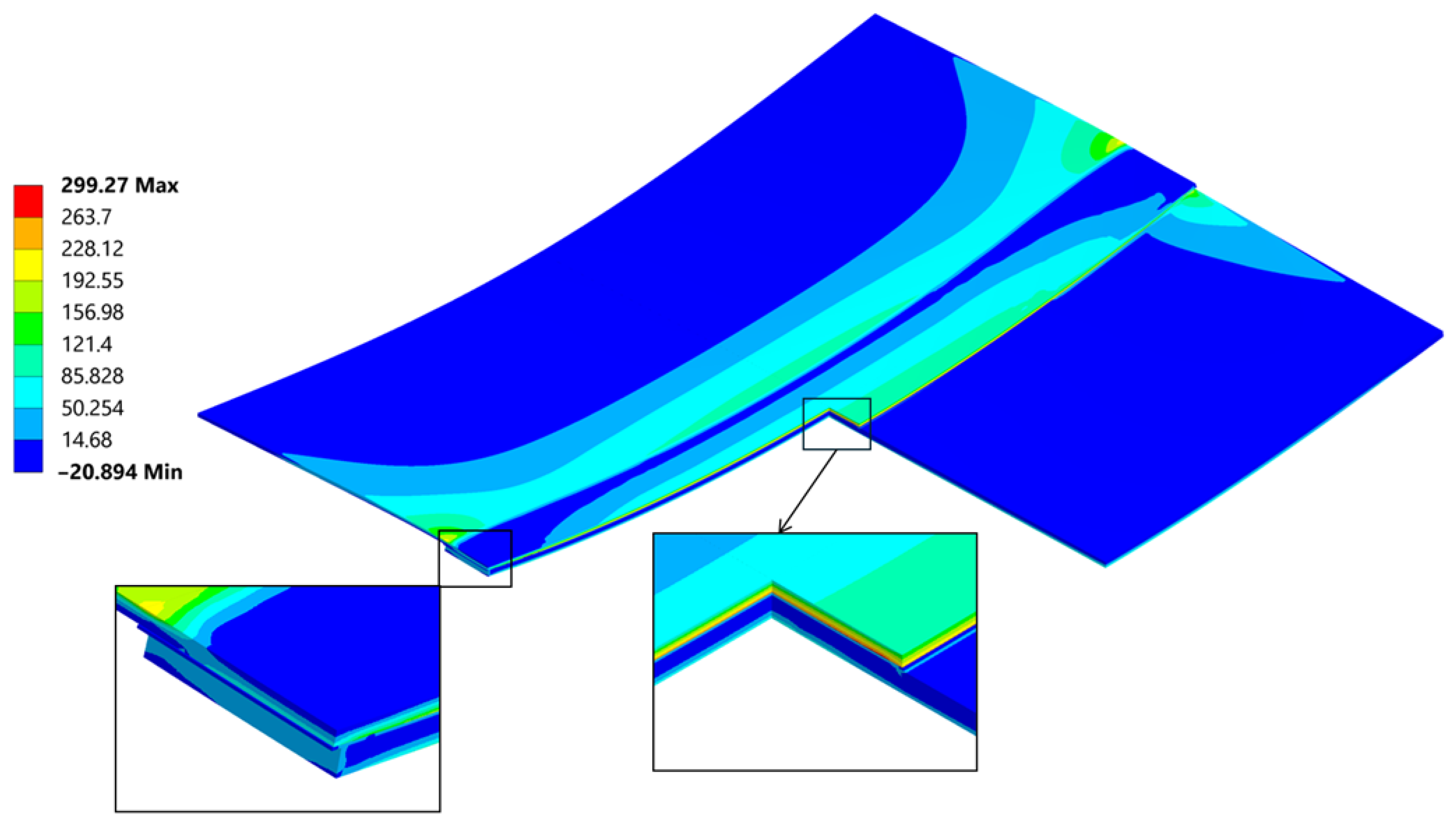
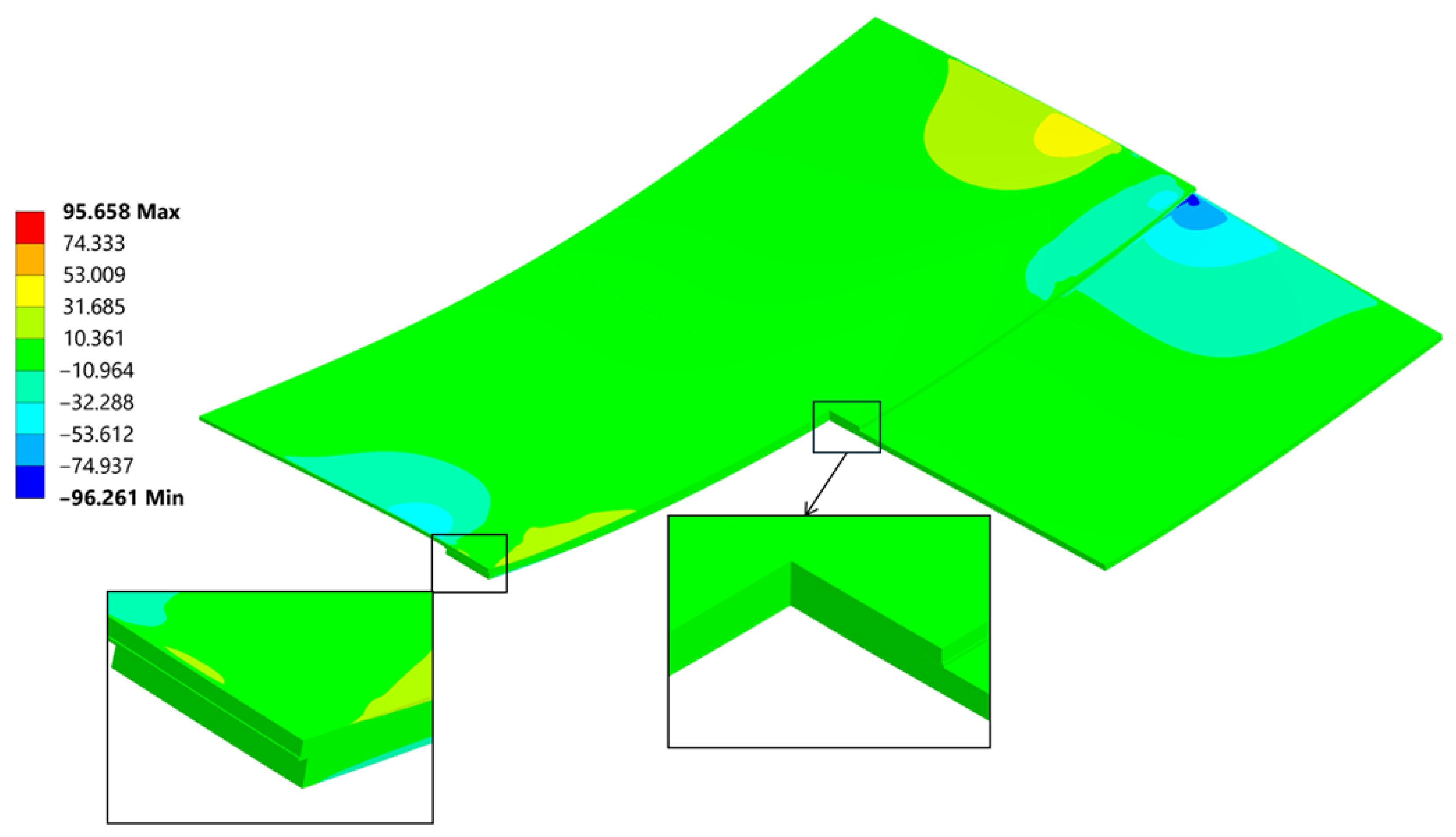
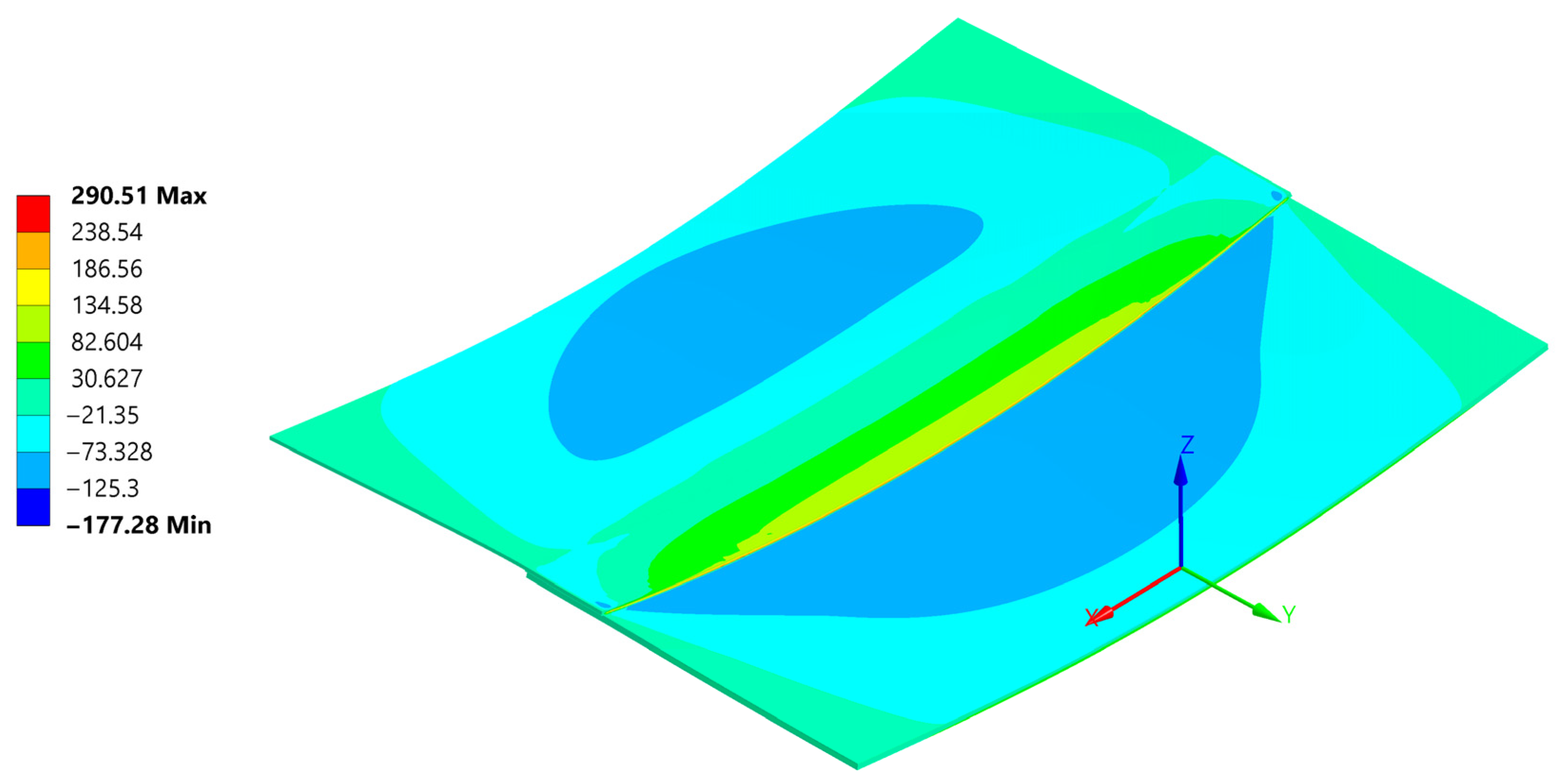
5.3. Stress
5.4. Deformation and σxx Stress Comparison Throughout Different Thermal Cycles
6. Summary
6.1. Conclusions
- -
- PC flow/viscoelastic relaxation above Tg: Mismatch strains relax before lock-in, so the residual curvature is less temperature-sensitive, and the behaviour is not represented in the elastic hand calculation or current FEM.
- -
- Al7075 hot softening/relaxation during dwell/early cooling reduces the recoverable bending moment, further flattening δ(ΔT) [53].
6.2. Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Valente, M.; Rossitti, I.; Sambucci, M. Different Production Processes for Thermoplastic Composite Materials: Sustainability versus Mechanical Properties and Processes Parameter. Polymers 2023, 15, 242. [Google Scholar] [CrossRef]
- Biron, M. Thermoplastics and Thermoplastic Composites, 3rd ed.; Plastics design library (PDL)—PDL Handbook Series; William Andrew Applied Science Publishers/Elsevier: Oxford, UK, 2018; ISBN 978-0-08-102501-7. [Google Scholar]
- Krueger, R.; Bergan, A. Advances in Thermoplastic Composites over Three Decades—A Literature Review; NASA Technical Memorandum; NASA/TM–20240005376; NASA: Washington, DC, USA, 2024. Available online: https://ntrs.nasa.gov/citations/20240005376 (accessed on 27 September 2025).
- Sastri, V.R. Plastics in Medical Devices: Properties, Requirements, and Applications, 1st ed.; PDL Handbook Series; Elsevier/William Andrew: Amsterdam, The Netherlands; Boston, MA, USA, 2010; ISBN 978-0-8155-2027-6. [Google Scholar]
- Murray, R.E.; Beach, R.; Barnes, D.; Snowberg, D.; Berry, D.; Rooney, S.; Jenks, M.; Gage, B.; Boro, T.; Wallen, S.; et al. Structural Validation of a Thermoplastic Composite Wind Turbine Blade with Comparison to a Thermoset Composite Blade. Renew. Energy 2021, 164, 1100–1107. [Google Scholar] [CrossRef]
- Kuleyin, H.; Gümrük, R. The Effect of Poly (Methyl Methacrylate) Content on Chemical, Thermomechanical, Mechanical, and Fatigue Life Characteristics of Ternary PC/ABS/PMMA Blends. Polymers 2025, 17, 1905. [Google Scholar] [CrossRef] [PubMed]
- Bondyra, A.; Łusiak, T. Analysis of Strenght Properties of Carbon Fibre-Reinforced Composites. Trans. Aerosp. Res. 2023, 2023, 45–66. [Google Scholar] [CrossRef]
- Nagel, L.; Herwig, A.; Schmidt, C.; Horst, P. Numerical Investigation of Residual Stresses in Welded Thermoplastic CFRP Structures. J. Compos. Sci. 2021, 5, 45. [Google Scholar] [CrossRef]
- Wu, T.; Ma, Y.; Xia, H.; Geng, P.; Niendorf, T.; Ma, N. Measurement and Simulation of Residual Stresses in Laser Welded CFRP/Steel Lap Joints. Compos. Struct. 2022, 292, 115687. [Google Scholar] [CrossRef]
- Sacchetti, F.; Grouve, W.J.B.; Warnet, L.L.; Villegas, I.F. Effect of Cooling Rate on the Interlaminar Fracture Toughness of Unidirectional Carbon/PPS Laminates. Eng. Fract. Mech. 2018, 203, 126–136. [Google Scholar] [CrossRef]
- Long, W.; Zhou, X.; Du, B.; Cheng, X.; Su, G.; Chen, L. Enhancing the Lap Shear Performance of Resistance-Welded GF/PP Thermoplastic Composite by Modifying Metal Heating Elements with Silane Coupling Agent. Materials 2024, 17, 4944. [Google Scholar] [CrossRef]
- Stankiewicz, K.; Lipkowski, A.; Kowalczyk, P.; Giżyński, M.; Waśniewski, B. Resistance Welding of Thermoplastic Composites, Including Welding to Thermosets and Metals: A Review. Materials 2024, 17, 4797. [Google Scholar] [CrossRef]
- Lionetto, F.; Pappadà, S.; Buccoliero, G.; Maffezzoli, A. Finite Element Modeling of Continuous Induction Welding of Thermoplastic Matrix Composites. Mater. Des. 2017, 120, 212–221. [Google Scholar] [CrossRef]
- Gouin O’Shaughnessey, P.; Dubé, M.; Fernandez Villegas, I. Modeling and Experimental Investigation of Induction Welding of Thermoplastic Composites and Comparison with Other Welding Processes. J. Compos. Mater. 2016, 50, 2895–2910. [Google Scholar] [CrossRef]
- Jiao, J.; Xu, J.; Jing, C.; Sheng, L.; Ru, H.; Xia, H. Laser Welding Process and Strength Enhancement of Carbon Fiber Reinforced Thermoplastic Composites and Metals Dissimilar Joint: A Review. Chin. J. Aeronaut. 2023, 36, 13–31. [Google Scholar] [CrossRef]
- Wang, Q.; Jia, Z.; Zhang, B.; Gao, D.; Ma, Y.; Liu, J. Influence of Processing Parameters on Joint Shear Performance in Laser Direct Joining of CFRTP and Aluminum Alloy. Mater. Des. 2021, 209, 109996. [Google Scholar] [CrossRef]
- Wu, T.; Tinkloh, S.R.; Tröster, T.; Zinn, W.; Niendorf, T. Determination and Validation of Residual Stresses in CFRP/Metal Hybrid Components Using the Incremental Hole Drilling Method. J. Compos. Sci. 2020, 4, 143. [Google Scholar] [CrossRef]
- Guo, Y.; Li, P. Effect of Residual Stress and Microstructure on the Fatigue Crack Growth Behavior of Aluminum Friction Stir Welded Joints. Materials 2024, 17, 385. [Google Scholar] [CrossRef]
- Wang, L.; Ni, Z.; Xiao, Y.; Li, Y.; Liu, X.; Chen, Y.; Cui, S.; Zhang, D.; Mi, C.; He, Q. Numerical Strength Analysis of Laser-Welded Differential Housing and Gear Considering Residual Stress. Materials 2023, 16, 4721. [Google Scholar] [CrossRef]
- DOT/FAA/AR-MMPDS-01; Metallic Materials Properties Development and Standardization (MMPDS). U.S. Department of Transportation, Federal Aviation Administration: Washington, DC, USA, 2003.
- Tanaka, K.; Takemoto, K.; Suzue, M.; Katayama, T. Effects of the Molecular Weight of Polycarbonate on the Mechanical Properties of Carbon Fiber Reinforced Polycarbonate. In Proceedings of the International Conference, Tallinn, Estonia, 28 November–1 December 2017; pp. 327–335. [Google Scholar]
- Zhang, S.; Wang, B. Mechanical Properties and Fracture Microstructure of Polycarbonate under High Strain Rate Tension. Materials 2023, 16, 3386. [Google Scholar] [CrossRef]
- Dobrzański, P.; Oleksiak, W. Design and Analysis Methods for Composite Bonded Joints. Trans. Aerosp. Res. 2021, 2021, 45–63. [Google Scholar] [CrossRef]
- ECSS-E-HB-32-21; A Space Engineering Adhesive Boding Handbook. ESA Requirements and Standards Division: Noordwijk, The Netherlands, 2011.
- Baker, A.; Rose, F.; Jones, R. Advances in the Bonded Composite Repair of Metallic Aircraft Structure; Elsevier: Amsterdam, The Netherlands, 2003; Volume 1. [Google Scholar]
- Bonpain, B.; Stommel, M. Influence of Surface Roughness on the Shear Strength of Direct Injection Molded Plastic-Aluminum Hybrid-Parts. Int. J. Adhes. Adhes. 2018, 82, 290–298. [Google Scholar] [CrossRef]
- Waśniewski, B. Duroplasty oraz termoplasty wysokotemperaturowe w prepregach jako osłony kompozytów węglowych do wytwarzania struktur lotniczych. PIL 2016, 243, 28–39. [Google Scholar] [CrossRef]
- Dobrzański, P. Bonding of High Temperature Thermoplastic Carbon Composites with Resistance Welding Technique. Trans. Aerosp. Res. 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Hou, M.; Ye, L.; Mai, Y.-W. An Experimental Study of Resistance Welding of Carbon Fibre Fabric Reinforced Polyetherimide (CF Fabric/PEI) Composite Material. Appl. Compos. Mater. 1999, 6, 35–49. [Google Scholar] [CrossRef]
- Stavrov, D.; Bersee, H. Resistance Welding of Thermoplastic Composites-an Overview. Compos. Part A Appl. Sci. Manuf. 2005, 36, 39–54. [Google Scholar] [CrossRef]
- Hyla, B.; Sobczak, M.; Synaszko, P.; Roemer, J. Laser Spot Thermography and Pulse Thermography—Comparison of Performance for Non-Destructive Testing of Composite Structures. Int. J. Multiphys. 2023, 17, 91. [Google Scholar] [CrossRef]
- Kamińska, P.; Ziemkiewcz, J.; Synaszko, P.; Dragan, K. Comparison of Pulse Thermography (PT) and Step Heating (SH) Thermography in Non-Destructive Testing of Unidirectional GFRP Composites. Fatigue Aircr. Struct. 2019, 2019, 87–102. [Google Scholar] [CrossRef]
- Okolie, O.; Latto, J.; Faisal, N.; Jamieson, H.; Mukherji, A.; Njuguna, J. Manufacturing Defects in Thermoplastic Composite Pipes and Their Effect on the In-Situ Performance of Thermoplastic Composite Pipes in Oil and Gas Applications. Appl. Compos. Mater. 2023, 30, 231–306. [Google Scholar] [CrossRef]
- Tammas-Williams, S.; Withers, P.J.; Todd, I.; Prangnell, P.B. The Influence of Porosity on Fatigue Crack Initiation in Additively Manufactured Titanium Components. Sci. Rep. 2017, 7, 7308. [Google Scholar] [CrossRef]
- Young, W.C.; Budynas, R.G.; Roark, R.J. Roark’s Formulas for Stress and Strain, 7th ed.; McGraw-Hill International Edition, General Engineering Series; Reprint; McGraw-Hill: New York, NY, USA, 2011; ISBN 978-0-07-072542-3. [Google Scholar]
- Pradere, C.; Sauder, C. Transverse and Longitudinal Coefficient of Thermal Expansion of Carbon Fibers at High Temperatures (300–2500K). Carbon 2008, 46, 1874–1884. [Google Scholar] [CrossRef]
- Abdullah, F.; Okuyama, K.; Fajardo, I.; Urakami, N. In Situ Measurement of Carbon Fibre/Polyether Ether Ketone Thermal Expansion in Low Earth Orbit. Aerospace 2020, 7, 35. [Google Scholar] [CrossRef]
- Geng, Z.; Yu, S.; Wang, S.; Tian, Z.; Gao, Z.; Wang, K.; Li, Y. Advances in Resistance Welding of Fiber-Reinforced Thermoplastics. Materials 2024, 17, 4693. [Google Scholar] [CrossRef]
- Lan, S.; Lee, H.-J.; Lee, S.-H.; Ni, J.; Lai, X.; Lee, H.-W.; Song, J.-H.; Lee, M.G. Experimental and Numerical Study on the Viscoelastic Property of Polycarbonate near Glass Transition Temperature for Micro Thermal Imprint Process. Mater. Des. 2009, 30, 3879–3884. [Google Scholar] [CrossRef]
- Principles of Heat and Mass Transfer, 7th ed.; Incropera, F.P., DeWitt, D.P., Bergman, T.L., Lavine, A.S., Eds.; International Student Version; Wiley: Hoboken, NJ, USA, 2013; ISBN 978-0-470-50197-9. [Google Scholar]
- NASA. Materials Data Handbook: Aluminum Alloy 7075, 2nd ed.; Contract Number NAS8-25644; Western Applied Research & Development, Inc.: San Carlos, CA, USA, 1972.
- ISO-11359-2-2021; Plastics—Thermomechanical Analysis (TMA)—Part 2: Determination of Coefficient of Linear Thermal Expansion and Glass Transition Temperature. International Organization for Standardization: Geneva, Switzerland, 2021.
- Dong, C.; Li, K.; Jiang, Y.; Arola, D.; Zhang, D. Evaluation of Thermal Expansion Coefficient of Carbon Fiber Reinforced Composites Using Electronic Speckle Interferometry. Opt. Express 2018, 26, 531. [Google Scholar] [CrossRef]
- Tsivouraki, N.; Tserpes, K.; Sioutis, I. Modelling of Fatigue Delamination Growth and Prediction of Residual Tensile Strength of Thermoplastic Coupons. Materials 2024, 17, 362. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Tian, Y.; Gong, Y.; Zhang, J.; Qi, H.; Wang, C. Study of the Effect of Curing Residual Stress on the Bonding Strength of the Single Lap Joint Using a High-Temperature Phosphate Adhesive. Materials 2018, 11, 1198. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.T.; Nelson, C.W. Thermal Stressin Bonded Joints. IBM J. Res. Dev. 1979, 23, 179–188. [Google Scholar] [CrossRef]
- Timošenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells, 2nd ed.; McGraw-Hill Classic Textbook Reissue; [Nachdr.]; McGraw-Hill: New York, NY, USA, 1996; ISBN 978-0-07-064779-4. [Google Scholar]
- Reeder, J.R. 3D Mixed-Mode Delamination Fracture Criteria—An Experimentalist’s Perspective. In Damage in Composites; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Rodríguez, R.Q.; Sollero, P.; Rodrigues, M.B.; de Albuquerque, É.L. Stress analysis and failure criteria of adhesive bonded single lap joints. In Proceedings of the 21st International Congress of Mechanical Engineering, Natal, RN, Brazil, 24–28 October 2011. [Google Scholar]
- Zheng, X.; Li, D.; Liao, W.; Zhang, H. Residual Stress and Fatigue Strength Analysis of Stiffener Welds of Steel-Plate Composite Girder Bridge Considering Welding Sequence. Buildings 2024, 14, 1801. [Google Scholar] [CrossRef]
- El Shrief, E.; El-Megharbel, A.; El Domiaty, A.; Abd El-Hafez, H. Residual Stress Effects on Fatigue Crack Propagation in Butt–Welded Joints for 304 Stainless Steel Sheets. Manuf. Rev. 2021, 8, 19. [Google Scholar] [CrossRef]
- Malekinejad, H.; Carbas, R.J.C.; Akhavan-Safar, A.; Marques, E.A.S.; Castro Sousa, F.; Da Silva, L.F.M. Enhancing Fatigue Life and Strength of Adhesively Bonded Composite Joints: A Comprehensive Review. Materials 2023, 16, 6468. [Google Scholar] [CrossRef]
- Öchsner, A.; da Silva, L.F.M. Modeling of Adhesively Bonded Joints; Springer: Berlin/Heidelberg, Germany; London, UK, 2008; ISBN 978-3-540-79056-3. [Google Scholar]
- Withers, P.J.; Bhadeshia, H.K.D.H. Residual Stress. Part 1—Measurement Techniques. Mater. Sci. Technol. 2001, 17, 355–365. [Google Scholar] [CrossRef]
- Neto, D.M.; Borges, M.F.; Sérgio, E.R.; Antunes, F.V. Effect of Residual Stresses on Fatigue Crack Growth: A Numerical Study Based on Cumulative Plastic Strain at the Crack Tip. Materials 2022, 15, 2156. [Google Scholar] [CrossRef]








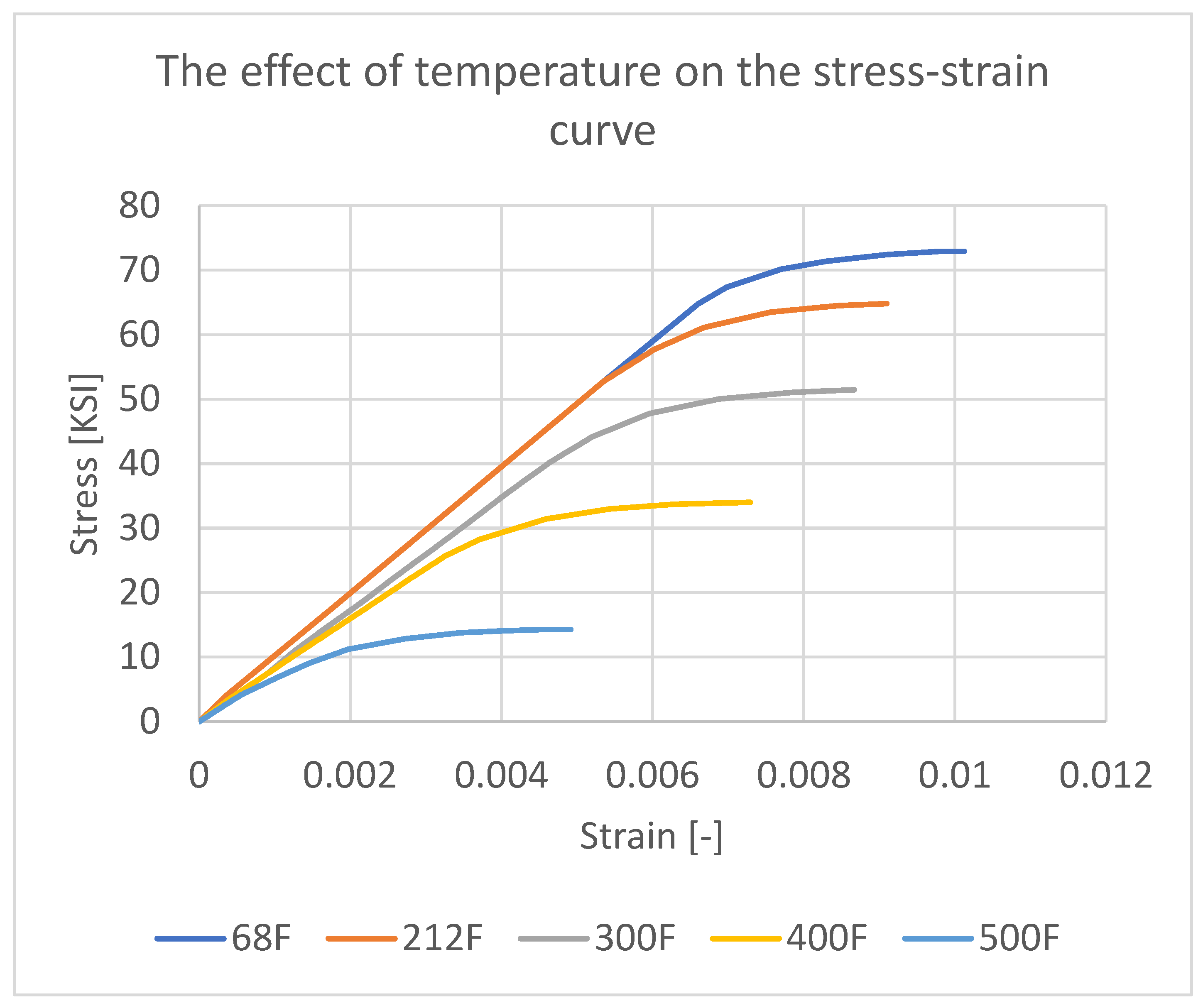

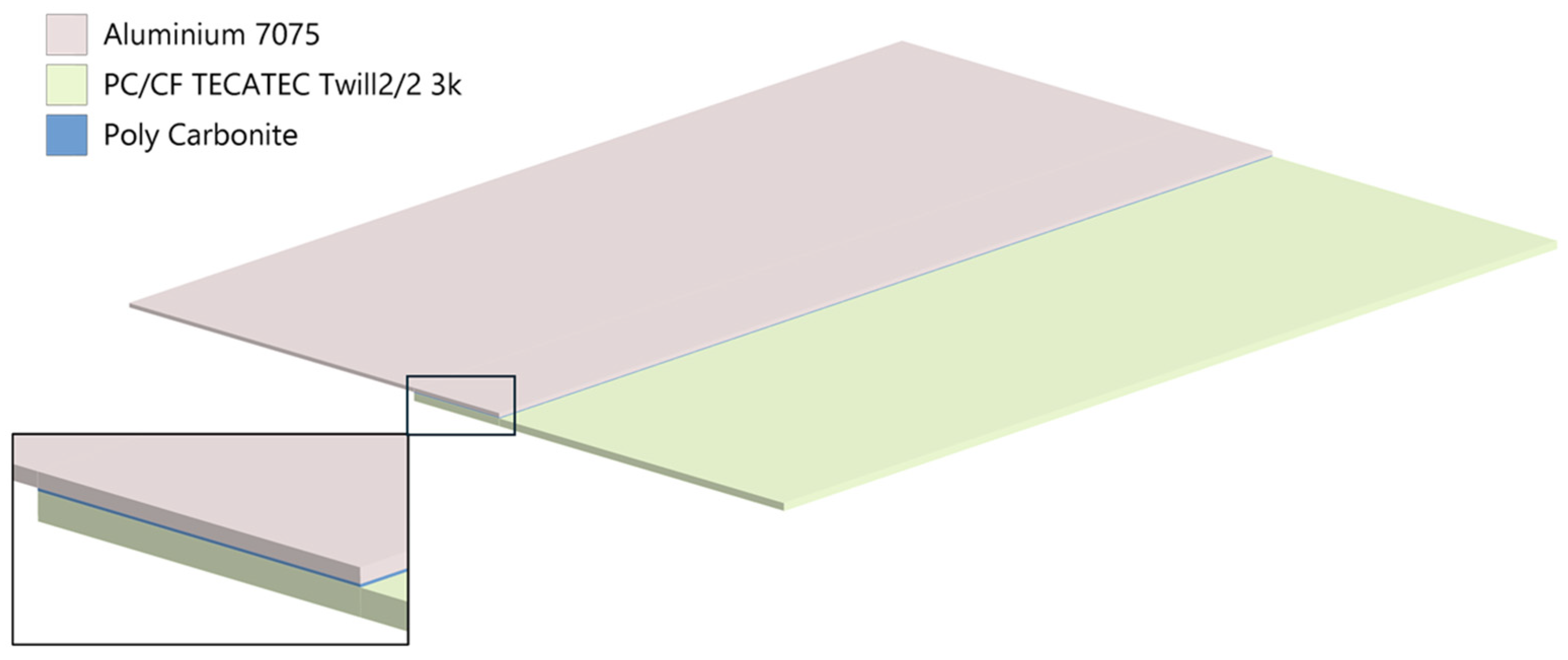

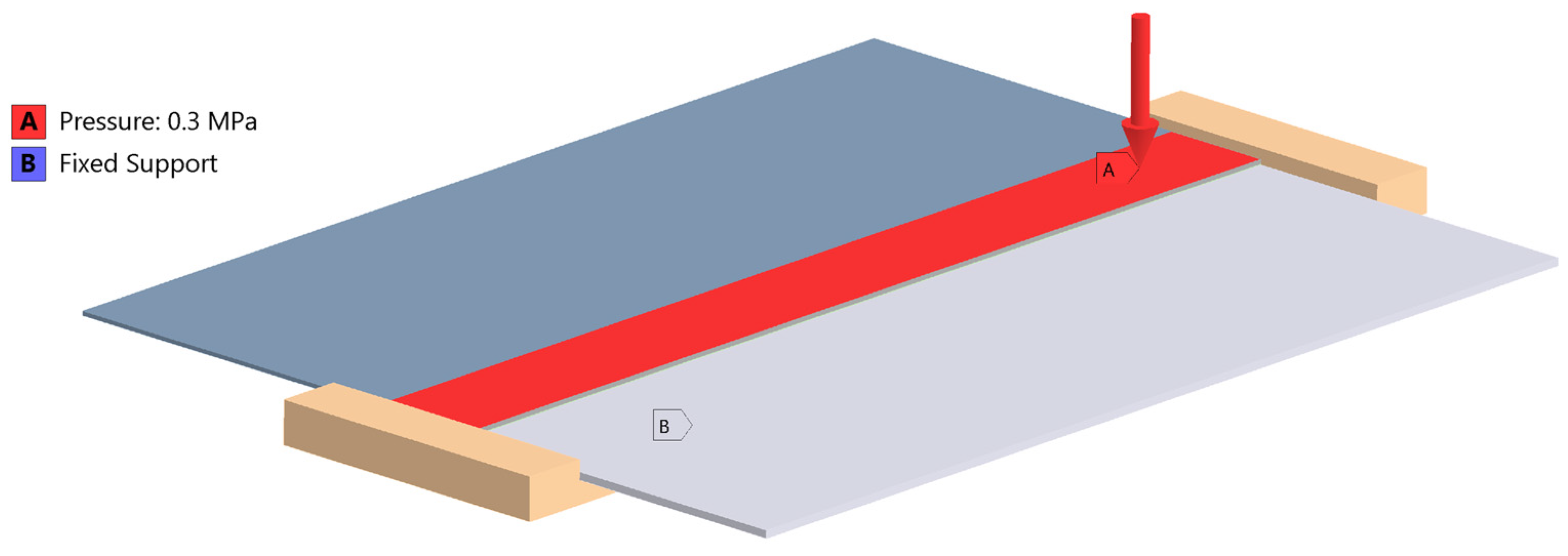
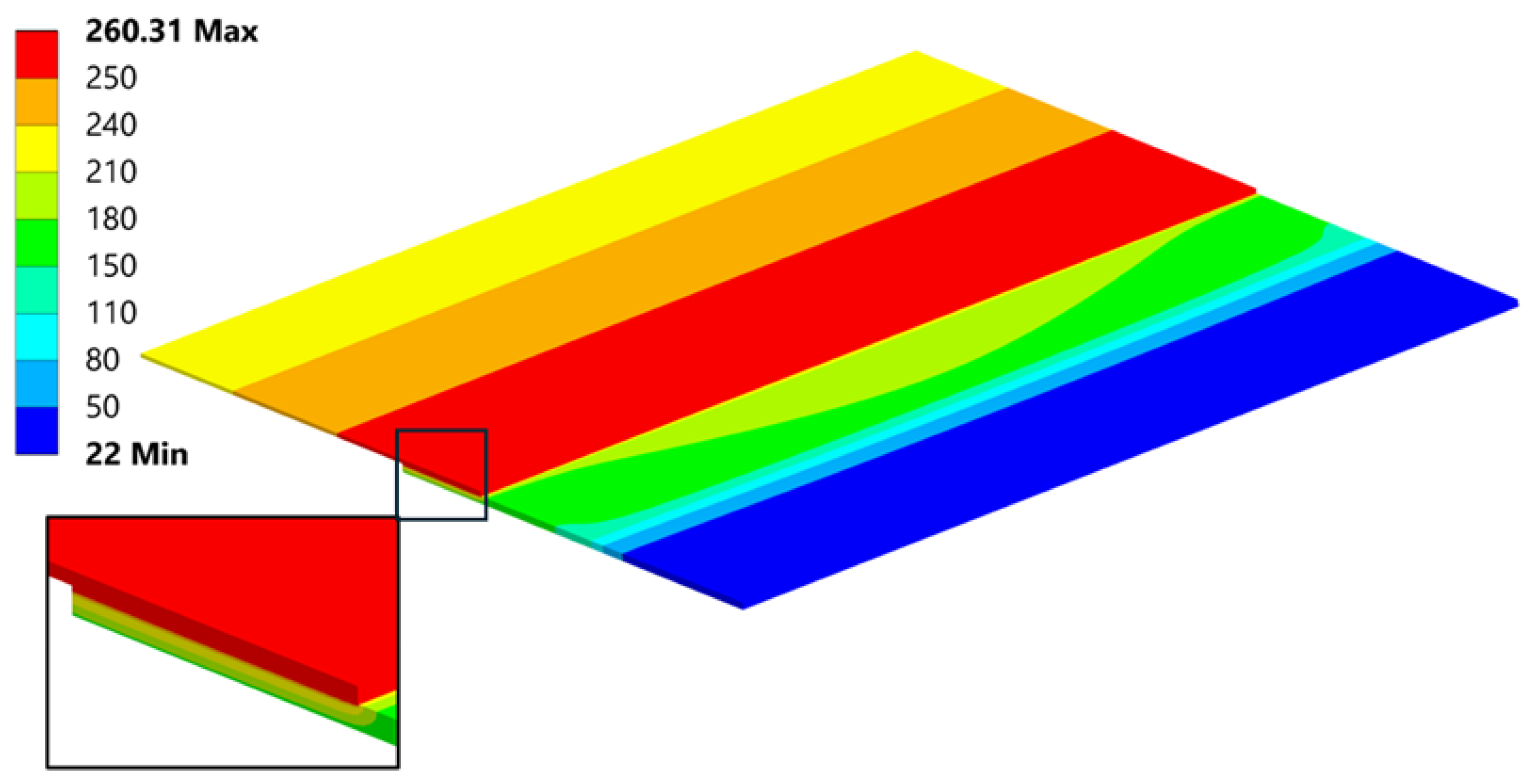


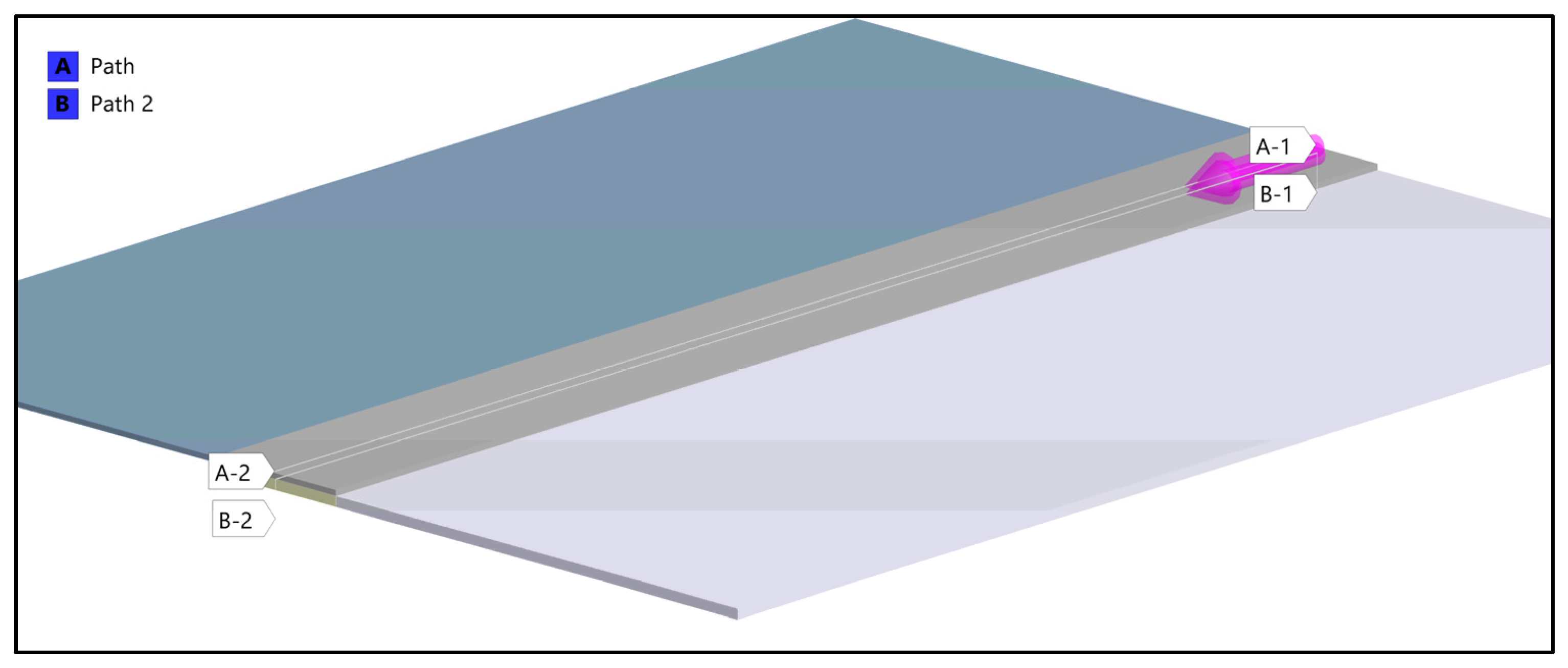
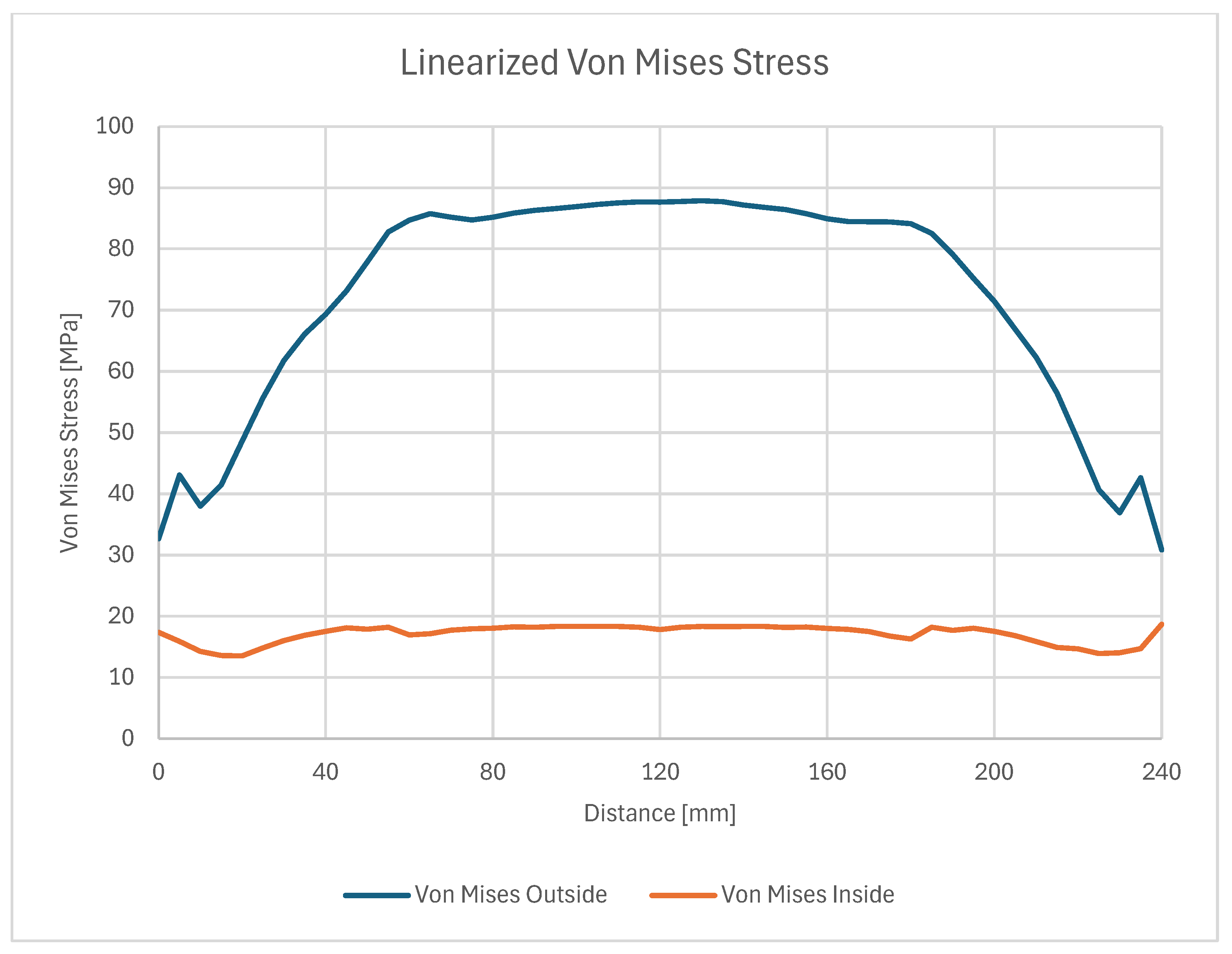
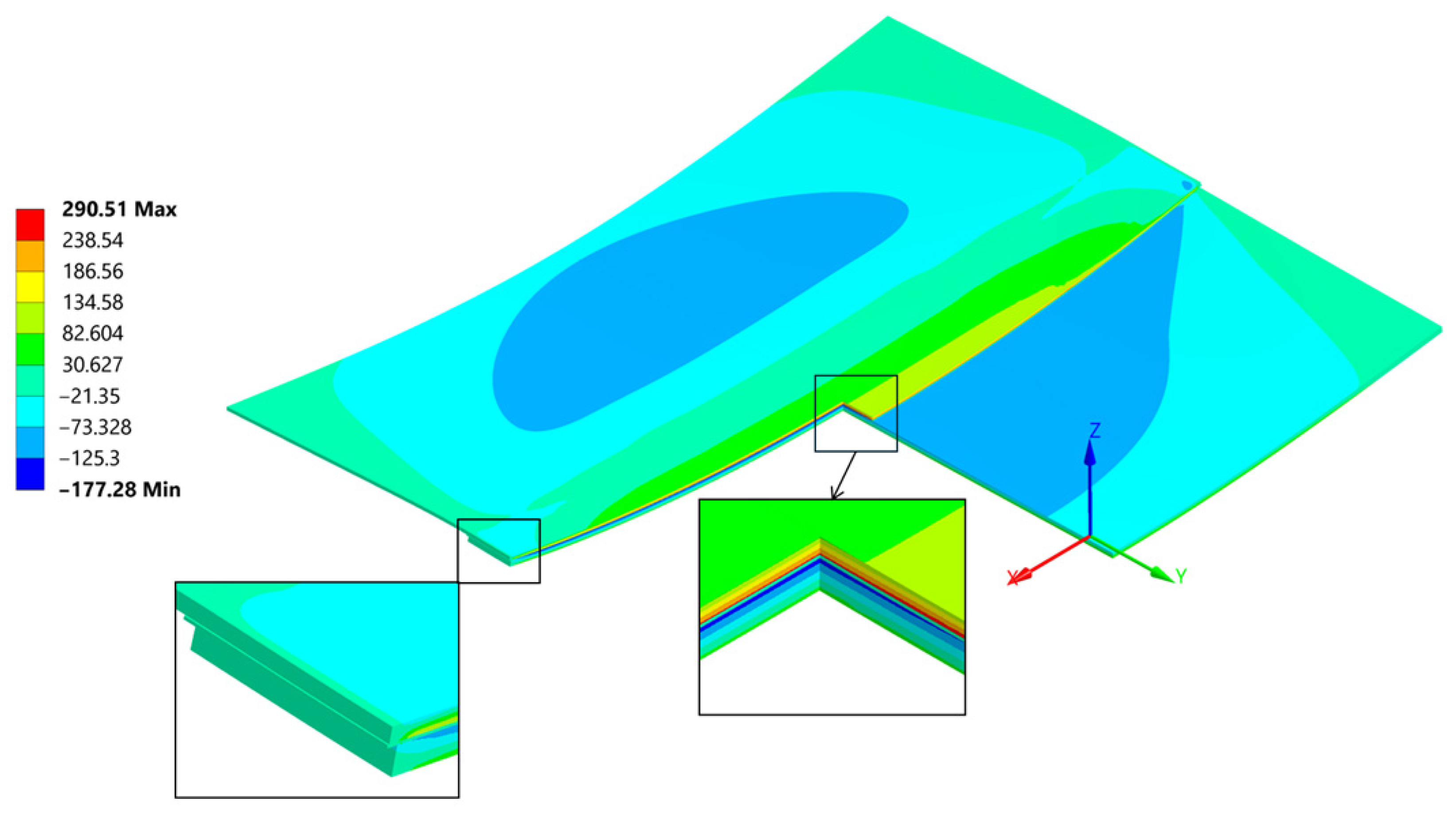

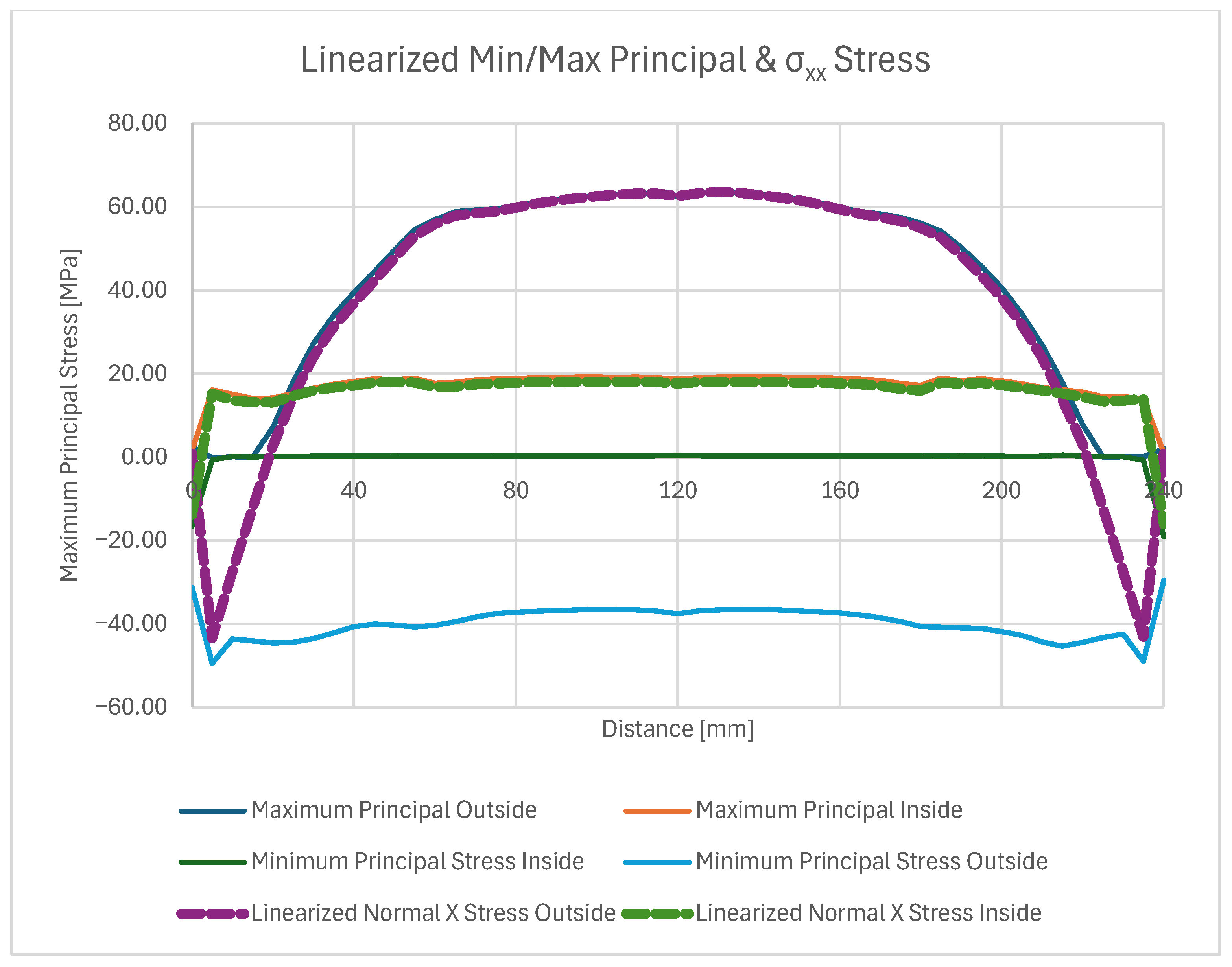


| Sample | T1 [°C] | T2 [°C] | t [mm] Thickness | Δ [mm] Displacement | L [mm] Length | B [mm] Width |
|---|---|---|---|---|---|---|
| AL-CPC-01 | 20 | 260 | 2.84 | 16.71 | 240 | 30 |
| AL-CPC-02 | 20 | 240 | 3.02 | 16.97 | 240 | 30 |
| AL-CPC-03 | 20 | 220 | 2.85 | 16.78 | 240 | 30 |
| Parameter * | PC/CF (Layer a) | Al 7075 (Layer b) |
|---|---|---|
| Thickness t [mm] | 1.8 | 1.0 |
| E [GPa] | 48 | 72 |
| υ [-] | 0.3 | 0.3 |
| CTE α [1/K] | 1.5 × 10−6 ** | 23 × 10−6 |
| ΔT [K] | Curvature κ [1/m] | Bow δ Calculated [mm] | Bow δ Measured [mm] | Error [%] | [MPa] |
|---|---|---|---|---|---|
| 200 | −1.872 | 13.48 | 16.779 | −19.66 | −159.9 |
| 220 | −2.059 | 14.83 | 16.542 | −10.35 | −175.8 |
| 240 | −2.246 | 16.17 | 16.71 | −3.23 | −191.8 |
| Parameter | Value | Unit |
|---|---|---|
| Fibre type | carbon HT 3 k | - |
| Fibre architecture | twill 2/2 | - |
| Fibre areal weight | 200 | g/m2 |
| Tensile strength | 440 | MPa |
| Modulus of elasticity (tensile test) | 48,000 | MPa |
| Flexural strength | 615 | MPa |
| Modulus of elasticity (flexural test) | 48,000 | MPa |
| Compression strength | 215 | MPa |
| Glass transition temperature | 143 | °C |
| Service temperature (short term) | 140 | °C |
| Service temperature (long term) | 120 | °C |
| Thermal expansion (CLTE) | 5 | 10−6 K−1 |
| Drying temperature | 120 | °C |
| Drying time | 3 | h |
| Property | Value |
|---|---|
| Young Modulus [GPa] | 2.5 |
| Poisson’s Coefficient | 0.34 |
| Coefficient of thermal expansion | 0.65 × 10−4 |
| Heat Conductivity [m−1K−1] | 0.2 |
| Specific Heat [kJ kg−1K−1] | 1.2 |
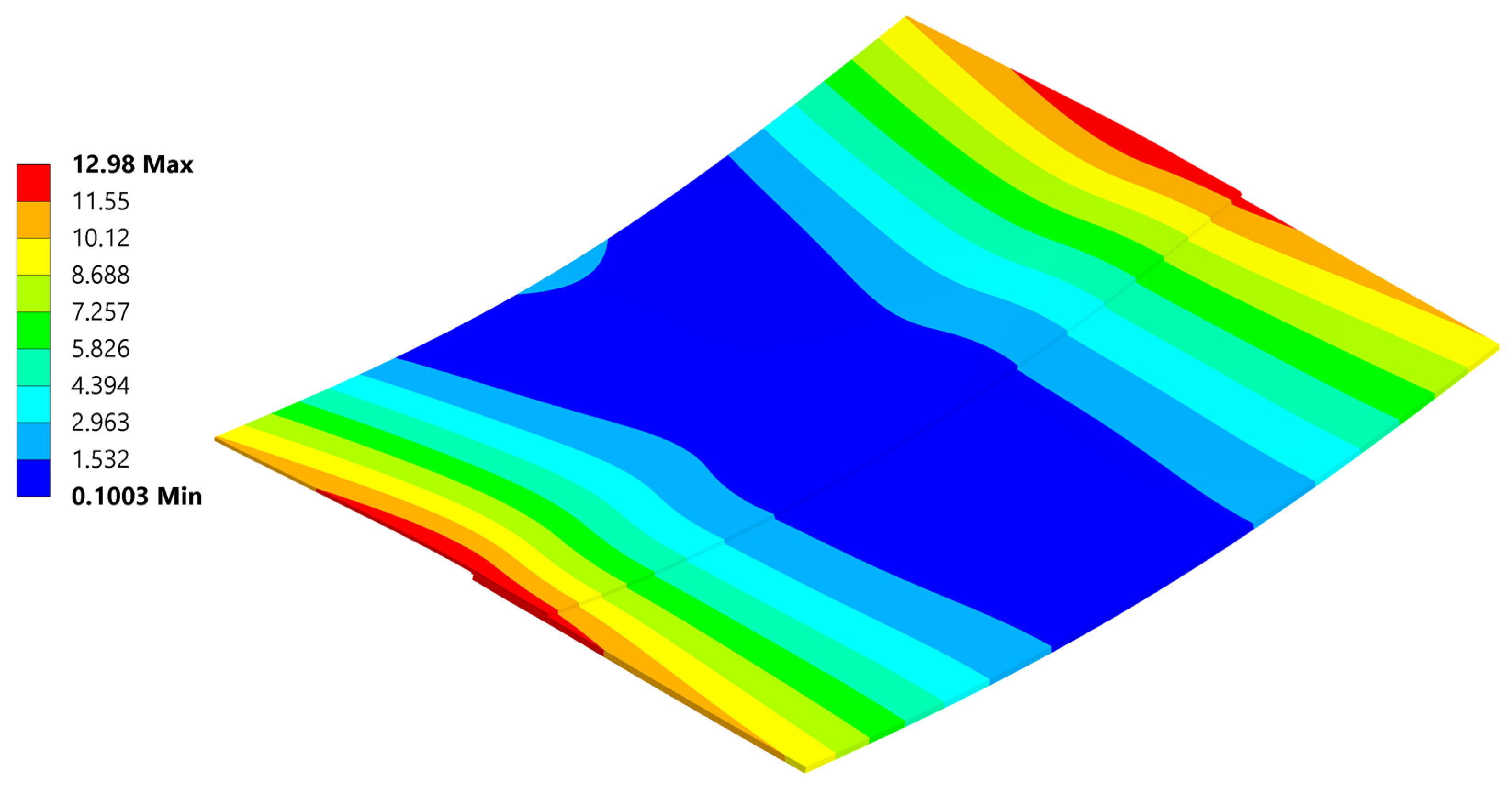
| Parameter | ΔT = 200 °C | ΔT = 220 °C | ΔT = 240 °C |
|---|---|---|---|
| δ test [mm] | 16.78 | 16.54 | 16.71 |
| δ analytical [mm] | 13.48 | 14.83 | 16.17 |
| δ error analytical [%] | −19.67 | −10.34 | −3.23 |
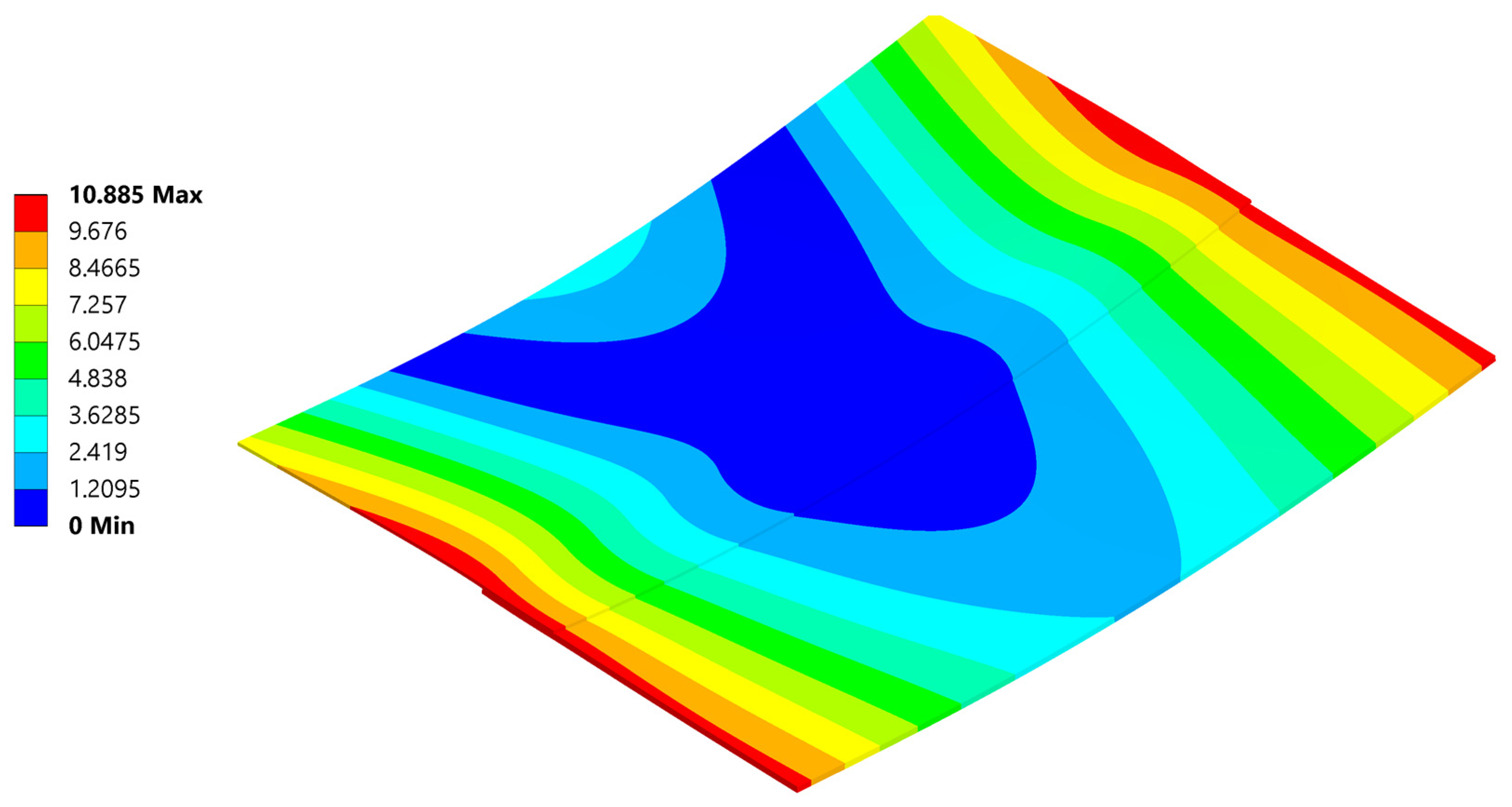
| δ FEM [mm] | 10.88 | 12.05 | 12.98 |
| δ error FEM [%] | −34.88 | −30.5 | −21.21 |
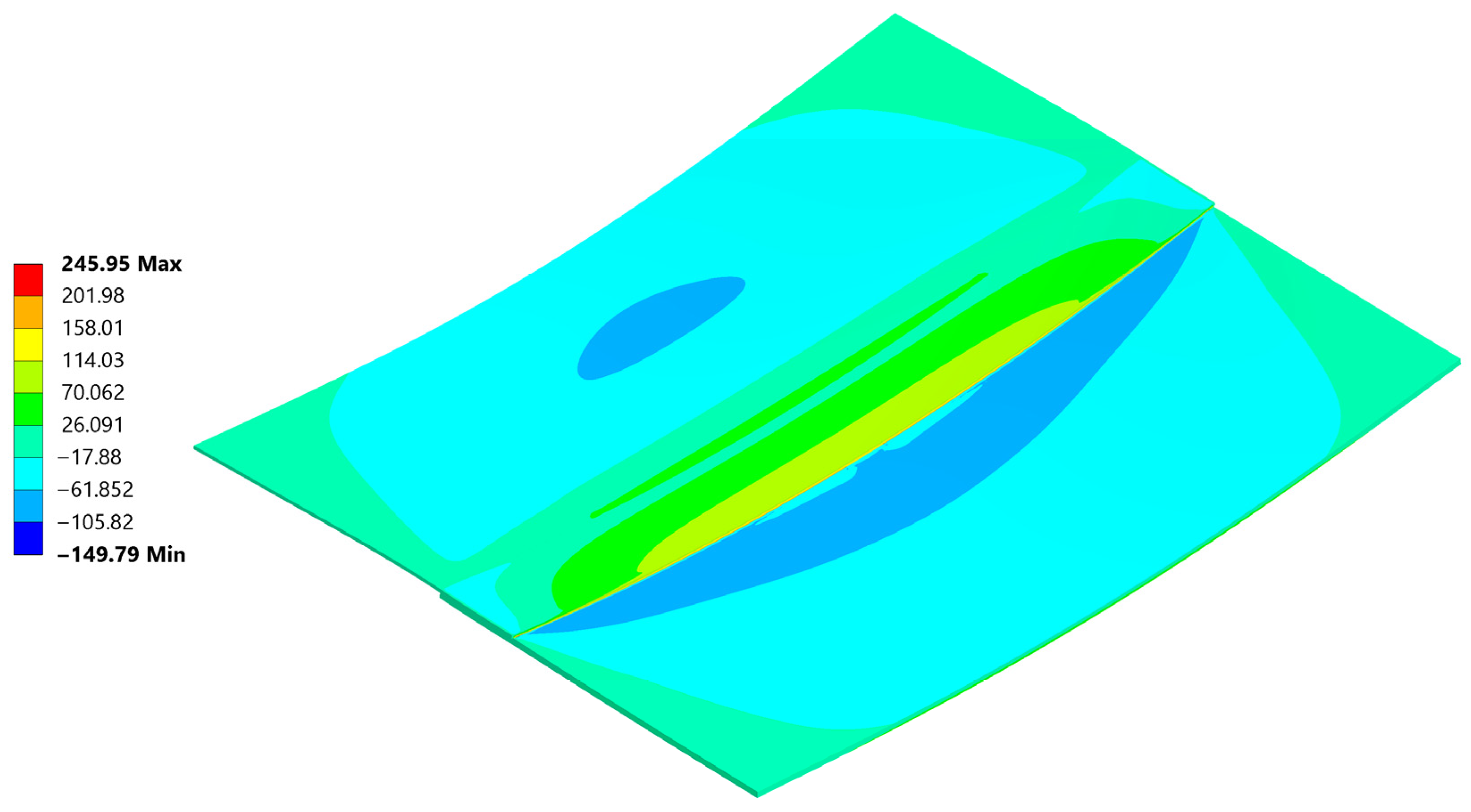
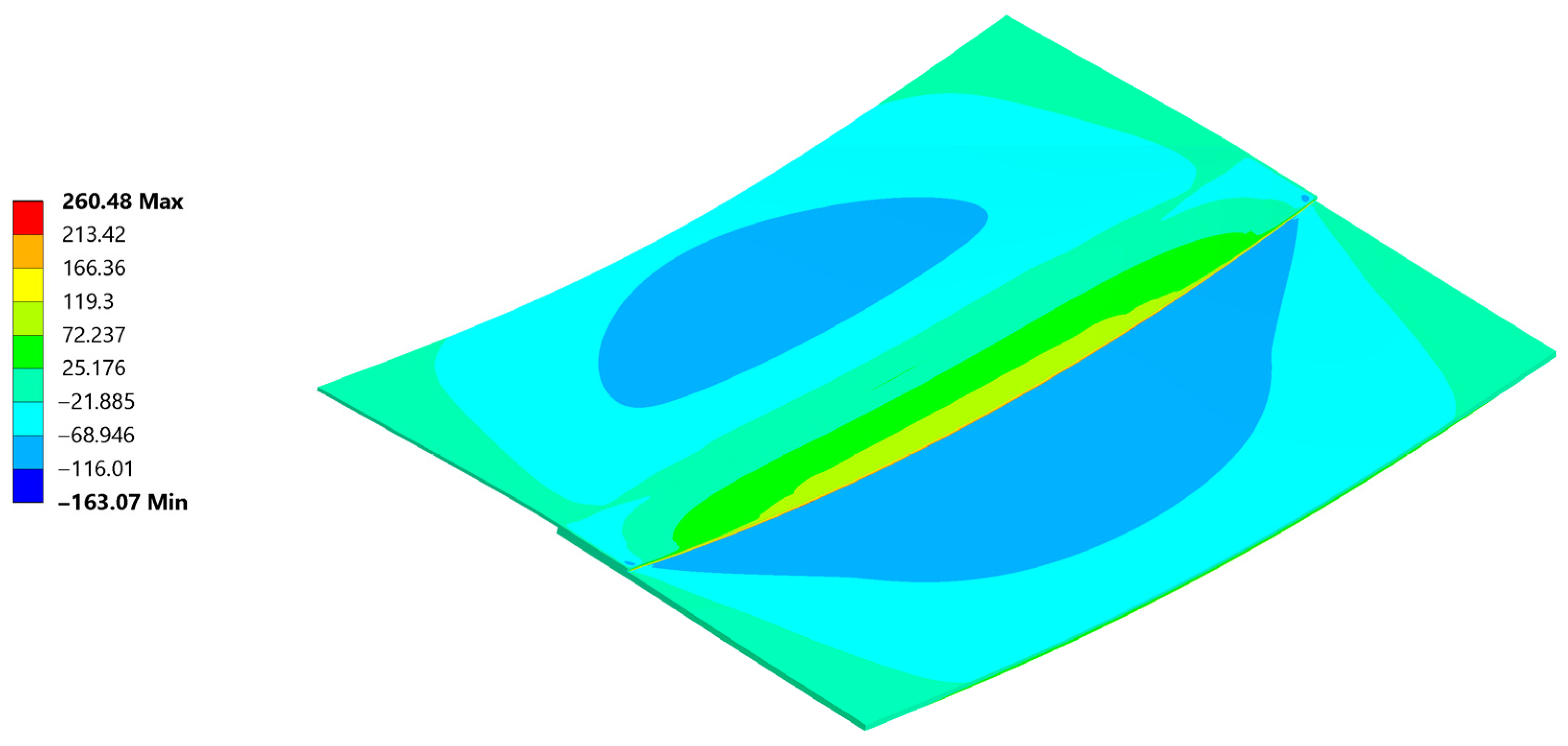
| σxx analytical [MPa] | −159.9 | −175.8 | −191.8 |
| Linearized σxx FEM [MPa] | 43.21 | 55.6 | 63.63 |
| Δσxx FEM vs. analytical [%] | 1.08 | 7.36 | 10.28 |
| Linearized σzz FEM (edge) [MPa] | −1.75 | −1.93 | −2.07 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Praski, M.; Kowalczyk, P.; Stankiewicz, K.; Szumowski, R.; Synaszko, P.; Leski, A. Analysis of Thermally Induced Residual Stress in Resistance Welded PC/CF Composite to Aluminum. Materials 2025, 18, 4962. https://doi.org/10.3390/ma18214962
Praski M, Kowalczyk P, Stankiewicz K, Szumowski R, Synaszko P, Leski A. Analysis of Thermally Induced Residual Stress in Resistance Welded PC/CF Composite to Aluminum. Materials. 2025; 18(21):4962. https://doi.org/10.3390/ma18214962
Chicago/Turabian StylePraski, Marcin, Piotr Kowalczyk, Karolina Stankiewicz, Radosław Szumowski, Piotr Synaszko, and Andrzej Leski. 2025. "Analysis of Thermally Induced Residual Stress in Resistance Welded PC/CF Composite to Aluminum" Materials 18, no. 21: 4962. https://doi.org/10.3390/ma18214962
APA StylePraski, M., Kowalczyk, P., Stankiewicz, K., Szumowski, R., Synaszko, P., & Leski, A. (2025). Analysis of Thermally Induced Residual Stress in Resistance Welded PC/CF Composite to Aluminum. Materials, 18(21), 4962. https://doi.org/10.3390/ma18214962





