Investigating the Effect of Wire Drawing and Heat Treatment on the Response of Ni50.9Ti49.1 R-Phase Actuators
Abstract
1. Introduction
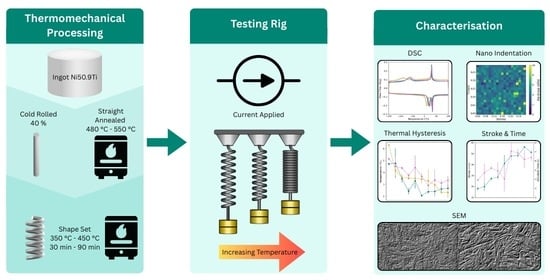
2. Materials and Method
2.1. Materials and Sample Preparation
2.2. Heat Treatment and Shape Setting
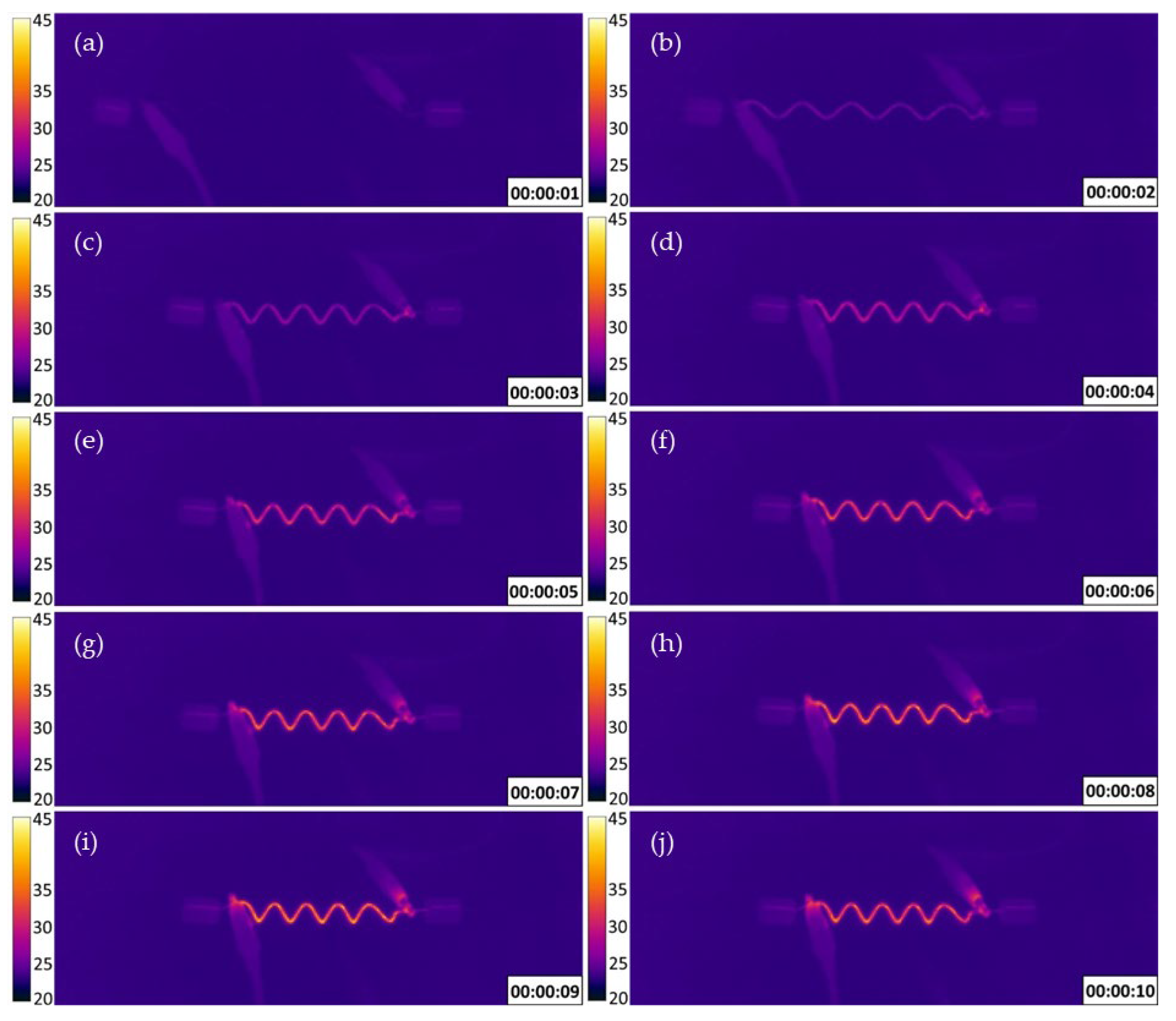
2.3. Stroke and Actuation Time
- The sample is loaded onto the rig at ‘A’ and attached on either end by the connector blocks ‘B’.
- Electrical connectors are attached at both ends of the sample at ‘C’.
- The bias load ‘D’ is attached, causing the sample to stretch.
- Using a LabVIEW program, a current of 2 A is applied to the sample via the electrical connectors.
- The application of current causes the sample to contract and lift the bias load.
- The distance sensor ‘E’ connected to the LabVIEW program records the change in distance between the sensor and the bias load w.r.t time.
- The thermal camera connected to the LabVIEW program records the temperature of the sample w.r.t time during heating.
- After 10 seconds, the current switches off and the sample is left to cool.
- The distance sensor and thermal camera continue to record data as the sample cools and stretches, lowering the bias load.
- The data from the displacement sensor is exported from the LabVIEW program and used to calculate the maximum stroke and the actuation.
2.4. Material Characterisation
3. Results and Discussion
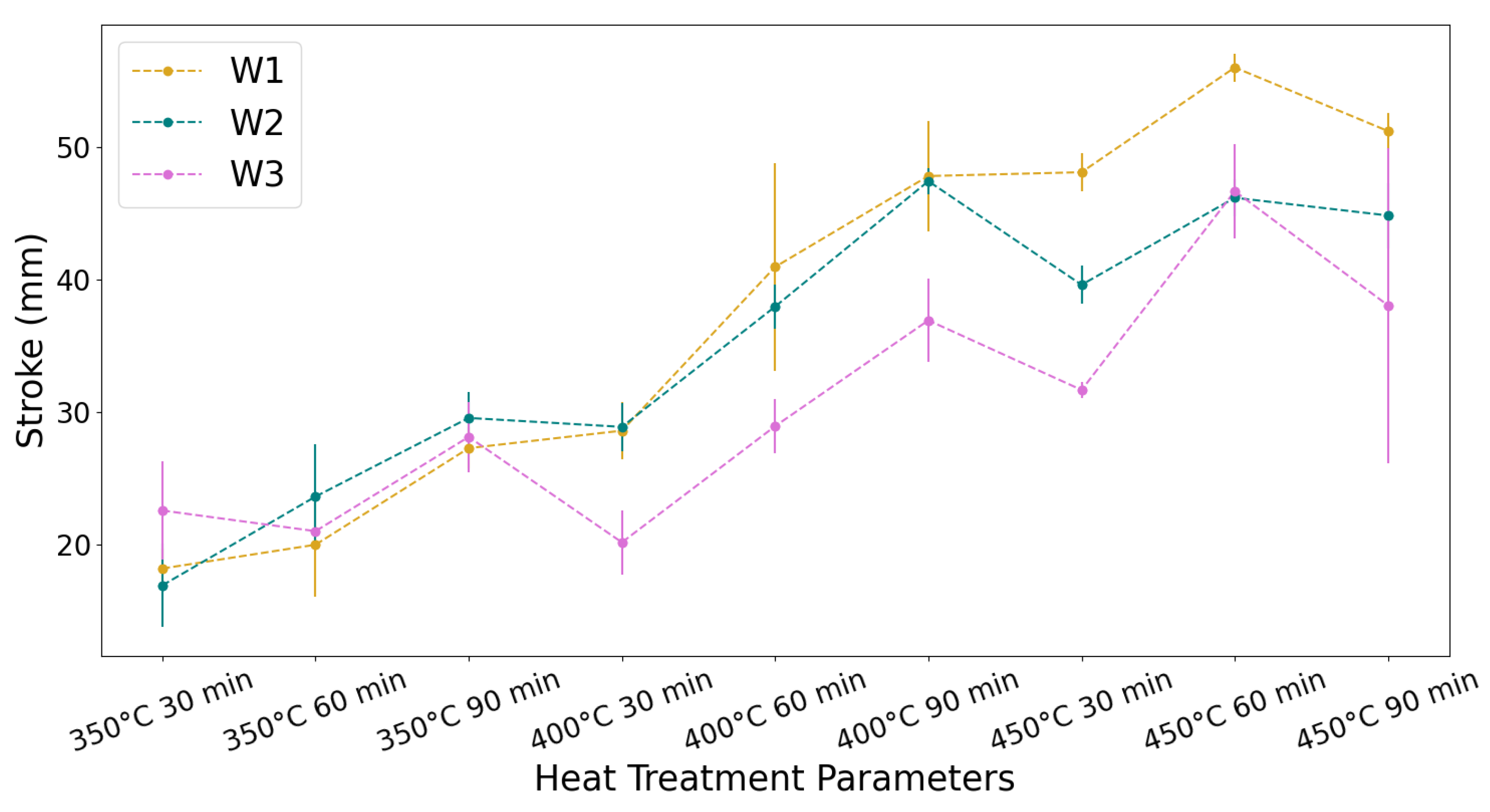
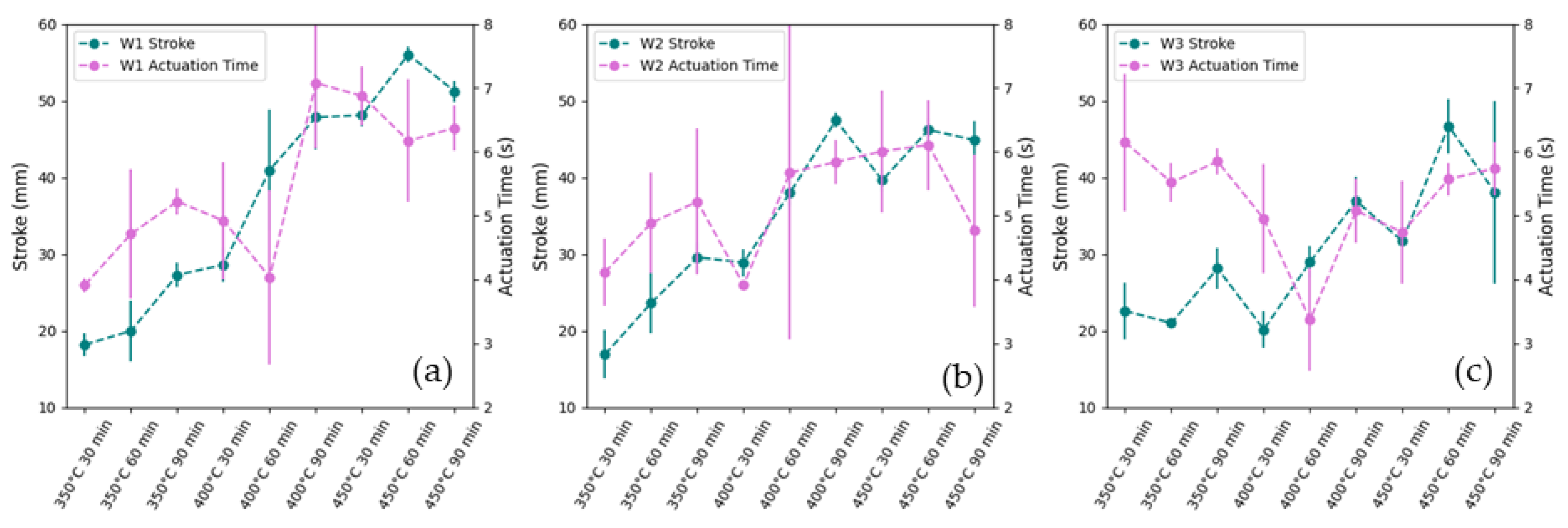
3.1. Effect of Low-Temperature Aging on Actuator Stroke
3.2. Effect of Low-Temperature Aging (350 °C to 450 °C) on Actuation Time
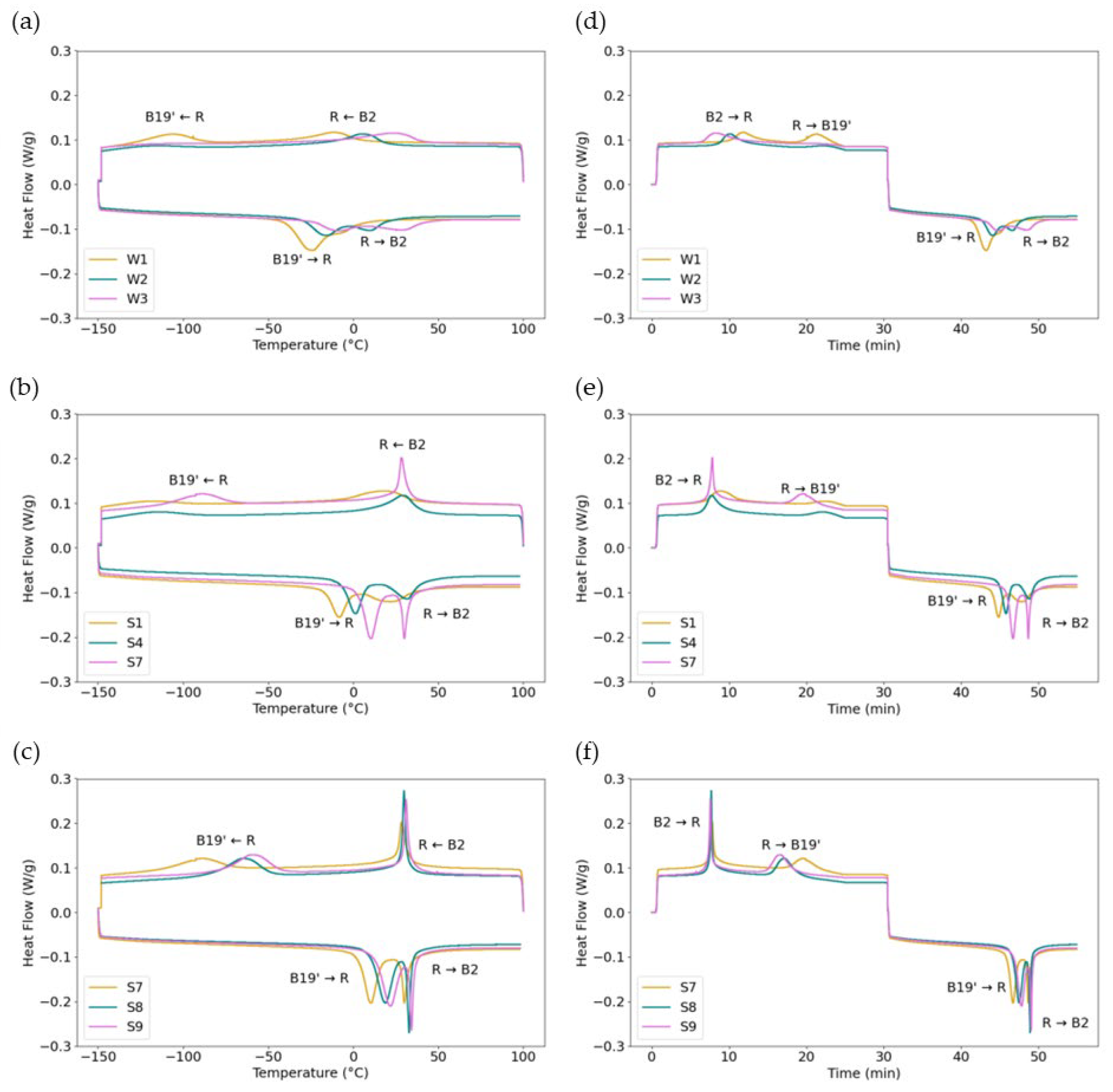
3.3. Phase Transformation Temperatures and DSC Results
3.3.1. DSC Peak Analysis
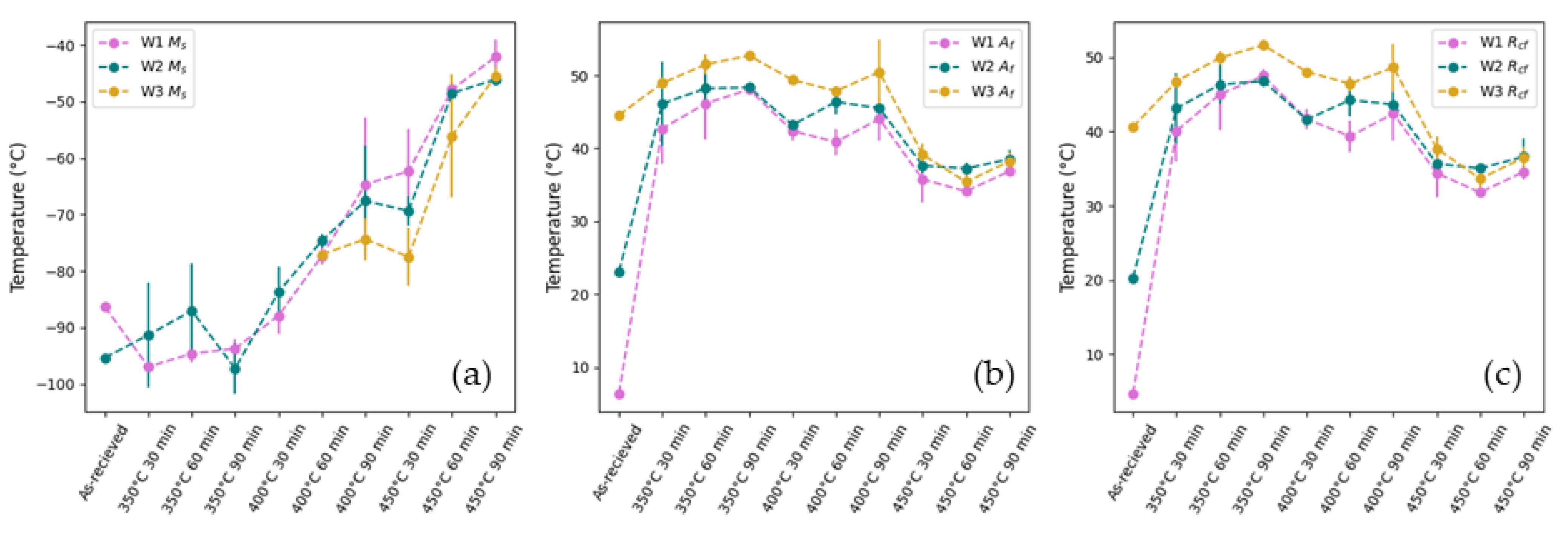
3.3.2. Transformation Temperatures
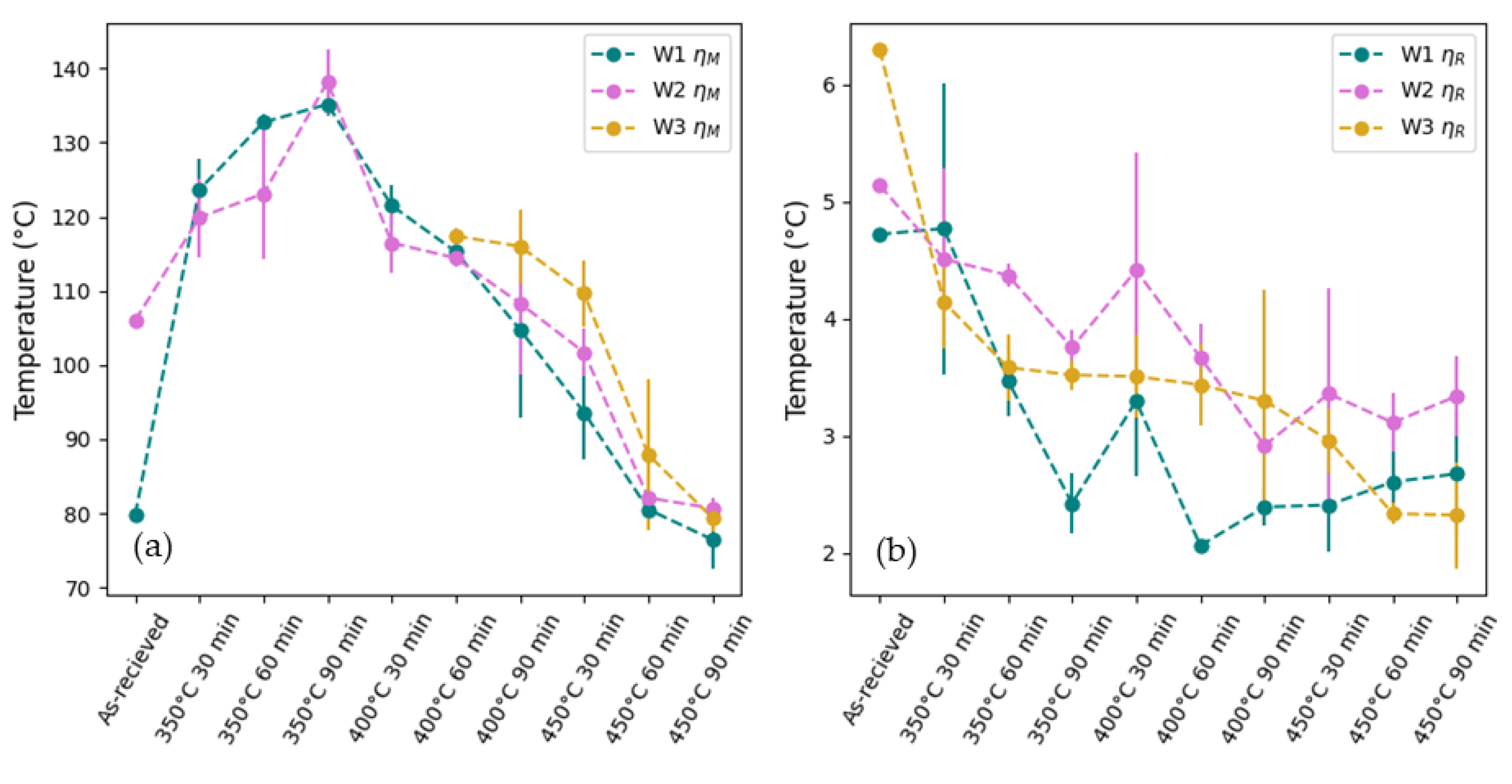
3.3.3. Thermal Hysteresis
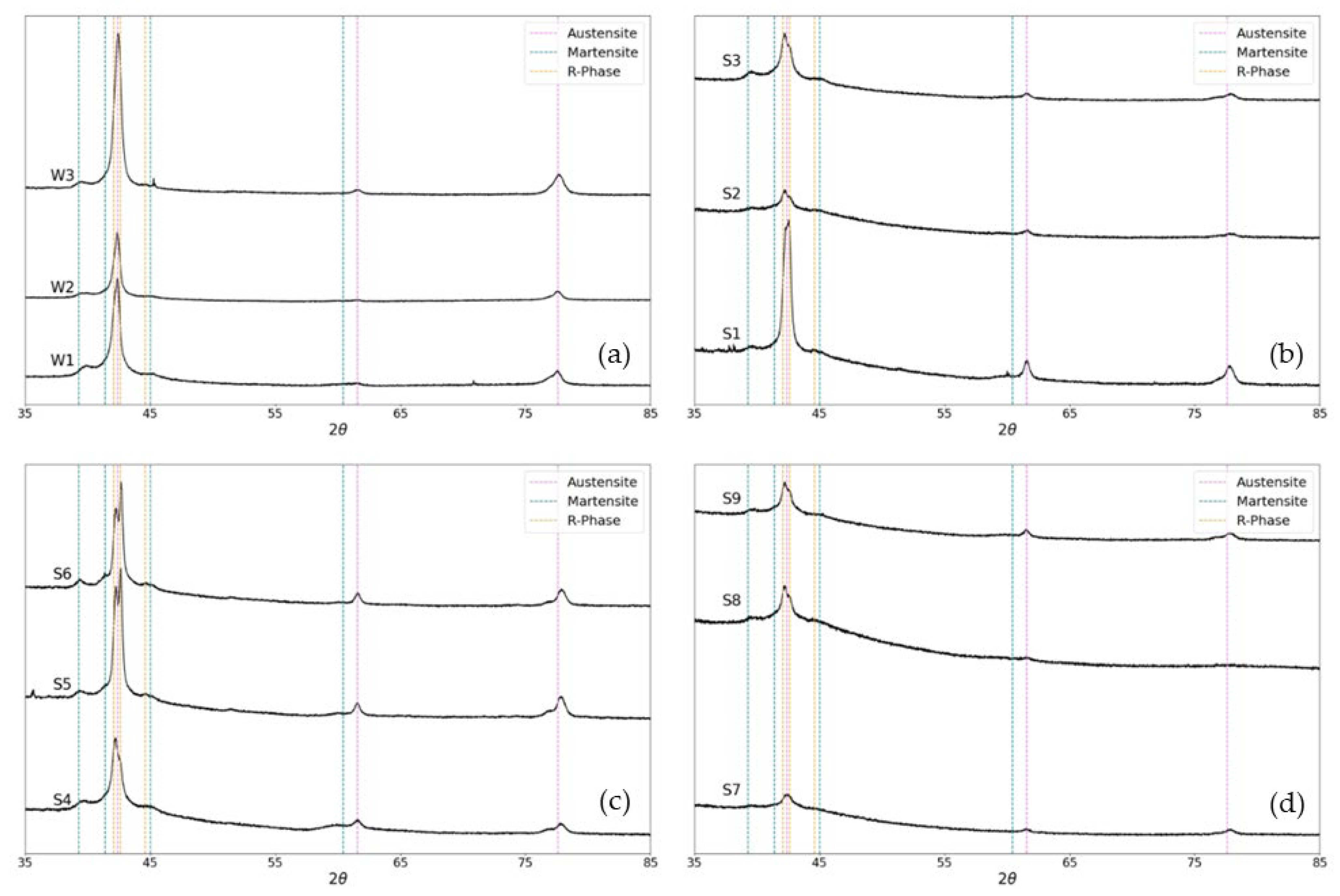
3.4. Phase and Microstructural Analysis
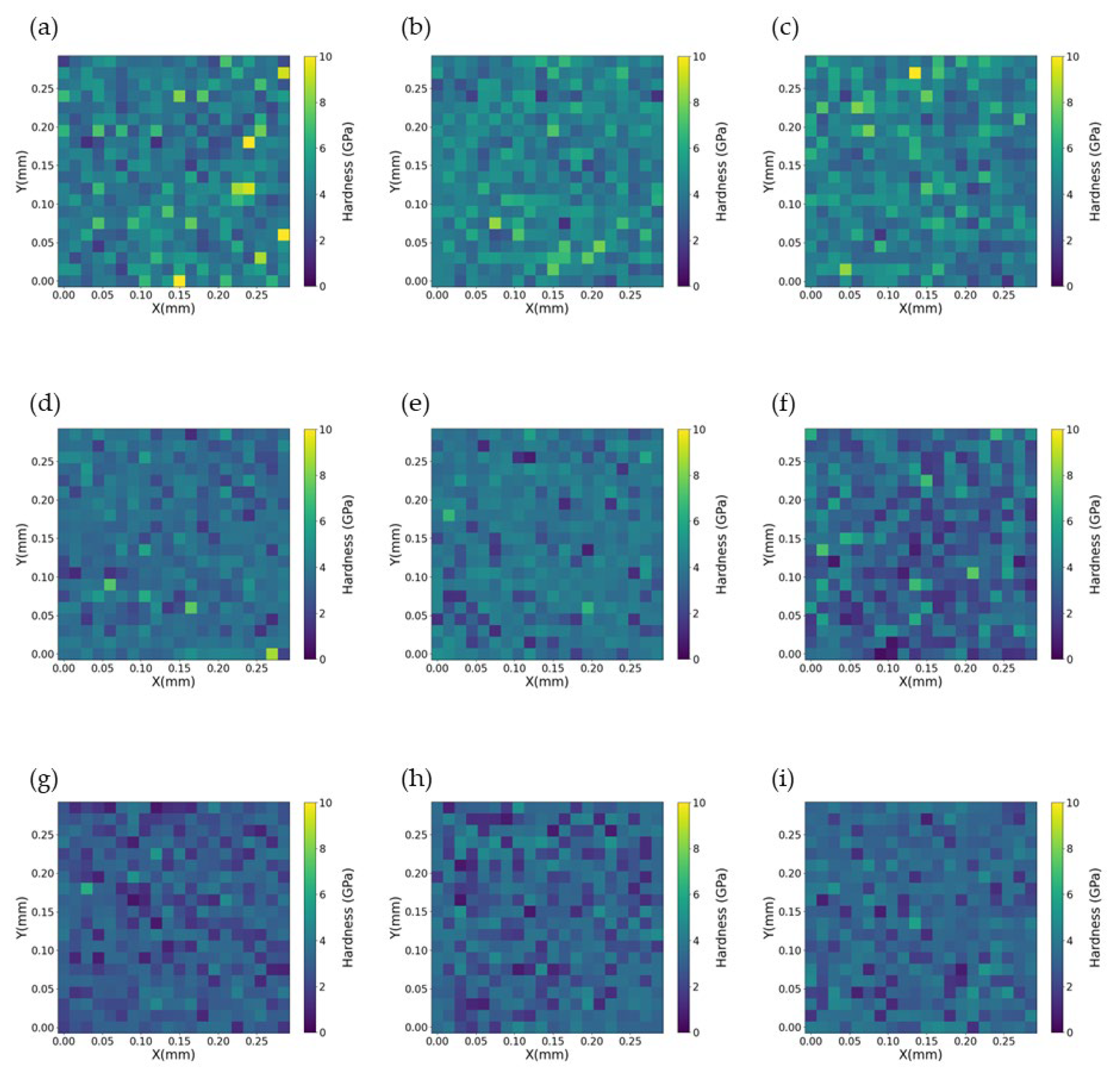
3.5. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kujala, S.; Pajala, A.; Kallioinen, M.; Pramila, A.; Tuukkanen, J.; Ryhänen, J. Biocompatibility and strength properties of nitinol shape memory alloy suture in rabbit tendon. Biomaterials 2004, 25, 353–358. [Google Scholar] [CrossRef] [PubMed]
- McNaney, J.M.; Imbeni, V.; Jung, Y.; Papadopoulos, P.; Ritchie, R.O. An experimental study of the superelastic effect in a shape-memory Nitinol alloy under biaxial loading. Mech. Mater. 2003, 35, 969–986. [Google Scholar] [CrossRef]
- Wang, Z.; Everaerts, J.; Salvati, E.; Korsunsky, A.M. Evolution of thermal and mechanical properties of Nitinol wire as a function of ageing treatment conditions. J. Alloys Compd. 2020, 819, 153024. [Google Scholar] [CrossRef]
- El Naggar, A.; Youssef, M.A. Shape memory alloy heat activation: State of the art review. AIMS Mater. Sci. 2020, 7, 836–858. [Google Scholar] [CrossRef]
- Reedlunn, B.; Daly, S.; Shaw, J. Superelastic shape memory alloy cables: Part I–Isothermal tension experiments. Int. J. Solids Struct. 2013, 50, 3009–3026. [Google Scholar] [CrossRef]
- Nespoli, A. The high potential of shape memory alloys in developing miniature mechanical devices: A review on shape memory alloy mini-actuators. Sens. Actuators A Phys. 2010, 158, 149–160. [Google Scholar] [CrossRef]
- Haberland, C.; Elahinia, M.; Walker, J.; Meier, H. Visions, Concepts and Strategies for Smart Nitinol Actuators and Complex Nitinol Structures Produced by Additive Manufacturing. In Volume 1: Development and Characterization of Multifunctional Materials; Modeling, Simulation and Control of Adaptive Systems; Integrated System Design and Implementation, Proceedings of the ASME 2013 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, Snowbird, UT, USA, 16–18 September 2013; American Society of Mechanical Engineers: Snowbird, UT, USA, 2013; p. V001T01A006. [Google Scholar] [CrossRef]
- Chekotu, J.; Groarke, R.; O’Toole, K.; Brabazon, D. Advances in Selective Laser Melting of Nitinol Shape Memory Alloy Part Production. Materials 2019, 12, 809. [Google Scholar] [CrossRef]
- Wen, S.; Liu, Y.; Zhou, Y.; Zhao, A.; Yan, C.; Shi, Y. Effect of Ni content on the transformation behavior and mechanical property of NiTi shape memory alloys fabricated by laser powder bed fusion. Opt. Laser Technol. 2021, 134, 106653. [Google Scholar] [CrossRef]
- Frenzel, J.; George, E.P.; Dlouhy, A.; Somsen, C.; Wagner, M.F.-X.; Eggeler, G. Influence of Ni on martensitic phase transformations in NiTi shape memory alloys. Acta Mater. 2010, 58, 3444–3458. [Google Scholar] [CrossRef]
- Jahanbazi Asl, J.; Kadkhodaei, M.; Karimzadeh, F. The effects of shape-setting on transformation temperatures of pseudoelastic shape memory alloy springs. J. Sci. Adv. Mater. Devices 2019, 4, 568–576. [Google Scholar] [CrossRef]
- Casati, R.; Tuissi, A.; Belochapkine, S.; Dickinson, C.; Tofail, S.A.M. Thin NiTi Wires with Reduced Thermal Hysteresis for Shape Memory Actuators. Funct. Mater. Lett. 2012, 5, 1250009. [Google Scholar] [CrossRef]
- Patel, M.; Plumley, D.; Bouthot, R.; Proft, J. The Effects of Varying Active Af Temperatures on the Fatigue Properties of Nitinol Wire. In Proceedings of the ASM Materials & Processes for Medical Devices Conference and Exposition (MDMD), Boston, MA, USA, 14–16 November 2005. [Google Scholar]
- Lygin, K.; Langbein, S.; Labenda, P.; Sadek, T. A Methodology for the Development, Production, and Validation of R-Phase Actuators. J. Mater. Eng. Perform. 2012, 21, 2657–2662. [Google Scholar] [CrossRef]
- Luo, Y.; Takagi, T.; Maruyama, S.; Yamada, M. A Shape Memory Alloy Actuator Using Peltier Modules and R-Phase Transition. J. Intell. Mater. Syst. Struct. 2000, 11, 503–511. [Google Scholar] [CrossRef]
- Gallardo Fuentes, J.M.; Gümpel, P.; Strittmatter, J. Phase Change Behavior of Nitinol Shape Memory Alloys. Adv. Eng. Mater. 2002, 4, 437–452. [Google Scholar] [CrossRef]
- Spaggiari, A.; Dragoni, E.; Tuissi, A. NiTi Alloy Negator Springs for Long-Stroke Constant-Force Shape Memory Actuators: Modeling, Simulation and Testing. J. Mater. Eng. Perform. 2014, 23, 2412–2419. [Google Scholar] [CrossRef]
- Benafan, O.; Brown, J.; Calkins, F.T.; Stebner, A.P.; Turner, T.L.; Vaidyanath, R.; Webster, J.; Young, M.L.; Young, M.L. Shape memory alloy actuator design: CASMART collaborative best practices and case studies. Int. J. Mech. Mater. Des. 2014, 10, 1–42. [Google Scholar] [CrossRef]
- Gédouin, P.-A.; Pino, L.; Chirani, S.A.; Calloch, S.; Delaleau, E.; Bourgeot, J.-M. R-phase shape memory alloy helical spring based actuators: Modeling and experiments. Sens. Actuators Phys. 2019, 289, 65–76. [Google Scholar] [CrossRef]
- Favier, D.; Liu, Y.; Orgéas, L.; Sandel, A.; Debove, L.; Comte-Gaz, P. Influence of thermomechanical processing on the superelastic properties of a Ni-rich Nitinol shape memory alloy. Mater. Sci. Eng. A 2006, 429, 130–136. [Google Scholar] [CrossRef]
- Benafan, O.; Padula, S.A.; Noebe, R.D.; Brown, D.W.; Clausen, B.; Vaidyanathan, R. An in situ neutron diffraction study of shape setting shape memory NiTi. Acta Mater. 2013, 61, 3585–3599. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Yang, D.; Qi, M. The effect of ageing treatment on shape-setting and superelasticity of a nitinol stent. Mater. Charact. 2008, 59, 402–406. [Google Scholar] [CrossRef]
- Assawakawintip, T.; Santiwong, P.; Khantachawana, A.; Sipiyaruk, K.; Chintavalakorn, R. The Effects of Temperature and Time of Heat Treatment on Thermo-Mechanical Properties of Custom-Made NiTi Orthodontic Closed Coil Springs. Materials 2022, 15, 3121. [Google Scholar] [CrossRef] [PubMed]
- Choi, E.; Ostadrahimi, A.; Park, J. On mechanical properties of NiTi SMA wires prestrained by cold rolling. Smart Mater. Struct. 2020, 29, 065009. [Google Scholar] [CrossRef]
- Li, G.; Yu, T.; Zhang, N.; Chen, M. The effect of Ni content on phase transformation behavior of NiTi alloys: An atomistic modeling study. Comput. Mater. Sci. 2022, 215, 111804. [Google Scholar] [CrossRef]
- De Oliveira, S.; Silva, S.A.; Souto, C.R.; Ries, A. Experimental Characterization and Control of a Force Actuator Based on Shape Memory Alloy Wire. J. Control Autom. Electr. Syst. 2018, 29, 670–676. [Google Scholar] [CrossRef]
- Costanza, G.; Tata, M.E.; Calisti, C. Nitinol one-way shape memory springs: Thermomechanical characterization and actuator design. Sens. Actuators Phys. 2010, 157, 113–117. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Nanoindentation. In Mechanical Engineering Series; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Farber, E.; Orlov, A.; Borisov, E.; Repnin, A.; Kuzin, S.; Golubkov, N.; Popovich, A. TiNi Alloy Lattice Structures with Negative Poisson’s Ratio: Computer Simulation and Experimental Results. Metals 2022, 12, 1476. [Google Scholar] [CrossRef]
- Jian, S.-R.; Chen, G.-J.; Lin, T.-C. Berkovich Nanoindentation on AlN Thin Films. Nanoscale Res. Lett. 2010, 5, 935–940. [Google Scholar] [CrossRef]
- Zhan, Y.; He, L.; Lu, X.; Zhu, X.; Chen, Q. The Effect of Ageing Treatment on Shape-Setting and Shape Memory Effect of a NiTi SMA Corrugated Structure. Adv. Mater. Sci. Eng. 2020, 2020, 2846721. [Google Scholar] [CrossRef]
- Miyazaki, S.; Otsuka, K. Deformation and transition behavior associated with the R-phase in Ti-Ni alloys. Metall. Trans. A 1986, 17, 53–63. [Google Scholar] [CrossRef]
- Vollach, S.; Shilo, D.; Shlagman, H. Mechanical Response of Shape Memory Alloys Under a Rapid Heating Pulse—Part II. Exp. Mech. 2016, 56, 1465–1475. [Google Scholar] [CrossRef]
- Motzki, P.; Gorges, T.; Kappel, M.; Schmidt, M.; Rizzello, G.; Seelecke, S. High-speed and high-efficiency shape memory alloy actuation. Smart Mater. Struct. 2018, 27, 075047. [Google Scholar] [CrossRef]
- Salman, K.D. Manufacture of shape memory alloys NiTi and NiTiCu by casting method and studying the effect of adding the copper element in different proportions to the binary alloy on the microstructure, phase transformations and conductivity. J. Phys. Conf. Ser. 2021, 1973, 012108. [Google Scholar] [CrossRef]
- Duerig, T.W.; Bhattacharya, K. The Influence of the R-Phase on the Superelastic Behavior of NiTi. Shape Mem. Superelast. 2015, 1, 153–161. [Google Scholar] [CrossRef]
- Uchil, J.; Kumara, K.G.; Mahesh, K.K. Effect of thermal cycling on R-phase stability in a NiTi shape memory alloy. Mater. Sci. Eng. A 2002, 332, 25–28. [Google Scholar] [CrossRef]
- Yan, K.; Yang, S.; Xu, J.; Ren, F.; Sun, Q. Effects of Gradient Annealing on the Microstructure and Rate-Dependent Thermomechanical Behavior of Nanocrystalline NiTi Shape Memory Alloy. Shape Mem. Superelast. 2022, 8, 308–319. [Google Scholar] [CrossRef]
- Uchil, J.; Mohanchandra, K.P.; Mahesh, K.K.; Kumara, K.G. Thermal and electrical characterization of R-phase dependence on heat-treat temperature in Nitinol. Phys. B Condens. Matter 1998, 253, 83–89. [Google Scholar] [CrossRef]
- Pattabi, M.; Murari, M.S. Effect of Cold Rolling on Phase Transformation Temperatures of NiTi Shape Memory Alloy. J. Mater. Eng. Perform. 2015, 24, 556–564. [Google Scholar] [CrossRef]
- Wang, X.; Yu, J.; Liu, J.; Chen, L.; Yang, Q.; Wei, H.; Sun, J.; Wang, Z.; Zhang, Z.; Zhao, G.; et al. Effect of process parameters on the phase transformation behavior and tensile properties of NiTi shape memory alloys fabricated by selective laser melting. Addit. Manuf. 2020, 36, 101545. [Google Scholar] [CrossRef]
- Morawiec, H.; Stróz, D.; Chrobak, D. Effect of Deformation and Thermal Treatment of NiTi Alloy on Transition Sequence. J. Phys. IV 1995, 5, C2-205–C2-210. [Google Scholar] [CrossRef][Green Version]
- Sadiq, H.; Wong, M.B.; Al-Mahaidi, R.; Zhao, X.L. The effects of heat treatment on the recovery stresses of shape memory alloys. Smart Mater. Struct. 2010, 19, 035021. [Google Scholar] [CrossRef]
- Choi, E.; Kim, Y.-W.; Chung, Y.-S.; Yang, K.-T. Bond strength of concrete confined by SMA wire jackets. Phys. Procedia 2010, 10, 210–215. [Google Scholar] [CrossRef][Green Version]
- Dos Santos Paula, A.; Mahesh, K.K.; Fernandes, F.M.B. Stability in Phase Transformation After Multiple Steps of Marforming in Ti-Rich Ni-Ti Shape Memory Alloy. J. Mater. Eng. Perform. 2011, 20, 771–775. [Google Scholar] [CrossRef]
- Drexel, M.J.; Selvaduray, G.S.; Pelton, A.R. The Effects of Cold Work and Heat Treatment on the Properties of Nitinol Wire. In Proceedings of the ASME 2007 2nd Frontiers in Biomedical Devices Conference, Irvine, CA, USA, 7–8 June 2007; pp. 88–89. [Google Scholar]
- Kaya, I.; Karaca, H.E.; Nagasako, M.; Kainuma, R. Effects of aging temperature and aging time on the mechanism of martensitic transformation in nickel-rich NiTi shape memory alloys. Mater. Charact. 2020, 159, 110034. [Google Scholar] [CrossRef]
- Wang, X.B.; Verlinden, B.; Van Humbeeck, J. R-phase transformation in NiTi alloys. Mater. Sci. Technol. 2014, 30, 1517–1529. [Google Scholar] [CrossRef]
- Sehitoglu, H.; Hamilton, R.; Maier, H.J.; Chumlyakov, Y. Hysteresis in NiTi alloys. J. Phys. IV Proc. 2004, 115, 3–10. [Google Scholar] [CrossRef]
- Mitwally, M.E.; Farag, M. Effect of cold work and annealing on the structure and characteristics of NiTi alloy. Mater. Sci. Eng. A 2009, 519, 155–166. [Google Scholar] [CrossRef]
- Yang, Z.; Tirry, W.; Lamoen, D.; Kulkova, S.; Schryvers, D. Electron energy-loss spectroscopy and first-principles calculation studies on a Ni–Ti shape memory alloy. Acta Mater. 2008, 56, 395–404. [Google Scholar] [CrossRef]
- Monu, M.C.C.; Kumar, S.S.; Brabazon, D. Heat treatment of NiTi alloys: Influence of volumetric energy density on ageing parameters and the resulting physical properties. J. Mater. Res. Technol. 2023, 26, 9532–9555. [Google Scholar] [CrossRef]
- Kumar, S.S.; Marandi, L.; Balla, V.K.; Bysakh, S.; Piorunek, D.; Eggeler, G.; Das, M.; Sen, I.S. Microstructure—Property correlations for additively manufactured NiTi based shape memory alloys. Materialia 2019, 8, 100456. [Google Scholar] [CrossRef]
- Kumar, S.S.; Kumar, I.A.; Marandi, L.; Sen, I. Assessment of small-scale deformation characteristics and stress-strain behavior of NiTi based shape memory alloy using nanoindentation. Acta Mater. 2020, 201, 303–315. [Google Scholar] [CrossRef]
- Obeidi, M.A. Achieving high quality nitinol parts with minimised input thermal energy by optimised pulse wave laser powder bed fusion process. Results Mater. 2022, 14, 100279. [Google Scholar] [CrossRef]
- Huang, X.; Nohava, J.; Zhang, B.; Ramirez, A.G. Nanoindentation of NiTi shape memory thin films at elevated temperatures. Int. J. Smart Nano Mater. 2011, 2, 39–49. [Google Scholar] [CrossRef]
- Wagner, M.F.-X.; Windl, W. Elastic anisotropy of Ni4Ti3 from first principles. Scr. Mater. 2009, 60, 207–210. [Google Scholar] [CrossRef]
- Adharapurapu, R.R.; Jiang, F.; Vecchio, K.S. Aging effects on hardness and dynamic compressive behavior of Ti–55Ni (at.%) alloy. Mater. Sci. Eng. A 2010, 527, 1665–1676. [Google Scholar] [CrossRef]
- Tahaei, A.; Aghajani, A.; Abbasi, M.; Bagheri, B.; Merlin, M.; Garagnani, G.L. Effects of Predefined Thermomechanical Procedure on the Microstructure and Mechanical Properties of the Two-Way Shape Memory Effect in the NiTi Alloy. Adv. Mater. Sci. Eng. 2023, 2023, 1524836. [Google Scholar] [CrossRef]
- Frick, C.P.; Ortega, A.M.; Tyber, J.; Maksound, A.; Maier, H.J.; Liu, Y.; Gall, K. Thermal processing of polycrystalline NiTi shape memory alloys. Mater. Sci. Eng. A 2005, 405, 34–49. [Google Scholar] [CrossRef]


| Level | −1 | 0 | +1 |
| Starting Wire | W1 | W2 | W3 |
| Treatment Temperature (°C) | 350 | 400 | 450 |
| Treatment Time (min) | 30 | 60 | 90 |
| Sample Name | Starting Wire | Heat Treatment Temperature (°C) | Heat Treatment Time (min) |
|---|---|---|---|
| S1 | W1 | 350 | 30 |
| S2 | W1 | 350 | 60 |
| S3 | W1 | 350 | 90 |
| S4 | W1 | 400 | 30 |
| S5 | W1 | 400 | 60 |
| S6 | W1 | 400 | 90 |
| S7 | W1 | 450 | 30 |
| S8 | W1 | 450 | 60 |
| S9 | W1 | 450 | 90 |
| S10 | W2 | 350 | 30 |
| S11 | W2 | 350 | 60 |
| S12 | W2 | 350 | 90 |
| S13 | W2 | 400 | 30 |
| S14 | W2 | 400 | 60 |
| S15 | W2 | 400 | 90 |
| S16 | W2 | 450 | 30 |
| S17 | W2 | 450 | 60 |
| S18 | W2 | 450 | 90 |
| S19 | W3 | 350 | 30 |
| S20 | W3 | 350 | 60 |
| S21 | W3 | 350 | 90 |
| S22 | W3 | 400 | 30 |
| S23 | W3 | 400 | 60 |
| S24 | W3 | 400 | 90 |
| S25 | W3 | 450 | 30 |
| S26 | W3 | 450 | 60 |
| S27 | W3 | 450 | 90 |
| Sample | E (GPa) | H (GPa) |
|---|---|---|
| W1 (as-received) | 55.8 ± 12.5 | 4.17 ± 1.36 |
| S3 (W1, 350 °C, 90 min) | 65.5 ± 10.5 | 3.52 ± 0.83 |
| S8 (W1, 450 °C, 60 min) | 60.7 ± 11.5 | 2.79 ± 0.84 |
| W2 (as-received) | 59.20 ± 8.81 | 4.34 ± 1.01 |
| S12 (W2, 350 °C, 90 min) | 64.80 ± 9.44 | 3.73 ± 0.84 |
| S17 (W2, 450 °C, 60 min) | 60.4 ± 12.6 | 3.06 ± 0.96 |
| W3 (as-received) | 59.9 ± 10.2 | 4.24 ± 1.13 |
| S21 (W3, 350 °C, 90 min) | 56.1 ± 14.3 | 3.16 ± 1.18 |
| S26 (W3, 450 °C, 60 min) | 60.5 ± 10.5 | 3.20 ± 0.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ryan Murphy, J.; Obeidi, M.A.; Ahad, I.U.; Brabazon, D. Investigating the Effect of Wire Drawing and Heat Treatment on the Response of Ni50.9Ti49.1 R-Phase Actuators. Materials 2025, 18, 4931. https://doi.org/10.3390/ma18214931
Ryan Murphy J, Obeidi MA, Ahad IU, Brabazon D. Investigating the Effect of Wire Drawing and Heat Treatment on the Response of Ni50.9Ti49.1 R-Phase Actuators. Materials. 2025; 18(21):4931. https://doi.org/10.3390/ma18214931
Chicago/Turabian StyleRyan Murphy, Josephine, Muhannad Ahmed Obeidi, Inam Ul Ahad, and Dermot Brabazon. 2025. "Investigating the Effect of Wire Drawing and Heat Treatment on the Response of Ni50.9Ti49.1 R-Phase Actuators" Materials 18, no. 21: 4931. https://doi.org/10.3390/ma18214931
APA StyleRyan Murphy, J., Obeidi, M. A., Ahad, I. U., & Brabazon, D. (2025). Investigating the Effect of Wire Drawing and Heat Treatment on the Response of Ni50.9Ti49.1 R-Phase Actuators. Materials, 18(21), 4931. https://doi.org/10.3390/ma18214931