Experimental and DEM Study on the Mechanical Behaviors of Sand–Fines Mixtures with Different Fines Contents and Particle Size Ratios
Abstract
1. Introduction
2. Materials and Testing Program
2.1. Testing Materials
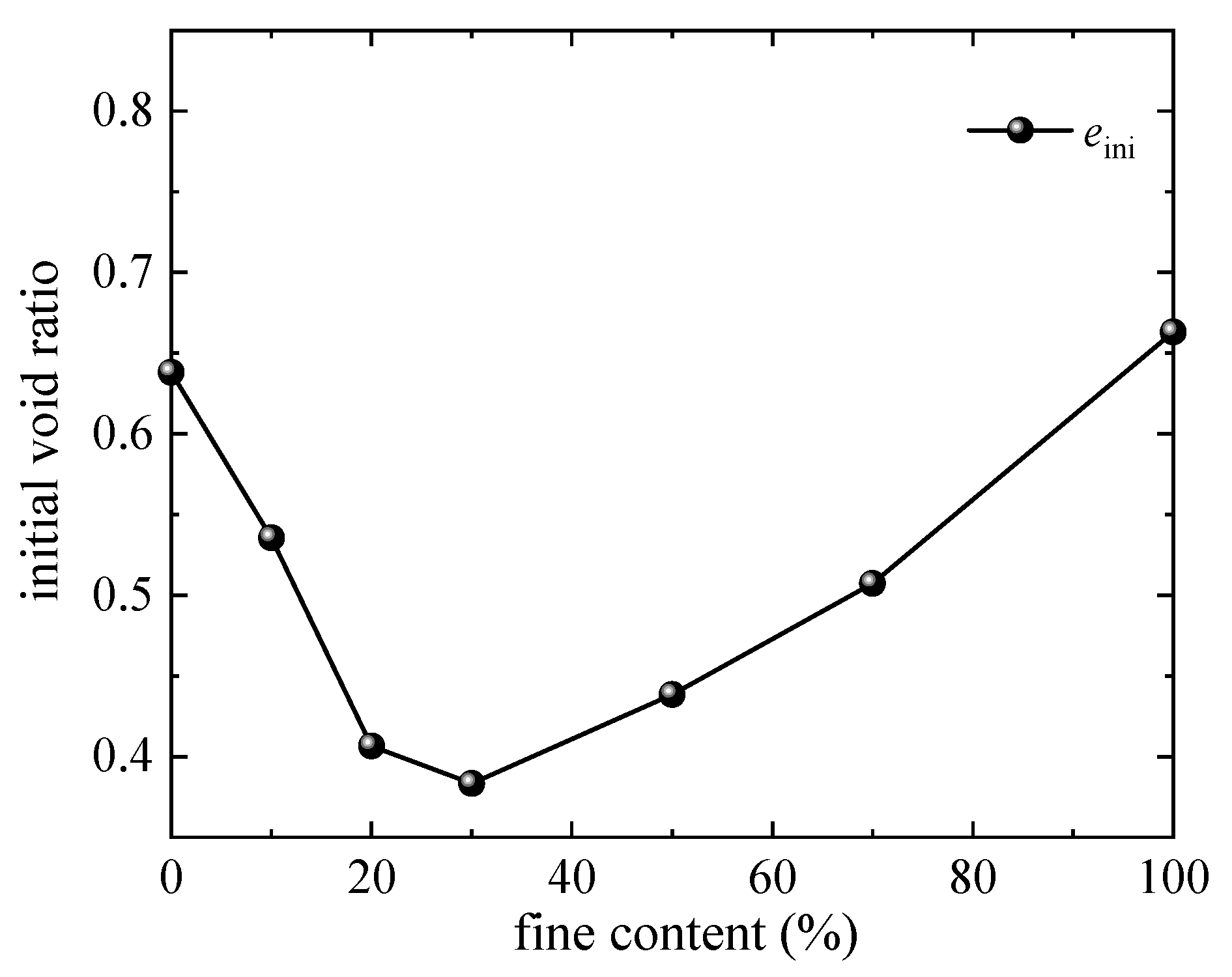
2.2. Testing Procedure
3. Testing Results
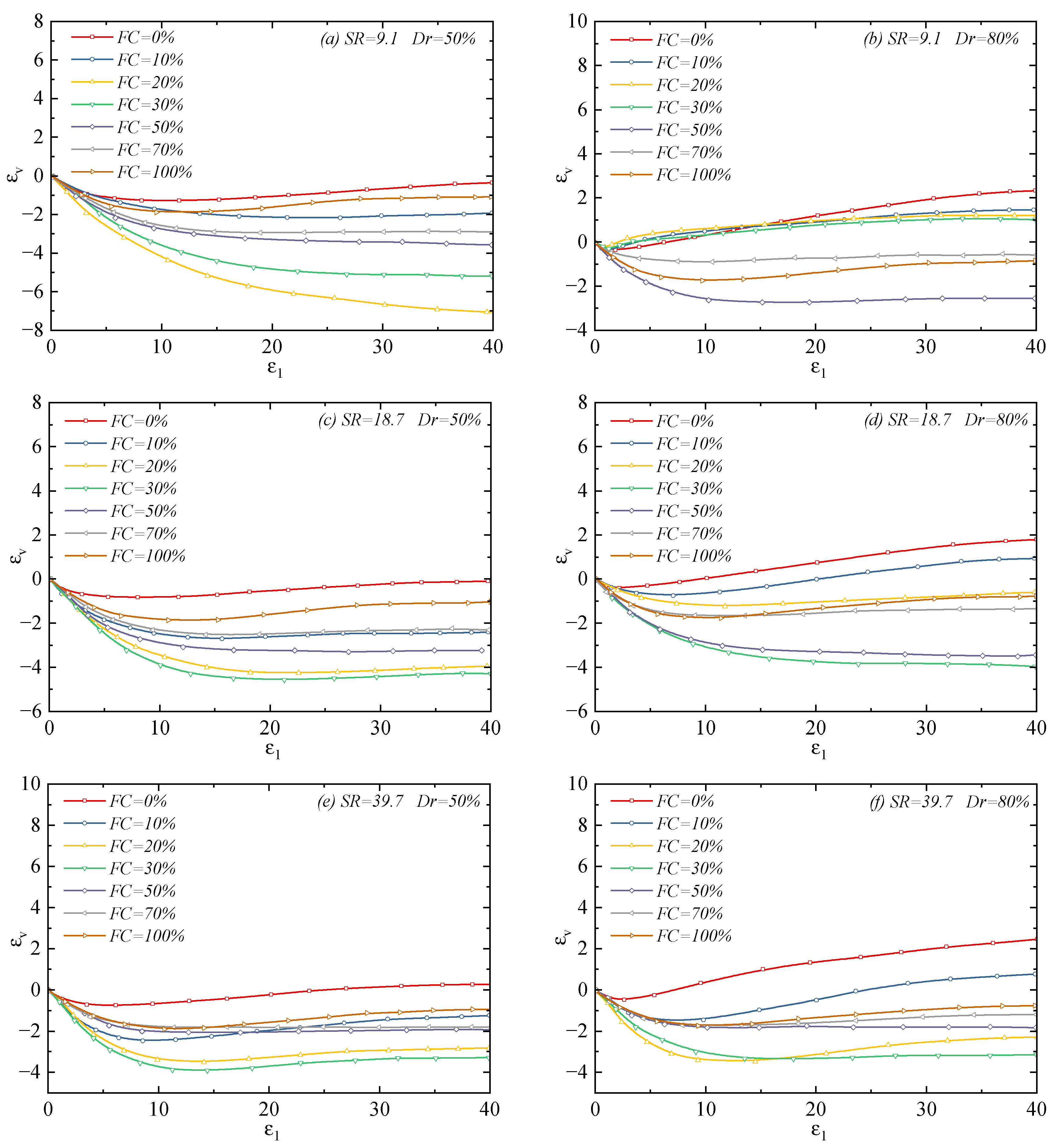
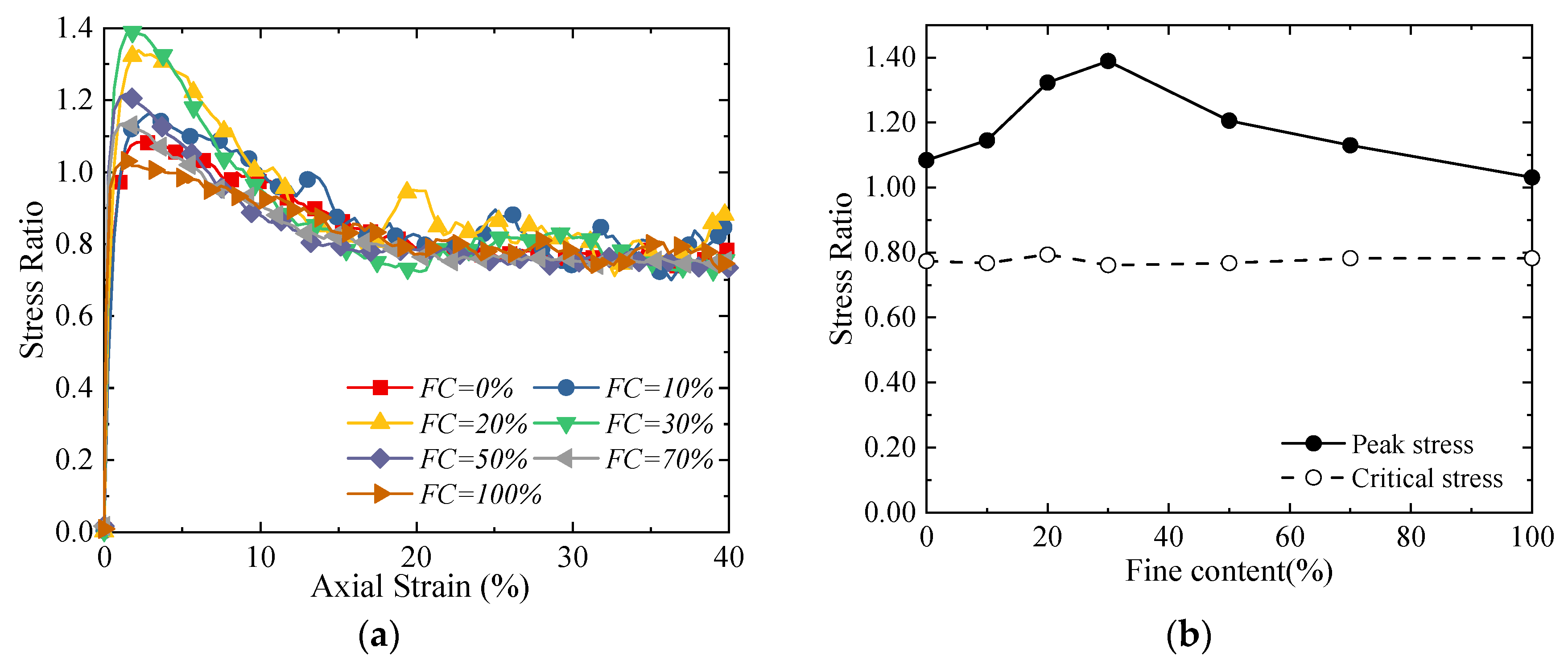
3.1. Stress–Strain and Volumetric Change Responses
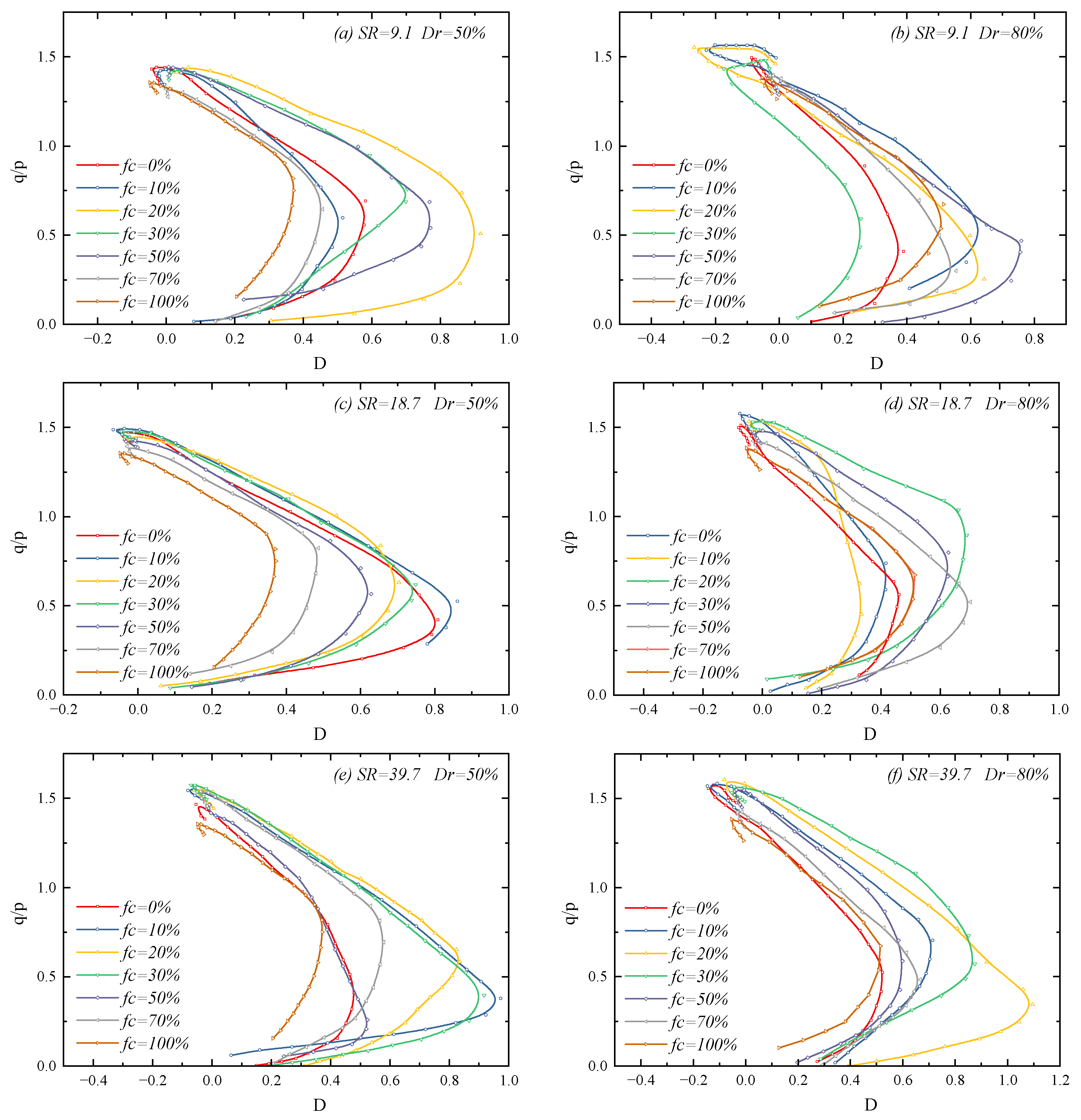
3.2. Stress–Dilatancy Relationship
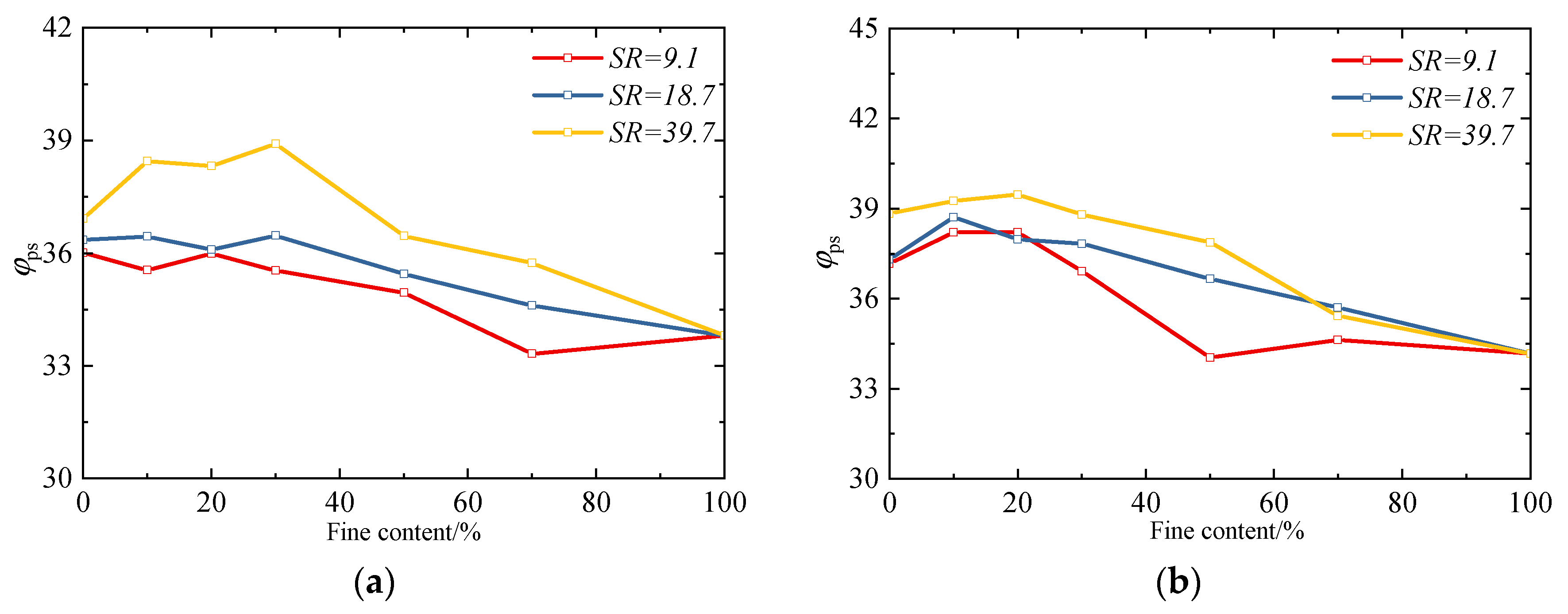
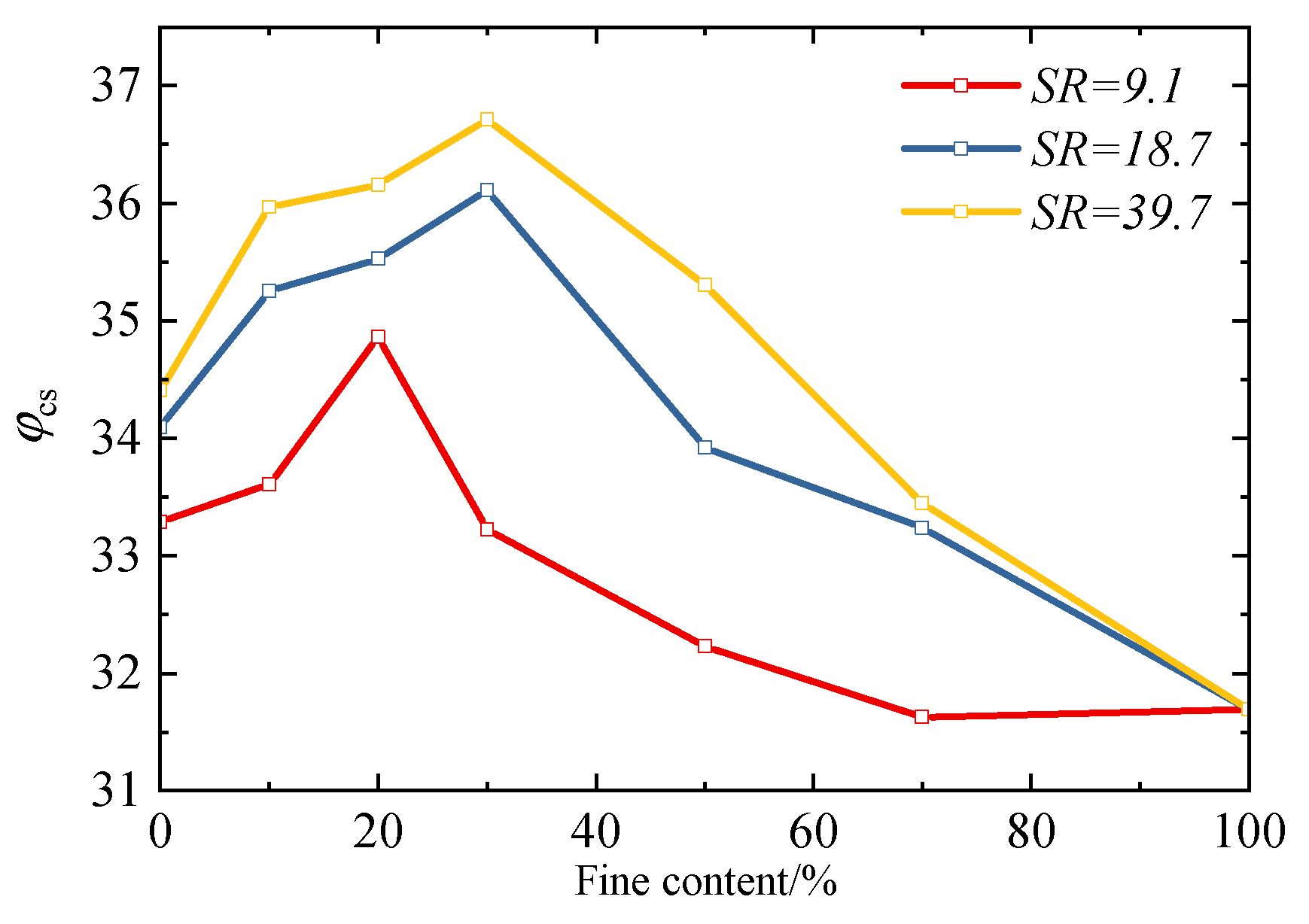
3.3. Peak State Friction Angle
3.4. Critical-State Friction Angle
4. DEM Modeling
4.1. Contact Model
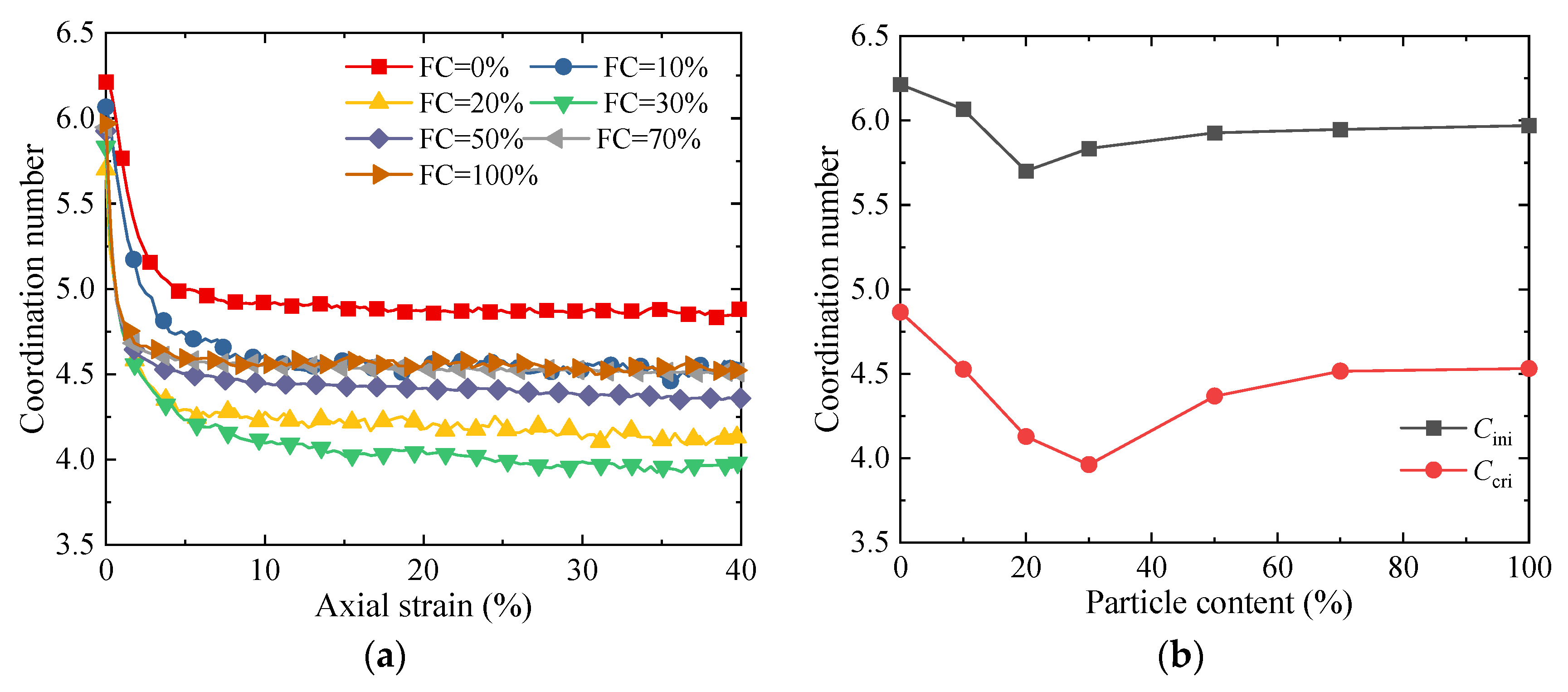
4.2. Analysis of Micro-Mechanical Responses
5. Conclusions
- (1)
- Both the peak friction angle (φps) and critical-state friction angle (φcs) of sand–silt mixtures exhibit a trend of “first increase, and then decrease” with an increasing fines content. The peak inflection point of their variation curves corresponds to the threshold fines content. When the FC is below the threshold, fines fill the pores of coarse particles and enhance inter-particle interlocking, thereby improving the strength; when the FC exceeds the threshold, excessive fines disrupt the force-transmitting skeleton of coarse particles, leading to strength attenuation. Moreover, the smaller the SR, the lower the threshold FC, and the narrower the transitional range of the FC on the strength. Specifically, the threshold FC of mixtures with SR = 9.1 is approximately 10% lower than that of mixtures with SR = 18.1 and 39.7, and its transitional range of the FC is also approximately 10% narrower than theirs.
- (2)
- The fines contents and size ratio jointly regulate the deformation mode of the mixtures: when the FC is below the threshold, the contraction behaviors of the mixtures becomes more significant with an increasing FC, while dilatancy is inhibited; when the FC is above the threshold, dilatancy gradually strengthens with an increasing FC. Additionally, mixtures with a smaller SR show more significant post-peak stress softening and greater dilatancy in the low FC range: Mixtures with SR = 9.1 exhibit more significant post-peak stress softening with a softening amplitude of 15–20% and greater dilatancy with a dilatancy ratio of 0.8–1.2; in contrast, mixtures with SR = 39.7 display weaker post-peak stress softening with a softening amplitude of only 5–8% and smaller dilatancy with a dilatancy ratio of 0.2–0.5.
- (3)
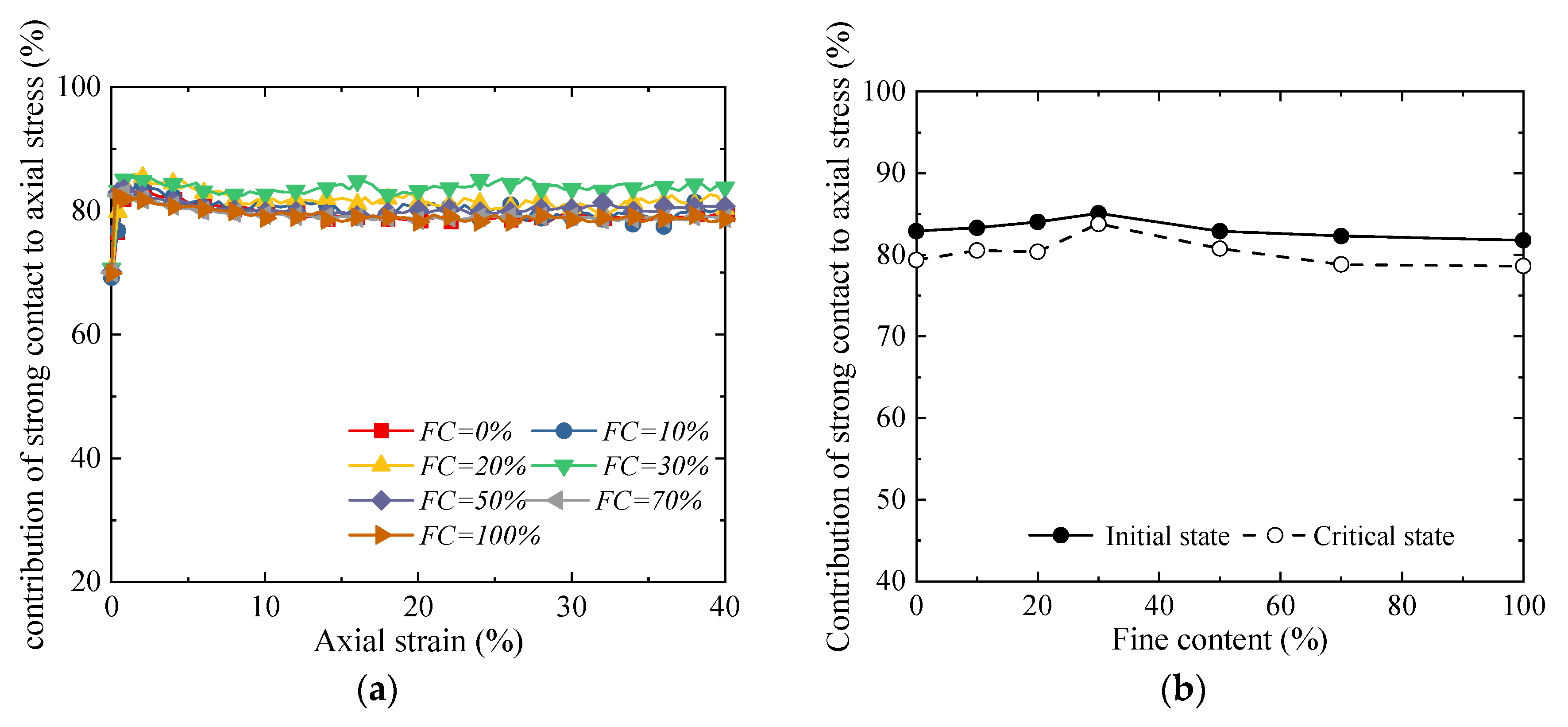
- The results from microscopic simulations indicate that, when the fines content is approximately 30%, although the proportion of strong contacts is the lowest, their contribution to the axial stress is the highest. Meanwhile, a large number of weak contacts form a stable lateral support, effectively constraining the deformation of the strong contact skeleton. At this point, the coordination between load-bearing and support within the material is achieved, resulting in the peak macroscopic strength.
- (4)
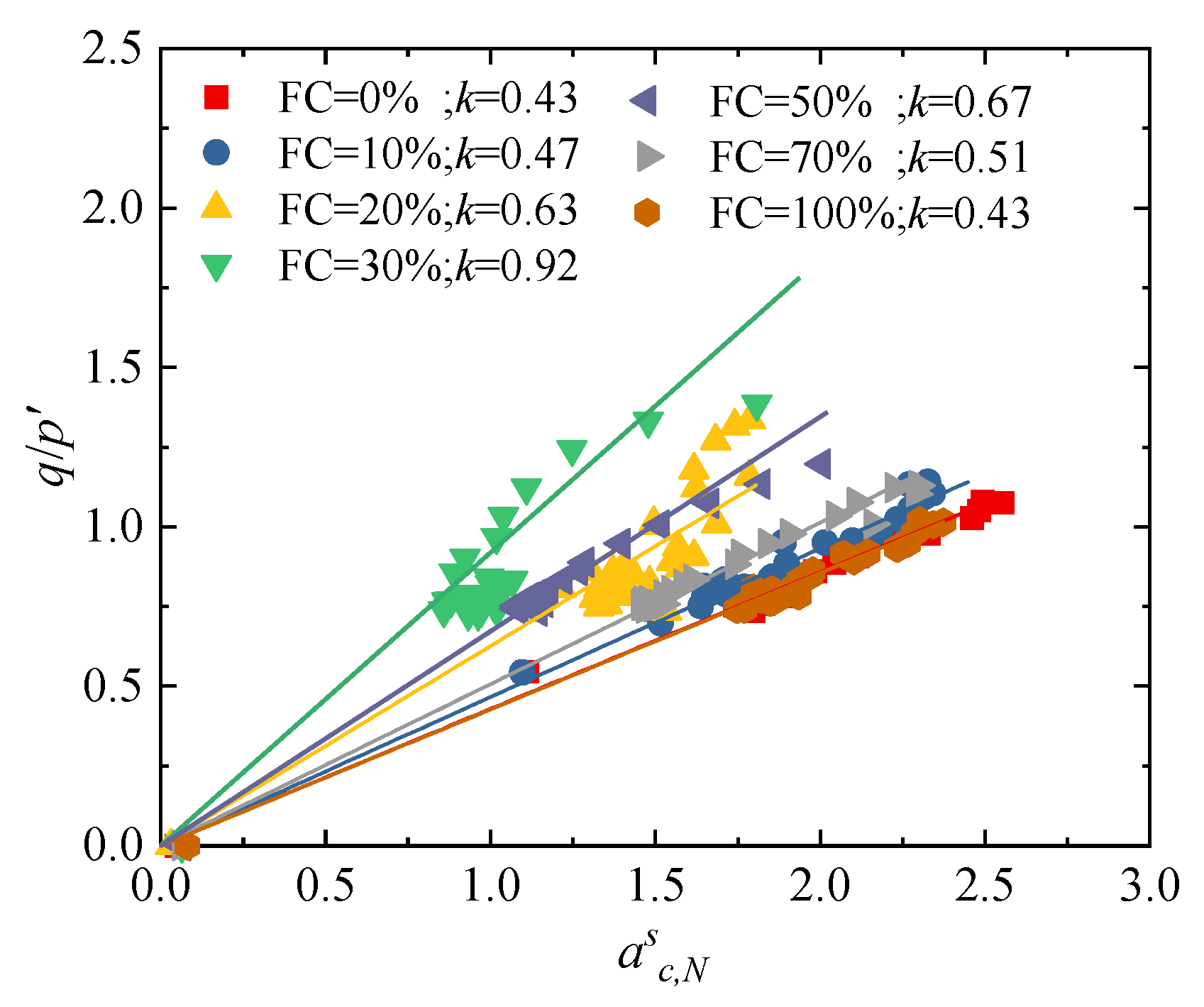
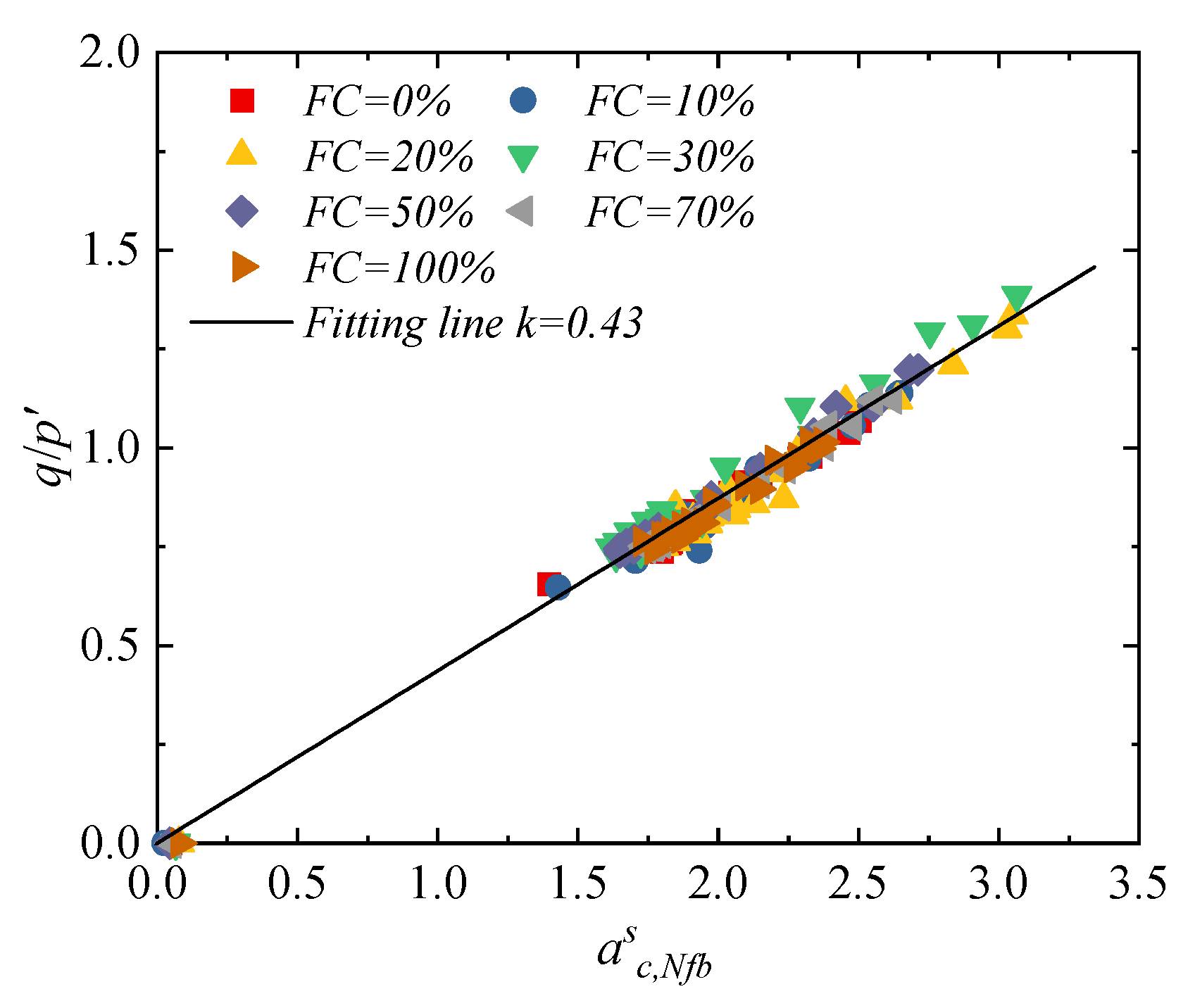
- By considering the influence of the contact number, average normal contact force, and average branch vector length on the weight coefficient of fabric anisotropy, a unique linear relationship between the fabric anisotropy of strong contacts and the stress ratio is established. This indicates that, at the microscopic scale, the strong contact network plays a similar core role in sand–silt mixtures with different fines contents, providing a unified theoretical framework and evaluation criterion for exploring the microscopic essence of instability and failure in sand–silt mixtures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nikbakht, M.; Sarand, F.B.; Irani, A.E.; Bonab, M.H.; Azarafza, M.; Derakhshani, R. An Experimental Study for Swelling Effect on Repairing of Cracks in Fine-Grained Clayey Soils. Appl. Sci. 2022, 12, 8596. [Google Scholar] [CrossRef]
- Thevanayagam, S.; Shenthan, T.; Mohan, S.; Liang, J. Undrained Fragility of Clean Sands, Silty Sands, and Sandy Silts. J. Geotech. Geoenviron. Eng. 2002, 128, 849–859. [Google Scholar] [CrossRef]
- Carraro, J.A.H.; Prezzi, M.; Salgado, R. Shear Strength and Stiffness of Sands Containing Plastic or Nonplastic Fines. J. Geotech. Geoenviron. Eng. 2009, 135, 1167–1178. [Google Scholar] [CrossRef]
- Yilmaz, Y.; Deng, Y.B.; Chang, C.S.; Gokce, A. Strength-dilatancy and critical state behaviours of binary mixtures of graded sands influenced by particle size ratio and fines content. Géotechnique 2023, 73, 202–217. [Google Scholar] [CrossRef]
- Naeini, S.A.; Baziar, M.H. Effect of fines content on steady-state strength of mixed and layered samples of a sand. Soil Dyn. Earthq. Eng. 2004, 24, 181–187. [Google Scholar] [CrossRef]
- Zuo, L.; Baudet, B.A. Determination of the transitional fines content of sand-non plastic fines mixtures. Soils Found. 2015, 55, 213–219. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, Y.; Zhao, D. Instability of binary mixtures subjected to constant shear drained stress path: Insight from macro and micro perspective. Int. J. Numer. Anal. Methods Geomech. 2024, 48, 3997–4013. [Google Scholar] [CrossRef]
- Harehdasht, S.A.; Karray, M.; Hussien, M.N.; Chekired, M. Influence of Particle Size and Gradation on the Stress-Dilatancy Behavior of Granular Materials during Drained Triaxial Compression. Int. J. Geomech. 2017, 17, 04017077. [Google Scholar] [CrossRef]
- Gong, J.; Nie, Z.H.; Zhu, Y.G.; Liang, Z.Y.; Wang, X. Exploring the effects of particle shape and content of fines on the shear behavior of sand-fines mixtures via the DEM. Comput. Geotech. 2019, 106, 161–176. [Google Scholar] [CrossRef]
- Salgado, R.; Bandini, P.; Karim, A. Shear strength and stiffness of silty sand. J. Geotech. Geoenviron. Eng. 2000, 126, 451–462. [Google Scholar] [CrossRef]
- Ueda, T.; Matsushima, T.; Yamada, Y. Effect of particle size ratio and volume fraction on shear strength of binary granular mixture. Granul. Matter 2011, 13, 731–742. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, K.; Ma, G.; Yang, L.F.; Chang, X.L. Effects of particle size ratio on the macro- and microscopic behaviors of binary mixtures at the maximum packing efficiency state. Granul. Matter 2016, 18, 81. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, H.L.; Chen, Y.M.; Chu, J. Strength and Dilatancy of Silty Sand. J. Geotech. Geoenviron. Eng. 2014, 140, 06014007. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.H.; Liu, J.K.; Wang, C. Influence of non-plastic fines and density state on stress-dilatancy behavior of coral sand: An experimental investigation. Acta Geotech. 2024, 19, 5757–5779. [Google Scholar] [CrossRef]
- Xiao, Y.; Xiang, J.; Liu, H.; Ma, Q. Strength-dilatancy relation of sand containing non-plastic fines. Geotech. Lett. 2017, 7, 204–210. [Google Scholar] [CrossRef]
- Ni, Q.; Tan, T.S.; Dasari, G.R.; Hight, D.W. Contribution of fines to the compressive strength of mixed soils. Géotechnique 2004, 54, 561–569. [Google Scholar] [CrossRef]
- Bouckovalas, G.D.; Andrianopoulos, K.I.; Papadimitriou, A.G. A critical state interpretation for the cyclic liquefaction resistance of silty sands. Soil Dyn. Earthq. Eng. 2003, 23, 115–125. [Google Scholar] [CrossRef]
- Rahman, M.M.; Lo, S.C.R.; Dafalias, Y.F. Modelling the static liquefaction of sand with low-plasticity fines. Géotechnique 2014, 64, 881–894. [Google Scholar] [CrossRef]
- Zhu, Y.; Nie, Z.; Gong, J.; Zou, J.; Zhao, L.; Li, L. An analysis of the effects of the size ratio and fines content on the shear behaviors of binary mixtures using DEM. Comput. Geotech. 2020, 118, 103353. [Google Scholar] [CrossRef]
- Li, X.; Zhou, W.-H.; Liu, J. Stress-dilatancy behavior of marine coral sand incorporating non-plastic fines. Eng. Geol. 2024, 342, 107764. [Google Scholar] [CrossRef]
- Xiao, Y.; Yang, H.; Fang, Q.; Ling, Y.; Liu, H. Effect of Shape Discrepancies on Strength of Binary Soils. Transp. Geotech. 2025, 54, 101609. [Google Scholar] [CrossRef]
- Yang, J.; Wei, L.M. Collapse of loose sand with the addition of fines: The role of particle shape. Géotechnique 2012, 62, 1111–1125. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, Z.; Zheng, Y.; Wu, Q. Influences of particle size ratio and fines content on the suffusion characteristics of gap-graded soils. Granul. Matter 2024, 26, 52. [Google Scholar] [CrossRef]
- Yang, D.; Chu, X. The Effects of the Particle Size Ratio on the Behaviors of Binary Granular Materials. Cmes-Comput. Model. Eng. Sci. 2023, 136, 63–85. [Google Scholar] [CrossRef]
- Wiacek, J.; Parafiniuk, P.; Stasiak, M. Effect of particle size ratio and contribution of particle size fractions on micromechanics of uniaxially compressed binary sphere mixtures. Granul. Matter 2017, 19, 34. [Google Scholar] [CrossRef][Green Version]
- Wiacek, J. Geometrical parameters of binary granular mixtures with size ratio and volume fraction: Experiments and DEM simulations. Granul. Matter 2016, 18, 42. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, W.; Ma, G.; Yang, S.; Chang, X. Strong contacts, connectivity and fabric anisotropy in granular materials: A 3D perspective. Powder Technol. 2020, 366, 747–760. [Google Scholar] [CrossRef]
- Sufian, A.; Russell, A.R.; Whittle, A.J. Anisotropy of contact networks in granular media and its influence on mobilised internal friction. Géotechnique 2017, 67, 1067–1080. [Google Scholar] [CrossRef]
- Imseeh, W.H.; Druckrey, A.M.; Alshibli, K.A. 3D experimental quantification of fabric and fabric evolution of sheared granular materials using synchrotron micro-computed tomography. Granul. Matter 2018, 20, 24. [Google Scholar] [CrossRef]
- Lopez, R.D.F.; Silfwerbrand, J.; Jelagin, D.; Birgisson, B. Force transmission and soil fabric of binary granular mixturese. Géotechnique 2016, 66, 578–583. [Google Scholar] [CrossRef]
- Fonseca, J.; O’Sullivan, C.; Coop, M.R.; Lee, P.D. Quantifying the evolution of soil fabric during shearing using scalar parameters. Géotechnique 2013, 63, 818–829. [Google Scholar] [CrossRef]
- Liu, Y.; Yan, Z. Study on strong contact system by sub-network partitioning method for binary mixtures. Eur. J. Environ. Civ. Eng. 2024, 28, 1589–1613. [Google Scholar] [CrossRef]
- Cao, X.; Zhu, Y.; Gong, J. Effect of the intermediate principal stress on the mechanical responses of binary granular mixtures with different fines contents. Granul. Matter 2021, 23, 37. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, F.; Dupla, J.-C.; Canou, J.; Foerster, E.; Peng, Q. Assessment of tamping-based specimen preparation methods on static liquefaction of loose silty sand. Soil Dyn. Earthq. Eng. 2021, 143, 106592. [Google Scholar] [CrossRef]
- Mousavi, M.; Disfani, M.M.; Black, J.R.; Mehdizadeh, A. Impact of sample preparation on erosion characteristics and subsequent mechanical behaviour of gap-graded soils: An imaging-based analysis. Can. Geotech. J. 2025, 62, 1–19. [Google Scholar] [CrossRef]
- Selig, E.; Ladd, R. Preparing Test Specimens Using Undercompaction. Geotech. Test. J. 1978, 1, 16–23. [Google Scholar] [CrossRef]
- Rahman, M.M.; Lo, S.R.; Baki, M.A.L. Equivalent granular state parameter and undrained behaviour of sand–fines mixtures. Acta Geotech. 2011, 6, 183–194. [Google Scholar] [CrossRef]
- Cabalar, A.F. The effects of fines on the behaviour of a sand mixture. Geotech. Geol. Eng. 2011, 29, 91–100. [Google Scholar] [CrossRef]
- Bolton, M.D. The strength and dilatancy of sands. Géotechnique 1986, 36, 65–78. [Google Scholar] [CrossRef]
- Kuerbis, R.; Negussey, D.; Vaid, Y.P. Effect of Gradation and Fines Content on the Undrained Response of Sand. Geotech. Spec. Publ. 1988, 330–345. [Google Scholar]
- Liu, Y.; Zhang, D.; Wu, S.; Yu, P. DEM Investigation on the Evolution of Fabric under True Triaxial Conditions in Granular Materials. Int. J. Geomech. 2020, 20, 04020110. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Hu, W. Competition mechanism between dilation and interlocking in granular soils: DEM simulation and constitutive modeling. Acta Geotech. 2023, 18, 149–169. [Google Scholar] [CrossRef]
- Yang, Z.X.; Yang, J.; Wang, L.Z. On the influence of inter-particle friction and dilatancy in granular materials: A numerical analysis. Granul. Matter 2012, 14, 433–447. [Google Scholar] [CrossRef]
- Gu, X.; Huang, M.; Qian, J. DEM investigation on the evolution of microstructure in granular soils under shearing. Granul. Matter 2014, 16, 91–106. [Google Scholar] [CrossRef]
- Yan, Z.; Liu, Y. Investigation of the macro-and micro-mechanical behaviors of binary mixtures under proportional strain loading path via DEM simulation. Comput. Part. Mech. 2025, 1–19. [Google Scholar] [CrossRef]
- Chang, C.; Wang, J.; Ge, L. Maximum and minimum void ratios for sand-silt mixtures. Eng. Geol. 2016, 211, 7–18. [Google Scholar] [CrossRef]
- Chang, C.S.; Wang, J.-Y.; Ge, L. Modeling of minimum void ratio for sand–silt mixtures. Eng. Geol. 2015, 196, 293–304. [Google Scholar] [CrossRef]
- Lopera Pereza, J.; Kwok, C.; O’Sullivan, C.; Huang, X.; Hanley, K. Assessing the quasi-static conditions for shearing in granular media within the critical state soil mechanics framework. Soils Found. 2016, 56, 152–159. [Google Scholar] [CrossRef]
- Li, Y.; Huang, R.; Chan, L.S.; Chen, J. Effects of particle shape on shear strength of clay-gravel mixture. KSCE J. Civ. Eng. 2013, 17, 712–717. [Google Scholar] [CrossRef]
- Thornton, C.; Sun, G. Axisymmetric compression of 3D polydisperse systems of spheres. Powders Grains 1993, 93, 129–134. [Google Scholar]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Guo, N.; Zhao, J. The signature of shear-induced anisotropy in granular media. Comput. Geotech. 2013, 47, 1–15. [Google Scholar] [CrossRef]
- Oda, M. Fabric tensor for discontinuous geological materials. Soils Found. 1982, 22, 96–108. [Google Scholar] [CrossRef] [PubMed]
- Ouadfel, H.; Rothenburg, L. ‘Stress-force-fabric’ relationship for assemblies of ellipsoids. Mech. Mater. 2001, 33, 201–221. [Google Scholar] [CrossRef]
- Decky, M.; Papanova, Z.; Juhas, M.; Kudelcikova, M. Evaluation of the Effect of Average Annual Temperatures in Slovakia between 1971 and 2020 on Stresses in Rigid Pavements. Land 2022, 11, 764. [Google Scholar] [CrossRef]

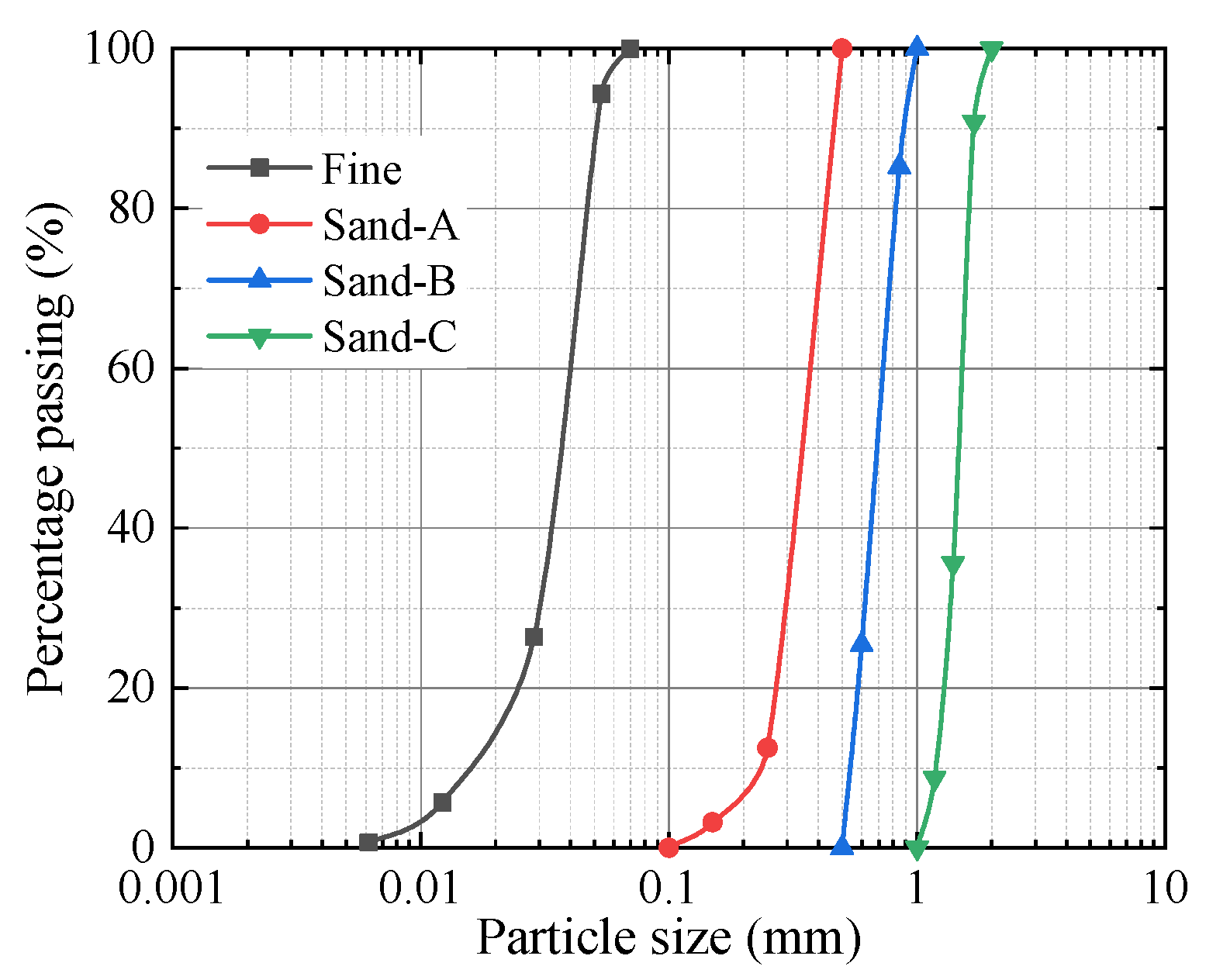



| Soils | Sand-A | Sand-B | Sand-C | Fine |
|---|---|---|---|---|
| Median particle diameter D50/mm | 0.338 | 0.693 | 1.46 | 0.037 |
| Specific gravity GS/g·cm−3 | 2.654 | 2.642 | 2.640 | 2.653 |
| SR * | FC */% | emax | emin | /% | e0 | SR | FC/% | emax | emin | /% | e0 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 9.1 | 0 | 1.235 | 0.779 | 50 | 1.007 | 18.7 | 0 | 1.152 | 0.746 | 50 | 0.949 |
| 80 | 0.870 | 80 | 0.827 | ||||||||
| 10 | 1.130 | 0.669 | 50 | 0.899 | 10 | 1.013 | 0.603 | 50 | 0.808 | ||
| 80 | 0.761 | 80 | 0.685 | ||||||||
| 20 | 1.089 | 0.568 | 50 | 0.829 | 20 | 0.853 | 0.498 | 50 | 0.676 | ||
| 80 | 0.672 | 80 | 0.569 | ||||||||
| 30 | 1.016 | 0.534 | 50 | 0.775 | 30 | 0.881 | 0.458 | 50 | 0.669 | ||
| 80 | 0.630 | 80 | 0.542 | ||||||||
| 50 | 0.937 | 0.449 | 50 | 0.693 | 50 | 0.848 | 0.468 | 50 | 0.658 | ||
| 80 | 0.546 | 80 | 0.544 | ||||||||
| 70 | 1.080 | 0.560 | 50 | 0.820 | 70 | 0.908 | 0.546 | 50 | 0.727 | ||
| 80 | 0.664 | 80 | 0.618 | ||||||||
| 39.7 | 0 | 1.140 | 0.733 | 50 | 0.937 | 39.7 | 10 | 1.019 | 0.596 | 50 | 0.808 |
| 80 | 0.815 | 80 | 0.681 | ||||||||
| 20 | 0.930 | 0.442 | 50 | 0.686 | 30 | 0.852 | 0.341 | 50 | 0.597 | ||
| 80 | 0.540 | 80 | 0.443 | ||||||||
| 50 | 0.826 | 0.377 | 50 | 0.602 | 70 | 0.897 | 0.530 | 50 | 0.713 | ||
| 80 | 0.467 | 80 | 0.603 | ||||||||
| 100 | 1.138 | 0.736 | 50 | 0.937 | 100 | 1.138 | 0.736 | 80 | 0.817 |
| Parameter | Value |
|---|---|
| particle radius r/mm | 0.1, 0.025 |
| particle density ρ/kg·m−3 | 2600 |
| particle–particle friction coefficient μ | 0, 0.5 |
| Wall–particle friction coefficient μwp | 0 |
| stiffness constant k0/MPa | 1.0 × 103, 4.0 × 103 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, K.; Lv, B.; Baoyin, H.; Li, D.; Yan, Z.; Yu, P.; Liu, Y. Experimental and DEM Study on the Mechanical Behaviors of Sand–Fines Mixtures with Different Fines Contents and Particle Size Ratios. Materials 2025, 18, 4929. https://doi.org/10.3390/ma18214929
Wu K, Lv B, Baoyin H, Li D, Yan Z, Yu P, Liu Y. Experimental and DEM Study on the Mechanical Behaviors of Sand–Fines Mixtures with Different Fines Contents and Particle Size Ratios. Materials. 2025; 18(21):4929. https://doi.org/10.3390/ma18214929
Chicago/Turabian StyleWu, Kejia, Bing Lv, Hexige Baoyin, Dongsheng Li, Zhouyi Yan, Pengqiang Yu, and Yang Liu. 2025. "Experimental and DEM Study on the Mechanical Behaviors of Sand–Fines Mixtures with Different Fines Contents and Particle Size Ratios" Materials 18, no. 21: 4929. https://doi.org/10.3390/ma18214929
APA StyleWu, K., Lv, B., Baoyin, H., Li, D., Yan, Z., Yu, P., & Liu, Y. (2025). Experimental and DEM Study on the Mechanical Behaviors of Sand–Fines Mixtures with Different Fines Contents and Particle Size Ratios. Materials, 18(21), 4929. https://doi.org/10.3390/ma18214929






