Study on the γ/γ′ Eutectic Inhomogeneity of a Novel 3rd Generation Nickel-Based Single-Crystal Superalloy Casting
Abstract
1. Introduction
2. Experimental Design and Methods
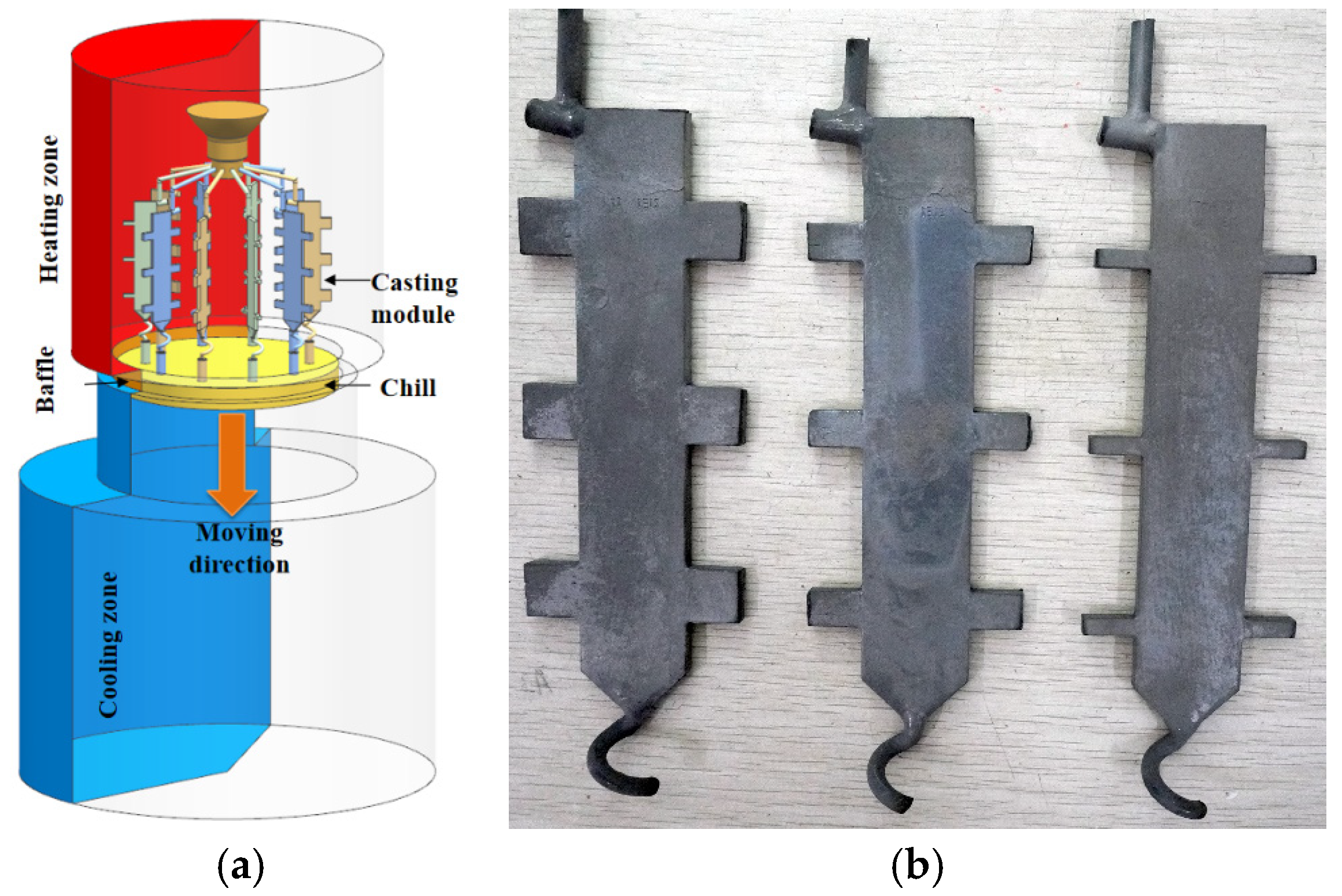
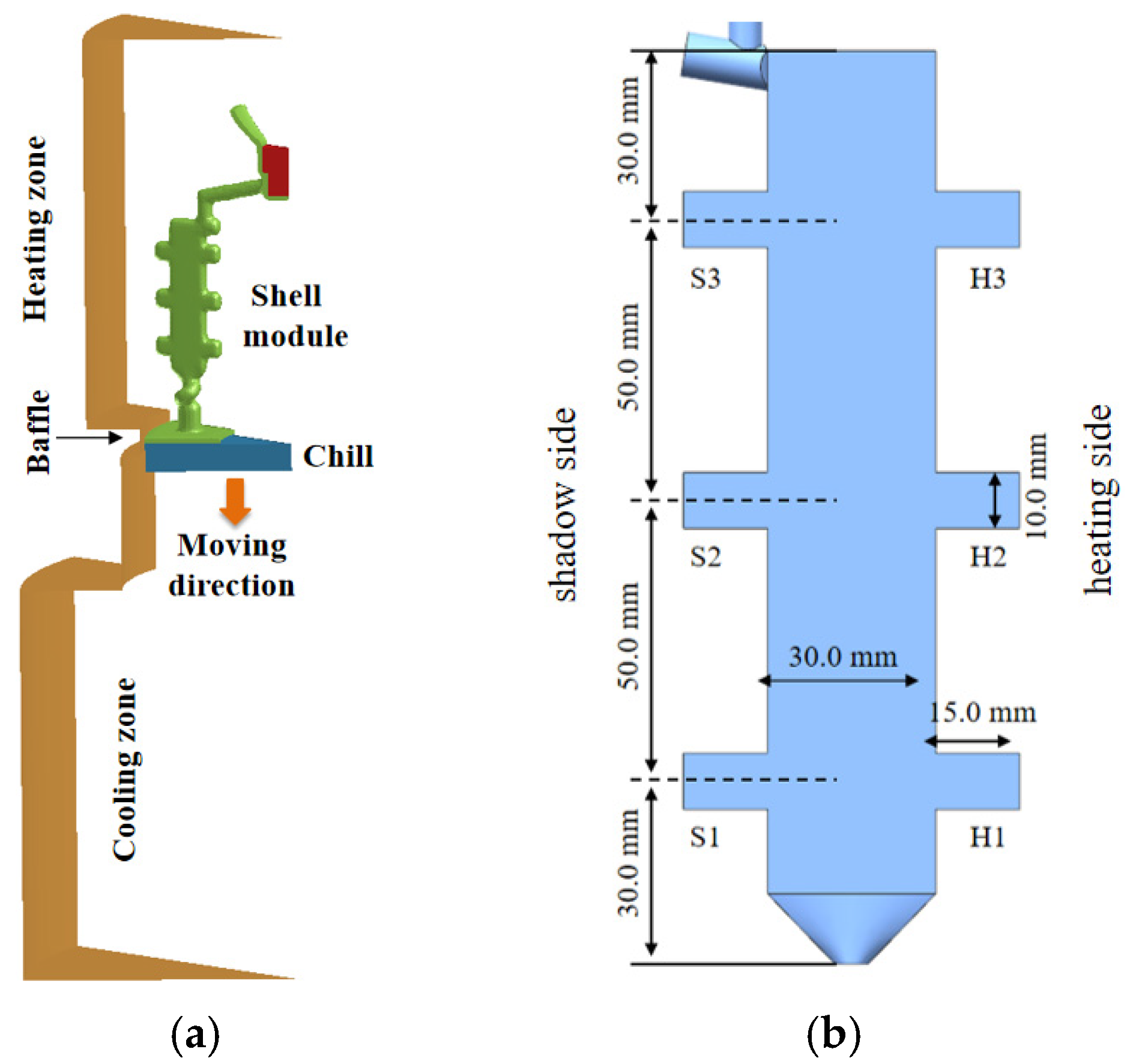
2.1. Experimental Design
2.2. Experimental Methods
3. Experimental Results and Analysis
3.1. Experimental Results
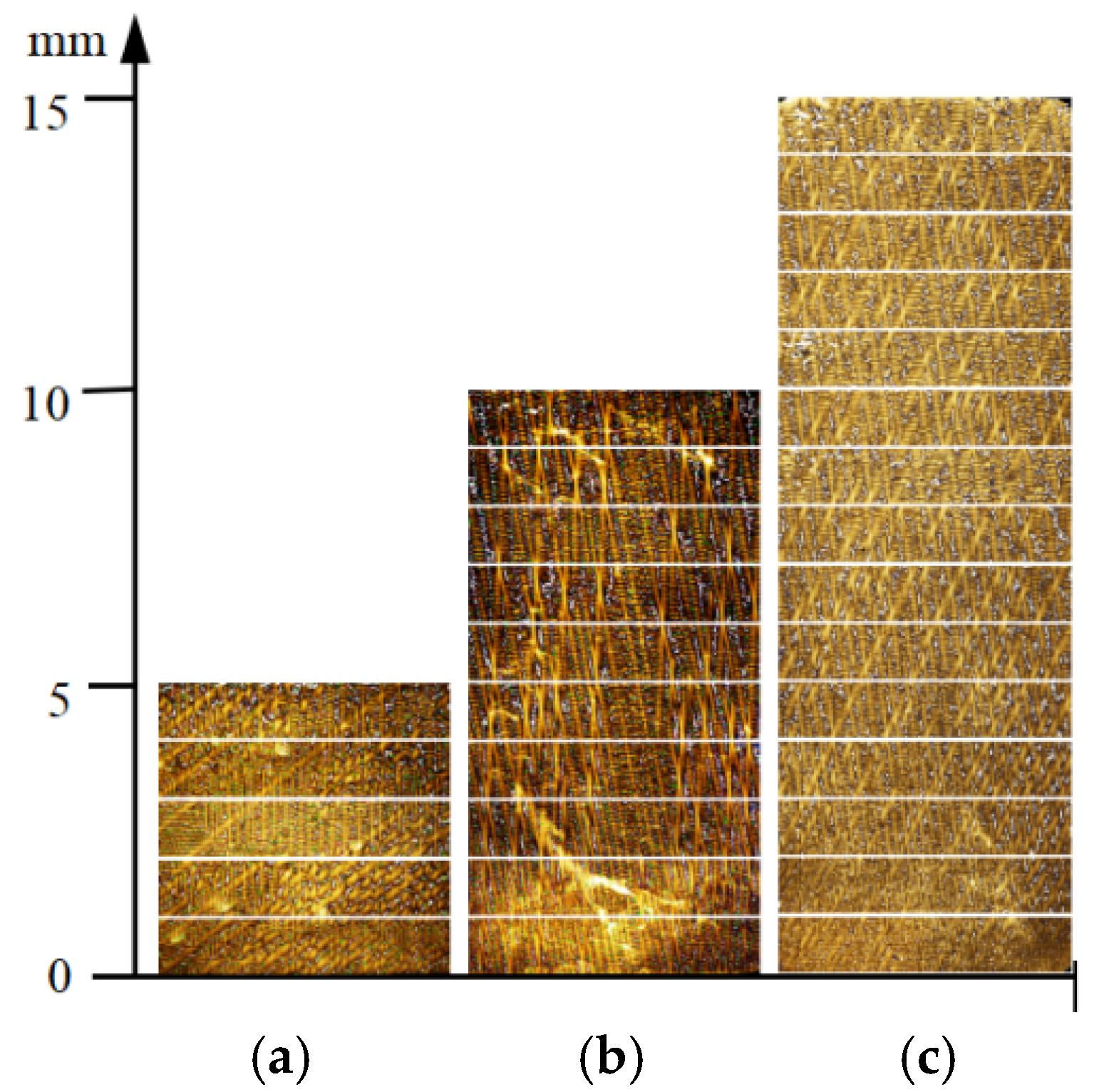
3.1.1. Comparison of Eutectic Distribution on the Top and Bottom Surfaces of the Platform
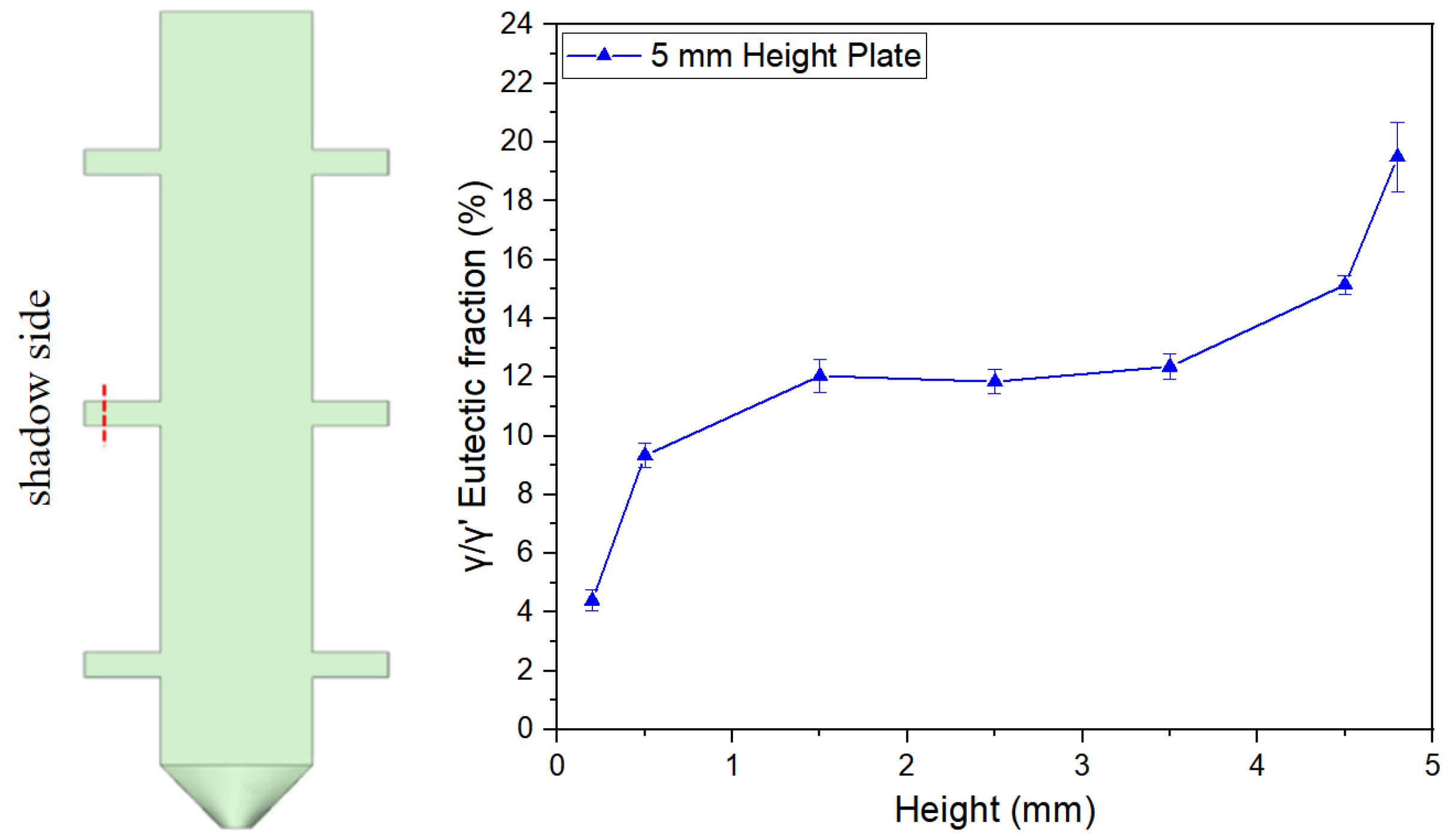
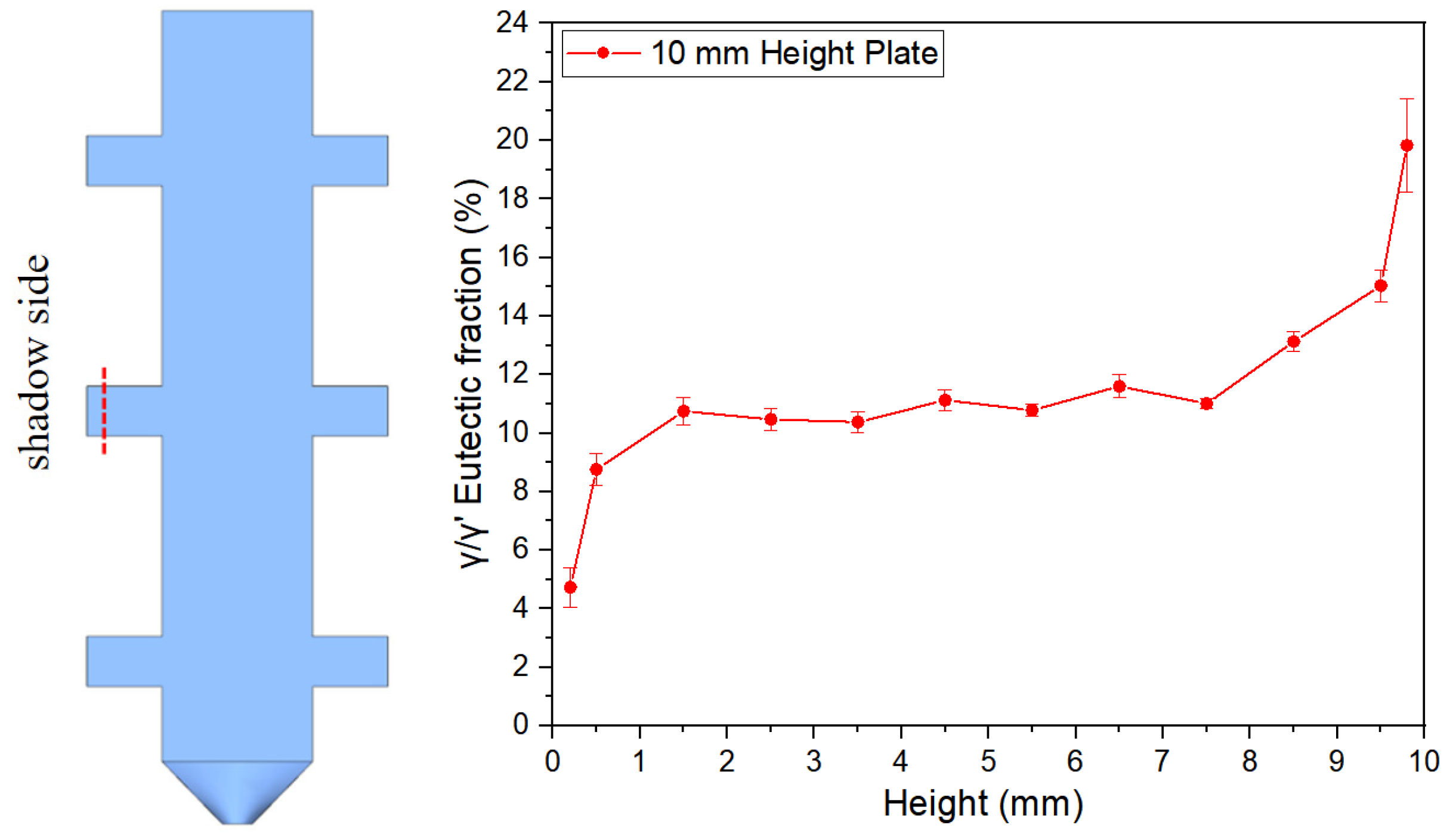
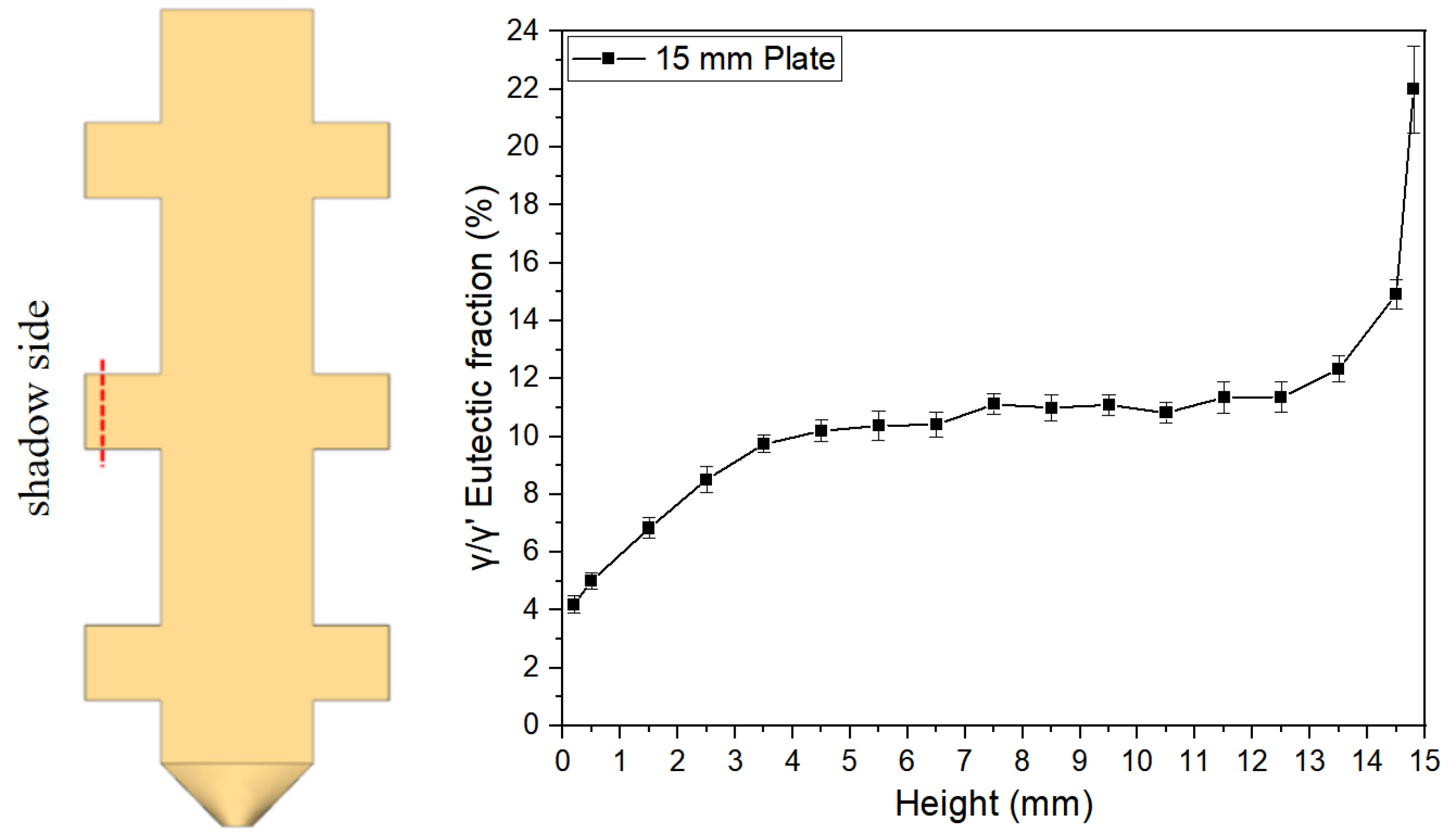
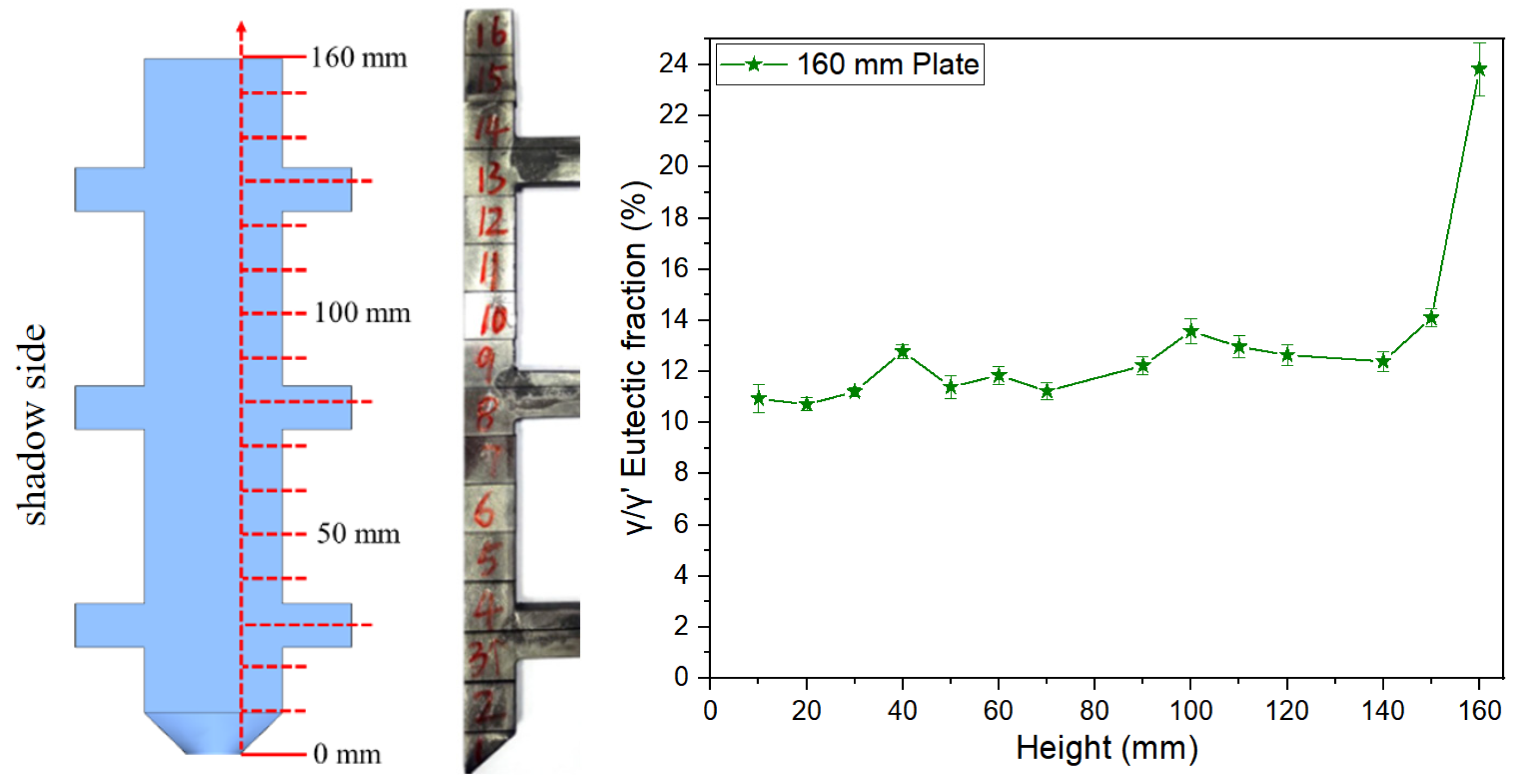
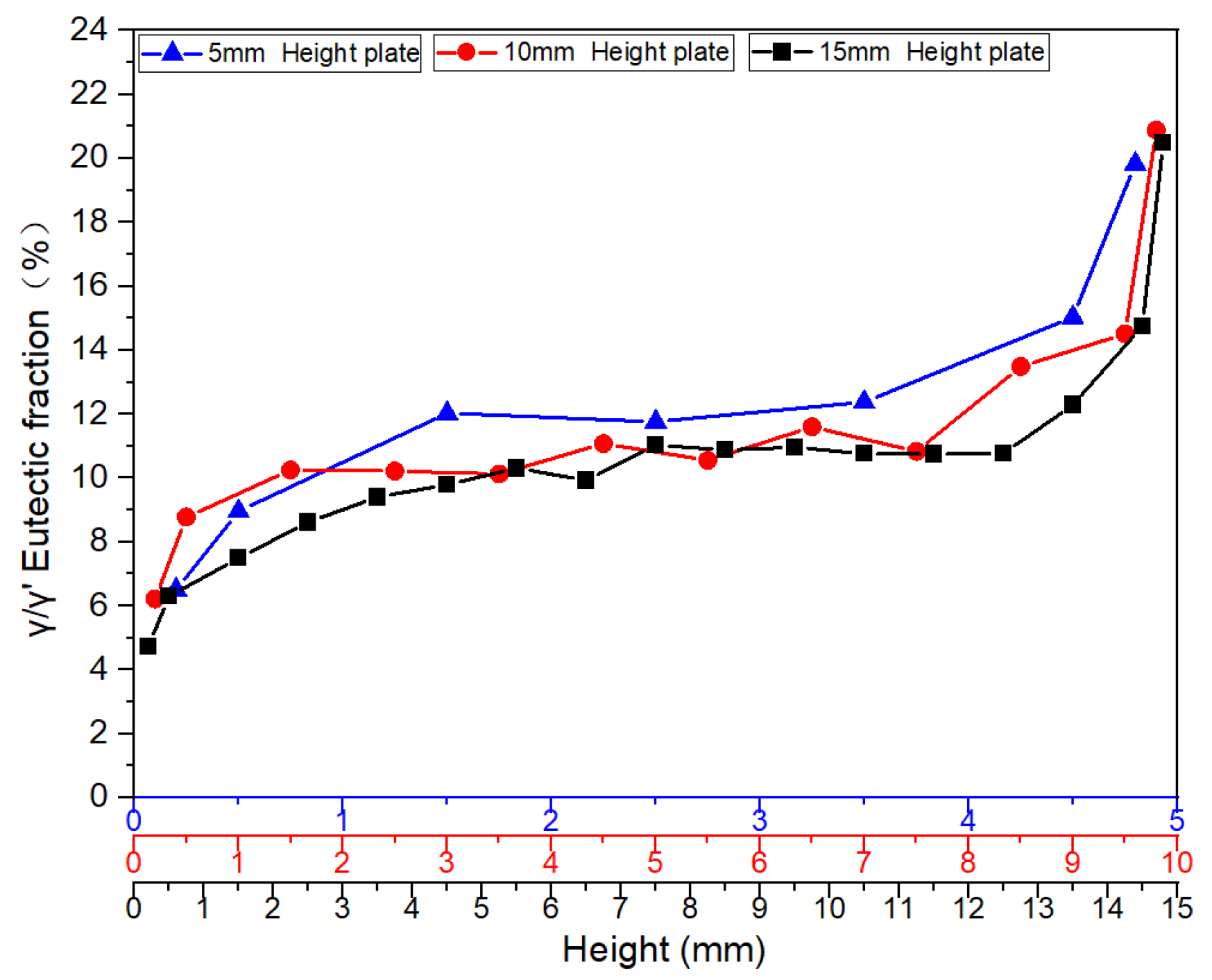
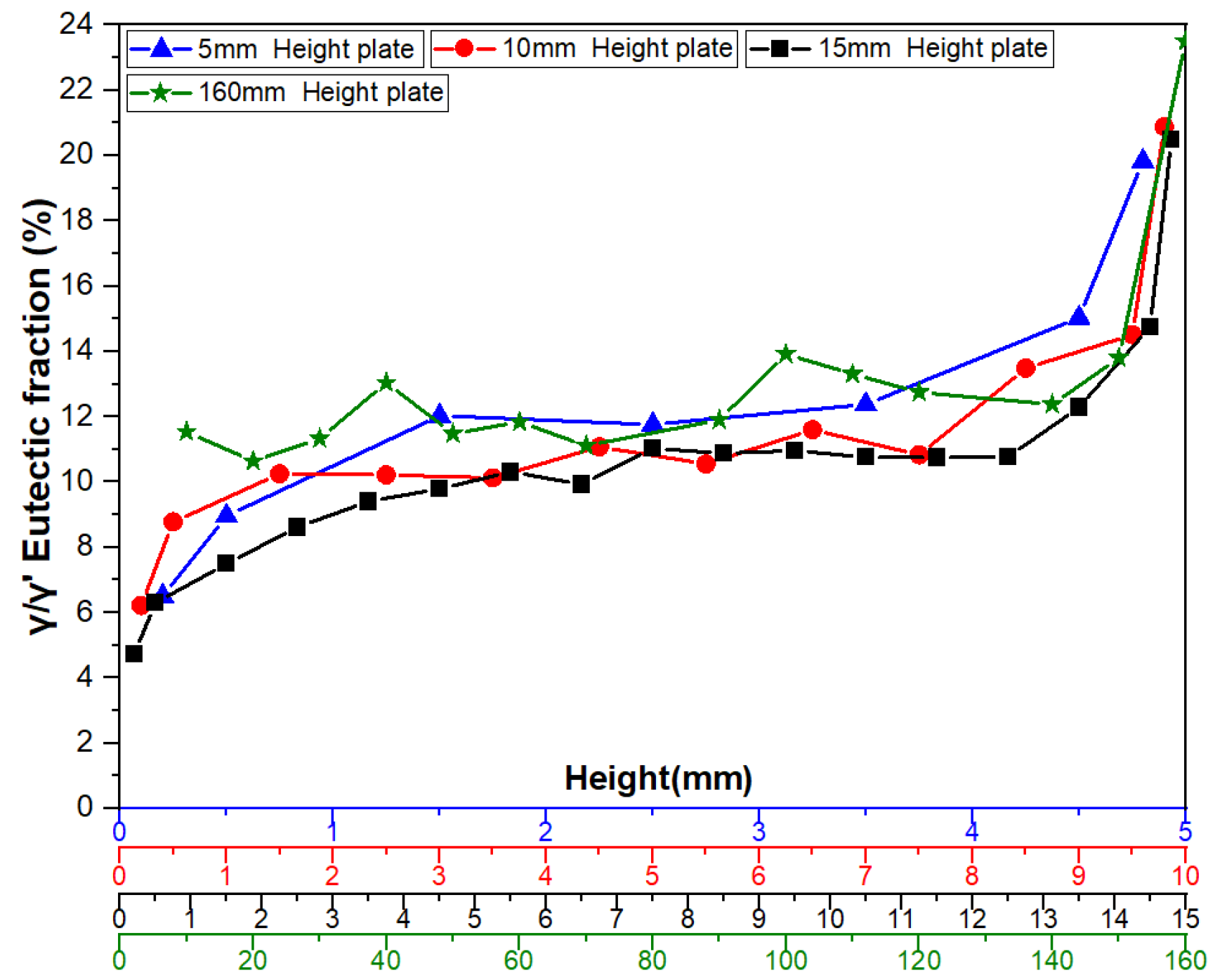
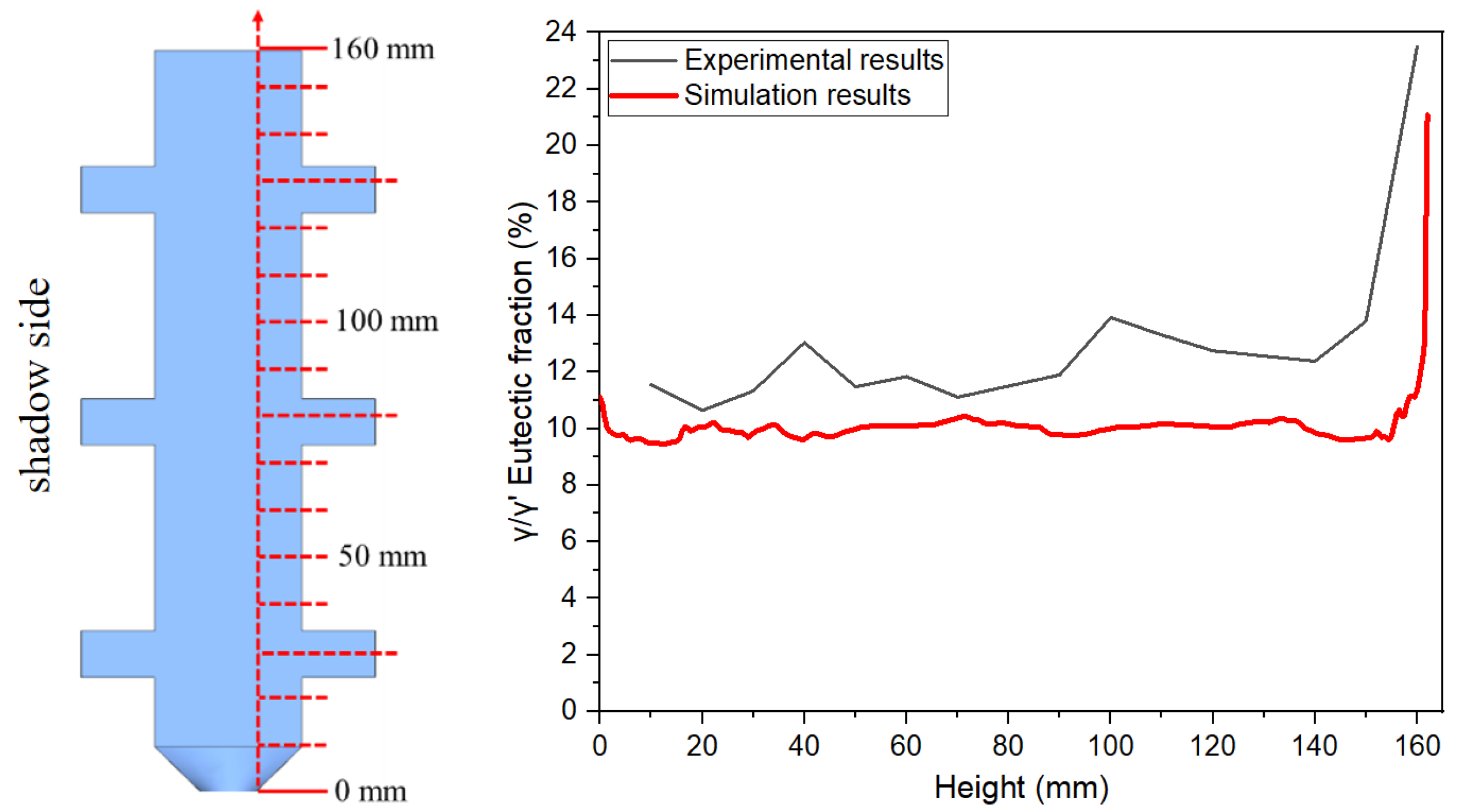
3.1.2. Distribution of γ/γ’ Eutectic Along the Height Direction of Platforms
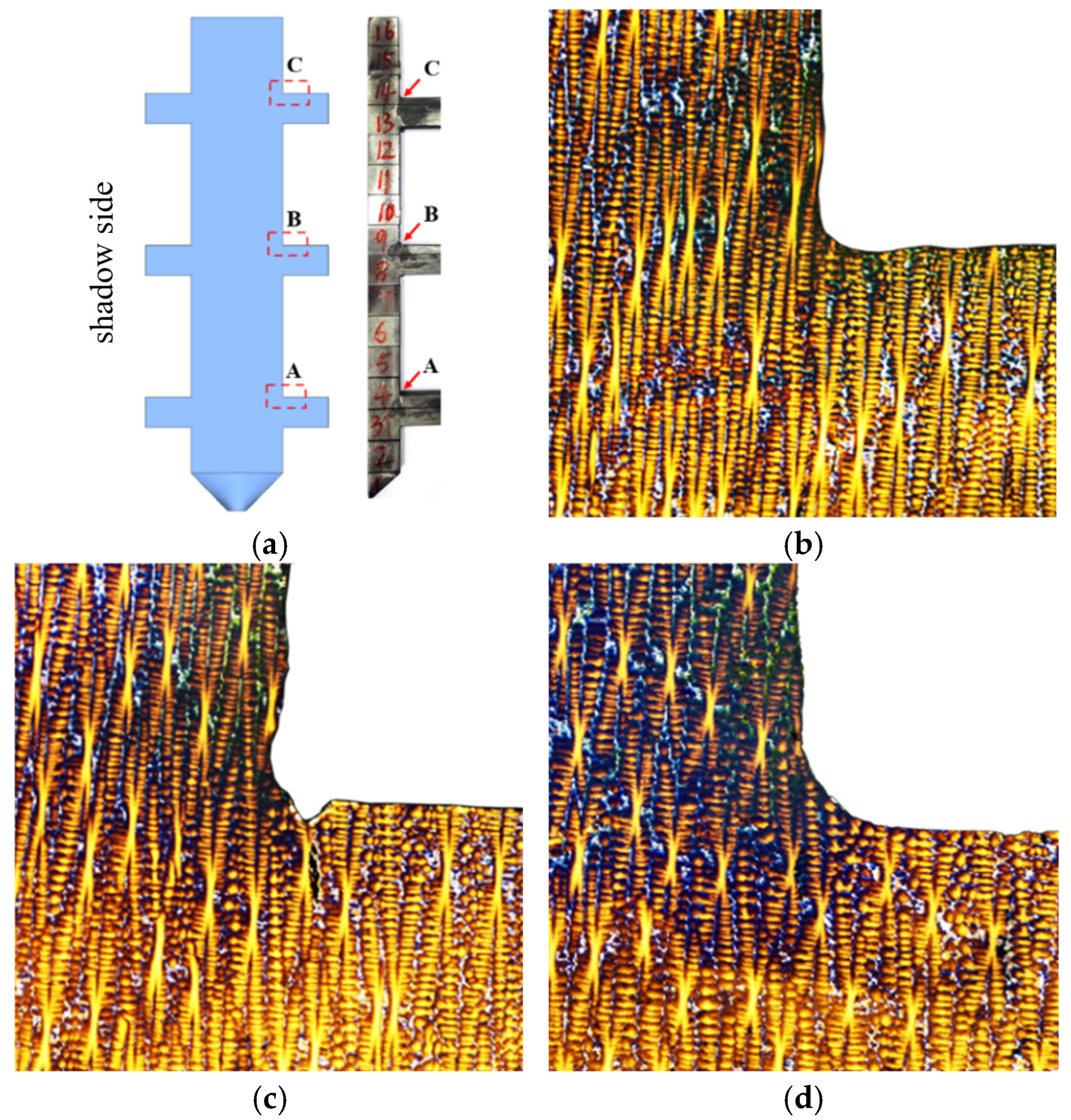
3.1.3. Eutectic Distribution at Corner Regions of the 10 mm Boss-Plate Junction
3.2. Analysis of Experimental Results
3.2.1. Interpretation of γ/γ’ Eutectic Distribution Patterns
3.2.2. Mechanism Discussion of γ/γ’ Eutectic Distribution Patterns
4. Numerical Simulation of γ/γ’ Eutectic Evolution
4.1. Multiphysics-Coupled Modeling and Numerical Solution Strategy
4.1.1. Computational Model
4.1.2. Numerical Solution Strategy
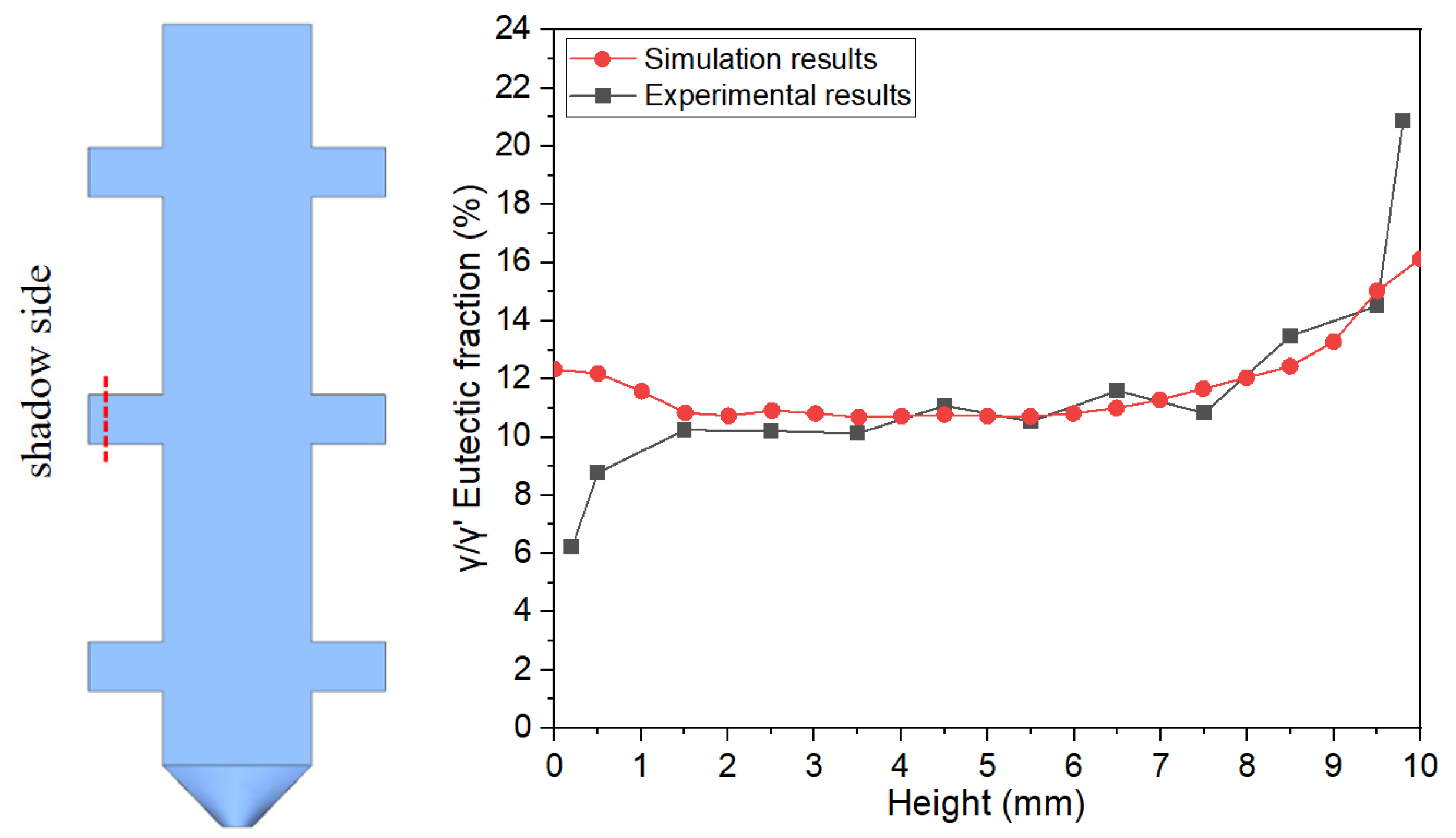
4.2. Discussion and Analysis of Computational Results
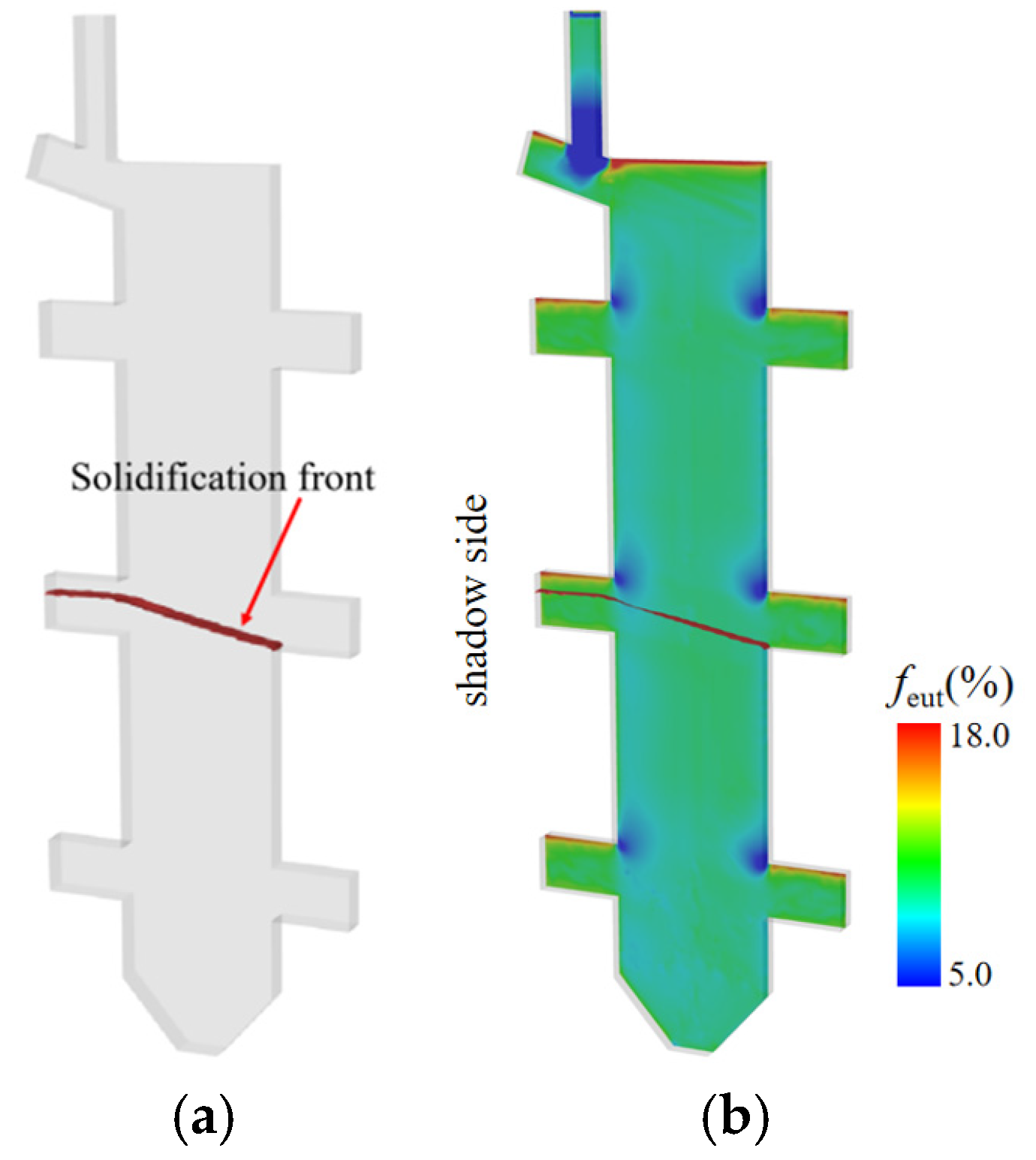
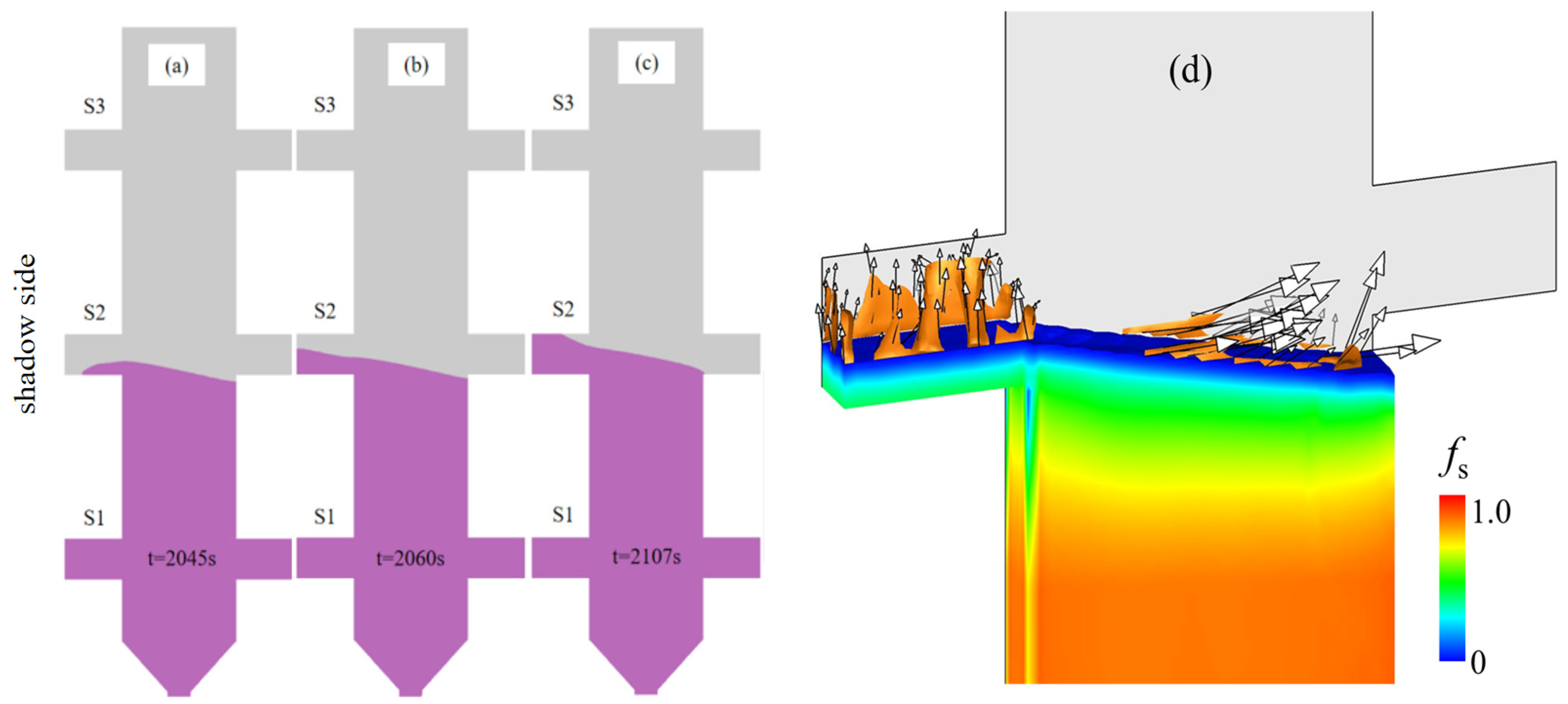
4.2.1. Eutectic Distribution Characteristics in the Casting
4.2.2. Eutectic Distribution Mechanism in the Plate Region of the Casting
4.2.3. Analysis of γ/γ’ Eutectic Distribution Patterns in Corner Regions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Wang, L.; Xie, G.; Wang, D.; Shen, J.; Lu, Y.Z.; Huang, Y.Q.; Li, Y.W. Recent advances in Ni-based single crystal superalloys. Acta Met. Sin 2023, 59, 1109–1124. [Google Scholar] [CrossRef]
- Cao, K.L.; Yang, W.C.; Qu, P.F.; Huang, T.W.; Guo, M.; Su, H.J.; Zhang, J.; Liu, L. Research progress in effect of Ru on solidification characteristics, precipitation of topologically close-packed phases and creep property of nickel-based single crystal superalloy. J. Mater. Eng. 2022, 50, 80–92. [Google Scholar] [CrossRef]
- Liu, L. Progress in precision casting technology for superalloys. Foundry 2012, 61, 1273–1285. [Google Scholar] [CrossRef]
- Fuchs, G.E. Solution heat treatment response of a third generation single crystal Ni-base superalloy. Mater. Sci. Eng. A 2001, 300, 52–60. [Google Scholar] [CrossRef]
- Seo, S.M.; Jeong, H.W.; Ahn, Y.K.; Yun, D.W.; Lee, J.H.; Yoo, Y.S. A comparative study of quantitative microsegregation analyses performed during the solidification of the Ni-base superalloy CMSX-10. Mater. Charact. 2014, 89, 43–55. [Google Scholar] [CrossRef]
- Seo, S.M.; Lee, J.H.; Yoo, Y.S.; Jo, C.Y.; Miyahara, H.; Ogi, K. A Comparative Study of the γ/γ′ Eutectic Evolution During the Solidification of Ni-Base Superalloys. Metall. Mater. Trans. A 2011, 42, 3150–3159. [Google Scholar] [CrossRef]
- Aveson, J.W.; Reinhart, G.; Goddard, C.J.L.; Nguyen-Thi, H.; Mangelinck-Noël, N.; Tandjaoui, A.; Davenport, J.R.; Warnken, N.; Gioacchino, F.D.; Lafford, T.A.; et al. On the Deformation of Dendrites During Directional Solidification of a Nickel-Based Superalloy. Metall. Mater. Trans. A 2019, 50, 5234–5241. [Google Scholar] [CrossRef]
- Ai, C.; Li, Q.; Chen, X.; Guo, M.; Huang, T.W.; Liu, L. Research progress on γ/γ′ elemental partitioning behavior in Ni-based single crystal superalloys. Chin. J. Nonferrous Met. 2022, 32, 3694–3705. [Google Scholar] [CrossRef]
- Zhao, X.B.; Liu, L.; Zhang, J. Investigation of grain competitive growth during directional solidification of single-crystal nickel-based superalloys. Appl. Phys. A Mater. Sci. Process. 2015, 120, 793–800. [Google Scholar] [CrossRef]
- Zhao, Z.; Liang, Z.; Li, Q.; Zhang, F.; Chen, B. Crack initiation and propagation behaviour under high-temperature very-high-cycle fatigue: Directionally solidified columnar-grained vs. single-crystal superalloys. Mater. Sci. Eng. A 2022, 836, 142711. [Google Scholar] [CrossRef]
- Pei, H.Q.; Wang, S.S.; Gao, X.A.; Wen, Z.X.; Wang, J.D.; Ai, X.; Yue, Z.F. Thermomechanical fatigue behavior and failure mechanism of a nickel-based directional solidification column crystal superalloy. Eng. Fract. Mech. 2023, 292, 109674. [Google Scholar] [CrossRef]
- Yuan, X.Y.; Long, H.B.; Zhao, J.B.; Fan, H.; Mao, S.C.; Wang, L.H.; Zhang, Z.; Han, X.D. Improved creep properties of a Ni-based single crystal superalloy by optimized solid solution treatments. J. Mater. Res. Technol. 2025, 36, 6257–6267. [Google Scholar] [CrossRef]
- Zhao, G.Q.; Tian, S.G.; Liu, L.R.; Tian, N.; Jin, F.W. Deformation Mechanism of Single-Crystal Nickel-based Superalloys During Ultra-High-Temperature Creep. Rare Met. Mater. Eng. 2022, 51, 52–59. [Google Scholar] [CrossRef]
- Yang, M.; Yang, F.; Chen, J.; Guo, M.; Su, H.J.; Zhang, J. Influence of γʹ volume fraction on creep of Ni-based superalloy through phase-field simulations. Trans. Nonferrous Met. Soc. China 2025, 35, 1168–1181. [Google Scholar] [CrossRef]
- Brewster, G.; Dong, H.B.; Green, N.R.; D’Souza, N. Surface Segregation during Directional Solidification of Ni-Base Superalloys. Metall. Mater. Trans. B 2008, 39, 87–93. [Google Scholar] [CrossRef]
- Cao, L.; Yao, L.; Zhou, Y.Z.; Jin, T.; Sun, X.F. Formation of the Surface Eutectic of a Ni-based Single Crystal Superalloy. J. Mater. Sci. Technol. 2017, 33, 347–351. [Google Scholar] [CrossRef]
- Cao, L.; Zhou, Y.Z.; Jin, T.; Sun, X.F. Effects of Re on surface eutectic formation for Ni-base single crystal superalloys during directional solidification. J. Mater. Sci. Technol. 2017, 33, 1308–1313. [Google Scholar] [CrossRef]
- Ma, D.X.; Zhao, Y.X.; Xu, W.T.; Pi, L.B.; Li, Z.X. Surface effects on eutectic distribution in single crystal superalloy castings. Acta Met. Sin 2021, 57, 1539–1548. [Google Scholar] [CrossRef]
- Hu, Y.Y.; Ma, J.H.; Xu, Q.Y. Numerical simulation on directional solidification and heat treatment processes of turbine blades. China Foundry 2024, 21, 476–490. [Google Scholar] [CrossRef]
- Mo, J.; Li, X.M.; Luo, L.; Peng, B.B. Research on evolution of tilted eutectic structure based on phase field simulation. Mater. Res. Express 2021, 8, 036502. [Google Scholar] [CrossRef]
- Eck, S.; Mogeritsch, J.; Ludwig, A. Experimental Observation of Convection during Equiaxed Solidification of Transparent Alloys. Mater. Ence Forum 2006, 508, 157–162. [Google Scholar] [CrossRef]
- Zhang, H.J.; Liu, X.S.; Ma, D.X.; Song, M.; Ludwig, A.; Kharicha, A.; Wu, M.H. Digital twin for directional solidification of a single-crystal turbine blade. Acta Mater. 2023, 244, 118579. [Google Scholar] [CrossRef]
- Wu, M.; Ludwig, A. Using a Three-Phase Deterministic Model for the Columnar-to-Equiaxed Transition. Met. Mater. Trans. A 2007, 38, 1465–1475. [Google Scholar] [CrossRef]
- Zhang, H.; Zhao, Y.; Xiong, W.; Ma, D.; Ludwig, A.; Kharicha, A.; Wu, M. Modelling freckles and spurious grain formation in directionally solidified superalloy castings. Commun. Mater. 2024, 5, 232. [Google Scholar] [CrossRef]
- Wu, M.; Ludwig, A.; Kharicha, A. Volume-averaged modeling of multiphase flow phenomena during alloy solidification. Metals 2019, 9, 229. [Google Scholar] [CrossRef]
- Lipton, J.; Glicksman, M.E.; Kurz, W. Equiaxed dendrite growth in alloys at small supercooling. Met. Trans. A 1987, 18, 341–345. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, M.; Zheng, Y.; Ludwig, A.; Kharicha, A. Numerical study of the role of mush permeability in the solidifying mushy zone under forced convection. Mater. Today Commun. 2020, 22, 100842. [Google Scholar] [CrossRef]
- Wang, L.S.; Shen, J.; Xiong, Y.L.; Du, Y.J.; Fu, H.Z. Phase and Microstructure Selection During Directional Solidification of Peritectic Alloy Under Convection Condition. Acta Metall. Sin 2014, 27, 585–592. [Google Scholar] [CrossRef]
- Xing, H.; Dong, X.L.; Wang, J.Y.; Jin, K.X. Orientation Dependence of Columnar Dendritic Growth with Sidebranching Behaviors in Directional Solidification: Insights from Phase-Field Simulations. Met. Mater. Trans. B 2018, 49, 1547–1559. [Google Scholar] [CrossRef]
- Hu, M.D.; Sun, C.; Fang, H.; Zhu, M.F. Competitive dendrite growth during directional solidification of a transparent alloy: Modeling and experiment. Eur. Phys. J. E 2020, 43, 16. [Google Scholar] [CrossRef]
- Flemings, M.C. Solidification Processing; McGraw-Hill: New York, NY, USA, 1974. [Google Scholar]
- Zhang, H.J.; Liu, X.S.; Ma, D.X.; Ludwig, A.; Kharicha, A.; Wu, M.H. Potential eutectic accumulation in single crystal turbine blade due to geometry effect: A numerical study. IOP Conf. Ser. Mater. Sci. Eng. 2023, 1274, 012026. [Google Scholar] [CrossRef]
- Ren, N.; Panwisawas, C.; Li, J.; Xia, M.X.; Dong, H.B.; Li, J.G. Solute enrichment induced dendritic fragmentation in directional solidification of nickel-based superalloys. Acta Mater. 2021, 215, 117043. [Google Scholar] [CrossRef]
- Felicelli, S.D.; Heinrich, J.C.; Poirier, D.R. Three-dimensional simulations of freckles in binary alloys. J. Cryst. Growth 1998, 191, 879–888. [Google Scholar] [CrossRef]
- Quested, P.N.; Brooks, R.F.; Chapman, L.; Morrell, R.; Youssef, Y.; Mills, K.C. Measurement and estimation of thermophysical properties of nickel based superalloys. Mater. Sci. Technol. 2009, 25, 154–162. [Google Scholar] [CrossRef]
- Dantzig, J.A.; Rappaz, M. Solidification; EPFL Press: Lausanne, Switzerland, 2009. [Google Scholar]
- Kurz, W.; Fisher, D.J. Fundamentals of Solidification, 4th ed.; Trans Tech Publications: Aedermannsdorf, Switzerland, 1989. [Google Scholar]







| Element | Al | Co | Cr | Fe | Hf | Mo | Nb | Re | Ta | Ti | W | Ni |
| Content | 5.69 | 5.97 | 3.39 | 0.21 | 0.03 | 0.41 | 0.10 | 4.89 | 8.07 | 0.15 | 6.52 | Base |
| Properties/Parameters | Symbol | Units | Values |
|---|---|---|---|
| Thermophysical | |||
| Specific heat of the alloy | cp,l; cp,s | J·kg−1·K−1 | 500.0 |
| Latent heat | Δhf | J·kg−1 | 2.4 × 105 |
| Liquid diffusion coefficient | D1 | m2·s−1 | 3.6 × 10−9 |
| Liquid thermal conductivity | k1 | W·m−1·K−1 | 33.5 |
| Solid thermal conductivity | ks | W·m−1·K−1 | 24.6 |
| Thermal expansion coefficient | βT | K−1 | −1.16 × 10−4 |
| Solutal expansion coefficient | βc | wt.%−1 | −0.228 |
| Density | P | kg·m−3 | 7646.0 |
| Viscosity | μ1 | kg·m−1·s−1 | 4.9 × 10−3 |
| Thermodynamic | |||
| Eutectic temperature | Teut | K | 1627.0 |
| Liquidus slope | m | K (wt.%)−1 | −1.145 |
| Equilibrium partition coefficient | k | - | 0.57 |
| Primary dendritic arm spacing | λ1 | µm | 500.0 |
| Melting point of the solvent | Tf | K | 1728.0 |
| Others | |||
| Initial concentration | wt.% | 35.09 | |
| Initial temperature | T0 | K | 1773.0 |
| Withdrawal velocity | v | mm/min | 3.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Long, A.; Zhang, H.; Ma, D.; Song, M.; Wu, M.; Guo, J. Study on the γ/γ′ Eutectic Inhomogeneity of a Novel 3rd Generation Nickel-Based Single-Crystal Superalloy Casting. Materials 2025, 18, 4872. https://doi.org/10.3390/ma18214872
Liu X, Long A, Zhang H, Ma D, Song M, Wu M, Guo J. Study on the γ/γ′ Eutectic Inhomogeneity of a Novel 3rd Generation Nickel-Based Single-Crystal Superalloy Casting. Materials. 2025; 18(21):4872. https://doi.org/10.3390/ma18214872
Chicago/Turabian StyleLiu, Xiaoshan, Anping Long, Haijie Zhang, Dexin Ma, Min Song, Menghuai Wu, and Jianzheng Guo. 2025. "Study on the γ/γ′ Eutectic Inhomogeneity of a Novel 3rd Generation Nickel-Based Single-Crystal Superalloy Casting" Materials 18, no. 21: 4872. https://doi.org/10.3390/ma18214872
APA StyleLiu, X., Long, A., Zhang, H., Ma, D., Song, M., Wu, M., & Guo, J. (2025). Study on the γ/γ′ Eutectic Inhomogeneity of a Novel 3rd Generation Nickel-Based Single-Crystal Superalloy Casting. Materials, 18(21), 4872. https://doi.org/10.3390/ma18214872





