Effects of Cooling Rate and Solid Fraction on α-Al Phase Evolution in Rheo-Die Casting: Phase-Field Simulation and Experimental Investigation
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiment Methods
2.2. Phase Field Model
3. Results and Discussion
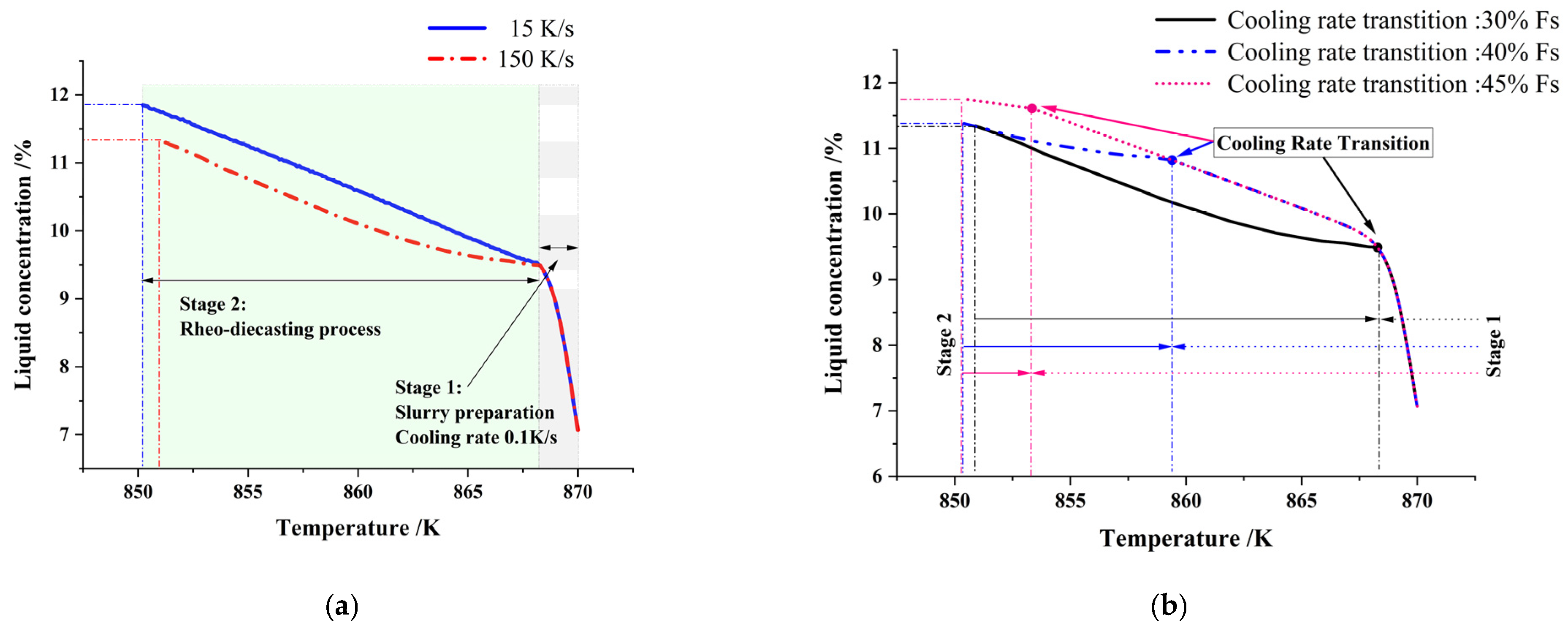
3.1. Rheo-Die Casting Experiment Results
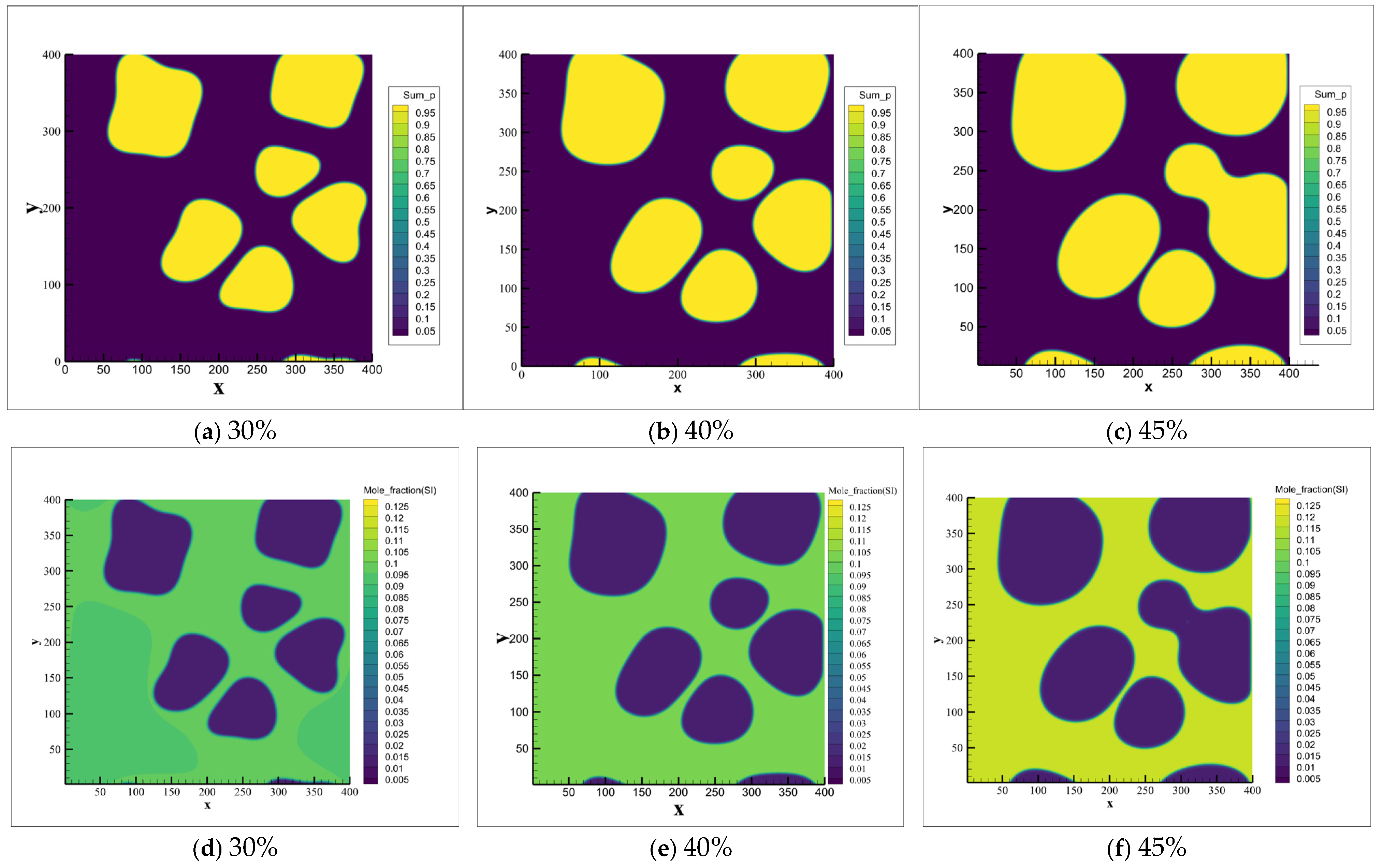
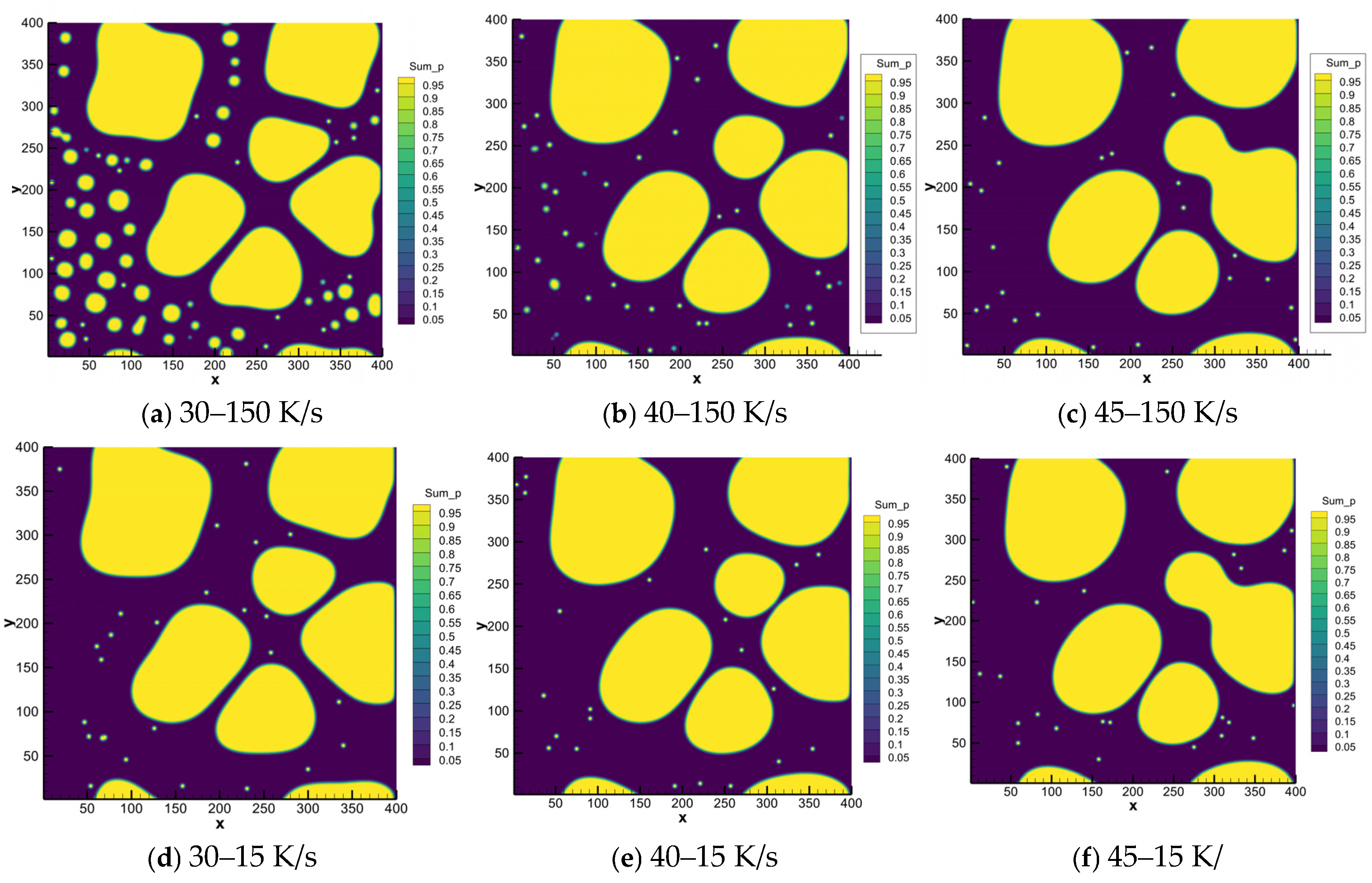
3.2. Phase Field Simulation Results
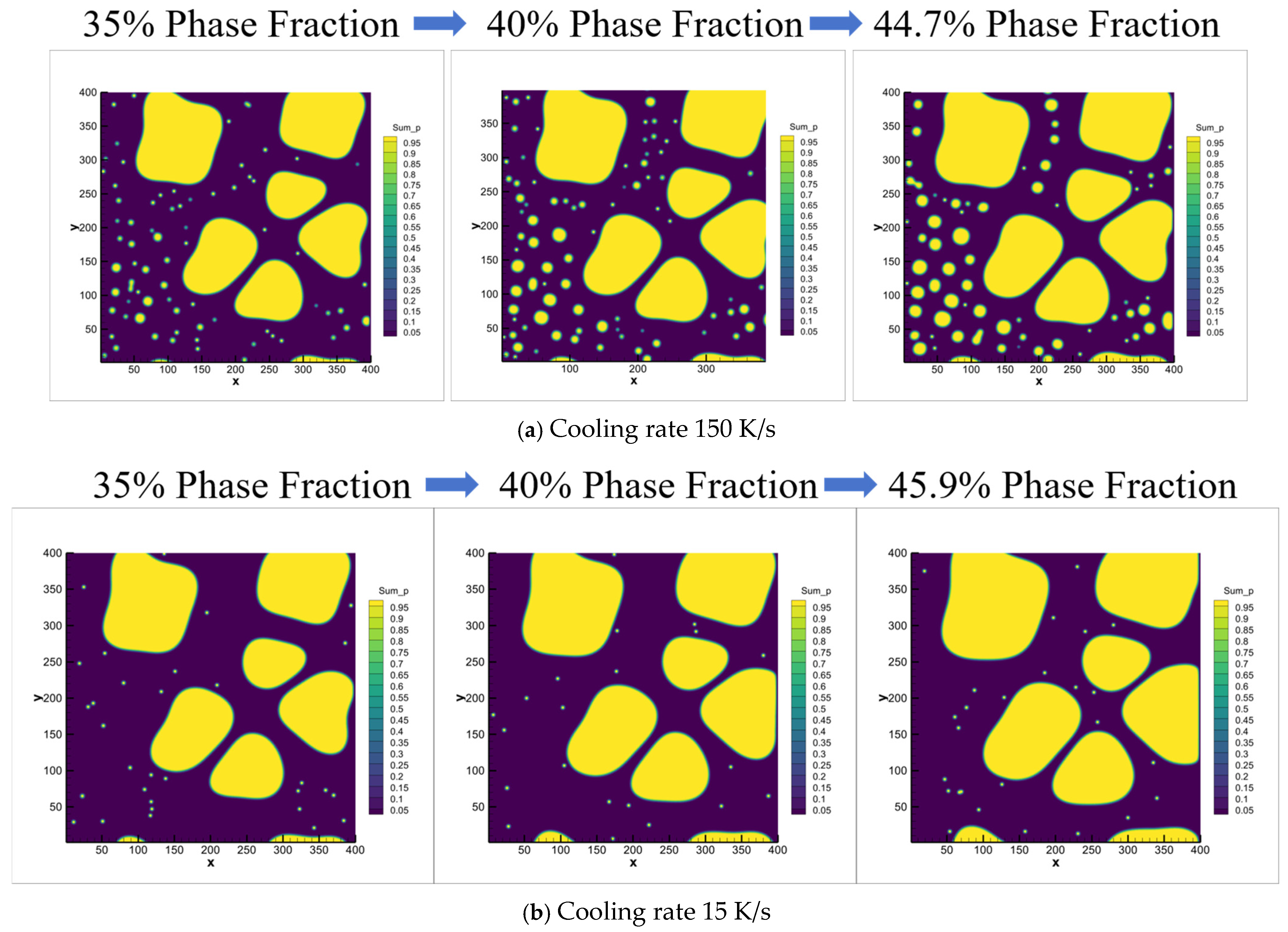
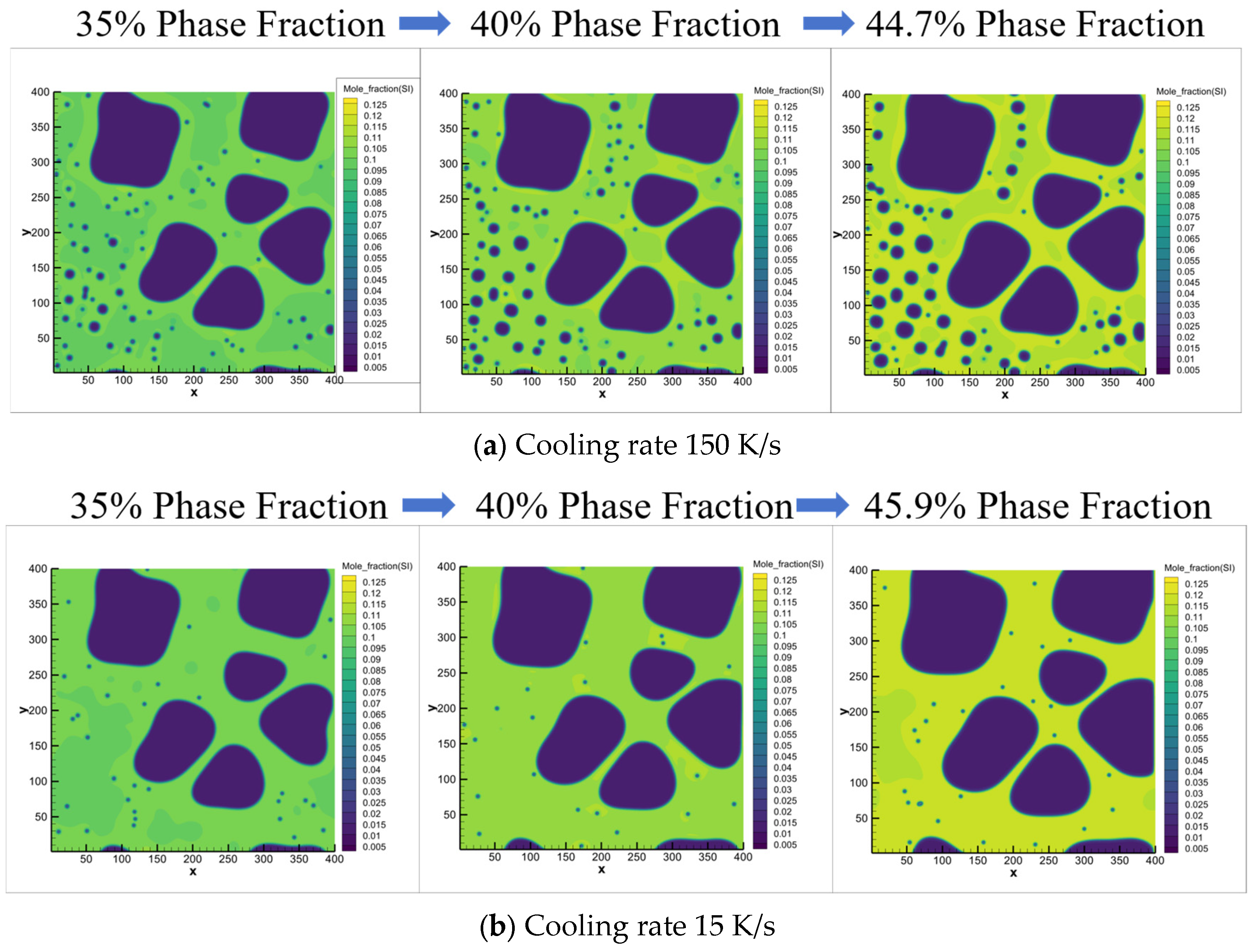
3.3. Microstructural Evolution Mechanisms of Primary and Secondary α Phase During Semi-Solid Rheo-Die Casting Process
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ji, S.; Wang, K.; Dong, X. An overview on the process development and the formation of non-dendritic microstructure in semi-solid processing of metallic materials. Crystals 2022, 12, 1044. [Google Scholar] [CrossRef]
- Pola, A.; Tocci, M.; Kapranos, P. Microstructure and properties of semi-solid aluminum alloys: A literature review. Metals 2018, 8, 181. [Google Scholar] [CrossRef]
- Flemings, M.C.; Riek, R.G.; Young, K.P. Rheocasting. Mater. Sci. Eng. 1976, 25, 103–117. [Google Scholar] [CrossRef]
- Martinez, R.A.; Flemings, M.C. Evolution of particle morphology in semisolid processing. Metall. Mater. Trans. A 2005, 36, 2205–2210. [Google Scholar] [CrossRef]
- Hu, X.G.; Zhu, Q.; Midson, S.P.; Atkinson, H.V.; Dong, H.B.; Zhang, F.; Kang, Y.L. Blistering in semi-solid die casting of aluminium alloys and its avoidance. Acta Mater. 2017, 124, 446–455. [Google Scholar] [CrossRef]
- Kapranos, P. Current state of semi-solid net-shape die casting. Metals 2019, 9, 1301. [Google Scholar] [CrossRef]
- Li, D.Q.; Liang, X.K.; Zhang, F.; Chen, S.; Zhang, F.; Feng, J. Recent Industrial Application and Perspectives of Rheo-Diecast Process in China. Solid. State Phenom. 2022, 327, 238–243. [Google Scholar] [CrossRef]
- Luo, M.; Li, D.; Qu, W.; Hu, X.; Zhu, Q.; Fan, J. Mold–Slug Interfacial Heat Transfer Characteristics of Different Coating Thicknesses: Effects on Slug Temperature and Microstructure in Swirled Enthalpy Equilibration Device Process. Materials 2019, 12, 1836. [Google Scholar] [CrossRef]
- Li, G.; Lu, H.; Hu, X.; Lin, F.; Li, X.; Zhu, Q. Current Progress in Rheoforming of Wrought Aluminum Alloys: A Review. Metals 2020, 10, 238. [Google Scholar] [CrossRef]
- Nafisi, S.; Lashkari, O.; Ghomashchi, R.; Ajersch, F.; Charette, A. Microstructure and rheological behavior of grain refined and modified semi-solid A356 Al-Si slurries. Acta Mater. 2006, 54, 3503–3511. [Google Scholar] [CrossRef]
- Liang, X.K.; Zhu, Q.; Luo, M.; Li, D.Q. Application of polarized light microscopy on microstructural characterization of semisolid slurry. Rare Met. 2023, 42, 3545–3552. [Google Scholar] [CrossRef]
- Ji, S.; Das, A.; Fan, Z. Solidification behavior of the remnant liquid in the sheared semisolid slurry of Sn-15 wt.% Pb alloy. Scripta Mater. 2002, 46, 205–210. [Google Scholar] [CrossRef]
- Hitchcock, M.; Wang, Y.; Fan, Z. Secondary solidification behaviour of the Al-Si-Mg alloy prepared by the rheo-diecasting process. Acta Mater. 2007, 55, 1589–1598. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, M.; Meng, S.; Fu, Y.; Li, W.; Li, C.; Guan, R. Solidification behavior and enhanced properties of semi-solid Al-8Si-0.5 Fe alloys fabricated by rheo-diecasting. J. Mater. Res. Technol. 2022, 19, 3160–3171. [Google Scholar] [CrossRef]
- Ginzburg, V.L.; Landau, L.D. On the Theory of Superconductivity. In On Superconductivity and Superfluidity; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Karma, A. Phase-field formulation for quantitative modeling of alloy solidification. Phys. Rev. Lett. 2001, 87, 115701. [Google Scholar] [CrossRef]
- Qu, W.; Luo, M.; Guo, Z.; Hu, X.; Zhang, A.; Zhang, F.; Li, D.; Zhang, Y. Effect of Temperature Gradient on the Grain Size Homogeneity of SEED Produced Semi-Solid Slurries by Phase-Field Simulation. Materials 2019, 12, 3309. [Google Scholar] [CrossRef]
- Qu, W.; Luo, M.; Guo, Z.; Hu, X.; Zhang, A.; Zhang, F.; Li, D. Microstructural evolution mechanism of semi-solid slurry: A study using Phase-Field-Lattice-Boltzmann scheme. J. Mater. Res. Technol. 2020, 280, 116592. [Google Scholar] [CrossRef]
- Guo, H.M.; Wei, T.; Yang, X.J. Phase Field Simulation of Solidified Multiple Grains. Adv. Mater. Res. 2013, 602, 1874–1877. [Google Scholar] [CrossRef]
- Li, J.; Guo, C.; Ma, Y.; Wang, Z.; Wang, J. Effect of initial particle size distribution on the dynamics of transient Ostwald ripening: A phase field study. Acta Mater. 2015, 90, 10–26. [Google Scholar] [CrossRef]
- Das, P.; Dutta, P. Phase field modelling of microstructure evolution and ripening driven grain growth during cooling slope processing of A356 Al alloy. Comp. Mater. Sci. 2016, 125, 8–19. [Google Scholar] [CrossRef]
- Qin, R.S.; Wallach, E.R. Phase-field simulation of semisolid metal processing under conditions of laminar and turbulent flow. Metall. Mater. Trans. A 2003, 357, 45–54. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Phase-field method for computationally efficient modeling of solidification with arbitrary interface kinetics. Phys. Rev. E 1996, 53, R3015. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.K. Thermodynamics and its prediction and CALPHAD modeling: Review, state of the art, and perspectives. Calphad 2024, 82, 273–348. [Google Scholar] [CrossRef]
- Gröbner, J.; Lukas, H.L.; Aldinger, F. Thermodynamic calculation of the ternary system Al-Si-C. Calphad 1996, 20, 247–254. [Google Scholar] [CrossRef]
- Allen, S.M.; Cahn, J.W. A microscopic theory for antiphase boundary motion and its application to antiphase domain coarsening. Acta Metall. 1979, 27, 1085–1095. [Google Scholar] [CrossRef]
- Paul, A.; Laurila, T.; Vuorinen, V.; Divinski, S.V. Fick’s Laws of Diffusion. In Thermodynamics, Diffusion and the Kirkendall Effect in Solids; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar] [CrossRef]
- Ofori-Opoku, N.; Provatas, N. A quantitative multi-phase field model of poly crystalline alloy solidification. Acta Mater. 2010, 58, 2155–2164. [Google Scholar] [CrossRef]
- Yang, L.; Dong, Z.; Wang, L.; Provatas, N. Improved multi-order parameter and multi-component model of polycrystalline solidification. J. Mater. Sci. Technol. 2022, 101, 217–225. [Google Scholar] [CrossRef]
- Simmons, J.P.; Shen, C.; Wang, Y. Phase field modeling of simultaneous nucleation and growth by explicitly incorporating nucleation events. Scr. Mater. 2000, 43, 935–942. [Google Scholar] [CrossRef]
- Ramirez, J.C.; Beckermann, C.; Karma, A.; Diepers, H.J. Phase-field modeling of binary alloy solidification with coupled heat and solute diffusion. Phys. Rev. E 2004, 69, 051607. [Google Scholar] [CrossRef]
- Turnbull, D.J. Formation of crystal nuclei in liquid metals. J. Appl. Phys. 1950, 21, 1022–1028. [Google Scholar] [CrossRef]
- Mullin, W.W.; Sekerka, R.F. Morphological stability of a particle growing by diffusion or heat flow. J. Appl. Phys. 1963, 34, 323–329. [Google Scholar] [CrossRef]
- Aziz, M.J. Interface Attachment Kinetics in Alloy Solidification. Metall. Mater. Trans. A 1996, 27A, 671–686. [Google Scholar] [CrossRef]
- Tiller, W.A.; Jackson, K.A.; Rutter, J.W.; Chalmers, B. The redistribution of solute atoms during the solidification of metals. Acta Metall. 1953, 1, 428–437. [Google Scholar] [CrossRef]
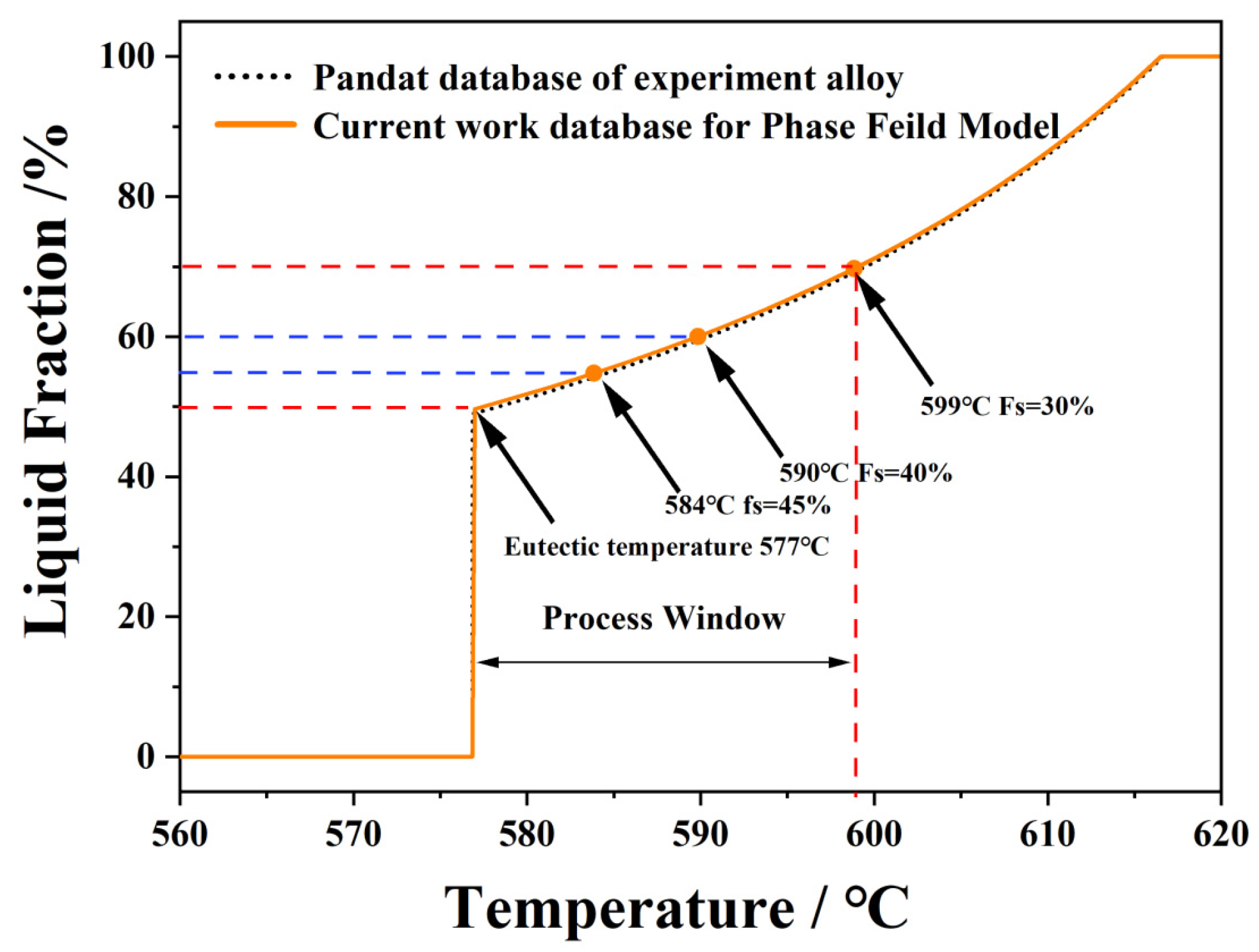

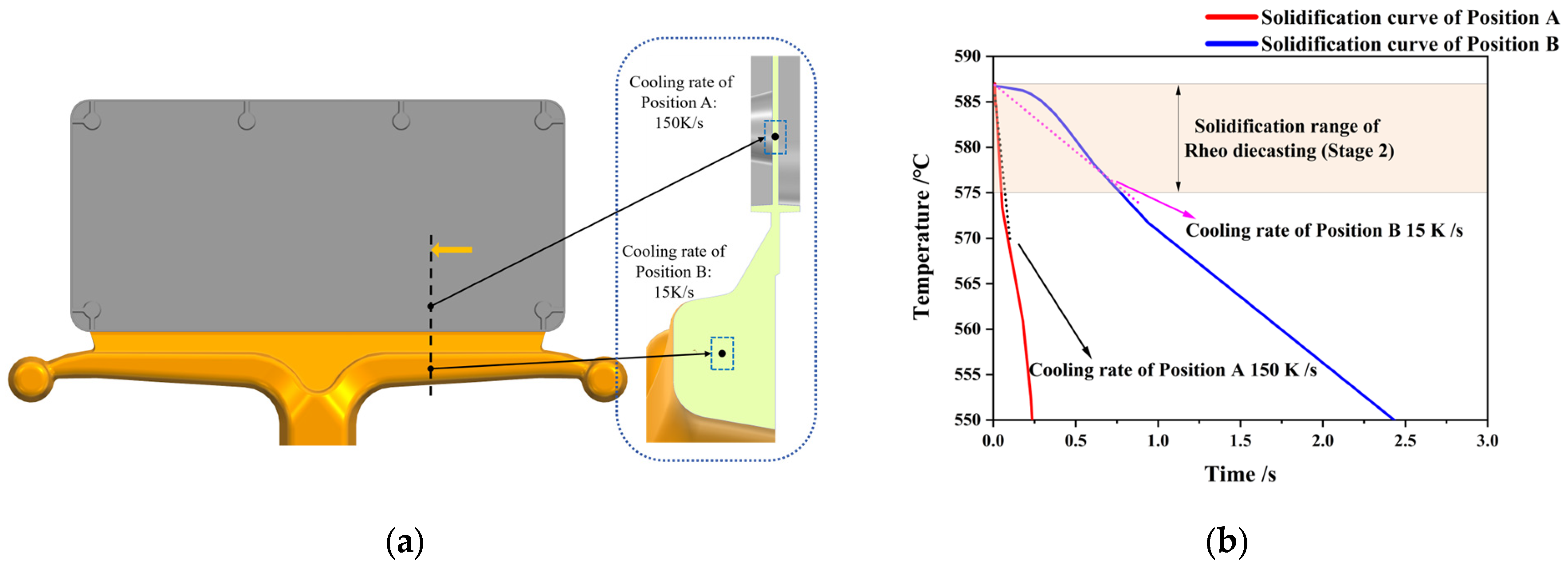
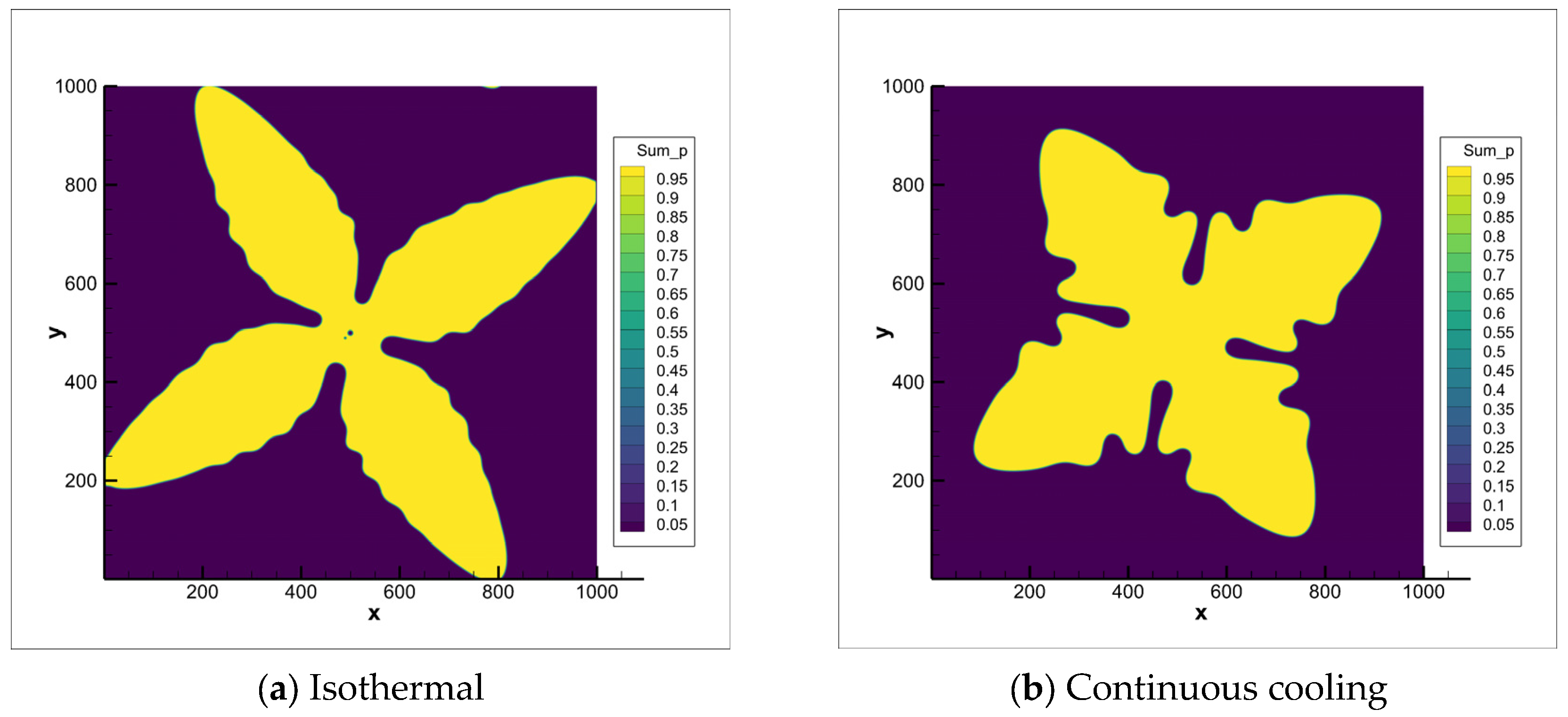
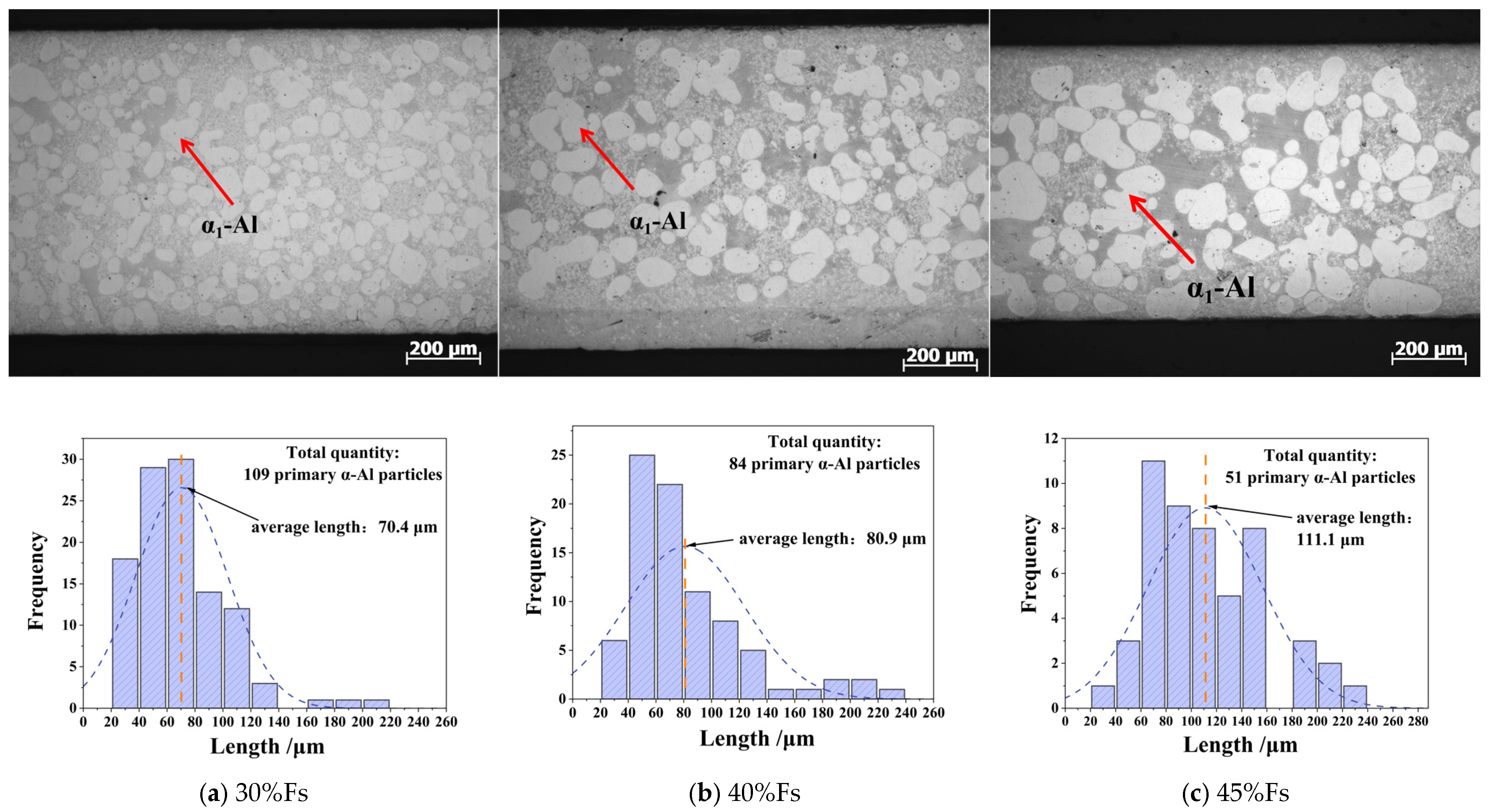


| Alloy | Si | Fe | Al |
|---|---|---|---|
| Al-7Si | 7.06 | 0.115 | Bal. |
| Definition | Symbol | Value [Unit] |
|---|---|---|
| Phase-field mobility | MΦ | 0.34 [m3·J−1s−1] |
| Anisotropy strength | 0.01 | |
| Initial solute concentration | c0 | 7 [mass%] |
| Diffusion coefficient for in liquid | DL | 1 × 10−9 [m2·s−1] |
| Diffusion coefficient for in solid | DS | 1 × 10−13 [m2·s−1] |
| Coupling constant | λ | 5.0 |
| Capillary length | d | 0.2 [μm] |
| Solute partition coefficient | k | CALPHAD calculated |
| Liquidus | TLiquidus | CALPHAD calculated |
| Eutectic temperature | Teutectic | CALPHAD calculated |
| Melting point of pure solvent | TM | CALPHAD calculated |
| Nucleation parameter | k1 | 5 × 10−2 |
| Nucleation parameter | k2 | 240 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Kuang, W.; Feng, J.; Wang, H.; Zhang, F.; Li, D. Effects of Cooling Rate and Solid Fraction on α-Al Phase Evolution in Rheo-Die Casting: Phase-Field Simulation and Experimental Investigation. Materials 2025, 18, 4169. https://doi.org/10.3390/ma18174169
Chen S, Kuang W, Feng J, Wang H, Zhang F, Li D. Effects of Cooling Rate and Solid Fraction on α-Al Phase Evolution in Rheo-Die Casting: Phase-Field Simulation and Experimental Investigation. Materials. 2025; 18(17):4169. https://doi.org/10.3390/ma18174169
Chicago/Turabian StyleChen, Song, Wangwang Kuang, Jian Feng, Hongmiao Wang, Fan Zhang, and Daquan Li. 2025. "Effects of Cooling Rate and Solid Fraction on α-Al Phase Evolution in Rheo-Die Casting: Phase-Field Simulation and Experimental Investigation" Materials 18, no. 17: 4169. https://doi.org/10.3390/ma18174169
APA StyleChen, S., Kuang, W., Feng, J., Wang, H., Zhang, F., & Li, D. (2025). Effects of Cooling Rate and Solid Fraction on α-Al Phase Evolution in Rheo-Die Casting: Phase-Field Simulation and Experimental Investigation. Materials, 18(17), 4169. https://doi.org/10.3390/ma18174169





