Effect of Energy-Dependent Proton Irradiation in Thin-Film YBa2Cu3O7−δ Superconductor
Abstract
1. Introduction
2. Material and Methods
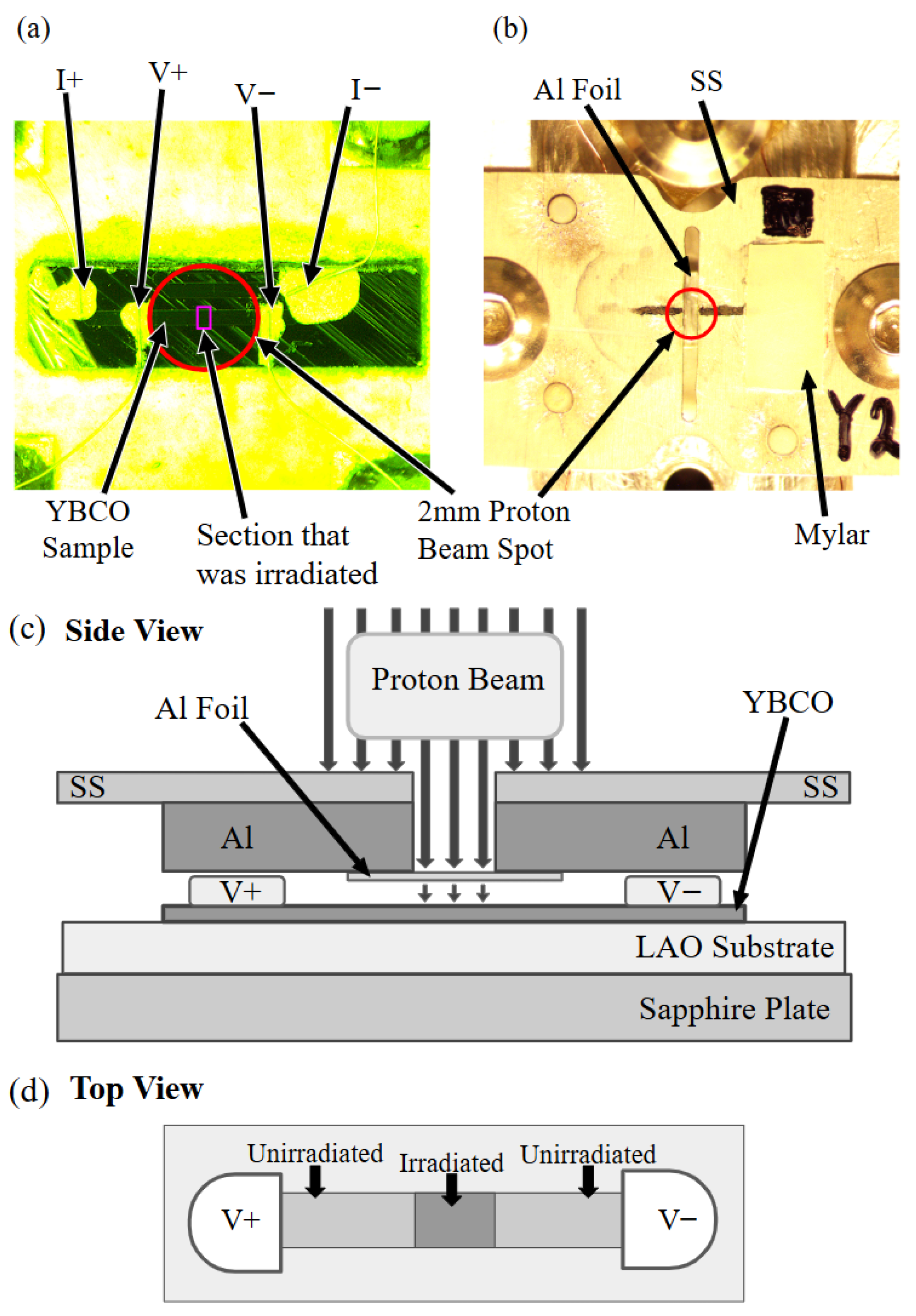
2.1. YBCO Thin Film and Resistance Measurements
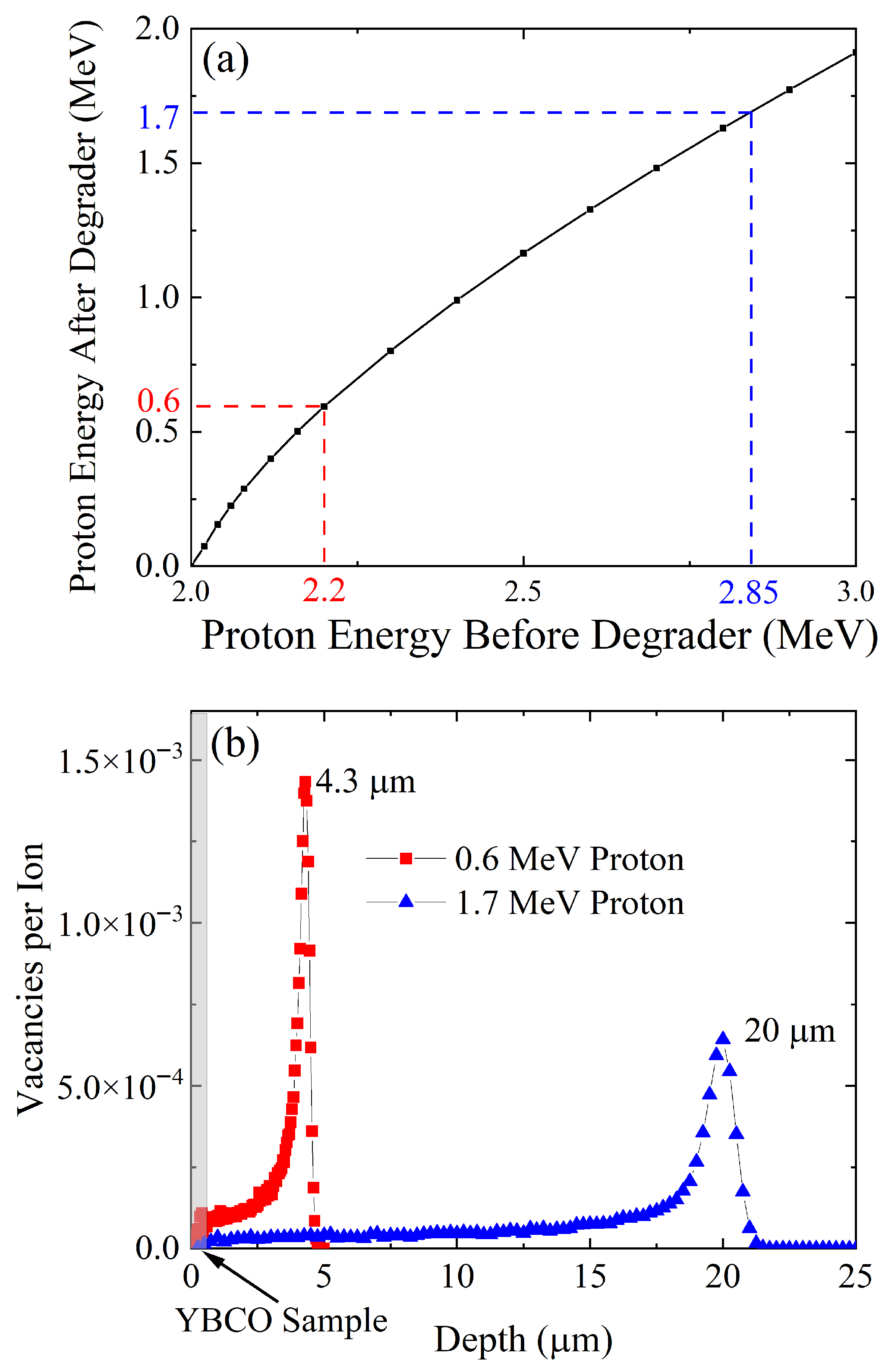
2.2. Energy Degrader and Homogeneous Proton Beam
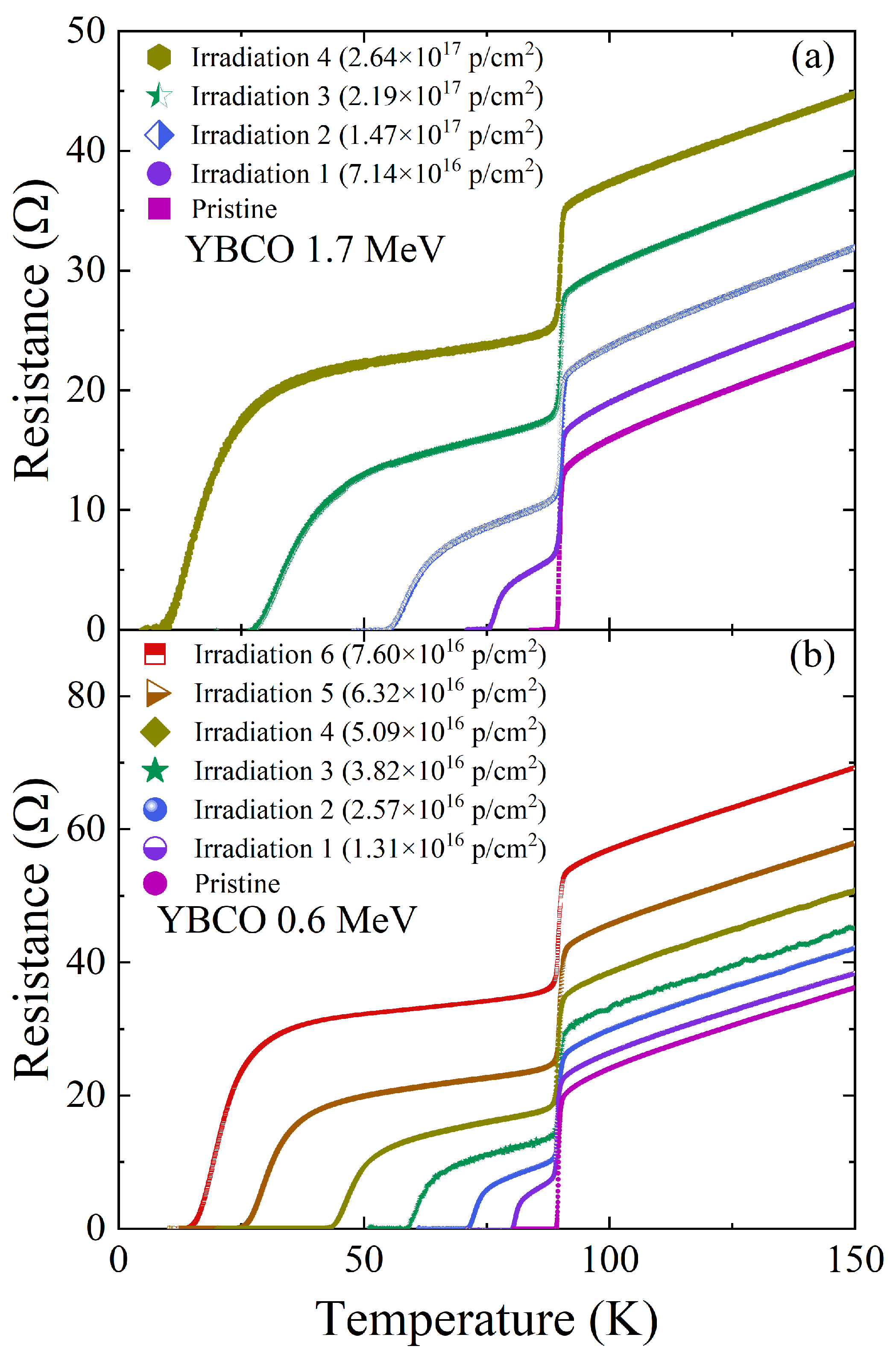
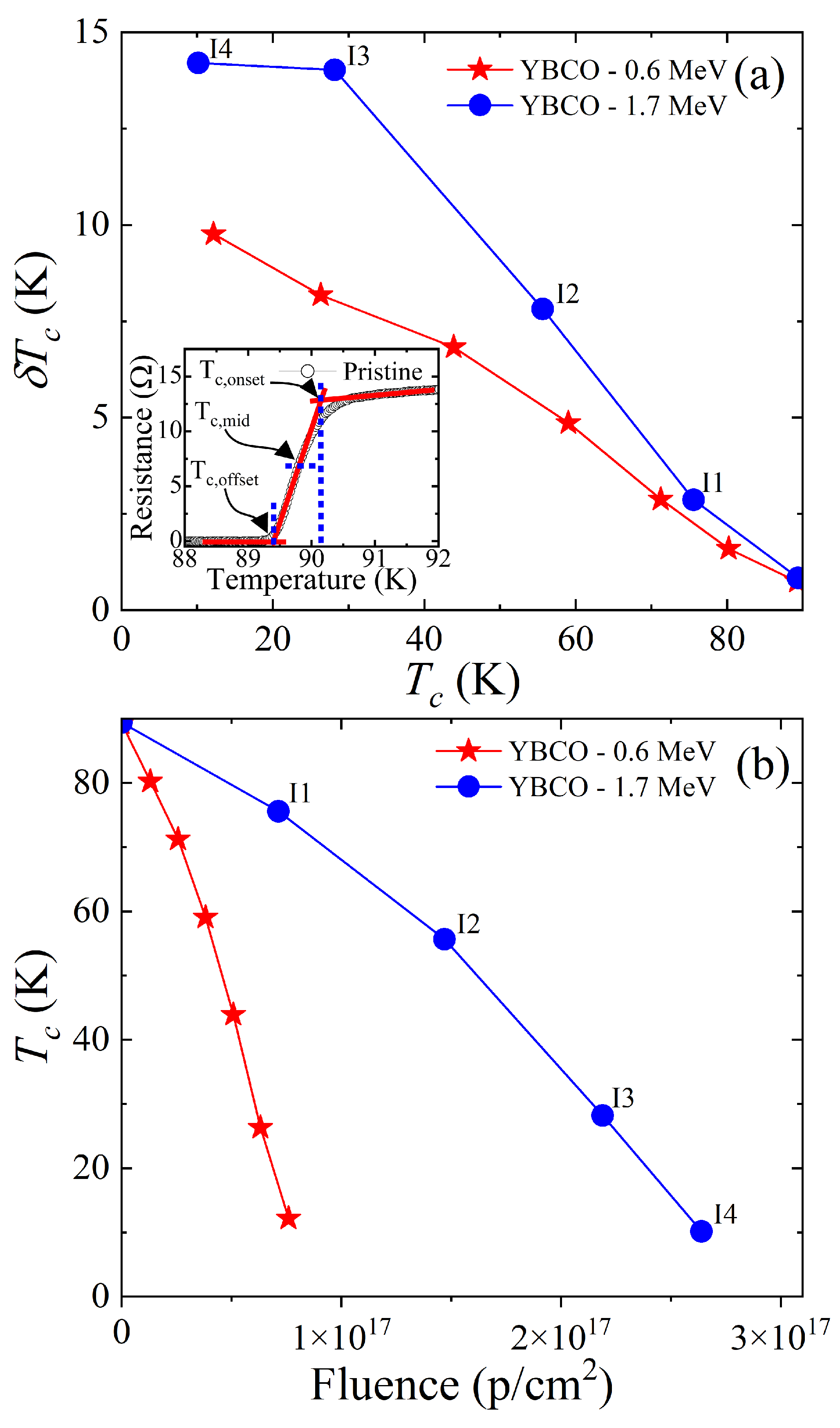
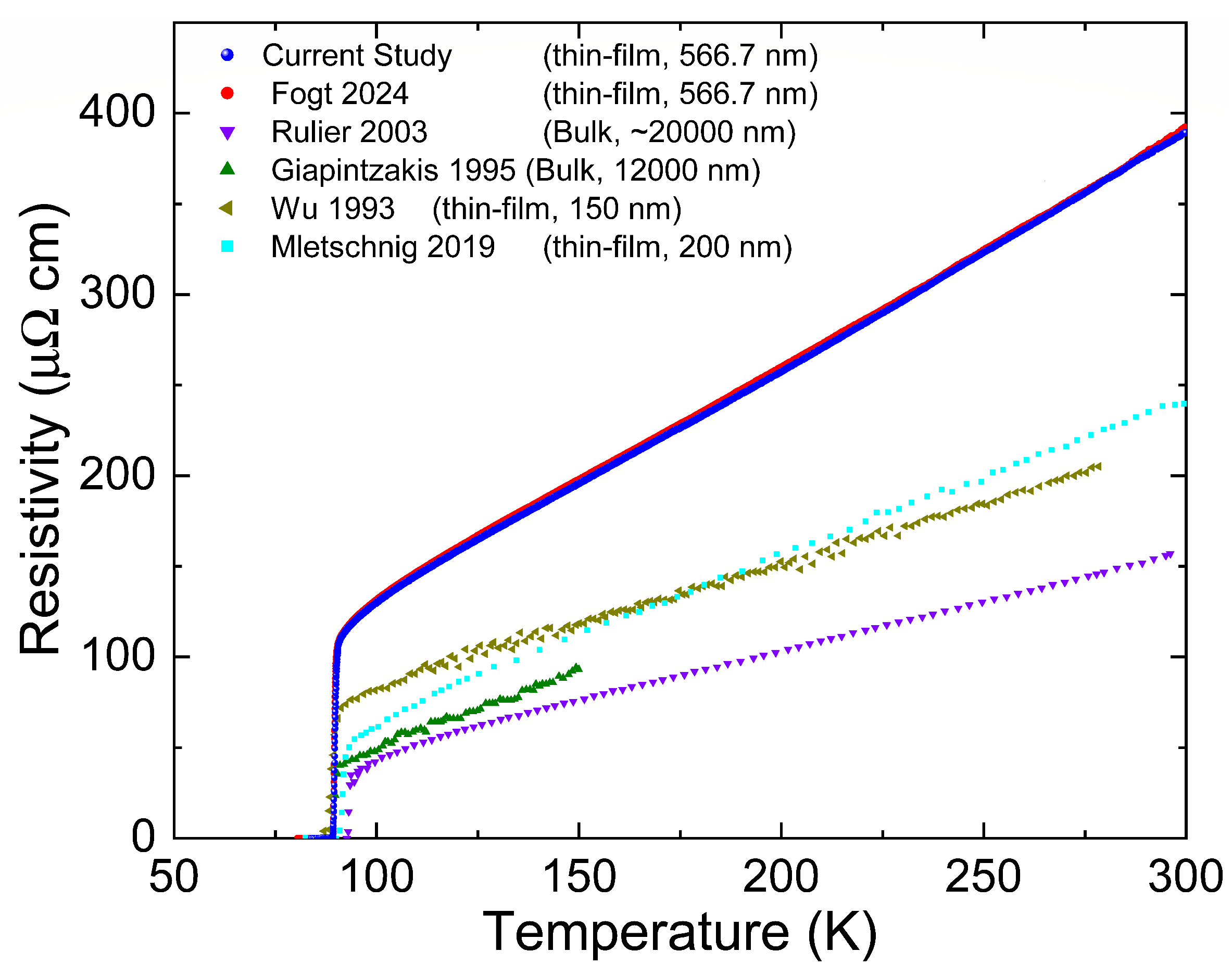
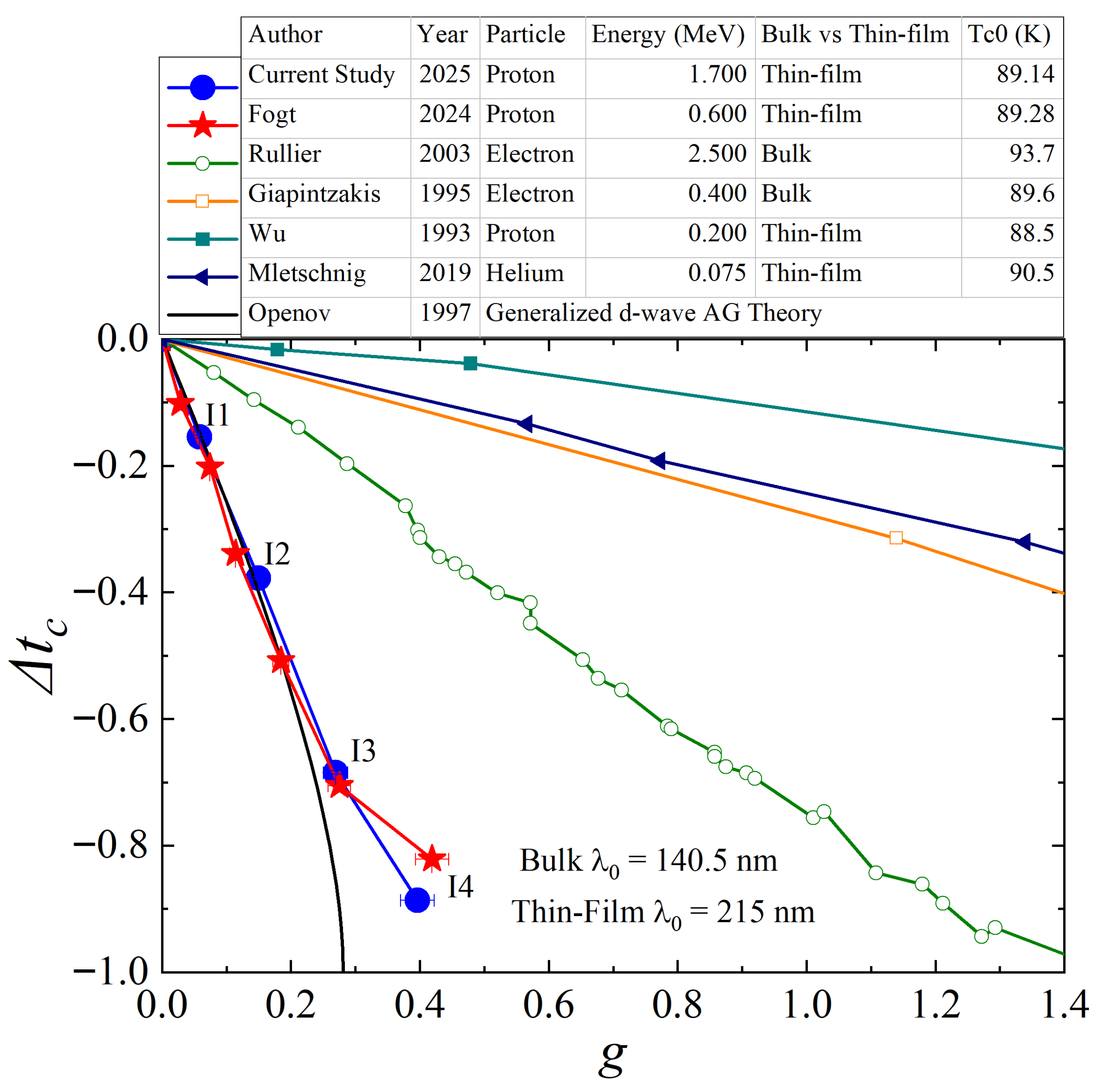
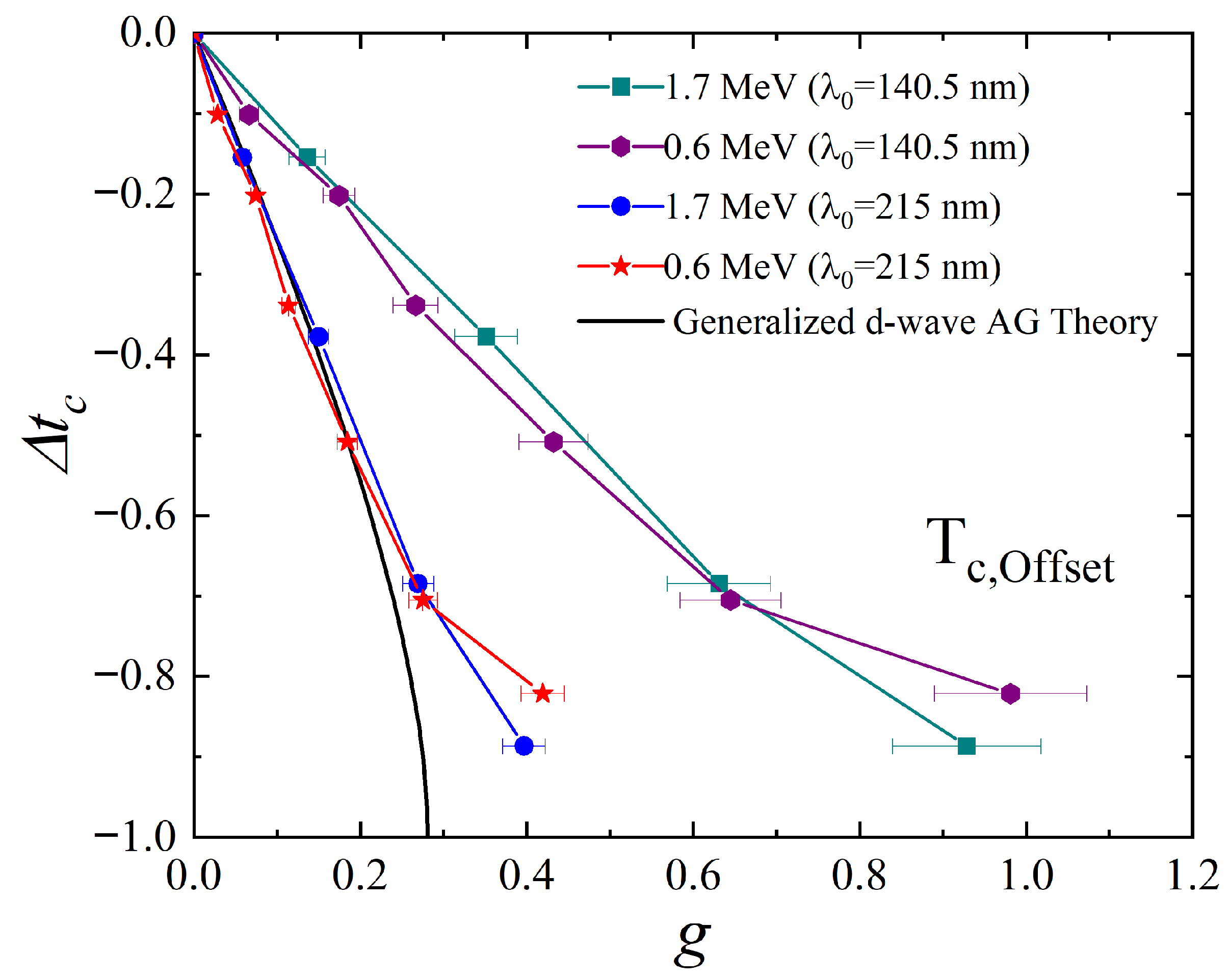
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bednorz, J.G.; Mueller, K.A. Possible high Tc superconductivity in the barium-lanthanum-copper-oxygen system. Z. Phys. B Condens. Matter 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Wu, M.K.; Ashburn, J.R.; Torng, C.J.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, Z.J.; Wang, Y.Q.; Chu, C.W. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure. Phys. Rev. Lett. 1987, 58, 908–910. [Google Scholar] [CrossRef]
- Hahn, S.; Kim, K.; Kim, K.; Hu, X.; Painter, T.; Dixon, I.; Kim, S.; Bhattarai, K.R.; Noguchi, S.; Jaroszynski, J.; et al. 45.5-tesla direct-current magnetic field generated with a high-temperature superconducting magnet. Nature 2019, 570, 496–499. [Google Scholar] [CrossRef] [PubMed]
- Molodyk, A.; Samoilenkov, S.; Markelov, A.; Degtyarenko, P.; Lee, S.; Petrykin, V.; Gaifullin, M.; Mankevich, A.; Vavilov, A.; Sorbom, B.; et al. Development and large volume production of extremely high current density YBa2Cu3O7 superconducting wires for fusion. Sci. Rep. 2021, 11, 2084. [Google Scholar] [CrossRef] [PubMed]
- Tsuei, C.C.; Kirtley, J.R. Pairing symmetry in cuprate superconductors. Rev. Mod. Phys. 2000, 72, 969–1016. [Google Scholar] [CrossRef]
- Anderson, P.W. Theory of dirty superconductors. J. Phys. Chem. Solids 1959, 11, 26–30. [Google Scholar] [CrossRef]
- Abrikosov, A.A.; Gor’kov, L.P. Contribution to the theory of superconducting alloys with paramagnetic impurities. Zh. Eksp. Teor. Fiz. 1960, 39, 1781. [Google Scholar]
- Ambegaokar, V.; Griffin, A. Theory of the Thermal Conductivity of Superconducting Alloys with Paramagnetic Impurities. Phys. Rev. 1965, 137, A1151–A1167. [Google Scholar] [CrossRef]
- Radtke, R.J.; Levin, K.; Schüttler, H.B.; Norman, M.R. Predictions for impurity-induced Tc suppression in the high-temperature superconductors. Phys. Rev. B 1993, 48, 653–656. [Google Scholar] [CrossRef]
- Openov, L.A. Combined effect of nonmagnetic and magnetic scatterers on the critical temperatures of superconductors with different anisotropies of the gap. J. Exp. Theor. Phys. Lett. 1997, 66, 661–667. [Google Scholar] [CrossRef]
- Wang, C.; Hirota, Y.; Wang, L.; Sakagami, R.; Li, Y.; Yi, X.; Li, W.; Chen, Y.; Yu, C.; Wang, Z.; et al. Peak effects in the kagome superconductors CsV3Sb5 and Cs(V0.93Nb0.07)3Sb5. Phys. Rev. B 2024, 109, 024514. [Google Scholar] [CrossRef]
- Remillard, S.K.; Wormmeester, A.E.; Huizen, R.A. Local Whole-Device Scanning of Distortion in Superconducting Microwave Resonators. IEEE Trans. Appl. Supercond. 2018, 28, 1500505. [Google Scholar] [CrossRef]
- Cho, K.; Kończykowski, M.; Teknowijoyo, S.; Tanatar, M.A.; Prozorov, R. Using electron irradiation to probe iron-based superconductors. Supercond. Sci. Technol. 2018, 31, 064002. [Google Scholar] [CrossRef]
- Ghigo, G.; Torsello, D.; Ummarino, G.A.; Gozzelino, L.; Tanatar, M.A.; Prozorov, R.; Canfield, P.C. Disorder-Driven Transition from s± to s++ Superconducting Order Parameter in Proton Irradiated Ba(Fe1−xRhx)2As2 Single Crystals. Phys. Rev. Lett. 2018, 121, 107001. [Google Scholar] [CrossRef]
- Smylie, M.P.; Leroux, M.; Mishra, V.; Fang, L.; Taddei, K.M.; Chmaissem, O.; Claus, H.; Kayani, A.; Snezhko, A.; Welp, U.; et al. Effect of proton irradiation on superconductivity in optimally doped BaFe2(As1−xPx)2 single crystals. Phys. Rev. B 2016, 93, 115119. [Google Scholar] [CrossRef]
- Mletschnig, K.; Lang, W. Nano-patterning of cuprate superconductors by masked He+ ion irradiation: 3-dimensional profiles of the local critical temperature. Microelectron. Eng. 2019, 215, 110982. [Google Scholar] [CrossRef]
- Rullier-Albenque, F.; Alloul, H.; Tourbot, R. Influence of Pair Breaking and Phase Fluctuations on Disordered High Tc Cuprate Superconductors. Phys. Rev. Lett. 2003, 91, 047001. [Google Scholar] [CrossRef] [PubMed]
- Giapintzakis, J.; Ginsberg, D.M.; Kirk, M.A. Determination of the Symmetry of the Superconducting Pairing State and Formation of a Low-Temperature Normal Metallic State in YBCO by Electron Irradiation; Technical Report; Argonne National Lab: Argonne, IL, USA, 1995. [Google Scholar]
- Cho, K.; Kończykowski, M.; Teknowijoyo, S.; Tanatar, M.A.; Liu, Y.; Lograsso, T.A.; Straszheim, W.E.; Mishra, V.; Maiti, S.; Hirschfeld, P.J.; et al. Energy gap evolution across the superconductivity dome in single crystals of Ba1−xKxFe2As2. Sci. Adv. 2016, 2, e1600807. [Google Scholar] [CrossRef]
- Cho, K.; Kończykowski, M.; Teknowijoyo, S.; Ghimire, S.; Tanatar, M.A.; Mishra, V.; Prozorov, R. Intermediate scattering potential strength in electron-irradiated YBa2Cu3O7−δ from London penetration depth measurements. Phys. Rev. B 2022, 105, 014514. [Google Scholar] [CrossRef]
- Wu, J.Z.; Yu, N.; Chu, W.K. Anisotropy of the ion-beam radiation effect in YBa2Cu3O7−δ (110) thin films. Phys. Rev. B 1993, 48, 9929–9931. [Google Scholar] [CrossRef]
- Torsello, D.; Fracasso, M.; Gerbaldo, R.; Ghigo, G.; Laviano, F.; Napolitano, A.; Iebole, M.; Cialone, M.; Manca, N.; Martinelli, A.; et al. Proton Irradiation Effects on the Superconducting Properties of Fe(Se,Te) Thin Films. IEEE Trans. Appl. Supercond. 2022, 32, 7500105. [Google Scholar] [CrossRef]
- Konczykowski, M.; Rullier-Albenque, F.; Yacoby, E.R.; Shaulov, A.; Yeshurun, Y.; Lejay, P. Effect of 5.3-GeV Pb-ion irradiation on irreversible magnetization in Y-Ba-Cu-O crystals. Phys. Rev. B 1991, 44, 7167–7170. [Google Scholar] [CrossRef]
- Nakajima, Y.; Tsuchiya, Y.; Taen, T.; Tamegai, T.; Okayasu, S.; Sasase, M. Enhancement of critical current density in Co-doped BaFe2As2 with columnar defects introduced by heavy-ion irradiation. Phys. Rev. B 2009, 80, 012510. [Google Scholar] [CrossRef]
- Openov, L.A. Critical temperature of an anisotropic superconductor containing both nonmagnetic and magnetic impurities. Phys. Rev. B 1998, 58, 9468–9478. [Google Scholar] [CrossRef][Green Version]
- Graser, S.; Hirschfeld, P.J.; Zhu, L.Y.; Dahm, T. Tc suppression and resistivity in cuprates with out of plane defects. Phys. Rev. B 2007, 76, 054516. [Google Scholar] [CrossRef]
- Garg, A.; Randeria, M.; Trivedi, N. Strong correlations make high-temperature superconductors robust against disorder. Nat. Phys. 2008, 4, 762–765. [Google Scholar] [CrossRef]
- Kemper, A.F.; Doluweera, D.G.S.P.; Maier, T.A.; Jarrell, M.; Hirschfeld, P.J.; Cheng, H.P. Insensitivity of d-wave pairing to disorder in the high-temperature cuprate superconductors. Phys. Rev. B 2009, 79, 104502. [Google Scholar] [CrossRef]
- Tang, S.; Dobrosavljević, V.; Miranda, E. Strong correlations generically protect d-wave superconductivity against disorder. Phys. Rev. B 2016, 93, 195109. [Google Scholar] [CrossRef]
- Fogt, J.; Weeda, H.; Harrison, T.; Miles, N.; Cho, K. Effect of Proton Irradiation on Thin-Film YBa2Cu3O7 Superconductor. Materials 2024, 17, 4601. [Google Scholar] [CrossRef] [PubMed]
- Remillard, S.K.; Kirkendall, D.; Ghigo, G.; Gerbaldo, R.; Gozzelino, L.; Laviano, F.; Yang, Z.; Mendelsohn, N.A.; Ghamsari, B.G.; Friedman, B.; et al. Microwave nonlinearity and photoresponse of superconducting resonators with columnar defect micro-channels. Supercond. Sci. Technol. 2014, 27, 095006. [Google Scholar] [CrossRef][Green Version]
- Ziegler, J.F.; Ziegler, M.; Biersack, J. SRIM–The stopping and range of ions in matter. Nucl. Instrum. Methods Phys. Res. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Miles, N.; Fogt, J.; Harrison, T.; Weeda, H.; Bunnell, A.; DeYoung, P.; Cho, K. Correcting Faraday Cup Measurements with Rutherford Backscattering Spectroscopy. J. Undergrad. Res. Phys. Astron. 2025, 34, 46. [Google Scholar]
- Prozorov, R.; Kończykowski, M.; Tanatar, M.A.; Thaler, A.; Bud’ko, S.L.; Canfield, P.C.; Mishra, V.; Hirschfeld, P.J. Effect of Electron Irradiation on Superconductivity in Single Crystals of Ba(Fe1−xRux)2As2 (x = 0.24). Phys. Rev. X 2014, 4, 041032. [Google Scholar] [CrossRef]
- Prozorov, R.; Giannetta, R.W.; Carrington, A.; Fournier, P.; Greene, R.L.; Guptasarma, P.; Hinks, D.G.; Banks, A.R. Measurements of the absolute value of the penetration depth in high-Tc superconductors using a low-Tc superconductive coating. Appl. Phys. Lett. 2000, 77, 4202–4204. [Google Scholar] [CrossRef]
- Bernhard, C.; Niedermayer, C.; Binninger, U.; Hofer, A.; Wenger, C.; Tallon, J.L.; Williams, G.V.M.; Ansaldo, E.J.; Budnick, J.I.; Stronach, C.E.; et al. Magnetic penetration depth and condensate density of cuprate high-Tc superconductors determined by muon-spin-rotation experiments. Phys. Rev. B 1995, 52, 10488–10498. [Google Scholar] [CrossRef] [PubMed]
- Djordjevic, S.; de Vaulchier, L.A.; Bontemps, N.; Vieren, J.P.; Guldner, Y.; Moffat, S.; Preston, J.; Castel, X.; Guilloux-Viry, M.; Perrin, A. Low temperature penetration depth and the effect of quasi-particle scattering measured by millimeter wave transmission in YBa2Cu3O7-δ thin films. Eur. Phys. J. B Condens. Matter Complex Syst. 1998, 5, 847–858. [Google Scholar] [CrossRef][Green Version]
- Zaitsev, A.G.; Schneider, R.; Linker, G.; Ratzel, F.; Smithey, R.; Schweiss, P.; Geerk, J.; Schwab, R.; Heidinger, R. Microwave measurements of the absolute London penetration depth in double-sided YBa2Cu3O7−x thin films on sapphire. Rev. Sci. Instrum. 2002, 73, 335–344. [Google Scholar] [CrossRef]
- Bonn, D.A.; Liang, R.; Riseman, T.M.; Baar, D.J.; Morgan, D.C.; Zhang, K.; Dosanjh, P.; Duty, T.L.; MacFarlane, A.; Morris, G.D.; et al. Microwave determination of the quasiparticle scattering time in YBa2Cu3O6.95. Phys. Rev. B 1993, 47, 11314–11328. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; McGraw Hill: New York, NY, USA, 1996. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harrison, T.; Kim, J.; Cook, K.; Weeda, H.; Fogt, J.; Miles, N.; Cho, K. Effect of Energy-Dependent Proton Irradiation in Thin-Film YBa2Cu3O7−δ Superconductor. Materials 2025, 18, 4845. https://doi.org/10.3390/ma18214845
Harrison T, Kim J, Cook K, Weeda H, Fogt J, Miles N, Cho K. Effect of Energy-Dependent Proton Irradiation in Thin-Film YBa2Cu3O7−δ Superconductor. Materials. 2025; 18(21):4845. https://doi.org/10.3390/ma18214845
Chicago/Turabian StyleHarrison, Trevor, Joshua Kim, Katharina Cook, Hope Weeda, Joseph Fogt, Nolan Miles, and Kyuil Cho. 2025. "Effect of Energy-Dependent Proton Irradiation in Thin-Film YBa2Cu3O7−δ Superconductor" Materials 18, no. 21: 4845. https://doi.org/10.3390/ma18214845
APA StyleHarrison, T., Kim, J., Cook, K., Weeda, H., Fogt, J., Miles, N., & Cho, K. (2025). Effect of Energy-Dependent Proton Irradiation in Thin-Film YBa2Cu3O7−δ Superconductor. Materials, 18(21), 4845. https://doi.org/10.3390/ma18214845





