Fabrication Process and Surface Morphology Prediction of Radial Straight Groove-Structured CBN Grinding Wheel by Laser Cladding
Abstract
1. Introduction
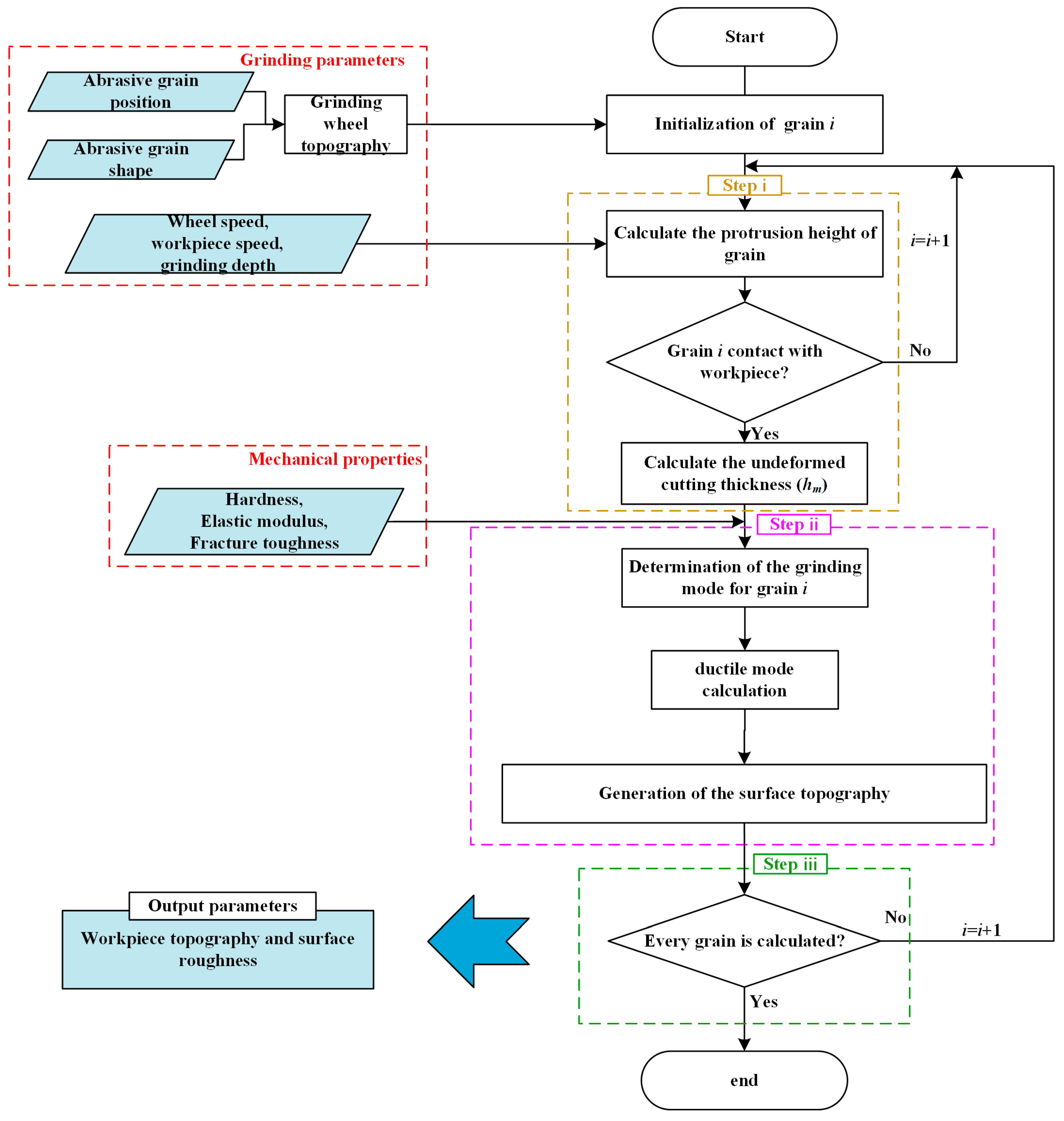
2. Modelling
2.1. Grinding Wheel Modeling
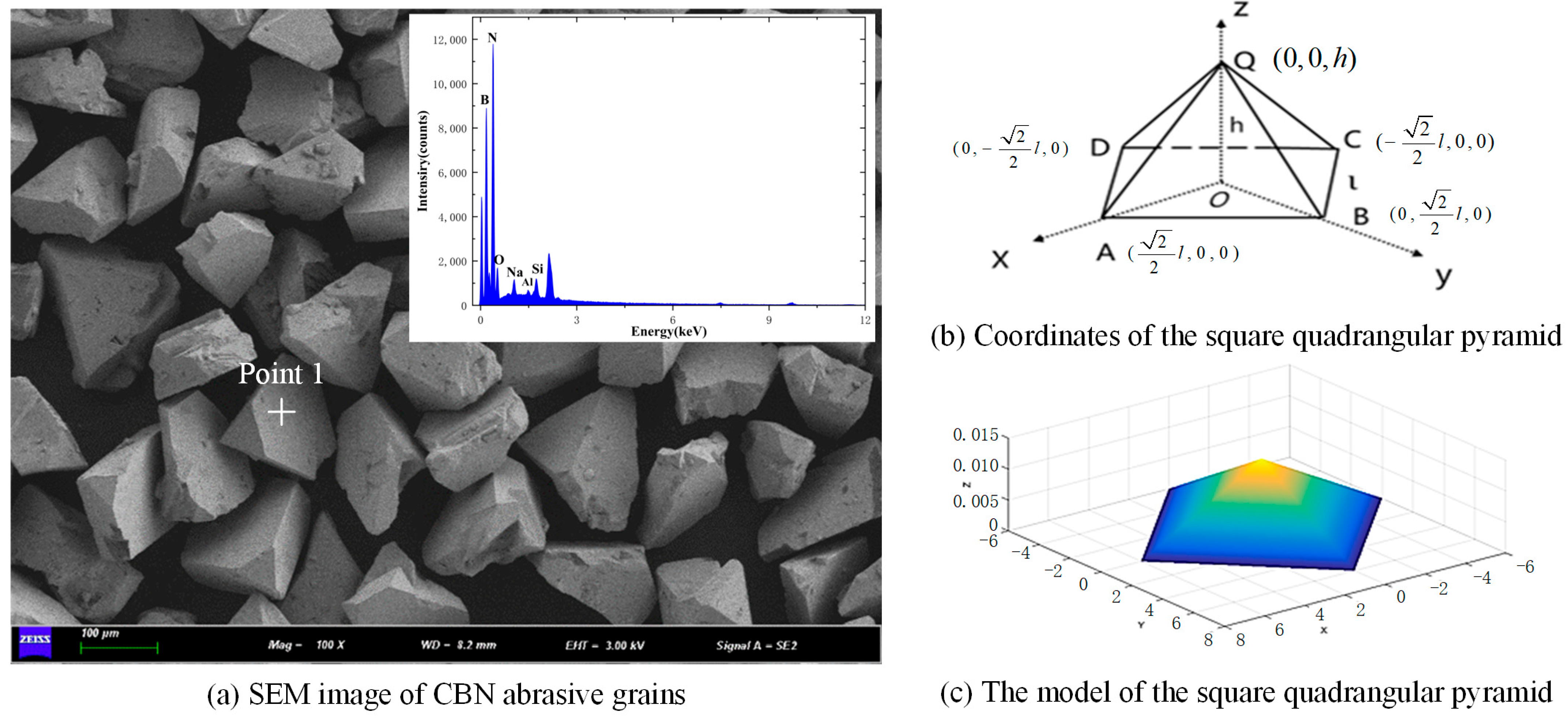
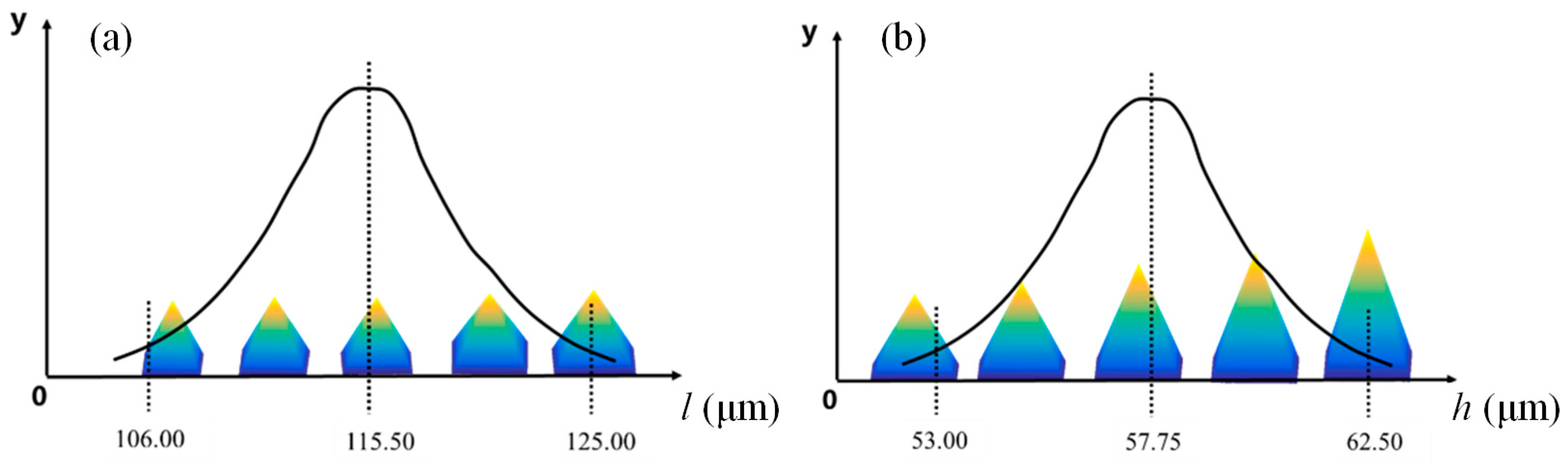
2.1.1. CBN Abrasive Grain Model
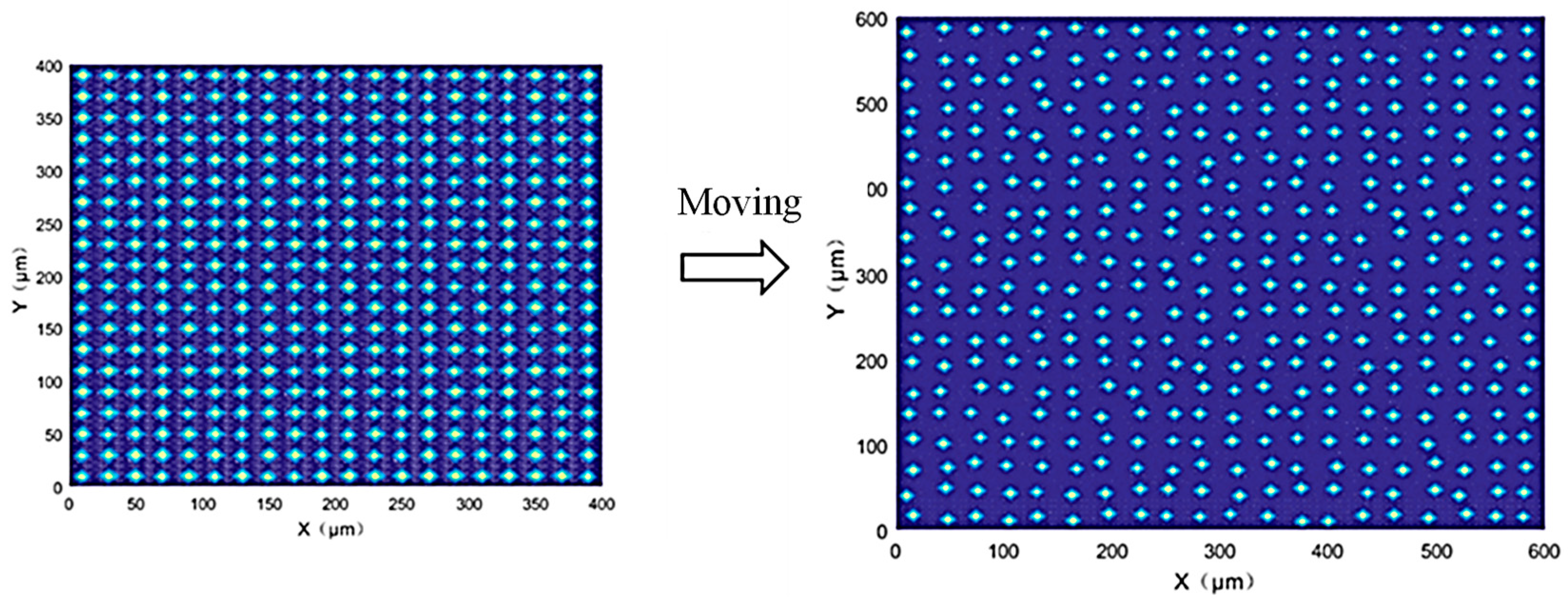
2.1.2. Grinding Wheel Morphology
2.2. Simulation of Ground Surface Morphology
- (1)
- Abrasive grain deformation and wear are neglected, and grains are considered rigid bodies during the grinding process.
- (2)
- Workpiece material deformation is ignored; material in contact with grains is directly removed.
- (3)
- The vibrations of the machine and grinding wheel during grinding are not considered.
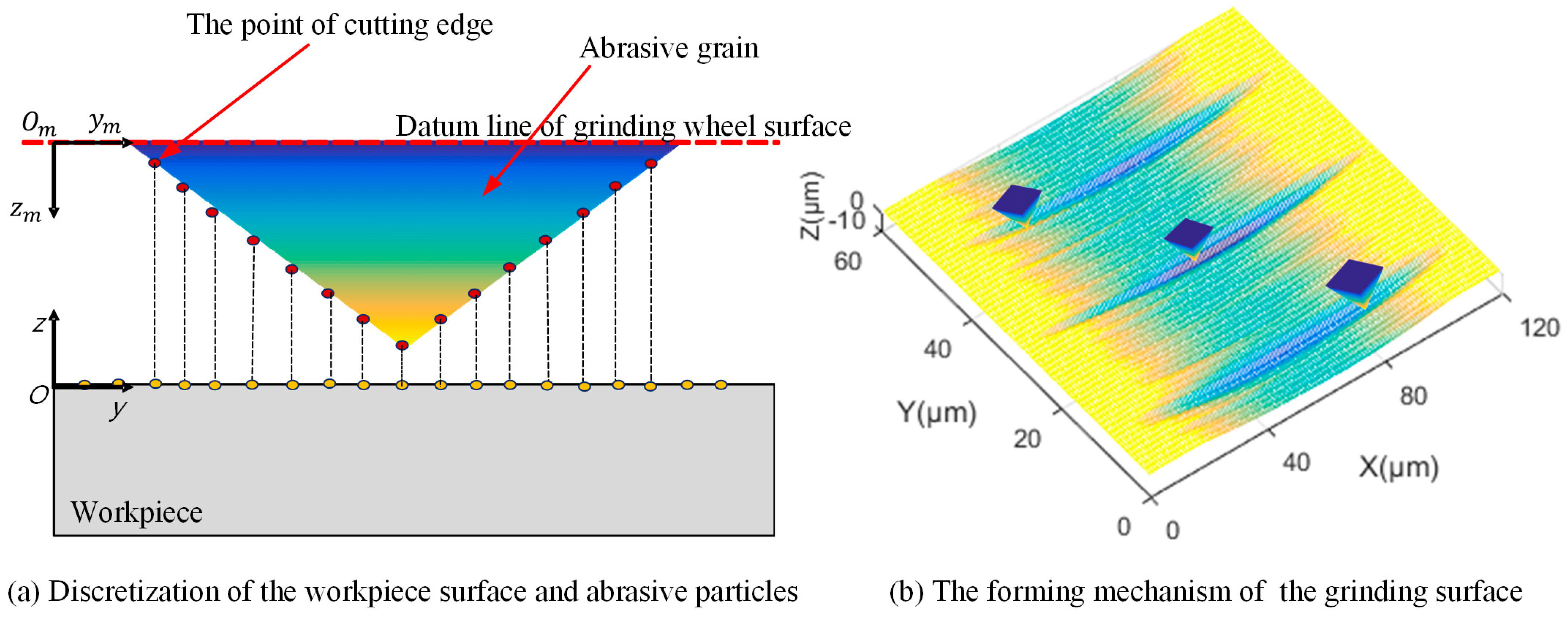
2.2.1. Motion Trajectory of Abrasive Grain
2.2.2. Model of Surface Morphology Generation
3. Experiment Method
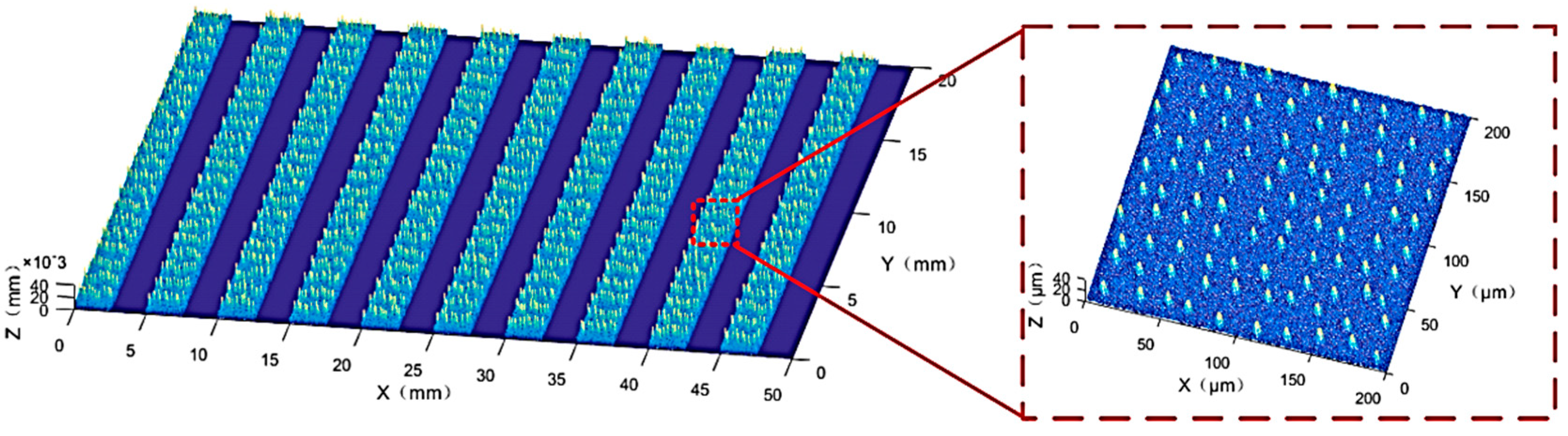
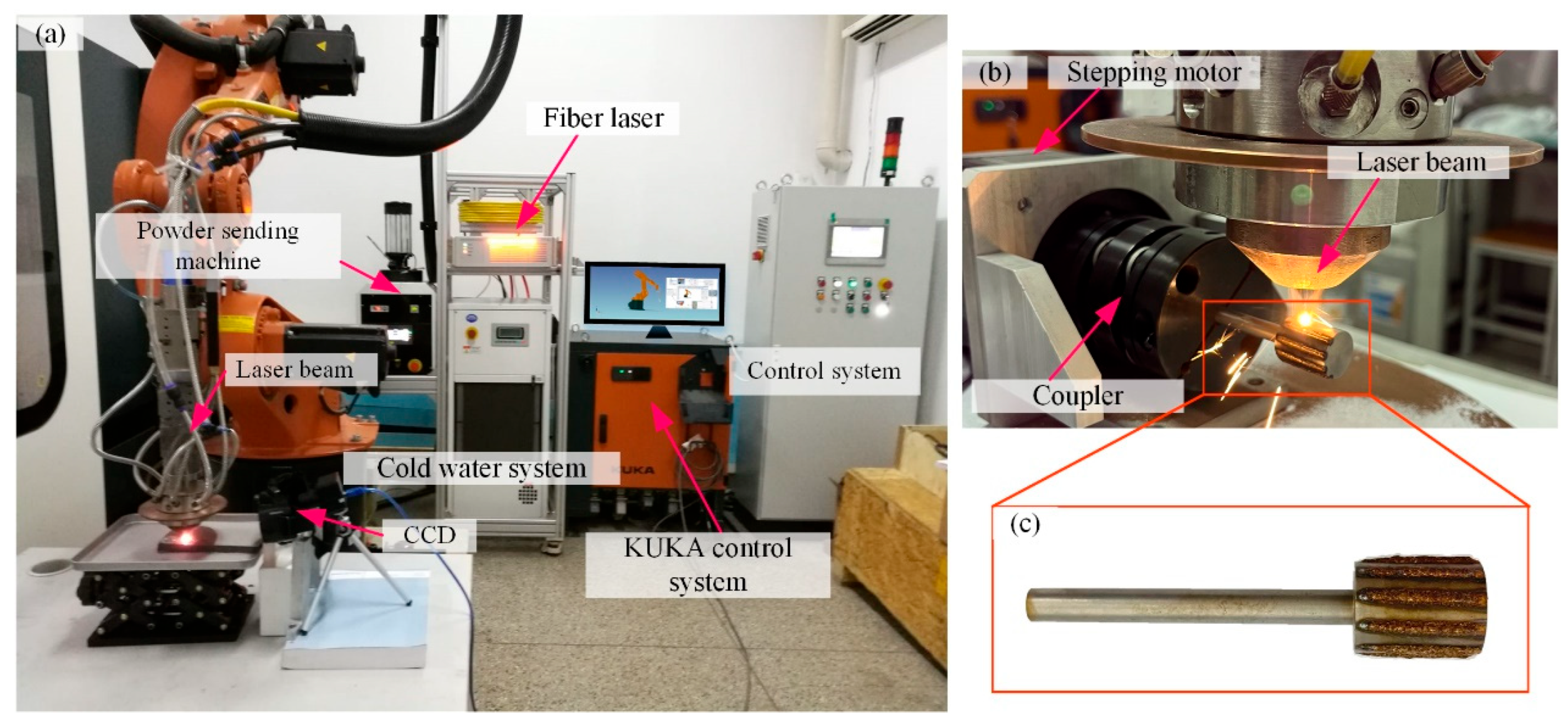
3.1. Fabrication of Laser-Melting Structured CBN Grinding Wheel
3.2. Grinding Experiment
4. Discussion and Analysis
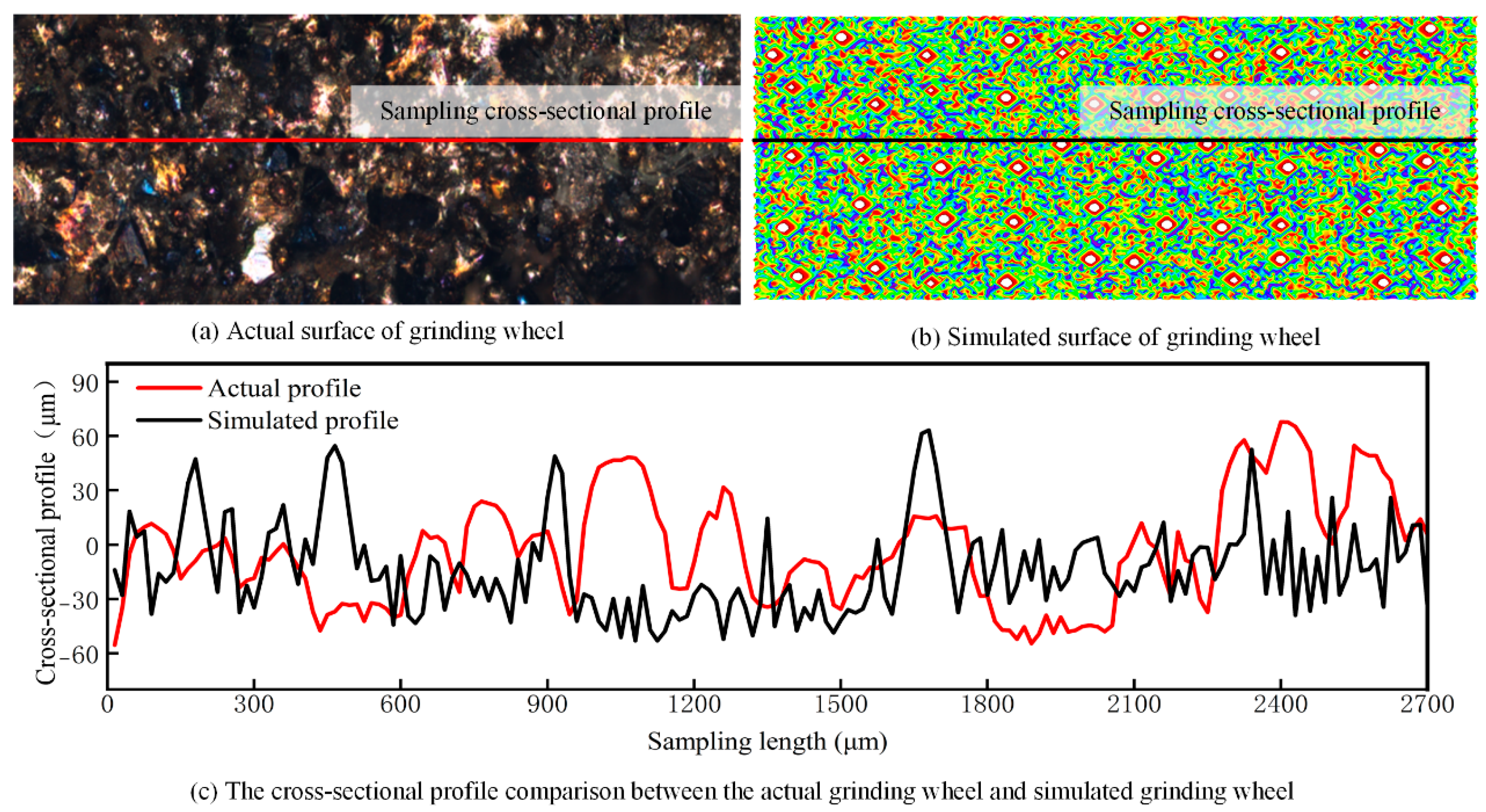
4.1. Comparison of Grinding Wheel Models
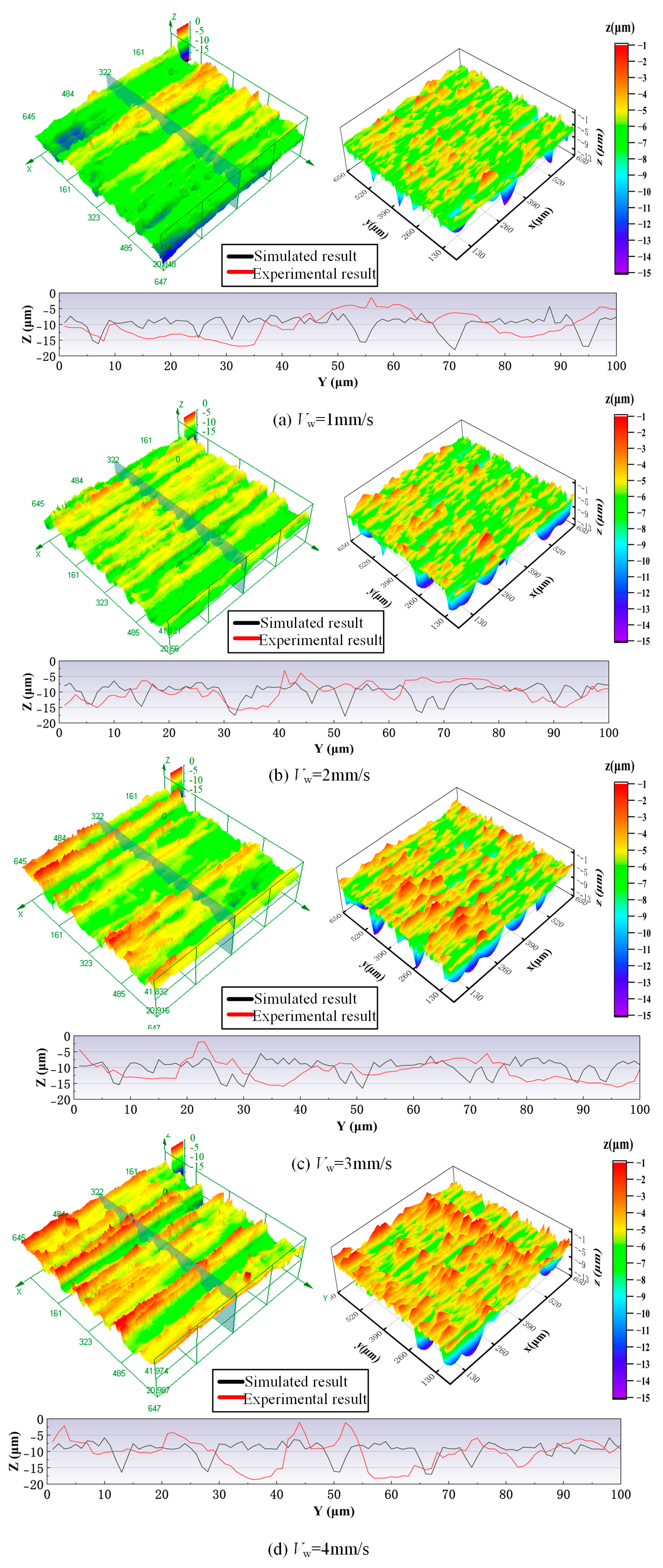
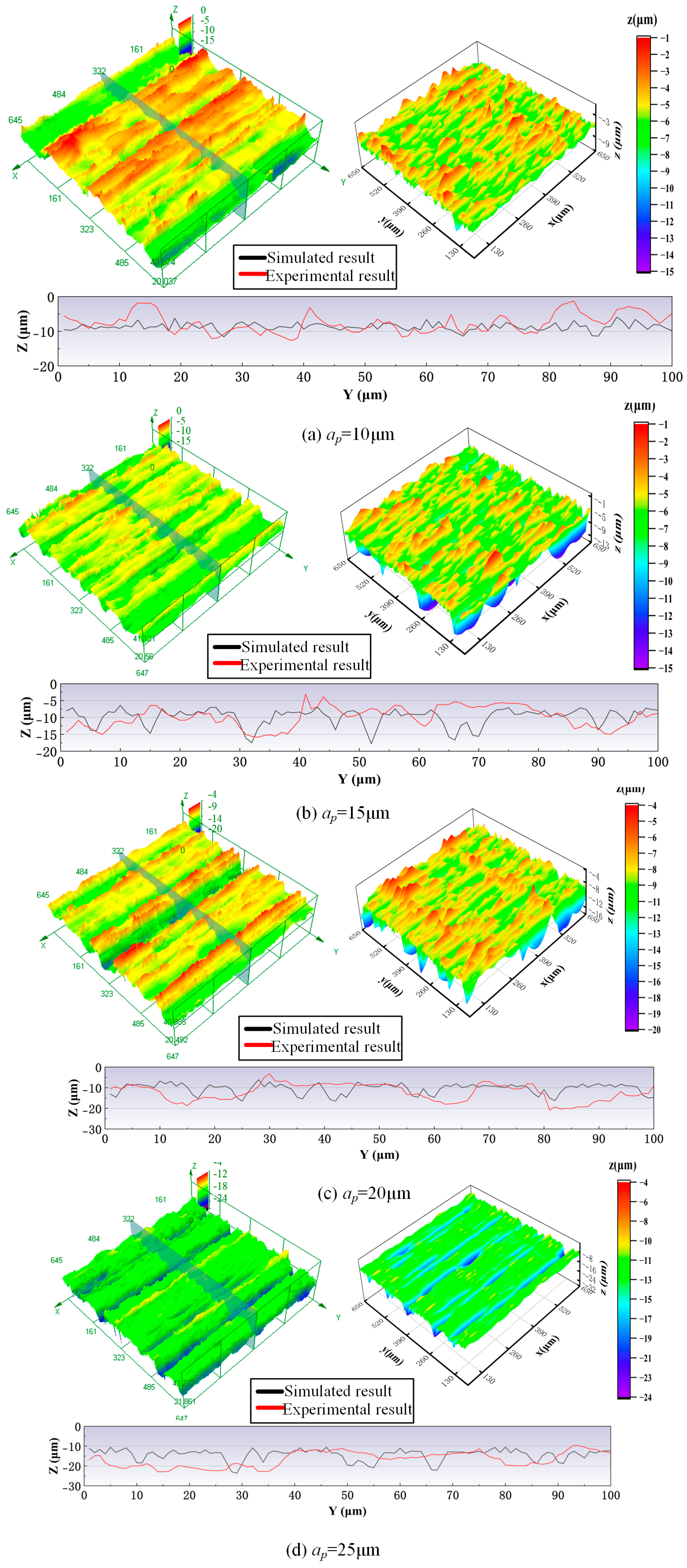
4.2. Analysis of Grinding Surface Morphology
4.2.1. Wheel Speed
4.2.2. Feeding Speed
4.2.3. Grinding Depth
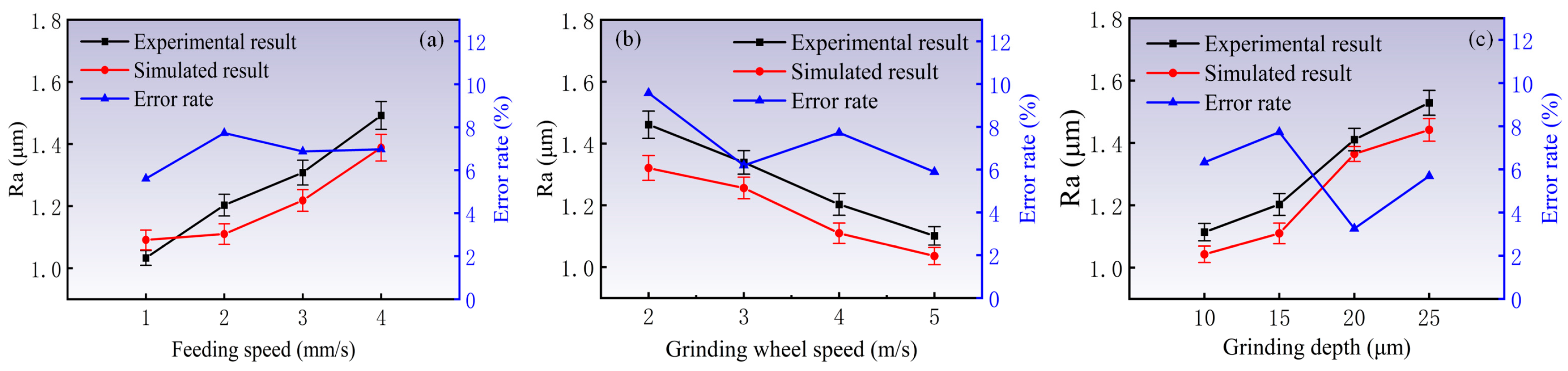
4.3. Analysis of Surface Roughness
5. Conclusions
- (1)
- Additive manufacturing technology was used to fabricate a radial straight groove-structured grinding wheel. Meanwhile, a corresponding mathematical model of the grinding wheel was also established considering the shape and position of the abrasive grains. A comparison of the wheel surface morphology substantiated the reliability and rationality of the simulated grinding wheel. The results showed that although the wheel surface morphology had different peak–valley pairs, their overall fluctuation ranges were essentially the same, with an error rate of less than 5%. Therefore, the simulated grinding wheel model closely matched the real one.
- (2)
- The ground surface morphologies of the fabricated wheel and simulated wheel under different machining parameter conditions were compared to further prove the rationality of the simulated grinding wheel. The results showed that the ground surfaces of the fabricated wheel and simulated wheel had similar morphological characteristics, which proved the correctness of the grinding mechanism analysis for the radial straight groove-structured grinding wheel.
- (3)
- The trend in the surface roughness under different machining parameter conditions was also analyzed and showed the same variation for the fabricated and simulated wheels; the error rate was confined within 8%. The discrepancy is attributable to inherent systematic errors in the simulation model, which considers only idealized grain–workpiece pure cutting while neglecting additional phenomena that influence the real surface morphology.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, Y.; Chen, B.; Liu, Z.; Sun, S.; Liu, G.; Guo, B. Research Progress of Abrasive Groups Ordered Grinding Wheels. Chin. J. Mech. Eng. 2025, 1–32. [Google Scholar] [CrossRef]
- Forbrigger, C.; Bauer, R.; Warkentin, A. A review of state-of-the-art vitrified bond grinding wheel grooving processes. Int. J. Adv. Manuf. Technol. 2016, 90, 2207–2216. [Google Scholar] [CrossRef]
- Li, H.N.; Axinte, D. Textured grinding wheels: A review. Int. J. Mach. Tools Manuf. 2016, 109, 8–35. [Google Scholar] [CrossRef]
- Chen, C.; Tang, J.; Chen, H.; Zhao, B. An active manufacturing method of surface micro structure based on ordered grinding wheel and ultrasonic-assisted grinding. Int. J. Adv. Manuf. Technol. 2018, 97, 1627–1635. [Google Scholar] [CrossRef]
- Azarhoushang, B.; Daneshi, A.; Lee, D.H. Evaluation of thermal damages and residual stresses in dry grinding by structured wheels. J. Clean. Prod. 2017, 142, 1922–1930. [Google Scholar] [CrossRef]
- He, Q.; Xie, Y.; Liu, T.; Zhao, Y.; Li, S.; Cui, Z. Experimental investigation on performance of electroplated CBN wheel with ordered arrangement of abrasives in dry grinding. Int. J. Adv. Manuf. Technol. 2022, 121, 4919–4927. [Google Scholar] [CrossRef]
- Zhang, Y.; Fang, C.; Huang, G.; Xu, X. Modeling and simulation of the distribution of undeformed chip thicknesses in surface grinding. Int. J. Mach. Tools Manuf. 2018, 127, 14–27. [Google Scholar] [CrossRef]
- Azarhoushang, B.; Zahedi, A. Laser conditioning and structuring of grinding tools—A review. Adv. Manuf. 2017, 5, 35–49. [Google Scholar] [CrossRef]
- Yu, H.; Han, Z.; Zhang, J.; Zhang, S. Bionic design of tools in cutting: Reducing adhesion, abrasion or friction. Wear 2021, 482-483. [Google Scholar] [CrossRef]
- Yu, H.; Lu, Y.; Wang, J. Study on wear of the grinding wheel with an abrasive phyllotactic pattern. Wear 2016, 358-359, 89–96. [Google Scholar] [CrossRef]
- Deng, H.; Wu, X.; Yuchi, G.; Liu, G.; Xu, Z.; Yi, J. Research on laser preparation and grinding performance of hydrophilic structured grinding wheels. Ceram. Int. 2022, 49, 7649–7661. [Google Scholar] [CrossRef]
- Yu, H.; Zhang, W.; Zhang, S.; Zhang, J.; Han, Z. Optimization of hydrodynamic properties of structured grinding wheels based on combinatorial bionics. Tribol. Int. 2022, 173. [Google Scholar] [CrossRef]
- Yu, H.; Sun, K.; Ren, W.; Zhang, J.; Han, Z. Synergistic improvement of grinding fluid utilization and workpiece surface quality using combinatorial bionic structured grinding wheels. J. Manuf. Process. 2024, 130, 102–117. [Google Scholar] [CrossRef]
- Yi, J.; Yi, T.; Deng, H.; Chen, B.; Zhou, W. Theoretical modeling and experimental study on grinding force of straight groove structured grinding wheel. Int. J. Adv. Manuf. Technol. 2022, 124, 3407–3421. [Google Scholar] [CrossRef]
- Jia, J.; Zhang, Q.; Yang, W.; Yao, H.; Wu, G.; Zhao, H.; Zhu, J.; Li, K.; Guo, B.; Qin, J. Analysis and optimization of microchannel array precision grinding processes with micro-structured micro-grinding tool. Chin. J. Aeronaut. 2024, 38, 103261. [Google Scholar] [CrossRef]
- Wu, M.; Guo, B.; Zhao, Q.; Fan, R.; Dong, Z.; Yu, X. The influence of the focus position on laser machining and laser micro-structuring monocrystalline diamond surface. Opt. Lasers Eng. 2018, 105, 60–67. [Google Scholar] [CrossRef]
- Wu, M.; Guo, B.; Zhao, Q.; He, P. Precision grinding of a microstructured surface on hard and brittle materials by a microstructured coarse-grained diamond grinding wheel. Ceram. Int. 2018, 44, 8026–8034. [Google Scholar] [CrossRef]
- Yang, Z.; He, D.; Sun, W.; Zhang, Y.; Zhang, S.; Shi, H.; Liu, S.; Zhang, Y. Determination of the grinding force on optical glass based on a diamond wheel with an ordered arrangement of abrasive grains. Int. J. Adv. Manuf. Technol. 2021, 115, 1237–1248. [Google Scholar] [CrossRef]
- Zhang, F.-L.; Li, M.-C.; Wang, J.; Huang, H.-P.; Wang, C.-Y.; Zhou, Y.-M. Effect of arraying parameters on dry grinding performance of patterned monolayer brazed CBN wheel. Int. J. Adv. Manuf. Technol. 2020, 107, 2081–2089. [Google Scholar] [CrossRef]
- Ding, W.; Linke, B.; Zhu, Y.; Li, Z.; Fu, Y.; Su, H.; Xu, J. Review on monolayer CBN superabrasive wheels for grinding metallic materials. Chin. J. Aeronaut. 2017, 30, 109–134. [Google Scholar] [CrossRef]
- Costa, S.; Pereira, M.; Ribeiro, J.; Soares, D. Texturing Methods of Abrasive Grinding Wheels: A Systematic Review. Materials 2022, 15, 8044. [Google Scholar] [CrossRef]
- Buravlev, I.; Shichalin, O.; Marmaza, P.; Kolodeznikov, E.; Dvornik, M.; Sakhnevich, A.; Buravleva, A.; Chuklinov, S.; Papynov, E. Microstructural evolution and mechanical behavior of WC–4wt.% TiC–3wt.% TaC–12wt.% Co refractory cermet consolidated by spark plasma sintering of mechanically activated powder mixtures. Adv. Powder Technol. 2024, 35. [Google Scholar] [CrossRef]
- Wang, C.; Wang, D.; Tian, C.; Wang, L.; Rong, Y.; Li, X. Grinding performance evaluation of 3D-printed porous metal-bonded grinding wheel in BK7 glass grinding. Int. J. Adv. Manuf. Technol. 2021, 117, 1445–1457. [Google Scholar] [CrossRef]
- Tian, C.; Wan, Y.; Li, X.; Rong, Y. Study on the additively manufactured porous metal-bonded grinding wheel designed by octahedron lattice structure. Int. J. Adv. Manuf. Technol. 2023, 125, 1743–1756. [Google Scholar] [CrossRef]
- Ye, M.; Wang, D.; Wang, L.; Zhang, Y.; Li, X. Optimal design and performance evaluation of grinding wheels with triply periodic minimal surface lattice structure. J. Mater. Res. Technol. 2024, 32, 3181–3193. [Google Scholar] [CrossRef]
- Barmouz, M.; Azarhoushang, B.; Zahedi, A.; Rabiei, F.; Steinhäuser, F. Progress in grinding performance by additive manufacturing of grinding wheels integrated with internal venturi cooling channels and surface slots. J. Manuf. Process. 2023, 99, 485–500. [Google Scholar] [CrossRef]
- Yang, Z.; Zhang, M.; Zhang, Z.; Liu, A.; Yang, R.; Liu, S. A study on diamond grinding wheels with regular grain distribution using additive manufacturing (AM) technology. Mater. Des. 2016, 104, 292–297. [Google Scholar] [CrossRef]
- Wang, B.; Zhao, Y.; Liu, G.; Thein, C.K.; Su, W.; Long, S.; Qi, H.; Wei, P.; He, Y.; Li, H.N. Preventing thermal osteonecrosis through 3D printed ceramic grinding tool. Addit. Manuf. 2023, 78. [Google Scholar] [CrossRef]
- Yang, Z.; Zhu, L.; Ni, C.; Ning, J. Investigation of surface topography formation mechanism based on abrasive-workpiece contact rate model in tangential ultrasonic vibration-assisted CBN grinding of ZrO2 ceramics. Int. J. Mech. Sci. 2019, 155, 66–82. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Q.; Chen, H.; Chen, L.; Meng, F.; Chen, X.; Qu, S.; Wang, Z.; Yu, T. Surface prediction in laser-assisted grinding process considering temperature-dependent mechanical properties of zirconia ceramic. J. Manuf. Process. 2022, 80, 491–503. [Google Scholar] [CrossRef]
- Sales, W.F.; Schoop, J.; da Silva, L.R.; Machado, Á.R.; Jawahir, I. A review of surface integrity in machining of hardened steels. J. Manuf. Process. 2020, 58, 136–162. [Google Scholar] [CrossRef]
- Ma, Z.; Wang, Z.; Wang, X.; Yu, T. Effects of laser-assisted grinding on surface integrity of zirconia ceramic. Ceram. Int. 2020, 46, 921–929. [Google Scholar] [CrossRef]


| Parameters | Value | |
|---|---|---|
| Bond Layer | Grain Layer | |
| Laser power (W) | 400 | 360 |
| Powder feeding speed (r/min) | 1.3 | 1.6 |
| Powder feed gas rate (L/min) | 8 | 8 |
| Shielding gas rate (L/min) | 15 | 15 |
| Scanning speed (mm/s) | 6.5 | 5 |
| Mechanical Property | Value |
|---|---|
| Density (g/cm3) | 7850 |
| Poisson’s ratio | 0.269 |
| Elasticity modulus (Gpa) | 210 |
| Hardness (HRC) | 48 |
| Yield strength (MPa) | 205 |
| Parameters | Value |
|---|---|
| Grinding condition | Up-grinding (without cooling liquid) |
| The size of the workpiece (mm) | 180 × 60 × 30 |
| Wheel speed (m/s) | 2, 3, 4, 5 |
| Feeding speed (mm/s) | 1, 2, 3, 4 |
| Grinding depth (μm) | 10, 15, 20, 25 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, Z.; Zhang, W.; Liu, Q.; Chen, L.; Zhang, C.; Liu, C.; Yu, T.; Wang, Q. Fabrication Process and Surface Morphology Prediction of Radial Straight Groove-Structured CBN Grinding Wheel by Laser Cladding. Materials 2025, 18, 4733. https://doi.org/10.3390/ma18204733
Ma Z, Zhang W, Liu Q, Chen L, Zhang C, Liu C, Yu T, Wang Q. Fabrication Process and Surface Morphology Prediction of Radial Straight Groove-Structured CBN Grinding Wheel by Laser Cladding. Materials. 2025; 18(20):4733. https://doi.org/10.3390/ma18204733
Chicago/Turabian StyleMa, Zhelun, Wei Zhang, Qi Liu, Liaoyuan Chen, Chao Zhang, Changsheng Liu, Tianbiao Yu, and Qinghua Wang. 2025. "Fabrication Process and Surface Morphology Prediction of Radial Straight Groove-Structured CBN Grinding Wheel by Laser Cladding" Materials 18, no. 20: 4733. https://doi.org/10.3390/ma18204733
APA StyleMa, Z., Zhang, W., Liu, Q., Chen, L., Zhang, C., Liu, C., Yu, T., & Wang, Q. (2025). Fabrication Process and Surface Morphology Prediction of Radial Straight Groove-Structured CBN Grinding Wheel by Laser Cladding. Materials, 18(20), 4733. https://doi.org/10.3390/ma18204733








