Machine Learning Phase Classification of Thermoelectric Materials
Abstract
1. Introduction
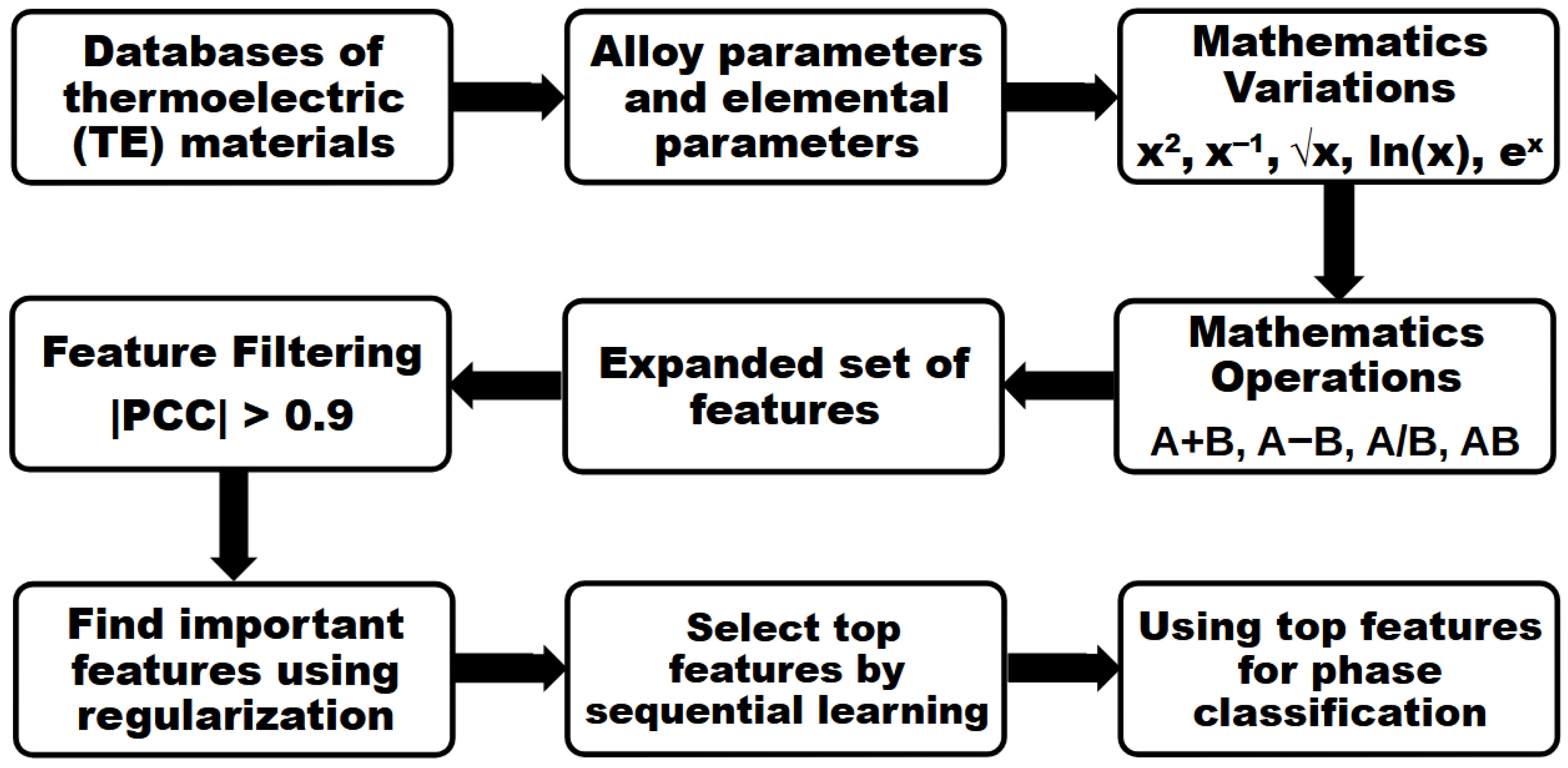
2. Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- He, J.; Tritt, T.M. Advances in thermoelectric materials research: Looking back and moving forward. Science 2017, 357, eaak9997. [Google Scholar] [CrossRef] [PubMed]
- Wei, J.; Yang, L.; Ma, Z.; Song, P.; Zhang, M.; Ma, J.; Yang, F.; Wang, X. Review of current high-ZT thermoelectric materials. J. Mater. Sci. 2020, 55, 12642–12704. [Google Scholar] [CrossRef]
- Shi, X.L.; Zou, J.; Chen, Z.G. Advanced Thermoelectric Design: From Materials and Structures to Devices. Chem. Rev. 2020, 120, 7399–7515. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.N.; Wahid, H.; Nayan, N.; Mohamed Ali, M.S. Inorganic thermoelectric materials: A review. Int. J. Energy Res. 2020, 44, 6170–6222. [Google Scholar] [CrossRef]
- Mukherjee, M.; Srivastava, A.; Singh, A.K. Recent advances in designing thermoelectric materials. J. Mater. Chem. C 2022, 10, 12524–12555. [Google Scholar] [CrossRef]
- Qi, W.; Lan, P.; Yang, J.; Chen, Y.; Zhang, Y.; Wang, G.; Peng, F.; Hong, J. Multi-U-Style micro-channel in liquid cooling plate for thermal management of power batteries. Appl. Therm. Eng. 2024, 256, 123984. [Google Scholar] [CrossRef]
- Qi, W.; Yang, J.; Zhang, Z.; Wu, J.; Lan, P.; Xiang, S. Investigation on thermal management of cylindrical lithium-ion batteries based on interwound cooling belt structure. Energy Convers. Manag. 2025, 340, 119962. [Google Scholar] [CrossRef]
- Zhu, T.; Fu, C.; Xie, H.; Liu, Y.; Zhao, X. High Efficiency Half-Heusler Thermoelectric Materials for Energy Harvesting. Adv. Energy Mater. 2015, 5, 1500588. [Google Scholar] [CrossRef]
- Poon, S.J. Half Heusler compounds: Promising materials for mid-to-high temperature thermoelectric conversion. J. Phys. D Appl. Phys. 2019, 52, 493001. [Google Scholar] [CrossRef]
- Rogl, G.; Rogl, P.F. Development of Thermoelectric Half-Heusler Alloys over the Past 25 Years. Crystals 2023, 13, 1152. [Google Scholar] [CrossRef]
- Mitra, M.; Benton, A.; Akhanda, M.S.; Qi, J.; Zebarjadi, M.; Singh, D.J.; Poon, S.J. Conventional Half-Heusler alloys advance state-of-the-art thermoelectric properties. Mater. Today Phys. 2022, 28, 100900. [Google Scholar] [CrossRef]
- Cao, T.; Shi, X.L.; Li, M.; Hu, B.; Chen, W.; Liu, W.D.; Lyu, W.; MacLeod, J.; Chen, Z.G. Advances in bismuth-telluride-based thermoelectric devices: Progress and challenges. eScience 2023, 3, 100122. [Google Scholar] [CrossRef]
- Kim, S.I.; Lee, K.H.; Mun, H.A.; Kim, H.S.; Hwang, S.W.; Roh, J.W.; Yang, D.J.; Shin, W.H.; Li, X.S.; Lee, Y.H.; et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science 2015, 348, 109–114. [Google Scholar] [CrossRef]
- Guo, F.; Sun, Y.; Qin, H.; Zhu, Y.; Ge, Z.; Liu, Z.; Cai, W.; Sui, J. BiSbTe alloy with high thermoelectric and mechanical performance for power generation. Scr. Mater. 2022, 218, 114801. [Google Scholar] [CrossRef]
- Hong, M.; Li, M.; Wang, Y.; Shi, X.L.; Chen, Z.G. Advances in Versatile GeTe Thermoelectrics from Materials to Devices. Adv. Mater. 2023, 35, 2208272. [Google Scholar] [CrossRef]
- Li, M.; Shi, X.L.; Chen, Z.G. Trends in GeTe Thermoelectrics: From Fundamentals to Applications. Adv. Funct. Mater. 2024, 34, 2403498. [Google Scholar] [CrossRef]
- Vankayala, R.K.; Lan, T.W.; Parajuli, P.; Liu, F.; Rao, R.; Yu, S.H.; Hung, T.L.; Lee, C.H.; Yano, S.i.; Hsing, C.R.; et al. High zT and Its Origin in Sb-doped GeTe Single Crystals. Adv. Sci. 2020, 7, 2002494. [Google Scholar] [CrossRef]
- Gelbstein, Y.; Dashevsky, Z.; Dariel, M. High performance n-type PbTe-based materials for thermoelectric applications. Phys. B Condens. Matter 2005, 363, 196–205. [Google Scholar] [CrossRef]
- Xiao, Y.; Zhao, L.D. Charge and phonon transport in PbTe-based thermoelectric materials. NPJ Quantum Mater. 2018, 3, 55. [Google Scholar] [CrossRef]
- Wang, L.; Wen, Y.; Bai, S.; Chang, C.; Li, Y.; Liu, S.; Liu, D.; Wang, S.; Zhao, Z.; Zhan, S.; et al. Realizing thermoelectric cooling and power generation in N-type PbS0.6Se0.4 via lattice plainification and interstitial doping. Nat. Commun. 2024, 15, 3782. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Sturm, C.; Kleinke, H. Chalcogenides as thermoelectric materials. J. Solid State Chem. 2019, 270, 273–279. [Google Scholar] [CrossRef]
- Yu, Y.; Cagnoni, M.; Cojocaru-Mirédin, O.; Wuttig, M. Chalcogenide Thermoelectrics Empowered by an Unconventional Bonding Mechanism. Adv. Funct. Mater. 2020, 30, 1904862. [Google Scholar] [CrossRef]
- Wei, T.R.; Qiu, P.; Zhao, K.; Shi, X.; Chen, L. Ag2Q-Based (Q = S, Se, Te) Silver Chalcogenide Thermoelectric Materials. Adv. Mater. 2023, 35, 2110236. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Liu, Y.; Funahashi, R. Oxide thermoelectrics: The challenges, progress, and outlook. J. Mater. Res. 2011, 26, 1762–1772. [Google Scholar] [CrossRef]
- Yin, Y.; Tudu, B.; Tiwari, A. Recent advances in oxide thermoelectric materials and modules. Vacuum 2017, 146, 356–374. [Google Scholar] [CrossRef]
- Banerjee, R.; Chatterjee, S.; Ranjan, M.; Bhattacharya, T.; Mukherjee, S.; Jana, S.S.; Dwivedi, A.; Maiti, T. High-Entropy Perovskites: An Emergent Class of Oxide Thermoelectrics with Ultralow Thermal Conductivity. ACS Sustain. Chem. Eng. 2020, 8, 17022–17032. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, C.; Yao, H.; Bai, F.; Yin, L.; Li, X.; Li, S.; Xue, W.; Wang, Y.; Cao, F.; et al. High-Performance N-type Mg3Sb2 towards Thermoelectric Application near Room Temperature. Adv. Funct. Mater. 2020, 30, 1906143. [Google Scholar] [CrossRef]
- Zhang, J.; Song, L.; Mamakhel, A.; Jørgensen, M.R.V.; Iversen, B.B. High-Performance Low-Cost n-Type Se-Doped Mg3Sb2-Based Zintl Compounds for Thermoelectric Application. Chem. Mater. 2017, 29, 5371–5383. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, W.; Back, S.Y.; Kawamoto, N.; Nguyen, D.H.; Mori, T. High-performance Mg3Sb2-based thermoelectrics with reduced structural disorder and microstructure evolution. Nat. Commun. 2024, 15, 6800. [Google Scholar] [CrossRef]
- Islam, N.; Huang, W.; Zhuang, H.L. Machine learning for phase selection in multi-principal element alloys. Comput. Mater. Sci. 2018, 150, 230–235. [Google Scholar] [CrossRef]
- Hart, G.L.; Mueller, T.; Toher, C.; Curtarolo, S. Machine learning for alloys. Nat. Rev. Mater. 2021, 6, 730–755. [Google Scholar] [CrossRef]
- Lee, K.; Ayyasamy, M.V.; Ji, Y.; Balachandran, P.V. A comparison of explainable artificial intelligence methods in the phase classification of multi-principal element alloys. Sci. Rep. 2022, 12, 11591. [Google Scholar] [CrossRef] [PubMed]
- Qi, J.; Hoyos, D.I.; Poon, S.J. Machine learning-based classification, interpretation, and prediction of high-entropy-alloy intermetallic phases. High Entropy Alloy. Mater. 2023, 1, 312–326. [Google Scholar] [CrossRef]
- Bilińska, K.; Winiarski, M.J. Machine learning-based predictions for half-Heusler phases. Inorganics 2023, 12, 5. [Google Scholar] [CrossRef]
- Chen, Z.; Shang, Y.; Liu, X.; Yang, Y. Accelerated discovery of eutectic compositionally complex alloys by generative machine learning. NPJ Comput. Mater. 2024, 10, 204. [Google Scholar] [CrossRef]
- Oñate, A.; Seidou, H.; Tchoufang-Tchuindjang, J.; Tuninetti, V.; Miranda, A.; Sanhueza, J.P.; Mertens, A. New analytical parameters for B2 phase prediction as a complement to multiclass phase prediction using machine learning in multicomponent alloys: A computational approach with experimental validation. J. Alloys Compd. 2025, 1022, 179950. [Google Scholar] [CrossRef]
- Beniwal, D.; Ray, P.K. FCC vs. BCC phase selection in high-entropy alloys via simplified and interpretable reduction of machine learning models. Materialia 2022, 26, 101632. [Google Scholar] [CrossRef]
- Jin, T.; Park, I.; Park, T.; Park, J.; Shim, J.H. Accelerated crystal structure prediction of multi-elements random alloy using expandable features. Sci. Rep. 2021, 11, 5194. [Google Scholar] [CrossRef]
- Bansal, A.; Kumar, P.; Yadav, S.; Hariharan, V.; MR, R.; Phanikumar, G. Accelerated design of high entropy alloys by integrating high throughput calculation and machine learning. J. Alloys Compd. 2023, 960, 170543. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, Y.; Ning, J.; Xi, J.; Xi, L.; Qiu, D.; Yang, J.; Ke, X. A Critical Review of Machine Learning Techniques on Thermoelectric Materials. J. Phys. Chem. Lett. 2023, 14, 1808–1822. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Liu, X.; Wang, J. Prediction of thermoelectric-figure-of-merit based on autoencoder and light gradient boosting machine. J. Appl. Phys. 2024, 135, 074901. [Google Scholar] [CrossRef]
- Vaitesswar, U.S.; Bash, D.; Huang, T.; Recatala-Gomez, J.; Deng, T.; Yang, S.W.; Wang, X.; Hippalgaonkar, K. Machine learning based feature engineering for thermoelectric materials by design. Digit. Discov. 2024, 3, 210–220. [Google Scholar] [CrossRef]
- Juneja, R.; Yumnam, G.; Satsangi, S.; Singh, A.K. Coupling the high-throughput property map to machine learning for predicting lattice thermal conductivity. Chem. Mater. 2019, 31, 5145–5151. [Google Scholar] [CrossRef]
- Iwasaki, Y.; Takeuchi, I.; Stanev, V.; Kusne, A.G.; Ishida, M.; Kirihara, A.; Ihara, K.; Sawada, R.; Terashima, K.; Someya, H.; et al. Machine-learning guided discovery of a new thermoelectric material. Sci. Rep. 2019, 9, 2751. [Google Scholar] [CrossRef]
- Barua, N.K.; Lee, S.; Oliynyk, A.O.; Kleinke, H. Thermoelectric Material Performance (zT) Predictions with Machine Learning. ACS Appl. Mater. Interfaces 2025, 17, 1662–1673. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Yokoyama, Y.; Onda, T.; Adachi, Y.; Chen, Z.C. Improved Thermoelectric Properties of Hot-Extruded Bi–Te–Se Bulk Materials with Cu Doping and Property Predictions via Machine Learning. Adv. Electron. Mater. 2019, 5, 1900079. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Song, Y.; Qi, W.; Guo, Q.; Li, X.; Kong, L.; Chen, J. Real-Time Global Optimal Energy Management Strategy for Connected PHEVs Based on Traffic Flow Information. IEEE Trans. Intell. Transp. Syst. 2024, 25, 20032–20042. [Google Scholar] [CrossRef]
- Zhang, R.; Zhang, S.; He, Z.; Jing, J.; Sheng, S. Miedema Calculator: A thermodynamic platform for predicting formation enthalpies of alloys within framework of Miedema’s Theory. Comput. Phys. Commun. 2016, 209, 58–69. [Google Scholar] [CrossRef]
- Ward, L.; Dunn, A.; Faghaninia, A.; Zimmermann, N.E.; Bajaj, S.; Wang, Q.; Montoya, J.; Chen, J.; Bystrom, K.; Dylla, M.; et al. Matminer: An open source toolkit for materials data mining. Comput. Mater. Sci. 2018, 152, 60–69. [Google Scholar] [CrossRef]
| Definition | Comments |
|---|---|
| R = the gas constant | |
| = the atomic percentage of the i-th element for an N-element alloy | |
| = the binary mixing enthalpy obtained from Miedama’s model [48] of i-j elemental pair | |
| = alloy melting temperature | |
| = the Gibbs free energy change for forming a fully disordered solid solution phase | |
| = the largest absolute Gibbs free energy for forming the strongest binary compound | |
| = annealing temperature, or if is unknown, = 0.8 | |
| where is the melting temperature of the i-j elements | |
| = the most negative binary mixing enthalpy for forming inter-metallics | |
| = mixing enthalpy for forming inter-metallics | |
| = the atomic radius of the i-th element | |
| = average atomic radius | |
| = electronegativity of i-th element | |
| = valence electron count of the i-th element |
| Materials Group | Accuracy |
|---|---|
| HH | () |
| + (Si or Sb)-based | () |
| BiTe-based | () |
| TM Chalcogenides | () |
| (Pb, Ge, or Sn) Chalcogenides | () |
| Oxides (Hexagonal) | () |
| Oxides (Perovskites) | () |
| Oxides (Orthorhombic) | () |
| Oxides (Rhombohedral) | () |
| Materials Group | Accuracy |
|---|---|
| HH | () |
| + (Si or Sb)-based | () |
| BiTe-based | () |
| TM Chalcogenides | () |
| (Pb, Ge, or Sn) Chalcogenides | () |
| Oxides (Hexagonal) | () |
| Oxides (Perovskites) | () |
| Oxides (Orthorhombic) | () |
| Oxides (Rhombohedral) | () |
| Training Sets → Targeted Alloys ↓ | HH | + (Si or Sb)-Based | BiTe-Based | TM Chalcogenides | (Pb, Ge, or Sn) Chalcogenides | Oxides |
|---|---|---|---|---|---|---|
| HH | 0.91 | 0.06 | 0.03 | 0.10 | 0.04 | 0.02 |
| + (Si or Sb)-based | 0.05 | 0.84 | 0.03 | 0.08 | 0.02 | 0.02 |
| BiTe-based | 0.01 | 0.02 | 0.85 | 0.01 | 0.02 | 0.01 |
| TM Chalcogenides | 0.07 | 0.05 | 0.02 | 0.84 | 0.21 | 0.02 |
| (Pb, Ge, or Sn) Chalcogenides | 0.01 | 0.01 | 0.02 | 0.28 | 0.80 | 0.01 |
| Oxides | 0.01 | 0.01 | 0.01 | 0.01 | 0.01 | 0.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.T.; Poon, S.J. Machine Learning Phase Classification of Thermoelectric Materials. Materials 2025, 18, 4726. https://doi.org/10.3390/ma18204726
Ma CT, Poon SJ. Machine Learning Phase Classification of Thermoelectric Materials. Materials. 2025; 18(20):4726. https://doi.org/10.3390/ma18204726
Chicago/Turabian StyleMa, Chung T., and S. Joseph Poon. 2025. "Machine Learning Phase Classification of Thermoelectric Materials" Materials 18, no. 20: 4726. https://doi.org/10.3390/ma18204726
APA StyleMa, C. T., & Poon, S. J. (2025). Machine Learning Phase Classification of Thermoelectric Materials. Materials, 18(20), 4726. https://doi.org/10.3390/ma18204726







