Abstract
The dynamics of thin elastic one-directional non-periodic plates are considered in this paper. The structure of these plates is, at a macro level, functionally graded along the x1-axis, but at the micro level it is non-periodic (tolerance-periodic). In the plates, the effect of a microstructure size on their behaviour can play a crucial role. The tolerance modelling method allows for this effect to be taken into account. This paper mainly proposes that tolerance modelling leads to model equations of two different tolerance models for one-directional functionally graded plates with two kinds of tolerance-periodic microstructures, i.e., (a) those having a microstructure size that is an order of the plate thickness, d~l, and (b) those having the plate thickness that is smaller than a microstructure size, d << l. Derived model equations are characterised by slowly varying coefficients. A subset of these coefficients is contingent on the microstructure size. The models presented herein determine formulas for both fundamental lower-order vibration frequencies and higher-order vibration frequencies, which are related to the microstructure. These models of such plates are implemented in a rudimentary example of free vibrations. Using the Ritz method, formulas of frequencies are obtained.
1. Introduction
Functionally graded (FG) plates with two kinds of tolerance-periodic (non-periodic) microstructures are considered: (a) those with an a-type tolerance-periodic microstructure, in which the size of the microstructure is of an order of the plate thickness, d~l, and (b) those with a b-type tolerance-periodic microstructure, having the plate thickness that is smaller than a microstructure size, d << l. These plates consist of many small elements, called cells, cf. Figure 1 and Figure 2. An example of an FG plate with an a-type microstructure is shown in Figure 1a, with a cell of the plate in Figure 1b. Conversely, Figure 2a presents a fragment of an FG plate with a b-type microstructure, and Figure 2b shows a cell of this plate.
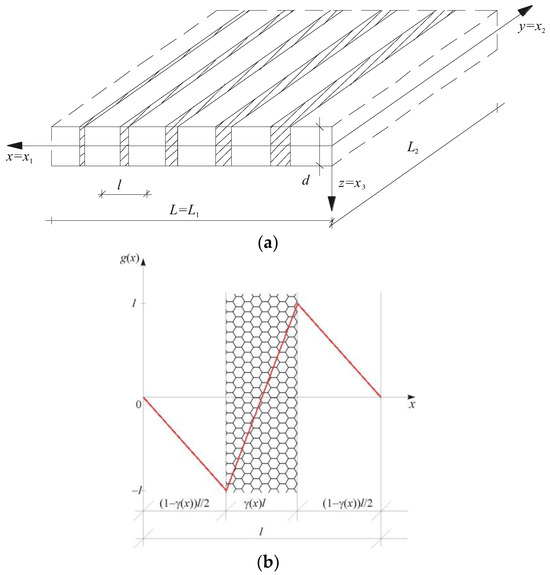
Figure 1.
(a) A fragment of a thin functionally graded plate with an a-type tolerance-periodic (non-periodic) microstructure; (b) a cell of the plate with a saw-type fluctuation shape function.
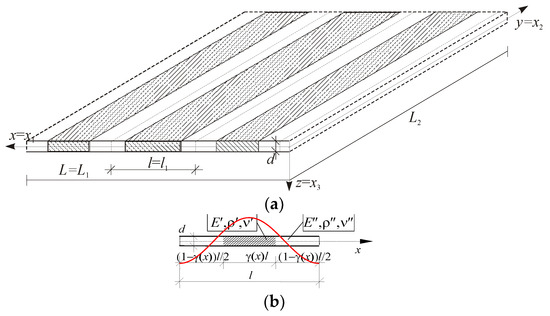
Figure 2.
(a) A fragment of a thin functionally graded plate with a b-type tolerance-periodic (non-periodic) microstructure; (b) a cell of the plate with a fluctuation shape function.
In view of the fact that the microstructure of the plates is non-periodic along the x1 = x axis, a macrostructure is exhibited as functionally graded along that same axis, cf. Suresh and Mortensen [1] and Woźniak et al. [2]. These plates are frequently utilised in diverse engineering disciplines.
The dynamic problems of the thin FG plates under consideration are determined by a partial differential equation having non-continuous, highly oscillating, and tolerance-periodic coefficients. However, it is important to note that the present form of the governing equations is not an effective tool for investigating specific problems. Hence, different approximated averaging methods have been proposed.
Some averaging approaches are used for the analysis of periodic structures. Such techniques are frequently employed in the study of microstructured, functionally graded media (also of plates) [1,2]. Averaged models with the concept of effective (averaged) properties of the structure, e.g., a plate, are formulated in the framework of many of these methods. Between them, models based on asymptotic homogenisation, as in the study of Bensoussan et al. [3], can be highlighted. Effective rigidity plate theories were used to investigate periodic plates in a series of papers, e.g., in Kohn and Vogelius [4], Duvaut and Metellus [5], and Caillerie [6]. In the aforementioned models, plates are described by governing equations. These are of particular plates, with constant averaged rigidities and averaged mass densities. In order to obtain averaged properties in the context of asymptotic homogenisation, it is necessary to solve a certain boundary value problem on the periodicity cell. This problem is solved for every periodic structure. It is important to note that these procedures are usually restricted to the first approximation. However, the effect of the microstructure size usually vanishes in the model equations.
It is important to note that a range of other modelling approaches has also been proposed and developed for the purpose of describing various composite media. Several works on this type of issue can be mentioned. Some of such articles, mainly dealing with plates and shells, are indicated in this section. Homogenisation with microlocal parameters has been used to analyse periodic plates [7] and to model certain problems for a micro-periodic composite half-plane with slant lamination [8,9]. Free vibration frequencies of thick square panels made of various materials, e.g., orthotropic or hexagonal ones, were investigated in [10]. Stability problems of multi-cell thin-walled columns were analysed in [11].
Dynamic problems of three-layered, annular plates with a viscoelastic core were considered using two approximation methods—orthogonalisation and finite differences—in [12]. The buckling and post-buckling behaviours of shells of a revolution with non-classical shapes are presented in [13], using analytical–numerical models. Also, analytical–numerical methods were applied in [14,15] to analyse interesting problems of the buckling of three-layered polyethylene plates under a magnetic field. The stability of three-layered annular plates with differently damaged laminate facings under temperature fields was considered in [16], applying mainly numerical methods. In [17], computer simulations made it possible to investigate effective properties and the dynamic response of a sandwich panel made of two-faced sheets and an auxetic core. An analytical–numerical model was used to analyse dynamic problems induced by fluid flow in plates having different Poisson’s ratios in [18]. The finite element method was applied to compare the blast resistance of auxetic and non-auxetic sandwich plates in [19]. Sandwich plates with an auxetic anti-tetrachiral core have been analysed under puncture [20] and with a steady-state harmonic base motion [21] using the finite element method. The results obtained for auxetic sandwich plates were compared with the results calculated for sandwich plates having standard hexagonal honeycomb cores. Orthogonalisation and finite difference methods have been applied for annular composite plates made of layers with auxetic properties to static stability [22] and dynamic stability problems [23].
The exact strong form of governing equations for the Timoshenko–Ehrenfest beam, with geometrical nonlinearity, was formulated in [24], and then a nonlinear finite element analysis was used to obtain the weak form. Natural frequencies and mode shapes and the nonlinear free vibration were computed by applying the finite element method. In [25], the dynamic stability of a Mindlin–Reissner plate was considered, where a variational approach was used to obtain the finite element formulation of a four-node plate element. The Floquet theory and first-order approximation based on the averaging method were also applied to evaluate stability of the time-periodic system.
Many articles, which present theoretical and numerical results connected to a variety of problems concerning functionally graded media, have been published. Thermomechanical problems of functionally graded fibre-reinforced microstructure composites were considered using the higher-order theory in [26,27,28,29]. Numerous papers have successfully applied the known numerical methods for functionally graded media. For instance, the thermal analysis of composites with fibres applying the boundary element method was shown in [30]. Furthermore, the finite element method was implemented in [31] specifically for functionally graded materials. The stability analysis of functionally graded cylindrical shells demonstrated its conformity to Donnell type dynamic stability equations [32]. Meshless methods have been used in numerous papers to investigate natural frequencies of functionally graded plates [33] and sandwich beams with a functionally graded core of the structure [34]. In [35], the successful application of higher-order plate theories and a collocation method to the dynamic of functionally graded plates was presented. A GDQ solution was shown in [36] to investigate the free vibrations of shells, and higher-order deformation theories were successfully used to consider the thermomechanical problems of plates and shells with a functionally graded structure in [37,38]. In [39,40,41], the static behaviour of doubly curved functionally graded shells was analysed, while in [42] the thermal buckling of functionally graded annular plates was examined and a non-classical functionally gradient plate (FGM) model based on the modified couple stress theory was proposed. The size effect was also examined, in relation to the couple stress theory.
The free vibrations of functionally graded thick plates were investigated in [43], with consideration of the effects of normal and shear deformations. Using a higher-order normal and shear deformable plate theory, the authors of [44] analysed the vibrations of functionally graded rectangular plates. In [45], a nonlinear analysis under a shear deformation theory for functionally graded plates was presented, while in the study [46] the chaos problem pertinent to a functionally graded rectangular plate was investigated. The development of a robust formulation based on the finite element method and the GDQ technique for multilayered plates was shown in [47]. Another work on laminated composite plates can be found in [48], where the presentation of a substantial formulation of isogeometric analysis is shown. In [49], the layer-wise theory with the differential quadrature method was employed for composite plates.
In the study referenced in [50], a new low-order shell element was developed and employed for shells with functionally graded material properties. The differential quadrature method was successfully applied in the variety of issues related to functionally graded shells and plates. For instance, it was used to determine the natural frequencies of sandwich shells in [51] and to assess the dynamic stability of layered shells in [52]. In [53,54], the theory of sinusoidal shear deformation was applied to analyse the bending of piezoelectric functionally graded plates on a foundation and/or free vibrations of functionally graded composite polymer nanoplates. In addition, in [55] a semi-analytical method for investigating specific buckling, post-buckling, and dynamic problems for functionally graded thin plates was developed using the classical laminated plate theory. The same approach was also used to analyse columns made of such plates and having closed/open cross-sections (references [56,57,58]). The investigation of the free vibrations of thermally loaded functionally graded sandwich plates was conducted with the use of three-dimensional finite element modelling in [59]. Furthermore, the transient behaviour of functionally graded plates was addressed in [60] by applying a novel semi-analytical algorithm, which encompassed in-plane displacements and temperature fluctuations. The complex variable approach is used in the analysis of forces and moments acting on infinite, symmetric, functionally graded plates with a triangular hole in [61]. Another novel analytical model for sandwich structures was shown in [62], where the authors generalised the model to encompass the continuous variation in mechanical properties in the thickness direction of the structure. The individual nonlinear theory of deformation of a straight line normal to the neutral surface was applied to develop this model. In [63], an axisymmetric bending of a generalised circular sandwich plate with continuous variation in mechanical properties in the thickness direction of the core, under a concentrated force, was considered analytically with the aim of improving the shear deformation theory. Another analytical model of the elastic buckling of a sandwich plate with a functionally graded core was presented in [64] under the assumption of the nonlinear shear deformation theory of a straight normal line. In [65], the first-order shear deformation theory alongside the variational method and the Galerkin–Vlasov method were applied to analyse the dynamics of a functionally graded material porous plate resting on Winkler’s elastic foundation. Vibrations of functionally graded plates were considered in [66] using the dynamic stiffness method. In paper [67], the combination of the Jacobi–Ritz method and the multi-segment strategy, based on the higher-order shear deformation theory variational equation, were applied to propose a unified solution for the transient state vibration problem of functionally graded porous plates. Dynamical problems of nanocomposite functionally graded shells were modelled in some papers [68,69,70] using a generalised differential quadrature method. In [71], a highly accurate model was presented for the analysis of the static mechanics of pressurised annular functionally graded structures with arbitrary elastic properties along the radial direction. In the work [72], an investigation of the low-frequency vibrations of a functionally graded thin-walled cylinder in the plane state of strain was conducted. Subsequently, an asymptotic analysis of the dynamic relations in elasticity was performed across the cross-section of the cylinder, resulting in the formulation of a consistent approximate equation of motion on the mid-surface.
It is important to acknowledge that the model equations derived within the framework of the proposed modelling approaches for microstructured media tend to neglect the impact of microstructure size. On the contrary, this effect can be of significant importance in the context of vibrations in these media. As observed by Brillouin [73], a relation between macro- and microvibrations exists. To address similar issues, specific methodologies have been employed to take into account this effect. Their considerations have been extended to periodic structures in several studies, a number of which are referenced herein. In [74], the authors employed a spectral element method to analyse the characteristics of vibration band gaps in Mindlin’s periodic plates. In [75,76], the band gaps in periodic thin plates with and without damping were investigated using a centre finite difference method. Flexural wave band gaps in composite periodic plates were examined in [77] applying the differential quadrature element method.
The tolerance modelling method (or the tolerance method) is an alternative approach to the analysis of mechanical problems in microstructured media, either periodic or non-periodic. For further details, it is recommended to refer to the books by Woźniak and Wierzbicki [78], as well as Woźniak et al. (eds) [2,79]. The method has been demonstrated to be applicable in a range of problems described by differential equations with non-continuous, highly oscillating functional coefficients. The modelling procedure of the method involves substituting the exact governing equations with the averaged model equations, which are characterised by constant (or slowly varying) coefficients. It is important to note that a proportion of these coefficients are explicitly dependent on the size of the microstructure.
The tolerance modelling method enables the investigation of a range of dynamical, stability, and thermoelastic problems associated with periodic structures, as discussed in a series of articles. Some notable examples include the analysis of fluid-saturated periodic grounds, as presented in [80]. In the paper [81], the authors analysed the dynamics of periodic plane structures. An application to the vibrations of periodic medium-thickness plates was demonstrated in [82,83]. Vibrations of thin, one-directional periodic plates with a thickness smaller than the length of the periodic cell were considered in [84]. The vibrations of wavy-type periodic plates were subjected to analysis in [85]. The dynamics of thin periodic plates reinforced by stiffeners was described in [86]. The dynamics of periodic thin plates with the size of microstructure of the order of the thickness of plate was investigated in [87]. The applications of the method to various thermomechanical problems, including dynamics and stability, for thin cylindrical shells with one-directional or two-directional micro-periodic structures were presented in [88,89,90,91]. The geometrically nonlinear behaviour of thin periodically microstructured plates was investigated in [92], while the geometrically nonlinear vibrations of periodically microstructured beams were examined in [93]. A specific tolerance model for vibrations in periodic three-layered plates was proposed in [94], and the comparison of several dynamic models was discussed in [95]. The tolerance method, in conjunction with the finite difference algorithm, was employed to analyse the issue of heat transfer in biperiodic composites with third-type boundary conditions, as outlined in [96]. An investigation into the multi-scale analysis of stress distribution in thin periodic composite plates was presented in [97].
The modelling of functionally graded media with a non-periodic microstructure was also successfully achieved using the tolerance method. The thermoelasticity of transversally graded laminates, with consideration of the effect of microstructure, was analysed in [98,99]. The vibration behaviour of longitudinally graded plates was investigated in [100,101], while the stability of similar plates was examined in [102]. In [103,104], the authors analysed the dynamics of thin-walled structures having a dense system of ribs using tolerance models. The transfer of heat in composite cylindrical conductors with a non-uniform constituent distribution was described in [105,106]. Further investigations of heat conduction phenomena in laminates with functionally graded material properties and the third-type boundary conditions were conducted by [107]. The dynamics of transversally graded thin plates with a thickness smaller than the microstructure size was demonstrated in [2,108]. In the work [109], the free vibrations of thin functionally graded plates with a one-directional microstructure, having a microstructure size of the order of the plate thickness, were considered. The vibrations of functionally graded thin shells with a microstructure were presented in [110,111,112], and the dynamics and stability of them were discussed in [113]. However, it is important to note that these works do not address every issue that has been previously discussed in the literature on the tolerance modelling method for microstructured media and therefore do not represent a complete account of this field.
The principal objective of this paper is to put forth two novel tolerance models for thin, one-directional, functionally graded plates exhibiting two distinct forms of tolerance-periodic (non-periodic) microstructures: (a) an a-type tolerance-periodic microstructure, with the dimension of the microstructure of the order of the plate thickness, d~l; (b) a b-type tolerance-periodic microstructure, with the plate thickness smaller than the dimension of the microstructure d << l. The impact of the microstructure on the overall behaviour of the functionally graded plates with the microstructure is taken into account within the governing equations of both models. The microstructural effect of these plates can be of significant consequence in the context of dynamical issues, including free or forced vibrations. The tolerance models allow the investigation of higher-order frequencies (and higher-order vibrations, cf. Brillouin [73]) associated with the microstructure of the plate, in addition to fundamental lower frequencies (and vibrations) related to the macrostructure of the plate. Moreover, the governing equations of the asymptotic model are derived using the asymptotic homogenisation procedure, thereby eliminating the microstructural effect. This procedure is used to assess the correctness of the obtained results. The considerations presented in this paper are limited to the theoretical aspect, and as a means of illustrating the applications of the aforementioned models, formulas for the free vibration frequencies of functionally graded plate bands are derived using the Ritz method.
The main novelty of this paper is to compare and contrast two averaged tolerance models of tolerance-periodic thin plates. It is shown how the use of different formulations of one of the fundamental tolerance modelling assumptions, adapted to the nature of the microstructure of the plate under consideration, affects the obtained equations of tolerance models. All investigations are supplemented by calculation example devoted to the derivation of lower- and higher-order free vibration frequencies.
2. Modelling Preliminaries
Let the orthogonal Cartesian coordinate system be denoted by Ox1x2x3, and the time coordinate by t. Also denote x≡x1, z≡x3. Let be the region of the undeformed plate, where d(·) is the plate thickness; Π is the plate midplane with L1, L2 being the lengths of the plate along the x1-, x2-axis, respectively. Let subscripts i,k,l run over 1, 2, 3 but α,β,γ run over 1, 2. Derivatives of xα are denoted by ∂α and also ∂α...δ≡∂α...∂δ, and those of t by an overdot. Let Δ≡[−l/2,l/2]×{0} be the “basic cell” on Ox1x2, with l as its length dimension along the x1-axis. This length l is called the microstructure parameter.
In this paper, two types of microstructured plates are considered:
- (a)
- Where the size of the microstructure is of an order of the plate thickness, called the a-type microstructure, this parameter hence satisfies the condition dmax~l << L1;
- (b)
- Where the plate thickness is smaller than the size of the microstructure, called the b-type microstructure, the condition can hence be stated as dmax << l << L1.
Thickness d(·) can be a tolerance-periodic function in x1, but elastic moduli aijlm = aijlm(·,x2,z) and a mass density ρ = ρ(·,x2,z) can be tolerance-periodic functions in x1 and even functions in z. It is assumed that the geometric and material properties of the considered plates are constant along the x2-axis direction. Using the non-zero components of the elastic moduli tensor aαβγδ, aαβ33, aα3γ3, a3333, let us denote cαβγδ≡aαβγδ − aαβ33aγδ33(a3333)−1, cα3γ3≡aα3γ3 − aα333a33γ3(a3333)−1. Let ui(x1,x2,x3,t) and i = 1, 2, 3 be displacements of the plate along the xi-axis directions; w(x1,x2,t) = u(x1,x2,t) = u3(x1,x2,x3,t) be a plate deflection; and p be the total loadings in the z-axis direction.
Introducing the following denotations for the tolerance-periodic functions in x, the stiffnesses of the plate bαβγδ(·), the mass density μ(·), and the rotational mass inertia ϑ(·) are as follows:
and applying the assumptions of the Kirchhoff type plate theory to thin functionally graded plates with a microstructure, the Lagrangean Λ can be written as follows:
for which the Euler–Lagrange equation takes the following form:
Combining Equations (2) and (3) for deflection w(x1,x2), the following equation is derived:
which is the known fourth-order partial differential equation for thin plates and has coefficients being the non-continuous, highly oscillating, tolerance-periodic functions in x1.
3. Tolerance Modelling Preliminaries
3.1. Basic Concepts of Tolerance Method
Some basic concepts of the tolerance modelling method are introduced in the general form in the books of [2,78,79]. These concepts are shown and used in different works, e.g., in [108,109]. However, some of them are recalled here for this paper to be self-consistent.
Keeping in mind that x = x1, let us denote y = x2 and introduce an interval along the x-axis Γ = (0,L1).
Denoting a cell at x∈ΓΔ by Δ(x)≡x + Δ, ΓΔ = {x∈Γ: Δ(x)⊂Γ}, for an integrable function f the averaging operator is defined by the following:
If a function f is tolerance-periodic, the averaged value obtained from (5) is a slowly varying function in x, but for the periodic function, this value is constant.
Let the following be denoted by , , and the k-th gradient of function . (For problems of the considered plates, s = 2 or/and s = 1.) Let and be a function defined in . Let us introduce the parameter δ, called the tolerance parameter, which is small, δ << 1. This parameter is related to and dependent on every considered problem.
The tolerance-periodic function, , is a function , and if for the following conditions are satisfied:
where function is the periodic approximation of in and .
The slowly varying function, , is a function if
The highly oscillating function, , is a function if
Let us denote for k = 0.
At this stage of investigation, two kinds of highly oscillating functions, which are g(·) and h(·), are introduced.
For FG plates with an a-type microstructure, let a highly oscillating function g(·) be defined on , , and being continuous. Gradient ∂1g is piecewise continuous and bounded. Function g(·) is the fluctuation shape function of the first kind, , if it depends on l as a parameter and the following conditions are held:
- ∂kg∈O(ls−k) for k = 0,1, s = 1, ∂0g≡g;
- <μg>(x)≈0 for every .
- Where l is the microstructure parameter, μ > 0 is a certain tolerance-periodic function.
For FG plates with a b-type microstructure let a highly oscillating function h(·) be defined on , , which is continuous together with gradient ∂1h. Gradient ∂2h is piecewise continuous and bounded. Function h(·) is the fluctuation shape function of the second kind, , if it depends on l as a parameter and if it satisfies the conditions:
- ∂kh∈O(ls−k) for k = 0, 1, s = 2, ∂0h≡h;
- <μh>(x)≈0 for every .
- With l as the microstructure parameter; μ > 0 is a certain tolerance-periodic function.
3.2. Tolerance Modelling Assumptions
Tolerance modelling assumptions were formulated in a general form in books [2,78,79]. In a series of papers for special problems of various structures, they were adopted applying the basic introductory concepts. Here, these assumptions are recalled for two kinds of plates under consideration.
- FG plates with an a-type microstructure (d~l).
The first assumption is the micro–macro decomposition, which is introduced as formulations of displacements of the plate:
where functions u(·,t) and rα(·,t) are kinematic unknowns, named the macrodeflection and the fluctuation amplitudes, respectively. They are assumed to be slowly varying functions: the macrodeflection of the second kind, i.e., , and the fluctuation amplitudes of the first kind, i.e., . It is assumed that function g(·) is the known fluctuation shape function, postulated a priori in the considered problem and describing the unknown fields (here: displacements uα, α = 1, 2) of oscillations caused by an a-type microstructure of the plate. Figure 1b shows an example of this function. This function satisfies the following restrictions:
∂kg∈O(l1−k) for k = 0, 1;
<μg> = 0;
<μgg> = 0.
The second assumption is the tolerance averaging approximation, in which it is assumed that terms O(δ) are negligibly small, e.g., for , , or in
- FG plates with b-type microstructure (d << l).
The first assumption is the micro–macro decomposition, which is introduced as formulations of deflection of the plate u:
where functions W(·,t) and VA(·,t) are new kinematic unknowns, called the macrodeflection and the fluctuation amplitudes, respectively. They are assumed to be slowly varying functions of the second kind, i.e., . Functions hA(·), A = 1,…,N are assumed to be known fluctuation shape functions, a priori postulated in the considered problem and describing the unknown fields (here, the deflection) of oscillations caused by a b-type microstructure of the plate. An example of this function is shown in Figure 2b. These functions satisfy the following restrictions:
∂khA∈O(l2−k) for k = 0, 1, 2;
<μhA> = 0;
<μhAhB> = 0 for A ≠ B, A, B = 1,…,N.
The second assumption is the tolerance averaging approximation, in which it is assumed that terms O(δ) are negligibly small, e.g., for , and in
4. Tolerance Modelling Procedure
The tolerance modelling procedure was shown in various forms in the books of [2,78,79]. In order to make this paper self-consistent, the procedure is shortly presented below, similarly to that in [2,108]. Using the Kirchhoff type plate theory assumptions with the tolerance modelling assumptions ((6) and (7) or (8) and (9)) for FG plates with an a-type or b-type microstructure and then the averaging operator (5) instead of the Lagrangean (2), one obtains the appropriate averaged Lagrangean.
4.1. Tolerance Modelling for FG Pates with a-Type Microstructure (d~l)
Applying the tolerance modelling for FG plates with an a-type microstructure, the tolerance-averaged Lagrangean is derived in the following form:
The averaged Euler–Lagrange equations for u(·,x2,t) and rα(·,x2,t) are obtained from the principle of stationary action applied to (10) in the following form:
4.2. Tolerance Modelling for FG Pates with b-Type Microstructure (d << l)
Similarly, by applying the tolerance modelling for FG plates with a b-type microstructure the tolerance-averaged Lagrangean is derived in the following form:
The averaged Euler–Lagrange equations for W(·,x2,t) and VA(·,x2,t) are obtained from the principle of stationary action applied to (12) in the following form:
In Lagrangeans (10) and (12), the underlined terms are dependent on the microstructure parameter l.
5. Asymptotic Modelling Approach
In order to assess the quality of results obtained by the tolerance model, an approximate asymptotic model can be applied. This model neglects the effect of microstructure size. Equations of the asymptotic model can be derived using the proper asymptotic modelling procedure, cf. [79,108,109], which is briefly sketched in the following subsections for both kinds of FG plates.
5.1. Tolerance Modelling for FG Pates with a-Type Microstructure (d~l)
The procedure starts with the introduction of the following: a small parameter ε∈(0,1]; an interval Δε≡[−εl/2, εl/2]; and ε-cell Δε(x)≡x + Δε, . Then, instead of the tolerance decomposition (6), the asymptotic decomposition is formulated, cf. [109]. Moreover, the tolerance averaging approximation (7) is replaced by the asymptotic approximation, cf. [109]. Because the parameter ε tends to zero terms of an order ε (or higher), O(ε) can be neglected.
Let us introduce Lagrange’s function , , , t∈(t0,t1).
In the asymptotic modelling, for ε→0 function Λε of variable tends to an averaged Lagrangean Λ0g in the following form:
The averaged asymptotic Euler–Lagrange equations for u(·,x2,t) and rα(·,x2,t) are obtained from the principle of stationary action applied to (14) in the following form:
The asymptotic model equations of the FG plates with an a-type microstructure can be derived by applying (14) to the averaged asymptotic Euler–Lagrange Equation (15).
5.2. Tolerance Modelling for FG Pates with b-Type Microstructure (d << l)
Similarly to Section 5.1, a small parameter ε∈(0,1]; an interval Δε≡[−εl/2,εl/2]; and ε-cell Δε(x)≡x + Δε, are introduced. Then, instead of the tolerance decomposition (8), the asymptotic decomposition is formulated, cf. [108]. Moreover, the tolerance averaging approximation (9) is replaced by the asymptotic approximation, cf. [108]. Because the parameter ε tends to zero terms of an order ε (or higher), O(ε) can be omitted.
Let us introduce Lagrange’s function , , , t∈(t0,t1).
In the asymptotic modelling, for ε→0 function Λε of variable tends to an averaged Lagrangean Λ0h in the following form:
The averaged asymptotic Euler–Lagrange equations for W(·,x2,t) and VA(·,x2,t) are obtained from the principle of stationary action applied to (16) in the following form:
The asymptotic model equations of the FG plates with a b-type microstructure can be derived using the averaged asymptotic Euler–Lagrange Equation (17) with Lagrangean (16).
6. Governing Equations
6.1. Model Equations for FG Plates with a-Type Microstructure (d~l)
6.1.1. Tolerance Model Equations
Combining Lagrangean (10) with Euler–Lagrange Equation (12), the averaged equations of the tolerance model of the FG plates with an a-type microstructure for u(·,x2,t) and rα(·,x2,t) are derived (α = 1, 2):
The coefficients of Equation (18) are slowly varying functions in x. These equations describe the effect of the microstructure size on the overall dynamic and static behaviour of the considered FG plates, as the underlined coefficients involve the microstructure parameter l. Double-underlined terms allow us to analyse this influence on some static issues. Equation (18) stands for the system of three differential equations for the unknowns: the macrodeflection u and the fluctuation amplitudes rα, α = 1, 2. These functions have to be slowly varying functions in x. For the macrodeflection u, two boundary conditions have to be formulated at all edges of the plate, but for the fluctuation amplitudes rα, α = 1, 2, two boundary conditions have to be formulated at both edges parallel to the microstructure of the plate.
6.1.2. Asymptotic Model Equations
After combining Lagrangean (14) with Euler–Lagrange Equation (15), the averaged equations of the asymptotic model of the FG plates with an a-type microstructure for u(·,x2,t) and rα(·,x2,t) are derived (α = 1, 2):
Similarly to (18), Equation (19) has coefficients being slowly varying functions in x. These equations neglect the effect of the microstructure size on the overall behaviour of the considered FG plates. Equation (19) stands for the system of one differential equation for the unknown macrodeflection u and two algebraic equations for the fluctuation amplitudes rα, α = 1, 2. These functions have to be slowly varying functions in x. For these plates, two boundary conditions have to be formulated at all edges of the plate only for the macrodeflection u. It can be observed that neglecting terms with the microstructure parameter l in Equation (18) leads directly to Equation (19).
6.2. Model Equations for FG Plates with b-Type Microstructure (d << l)
6.2.1. Tolerance Model Equations
Combining Lagrangean (12) with Euler–Lagrange Equation (13), the averaged equations of the tolerance model of the FG plates with a b-type microstructure for W(·,x2,t) and VA(·,x2,t), A = 1,…, N are derived:
Equation (20) also has slowly varying functional coefficients in x. These equations describe the effect of the microstructure size on the overall dynamic and static behaviour of the considered FG plates, as the underlined coefficients involve the microstructure parameter l. Double-underlined terms allow us to analyse this effect on some static issues. Equation (20) stands for the system of N + 1 differential equations for the unknowns: the macrodeflection is W and the fluctuation amplitudes are VA(·,x2,t), A = 1,…, N. These functions have to be slowly varying functions in x. For the macrodeflection W, two boundary conditions have to be formulated at all edges of the plate, but for the fluctuation amplitudes VA(·,x2,t), A = 1,…, N, two boundary conditions have to be formulated at both edges parallel to the microstructure of the plate.
6.2.2. Asymptotic Model Equations
After combining Lagrangean (16) with Euler–Lagrange Equation (17), the averaged equations of the asymptotic model of the FG plates with a b-type microstructure for W(·,x2,t) and VA(·,x2,t), A = 1,…, N are derived:
Similarly to (20), Equation (21) has coefficients being slowly varying functions in x. These equations neglect the effect of the microstructure size on the overall behaviour of the considered FG plates. Equation (21) stands for the system of one differential equation for the unknown macrodeflection W and N algebraic equations for the fluctuation amplitudes VA(·,x2,t), A = 1,…, N. These functions have to be slowly varying functions in x. For these plates, two boundary conditions have to be formulated at all edges of the plate only for the macrodeflection W. It can be observed that neglecting terms with the microstructure parameter l in Equation (20) leads directly to Equation (21).
7. An Example: Formulas of Free Vibration Frequencies for a Special FG Plate Band
7.1. Preliminaries
Let us consider two kinds of FG plate bands: case (1) with a span L along the x-axis, simply supported on the edges x = 0, L; case (2) with a span L2 along the y-axis, simply supported on the edges y = 0, L2. It is assumed that the plate bands are made of two component elastic isotropic materials, described by the following: Young’s moduli E′, E″, as well as mass densities ρ′, ρ″. Let the plate thickness d and Poisson’s ratio ν be constant; load p = 0 and . Moreover, all geometrical and material properties are constant along the y-axis.
It is assumed that the tolerance-periodic distribution of Young’s modulus E and mass density is described as follows:
where γ(x), x∈[0,L] is a distribution function of material properties.
For the FG plate bands with an a-type microstructure, the form of the fluctuation shape function g is related to the structure of the “basic cell” shown in Figure 1b. Hence, the periodic approximation of this function can be assumed as follows:
where is the periodic approximation of the distribution function of material properties γ(x).
For the FG plate bands with a b-type microstructure, only one fluctuation shape function is assumed, i.e., h = h1, A = M = 1 (hence, also denote V = V1). Similarly to function g, the form of function h should be related to the structure of the “basic cell” presented in Figure 2b. Thus, the fluctuation shape function can be approximated by the periodic approximation function in the following form:
where function c(x) is a slowly varying one in x, determined by ; function is the periodic approximation of the distribution function γ(x). Function c(x) is treated as constant in calculations of derivatives .
7.2. Free Vibration Equations
7.2.1. Case (1): FG Plate Bands with a Span L Along the x-Axis
Assuming that the central part of the cells of these bands (cf. Figure 1b and Figure 2b) is the reinforcement or the rib of the plate, it can be observed that this case (1) corresponds to plate bands with reinforcement ribs parallel to the edges of support.
- FG plate bands with a-type microstructure
Let us introduce some denotations:
- The tolerance model for an a-type microstructure
The tolerance model equations of free vibrations for FG plate bands with an a-type microstructure are obtained from (18) with the averaged coefficients (25) in the following form:
The above equations describe both macrovibrations (related to the averaged macrostructure of the plate band under consideration) and microvibrations (related to the plate band microstructure) for two fluctuation amplitudes rα, α = 1, 2. It can be observed that the equation of r2 is independent.
- The asymptotic model for an a-type microstructure
For the considered plate band, by applying coefficients (25), the asymptotic model equations of free vibrations for FG plate bands with an a-type microstructure are derived from (19) in the following form:
Because terms with the microstructure parameter l are omitted in the above equations, the effect of the microstructure size is neglected. Equation (27) only describes the macrovibrations of the plate band.
- 2.
- FG plate bands with b-type microstructure
Let us introduce some denotations:
- The tolerance model for a b-type microstructure
The tolerance model equations of free vibrations for FG plate bands with a b-type microstructure are obtained from (20) with the averaged coefficients (28) in the following form:
The above equations describe both macrovibrations (related to the averaged macrostructure of the plate band under consideration) and microvibrations (related to the plate band microstructure).
- The asymptotic model for a b-type microstructure
For the considered plate band, by applying coefficients (28), the asymptotic model equations of free vibrations for FG plate bands with a b-type microstructure are derived from (21) in the following form:
Because terms with the microstructure parameter l are neglected in the above equations, the effect of the microstructure size is neglected. Equation (30) only describes the macrovibrations of the plate band.
It should be observed that model Equations (26), (27), (29), and (30) have slowly varying functional coefficients in x.
7.2.2. Case (2): FG Plate Bands with a Span L2 Along the y-Axis
By analogy with Section 7.2.1, it can be seen that case (2) corresponds to plate bands with reinforcement ribs perpendicular to the edges of support.
- FG plate bands with a-type microstructure
In this case, the following denotations are introduced:
- The tolerance model for an a-type microstructure
The tolerance model equations of free vibrations for FG plate bands with an a-type microstructure are obtained from (18) with the averaged coefficients (31) in the following form:
Equation (32) determines both macrovibrations (related to the averaged macrostructure of a considered plate band) and microvibrations (related to the plate band microstructure) for macrodeflection u and two fluctuation amplitudes rα, α = 1, 2. It can be observed that the equation of r2 is independent.
- The asymptotic model for an a-type microstructure
For this plate band, by applying denotations (31), the asymptotic model equations of free vibrations for FG plate bands with an a-type microstructure are derived from (19) as follows:
Since the coefficients with the microstructure parameter l are neglected in (33), then the effect of the microstructure size is omitted in these equations. Equation (33) only describes macrovibrations of the plate band.
- 2.
- FG plate bands with b-type microstructure
In this case, the following denotations are used:
- The tolerance model for a b-type microstructure
The tolerance model equations of free vibrations for FG plate bands with a b-type microstructure are obtained from (20) with the averaged coefficients (34) in the following form:
Equation (35) determines both macrovibrations (related to the averaged macrostructure of the plate band) and microvibrations (related to the plate band microstructure).
- The asymptotic model for a b-type microstructure
For the considered plate band, by applying coefficients (34), the asymptotic model equations of free vibrations for FG plate bands with a b-type microstructure derived from (21) take the following form:
The effect of the microstructure size is neglected in the above equations because there are no terms dependent on the microstructure parameter l within them. Hence, Equation (36) describes macrovibrations of the plate band only.
It should be observed that model Equations (32), (33), (35), and (36) have slowly varying functional coefficients in x.
7.3. Free Vibration Frequencies—The Ritz Method Applied to the Model Equations
In this section, formulas of free vibration frequencies for FG plate with the tolerance-periodic microstructure introduced above are obtained.
Because Equations (26), (27), (29), (30), (32), (33), (35), and (36) have slowly varying functional coefficients, analytical solutions of these equations are difficult to find. Approximate formulas of free vibration frequencies can be obtained by applying, for instance, the known Ritz method, cf. [2,79]. In this method, the relation between the maximal strain energy and the maximal kinetic energy have to be derived.
7.3.1. Case (1): FG Plate Bands with a Span L Along the x-Axis
- FG plate bands with a-type microstructure
Solutions to Equations (26) and (27) can be assumed in the following form:
where k is a wave number; ω is a free vibration frequency; functions Φ(x), Ψ(x) satisfy boundary conditions for the considered FG plate band with an a-type microstructure, in x = 0, L; and are amplitudes. The derivatives of functions Φ(x), Ψ(x) are denoted as follows:
Using functions (37) and (38), and also coefficients (25), the following denotations can be introduced:
Then, the formulas of the maximal energies—strain and kinetic —can be derived for both models of FG plates with an a-type microstructure—the tolerance and the asymptotic one.
Using the conditions of the Ritz method in the following form:
the following characteristic equations can be derived for these models:
- The tolerance model
- The asymptotic modelSolutions of the above equations stand for the free vibration frequencies for the considered models.
Equation (41) leads to the formulas of the free vibration frequencies for the tolerance model in the following form:
where ω− is the fundamental lower free vibration frequency related to the averaged macrostructure of the considered FG plate band; ω+1, ω+2 are the higher free vibration frequencies related to an a-type microstructure of the plate band.
However, only one formula of the free vibration frequency for the asymptotic model is obtained from Equation (42):
which is the fundamental lower free vibration frequency related to the averaged macrostructure of the FG plate band.
It can be observed that in the tolerance model for the considered FG plate bands, only fundamental lower-order vibrations (macrovibrations) and higher-order vibrations (microvibrations) along the x-axis are coupled.
- 2.
- FG plate bands with b-type microstructure
Solutions to Equations (29) and (30) are assumed in the following form:
where k is a wave number; ω is a free vibration frequency; functions Θ(x), Ξ(x) satisfy boundary conditions for the considered FG plate band with a b-type microstructure in x = 0, L; and are amplitudes. Let derivatives of functions Θ(x), Ξ(x) be denoted as follows:
Using functions (45) and (46), and also coefficients (28), let us introduce the following denotations:
Then, the formulas of the maximal energies—strain and kinetic —can be obtained for both models of FG plates with a b-type microstructure—the tolerance and the asymptotic one.
Applying the conditions of the Ritz method
the following characteristic equations are obtained for these models:
- The tolerance model
- The asymptotic modelFormulas of the free vibration frequencies for the considered models are obtained as solutions of Equations (49) and (50).
Hence, the formulas of the free vibration frequencies for the tolerance model take the following form:
where is the fundamental lower free vibration frequency related to the averaged macrostructure of the considered FG plate band; is the higher free vibration frequency related to the microstructure of the FG plate band.
Similarly to plates with an a-type microstructure, only one formula of the free vibration frequency for the asymptotic model is derived:
This is the fundamental lower free vibration frequency related to the averaged macrostructure of the FG plate band.
Moreover, in the tolerance model for the considered FG plate bands with a b-type microstructure, fundamental macrovibrations and microvibrations are coupled.
7.3.2. Case (2): FG Plate Bands with a Span L2 Along the y-Axis
- FG plate bands with a-type microstructure
Solutions to Equations (32) and (33) are assumed in the form similar to (37), i.e., as follows:
where k is a wave number; ω is a free vibration frequency; functions Φ(y), Ψ(y) satisfy boundary conditions for the considered FG plate band with an a-type microstructure, in y = 0, L2; and are amplitudes. The first and second derivatives of functions Φ(y), Ψ(y) are denoted as follows:
The length of the plate band is assumed as L2 = L. Applying functions (53) and (54) and coefficients (31), the following denotations are introduced:
Then, the formulas of the maximal energies—strain and kinetic —can be obtained for both models of FG plates with an a-type microstructure—the tolerance and the asymptotic one.
Applying the conditions of the Ritz method in the following form:
the following characteristic equations are derived for these models:
- The tolerance model
- The asymptotic modelFormulas of the free vibration frequencies for the considered models are obtained as solutions of the above equations.
Solving Equation (57), the formulas of the free vibration frequencies for the tolerance model are derived:
where the fundamental lower free vibration frequency related to the averaged macrostructure of the considered FG plate band is denoted by , and the higher free vibration frequencies related to the plate band a-type microstructure are denoted by .
But from Equation (58), only one formula of the free vibration frequency for the asymptotic model is obtained:
which is the fundamental lower free vibration frequency related to the averaged macrostructure of the FG plate band.
For the considered FG plate bands, the fundamental lower-order vibrations and higher-order vibrations along the x-axis are coupled in the tolerance model only, but higher-order vibrations along the y-axis are independent of them.
- 2.
- FG plate bands with b-type microstructure
Solutions to Equations (35) and (36) are assumed as follows:
where k is a wave number; ω is a free vibration frequency; functions Θ(y), Ξ(y) satisfy boundary conditions for the considered FG plate band with a b-type microstructure in y = 0, L2; and are amplitudes. Let the first and second derivatives of functions Θ(y), Ξ(y) be denoted as follows:
In the following transformations, it is assumed that L2 = L. Using functions (61) and (62) and also coefficients (34), the following denotations are introduced:
Similarly to case (1) for FG plates with a b-type microstructure, the formulas of the maximal energies—strain and kinetic —are obtained for both tolerance and asymptotic models.
From the conditions of the Ritz method
the following characteristic equations are obtained for these models:
- The tolerance model
- The asymptotic modelSolving Equation (65), the formulas of the free vibration frequencies for the tolerance model of the considered FG plate bands are obtained:where the fundamental lower free vibration frequency related to the averaged macrostructure of the considered FG plate band is denoted by ; but the higher free vibration frequency is related to the b-type microstructure of the plate band by .
However, only one formula of the free vibration frequency for the asymptotic model is obtained, similarly to plates with an a-type microstructure:
which is the fundamental lower free vibration frequency related to the averaged macrostructure of the FG plate band.
Moreover, it should be noticed that fundamental macrovibrations and microvibrations in the tolerance model are coupled for the considered FG plate bands with a b-type microstructure.
8. Final Remarks
Vibrations of thin functionally graded plates with two kinds of tolerance-periodic (non-periodic) microstructures have been considered in this paper: (a) with an a-type tolerance-periodic microstructure, in which the size of the microstructure is of an order of the plate thickness, d~l; (b) with a b-type tolerance-periodic microstructure, having a size of the microstructure higher than the plate thickness, d << l.
The work is theoretical in nature, and so are the presented simple examples of calculations. It considers the free vibrations of two cases of plate bands, i.e., case (1) spanning along the microstructure (along the x-axis); case (2) spanning across the microstructure (along the y-axis), simply supported at the ends. This can be illustrated by assuming that the central part of the cells of these bands (cf. Figure 1b and Figure 2b) is the reinforcement—the rib of the plate. Then, the considered case (1) corresponds to bands with reinforcement ribs parallel to the edges of support, while case (2) concerns bands with reinforcement ribs perpendicular to the edges of support.
It is shown that formulas for the free vibration frequencies can be obtained within the derived models (whereby equations are characterised by continuous, smooth, but still functional coefficients) using well-known methods, such as the Ritz method.
From the derived equations describing the free vibrations of the plate bands considered in the example, as well as the formulae for the free vibration frequencies, the following can be seen:
- -
- In the tolerance models for functionally graded plates with a-type or b-type tolerance-periodic microstructures, a single equation of macrovibrations along the z-axis is obtained. Additionally, in the model for FG plates with the a-type microstructure, equations of microvibrations along the x- and y-axes are derived, while for the FG plates with a b-type microstructure the equations of microvibrations occur along the z-axis.
- -
- According to the tolerance models for the considered plate bands with an a-type tolerance-periodic microstructure, the fundamental lower-order vibrations (macrovibrations along the z-axis), corresponding to the macrostructure, and higher-order vibrations (microvibrations) along the x-axis, corresponding to the microstructure, are coupled; meanwhile, higher-order vibrations along the y-axis are independent.
- -
- However, for the plate bands with a b-type microstructure, the macrovibrations along the z-axis and microvibrations along the z-axis are coupled.
- -
- Within the framework of tolerance models for functionally graded plate bands with an a-type tolerance-periodic microstructure, one fundamental lower-order free vibration frequency, corresponding to the macrostructure, and two higher-order free vibration frequencies, corresponding to the microstructure, are obtained.
- -
- However, for FG plate bands with a b-type microstructure, one lower-order free vibration frequency and one higher-order free vibration frequency are obtained.
- -
- In the asymptotic models for all cases of functionally graded plates under consideration, one equation describing macrovibrations along the z-axis and one fundamental lower free vibration frequency are obtained.
- -
- In forthcoming papers, the tolerance model equations of the aforementioned plates will be used to investigate a number of additional, more complex, and interesting problems. The obtained calculation results obtained with both tolerance models will be compared with each other. Furthermore, the selected results will be validated using the finite element method.
Author Contributions
J.J. conceived and designed the tolerance and asymptotic models of thin functionally graded plates with an a-type microstructure; M.K.-S. conceived and designed the tolerance and asymptotic models of thin functionally graded plates with a b-type microstructure; J.J. and M.K.-S. performed the examples and analysis; J.J. and M.K.-S. made figures for the paper, discussed the obtained results, and wrote the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding authors.
Conflicts of Interest
The authors declares no conflict of interest.
List of Basic Symbols
| <Λg>, <Λh> | averaged Lagrangean of plate |
| <·> | averaging operator |
| Δ | basic cell |
| bαβγδ | bending stiffnesses of plate |
| ∂ | derivative of x1 |
| derivative of x2 | |
| ∂α, ∂α...δ≡∂α...∂δ | derivatives of xα |
| γ(x) | distribution function of material properties |
| rα, r; VA, V | fluctuation amplitudes |
| fluctuation shape functions | |
| highly oscillating function | |
| Λ | Lagrangean of plate |
| L | length of the plate band along the x1- or x2-axis |
| L1, L2 | lengths of the plate along the x1-, x2-axis, respectively |
| u, W | macrodeflection |
| μ | mass density of plate |
| l | microstructure parameter |
| periodic approximation (of function f) | |
| Π | plate midplane |
| ν | Poisson’s ratio of plate material |
| ϑ | rotational mass inertia of plate |
| slowly varying function | |
| d | thickness of plate |
| δ | tolerance parameter |
| tolerance-periodic function | |
| E | Young’s modulus of plate material |
References
- Suresh, S.; Mortensen, A. Fundamentals of Functionally Graded Materials; The University Press: Cambridge, UK, 1998. [Google Scholar]
- Woźniak, C.; Michalak, B.; Jędrysiak, J. (Eds.) Thermomechanics of Microheterogeneous Solids and Structures: Tolerance Averaging Approach; Publishing House of Łódź University of Technology: Lodz, Poland, 2008. [Google Scholar]
- Bensoussan, A.; Lions, J.-L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North-Holland: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Kohn, R.V.; Vogelius, M. A new model of thin plates with rapidly varying thickness. Int. J. Solid Struct. 1984, 20, 333–350. [Google Scholar] [CrossRef]
- Duvaut, G.; Metellus, A.M. Homogéneisation d’une plaque mince en flexion des structure périodique et symmetrique. C.R. Acad. Sci. 1976, 283, 947–950. [Google Scholar]
- Caillerie, D. Thin elastic and periodic plates. Math. Meth. Appl. Sci. 1984, 6, 159–191. [Google Scholar] [CrossRef]
- Matysiak, S.J.; Nagórko, W. Microlocal parameters in the modelling of microperiodic plates. Ing. Arch. 1989, 59, 434–444. [Google Scholar] [CrossRef]
- Sebestianiuk, P.; Perkowski, D.M.; Kulchytsky-Zhyhailo, R. On stress analysis of load for microperiodic composite half-plane with slant lamination. Meccanica 2019, 54, 573–593. [Google Scholar] [CrossRef]
- Sebestianiuk, P.; Perkowski, D.M.; Kulchytsky-Zhyhailo, R. On contact problem for the microperiodic composite half-plane with slant layering. Int. J. Mech. Sci. 2020, 182, 105734. [Google Scholar] [CrossRef]
- Batra, R.C.; Qian, L.F.; Chen, L.M. Natural frequencies of thick square plates made of orthotropic, trigonal, monoclinic, hexagonal and triclinic materials. J. Sound Vib. 2004, 270, 1074–1086. [Google Scholar] [CrossRef]
- Królak, M.; Kowal-Michalska, K.; Mania, R.J.; Świniarski, J. Stability and load carrying capacity of multi-cell thin-walled columns of rectangular cross-sections. J. Theor. Appl. Mech. 2009, 47, 435–456. [Google Scholar]
- Pawlus, D. Dynamic behaviour of three-layered annular plates with viscoelastic core under lateral loads. J. Sound Vib. 2015, 53, 775–788. [Google Scholar] [CrossRef][Green Version]
- Grygorowicz, M.; Jasion, P.; Magnucki, K. Elastic buckling and post-buckling behaviour of shells of revolution with special meridian. In Insights and Innovations in Structural Engineering, Mechanics and Computation, Proceedings of the 6th International Conference on Structural Engineering, Mechanics and Computation (SEMC), Cape Town, South Africa, 5–7 September 2016; Zingoni, A., Ed.; Zingoni, A., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 789–792. [Google Scholar]
- Grygorowicz, M.; Kędzia, P. Homogeneity of magnetic field influence on buckling of three layer polyethylene plate. In Insights and Innovations in Structural Engineering, Mechanics and Computation, Proceedings of the 6th International Conference on Structural Engineering, Mechanics and Computation (SEMC), Cape Town, South Africa, 5–7 September 2016; Zingoni, A., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 912–917. [Google Scholar]
- Smyczyński, M.J.; Grygorowicz, M.; Kędzia, P. Buckling of three layer rectangular polyethylene plate with ferrofluid under magnetic field. In Insights and Innovations in Structural Engineering, Mechanics and Computation, Proceedings of the 6th International Conference on Structural Engineering, Mechanics and Computation (SEMC), Cape Town, South Africa, 5–7 September 2016; Zingoni, A., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 924–928. [Google Scholar]
- Pawlus, D. Temperature effect on stability of clamped–clamped composite annular plate with damages. Materials 2021, 14, 4559. [Google Scholar] [CrossRef]
- Stręk, T.; Jopek, H.; Nienartowicz, M. Dynamic response of sandwich panels with auxetic cores. Phys. Status Solidi (B) Basic Res. 2015, 252, 1540–1550. [Google Scholar] [CrossRef]
- Burlaga, B.; Stręk, T. The vibrations induced by fluid flow in plates with different Poisson’s ratios. Vib. Phys. Syst. 2020, 31, 2020301. [Google Scholar]
- Michalski, J.; Stręk, T. Blast resistance of sandwich plate with auxetic anti-tetrachiral core. Vib. Phys. Syst. 2020, 31, 2020316. [Google Scholar]
- Michalski, J.; Stręk, T. Response of a sandwich plate with auxetic anti-tetrachiral core to puncture. In Lecture Notes in Mechanical Engineering, Proceedings of the 7th International Scientific-Technical Conference, MANUFACTURING 2022, Poznań, Poland, 16–19 May 2022; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1–14. [Google Scholar]
- Michalski, J.; Stręk, T. Numerical analysis of an auxetic anti-tetrachiral sandwich panel subjected to steady-state harmonic base motion. Vib. Phys. Syst. 2022, 33, 2022323. [Google Scholar]
- Pawlus, D. Static stability of composite annular plates with auxetic properties. Materials 2022, 15, 3579. [Google Scholar] [CrossRef]
- Pawlus, D. The dynamic stability problem of composite annular plates with auxetic properties. Eng. Trans. 2023, 71, 329–349. [Google Scholar]
- Firouzi, N.; Lenci, S.; Amabili, M.; Rabczuk, T. Nonlinear free vibrations of Timoshenko–Ehrenfest beams using finite element analysis and direct scheme. Nonlinear Dyn. 2024, 112, 7199–7213. [Google Scholar] [CrossRef]
- Firouzi, N.; Dohnal, F. Dynamic stability of the Mindlin-Reissner plate using a time-modulated axial force. Mech. Based Des. Struct. Mach. 2024, 53, 446–463. [Google Scholar] [CrossRef]
- Aboudi, J.; Pindera, M.-J.; Arnold, S.M. Thermo-inelastic response of functionally graded composites. Int. J. Solid Struct. 1995, 32, 1675–1710. [Google Scholar] [CrossRef]
- Aboudi, J.; Pindera, M.-J.; Arnold, S.M. A coupled higher-order theory for functionally graded composites with partial homogenization. Compos. Eng. 1995, 5, 771–792. [Google Scholar] [CrossRef]
- Pindera, M.-J.; Dunn, P. Evaluation of the higher-order theory for functionally graded materials via the finite-element method. Compos. Part B 1997, 28, 109–119. [Google Scholar] [CrossRef]
- Aboudi, J.; Pindera, M.-J.; Arnold, S.M. Higher-order theory for functionally graded materials. Compos. Part B 1999, 30, 777–832. [Google Scholar] [CrossRef]
- Goldberg, R.K.; Hopkins, D.A. Thermal analysis of a functionally graded material subject to a thermal gradient using the boundary element method. Compos. Eng. 1995, 5, 793–806. [Google Scholar] [CrossRef]
- Martínez-Pañeda, M. On the finite element implementation of functionally graded materials. Materials 2019, 12, 287. [Google Scholar] [CrossRef] [PubMed]
- Sofiyev, A.H.; Schnack, E. The stability of functionally graded cylindrical shells under linearly increasing dynamic torsional loading. Eng. Struct. 2004, 26, 1321–1331. [Google Scholar] [CrossRef]
- Ferreira, A.J.M.; Batra, R.C.; Roque, C.M.C.; Qian, L.F.; Jorge, R.M.N. Natural frequencies of functionally graded plates by a meshless method. Compos. Struct. 2006, 75, 593–600. [Google Scholar] [CrossRef]
- Bui, T.Q.; Khosravifard, A.; Zhang, C.; Hematiyan, M.R.; Golu, M.V. Dynamic analysis of sandwich beams with functionally graded core using a truly meshfree radial point interpolation method. Eng. Struct. 2013, 47, 90–104. [Google Scholar] [CrossRef]
- Roque, C.M.C.; Ferreira, A.J.M.; Jorge, R.M.N. A radial basis function approach for the free vibration analysis of functionally graded plates using a refined theory. J. Sound Vib. 2007, 300, 1048–1070. [Google Scholar] [CrossRef]
- Tornabene, F.; Liverani, A.; Caligiana, G. FGM and laminated doubly curved shells and panels of revolution with a free-form meridian: A 2-D GDQ solution for free vibrations. Int. J. Mech. Sci. 2011, 53, 443–470. [Google Scholar] [CrossRef]
- Akbarzadeha, A.H.; Abbasib, M.; Eslami, M.R. Coupled thermoelasticity of functionally graded plates based on the third-order shear deformation theory. Thin-Walled Struct. 2012, 53, 141–155. [Google Scholar] [CrossRef]
- Oktem, A.S.; Mantari, J.L.; Guedes Soares, C. Static response of functionally graded plates and doubly-curved shells based on a higher order shear deformation theory. Eur. J. Mech. A/Solids 2012, 36, 163–172. [Google Scholar] [CrossRef]
- Tornabene, F.; Viola, E. Static analysis of functionally graded doubly-curved shells and panels of revolution. Meccanica 2013, 48, 901–930. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Batra, R.C. Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos. Struct. 2015, 119, 67–89. [Google Scholar] [CrossRef]
- Tornebene, F.; Fantuzzi, N.; Bacciocchi, M. On the mechanics of laminated doubly-curved shells subjected to point and line loads. Int. J. Eng. Sci. 2016, 109, 115–164. [Google Scholar] [CrossRef]
- Ashoori, A.R.; Sadough Vanini, S.A. Thermal buckling of annular microstructure-dependent functionally graded material plates resting on an elastic medium. Compos. Part B Eng. 2016, 87, 245–255. [Google Scholar] [CrossRef]
- Jha, D.K.; Kant, T.; Singh, R.K. Free vibration response of functionally graded thick plates with shear and normal deformations effects. Compos. Struct. 2013, 96, 799–823. [Google Scholar] [CrossRef]
- Sheikholeslami, S.A.; Saidi, A.R. Vibration analysis of functionally graded rectangular plates resting on elastic foundation using higher-order shear and normal deformable plate theory. Compos. Struct. 2013, 106, 350–361. [Google Scholar] [CrossRef]
- Derras, M.; Kaci, A.; Draiche, K.; Tounsi, A. Non-linear analysis of functionally graded plates in cylindrical bending based on a new refined shear deformation theory. J. Theor. Appl. Mech. 2013, 51, 339–348. [Google Scholar]
- Huangfu, Y.-G.; Chen, F.-Q. Single-pulse chaotic dynamics of functionally graded materials plate. Acta Mech. Sin. 2013, 29, 593–601. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F.; Viola, E.; Ferreira, A.J.M. A strong formulation finite element method (SFEM) based on RBF and GDQ techniques for the static and dynamic analyses of laminated plates of arbitrary shape. Meccanica 2014, 49, 2503–2542. [Google Scholar] [CrossRef]
- Fantuzzi, N.; Tornabene, F. Strong Formulation Isogeometric Analysis (SFIGA) for laminated composite arbitrarily shaped plates. Compos. Part B Eng. 2016, 96, 173–203. [Google Scholar] [CrossRef]
- Liu, B.; Ferreira, A.J.M.; Xing, Y.F.; Neves, A.M.A. Analysis of composite plates using a layerwise theory and a differential quadrature finite element method. Compos. Struct. 2016, 156, 393–398. [Google Scholar] [CrossRef]
- Kugler, S.; Fotiu, P.A.; Murin, J. The numerical analysis of FGM shells with enhanced finite elements. Eng. Struct. 2013, 49, 920–935. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Bacciocchi, M.; Viola, E.; Reddy, J.N. A numerical investigation on the natural frequencies of FGM sandwich shells with variable thickness by the local generalized differential quadrature method. Appl. Sci. 2017, 7, 131. [Google Scholar] [CrossRef]
- Tornabene, F.; Bacciocchi, M. Dynamic stability of doubly-curved multilayered shells subjected to arbitrarily oriented angular velocities: Numerical evaluation of the critical speed. Compos. Struct. 2018, 201, 1031–1055. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Bacciocchi, M.; Tornabene, F. Application of sinusoidal shear deformation theory and physical neutral surface to analysis of functionally graded piezoelectric plate. Compos. Part B Eng. 2018, 151, 35–50. [Google Scholar] [CrossRef]
- Arefi, M.; Bidgoli, E.M.R.; Dimitri, R.; Tornabene, F. Free vibrations of functionally graded polymer composite nanoplates reinforced with graphene nanoplatelets. Aerosp. Sci. Technol. 2018, 81, 108–117. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Mania, R.J. Dynamic response of thin FG plates with a static unsymmetrical stable postbuckling path. Thin-Walled Struct. 2015, 86, 10–17. [Google Scholar] [CrossRef]
- Mania, R.J.; Madeo, A.; Zucco, G.; Kubiak, T. Imperfection sensitivity of post-buckling of FML channel section column. Thin-Walled Struct. 2017, 114, 32–38. [Google Scholar] [CrossRef]
- Teter, A.; Mania, R.J.; Kołakowski, Z. Non-linear multi-mode buckling of non-symmetric FML/FGM thin-walled columns with open cross-sections under compression. Compos. Struct. 2017, 167, 38–49. [Google Scholar] [CrossRef]
- Kołakowski, Z.; Mania, R.J. Influence of the coupling matrix B on the interactive buckling of FML-FGM columns with closed cross-sections under axial compression. Compos. Struct. 2017, 173, 70–77. [Google Scholar] [CrossRef]
- Sadowski, T.; Burlayenko, V.N. Three-dimensional free vibration analysis of thermally loaded FGM sandwich plates. Materials 2019, 12, 2377. [Google Scholar] [CrossRef] [PubMed]
- Cao, Z.; Liang, X.; Deng, Y.; Zha, X.; Zhu, R.; Leng, J. Novel semi-analytical solutions for the transient behaviors of functionally graded material plates in the thermal environment. Materials 2019, 12, 4084. [Google Scholar] [CrossRef]
- Jafari, M.; Chaleshtari, M.H.B.; Abdolalian, H.; Craciun, E.-M.; Feo, L. Determination of forces and moments per unit length in symmetric exponential FG plates with a quasi-triangular hole. Symmetry 2020, 12, 834. [Google Scholar] [CrossRef]
- Magnucki, K.; Magnucka-Blandzi, E. Generalization of a sandwich structure model: Analytical studies of bending and buckling problems of rectangular plate. Compos. Struct. 2021, 255, 112944. [Google Scholar] [CrossRef]
- Magnucki, K.; Magnucka-Blandzi, E.; Wittenbeck, L. Bending of a generalized circular sandwich plate under a concentrated force with consideration of an improved shear deformation theory. Arch. Mech. 2022, 74, 267–282. [Google Scholar]
- Magnucki, K.; Magnucka-Blandzi, E.; Sowinski, K. Elastic buckling of a rectangular sandwich plate with an individual functionally graded core. J. Theor. Appl. Mech. 2024, 62, 171–185. [Google Scholar] [CrossRef]
- Kumar, V.; Singh, S.J.; Saran, V.H.; Harsha, S.P. Vibration Response Analysis of Tapered Porous FGM Plate Resting on Elastic Foundation. Int. J. Struct. Stab. Dyn. 2022, 23, 2350024. [Google Scholar] [CrossRef]
- Kumar, R.; Jana, P. Free vibration analysis of uniform thickness and stepped P-FGM plates: A FSDT-based dynamic stiffness approach. Mech. Based Des. Struct. Mach. 2022, 52, 447–476. [Google Scholar] [CrossRef]
- Zhao, Y.; Qin, B.; Wang, Q.; Liang, X. A unified Jacobi–Ritz approach for vibration analysis of functionally graded porous rectangular plate with arbitrary boundary conditions based on a higher-order shear deformation theory. Thin-Walled Struct. 2022, 173, 108930. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R. Natural frequency responses of hybrid polymer/carbon fiber/FG-GNP nanocomposites paraboloidal and hyperboloidal shells based on multiscale approaches. Aerosp. Sci. Technol. 2021, 119, 107111. [Google Scholar] [CrossRef]
- Sobhani, E.; Masoodi, A.R. On the circumferential wave responses of connected elliptical-cylindrical shell-like submerged structures strengthened by nano-reinforcer. Ocean Eng. 2022, 247, 110718. [Google Scholar] [CrossRef]
- Sobhani, E.; Moradi-Dastjerdi, R.; Behdinan, K.; Masoodi, A.R.; Ahmadi-Pari, A.R. Multifunctional trace of various reinforcements on vibrations of three-phase nanocomposite combined hemispherical-cylindrical shells. Compos. Struct. 2022, 279, 114798. [Google Scholar] [CrossRef]
- Shi, P.; Xie, J.; Li, X. Multilayer heterostructure inhomogeneous model for pressurized functionally graded annular structures (cylinder/sphere/annulus) with arbitrary elastic property along the radial direction. Compos. Struct. 2023, 322, 117425. [Google Scholar] [CrossRef]
- Ege, N.; Erbaş, B.; Kaplunov, J.; Noori, N. Low-frequency vibrations of a thin-walled functionally graded cylinder (plane strain problem). Mech. Adv. Mater. Struct. 2023, 30, 1172–1180. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures; Dover Pub. Inc.: Dover, UK, 1953. [Google Scholar]
- Wu, Z.-J.; Li, F.-M.; Wang, Y.-Z. Vibration band gap properties of periodic Mindlin plate structure using the spectral element method. Meccanica 2014, 49, 725–737. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Yu, D.Y.; Shao, X.; Wang, S.; Tian, Y.H. Band gap characteristics of periodically stiffened-thin-plate based on center-finite-difference-method. Thin-Walled Struct. 2014, 82, 115–123. [Google Scholar] [CrossRef]
- Zhou, X.Q.; Yu, D.Y.; Shao, X.; Wang, S.; Zhang, S.Q. Simplified-super-element-method for analyzing free flexural vibration characteristics of periodically stiffened-thin-plate filled with viscoelastic damping material. Thin-Walled Struct. 2015, 94, 234–252. [Google Scholar] [CrossRef]
- Cheng, Z.B.; Xu, Y.G.; Zhang, L.L. Analysis of flexural wave bandgaps in periodic plate structures using differential quadrature element method. Int. J. Mech. Sci. 2015, 100, 112–125. [Google Scholar] [CrossRef]
- Woźniak, C.; Wierzbicki, E. Averaging Techniques in Thermomechanics of Composite Solids: Tolerance Averaging Versus Homogenization; Publishing House Częstochowa University Technology: Częstochowa, Poland, 2000. [Google Scholar]
- Jan Awrejcewicz, G.; Jemielita, Z.; Kołakowski, S.J.; Matysiak, W.; Nagórko, W.; Pietraszkiewicz, P.; Śniady, R.; Świtka, G.; Szafer, M.; Wągrowska, K.; et al. (Eds.) Mathematical Modelling and Analysis in Continuum Mechanics of Microstructured Media; Publishing House Silesian University of Technology: Gliwice, Poland, 2010. [Google Scholar]
- Dell’Isola, F.; Rosa, L.; Woźniak, C. A micro-structural continuum modelling compacting fluid-saturated grounds. Acta Mech. 1998, 127, 165–182. [Google Scholar] [CrossRef]
- Wierzbicki, E.; Woźniak, C. On the dynamics of combined plane periodic structures. Arch. Appl. Mech. 2000, 70, 387–398. [Google Scholar] [CrossRef]
- Baron, E.; Woźniak, C. On the micro-dynamics of composite plates. Arch. Appl. Mech. 1995, 66, 126–133. [Google Scholar] [CrossRef]
- Baron, E. On dynamic behaviour of medium-thickness plates with uniperiodic structure. Arch. Appl. Mech. 2003, 73, 505–516. [Google Scholar] [CrossRef]
- Jędrysiak, J. On vibrations of thin plates with one-dimensional periodic structure. Int. J. Eng. Sci. 2000, 38, 2023–2043. [Google Scholar] [CrossRef]
- Michalak, B. The meso-shape functions for the meso-structural models of wavy-plates. ZAMM 2001, 81, 639–641. [Google Scholar] [CrossRef]
- Nagórko, W.; Woźniak, C. Nonasymptotic modelling of thin plates reinforced by a system of stiffeners. Electr. J. Pol. Agric. Univ. Civ. Eng. 2002, 5, 8. [Google Scholar]
- Mazur-Śniady, K.; Woźniak, C.; Wierzbicki, E. On the modelling of dynamic problems for plates with a periodic structure. Arch. Appl. Mech. 2004, 74, 179–190. [Google Scholar] [CrossRef]
- Tomczyk, B. A non-asymptotic model for the stability analysis of thin biperiodic cylindrical shells. Thin-Walled Struct. 2007, 45, 941–944. [Google Scholar] [CrossRef]
- Tomczyk, B. Dynamic stability of micro-periodic cylindrical shells. Mech. Mech. Eng. 2010, 14, 137–150. [Google Scholar]
- Tomczyk, B.; Gołąbczak, M.; Litawska, A.; Gołąbczak, A. Extended tolerance modelling of dynamic problems for thin uniperiodic cylindrical shells. Contin. Mech. Thermodyn. 2023, 35, 183–210. [Google Scholar] [CrossRef]
- Tomczyk, B.; Bagdasaryan, V.; Gołąbczak, M.; Litawska, A. A new combined asymptotic-tolerance model of thermoelasticity problems for thin biperiodic cylindrical shells. Compos. Struct. 2023, 309, 116708. [Google Scholar] [CrossRef]
- Domagalski, Ł.; Jędrysiak, J. On the elastostatics of thin periodic plates with large deflections. Meccanica 2012, 47, 1659–1671. [Google Scholar] [CrossRef]
- Domagalski, Ł.; Świątek, M.; Jędrysiak, J. An analytical-numerical approach to vibration analysis of periodic Timoshenko beams. Compos. Struct. 2019, 211, 490–501. [Google Scholar] [CrossRef]
- Marczak, J.; Jędrysiak, J. Some remarks on modelling of vibrations of periodic sandwich structures with inert core. Compos. Struct. 2018, 202, 752–758. [Google Scholar] [CrossRef]
- Marczak, J. A comparison of dynamic models of microheterogeneous asymmetric sandwich plates. Compos. Struct. 2021, 256, 113054. [Google Scholar] [CrossRef]
- Kubacka, E.; Ostrowski, P. A finite difference algorithm applied to the averaged equations of the heat conduction issue in biperiodic composites – Robin boundary conditions. Materials 2021, 14, 6329. [Google Scholar] [CrossRef]
- Marczak, J.; Michalak, B.; Wirowski, A. A multi-scale analysis of stress distribution in thin composite plates with dense system of ribs in two directions. Adv. Eng. Softw. 2021, 153, 102960. [Google Scholar] [CrossRef]
- Jędrysiak, J. On the tolerance modeling of thermoelasticity problems for transversally graded laminates. Arch. Civ. Mech. Eng. 2011, 11, 61–74. [Google Scholar] [CrossRef]
- Pazera, E.; Jędrysiak, J. Effect of microstructure in thermoelasticity problems of functionally graded laminates. Compos. Struct. 2018, 202, 296–303. [Google Scholar] [CrossRef]
- Michalak, B.; Wirowski, A. Dynamic modelling of thin plate made of certain functionally graded materials. Meccanica 2012, 47, 1487–1498. [Google Scholar] [CrossRef][Green Version]
- Wirowski, A.; Michalak, B.; Gajdzicki, M. Dynamic modelling of annular plates of functionally graded structure resting on elastic heterogeneous foundation with two modules. J. Mech. 2015, 31, 493–504. [Google Scholar] [CrossRef]
- Perliński, W.; Gajdzicki, M.; Michalak, B. Modelling of annular plates stability with functionally graded structure interacting with elastic heterogeneous subsoil. J. Theor. Appl. Mech. 2014, 52, 485–498. [Google Scholar]
- Michalak, B. 2D tolerance and asymptotic models in elastodynamics of a thin-walled structure with dense system of ribs. Arch. Civ. Mech. Eng. 2015, 15, 449–455. [Google Scholar] [CrossRef]
- Rabenda, M.; Michalak, B. Natural vibrations of prestressed thin functionally graded plates with dense system of ribs in two directions. Compos. Struct. 2015, 133, 1016–1023. [Google Scholar] [CrossRef]
- Ostrowski, P.; Michalak, B. The combined asymptotic-tolerance model of heat conduction in a skeletal micro-heterogeneous hollow cylinder. Compos. Struct. 2015, 134, 343–352. [Google Scholar] [CrossRef]
- Ostrowski, P.; Michalak, B. A contribution to the modelling of heat conduction for cylindrical composite conductors with non-uniform distribution of constituents. Int. J. Heat Mass Transf. 2016, 92, 435–448. [Google Scholar] [CrossRef]
- Pazera, E.; Ostrowski, P. Heat transfer in functionally graded laminate—Third type boundary conditions. AIP Conf. Proc. 2020, 2239, 020040. [Google Scholar]
- Kaźmierczak, M.; Jędrysiak, J. A new combined asymptotic-tolerance model of vibrations of thin transversally graded plates. Eng. Struct. 2013, 46, 322–331. [Google Scholar] [CrossRef]
- Jędrysiak, J. Tolerance modelling of free vibration frequencies of thin functionally graded plates with one-directional microstructure. Compos. Struct. 2017, 161, 453–468. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Tolerance and asymptotic modelling of dynamic problems for thin microstructured transversally graded shells. Compos. Struct. 2017, 162, 365–373. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. Combined asymptotic-tolerance modelling of dynamic problems for functionally graded shells. Compos. Struct. 2018, 183, 176–184. [Google Scholar] [CrossRef]
- Tomczyk, B.; Szczerba, P. A new asymptotic-tolerance model of dynamic and stability problems for longitudinally graded cylindrical shells. Compos. Struct. 2018, 202, 473–481. [Google Scholar] [CrossRef]
- Tomczyk, B.; Gołąbczak, M.; Gołąbczak, M.; Kubacka, E.; Bagdasaryan, V. Mathematical modelling of stability problems for thin transversally graded cylindrical shells. Contin. Mech. Thermodyn. 2024, 36, 1661–1684. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).