Micro-Interface Slip Damping in a Compressed Coir Vibration Isolator
Abstract
1. Introduction
1.1. Background
1.2. Overview of This Study
1.3. Technical Challenge and Solution Strategy
1.4. Mem-Models
- A mem-dashpot for restoring the force-displacement level can be defined in two differential forms as in Equations (7) and (23), where the former and latter are for flow- and effort-controlled settings, respectively. These two forms facilitate connecting the mem-dasphot with other modeling elements in parallel and series, respectively. These differential forms are featured with the “zero-crossing” property meaning that the input and output, and r, or r and , become zero simultaneously. Equations (13) and (19) are the integral forms for the mem-dashpot under flow- and effort-controlled settings, respectively. These integral forms are featured with one-to-one mapping from to , or to . The terminologies and usefulness of the differential and integral forms can be referred to [28].
- A mem-spring for restoring the force-displacement level can be defined in two differential forms as in Equations (8) and (24) under flow- and effort-controlled settings, respectively. These differential forms are featured with the “zero-crossing” property meaning that the input and output, x and r, or r and x, become zero simultaneously. Equations (14) and (20) are the integral forms for the mem-spring under flow- and effort-controlled settings, respectively. These integral forms are featured with one-to-one mapping from to , or to .
1.5. Intended Contribution and Structure of This Paper
- At restoring force-displacement level, we havewhere and K, the two parameters with fixed values in Equation (1) are replaced with two functions of absement. The first function is about how the yield strength is affected by absement, while the second function is about how the initial stiffness is affected by absement.
- At the stress–strain level, we havewhere and E, the two parameters with fixed values in Equation (2) are replaced with two functions of generalized momentum. The first function is about how the yield strength is affected by generalized momentum, while the second function is about how the initial stiffness is affected by generalized momentum.
2. Manufacturing and Testing
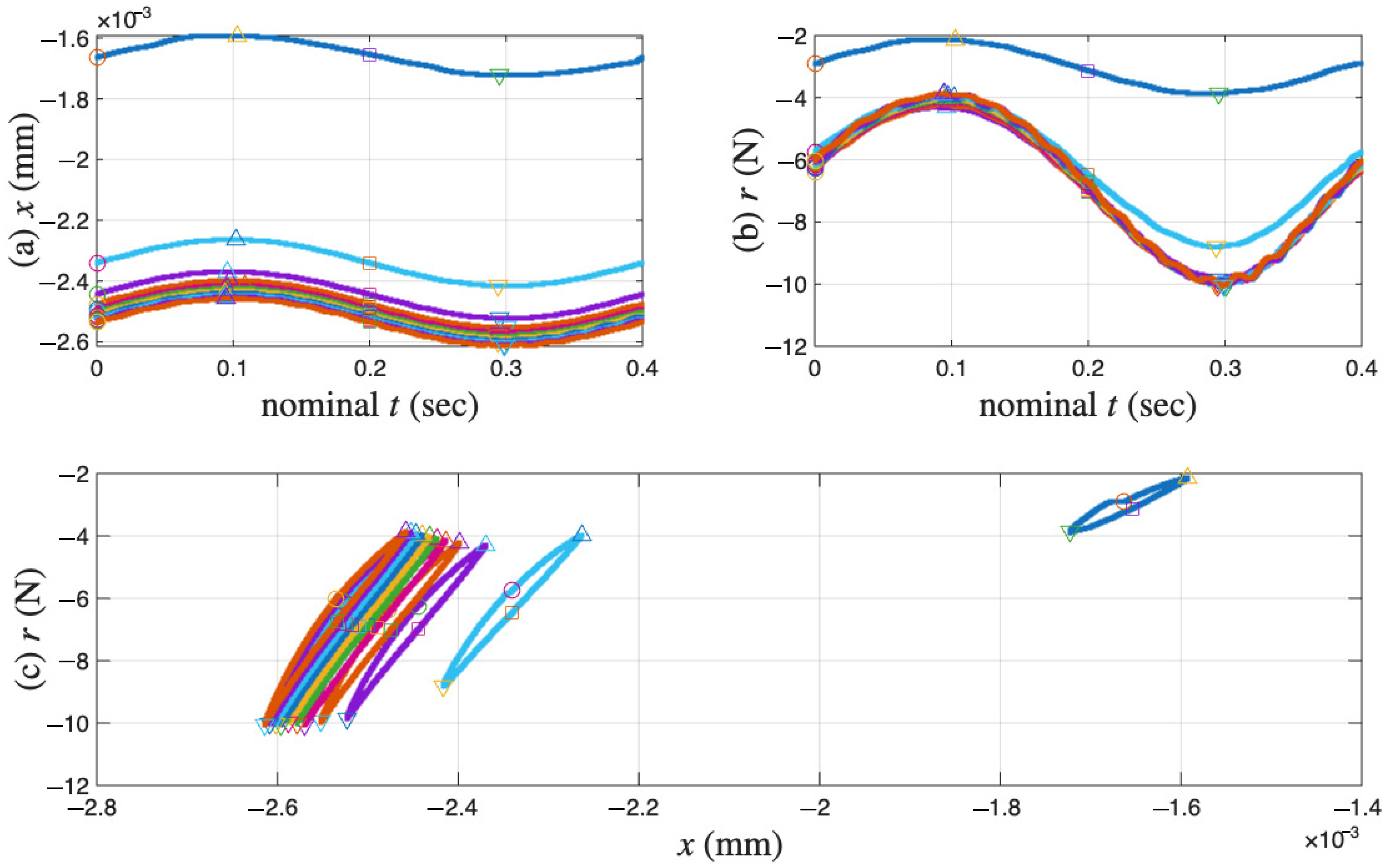
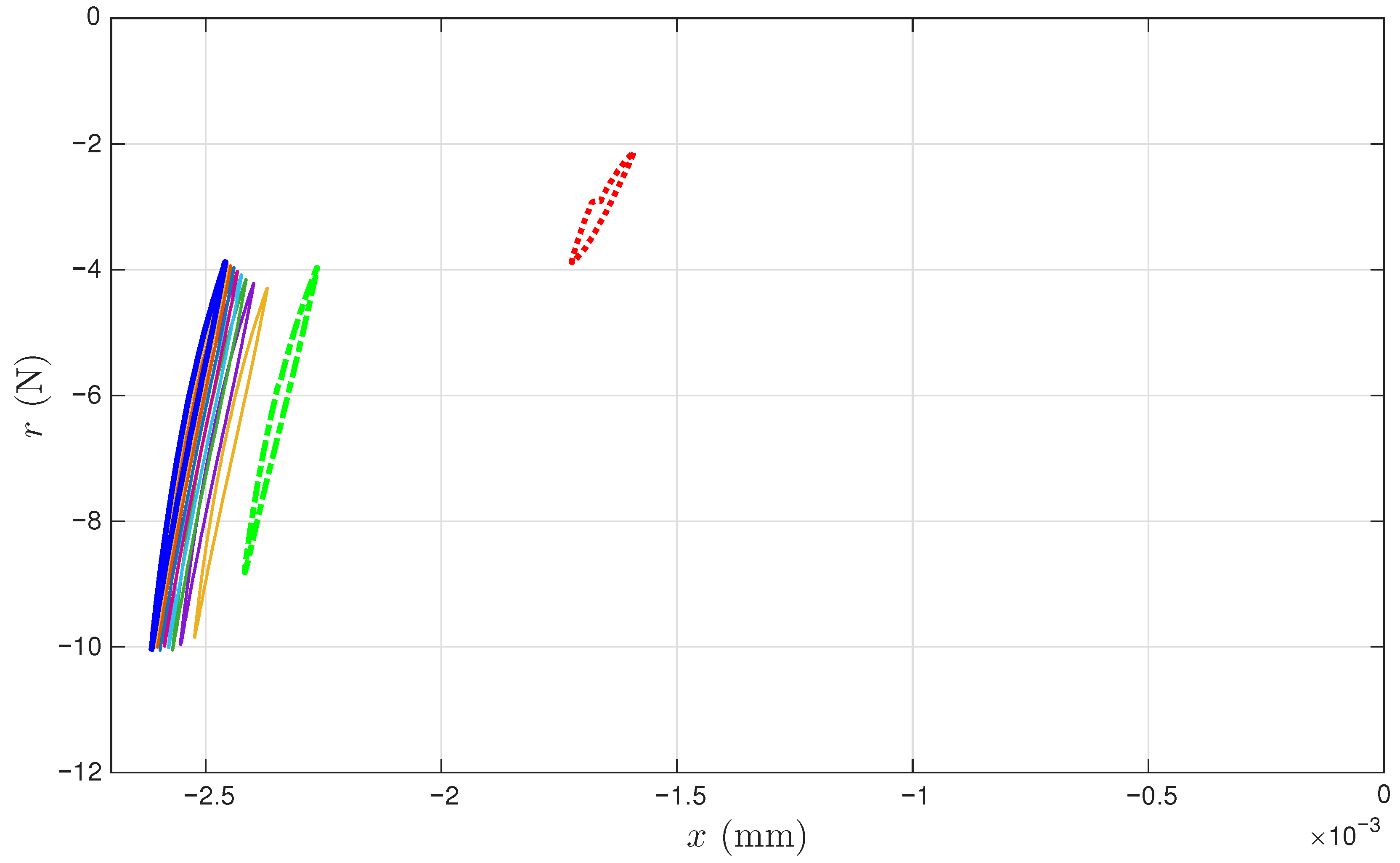
2.1. Coir Isolators
- (i)
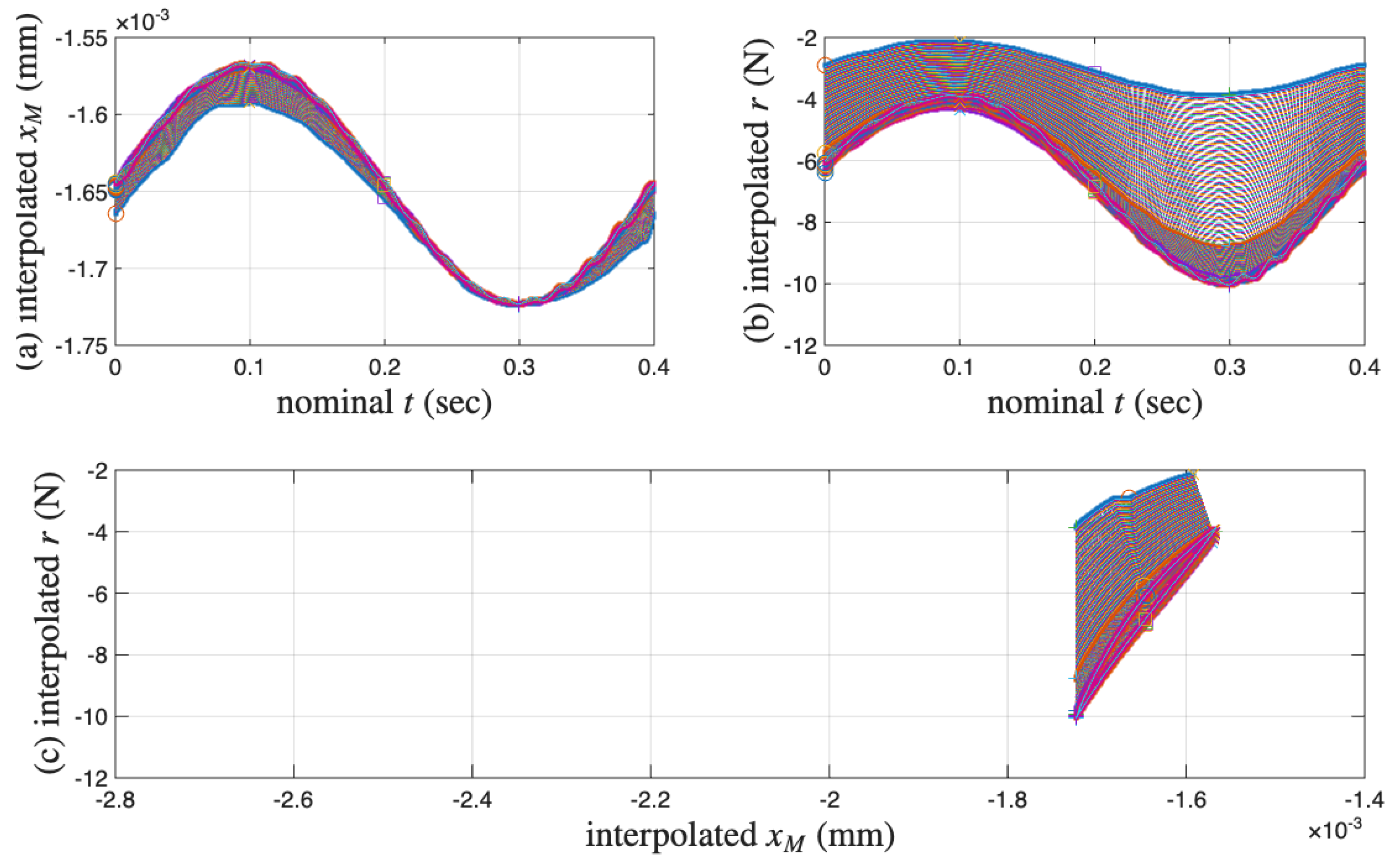
- Starts the first point with a circle marker, where there is an approximately maximum positive velocity on an unloading branch.
- (ii)
- Goes over the maximum displacement point, a velocity turning point to start a reloading branch. This point is not exactly the 2001st point but will be approximated using it later.
- (iii)
- Passes the 4001st point, an approximately maximum negative velocity point marked with a square.
- (iv)
- Reaches the minimum displacement point, the other velocity turning point to start a unloading branch. This point is not exactly the 6001st point but will be approximated using it later.
- (v)
- Completes the cycle at the 8001st point, just before the circle marker for the next cycle (which is not measured).
2.2. Clayey Soil Specimens
3. Proposed Models
3.1. More Review of Original Extended Masing Models
3.2. Proposed Enriched Extended Masing Models
4. Data Analysis and Modeling of Coir Isolator
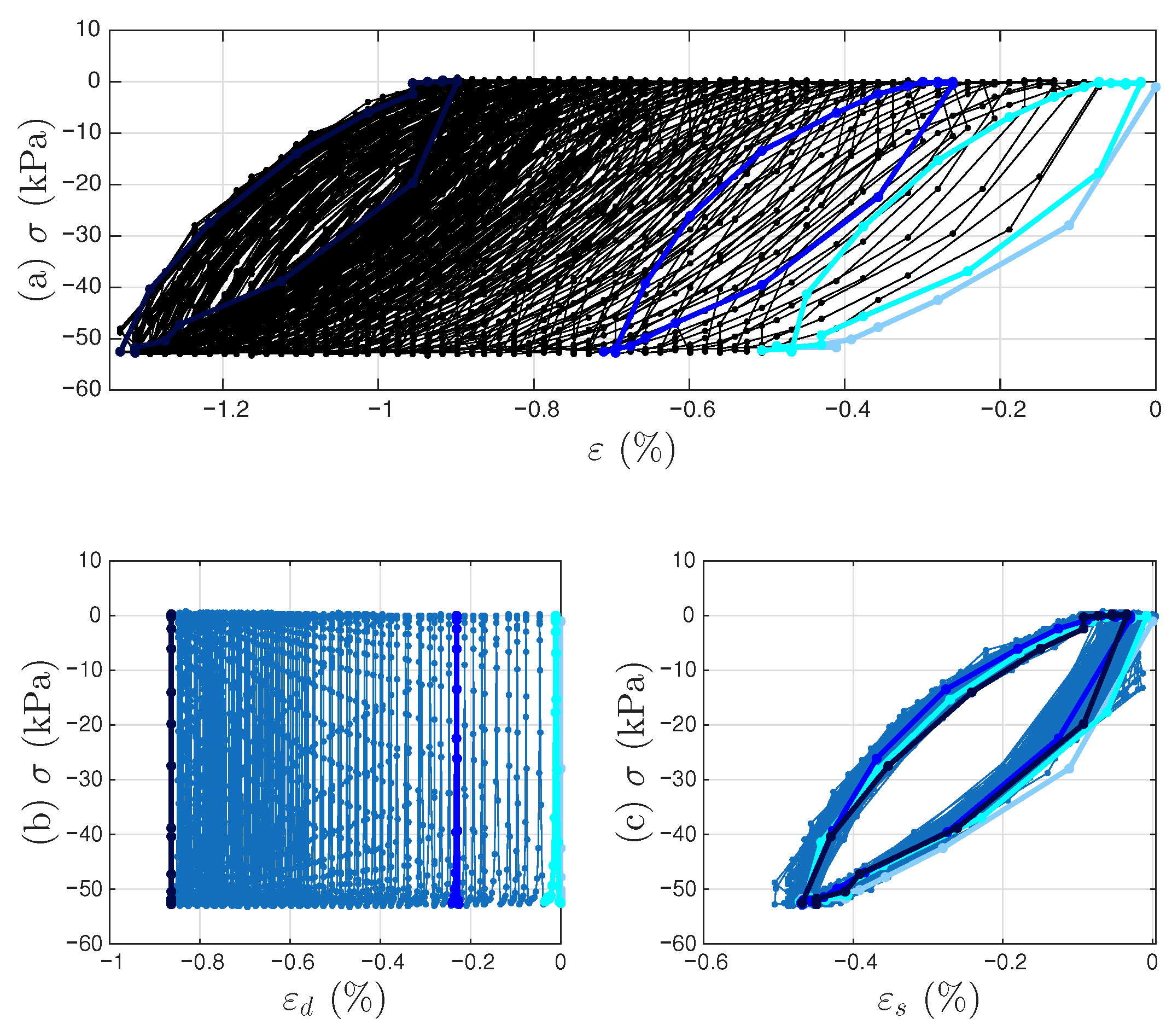
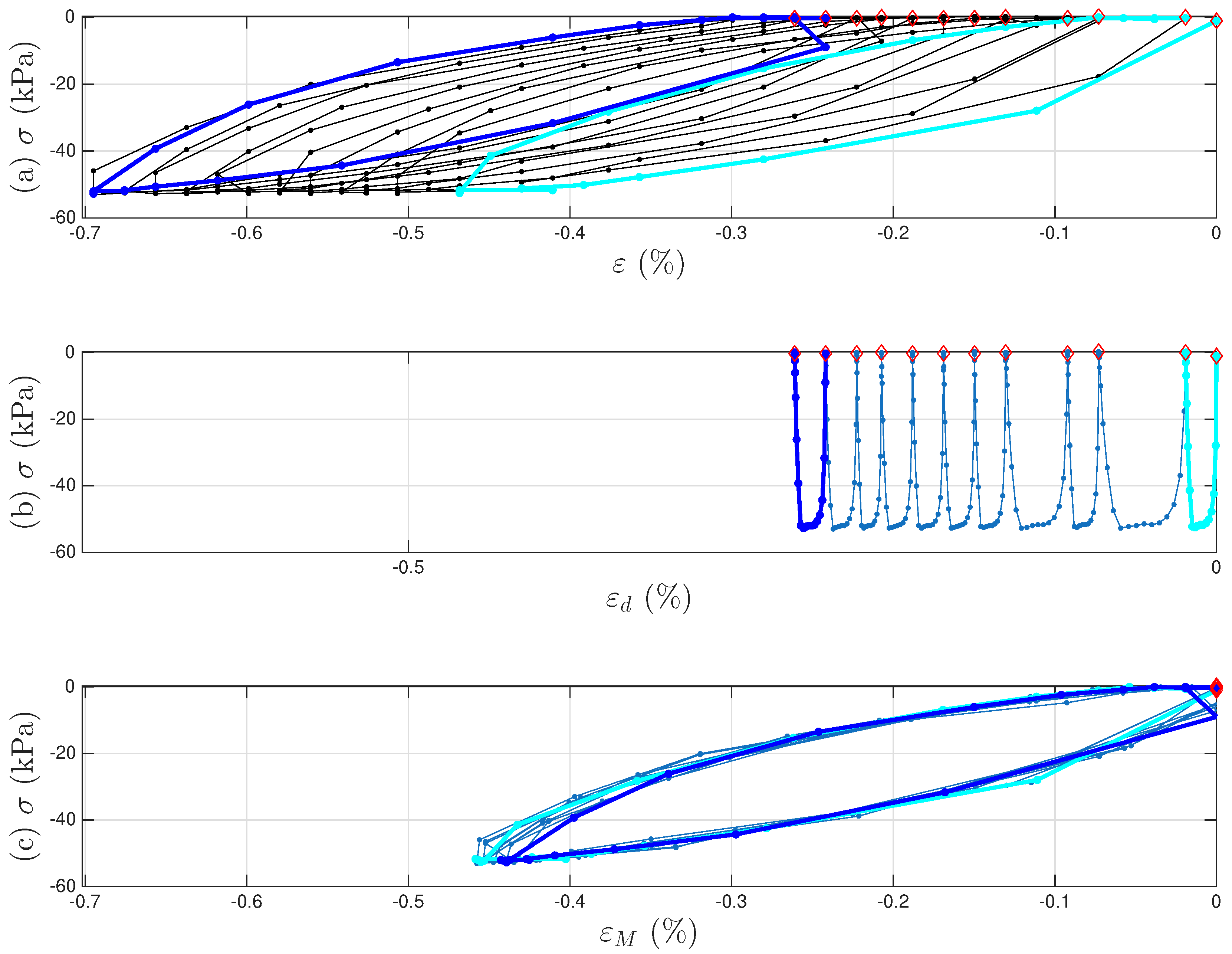
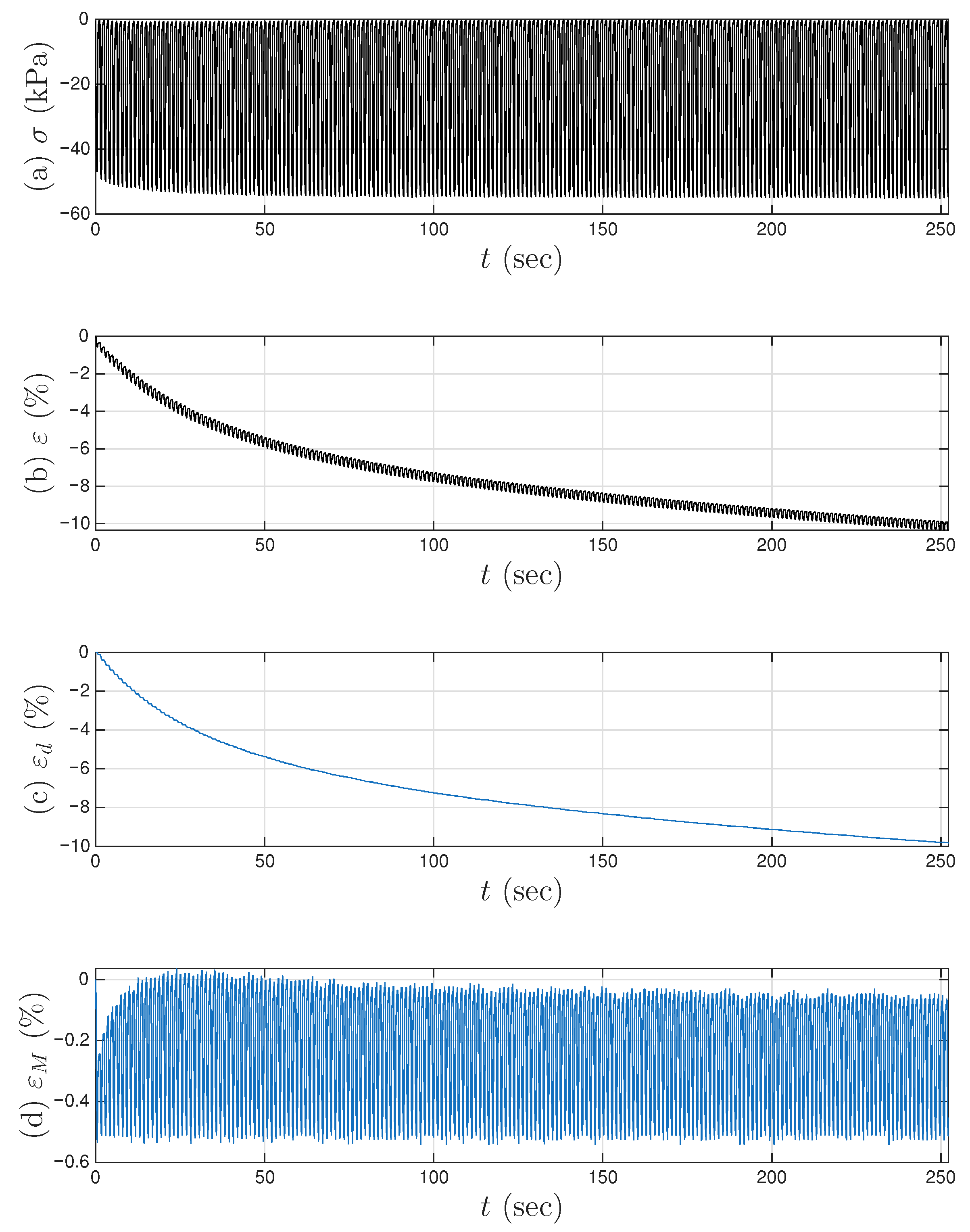
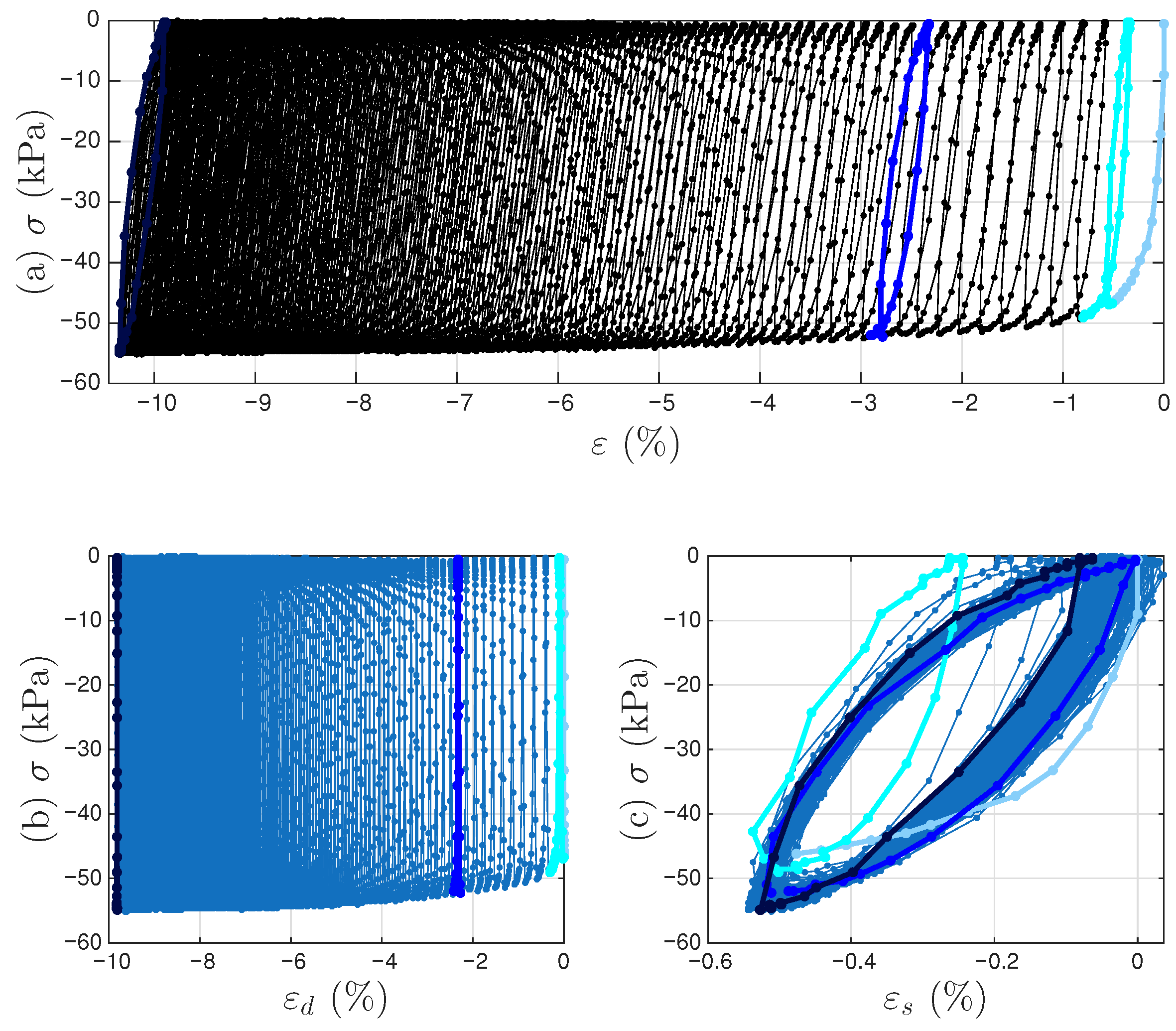
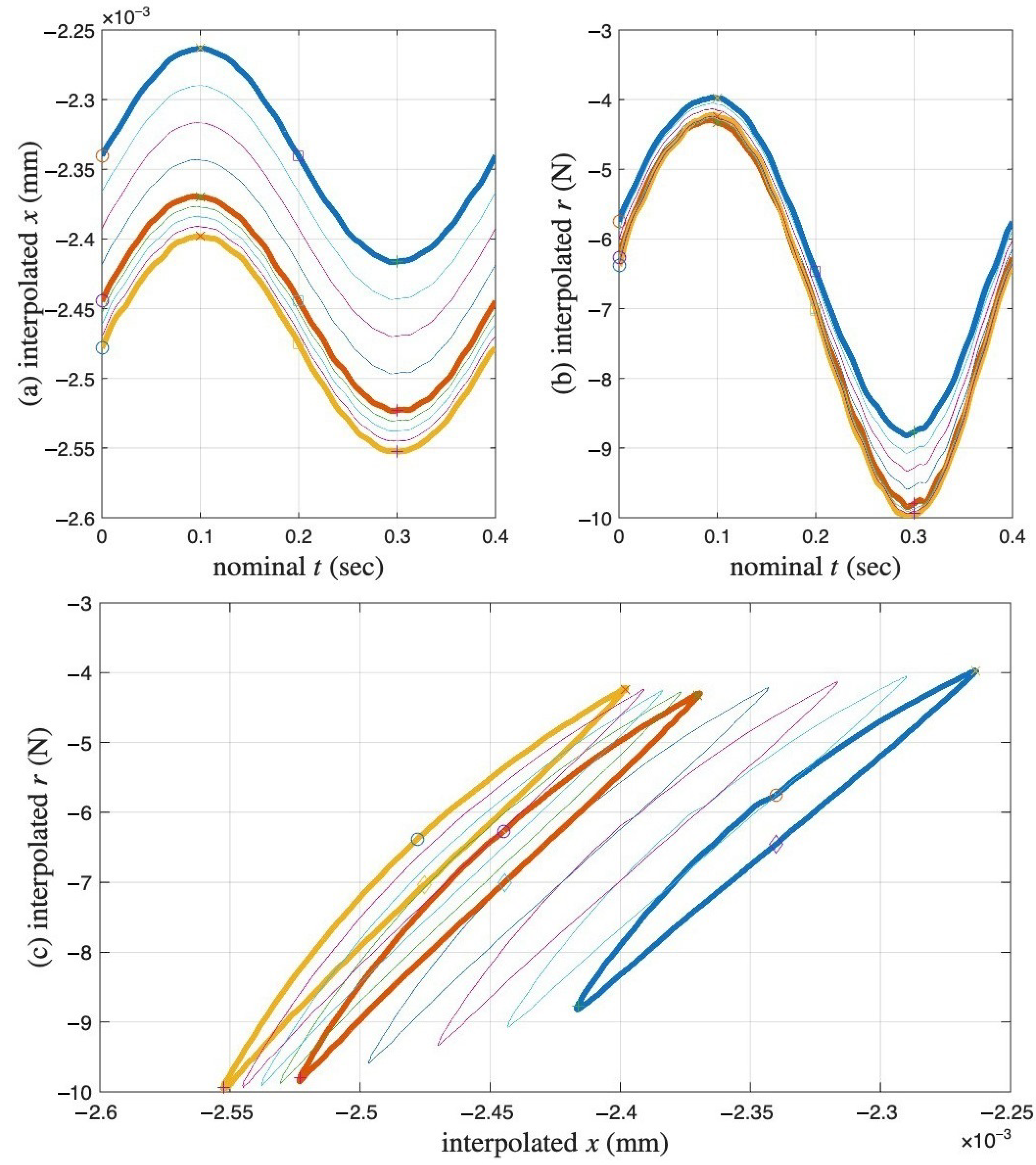
4.1. Analysis
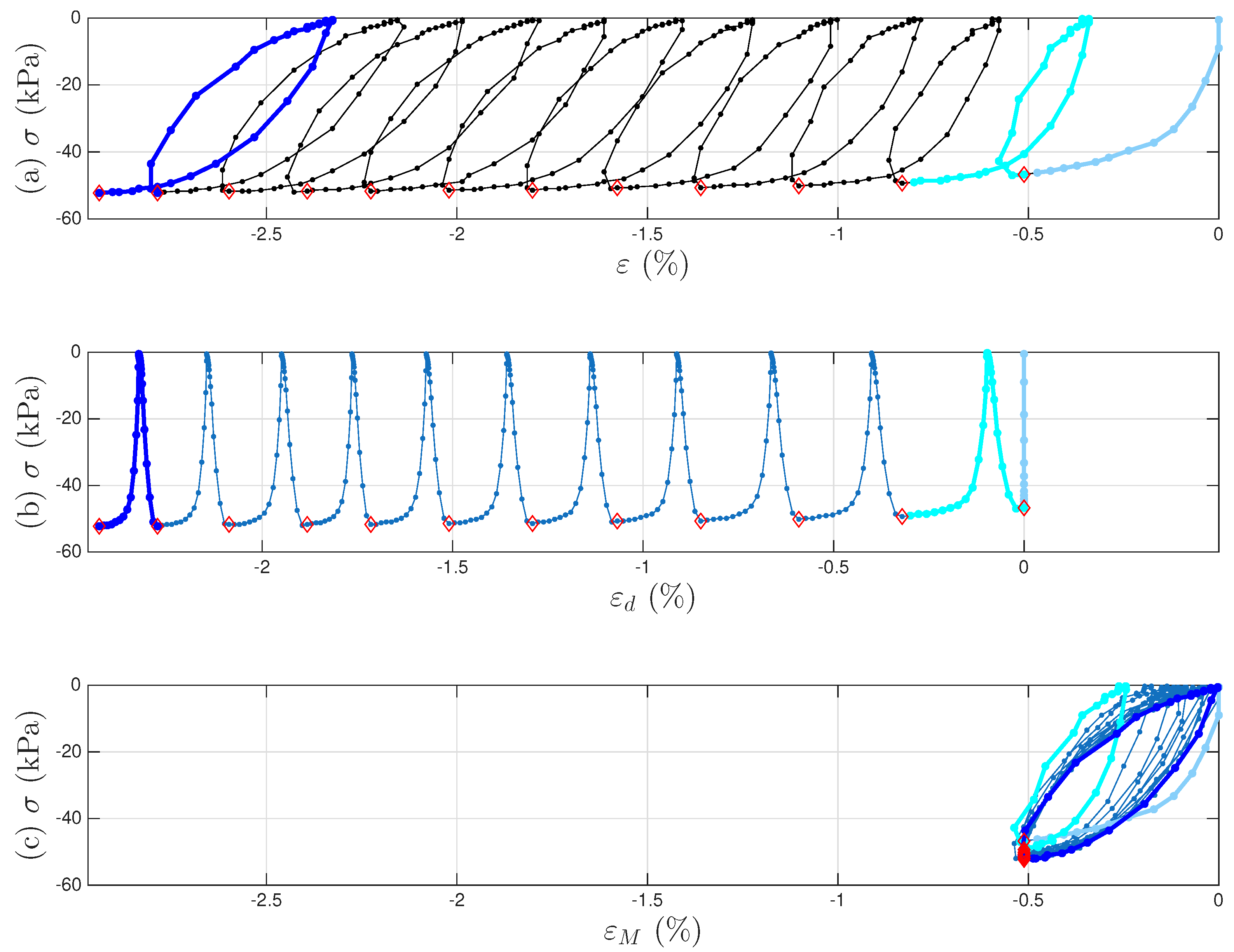
- The virgin loading curve goes through zero displacement and zero force.
- Referring to Figure 6a,c, the minimum displacement point (to be approximated with the 6001st point later) in a segmented measurement is where the minor loop closes on the virgin loading curve because it is a velocity turning point.
- The initial tangent stiffness of the unloading branch of the minor loop is equal to K, the initial tangent stiffness of the virgin loading curve.
- We assume that the yield plateau is equal to the r value at the minimum displacement point (to be approximated with the 6001st point later). That is, the Masing model is yielded when the minor loop starts to take place. This is one of the assumptions made to overcome the unidentifiable difficulty stated in Section 1.3. This is the major assumption made for mentioned at the end of Section 3.2.
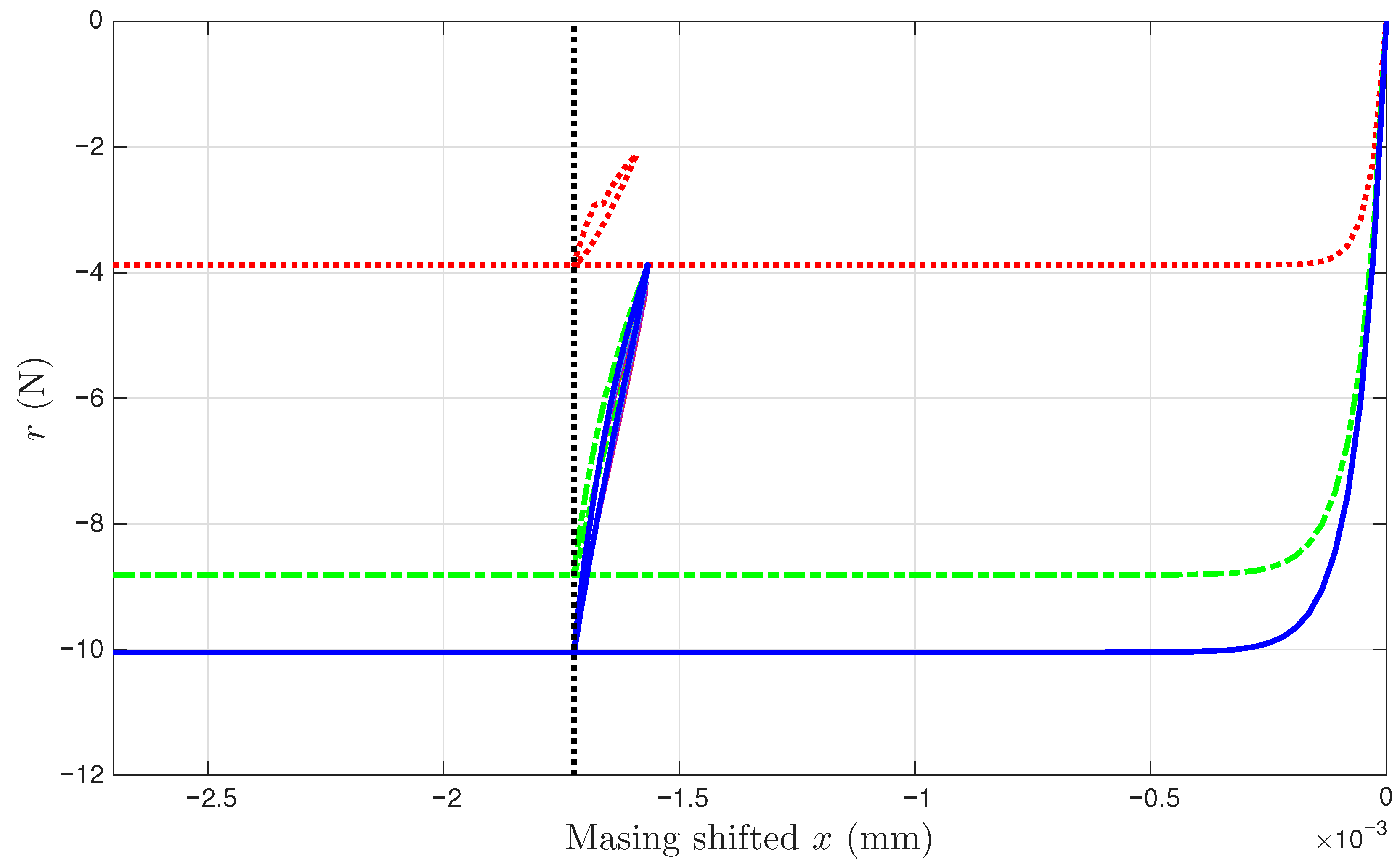
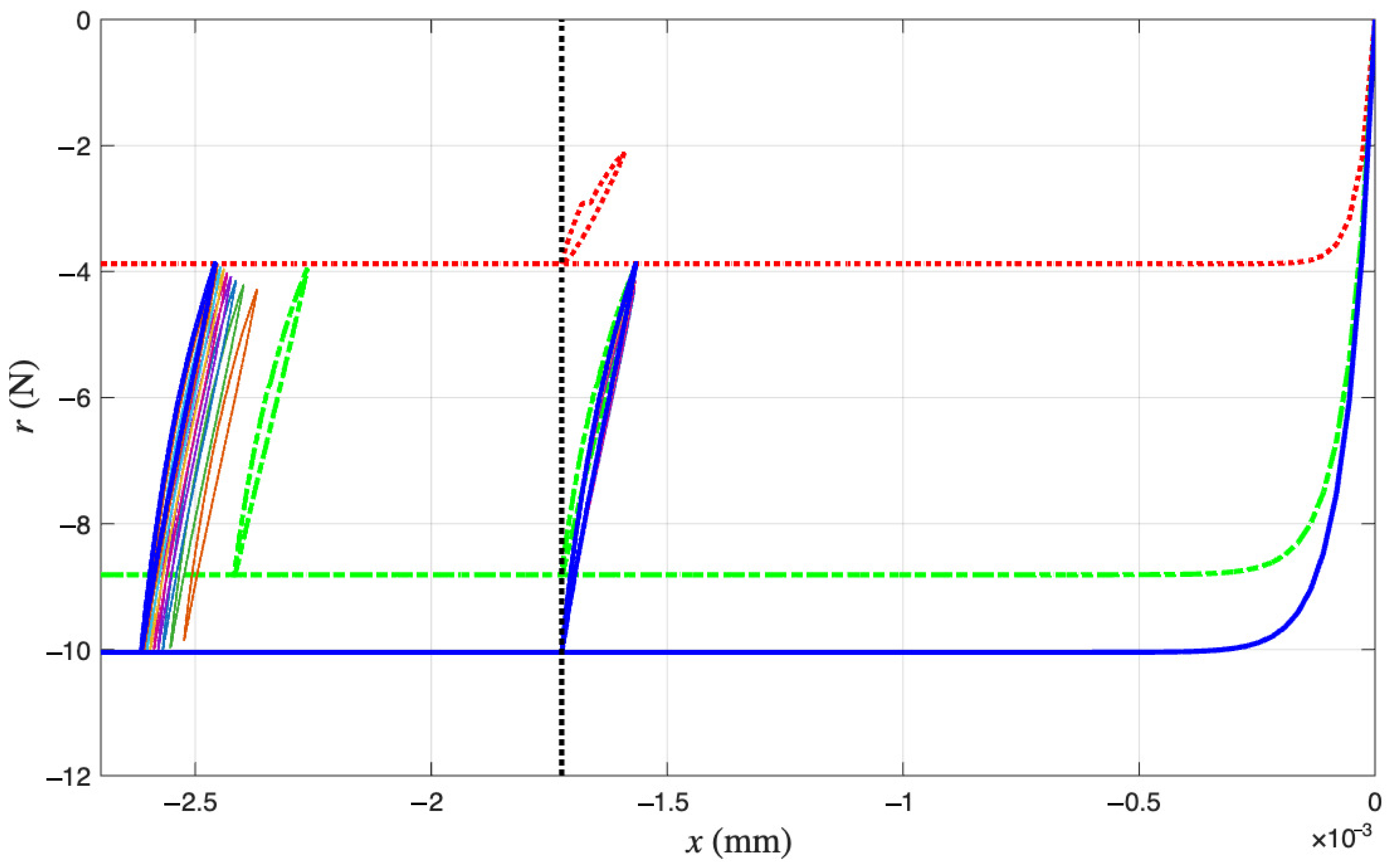
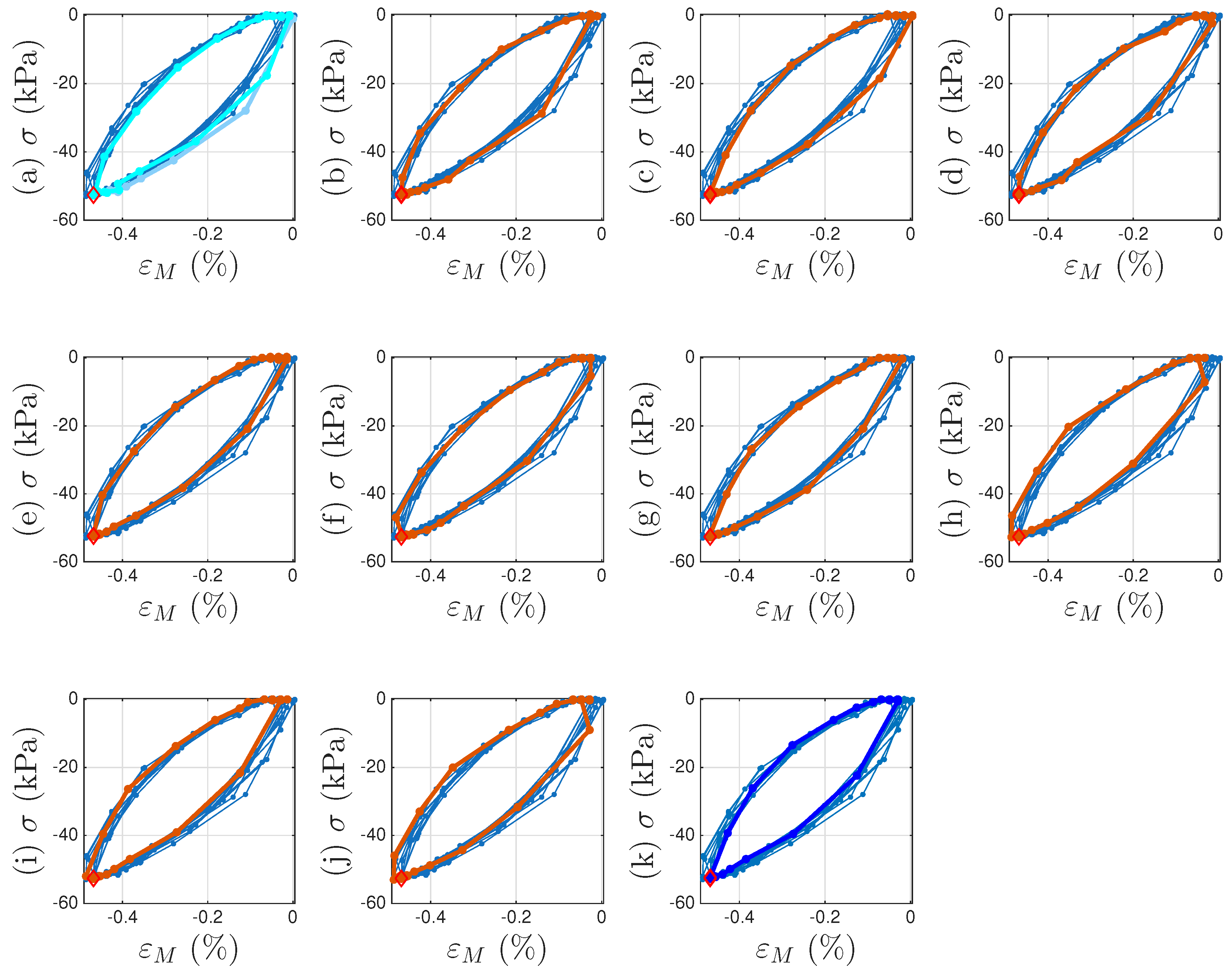
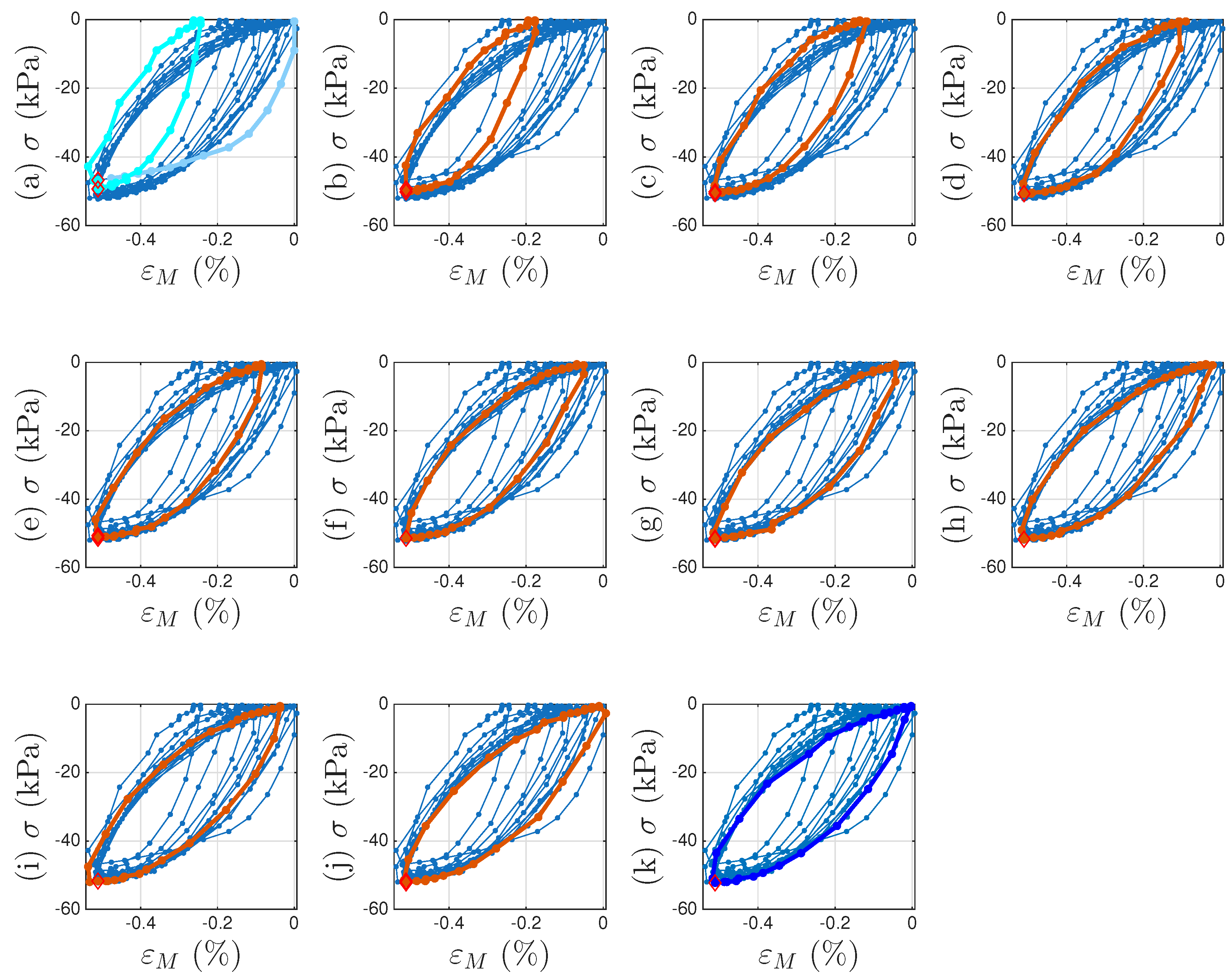
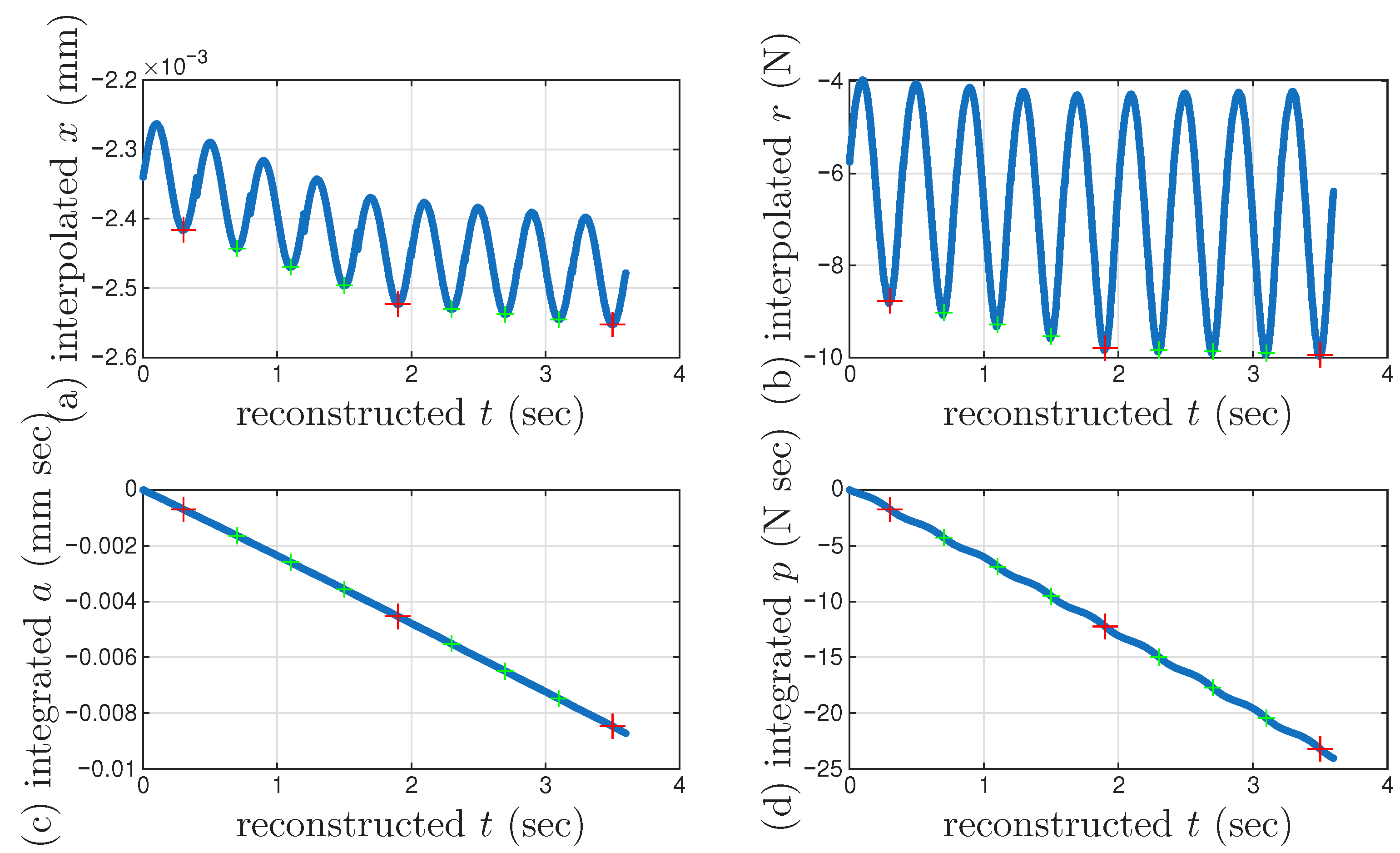
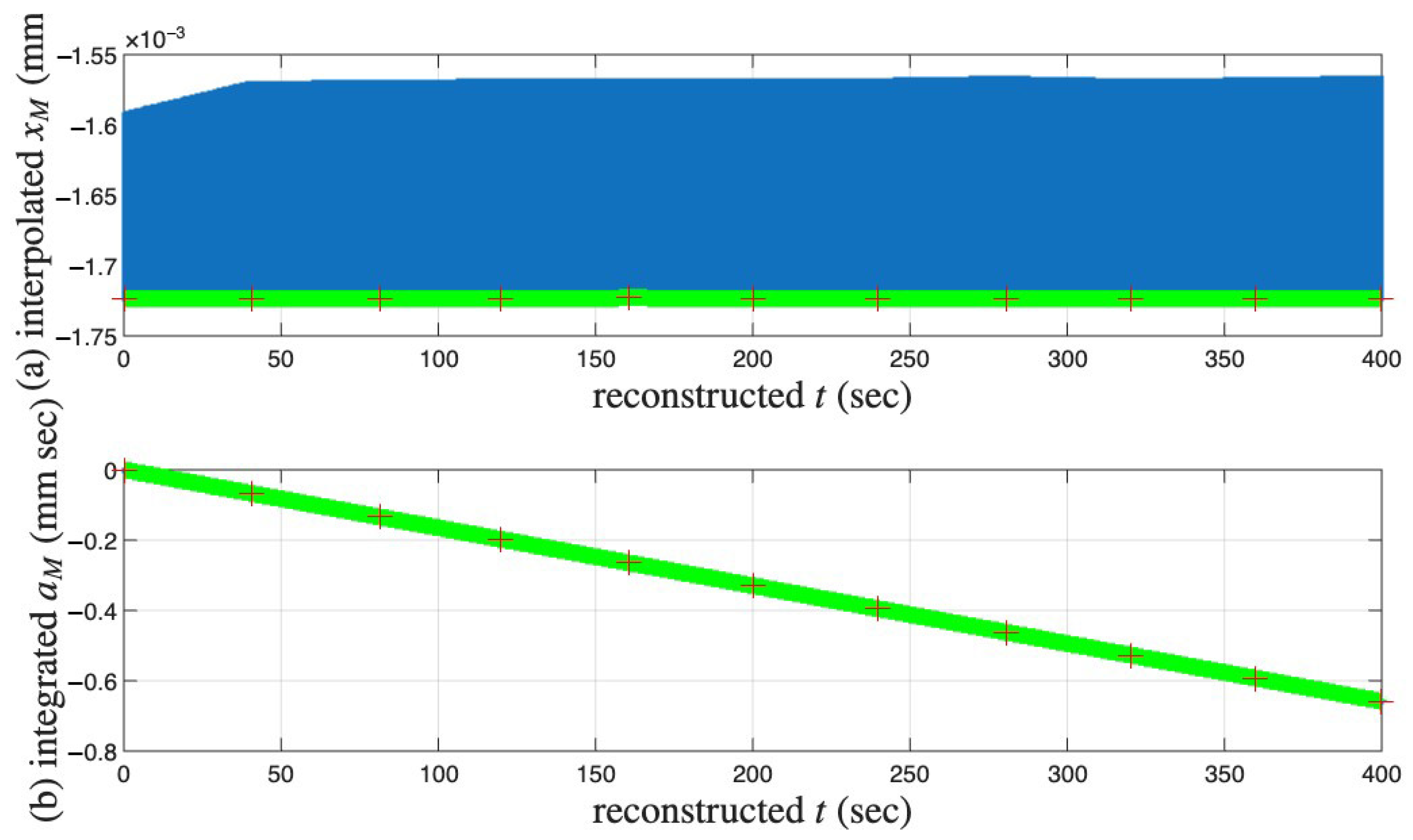
4.2. Approximating Unmeasured Cycles
4.3. Identification Procedure
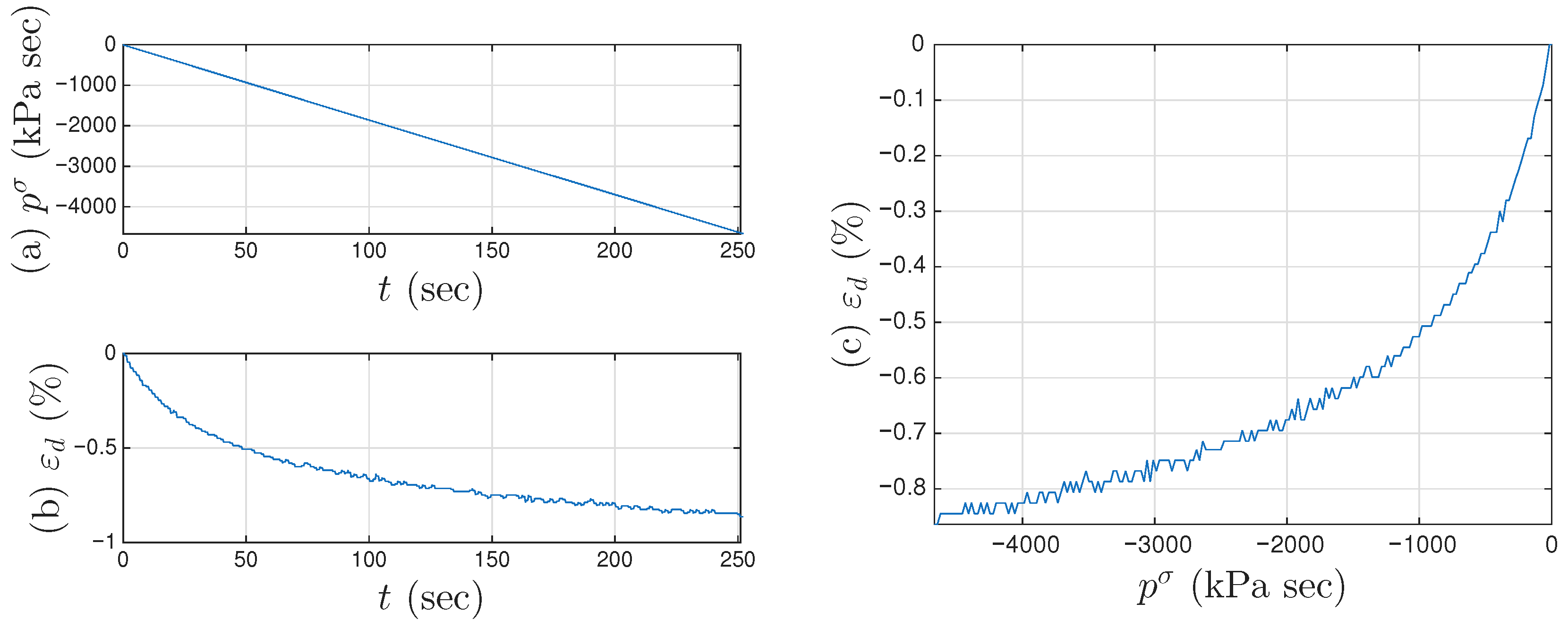
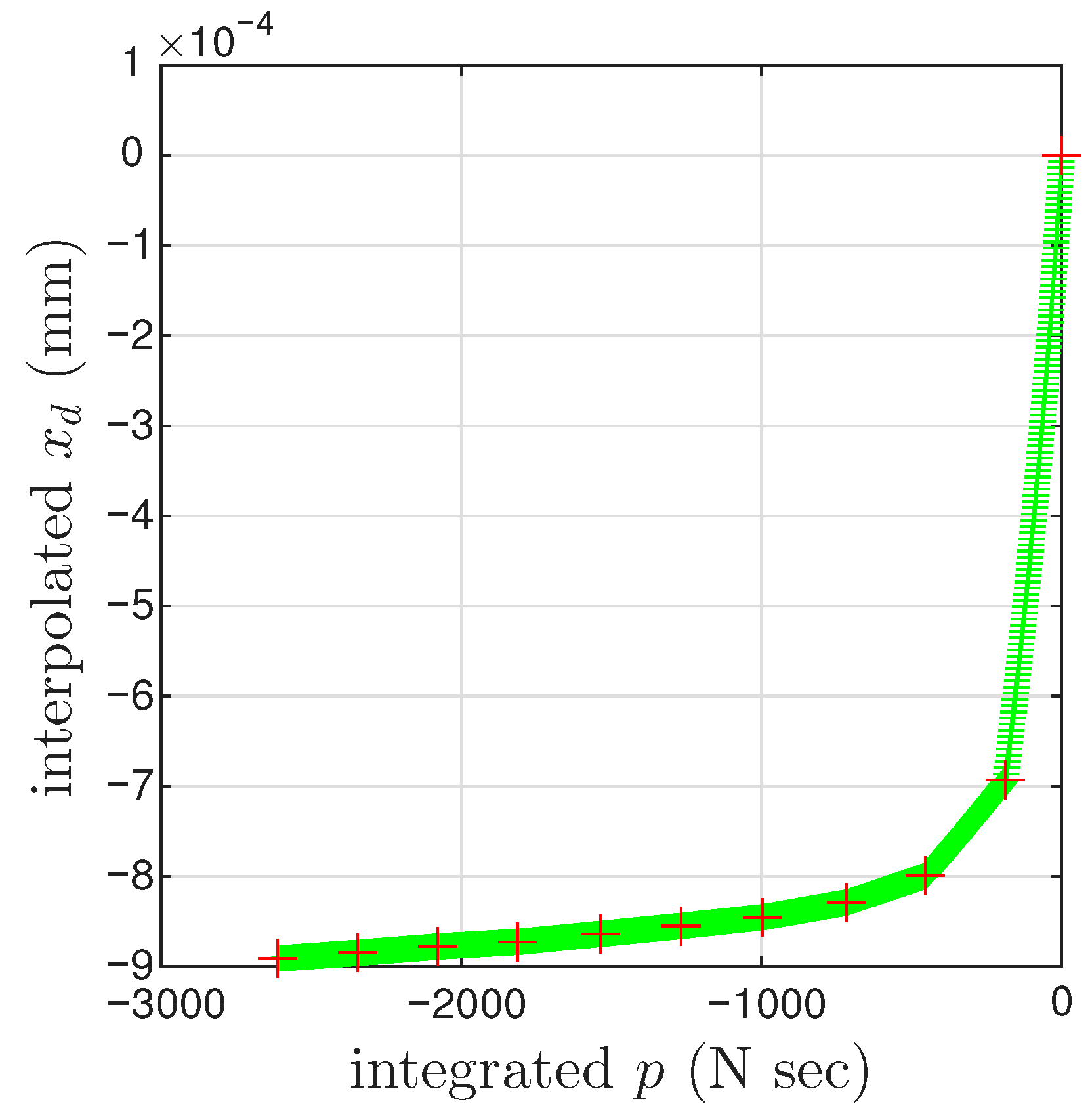
- Collect all minor loop closure points, the 6001st point of every cycle (including both segmented measurements and interpolated), marked with a cross +. Since the Masing minor loops close at these points, we only observe the displacement ratcheting. Because we assume that the displacement ratcheting starts at the closure point of the first minor loop, the coordinates of the closure point of the first minor loop are and . The x values of these 1000 points will be minus the x value of the first point throughout to obtain the values of these 1000 points. The p values of these 1000 points are ready. The nonlinear one-to-one mapping of as in Equation (19) will be ready to be identified by curve fitting.
- Use the approximated full time history of to interpolate the pair of p and of the 1000 points to obtain a full time history of .
- Use the approximated full time histories of x and to compute a full time history of , which is called the approximated full time history of .
- Integrate the approximated full time history of for , which is called the approximated full time history of .
- Estimate using the 6001st point of every cycle (including both segmented measurements and interpolated). Because we assume that the yield plateau is equal to the r value at such a point, collect all these 1000 r values. The values of these 1000 points are ready. The nonlinear one-to-one mapping of will be ready to be identified by curve fitting.
- Estimate using the 6001st point of every cycle (including both segmented measurements and interpolated). Because when , we have based on Equation (33), compute all these 1000 values when , or equivalently, . The values of these 1000 points are ready. The nonlinear one-to-one mapping of will be ready to be identified by curve fitting.
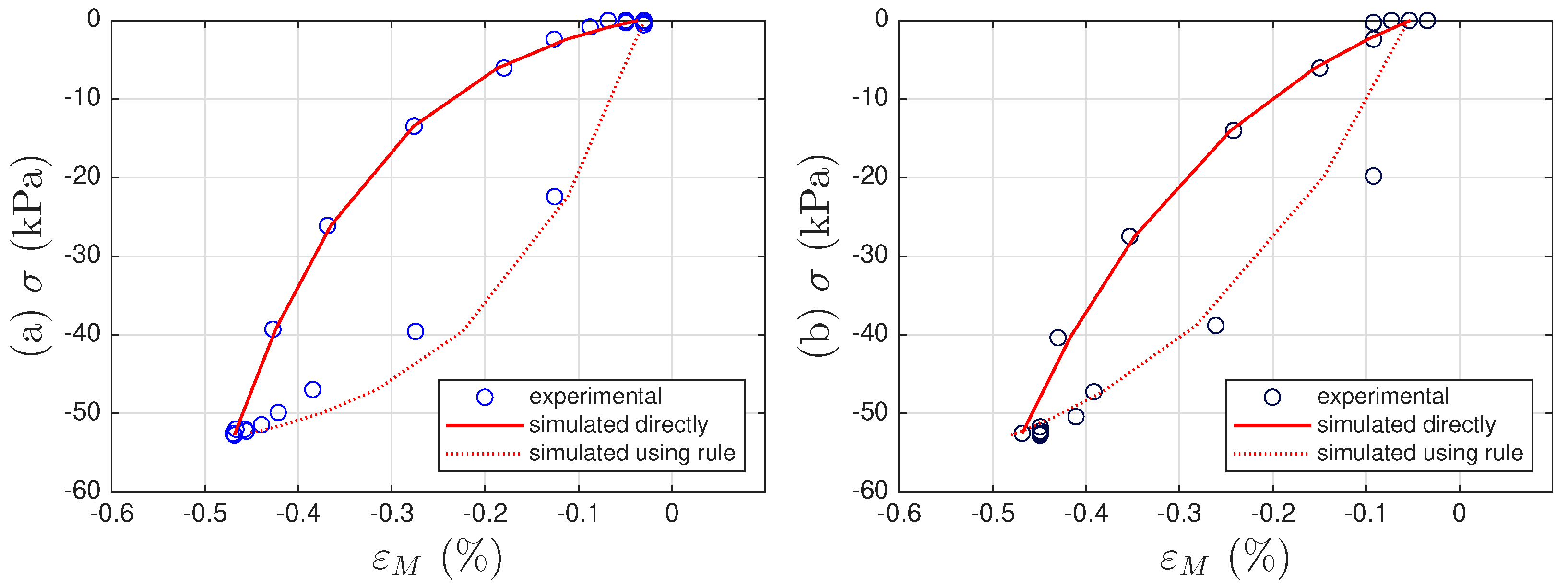
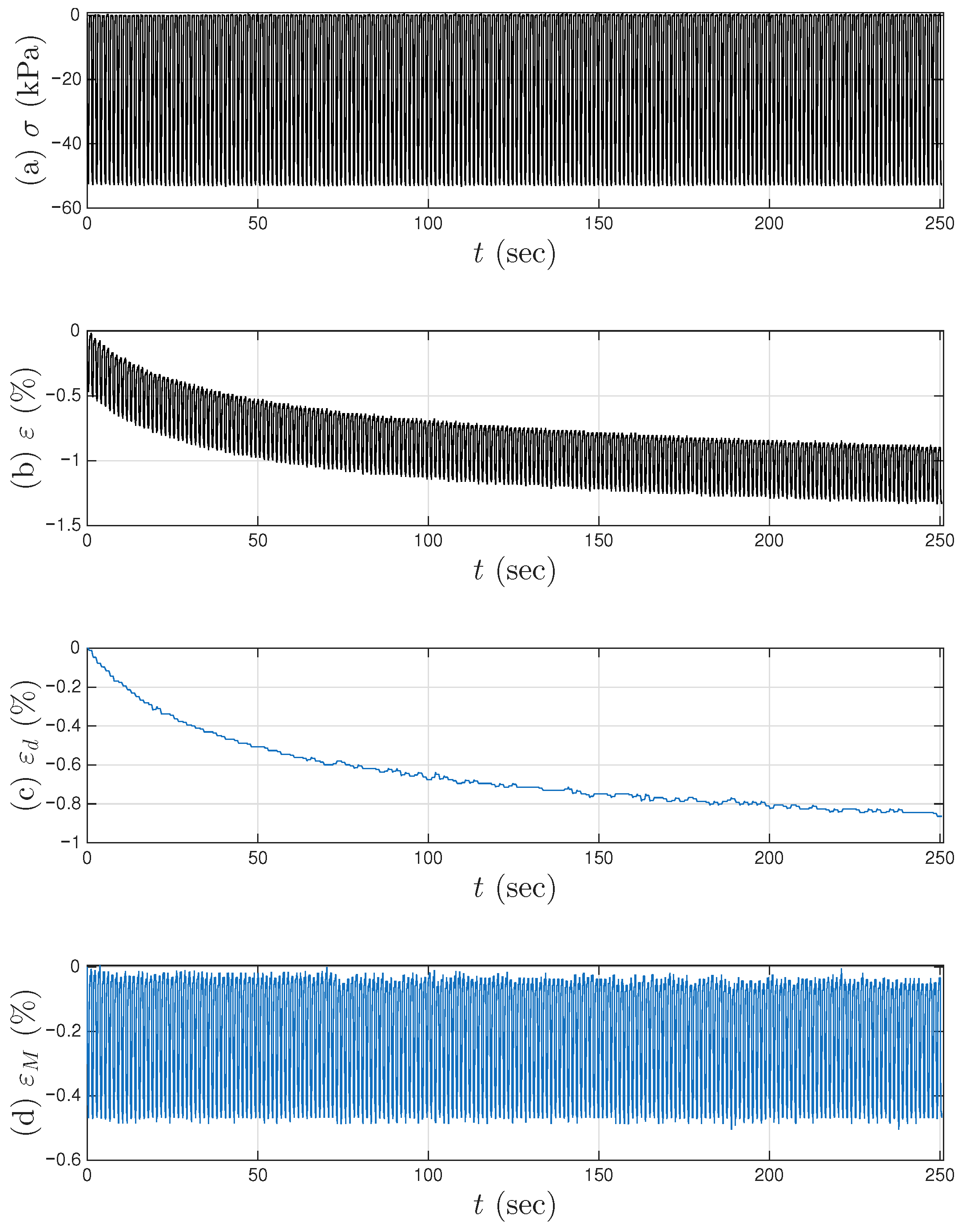
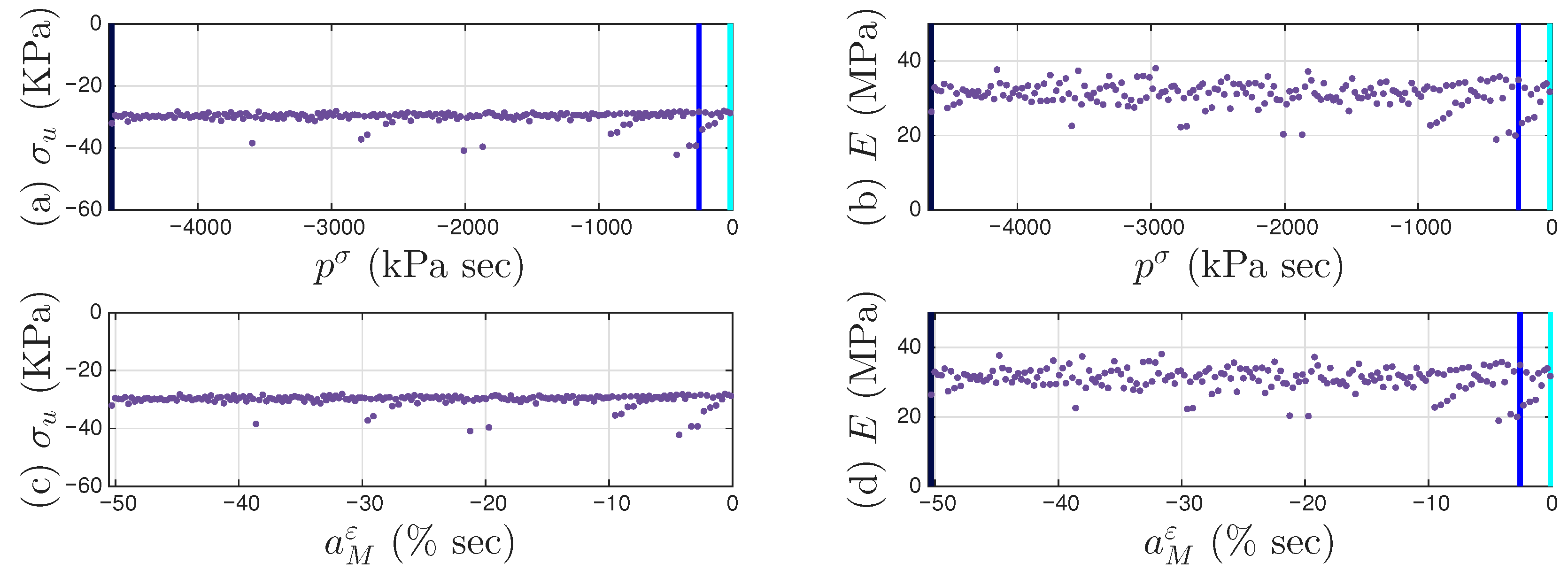
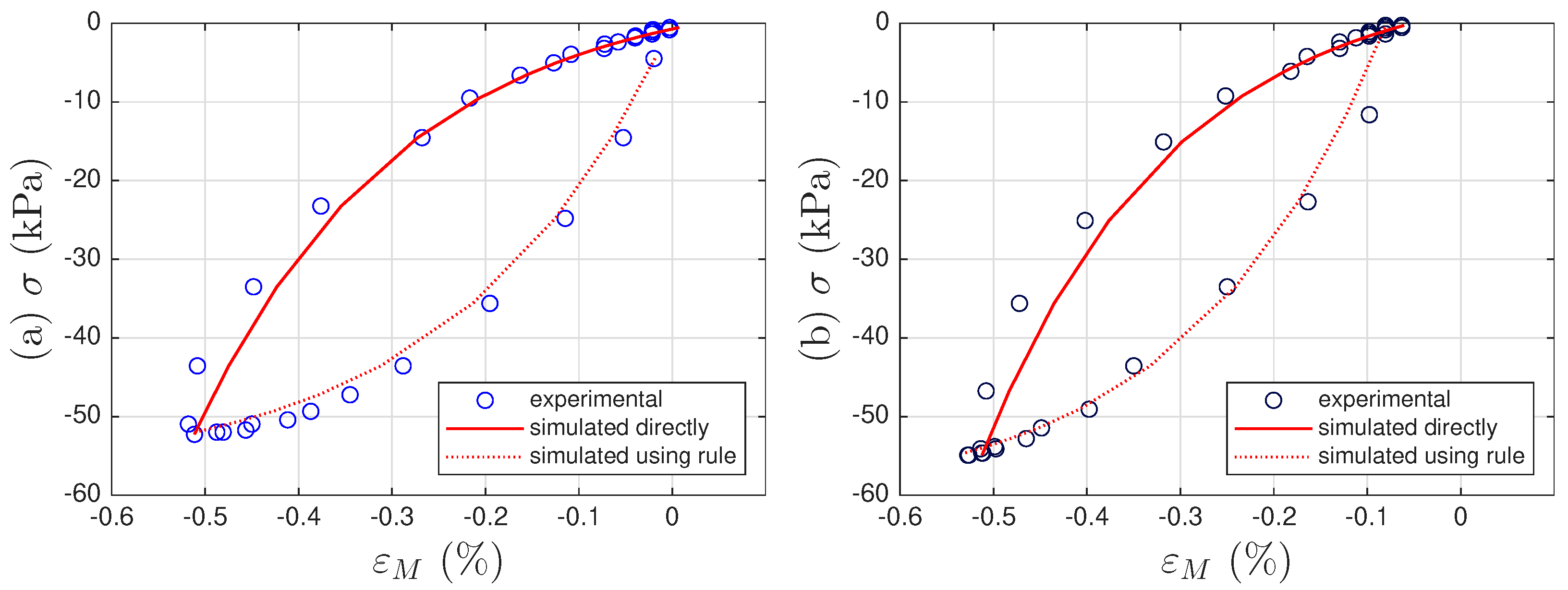
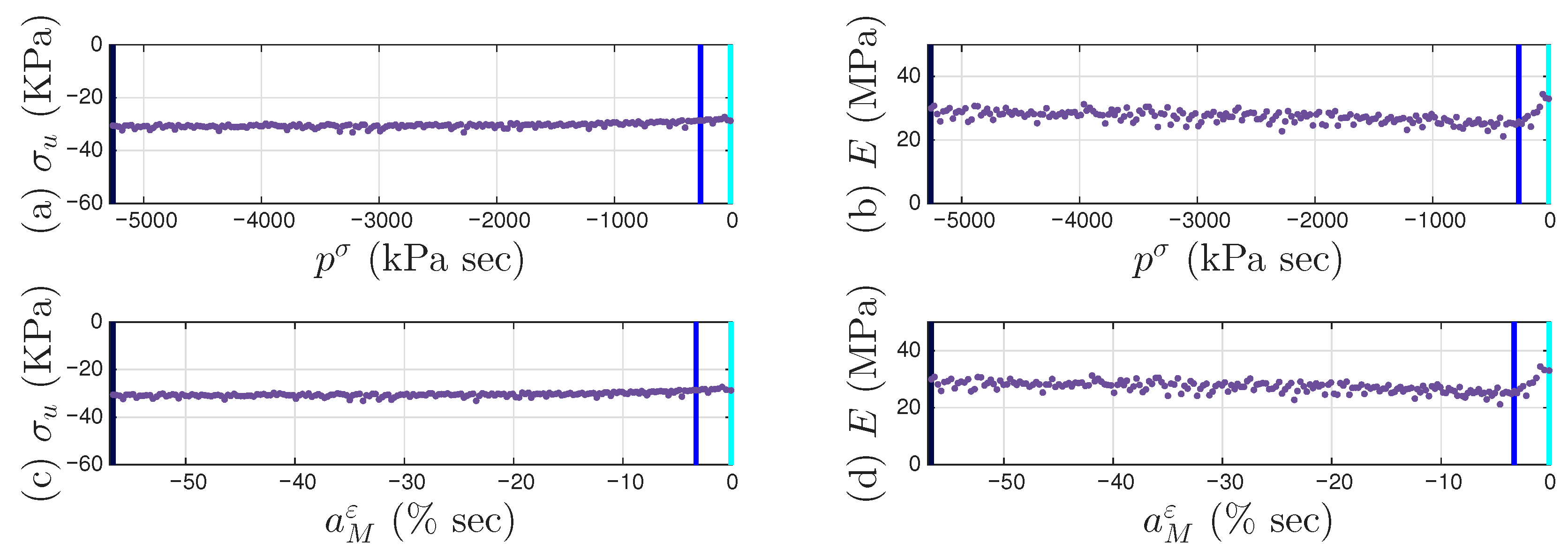
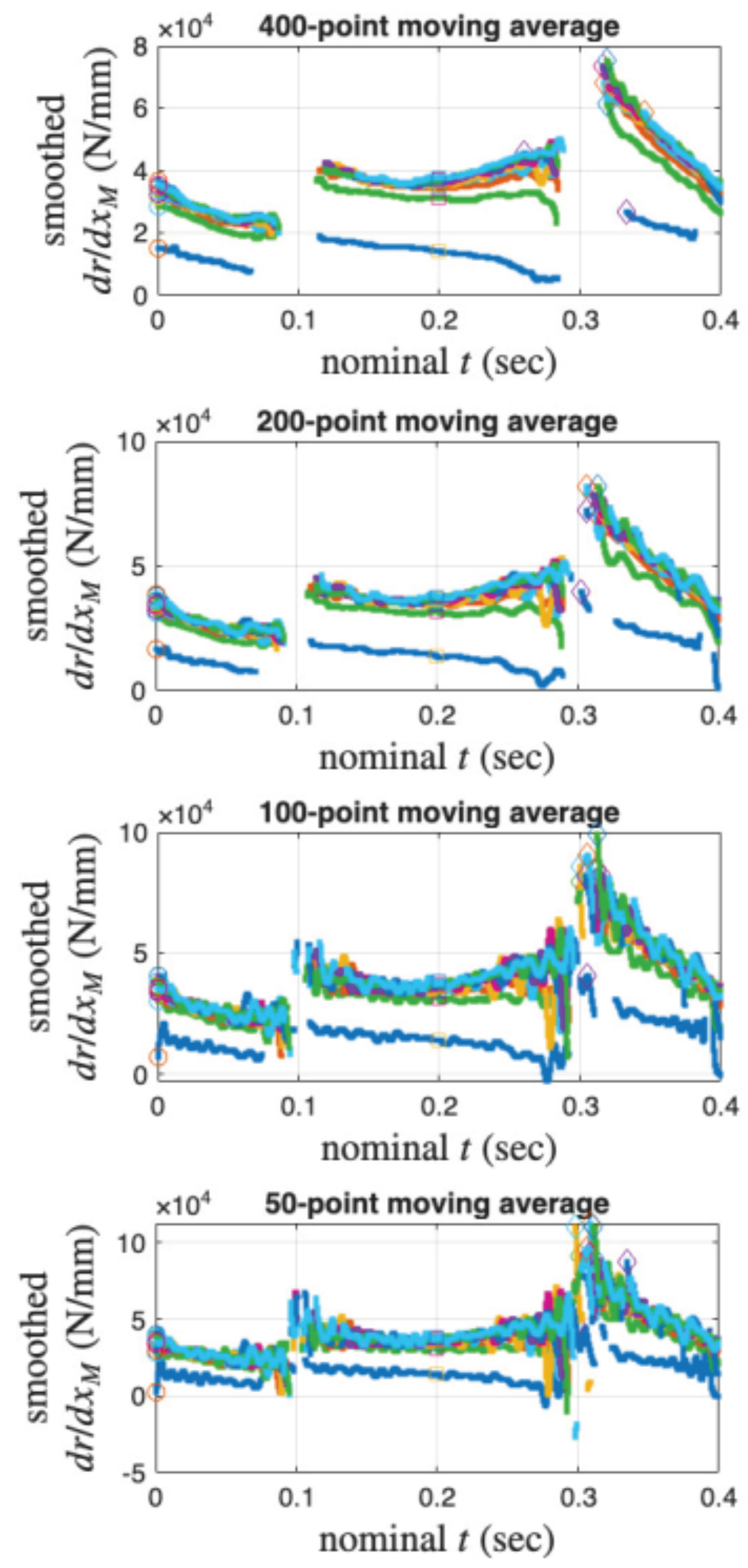
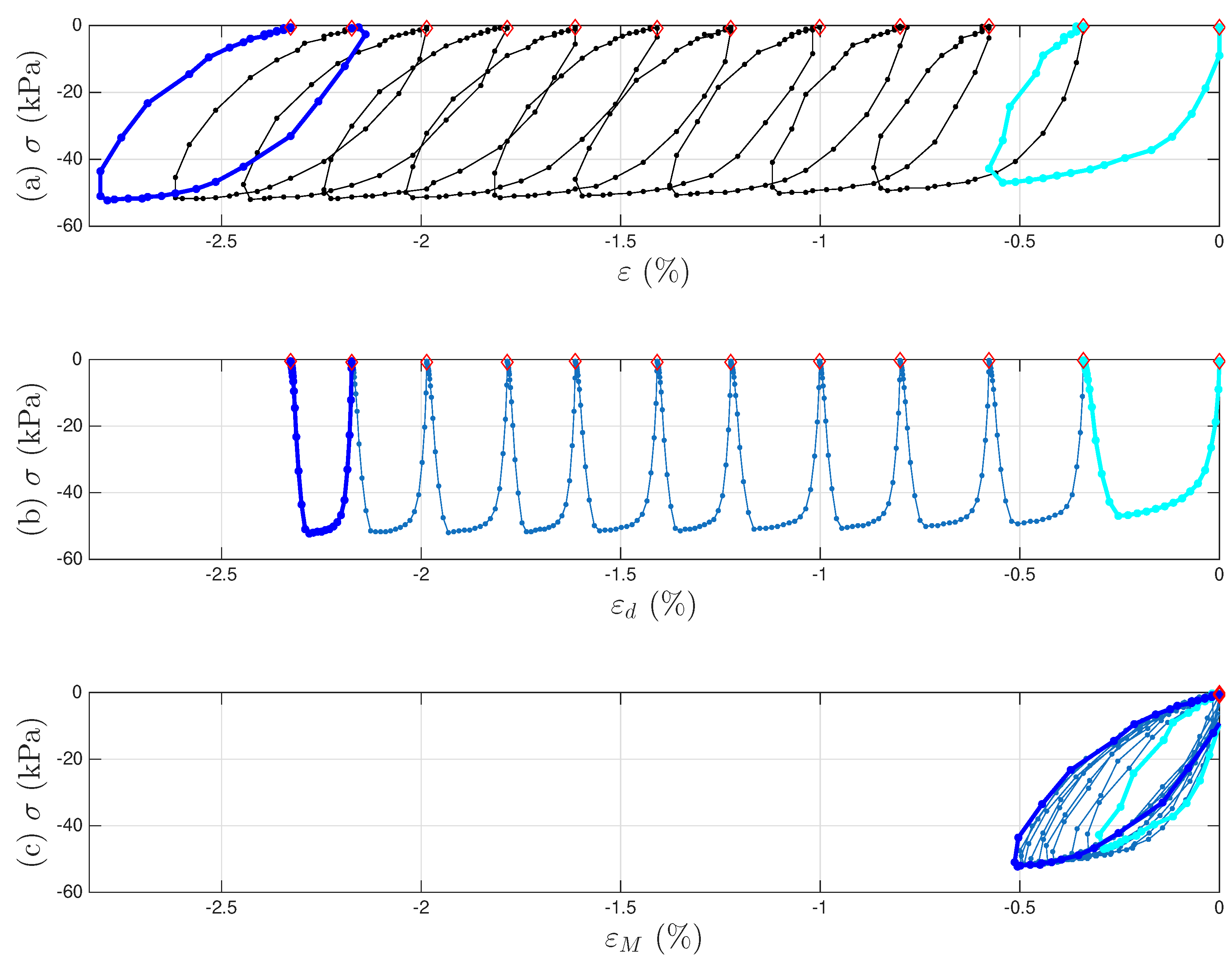
4.4. Results
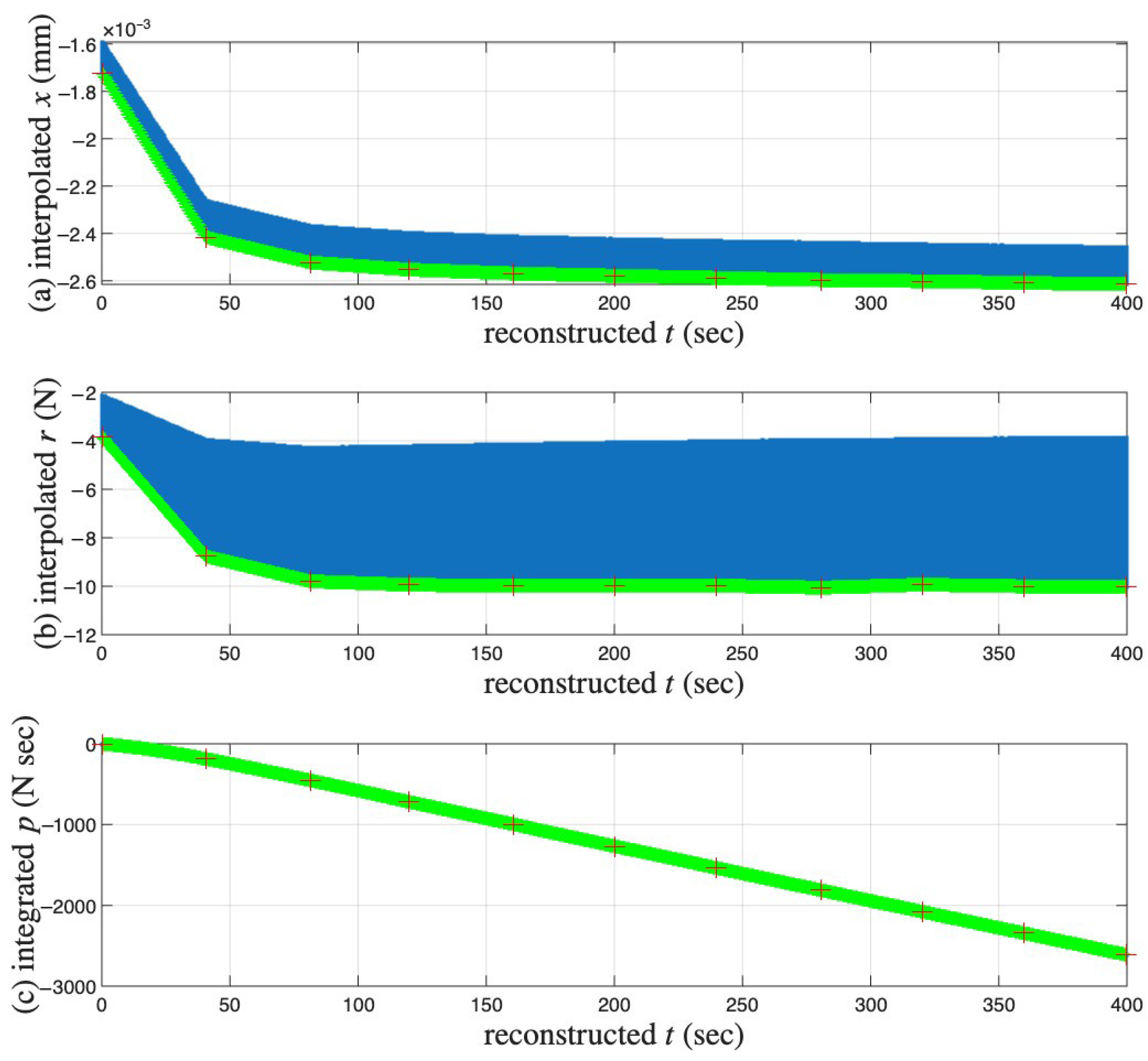
5. Modeling of Soil Specimens
6. Discussions
7. Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
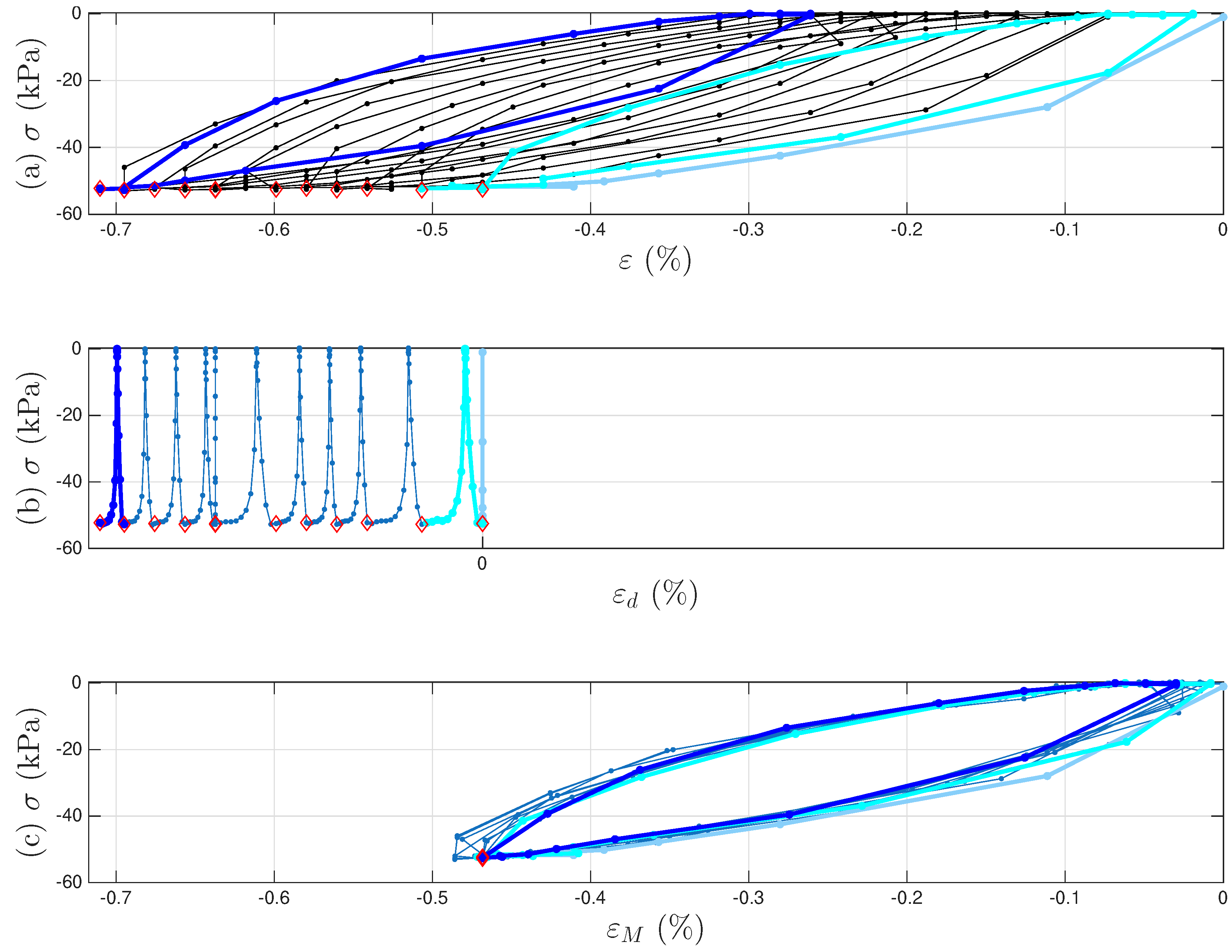
Appendix A. Additional Figures for Test 2 of Soil Data
References
- Jones, D.I. Handbook of Viscoelastic Vibration Damping; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Tassini, N.; Lambrinou, K.; Mircea, I.; Bartsch, M.; Patsias, S.; Van der Biest, O. Study of the amplitude-dependent mechanical behaviour of yttria-stabilised zirconia thermal barrier coatings. J. Eur. Ceram. Soc. 2007, 27, 1487–1491. [Google Scholar] [CrossRef]
- Chandrasekhar, K.; Rongong, J.A.; Cross, E. Mechanical behaviour of tangled metal wire devices. Mech. Syst. Signal Process. 2019, 118, 13–29. [Google Scholar] [CrossRef]
- Tinker, M.L.; Cutchins, M.A. Damping phenomena in a wire rope vibration isolation system. J. Sound Vib. 1992, 157, 7–18. [Google Scholar] [CrossRef]
- Panossian, H.V. Structural Damping Enhancement Via Non-Obstructive Particle Damping Technique. J. Vib. Acoust. 1992, 114, 101–105. [Google Scholar] [CrossRef]
- Satyanarayana, K.G.; Kulkarni, A.G.; Rohatgi, P.K. Structure and properties of coir fibres. Proc. Indian Acad. Sci. Sect. C Eng. Sci. 1981, 4, 419–436. [Google Scholar] [CrossRef]
- Perez, A.; Ferreno, D.; Carrasco, I.A.; Polanco, J.A.; Casado, J.A.; Diego, S. Metal cushion dampers for railway applications: A review. Constr. Build. Mater. 2020, 238, 117711. [Google Scholar] [CrossRef]
- Miller, G.; Teh, S.; Li, D.; Zaman, M. Cyclic Shear Strength of Soft Railroad Subgrade. ASCE J. Geotech. Geoenviron. Eng. 2000, 126, 139–147. [Google Scholar] [CrossRef]
- Pei, J.S.; Wright, J.P.; Miller, G.A.; Gay-Balmaz, F.; Quadrelli, M.B. Mem-modeling of strain ratcheting using early-time soil fatigue data. Nonlinear Dyn. 2025, 113, 9189–9215. [Google Scholar] [CrossRef]
- Mathis, A.T.; Balaji, N.N.; Kuether, R.J.; Brink, A.R.; Brake, M.R.W.; Quinn, D.D. A Review of Damping Models for Structures with Mechanical Joints. Appl. Mech. Rev. 2020, 72, 040802. [Google Scholar] [CrossRef]
- Masing, G. Eigenspannungen und Verfestigung beim Messing. In Proceedings of the 2nd International Congress for Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 332–335. (In German). [Google Scholar]
- Beck, J.L.; Pei, J.S. Demonstrating the power of extended Masing models for hysteresis through model equivalencies and numerical investigation. Nonlinear Dyn. 2022, 108, 827–856. [Google Scholar] [CrossRef]
- Caughey, T.K. Random Excitation of a System with Bilinear Hysteresis. J. Appl. Mech. 1960, 27, 649–652. [Google Scholar] [CrossRef]
- Caughey, T.K. Sinusoidal Excitation of a System with Bilinear Hysteresis. J. Appl. Mech. 1960, 27, 640–643. [Google Scholar] [CrossRef]
- Chiang, D.Y.; Beck, J.L. A New Class of Distributed-Element Models for Cyclic Plasticity—Part 1: Theory and Application. Int. J. Solids Struct. 1994, 31, 469–484. [Google Scholar] [CrossRef]
- Chiang, D.Y.; Beck, J.L. A New Class of Distributed-Element Models for Cyclic Plasticity—Part 2: On Important Properties of Material Behavior. Int. J. Solids Struct. 1994, 31, 485–496. [Google Scholar] [CrossRef]
- Chiang, D.Y. The generalized Masing models for deteriorating hysteresis and cyclic plasticity. Appl. Math. Model. 1999, 23, 847–863. [Google Scholar] [CrossRef]
- Ashrafi, S.A.; Smyth, A.W. A Generalized Masing Approach to Modeling Hysteretic Deteriorating Behavior. ASCE J. Eng. Mech. 2007, 133, 495–505. [Google Scholar] [CrossRef]
- Ashrafi, S.A.; Smyth, A.W. Adaptive Parametric Identification Scheme for a Class of Nondeteriorating and Deteriorating Nonlinear Hysteretic Behavior. ASCE J. Eng. Mech. 2008, 134, 482–494. [Google Scholar] [CrossRef]
- Jayakumar, P. Modeling and Identification in Structural Dynamics. Ph.D Thesis, California Institute of Technology, Pasadena, CA, USA, 1987. [Google Scholar]
- Jayakumar, P.; Beck, J.L. System Identification Using Nonlinear Structural Models. In Structural Safety Evaluation Based on System Identification Approaches; Natke, H.G., Yao, J.T.P., Eds.; Proceedings of the Workshop at Lambrecht/Pfalz, Vieweg International Scientific Book Series; Friedr. Vieweg & Sohn: Braunschweig/Wiesbaden, Germany, 1988; pp. 82–102. [Google Scholar]
- Beck, J.L.; Jayakumar, P. Class of Masing Models for Plastic Hysteresis in Structures. In Proceedings of the Proceedings 14th ASCE Structures Congress, Chicago, IL, USA, 14–18 April 1996. [Google Scholar]
- Pei, J.S.; Gay-Balmaz, F.; Luscher, D.J.; Beck, J.L.; Todd, M.D.; Wright, J.P.; Qiao, Y.; Quadrelli, M.B.; Farrar, C.R.; Lieven, N.A.J. Connecting mem-models with classical theories. Nonlinear Dyn. 2021, 103, 1321–1344. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Pintelon, R.; Schoukens, J. System Identification: A Frequency Domain Approach; IEEE Press: Piscataway, NJ, USA, 2001. [Google Scholar]
- Katafygiotis, L.S.; Beck, J.L. Updating Models and Their Uncertainties. II: Model Identifiability. ASCE J. Eng. Mech. 1998, 124, 463–467. [Google Scholar] [CrossRef]
- Pei, J.S.; Wright, J.P.; Todd, M.D.; Masri, S.F.; Gay-Balmaz, F. Understanding memristors and memcapacitors for engineering mechanical applications. Nonlinear Dyn. 2015, 80, 457–489. [Google Scholar] [CrossRef]
- Pei, J.S.; Gay-Balmaz, F.; Wright, J.P.; Todd, M.D.; Masri, S.F. Dual input-output pairs for modeling hysteresis inspired by mem-models. Nonlinear Dyn. 2017, 88, 2435–2455. [Google Scholar] [CrossRef]
- Chua, L.O. Memrister—The Missing Circuit Element. IEEE Trans. Circuit Theory 1971, CT-18, 507–519. [Google Scholar] [CrossRef]
- Chua, L.O.; Kang, S.M. Memristive Devices and Systems. Proc. IEEE 1976, 64, 209–223. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Di Ventra, M.; Pershin, Y.V.; Chua, L.O. Circuit Elements with Memory: Memristors, Memcapacitors, and Meminductors. Proc. IEEE 2009, 97, 1717–1724. [Google Scholar] [CrossRef]
- Oster, G.F.; Auslander, D.M. The Memristor: A New Bond Graph Element. ASME J. Dyn. Syst. Meas. Control 1973, 94, 249–252. [Google Scholar] [CrossRef]
- Jeltsema, D. Memory Elements: A Paradigm Shift in Lagrangian Modeling of Electrical Circuits. In Proceedings of the MathMod Conference, Vienna, Austria, 15–17 February 2012. [Google Scholar]
- Paynter, H.M. Analysis and Design of Engineering Systems: Class Notes for M.I.T. Course 2.751; M.I.T. Press: Cambridge, MA, USA, 1961. [Google Scholar]
- Paynter, H.M. The Gestation and Birth of Bond Graphs. 2000. Available online: https://sites.utexas.edu/longoria/files/2020/10/Birth_of_-Bond_Graphs.pdf (accessed on 21 September 2025).
- Pyke, R. Nonlinear Soil Models for Irregular Cyclic Loadings. J. Geotech. Eng. Div. ASCE 1979, 105, 715–726. [Google Scholar] [CrossRef]
- Pyke, R. Evolution of Soil Models Since the 1970s. In International Workshop on Uncertainties in Nonlinear Soil Properties and Their Impact on Modeling Dynamic Soil Response; University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- The Mathworks, Inc. MATLAB; The Mathworks, Inc.: Natick, MA, USA, 2025; Available online: http://www.mathworks.com/ (accessed on 21 September 2025).
- Canfield, R. central_diff.m. 2015. Available online: http://www.mathworks.com/matlabcentral/fileexchange/12-central-diff-m/content/central_diff.m (accessed on 21 September 2025).
- Tran, L.Q.N.; Minh, T.N.; Fuentes, C.A.; Chi, T.T.; Van Vuure, A.W.; Verpoest, I. Investigation of microstructure and tensile properties of porous natural coir fibre for use in composite materials. Ind. Crops Prod. 2015, 65, 437–445. [Google Scholar] [CrossRef]
- Krasnosel’skiǐ, M.A.; Pokrovskiǐ, A.V. Systems with Hysteresis; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Lazan, B.J. Damping of Materials and Members in Structural Mechanics; Pergamon Press: Oxford, UK, 1968. [Google Scholar]






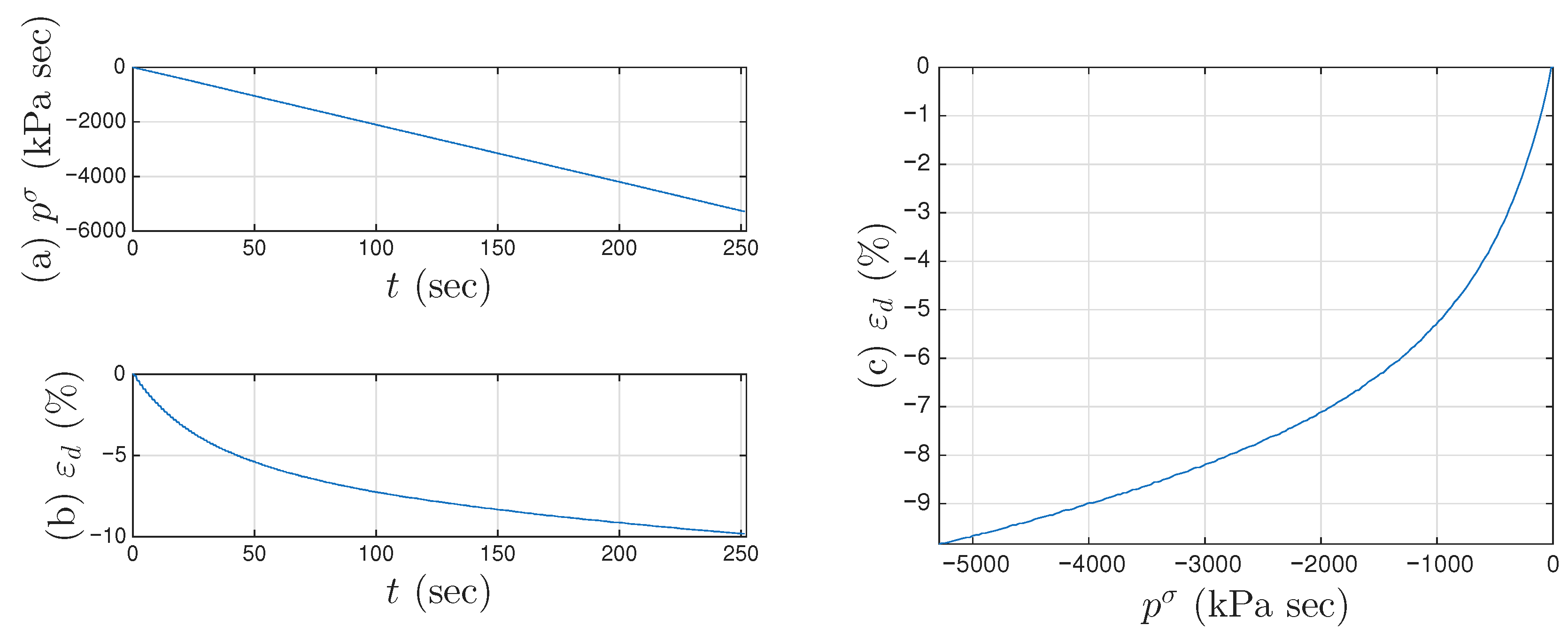
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rongong, J.A.; Pei, J.-S.; Wright, J.P.; Miller, G.A. Micro-Interface Slip Damping in a Compressed Coir Vibration Isolator. Materials 2025, 18, 4521. https://doi.org/10.3390/ma18194521
Rongong JA, Pei J-S, Wright JP, Miller GA. Micro-Interface Slip Damping in a Compressed Coir Vibration Isolator. Materials. 2025; 18(19):4521. https://doi.org/10.3390/ma18194521
Chicago/Turabian StyleRongong, Jem A., Jin-Song Pei, Joseph P. Wright, and Gerald A. Miller. 2025. "Micro-Interface Slip Damping in a Compressed Coir Vibration Isolator" Materials 18, no. 19: 4521. https://doi.org/10.3390/ma18194521
APA StyleRongong, J. A., Pei, J.-S., Wright, J. P., & Miller, G. A. (2025). Micro-Interface Slip Damping in a Compressed Coir Vibration Isolator. Materials, 18(19), 4521. https://doi.org/10.3390/ma18194521






