A Comparison of Discrete Crack and Smeared Crack Methods Applied to CFRP/Al Riveting Damage Modeling
Abstract
1. Introduction
2. Numerical Simulation Method
2.1. FNM Theory
2.2. Progressive Damage Modeling
2.2.1. Onset of Damage Model
- (1)
- Onset of fiber damage model
- (2)
- Onset of matrix damage model
- (3)
- Onset of delamination model
2.2.2. Damage Evolution
- (1)
- Fiber damage evolution
- (2)
- Matrix damage evolution for SCM
- (3)
- CZM damage evolution
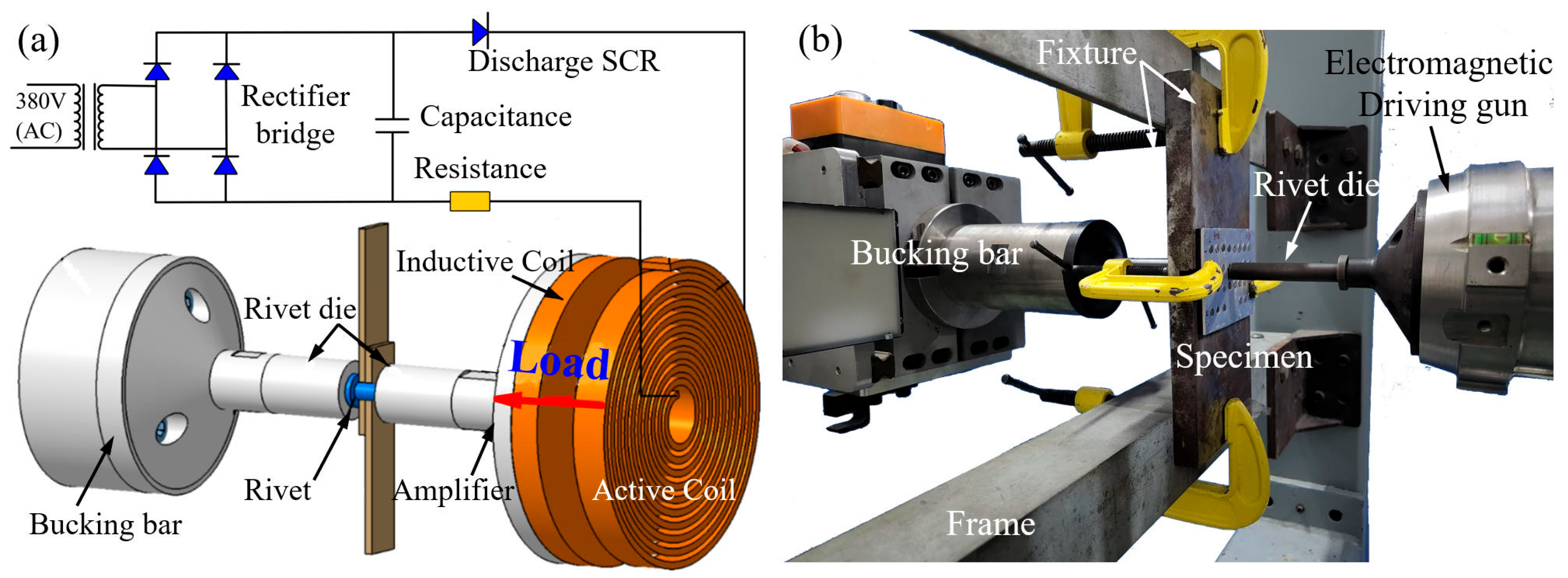
2.3. EMR Experiment
2.4. FE Analysis
2.4.1. FE Model
2.4.2. Material Properties and Constitutive Equation for Metal
3. Results and Discussion
3.1. Riveting Deformation Process
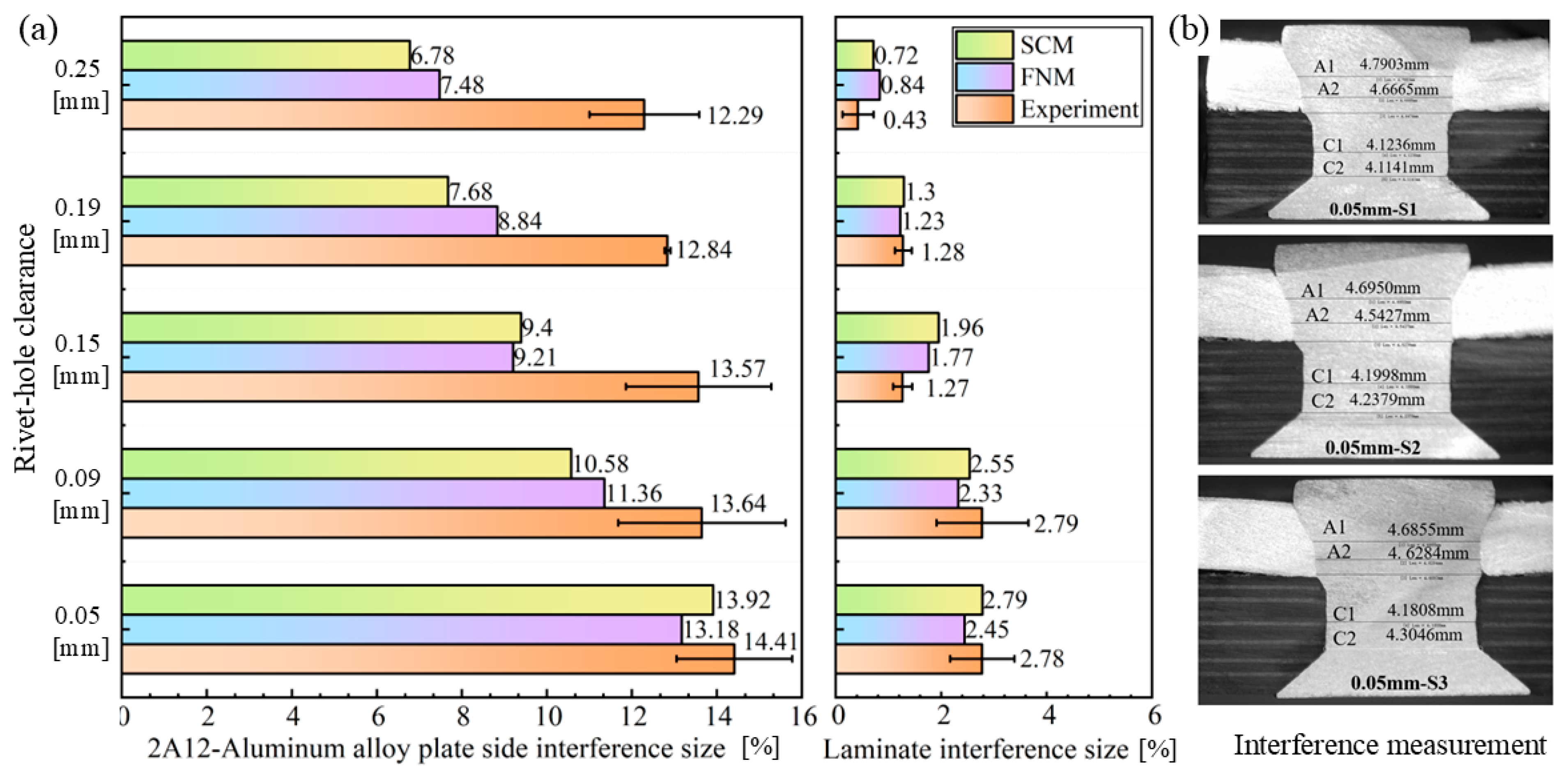
3.2. Interference Behavior
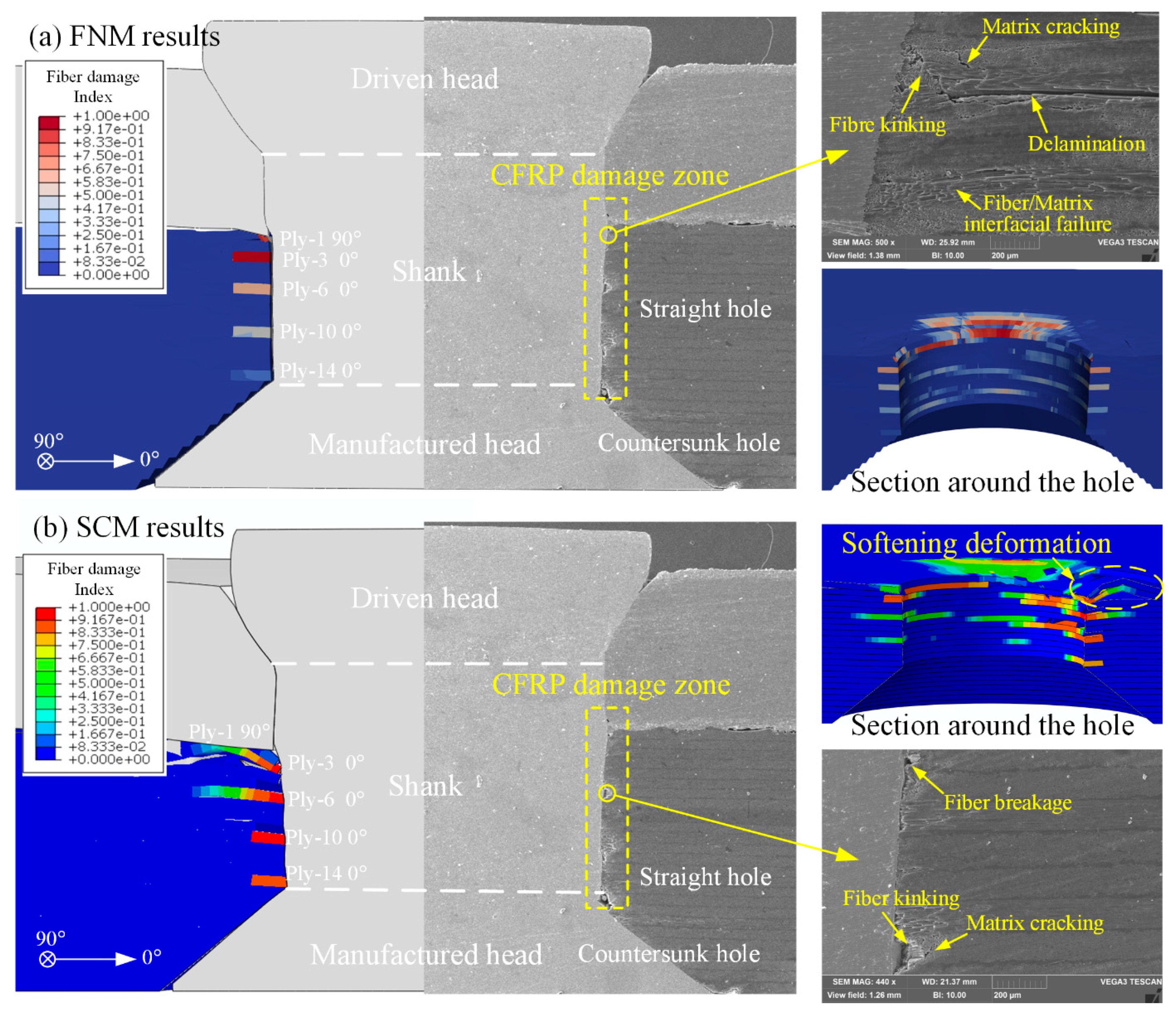
3.3. CFRP Damage Analysis
3.4. Computational Efficiency
4. Conclusions
- (1)
- The CFRP/Al double-sided countersunk riveting process can be divided into four stages. The axial interference distribution is non-uniform, with significantly higher interference sizes on the Al plate side than on the CFRP laminate side. Both the SCM and FNM models accurately predict the interference sizes on the laminate side but show deviations from experimental results on the Al plate side.
- (2)
- The initial damage in CFRP/Al double-sided countersunk riveted joints primarily concentrates in the laminate’s straight hole part, while damage caused by rivet expansion rarely occurs in the countersunk hole part. Excessive normal stress in the fiber direction during riveting is the direct cause of fiber damage. The joint section fiber damage distribution predictions for FNM and SCM showed consistency; however, the degradation of the element stiffness in SCM resulted in severe element distortion around the hole.
- (3)
- When the rivet-hole clearance increased from 0.05 mm to 0.25 mm, the number of fiber, matrix, and delamination damaged elements in the SCM model decreased by 45.71%, 31.86%, and 44.89%, respectively. And the corresponding numbers in the FNM model were 39.43%, 31.86%, and 14.97%. Increasing the clearance effectively reduces the damage severity, although this effect diminishes as the clearance increases beyond 0.22 mm. This suggests that there is an optimal clearance to minimize damage, although this is likely to depend on joint configurations and materials.
- (4)
- Compared to the SCM model, the FNM model demonstrates enhanced accuracy in capturing the onset and propagation of matrix-dominated cracks. However, this improvement comes at the expense of computational efficiency. The FNM mode, with a mass scaling factor of 104, requires 1.12 times more computation time than the SCM model. The FNM model’s CPU utilization is approximately 5% lower than that of the SCM model. Although FNM can track the crack propagation process with high fidelity, SCM has more advantages in engineering analyses of large-scale structures when efficiency is a priority.
- (5)
- The specific selection of rivet-hole parameters still needs to be determined in future studies by considering both the static strength and fatigue performance of the joints. The results demonstrate that the FNM-based DCM approach can serve as an effective tool to support the manufacturing and design processes of CFRP structures. Due to the challenges in damage detection, this study does not address the issue of balancing prediction accuracy and computational efficiency. This issue will be further investigated in future work by comparing SCM and FNM in simulations based on material property-oriented benchmark problems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Notation and Abbreviations
| σ11, σ22, σ33 | normal stress components with local material coordinates |
| τ12, τ23, τ31 | shear stress components with local material coordinates |
| τ1, τ2, τ3 | interlaminar stress for the delamination |
| N, S, T | interlaminar interface strengths |
| XT/XC | longitudinal tensile/compressive strength |
| YT/YC | transverse tensile/compressive strength |
| ST/SL | transverse/longitudinal shear strength |
| E11/E22, E33 | longitudinal/transverse elastic modulus |
| G12, G13, G23 | shear modulus |
| ν12, ν13, ν23 | Poisson ratio |
| μT, μL | friction-like parameters |
| εfc, εffc | fiber longitudinal strain and final failure longitudinal strain |
| εmc, εfmc | matrix longitudinal strain and final failure longitudinal strain |
| Gfc/Gmc | fiber/matrix longitudinal fracture toughness |
| σeff, deff | effective stress and effective displacement |
| df/dm | fiber/matrix damage index |
| Gn, Gs, Gt | current fracture energies in the normal and shear directions |
| Gnc, Gsc, Gtc | critical fracture energies in the normal and shear directions |
| le | element length |
| H | fracture criterion exponent |
| dn | expanded rivet diameter |
| Tr | reference temperature |
| actual strain rate | |
| CFRP | carbon fiber reinforced polymer |
| CT | computed tomography |
| SCM | smeared crack method |
| DCM | discrete crack method |
| DoF | degree of freedom |
| EMR | electromagnetic riveting |
| Kn | penalty stiffness |
| D | rivet-hole diameter |
| I | interference size |
| Tm | melting point temperature |
| static tensile strain rate | |
| Al | aluminum alloy |
| SEM | scanning electron microscopy |
| CDM | continuum damage mechanics |
| FNM | floating node method |
| CZM | cohesive zone model |
| FEA | finite element analysis |
Appendix A
| M1 | M2 | M3 | M4 | M5 | M6 | Average dn | Interference Size (dn − D)/D × 100% | ||
|---|---|---|---|---|---|---|---|---|---|
| D = 4.08 mm (c = 0.05 mm) | Al | 4.6950 | 4.5427 | 4.7903 | 4.6665 | 4.6855 | 4.6284 | 4.6681 | 14.41% |
| CFRP | 4.1998 | 4.2379 | 4.1236 | 4.1141 | 4.1808 | 4.3046 | 4.1935 | 2.78% | |
| D = 4.12 mm (c = 0.09 mm) | Al | 4.7903 | 4.6950 | 4.7426 | 4.6855 | 4.6474 | 4.5331 | 4.6823 | 13.65% |
| CFRP | 4.2379 | 4.1903 | 4.3522 | 4.5998 | 4.0379 | 3.9903 | 4.2347 | 2.79% | |
| D = 4.18 mm (c = 0.15 mm) | Al | 4.6950 | 4.6569 | 4.8664 | 4.7712 | / | / | 4.7474 | 13.57% |
| CFRP | 4.1331 | 4.2379 | 4.2189 | 4.3427 | / | / | 4.2332 | 1.27% | |
| D = 4.22 mm (c = 0.19 mm) | Al | 4.7860 | 4.7362 | 4.7807 | 4.7426 | / | / | 4.7614 | 12.84% |
| CFRP | 4.2671 | 4.2674 | 4.2951 | 4.2665 | / | / | 4.2740 | 1.28% | |
| D = 4.28 mm (c = 0.25 mm) | Al | 4.7183 | 4.767 | 4.8569 | 4.8284 | 4.8188 | 4.8474 | 4.8061 | 12.29% |
| CFRP | 4.2279 | 4.2003 | 4.3522 | 4.3046 | 4.3331 | 4.3712 | 4.2982 | 0.43% |
References
- Ma, Q.; Nie, N.; Zhang, S.; Gan, X. Comprehensive evaluation of energy absorption characteristics ofal-CFRP hybrid tube under radial impacts. Polym. Compos. 2024, 45, 6059–6076. [Google Scholar] [CrossRef]
- Pramanik, A.; Basak, A.K.; Dong, Y.; Sarker, P.K.; Uddin, M.S.; Littlefair, G.; Dixit, A.R.; Chattopadhyaya, S. Joining of carbon fibre reinforced polymer (CFRP) composites and aluminium alloys—A review. Compos. Part A Appl. Sci. Manuf. 2017, 101, 1–29. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, W.; Wu, Y.; Chen, Y. The damage investigation of wedge-shaped electromagnetic riveting structure of CFRP/aluminium alloy. J. Test. Eval. 2013, 41, 188–193. [Google Scholar] [CrossRef]
- Suo, H.; Zhou, H.; Wei, Z.; Li, R.; Zhang, Y.; Guan, W.; Cheng, H.; Luo, B.; Zhang, K. Degradation mechanisms and mechanical behavior of composite-metal bolted/riveted joints in complex service conditions: A comprehensive review. Eng. Fail. Anal. 2025, 182, 110037. [Google Scholar] [CrossRef]
- Li, M.; Tian, W.; Hu, J.; Wang, C.; Liao, W. Effect of hole perpendicularity error and squeeze force on the mechanical behaviors of riveted joints. Microsc. Res. Tech. 2022, 85, 1075–1088. [Google Scholar] [CrossRef]
- Korbel, A. Effect of aircraft rivet installation process and production variables on residual stress, clamping force and fatigue behaviour of thin sheet riveted lap joints. Thin-Walled Struct. 2022, 181, 110041. [Google Scholar] [CrossRef]
- Egan, B.; Mccarthy, C.T.; Mccarthy, M.A.; Frizzell, R.M. Stress analysis of single-bolt, single-lap, countersunk composite joints with variable bolt-hole clearance. Compos. Struct. 2012, 94, 1038–1051. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, Z.; Zheng, G.; Zuo, D.; Guo, C.; Wang, Y. Quasi-static tensile failure mechanism analysis of CFRP/al countersunk electromagnetic riveted joints with different rivet-hole clearances. Eng. Fail. Anal. 2024, 155, 107759. [Google Scholar] [CrossRef]
- Zhang, M.; Cao, Z.; Guo, Y.; Cao, Y.; Zheng, G.; Huo, L. Stress, damage, and fatigue performance analysis of CFRP/al double-sided countersunk riveted joints with variable rivet-hole clearance. Int. J. Fatigue 2024, 186, 108385. [Google Scholar] [CrossRef]
- Garcea, S.C.; Wang, Y.; Withers, P.J. X-ray computed tomography of polymer composites. Compos. Sci. Technol. 2018, 156, 305–319. [Google Scholar] [CrossRef]
- Lin, Y.; Liu, H.; Yu, J.; Cheng, Z.; Song, Y.; Zeng, L.; Ji, X. Non-destructive testing of metal/CFRP composite defects using continuous-wave laser ultrasonic technique. Opt. Laser Technol. 2025, 189, 113113. [Google Scholar] [CrossRef]
- Wang, A.; Wang, Z.; Zhao, M.; Zhao, Y.; Chang, Z. Effects of ply thickness and interference-fit on the bearing strength of single-lap countersunk composite joints. Thin-Walled Struct. 2023, 189, 110878. [Google Scholar] [CrossRef]
- Hassan, J.; O’Higgins, R.M.; Mccarthy, C.T.; Toso, N.; Mccarthy, M.A. Mesoscale modelling of extended bearing failure in tension-absorber joints. Int. J. Mech. Sci. 2020, 182, 105777. [Google Scholar] [CrossRef]
- Wang, A.; Wang, Z.; Wang, S.; Zhao, M.; Zhao, Y.; Cao, Y.; Chang, Z. Mechanical behaviour and damage mechanism of static/dynamic interference-fit installation in laminated bolted joint using ultra-thin plies. Tribol. Int. 2024, 194, 109482. [Google Scholar] [CrossRef]
- Xu, G.; Cheng, H.; Zhang, K.; Liang, B.; Cheng, Y.; Hu, J.; Liu, C. Modeling of damage behavior of carbon fiber reinforced plastic composites interference bolting with sleeve. Mater. Des. 2020, 194, 108904. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Li, H.; Qin, X.; Wu, X.; Gui, L. Numerical and experimental investigation of fitting tolerance effects on bearing strength of CFRP/al single-lap blind riveted joints. Compos. Struct. 2022, 281, 115022. [Google Scholar] [CrossRef]
- Kong, D.; Wang, D.; Xie, C.; Wang, S.; Zhang, X.; Zhang, Z. Investigation and optimization of structural parameters for the forming quality and mechanical properties of CFRP/al self-piercing riveting. Int. J. Adv. Manuf. Technol. 2023, 127, 3297–3313. [Google Scholar] [CrossRef]
- Lu, X.; Guo, X.M. An interactive orthotropic non-local damage model for progressive failure analysis of composite laminates. Compos. Struct. 2022, 295, 115841. [Google Scholar] [CrossRef]
- Chen, B.Y.; Pinho, S.T.; De Carvalho, N.V.; Baiz, P.M.; Tay, T.E. A floating node method for the modelling of discontinuities in composites. Eng. Fract. Mech. 2014, 127, 104–134. [Google Scholar] [CrossRef]
- Funari, M.F.; Spadea, S.; Fabbrocino, F.; Luciano, R. A moving interface finite element formulation to predict dynamic edge debonding in FRP-strengthened concrete beams in service conditions. Fibers 2020, 8, 42. [Google Scholar] [CrossRef]
- Funari, M.F.; Greco, F.; Lonetti, P.; Luciano, R.; Penna, R. An interface approach based on moving mesh and cohesive modeling in z-pinned composite laminates. Compos. Part B Eng. 2018, 135, 207–217. [Google Scholar] [CrossRef]
- Lu, X.; Chen, B.Y.; Tan, V.B.C.; Tay, T.E. Adaptive floating node method for modelling cohesive fracture of composite materials. Eng. Fract. Mech. 2018, 194, 240–261. [Google Scholar] [CrossRef]
- Zhi, J.; Tay, T. Interrogating failure mechanisms of notched composites through a discrete crack modeling approach. Compos. Sci. Technol. 2020, 196, 108203. [Google Scholar] [CrossRef]
- Tian, K.; Zhi, J.; Tan, V.B.C.; Tay, T.E. An explicit finite element discrete crack analysis of open hole compression failure in composites. Compos. Struct. 2025, 364, 119167. [Google Scholar] [CrossRef]
- Tian, K.; Zhi, J.; Tan, V.B.C.; Tay, T.E. An explicit finite element discrete crack analysis of open hole tension failure in composites. Compos. Struct. 2024, 345, 118411. [Google Scholar] [CrossRef]
- Chen, B.Y.; Tay, T.E.; Pinho, S.T.; Tan, V.B.C. Modelling the tensile failure of composites with the floating node method. Comput. Methods Appl. Mech. Eng. 2016, 308, 414–442. [Google Scholar] [CrossRef]
- Li, S. The maximum stress failure criterion and the maximum strain failure criterion: Their unification and rationalization. J. Compos. Sci. 2020, 4, 157. [Google Scholar] [CrossRef]
- Pinho, S.T.; Iannucci, L.; Robinson, P. Physically-based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part I: Development. Part A Appl. Sci. Manuf. 2006, 37, 63–73. [Google Scholar] [CrossRef]
- Puck, A.; Schurmann, H. Failure analysis of FRP laminates by means of physically based phenomenological models. Compos. Sci. Technol. 1998, 58, 1045–1067. [Google Scholar] [CrossRef]
- Pinho, S.T.; Iannucci, L.; Robinson, P. Physically based failure models and criteria for laminated fibre-reinforced composites with emphasis on fibre kinking. Part II: FE implementation. Compos. Part A Appl. Sci. Manuf. 2006, 37, 766–777. [Google Scholar] [CrossRef]
- Su, Z.C.; Tay, T.E.; Ridha, M.; Chen, B.Y. Progressive damage modeling of open-hole composite laminates under compression. Compos. Struct. 2015, 122, 507–517. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 4, 439–449. [Google Scholar] [CrossRef]
- Qin, Y.; Liao, Y.; Li, G.; Cui, J.; Jiang, H. Numerical simulation and parameter analysis of electromagnetic riveting process for ti-6al-4v titanium rivet. Coatings 2021, 11, 878. [Google Scholar] [CrossRef]
- Cui, J.; Dong, D.; Zhang, X.; Huang, X.; Lu, G.; Jiang, H.; Li, G. Influence of thickness of composite layers on failure behaviors of carbon fiber reinforced plastics/aluminum alloy electromagnetic riveted lap joints under high-speed loading. Int. J. Impact Eng. 2018, 115, 1–9. [Google Scholar] [CrossRef]
- Jiang, H.; Li, G.; Zhang, X.; Cui, J. Fatigue and failure mechanism in carbon fiber reinforced plastics/aluminum alloy single lap joint produced by electromagnetic riveting technique. Compos. Sci. Technol. 2017, 152, 1–10. [Google Scholar] [CrossRef]
- Zhang, Q.; Zuo, Y.; Hu, Z.; Xu, Y.; Liu, X. Advances and challenges in interference-fit technology for enhancing the mechanical performance of joints. J. Mater. Eng. Perform. 2025, 34, 3585–3607. [Google Scholar] [CrossRef]
- GJB715.25-90; TNDS. Fastener Test Methods. Military Standards Press of National Defense Science and Industry Commission: Beijing, China, 1990.
- Wang, J.; Zhang, Y.; Cheng, L.; Yang, Y.; Bi, Y. Effect of riveting parameters on the forming quality of riveted lap joints with reduced countersunk head half-crown rivet. Int. J. Adv. Manuf. Technol. 2022, 121, 8083–8098. [Google Scholar] [CrossRef]
- Shan, M.; Zhao, L.; Liu, F.; Qi, D.; Zhang, J. Revealing the competitive fatigue failure behaviour of CFRP-aluminum two-bolt, double-lap joints. Compos. Struct. 2020, 244, 112166. [Google Scholar] [CrossRef]
- Yang, B. Mechanical Behaviour of Carbon Fiber/BMI Composites and Joints at Space Environment Temperature. Ph.D. Thesis, Northwestern Polytechnical University, Xi’an, China, 2018. [Google Scholar]
- Institute ACAD. Specification of ZT7h/QY9611 Carbon Fiber Reinforced Bismaleimide Matrix Composite; Chengdu, China.
- Zhu, L.; Cui, H.; Li, Y.; Sun, W. Numerical simulation of the failure of composite t-joints with defects. Acta Aeronaut. Astronaut. Sin. 2012, 33, 287–296. [Google Scholar]
- Rao, Y. Study on Parameter Inversion of Cohesive Zone Model for Delamination in Composite. Masters’s Thesis, Nanjing University of Aeronautics and Astronautics, Nanjing, China, 2020. [Google Scholar]
- Zhang, X.; Li, C. The effect of loading rate on deformation of TA1 titanium alloy bars subjected to electromagnetic heading. Mater. Sci. Eng. A 2017, 679, 511–519. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, H.P.; Su, H.; Li, C.F. Experimental evaluation on mechanical properties of a riveted structure with electromagnetic riveting. Int. J. Adv. Manuf. Technol. 2016, 83, 2071–2082. [Google Scholar] [CrossRef]
- Zhang, X. Dynamic Plastic Deformation Behavior and Microstructure Properties of Rivets During Electromagnetic Riveting Process. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2016. [Google Scholar]
- Wang, L.; Li, Y.; Suo, T.; Guo, Y. Mechanical behavior of commonly used aeronautical aluminum alloys under dynamic tension. J. Aeronaut. Mater. 2013, 4, 71–77. [Google Scholar]
- Chang, Z.; Wang, Z.; Wang, B.; Kang, Y.; Luo, Q. Riveting force computation model based on formed head inhomogeneous deformation. Acta Aeronaut. Astronaut. Sin. 2016, 37, 2312–2320. [Google Scholar]
- Sogalad, I.; Ashoka, H.N.; Udupa, N.G.S. Influence of cylindricity and surface modification on load bearing ability of interference fitted assemblies. Precis. Eng. 2012, 36, 629–640. [Google Scholar] [CrossRef]
- Zeng, C.; Xue, J.T.; Liu, X.Y.; Tian, W. Design variables influencing the fatigue of al 2024-t3 in riveted aircraft lap joints: Squeeze force and initial fit tolerance. Int. J. Fatigue 2020, 140, 105751. [Google Scholar] [CrossRef]
- Tarpani, A.C.S.P.; Barreto, T.A.; Tarpani, J.R. Fatigue failure analysis of riveted fibre-metal laminate lap joints. Eng. Fract. Mech. 2020, 239, 107275. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, K. An experimental study on fatigue life of interference-fit fastened joint in a laminated. Chin. J. Aeronaut. 1993, 6, 13–17. [Google Scholar]











| Group A | Group B | Group C | Group D | Group E | |
|---|---|---|---|---|---|
| Nominal hole diameter D | 4.08 | 4.12 | 4.18 | 4.22 | 4.28 |
| Clearance c | 0.05 | 0.09 | 0.15 | 0.19 | 0.25 |
| Contact Property | Contact Surface Pairs | Friction Coefficient |
|---|---|---|
| Tangential behavior: Penalty Normal behavior: “Hard” Contact | Rivet die and rivet (driven head) | 0.1 |
| Rivet and Al plate hole wall | 0.1 | |
| Lower Al plate and upper CFRP laminate | 0.5 | |
| Rivet and CFRP laminate hole wall | 0.3 |
| Elastic Modulus | Shear Modulus | ||||
|---|---|---|---|---|---|
| E11 | E22 | E33 | G12 | G13 | G23 |
| 146 GPa | 10.4 GPa | 10.4 GPa | 6.12 GPa | 6.12 GPa | 3.45 GPa |
| Poisson’s ratio | Tensile strength | ||||
| ν12 | ν13 | ν23 | XT | YT | |
| 0.278 | 0.3 | 0.42 | 2354 MPa | 58 MPa | |
| Compressive strength | Shear strength | ||||
| XC | YC | SL | ST | ||
| 1349 MPa | 236 MPa | 105 MPa | 105 MPa | ||
| Penalty Stiffness | Normal Interface Strength | Shear Interface Strength |
|---|---|---|
| Kn | N | S = T |
| 108 GPa/m | 60 MPa | 95 MPa |
| Mode-I fracture toughness | Mode-II fracture toughness | Fracture criterion exponent |
| Gnc | Gsc | η |
| 0.267 N/mm | 0.75 N/mm | 1.45 |
| Material | Mass Density (kg/m3) | Young’s Modulus (GPa) | Ultimate Tensile Strength (MPa) | Yield Strength (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| TA1 | 4510 | 108 | 353 | 260 | 0.34 |
| 2A12 | 7850 | 67.3 | 481 | 380 | 0.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Tian, K.; Cao, Z.; Tay, T.-E. A Comparison of Discrete Crack and Smeared Crack Methods Applied to CFRP/Al Riveting Damage Modeling. Materials 2025, 18, 4511. https://doi.org/10.3390/ma18194511
Zhang M, Tian K, Cao Z, Tay T-E. A Comparison of Discrete Crack and Smeared Crack Methods Applied to CFRP/Al Riveting Damage Modeling. Materials. 2025; 18(19):4511. https://doi.org/10.3390/ma18194511
Chicago/Turabian StyleZhang, Minghao, Kun Tian, Zengqiang Cao, and Tong-Earn Tay. 2025. "A Comparison of Discrete Crack and Smeared Crack Methods Applied to CFRP/Al Riveting Damage Modeling" Materials 18, no. 19: 4511. https://doi.org/10.3390/ma18194511
APA StyleZhang, M., Tian, K., Cao, Z., & Tay, T.-E. (2025). A Comparison of Discrete Crack and Smeared Crack Methods Applied to CFRP/Al Riveting Damage Modeling. Materials, 18(19), 4511. https://doi.org/10.3390/ma18194511







