Microscopic Phase-Field Modeling with Accurate Interface Thickness Representation: Applied to Ceramic Matrix Composites
Highlights
- A unified framework for smeared interface modeling in a phase-field model of microscopic fracture is proposed.
- The method resolves limitations in handling close fibers and varying interface thickness.
- The method captures variable interface thickness without explicit interface partitioning and greatly reduces modeling effort in numerical simulations.
- Simulations of SiCf/SiCm with PyC and h-BN interfaces match experimental results.
Abstract
1. Introduction
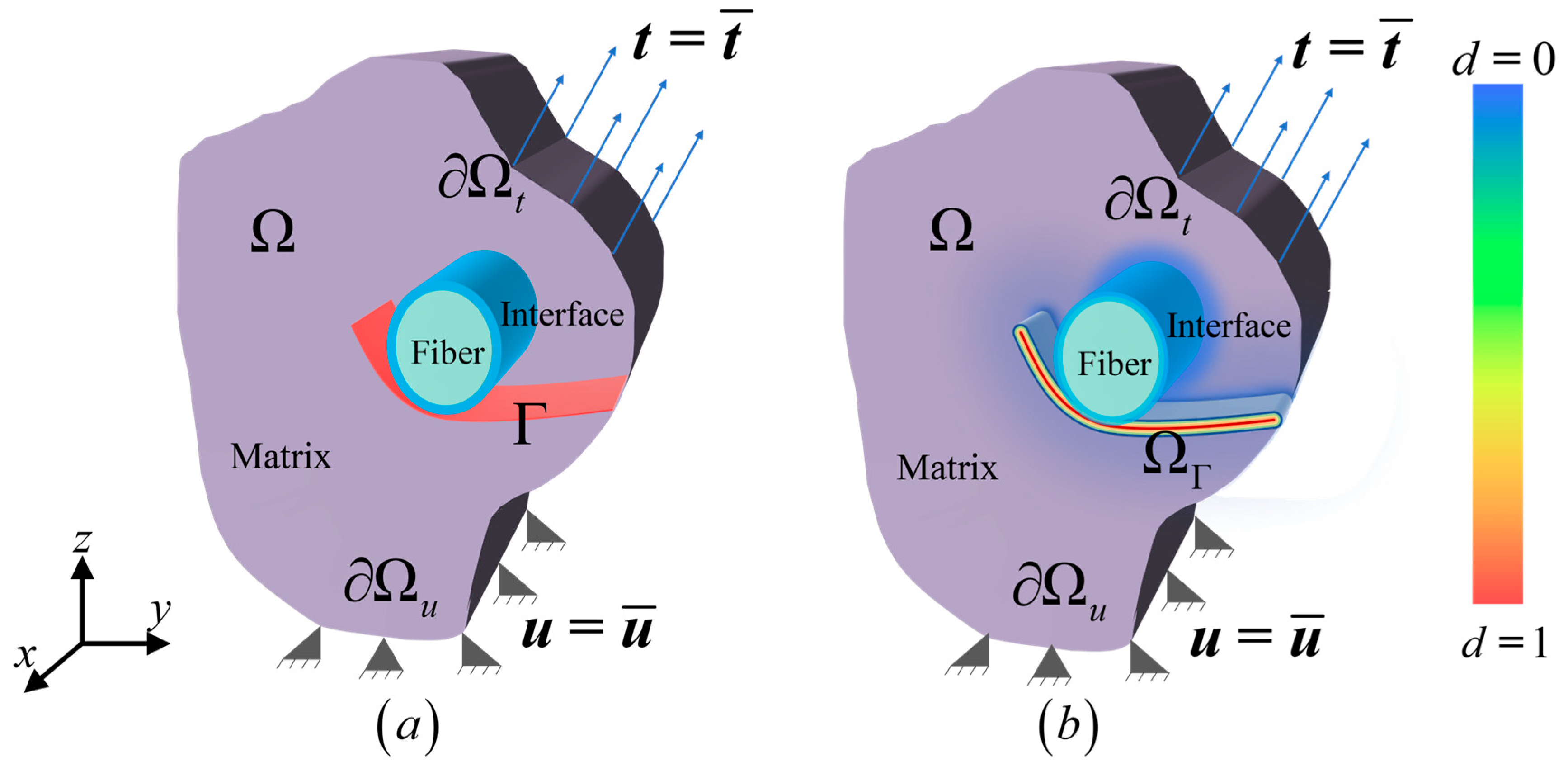
2. Conventional Phase-Field Modeling in Microscopic Composite Models: Methods and Limitations
2.1. Overview of Phase-Field Theory for Fracture
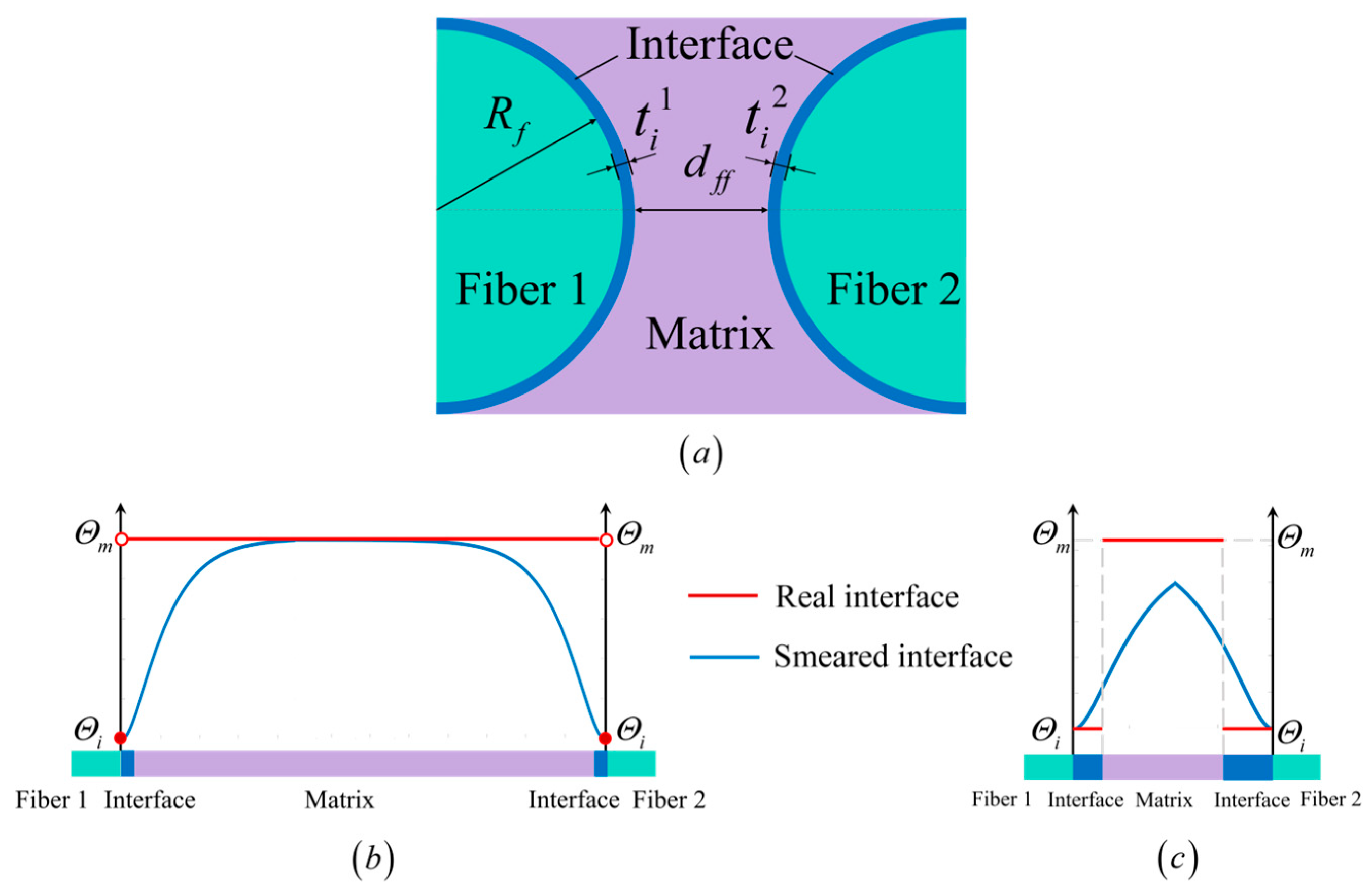
2.2. An Auxiliary Phase Field for Fiber-Matrix Interface
2.3. Limitations of Existing Interface Modeling Approaches
3. A Novel Unified Framework for Smeared Interface Modeling in Phase-Field Model of Microscopic Fracture
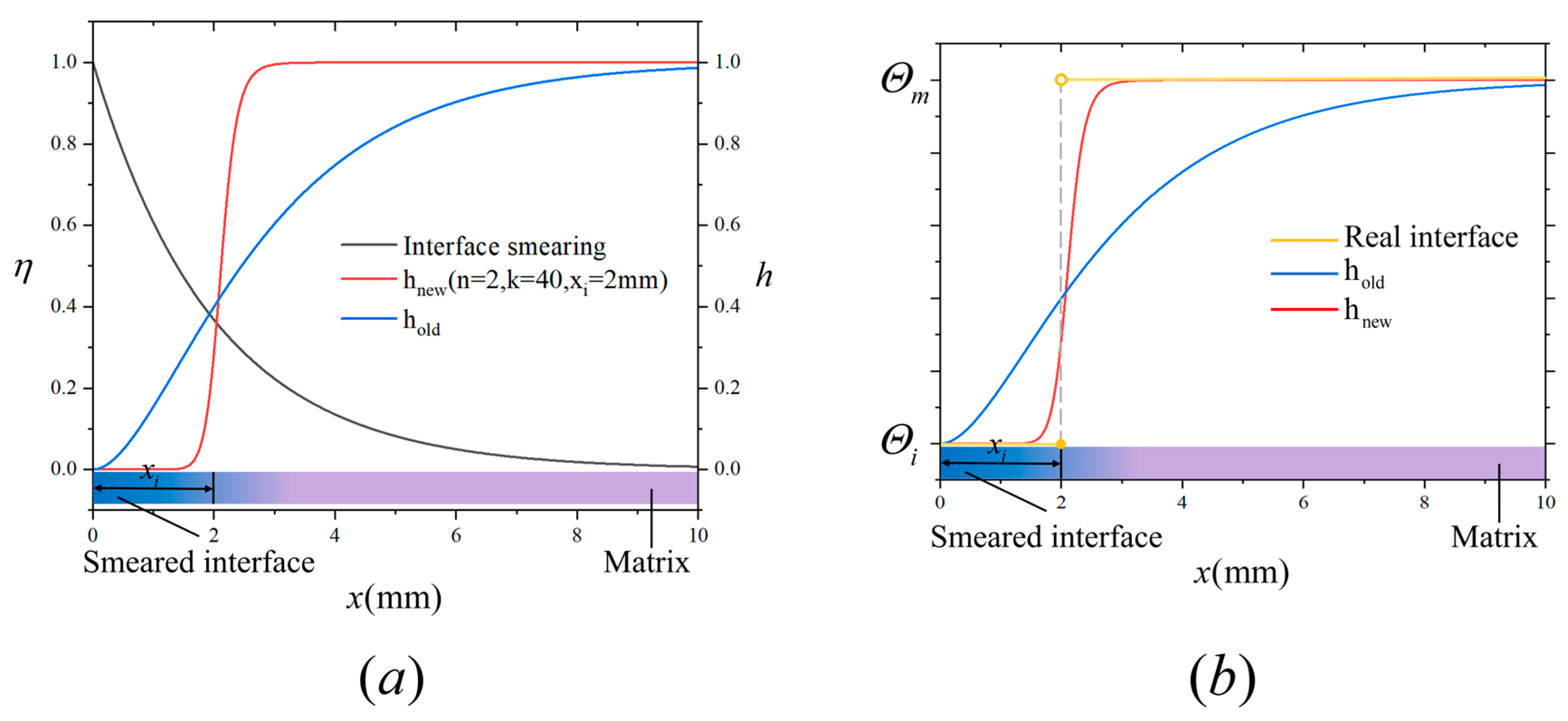
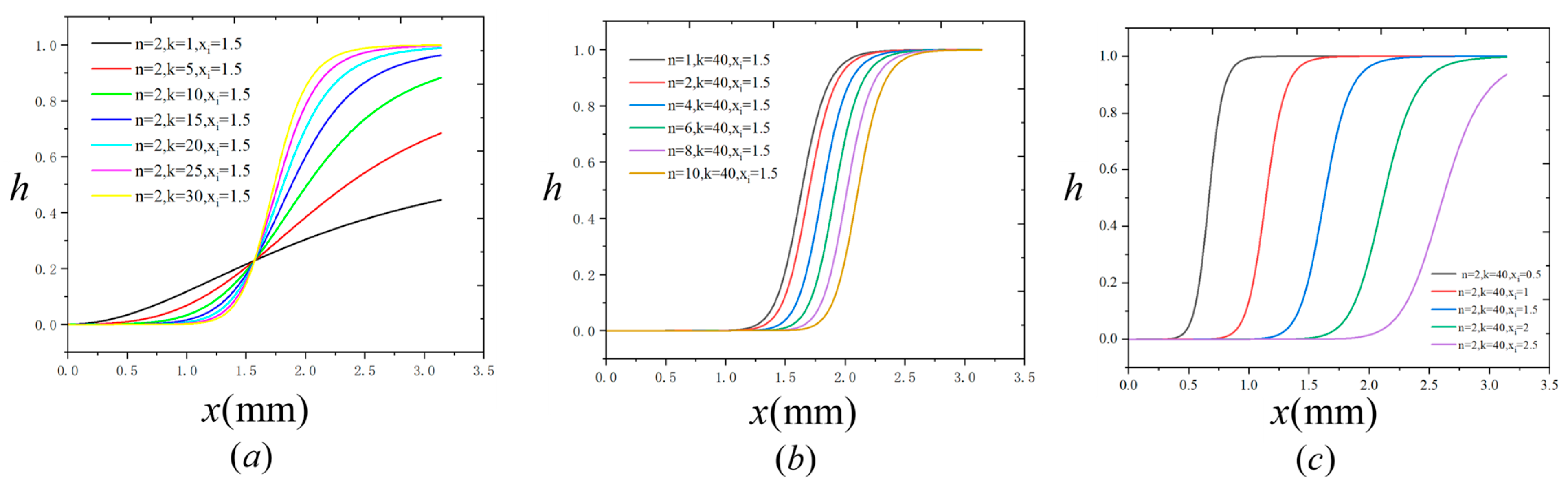
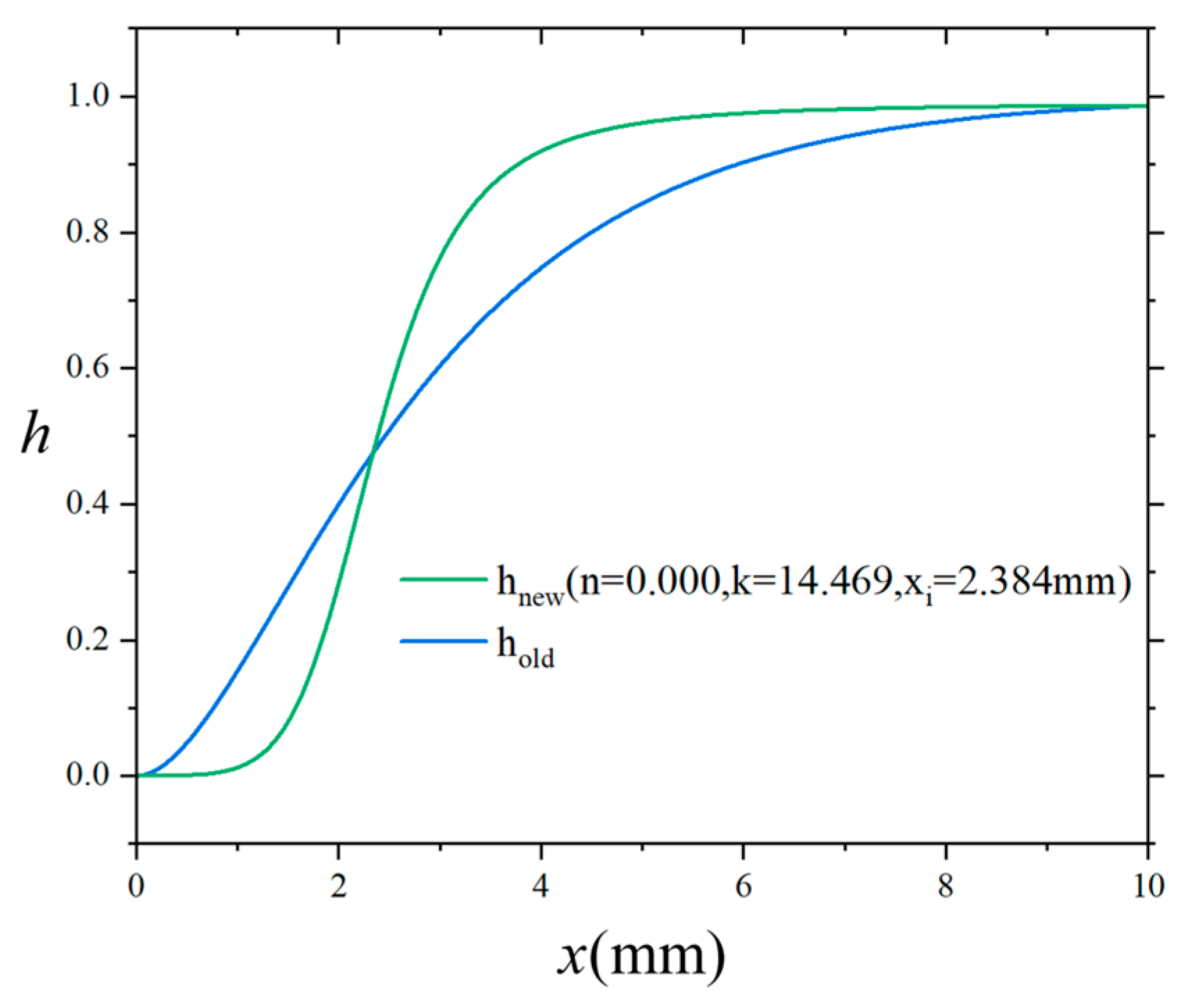
3.1. A Novel Interfacial Material Transition Function
3.2. Correction of Interface Energy Release Rate
3.3. Finite Element Formulation
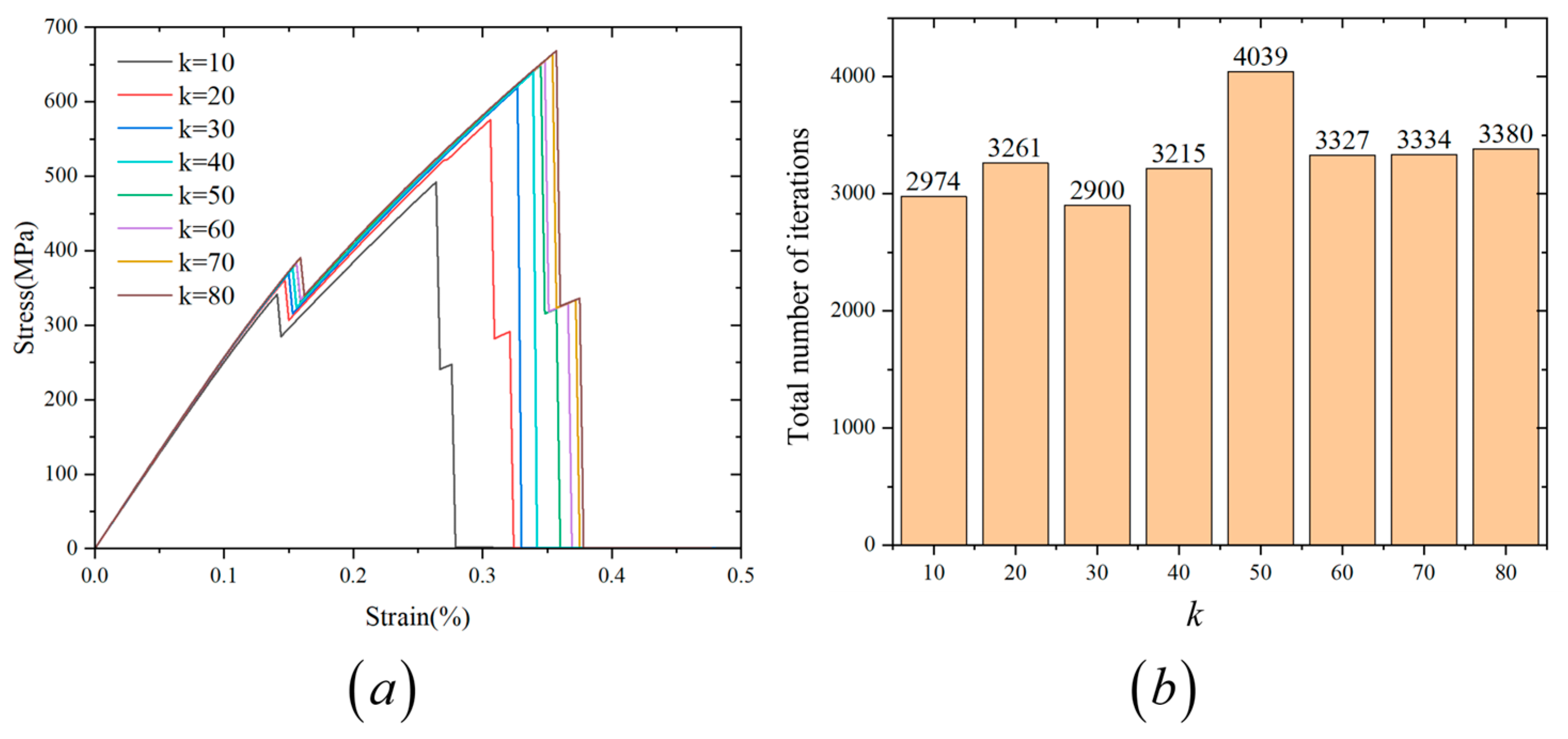
4. Verification
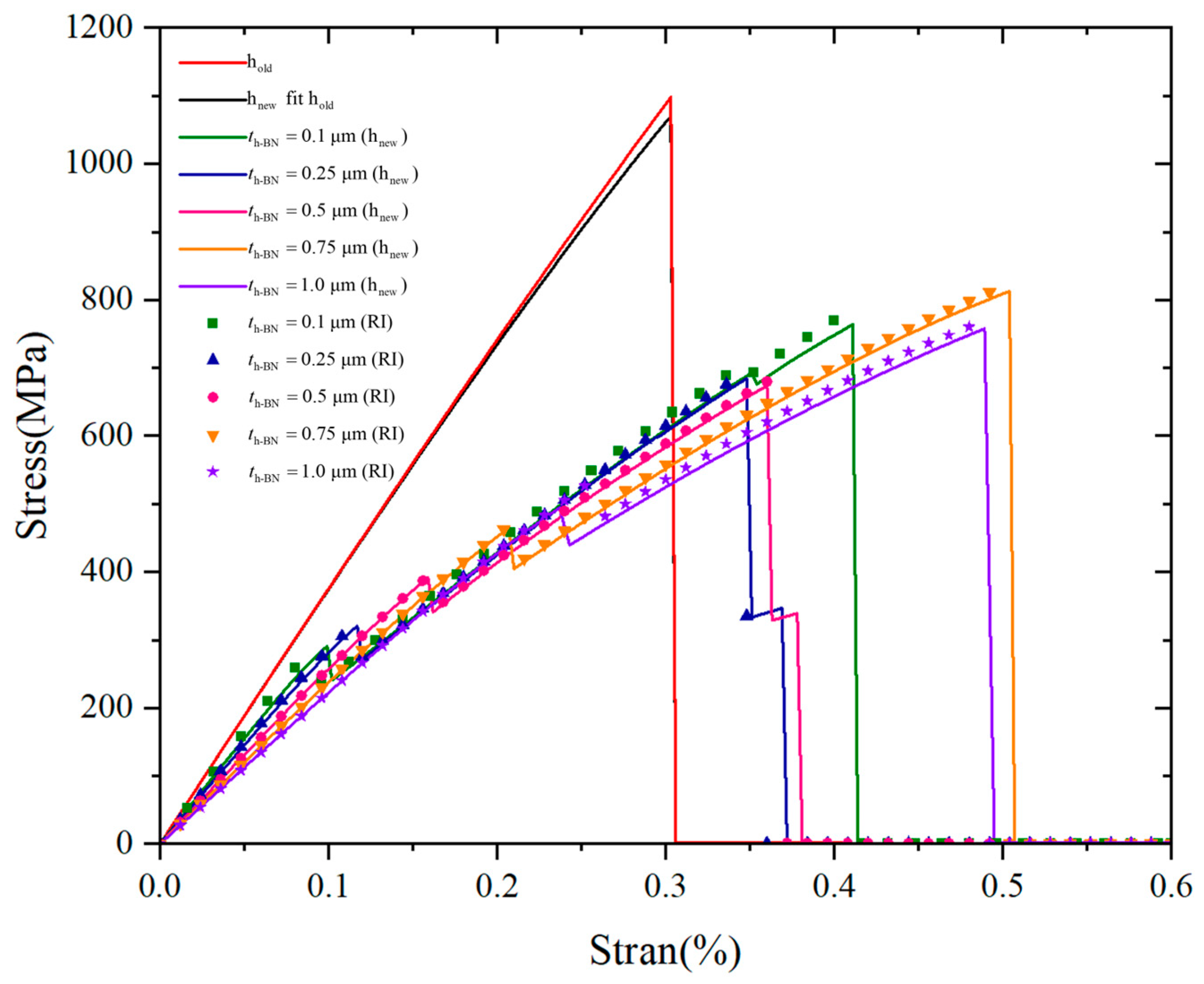
5. Validation
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Phillips, D. Fiber-reinforced ceramics. In Concise Encyclopedia of Advanced Ceramic Materials; Elsevier: Amsterdam, The Netherlands, 1991; pp. 155–160. [Google Scholar]
- Krenkel, W. Ceramic Matrix Composites: Fiber Reinforced Ceramics and Their Applications; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Arai, Y.; Inoue, R.; Goto, K.; Kogo, Y. Carbon fiber reinforced ultra-high temperature ceramic matrix composites: A review. Ceram. Int. 2019, 45, 14481–14489. [Google Scholar] [CrossRef]
- Kameda, T.; Itoh, Y.; Hijikata, T.; Okamura, T. Development of continuous fiber reinforced reaction sintered silicon carbide matrix composite for gas turbine hot parts application. In Turbo Expo: Power for Land, Sea, and Air; American Society of Mechanical Engineers: New York, NY, USA, 2000; p. V004T002A006. [Google Scholar]
- Jia, T.; Deng, Y.; Hao, Y.; Gao, X.; Zhang, C.; Cheng, T.; Li, W.; Yun, G. An analytical model for the high temperature fracture strength of SiC fiber reinforced ceramic matrix composites considering oxidation and residual thermal stresses. Compos. Part A Appl. Sci. Manuf. 2023, 173, 107668. [Google Scholar] [CrossRef]
- Fan, X.; Yin, X. Progress in research and development on matrix modification of continuous fiber-reinforced silicon carbide matrix composites. Adv. Compos. Hybrid Mater. 2018, 1, 685–695. [Google Scholar] [CrossRef]
- Zhao, M.; Zheng, J.; Wang, X.; Zhang, J.; Zhang, D. Gradient-structured SiCf/SiC hybrid woven metamaterials with superior broadband absorption and high-load bearing. Ceram. Int. 2024, 50, 49400–49411. [Google Scholar] [CrossRef]
- Li, L.; Song, Y.; Sun, Y. Modeling the tensile behavior of cross-ply C/SiC ceramic-matrix composites. Mech. Compos. Mater. 2015, 51, 359–376. [Google Scholar] [CrossRef]
- Li, L.; Song, Y.; Sun, Y.C. Modeling the tensile behavior of unidirectional C/SiC ceramic-matrix composites. Mech. Compos. Mater. 2014, 49, 659–672. [Google Scholar] [CrossRef]
- Erdman, D.; Weitsman, Y. The multi-fracture response of cross-ply ceramic composites. Int. J. Solids Struct. 1998, 35, 5051–5083. [Google Scholar] [CrossRef]
- Naslain, R.R.; Pailler, R.J.F.; Lamon, J.L. Single-and multilayered interphases in SiC/SiC composites exposed to severe environmental conditions: An overview. Int. J. Appl. Ceram. Technol. 2010, 7, 263–275. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, J.; Dong, S.; Li, Y. Influence of the thickness of pyrolytic carbon interphase on the mechanical behavior of SiC/(BN/PyC)/SiC composites. Ceram. Int. 2024, 50, 22085–22093. [Google Scholar] [CrossRef]
- Lv, X.; Yue, M.; Yang, W.; Feng, X.; Li, X.; Wang, Y.; Wang, J.; Zhang, J.; Wang, J. Tunable strength of SiCf/β-Yb2Si2O7 interface for different requirements in SiCf/SiC CMC: Inspiration from model composite investigation. J. Mater. Sci. Technol. 2021, 67, 165–173. [Google Scholar] [CrossRef]
- Yang, B.; Zhou, X.; Chai, Y. Mechanical properties of SiCf/SiC composites with PyC and the BN interface. Ceram. Int. 2015, 41, 7185–7190. [Google Scholar] [CrossRef]
- Petrie, C.M.; Koyanagi, T.; McDuffee, J.L.; Deck, C.P.; Katoh, Y.; Terrani, K.A. Experimental design and analysis for irradiation of SiC/SiC composite tubes under a prototypic high heat flux. J. Nucl. Mater. 2017, 491, 94–104. [Google Scholar] [CrossRef]
- Inghels, E.; Lamon, J. An approach to the mechanical behaviour of SiC/SiC and C/SiC ceramic matrix composites: Part 1 Experimental results. J. Mater. Sci. 1991, 26, 5403–5410. [Google Scholar] [CrossRef]
- Giusti, R.; Lucchetta, G. Cohesive Zone Modeling of the Interface Fracture in Full-Thermoplastic Hybrid Composites for Lightweight Application. Polymers 2023, 15, 4459. [Google Scholar] [CrossRef]
- Jia, W.; Fang, L.; Chen, Z.; Zhao, K.; Huang, H.; Pan, L. A microscopic cohesive zone model and effects of interface on the transverse mechanical properties for composites. Fibers Polym. 2021, 22, 1352–1365. [Google Scholar] [CrossRef]
- Kang, F.; Mei, H.; Gao, X.; Zhang, D.; Ye, F.; Zhang, Y.; Cheng, L. Three-dimensional in-situ observation and cohesive zone modeling of tension-induced delamination of two-dimensional C/SiC composites via deep learning-based damage identification. Carbon 2025, 233, 119842. [Google Scholar] [CrossRef]
- Jia, L.; Zhang, C.; Hu, Z.; Song, P.; Yu, L.; Tang, C. Failure analysis of composite laminates under transverse shear load via XFEM. Compos. Struct. 2021, 262, 113615. [Google Scholar] [CrossRef]
- Liu, G.; Guo, J.; Bao, Y.; Zhu, H.; Sun, K. Multiscale simulation of debonding in fiber-reinforced composites by a combination of MsFEM and XFEM. Eng. Fract. Mech. 2024, 306, 110216. [Google Scholar] [CrossRef]
- Vellwock, A.E.; Libonati, F. XFEM for composites; biological; bioinspired materials: A review. Materials 2024, 17, 745. [Google Scholar] [CrossRef]
- Kumar, V.; Dewangan, H.C.; Sharma, N.; Panda, S.K. Combined damage influence prediction of curved composite structural responses using VCCT technique and experimental verification. Int. J. Appl. Mech. 2021, 13, 2150086. [Google Scholar] [CrossRef]
- Martulli, L.; Bernasconi, A. An efficient and versatile use of the VCCT for composites delamination growth under fatigue loadings in 3D numerical analysis: The Sequential Static Fatigue algorithm. Int. J. Fatigue 2023, 170, 107493. [Google Scholar] [CrossRef]
- Buryachenko, V.A. Peridynamic micromechanics of composites: A review. J. Peridynamics Nonlocal Model. 2024, 6, 531–601. [Google Scholar] [CrossRef]
- Yin, B.; Huang, J.; Sun, W. Peridynamics-fueled convolutional neural network for predicting mechanical constitutive behaviors of fiber reinforced composites. Comput. Methods Appl. Mech. Eng. 2024, 431, 117309. [Google Scholar] [CrossRef]
- Shao, Y.; Duan, Q.; Qiu, S. Adaptive analysis for phase-field model of brittle fracture of functionally graded materials. Eng. Fract. Mech. 2021, 251, 107783. [Google Scholar] [CrossRef]
- Molnár, G.; Gravouil, A. 2D and 3D Abaqus implementation of a robust staggered phase-field solution for modeling brittle fracture. Finite Elem. Anal. Des. 2017, 130, 27–38. [Google Scholar] [CrossRef]
- Msekh, M.A.; Sargado, J.M.; Jamshidian, M.; Areias, P.M.; Rabczuk, T. Abaqus implementation of phase-field model for brittle fracture. Comput. Mater. Sci. 2015, 96, 472–484. [Google Scholar] [CrossRef]
- Storvik, E.; Both, J.W.; Sargado, J.M.; Nordbotten, J.M.; Radu, F.A. An accelerated staggered scheme for variational phase-field models of brittle fracture. Comput. Methods Appl. Mech. Eng. 2021, 381, 113822. [Google Scholar] [CrossRef]
- Zhuang, X.; Ren, H.; Rabczuk, T. Nonlocal operator method for dynamic brittle fracture based on an explicit phase field model. Eur. J. Mech. -A/Solids 2021, 90, 104380. [Google Scholar] [CrossRef]
- Peng, F.; Huang, W.; Zhang, Z.-Q.; Guo, T.F.; Ma, Y.E.; Zhang, Y. Conservational integrals of the fourth-order phase field model for brittle fracture via Noether theorem. Eng. Fract. Mech. 2021, 245, 107590. [Google Scholar] [CrossRef]
- Xue, T.; Adriaenssens, S.; Mao, S. Mapped phase field method for brittle fracture. Comput. Methods Appl. Mech. Eng. 2021, 385, 114046. [Google Scholar] [CrossRef]
- Nguyen, K.D.; Augarde, C.E.; Coombs, W.M.; Nguyen-Xuan, H.; Abdel-Wahab, M. Non-conforming multipatches for NURBS-based finite element analysis of higher-order phase-field models for brittle fracture. Eng. Fract. Mech. 2020, 235, 107133. [Google Scholar] [CrossRef]
- Nguyen-Thanh, N.; Nguyen-Xuan, H.; Li, W. Phase-field modeling of anisotropic brittle fracture in rock-like materials and polycrystalline materials. Comput. Struct. 2024, 296, 107325. [Google Scholar] [CrossRef]
- Tarafder, P.; Dan, S.; Ghosh, S. Finite deformation cohesive zone phase field model for crack propagation in multi-phase microstructures. Comput. Mech. 2020, 66, 723–743. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, X.; Yang, S.; Yao, W. Modelling progressive failure in multi-phase materials using a phase field method. Eng. Fract. Mech. 2019, 209, 105–124. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Réthoré, J.; Yvonnet, J.; Baietto, M.C. Multi-phase-field modeling of anisotropic crack propagation for polycrystalline materials. Comput. Mech. 2017, 60, 289–314. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. Numerical experiments in revisited brittle fracture. J. Mech. Phys. Solids 2000, 48, 797–826. [Google Scholar] [CrossRef]
- Ambati, M.; Gerasimov, T.; De Lorenzis, L. A review on phase-field models of brittle fracture and a new fast hybrid formulation. Comput. Mech. 2015, 55, 383–405. [Google Scholar] [CrossRef]
- Francfort, G.A.; Marigo, J.J. Revisiting brittle fracture as an energy minimization problem. J. Mech. Phys. Solids 1998, 46, 1319–1342. [Google Scholar] [CrossRef]
- Bourdin, B.; Francfort, G.A.; Marigo, J.J. The variational approach to fracture. J. Elast. 2008, 91, 5–148. [Google Scholar] [CrossRef]
- Gao, J.; Bai, Y.; Fan, H.; Song, G.; Zou, X.; Zheng, Y.; He, X. Phase-field simulation of microscale crack propagation/deflection in SiCf/SiC composites with weak interphase. J. Am. Ceram. Soc. 2023, 106, 4877–4890. [Google Scholar] [CrossRef]
- Xiao, Y.; Liu, Z.; Peng, X.; Zhu, W.; Zhou, Y.; Yang, L. Spallation mechanism of thermal barrier coatings with real interface morphology considering growth and thermal stresses based on fracture phase field. Surf. Coat. Technol. 2023, 458, 129356. [Google Scholar] [CrossRef]
- Gljušćić, M.; Lanc, D.; Franulović, M.; Žerovnik, A. Microstructural analysis of the transverse and shear behavior of additively manufactured CFRP composite RVEs based on the phase-field fracture theory. J. Compos. Sci. 2023, 7, 38. [Google Scholar] [CrossRef]
- Zhang, P.; Yao, W.; Hu, X.; Bui, T.Q. 3D micromechanical progressive failure simulation for fiber-reinforced composites. Compos. Struct. 2020, 249, 112534. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, P.; Yao, W. Phase field modelling of microscopic failure in composite laminates. J. Compos. Mater. 2021, 55, 1853–1865. [Google Scholar] [CrossRef]
- Wang, T.; Sun, Z.; Hu, X.; Xu, H.; Zhang, P.; Yao, W. Simulation of progressive failure process in solid rocket propellants using a phase-field model. Eng. Fract. Mech. 2024, 312, 110577. [Google Scholar] [CrossRef]
- Zhou, S.; Wang, T.; Wu, X.; Sun, Z.; Li, Y.; Berto, F. Three-dimensional phase field modeling of progressive failure in aramid short fiber reinforced paper. Mech. Adv. Mater. Struct. 2023, 30, 5106–5121. [Google Scholar] [CrossRef]
- Michel, J.-C.; Moulinec, H.; Suquet, P. Effective properties of composite materials with periodic microstructure: A computational approach. Comput. Methods Appl. Mech. Eng. 1999, 172, 109–143. [Google Scholar] [CrossRef]
- Mikdam, A.; Makradi, A.; Koutsawa, Y.; Belouettar, S. Microstructure effect on the mechanical properties of heterogeneous composite materials. Compos. Part B: Eng. 2013, 44, 714–721. [Google Scholar] [CrossRef]
- Bourdin, B.; Chambolle, A. Implementation of an adaptive finite-element approximation of the Mumford-Shah functional. Numer. Math. 2000, 85, 609–646. [Google Scholar] [CrossRef]
- Wu, J.Y. A unified phase-field theory for the mechanics of damage and quasi-brittle failure. J. Mech. Phys. Solids 2017, 103, 72–99. [Google Scholar] [CrossRef]
- Miehe, C.; Welschinger, F.; Hofacker, M. Thermodynamically consistent phase-field models of fracture: Variational principles and multi-field FE implementations. Int. J. Numer. Methods Eng. 2010, 83, 1273–1311. [Google Scholar] [CrossRef]
- Miehe, C.; Hofacker, M.; Welschinger, F. A phase field model for rate-independent crack propagation: Robust algorithmic implementation based on operator splits. Comput. Methods Appl. Mech. Eng. 2010, 199, 2765–2778. [Google Scholar] [CrossRef]
- Sudhir, A.; Talreja, R. Simulation of manufacturing induced fiber clustering and matrix voids and their effect on transverse crack formation in unidirectional composites. Compos. Part A Appl. Sci. Manuf. 2019, 127, 105620. [Google Scholar] [CrossRef]
- Hu, X.; Tan, S.; Xu, H.; Sun, Z.; Wang, T.; Min, L.; Wang, Z.; Yao, W. Modelling high temperature progressive failure in C/SiC composites using a phase field model: Oxidation rate controlled process. Comput. Methods Appl. Mech. Eng. 2025, 433, 117544. [Google Scholar] [CrossRef]
- Braginsky, M.; Przybyla, C.P. Simulation of crack propagation/deflection in ceramic matrix continuous fiber reinforced composites with weak interphase via the extended finite element method. Compos. Struct. 2016, 136, 538–545. [Google Scholar] [CrossRef]
- Shimoda, K.; Park, J.-S.; Hinoki, T.; Kohyama, A. Influence of pyrolytic carbon interface thickness on microstructure and mechanical properties of SiC/SiC composites by NITE process. Compos. Sci. Technol. 2008, 68, 98–105. [Google Scholar] [CrossRef]
- Shimoda, K.; Park, J.S.; Hinoki, T.; Kohyama, A. Microstructural optimization of high-temperature SiC/SiC composites by NITE process. J. Nucl. Mater. 2009, 386–388, 634–638. [Google Scholar] [CrossRef]
- Morishita, K.; Ochiai, S.; Okuda, H.; Inshikawa, T.; Sato, M.; Inoue, T. Fracture Toughness of a Crystalline Silicon Carbide Fiber (Tyranno-SA3®). J. Am. Ceram. Soc. 2006, 89, 2571–2576. [Google Scholar] [CrossRef]
- Yin, X.W.; Cheng, L.F.; Zhang, L.T.; Travitzky, N.; Greil, P. Fibre-reinforced multifunctional SiC matrix composite materials. Int. Mater. Rev. 2016, 62, 117–172. [Google Scholar] [CrossRef]
- Kabel, J.; Hosemann, P.; Zayachuk, Y.; Armstrong, D.E.J.; Koyanagi, T.; Katoh, Y.; Deck, C. Ceramic composites: A review of toughening mechanisms and demonstration of micropillar compression for interface property extraction. J. Mater. Res. 2018, 33, 424–439. [Google Scholar] [CrossRef]
- Jin, E.; Sun, W.; Liu, H.; Wu, K.; Ma, D.; Sun, X.; Feng, Z.; Li, J.; Yuan, Z. Effect of Interface Coating on High Temperature Mechanical Properties of SiC–SiC Composite Using Domestic Hi–Nicalon Type SiC Fibers. Coatings 2020, 10, 477. [Google Scholar] [CrossRef]
- Friedrich, K. Fractographic analysis of polymer composites. In Composite Materials Series; Elsevier: Amsterdam, The Netherlands, 1989; pp. 425–487. [Google Scholar]
- Pantazopoulos, G.A. A short review on fracture mechanisms of mechanical components operated under industrial process conditions: Fractographic analysis and selected prevention strategies. Metals 2019, 9, 148. [Google Scholar] [CrossRef]
- Shimoda, K.; Eto, M.; Lee, J.; Park, J.; Hinoki, T.; Kohyama, A. Influence of surface micro-chemistry of SiC nano-powder on the sinterability of NITE-SiC. Appl. Surf. Sci. 2004, 253, 9450–9456. [Google Scholar] [CrossRef]
- Gomez, E.; Echeberria, J.; Iturriza, I.; Castro, F. Liquid phase sintering of SiC with additions of Y2O3, Al2O3 and SiO2. J. Eur. Ceram. Soc. 2004, 24, 2895–2903. [Google Scholar] [CrossRef]






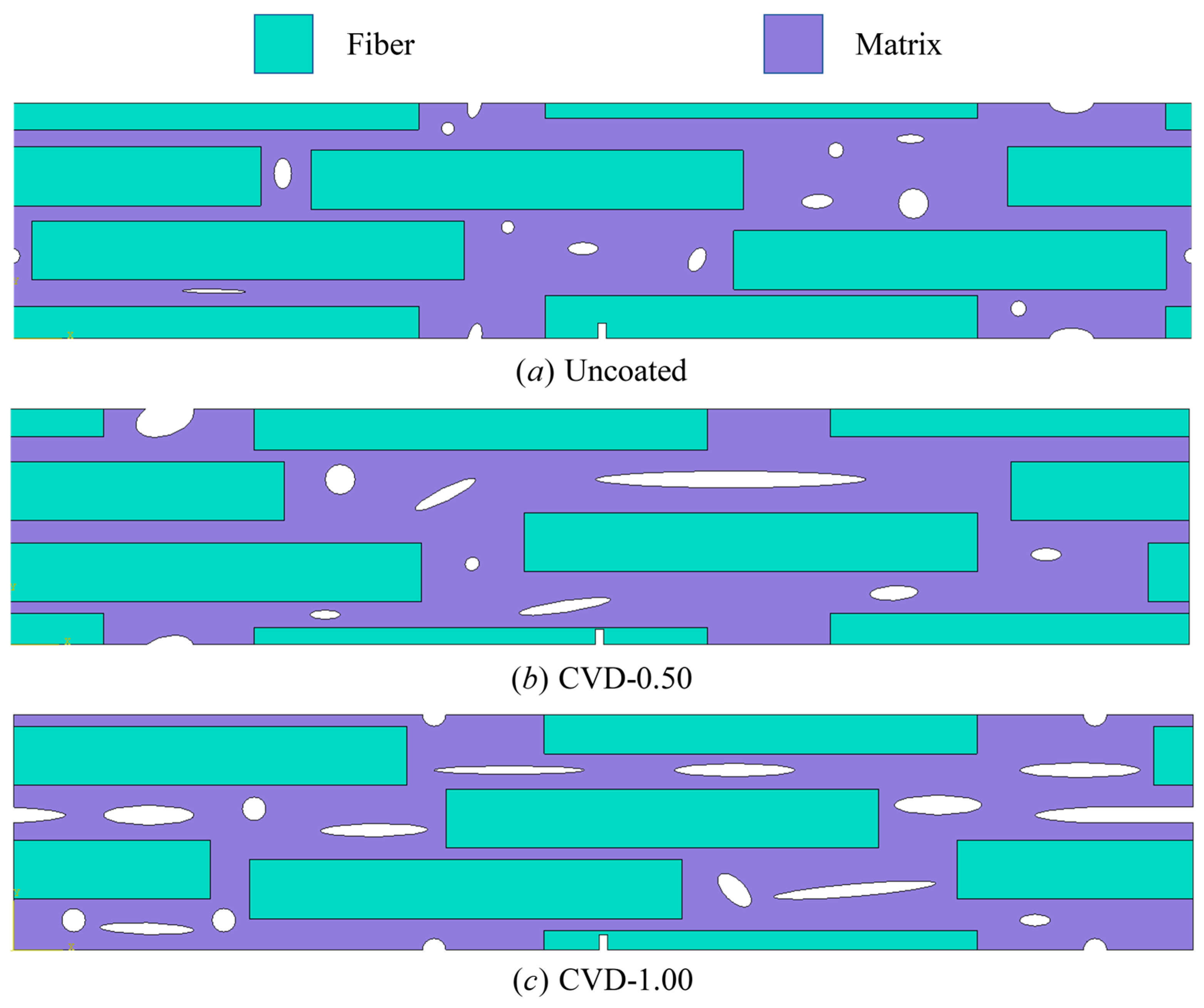
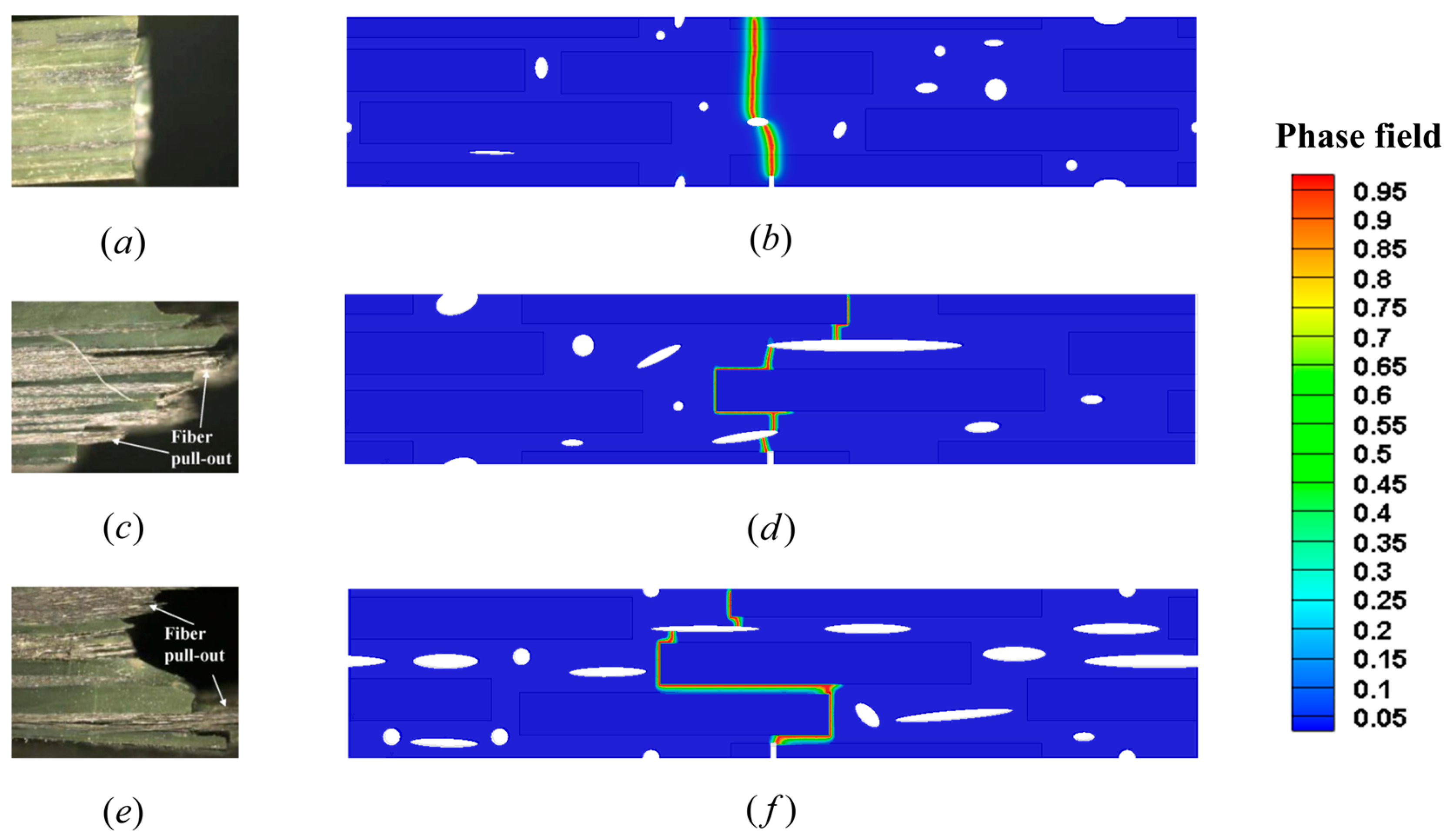
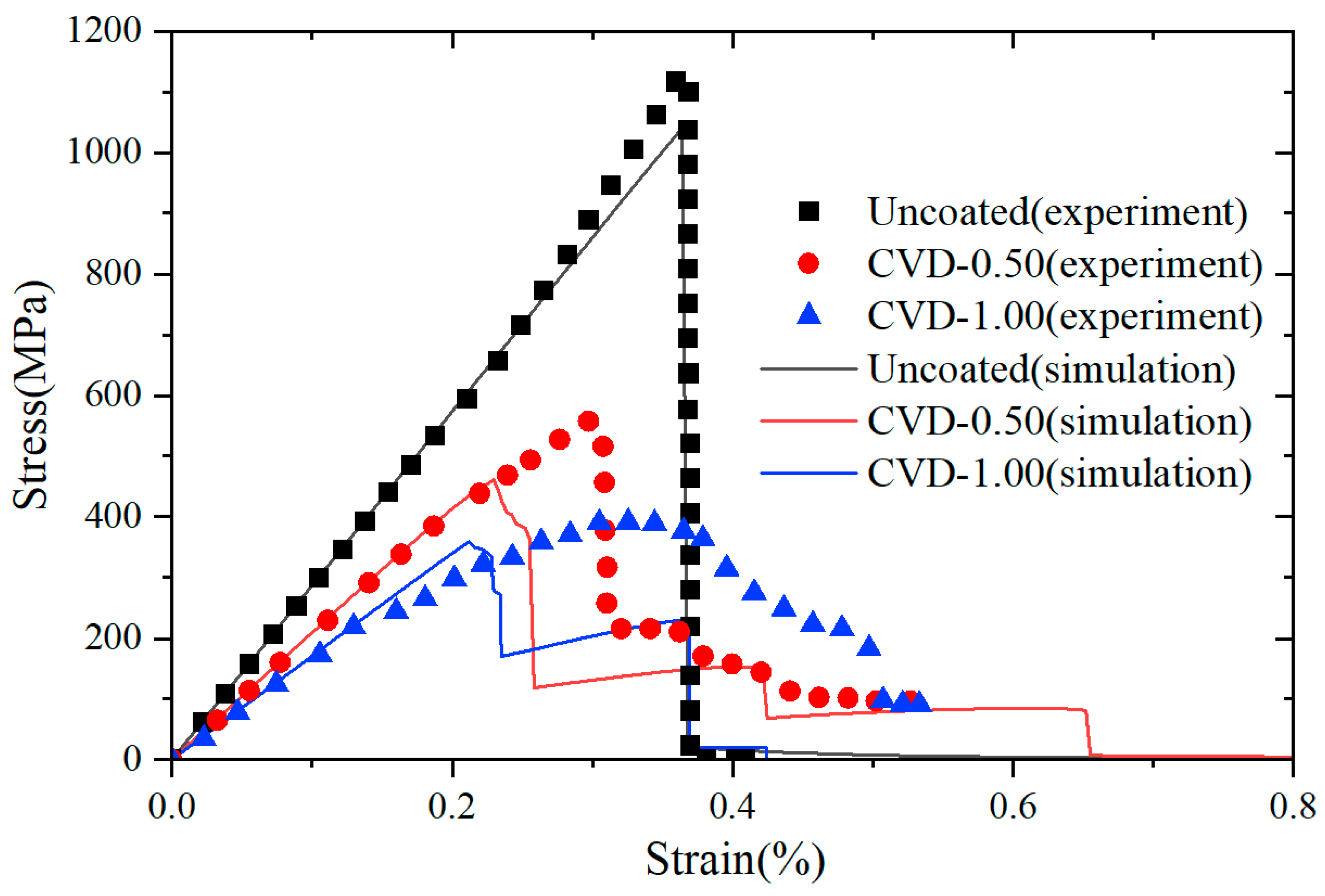
| Model | AT2 | PF-CZM | |||
|---|---|---|---|---|---|
| Type | Linear | Cornelissen | |||
| 2 | 2 | ||||
| −0.5 | 1.3868 | ||||
| 0 | 0.6567 | ||||
| 0.1 | 0.000 | 14.469 | 0.596 |
| 0.5 | 0.000 | 14.469 | 1.192 |
| 1.0 | 0.000 | 14.469 | 1.788 |
| 1.5 | 0.000 | 14.469 | 2.384 |
| 2.0 | 0.000 | 14.469 | 2.979 |
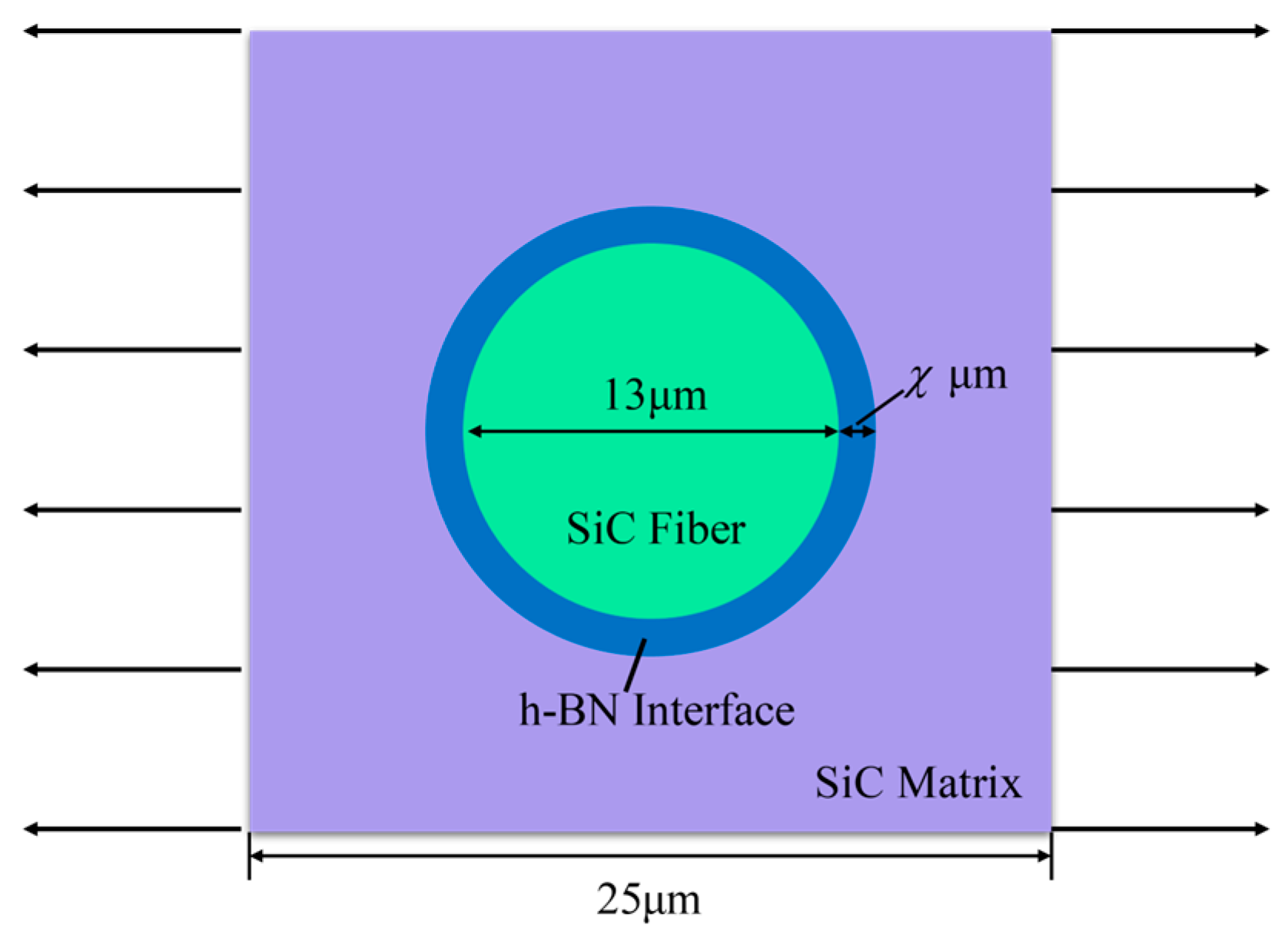
| Material Property | SiC Fiber | SiC Matrix | h-BN Interface |
|---|---|---|---|
| Young’s modulus | |||
| Poisson’s ratio | |||
| Critical energy release rate | |||
| Fracture strength |
| Fiber Volume () | Open Porosity () | Density () | |
|---|---|---|---|
| Uncoated | |||
| CVD-0.50 | |||
| CVD-1.00 |
| Material Property | SiC Fiber [59,61] | SiC Matrix [62] | PyC Interface [63,64] |
|---|---|---|---|
| Young’s modulus | |||
| Poisson’s ratio | |||
| Critical energy release rate | |||
| Fracture strength |
| Real PyC Thickness () | Simulation PyC Thickness () | Experimental Flexural Strength () | Simulation Flexural Strength () | The Relative Error Compared to the Central Value of the Experiment () | |
|---|---|---|---|---|---|
| Uncoated | |||||
| CVD-0.50 | |||||
| CVD-1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Hu, X.; Sun, Z.; Yao, W. Microscopic Phase-Field Modeling with Accurate Interface Thickness Representation: Applied to Ceramic Matrix Composites. Materials 2025, 18, 4496. https://doi.org/10.3390/ma18194496
Wang T, Hu X, Sun Z, Yao W. Microscopic Phase-Field Modeling with Accurate Interface Thickness Representation: Applied to Ceramic Matrix Composites. Materials. 2025; 18(19):4496. https://doi.org/10.3390/ma18194496
Chicago/Turabian StyleWang, Tong, Xiaofei Hu, Zhi Sun, and Weian Yao. 2025. "Microscopic Phase-Field Modeling with Accurate Interface Thickness Representation: Applied to Ceramic Matrix Composites" Materials 18, no. 19: 4496. https://doi.org/10.3390/ma18194496
APA StyleWang, T., Hu, X., Sun, Z., & Yao, W. (2025). Microscopic Phase-Field Modeling with Accurate Interface Thickness Representation: Applied to Ceramic Matrix Composites. Materials, 18(19), 4496. https://doi.org/10.3390/ma18194496







