DFT-Based Analysis on Structural, Electronic and Mechanical Properties of NiCoCr Medium-Entropy Alloy with C/N/O
Highlights
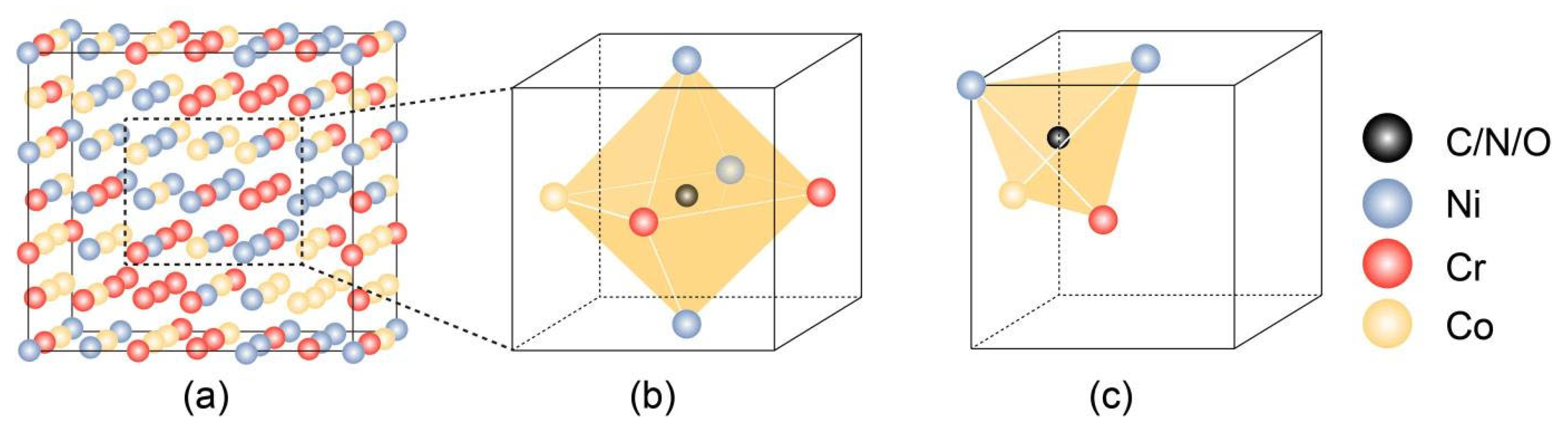
- Nonmetallic C/N/O atom occupies octahedral site of NiCoCr with obvious lattice distortion.
- Enhanced stacking fault energy can be achieved with 1 at% C/N/O doping.
- Improvement of strength–ductility balance is expected by nonmetallic doping through impediment to dislocation glide.
- The improvement effect is predicted to be O>N>C.
Abstract
1. Introduction
2. Calculation Details
2.1. DFT Calculation
2.2. Formation Energy Calculation
2.3. Stacking Fault Energy Calculation
3. Results
3.1. Atomic Distribution of Solid Solution
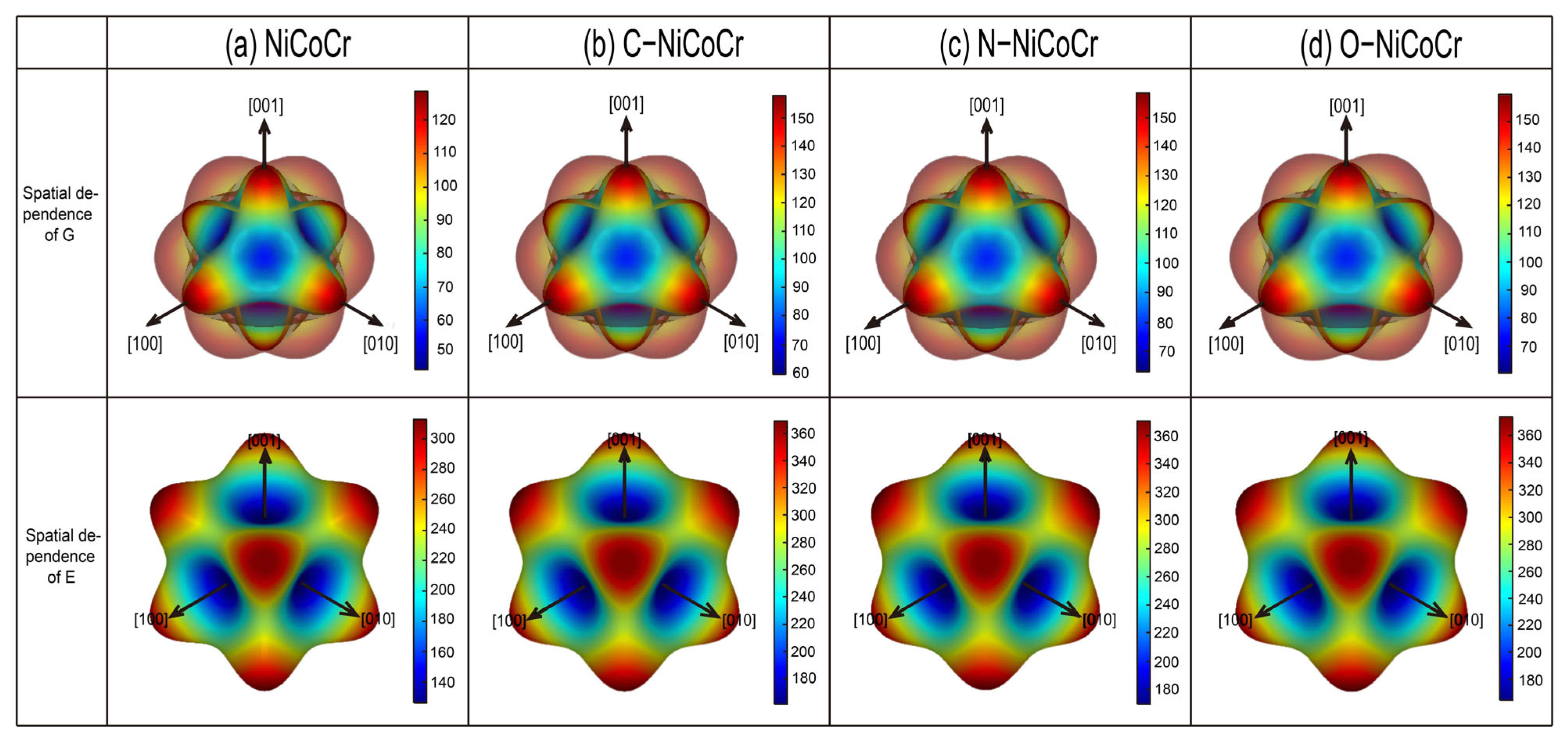
3.2. Elastic Constants
3.3. Stacking Fault Energy
4. Discussion
5. Conclusions
- (1)
- Interstitial site preference and lattice distortion: C and N preferentially occupy octahedral interstitial sites, while O exhibits a higher diffusion rate between octahedral and tetrahedral sites, effectively alleviating stress concentration. The dissolution of these interstitial atoms causes significant lattice distortion, with O causing the most noticeable distortion (16.82%), followed by N (10.84%) and C (9.27%).
- (2)
- Mechanical properties: The introduction of interstitial atoms increases the elastic constants and SFE, indicating an improvement in stiffness and resistance to plastic deformation. O doping leads to the most significant increase in SFE (69 mJ/m2, from −35 mJ/m2 to 34 mJ/m2), followed by N (58 mJ/m2) and C (54 mJ/m2). It optimizes the strength–ductility balance of the alloy by suppressing twinning and promoting dislocation glide.
- (3)
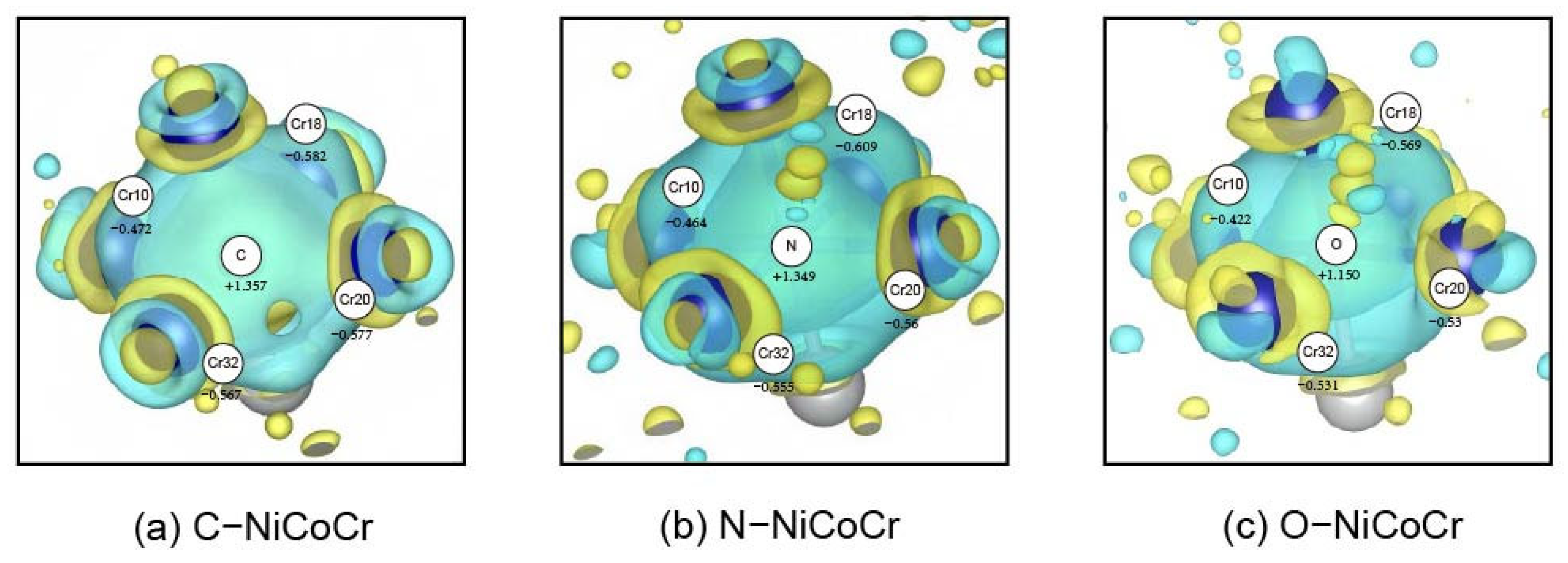
- Electronic interactions: Differential charge density analysis shows that C, N, and O atoms significantly alter the surrounding electronic environment, strengthening the ionic bonds between the solute and metal atoms. C exhibits the strongest directional charge interactions, indicating covalent characteristics, while O shows the weakest interactions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ron, T.; Shirizly, A.; Aghion, E. Additive Manufacturing Technologies of High Entropy Alloys (HEA): Review and Prospects. Materials 2023, 16, 2454. [Google Scholar] [CrossRef]
- Slone, C.; Miao, J.; George, E.; Mills, M. Achieving ultra-high strength and ductility in equiatomic CrCoNi with partially recrystallized microstructures. Acta Mater. 2019, 165, 496–507. [Google Scholar] [CrossRef]
- Zhang, Z.; Sheng, H.; Wang, Z.; Gludovatz, B.; Zhang, Z.; George, E.P.; Yu, Q.; Mao, S.X.; Ritchie, R.O. Dislocation mechanisms and 3D twin architectures generate exceptional strength-ductility-toughness combination in CrCoNi medium-entropy alloy. Nat. Commun. 2017, 8, 14390. [Google Scholar] [CrossRef]
- Gludovatz, B.; Hohenwarter, A.; Catoor, D.; Chang, E.H.; George, E.P.; Ritchie, R.O. A fracture-resistant high-entropy alloy for cryogenic applications. Science 2014, 345, 1153–1158. [Google Scholar] [CrossRef] [PubMed]
- Miao, J.; Li, T.; Li, Q.; Chen, X.; Ren, Z.; Lu, Y. Enhanced Surface Properties of the Al0.65CoCrFeNi High-Entropy Alloy via Laser Remelting. Materials 2023, 16, 1085. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Luo, X.; Ma, L.; Hou, L.; Huang, B.; Hu, R. Study on Microstructure and Properties of WC Particle-Reinforced FeCoCrNi-Matrix High Entropy Alloy Composites. Materials 2023, 16, 7380. [Google Scholar] [CrossRef]
- Ke, C.; Wang, C.; Wang, X. Superior low temperature mechanical properties and microstructure of (NiCoCr)95V5 medium entropy alloy. Intermetallics 2023, 162, 108034. [Google Scholar] [CrossRef]
- Peng, H.; Yi, Y.; Fang, W.; Hu, L.; Baker, I.; Li, L.; Luo, B. Optimization of the microstructure and mechanical properties of electron beam welded high-strength medium-entropy alloy (NiCoCr)94Al3Ti3. Intermetallics 2022, 141, 107439. [Google Scholar] [CrossRef]
- Huang, G.Q.; Chou, T.H.; Liu, S.F.; Xiao, B.; Ju, J.; Gan, J.; Yang, T.; Zhang, P.; Yang, J.X.; Lu, C.Y.; et al. Unveiling the microstructure evolution and mechanical properties of submerged friction stir welded joint of fine-grained NiCoCr medium entropy alloy. Mater. Charact. 2023, 200, 112903. [Google Scholar] [CrossRef]
- Han, B.; Zhang, C.; Feng, K.; Li, Z.; Zhang, X.; Shen, Y.; Wang, X.; Kokawa, H.; Li, R.; Wang, Z.; et al. Additively manufactured high strength and ductility CrCoNi medium entropy alloy with hierarchical microstructure. Mater. Sci. Eng. A 2021, 820, 141545. [Google Scholar] [CrossRef]
- An, Z.; Mao, S.; Liu, Y.; Zhou, H.; Zhai, Y.; Tian, Z.; Liu, C.; Zhang, Z.; Han, X. Hierarchical grain size and nanotwin gradient microstructure for improved mechanical properties of a non-equiatomic CoCrFeMnNi high-entropy alloy. J. Mater. Sci. Technol. 2021, 92, 195–207. [Google Scholar] [CrossRef]
- Du, X.H.; Li, W.P.; Chang, H.T.; Yang, T.; Duan, G.S.; Wu, B.L.; Huang, J.C.; Chen, F.R.; Liu, C.T.; Chuang, W.S.; et al. Dual heterogeneous structures lead to ultrahigh strength and uniform ductility in a Co-Cr-Ni medium-entropy alloy. Nat. Commun. 2020, 11, 2390. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Zhang, M.; Ma, Y.; Dong, W.; Li, R.; Lu, Y.; Zhang, Y.; Yu, P.; Gao, Y.; Li, G. Achieving ultrahigh strength in CoCrNi-based medium-entropy alloys with synergistic strengthening effect. Mater. Sci. Eng. A 2020, 776, 139028. [Google Scholar] [CrossRef]
- Chen, J.-X.; Li, T.; Tan, Y.-Y.; Chen, Y.; Wang, H.-Y.; Dai, L.-H. Tailoring nanoprecipitates to achieve ultrahigh strength (CoCrNi)94.5W3Ta2.5 medium-entropy alloys. Mater. Sci. Eng. A 2024, 892, 146046. [Google Scholar] [CrossRef]
- Liu, C.; Lu, W.; Xia, W.; Du, C.; Rao, Z.; Best, J.P.; Brinckmann, S.; Lu, J.; Gault, B.; Dehm, G.; et al. Massive interstitial solid solution alloys achieve near-theoretical strength. Nat. Commun. 2022, 13, 1102. [Google Scholar] [CrossRef]
- Shang, Y.Y.; Wu, Y.; He, J.Y.; Zhu, X.Y.; Liu, S.F.; Huang, H.L.; An, K.; Chen, Y.; Jiang, S.H.; Wang, H.; et al. Solving the strength-ductility tradeoff in the medium-entropy NiCoCr alloy via interstitial strengthening of carbon. Intermetallics 2019, 106, 77–87. [Google Scholar] [CrossRef]
- Ahn, J.-E.; Kim, Y.-K.; Yang, S.; Lee, K.-A. Interstitial carbon content effect on the microstructure and mechanical properties of additively manufactured NiCoCr medium-entropy alloy. J. Alloys Compd. 2022, 918, 165601. [Google Scholar] [CrossRef]
- Park, S.-Y.; Ahn, J.-E.; Kim, Y.-K.; Ravi, K.; Lee, K.-A. Substructure boundary’s enhancing strain hardening ability in additively manufactured 0.75 at%C doping NiCoCr medium entropy alloy. J. Mater. Res. Technol. 2024, 33, 1087–1096. [Google Scholar] [CrossRef]
- Moravcik, I.; Hadraba, H.; Li, L.; Dlouhy, I.; Raabe, D.; Li, Z. Yield strength increase of a CoCrNi medium entropy alloy by interstitial nitrogen doping at maintained ductility. Scr. Mater. 2020, 178, 391–397. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, H.; Zhang, Y.; Yu, J.; Zhang, X.; Yang, Z.; Hu, T.; Ren, Z. Enhanced strength of N-doped NiCoCr medium-entropy alloy produced by plasma arc melting in nitrogen atmosphere. Mater. Sci. Eng. A 2024, 918, 147474. [Google Scholar] [CrossRef]
- Song, Y.; Li, T.; Fu, X.; Zhang, Z.; Sheng, G.; Zhu, Y.; Lu, Y.; Yu, Q. Dislocation-twin interaction in medium entropy alloy containing a high density of oxygen interstitials. J. Alloys Compd. 2023, 947, 169522. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, B.; Li, T.; Fu, X.; Zou, J.; Chen, Y.; Fang, Y.; Zhang, Q.; Gu, L.; Lu, Y.; et al. Dynamic Homogenization of Internal Strain in Multi-Principal Element Alloy via High-Concentration Doping of Oxygen with Large Mobility. Small Methods 2023, 8, e2300871. [Google Scholar] [CrossRef] [PubMed]
- Pei, Z.; Li, R.; Gao, M.C.; Stocks, G.M. Statistics of the NiCoCr medium-entropy alloy: Novel aspects of an old puzzle. Npj Comput. Mater. 2020, 6, 122. [Google Scholar] [CrossRef]
- Yu, C.-F.; Cheng, H.-C. In-Depth DFT-Based Analysis of the Structural, Mechanical, Thermodynamic, and Electronic Characteristics of CuP2 and Cu3P: Insights into Material Stability and Performance. Metals 2025, 15, 369. [Google Scholar] [CrossRef]
- Skylaris, C.-K. A benchmark for materials simulation. Science 2016, 351, 1394–1395. [Google Scholar] [CrossRef]
- Hu, Y.-J. First-principles approaches and models for crystal defect energetics in metallic alloys. Comput. Mater. Sci. 2023, 216, 111831. [Google Scholar] [CrossRef]
- Shin, D.; Wolverton, C. First-principles density functional calculations for Mg alloys: A tool to aid in alloy development. Scr. Mater. 2010, 63, 680–685. [Google Scholar] [CrossRef]
- Feng, R.; Liaw, P.K.; Gao, M.C.; Widom, M. First-principles prediction of high-entropy-alloy stability. Npj Comput. Mater. 2017, 3, 50. [Google Scholar] [CrossRef]
- Casillas-Trujillo, L.; Jansson, U.; Sahlberg, M.; Ek, G.; Nygård, M.M.; Sørby, M.H.; Hauback, B.C.; Abrikosov, I.A.; Alling, B. Interstitial carbon in bcc HfNbTiVZr high-entropy alloy from first principles. Phys. Rev. Mater. 2020, 4, 123601. [Google Scholar] [CrossRef]
- Aladerah, B.; Obeidat, A.; Aledealat, K. A Computational exploration of the electronic, mechanical, and magnetic properties of Co2A1−xBxAl full heusler alloys (A, B = Cr, Mn, and Fe). Mater. Today Commun. 2024, 38, 108378. [Google Scholar] [CrossRef]
- PA Subramanyam, A.; Azócar Guzmán, A.; Vincent, S.; Hartmaier, A.; Janisch, R. Ab Initio Study of the Combined Effects of Alloying Elements and H on Grain Boundary Cohesion in Ferritic Steels. Metals 2019, 9, 291. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set—ScienceDirect. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.X.; Zhao, S.; Jin, K.; Xue, H.; Velisa, G.; Bei, H.; Huang, R.; Ko, J.Y.P.; Pagan, D.C.; Neuefeind, J.C.; et al. Local Structure and Short-Range Order in a NiCoCr Solid Solution Alloy. Phys. Rev. Lett. 2017, 118, 205501. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Qiu, S.; Jiao, Z.-B. Atomic-scale understanding of interstitial-strengthened high-entropy alloys. Rare Metals 2025, 149, 388–396. [Google Scholar] [CrossRef]
- Akter, R.; Khan, M.; Nobin, N.M.; Ali, S.; Hossain, M.; Rahaman, Z.; Ali, L. Effects of grain boundary and chemical short-range order on mechanical properties of NiCoCr multi-principal element alloys: A molecular dynamics simulations. Mater. Today Commun. 2023, 36, 106630. [Google Scholar] [CrossRef]
- Huang, H.; Li, X.; Dong, Z.; Li, W.; Huang, S.; Meng, D.; Lai, X.; Liu, T.; Zhu, S.; Vitos, L. Critical stress for twinning nucleation in CrCoNi-based medium and high entropy alloys. Acta Mater. 2018, 149, 388–396. [Google Scholar] [CrossRef]
- Zhao, S.; Stocks, G.M.; Zhang, Y. Stacking fault energies of face-centered cubic concentrated solid solution alloys. Acta Mater. 2017, 134, 334–345. [Google Scholar] [CrossRef]
- Moravcik, I.; Zelený, M.; Dlouhy, A.; Hadraba, H.; Moravcikova-Gouvea, L.; Papež, P.; Fikar, O.; Dlouhy, I.; Raabe, D.; Li, Z. Impact of interstitial elements on the stacking fault energy of an equiatomic CoCrNi medium entropy alloy: Theory and experiments. Sci. Technol. Adv. Mater. 2022, 23, 376–392. [Google Scholar] [CrossRef]
- Gu, X.; Liu, C.; Gao, X.; Zhang, K.; Zheng, W.; Chen, C. Solving Strength–Toughness Dilemma in Superhard Transition-Metal Diborides via a Distinct Chemically Tuned Solid Solution Approach. Research 2023, 6, 35. [Google Scholar] [CrossRef]
- Ouadah, O.; Merad, G.; Abdelkader, H.S. Energetic segregation of B, C, N, O at the γ-TiAl/α2-Ti3Al interface via DFT approach. Vacuum 2021, 186, 110045. [Google Scholar] [CrossRef]


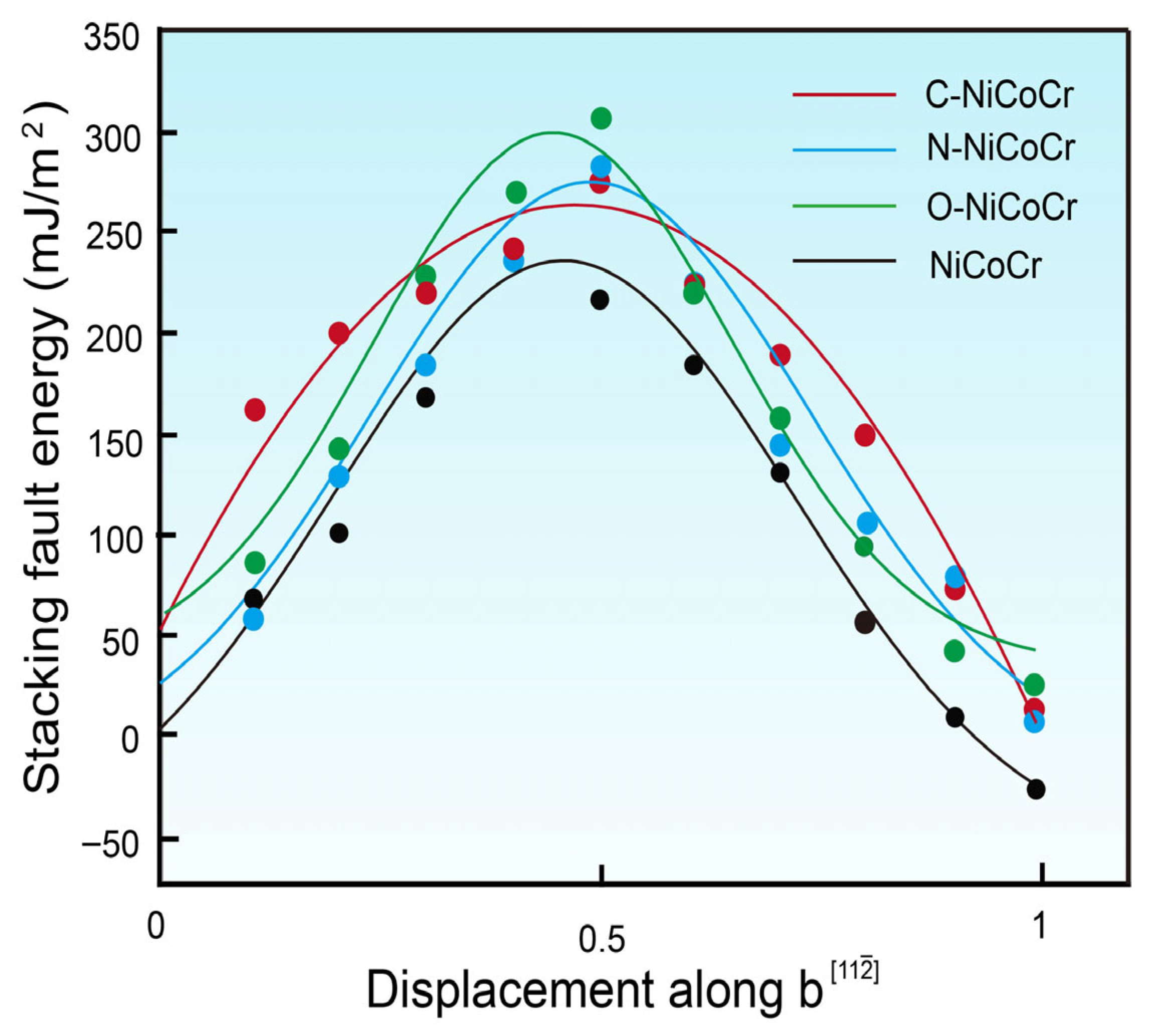

| C11 | C12 | C44 | Pugh’s Ratio | γisf, mJ/m2 | γus, mJ/m2 | |
|---|---|---|---|---|---|---|
| NiCoCr | 245 ± 4 | 155 ± 6 | 129 ± 3 | 2.40 | −35 | 245 |
| (250 calc [37]) | (175 calc [37]) | (100 calc [37]) | (−24 calc [3]) | (264 calc [3]) | ||
| (−26 calc [38]) | (313 calc [38]) | |||||
| (−60 calc [39]) | (269 calc [39]) | |||||
| C-NiCoCr | 264 ± 5 | 146 ± 7 | 158 ± 2 | 2.45 | 19 | 264 |
| (29 calc [40]) | ||||||
| N-NiCoCr | 269 ± 6 | 144 ± 7 | 158 ± 4 | 2.41 | 23 | 278 |
| (42 expt [40]) | ||||||
| O-NiCoCr | 270 ± 7 | 150 ± 6 | 159 ± 4 | 2.40 | 34 | 295 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, S.; Luo, Y.; Yao, Y.; Wang, Y.; Cao, F. DFT-Based Analysis on Structural, Electronic and Mechanical Properties of NiCoCr Medium-Entropy Alloy with C/N/O. Materials 2025, 18, 4494. https://doi.org/10.3390/ma18194494
Cheng S, Luo Y, Yao Y, Wang Y, Cao F. DFT-Based Analysis on Structural, Electronic and Mechanical Properties of NiCoCr Medium-Entropy Alloy with C/N/O. Materials. 2025; 18(19):4494. https://doi.org/10.3390/ma18194494
Chicago/Turabian StyleCheng, Shuqin, Yunfeng Luo, Yufan Yao, Yiren Wang, and Fuhua Cao. 2025. "DFT-Based Analysis on Structural, Electronic and Mechanical Properties of NiCoCr Medium-Entropy Alloy with C/N/O" Materials 18, no. 19: 4494. https://doi.org/10.3390/ma18194494
APA StyleCheng, S., Luo, Y., Yao, Y., Wang, Y., & Cao, F. (2025). DFT-Based Analysis on Structural, Electronic and Mechanical Properties of NiCoCr Medium-Entropy Alloy with C/N/O. Materials, 18(19), 4494. https://doi.org/10.3390/ma18194494







