Abrasive Waterjet Machining of r-GO Infused Mg Fiber Metal Laminates: ANFIS Modelling and Optimization Through Antlion Optimizer Algorithm
Abstract
1. Introduction
2. Materials and Methods
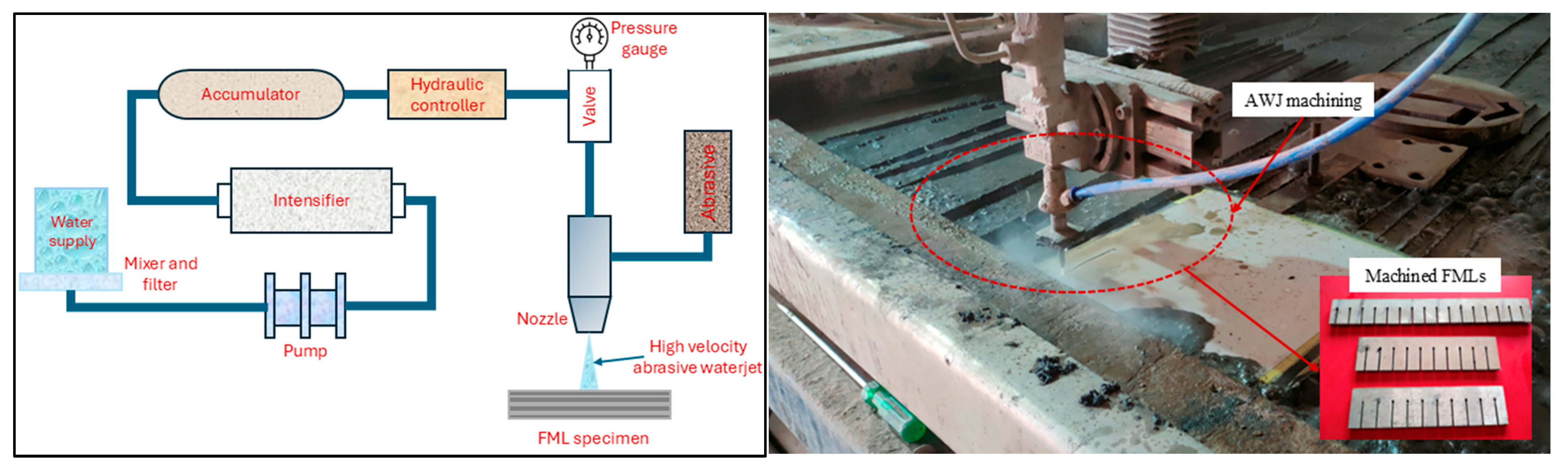
2.1. Experimental Methodology
2.2. Adaptive Neuro Fuzzy Inference System
- Step 1: Data Collection and Pre-processing
- Step 2: Define the Fuzzy Inference System (FIS)
- Step 3: Initialize the ANFIS Structure
- Step 4: Train the ANFIS Model
- Step 5: Validate the Model
- Step 6: Refine the Model
- Step 7: Implement and Interpret the Results
2.3. The Antlion Optimization Algorithm
- Initialization of antlion parameters
- Random walks of ants
- Trapping in antlions’ pits
- Building the trap
- Sliding the ants towards the antlion
- Catching prey and rebuilding the pit
- Elitism
2.4. AWJ Cutting Experiments of Mg FMLs
3. Result and Discussions
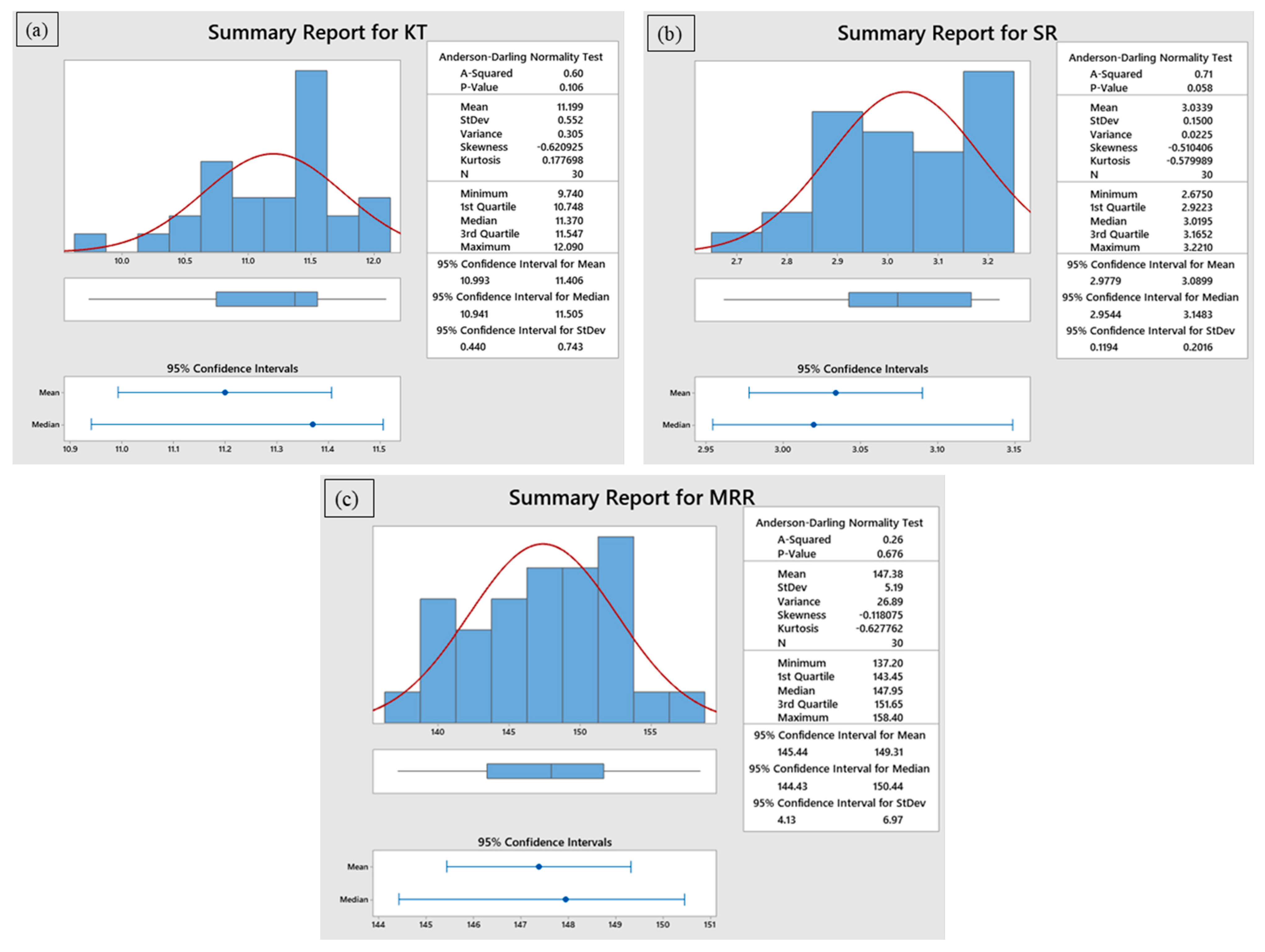
3.1. Statistical Analysis of Regression Models
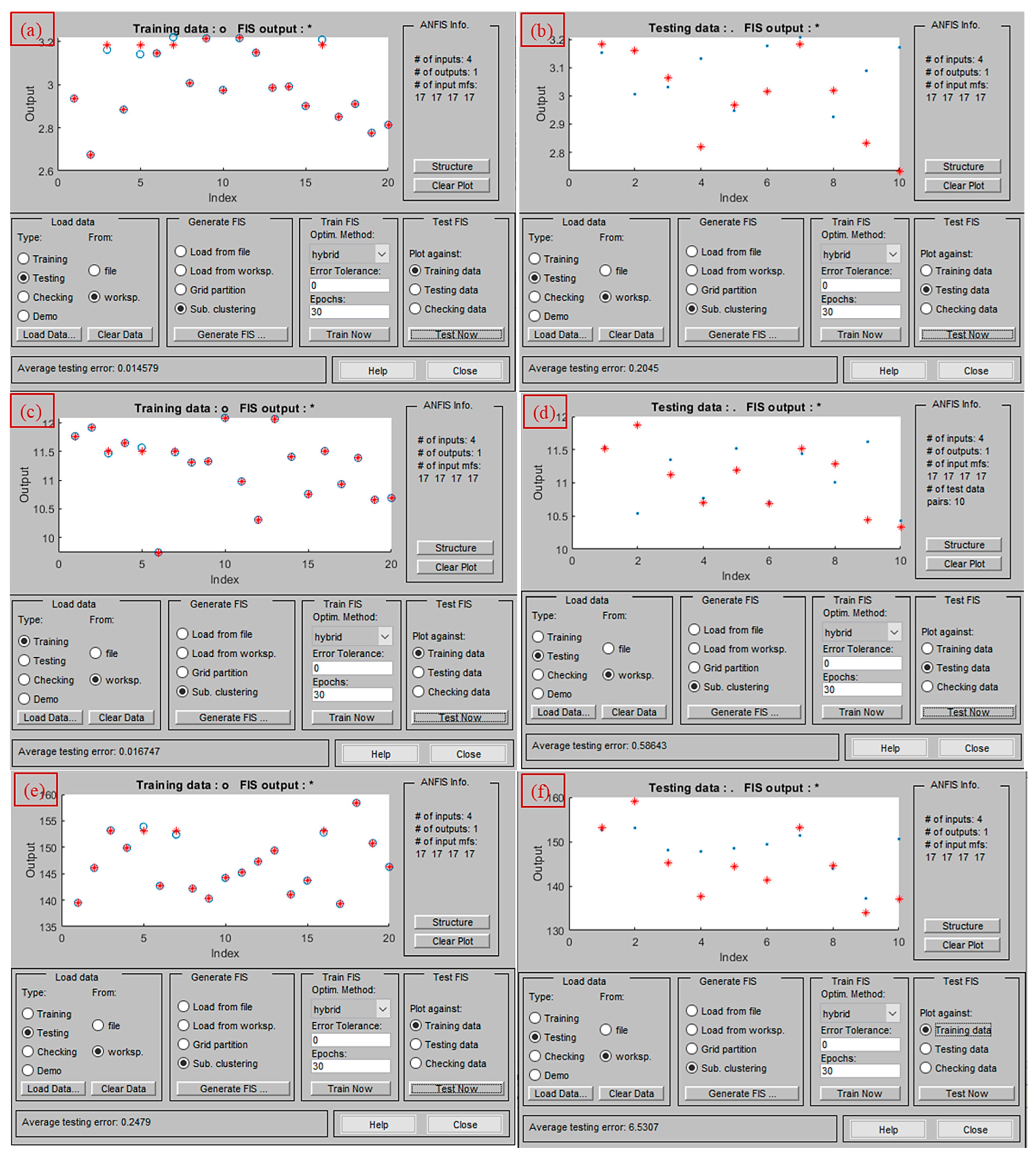
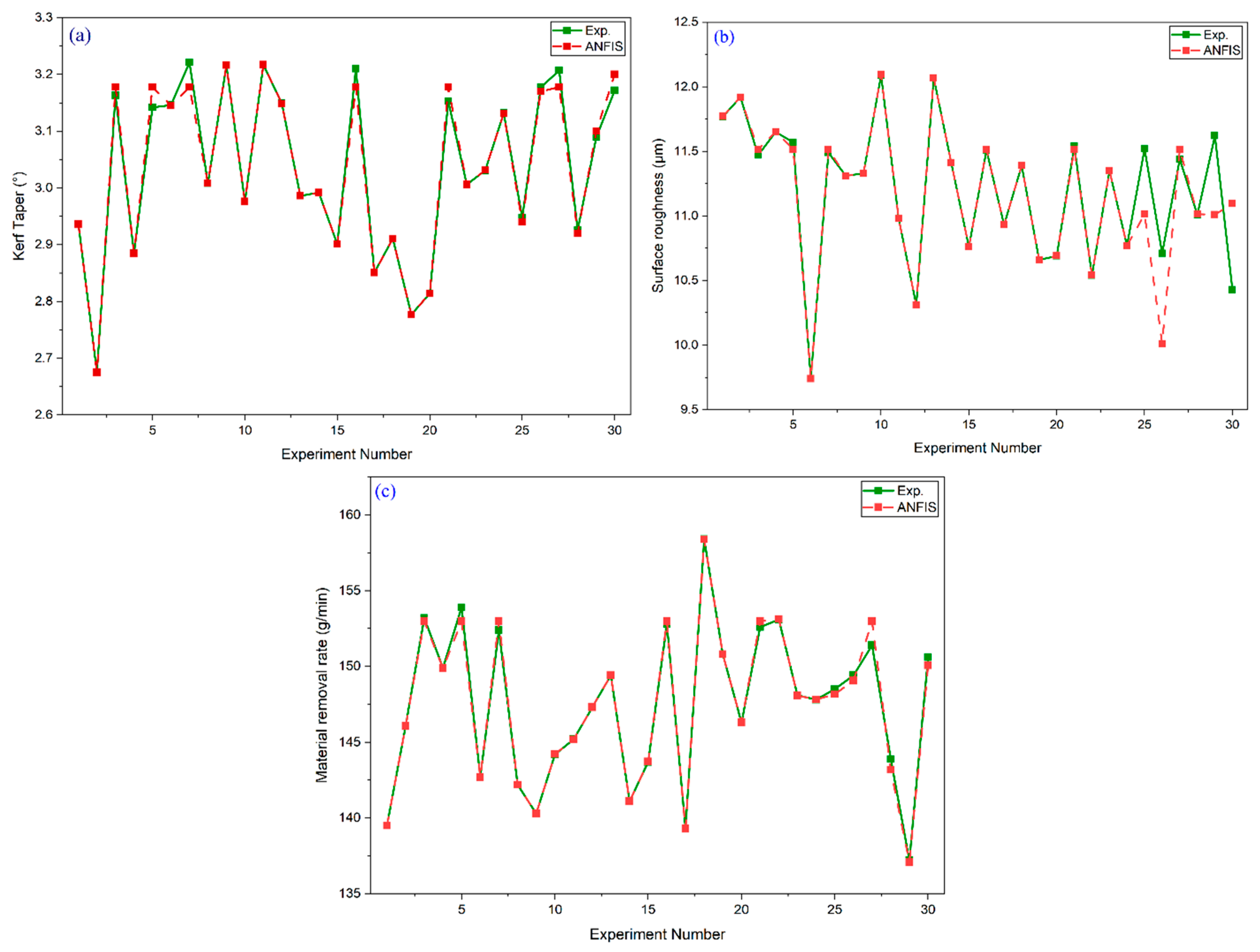
3.2. ANFIS Modeling of AWJ Performance Characteristics
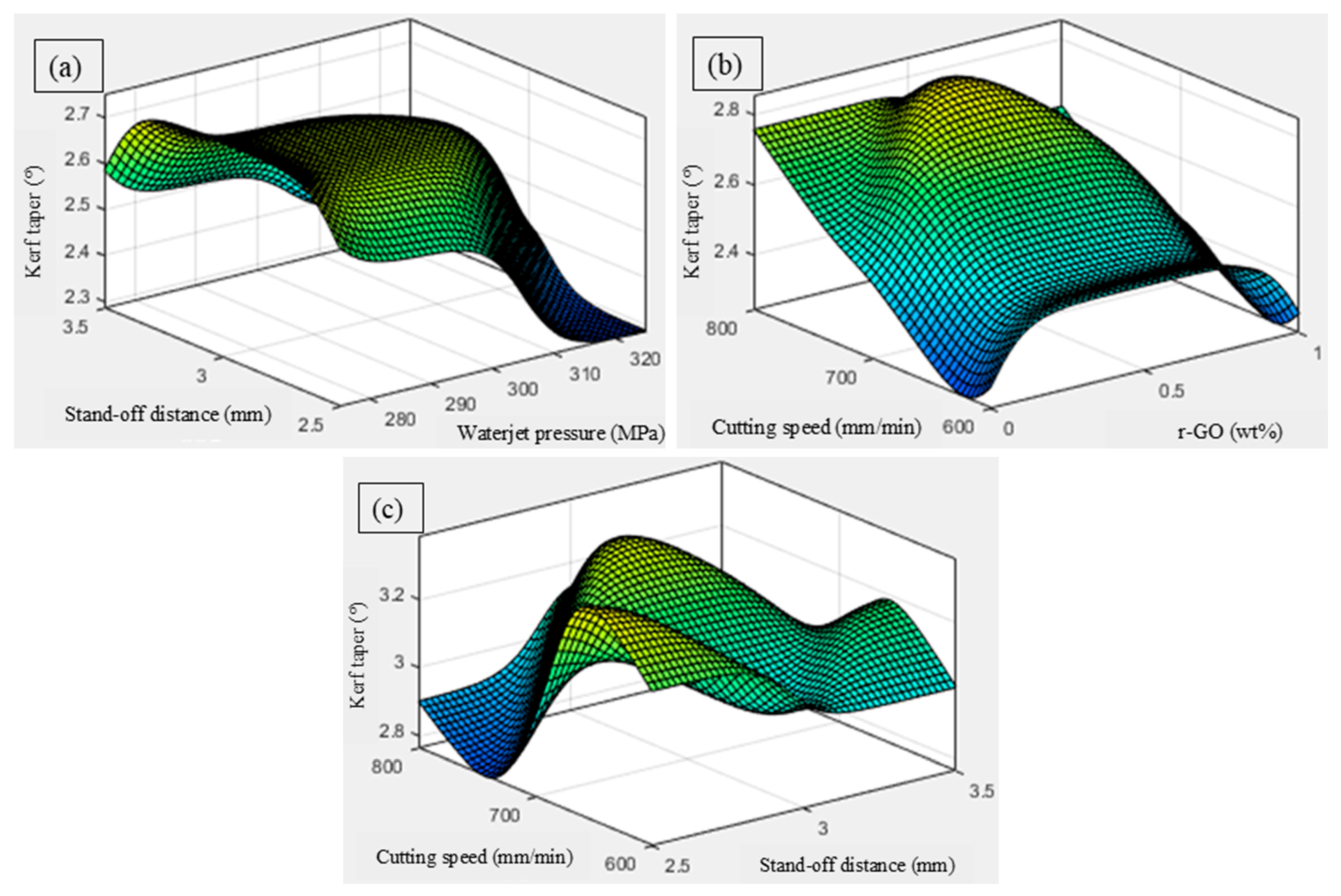
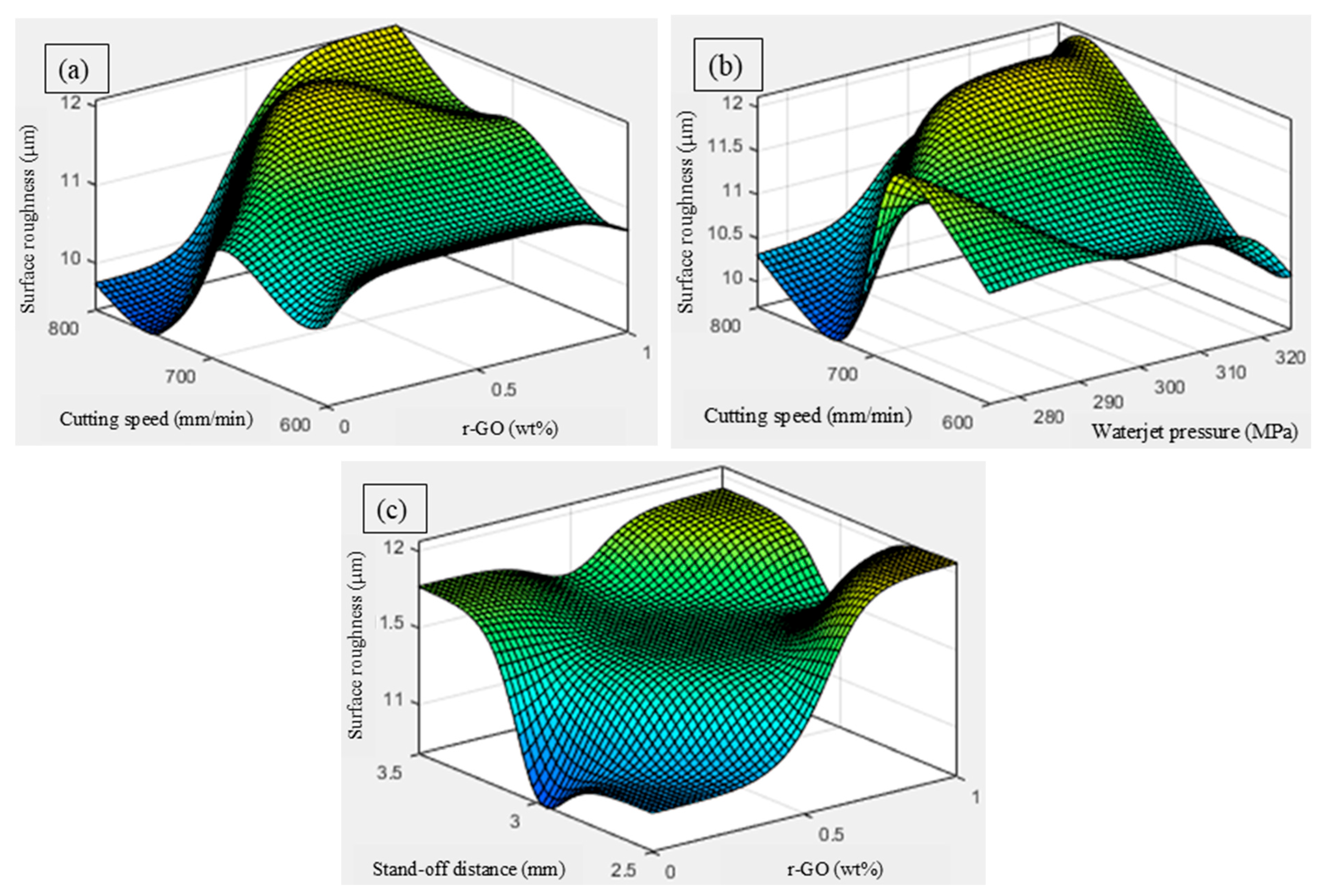
3.3. Influence of AWJ Cutting Parameters on the Response Characteristics
- Influence on Kerf Taper (Kt)
- Influence on Surface Roughness (Ra)
- Influence on Material Removal Rate (MRR)
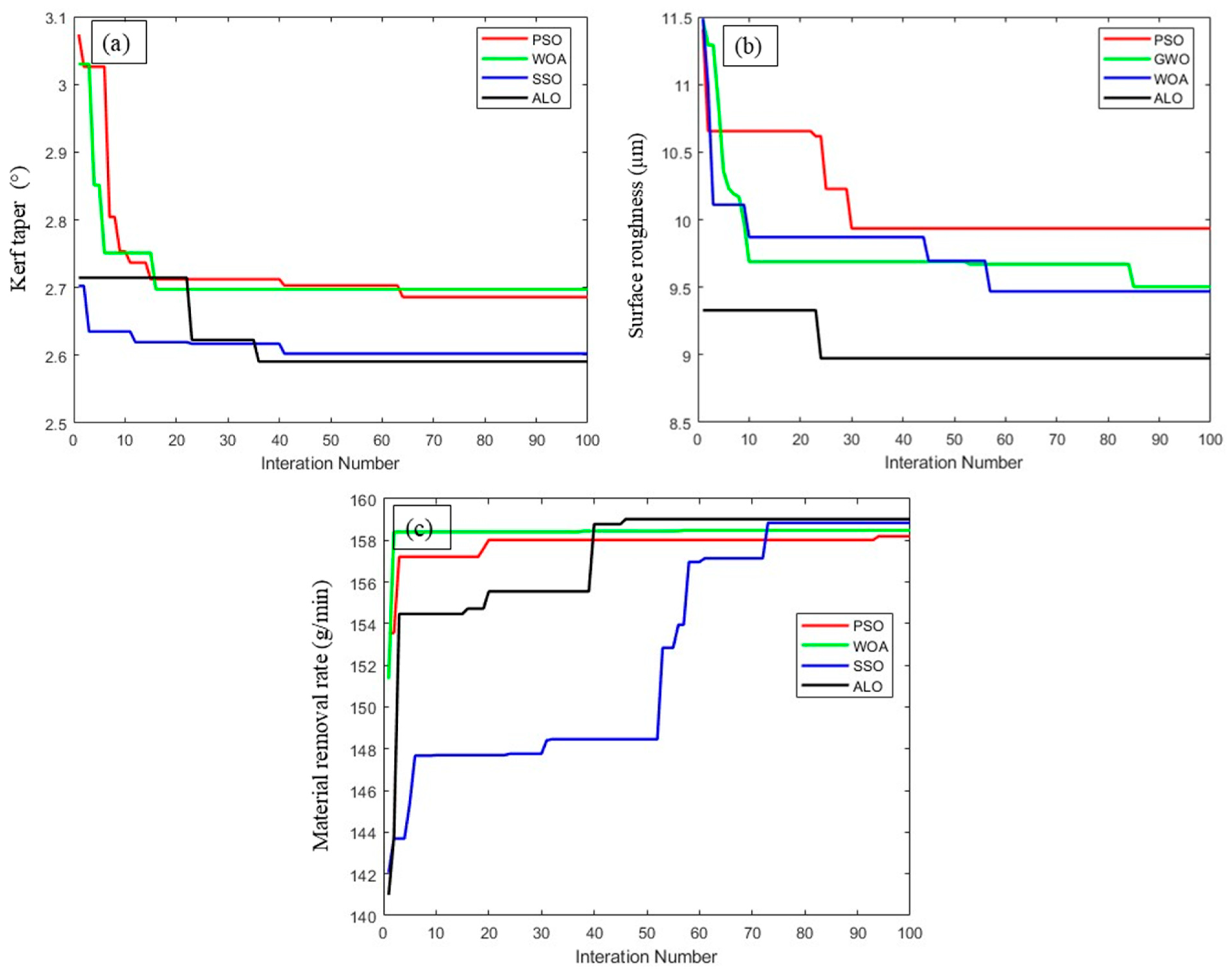
3.4. Multi-Response Optimization of AWJ Cutting Parameters Through ALO
4. Conclusions
- The DFO-assisted ANFIS approach successfully modeled the nonlinear relationships between process parameters and output characteristics, achieving consistently low RMSE and MAPE values with close alignment to experimental data.
- Each performance measure required distinct ANFIS parameter settings: Kt modeling was optimal at a cluster radius of 0.4074, Ra at 0.2221, and MRR at 0.4258, highlighting variation in response sensitivity.
- ANOVA indicated that inclusion of r-GO in the FMLs and waterjet pressure most strongly influenced Kt and MRR, whereas waterjet pressure and traverse speed were dominant for Ra.
- Comparative analysis of metaheuristic optimizers confirmed ALO’s superior convergence behavior, stability, and multi-response performance index. The optimal cutting conditions determined by ALO are 325 MPa waterjet pressure, 2.5 mm stand-off distance, 800 mm/min traverse speed, and 0.00602 wt% r-GO, which yielded minimal kerf taper (2.595°), improved surface quality (8.9897 µm), and a competitive material removal rate (138.13 g/min).
- The hybrid ANFIS–ALO methodology offers a reliable and adaptable framework for process optimization in AWJM, with promising applicability to other composite machining scenarios.
- The results of this study demonstrate that AWJM is a highly suitable process for machining r-GO-infused Mg-based FMLs due to its ability to produce burr-free cuts without thermal damage or delamination. This makes it advantageous for manufacturing high-performance lightweight components in sectors such as aerospace and automotive, where dimensional accuracy and structural integrity are critical.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, Z.; Wang, H.; Luo, J.; Li, N. A Review on Forming Technologies of Fibre Metal Laminates. Int. J. Lightweight Mater. Manuf. 2021, 4, 110–126. [Google Scholar] [CrossRef]
- Pai, A.; Rodriguez-Millan, M.; Kini, C.R.; Mallya, R.; Bekal, C.; Yeshwant Nayak, S.; Shenoy, S.B. Fiber Metal Laminates for High Strain Rate Applications with Layerwise Shock Impedance Tuning. Sci. Rep. 2023, 13, 18474. [Google Scholar] [CrossRef]
- Ghiotti, A.; Bruschi, S.; Kain, M.; Lizzul, L.; Simonetto, E.; Tosello, G. Simultaneous Bonding and Forming of Mg Fibre Metal Laminates at High Temperature. J. Manuf. Process. 2021, 72, 105–114. [Google Scholar] [CrossRef]
- Priya, I.I.M.; Arul Jeya Kumar, A. Tribo-Mechanical Analysis of Magnesium-Based Fibre Metal Laminates for Structural Applications. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2022, 237, 611–620. [Google Scholar] [CrossRef]
- Megahed, M.; Abd El-Baky, M.A.; Alsaeedy, A.M.; Alshorbagy, A.E. An Experimental Investigation on the Effect of Incorporation of Different Nanofillers on the Mechanical Characterization of Fiber Metal Laminate. Compos. B Eng. 2019, 176, 107277. [Google Scholar] [CrossRef]
- Vijayan, M.; Selladurai, V.; Balaganesan, G.; Suganya Priyadharshini, G. Comprehensive Characterization of AA 2024T3 Fiber Metal Laminate with Nanosilica-Reinforced Epoxy Based Polymeric Composite Panel for Lightweight Applications. Polym. Compos. 2022, 43, 8274–8296. [Google Scholar] [CrossRef]
- Giasin, K.; Atif, M.; Ma, Y.; Jiang, C.; Koklu, U.; Sinke, J. Machining GLARE Fibre Metal Laminates: A Comparative Study on Drilling Effect between Conventional and Ultrasonic-Assisted Drilling. Int. J. Adv. Manuf. Technol. 2022, 123, 3657–3672. [Google Scholar] [CrossRef]
- Karthikeyan, M.; Pandian, S.M.V.; Vijayakumar, R. Investigation on Metal Hybrid Fibres Laminate (MHFL) in Hybrid Machining. J. Manuf. Process. 2023, 101, 835–853. [Google Scholar] [CrossRef]
- Selvam, R.; Subramanian, M.; Diviya, M.; Khan, T.M.Y.; Baig, R.U.; Ahamad, T.; Kalam, M.d.A.; Razak, A.; Monish, N.; Wodajo, A.W. Effect of Silicon Carbide on Kerf Convergence and Irregularity of the Surface during Abrasive Water Jet Machining of Fiber-Metal Hybrid Composites. Sci. Rep. 2023, 13, 17391. [Google Scholar] [CrossRef]
- Kartal, F. Abrasive Water Jet Machining of Carbon Fiber-Reinforced PLA Composites: Optimization of Machinability and Surface Integrity for High-Precision Applications. Polymers 2025, 17, 445. [Google Scholar] [CrossRef]
- Sharun, V.; Ronald, B.A. Optimization of Process Parameters in Abrasive Water Jet Machining of Austempered Ductile Iron (ADI). J. Mater. Eng. Perform. 2024, 33, 4867–4882. [Google Scholar] [CrossRef]
- Tripathi, D.R.; Vachhani, K.H.; Bandhu, D.; Kumari, S.; Kumar, V.R.; Abhishek, K. Experimental Investigation and Optimization of Abrasive Waterjet Machining Parameters for GFRP Composites Using Metaphor-Less Algorithms. Mater. Manuf. Process. 2021, 36, 803–813. [Google Scholar] [CrossRef]
- Devaraj, R.; Mahalingam, S.K.; Esakki, B.; Astarita, A.; Mirjalili, S. A Hybrid GA-ANFIS and F-Race Tuned Harmony Search Algorithm for Multi-Response Optimization of Non-Traditional Machining Process. Expert Syst. Appl. 2022, 199, 116965. [Google Scholar] [CrossRef]
- Siva Kumar, M.; Rajamani, D.; El-Sherbeeny, A.M.; Balasubramanian, E.; Karthik, K.; Hussein, H.M.A.; Astarita, A. Intelligent Modeling and Multi-Response Optimization of AWJC on Fiber Intermetallic Laminates through a Hybrid ANFIS-Salp Swarm Algorithm. Materials 2022, 15, 7216. [Google Scholar] [CrossRef] [PubMed]
- Duranoğlu, D.; Sinan Altın, E.; Küçük, İ. Optimization of Adaptive Neuro–Fuzzy Inference System (ANFIS) Parameters via Box-Behnken Experimental Design Approach: The Prediction of Chromium Adsorption. Heliyon 2024, 10, e25813. [Google Scholar] [CrossRef]
- Singh, D.P.; Mishra, S.; Porwal, R.K. Parametric Analysis through ANFIS Modelling and Optimization of Micro-Hole Machining in Super Duplex Stainless Steel by Die-Sinking EDM. Adv. Mater. Process. Technol. 2023, 9, 1885–1902. [Google Scholar] [CrossRef]
- Rajamani, D.; Siva Kumar, M.; Balasubramanian, E.; Tamilarasan, A. Nd: YAG Laser Cutting of Hastelloy C276: ANFIS Modeling and Optimization through WOA. Mater. Manuf. Process. 2021, 36, 1746–1760. [Google Scholar] [CrossRef]
- Eaysin, A.; Kabir, S.; Gunister, E.; Jahan, N.; Hamza, A.; Zinnah, M.A.; Rashid, A. Bin Process Parameter Optimization of Laser Beam Machining for AISI -P20 Mold Steel Using ANFIS Method. Results Surf. Interfaces 2025, 18, 100357. [Google Scholar] [CrossRef]
- Denic, N.; Cirkovic, B.; Stevanovic, V.; Stevanovic, M.; Petković, D. ANFIS Estimation of Optimal Parameters for Dross Formation in Plasma Arc Cutting Process. Adv. Eng. Softw. 2022, 173, 103270. [Google Scholar] [CrossRef]
- Siva Kumar, M.; Rajamani, D.; Abouel Nasr, E.; Balasubramanian, E.; Mohamed, H.; Astarita, A. A Hybrid Approach of ANFIS—Artificial Bee Colony Algorithm for Intelligent Modeling and Optimization of Plasma Arc Cutting on Monel™ 400 Alloy. Materials 2021, 14, 6373. [Google Scholar] [CrossRef]
- Abdelaoui, F.Z.E.; Jabri, A.; Barkany, A.E. Optimization Techniques for Energy Efficiency in Machining Processes—A Review. Int. J. Adv. Manuf. Technol. 2023, 125, 2967–3001. [Google Scholar] [CrossRef]
- Song, J.; Wang, B.; Hao, X. Optimization Algorithms and Their Applications and Prospects in Manufacturing Engineering. Materials 2024, 17, 4093. [Google Scholar] [CrossRef]
- Abualigah, L.; Shehab, M.; Alshinwan, M.; Mirjalili, S.; Elaziz, M.A. Ant Lion Optimizer: A Comprehensive Survey of Its Variants and Applications. Arch. Comput. Methods Eng. 2021, 28, 1397–1416. [Google Scholar] [CrossRef]
- El Bakrawy, L.M.; Cifci, M.A.; Kausar, S.; Hussain, S.; Islam, M.d.A.; Alatas, B.; Desuky, A.S. A Modified Ant Lion Optimization Method and Its Application for Instance Reduction Problem in Balanced and Imbalanced Data. Axioms 2022, 11, 95. [Google Scholar] [CrossRef]
- Vu Hong Son, P.; Soulisa, F.V. A Hybrid Ant Lion Optimizer (ALO) Algorithm for Construction Site Layout Optimization. J. Soft Comput. Civ. Eng. 2023, 7, 50–71. [Google Scholar] [CrossRef]
- Jabari, M.; Izci, D.; Ekinci, S.; Bajaj, M.; Blazek, V.; Prokop, L. Hybrid Adaptive Ant Lion Optimization with Traditional Controllers for Driving and Controlling Switched Reluctance Motors to Enhance Performance. Sci. Rep. 2025, 15, 12898. [Google Scholar] [CrossRef]
- Wen, C.; Li, J.; Hou, B.; Liao, Y.; Fan, Y.; Guo, H.; Wu, J.; Zhao, X.; Liang, Y.; Liang, K. Multi-Objective Ant Lion Optimization for Parameter Optimization of Wireless Power Transfer Systems. AIP Adv. 2023, 13, 115116. [Google Scholar] [CrossRef]
- Fnides, M.; Amroune, S.; Slamani, M.; Elhadi, A.; Arslane, M.; Jawaid, M. Optimization of Manufacturing Parameters for Minimizing Vibrations and Surface Roughness in Milling Using Box–Behnken Design. J. Vib. Eng. Technol. 2025, 13, 22. [Google Scholar] [CrossRef]
- Sagias, V.D.; Zacharia, P.; Tempeloudis, A.; Stergiou, C. Adaptive Neuro-Fuzzy Inference System-Based Predictive Modeling of Mechanical Properties in Additive Manufacturing. Machines 2024, 12, 523. [Google Scholar] [CrossRef]
- AbouElaz, M.A.; Alhasnawi, B.N.; Sedhom, B.E.; Bureš, V. ANFIS-Optimized Control for Resilient and Efficient Supply Chain Performance in Smart Manufacturing. Results Eng. 2025, 25, 104262. [Google Scholar] [CrossRef]
- Mirjalili, S. The Ant Lion Optimizer. Adv. Eng. Softw. 2015, 83, 80–98. [Google Scholar] [CrossRef]
- Rajamani, D.; Balasubramanian, E.; Murugan, A.; Tamilarasan, A. AWJC of NiTi Interleaved R-GO Embedded Carbon/Aramid Fibre Intermetallic Laminates: Experimental Investigations and Optimization through BMOA. Mater. Manuf. Process. 2023, 38, 1144–1158. [Google Scholar] [CrossRef]
- Kumar, D.; Gururaja, S. Abrasive Waterjet Machining of Ti/CFRP/Ti Laminate and Multi-Objective Optimization of the Process Parameters Using Response Surface Methodology. J. Compos. Mater. 2019, 54, 1741–1759. [Google Scholar] [CrossRef]
- Naresh Babu, M.; Muthukrishnan, N. Investigation on Surface Roughness in Abrasive Water-Jet Machining by the Response Surface Method. Mater. Manuf. Process. 2014, 29, 1422–1428. [Google Scholar] [CrossRef]
- Rajesh, M.; Rajkumar, K.; Annamalai, V.E. Abrasive Water Jet Machining on Ti Metal-Interleaved Basalt-Flax Fiber Laminate. Mater. Manuf. Process. 2021, 36, 329–340. [Google Scholar] [CrossRef]
- Ghasemian Fard, M.; Nag, A.; Petru, J.; Hloch, S. Towards sustainable precision: A review of water jet meso and micromachining. Results in Engineering 2025, 27, 106447. [Google Scholar] [CrossRef]
- Rajamani, D.; Balasubramanian, E.; Dilli Babu, G.; Ananthakumar, K. Experimental Investigations on High Precision Abrasive Waterjet Cutting of Natural Fibre Reinforced Nano Clay Filled Green Composites. J. Ind. Text. 2020, 51, 3786S–3810S. [Google Scholar] [CrossRef]
- Palleda, M. A Study of Taper Angles and Material Removal Rates of Drilled Holes in the Abrasive Water Jet Machining Process. J. Mater. Process. Technol. 2007, 189, 292–295. [Google Scholar] [CrossRef]
- Sathees Kumar, S.; Isaac Premkumar, I.J.; Muthalagu, R.; Vijayakumar, S.; Pradeep, A.; Naga Swapna Sri, M. Examination of Abrasive water jet machining for Al hybrid composites using RSM-Central composite design. Interactions 2024, 245, 220. [Google Scholar] [CrossRef]
- Karthikeyan, R.; Madhu, S.; Geo Varuvel, E.; Pethuthraj, M. Influence of brown algae filler and process parameters on the surface roughness and MRR of jute fiber polymeric composite machined by abrasive water jet. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2024. [Google Scholar] [CrossRef]


| Exp. No | Input Parameters | Response Characteristics | |||||
|---|---|---|---|---|---|---|---|
| r-GO (wt%) | Waterjet Pressure (MPa) | Stand-Off Distance (mm) | Cutting Speed (mm/min) | Surface Roughness (µm) | Kerf Taper (°) | Material Removal Rate (g/min) | |
| 1 | 0 | 275 | 3 | 700 | 10.71 | 3.177 | 149.4 |
| 2 | 1 | 275 | 3 | 700 | 11.52 | 2.948 | 148.5 |
| 3 | 0 | 325 | 3 | 700 | 10.69 | 2.814 | 146.3 |
| 4 | 1 | 325 | 3 | 700 | 11.39 | 2.911 | 158.4 |
| 5 | 0.5 | 300 | 2.5 | 600 | 11.33 | 3.216 | 140.3 |
| 6 | 0.5 | 300 | 3.5 | 600 | 11.31 | 3.008 | 142.2 |
| 7 | 0.5 | 300 | 2.5 | 800 | 10.76 | 2.901 | 143.7 |
| 8 | 0.5 | 300 | 3.5 | 800 | 11.41 | 2.992 | 141.1 |
| 9 | 0 | 300 | 3 | 600 | 11.62 | 3.089 | 137.2 |
| 10 | 1 | 300 | 3 | 600 | 10.77 | 3.132 | 147.8 |
| 11 | 0 | 300 | 3 | 800 | 9.74 | 3.146 | 142.7 |
| 12 | 1 | 300 | 3 | 800 | 12.09 | 2.976 | 144.2 |
| 13 | 0.5 | 275 | 2.5 | 700 | 11.35 | 3.031 | 148.1 |
| 14 | 0.5 | 325 | 2.5 | 700 | 10.66 | 2.777 | 150.8 |
| 15 | 0.5 | 275 | 3.5 | 700 | 11.01 | 2.926 | 143.9 |
| 16 | 0.5 | 325 | 3.5 | 700 | 11.65 | 2.885 | 149.9 |
| 17 | 0 | 300 | 2.5 | 700 | 10.93 | 2.851 | 139.3 |
| 18 | 1 | 300 | 2.5 | 700 | 12.07 | 2.986 | 149.4 |
| 19 | 0 | 300 | 3.5 | 700 | 11.77 | 2.936 | 139.5 |
| 20 | 1 | 300 | 3.5 | 700 | 11.92 | 2.675 | 146.1 |
| 21 | 0.5 | 275 | 3 | 600 | 10.98 | 3.217 | 145.2 |
| 22 | 0.5 | 325 | 3 | 600 | 10.43 | 3.172 | 150.6 |
| 23 | 0.5 | 275 | 3 | 800 | 10.31 | 3.149 | 147.3 |
| 24 | 0.5 | 325 | 3 | 800 | 10.54 | 3.006 | 153.1 |
| 25 | 0.5 | 300 | 3 | 700 | 11.54 | 3.153 | 152.6 |
| 26 | 0.5 | 300 | 3 | 700 | 11.51 | 3.21 | 152.8 |
| 27 | 0.5 | 300 | 3 | 700 | 11.47 | 3.163 | 153.2 |
| 28 | 0.5 | 300 | 3 | 700 | 11.49 | 3.221 | 152.4 |
| 29 | 0.5 | 300 | 3 | 700 | 11.57 | 3.142 | 153.9 |
| 30 | 0.5 | 300 | 3 | 700 | 11.44 | 3.207 | 151.4 |
| Source | Sum of Squares | DF | Mean Square | F | Prob. > F |
|---|---|---|---|---|---|
| Kt | |||||
| Model | 8.81 | 12 | 0.7339 | 298.81 | <0.0001 |
| A—r-GO | 1.54 | 1 | 1.54 | 627.37 | <0.0001 |
| B—Waterjet pressure | 0.0225 | 1 | 0.0225 | 9.17 | 0.0076 |
| C—Stand-off distance | 0.3234 | 1 | 0.3234 | 131.68 | <0.0001 |
| D—Cutting speed | 0.2107 | 1 | 0.2107 | 85.78 | <0.0001 |
| Residual | 0.0418 | 17 | 0.0025 | ||
| Lack of fit | 0.0306 | 12 | 0.0026 | 1.15 | 0.4726 |
| Pure error | 0.0111 | 5 | 0.0022 | ||
| Total | 8.85 | 29 | |||
| R2 | 99.53% | Adj. R2 | 99.2% | ||
| Ra | |||||
| Model | 0.6251 | 13 | 0.0481 | 28.32 | <0.0001 |
| A—r-GO | 0.0124 | 1 | 0.0124 | 7.27 | 0.0159 |
| B—Waterjet pressure | 0.065 | 1 | 0.065 | 38.27 | <0.0001 |
| C—Stand-off distance | 0.0096 | 1 | 0.0096 | 5.67 | 0.03 |
| D—Cutting speed | 0.0367 | 1 | 0.0367 | 21.64 | 0.0003 |
| Residual | 0.0272 | 16 | 0.0017 | ||
| Lack of fit | 0.0214 | 11 | 0.0019 | 1.7 | 0.2903 |
| Pure error | 0.0057 | 5 | 0.0011 | ||
| Total | 0.6522 | 29 | |||
| R2 | 95.83% | Adj. R2 | 92.45% | ||
| MRR | |||||
| Model | 757.47 | 11 | 68.86 | 55.77 | <0.0001 |
| A—r-GO | 133.33 | 1 | 133.33 | 107.99 | <0.0001 |
| B—Waterjet pressure | 59.41 | 1 | 59.41 | 48.12 | <0.0001 |
| C—Stand-off distance | 6.6 | 1 | 6.6 | 5.35 | 0.0328 |
| D—Cutting speed | 6.45 | 1 | 6.45 | 5.23 | 0.0346 |
| Residual | 22.22 | 18 | 1.23 | ||
| Lack of fit | 18.74 | 13 | 1.44 | 2.07 | 0.2178 |
| Pure error | 3.49 | 5 | 0.6977 | ||
| Total | 779.69 | 29 | |||
| R2 | 97.15% | Adj. R2 | 95.41% |
| ANFIS Parameters | Representation | Range |
|---|---|---|
| RADII | Four input parameters and a response value (either kt or Ra or MRR) | 0.1 to 0.5 |
| Quash factor | Used to multiply with RADII values | 2 to 3 |
| % of data for training ANFIS model | Number of experiments | 60% to 85% |
| Parameters | Value/Equation |
|---|---|
| Number of dragonflies (nd) | 100 |
| Number of iterations (nitr) | 100 |
| Inertia wt. (w) (wmax = 0.8 and wmin = 0.2) | |
| Separation wt. | |
| Alignment wt. | |
| Cohesion wt. | |
| Food factor | |
| Enemy factor | |
| Achieve size | 100 |
| RADII Value | %Testing Data | Quash Factor | TError | CError | RMSE | MAPE | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| r-GO | WP | SOD | CS | KT/Ra/MRR | ||||||
| 0.2960 | 0.2627 | 0.4509 | 0.3421 | 0.4074 | 0.7895 | 2.5210 | 0.0145 | 0.204 | 0.0151 | 0.2563 |
| 0.3906 | 0.4137 | 0.2894 | 0.1424 | 0.2221 | 0.7856 | 2.7530 | 0.0167 | 0.586 | 0.2288 | 0.8238 |
| 0.2334 | 0.4921 | 0.3187 | 0.4939 | 0.4258 | 0.7904 | 2.2142 | 0.2479 | 6.530 | 0.4064 | 0.1364 |
| Algorithm | Algorithm Parameters | Range/Value of Parameters |
|---|---|---|
| PSO | Learning factors (C1 and C2) | 2 and 2 |
| Inertia weight (ω) | 0.6 | |
| Particle size (N) | 30 | |
| No. of iterations (nitr) | 100 | |
| SSO | C1-coefficient to exploration and exploitation | |
| C2 and C3 | Random values between 0 and 1 | |
| No. of salps (N) | 30 | |
| No. of iterations (nitr) | 100 | |
| WOA | Number of whales (i = 1, 2, 3,…nw) | Number of solutions |
| Position of whale (Xi.) | Combination of variables within their boundary conditions | |
| Number of dimensions involved in defining the position of whale (j = 1, 2…nd) | Number of independent variables | |
| Position of prey (Xp.) | Value of best variables | |
| Fitness of whale (Fik) (k = 1, 2…no) | Response variable | |
| Stopping criteria | Number of iterations | |
| ALO | No. of antlions (na) | 100 |
| No. of iterations (nitr) | 100 | |
| Accuracy of exploitation | 3 to 6 Based on % of no. of iterations | |
| Achieve size | 100 |
| Performance Metric | Probability | Rank Values | |||
|---|---|---|---|---|---|
| PSO | WOA | SSO | ALO | ||
| Objective value | 0.006983 | 2.43 | 2.39 | 2.53 | 2.65 |
| CI_Kt | 3.06 × 10−7 | 3.9 | 1.825 | 2.025 | 2.25 |
| CI_Ra | 3.52 × 10−10 | 3.325 | 3.5 | 1.325 | 1.85 |
| CI_MRR | 8.72 × 10−5 | 2.1 | 3.65 | 2.1 | 2.15 |
| CV_Kt | 2.4 × 10−12 | 1.1 | 2.925 | 1.975 | 4 |
| CV_Ra | 6.19 × 10−12 | 1.65 | 1.475 | 2.875 | 4 |
| CV_MRR | 2.43 × 10−11 | 1.9 | 1.1 | 3.45 | 3.55 |
| Computational time | 2.54 × 10−10 | 1.35 | 3.95 | 2.85 | 1.85 |
| Diversity | 3 | 2 | 1 | 4 | |
| Spacing value | 4 | 2 | 3 | 1 | |
| Overall Performance | 0.5875 | 0.5533 | 0.5793 | 0.6205 | |
| Algorithms | r-GO (wt%) | WP (MPa) | SOD (mm) | CS (mm/min) | Kt (°) | Ra (µm) | MRR (g/min) |
|---|---|---|---|---|---|---|---|
| PSO | 0.01810 | 322.31 | 2.516 | 785.64 | 2.663 | 9.3958 | 139.53 |
| WOA | 0.02668 | 323.70 | 2.558 | 796.12 | 2.693 | 9.2368 | 140.05 |
| SSO | 0.02806 | 325 | 2.5 | 800 | 2.610 | 9.0481 | 138.69 |
| ALO | 0.00602 | 325 | 2.5 | 800 | 2.595 | 8.9897 | 138.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rajamani, D.; Siva Kumar, M.; Tamilarasan, A. Abrasive Waterjet Machining of r-GO Infused Mg Fiber Metal Laminates: ANFIS Modelling and Optimization Through Antlion Optimizer Algorithm. Materials 2025, 18, 4480. https://doi.org/10.3390/ma18194480
Rajamani D, Siva Kumar M, Tamilarasan A. Abrasive Waterjet Machining of r-GO Infused Mg Fiber Metal Laminates: ANFIS Modelling and Optimization Through Antlion Optimizer Algorithm. Materials. 2025; 18(19):4480. https://doi.org/10.3390/ma18194480
Chicago/Turabian StyleRajamani, Devaraj, Mahalingam Siva Kumar, and Arulvalavan Tamilarasan. 2025. "Abrasive Waterjet Machining of r-GO Infused Mg Fiber Metal Laminates: ANFIS Modelling and Optimization Through Antlion Optimizer Algorithm" Materials 18, no. 19: 4480. https://doi.org/10.3390/ma18194480
APA StyleRajamani, D., Siva Kumar, M., & Tamilarasan, A. (2025). Abrasive Waterjet Machining of r-GO Infused Mg Fiber Metal Laminates: ANFIS Modelling and Optimization Through Antlion Optimizer Algorithm. Materials, 18(19), 4480. https://doi.org/10.3390/ma18194480








