Electrocaloric Effect on Lead-Free Ferroelectrics: Challenges in Identifying Trends and Evaluating Predictive Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Measurement Techniques of the Electrocaloric Effect
2.1.1. Formalism Based on Maxwell’s Relations
2.1.2. Differential Scanning Calorimetry (DSC)
2.1.3. Heat Flux Measurement Methods (Direct Calorimetry)
2.2. Literature Data Collection
3. Results
3.1. Literature Overview of Electrocaloric Effect in BaTiO3-Based Materials
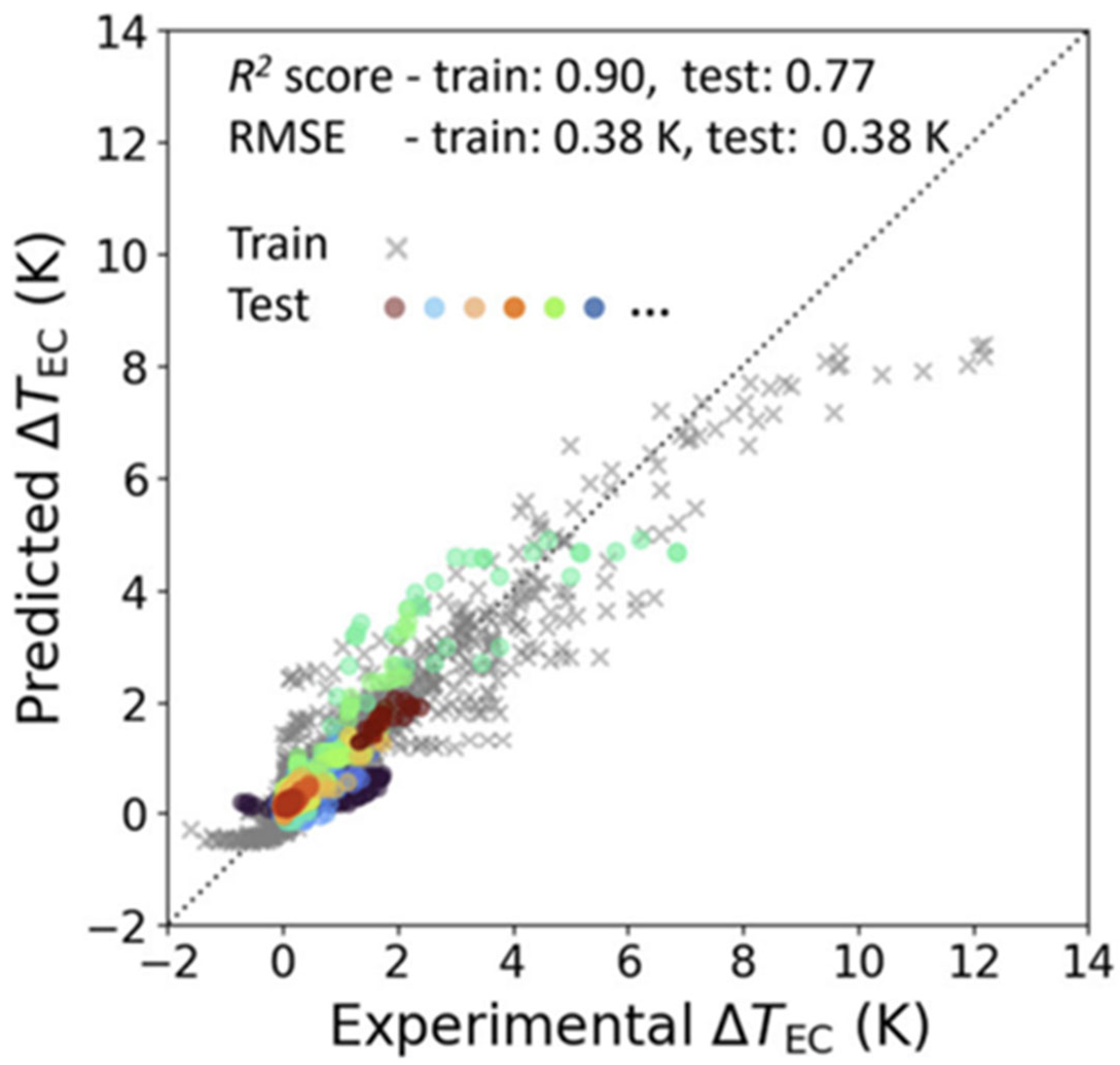
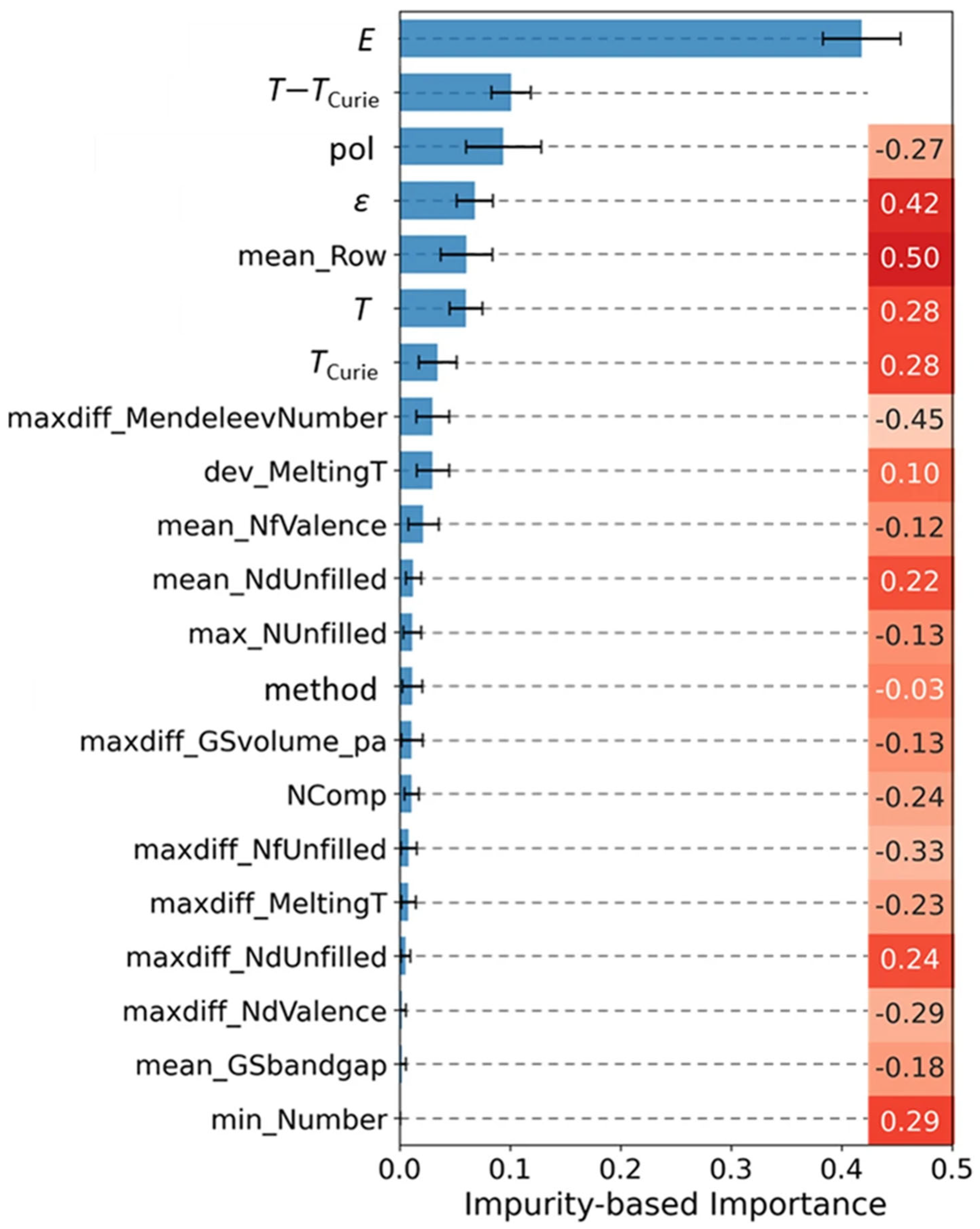
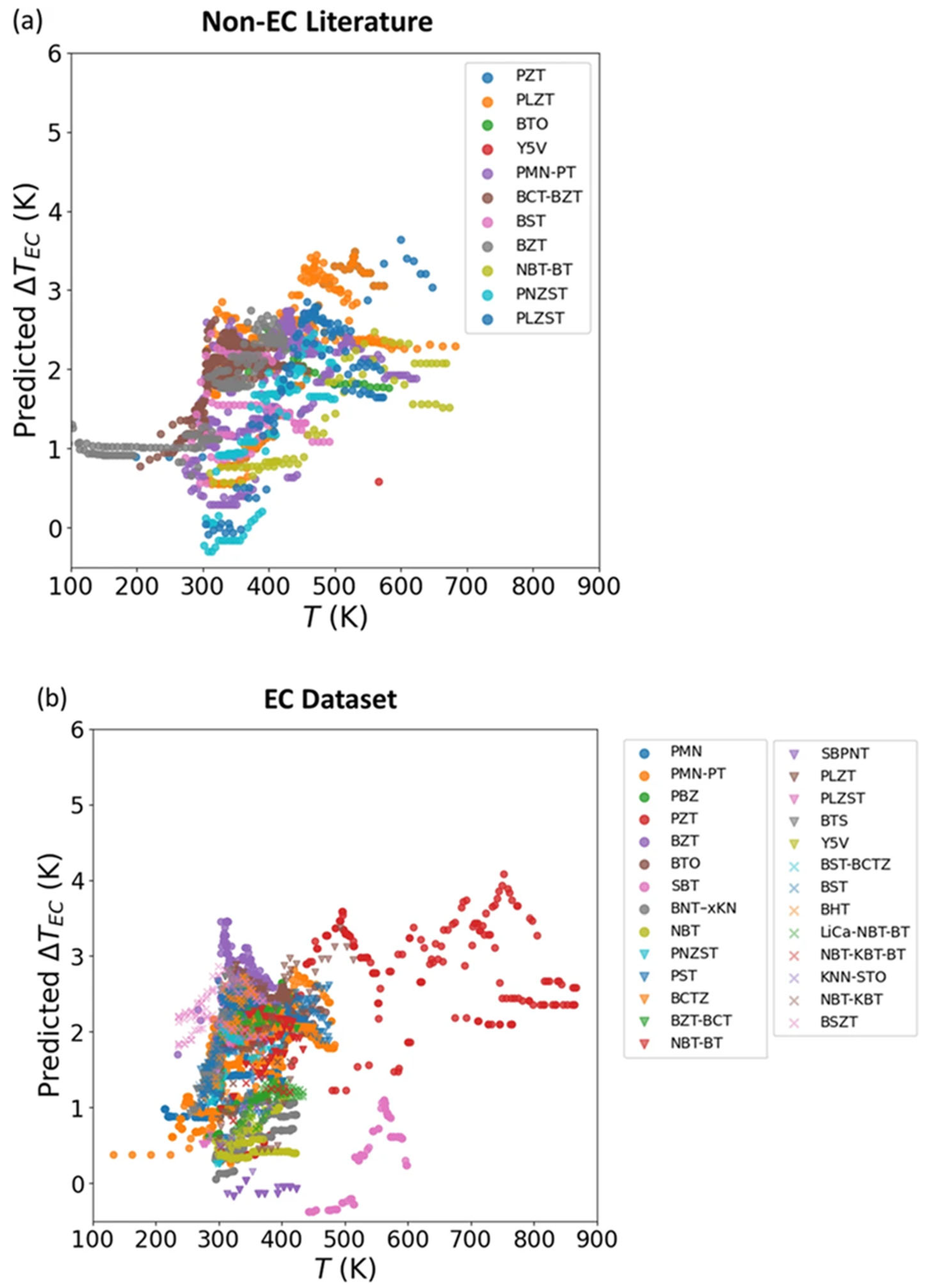
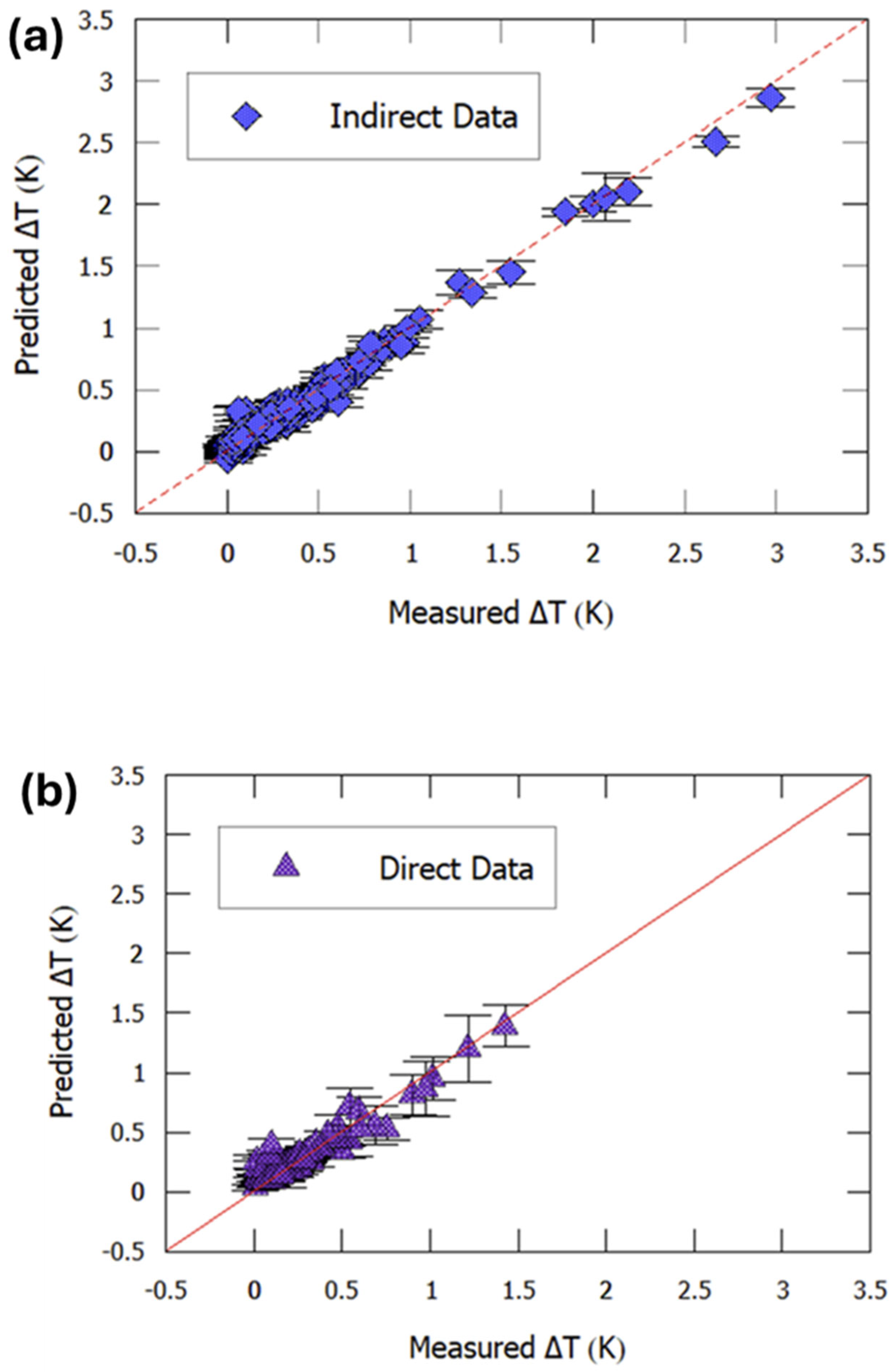
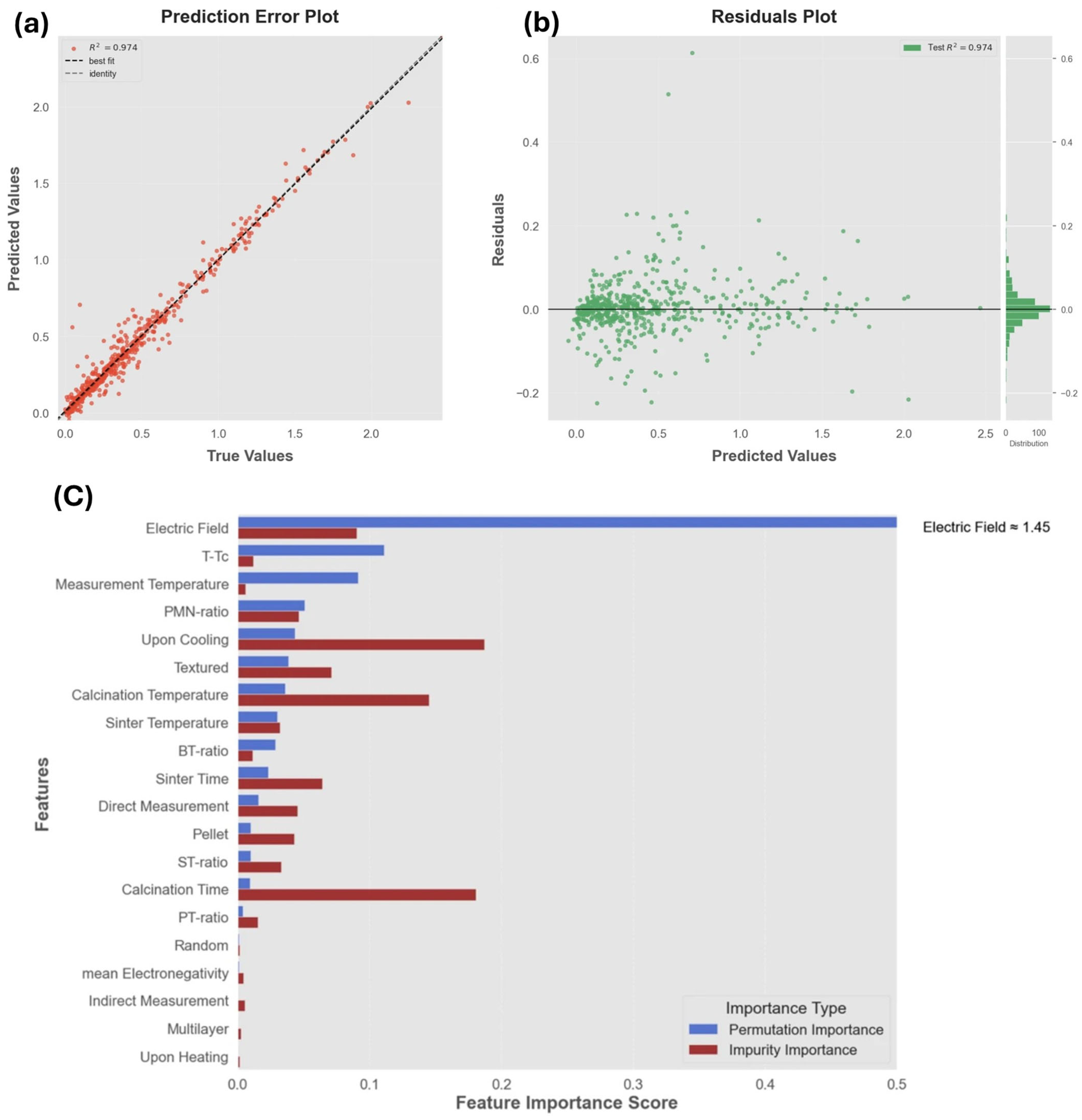
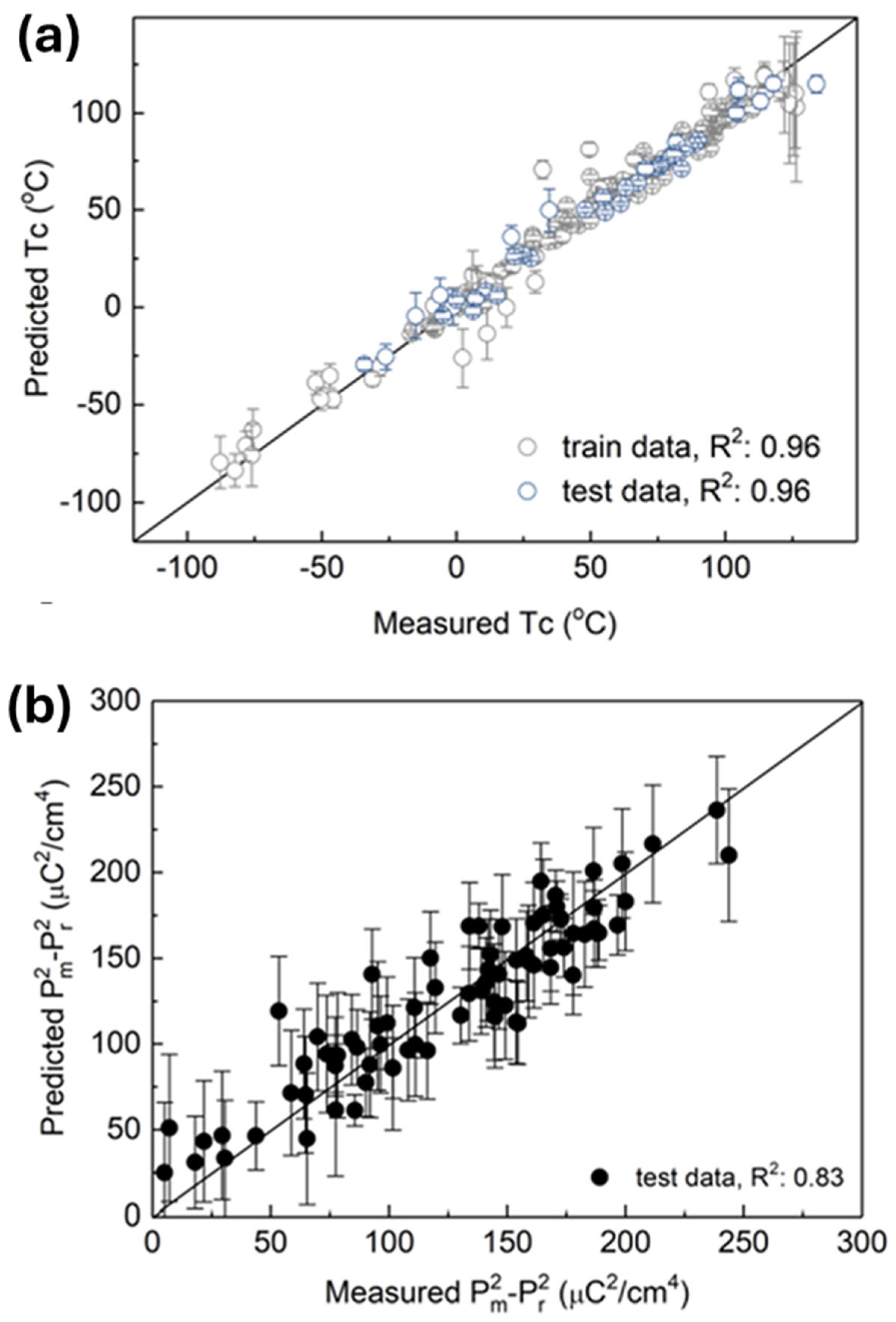
3.2. Electrocaloric Effect Predictions from Machine Learning Models in the Literature
- Feature engineering: Magpie descriptors, ionic radii, tolerance factors, and polarization parameters;
- Dimensionality reduction and filtering: variance analysis, correlation thresholds, backward elimination;
- Models: ensemble regression (XGBoost, random forest, SVR), surrogate modeling (Gaussian process), and classification (SVC);
- Validation: bootstrap resampling, group-aware cross-validation, ShuffleSplit, and exhaustive grid/Bayesian optimization;
- Software frameworks: Scikit-learn, TensorFlow, PyTorch, RStudio (e1071), Optuna.
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Composition | ΔT [K] | E [kV/cm] | T [K] | ΔT/E [K∙cm/kV] | M | Ref. |
|---|---|---|---|---|---|---|
| BaTi0.975Y0.025O3 | 1.260 | 50.0 | 375 | 0.0252 | I | [20] |
| BaTi0.9625Y0.0375O3 | 1.030 | 50.0 | 362 | 0.0206 | I | |
| BaTi0.95Y0.05O3 | 1.150 | 50.0 | 345 | 0.0230 | I | |
| BaTi0.9375Y0.0625O3 | 0.370 | 50.0 | 340 | 0.0074 | I | |
| (0.6BaTi0.8Hf0.2O3)–(0.4Ba0.94Sm0.04TiO3) | 0.340 | 30.0 | 334 | 0.0113 | I | [21] |
| (0.5BaTi0.8Hf0.2O3)–(0.5Ba0.94Sm0.04TiO3) | 0.390 | 30.0 | 341 | 0.0130 | I | |
| (0.3BaTi0.8Hf0.2O3)–(0.7Ba0.94Sm0.04TiO3) | 0.460 | 30.0 | 337 | 0.0153 | I | |
| Ba0.94Sm0.04TiO3 | 0.920 | 30.0 | 350 | 0.0307 | I | [22] |
| Ba0.94Dy0.04TiO3 | 1.040 | 30.0 | 412 | 0.0347 | I | |
| Ba0.94La0.04TiO3 | 0.680 | 30.0 | 319 | 0.0227 | I | |
| Ba0.94Ce0.04TiO3 | 0.720 | 30.0 | 325 | 0.0240 | I | |
| Ba0.94Nd0.04TiO3 | 0.790 | 30.0 | 337 | 0.0263 | I | |
| Ba0.94Eu0.04TiO3 | 0.890 | 30.0 | 359 | 0.0297 | I | |
| Ba0.94Gd0.04TiO3 | 0.860 | 30.0 | 367 | 0.0287 | I | |
| BaTiO3 + 4% Li | 0.545 | 20.0 | 392 | 0.0273 | I | [23] |
| BaTiO3 + 6% Li | 0.575 | 20.0 | 393 | 0.0288 | I | |
| BaTiO3 + 8% Li | 0.525 | 20.0 | 393 | 0.0263 | I | |
| Ba0.995Ce0.005Ti0.99Mn0.01O3 | 1.220 | 30.0 | 393 | 0.0407 | I | [24] |
| Ba0.985Ce0.015Ti0.99Mn0.01O3 | 1.070 | 30.0 | 370 | 0.0357 | I | |
| Ba0.97Ce0.03Ti0.99Mn0.01O3 | 0.410 | 30.0 | 328 | 0.0137 | I | |
| Ba0.96Ce0.04Ti0.99Mn0.01O3 | 0.500 | 30.0 | 298 | 0.0167 | I | |
| Ba0.955Ce0.045Ti0.99Mn0.01O3 | 0.420 | 30.0 | 293 | 0.0140 | I | |
| BaTiO3 | 0.010 | 10.0 | 396 | 0.0010 | I | [25] |
| BaTi0.98Sn0.02O3 | 0.160 | 9.8 | 370 | 0.0163 | I | |
| BaTi0.95Sn0.05O3 | 0.079 | 3.6 | 343 | 0.0218 | I | |
| BaTi0.9Sn0.1O3 | 0.050 | 10.1 | 306 | 0.0049 | I | |
| Ba0.98Ca0.02Ti0.95Sn0.05O3 | 0.200 | 7.9 | 370 | 0.0253 | I | [26] |
| Ba0.95Ca0.05Ti0.95Sn0.05O3 | 0.530 | 10.8 | 383 | 0.0490 | I | |
| Ba0.9Ca0.1Ti0.95Sn0.05O3 | 0.340 | 12.7 | 398 | 0.0268 | I | |
| 0.8BaTi0.82Zr0.18O3–0.2BaTi0.89Sn0.11O3 | 3.500 | 100.0 | 0.0350 | D | [27] | |
| BaTi0.82Hf0.18O3 | 0.330 | 20.0 | n/i | 0.0165 | I | [28] |
| BaTi0.82Hf0.18O3 | 0.370 | 20.0 | n/i | 0.0185 | D | |
| (Ba0.98Ca0.02)(Ti0.98Hf0.02)O3 | 0.790 | 20.0 | 394 | 0.0395 | I | |
| (Ba0.87Ca0.13)(Ti0.87Hf0.13)O3 | 0.470 | 20.0 | 328 | 0.0235 | I | |
| (Ba0.87Ca0.13)(Ti0.87Hf0.13)O3 | 0.480 | 20.0 | 328 | 0.0240 | D | |
| (Ba0.86Ca0.14)(Ti0.86Hf0.14)O3 | 0.350 | 20.0 | 324 | 0.0175 | I | |
| (Ba0.82Ca0.18)(Ti0.82Hf0.18)O3 | 0.160 | 20.0 | 308 | 0.0080 | I | |
| BaTiO3 + 0.1% Eu | 0.390 | 14.0 | 394 | 0.0279 | I | [29] |
| BaTiO3 + 1% Eu | 0.300 | 10.0 | 387 | 0.0300 | I | |
| BaTiO3 + 2% Eu | 0.120 | 10.0 | 363 | 0.0120 | I | |
| BaTiO3 + 3% Eu | 0.070 | 10.0 | 391 | 0.0070 | I | |
| BaTiO3 | 0.970 | 20.0 | 396 | 0.0485 | I | [30] |
| BaTi0.998Nb0.002O3 | 0.820 | 20.0 | 396 | 0.0410 | I | |
| BaTi0.996Nb0.004O3 | 0.790 | 20.0 | 392 | 0.0395 | I | |
| BaTi0.994Nb0.006O3 | 0.660 | 20.0 | 385 | 0.0330 | I | |
| BaTi0.992Nb0.008O3 | 0.500 | 20.0 | 384 | 0.0250 | I | |
| BaTi0.99Nb0.01O3 | 0.440 | 20.0 | n/i | 0.0220 | I | |
| BaTi0.94Sn0.06O3-Y | 1.100 | 50.0 | 316 | 0.0220 | I | [31] |
| BaTi0.92Sn0.08O3-Y | 1.250 | 50.0 | 344 | 0.0250 | I | |
| BaTi0.89Sn0.11O3-Y | 1.400 | 50.0 | 328 | 0.0280 | I | |
| BaTi0.87Sn0.13O3-Y | 1.200 | 50.0 | 300 | 0.0240 | I | |
| Ba(Zr0.15Ti0.85)O3 | 4.200 | 150.0 | 342 | 0.0280 | D | [32] |
| Ba(Zr0.2Ti0.8)O3 | 4.500 | 145.0 | 312 | 0.0310 | D | |
| (Ba0.86Ca0.14)0.995La0.005Ti0.92Sn0.08O3 | 0.850 | 40.0 | 0.0213 | D | [33] | |
| (Ba0.86Ca0.14)0.99La0.01Ti0.92Sn0.08O3 | 1.160 | 60.0 | 0.0193 | D | ||
| (Ba0.86Ca0.14)0.985La0.015Ti0.92Sn0.08O3 | 1.450 | 100.0 | 0.0145 | D | ||
| (Ba0.86Ca0.14)0.98La0.02Ti0.92Sn0.08O3 | 1.600 | 140.0 | 0.0114 | D | ||
| (Ba0.86Ca0.14)0.975La0.025Ti0.92Sn0.08O3 | 1.620 | 160.0 | 0.0101 | D | ||
| Ba0.96Pb0.04TiO3 | 2.190 | 18.0 | 420 | 0.1217 | I | [34] |
| Ba0.99La0.01TiO3 | 0.600 | 60.0 | 420 | 0.0100 | I | [35] |
| Ba0.98La0.02TiO3 | 0.650 | 60.0 | 370 | 0.0108 | I | |
| Ba0.97La0.03TiO3 | 0.750 | 60.0 | 327 | 0.0125 | I | |
| Ba0.96La0.04TiO3 | 1.810 | 60.0 | 303 | 0.0302 | I | |
| (Ba0.8Ca0.2)TiO3 | 0.120 | 8.0 | 400 | 0.0151 | I | [36] |
| (Ba0.8Ca0.2)0.98La0.013TiO3 | 0.115 | 9.9 | 370 | 0.0116 | I | |
| (Ba0.8Ca0.2)0.97La0.02TiO3 | 0.150 | 9.9 | 310 | 0.0152 | I | |
| (Ba0.8Ca0.2)0.95La0.033TiO3 | 0.250 | 9.9 | 260 | 0.0253 | I | |
| Ba0.85Ca0.15Ti0.94Hf0.06O3 | 1.030 | 40.0 | 383 | 0.0258 | D | [37] |
| Ba0.85Ca0.15Ti0.9Hf0.1O3 | 0.800 | 40.0 | 373 | 0.0200 | D | |
| Ba0.85Ca0.15Ti0.85Hf0.15O3 | 0.540 | 40.0 | 333 | 0.0135 | D | |
| Ba0.96Sm0.04TiO3 | 0.240 | 7.0 | 342 | 0.0343 | D | [38] |
| Ba0.7Sr0.3TiO3 + 1mol% Br+ + 0.3 mol% Mn2+ | 0.650 | 20.0 | 313 | 0.0325 | I | [39] |
| Ba0.7Sr0.3TiO3 + 1mol% Br+ + 0.5 mol% Mn2+ | 0.860 | 20.0 | 311 | 0.0430 | I | |
| Ba0.7Sr0.3TiO3 + 1mol% Br+ + 1.5 mol% Mn2+ | 0.400 | 20.0 | 308 | 0.0200 | I | |
| BaTi0.9Hf0.1O3 | 1.990 | 50.0 | 353 | 0.0398 | D | [40] |
| 0.2BaTi0.93 Sn0.07O3–0.8BaTi0.9Hf0.1O3 | 2.160 | 50.0 | 353 | 0.0432 | D | |
| BaTi0.93Sn0.07O3 | 1.140 | 50.0 | 353 | 0.0228 | D | |
| BaTi0.9Sn0.1O3 | 0.480 | 15.0 | 337 | 0.0320 | I | [41] |
| Ba0.94Sr0.06Ti0.9Sn0.1O3 | 0.460 | 15.0 | 320 | 0.0307 | I | |
| Ba0.93Sr0.07Ti0.9Sn0.1O3 | 0.370 | 15.0 | 315 | 0.0247 | I | |
| Ba0.92Sr0.08Ti0.9Sn0.1O3 | 0.340 | 15.0 | 304 | 0.0227 | I | |
| Ba0.6Sr0.4TiO3 | 2.460 | 50.0 | 303 | 0.0492 | D | [42] |
| Ba0.6Sr0.4Mn0.001Ti0.999O3 | 2.750 | 50.0 | 294 | 0.0550 | D | |
| Ba0.6Sr0.4Mn0.002Ti0.998O3 | 2.570 | 50.0 | 283 | 0.0514 | D | |
| Ba0.6Sr0.4Mn0.003Ti0.997O3 | 2.450 | 50.0 | 273 | 0.0490 | D | |
| Ba0.6Sr0.4Mn0.004Ti0.996O3 | 2.290 | 50.0 | 263 | 0.0458 | D | |
| Ba0.6Sr0.4Mn0.005Ti0.995O3 | 2.090 | 50.0 | 243 | 0.0418 | D | |
| Ba0.65Sr0.35TiO3 | 2.420 | 50.0 | 283 | 0.0484 | D | |
| Ba0.65Sr0.35Mn0.001Ti0.999O3 | 2.580 | 50.0 | 263 | 0.0516 | D | |
| Ba0.65Sr0.35Mn0.002Ti0.998O3 | 2.340 | 50.0 | 263 | 0.0468 | D | |
| Ba0.65Sr0.35Mn0.003Ti0.997O3 | 2.280 | 50.0 | 263 | 0.0456 | D | |
| Ba0.65Sr0.35Mn0.004Ti0.996O3 | 2.260 | 50.0 | 281 | 0.0452 | D | |
| Ba0.65Sr0.35Mn0.005Ti0.995O3 | 1.980 | 50.0 | 243 | 0.0396 | D | |
| Ba0.80Ca0.20Ti0.9925Fe0.01O3 | 0.370 | 25.0 | 396 | 0.0148 | I | [43] |
| Ba0.80Ca0.20Ti0.9888Fe0.015O3 | 0.410 | 25.0 | 408 | 0.0164 | I | |
| Ba0.80Ca0.20Ti0.985Fe0.02O3 | 0.440 | 25.0 | 368 | 0.0176 | I | |
| Ba(Ge0.02Ti0.98)O3 | 0.550 | 8.0 | 400 | 0.0692 | I | [44] |
| Ba(Ge0.03Ti0.97)O3 | 0.590 | 8.0 | 401 | 0.0742 | I | |
| Ba(Ge0.05Ti0.95)O3 | 0.530 | 8.0 | 402 | 0.0667 | I | |
| Ba(Ge0.06Ti0.94)O3 | 0.810 | 8.0 | 403 | 0.1019 | I | |
| Ba(Ge0.09Ti0.91)O3 | 0.380 | 8.0 | 404 | 0.0478 | I | |
| Ba(Ge0.06Ti0.94)O3 | 0.904 | 8.0 | 400 | 0.1130 | D | |
| (Ba0.865Ca0.135)(Zr0.1089Ti0.8811Fe0.01)O3 | 0.450 | 30.0 | 347 | 0.0150 | I | [45] |
| Ba0.8Sr0.2TiO3 | 0.620 | 20.0 | 351 | 0.0310 | I | [46] |
| Ba0.8Sr0.2Ti0.97Zr0.03O3 | 0.420 | 20.0 | 351 | 0.0210 | I | |
| Ba0.8Sr0.2Ti0.95Zr0.05O3 | 0.430 | 20.0 | 351 | 0.0215 | I | |
| Ba0.8Sr0.2Ti0.93Zr0.07O3 | 0.400 | 20.0 | 351 | 0.0200 | I | |
| Ba0.8Sr0.2Ti0.9Zr0.1O3 | 0.350 | 20.0 | 342 | 0.0175 | I | |
| Ba0.85Ca0.15Ti0.9Zr0.1O3 | 0.410 | 22.0 | 362 | 0.0186 | I | [47] |
| Ba0.85Ca0.1Sr0.05Ti0.9Zr0.1O3 | 0.600 | 30.0 | 333 | 0.0200 | I | |
| Ba0.85Ca0.05Sr0.1Ti0.9Zr0.1O3 | 1.000 | 30.0 | 323 | 0.0333 | I | |
| Ba0.85Sr0.15Ti0.9Zr0.1O3 | 2.400 | 37.0 | 303 | 0.0649 | I | |
| 0.8Ba(Hf0.2Ti0.8)O3-0.2(Ba0.7Ca0.3)TiO3 | 0.130 | 10.0 | 324 | 0.0130 | I | [48] |
| 0.7Ba(Hf0.2Ti0.8)O3-0.3(Ba0.7Ca0.3)TiO3 | 0.155 | 10.0 | 334 | 0.0155 | I | |
| 0.6Ba(Hf0.2Ti0.8)O3-0.4(Ba0.7Ca0.3)TiO3 | 0.140 | 10.0 | 352 | 0.0140 | I | |
| 0.5Ba(Hf0.2Ti0.8)O3-0.5(Ba0.7Ca0.3)TiO3 | 0.240 | 10.0 | 362 | 0.0240 | D | |
| 0.8Ba(Hf0.2Ti0.8)O3-0.2(Ba0.7Ca0.3)TiO3 | 0.125 | 10.0 | 313 | 0.0125 | D | |
| 0.7Ba(Hf0.2Ti0.8)O3-0.3(Ba0.7Ca0.3)TiO3 | 0.200 | 10.0 | 333 | 0.0200 | D | |
| 0.6Ba(Hf0.2Ti0.8)O3-0.4(Ba0.7Ca0.3)TiO3 | 0.150 | 10.0 | 343 | 0.0150 | D | |
| 0.5Ba(Hf0.2Ti0.8)O3-0.5(Ba0.7Ca0.3)TiO3 | 0.270 | 10.0 | 363 | 0.0270 | ||
| (Ba0.85Ca0.15)(Zr0.1Ti0.9)O3 | 0.750 | 60.0 | 360 | 0.0125 | D | [49] |
| (Ba0.85Ca0.15)(Zr0.1Ti0.9)O3 1 mol. % Bi2O3 | 0.450 | 60.0 | 380 | 0.0075 | D | |
| (Ba0.85Ca0.15)(Zr0.1Ti0.9)O3 | 0.260 | 20.0 | 343 | 0.0130 | I | [50] |
| (Ba0.85Ca0.15)(Zr0.1Ti0.9)O3 | 0.464 | 60.0 | 373 | 0.0077 | D | |
| 0.68Ba(Zr0.2Ti0.8)O3–0.32(Ba0.7Ca0.3)TiO3 | 0.318 | 20.0 | 352 | 0.0159 | I | [51] |
| 0.65Ba(Zr0.2Ti0.8)O3–0.35(Ba0.7Ca0.3)TiO3 | 0.188 | 20.0 | 348 | 0.0094 | I | |
| 0.63Ba(Zr0.2Ti0.8)O3–0.37(Ba0.7Ca0.3)TiO3 | 0.155 | 20.0 | 359 | 0.0078 | I | |
| 0.6Ba(Zr0.2Ti0.8)O3–0.4(Ba0.7Ca0.3)TiO3 | 0.225 | 20.0 | 361 | 0.0113 | I | |
| 0.55Ba(Zr0.2Ti0.8)O3–0.45(Ba0.7Ca0.3)TiO3 | 0.205 | 20.0 | 363 | 0.0103 | I | |
| 0.68Ba(Zr0.2Ti0.8)O3–0.32(Ba0.7Ca0.3)TiO3 | 0.330 | 20.0 | 337 | 0.0165 | D | |
| 0.65Ba(Zr0.2Ti0.8)O3–0.35(Ba0.7Ca0.3)TiO3 | 0.250 | 20.0 | 338 | 0.0125 | D | |
| 0.63Ba(Zr0.2Ti0.8)O3–0.37(Ba0.7Ca0.3)TiO3 | 0.195 | 20.0 | 343 | 0.0098 | D | |
| 0.6Ba(Zr0.2Ti0.8)O3–0.4(Ba0.7Ca0.3)TiO3 | 0.230 | 20.0 | 348 | 0.0115 | D | |
| 0.55Ba(Zr0.2Ti0.8)O3–0.45(Ba0.7Ca0.3)TiO3 | 0.255 | 20.0 | 362 | 0.0128 | D | |
| 0.9Ba(Zr0.2Ti0.8)O3–0.1(Ba0.7Ca0.3)TiO3 | 0.190 | 20.0 | 323 | 0.0095 | I | [52] |
| 0.7Ba(Zr0.2Ti0.8)O3–0.3(Ba0.7Ca0.3)TiO3 | 0.300 | 20.0 | 330 | 0.0150 | I | |
| 0.65Ba(Zr0.2Ti0.8)O3–0.35(Ba0.7Ca0.3)TiO3 | 0.280 | 20.0 | 348 | 0.0140 | I | |
| 0.5 0.5Ba(Zr0.2Ti0.8)O3–0.5(Ba0.7Ca0.3)TiO3 | 0.290 | 20.0 | 363 | 0.0145 | I | |
| 0.3Ba(Zr0.2Ti0.8)O3–0.7(Ba0.7Ca0.3)TiO3 | 0.330 | 20.0 | 375 | 0.0165 | I | |
| Ba0.6Sr0.4TiO3 | 0.600 | 20.0 | 300 | 0.0300 | D | [53] |
| Ba0.7Sr0.3TiO3 | 0.670 | 33.0 | 313 | 0.0203 | I | [54] |
| Ba0.8Sr0.2TiO3 | 0.830 | 33.0 | 338 | 0.0252 | I | |
| Ba0.9Sr0.1TiO3 | 0.610 | 33.0 | 360 | 0.0185 | I | |
| BaTi0.99In0.01O2.995 | 0.220 | 10.0 | 290 | 0.0220 | I | [55] |
| BaTi0.97In0.03O2.985 | 0.290 | 26.0 | 324 | 0.0112 | I | |
| BaTi0.95In0.05O2.975 | 0.420 | 26.0 | 314 | 0.0162 | I | |
| BaTi0.944Y0.056O2.972 | 0.400 | 45.0 | 356 | 0.0089 | I | [56] |
| BaTi0.942Y0.058O2.971 | 0.375 | 45.0 | 344 | 0.0083 | I | |
| BaTi0.94Y0.06O2.97 | 0.340 | 45.0 | 338 | 0.0076 | I | |
| BaTi0.938Y0.062O2.969 | 0.340 | 45.0 | 338 | 0.0076 | I | |
| BaTi0.936Y0.064O2.968 | 0.330 | 45.0 | 338 | 0.0073 | I | |
| BaTi0.97Hf0.03O3 | 0.190 | 10.0 | 318 | 0.0190 | D | [57] |
| BaTi0.89Hf0.11O3 | 0.350 | 10.0 | 343 | 0.0350 | D | |
| BaTi0.83Hf0.17O3 | 0.320 | 10.0 | 313 | 0.0320 | D | |
| BaTiO3 | 0.925 | 24.0 | 396 | 0.0385 | I | [58] |
| BaTi0.99Ce0.1O3 | 0.450 | 24.0 | 371 | 0.0188 | I | |
| BaTi0.88Ce0.12O3 | 0.825 | 24.0 | 351 | 0.0344 | I | |
| BaTi0.85Ce0.15O3 | 0.650 | 24.0 | 338 | 0.0271 | I | |
| BaTi0.8 Zr0.2O3 | 0.330 | 30.0 | 303 | 0.0110 | I | [59] |
| BaTi0.88Zr0.12O3 | 0.500 | 20.0 | 355 | 0.0250 | D | [60] |
| BaTi0.8Zr0.2O3 | 0.300 | 20.0 | 314 | 0.0150 | D | |
| 0.05 BaTi0.95Sn0.05O3 | 1.450 | 30.0 | 368 | 0.0483 | D | [61] |
| 0.1BaTi0.9Sn0.1O3 | 1.240 | 30.0 | 338 | 0.0413 | D | |
| BaTi0.85Sn0.15O3 | 1.490 | 30.0 | 299 | 0.0497 | D | |
| BaTi0.9Sn0.1O3 | 0.400 | 20.0 | 343 | 0.0200 | I | [62] |
| BaTi0.88Sn0.12O3 | 0.450 | 20.0 | 325 | 0.0225 | I | |
| BaTi0.85Sn0.15O3 | 0.420 | 20.0 | 301 | 0.0210 | I | |
| BaTi0.82Sn0.18O3 | 0.318 | 20.0 | 298 | 0.0159 | I | |
| BaTi0.92Sn0.08O3 | 0.490 | 20.0 | 341 | 0.0245 | D | [63] |
| BaTi0.89Sn0.11O3 | 0.630 | 20.0 | 317 | 0.0315 | D | |
| BaTi0.86Sn0.14O3 | 0.390 | 20.0 | 291 | 0.0195 | D | |
| BaTi0.85Sn0.15O3 | 0.310 | 20.0 | 289 | 0.0155 | D | |
| BaTi0.92Sn0.08O3 | 0.520 | 20.0 | 331 | 0.0260 | I | [64] |
| BaTi0.895Sn0.105O3 | 0.610 | 20.0 | 301 | 0.0305 | I | |
| BaTi0.86Sn0.14O3 | 0.470 | 20.0 | 282 | 0.0235 | I | |
| Ba0.8Ca0.2TiO3 | 0.120 | 8.0 | 398 | 0.0151 | I | [65] |
| Ba0.8Ca0.2Ti0.96Zr0.04O3 | 0.270 | 8.0 | 386 | 0.0340 | I | |
| Ba0.8Ca0.2Ti0.9Zr0.1O3 | 0.170 | 8.0 | 360 | 0.0214 | I | |
| Ba0.94Ca0.06Ti0.95Sn0.05O3 | 0.580 | 20.0 | 358 | 0.0290 | I | [66] |
| Ba0.94Ca0.06Ti0.925Sn0.075O3 | 0.580 | 20.0 | 339 | 0.0290 | I | |
| Ba0.94Ca0.06Ti0.9Sn0.1O3 | 0.550 | 20.0 | 320 | 0.0275 | I | |
| Ba0.94Ca0.06Ti0.875Sn0.125O3 | 0.630 | 20.0 | 298 | 0.0315 | I | |
| Ba0.94Ca0.06Ti0.85Sn0.15O3 | 0.350 | 20.0 | 281 | 0.0175 | I | |
| Ba0.94Ca0.06Ti0.8Sn0.2O3 | 0.320 | 20.0 | 237 | 0.0160 | I | |
| Ba0.95Ca0.05Ti0.95Zr0.05O3 | 0.310 | 15.0 | 405 | 0.0207 | I | [67] |
| Ba0.92Ca0.08Ti0.92Zr0.08O3 | 0.380 | 15.0 | 409 | 0.0253 | I | |
| Ba0.9Ca0.1Ti0.92Zr0.08O3 | 0.230 | 15.0 | 406 | 0.0153 | I | |
| Ba0.8Sr0.2TiO3 | 0.390 | 20.0 | 349 | 0.0195 | I | [68] |
| Ba0.75Sr0.25TiO3 | 0.370 | 20.0 | 334 | 0.0185 | I | |
| Ba0.7Sr0.3TiO3 | 0.360 | 20.0 | 303 | 0.0180 | I | |
| Ba0.65Sr0.35TiO3 | 0.420 | 20.0 | 296 | 0.0210 | I | |
| Ba0.8Zr0.2TiO3 | 2.780 | 161.0 | 350 | 0.0173 | I | [69] |
| Ba0.7Sr0.3TiO3 con | 0.670 | 40.0 | 312 | 0.0168 | I | [70] |
| Ba0.7Sr0.3TiO3 SPS | 1.850 | 90.0 | 312 | 0.0206 | I | |
| Ba0.7Sr0.3Ti0.997Mn0.003O3 SPS | 2.530 | 120.0 | 303 | 0.0211 | I | |
| Bi0.5Na0.5TiO3–0.06BaTiO3 | 0.860 | 50.0 | 383 | 0.0172 | D | [71] |
| Ba0.95Ca0.05Ti0.94Sn0.06O3 | 1.600 | 180.0 | 300 | 0.0089 | I | [72] |
| 0.45BaTi0.8Zr0.2O3-0.55Ba0.7Ca0.3TiO3 | 0.460 | 12.0 | 404 | 0.0383 | I | [73] |
| 0.65BaTi0.8Zr0.2O3-0.35Ba0.7Ca0.3TiO3 | 0.330 | 20.0 | 338 | 0.0165 | D | [74] |
| Ba0.8Sr0.2TiO3 | 1.670 | 50.0 | 344 | 0.0334 | I | [75] |
| Ba0.65Sr0.35TiO3 Con | 0.830 | 90.0 | 303 | 0.0092 | I | [76] |
| Ba0.65Sr0.35TiO3 SPS | 2.100 | 90.0 | 303 | 0.0233 | I | |
| Ba0.65Sr0.35Ti0.997Mn0.003O3 SPS | 3.080 | 130.0 | 293 | 0.0237 | I |
References
- Greco, A.; Masselli, C. Electrocaloric Cooling: A Review of the Thermodynamic Cycles, Materials, Models, and Devices. Magnetochemistry 2020, 6, 67. [Google Scholar] [CrossRef]
- Singh, S.K.; Rakshit, D.; Kumar, K.R.; Agarwal, A. Recent advancements and sustainable solutions in adsorption-based cooling systems integrated with renewable energy sources and industrial waste heat: A review. Clean. Eng. Technol. 2024, 23, 100827. [Google Scholar] [CrossRef]
- Guzmán-Verri, G.G.; Littlewood, P.B. Why is the electrocaloric effect so small in ferroelectrics? APL Mater. 2016, 4, 064106. [Google Scholar] [CrossRef]
- Klinar, K.; Law, J.Y.; Franco, V.; Moya, X.; Kitanovski, A. Perspectives and Energy Applications of Magnetocaloric, Pyromagnetic, Electrocaloric, and Pyroelectric Materials. Adv. Energy Mater. 2024, 14, 2401739. [Google Scholar] [CrossRef]
- Bai, Y.; Ding, K.; Zheng, G.P.; Shi, S.Q.; Qiao, L.J.; Guo, D. The Electrocaloric Effect in BaTiO3 Thick Film Multilayer Structure at High Electric Field. Key Eng. Mater. 2012, 512, 1304–1307. [Google Scholar] [CrossRef]
- Mischenko, A.S.; Zhang, Q.; Scott, J.F.; Whatmore, R.W.; Mathur, N.D. Giant Electrocaloric Effect in Thin-Film PbZr0.95Ti0.05O3. Science 2006, 311, 1270–1271. [Google Scholar] [CrossRef]
- Sun, Y.; Shirsath, S.E.; Zhang, S.; Wang, D. A reflection on recent efforts in optimization of cooling capacity of electrocaloric thin films. APL Mater. 2023, 11, 090602. [Google Scholar] [CrossRef]
- Shi, J.; Han, D.; Li, Z.; Yang, L.; Lu, S.-G.; Zhong, Z.; Chen, J.; Zhang, Q.; Qian, X. Electrocaloric Cooling Materials and Devices for Zero-Global-Warming-Potential, High-Efficiency Refrigeration. Joule 2019, 3, 1200–1225. [Google Scholar] [CrossRef]
- Bai, Y.; Han, X.; Zheng, X.-C.; Qiao, L. Both High Reliability and Giant Electrocaloric Strength in BaTiO3 Ceramics. Sci. Rep. 2013, 3, 2895. [Google Scholar] [CrossRef]
- Patel, S.; Kumar, M. Influence of grain size on the electrocaloric and pyroelectric properties in non-reducible BaTiO3 ceramics. AIP Adv. 2020, 10, 085302. [Google Scholar] [CrossRef]
- Han, X.; Bai, Y.; Qiao, L.J. The Electrocaloric Effect of BaTiO3 Ceramics Using Hydrothermal Synthesized Nano-Sized Starting Powders. Adv. Mater. Res. 2013, 624, 138–141. [Google Scholar] [CrossRef]
- Gong, J.; Chu, S.; Mehta, R.K.; McGaughey, A.J.H. XGBoost model for electrocaloric temperature change prediction in ceramics. npj Comput. Mater. 2022, 8, 140. [Google Scholar] [CrossRef]
- Su, M.; Grimes, R.; Garg, S.; Xue, D.; Balachandran, P.V. Machine-Learning-Enabled Prediction of Adiabatic Temperature Change in Lead-Free BaTiO3-Based Electrocaloric Ceramics. ACS Appl. Mater. Interfaces 2021, 13, 53475–53484. [Google Scholar] [CrossRef]
- Bayir, M.C.; Mensur, E. Electrocaloric property optimization of PMN-PT ceramics using predictive modeling. J. Mater. Sci. Mater. Electron. 2025, 36, 1097. [Google Scholar] [CrossRef]
- Yuan, R.; Liu, Z.; Xu, Y.; Yin, R.; He, J.; Bai, Y.; Zhou, Y.; Li, J.; Xue, D.; Lookman, T. Optimizing Electrocaloric Effect in Barium Titanate-Based Room Temperature Ferroelectrics: Combining Landau Theory, Machine Learning and Synthesis. Acta Mater. 2022, 235, 118054. [Google Scholar] [CrossRef]
- Xu, P.; Ji, X.; Li, M.; Lu, W. Small data machine learning in materials science. npj Comput. Mater. 2023, 9, 42. [Google Scholar] [CrossRef]
- Oviedo, F.; Ferres, J.L.; Buonassisi, T.; Butler, K.T. Interpretable and Explainable Machine Learning for Materials Science and Chemistry. Accounts Mater. Res. 2022, 3, 597–607. [Google Scholar] [CrossRef]
- Chang, R.; Wang, Y.-X.; Ertekin, E. Towards overcoming data scarcity in materials science: Unifying models and datasets with a mixture of experts framework. npj Comput. Mater. 2022, 8, 242. [Google Scholar] [CrossRef]
- Kailkhura, B.; Gallagher, B.; Kim, S.; Hiszpanski, A.; Han, T.Y.-J. Reliable and explainable machine-learning methods for accelerated material discovery. npj Comput. Mater. 2019, 5, 108. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Q.; Lv, J.H.; Zhao, X.; Wang, C.M. Dielectric properties and electrocaloric effect of yttri-um-modified BaTiO3 ceramics. Ceram. Int. 2021, 47, 18610–18618. [Google Scholar] [CrossRef]
- Zhang, B.; Lou, X.; Zheng, K.; Xie, X.; Shi, P.; Guo, M.; Zhu, X.; Gao, Y.; Liu, Q.; Kang, R. Enhanced electrocaloric effect in the Sm and Hf co-doped BaTiO3 ceramics. Ceram. Int. 2021, 47, 1101–1108. [Google Scholar] [CrossRef]
- Han, F.; Bai, Y.; Qiao, L.-J.; Guo, D. A systematic modification of the large electrocaloric effect within a broad temperature range in rare-earth doped BaTiO3 ceramics. J. Mater. Chem. C 2016, 4, 1842–1849. [Google Scholar] [CrossRef]
- Guvenc, C.M.; Adem, U. Influence of aging on electrocaloric effect in Li+ doped BaTiO3 ceramics. J. Alloys Compd. 2019, 791, 674–680. [Google Scholar] [CrossRef]
- Liu, S.; Xie, Q.; Zhang, L.; Zhao, Y.; Wang, X.; Mao, P.; Wang, J.; Lou, X. Tunable electrocaloric and energy storage behavior in the Ce, Mn hybrid doped BaTiO3 ceramics. J. Eur. Ceram. Soc. 2018, 38, 4664–4669. [Google Scholar] [CrossRef]
- Upadhyay, S.K.; Reddy, V.R.; Bag, P.; Rawat, R.; Gupta, S.M.; Gupta, A. Electro-caloric effect in lead-free Sn doped BaTiO3 ceramics at room temperature and low applied fields. Appl. Phys. Lett. 2014, 105, 112907. [Google Scholar] [CrossRef]
- Upadhyay, S.K.; Fatima, I.; Reddy, V.R. Study of electro-caloric effect in Ca and Sn co-doped BaTiO3 ceramics. Mater. Res. Express 2017, 4, 046303. [Google Scholar] [CrossRef]
- Hou, Y.; Yang, L.; Qian, X.; Zhang, T.; Zhang, Q.M. Electrocaloric response near room temperature in Zr- and Sn-doped BaTiO3 systems. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20160055. [Google Scholar] [CrossRef]
- Zhao, L.; Ke, X.; Zhou, Z.; Liao, X.; Li, J.; Wang, Y.; Wu, M.; Li, T.; Bai, Y.; Ren, X. Large electrocaloric effect over a wide temperature range in BaTiO3-modified lead-free ceramics. J. Mater. Chem. C 2019, 7, 1353–1358. [Google Scholar] [CrossRef]
- Gwizd, P.; Sitko, D.; Jankowska-Sumara, I.; Krupska-Klimczak, M. The electrocaloric effect in BaTiO3:Eu ceramics determined by an indirect method. Phase Transit. 2021, 94, 192–198. [Google Scholar] [CrossRef]
- Bai, Y.; Han, X.; Qiao, L.-J. Effect of donor doping in B sites on the electrocaloric effect of BaTi1−xNbxO3 ceramics. RSC Adv. 2015, 5, 71873–71877. [Google Scholar] [CrossRef]
- Qiang, H.; Fu, S.; Xu, Z. Electrocaloric Effect in Sn- and Y-Codoped BaTiO3 Ceramics. Phys. Status Solidi (A) 2021, 218, 2100090. [Google Scholar] [CrossRef]
- Qian, X.; Ye, H.; Zhang, Y.; Gu, H.; Li, X.; Randall, C.A.; Zhang, Q.M. Giant Electrocaloric Response over a Broad Temperature Range in Modified BaTiO3 Ceramics. Adv. Funct. Mater. 2014, 24, 1300–1305. [Google Scholar] [CrossRef]
- Meng, Y.; Tang, S.; Wang, Z.; Niu, X.; Zhang, H.; Wang, D.; Bai, Y.; Peng, B.; Lu, S.-G.; Ke, Q.; et al. Significantly enhanced electrocaloric effect by composition modulation in lead-free BaTiO3-based ceramics. J. Mater. 2024, 11, 100903. [Google Scholar] [CrossRef]
- Krupska-Klimczak, M.; Ziewiec, K.; Jankowska-Sumara, I. The Influence of Measurement Conditions on the Electrocaloric Effect in Ferroelectric Ceramics of Modified Barium Titanate. Materials 2024, 17, 3329. [Google Scholar] [CrossRef]
- Lv, Z.; Wei, J.; Yang, T.; Sun, Z.; Xu, Z. Manipulation of Curie temperature and ferroelectric polarization for large electrocaloric strength in BaTiO3-based ceramics. Ceram. Int. 2020, 46, 14978–14984. [Google Scholar] [CrossRef]
- Asbani, B.; Gagou, Y.; Trček, M.; Dellis, J.-L.; Amjoud, M.; Lahmar, A.; Mezzane, D.; Kutnjak, Z.; El Marssi, M. Dielectric permittivity enhancement and large electrocaloric effect in the lead free (Ba0.8Ca0.2)1−xLa2x/3TiO3 ferroelectric ceramics. J. Alloys Compd. 2018, 730, 501–508. [Google Scholar] [CrossRef]
- Zhao, C.; Huang, Y.; Wu, X.; Gao, M.; Lin, T.; Lin, C. Evolution behavior of electrocaloric effect in BaTiO3-based ceramics with different phase structures and phase transitions. J. Am. Ceram. Soc. 2024, 107, 195–204. [Google Scholar] [CrossRef]
- Achkar, M.; Fasquelle, D.; Duponchel, B.; Poupin, C.; Sahraoui, A.H.; Longuemart, S. Electrocaloric characterization of samarium doped barium titanate ceramics synthesized by sol-gel process. Ceram. Int. 2024, 50, 13794–13801. [Google Scholar] [CrossRef]
- Xu, Z.; Wang, J.; Chen, Y. Improved electrocaloric effect of Ba0.7Sr0.3TiO3 ceramics doped with B and Mn. J. Sol-Gel Sci. Technol. 2023, 107, 483–489. [Google Scholar] [CrossRef]
- Niu, X.; Jian, X.; Gong, W.; Liang, W.; Gong, X.; Zhang, G.; Jiang, S.; Yu, K.; Zhao, X.; Yao, Y.; et al. Field-driven merging of polarizations and enhanced electrocaloric effect in BaTiO3-based lead-free ceramics. J. Adv. Ceram. 2022, 11, 1777–1788. [Google Scholar] [CrossRef]
- Qi, S.; Zhang, G.; Duan, L.; Zeng, T.; Cao, J. Electrocaloric effect in Pb-free Sr-doped BaTi0.9Sn0.1O3 ceramics. Mater. Res. Bull. 2017, 91, 31–35. [Google Scholar] [CrossRef]
- Niu, X.; Jian, X.; Chen, X.; Li, H.; Liang, W.; Yao, Y.; Tao, T.; Liang, B.; Lu, S.-G. Enhanced electrocaloric effect at room temperature in Mn2+ doped lead-free (BaSr)TiO3 ceramics via a direct measurement. J. Adv. Ceram. 2021, 10, 482–492. [Google Scholar] [CrossRef]
- Redhu, P.; Hooda, A.; Sharma, P.; Dahiya, S.; Punia, R.; Tandon, R.P. Study of energy storage and electrocaloric behavior of lead-free Fe-doped BCT ceramics. Ferroelectrics 2020, 569, 136–147. [Google Scholar] [CrossRef]
- Asbani, B.; Gagou, Y.; Ben Moumen, S.; Dellis, J.-L.; Lahmar, A.; Amjoud, M.; Mezzane, D.; El Marssi, M.; Rozic, B.; Kutnjak, Z. Large Electrocaloric Responsivity and Energy Storage Response in the Lead-Free Ba(GexTi1−x)O3 Ceramics. Materials 2022, 15, 5227. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Chauhan, A.; Vaish, R. Multiple caloric effects in (Ba0.865Ca0.135Zr0.1089Ti0.8811Fe0.01)O3 ferroelectric ceramic. Appl. Phys. Lett. 2015, 107, 042902. [Google Scholar] [CrossRef]
- Şanlı, K.; Adem, U. Electrocaloric properties of Ba0.8Sr0.2Ti1−xZrxO3 (0 ≤ x ≤ 0.1) system: The balance between the nature of the phase transition and phase coexistence. Ceram. Int. 2020, 46, 2213–2219. [Google Scholar] [CrossRef]
- Patel, S.; Chauhan, A.; Vaish, R. Large room temperature electrocaloric strength in bulk ferroelectric ceramics: An optimum solution. Phase Transit. 2016, 89, 1019–1028. [Google Scholar] [CrossRef]
- Wu, P.; Lou, X.; Li, J.; Li, T.; Gao, H.; Wu, M.; Wang, S.; Wang, X.; Bian, J.; Hao, X. Direct and indirect measurement of electrocaloric effect in lead-free (100-x)Ba(Hf0.2Ti0.8)O3-x(Ba0.7Ca0.3)TiO3 ceramics near multi-phase boundary. J. Alloys Compd. 2017, 725, 275–282. [Google Scholar] [CrossRef]
- Weyland, F.; Hayati, R.; Novak, N. Tuning of electrocaloric performance in (Ba0.85Ca0.15)(Zr0.1Ti0.9)O3 by induced relaxor-like behavior. Ceram. Int. 2019, 45, 11408–11412. [Google Scholar] [CrossRef]
- Lu, S.; Chen, G.; Zhang, Y.; Zhao, Z.; Li, F.; Lv, Z.; Ma, Z.; Wang, D.; Lu, C.; Li, S. Electrocaloric effect in lead-free 0.5Ba(Zr0.2Ti0.8)O3-0.5(Ba0.7Ca0.3)TiO3 ceramic measured by direct and indirect methods. Ceram. Int. 2018, 44, 21950–21955. [Google Scholar] [CrossRef]
- Sanlialp, M.; Shvartsman, V.V.; Acosta, M.; Lupascu, D.C.; Alford, N. Electrocaloric Effect in Ba(Zr,Ti)O3–(Ba,Ca)TiO3 Ceramics Measured Directly. J. Am. Ceram. Soc. 2016, 99, 4022–4030. [Google Scholar] [CrossRef]
- Bai, Y.; Han, X.; Qiao, L. Optimized electrocaloric refrigeration capacity in lead-free (1−x)BaZr0.2Ti0.8O3-xBa0.7Ca0.3TiO3 ceramics. Appl. Phys. Lett. 2013, 102, 252904. [Google Scholar] [CrossRef]
- Zhang, H.F.; Chen, X.; Gao, J.; Lam, K.H.; Liang, S.D.; Fei, L.F.; Mak, C.L.; Chen, J.F. The Fabrication and Electrocaloric Effect of Bimodal-Grain Structure (Ba0.60Sr0.40)TiO3 Using the Induced Abnormal Grain Growth Method. IOP Conf. Ser. Mater. Sci. Eng. 2019, 678, 012138. [Google Scholar] [CrossRef]
- Srikanth, K.S.; Patel, S.; Vaish, R. Electrocaloric behavior and temperature dependent scaling of dynamic hysteresis of BaxSr1-xTiO3 (x = 0.7, 0.8 and 0.9) bulk ceramics. J. Aust. Ceram. Soc. 2018, 54, 439–450. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Wu, S.; Chen, X. Effect of phase transition on electrocaloric effect in Indium substituted BaTiO3 ceramics. J. Alloys Compd. 2020, 822, 153632. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, X.; Wu, J.; Wu, S.; Chen, X. Electrocaloric effect in relaxor ferroelectric Ba(Ti1−xYx)O3−x/2 ceramics over a broad temperature range. J. Alloys Compd. 2017, 729, 57–63. [Google Scholar] [CrossRef]
- Li, J.; Zhang, D.; Qin, S.; Li, T.; Wu, M.; Wang, D.; Bai, Y.; Lou, X. Large room-temperature electrocaloric effect in lead-free BaHf TiO3 ceramics under low electric field. Acta Mater. 2016, 115, 58–67. [Google Scholar] [CrossRef]
- Srikanth, K.; Vaish, R. Enhanced electrocaloric, pyroelectric and energy storage performance of BaCexTi1−xO3 ceramics. J. Eur. Ceram. Soc. 2017, 37, 3927–3933. [Google Scholar] [CrossRef]
- Maiwa, H. Temperature dependences of the electromechanical and electrocaloric properties of Ba(Zr,Ti)O3 and (Ba,Sr)TiO3 ceramics. Jpn. J. Appl. Phys. 2017, 56, 10PC05. [Google Scholar] [CrossRef]
- Sanlialp, M.; Shvartsman, V.V.; Faye, R.; Karabasov, M.O.; Molin, C.; Gebhardt, S.; Defay, E.; Lupascu, D.C. Quasi-adiabatic calorimeter for direct electrocaloric measurements. Rev. Sci. Instruments 2018, 89, 034903. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Li, D.-D.; Lu, B.; Yao, Y.-B.; Tao, T.; Liang, B.; Lu, W.-H.; Luo, G.-L.; Lu, S.-G. Large electrocaloric effect obtained in Ba(SnxTi1−x)O3 lead-free ceramics using direct and indirect measurements. J. Adv. Dielectr. 2018, 8, 1850038. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, L.; Gao, S.; Liu, J.Q.; Xu, B.; Xia, Y.D.; Yin, J.; Liu, Z.G. Large electrocaloric effect in Ba(Ti1−xSnx)O3 ceramics over a broad temperature region. AIP Adv. 2015, 5, 047134. [Google Scholar] [CrossRef]
- Sanlialp, M.; Luo, Z.; Shvartsman, V.V.; Wei, X.; Liu, Y.; Dkhil, B.; Lupascu, D.C. Direct measurement of electrocaloric effect in lead-free Ba(SnxTi1−x)O3 ceramics. Appl. Phys. Lett. 2017, 111, 173903. [Google Scholar] [CrossRef]
- Luo, Z.; Zhang, D.; Liu, Y.; Zhou, D.; Yao, Y.; Liu, C.; Dkhil, B.; Ren, X.; Lou, X. Enhanced electrocaloric effect in lead-free BaTi1−xSnxO3 ceramics near room temperature. Appl. Phys. Lett. 2014, 105, 102904. [Google Scholar] [CrossRef]
- Asbani, B.; Dellis, J.-L.; Lahmar, A.; Courty, M.; Amjoud, M.; Gagou, Y.; Djellab, K.; Mezzane, D.; Kutnjak, Z.; El Marssi, M. Lead-free Ba0.8Ca0.2(ZrxTi1−x)O3 ceramics with large electrocaloric effect. Appl. Phys. Lett. 2015, 106, 042902. [Google Scholar] [CrossRef]
- Wang, X.; Tian, F.; Zhao, C.; Wu, J.; Liu, Y.; Dkhil, B.; Zhang, M.; Gao, Z.; Lou, X. Giant electrocaloric effect in lead-free Ba0.94Ca0.06Ti1−xSnxO3 ceramics with tunable Curie temperature. Appl. Phys. Lett. 2015, 107, 252905. [Google Scholar] [CrossRef]
- Singh, G.; Tiwari, V.S.; Gupta, P.K. Electro-caloric effect in (Ba1−xCax)(Zr0.05Ti0.95)O3: A lead-free ferroelectric material. Appl. Phys. Lett. 2013, 103, 202903. [Google Scholar] [CrossRef]
- Bai, Y.; Han, X.; Ding, K.; Qiao, L. Combined effects of diffuse phase transition and microstructure on the electrocaloric effect in Ba1−xSrxTiO3 ceramics. Appl. Phys. Lett. 2013, 103, 162902. [Google Scholar] [CrossRef]
- Zhang, Y. Thermal hysteresis and electrocaloric effect in Ba1−xZrxTiO. J. Phys. Chem. Solids 2018, 115, 326–331. [Google Scholar] [CrossRef]
- Liu, X.Q.; Chen, T.T.; Fu, M.S.; Wu, Y.J.; Chen, X.M. Electrocaloric effects in spark plasma sintered Ba0.7Sr0.3TiO3-based ceramics: Effects of domain sizes and phase constitution. Ceram. Int. 2014, 40, 11269–11276. [Google Scholar] [CrossRef]
- Li, F.; Chen, G.; Liu, X.; Zhai, J.; Shen, B.; Li, S.; Li, P.; Yang, K.; Zeng, H.; Yan, H. Type–I pseudo–first–order phase transition induced electrocaloric effect in lead–free Bi0.5Na0.5TiO3–0.06BaTiO3 ceramics. Appl. Phys. Lett. 2017, 110, 182904. [Google Scholar] [CrossRef]
- Du, H.; Chang, Y.; Li, C.; Hu, Q.; Pang, J.; Sun, Y.; Weyland, F.; Novak, N.; Jin, L. Ultrahigh room temperature electrocaloric response in lead-free bulk ceramics via tape casting. J. Mater. Chem. C 2019, 7, 6860–6866. [Google Scholar] [CrossRef]
- Singh, G.; Bhaumik, I.; Ganesamoorthy, S.; Bhatt, R.; Karnal, A.K.; Tiwari, V.S.; Gupta, P.K. Electro-caloric effect in 0.45BaZr0.2Ti0.8O3-0.55Ba0.7Ca0.3TiO3 single crystal. Appl. Phys. Lett. 2013, 102, 082902. [Google Scholar] [CrossRef]
- Sanlialp, M.; Shvartsman, V.V.; Acosta, M.; Dkhil, B.; Lupascu, D.C. Strong electrocaloric effect in lead-free 0.65Ba(Zr0.2Ti0.8)O3-0.35(Ba0.7Ca0.3)TiO3 ceramics obtained by direct measurements. Appl. Phys. Lett. 2015, 106, 062901. [Google Scholar] [CrossRef]
- Bai, Y.; Han, F.; Xie, S.; Li, J.; Qin, S.; Li, J.; Qiao, L.; Guo, D. Thickness dependence of electrocaloric effect in high-temperature sintered Ba0.8Sr0.2TiO3 ceramics. J. Alloys Compd. 2018, 736, 57–61. [Google Scholar] [CrossRef]
- Liu, X.Q.; Chen, T.T.; Wu, Y.J.; Chen, X.M.; Valant, M. Enhanced Electrocaloric Effects in Spark Plasma-Sintered Ba0.65Sr0.35TiO3-Based Ceramics at Room Temperature. J. Am. Ceram. Soc. 2013, 96, 1021–1023. [Google Scholar] [CrossRef]
- Kutnjak, Z.; Rožič, B.; Pirc, R. Electrocaloric Effect: Theory, Measurements, and Applications. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 1–19. [Google Scholar] [CrossRef]
- Valant, M. Electrocaloric materials for future solid-state refrigeration technologies. Prog. Mater. Sci. 2012, 57, 980–1009. [Google Scholar] [CrossRef]
- Liu, Y.; Scott, J.F.; Dkhil, B. Direct and indirect measurements on electrocaloric effect: Recent developments and perspectives. Appl. Phys. Rev. 2016, 3, 031102. [Google Scholar] [CrossRef]
- Pirc, R.; Kutnjak, Z.; Blinc, R.; Zhang, Q.M. Electrocaloric effect in relaxor ferroelectrics. J. Appl. Phys. 2011, 110, 074113. [Google Scholar] [CrossRef]
- Cheng, X.; Weyland, F.; Novak, N.; Li, Y. Indirect Electrocaloric Evaluation: Influence of Polarization Hysteresis Measurement Frequency. Phys. Status Solidi (A) 2019, 216, 1900684. [Google Scholar] [CrossRef]
- Bai, Y.; Zheng, G.; Shi, S. Direct measurement of giant electrocaloric effect in BaTiO3 multilayer thick film structure beyond theoretical prediction. Appl. Phys. Lett. 2010, 96, 192902. [Google Scholar] [CrossRef]
- Kaddoussi, H.; Lahmar, A.; Gagou, Y.; Asbani, B.; Dellis, J.-L.; Cordoyiannis, G.; Allouche, B.; Khemakhem, H.; Kutnjak, Z.; El Marssi, M. Indirect and direct electrocaloric measurements of (Ba1−xCax)(Zr0.1Ti0.9)O3 ceramics (x = 0.05, x = 0.20). J. Alloys Compd. 2016, 667, 198–203. [Google Scholar] [CrossRef]
- Asbani, B.; Dellis, J.L.; Gagou, Y.; Kaddoussi, H.; Lahmar, A.; Amjoud, M.; El Marssi, M. Electrocaloric effect in Ba0.2Ca0.8Ti0.95Ge0.05O3 determined by a new pyroelectric method. Europhys. Lett. 2015, 111, 57008. [Google Scholar] [CrossRef]
- Sebald, G.; Guyomar, D.; Agbossou, A. On thermoelectric and pyroelectric energy harvesting. Smart Mater. Struct. 2009, 18, 125006. [Google Scholar] [CrossRef]
- Moya Raposo, X.E. Effect of inactive volume on thermocouple measurements of electrocaloric temperature change in multilayer capacitors of 0.9Pb(Mg1/3Nb2/3)O3–0.1PbTiO3. J. Phys. D Appl. Phys. 2017, 50, 42. [Google Scholar] [CrossRef]
- Liu, Y.; Dkhil, B.; Defay, E. Spatially resolved imaging of electrocaloric effect and the resultant heat flux in multilayer capacitors. ACS Energy Lett. 2016, 1, 521–528. [Google Scholar] [CrossRef]
- Borkar, S.N.; Aggarwal, P.; Deshpande, V. Effect of calcium substitution on structural, dielectric, ferroelectric, piezoelectric, and energy storage properties of BaTiO3. Curr. Appl. Phys. 2022, 39, 205–213. [Google Scholar] [CrossRef]
- Ali, S.; Ahmad, S.; Farooq, J.; Uddin, S.; Chen, B.; Ullah, I.; Alam, M.M. The effect of A-site strontium substitution on the energy storage properties of ferroelectric BaZr0.2Ti0.8O3 system. Ceram. Int. 2025, 51, 14821–14833. [Google Scholar] [CrossRef]
- Younas, U.; Atif, M.; Anjum, A.; Nadeem, M.; Ali, T.; Shaheen, R.; Khalid, W.; Ali, Z. Fabrication of La3+ doped Ba1−xLaxTiO3 ceramics with improved dielectric and ferroelectric properties using a composite-hydroxide-mediated method. RSC Adv. 2023, 13, 5293–5306. [Google Scholar] [CrossRef]
- Xu, Q.; Li, Z. Dielectric and ferroelectric behaviour of Zr-doped BaTiO3 perovskites. Process. Appl. Ceram. 2020, 14, 188–194. [Google Scholar] [CrossRef]
- Tang, Q.; Shi, Z.; Xia, S.; Bie, X.; Yang, Y.; Bian, D.; Xu, D.; Fan, R. Enhanced dielectric properties of Sr2+ and Zr4+ doped BaTiO3 colossal permittivity metamaterials. EPJ Appl. Metamaterials 2024, 11, 13. [Google Scholar] [CrossRef]
- Anwar, S.; Sagdeo, P.; Lalla, N. Ferroelectric relaxor behavior in hafnium doped barium-titanate ceramic. Solid State Commun. 2006, 138, 331–336. [Google Scholar] [CrossRef]
- Brzozowski, E.; Castro, M. Influence of Nb5+ and Sb3+ dopants on the defect profile, PTCR effect and GBBL characteristics of BaTiO3 ceramics. J. Eur. Ceram. Soc. 2004, 24, 2499–2507. [Google Scholar] [CrossRef]
- Si, F.; Tang, B.; Fang, Z.; Zhang, S. Nb-Doped 0.8BaTiO3-0.2Bi(Mg0.5Ti0.5)O3 Ceramics with Stable Dielectric Properties at High Temperature. Crystals 2017, 7, 168. [Google Scholar] [CrossRef]
- Islam, A.; Momin, A.; Nesa, M. Effect of Fe doping on the structural, optical and electronic properties of BaTiO3: DFT based calculation. Chin. J. Phys. 2019, 60, 731–738. [Google Scholar] [CrossRef]
- Horchidan, N.; Lukacs, V.A.; Asandulesa, M.; Stoian, G.; Ciomaga, C.E.; Mitoseriu, L. Exploring grain size and composition effects on the functional properties of BaGexTi1−xO3 ceramics. J. Eur. Ceram. Soc. 2025, 45, 116997. [Google Scholar] [CrossRef]
- Sun, J.; Wang, S.; Tong, L.; Li, Q.; Yu, Y.; Li, Y.; Huang, S.; Guo, Y.; Wang, C. Enhanced dielectric properties in (In, Nb) co-doped BaTiO3 ceramics. Mater. Lett. 2017, 200, 51–54. [Google Scholar] [CrossRef]
- Sareecha, N.; Shah, W.; Mirza, M.; Maqsood, A.; Awan, M. Electrical investigations of Bi-doped BaTiO3 ceramics as a function of temperature. Phys. B Condens. Matter 2018, 530, 283–289. [Google Scholar] [CrossRef]
- Ismail, F.A.; Osman, R.A.M.; Idris, M.S. Review on dielectric properties of rare earth doped barium titanate. In Proceedings of the 2nd International Conference on Functional Materials and Metallurgy (ICOFM 2016), Penang, Malaysia, 28 May 2016; p. 090005. [Google Scholar]
- Lu, S.G.; Rožič, B.; Zhang, Q.M.; Kutnjak, Z.; Pirc, R.; Lin, M.; Li, X.; Gorny, L. Comparison of directly and indirectly measured electrocaloric effect in relaxor ferroelectric polymers. Appl. Phys. Lett. 2010, 97, 202901. [Google Scholar] [CrossRef]
- Rožič, B.; Kosec, M.; Uršič, H.; Holc, J.; Malič, B.; Zhang, Q.M.; Blinc, R.; Pirc, R.; Kutnjak, Z. Influence of the critical point on the electrocaloric response of relaxor ferroelectrics. J. Appl. Phys. 2011, 110, 064118. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Mohammed, A.; Kora, R. A comprehensive review on ensemble deep learning: Opportunities and challenges. J. King Saud Univ. Comput. Inf. Sci. 2023, 35, 757–774. [Google Scholar] [CrossRef]
- Mayr, A.; Binder, H.; Gefeller, O.; Schmid, M. The evolution of boosting algorithms. Methods Inf. Med. 2014, 53, 419–427. [Google Scholar] [PubMed]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Liu, W.; Ren, X. Large Piezoelectric Effect in Pb-Free Ceramics. Phys. Rev. Lett. 2009, 103, 257602. [Google Scholar] [CrossRef] [PubMed]
- He, J.; Li, J.; Liu, C.; Wang, C.; Zhang, Y.; Wen, C.; Xue, D.; Cao, J.; Su, Y.; Qiao, L.; et al. Machine learning identified materials descriptors for ferroelectricity. Acta Mater. 2021, 209, 116815. [Google Scholar] [CrossRef]
- He, J.; Wang, C.; Li, J.; Liu, C.; Xue, D.; Cao, J.; Su, Y.; Qiao, L.; Lookman, T.; Bai, Y. Machine learning assisted prediction of dielectric temperature spectrum of ferroelectrics. J. Adv. Ceram. 2023, 12, 1793–1804. [Google Scholar] [CrossRef]
- Sun, Z.; Gao, R.; Wang, P.; Liu, X.; Bai, Y.; Luo, J.; Yang, H.; Hu, W. Accelerating the prediction of remanent polarization in multicomponent ferroelectrics by using variational autoencoder-based data augmentation. J. Mater. Chem. C 2025. [Google Scholar] [CrossRef]
- Beckman, S.P.; Wan, L.F.; Barr, J.A.; Nishimatsu, T. Effective Hamiltonian methods for predicting the electrocaloric behavior of BaTiO3. Mater. Lett. 2012, 89, 254–257. [Google Scholar] [CrossRef]
- Marathe, M.; Grünebohm, A.; Nishimatsu, T.; Entel, P.; Ederer, C. First-principles-based calculation of the electrocaloric effect in BaTiO3: A comparison of direct and indirect methods. Phys. Rev. B 2016, 93, 054110. [Google Scholar] [CrossRef]
- Wojdeł, J.C.; Hermet, P.; Ljungberg, M.P.; Ghosez, P.; Íñiguez, J. First-principles model potentials for lattice-dynamical studies: General methodology and example of application to ferroic perovskite oxides. J. Physics Condens. Matter 2013, 25, 305401. [Google Scholar] [CrossRef]
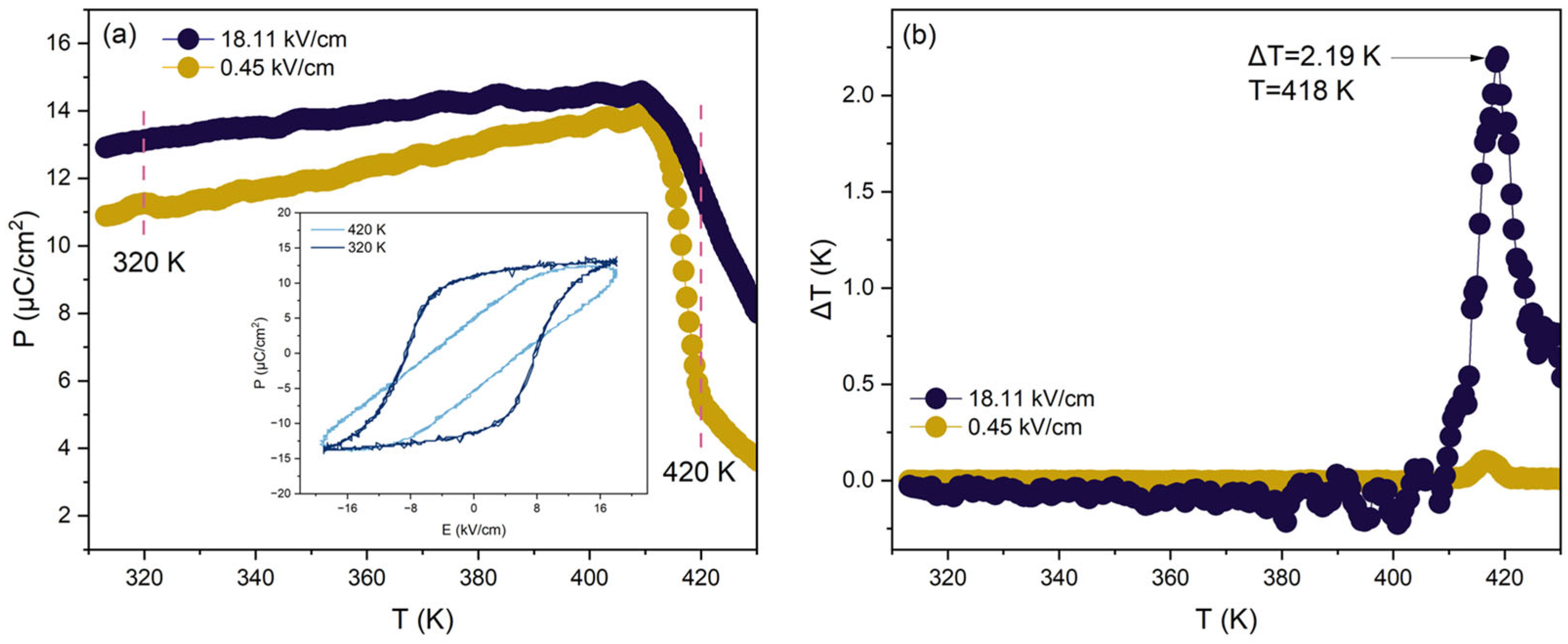
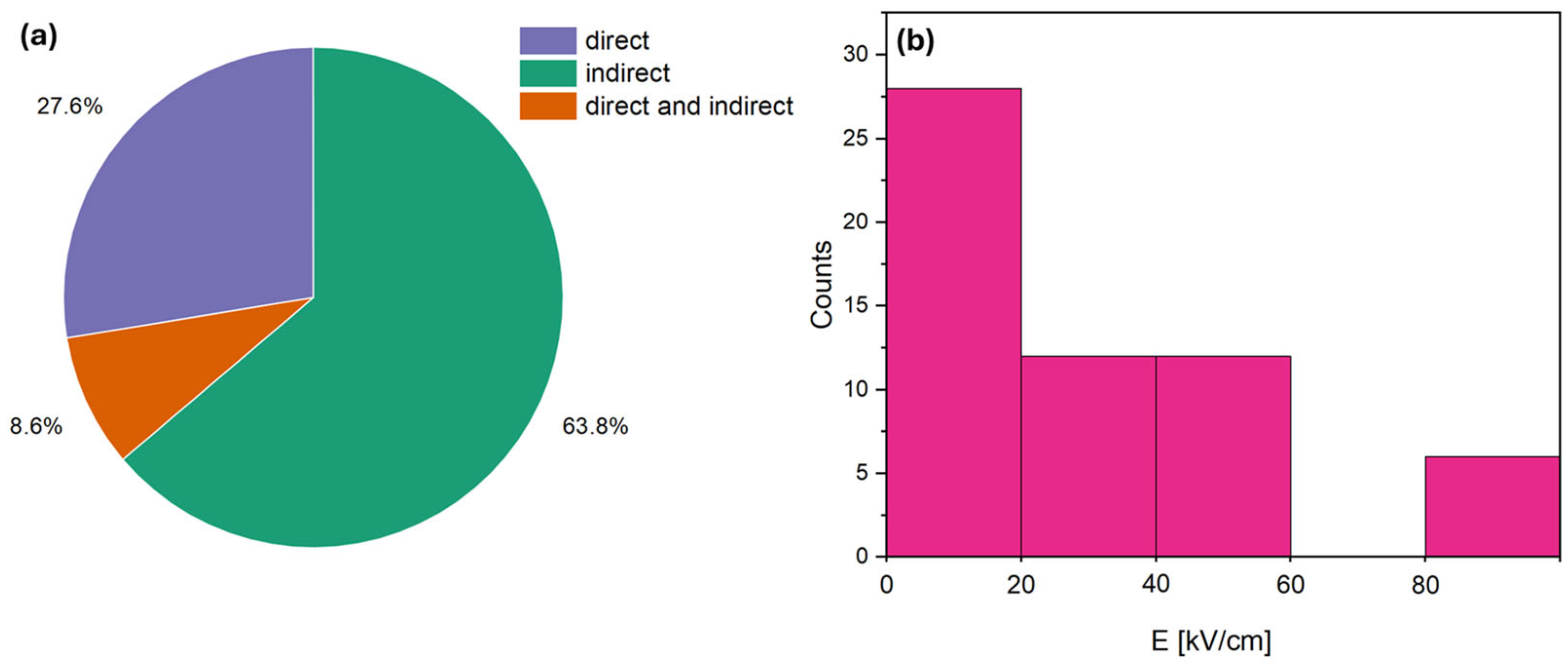
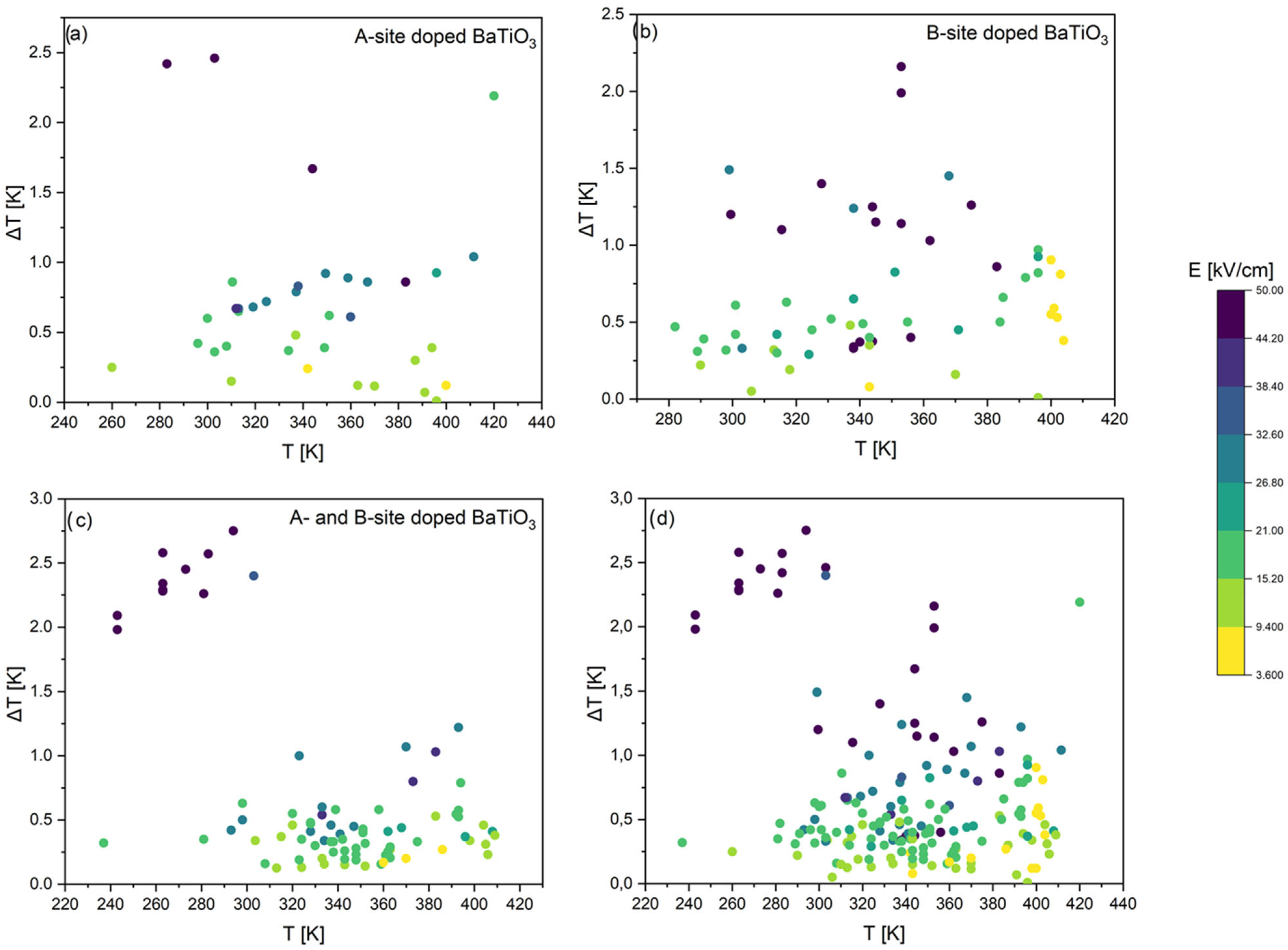
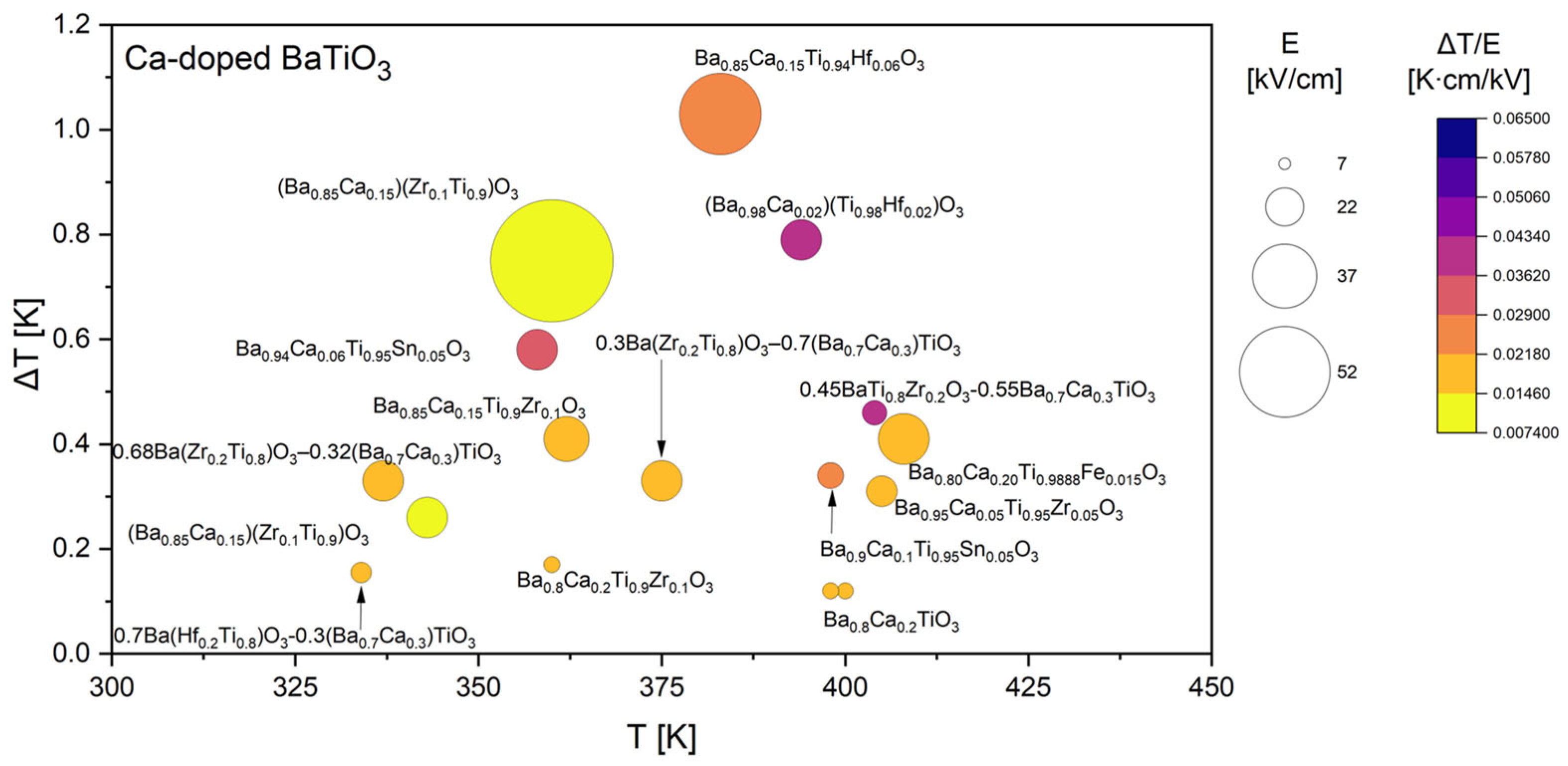
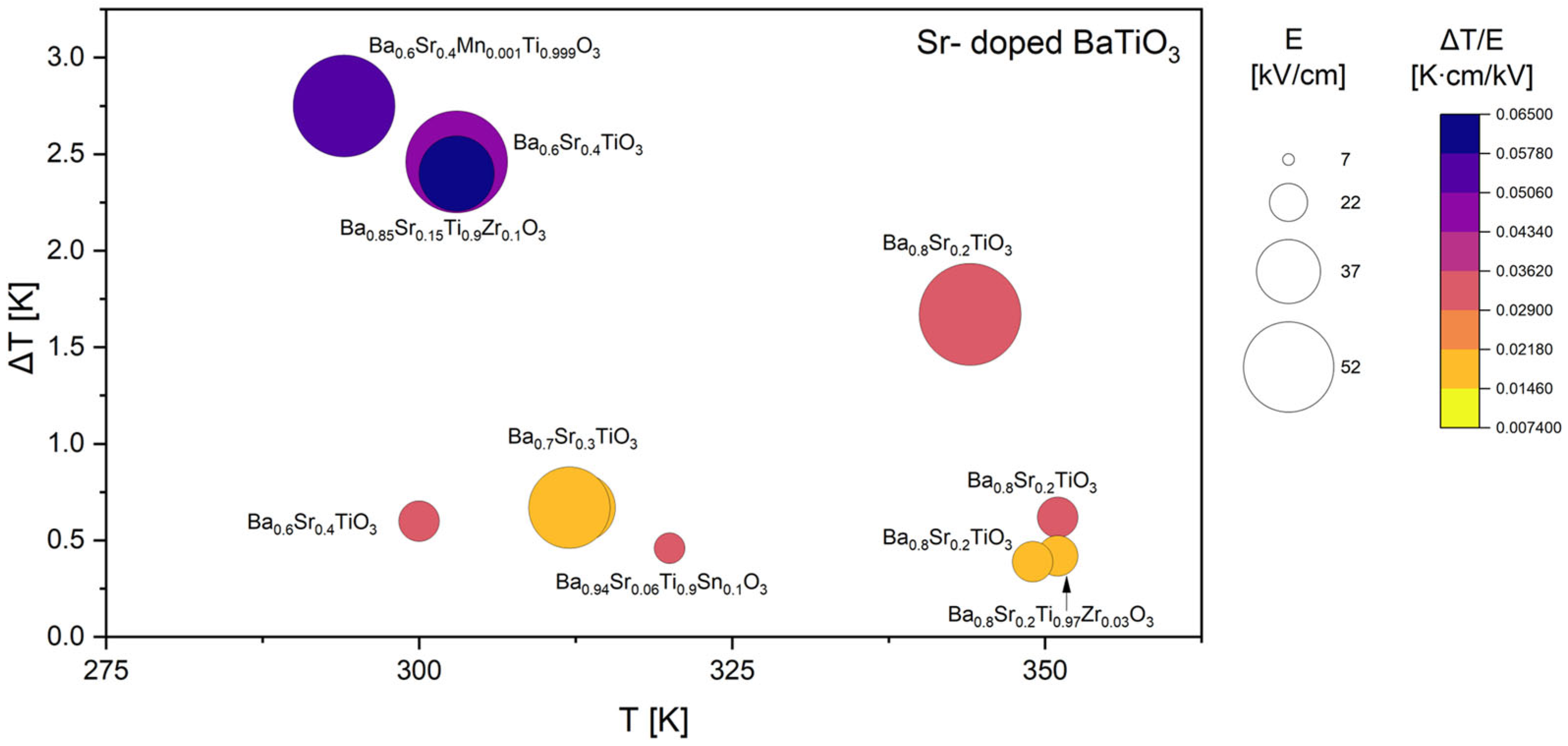

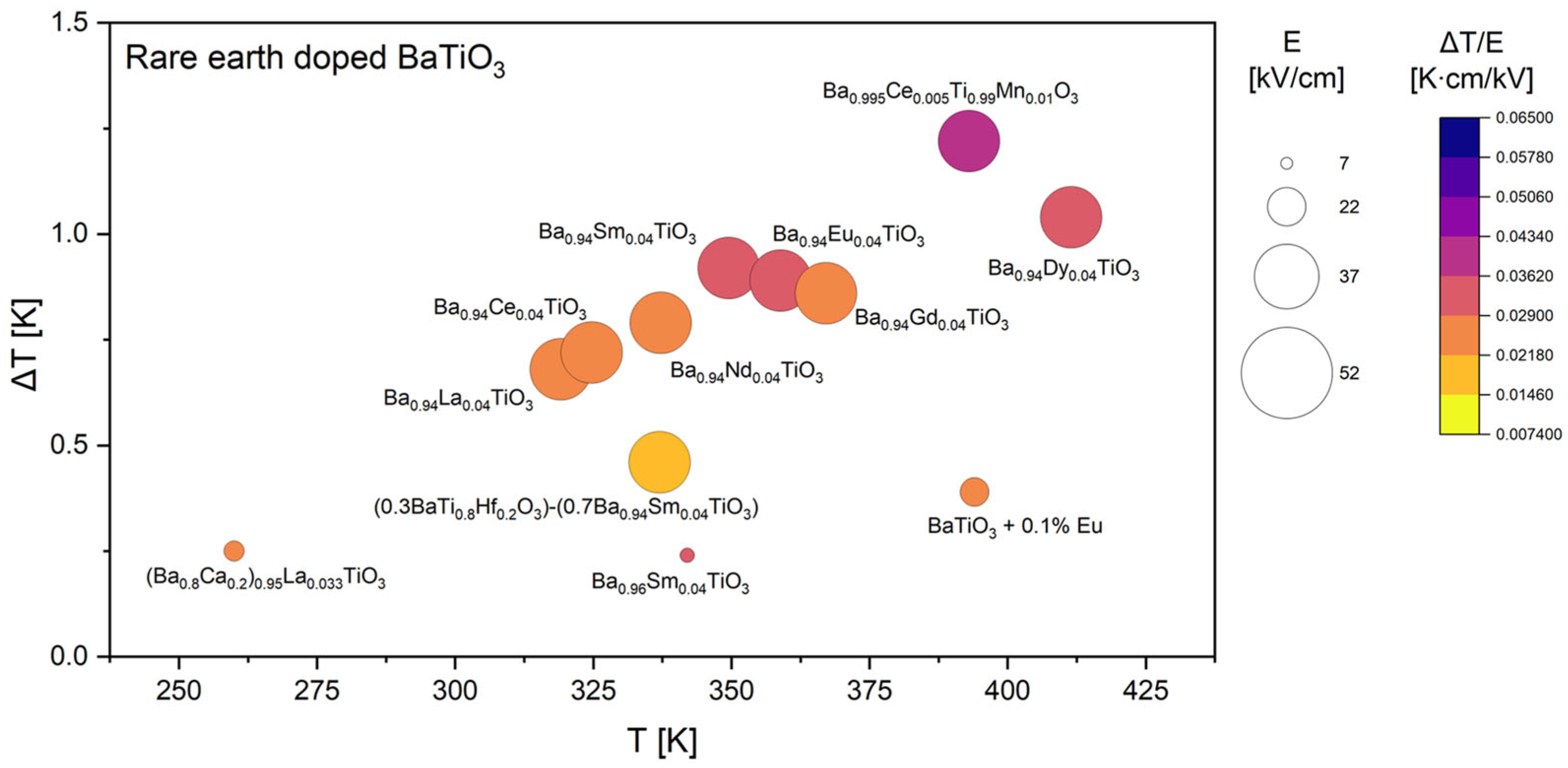
| Composition | ΔT [K] | E [kV/cm] | T [K] | [K·cm/kV] | Method | Ref. |
|---|---|---|---|---|---|---|
| Ba0.94Sm0.04TiO3 | 0.920 | 30 | 350 | 0.0307 | I | [22] |
| Ba0.94Dy0.04TiO3 | 1.040 | 30 | 412 | 0.0347 | I | |
| Ba0.94La0.04TiO3 | 0.680 | 30 | 319 | 0.0227 | I | |
| Ba0.94Ce0.04TiO3 | 0.720 | 30 | 325 | 0.0240 | I | |
| Ba0.94Nd0.04TiO3 | 0.790 | 30 | 337 | 0.0263 | I | |
| Ba0.94Eu0.04TiO3 | 0.890 | 30 | 359 | 0.0297 | I | |
| Ba0.94Gd0.04TiO3 | 0.860 | 30 | 367 | 0.0287 | I |
| Study | Dataset Size and Type | Features | ML Methods | Validation Strategy | Strengths | Limitations |
|---|---|---|---|---|---|---|
| Gong et al. [12] | ~97 compositions, >4000 datapoints (literature) | Magpie descriptors, dielectric constant, Curie temperature, experimental conditions | XGBoost regression | t-SNE + k-means clustering, extensive grid search | R2 ≈ 0.77, RMSE ~0.38 K; captured physical trends (EN differences, ionic charge) | Dependent on heterogeneous literature data |
| Su et al. [13] | BaTiO3-based ceramics, indirect and direct data separated | Ionic radii, electronegativity, tolerance factor, dopant encoding | SVR (Gaussian kernels), Random Forest, ensemble models | Bootstrap resampling, grid search + cross-validation | Robust predictions for both direct and indirect datasets; interactive web app | Limited by dataset size and diversity |
| Bayir and Mensur [14] | 2188 entries (BCZT ceramics, literature) | Magpie descriptors, Curie temperature, processing parameters | XGBoost + Bayesian optimization (Optuna TPE) | ShuffleSplit + group-aware cross-validation | R2 ≈ 0.99, MAE ≈ 0.02 °C; identified optimal BCZT composition | High accuracy but dataset-specific |
| Yuan et al. [15] | ~195 compositions (BaTiO3-based) | Compositional descriptors (NCT, tolerance factor, atomic volume, EN, etc.) | SVR (radial kernel), Gaussian process surrogate models | Bootstrap (1000 samples) + 10-fold CV | Predicted Tc and polarization; surrogate model links polarization → ΔS | Requires indirect inference, not direct ΔT data |
| Method | Mechanism Captured | Typical Simulation Scale | Strengths | Limitations | Ref. |
|---|---|---|---|---|---|
| Effective Hamiltonian | Polar soft modes, coupling to strain; can include disorder if parameterized | 103–105 unit cells, MC/MD | Mechanistic insight into ΔT, efficient for phase transitions, established for BTO/PTO, BZT | Requires careful DFT parametrization; difficult to include extrinsic defects; relaxors need large cells | [111] |
| Second principles | Anharmonic couplings, elasticity, mesoscale domains | 105–107 atoms, longer MD | Captures domain/nanoregion effects; scalable to realistic microstructures | Parametrization heavy, limited transferability; still idealized vs. experiments | [113] |
| First principles MD | Full electronic structure, phonons, vibrational entropy | 103 atoms, short times | Highest fidelity per atom; captures electronic contributions | Too small/short to capture domains/disorder; very costly | [112] |
| Machine learning | Correlations between composition/process descriptors and ΔT | data-dependent/no single typical scale | Fast screening; finds statistical trends | Accuracy limited by data quality; limited mechanistics insights | [12,13,14,15] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krupska-Klimczak, M.; Frontczak, M.; Świerczyński, Z.; Semenov, S.; Kajewski, D.; Jankowska-Sumara, I. Electrocaloric Effect on Lead-Free Ferroelectrics: Challenges in Identifying Trends and Evaluating Predictive Models. Materials 2025, 18, 4444. https://doi.org/10.3390/ma18194444
Krupska-Klimczak M, Frontczak M, Świerczyński Z, Semenov S, Kajewski D, Jankowska-Sumara I. Electrocaloric Effect on Lead-Free Ferroelectrics: Challenges in Identifying Trends and Evaluating Predictive Models. Materials. 2025; 18(19):4444. https://doi.org/10.3390/ma18194444
Chicago/Turabian StyleKrupska-Klimczak, Magdalena, Michał Frontczak, Zdobysław Świerczyński, Serhii Semenov, Dariusz Kajewski, and Irena Jankowska-Sumara. 2025. "Electrocaloric Effect on Lead-Free Ferroelectrics: Challenges in Identifying Trends and Evaluating Predictive Models" Materials 18, no. 19: 4444. https://doi.org/10.3390/ma18194444
APA StyleKrupska-Klimczak, M., Frontczak, M., Świerczyński, Z., Semenov, S., Kajewski, D., & Jankowska-Sumara, I. (2025). Electrocaloric Effect on Lead-Free Ferroelectrics: Challenges in Identifying Trends and Evaluating Predictive Models. Materials, 18(19), 4444. https://doi.org/10.3390/ma18194444










