Simulation-Based Study on the Performance of NSM-CFRP Strengthening in Prestressed Concrete T-Beams Under Seismic Loading
Abstract
1. Introduction
2. Novelty of the Research
3. Specimen Configuration
4. Development of the FE Model
4.1. Geometry and Element Description
4.2. Constitutive Models of Materials
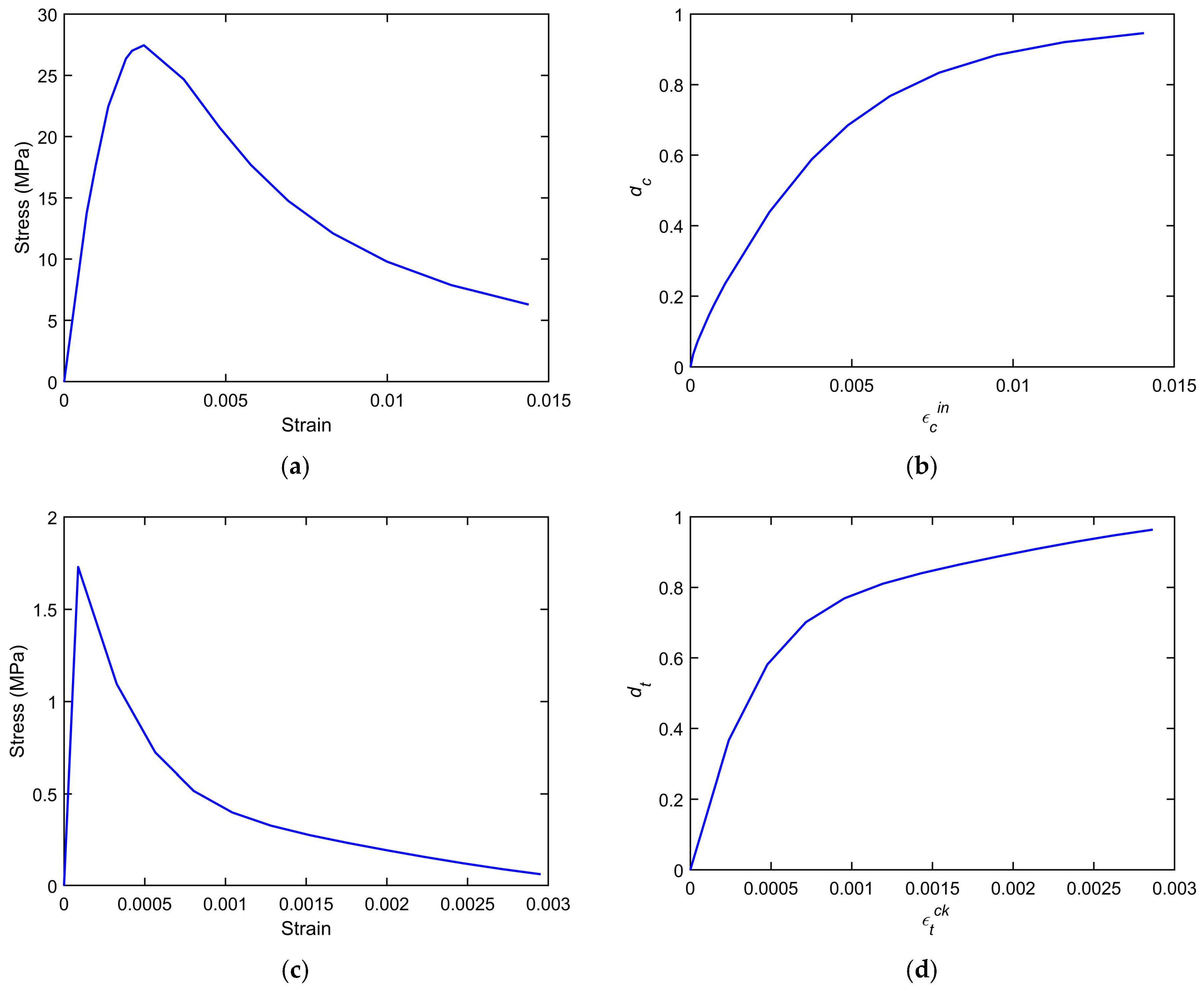
4.2.1. Concrete
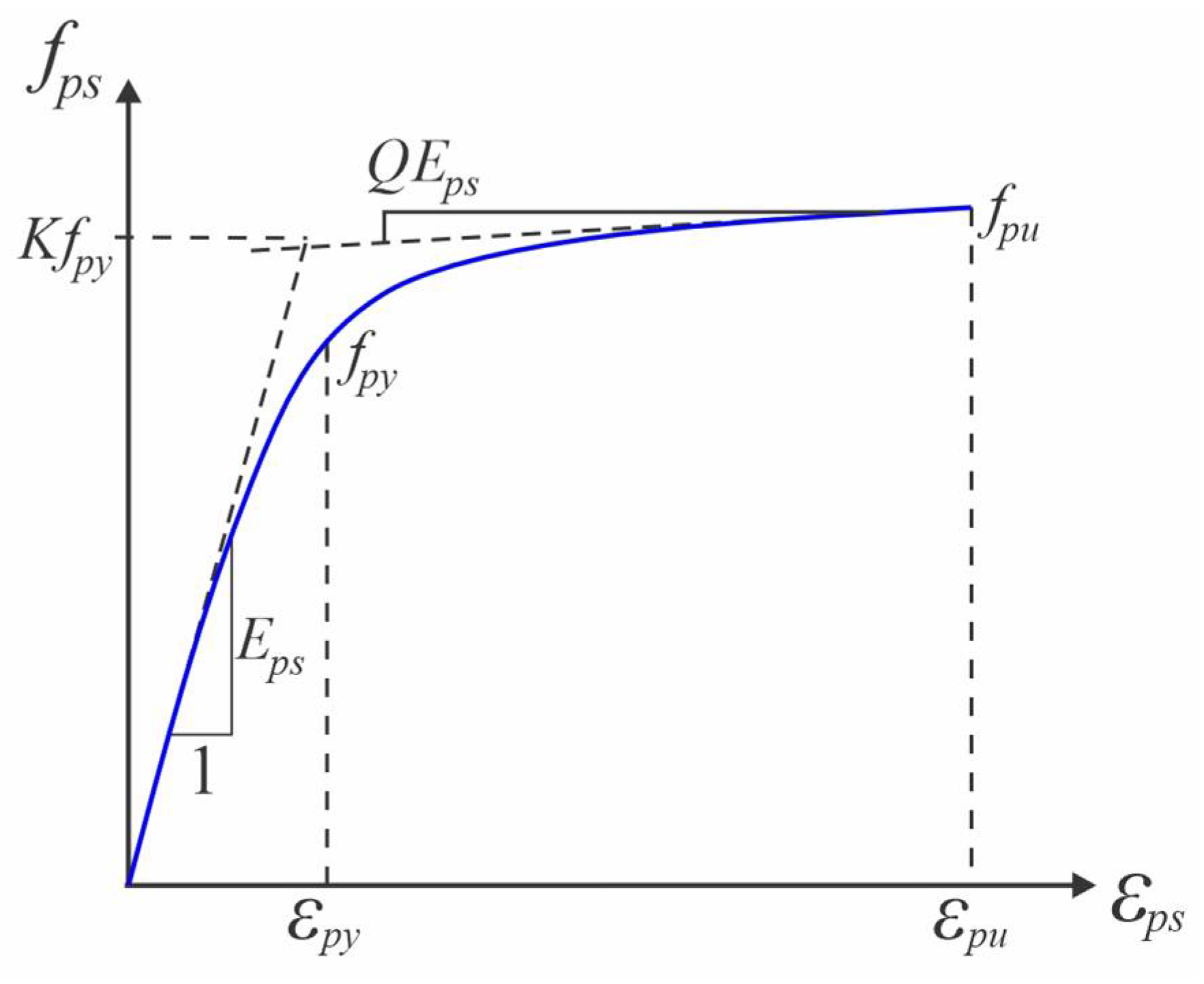
4.2.2. Steel Rebar and Prestressing Strand
4.2.3. CFRP Composites
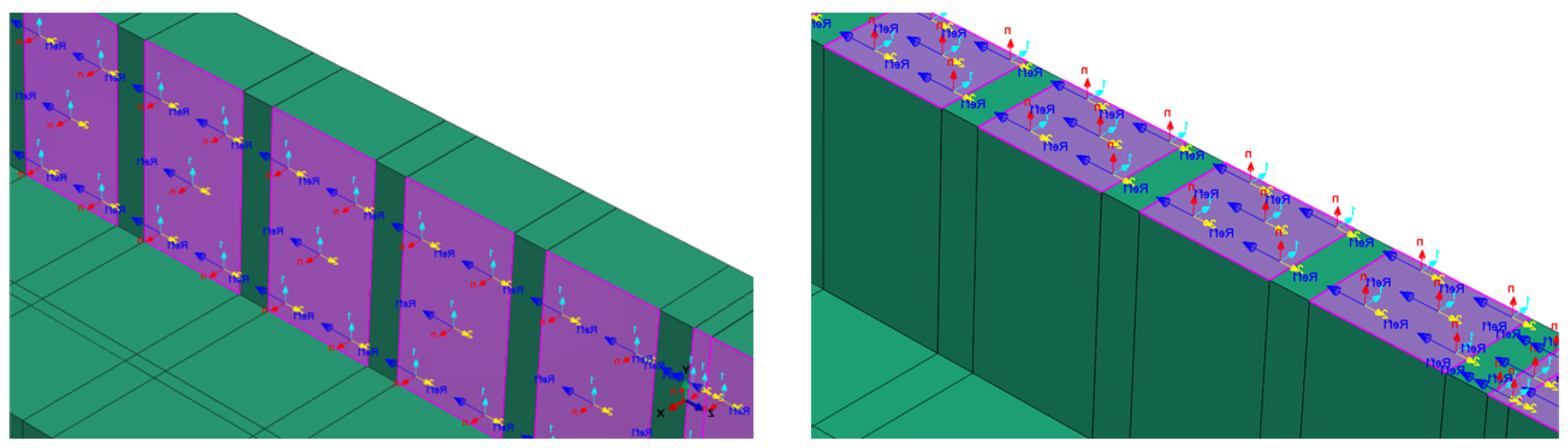
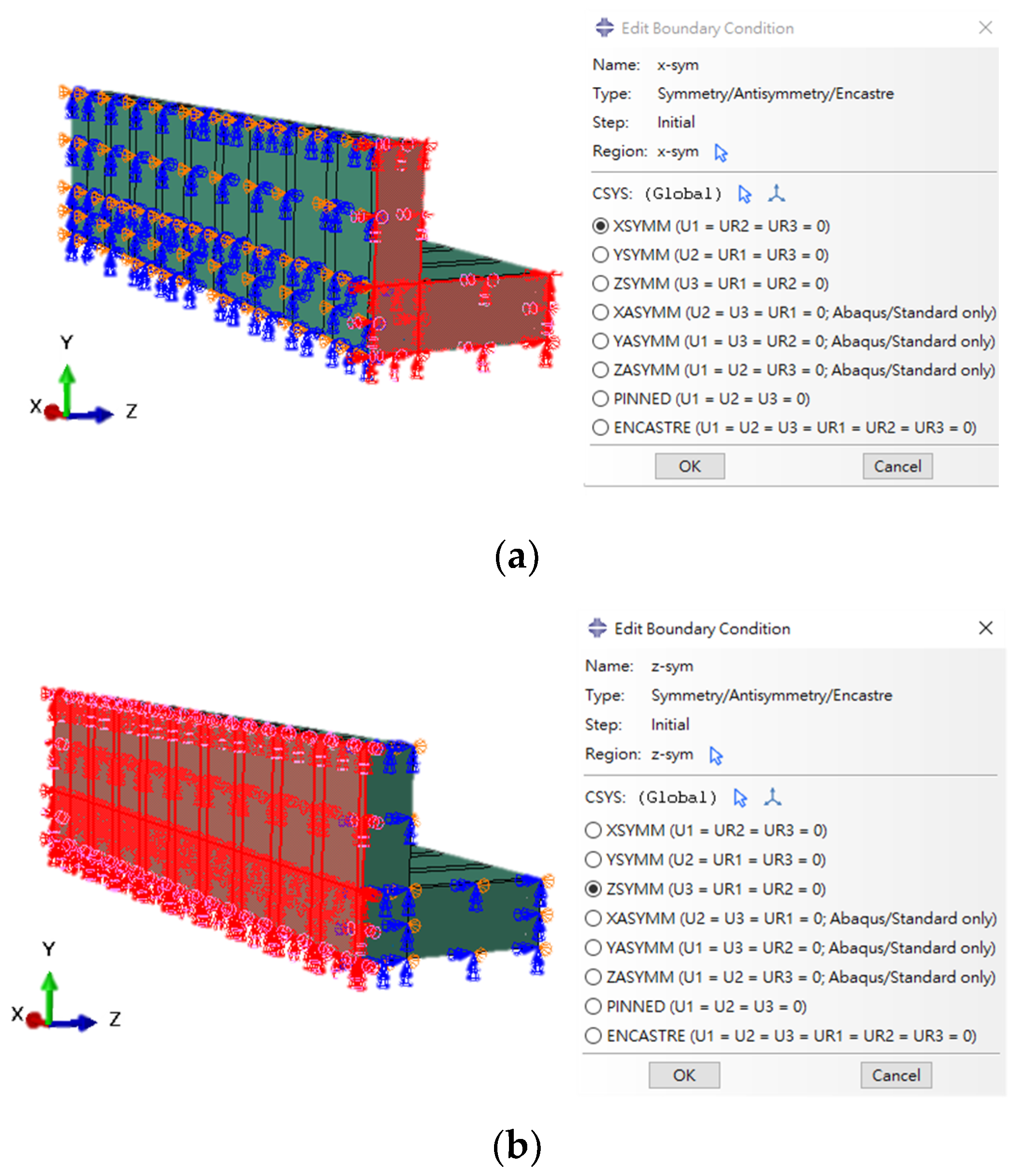
4.3. Boundary Conditions
4.4. Contact Interaction
4.5. Predefined Field
5. Results and Discussion
5.1. Assessment of Numerical Model Accuracy
5.1.1. RC T-Beams Strengthened with CFRP Subjected to Cyclic Loading
5.1.2. Prestressed Concrete I-Beam
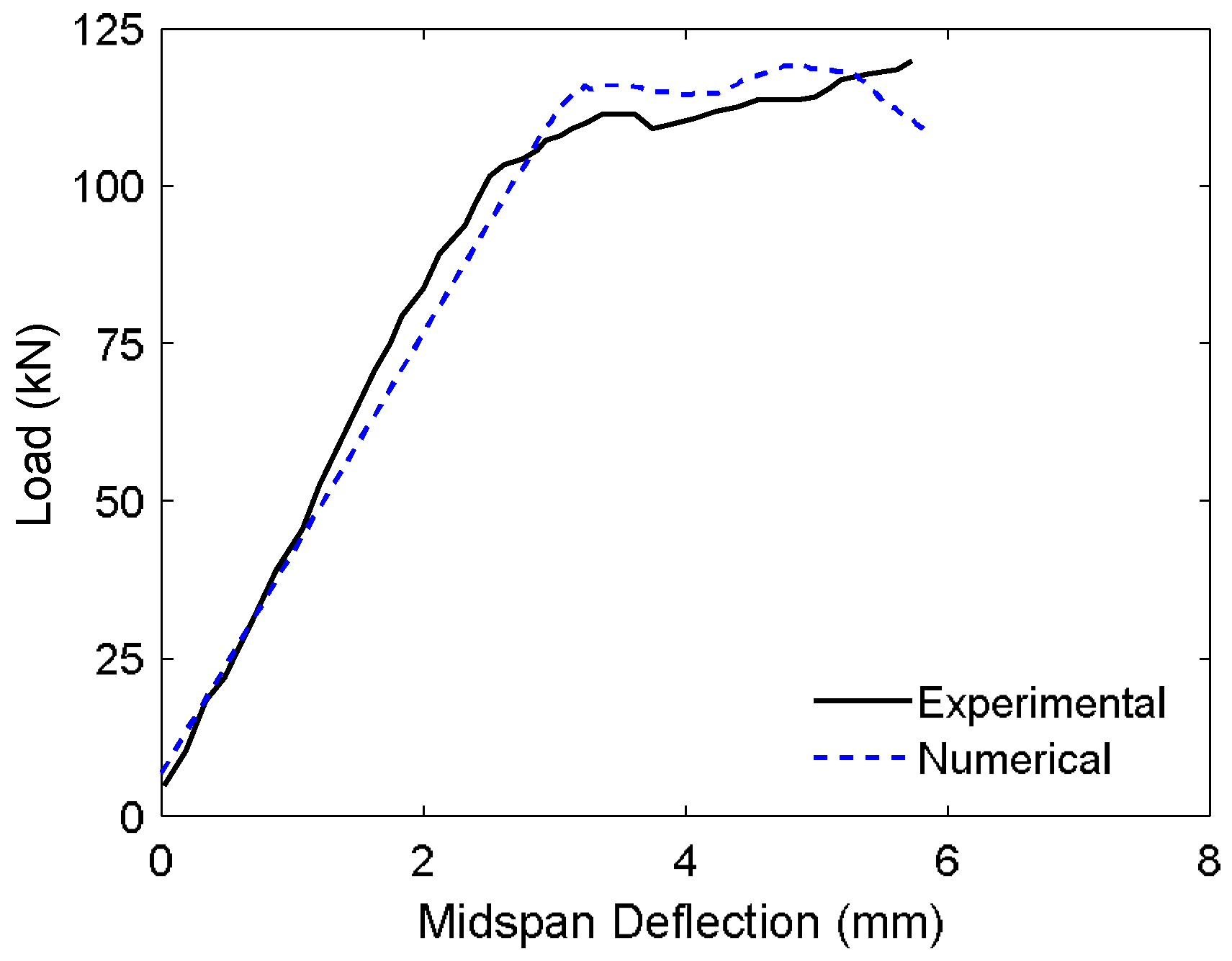
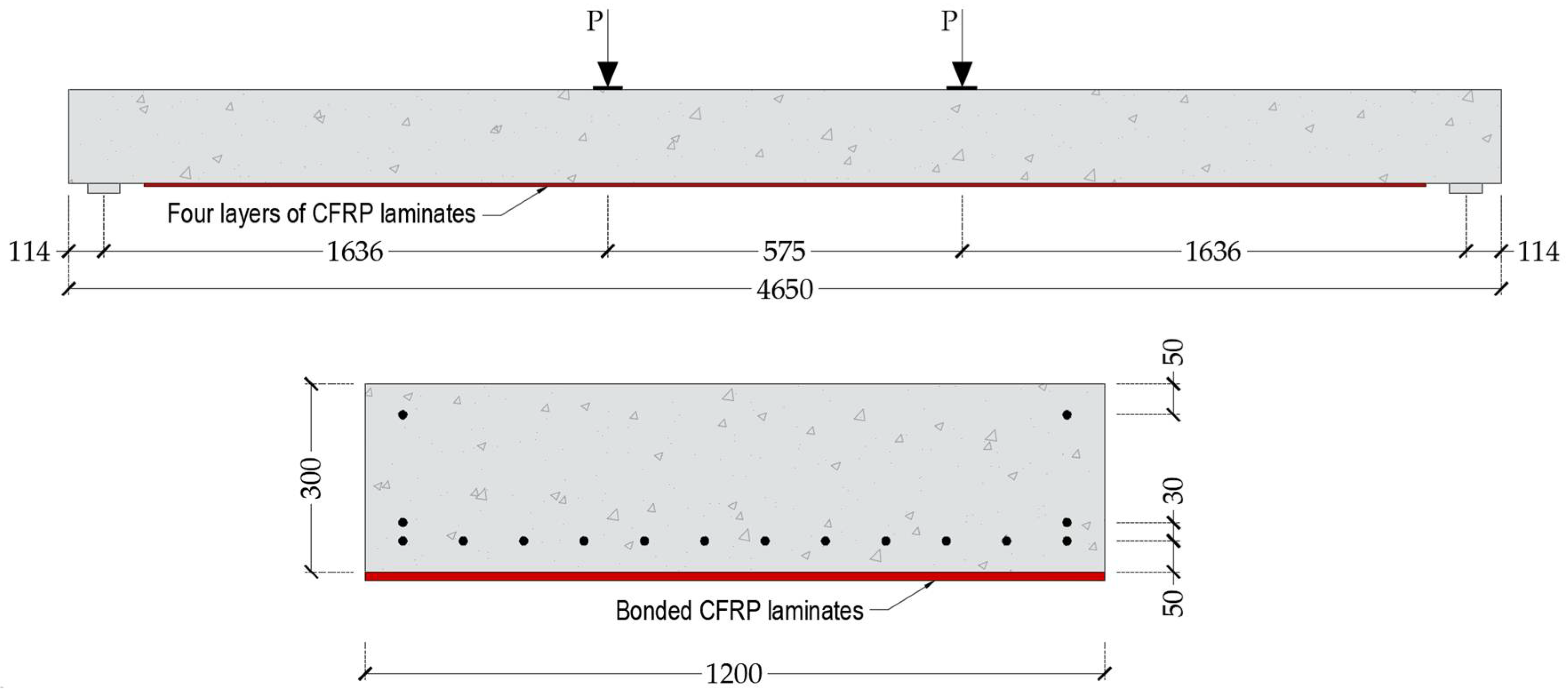
5.1.3. CFRP-Retrofitted Prestressed Concrete Slab
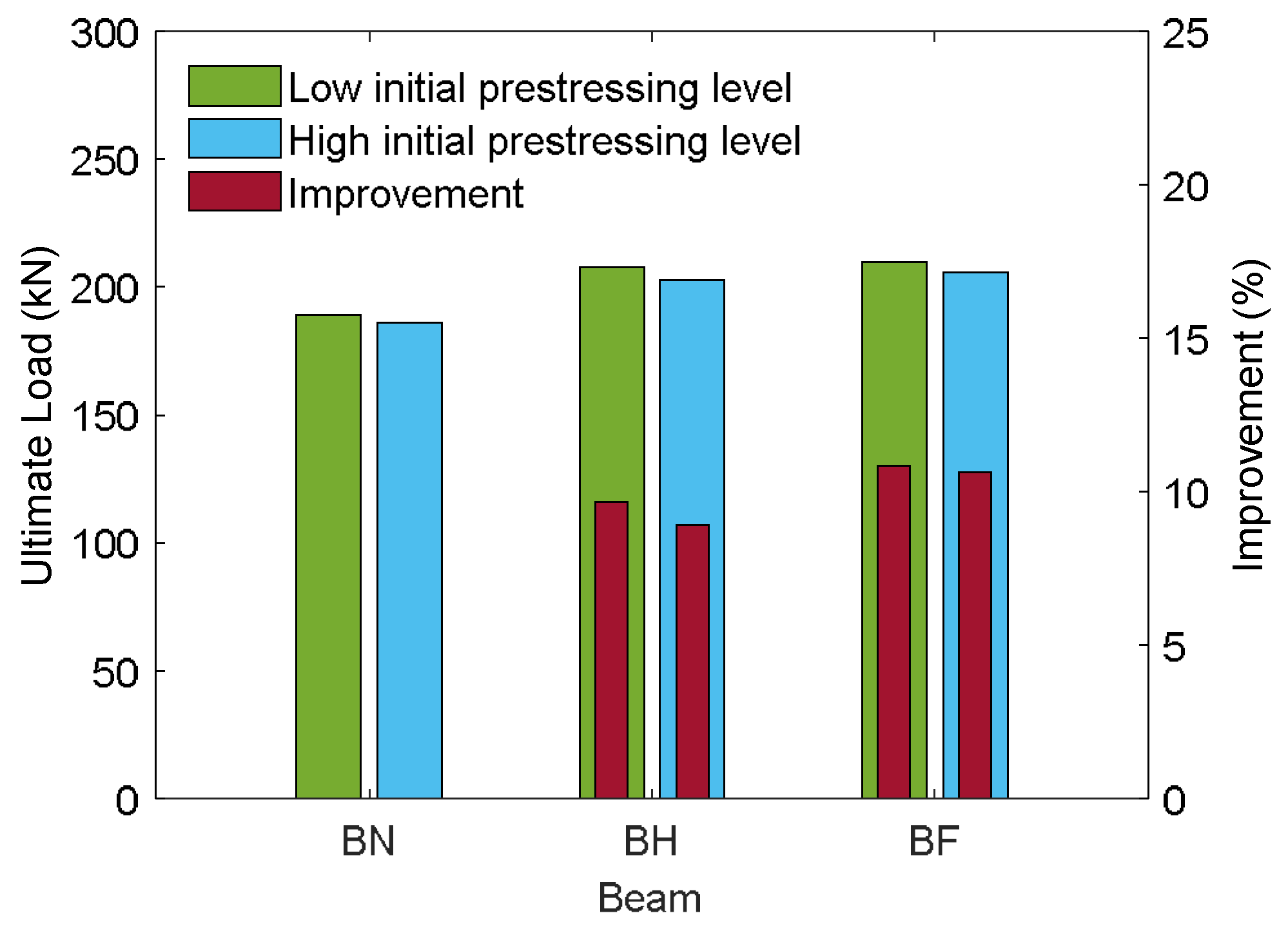
5.2. Parametric Study of CFRP-Strengthened Prestressed Concrete T-Beams
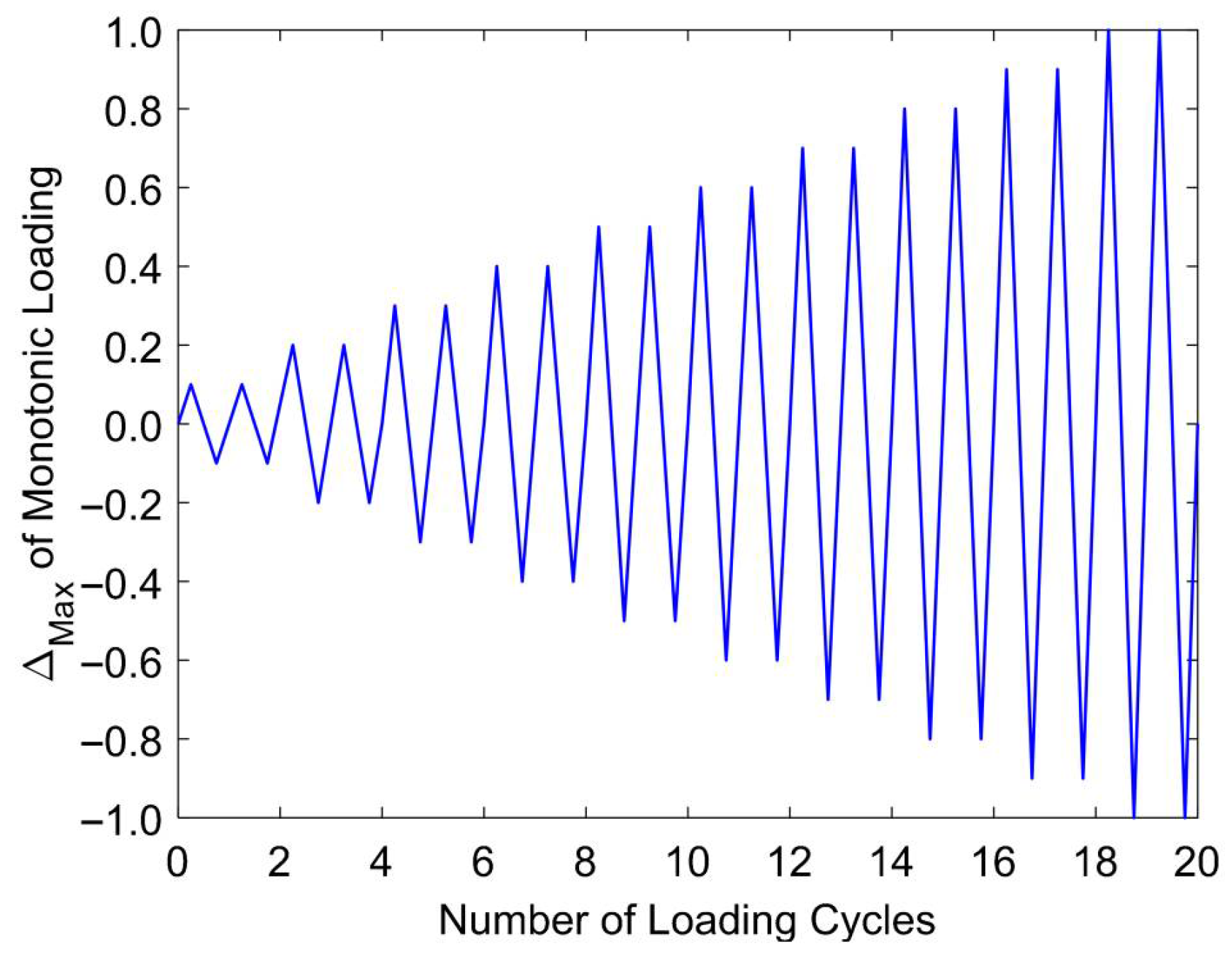
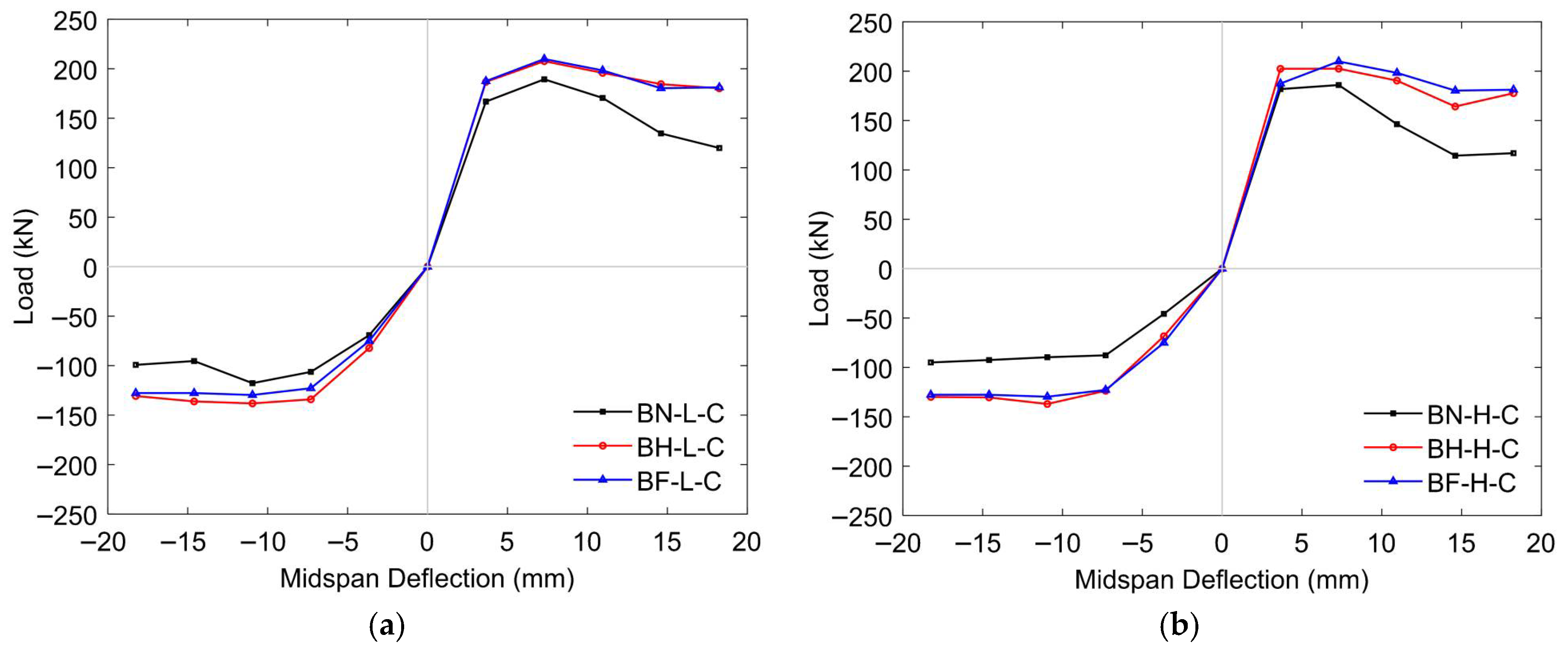
5.2.1. Response Under Reversed Cyclic Loading
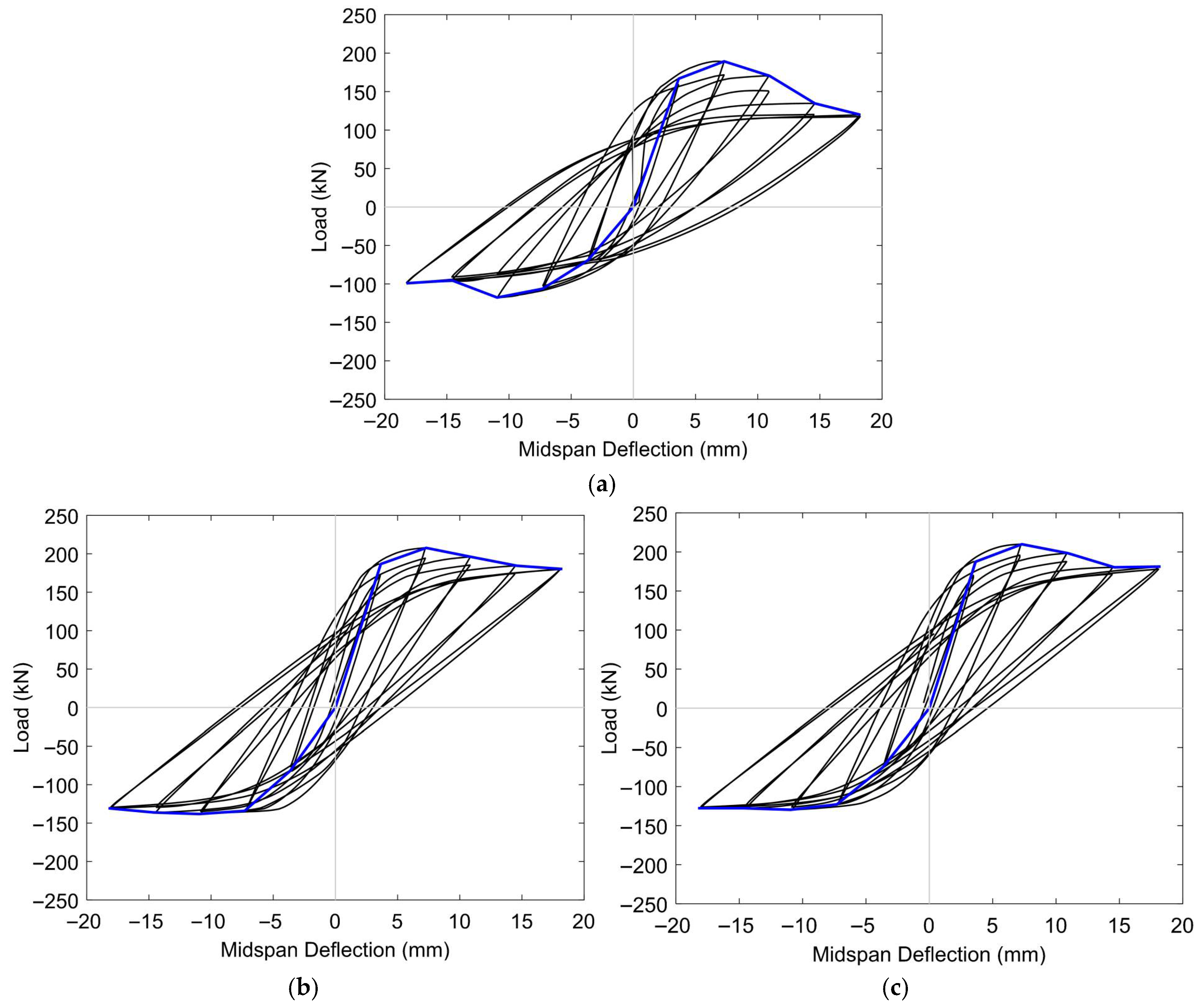
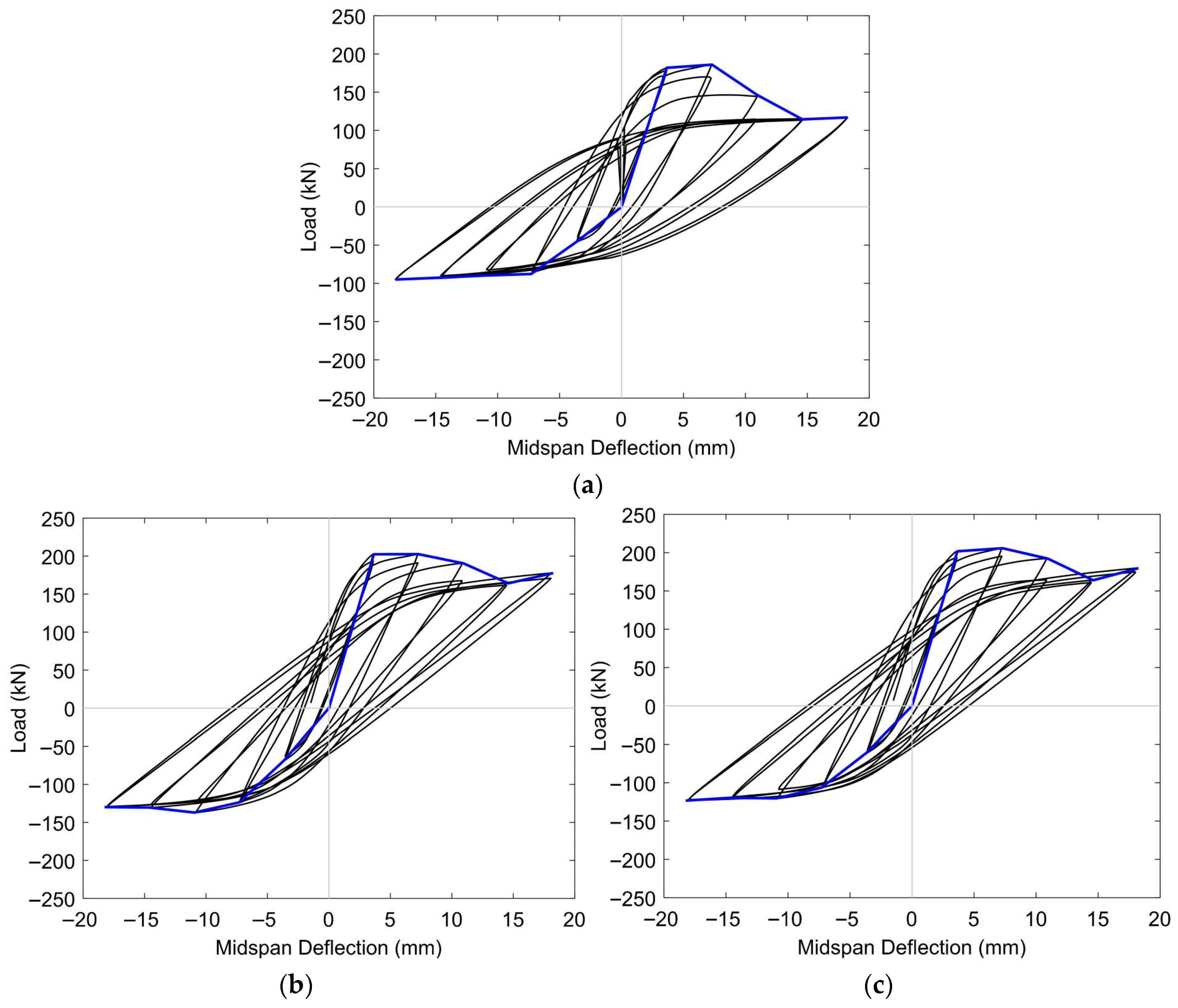
Hysteresis Responses
Envelope Curves
Stiffness Degradation
Displacement Ductility
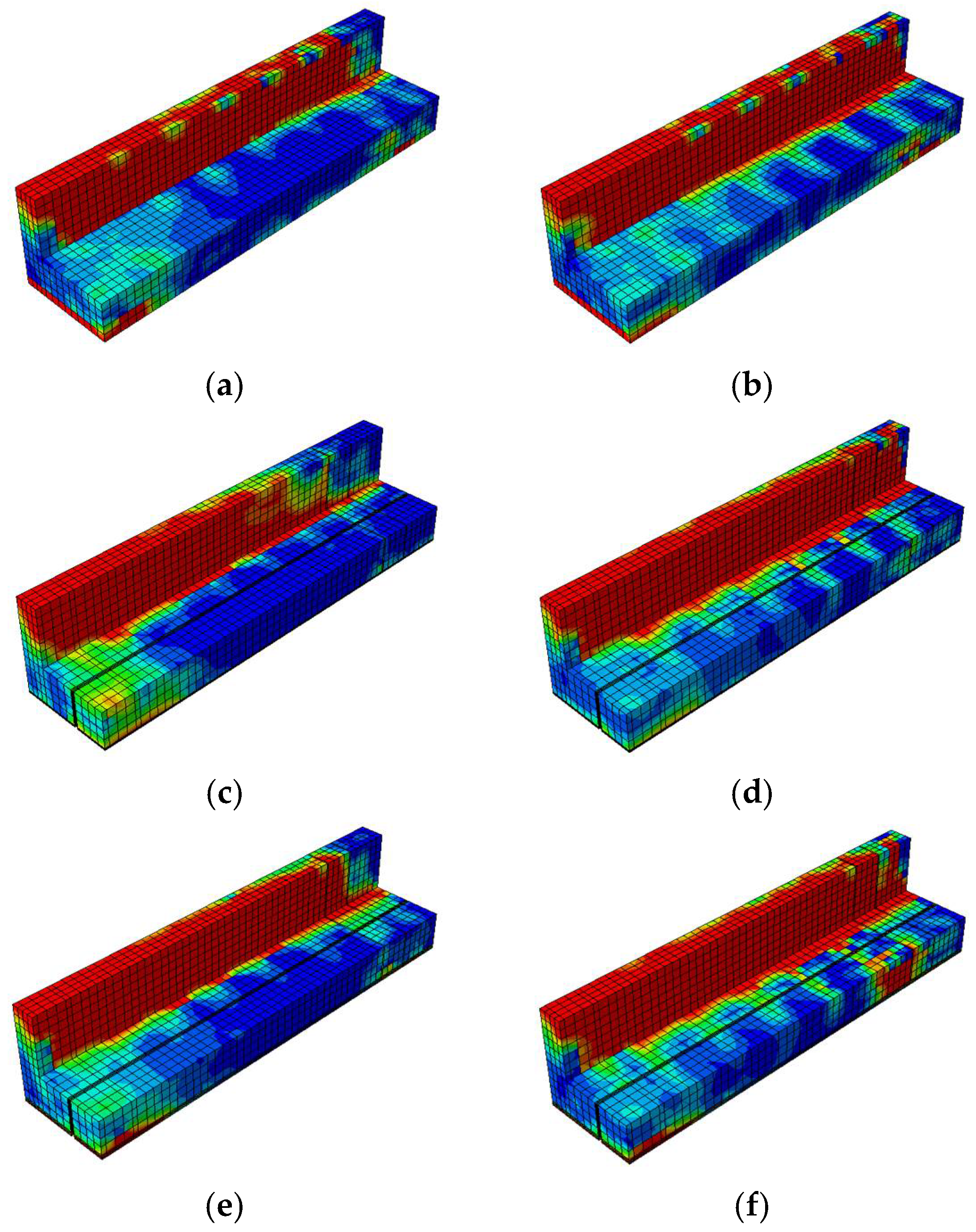
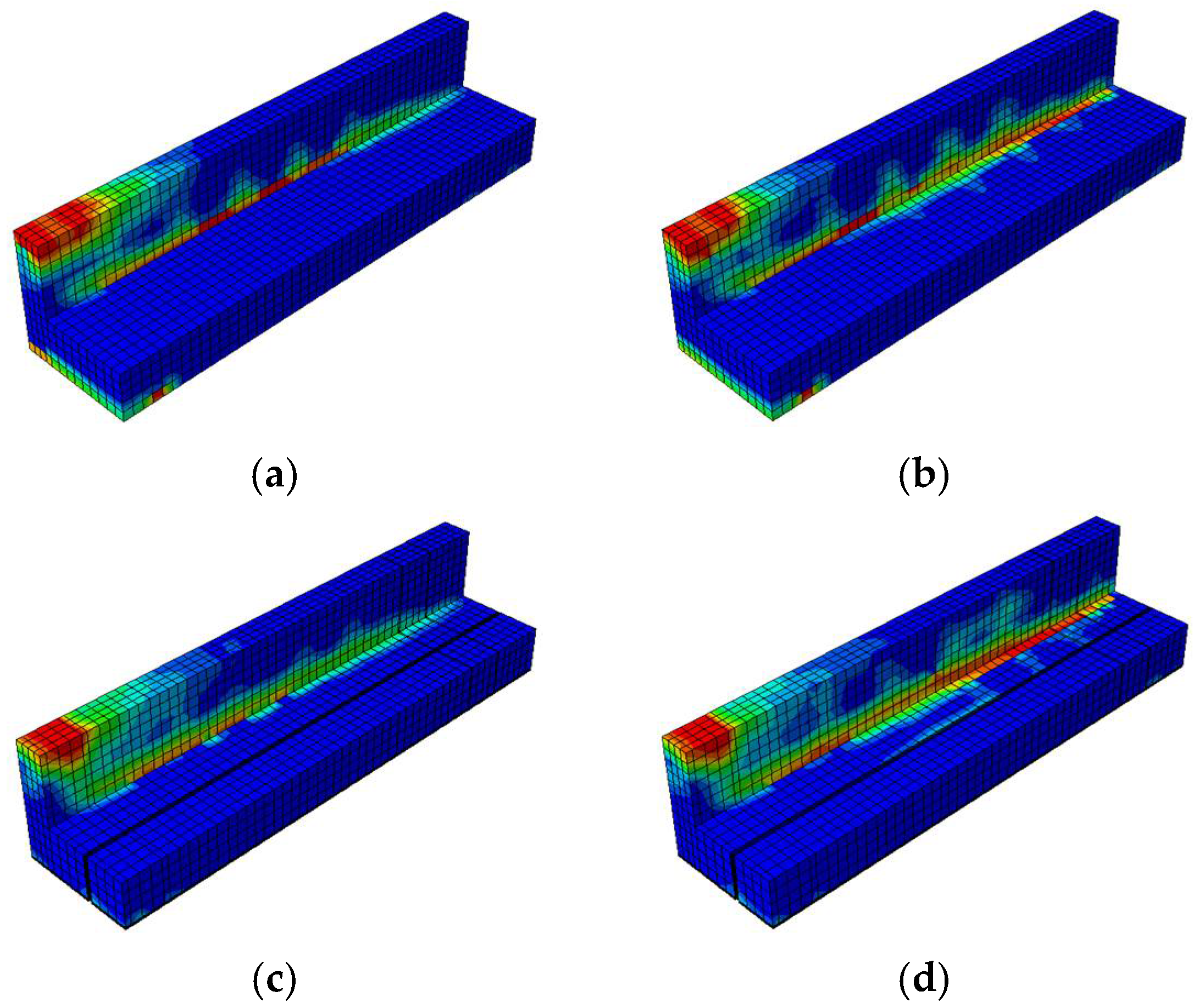
Damage Contours
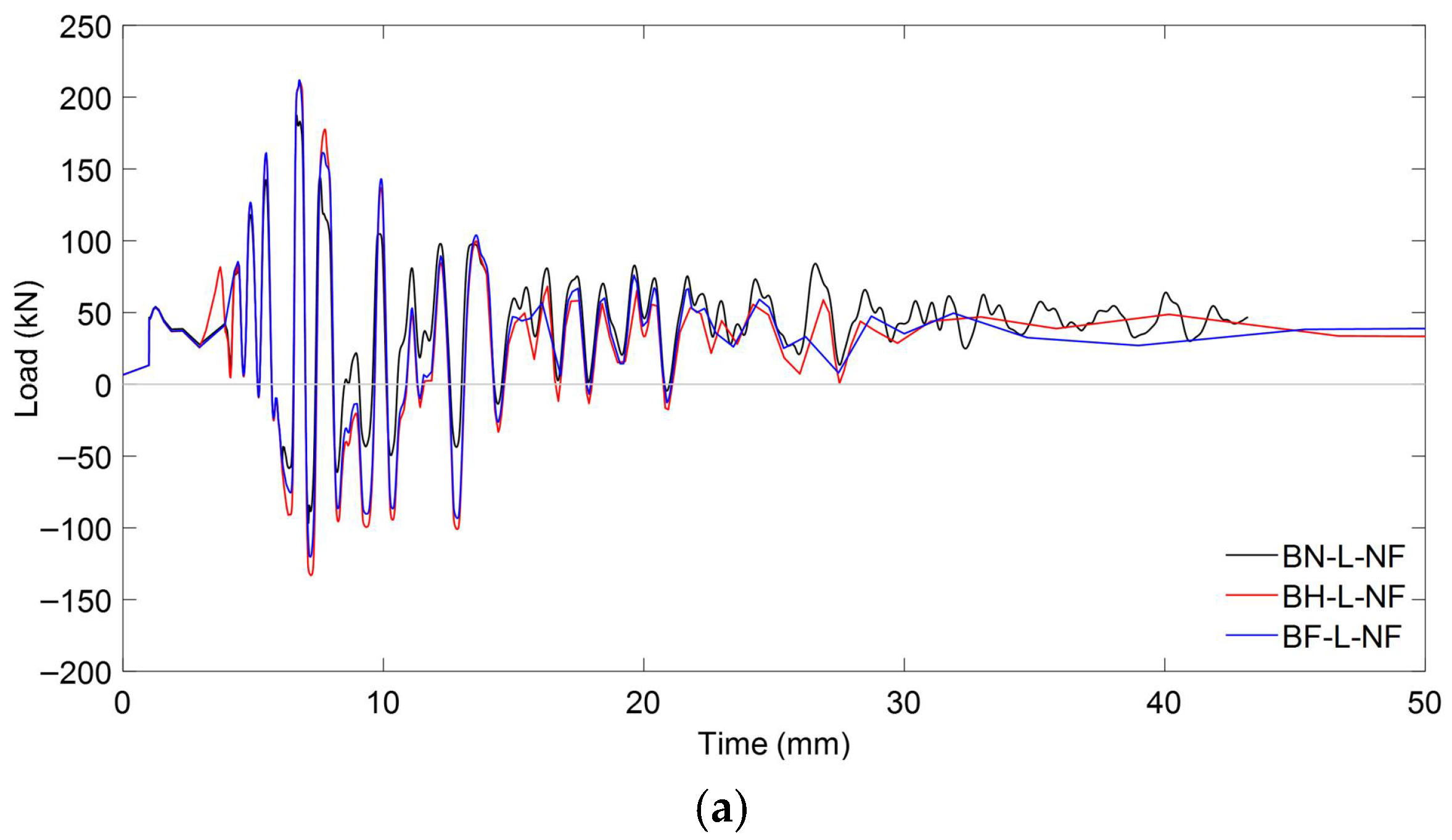
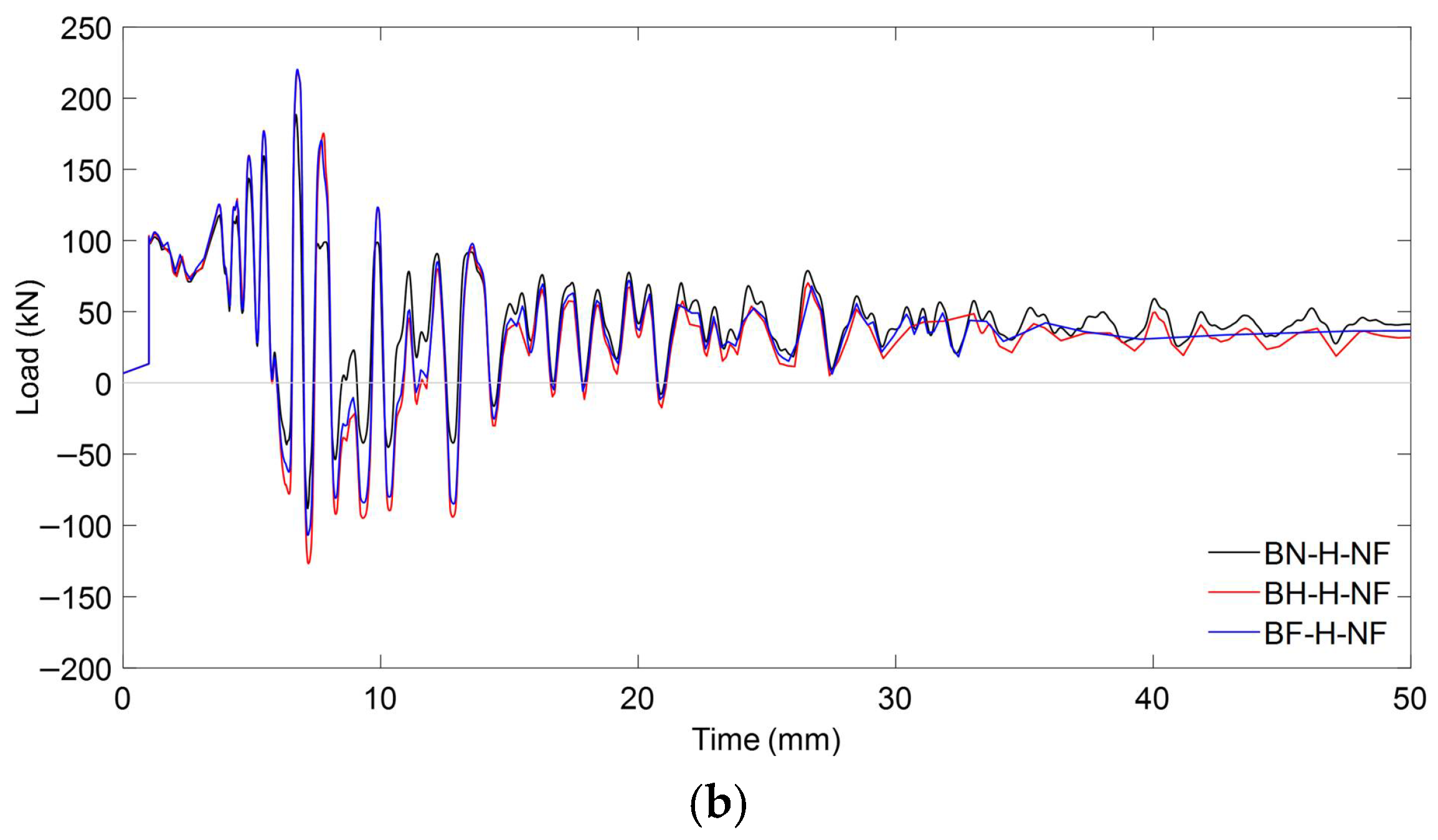
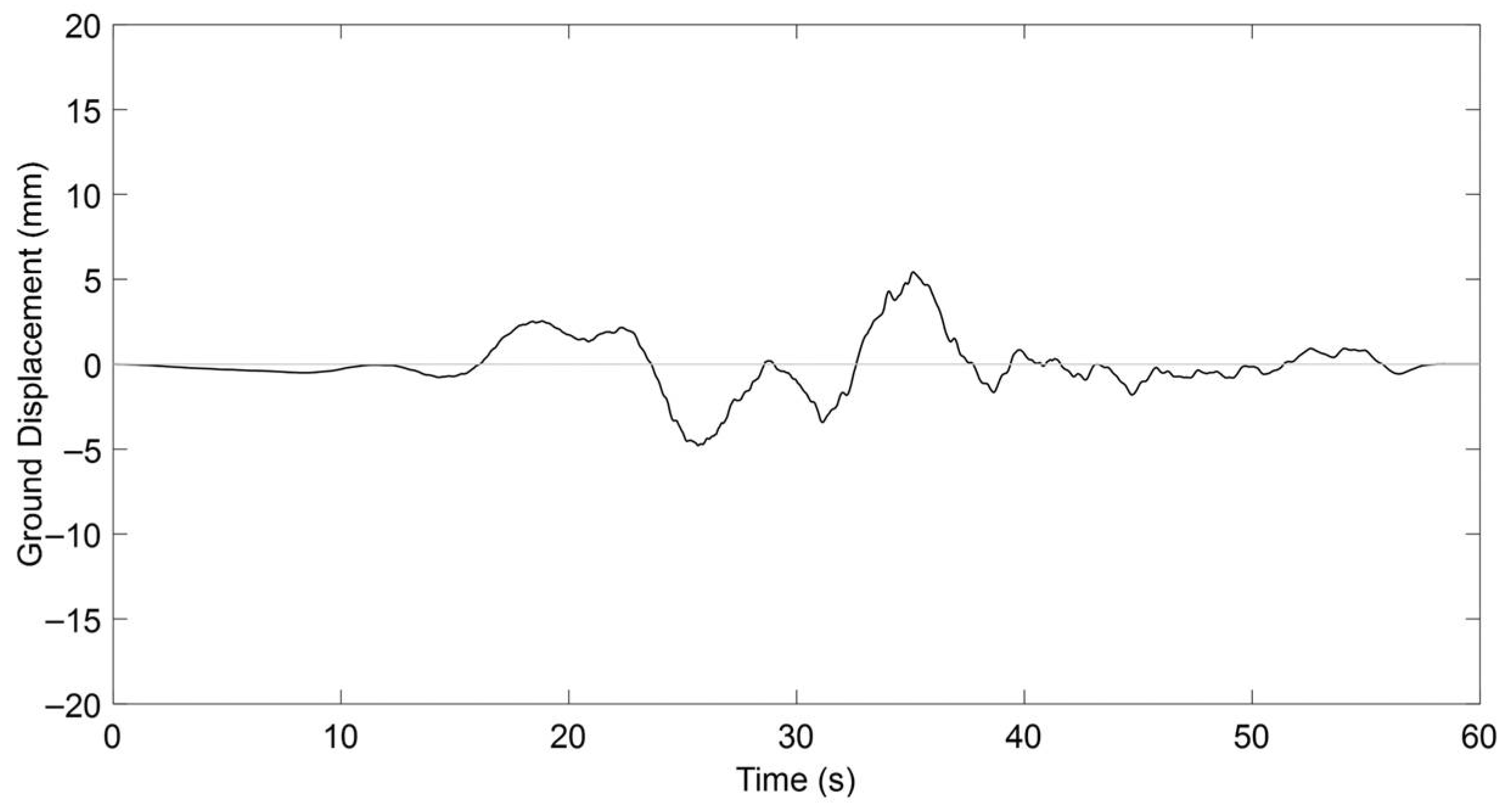
5.2.2. Response Under Near-Fault Ground Motion
Load Characteristics
Damage Contours
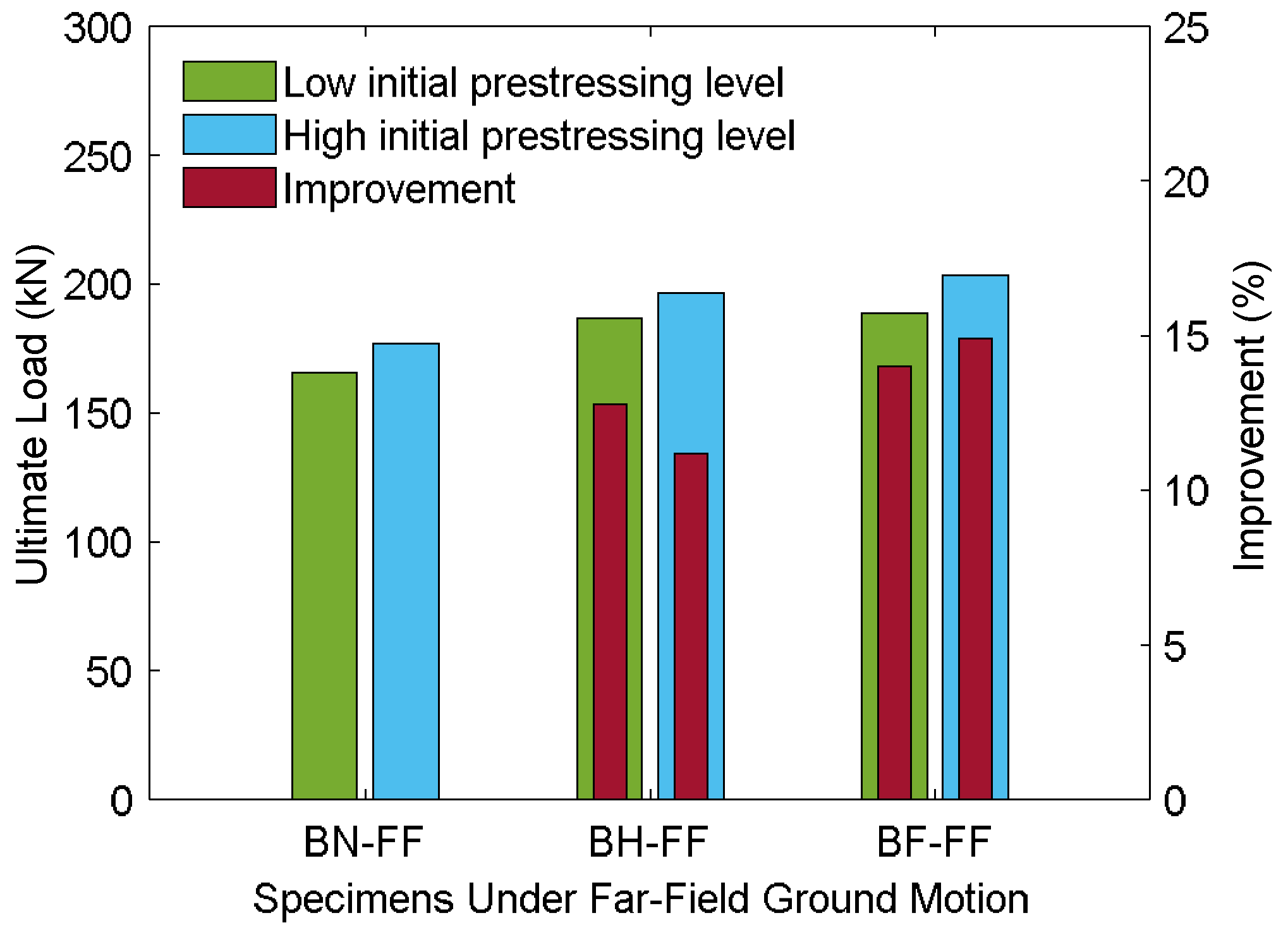
5.2.3. Response Under Far-Field Ground Motion
Load Characteristics
Damage Contours
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviation
| RC | Reinforced concrete |
| FRP | Fiber-reinforced polymer |
| EB | Externally bonded |
| NSM | Near-surface mounted |
| CFRP | Carbon fiber-reinforced polymer |
| FE | Finite element |
| FEM | Finite element method |
| SRC | Steel-reinforced concrete |
| ECC | Engineered cementitious composites |
| CDP | Concrete damage plasticity |
| NMSE | Normalized mean square error |
References
- Park, R. Reinforced Concrete. In Encyclopedia of Physical Science and Technology, 3rd ed.; Meyers, R.A., Ed.; Academic Press: New York, NY, USA, 2003; pp. 583–602. [Google Scholar]
- Hannant, D.J.; Venkata Siva, S.B.; Rama Sreekanth, P.S. Prestressed concrete. In Comprehensive Composite Materials II; Beaumont, P.W.R., Zweben, C.H., Eds.; Elsevier: Oxford, UK, 2018. [Google Scholar]
- Collins, M.P.; Mitchell, D. Prestressed Concrete Structures; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Chen, W.; Hao, H.; Chen, S. Numerical analysis of prestressed reinforced concrete beam subjected to blast loading. Mater. Des. (1980–2015) 2015, 65, 662–674. [Google Scholar] [CrossRef]
- Shahrbijari, K.B.; Barros, J.A.O.; Valente, I.B. Experimental study on the structural performance of concrete beams reinforced with prestressed GFRP and steel bars. Constr. Build. Mater. 2024, 438, 137031. [Google Scholar] [CrossRef]
- Du, Y.X.; Wei, J.; Yuan, J.; Lai, Y.F.; Sun, D.H. Experimental research on fatigue behavior of prestressed concrete beams under constant-amplitude and variable-amplitude fatigue loading. Constr. Build. Mater. 2020, 259, 119852. [Google Scholar] [CrossRef]
- Chen, X.; Jiang, R.; Bai, Z.; Au Francis, T.K. Shear failure in flanges of prestressed concrete bridges with corrugated steel webs. J. Bridge Eng. 2022, 27, 04022087. [Google Scholar] [CrossRef]
- da Silva, A.R.; Rosa, J.P.D. Nonlinear numerical analysis of prestressed concrete beams and slabs. Eng. Struct. 2020, 223, 111187. [Google Scholar] [CrossRef]
- Huang, Y.; Tao, Y.X.; Yi, W.J.; Zhou, Y.; Deng, L. Numerical investigation on compressive arch action of prestressed concrete beam-column assemblies against progressive collapse. J. Build. Eng. 2021, 44, 102991. [Google Scholar] [CrossRef]
- Liu, J.B.; Guo, Z.X.; Chen, L.Q. Research on precast roof truss of prestressed concrete square pile. Appl. Mech. Mater. 2014, 488–489, 359–364. [Google Scholar] [CrossRef]
- Zhao, G.Y.; Wang, Y.; Zhu, L.; Zhao, J.C. Shear behavior of prestressed concrete T-beams strengthened by steel plate-concrete composite. Eng. Struct. 2023, 291, 116440. [Google Scholar] [CrossRef]
- Hu, D. Chapter 10–Design of prestressed concrete flexural structures. In Analysis and Design of Prestressed Concrete; Hu, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2022; pp. 327–349. [Google Scholar]
- Al-Mosawe, D.; Neves, L.; Owen, J. Reliability analysis of deteriorated post-tensioned concrete bridges: The case study of Ynys-y-Gwas bridge in UK. Structures 2022, 41, 242–259. [Google Scholar] [CrossRef]
- Jiang, X.; Cao, D.Q.; Qiang, X.H.; Xu, C.L. Study on fatigue performance of steel bridge welded joints considering initial defects. J. Constr. Steel Res. 2024, 212, 108309. [Google Scholar] [CrossRef]
- Peng, J.X.; Tang, H.; Zhang, J.R. Structural behavior of corroded reinforced concrete beams strengthened with steel plate. J. Perform. Constr. Fac. 2017, 31, 04017013. [Google Scholar] [CrossRef]
- Sharif, A.; AlSulaimani, G.J.; Basunbul, I.A.; Baluch, M.H.; Husain, M. Strengthening of shear-damaged RC beams by external bonding of steel plates. Mag. Concrete Res. 1995, 47, 329–334. [Google Scholar] [CrossRef]
- Jiang, C.; Xiong, W.; Ye, J. Simplified design formula for the shear capacity of prestressed concrete T-beams strengthened by steel plates. KSCE J. Civ. Eng. 2024, 100013. [Google Scholar] [CrossRef]
- Eisa, A.S.; Kotrasova, K.; Sabol, P.; Mihaliková, M.; Attia, M.G. Experimental and numerical study of strengthening prestressed reinforced concrete beams using different techniques. Buildings 2024, 14, 29. [Google Scholar] [CrossRef]
- Campione, G.; Zizzo, M. Influence of strands corrosion on the flexural behavior of prestressed concrete beams. Structures 2022, 45, 1366–1375. [Google Scholar] [CrossRef]
- Jeon, C.H.; Oeurn, S.; Shim, C.S. Test database for corroded prestressing steel strands recovered from aged bridges. J. Mater. Civ. Eng. 2023, 35, 05022003. [Google Scholar] [CrossRef]
- Dai, L.; Bian, H.; Wang, L.; Potier-Ferry, M.; Zhang, J. Prestress loss diagnostics in pretensioned concrete structures with corrosive cracking. J. Struct. Eng. 2020, 146, 04020013. [Google Scholar] [CrossRef]
- Imperatore, S.; Benenato, A.; Spagnuolo, S.; Ferracuti, B.; Kioumarsi, M. Corrosion effects on the flexural performance of prestressed reinforced concrete beams. Constr. Build. Mater. 2024, 411, 134581. [Google Scholar] [CrossRef]
- Valente, M. Seismic upgrading strategies for non-ductile plan-wise irregular R/C structures. Procedia Eng. 2013, 45, 539–553. [Google Scholar] [CrossRef]
- Valente, M.; Milani, G. Alternative retrofitting strategies to prevent the failure of an underdesigned reinforced concrete frame. Eng. Fail. Anal. 2018, 89, 271–285. [Google Scholar] [CrossRef]
- Lin, C.T.; Wu, Y.H.; Chin, W.H.; Lin, M.L. Performance of CFRP-strengthened RC beams subjected to repeated loads. J. Chin. Inst. Eng. 2014, 37, 1007–1017. [Google Scholar] [CrossRef]
- Ashteyat, A.; Almahadin, W.; Abdel-Jaber, M.; Almuaythir, S. Shear repairing of reinforced concrete beams exposed to high temperature using basalt fiber reinforcing bars and CFRP ropes and strips. Compos. Part C Open 2024, 15, 100517. [Google Scholar] [CrossRef]
- Zapris, A.G.; Kytinou, V.K.; Chalioris, C.E. Innovative fiber-reinforced polymer rope-based closed-form retrofitting methods applied in reinforced concrete T-shaped beams under torsion. Polymers 2024, 16, 2634. [Google Scholar] [CrossRef] [PubMed]
- Xue, W.C.; Tan, Y.; Zeng, L. Flexural response predictions of reinforced concrete beams strengthened with prestressed CFRP plates. Compos. Struct. 2010, 92, 612–622. [Google Scholar] [CrossRef]
- Sharaky, I.A.; Torres, L.; Baena, M.; Miàs, C. An experimental study of different factors affecting the bond of NSM FRP bars in concrete. Compos. Struct. 2013, 99, 350–365. [Google Scholar] [CrossRef]
- Al-Bayati, G.; Al-Mahaidi, R.; Kalfat, R. Experimental investigation into the use of NSM FRP to increase the torsional resistance of RC beams using epoxy resins and cement-based adhesives. Constr. Build Mater. 2016, 124, 1153–1164. [Google Scholar] [CrossRef]
- Sabau, C.; Popescu, C.; Sas, G.; Schmid, J.W.; Blanksvärd, T.; Täljsten, B. Strengthening of RC beams using bottom and side NSM reinforcement. Compos. Part B-Eng. 2018, 14, 82–91. [Google Scholar] [CrossRef]
- Wang, Q.; Zhu, H.; Li, T.; Wu, G.; Hu, X.X. Bond performance of NSM FRP bars in concrete with an innovative additional ribs anchorage system: An experimental study. Constr. Build Mater. 2019, 207, 572–584. [Google Scholar] [CrossRef]
- Aljabbri, N.A.S.; Karim, A.A.; Majeed, F.H. Carbon fiber-reinforced polymer composites integrated beam–column joints with improved strength performance against seismic events: Numerical model simulation. Eng 2024, 5, 112–1139. [Google Scholar] [CrossRef]
- Xue, Y.J.; Wang, W.W.; Tian, J.; Wu, Z.H. Plate end debonding strength model for RC beams strengthened with FRP/ SMA composites. Eng. Struct. 2024, 302, 117421. [Google Scholar] [CrossRef]
- De Lorenzis, L.; Teng, J.G. Near-surface mounted FRP reinforcement: An emerging technique for strengthening structures. Compos. Part B-Eng. 2007, 38, 119–143. [Google Scholar] [CrossRef]
- ACI Committee 440. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures (ACI 440.2R-17); American Concrete Institute: Farmington Hills, MI, USA, 2017. [Google Scholar]
- Budipriyanto, A.; Han, A.L.; Hu, H.-T. Bond-shear behavior of FRP rods as a function of attachment configuration. J. Adv. Civ. Environ. Eng. (JACEE) 2018, 1, 9–17. [Google Scholar] [CrossRef]
- Biolzi, L.; Ghittoni, C.; Fedele, R.; Rosati, G. Experimental and theoretical issues in FRP-concrete bonding. Constr. Build Mater. 2013, 41, 182–190. [Google Scholar] [CrossRef]
- Saad, S.; Polak, M.A. Bond Behavior of Glass Fiber-Reinforced Polymer (GFRP) Bars Embedded in Concrete: A Review. Materials 2025, 18, 3367. [Google Scholar] [CrossRef]
- Tworzewski, P.; Bacharz, K. Flexural Strengthening of Reinforced Concrete Beams Using Near-Surface Mounted (NSM) Carbon Fiber-Reinforced Polymer (CFRP) Strips with Additional Anchorage. Materials 2025, 18, 2579. [Google Scholar] [CrossRef]
- Haryanto, Y.; Hsiao, F.-P.; Hu, H.-T.; Han, A.L.; Chua, A.W.; Salim, F.; Nugroho, L. Structural behavior of negative moment region NSM-CFRP strengthened RC T-beams with various embedment depth under monotonic and cyclic loading. Compos. Struct. 2022, 301, 116214. [Google Scholar] [CrossRef]
- Haryanto, Y.; Wariyatno, N.G.; Hsiao, F.-P.; Hu, H.-T.; Han, A.L.; Nugroho, L.; Hartono, H. RC T-beams with flexural strengthening in the negative moment region under different configurations of NSM CFRP rods. Eng. Fail. Anal. 2025, 173, 109458. [Google Scholar] [CrossRef]
- Han, A.L.; Hu, H.-T.; Gan, B.S.; Hsiao, F.-P.; Haryanto, Y. Carbon fiber-reinforced polymer rod embedment depth influence on concrete strengthening. Arab. J. Sci. Eng. 2022, 47, 12685–12695. [Google Scholar] [CrossRef]
- Nugroho, L.; Haryanto, Y.; Hu, H.-T.; Han, A.L.; Hsiao, F.-P.; Lin, C.-C.; Weng, P.-W.; Widiastuti, E.P. NSM-CFRP rods with varied embedment depths for strengthening RC T-beams in the negative moment region: Investigation on high cyclic response. Compos. Struct. 2024, 331, 117891. [Google Scholar] [CrossRef]
- Pham, T.D.; Hong, W.-K. Invesigation of strain evolutions in presressed reinforced concrete beams based on nonlinear finite element analyses considering concrete plasicity and concrete damaged plasicity. J. Asian Arch. Build. Eng. 2021, 21, 448–468. [Google Scholar] [CrossRef]
- Chira, A.; Puskás, A.; Bompa, D.V. Load-deformation response of long span prestressed concrete wide beams. J. Build. Eng. 2023, 65, 105631. [Google Scholar] [CrossRef]
- Nugroho, L.; Haryanto, Y.; Hu, H.-T.; Hsiao, F.-P.; Pamudji, G.; Setiadji, B.H.; Hsu, C.-N.; Weng, P.-W.; Lin, C.-C. Prestressed concrete T-beams strengthened with near-surface mounted carbon-fiber-reinforced polymer rods under monotonic loading: A Finite element analysis. Eng 2025, 6, 36. [Google Scholar] [CrossRef]
- Nguyen, M.H.; Ho, M.H.; Tran, V.R.; Phan, H.N.; Nguyen, D.D.N.; Huynh, P.N. Flexural performance of reinforced concrete beams strengthened with prestressed FRP sheets: Experiments and numerical investigations. Case Stud. Constr. Mat. 2024, 21, e03475. [Google Scholar] [CrossRef]
- Cutolo, A.; Guarracino, F.; Olivieri, C.; Mascolo, I. Nonlinear FE analysis of a masonry spiral staircase in Nisida: A refined numerical case study. Int. J. Multiscale Comput. Eng. 2022, 20, 105–114. [Google Scholar] [CrossRef]
- Verre, S. Numerical Strategy for Column Strengthened with FRCM/SRG System. Buildings 2022, 12, 2187. [Google Scholar] [CrossRef]
- Ji, J.; Qi, P.; Jiang, L.; Zhang, Z.; Chu, X.; Li, Y. Numerical study on the seismic behavior of novel precast prestressed SRC composite frames with fiber-reinforced ECC cast-in-place joints. Structures 2025, 71, 108024. [Google Scholar] [CrossRef]
- Nicoletti, V.; Carbonari, S.; Gara, F. Nomograms for the pre-dimensioning of RC beam-column joints according to Eurocode 8. Structures 2022, 39, 958–973. [Google Scholar] [CrossRef]
- Dassualt Systemes. ABAQUS/Standard User’s Manual, Version 6.14; Dassualt Systemes: Vélizy-Villacoublay, France, 2017. [Google Scholar]
- Zheng, Y.-Z.; Wang, W.-W.; Mosalam, K.M.; Fang, Q.; Chen, L.; Zhu, Z.-F. Experimental investigation and numerical analysis of RC beams shear strengthened with FRP/ECC composite layer. Compos. Struct. 2020, 246, 112436. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete and Commentary (ACI 318-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Construction Agency. General Rules for Revision of Design Code for Concrete Structures; Ministry of Interior: Taipei, Taiwan, 2019. [Google Scholar]
- Hsu, L.S.; Hsu, C.-T.T. Complete stress-strain behaviour of high-strength concrete under compression. Mag. Concrete Res. 1994, 46, 301–312. [Google Scholar] [CrossRef]
- Alfarah, B.; López-Almansa, F.; Oller, S. New methodology for calculating damage variables evolution in plastic damage model for RC structures. Eng. Struct. 2017, 132, 70–86. [Google Scholar] [CrossRef]
- Hordijk, D.A. Tensile and tensile fatigue behaviour of concrete; experiments, modelling and analyses. Heron J. 1992, 37, 1–79. [Google Scholar]
- Fédération internationale du béton (fib). Model Code 2010, Final Draft ed.; International Federation for Structural Concrete (fib): Lausanne, Switzerland, 2012. [Google Scholar]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Xiao, H.; Zhang, K.; Du, J. Numerical simulation analysis of uniaxial compression damage of reinforced concrete column based on ABAQUS. Highl. Sci. Eng. Technol. 2023, 51, 113–118. [Google Scholar] [CrossRef]
- Guo, L.; Mao, R.; Liu, Z.; Li, S.; Wu, G.; Wang, Z. Dynamic large deflection response of RC Beams under low-speed impact loading. Shock Vib. 2020, 2020, 8812890. [Google Scholar] [CrossRef]
- Lee, S.-H.; Abolmaali, A.; Shin, K.-J.; Lee, H.-D. ABAQUS modeling for post-tensioned reinforced concrete beams. J. Build. Eng. 2020, 30, 101273. [Google Scholar] [CrossRef]
- Hafezolghorani, M.; Hejazi, F.; Vaghei, R.; Bin Jaafar, M.S.; Karimzade, K. Simplified damage plasticity model for concrete. Struct. Eng. Int. 2017, 27, 68–78. [Google Scholar] [CrossRef]
- Wei, L.; Xu, M.; Chen, Z. Parameter calibration and verification of ABAQUS concrete damage plastic model. Ind. Bldg. 2014, 44, 167–171. (In Chinese) [Google Scholar] [CrossRef]
- Demir, A.; Ozturk, H.; Edip, K.; Stojmanovska, M.; Bogdanovic, A. Effect of viscosity parameter on the numerical simulation of reinforced concrete deep beam behavior. Online J. Sci. Technol. 2018, 8, 50–56. [Google Scholar]
- Menegotto, M.; Pinto, P.E. Method of Analysis for Cyclically Loaded R.C. Plane Frames Including Changes in Geometry and Non-Elastic Behaviour of Elements Under Combined Normal Force and Bending. In Rapports des Commissions de Travail AIPC = IVBH Berichte der Arbeitskommissionen = IABSE Reports of the Working Commissions; E-Periodica: Zürich, Switzerland, 1973; Volume 13. [Google Scholar] [CrossRef]
- Naaman, A.E. An approximate nonlinear design procedure for partially prestressed concrete beams. Comput. Struct. 1983, 17, 287–299. [Google Scholar] [CrossRef]
- Sika. Sika® CarboDur® BC. Pultruded Carbon Fibre Rods for Structural Strengthening as Part of the Sika®CarboDur® System; Sika UK: Welwyn Garden City, UK, 2016. [Google Scholar]
- Simulia. Abaqus Technology Brief Projectile Impact on a Carbon Fiber Reinforced Plate (TB-06-CRP-1); Abaqus Technology Brief; Simulia: Johnston, RI, USA, 2007. [Google Scholar]
- Hashin, Z. Failure criteria for unidirectional fiber composites. J. Appl. Mech. 1980, 47, 329–334. [Google Scholar] [CrossRef]
- Rabczuk, T.; Eibl, J. Numerical analysis of prestressed concrete beams using a coupled element free Galerkin/finite element approach. Int. J. Solids Struct. 2004, 41, 1061–1080. [Google Scholar] [CrossRef]
- Shahawy, M.A.; Beitelman, T.; Arockiasamy, M.; Sowrirajan, R. Experimental investigation on structural repair and strengthening of damaged prestressed concrete slabs utilizing externally bonded carbon laminates. Compos. Part B-Eng. 1996, 27, 217–224. [Google Scholar] [CrossRef]
- Haryanto, Y.; Sudibyo, G.H.; Nugroho, L.; Hu, H.-T.; Han, A.L.; Hsiao, F.-P.; Widyaningrum, A.; Susetyo, Y. Flexural performance of the negative moment region in bonded steel-wire-rope-strengthened reinforced concrete T-beams at different prestressing levels. Adv. Struct. Eng. 2024, 27, 2338–2358. [Google Scholar] [CrossRef]
- Atmajayanti, A.T.; Haryanto, Y.; Hsiao, F.-P.; Hu, H.-T.; Nugroho, L. Effective flexural strengthening of reinforced concrete T-beams using bonded fiber-core steel wire ropes. Fibers 2025, 13, 53. [Google Scholar] [CrossRef]
- Haryanto, Y.; Hsiao, F.-P.; Nugroho, L.; Hu, H.-T.; Sudibyo, G.H.; Wariyatno, N.G.; Hidayat, B.A.; Pamudji, G. Enhancing the negative moment flexural capacity of RC T-beams with bonded steel wire ropes—A parametric study. Eng. Fail. Anal. 2025, 180, 109883. [Google Scholar] [CrossRef]
- Nugroho, L.; Haryanto, Y.; Hsiao, F.-P.; Hu, H.-T.; Weng, P.-W.; Lin, C.-C.; Kristiawan, S.A.; Sangadji, S. Effectiveness of UHPC reinforced with steel rebars for flexural strengthening of RC T-beams in an idealized negative moment region. Structures 2025, 10, 109728. [Google Scholar] [CrossRef]
- Ye, L.P.; Lu, X.Z.; Ma, Q.L.; Cheng, G.Y.; Song, S.Y.; Miao, Z.W.; Pan, P. Study on the influence of post-yielding stiffness to the seismic response of building structures. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Wang, Z.; Wang, B.; Jiang, H.Z.; Zhuge, P. Experimental study on the flexural and shear performance of concrete beams strengthened with prestressed CFRP tendons. Appl. Sci. 2024, 14, 1237. [Google Scholar] [CrossRef]
- Omran, G.M.; Beygi, M.H.A.; Dehestani, M. Numerical analysis of externally prestressed concrete beams and parametric study of factors affecting their flexural performance. Int. J. Adv. Eng. Sci. Ap. 2020, 12, 142–157. [Google Scholar] [CrossRef]
- Lou, T.J.; Hu, H.; Pang, M. Effect of tendon-related variables on the behavior of externally CFRP prestressed concrete beams. Materials 2023, 16, 5197. [Google Scholar] [CrossRef]
- Stewart, J.P.; Chiou, S.J.; Bray, J.D.; Graves, R.W.; Somerville, P.G.; Abrahamson, N.A. Ground motion evaluation procedures for performance-based design. Soil Dyn. Earthq. Eng. 2022, 22, 765–772. [Google Scholar] [CrossRef]
- Bray, J.D.; Rodriguez-Marek, A. Characterization of forward-directivity ground motions in the near-fault region. Soil Dyn. Earthq. Eng. 2004, 24, 815–828. [Google Scholar] [CrossRef]
- Li, S.; Xie, L.L. Progress and trend on near-field problems in civil engineering. Acta Seismol. Sin. 2007, 20, 105–114. [Google Scholar] [CrossRef]
- Heydari, M.; Mousavi, M. The comparison of seismic effects of near-field and far-field earthquakes on relative displacement of seven-storey concrete building with shear wall. Curr. World Environ. 2015, 10, 40–46. [Google Scholar] [CrossRef]
- Moniri, H. Evaluation of seismic performance of reinforced concrete (RC) buildings under near-field earthquakes. Int. J. Adv. Struct. Eng. 2017, 9, 13–25. [Google Scholar] [CrossRef]
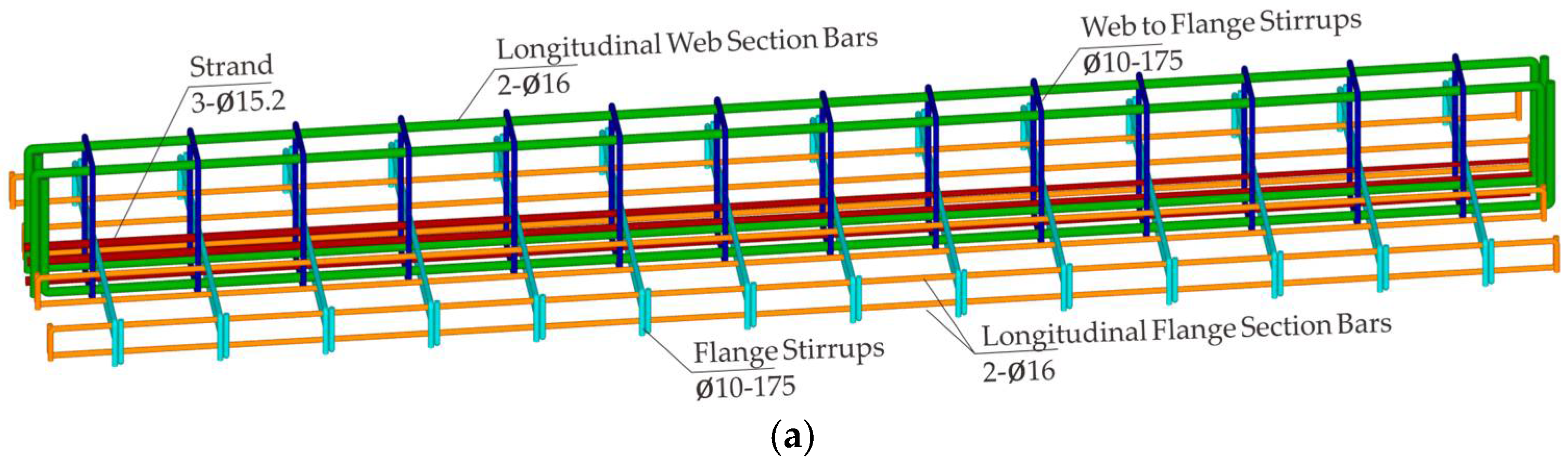
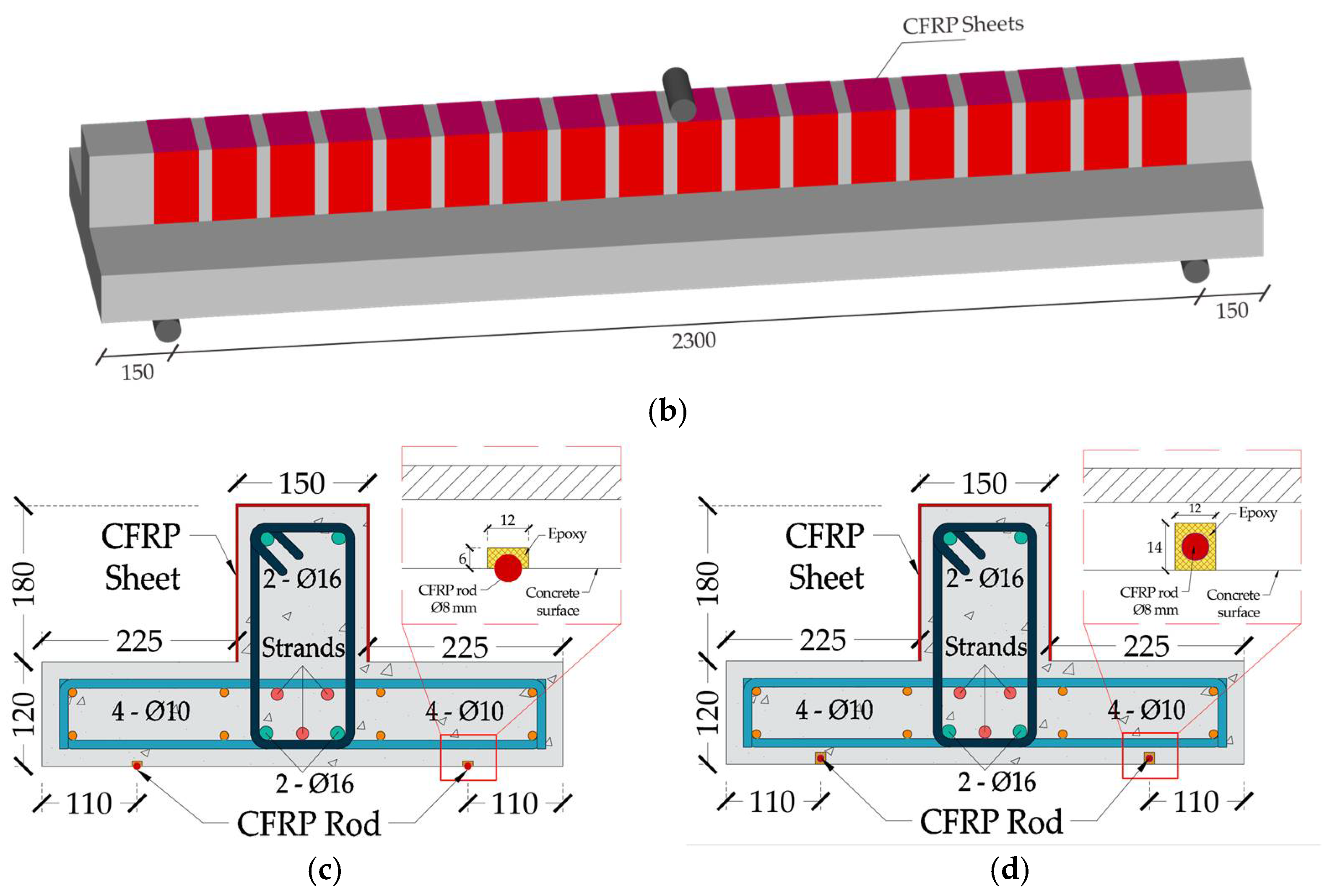

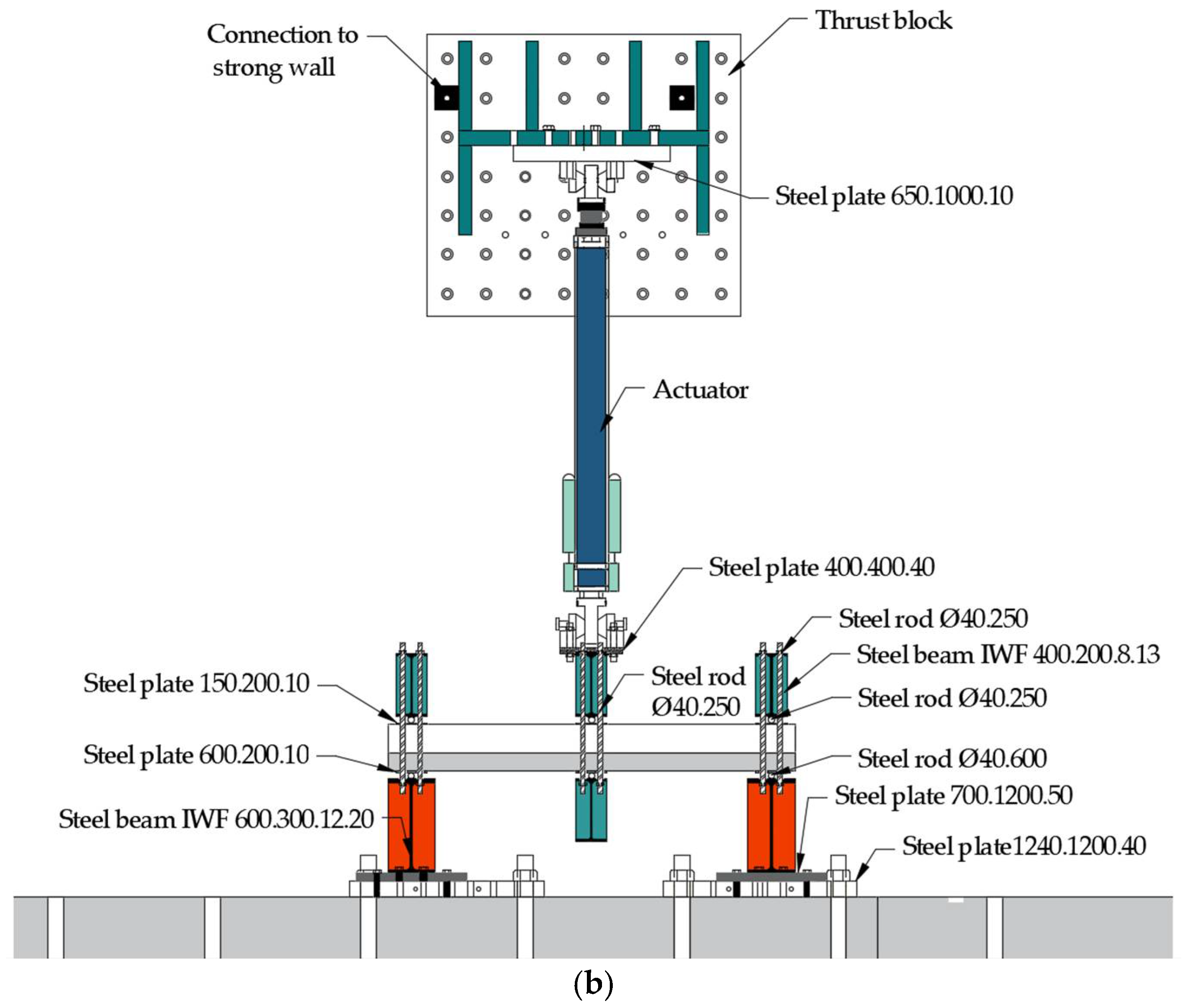
















| Specimen ID | Prestressing Level | CFRP Strengthening Configuration |
|---|---|---|
| BN-L | 35% (Low) | - |
| BN-H | 70% (High) | |
| BH-L | 35% (Low) | Half-embedded CFRP rods |
| BH-H | 70% (High) | |
| BF-L | 35% (Low) | Fully embedded CFRP rods |
| BF-H | 70% (High) |
| Dilation Angle | Eccentricity | Viscosity Parameter | ||
|---|---|---|---|---|
| 35° | 0.1 | 1.16 | 2/3 | 0.0005 |
| Properties | Value |
|---|---|
| Tensile strength along fiber direction, (MPa) | 3850 |
| Compressive strength along fiber direction, (MPa) | −2369.23 |
| Young’s modulus along fiber direction, (GPa) | 225 |
| Tensile strength perpendicular to fiber direction, (MPa) | 109.58 |
| Compressive strength perpendicular to fiber direction, (MPa) | −286.28 |
| Young’s modulus perpendicular to fiber direction, (GPa) | 16.28 |
| Shear strength, (MPa) | 118.46 |
| Shear modulus, (GPa) | 4.31 |
| Parameter | Description | Value (N/mm3) |
|---|---|---|
| Knn | Normal penalty stiffness | 3000 |
| Kss | Shear penalty stiffness in first direction | 8 |
| Ktt | Shear penalty stiffness in second direction | 8 |
| Specimen | Experimental [44] | Numerical | % Difference | |||
|---|---|---|---|---|---|---|
| Pu (kN) | Δu (mm) | Pu (kN) | Δu (mm) | Pu | Δu | |
| BN | 158.36 | 25.90 | 150.78 | 25.30 | 4.79 | 2.35 |
| BH | 197.06 | 14.49 | 183.09 | 14.46 | 7.09 | 0.17 |
| BF | 217.88 | 25.81 | 214.93 | 25.29 | 1.36 | 2.03 |
| Specimen | Positive Direction | Negative Direction | Ductility (µ) | ||
|---|---|---|---|---|---|
(mm) | (mm) | (mm) | (mm) | ||
| Low level of initial prestressing | |||||
| BN-L-C | 4.14 | 18.25 | −7.37 | −18.20 | 6.90 |
| BH-L-C | 4.06 | 18.25 | −6.87 | −18.20 | 7.10 |
| BF-L-C | 4.09 | 18.25 | −7.13 | −18.20 | 7.10 |
| High level of initial prestressing | |||||
| BN-H-C | 3.73 | 18.25 | −7.82 | −18.20 | 7.20 |
| BH-H-C | 3.65 | 18.25 | −7.89 | −18.20 | 7.30 |
| BF-H-C | 3.72 | 18.25 | −8.26 | −18.20 | 7.10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haryanto, Y.; Hu, H.-T.; Atmajayanti, A.T.; Hsiao, F.-P.; Nugroho, L.; Wariyatno, N.G. Simulation-Based Study on the Performance of NSM-CFRP Strengthening in Prestressed Concrete T-Beams Under Seismic Loading. Materials 2025, 18, 4386. https://doi.org/10.3390/ma18184386
Haryanto Y, Hu H-T, Atmajayanti AT, Hsiao F-P, Nugroho L, Wariyatno NG. Simulation-Based Study on the Performance of NSM-CFRP Strengthening in Prestressed Concrete T-Beams Under Seismic Loading. Materials. 2025; 18(18):4386. https://doi.org/10.3390/ma18184386
Chicago/Turabian StyleHaryanto, Yanuar, Hsuan-Teh Hu, Anggun Tri Atmajayanti, Fu-Pei Hsiao, Laurencius Nugroho, and Nanang Gunawan Wariyatno. 2025. "Simulation-Based Study on the Performance of NSM-CFRP Strengthening in Prestressed Concrete T-Beams Under Seismic Loading" Materials 18, no. 18: 4386. https://doi.org/10.3390/ma18184386
APA StyleHaryanto, Y., Hu, H.-T., Atmajayanti, A. T., Hsiao, F.-P., Nugroho, L., & Wariyatno, N. G. (2025). Simulation-Based Study on the Performance of NSM-CFRP Strengthening in Prestressed Concrete T-Beams Under Seismic Loading. Materials, 18(18), 4386. https://doi.org/10.3390/ma18184386







