Metrological Comparison of Indirect Calibration Methods for Nanoindentation: A Bootstrap-Based Approach
Abstract
1. Introduction
1.1. Calibration Methods for Area Shape Function and Frame Compliance
1.1.1. ISO 14577-2 Method #2 (M2)
1.1.2. ISO 14577-2 Method #4 (M4)
1.1.3. Remarks on ISO 14577-2 M2 and M4
1.1.4. Single-Step Calibration Method (ODR)
1.2. Criticalities of Indirect Calibration Methods
1.3. Scope of the Work
2. Materials and Methods
2.1. Experiment Set Up
2.2. Uncertainty Evaluation
2.3. Statistical Evaluation of Results
- The distribution shape of the calibrated value .
- The statistical relevance of the effect of calibration datasets by performing a hypothesis test based on the F-Fisher distribution, with the null hypothesis , where the degrees of freedom of the numerator are K − 1 and of the denominator are K(IJ − 1).
- The statistical difference in calibrated values by performing a hypothesis test based on the t-Student distribution, with the null hypothesis , where and are the calibrated parameters from any two methods from Table 3, and are the pooled degrees of freedom of the difference obtained by the Welch–Satterthwaite formula [55].
- The statistical difference in mechanical characterization results by performing a hypothesis test based on the t-Student distribution, with the null hypothesis .
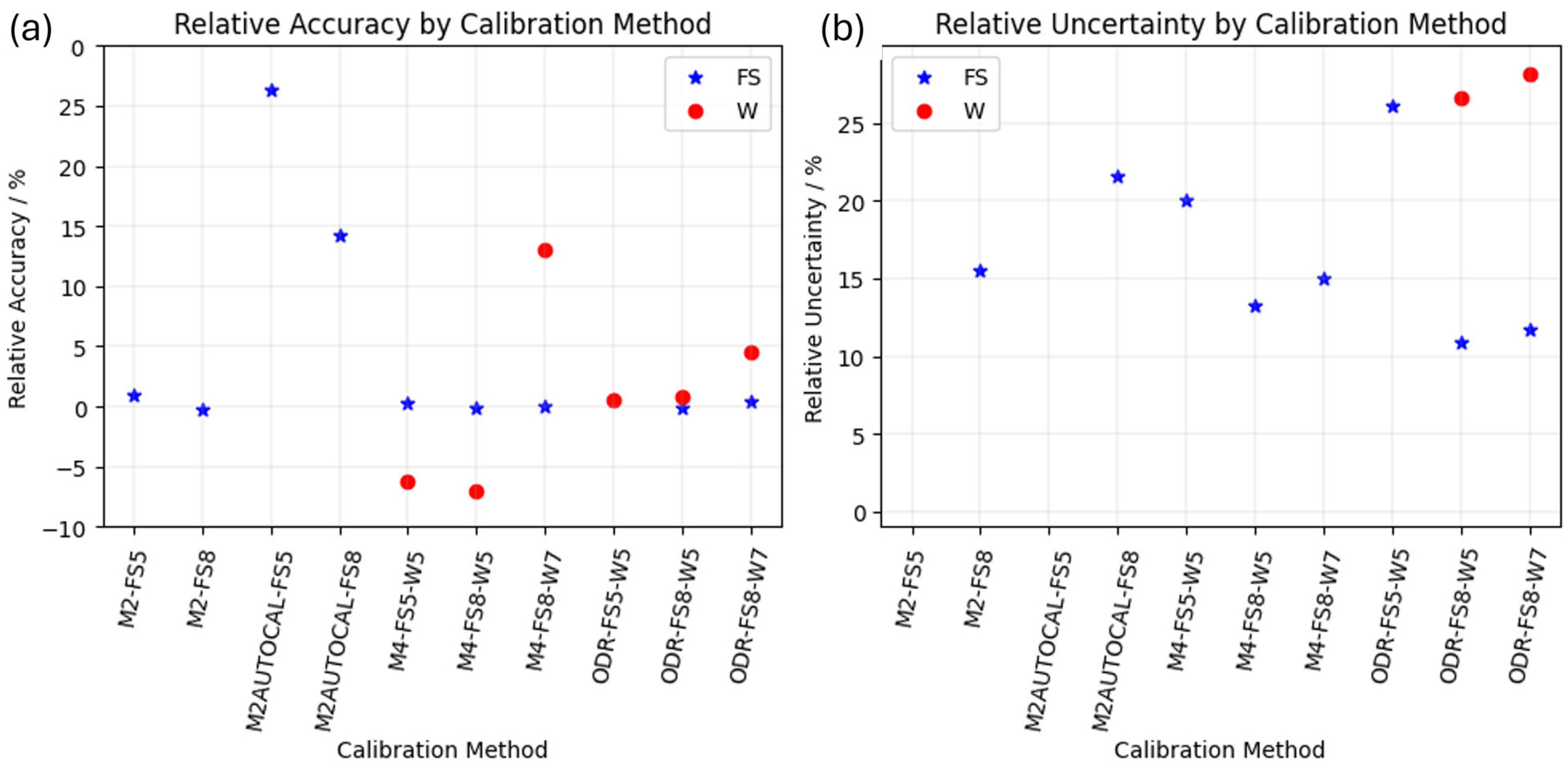
- Relative accuracy: , where represents the mechanical characterization from any of the considered calibration methods (in this case, i ranges from 1 to 10), and the is the reference value reported on the calibration certificate by an independent characterization method.
- Relative uncertainty: .
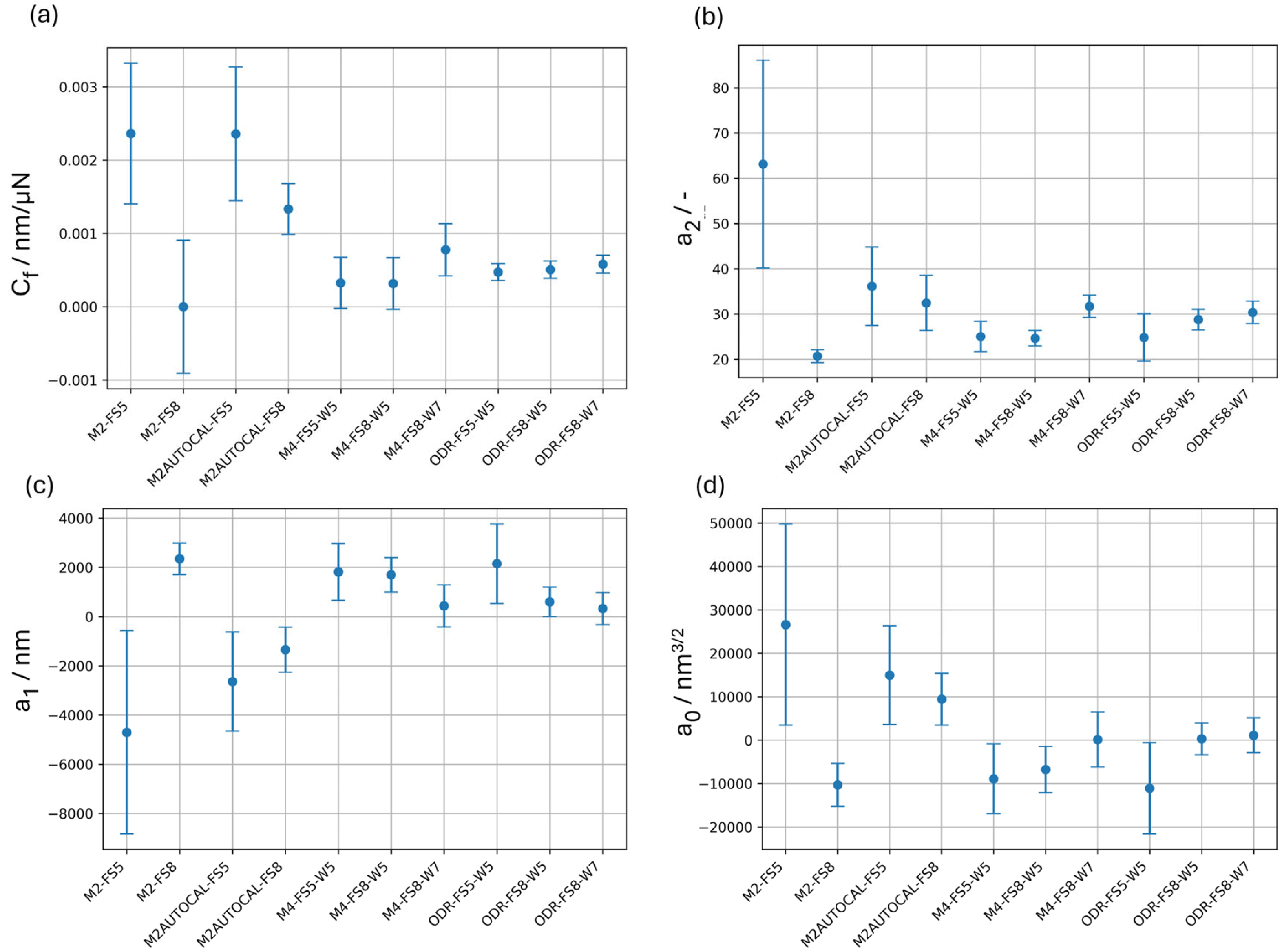
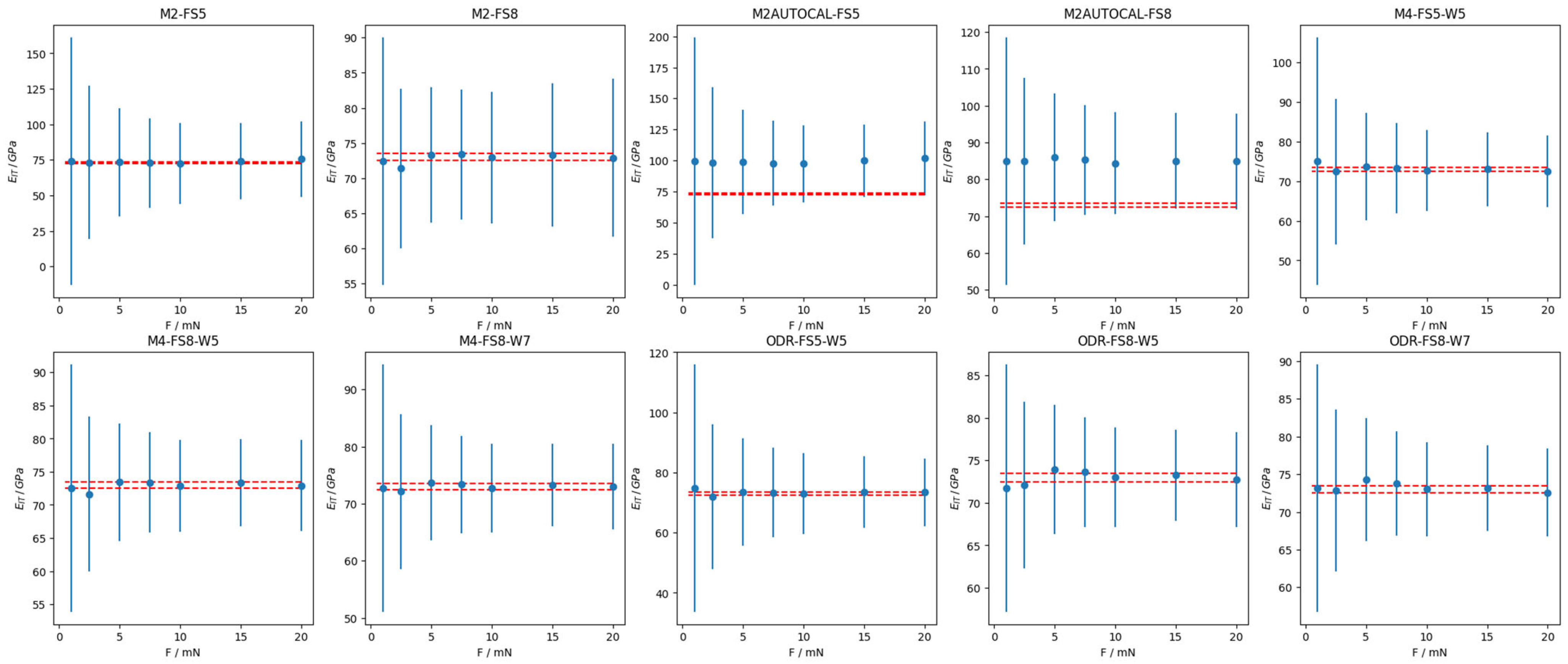
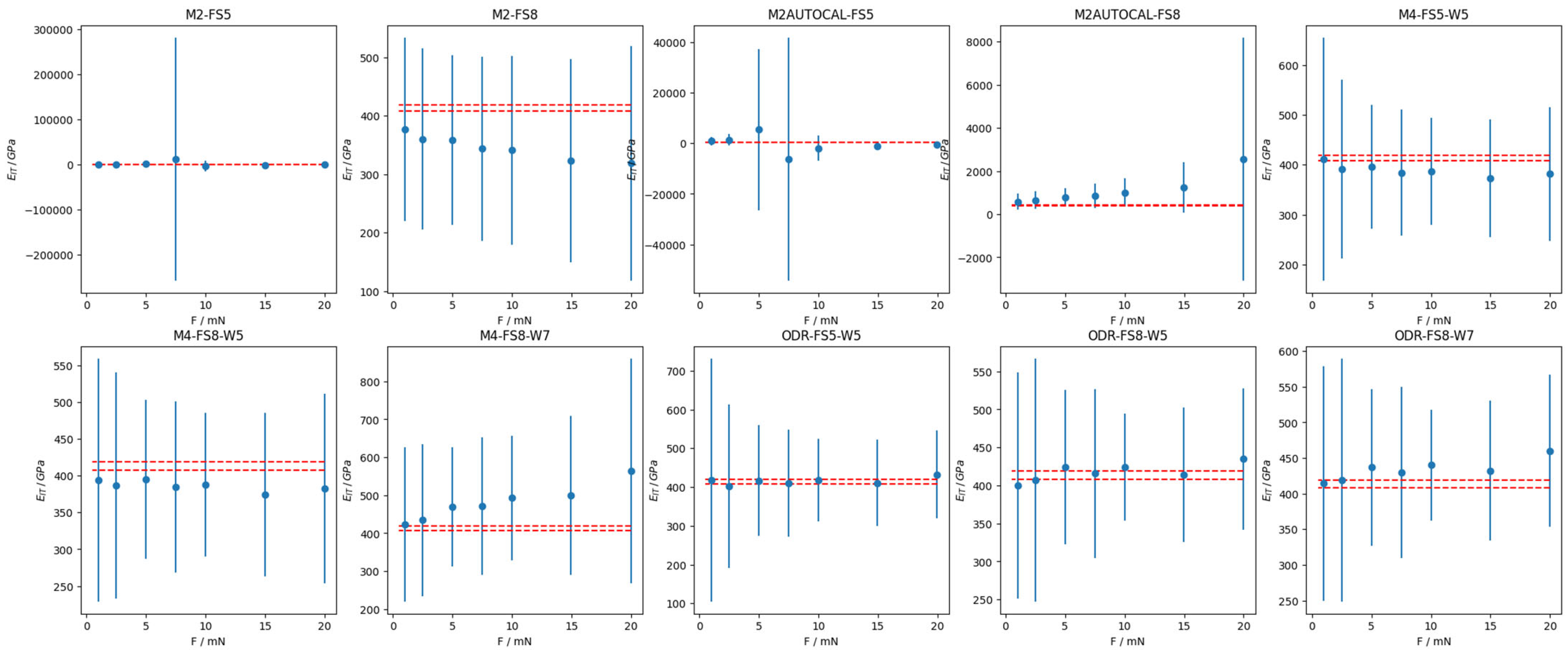
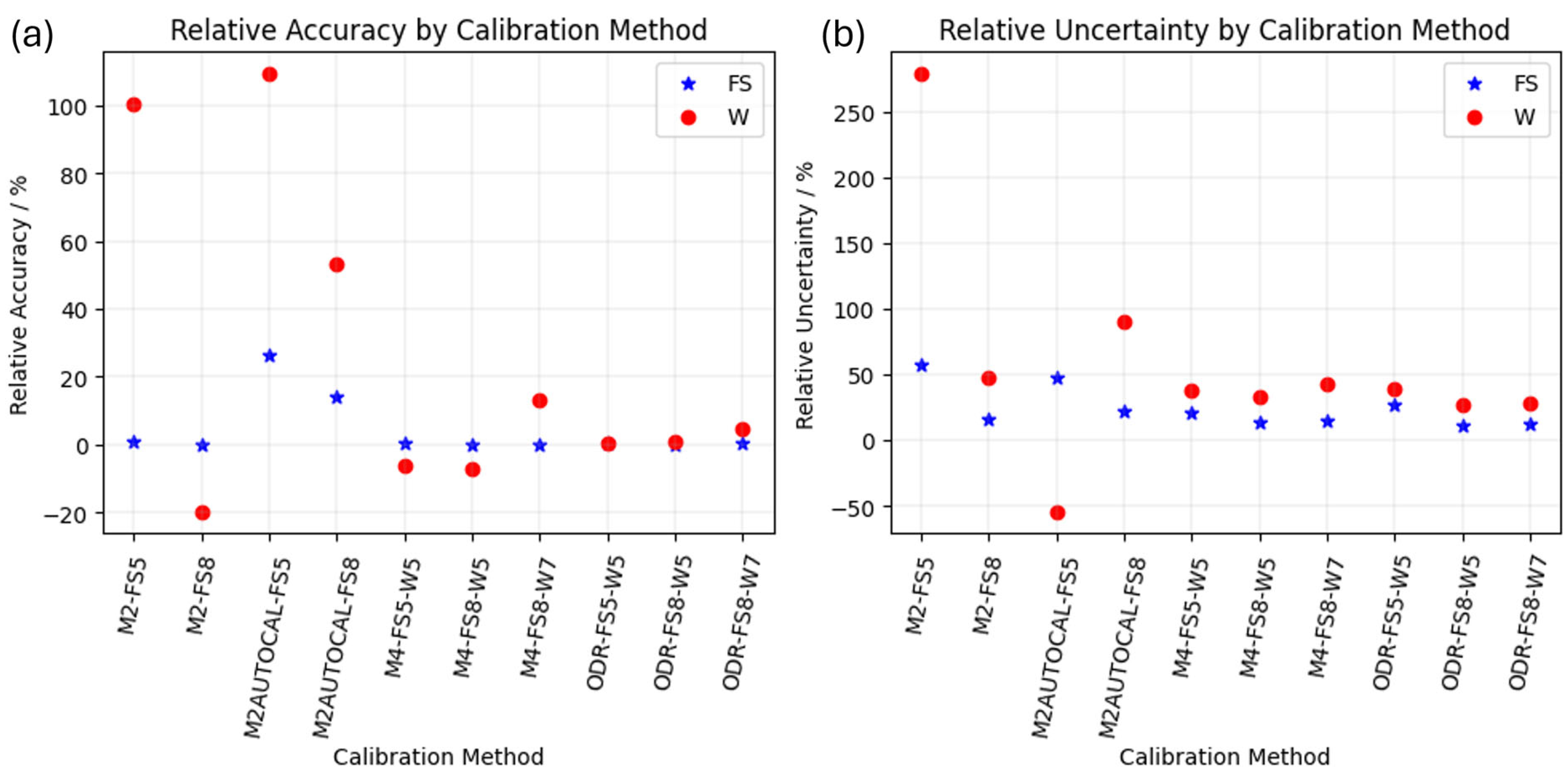
3. Results
4. Discussion
5. Conclusions
- -
- Calibration methods based on two certified reference materials, e.g., ISO 14577-2 method 4, optimize the accuracy and uncertainty of characterization.
- -
- Multiple calibration indentation datasets are needed to avoid the severe underestimation of calibration uncertainty.
- -
- A cost-effective approach to cater for the effect of the calibration indentation dataset can be obtained by the bootstrap simulation of such datasets.
- -
- Indentation on tungsten certified reference material shall be greater than 5 mN to avoid characterization bias.
- -
- The single-step method, based on orthogonal distance regression, further improves the accuracy and uncertainty of the ISO 14577-2 method 4.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CRM | Certified Reference Material |
| FS | Fused Silica (SiO2) |
| IIT | Instrumented Indentation Test |
| ISO | International Organization for Standardization |
Appendix A

References
- Oliver, W.C.; Pharr, G.M. An Improved Technique for Determining Hardness and Elastic Modulus Using Load and Displacement Sensing Indentation Experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of Hardness and Elastic Modulus by Instrumented Indentation: Advances in Understanding and Refinements to Methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Lucca, D.A.; Herrmann, K.; Klopfstein, M.J. Nanoindentation: Measuring Methods and Applications. CIRP Ann. Manuf. Technol. 2010, 59, 803–819. [Google Scholar] [CrossRef]
- Schulze, V.; Aurich, J.; Jawahir, I.S.; Karpuschewski, B.; Yan, J. Surface Conditioning in Cutting and Abrasive Processes. CIRP Ann. 2024, 73, 667–693. [Google Scholar] [CrossRef]
- ISO 14577-1:2015; Metallic Materials-Instrumented Indentation Test for Hardness and Materials Parameters—Part 1: Test Method. International Organization for Standardization: Geneva, Switzerland, 2015.
- Mughal, M.; Amanieu, H.-Y.; Moscatelli, R.; Sebastiani, M. A Comparison of Microscale Techniques for Determining Fracture Toughness of LiMn2O4 Particles. Materials 2017, 10, 403. [Google Scholar] [CrossRef]
- Mieczkowski, G.; Szpica, D.; Borawski, A. Comprehensive Analysis of Elastic–Plastic Behavior in Hybrid Metal Matrix Composites with Varied Reinforcement Geometry. Materials 2025, 18, 2763. [Google Scholar] [CrossRef]
- Slater, C.; Bandi, B.; Dastur, P.; Davis, C. Multiphase Identification Through Automatic Classification from Large-Scale Nanoindentation Mapping Compared to an EBSD-Machine Learning Approach. Metals 2025, 15, 636. [Google Scholar] [CrossRef]
- Li, Z.; Klapetek, P.; Brand, U.; Refino, A.D.; Xu, J.; Peiner, E. Nanomechanical Characterisation of Vertical Nanowires Used for Energy Harvesting. Meas. Sens. 2025, 38, 101671. [Google Scholar] [CrossRef]
- Lucca, D.A.; Klopfstein, M.J.; Ghisleni, R.; Cantwell, G. Investigation of Polished Single Crystal ZnO by Nanoindentation. CIRP Ann. 2002, 51, 483–486. [Google Scholar] [CrossRef]
- Yan, D.; Cuevas, A.; Stuckelberger, J.; Wang, E.C.; Phang, S.P.; Kho, T.C.; Michel, J.I.; Macdonald, D.; Bullock, J. Silicon Solar Cells with Passivating Contacts: Classification and Performance. Prog. Photovolt. Res. Appl. 2023, 31, 310–326. [Google Scholar] [CrossRef]
- Khataee, A.R.; Fathinia, M.; Aber, S.; Zarei, M. Optimization of Photocatalytic Treatment of Dye Solution on Supported TiO2 Nanoparticles by Central Composite Design: Intermediates Identification. J. Hazard. Mater. 2010, 181, 886–897. [Google Scholar] [CrossRef] [PubMed]
- George, J.; Mannepalli, S.; Mangalampalli, K.S.R.N. Understanding Nanoscale Plasticity by Quantitative In Situ Conductive Nanoindentation. Adv. Eng. Mater. 2021, 23, 2001494. [Google Scholar] [CrossRef]
- Lucca, D.A.; Zare, A.; Klopfstein, M.J.; Shao, L.; Xie, G.Q. Investigation of the Mechanical Behavior of Ion Irradiated Ni-Free Ti-Based Metallic Glass by Nanoindentation. CIRP Ann. 2014, 63, 533–536. [Google Scholar] [CrossRef]
- Genta, G.; Maculotti, G. Thin Coatings Thickness Measurement by Augmented Nanoindentation Data Fusion. CIRP Ann. Manuf. Technol. 2024, 73, 409–412. [Google Scholar] [CrossRef]
- Li, N.; Wang, C.; Li, C. Microstructures and High-Temperature Mechanical Properties of Inconel 718 Superalloy Fabricated via Laser Powder Bed Fusion. Materials 2024, 17, 3735. [Google Scholar] [CrossRef]
- Rickhey, F.; Marimuthu, K.; Lee, H. Investigation on Indentation Cracking-Based Approaches for Residual Stress Evaluation. Materials 2017, 10, 404. [Google Scholar] [CrossRef]
- Lee, Y.-H.; Kwon, D. Estimation of Biaxial Surface Stress by Instrumented Indentation with Sharp Indenters. Acta Mater. 2004, 52, 1555–1563. [Google Scholar] [CrossRef]
- Sleem, K.; Grima, G.; Cabibbo, M. A Nanoindentation Approach to Investigating Dislocation Density in Additive-Manufactured SS316L-Graded Lattice Structures. J. Manuf. Mater. Process. 2025, 9, 59. [Google Scholar] [CrossRef]
- Bertolini, R.; Bruschi, S.; Ghiotti, A.; Savio, E.; Ceseracciu, L.; Jawahir, I.S. Surface Integrity and Superelastic Response of Additively Manufactured Nitinol after Heat Treatment and Finish Machining. CIRP Ann. 2023, 72, 501–504. [Google Scholar] [CrossRef]
- Lucca, D.A.; Klopfstein, M.J.; Ghisleni, R.; Gude, A.; Mehner, A.; Datchary, W. Investigation of Sol-Gel Derived ZrO2 Thin Films by Nanoindentation. CIRP Ann. Manuf. Technol. 2004, 53, 475–478. [Google Scholar] [CrossRef]
- Hayes, S.A.; Goruppa, A.A.; Jones, F.R. Dynamic Nanoindentation as a Tool for the Examination of Polymeric Materials. J. Mater. Res. 2004, 19, 3298–3306. [Google Scholar] [CrossRef]
- Ovsik, M.; Manas, M.; Stanek, M.; Dockal, A.; Vanek, J.; Mizera, A.; Adamek, M.; Stoklasek, P. Polyamide Surface Layer Nano-Indentation and Thermal Properties Modified by Irradiation. Materials 2020, 13, 2915. [Google Scholar] [CrossRef]
- Tosini, M.; Tänzer, T.; Villata, S.; Baruffaldi, D.; Monica, V.; Peracino, B.; Primo, L.; Frascella, F.; Pirri, F.; Audenino, A.; et al. A Methodological Approach for Interpreting and Comparing the Viscoelastic Behaviors of Soft Biological Tissues and Hydrogels at the Cell-Length Scale. Appl. Sci. 2024, 14, 1093. [Google Scholar] [CrossRef]
- Xu, D.; Harvey, T.; Begiristain, E.; Domínguez, C.; Sánchez-Abella, L.; Browne, M.; Cook, R.B. Measuring the Elastic Modulus of Soft Biomaterials Using Nanoindentation. J. Mech. Behav. Biomed. Mater. 2022, 133, 105329. [Google Scholar] [CrossRef] [PubMed]
- Qian, L.; Zhao, H. Nanoindentation of Soft Biological Materials. Micromachines 2018, 9, 654. [Google Scholar] [CrossRef] [PubMed]
- Mostakhdemin, M.; Nand, A.; Ramezani, M. Articular and Artificial Cartilage, Characteristics, Properties and Testing Approaches—A Review. Polymers 2021, 13, 2000. [Google Scholar] [CrossRef]
- Erazo, O.; Jakes, J.E.; Plaza, N.Z.; Vergara-Figueroa, J.; Valenzuela, P.; Gacitúa, W. Quasistatic and Dynamic Nanoindentation Measurements of Pinus radiata D. Don S2 and CCML Cell Wall Layers. Forests 2023, 14, 1900. [Google Scholar] [CrossRef]
- Ezenwafor, T.; Anye, V.; Madukwe, J.; Amin, S.; Obayemi, J.; Odusanya, O.; Soboyejo, W. Nanoindentation Study of the Viscoelastic Properties of Human Triple Negative Breast Cancer Tissues: Implications for Mechanical Biomarkers. Acta Biomater. 2023, 158, 374–392. [Google Scholar] [CrossRef]
- Yallapu, M.M.; Katti, K.S.; Katti, D.R.; Mishra, S.R.; Khan, S.; Jaggi, M.; Chauhan, S.C. The Roles of Cellular Nanomechanics in Cancer. Med. Res. Rev. 2015, 35, 198–223. [Google Scholar] [CrossRef]
- ISO 14577-2:2015; Metallic Materials-Instrumented Indentation Test for Hardness and Materials Parameters—Part 2: Verification and Calibration of Testing Machines. International Organization for Standardization: Geneva, Switzerland, 2015.
- Barbato, G.; Genta, G.; Cagliero, R.; Galetto, M.; Klopfstein, M.J.; Lucca, D.A.; Levi, R. Uncertainty Evaluation of Indentation Modulus in the Nano-Range: Contact Stiffness Contribution. CIRP Ann. Manuf. Technol. 2017, 66, 495–498. [Google Scholar] [CrossRef]
- Barbato, G.; Brondino, G.; Galetto, M.; Vicario, G. “Zero-Point” in the Evaluation of Martens Hardness Uncertainty. In Proceedings of the 11th IMEKO TC5 Conference on Hardness Measurement 2002—Joint International Conference on Force, Mass, Torque, Hardness and Civil Engineering Metrology in the Age of Globalization, Celle, Germany, 24–26 September 2002; pp. 72–77. [Google Scholar]
- Cagliero, R.; Barbato, G.; Maizza, G.; Genta, G. Measurement of Elastic Modulus by Instrumented Indentation in the Macro-Range: Uncertainty Evaluation. Int. J. Mech. Sci. 2015, 101–102, 161–169. [Google Scholar] [CrossRef]
- Genta, G.; Maculotti, G.; Barbato, G.; Levi, R.; Galetto, M. Effect of Contact Stiffness and Machine Calibration in Nano-Indentation Testing. Procedia CIRP 2018, 78, 208–212. [Google Scholar] [CrossRef]
- Maculotti, G.; Genta, G.; Lorusso, M.; Pavese, M.; Ugues, D.; Galetto, M. Instrumented Indentation Test: Contact Stiffness Evaluation in the Nano-Range. Nanomanuf. Metrol. 2018, 2, 16–25. [Google Scholar] [CrossRef]
- Germak, A.; Herrmann, K.; Dai, G.; Li, Z. Development of Calibration Methods for Hardness Indenters. In VDI Berichte; Verlag: Düsseldorf, Germany, 2006; pp. 13–26. [Google Scholar]
- Maculotti, G.; Kholkhujaev, J.; Genta, G.; Galetto, M. Direct Calibration of Indenter Tip Geometry by Optical Surface Topography Measuring Instruments. J. Mater. Res. 2023, 38, 3336–3348. [Google Scholar] [CrossRef]
- Aldrich-Smith, G.; Jennett, N.J.; Hangen, U. Direct Measurement of Nanoindentation Area Function by Metrological AFM. Int. J. Mater. Res. 2005, 96, 1267–1271. [Google Scholar] [CrossRef]
- Degenhardt, J.; Hu, X.; Zackaria, M.; Menelao, F.; Tutsch, R.; Dai, G. Accurate AFM Calibration of Indenter Geometry for Instrumented Indentation. Nanomanuf. Metrol. 2025, 8, 15. [Google Scholar] [CrossRef]
- Vanlandingham, M.R.; Juliano, T.F.; Hagon, M.J. Measuring Tip Shape for Instrumented Indentation Using Atomic Force Microscopy. Meas. Sci. Technol. 2005, 16, 2173–2185. [Google Scholar] [CrossRef]
- Barone, A.C.; Salerno, M.; Patra, N.; Gastaldi, D.; Bertarelli, E.; Carnelli, D.; Vena, P. Calibration Issues for Nanoindentation Experiments: Direct Atomic Force Microscopy Measurements and Indirect Methods. Microsc. Res. Tech. 2010, 73, 996–1004. [Google Scholar] [CrossRef]
- Li, Z.; Brand, U. Towards Quantitative Characterisation of the Small Force Transducer Used in Nanoindentation Instruments. Mod. Instrum. 2013, 02, 61–67. [Google Scholar] [CrossRef][Green Version]
- Brand, U.; Chudoba, T.; Griepentrog, M.; Schwenk, D.; Bosch, G.; Scheerer, H.; Gärtner, E. Round Robin for Testing Instrumented Indenters with Silicon Reference Springs. Int. J. Mater. Res. 2015, 106, 1215–1223. [Google Scholar] [CrossRef]
- Galetto, M.; Barbato, G.; Maculotti, G. System, Method and Device for Measuring the Frame Compliance of a Durometer. WO2024116066A1, 28 November 2023. [Google Scholar]
- Doerner, M.F.; Nix, W.D. A Method for Interpreting the Data from Depth-Sensing Indentation Instruments. J. Mater. Res. 1986, 1, 601–609. [Google Scholar] [CrossRef]
- Meneve, J.L.; Smith, J.F.; Jennett, N.M.; Saunders, S.R.J. Surface Mechanical Property Testing by Depth Sensing Indentation. Appl. Surf. Sci. 1996, 100–101, 64–68. [Google Scholar] [CrossRef]
- Jennett, N.M.; McCartney, L.N.; Lawrence, K.; Hunt, R.; Maxwell, A.; Koskinen, J.; Meneve, J.; Wegener, W.; Gibson, N.; Bushby, A.J.; et al. Indicoat Final Report—Determination of Hardness and Modulus of Thin Films and Coatings by Nanoindentation. In NPL Report MATC(A); National Physical Laboratory: Teddington, UK, 2001. [Google Scholar]
- Herrmann, K.; Jennet, N.M.; Wegener, W.; Meneve, J.; Hasche, K.; Seeman, R. Progress in Determination of the Area Function of Indenters Used for Nanoindentation. Thin Solid Film. 2000, 377–378, 394–400. [Google Scholar] [CrossRef]
- Galetto, M.; Genta, G.; Maculotti, G. Single-Step Calibration Method for Nano Indentation Testing Machines. CIRP Ann. 2020, 69, 429–432. [Google Scholar] [CrossRef]
- Maculotti, G.; Genta, G.; Carbonatto, A.; Galetto, M. Uncertainty-Based Comparison of the Effect of the Area Shape Function on Material Characterisation in Nanoindentation Testing. In Proceedings of the 22nd International Conference and Exhibition of EUSPEN, Genève, Switzerland, 30 May–3 June 2022. [Google Scholar]
- Boggs, P.T.; Byrd, R.H.; Schnabel, R.B. A Stable and Efficient Algorithm for Nonlinear Orthogonal Distance Regression. SIAM J. Sci. Stat. Comput. 1987, 8, 1052–1078. [Google Scholar] [CrossRef]
- Maculotti, G.; Genta, G.; Galetto, M. Criticalities of Iterative Calibration Procedures for Indentation Testing Machines in the Nano-Range. In Proceedings of the 20th International Conference and Exhibition of EUSPEN, Genève, Switzerland, 8–12 June 2020; pp. 2–5. [Google Scholar]
- Maculotti, G.; Genta, G.; Galetto, M. An Uncertainty-Based Quality Evaluation Tool for Nanoindentation Systems. Measurement 2024, 225, 113974. [Google Scholar] [CrossRef]
- JCGM100; Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement (GUM). JCGM: Sèvres, France, 2008. [CrossRef]



| Method # | Ap Calibration | Cf Calibration | Input Required | Notes |
|---|---|---|---|---|
| 1 | Direct by AFM | Indirect | Ap calibration | CRM: W |
| 2 | Indirect | Indirect | None | CRM: Al, or SiO2 |
| 3 | Direct by AFM | Indirect | Ap calibration, calibrated Er | CRM: W |
| 4 | Indirect | Indirect | Calibrated Er,1, Er,2 | CRM 1 (Ap): SiO2; CRM 2 (Cf): W |
| 5 | Indirect | Indirect | Calibrated Er,1, Er,2, elastic deformation | For spherical indenters |
| 6 | Indirect | Indirect | None | For micro- and macro-range (CRM shall not exhibit indentation size effect, nor significant pile-up and sink-in) |
| Certified Reference Material | Calibrated Property | Tested Maximum Forces/mN |
|---|---|---|
| SiO2 (FS) | E = (73.0 ± 0.5) GPa | 0.5, 1, 2.5, 5, 7.5, 10, 15, 20 |
| υ = (0.163 ± 0.002) | ||
| HIT = (8.5 ± 0.5) GPa | ||
| W | E = (414.3 ± 5.6) GPa | 1, 2.5, 5, 7.5, 10, 15, 20 |
| υ = (0.279 ± 0.005) | ||
| HIT = (7.0 ± 0.5) GPa |
| Short Name | Applied Method | CRM | Used Force Range/mN | I |
|---|---|---|---|---|
| M2-FS5 | ISO 14577-2 M2 with use of calibrated Er | SiO2 | [1,2,3,4,5,6,7,8,9,10] | 5 |
| M2-FS8 | [0.5–20] | 8 | ||
| M2AUTOCAL-FS5 | ISO 14577-2 M2 | [1,2,3,4,5,6,7,8,9,10] | 5 | |
| M2AUTOCAL-FS8 | [0.5–20] | 8 | ||
| M4-FS5-W5 | ISO 14577-2 M4 | SiO2, W | SiO2: [1,2,3,4,5,6,7,8,9,10] W: [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] | 5 |
| M4-FS8-W5 | SiO2: [0.5–20] W: [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] | Ap: 8 Cf: 5 | ||
| M4-FS8-W7 | SiO2: [0.5–20] W: [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] | Ap: 8 Cf: 7 | ||
| ODR-FS5-W5 | ODR Single-step method | SiO2, W | SiO2: [1,2,3,4,5,6,7,8,9,10] W: [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] | 5 |
| ODR-FS8-W5 | SiO2: [0.5–20] W: [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] | Ap: 8 Cf: 5 | ||
| ODR-FS8-W7 | SiO2: [0.5–20] W: [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20] | Ap: 8 Cf: 7 |
| Method | p-Value | p-Value | p-Value | p-Value | ||||
|---|---|---|---|---|---|---|---|---|
| M2-FS5 | <0.001 | 95.7% | <0.001 | 80.2% | <0.001 | 87.6% | <0.001 | 97.0% |
| M2-FS8 | >0.99 | <1‰ | 25.8% | 32.8% | 43.1% | |||
| M2AUTOCAL-FS5 | <0.001 | 95.3% | 73.2% | 83.0% | 93.1% | |||
| M2AUTOCAL-FS8 | <0.001 | 68.2% | 36.8% | 58.6% | 95.8% | |||
| M4-FS5-W5 | >0.99 | 1.9% | 39.5% | 43.2% | 50.7% | |||
| M4-FS8-W5 | >0.99 | 1.8% | 27.7% | 35.8% | 53.7% | |||
| M4-FS8-W7 | <0.001 | 6.8% | 33.8% | 44.4% | 70.5% | |||
| ODR-FS5-W5 | <0.001 | 38.0% | 21.3% | 21.0% | 19.9% | |||
| ODR-FS8-W5 | <0.001 | 47.7% | 22.9% | 25.6% | 36.2% | |||
| ODR-FS8-W7 | <0.001 | 40.1% | 19.4% | 21.6% | 30.6% | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maculotti, G.; Giorio, L.; Genta, G.; Galetto, M. Metrological Comparison of Indirect Calibration Methods for Nanoindentation: A Bootstrap-Based Approach. Materials 2025, 18, 4382. https://doi.org/10.3390/ma18184382
Maculotti G, Giorio L, Genta G, Galetto M. Metrological Comparison of Indirect Calibration Methods for Nanoindentation: A Bootstrap-Based Approach. Materials. 2025; 18(18):4382. https://doi.org/10.3390/ma18184382
Chicago/Turabian StyleMaculotti, Giacomo, Lorenzo Giorio, Gianfranco Genta, and Maurizio Galetto. 2025. "Metrological Comparison of Indirect Calibration Methods for Nanoindentation: A Bootstrap-Based Approach" Materials 18, no. 18: 4382. https://doi.org/10.3390/ma18184382
APA StyleMaculotti, G., Giorio, L., Genta, G., & Galetto, M. (2025). Metrological Comparison of Indirect Calibration Methods for Nanoindentation: A Bootstrap-Based Approach. Materials, 18(18), 4382. https://doi.org/10.3390/ma18184382







