Author Contributions
Conceptualization, X.-C.Z. and Z.-Y.L.; methodology, X.-C.Z. and Z.-Y.L.; software, Z.-Y.L.; validation, X.-C.Z., Z.-Y.L. and K.-S.Z.; formal analysis, X.-C.Z. and Z.-Y.L.; data curation, Z.-Y.L.; writing—original draft preparation, X.-C.Z. and Z.-Y.L.; writing—review and editing, K.-S.Z.; project administration, X.-C.Z.; funding acquisition, X.-C.Z. All authors have read and agreed to the published version of the manuscript.
Figure 1.
Geometry of smooth Q235B specimen (unit: mm).
Figure 1.
Geometry of smooth Q235B specimen (unit: mm).
Figure 2.
The stress–strain hysteresis loops of a specimen under strain amplitude 0.004.
Figure 2.
The stress–strain hysteresis loops of a specimen under strain amplitude 0.004.
Figure 3.
The stress–strain hysteresis loops of a specimen under strain amplitude 0.005.
Figure 3.
The stress–strain hysteresis loops of a specimen under strain amplitude 0.005.
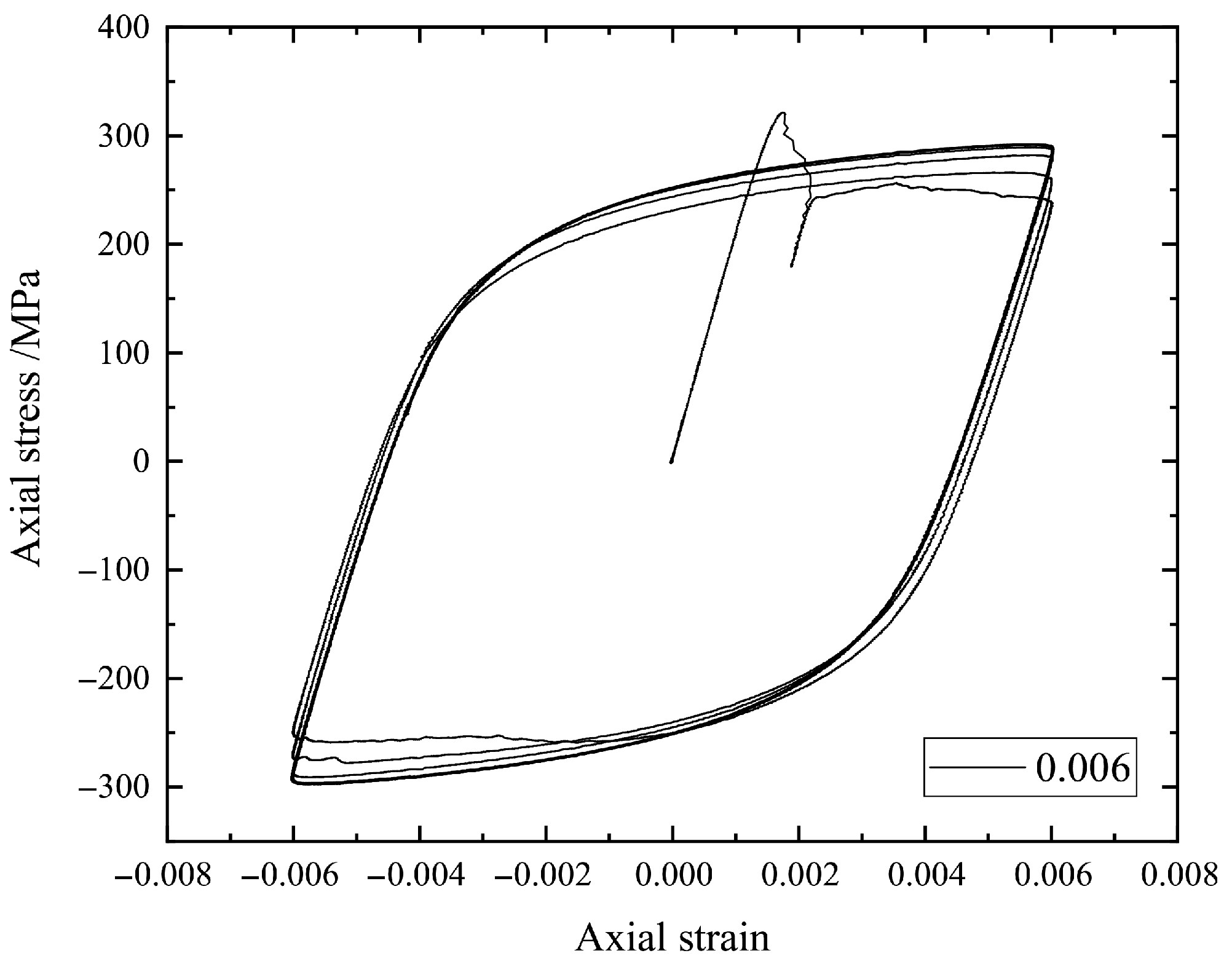
Figure 4.
The stress–strain hysteresis loops of a specimen under strain amplitude 0.006.
Figure 4.
The stress–strain hysteresis loops of a specimen under strain amplitude 0.006.
Figure 5.
The stress–strain hysteresis loops of a specimen under strain amplitude 0.008.
Figure 5.
The stress–strain hysteresis loops of a specimen under strain amplitude 0.008.
Figure 6.
Scheme of dataset compilation process.
Figure 6.
Scheme of dataset compilation process.
Figure 7.
Six key points by considering the characteristics of a hysteresis loop.
Figure 7.
Six key points by considering the characteristics of a hysteresis loop.
Figure 8.
Six key points of a hysteresis loop in polar coordinates.
Figure 8.
Six key points of a hysteresis loop in polar coordinates.
Figure 9.
BP neural network model driven by the dataset
Figure 9.
BP neural network model driven by the dataset
Figure 10.
Flowchart of SVR.
Figure 10.
Flowchart of SVR.
Figure 11.
Variations of versus by selecting , and respectively.
Figure 11.
Variations of versus by selecting , and respectively.
Figure 12.
Network structure of RF.
Figure 12.
Network structure of RF.
Figure 13.
The effects of the number of trees and the depth of trees on MSE.
Figure 13.
The effects of the number of trees and the depth of trees on MSE.
Figure 14.
Comparison between the predicted values and the experimental results of the training set based on the trained BP neural network models for cases 1–4, respectively.
Figure 14.
Comparison between the predicted values and the experimental results of the training set based on the trained BP neural network models for cases 1–4, respectively.
Figure 15.
Comparison between the predicted values and the experimental results of the test set based on the trained BP neural network models for cases 1–4, respectively.
Figure 15.
Comparison between the predicted values and the experimental results of the test set based on the trained BP neural network models for cases 1–4, respectively.
Figure 16.
Interval predictions of logarithm fatigue life for specimens A10–A12 based on the BP neural network models for cases 1–4, respectively. The blue points are the predicted values based on the randomly generated input data.
Figure 16.
Interval predictions of logarithm fatigue life for specimens A10–A12 based on the BP neural network models for cases 1–4, respectively. The blue points are the predicted values based on the randomly generated input data.
Figure 17.
Comparison between the predicted values and the experimental results of the training set based on the constructed SVR models for cases 1–4, respectively.
Figure 17.
Comparison between the predicted values and the experimental results of the training set based on the constructed SVR models for cases 1–4, respectively.
Figure 18.
Comparison between the predicted values and the experimental results of the test set based on the constructed SVR models for cases 1–4, respectively.
Figure 18.
Comparison between the predicted values and the experimental results of the test set based on the constructed SVR models for cases 1–4, respectively.
Figure 19.
Interval predictions of logarithm fatigue life for specimens A10–A12 based on the SVR models for cases 1–4, respectively. The blue points are the predicted values based on the randomly generated input data.
Figure 19.
Interval predictions of logarithm fatigue life for specimens A10–A12 based on the SVR models for cases 1–4, respectively. The blue points are the predicted values based on the randomly generated input data.
Figure 20.
Comparison between the predicted values and the experimental data of the training set based on the selected RF models for cases 1–4, respectively.
Figure 20.
Comparison between the predicted values and the experimental data of the training set based on the selected RF models for cases 1–4, respectively.
Figure 21.
Comparison between the predicted values and the experimental data of the test set based on the selected RF models for cases 1–4, respectively.
Figure 21.
Comparison between the predicted values and the experimental data of the test set based on the selected RF models for cases 1–4, respectively.
Figure 22.
Interval predictions of logarithm fatigue life for specimens A10–A12 based on the RF models for cases 1–4, respectively. The blue points are the predicted values based on the randomly generated input data.
Figure 22.
Interval predictions of logarithm fatigue life for specimens A10–A12 based on the RF models for cases 1–4, respectively. The blue points are the predicted values based on the randomly generated input data.
Table 1.
Mechanical properties of Q235B steel.
Table 1.
Mechanical properties of Q235B steel.
| Yield Strength/Mpa | Ultimate Strength/Mpa | Young’s Modulus/Mpa | Poisson’s Ratio | Elongation |
|---|
| 260 | 550 | 193900 | 0.277 | 20% |
Table 2.
Main chemical compositions of Q235B steel (%).
Table 2.
Main chemical compositions of Q235B steel (%).
| C | | | P | S | | |
|---|
| 0.14 | 0.032 | 0.4 | 0.03 | 0.019 | 0.031 | 0.42 |
Table 3.
Experimental data of Q235B.
Table 3.
Experimental data of Q235B.
| Axial Strain Amplitude |
|---|
| 0.004 | 0.005 | 0.006 | 0.008 |
|---|
| Specimen | | Specimen | | Specimen | | Specimen | |
|---|
| A1 | 3.9227 | A4 | 3.7782 | A7 | 3.4905 | A10 | 3.2586 |
| A2 | 3.9129 | A5 | 3.7455 | A8 | 3.464 | A11 | 3.1452 |
| A3 | 3.9946 | A6 | 3.7269 | A9 | 3.4984 | A12 | 3.4 |
Table 4.
Interval-valued data of Q235B smooth specimens.
Table 4.
Interval-valued data of Q235B smooth specimens.
| Class | Specimen | Strain Amplitude Interval | Hysteresis Loop | Fatigue Life (lg) |
|---|
| Training set | A1, A2, A3 | [0.00392, 0.00408] | | [3.9129, 3.9946] |
| A4, A5, A6 | [0.00492, 0.00508] | | [3.7269, 3.7455] |
| A7, A8, A9 | [0.00592, 0.00608] | | [3.464, 3.4984] |
| Test set | A10, A11, A12 | [0.00792, 0.00808] | | [3.1452, 3.4] |
Table 5.
Optimized hyperparameters in ML models.
Table 5.
Optimized hyperparameters in ML models.
| ML Model | Hyperparameter | Value |
|---|
| BP | Number of hidden layers | 3 |
| Numbers of neurons in hidden layers | 18, 13, 20 |
| Learning rate | 0.005 |
| Activation function | Sigmoid |
| SVR | Kernel | Radial basis function |
| Maximum allowable error | |
| Regularization parameter | |
| RF | Number of trees | |
| Depth of trees | |
Table 6.
Four cases of input data.
Table 6.
Four cases of input data.
| Case | Strain Amplitude? | Number of Early Hysteresis Loops | Dimension of Input Data |
|---|
| Case 1 | Yes | 10 | 61 |
| Case 2 | Yes | 5 | 31 |
| Case 3 | No | 10 | 60 |
| Case 4 | No | 5 | 30 |
Table 7.
Mean values and variances of probability distributions in interval predictions.
Table 7.
Mean values and variances of probability distributions in interval predictions.
| Case | BP Model | SVR Model | RF Model |
|---|
| Mean | Variance | Mean | Variance | Mean | Variance |
|---|
| Case 1 | 3.28 | 0.032 | 3.27 | 0.034 | 3.23 | 0.030 |
| Case 2 | 3.27 | 0.036 | 3.29 | 0.038 | 3.22 | 0.038 |
| Case 3 | 3.30 | 0.042 | 3.25 | 0.041 | 3.31 | 0.036 |
| Case 4 | 3.23 | 0.064 | 3.22 | 0.068 | 3.30 | 0.062 |
Table 8.
Performances of three models for fatigue life point predictions of Q235B.
Table 8.
Performances of three models for fatigue life point predictions of Q235B.
| Case | BP Model | SVR Model | RF Model |
|---|
| MSE | MSE | MSE |
|---|
| Case 1 | 0.0011 | 0.0041 | 0.0002 |
| Case 2 | 0.0058 | 0.0069 | 0.0149 |
| Case 3 | 0.0108 | 0.0119 | 0.0025 |
| Case 4 | 0.0260 | 0.0155 | 0.0202 |