Analysis of Filtration Coefficient of Selected Recycled Materials on the Example of Concrete Aggregate and Rubber Waste
Abstract
1. Introduction
2. Materials and Methods
2.1. fRCA
2.2. fRCA, RTWP and RTWG
- M1_R–fRCA with 10% addition of RTWP, 10% addition of RTWG, and 0% of FF content of fRCA,
- M3_R–fRCA with 10% addition of RTWP and 20% of FF content of fRCA.
2.3. RTWS
2.4. Equipment and Testing
3. Results and Discussion
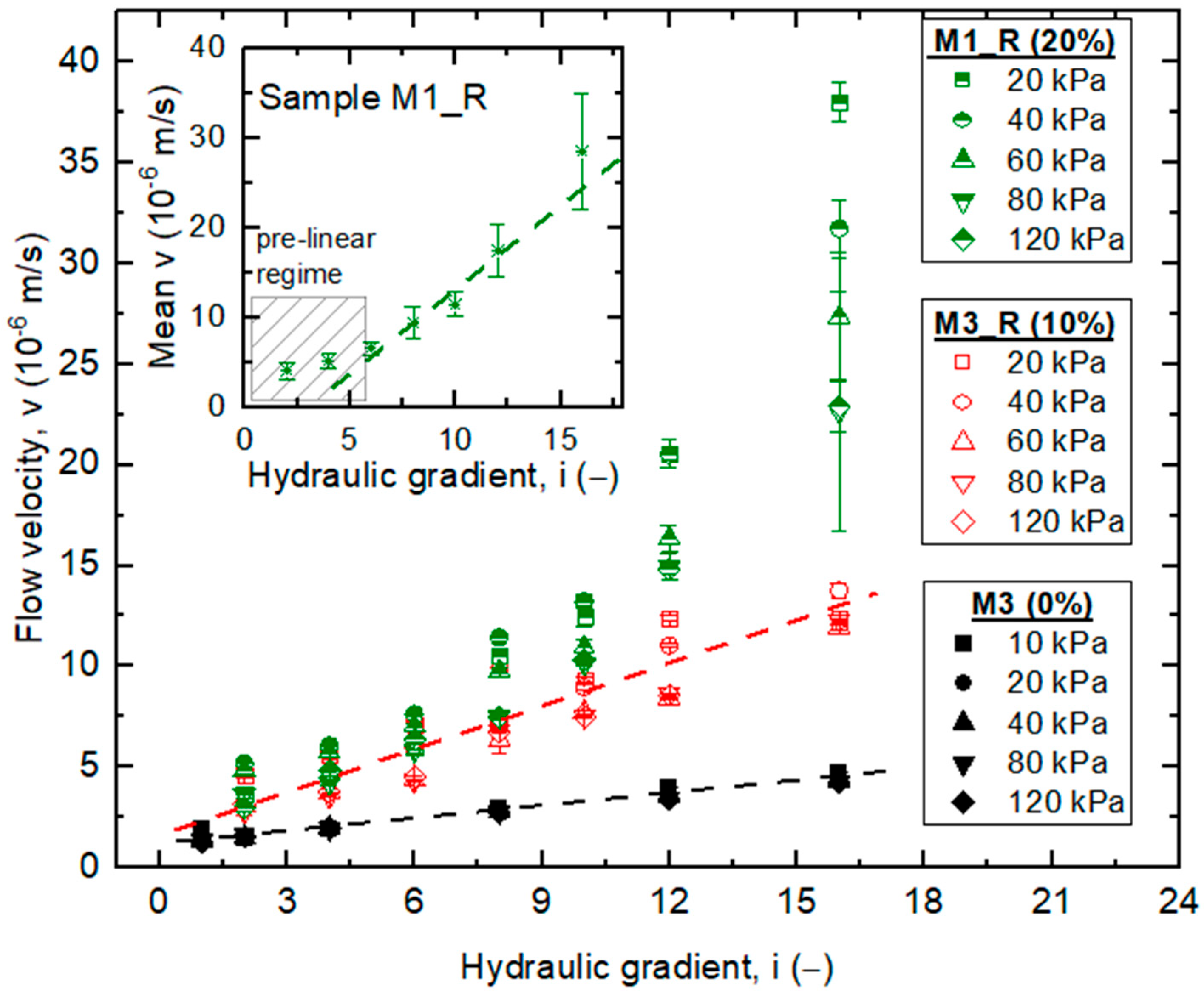
3.1. fRCA–RTW Mixtures
- Pre-linear filtration, where the relationship between velocity and gradient is curved, reflecting a gradual increase in permeability as interconnected pore channels open under increasing hydraulic forces.
- Linear filtration, where the flow aligns more closely with Darcy’s law at higher gradients.
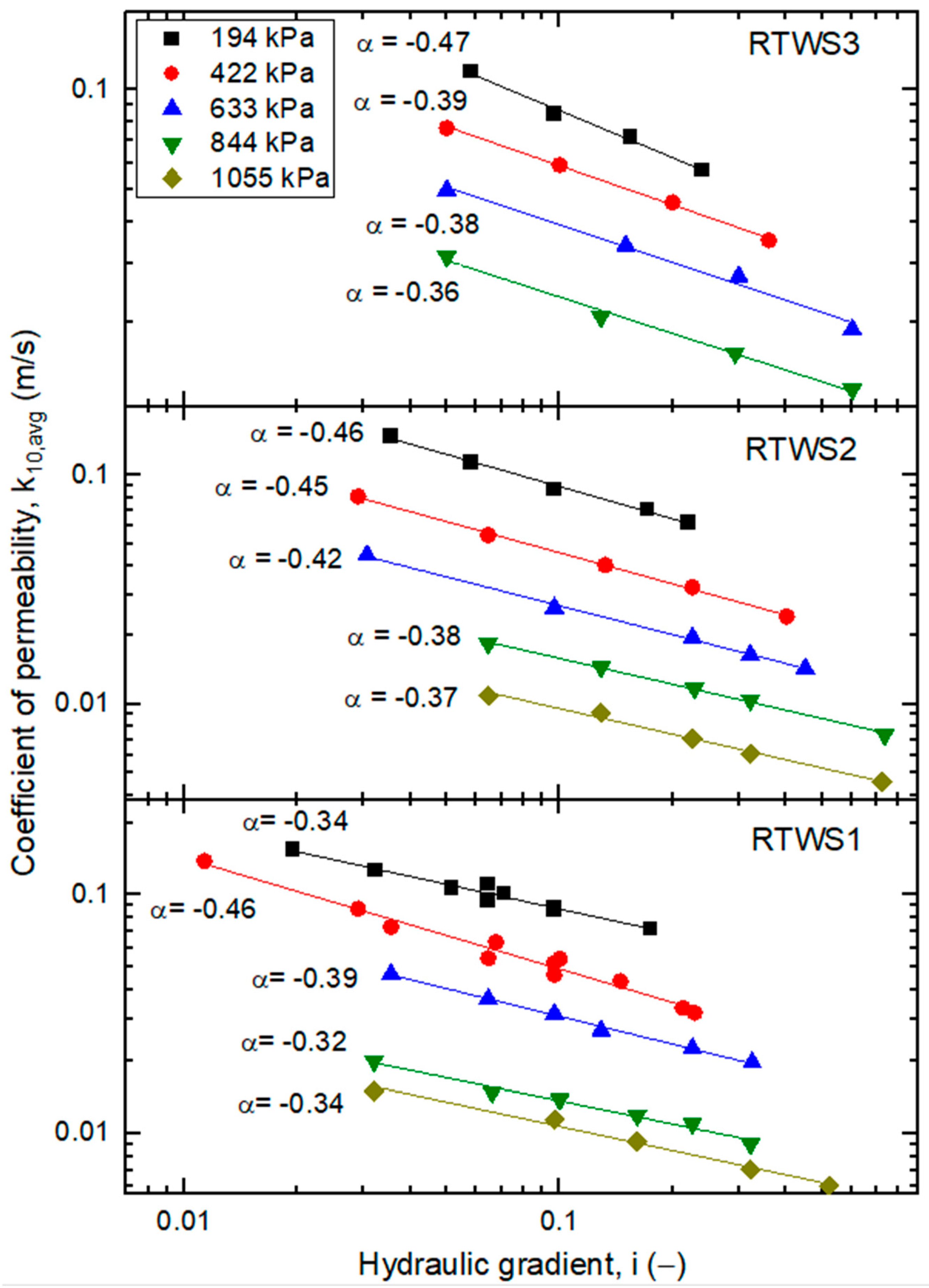
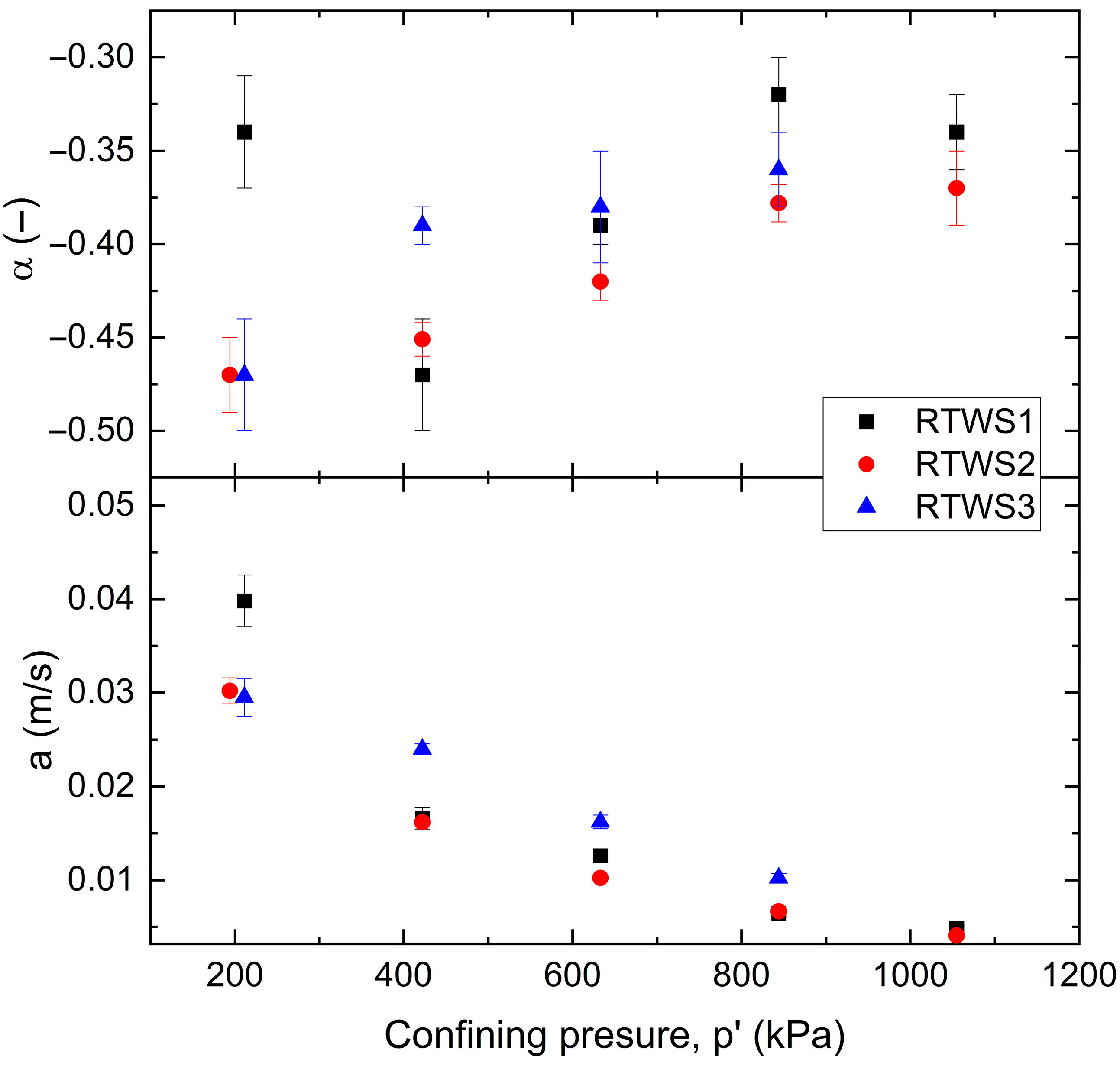
3.2. RTWS
4. Conclusions
- The tested crushed concrete aggregate has a filtration coefficient corresponding to semi-permeable, cohesive materials, e.g., clay. The filtration coefficient was found to be in the range of 10−6 to 10−7 m/s. This is undoubtedly associated with the composition of fine fractions, with a proportion of 20% in the M3 mixture.
- There is a non-linear relationship between the average coefficient of permeability of fRCA and hydraulic gradient: the former decreases as the latter increases. This may indicate the occurrence of clogging and obstruction of water flow caused by high flow velocities.
- No effect of consolidation pressure on fRCA filtration parameters was noted, although the tests were performed at low pressures. The experiments could be extended to higher pressures, as in the case of pure rubber waste.
- For fRCA, a linear increase in flow velocity was observed as the gradient increased. No characteristic filtration phases were observed, i.e., a pre-linear phase, a transition phase, and a linearisation phase. The initial gradient could not be determined, which may be related to the excessive gradients used in the studies.
- The addition of tire rubber waste modifies the permeability conditions of fRCA. In the mixtures, M1_R and M3_R, rubber was used as a partial replacement for coarser concrete aggregates, resulting in increased porosity and permeability. It is an increase of one order of magnitude. The presence of fine fractions in crushed concrete in the mixtures remains a concern.
- The higher the rubber content in the mixture (e.g., 20%), the more visible the division into two regimes: a low-pressure, aggregate-dominated regime where pore closure reduces flow, and a high-pressure, rubber-dominated regime where macropores associated with rubber particles increase flow; this two-phase behavior is absent in mixtures without rubber.
- The mixtures containing rubber (M1_R and M3_R) demonstrate significantly higher permeability coefficients at lower effective stresses compared to pure fRCA. The effect of consolidation for these materials is visible. There is a migration of finer particles and rubber particles into the pore spaces. The obtained hydraulic conductivity is a function of flow pressure and effective stress, especially for the M1_R mix.
- For the fRCA–RTW mixtures, an increase in flow velocity can be observed with an increase in the hydraulic gradient. The M1_R blend with 20% of rubber content exhibits the non-Darcian flow of water with threshold gradient occurrence. The M3_R mix, with a lower rubber content, i.e., 10%, performs more like pure fRCA and behaves according to Darcy’s law.
- Pure shredded tires in all studied cases, even at the highest possible compression pressure of 1055 kPa, are characterized by a high filtration coefficient similar to the water permeability of coarse-grained soils. This coefficient depends exponentially on the hydraulic gradient, i.e., the greater the gradient, the lower the filtration capacity. This is due to the uneven increase in water speed through the voids of the tire pieces, caused by a change in flow regime from laminar to turbulent.
- The influence of the water pressure height gradient depends on the compression pressure of the RTWS specimens. At a pressure greater than 800 kPa, the gradient i has little effect on the permeability coefficient.
- Restricted hydraulic gradient range. Future studies should consider applying a broader range of gradients (e.g., i < 1 to i > 20) to better define the transition between laminar and turbulent flow regimes.
- Absence of non-linear flow modeling. Future work should integrate such models like the Forchheimer or Hazen–Dupuit–Darcy to improve the interpretation and predictive capacity of filtration parameters.
- Limited consolidation pressures. Investigation at higher pressures—particularly for mixed and granular systems—would enhance the practical relevance of the findings.
- Lack of microstructural characterization. This study did not include microstructural analyses such as Scanning Electron Microscopy (SEM), Mercury Intrusion Porosimetry (MIP), or X-ray Computed Tomography (CT). Such techniques could elucidate key mechanisms influencing permeability, including pore connectivity, rubber–cement interaction, and clogging phenomena. Incorporating microstructural tools in future research would enable a more comprehensive understanding of how internal structure affects hydraulic behavior.
- Material heterogeneity and rubber content variability. Future experiments could benefit from controlled gradation of rubber particles and standardized RTW material specifications to reduce experimental scatter and isolate the effects of particle shape, size, and composition.
- Absence of temperature and/or saturation effect. Investigations could be extended to study thermal effects and unsaturated flow conditions, which would better reflect more realistic service environments, particularly in field conditions characterized by fluctuating temperatures and partial saturation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abbass, K.; Qasim, M.Z.; Song, H.; Murshed, M.; Mahmood, H.; Younis, I. A review of the global climate change impacts, adaptation, and sustainable mitigation measures. Environ. Sci. Pollut. Res. 2022, 29, 42539–42559. [Google Scholar] [CrossRef]
- Schilling, M.; Chiang, L. The effect of natural resources on a sustainable development policy: The approach of non-sustainable externalities. Energy Policy 2011, 39, 990–998. [Google Scholar] [CrossRef]
- A/RES/70/1-Transforming Our World: The 2030 Agenda for Sustainable Development. Available online: https://sdgs.un.org/2030agenda (accessed on 12 March 2025).
- Silva Vieira, C.; Pereira, P.; De Lurdes Lopes, M. Recycled Construction and Demolition Wastes as filling material for geosynthetic reinforced structures. Interface properties. J. Clean Prod. 2016, 124, 299–311. [Google Scholar] [CrossRef]
- Asanousi Lamma, O. The impact of recycling in preserving the environment. Int. J. Appl. Res. 2021, 7, 297–302. [Google Scholar]
- Kumbhar, S.; Gupta, A.; Desai, D. Recycling and Reuse of Construction and Demolition Waste for Sustainable Development. OIDA Int. J. Sustain. Dev. 2013, 6, 83–92. [Google Scholar]
- Moussa, A.; El Naggar, H.; Sadrekarimi, A. Dynamic characterization of tire derived aggregates using cyclic simple shear and bender element tests. Soil Dyn. Earth Eng. 2023, 165, 10700. [Google Scholar] [CrossRef]
- Farooq, M.A.; Nimbalkar, S.; Fatahi, B. Sustainable Applications of Tyre-Derived Aggregates for Railway Transportation Infrastructure. Sustainability 2022, 14, 11715. [Google Scholar] [CrossRef]
- Kumar, P.; Mina, U. Fundamentals of Ecology and Environment, 3rd ed.; Jamia Millia Islamia and Jawaharlal Nehru University: New Delhi, India, 2021. [Google Scholar]
- Dzięcioł, J.; Radziemska, M. Blast Furnace Slag, Post-Industrial Waste or Valuable Building Materials with Remediation Potential? Minerals 2022, 12, 478. [Google Scholar] [CrossRef]
- Khan, A.A.; Balunaini, U.; Costa, A.; Nguyen, N.H.T. A review on sustainable use of recycled construction and demolition waste aggregates in pavement base and subbase layers. Clean. Mater. 2024, 13, 100266. [Google Scholar] [CrossRef]
- Punetha, P.; Nimbalkar, S. Utilisation of construction and demolition waste and recycled glass for sustainable flexible pavements: A critical review. Transp. Geotech. 2025, 54, 101612. [Google Scholar] [CrossRef]
- Chen, S.H. Hydraulic Structures; Springer: Singapore, 2015. [Google Scholar]
- Elhakim, A.F. Estimation of soil permeability. Alex. Eng. J. 2016, 55, 2631–2638. [Google Scholar] [CrossRef]
- Malinowska, E.; Szymański, A.; Sas, W. Estimation of Flow Characteristics in Peat. Geotech. Test. J. 2010, 33, GTJ102783. [Google Scholar]
- Sobolewski, M. Various methods of the measurement of the permeability coefficient in soils-possibilities and application. EJPAU 2011, 34, 1–5. [Google Scholar] [CrossRef]
- ASTM D5084; Standard Test Method for Measurement of Hydraulic Conductivity of Saturated Porous Materials Using a Flexible Wall Permeameter. ASTM International: West Conshocken, PA, USA, 2024.
- Deshpande, Y.S.; Hiller, J.E. Pore characterization of manufactured aggregates: Recycled concrete aggregates and lightweight aggregates. Mater. Struct. 2011, 45, 67–79. [Google Scholar] [CrossRef]
- Gómez-Soberón, J.M. Porosity of recycled concrete with substitution of recycled concrete aggregate: An experimental study. Cem. Concr. Res. 2002, 32, 1301–1311. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Gao, X.F.; Tam, C.M.; Chan, C.H. New Approach in Measuring Water Absorption of Recycled Aggregates. Constr. Build. Mater. 2008, 22, 364–369. [Google Scholar] [CrossRef]
- Arulrajah, A.; Piratheepan, J.; Disfani, M.M.; Bo, M.W. Geotechnical and geoenvironmental properties of recycled construction and demolition materials in pavement subbase applications. J. Mater. Civ. Eng. 2013, 25, 1077–1088. [Google Scholar] [CrossRef]
- Poon, C.S.; Qiao, X.C.; Chan, D. The cause and influence of self-cementing properties of fine recycled concrete aggregates on the properties of unbound sub-base. Waste Manag. 2006, 26, 1166–1172. [Google Scholar] [CrossRef] [PubMed]
- Poon, C.S.; Chan, D. Feasible use of recycled concrete aggregates and crushed clay brick as unbound road sub-base. Constr. Build. Mater. 2006, 20, 578–585. [Google Scholar] [CrossRef]
- Głuchowski, A.; Sas, W.; Dzięcioł, J.; Soból, E.; Szymański, A. Permeability and Leaching Properties of Recycled Concrete Aggregate as an Emerging Material in Civil Engineering. Appl. Sci. 2019, 9, 81. [Google Scholar] [CrossRef]
- Gonzales, L.; Williams, J. Use of Shredded Tires as Lightweight Fill Backfill Material for Retaining Structures. Waste Manag. Res. 1996, 14, 433–451. [Google Scholar]
- Warith, M.A.; Evgin, E.; Benson, P.A.S.; Rao, S.M. Evaluation of Permeability of Tire Shreds Under Vertical Loading. J. Test. Eval. 2005, 33, 51–54. [Google Scholar] [CrossRef]
- Koohmishi, M.; Azarhoosh, A. Hydraulic conductivity of fresh railway ballast mixed with crumb rubber considering size and percentage of crumb rubber as well as aggregate gradation. Const. Build. Mater. 2020, 241, 118133. [Google Scholar] [CrossRef]
- Gesoğlu, M.; Güneyisi, E.; Khoshnaw, G.; İpek, S. Investigating properties of pervious concretes containing waste tire rubbers. Constr. Build. Mater. 2014, 63, 206–213. [Google Scholar] [CrossRef]
- Maguesvari Muthaiyan, U. Characteristics of pore structure and permeability prediction in binary blended pervious concrete. Matéria (Rio J.) 2024, 29, e20230251. [Google Scholar] [CrossRef]
- Huang, J.; Zhang, Y.; Sun, Y.; Ren, J.; Zhao, Z.; Zhang, J. Evaluation of pore size distribution and permeability reduction behavior in pervious concrete. Const. Build. Mater. 2021, 5, 123228. [Google Scholar] [CrossRef]
- Lyu, Q.; Dai, P.; Chen, A. Correlations among physical properties of pervious concrete with different aggregate sizes and mix proportions. Road Mater. Pavement Des. 2024, 25, 2747–2771. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Qian, D. Prediction of the Strength of Rubberized Concrete by an Evolved Random Forest Model. Adv. Civ. Eng. 2019, 2019, 5198583. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, J.; Li, G.; Wang, Y.; Sun, J.; Jiang, C. Optimized neural network using beetle antennae search for predicting the unconfined compressive strength of jet grouting coalcretes. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 801–813. [Google Scholar] [CrossRef]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior, 2nd ed.; John and Wiley and Sons Inc.: New York, NY, USA, 1993. [Google Scholar]
- Nedeljković, M.; Visser, J.; Šavija, B.; Valcke, S.; Schlangen, E. Use of fine recycled concrete aggregates in concrete: A critical review. J. Build. Eng. 2021, 38, 102196. [Google Scholar] [CrossRef]
- Villagrán-Zaccardi, Y.; Broodcoorens, L.; Van den Heede, P.; De Belie, N. Fine Recycled Concrete Aggregates Treated by Means of Wastewater and Carbonation Pretreatment. Sustainability 2023, 15, 6386. [Google Scholar] [CrossRef]
- Gabryś, K.; Radzevičius, A.; Szymański, A.; Šadzevičius, R. Shear Strength Characteristics of Recycled Concrete Aggregate and Recycled Tire Waste Mixtures from Monotonic Triaxial Tests. Materials 2021, 14, 7400. [Google Scholar] [CrossRef] [PubMed]
- Gabryś, K.; Šadzevičius, R.; Dapkienė, M.; Ramukevičius, D.; Sas, W. Effect of a Fine Fraction on Dynamic Properties of Recycled Concrete Aggregate as a Special Anthropogenic Soil. Materials 2023, 16, 4986. [Google Scholar] [CrossRef]
- Gabryś, K. Geomechanical Characterization of Crushed Concrete–Rubber Waste Mixtures. Sustainability 2023, 15, 14446. [Google Scholar] [CrossRef]
- ISO 14688-2:2017; Rozpoznanie i Badania Geotechniczne–Oznaczanie i Klasyfikowanie Gruntów–Część 2: Zasady Klasyfikowania (Geotechnical Investigation and Testing–Determination and Classification of Soils–Part 2: Classification Principles). International Organization for Standardization: Geneva, Switzerland, 2017.
- Humboldt Mfg. Co. Humboldt HM-4150-40-60 Manual: Vol. Testing Equipment for Construction Materials; Humboldt Mfg. Co.: Schiller Park, IL, USA, 2011. [Google Scholar]
- Raghunandan, M.E.; Juneja, A.; Benson Hsiung, B.C. Preparation of reconstituted sand samples in the laboratory. Int. J. Geotech. Eng. 2016, 6, 125–131. [Google Scholar] [CrossRef]
- Kandalai, S.; Singh, P.N.; Singh, K.K. Permeability of granular soil employing flexible wall permeameter. Arab. J. Geosci. 2018, 11, 28. [Google Scholar] [CrossRef]
- Fell, R.; MacGregor, P.; Stapledon, D.; Bell, G. Geotechnical Engineering of Dams; Taylor&Francis Group: London, UK, 2005; pp. 353–360. [Google Scholar]
- Azram, A.M.; Cameron, D.A. Geotechnical properties of blends of Recycled Clay Marsony and Recycled Concrete Aggregates in Unbound Pavement Construction. J. Mater. Civ. Eng. 2013, 25, 788–798. [Google Scholar] [CrossRef]
- Arulrajah, A.; Piratheepan, J.; Ali, M.M.Y.; Bo, M.W. Geotechnical properties of recycled concrete aggregate in pavement sub-base applications. Geotech. Test. J. 2012, 35, 743–751. [Google Scholar] [CrossRef]
- McCulloch, T.; Kang, D.; Shamet, R.; Lee, S.J.; Nam, B.H. Long-Term performance of recycled concrete aggregate for subsurface drainage. J. Perform. Constr. Facil. 2017, 31, 04017015. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhou, M.; Wang, B.; Xu, X. Enhancing permeability and mechanical properties of rubber cement-based materials through surface modification of waste tire rubber powder. Const. Build. Mater. 2024, 425, 136098. [Google Scholar] [CrossRef]
- Liu, H.; Luo, G.; Gong, Y.; Wei, H. Mechanical Properties, Permeability, and Freeze–Thaw Resistance of Pervious Concrete Modified by Waste Crumb Rubbers. Appl. Sci. 2018, 8, 1843. [Google Scholar] [CrossRef]
- Das, B.M. Principles of Geotechnical Engineering; PWS-Kent: Boston, MA, USA, 1990; Chapter 4. [Google Scholar]
- Chapuis, R.P. Similarity of internal stability criteria for granular soils. Can. Geotech. J. 1992, 29, 711–713. [Google Scholar] [CrossRef]
- Chapuis, R.P. Predicting the saturated hydraulic conductivity of soils: A review. Bull. Eng. Geol. Environ. 2012, 71, 401–434. [Google Scholar] [CrossRef]
- Daniel, D.E. State of the art: Laboratory hydraulic conductivity tests for saturated soils. In Hydraulic Conductivity and Waste Contaminant Transport in Soil; ASTM STP 1142; Daniel, D.E., Trautwein, S.J., Eds.; ASTM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Wang, F.; Sun, C.; Zhao, H.; Liu, Y. Effect of waste tire rubber crumb on impermeability of cement-stabilized soil. Environ. Technol. 2023, 45, 4243–4254. [Google Scholar] [CrossRef]
- Akhtar, A.Y.; Tsang, H.H. Dynamic leaching assessment of recycled polyurethane-coated tire rubber for sustainable engineering applications. Chem. Eng. J. 2024, 495, 153351. [Google Scholar] [CrossRef]
- Fiorillo, F.; Esposito, L.; Ginolfi, M.; Leone, G. New Insights into Turbulent and Laminar Flow Relationships Using Darcy–Weisbach and Poiseuille Laws. Water 2024, 16, 1452. [Google Scholar] [CrossRef]
- Hansbo, S. Consolidation equation valid for both Darcian and non-Darcian flow. Géotechnique 2001, 51, 51–58. [Google Scholar] [CrossRef]
- Sas, W.; Dzięcioł, J.; Głuchowski, A. Estimation of Recycled Concrete Aggregate’s Water Permeability Coefficient as Earth Construction Material with the Application of an Analytical Method. Materials 2019, 12, 2920. [Google Scholar] [CrossRef] [PubMed]
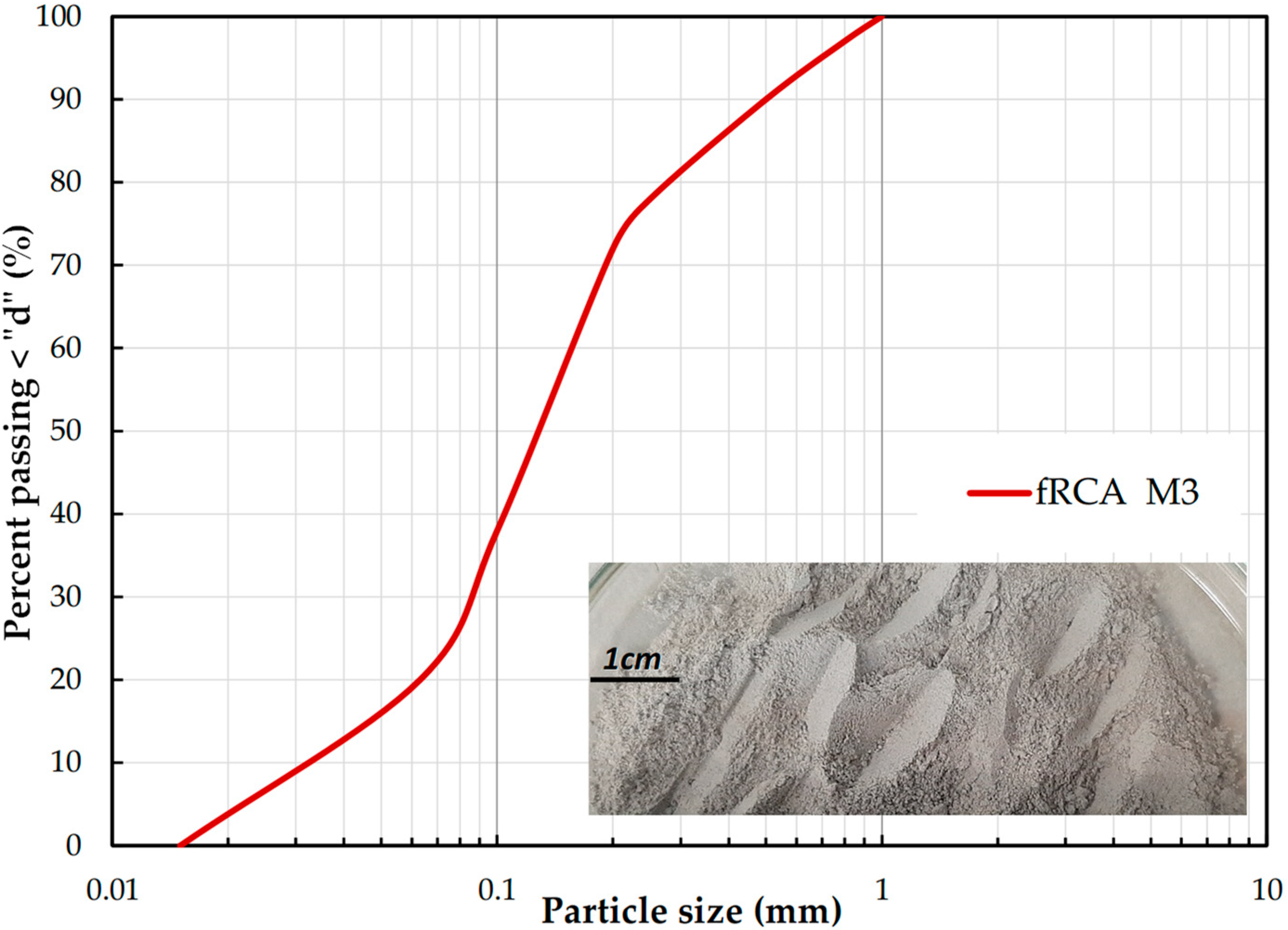
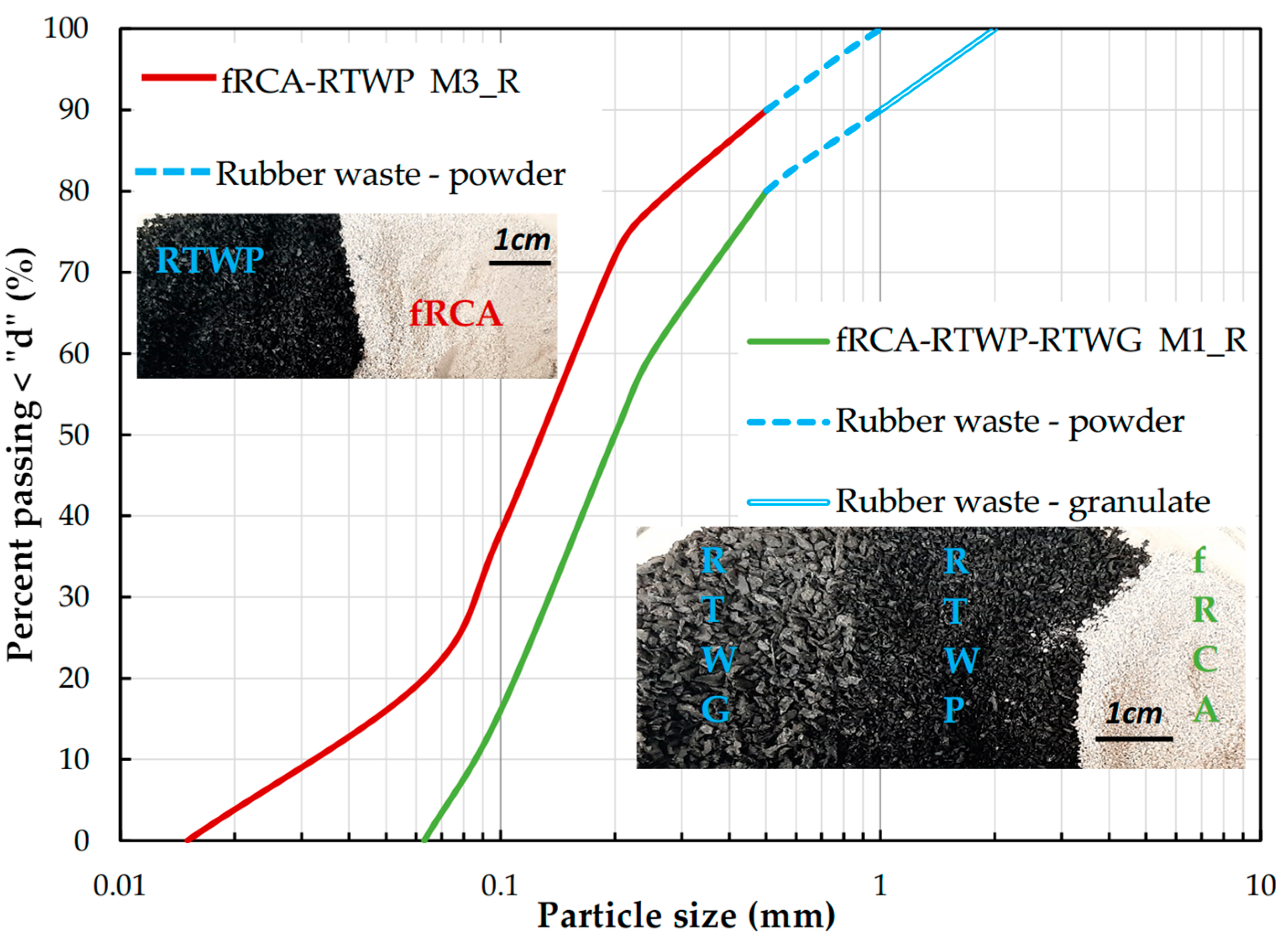

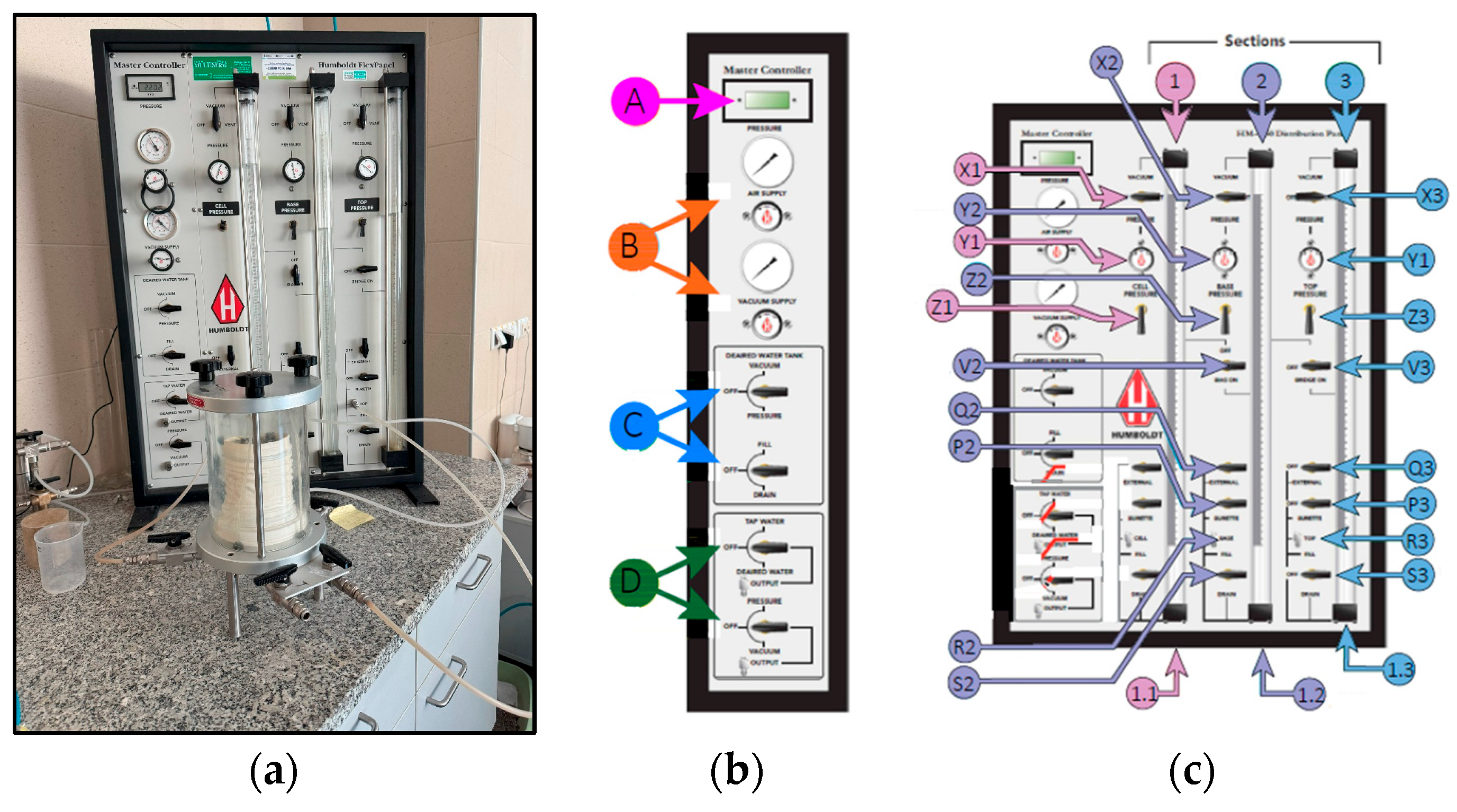



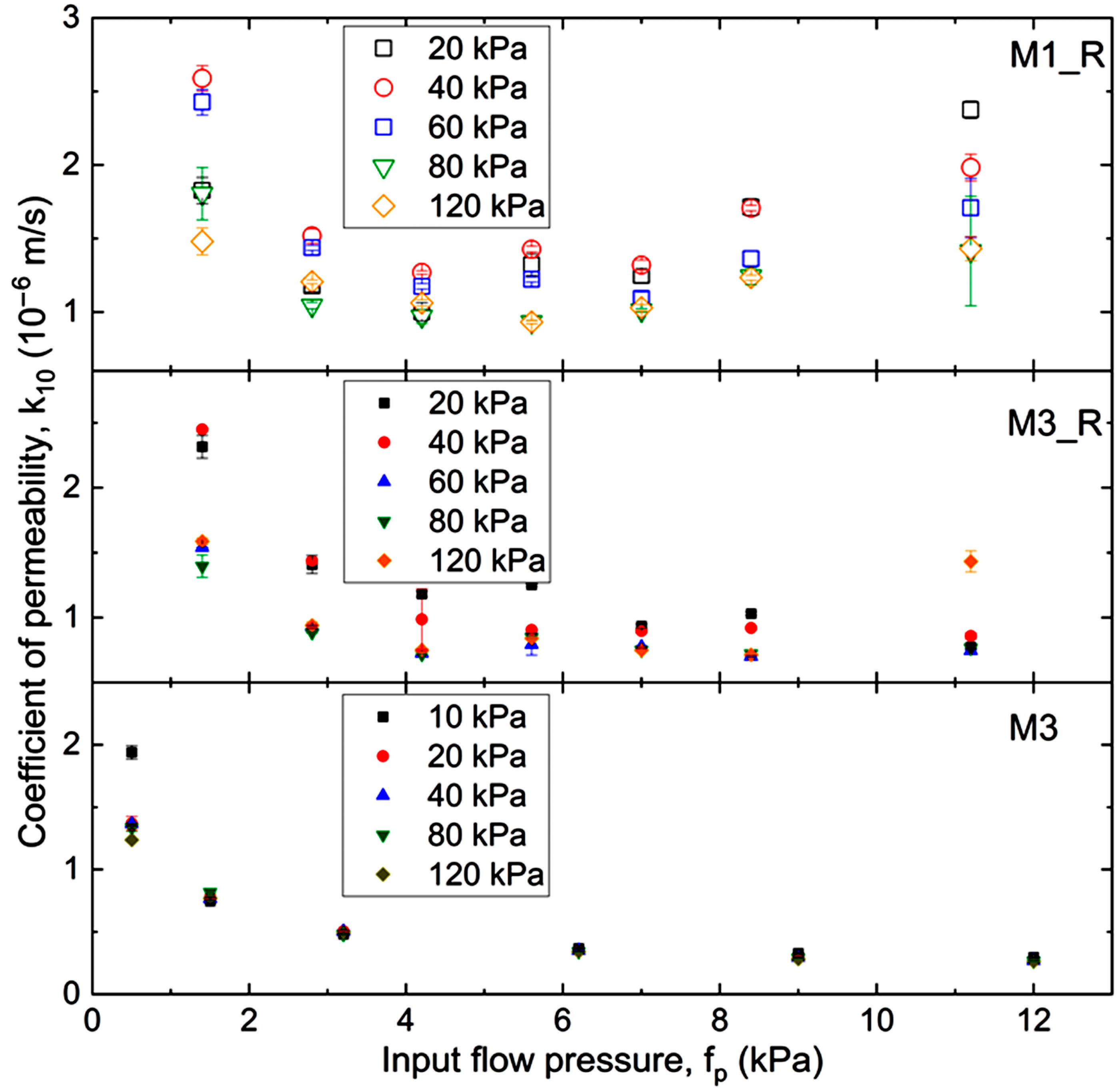
| Sample/Material | Research Content | Major Conclusion | Reference |
|---|---|---|---|
| RCA | Pore characterization of manufactured aggregates | High roughness grains with irregular shapes complicate the flow path of water. | [18] |
| RCA | Porosity of recycled concrete with the substitution of RCA | Void ratio, porosity, and, therefore, hydraulic conductivity of RCA are higher than natural aggregates. | [19] |
| RCA | Water absorption of recycled aggregates—new approach | Patches of cement paste attached to the surface of recycled aggregate may affect water absorption in a manner different from conventional aggregate. Because of this, the standard duration of 24 h of saturation is not suitable for RCA. | [20] |
| RCA | Geotechnical and geoenvironmental properties of recycled construction and demolition materials | The coefficient of permeability is equal to 3.3 × 10−8 m/s, which is similar to cohesive soils and materials used for dam and levee cores. | [21] |
| RCA | Replacement of RCA by crushed clay brick as an unbound road sub-base | The hydraulic conductivity of RCA ranges from 2.04 × 10−3 m/s to 2.67 × 10−3 m/s. | [22,23] |
| RCA | Permeability and leaching properties of RCA | The average coefficient of permeability for linear flow in RCA is equal from ~1.02 × 10−4 m/s to ~2.08 × 10−5 m/s for aggregates from 0.05–16 mm to 0–8 mm, respectively. RCA proves its good quality as a permeable material. | [24] |
| Tire shreds | Shredded tires as lightweight fill backfill material for retaining structures | Tire shreds have a hydraulic conductivity of ~3 × 10−2 cm/s, indicating that they are well suited for use as drainage material in landfill leachate collection systems. | [25] |
| Tire shreds | Evaluation of the permeability of tire shreds under vertical loading | Despite experiencing large axial strains, the average permeability of the tire shred sample consistently remained two to three orders of magnitude higher than the design performance criterion of 0.01 cm/s for landfill drainage layers, suggesting that the compressible nature of tire shreds will not interfere with their use as a leachate collection drainage layer in municipal solid waste landfills. | [26] |
| Crumb rubber particles and ballast aggregates | The effect of size and percentage of crumb rubber particles on hydraulic conductivity of rubber-modified railway ballast | The nonlinear relationship between applied hydraulic gradient and water flow velocity is observed for different characterized conditions. Rubber-modified ballast under extreme conditions (using a higher percentage of smaller-sized CR particles) shows a flow regime between laminar and turbulent (with n value around 0.8). | [27] |
| Rubberized pervious concretes | Permeability of rubberized plain pervious concrete | Permeability is significantly reduced with tire rubber. A 10% rubber replacement diminished the permeability coefficient by 28%. | [28] |
| Pervious concrete (binary blended) | Characteristics of pore structure and permeability prediction, with partial fly ash replacement (10–20%) | Image-based porosity (area fraction) slightly exceeds volumetric porosity. Pore characteristics (via morphological techniques) agree across methods, with a strong match between experimental and predicted permeability. | [29] |
| Pervious concrete (aggregate mix) | Evaluation of pore size distribution and permeability reduction behaviour | Lower aggregate-to-cement ratio and higher water-to-cement ratio decrease porosity and permeability but increase compressive strength, thermal conductivity, and abrasion resistance; porosity, permeability, and compressive strength correlate via a power–law. | [30,31] |
| Rubberized concrete (RC) | Prediction of compressive strength using an evolved random forest model (RF optimized by BAS algorithm) | High predictive accuracy (correlation coefficient ≈ 0.96). Key influencing variables: RC age (most significant), followed by water–cement ratio, fine rubber aggregate content, coarse rubber aggregate content, and coarse aggregate. | [32] |
| Jet-grouting coalcretes (coalcrete) | Optimized neural network (BPNN tuned via BAS) to predict unconfined compressive strength (UCS) | The BAS-optimized BPNN model outperforms MLR, LR, and SVM in accuracy and reliability. Sensitivity analysis shows curing time is the most critical variable, followed by water–cement ratio and coal–grout ratio. | [33] |
| Mixture fRCA–RTW | Cell Pressure | Effective Stress | Hydraulic Gradient |
|---|---|---|---|
| kPa | kPa | - | |
| M3 | 210 | 10 | 1, 2, 4, 8, 12, 16 |
| 220 | 20 | 1, 2, 4, 8, 12, 16 | |
| 240 | 40 | 1, 2, 4, 8, 12, 16 | |
| 280 | 80 | 1, 2, 4, 8, 12, 16 | |
| 320 | 120 | 1, 2, 4, 8, 12, 16 | |
| M1_R; M3_R | 220 | 20 | 2, 4, 6, 8, 10, 12, 16 |
| 240 | 40 | 2, 4, 6, 8, 10, 12, 16 | |
| 260 | 60 | 2, 4, 6, 8, 10, 12, 16 | |
| 280 | 80 | 2, 4, 6, 8, 10, 12, 16 | |
| 320 | 120 | 2, 4, 6, 8, 10, 12, 16 |
| Mixture fRCA–RTW | Top Pressure | Base Pressure | Input Pressure | Hydraulic Gradient |
|---|---|---|---|---|
| kPa | kPa | kPa | - | |
| M3-1 | 199.2 | 199.7 | 0.5 | 1 |
| M3-2 | 199.1 | 200.6 | 1.5 | 2 |
| M3-3 | 200.0 | 203.2 | 3.2 | 4 |
| M3-4 | 200.3 | 206.5 | 6.2 | 8 |
| M3-5 | 200.0 | 209.0 | 9.0 | 12 |
| M3-6 | 200.0 | 212.0 | 12.0 | 16 |
| M1_R-1 | 200.0 | 201.4 | 1.4 | 2 |
| M1_R-2 | 200.0 | 202.8 | 2.8 | 4 |
| M1_R-3 | 200.0 | 204.2 | 4.2 | 6 |
| M1_R-4 | 200.0 | 205.6 | 5.6 | 8 |
| M1_R-5 | 200.0 | 207.0 | 7.0 | 10 |
| M1_R-6 | 200.0 | 208.4 | 8.4 | 12 |
| M1_R-7 | 200.0 | 211.2 | 11.2 | 16 |
| M3_R-1 | 200.0 | 201.4 | 1.4 | 2 |
| M3_R-2 | 200.0 | 202.8 | 2.8 | 4 |
| M3_R-3 | 200.0 | 204.2 | 4.2 | 6 |
| M3_R-4 | 200.0 | 205.6 | 5.6 | 8 |
| M3_R-5 | 200.0 | 207.0 | 7.0 | 10 |
| M3_R-6 | 200.0 | 208.4 | 8.4 | 12 |
| M3_R-7 | 200.0 | 211.2 | 11.2 | 16 |
| Tire Shreds Sample | Length | Width | Thickness | Total Sample Mass | Compression Stress | Hydraulic Gradient |
|---|---|---|---|---|---|---|
| mm | mm | mm | kg | kPa | - | |
| RTWS1 | 260 | 140 | 16 | 12.3 | 211/422/633/844/1055 | ~0.02–0.52 |
| RTWS2 | 250 | 90 | 17 | 13.1 | 194/422/633/844/1055 | ~0.04–0.72 |
| RTWS3 | 470 | 145 | 16 | 11.0 | 211/422/633/844 | ~0.05–0.60 |
| Mixture fRCA–RTW | M1_R | M3_R | M3 |
|---|---|---|---|
| y = ax + b | |||
| a (10−6 m/s) | 1.6 ± 0.3 | 6.2 ± 0.5 | 1.15 ± 0.03 |
| b (10−6 m/s) | 3.0 ± 2.0 | 2.1 ± 0.4 | 0.20 ± 0.003 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabryś, K.; Damska, K.; Šadzevičius, R.; Ramukevičius, D.; Sas, W.; Camargo, B.; Radzevičius, A.; Dapkienė, M. Analysis of Filtration Coefficient of Selected Recycled Materials on the Example of Concrete Aggregate and Rubber Waste. Materials 2025, 18, 4240. https://doi.org/10.3390/ma18184240
Gabryś K, Damska K, Šadzevičius R, Ramukevičius D, Sas W, Camargo B, Radzevičius A, Dapkienė M. Analysis of Filtration Coefficient of Selected Recycled Materials on the Example of Concrete Aggregate and Rubber Waste. Materials. 2025; 18(18):4240. https://doi.org/10.3390/ma18184240
Chicago/Turabian StyleGabryś, Katarzyna, Karolina Damska, Raimondas Šadzevičius, Dainius Ramukevičius, Wojciech Sas, Bruno Camargo, Algirdas Radzevičius, and Midona Dapkienė. 2025. "Analysis of Filtration Coefficient of Selected Recycled Materials on the Example of Concrete Aggregate and Rubber Waste" Materials 18, no. 18: 4240. https://doi.org/10.3390/ma18184240
APA StyleGabryś, K., Damska, K., Šadzevičius, R., Ramukevičius, D., Sas, W., Camargo, B., Radzevičius, A., & Dapkienė, M. (2025). Analysis of Filtration Coefficient of Selected Recycled Materials on the Example of Concrete Aggregate and Rubber Waste. Materials, 18(18), 4240. https://doi.org/10.3390/ma18184240










