Heat Source Parameter Identification Based on Attention-Enhanced Residual Convolutional Neural Network
Abstract
1. Introduction
2. Theoretical Analysis
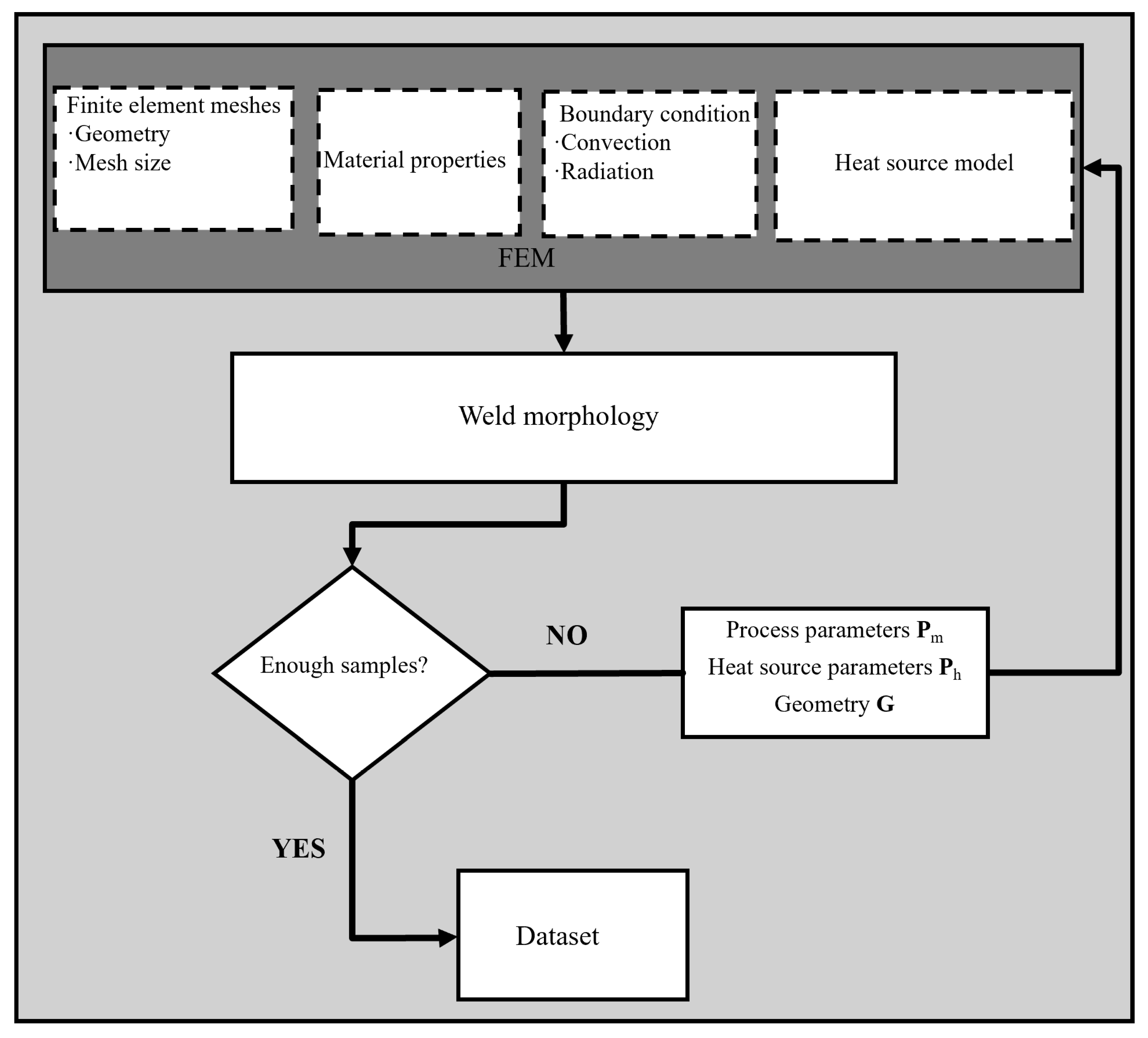
3. Dataset Construction
3.1. Weld Morphology Simulation
3.1.1. Finite Element Model
3.1.2. Heat Source Model
3.2. Analysis and Validation of FEM Simulation Results
3.3. Sample Generation
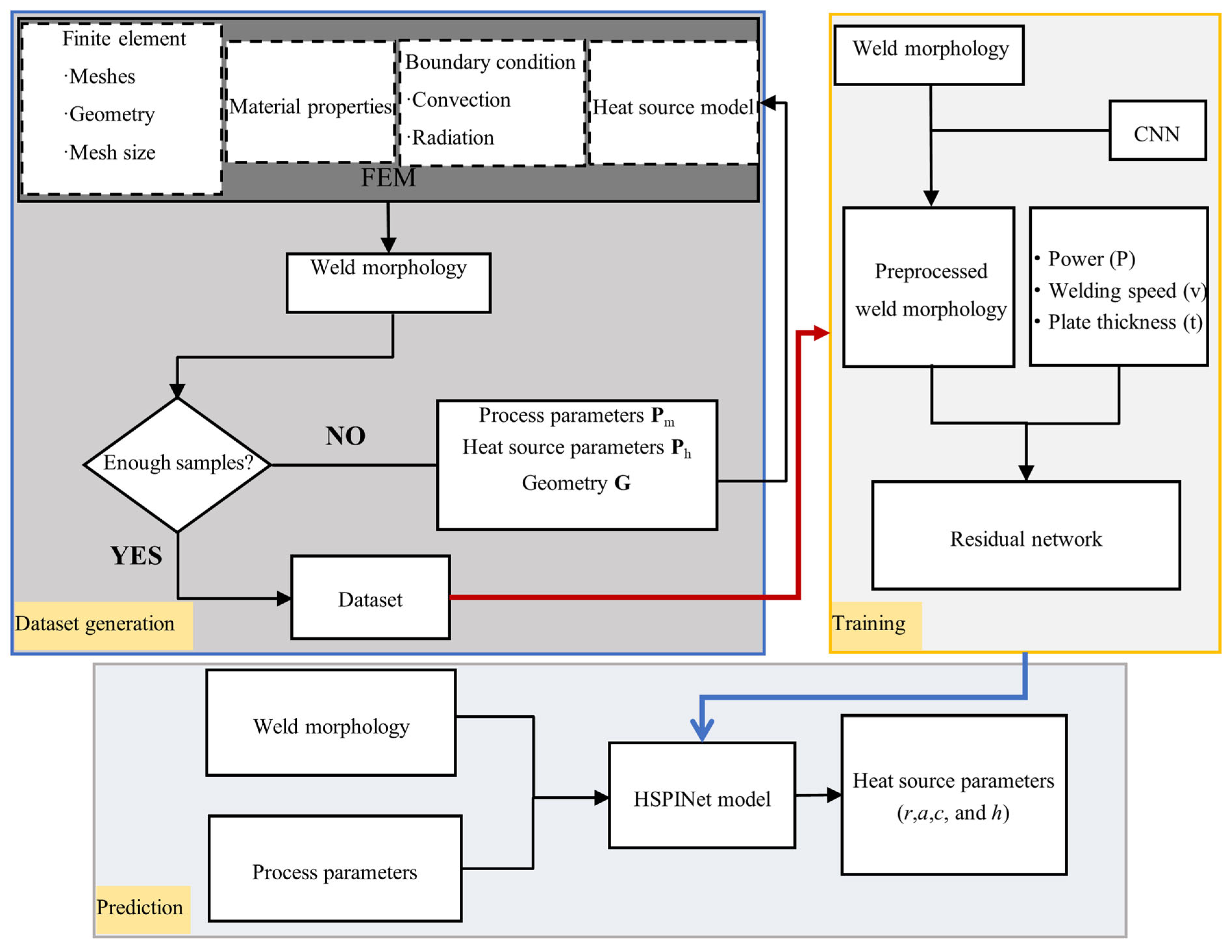
4. Development of the HSPINet Model
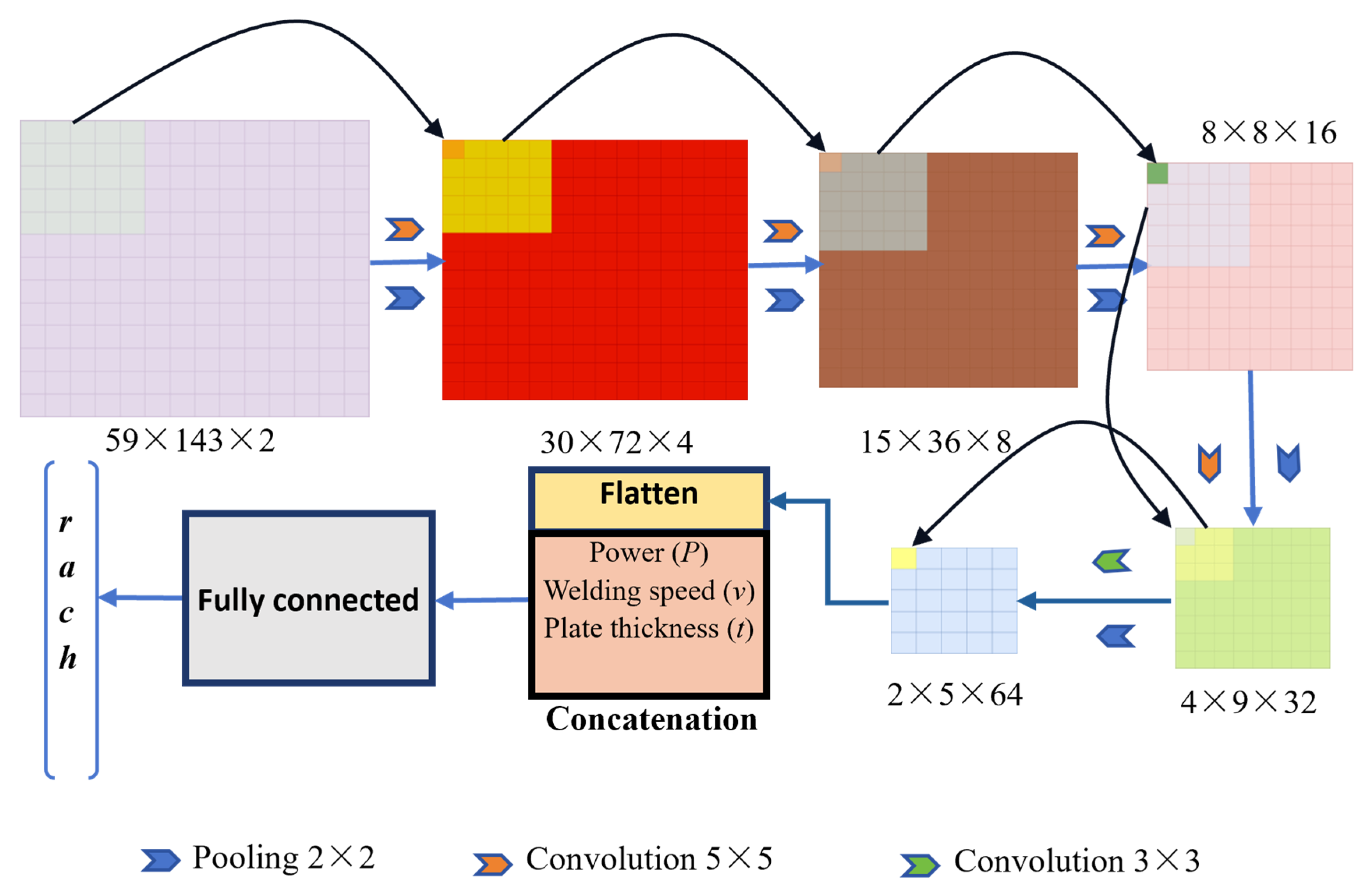
4.1. Residual Convolutional Neural Network
- (1)
- Average pooling and max pooling of the feature map. The input feature map is processed by average pooling and max pooling along the channel dimension, producing two one-dimensional vectors. These vectors encode the mean and maximum responses across channels, thereby capturing complementary global information from the feature map.
- (2)
- Activation and application of the attention map. The two vectors produced by average and max pooling are concatenated and subsequently passed through a convolutional layer to achieve feature fusion, generating an attention map. Each element of this map indicates the relative importance of the corresponding spatial location in the feature map. In the model proposed in this study, the spatial attention mechanism is embedded between the convolutional and pooling layers. By introducing the spatial attention mechanism, the model can better capture key features in weld morphology images, thereby improving the prediction accuracy of heat source parameters.
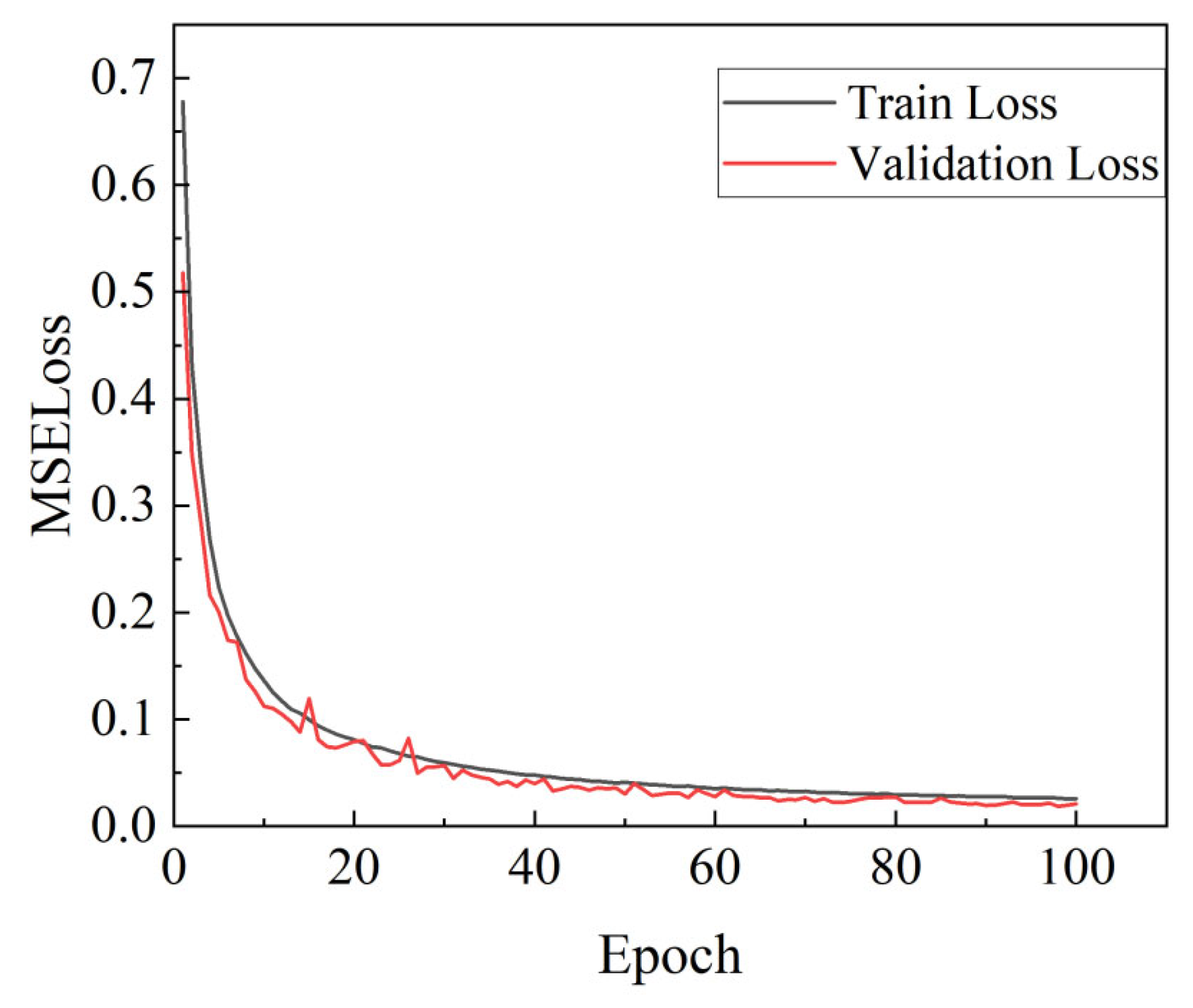
4.2. Model Training and Validation
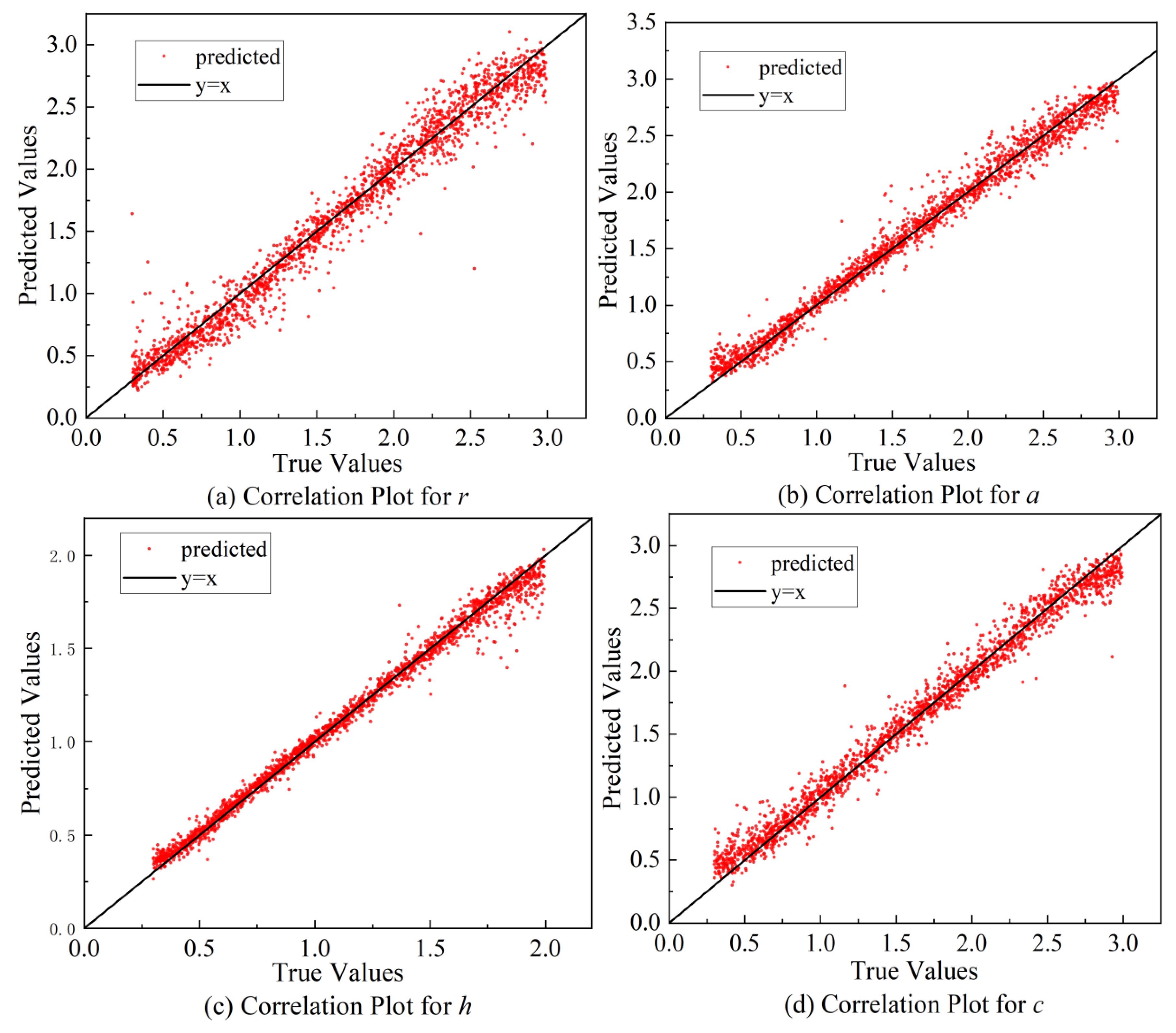
4.3. Results and Discussion
5. Conclusions
- (1)
- A high-fidelity dataset was constructed by performing the finite element thermal analyses under diverse process parameters and heat source conditions. The dataset effectively captured the relationship between weld pool geometries and heat source characteristics, providing a robust foundation for training the deep learning model.
- (2)
- The proposed HSPINet successfully established mapping between multi-angle weld cross-sectional morphologies, process parameters, and the underlying composite heat source parameters. The model demonstrated an excellent predictive performance, achieving an RPE below 7% and an average coefficient of determination (R2) of 0.98 on the testing dataset, indicating strong prediction accuracy and generalization capability.
- (3)
- The results confirm that the method can reliably identify heat source parameters across varying process settings and joint dimensions, significantly enhancing the efficiency and precision of heat source parameter identification. This work provides a valuable technical basis for improving the fidelity of welding thermal simulations and mechanical performance evaluations in complex engineering applications.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CWM | Computational Welding Mechanics |
| FEM | Finite Element Method |
| CNN | Convolutional Neural Network |
| ResNet | Residual Network |
| HSPINet | Heat Source Parameter Identification Network |
| RPE | Relative Percentage Error |
| MSE | Mean Squared Error |
| R2 | Coefficient of Determination |
| RSM | Response Surface Model |
| LBW | Laser Beam Welding |
| GTAW | Gas Tungsten Arc Welding |
| HAZ | Heat-Affected Zone |
References
- Chen, Q.; Zhang, L.; Chen, M.-T.; Zhao, O. Experimental Investigation and Predictive Models of Membrane Residual Stresses in S690 High Strength Steel Welded π-Shaped and Cruciform Sections. Eng. Struct. 2024, 303, 117501. [Google Scholar] [CrossRef]
- Guo, Z.; Bai, R.; Lei, Z.; Jiang, H.; Zou, J.; Yan, C. Experimental and Numerical Investigation on Ultimate Strength of Laser-Welded Stiffened Plates Considering Welding Deformation and Residual Stresses. Ocean Eng. 2021, 234, 109239. [Google Scholar] [CrossRef]
- Bai, R.; Guo, Z.; Lei, Z.; Wu, W.; Yan, C. Hybrid Inversion Method and Sensitivity Analysis of Inherent Deformations of Welded Joints. Adv. Eng. Softw. 2019, 131, 186–195. [Google Scholar] [CrossRef]
- Liu, Z.; Jin, X.; Li, J.; Hao, Z.; Zhang, J. Numerical Simulation and Experimental Analysis on the Deformation and Residual Stress in Trailing Ultrasonic Vibration Assisted Laser Welding. Adv. Eng. Softw. 2022, 172, 103200. [Google Scholar] [CrossRef]
- Xu, J.; Ma, Y.; Wang, L.; Lu, X. Numerical Simulation of Arc and Metal Transfer Behaviors in Double-Wire Gas Metal Arc Welding. Weld. World 2022, 66, 2521–2531. [Google Scholar] [CrossRef]
- Farias, R.M.; Teixeira, P.R.F.; Vilarinho, L.O. Variable Profile Heat Source Models for Numerical Simulations of Arc Welding Processes. Int. J. Therm. Sci. 2022, 179, 107593. [Google Scholar] [CrossRef]
- Yan, H.; Zeng, X.; Cui, Y.; Zou, D. Numerical and Experimental Study of Residual Stress in Multi-Pass Laser Welded 5A06 Alloy Ultra-Thick Plate. J. Mater. Res. Technol. 2024, 28, 4116–4130. [Google Scholar] [CrossRef]
- Sun, J.; Klassen, J.; Nitschke-Pagel, T.; Dilger, K. Effects of Heat Source Geometric Parameters and Arc Efficiency on Welding Temperature Field, Residual Stress, and Distortion in Thin-Plate Full-Penetration Welds. Int. J. Adv. Manuf. Technol. 2018, 99, 497–515. [Google Scholar] [CrossRef]
- Raftar, H.R.; Ahola, A.; Lipiäinen, K.; Björk, T. Simulation and Experiment on Residual Stress and Deflection of Cruciform Welded Joints. J. Constr. Steel Res. 2023, 208, 108023. [Google Scholar] [CrossRef]
- Yan, L.; Guan, Y.; Luo, K.; Wang, Q. Corrugated Steel Web I-Girder Welding Deformation and Residual Stress Research. Structures 2023, 58, 105602. [Google Scholar] [CrossRef]
- Ghafouri, M.; Ahola, A.; Ahn, J.; Björk, T. Numerical and Experimental Investigations on the Welding Residual Stresses and Distortions of the Short Fillet Welds in High Strength Steel Plates. Eng. Struct. 2022, 260, 114269. [Google Scholar] [CrossRef]
- Walker, T.R.; Bennett, C.J. An Automated Inverse Method to Calibrate Thermal Finite Element Models for Numerical Welding Applications. J. Manuf. Process. 2019, 47, 263–283. [Google Scholar] [CrossRef]
- Farias, R.M.; Teixeira, P.R.F.; Vilarinho, L.O. An Efficient Computational Approach for Heat Source Optimization in Numerical Simulations of Arc Welding Processes. J. Constr. Steel Res. 2021, 176, 106382. [Google Scholar] [CrossRef]
- Jiao, H.; Jin, H. An Automated Optimization Procedure for Geometry Parameters Calibration of Two-Curvature Conical Heat Source Model. Int. J. Therm. Sci. 2024, 197, 108788. [Google Scholar] [CrossRef]
- Bai, R.; Guo, Z.; Tian, C.; Lei, Z.; Yan, C.; Tao, W. Study on Welding Sequence of Butt-Welded Structures Based on Equivalent Heat Source Parameter. Int. J. Press. Vessel. Pip. 2018, 163, 15–22. [Google Scholar] [CrossRef]
- Bai, R.; Guo, Z.; Tian, C.; Lei, Z.; Yan, C.; Tao, W. Investigation on Welding Sequence of I-Beam by Hybrid Inversion. Mar. Struct. 2018, 62, 23–39. [Google Scholar] [CrossRef]
- Jiao, H.; Jin, H. An Inverse Method for Determining Geometric Parameters of Heat Source Models Using Analytical Solutions and Regression Analysis. J. Mech. Sci. Technol. 2023, 37, 6739–6747. [Google Scholar] [CrossRef]
- Guo, Z.; Jiang, H.; Bai, R.; Lei, Z. Prediction of Laser-Welded Deformation Using Artificial Neural Networks. J. Laser Appl. 2024, 36, 022014. [Google Scholar] [CrossRef]
- Zhang, Z.; Wen, G.; Chen, S. Weld Image Deep Learning-Based on-Line Defects Detection Using Convolutional Neural Networks for Al Alloy in Robotic Arc Welding. J. Manuf. Process. 2019, 45, 208–216. [Google Scholar] [CrossRef]
- Fu, G.; Lourenço, M.I.; Duan, M.; Estefen, S.F. Influence of the Welding Sequence on Residual Stress and Distortion of Fillet Welded Structures. Mar. Struct. 2016, 46, 30–55. [Google Scholar] [CrossRef]
- Fu, G.; Gu, J.; Lourenco, M.I.; Duan, M.; Estefen, S.F. Parameter Determination of Double-Ellipsoidal Heat Source Model and Its Application in the Multi-Pass Welding Process. Ships Offshore Struct. 2015, 10, 204–217. [Google Scholar] [CrossRef]
- Kitano, H.; Mikami, Y. Constructing a Heat Source Parameter Estimation Model for Heat Conduction Finite Element Analysis Using Deep Convolutional Neural Network. Mater. Today Commun. 2022, 31, 103387. [Google Scholar] [CrossRef]
- Guo, Z.; Jiang, H.; He, L.; Lei, Z.; Bai, R. CNN-Empowered Identification of Heat Source Parameters from the Cross-Section Profile of Laser-Welded Zone. Int. J. Adv. Manuf. Technol. 2024, 130, 5441–5455. [Google Scholar] [CrossRef]
- Tsirkas, S.A. Numerical Simulation of the Laser Welding Process for the Prediction of Temperature Distribution on Welded Aluminium Aircraft Components. Opt. Laser Technol. 2018, 100, 45–56. [Google Scholar] [CrossRef]
- Brown, S.; Song, H. Finite Element Simulation of Welding of Large Structures. J. Eng. Ind. 1992, 114, 441–451. [Google Scholar] [CrossRef]
- Russo Spena, P.; De Maddis, M.; Razza, V.; Santoro, L.; Mamarayimov, H.; Basile, D. Infrared-Guided Thermal Cycles in FEM Simulation of Laser Welding of Thin Aluminium Alloy Sheets. Metals 2025, 15, 830. [Google Scholar] [CrossRef]
- Li, S.; Ren, S.; Zhang, Y.; Deng, D.; Murakawa, H. Numerical Investigation of Formation Mechanism of Welding Residual Stress in P92 Steel Multi-Pass Joints. J. Mater. Process. Technol. 2017, 244, 240–252. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, B.; Xue, H.; Wang, Z. Influence of Material Randomness on Welding Residual Stress in Dissimilar Metal Welded Joints of Nuclear Power Plants. Int. J. Front. Eng. Technol. 2022, 4, 0802. [Google Scholar] [CrossRef]
- Guo, W.; Kar, A. Determination of Weld Pool Shape and Temperature Distribution by Solving Three-Dimensional Phase Change Heat Conduction Problem. Sci. Technol. Weld. Join. 2000, 5, 317–323. [Google Scholar] [CrossRef]
- Jin, Y.; Wang, S.; Huang, W.; Li, L. Numerical Simulation Analysis and Experimental Verification of Laser Beam Welding of New Type Al-Li Alloy. Hot Work. Technol. 2019, 48, 163–169. [Google Scholar] [CrossRef]
- Mwema, F.M. Transient Thermal Modeling in Laser Welding of Metallic/Nonmetallic Joints Using SolidWorks® Software. IJNM 2017, 6, 1–16. (In Chinese) [Google Scholar] [CrossRef][Green Version]
- Escribano-García, R.; Álvarez, P.; Marquez-Monje, D. Calibration of Finite Element Model of Titanium Laser Welding by Fractional Factorial Design. JMMP 2022, 6, 130. [Google Scholar] [CrossRef]
- Yang, Z.; Tao, W.; Li, L.; Chen, Y.; Shi, C. Numerical Simulation of Heat Transfer and Fluid Flow during Double-Sided Laser Beam Welding of T-Joints for Aluminum Aircraft Fuselage Panels. Opt. Laser Technol. 2017, 91, 120–129. [Google Scholar] [CrossRef]
- Tao, W.; Yang, Z.; Shi, C.; Dong, D. Simulating Effects of Welding Speed on Melt Flow and Porosity Formation during Double-Sided Laser Beam Welding of AA6056-T4/AA6156-T6 Aluminum Alloy T-Joint. J. Alloys Compd. 2017, 699, 638–647. [Google Scholar] [CrossRef]
- Lundbäck, A.; Runnemalm, H. Validation of Three-Dimensional Finite Element Model for Electron Beam Welding of Inconel 718. Sci. Technol. Weld. Join. 2005, 10, 717–724. [Google Scholar] [CrossRef]
- Ilesanmi, A.E.; Ilesanmi, T.O. Methods for Image Denoising Using Convolutional Neural Network: A Review. Complex Intell. Syst. 2021, 7, 2179–2198. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. arXiv 2015, arXiv:1502.03167. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26–30 June 2016; IEEE: New York, NY, USA, 2016; pp. 770–778. [Google Scholar]
- Whitman, S.E.; Latypov, M.I. Machine Learning of Microstructure–Property Relationships in Materials Leveraging Microstructure Representation from Foundational Vision Transformers. Acta Mater. 2025, 296, 121217. [Google Scholar] [CrossRef]
- Fan, Z.; Ma, E. Predicting Orientation-Dependent Plastic Susceptibility from Static Structure in Amorphous Solids via Deep Learning. Nat. Commun. 2021, 12, 1506. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Wang, Y.; Islam, M.; Hwang, J.; Wang, Y.; Fan, Y. Concurrent Prediction of Metallic Glasses’ Global Energy and Internal Structural Heterogeneity by Interpretable Machine Learning. Acta Mater. 2023, 259, 119281. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Computer Vision–ECCV 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Lecture Notes in Computer Science; Springer International Publishing: Cham, Switzerland, 2018; Volume 11211, pp. 3–19. [Google Scholar]
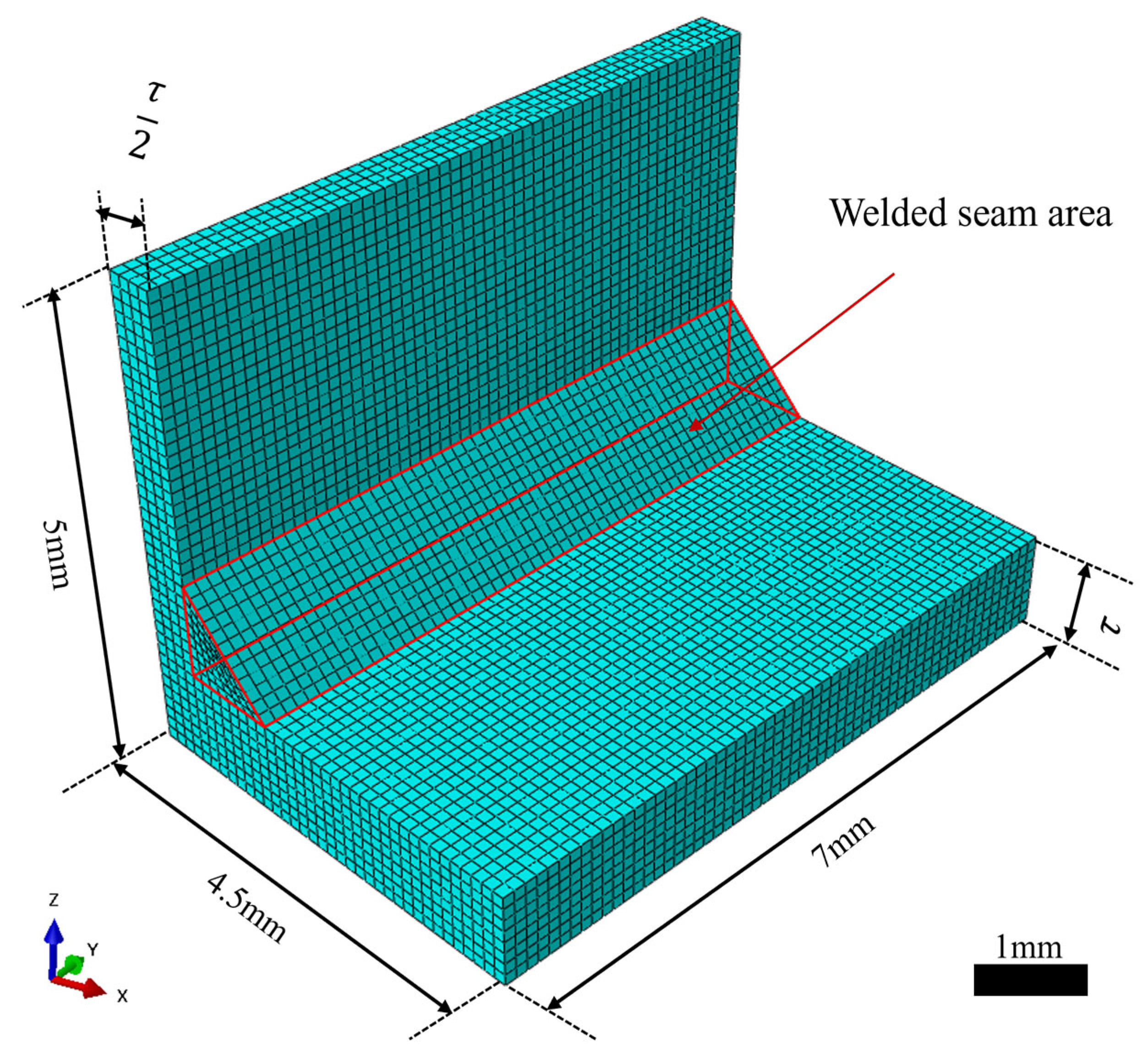
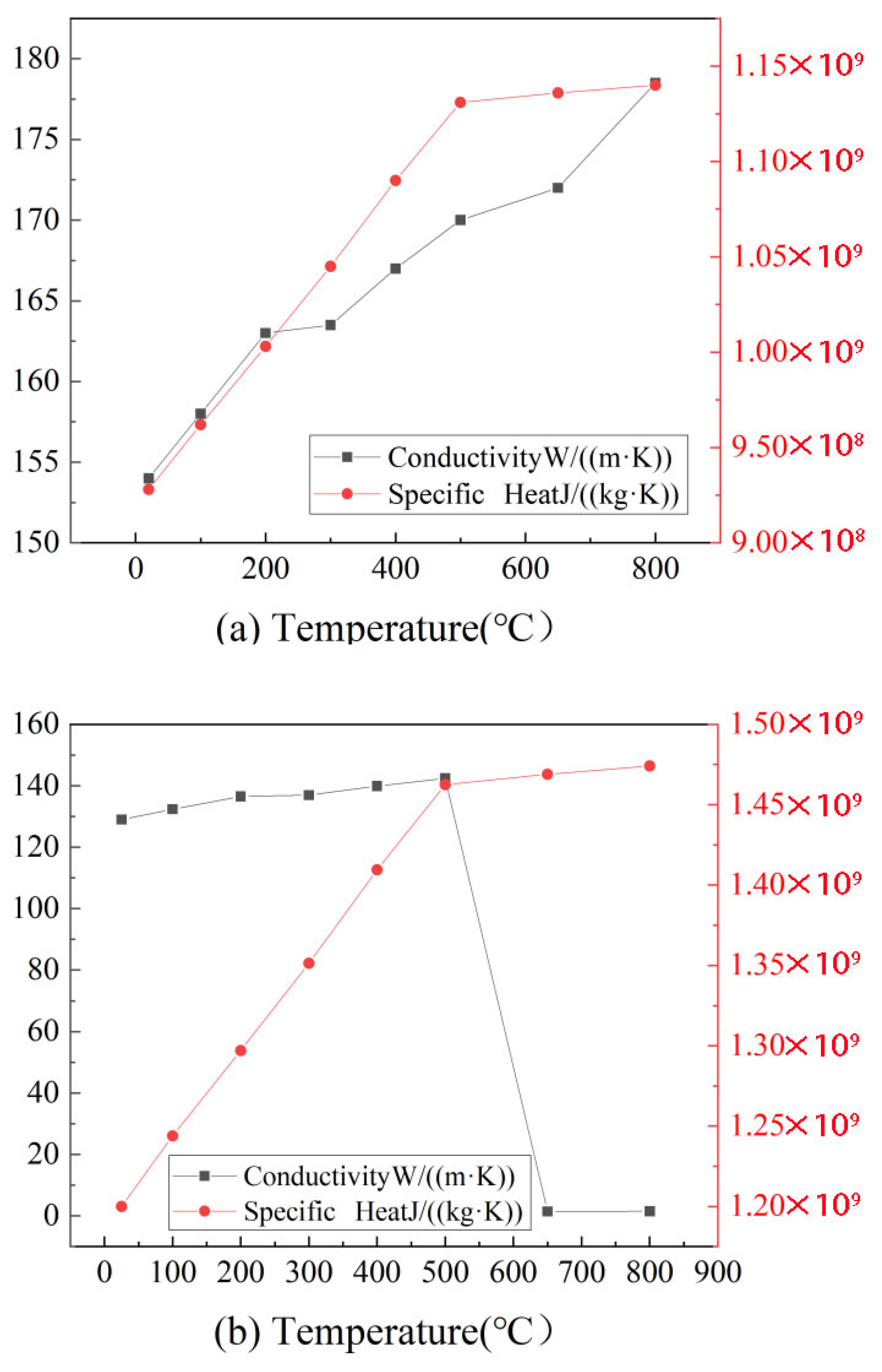
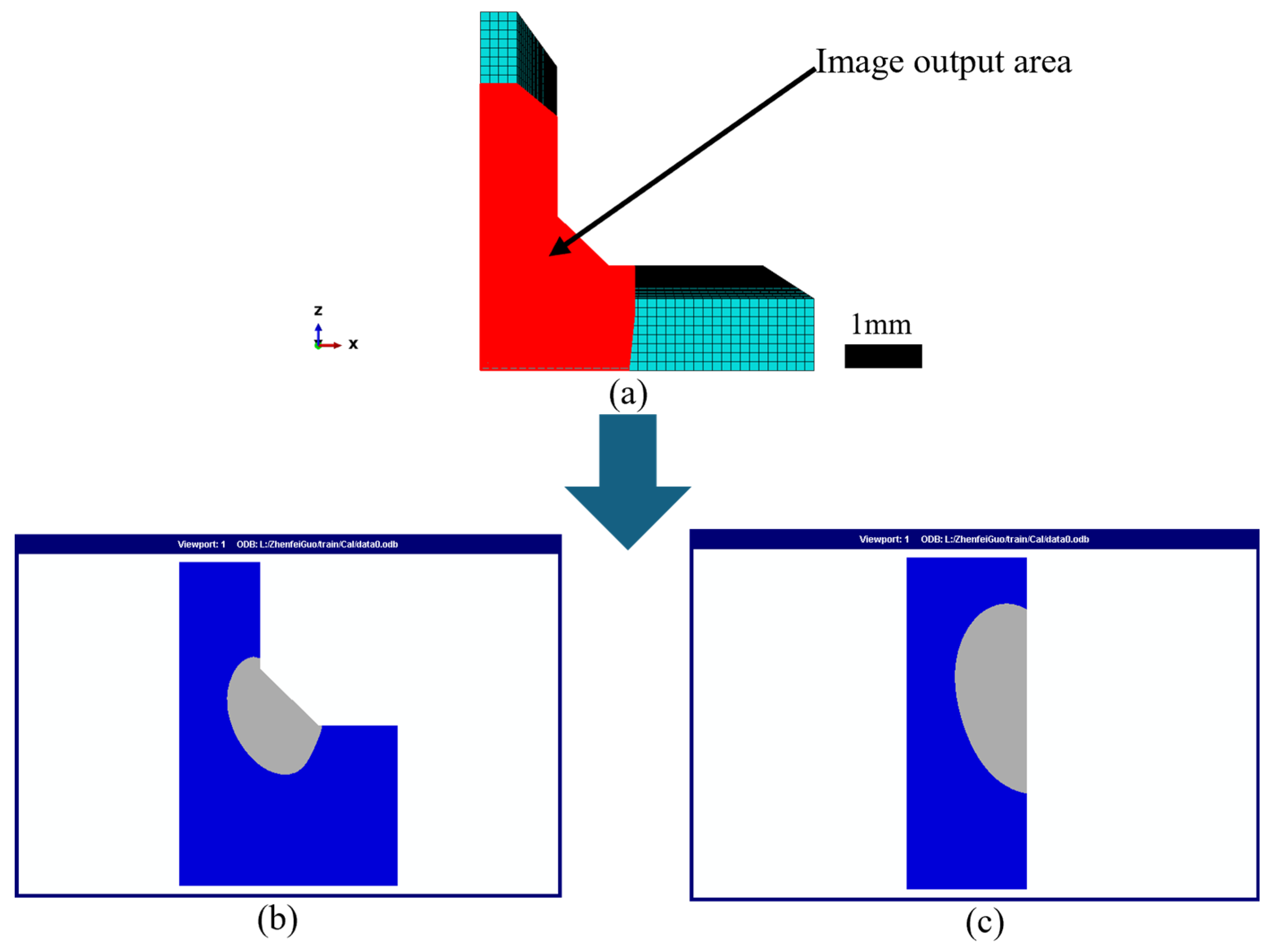
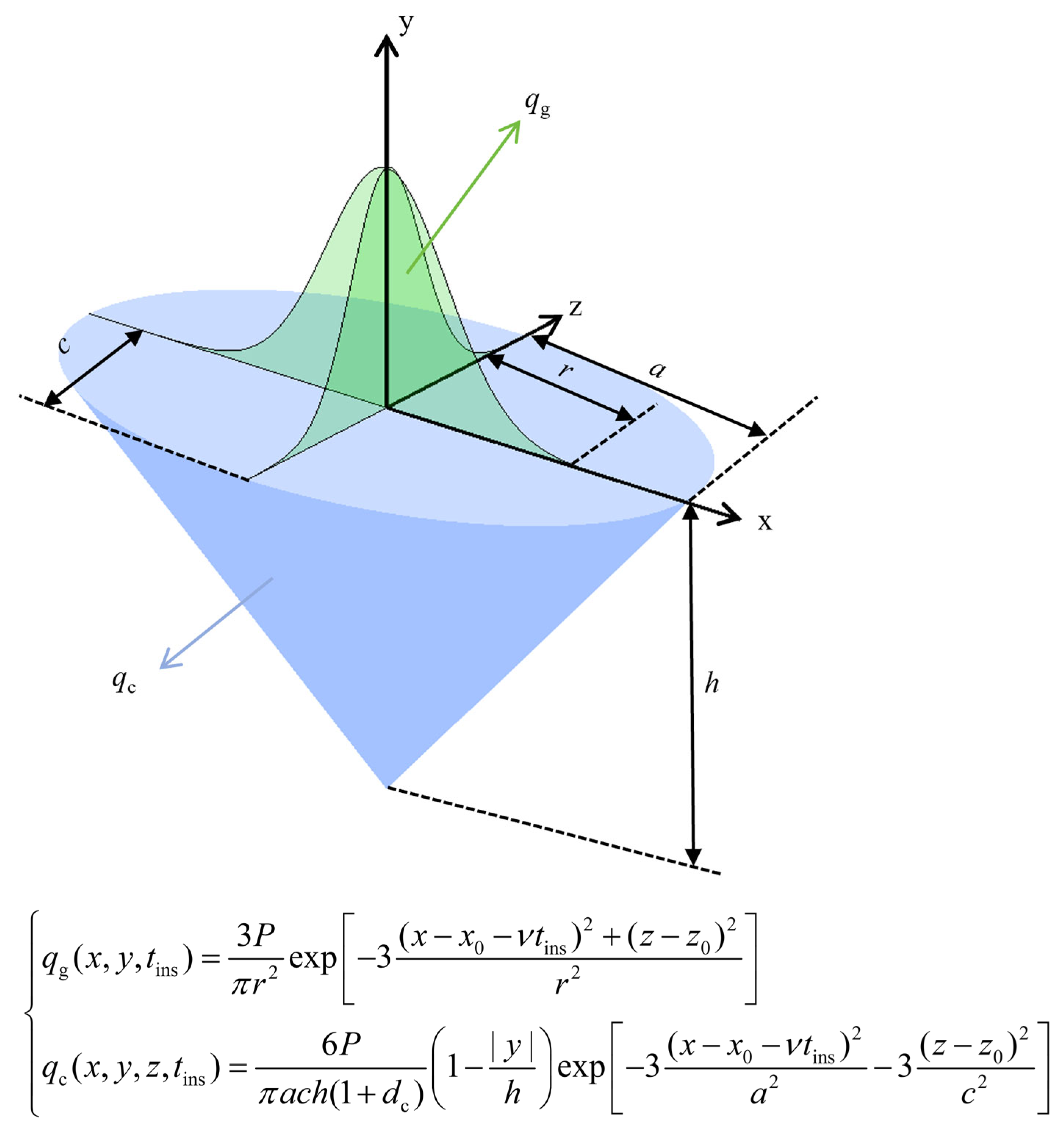
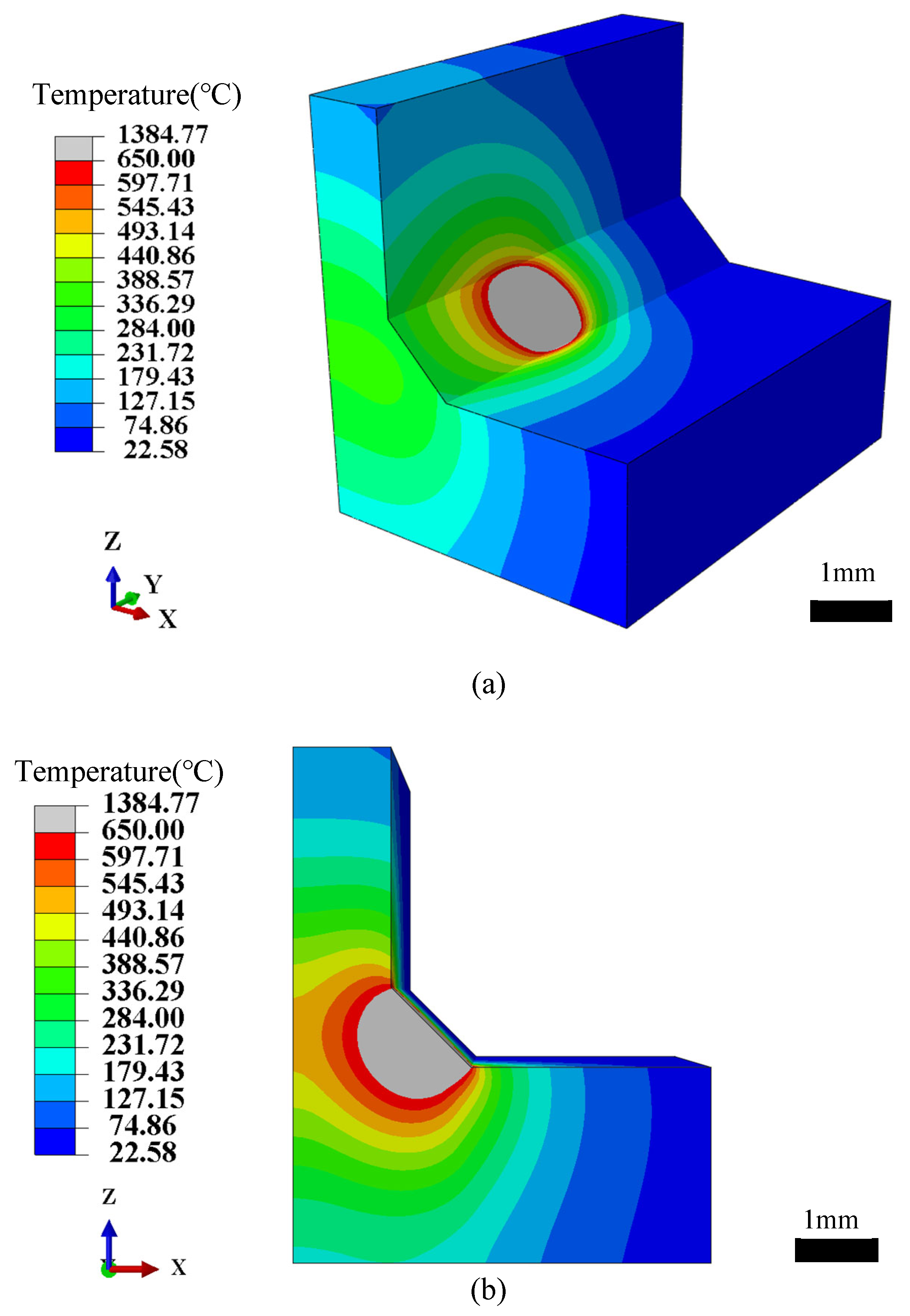
| Temperature (°C) | 20 | 100 | 500 | 750 | 1000 | 1500 | 2000 | 2500 | 3000 |
|---|---|---|---|---|---|---|---|---|---|
| Convection coefficient (W/m2·K) | 1.366 | 6.680 | 33.400 | 91.150 | 148.900 | 264.400 | 379.900 | 580.000 | 800.000 |
| Input Parameters of the Finite Element Model | Range | |
|---|---|---|
| Process Parameters | Power (W) | [2000, 3500] |
| Welding Speed (m/min) | [3, 4.5] | |
| Thickness (mm) | [1, 3] | |
| Heat Source Parameters | r (mm) | [0.3, 3] |
| a (mm) | [0.3, 3] | |
| c (mm) | [0.3, 3] | |
| h (mm) | [0.3, 2] | |
| Name | Operation | Kernel Size | Stride | Quantity/Method | Padding | Activation Function |
|---|---|---|---|---|---|---|
| L1-C | Convolution | 5 × 5 | (1, 1) | Kernels. 4 | padding = 2 | ReLU |
| L1-P | Pooling | 2 × 2 | (2, 2) | Max Pooling | padding = (1, 1) | - |
| L2-C | Convolution | 5 × 5 | (1, 1) | Kernels. 8 | padding = 2 | ReLU |
| L2-P | Pooling | 2 × 2 | (2, 2) | Max Pooling | padding = (0, 0) | - |
| L3-C | Convolution | 5 × 5 | (1, 1) | Kernels. 16 | padding = 2 | ReLU |
| L3-P | Pooling | 2 × 2 | (2, 2) | Max Pooling | padding = (1, 0) | - |
| L4-C | Convolution | 5 × 5 | (1, 1) | Kernels. 32 | padding = 2 | ReLU |
| L4-P | Pooling | 2 × 2 | (2, 2) | Max Pooling | padding = (0, 0) | - |
| L5-C | Convolution | 3 × 3 | (1, 1) | Kernels. 64 | padding = 2 | ReLU |
| L5-P | Pooling | 2 × 2 | (2, 2) | Max Pooling | padding = (0, 1) | - |
| L6-F | Fully Connected | - | - | Dimension. 1024 | - | - |
| L7-F | Fully Connected | - | - | Dimension. 1500 | - | - |
| L8-F | Fully Connected | - | - | Dimension. 4 | - | - |
| Evaluation Metric | Test Set Average Loss | R2 for r | R2 for a | R2 for h | R2 for c | Test Set RPE |
|---|---|---|---|---|---|---|
| Value | 0.02 | 0.96 | 0.98 | 0.99 | 0.98 | 6.38% |
| Parameter | Model Input | Actual Input Value/ Output Error | Predicted Result | Actual Output Value |
|---|---|---|---|---|
| Power (W) | 3413.25 | 3413.25 | - | - |
| Welding Speed (m/min) | 3.79 | 3.79 | - | - |
| Joint Thickness (mm) | 1.84 | 1.84 | - | - |
| r (mm) | - | 2.55% | 2.28 | 2.34 |
| a (mm) | - | 2.36% | 1.16 | 1.13 |
| h (mm) | - | 2.23% | 1.25 | 1.28 |
| c (mm) | - | 1.01% | 1.33 | 1.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, H.; Liu, X.; Guo, Z.; Yang, T.; Chen, M.; Man, Z.; Wei, X.; Zhou, J.; Liu, D. Heat Source Parameter Identification Based on Attention-Enhanced Residual Convolutional Neural Network. Materials 2025, 18, 4174. https://doi.org/10.3390/ma18174174
Jiang H, Liu X, Guo Z, Yang T, Chen M, Man Z, Wei X, Zhou J, Liu D. Heat Source Parameter Identification Based on Attention-Enhanced Residual Convolutional Neural Network. Materials. 2025; 18(17):4174. https://doi.org/10.3390/ma18174174
Chicago/Turabian StyleJiang, Hao, Xinyu Liu, Zhenfei Guo, Tianlei Yang, Mengyi Chen, Zongzhe Man, Xiao Wei, Jiangfan Zhou, and Da Liu. 2025. "Heat Source Parameter Identification Based on Attention-Enhanced Residual Convolutional Neural Network" Materials 18, no. 17: 4174. https://doi.org/10.3390/ma18174174
APA StyleJiang, H., Liu, X., Guo, Z., Yang, T., Chen, M., Man, Z., Wei, X., Zhou, J., & Liu, D. (2025). Heat Source Parameter Identification Based on Attention-Enhanced Residual Convolutional Neural Network. Materials, 18(17), 4174. https://doi.org/10.3390/ma18174174






