Arc Jet Testing and Modeling Study for Ablation of SiFRP Composites in Shear Environment
Abstract
1. Introduction
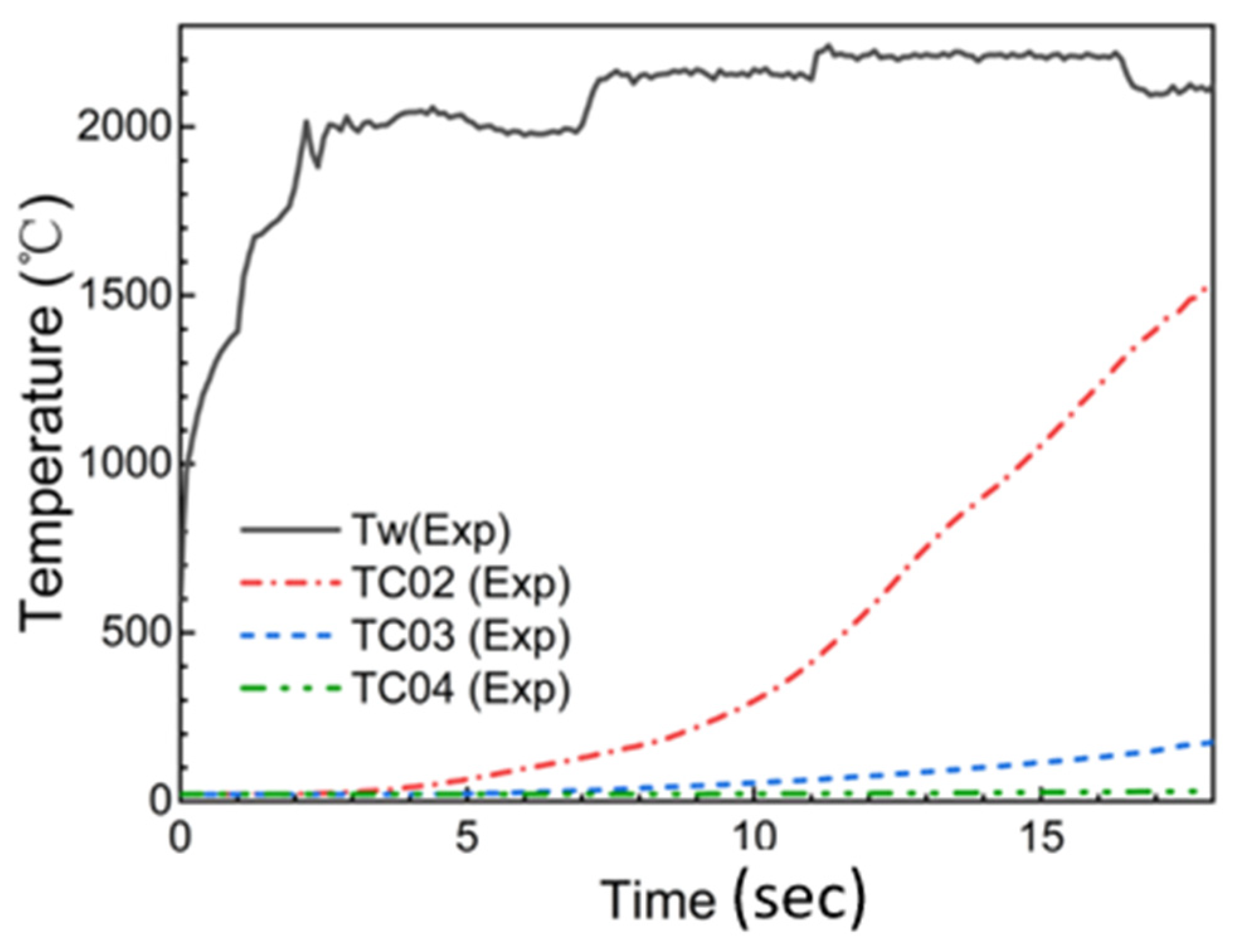
2. Ablation Test Methods and Typical Experimental Results of SiFPR Composites
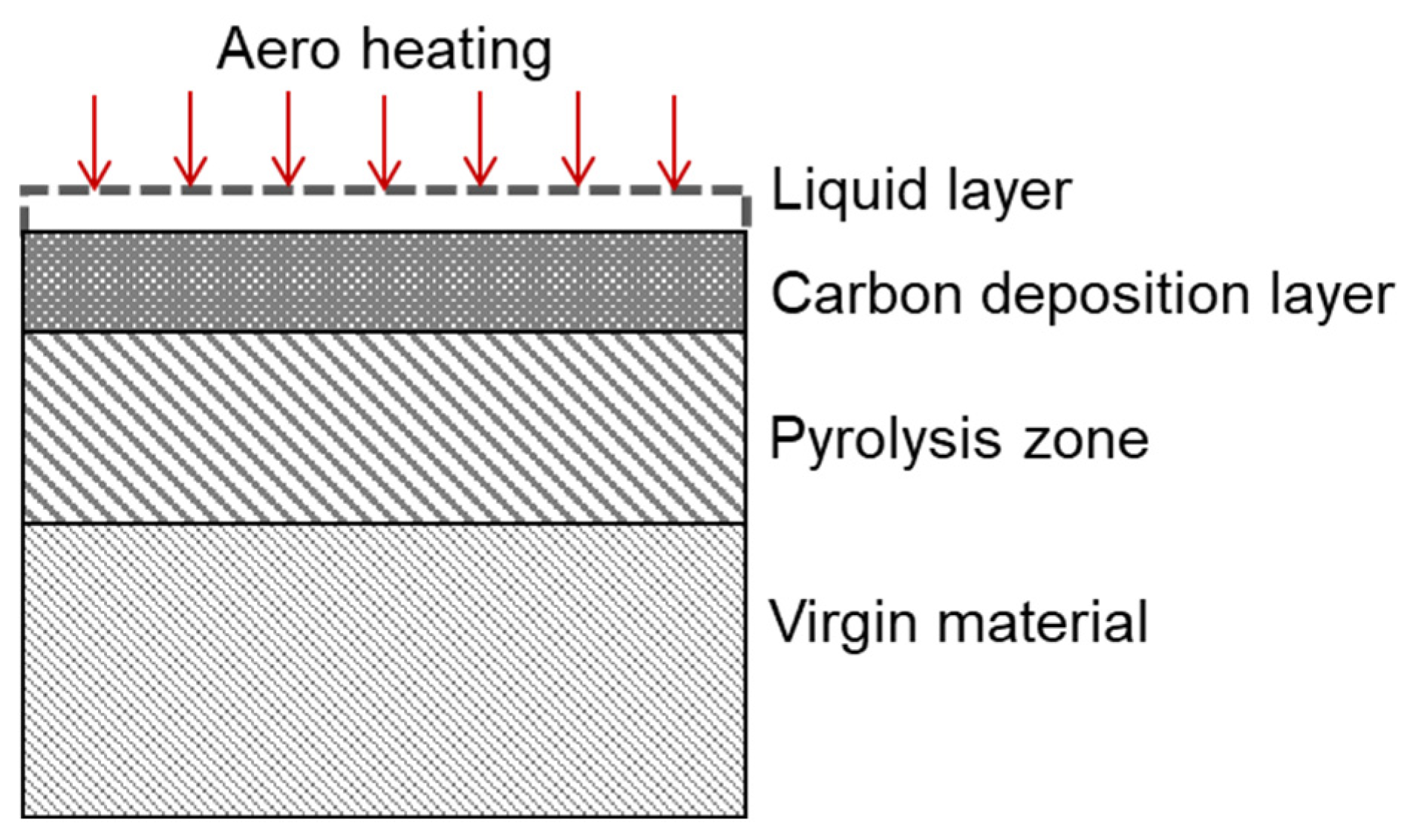
3. Ablation Model
3.1. Surface Ablation Model
3.2. Volumetric Ablation Model
3.2.1. Mass Conservation Equation Including Carbon Deposition
3.2.2. Energy Conservation Equation Including Carbon Deposition
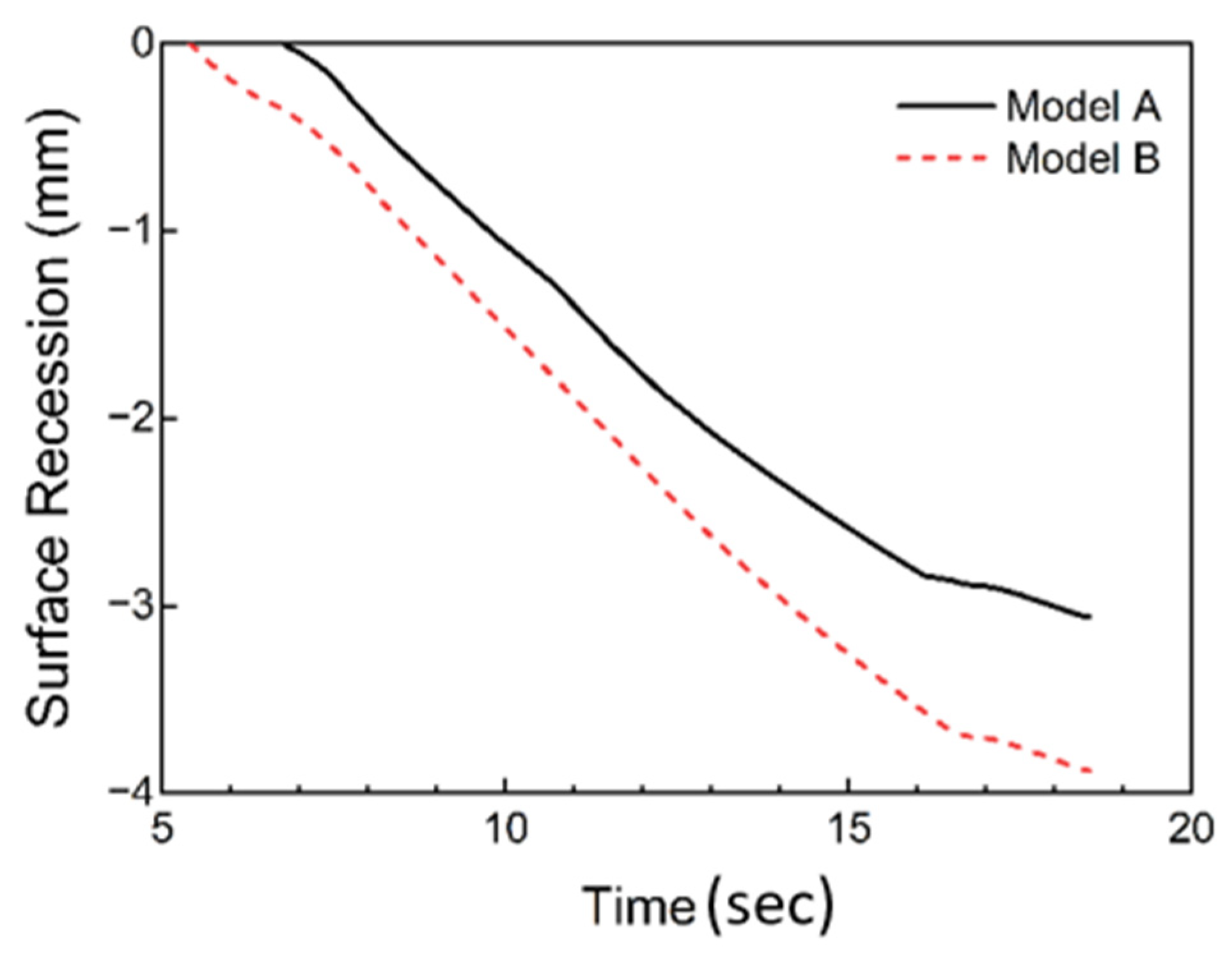
4. Analysis
- The thickness of the liquid layer is assumed to be constant.
- The specific heat, density, and thermal conductivity of the melt are assumed to be constant in the analysis, although they vary somewhat with the temperature. The effective thermal conductivity and density of the liquid layer are assumed to be linearly correlated with the porosity.
- The aerodynamic shear force acting on the liquid layer is assumed to be great enough, so that the liquid phase transformed from the solid phase instantly leaves its original position. The melting temperature of the silica fibers is 1700 °C.
- The thermal expansion due to pyrolysis is neglected since the thickness of the charred layer is small.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, S.; Tang, S. Surface and volumetric ablation behaviors of SiFRP composites at high heating rates for thermal protection applications. Int. J. Heat Mass Transf. 2016, 102, 1190–1198. [Google Scholar] [CrossRef]
- Farrukh, S.; Tahir, N.A.; Hussain, A.; Ayoub, M.; Rafiq, M.; Khan, M.H. Fabrication and analysis of HNBR-Silica/Carbon Phenolic ablative composites as an effective thermal protection system (TPS). IOP Conf. Ser. Mater. Sci. Eng. 2018, 458, 012015. [Google Scholar] [CrossRef]
- Zhou, L.; Sun, X.; Chen, M.; Zhu, Y.; Wu, H. Multiscale modeling and theoretical prediction for the thermal conductivity of porous plain-woven carbonized silica/phenolic composites. Compos. Struct. 2019, 215, 278–288. [Google Scholar] [CrossRef]
- AJ, A.J.; Panigrahi, S.K.; Sasikumar, P.; Rao, K.S.; Krishnakumar, G. Ablative properties, thermal stability, and compressive behaviour of hybrid silica phenolic ablative composites. Polym. Degrad. Stab. 2022, 203, 110063. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Q.; Lv, S.; Zuo, B.; Chen, L.; Cao, T.; Chen, C.; Tao, W.Q. Investigation on thermal conductivities of plain-woven carbon/phenolic and silica/phenolic composites at high temperature: Theoretical prediction and experiment. Compos. Sci. Technol. 2024, 256, 110771. [Google Scholar] [CrossRef]
- Hsieh, C.-L.; Seader, J.D. Surface ablation of silica-reinforced composites. AIAA J. 1973, 11, 1181–1187. [Google Scholar] [CrossRef]
- Henderson, J.B.; Wiebelt, J.A.; Tant, M.R. A Model for the thermal response of polymer composite materials with experimental verification. J. Compos. Mater. 1985, 19, 579–595. [Google Scholar] [CrossRef]
- Adams, M.C.; Powers, W.E.; Georgiev, S. An experimental and theoretical study of quartz ablation at the stagnation point. J. Aerosp. Sci. 1960, 27, 535–543. [Google Scholar] [CrossRef]
- Hidalgo, H. Ablation of glassy material around blunt bodies of revolution. ARS J. 1960, 30, 806–814. [Google Scholar] [CrossRef]
- Rosensweig, R.E.; Beecher, N. Theory for the ablation of fiber glass-reinforced phenolic resin. AIAA J. 1963, 1, 1802–1809. [Google Scholar] [CrossRef]
- Xu, Y.; Ye, H.; Zhang, L.; Cai, Q. Investigation on the effective thermal conductivity of carbonized high silica/phenolic ablative material. Int. J. Heat Mass Transf. 2017, 115, 597–603. [Google Scholar] [CrossRef]
- Duffa, G. Ablative Thermal Protection Systems Modeling; AIAA education series; American Institute of Aeronautics and Astronautics, Inc.: Reston, VA, USA, 2013. [Google Scholar]
- Henderson, J.B.; Verma, Y.P.; Tant, M.R.; Moore, G.R. Measurement of the thermal conductivity of polymer composites to high temperatures using the line source technique. Polym. Compos. 1983, 4, 219–224. [Google Scholar] [CrossRef]
- Meicong, W.; Xin, Y.; Jixiang, S.; Yonggang, L.; Yanru, H.; Zhiwei, D.; Yupeng, H. Effect of Phenolic Resin Pyrolysis on Thermal Properties of SiFRP Composites under High Heating Rates. J. Phys. Conf. Ser. 2024, 2891, 112023. [Google Scholar] [CrossRef]
- Torre, L.; Kenny, J.M.; Maffezzoli, A.M. Degradation behaviour of a composite material for thermal protection systems Part I–Experimental characterization. J. Mater. Sci. 1998, 33, 3137–3143. [Google Scholar] [CrossRef]
- Torre, L.; Kenny, J.M. Degradation behaviour of a composite material for thermal protection systems Part III–Experimental characterization. J. Mater. Sci. 2000, 35, 4563–4566. [Google Scholar] [CrossRef]
- Milos, F.S.; Chen, Y.-K. Ablation and Thermal Response Property Model Validation for Phenolic Impregnated Carbon Ablator. J. Spacecr. Rockets. 2010, 47, 786–805. [Google Scholar] [CrossRef]
- Ayasoufi, A.; Rahmani, R.; Cheng, G.; Koomullil, R.; Neroorkar, K. Numerical Simulation of Ablation for Reentry Vehicles. In Proceedings of the 9th AIAA/ASME Joint Thermophysics and Heat Transfer Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar] [CrossRef]
- Beecher, N.; Rosensweig, R.E. Ablation Mechanisms in Plastics With Inorganic Reinforcement. ARS J. 1961, 31, 532–539. [Google Scholar] [CrossRef]
- Driver, D.M.; Carballo, J.E.; Beck, R.; Prabhu, D.; Santos, J.A.; Cassell, A.; Skokova, K.; Tang, C.; Hwang, H.H.; Slimko, E.; et al. Arcjet Testing in Shear Environment for Mars Science Laboratory Thermal Protection System. J. Spacecr. Rockets 2014, 51, 1151–1166. [Google Scholar] [CrossRef]
- Driver, D.; Olson, M.; Barnhardt, M.; MacLean, M.; MacLean, M. Understanding High Recession Rates of Carbon Ablators Seen in Shear Tests in an Arc Jet. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef]
- Driver, D.; MacLean, M. Improved Predictions of PICA Recession in Arc Jet Shear Tests. In Proceedings of the 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2011. [Google Scholar] [CrossRef]
- Weger, E.; Brew, J.R.; Servais, R.A. An Investigation of Carbon Deposition in Chars. II. 1968. Available online: https://api.semanticscholar.org/CorpusID:91211581 (accessed on 1 May 2024).
- Isabelle, Z.-D.; Fournet, R.; Marquaire, P.-M. Pyrolysis of propane for CVI of pyrocarbon: Part III: Experimental and modeling study of the formation of pyrocarbon. J. Anal. Appl. Pyrolysis 2006, 79, 268–277. [Google Scholar] [CrossRef]
- Becker, A.; Hüttinger, K.J. Chemistry and kinetics of chemical vapor deposition of pyrocarbon–IV pyrocarbon deposition from methane in the low temperature regime. Carbon 1998, 36, 213–224. [Google Scholar] [CrossRef]
- Jiang, L.; Kun, X.; Xiang, L. Characteristics and formation mechanism of compact/porous structures in char layers of EPDM insulation materials. Carbon 2018, 127, 498–509. [Google Scholar] [CrossRef]
- Blumenthal, J.L.; Santy, M.J. Kinetic studies of high-temperature carbon- silica reactions in charred silica-reinforced phenolic resins. AIAA J. 1966, 4, 1053–1057. [Google Scholar] [CrossRef]
- Cagliostro, D.E.; Goldstein, H.; Parker, J.A. Silica Reinforcement and Char Reactions in the Apollo Heat Shield. J. Spacecr. Rockets. 1972, 9, 346–350. [Google Scholar] [CrossRef]
- Henderson, J.B.; Tant, M.R. A study of the kinetics of high-temperature carbon-silica reactions in an ablative polymer composite. Polym. Compos. 1983, 4, 233–237. [Google Scholar] [CrossRef]
- Yinda, H. Experimental research on the effect of separation flow on ablation in supersonic turbulent flow. In Proceedings of the 20th Thermophysics Conference, Williamsburg, VA, USA, 19–21 June 1985. [Google Scholar] [CrossRef]
- Tarasiuk, J.; Mnich, B.; Wroński, S.; Lisowska-Gaczorek, A.; Szostek, K. Application of the microtomography technique in density studies of prehistoric and historical human skeletal materials. Int. J. Osteoarchaeol. 2023, 33, 829–840. [Google Scholar] [CrossRef]
- Bartlett, E.P.; Kendall, R.M.; Rindal, R.A. An analysis of the coupled chemically reacting boundary layer and charring ablator, part 1 Summary report. In NASA Technical Report; NASA: Washington, DC, USA, 1968; p. CR-1062. [Google Scholar]
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]



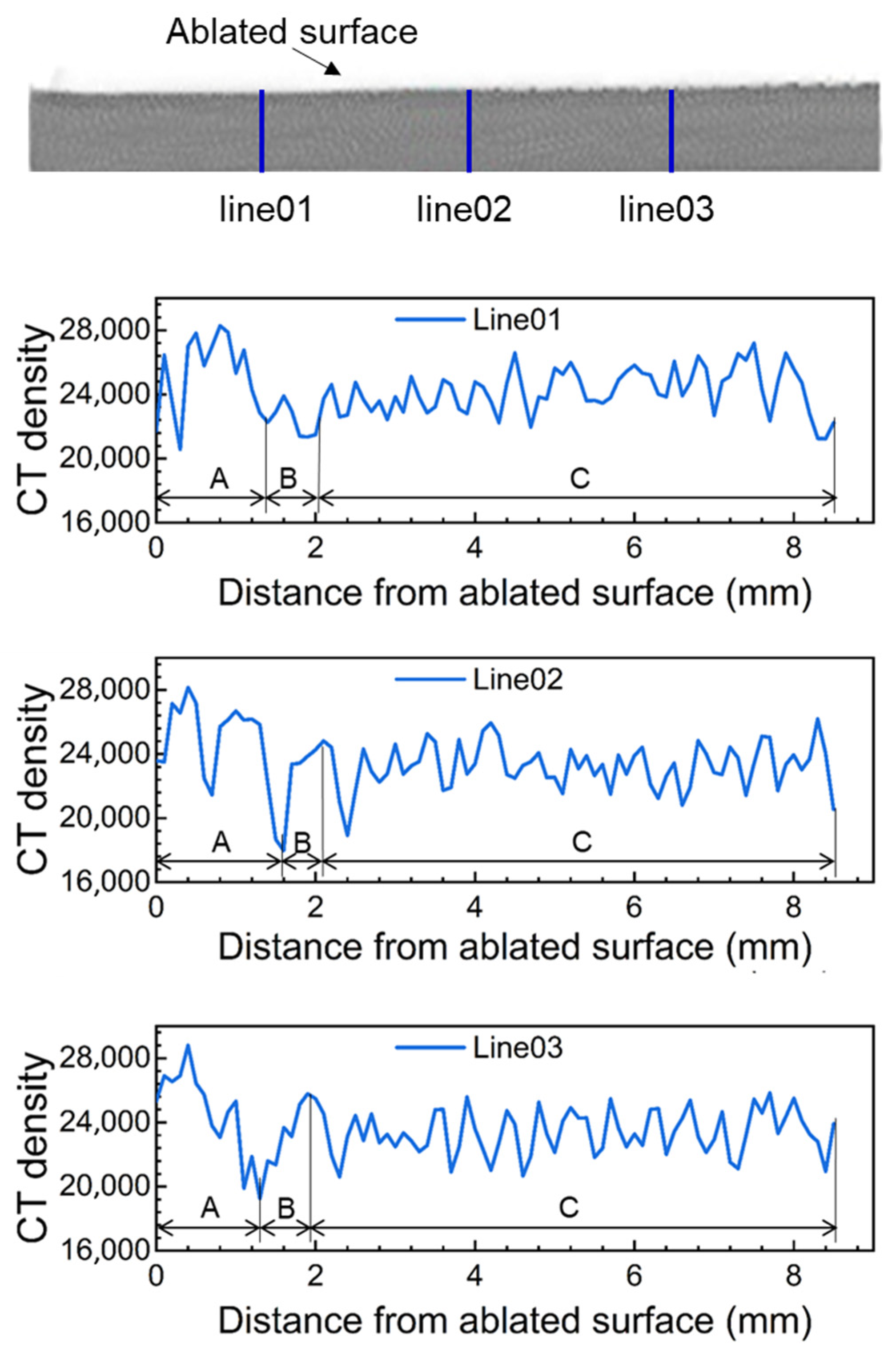


| Average CT Density of Area A | Average CT Density of Area B | Average CT Density of Area C | Average CT Density of All Areas | |
|---|---|---|---|---|
| Line01 | 26,299 | 22,505 | 24,227 | 24,254 |
| Line02 | 24,211 | 22,868 | 23,342 | 23,511 |
| Line03 | 23,884 | 23,326 | 23,409 | 23,594 |
| Property | Value | Source |
|---|---|---|
| Density of virgin material, ρvir (kg/m3) | 1640 | Manufacturer (China space sanjiang group CO., LTD., Xiaogan, China) |
| Thermal conductivity of virgin material (room temperature to 250 °C), kvir (W/m K) | 0.4–0.7 | |
| Specific heat capacity of virgin material (room temperature to 250 °C), Cpvir (J/kg K) | ≥800 | |
| Coefficient of thermal expansion of virgin material (room temperature to 250 °C), βvir (1/K) | 12 × 10−6 | |
| Density of char material, ρchar (kg/m3) | 1230 | [7] |
| Thermal conductivity of char material (room temperature to 850 °C), kchar (W/m K) | 0.955 + 8.42 × 10−4 T − 4.07 × 10−6 T2 + 5.35 × 10−9 T3 | [7] |
| Specific heat capacity of char material (room temperature to 850 °C), Cpchar (J/kg K) | 1120.8 + 1.025 T | [7] |
| Density of molten layer, ρL (kg/m3) | 2250 | [6] |
| Thermal conductivity of molten layer, kL (W/m K) | 2.93 | [6] |
| Specific heat capacity of molten layer, CpL (J/kg K) | 1046 | [6] |
| Heat of pyrolysis, hp (kJ/kg) | 418 | [1] |
| Average activation energy (phenolic resin pyrolysis), Ep (J/mol) | 64,081 | TGA |
| Pre-exponential factor (phenolic resin pyrolysis), Ap (1/s) | 333 | TGA |
| Order of reaction (phenolic resin pyrolysis), np (-) | 1 | TGA |
| Heat of carbon–silica reaction, hR (kJ/kg) | 5941 | [6] |
| Average activation energy (carbon–silica reactions), ER (J/mol) | 353,758 | [29] |
| Pre-exponential factor (carbon–silica reactions), AR (1/s) | 2.6167 × 10−7 | [29] |
| Order of reaction (carbon–silica reactions), nR (-) | 0.532 | [29] |
| Initial temperature of deposition, Td,1 | 1000 °C | [23] |
| End temperature of deposition, Td,2 | 1700 °C | Manufacturer (China space sanjiang group CO., Ltd., Xiaogan, China) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Shan, J.; Yang, X.; Chen, Q.; Lu, Y.; Hu, Y. Arc Jet Testing and Modeling Study for Ablation of SiFRP Composites in Shear Environment. Materials 2025, 18, 4142. https://doi.org/10.3390/ma18174142
Wang M, Shan J, Yang X, Chen Q, Lu Y, Hu Y. Arc Jet Testing and Modeling Study for Ablation of SiFRP Composites in Shear Environment. Materials. 2025; 18(17):4142. https://doi.org/10.3390/ma18174142
Chicago/Turabian StyleWang, Meicong, Jixiang Shan, Xin Yang, Qianghong Chen, Yonggang Lu, and Yupeng Hu. 2025. "Arc Jet Testing and Modeling Study for Ablation of SiFRP Composites in Shear Environment" Materials 18, no. 17: 4142. https://doi.org/10.3390/ma18174142
APA StyleWang, M., Shan, J., Yang, X., Chen, Q., Lu, Y., & Hu, Y. (2025). Arc Jet Testing and Modeling Study for Ablation of SiFRP Composites in Shear Environment. Materials, 18(17), 4142. https://doi.org/10.3390/ma18174142





