Microstructural Stability and Transition to Unstable Friction for FCC Metals: Ag and Ni
Abstract
1. Introduction
2. Theoretical Background: Microstructural Stability of FCC Metals and Alloys
3. Materials and Methods
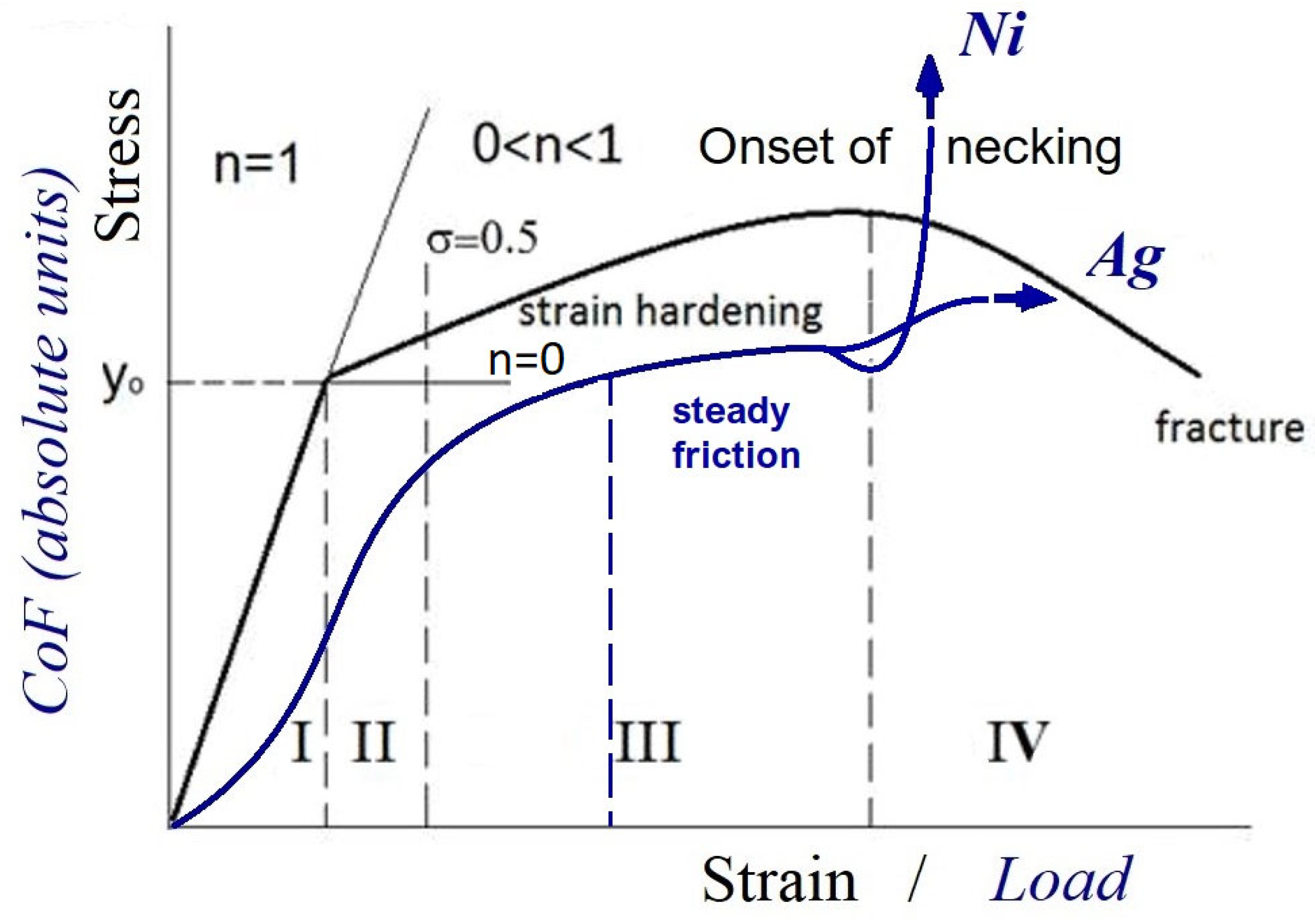
3.1. Friction and Wear of Ag and Ni
3.2. Characterization Methods
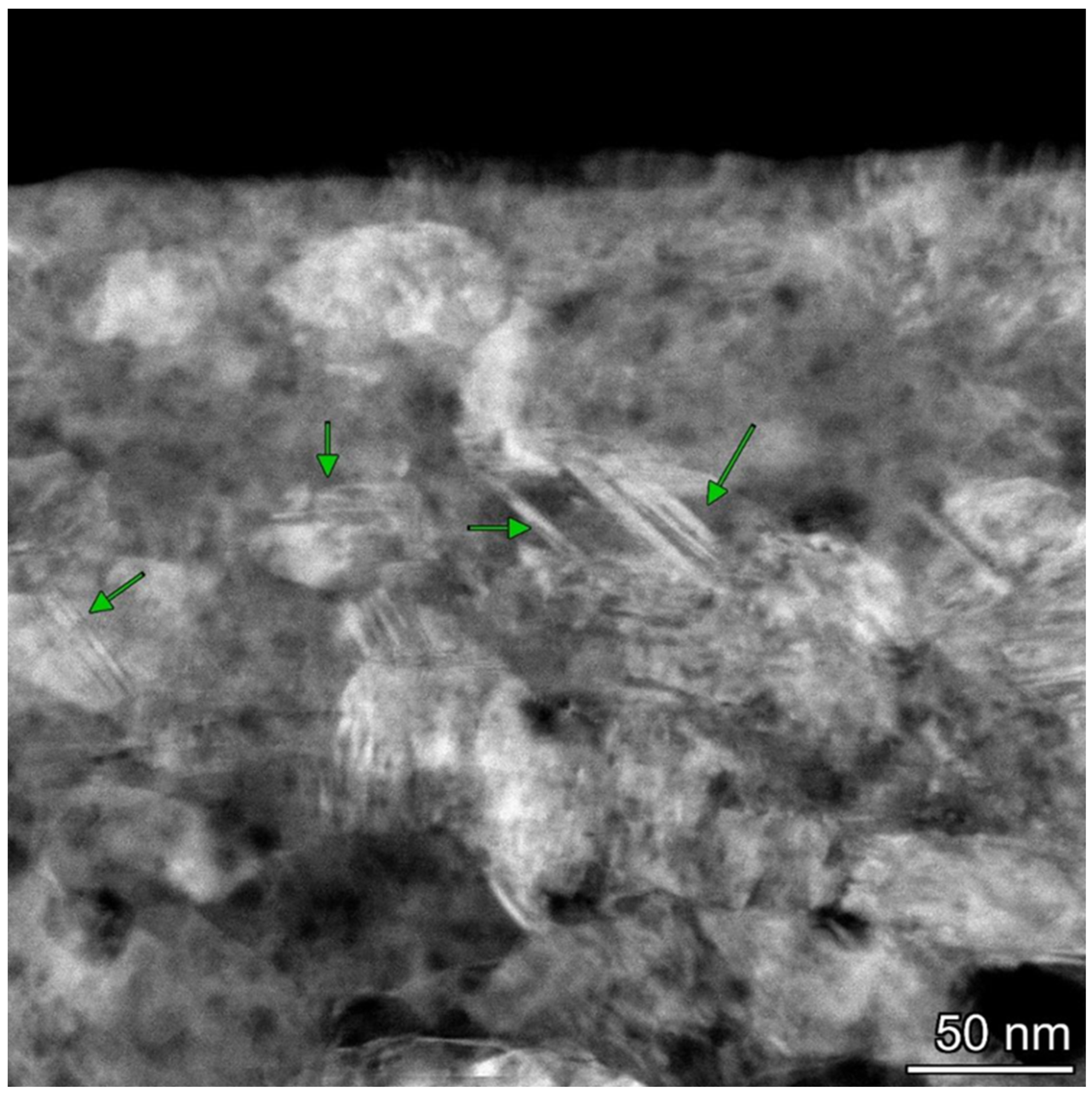
3.3. Analysis of Plastic Deformation of Ag and Ni in a Steady Friction State
3.4. Deformation Twinning and Dynamic Recovery in the Transition to Unstable Friction
4. Discussion
4.1. Analysis of Crystal Plasticity Under Friction of Ag and Ni
4.2. Microstructural Instability
4.3. Model of Strength–Ductility Trade-Off and Microstructural Instability
5. Conclusions
- (1)
- The effect of dislocation pile-ups responsible for the generation or annihilation of dislocations during friction was considered. Ag’s top surface layer exhibits steady-state friction under the formation of twin bundles, intersecting twins, and dislocations. With increasing deformation depths (>1 μm), adiabatic elongated shear bands (ASBs) were observed. The intense dynamic recrystallization (DRX) process was associated with minimal slip resistance and applied stresses in the lower regions of ASBs. The mechanisms of microstructural stability and friction instability and the theoretical models of dislocation generation and annihilation in ultrafine-grained (UFG) or nanocrystalline (NC) FCC metals were investigated, particularly in the context of plastic deformation and failure development under friction.
- (2)
- The transition to unstable friction was estimated. Plastic deformation in Ag’s surface layers was limited due to the interaction of deformation twins and dislocation slip in a hydrostatic compression field. The damaged surface of Ag exhibited numerous pores, reducing the contact area and significantly increasing the shear stress. The brittle fracture of Ni represents a catastrophic failure associated with the formation of super-hard nickel oxide. It is worth noting that the Gibbs energy absorbed per unit area in intergranular brittle fractures is similar to the effective shear stress considered in our work.
- (3)
- Deformation resistance of the mesoscale dislocation structure was compared to the applied shear stress at the macroscale. The coefficient of similitude (K) has been introduced in this work to compare plastic deformation at different scales. The maximum calculated values of shear flow stress (τ*) and critical strain (ε*) were compared with experimental results. The model of the strength–ductility trade-off and microstructural instability is considered. The interaction between the migration of dislocation pile-ups and the driving forces applied to the grain boundaries was estimated. It is suggested that driving forces provide deformation resistance to dislocation pile-ups formed due to the applied stress and temperature during friction. The phase transformation and plastic deformation in the literature are attributed to the thermodynamically induced kinetics of atoms, which is similar to our effective shear stress, τeff = τap − τcr.
- (4)
- Nanostructure stabilization through the addition of a polycrystalline element (solute) to the crystal interiors in order to reduce the free energy of grain boundary interfaces was investigated. Nanocrystalline GS can be stabilized via solute segregation, especially at high temperatures. It is suggested that further refinement of these complex systems is key to the development of new strengthening materials. A method for suppressing strain localization was proposed, involving selective doping for grain resistance. The thermodynamic driving force and kinetic energy barrier involved in strengthening, brittleness, or annealing under plastic deformation and phase formation in alloys and composite materials were examined.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| 2y | dislocation length | j | dislocation flux |
| a | lattice parameter | k | Archard wear coefficient |
| Ar | real contact area | Boltzmann constant | |
| Adefect | grain boundary area | K | coefficient of similitude |
| ASB | adiabatic shear bands | K* | fitting parameter |
| α | slip system | L | obstacle spacing |
| α0 | dimensionless constant | width of twin embryo | |
| b | magnitude of the Burger’s vector | µ | coefficient of friction (COF) |
| Burger’s vector of a partial dislocation | Λ | geometrical length scale of the microstructure | |
| bs | Burger’s vector of the Shockley partial | νD | Debye frequency |
| d | size of grain | m | strain rate sensitivity exponent |
| DRX | dynamic recrystallization | migration of pile-up dislocations | |
| energy of the single crystal | number of dislocations | ||
| energy of the polycrystal | saturated number of piled-up dislocations | ||
| Eseg | segregation energy, | n | strain hardening exponent |
| εcr | critical strain | P | driving pressure |
| H | hardness | ρ | dislocation density |
| F | Gibbs energy absorbed per unit area | ρSSD | density of statistically stored dislocations |
| FN | normal friction force | Q | activation energy |
| G | shear modulus | σtw | twinning stress |
| GBs | grain boundaries | σap | applied stress |
| activation Gibbs energy | Gibbs energies of the free surface | ||
| ΔGchem | strain energy | Gibbs energies of grain boundary | |
| migration Gibbs energy | tl | thickness of twin lamellas | |
| ΔGstrain | interface energy | t | time |
| ΔG | interface energy | T | temperature |
| ΔG SE, I | strengthening/embrittling energy | Tc | recrystallization temperature |
| λ | fitting parameter | Tt | test temperature |
| λp | mean free path | Tm | temperature of melting |
| γ | atomic diameter | τ | shear strength |
| shear strain rate | lattice friction stress | ||
| γb | grain boundary energy | critical shear stress of slip system α | |
| γSF | stacking fault energy | internal backstress | |
| shear stress concentration | V | wearing volume | |
| stress of forest dislocations | Ω | atomic volume | |
| twin stress | w | interaction parameters | |
| critical twinning stress | W | dimensional wear coefficient | |
| controllable parameter | UFG | ultrafine-grained crystals |
References
- Lu, K. Making strong nanomaterials ductile with gradients. Science 2014, 345, 1455–1456. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Han, Z.; Li, X.; Lu, K. Lowering coefficient of friction in Cu alloys with stable gradient nanostructures. Sci. Adv. 2016, 2, e1601942. [Google Scholar] [CrossRef]
- Cao, H.M.; Zhou, X.; Li, X.Y.; Lu, K. Friction mechanism in the running-in stage of copper: From plastic deformation to delamination and oxidation. Trib. Int. 2017, 115, 3–7. [Google Scholar] [CrossRef]
- Hu, J.; Shi, Y.N.; Sauvage, X.; Sha, G.; Lu, K. Grain boundary stability governs hardening and softening in extremely fine nanograined metals. Science 2017, 355, 1292–1296. [Google Scholar] [CrossRef]
- Li, Y.S.; Tao, N.R.; Lu, K. Microstructural evolution and nanostructure formation in copper during dynamic plastic deformation at cryogenic temperatures. Acta Mater. 2008, 56, 230–241. [Google Scholar] [CrossRef]
- Chen, X.; Han, Z.; Li, X.Y.; Lu, K. Friction of stable gradient nano-grained metals. Scr. Mater. 2020, 185, 82–87. [Google Scholar] [CrossRef]
- Wang, P.F.; Han, Z.; Lu, K. Enhanced tribological performance of a gradient nanostructured interstitial-free steel. Wear 2018, 402–403, 100–108. [Google Scholar] [CrossRef]
- Wang, P.F.; Han, Z.J. Friction and wear behaviors of a gradient nano-grained AISI 316. Mater. Sci. Technol. 2018, 34, 1835–1842. [Google Scholar] [CrossRef]
- Ma, E.; Zhu, T. Towards strength-ductility synergy through the design of heterogeneous nanostructures in metals. Mater. Today 2017, 20, 323–331. [Google Scholar] [CrossRef]
- Xing, W.; Yu, Z.; Li, X.; Zhang, H.; Wu, H.; Zhang, Z.; Zhang, Z.; Liu, C.; Zhao, H. Multiscale heterostructure construction and dislocation density modulation for enhanced wear resistance in novel Al0.25FeCoNiVTi0.1 high-entropy alloy. Wear 2025, 576–577, 206120. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, J.; Cao, Y.; Meng, A.; Liu, R.; Li, J.; Li, Z.; Zhao, Y.; Zhao, Y. Tribo-induced microstructural evolutions and wear mechanisms of AlCoCrFeNi2.1 eutectic high-entropy alloy at elevated temperatures. Acta Mater. 2025, 296, 121272. [Google Scholar] [CrossRef]
- Greiner, C.; Liu, Z.; Schneider, R.; Pastewka, L.; Gumbsch, P. The origin of surface microstructure evolution in sliding friction. Scr. Mater. 2018, 153, 63–67. [Google Scholar] [CrossRef]
- Haug, C.; Molodov, D.; Gumbsch, P.; Greiner, C. Tribologically induced crystal rotation kinematics revealed by electron backscatter diffraction. Acta Mater. 2022, 225, 117566. [Google Scholar] [CrossRef]
- Lee, S.H.; Wieners, C.; Schulz, K. Continuum modeling of dislocation microstructures under tribological loading. Trib. Int. 2025, 209, 110731. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Liao, X.Z.; Zhu, Y.T.; Horita, Z.; Langdon, T.G. Influence of stacking fault energy on nanostructure formation under high pressure torsion. Mater. Sci. Eng. A 2005, 410–411, 188–193. [Google Scholar] [CrossRef]
- Wang, Y.B.; Liao, X.Z.; Zhao, Y.H.; Lavernia, E.J.; Ringer, S.P.; Horita, Z.; Langdon, T.G.; Zhug, Y.T. The role of stacking faults and twin boundaries in grain refinement of a Cu–Zn alloy processed by high-pressure torsion. Mater. Sci. Eng. A 2010, 527, 4959–4966. [Google Scholar] [CrossRef]
- Edalati, K.; Horita, Z. High-pressure torsion of pure metals: Influence of atomic bond parameters and stacking fault energy on grain size and correlation with hardness. Acta Mater. 2011, 59, 6831–6836. [Google Scholar] [CrossRef]
- Balogh, L.; Ungar, T.; Zhao, Y.; Zhu, Y.T.; Horita, Z.; Xu, C.; Langdon, T.G. Influence of stacking-fault energy on microstructural characteristics of ultrafine-grain copper and copper-zinc. Acta Mater. 2008, 56, 809–820. [Google Scholar] [CrossRef]
- Meyers, M.A.; Vöhringer, O.; Lubarda, V.A. The onset of twinning in metals: A constitutive description. Acta Mater. 2001, 49, 4025–4039. [Google Scholar] [CrossRef]
- Frøseth, A.; Swygenhoven, H.V.; Derlet, P.M. The influence of twins on the mechanical properties of nc-Al. Acta Mater. 2004, 52, 2259–2268. [Google Scholar] [CrossRef]
- Huang, C.; Wang, K.; Wu, S.; Zhang, Z.; Li, G.; Li, S. Deformation twinning in polycrystalline copper at room temperature and low strain rate. Acta Mater. 2006, 54, 655–665. [Google Scholar] [CrossRef]
- Yan, J.; Lindo, A.; Schwaiger, R.; Hodge, A.M. Sliding wear behavior of fully nanotwinned Cu alloys. Friction 2019, 7, 260–267. [Google Scholar] [CrossRef]
- Liu, Z.; Messer-Hannemann, P.; Laube, S.; Greiner, C. Tribological performance and microstructural evolution of α-brass alloys as a function of zinc concentration. Friction 2020, 8, 1117–1136. [Google Scholar] [CrossRef]
- Wu, B.; Fu, H.; Sun, W.; Yang, W.; Luo, J.; Yang, X.S. Significantly lowered coefficient of friction in copper alloy with a gradient nanograined-nanotwinned surface layer. Wear 2022, 510–511, 204517. [Google Scholar] [CrossRef]
- Li, X.; Wei, Y.; Lu, L.; Lu, K.; Gao, H. Dislocation nucleation governed softening and maximum strength in nano-twinned metals. Nature 2010, 464, 877–880. [Google Scholar] [CrossRef]
- Hansen, N.; Huang, X.; Hughes, D.A. Microstructural evolution and hardening parameters. Mater. Sci. Eng. A 2001, 317, 3–11. [Google Scholar] [CrossRef]
- Mirmohammad, H.; Sarker, S.; Berke, R.; Kingstedt, O. A multi-length-scale investigation of the applicability of ductility laws for annealed and work-hardened copper. Mater. Sci. Eng. A 2023, 883, 145464. [Google Scholar] [CrossRef]
- Kad, B.K.; Gebert, J.M.; Perez-Prado, M.T.; Kassner, M.E.; Meyers, M.A. Ultrafine-grain-sized zirconium by dynamic deformation. Acta Mater. 2006, 54, 4111–4127. [Google Scholar] [CrossRef]
- Meyers, M.A.; Andrade, U.R.; Chokshi, A.H. The effect of grain size on the high-strain, high-strain-rate behavior of copper. Metal. Mater. Trans. A 1995, 26, 2881–2893. [Google Scholar] [CrossRef]
- Vo, N.Q.; Averback, R.S.; Bellon, P.; Caro, A. Yield strength in nanocrystalline Cu during high strain rate deformation. Scr. Mater. 2009, 61, 76–79. [Google Scholar] [CrossRef]
- Xu, Z.; Shen, Y.F.; Naghibzadeh, S.K.; Peng, X.; Muralikrishnan, V.; Maddali, S.; Menasche, D.; Krause, A.R.; Dayal, K.; Suter, R.M.; et al. Grain boundary migration in polycrystalline α-Fe. Acta Mater. 2024, 264, 119541. [Google Scholar] [CrossRef]
- Kang, S.; Jung, J.G.; Kang, M.; Woo, W.; Lee, Y.K. The effects of grain size on yielding, strain hardening, and mechanical twinning in Fe–18Mn–0.6C–1.5Al twinning-induced plasticity steel. Mater. Sci. Eng. A 2016, 652, 212–220. [Google Scholar] [CrossRef]
- Haddou, H.; Risbet, M.; Marichal, G.; Feaugas, X. The effects of grain size on the cyclic deformation behaviour of polycrystalline nickel. Mater. Sci. Eng. A 2004, 379, 102–111. [Google Scholar] [CrossRef]
- Valiev, R.; Islamgaliev, R.; Alexandrov, I. Bulk nanostructured materials from severe plastic deformation. Prog. Mater. Sci. 2000, 45, 103–190. [Google Scholar] [CrossRef]
- Ma, E. Instabilities and ductility of nanocrystalline and ultrafine-grained metals. Scr. Mater. 2003, 49, 663–668. [Google Scholar] [CrossRef]
- Li, Z.; Pradeep, K.G.; Deng, Y.; Raabe, D.; Tasan, C.C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 2016, 534, 227–230. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.W.; Wang, G.Q.; Jia, Y.D.; Yi, J.; Zhai, Q.J.; Liu, J.B.; Sun, B.A.; Chu, H.J.; Shen, J.; Liaw, P.K.; et al. Enhancement of strength-ductility trade-off in a high-entropy alloy through a heterogeneous structure. Acta Mater. 2019, 165, 444–458. [Google Scholar] [CrossRef]
- Zheng, G.; Tang, B.; Zhao, S.; Wang, J.; Xie, Y.; Chen, X.; Wang, W.Y.; Liu, D.; Yang, R.; Li, J. Breaking the high-temperature strength-ductility trade-off in TiAl alloys through microstructural optimization. Inter J. Plast. 2023, 170, 103756. [Google Scholar] [CrossRef]
- Ma, E.; Liu, C. Chemical inhomogeneities in high-entropy alloys help mitigate the strength-ductility trade-off. Prog. Mater. Sci. 2024, 143, 101252. [Google Scholar] [CrossRef]
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Li, Y.; Zhu, L.; Liu, Y.; Lei, X.; Wang, G.; Wu, Y.; Mi, Z.; Liu, J.; Wang, H.; et al. Evading the strength–ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 2014, 5, 3580. [Google Scholar] [CrossRef]
- Owen, W.S.; Grujicic, M. Strain aging of austenitic Hadfield manganese steel. Acta Mater. 1998, 47, 111–126. [Google Scholar] [CrossRef]
- Grässel, O.; Krüger, L.; Frommeyer, G.; Meyer, L.W. High strength Fe–Mn-(Al, Si) TRIP/TWIP steels development–properties–application. Int. J. Plast. 2000, 16, 1391–1409. [Google Scholar] [CrossRef]
- Yeh, J.W.; Chen, S.K.; Lin, S.J.; Gan, J.Y.; Chin, T.S.; Shun, T.T.; Tsau, C.H.; Chang, S.Y. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 2004, 6, 299–303. [Google Scholar] [CrossRef]
- Fan, J.; Zhu, L.; Lu, J.; Fu, T.; Chen, A. Theory of designing the gradient microstructured metals for overcoming strength-ductility trade-off. Scr. Mater. 2020, 184, 41–45. [Google Scholar] [CrossRef]
- Fang, T.H.; Li, W.L.; Tao, N.R.; Lu, K. Revealing extraordinary intrinsic tensile plasticity in gradient nano-grained copper. Sci. 2011, 331, 1587–1590. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Li, X.; Xu, D.; Lu, L.; Gao, H.; Zhu, T. Gradient plasticity in gradient nano-grained metals. Ext. Mech. Lett. 2016, 8, 213–219. [Google Scholar] [CrossRef]
- Torre, F.D.; Lapovok, R.; Sandlin, J.; Thomson, P.F.; Davies, C.H.J.; Pereloma, E.V. Microstructures and properties of copper processed by equal channel angular extrusion for 1–16 passes. Acta Mater. 2004, 52, 4819–4832. [Google Scholar] [CrossRef]
- Mishra, A.; Kad, B.K.; Gregori, F.; Meyers, M.A. Microstructural evolution in copper subjected to severe plastic deformation: Experiments and analysis. Acta Mater. 2007, 55, 13–28. [Google Scholar] [CrossRef]
- Hebesberger, T.; Stüwe, H.P.; Vorhauer, A.; Wetscher, F.; Pippan, R. Structure of Cu deformed by high pressure torsion. Acta Mater. 2005, 53, 393–402. [Google Scholar] [CrossRef]
- Estrin, Y.; Molotnikov, A.; Davies, C.H.J.; Lapovok, R. Strain gradient plasticity modelling of high-pressure torsion. J. Mech. Phys. Solids 2008, 56, 1186–1202. [Google Scholar] [CrossRef]
- Huang, C.X.; Wang, Y.F.; Ma, X.L.; Yin, S.; Höppel, H.W.; Göken, M.; Wu, X.L.; Gao, H.J.; Zhu, Y.T. Interface affected zone for optimal strength and ductility in heterogeneous laminate. Mater. Today 2018, 21, 713–719. [Google Scholar] [CrossRef]
- Huang, X.; Hansen, N.; Tsuji, N. Hardening by annealing and softening by deformation in nanostructured metals. Science 2006, 312, 249–251. [Google Scholar] [CrossRef] [PubMed]
- Roters, F.; Raabe, D.; Gottstein, G. Work hardening in heterogeneous alloys—A microstructural approach based on three internal state variables. Acta Mater. 2000, 48, 4181–4189. [Google Scholar] [CrossRef]
- Yu, T.; Hansen, N.; Huang, X.; Godfrey, A. Observation of a new mechanism balancing hardening and softening in metals. Math. Res. Lett. 2014, 2, 160–165. [Google Scholar] [CrossRef]
- Nes, E.; Marthinsen, K.; Brechet, Y. On the mechanisms of dynamic recovery. Scr. Mater. 2002, 47, 607–611. [Google Scholar] [CrossRef]
- Kubin, L.; Hoc, T.; Devincre, B. Dynamic recovery and its orientation dependence in face-centered cubic crystals. Acta Mater. 2009, 57, 2567–2575. [Google Scholar] [CrossRef]
- Pantleon, W. Stage IV work-hardening related to disorientations in dislocation structures. Mater. Sci. Eng. A 2004, 387–389, 257–261. [Google Scholar] [CrossRef]
- Kocks, U.F. Laws for work-hardening and low-temperature creep. J. Eng. Mater. Technol. 1976, 98, 76–85. [Google Scholar] [CrossRef]
- Kumar, K.S.; Swygenhoven, H.V.; Suresh, S. Mechanical behavior of nanocrystalline metals and alloys. Acta Mater. 2003, 51, 5743–5774. [Google Scholar] [CrossRef]
- Frøseth, A.G.; Derlet, P.M.; Swygenhoven, H.V. Dislocations emitted from boundaries: Nucleation and splitting distance. Acta Mater. 2004, 52, 5863–5870. [Google Scholar] [CrossRef]
- Dao, M.; Lu, L.; Asaro, R.J.; De Hosson, J.T.M.; Ma, E. Toward a quantitative understanding of mechanical behavior of nanocrystalline metals. Acta Mater. 2007, 55, 4041–4065. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, F.; Wang, H.F.; Yang, W.; Yang, G.C.; Zhou, Y.H. A thermokinetic description for grain growth in nanocrystalline materials. Acta Mater. 2009, 57, 1466–1475. [Google Scholar] [CrossRef]
- Gong, M.M.; Liu, F.; Zhang, K. Thermodynamic stability of binary nanocrystalline alloys: Analysis of solute and excess vacancy. Appl. Phys. A 2011, 105, 927–934. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, F.; Yang, X.Q.; Shen, C.J. A thermokinetic description of nanoscale grain growth: Analysis of the activation energy effect. Acta Mater. 2012, 60, 4833–4844. [Google Scholar] [CrossRef]
- Darling, K.A.; Roberts, A.J.; Mishin, Y.; Mathaudhu, S.N.; Kecskes, L.J. Grain size stabilization of nanocrystalline copper at high temperatures by alloying with tantalum. J. Alloys Comp. 2013, 573, 142–150. [Google Scholar] [CrossRef]
- Chookajorn, T.J.; Murdoch, H.A.; Schuh, C.A. Design of stable nanocrystalline alloys. Science 2012, 337, 951–954. [Google Scholar] [CrossRef]
- Wise, G.J.; Miller, J.R.; Church, N.L.; Mignanelli, P.M.; Hardy, M.C.; Jones, N.G.; Stone, H.J. Microstructural stability and properties of new nickel-base superalloys with varying aluminium: Niobium ratio. Adv. Eng. Mater. 2023, 25, 2201669. [Google Scholar] [CrossRef]
- Millett, P.C.; Selvam, R.P.; Saxena, A. Stabilizing nanocrystalline materials with dopants. Acta Mater. 2007, 55, 2329–2336. [Google Scholar] [CrossRef]
- Cunningham, W.S.; Shin, J.; Lei, T.; Rupert, T.J.; Gianola, D.S. High-throughput assessment of the microstructural stability of segregation-engineered nanocrystalline Al-Ni-Y alloys. Materialia 2023, 31, 101940. [Google Scholar] [CrossRef]
- Derlet, P.M.; Hasnaoui, A.; Swygenhoven, H.V. Atomistic simulations as guidance to experiments. Scr. Mater. 2003, 49, 629–635. [Google Scholar] [CrossRef]
- Rupert, T.J. Strain localization in a nanocrystalline metal: Atomic mechanisms and the effect of testing conditions. J. Appl. Phys. 2013, 114, 033527. [Google Scholar] [CrossRef]
- Araki, S.; Mashima, K.; Masumura, T.; Tsuchiyama, T.; Takaki, S.; Ohmur, T. Effect of grain boundary segregation of carbon on critical grain boundary strength of ferritic steel. Scr. Mater. 2019, 169, 38–41. [Google Scholar] [CrossRef]
- Peng, H.R.; Huo, W.T.; Zhang, W.; Tang, Y.; Zhang, S.; Huang, L.K.; Hou, H.Y.; Ding, Z.G.; Liu, F. Correlation between stabilizing and strengthening effects due to grain boundary segregation in iron-based alloys: Theoretical models and first-principles calculations. Acta Mater. 2023, 251, 118899. [Google Scholar] [CrossRef]
- Heckman, N.M.; Barrios, A.; Barr, C.M.; Adams, D.P.; Furnish, T.A.; Hattar, K.; Boyce, B.L. Solute segregation improves the high-cycle fatigue resistance of nanocrystalline Pt-Au. Acta Mater. 2022, 229, 117794. [Google Scholar] [CrossRef]
- Zhou, Q.; Jiao, Z.; Huang, Z.; Shi, Y.; Li, Y.; Yin, C.; Wang, H.; Pinto, H.C.; Greiner, H.; Liu, W. Wear-resistant CrCoNi nanocrystalline film via friction-driven surface segregation. Acta Mater. 2024, 279, 120299. [Google Scholar] [CrossRef]
- Song, R.G.; Zhang, B.J.; Tseng, M.K. Role of grain boundary segregation in corrosion fatigue process of high strength aluminium alloy. Mater. Chem. Phys. 1996, 45, 84–87. [Google Scholar] [CrossRef]
- Watanabe, T. Grain boundary engineering: Historical perspective and future prospects. J. Mater. Sci. 2011, 46, 4095–4115. [Google Scholar] [CrossRef]
- Randle, V.; Owen, G. Mechanisms of grain boundary engineering. Acta Mater. 2006, 54, 1777–1783. [Google Scholar] [CrossRef]
- Schuh, C.A.; Kumar, M.; King, W.E. Analysis of grain boundary networks and their evolution during grain boundary engineering. Acta Mater. 2003, 51, 687–700. [Google Scholar] [CrossRef]
- Raabe, D.; Sandlöbes, S.; Millán, J.; Ponge, D.; Assadi, H.; Herbig, M.; Choi, P.P. Segregation engineering enables nanoscale martensite to austenite phase transformation at grain boundaries: A pathway to ductile martensite. Acta Mater. 2013, 61, 6132–6152. [Google Scholar] [CrossRef]
- Raabe, D.; Herbig, M.; Sandlöbes, S.; Li, Y.; Tytko, D.; Kuzmina, M.; Ponge, D.; Choi, P.P. Grain boundary segregation engineering in metallic alloys: A pathway to the design of interfaces. Curr. Opin. Solid State Mater. Sci. 2014, 18, 253–261. [Google Scholar] [CrossRef]
- Gibson, M.A.; Schuh, C.A. Segregation-induced changes in grain boundary cohesion and embrittlement in binary alloys. Acta Mater. 2015, 95, 145–155. [Google Scholar] [CrossRef]
- He, Y.; Song, S.; Du, J.; Peng, H.; Ding, Z.; Hou, H.; Huang, L.; Liu, Y.; Liu, F. Thermo-kinetic connectivity by integrating thermo-kinetic correlation and generalized stability. J. Mater. Sci. Technol. 2022, 127, 225–235. [Google Scholar] [CrossRef]
- Devaraj, A.; Wang, W.; Vemuri, R.; Kovarik, L.; Jiang, X.; Bowden, M.; Trelewicz, J.R.; Mathaudhu, S.; Rohatgi, A. Grain boundary segregation and intermetallic precipitation in coarsening resistant nanocrystalline aluminum alloys. Acta Mater. 2019, 165, 698–708. [Google Scholar] [CrossRef]
- Popov, I.; Moshkovich, A.; Cohen, S.R.; Perfilyev, V.; Vakahy, A.; Rapoport, L. Microstructure and nanohardness of Ag and Ni under friction in boundary lubrication. Wear 2018, 404–405, 62–70. [Google Scholar] [CrossRef]
- Moshkovich, A.; Rapoport, L.S. The effect of the structural parameters on the friction and wear properties of some FCC metals. J. Mater. Res. Technol. 2023, 24, 3913–3924. [Google Scholar] [CrossRef]
- Murr, L.E. Interfacial Phenomena in Metals and Alloys; Addison-Wesley: Reading, MA, USA, 1975. [Google Scholar] [CrossRef]
- Gallagher, P.C.J. The influence of alloying, temperature and related effects on the stacking fault energy. Metall. Trans. 1970, 1, 2429–2461. [Google Scholar] [CrossRef]
- Conrad, H.; Jung, K. Effect of grain size from millimeters to nanometers on the flow stress and deformation kinetics of Ag. Mater. Sci. Eng. A 2005, 391, 272–284. [Google Scholar] [CrossRef]
- Estrin, Y.; Kubin, L.P. Plastic instabilities: Phenomenology and theory. Mater. Sci. Eng. A 1991, 137, 125–134. [Google Scholar] [CrossRef]
- Sinclair, W.; Poole, W.J.; Bréchet, Y. A model for the grain size dependent work hardening of copper. Scr. Mater. 2006, 55, 739–742. [Google Scholar] [CrossRef]
- Hong, C.S.; Tao, N.R.; Lua, K.; Huang, X. Grain orientation dependence of deformation twinning in pure Cu subjected to dynamic plastic deformation. Scr. Mater. 2009, 61, 289–292. [Google Scholar] [CrossRef]
- Bouaziz, O.; Allain, S.; Scott, C. Effect of grain and twin boundaries on the hardening mechanisms of twinning-induced plasticity steels. Scr. Mater. 2008, 58, 484–487. [Google Scholar] [CrossRef]
- Steinmetz, D.R.; Jäpel, T.; Wietbrock, B.; Eisenlohr, P.; Gutierrez-Urrutia, I.; Saeed-Akbari, A.; Hickel, T.; Roters, F.; Raabe, D. Revealing the strain-hardening behavior of twinning-induced plasticity steels: Theory, simulations, experiments. Acta Mater. 2013, 61, 494–510. [Google Scholar] [CrossRef]
- Foley, D.L.; Huang, S.H.; Anber, E.; Shanahan, L.; Shen, Y.; Lang, A.C.; Barr, C.M.; Spearot, D.; Lamberson, L.; Taheri, M.L. Simultaneous twinning and microband formation under dynamic compression in a high entropy alloy with a complex energetic landscape. Acta Mater. 2020, 200, 1–11. [Google Scholar] [CrossRef]
- Pan, X.; Xin, S.; Sun, J.; Zhang, S.; Zhou, W.; Cai, J. Achieving improved dynamic mechanical properties in twinning-dominated titanium alloys. Mater. Sci. Eng. A 2025, 920, 147570. [Google Scholar] [CrossRef]
- Shute, C.J.; Meyers, B.D.; Xie, S.; Barbee, T.W., Jr.; Hodge, A.M.; Weertman, J.R. Microstructural stability during cyclic loading of multilayer copper/copper samples with nanoscale twinning. Scr. Mater. 2009, 60, 1073–1077. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Liao, X.Z.; Wu, X.L. Deformation twinning in nanocrystalline materials. Prog. Mater. Sci. 2012, 57, 1–62. [Google Scholar] [CrossRef]
- Duong, T.; Dingreville, R.; Demkowicz, M.J. Mobility of twinning dislocations in copper up to supersonic speeds. Acta Mater. 2024, 275, 120050. [Google Scholar] [CrossRef]
- Zhu, Y.T.; Liao, X.Z.; Wu, X.L.; Narayan, J. Grain size effect on deformation twinning and detwinning. J. Mater. Sci. 2013, 48, 4467–4475. [Google Scholar] [CrossRef]
- Humphreys, F.J.; Hatherly, M. Recrystallization and Related Annealing Phenomena, 2nd ed.; Pergamon: Oxford, UK, 2004. [Google Scholar] [CrossRef]
- Zhang, W.; He, L.; Lu, Z.; Kennedy, G.B.; Thadhani, N.N.; Li, P. Microstructural characteristics and formation mechanism of adiabatic shear bands in Al–Zn–Mg–Cu alloy under dynamic shear loading. Mater. Sci. Eng. A 2020, 791, 139430. [Google Scholar] [CrossRef]
- He, J.; Yang, Y. Quantitative investigation on deformation mechanism and dynamic recrystallization during localized adiabatic shearing of single crystal copper. Mater. Sci. Eng. A 2023, 869, 144814. [Google Scholar] [CrossRef]
- Wang, M.; Sun, C.; Fu, M.W.; Liu, Z.; Wang, C. Experimental investigations and constitutive modeling of the dynamic recrystallization behavior of Inconel 740 superalloy. Mater. Sci. Eng. A 2020, 793, 139939. [Google Scholar] [CrossRef]
- Wei, Q.; Kecskes, L.; Jiao, T.; Hartwig, K.T.; Ramesh, K.T.; Ma, E. Adiabatic shear banding in ultrafine-grained Fe processed by severe plastic deformation. Acta Mater. 2004, 52, 1859–1869. [Google Scholar] [CrossRef]
- Chen, S.; Feng, B.; Wei, Y.; Wang, T. Prediction of the initial thickness of shear band localization based on a reduced strain gradient theory. Int. J. Solids Struct. 2011, 48, 3099–3111. [Google Scholar] [CrossRef][Green Version]
- Rittel, D.; Wang, Z.G.; Merzer, M. Adiabatic shear failure and dynamic stored energy of cold work. Phys. Rev. Lett. 2006, 96, 075502. [Google Scholar] [CrossRef] [PubMed]
- Osovski, S.; Rittel, D.; Landau, P.; Venkert, A. Microstructural effects on adiabatic shear band formation. Scr. Mater. 2012, 66, 9–12. [Google Scholar] [CrossRef]
- Rittel, D.; Wang, Z.G. Thermo-mechanical aspects of adiabatic shear failure of AM50 and Ti6Al4V alloys. Mech. Mater. 2008, 40, 629–635. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Huang, C.; Suo, T.; Wei, Q. On adiabatic shear localization in nanostructured face-centered cubic alloys with different stacking fault energies. Acta Mater. 2017, 141, 163–182. [Google Scholar] [CrossRef]
- Lu, X.C.; Zhao, J.F.; Wang, Z.W.; Gan, B.; Zhao, J.W.; Kang, G.Z.; Zhang, X. Crystal plasticity finite element analysis of gradient nanostructured TWIP steel. Int. J. Plast. 2020, 130, 102703. [Google Scholar] [CrossRef]
- Cai, W.; Sun, C.Y.; Wang, C.H.; Qian, L.Y.; Li, Y.M.; Fu, M.W. Modelling of the intergranular fracture of TWIP steels working at high temperature by using CZM-CPFE method. Int. J. Plast. 2022, 156, 103366. [Google Scholar] [CrossRef]
- Guo, X.; Mao, N.; Kong, T.; Zhang, J.; Shen, J.; Wang, C.; Sun, C.; Li, P.; Xiong, Z. Strain rate-dependent plastic behavior of TWIP steel investigated by crystal plasticity model. Mater. Sci. Eng. A 2024, 891, 145986. [Google Scholar] [CrossRef]
- Taylor, G.I. The mechanism of plastic deformation of crystals. Part I.—Theoretical. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1934, 145, 362–387. [Google Scholar] [CrossRef]
- Meyers, M.A.; Mishra, A.; Benson, D.J. Mechanical properties of nanocrystalline materials. Prog. Mater. Sci. 2006, 51, 427–556. [Google Scholar] [CrossRef]
- Sauzay, M. Analytical modelling of intragranular backstresses due to deformation induced dislocation microstructures. Int. J. Plast. 2008, 24, 727–745. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, M.; Ma, X.; Wang, M.; Yin, K.; Huang, A.; Huang, C. Improved back stress and synergetic strain hardening in coarse-grain/nanostructure laminates. Mater. Sci. Eng. A 2018, 727, 113–118. [Google Scholar] [CrossRef]
- Lee, M.G.; Lim, H.; Adams, B.L.; Hirth, J.P.; Wagoner, R.H. A dislocation density-based single crystal constitutive equation. Int. J. Plast. 2010, 26, 925–938. [Google Scholar] [CrossRef]
- Youngdahl, C.J.; Sanders, P.G.; Eastman, J.A.; Weertman, J.R. Compressive yield strengths of nanocrystalline Cu and Pd. Scr. Mater. 1997, 37, 809–813. [Google Scholar] [CrossRef]
- Jones, R.M. Deformation Theory of Plasticity; Bull Ridge Corporation: Blacksburg, VA, USA, 2009; 622p. [Google Scholar]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Prog. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Mecking, H.; Kocks, U.F. Kinetics of flow and strain-hardening. Acta Metall. 1981, 29, 1865–1875. [Google Scholar] [CrossRef]
- Estrin, Y.; Mecking, H. A unified phenomenological description of work hardening and creep based on one-parameter models. Acta Metall. 1984, 32, 57–70. [Google Scholar] [CrossRef]
- Li, Y.L.; Wu, W.P.; Sopu, D.; Eckert, J. Effects of void shape and location on the fracture and plastic deformation of Cu (crystalline)/Cu64Zr36 (amorphous) composites. J. Mater. Res. Technol. 2023, 24, 4177–4189. [Google Scholar] [CrossRef]
- Gerstein, G.; Besserer, H.B.; Nürnberger, F.; Barrales-Mora, L.A.; Shvindlerman, L.S. Formation and growth of voids in dual-phase steel at microscale and nanoscale levels. J. Mater. Sci. 2017, 52, 4234–4243. [Google Scholar] [CrossRef]
- Kováčik, J. Correlation between Young’s modulus and porosity in porous materials. J. Mater. Sci. Lett. 1999, 18, 1007–1010. [Google Scholar] [CrossRef]
- Choren, J.A.; Heinrich, S.M.; Silver-Thorn, B. Young’s modulus and volume porosity relationships for additive manufacturing applications. J. Mater. Sci. 2013, 48, 5103–5112. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, Y.T.; Liu, Y.X.; Feng, S.P.; Huang, M.X. Thermal instability of nanocrystalline Cu enables Cu-Cu direct bonding in interconnects at low temperature. Scr. Mater. 2022, 220, 114900. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, J.; Wang, L.; Wang, Y.; Dong, S. Effect of twin boundaries on nanovoid growth based on dislocation emission. Mater. Sci. Eng. A 2013, 582, 29–35. [Google Scholar] [CrossRef]
- Zhevnenko, S.N.; Petrov, I.S.; Scheiber, D.; Razumovskiy, V.I. Surface and segregation energies of Ag based alloys with Ni, Co and Fe: Direct experimental measurement and DFT study. Acta Mater. 2021, 205, 116565. [Google Scholar] [CrossRef]
- Yang, P.; Zhao, P. Void nucleation at dislocation boundaries aided by the synergy of multiple dislocation pile-ups. Int. J. Plast. 2023, 171, 103779. [Google Scholar] [CrossRef]
- Najafahadi, R.; Wang, H.Y.; Srolovitz, D.J.; LeSar, R. The Effects of segregation on grain boundary cohesive energies in Ni3-xAI1+x. Scr. Metall. Mater. 1991, 25, 2497–2502. [Google Scholar] [CrossRef]
- Lee, B.J.; Choi, S.H. Computation of grain boundary energies. Model. Simul. Mater. 2004, 12, 621–632. [Google Scholar] [CrossRef]
- Detor, A.J.; Schuh, C.A. Grain boundary segregation, chemical ordering and stability of nanocrystalline alloys: Atomistic computer simulations in the Ni–W system. Acta Mater. 2007, 55, 4221–4232. [Google Scholar] [CrossRef]
- Qi, Y.; Bruckel, P.; Lours, P. Interfacial toughness of the nickel-nickel oxide system. J. Mater. Sci. Lett. 2003, 22, 371–374. [Google Scholar] [CrossRef]
- Xiao, Z.; Bai, X.M. First-principle studies of oxidation effects on grain boundary strength in nickel. Materialia 2023, 28, 101745. [Google Scholar] [CrossRef]
- Lejček, P.; Šob, M. Entropy: A controversy between experiment and calculations in grain boundary segregation. Prog. Mater. Sci. 2025, 151, 101431. [Google Scholar] [CrossRef]
- Lejček, P.; Šob, M.; Paidar, V.; Vitek, V. Why calculated energies of grain boundary segregation are unreliable when segregant solubility is low. Scr. Mater. 2013, 68, 547–550. [Google Scholar] [CrossRef]
- Gottstein, G.; Shvindlerman, L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2009; 711p. [Google Scholar] [CrossRef]
- Murdoch, H.A.; Schuh, C.A. Stability of binary nanocrystalline alloys against grain growth and phase separation. Acta Mater. 2013, 61, 2121–2132. [Google Scholar] [CrossRef]
- Liu, F.; Kirchheim, R. Grain boundary saturation and grain growth. Scr. Mater. 2004, 51, 521–525. [Google Scholar] [CrossRef]










| Material | Load FN, N | COF | Hi, GPa | Hf, GPa | γSF, mJm−2 [88,89] | d, nm (XRD) | T/Tm | G, GPa |
|---|---|---|---|---|---|---|---|---|
| Ag | 220 ± 20 | 0.10 ± 0.02 | 0.27 ± 0.01 | 0.78 ± 0.12 | 16 | 33 ± 3 | 0.26 | 30 |
| Ni | 1820 ± 200 | 0.08 ± 0.01 | 0.78 ± 0.03 | 2.60 ± 0.25 | 125 | 160 ± 5 | 0.31 | 75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moshkovich, A.; Popov, I.; Remennik, S.; Rapoport, L.S. Microstructural Stability and Transition to Unstable Friction for FCC Metals: Ag and Ni. Materials 2025, 18, 4123. https://doi.org/10.3390/ma18174123
Moshkovich A, Popov I, Remennik S, Rapoport LS. Microstructural Stability and Transition to Unstable Friction for FCC Metals: Ag and Ni. Materials. 2025; 18(17):4123. https://doi.org/10.3390/ma18174123
Chicago/Turabian StyleMoshkovich, Alexey, Inna Popov, Sergei Remennik, and Lev S. Rapoport. 2025. "Microstructural Stability and Transition to Unstable Friction for FCC Metals: Ag and Ni" Materials 18, no. 17: 4123. https://doi.org/10.3390/ma18174123
APA StyleMoshkovich, A., Popov, I., Remennik, S., & Rapoport, L. S. (2025). Microstructural Stability and Transition to Unstable Friction for FCC Metals: Ag and Ni. Materials, 18(17), 4123. https://doi.org/10.3390/ma18174123







