Multiscale Mechanical Responses of the Racetrack NbTi Superconducting Coil Under Dynamic Pressures
Abstract
1. Introduction
2. The Model and Methodology of Multiscale Analysis
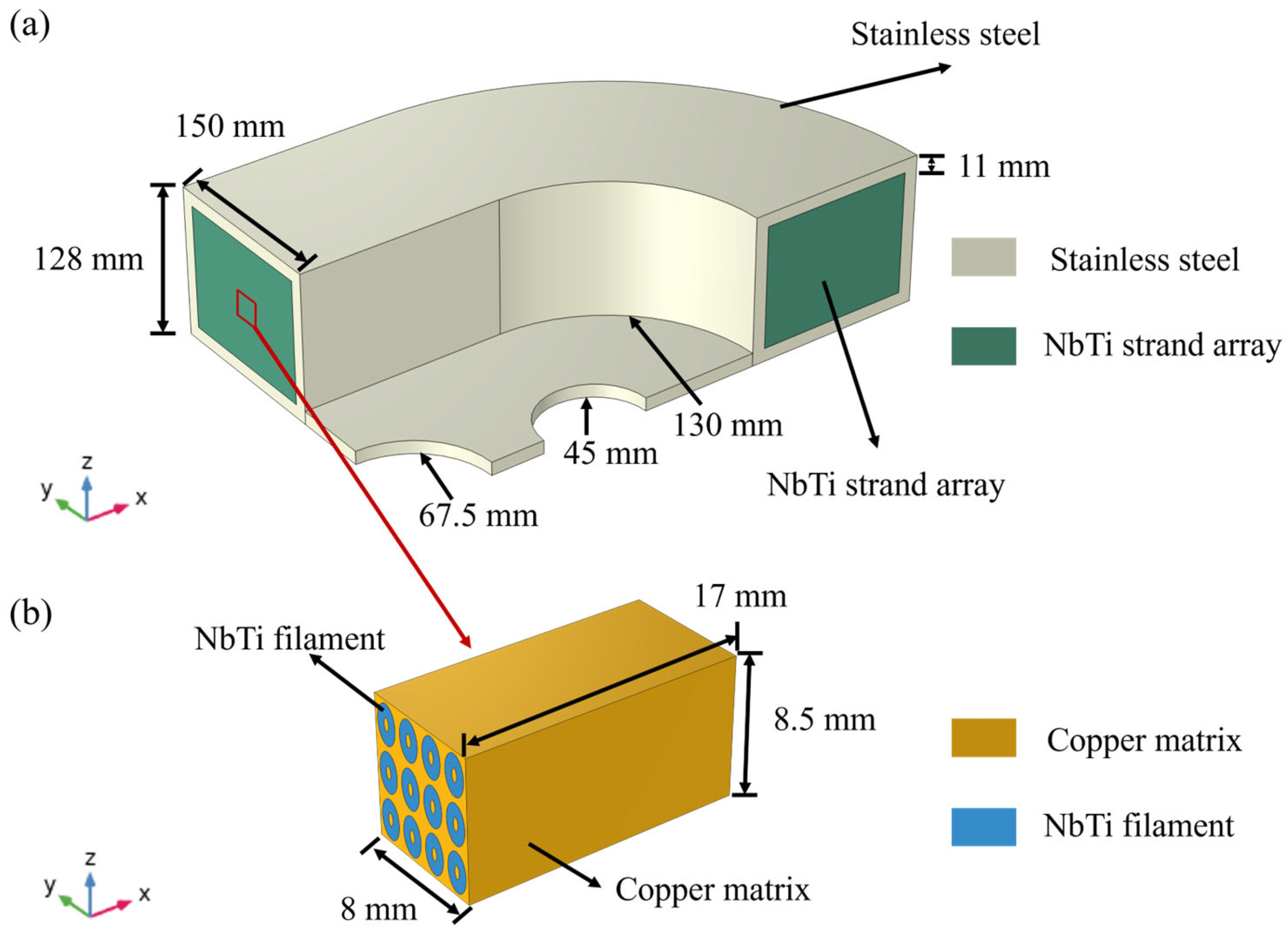
2.1. The Multiscale Geometry Model of the Racetrack NbTi Superconducting Coil
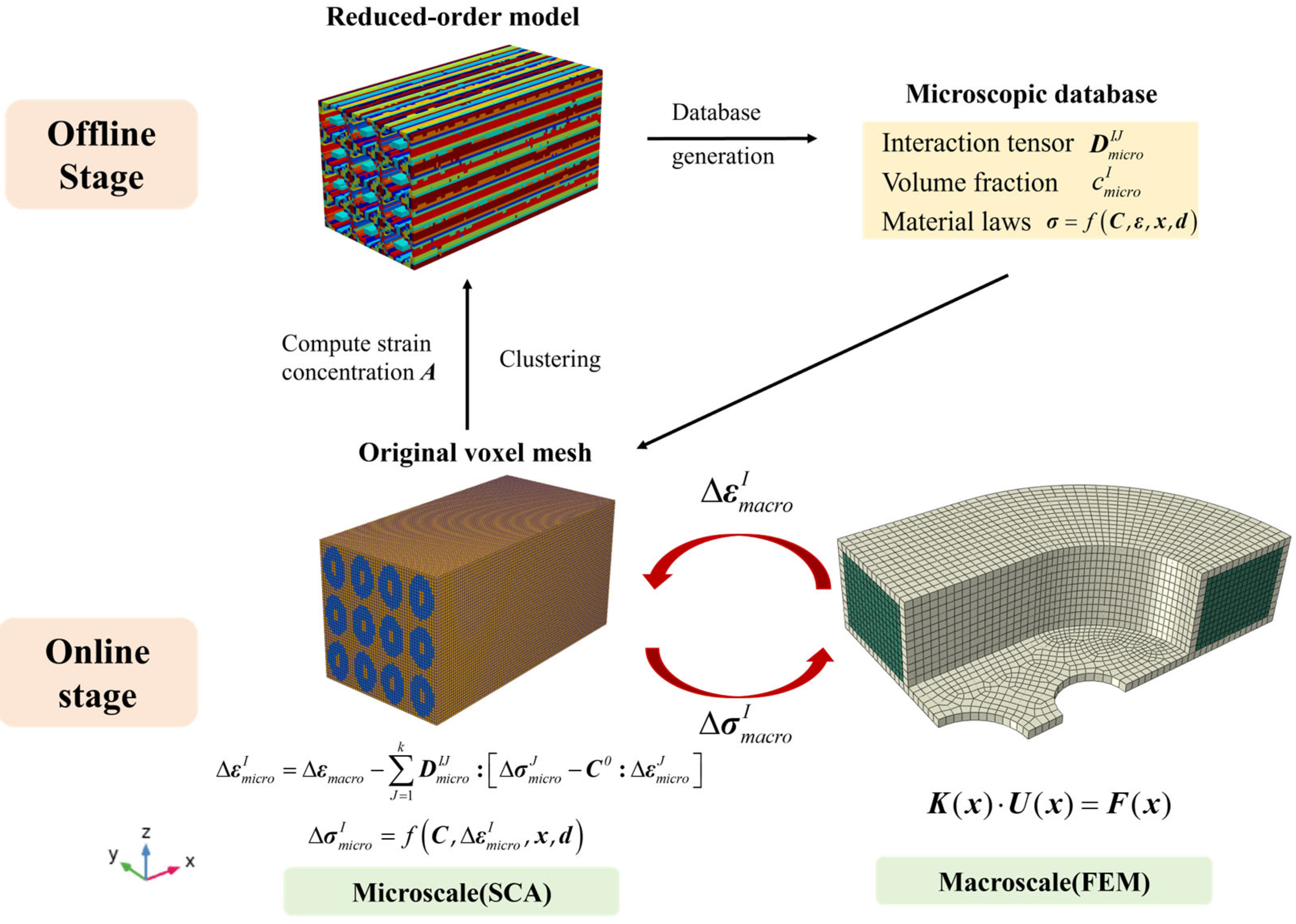
2.2. The Self-Consistent Analysis for the Microscale Model
2.3. The Multiscale Analysis Based on Self-Consistent Analysis
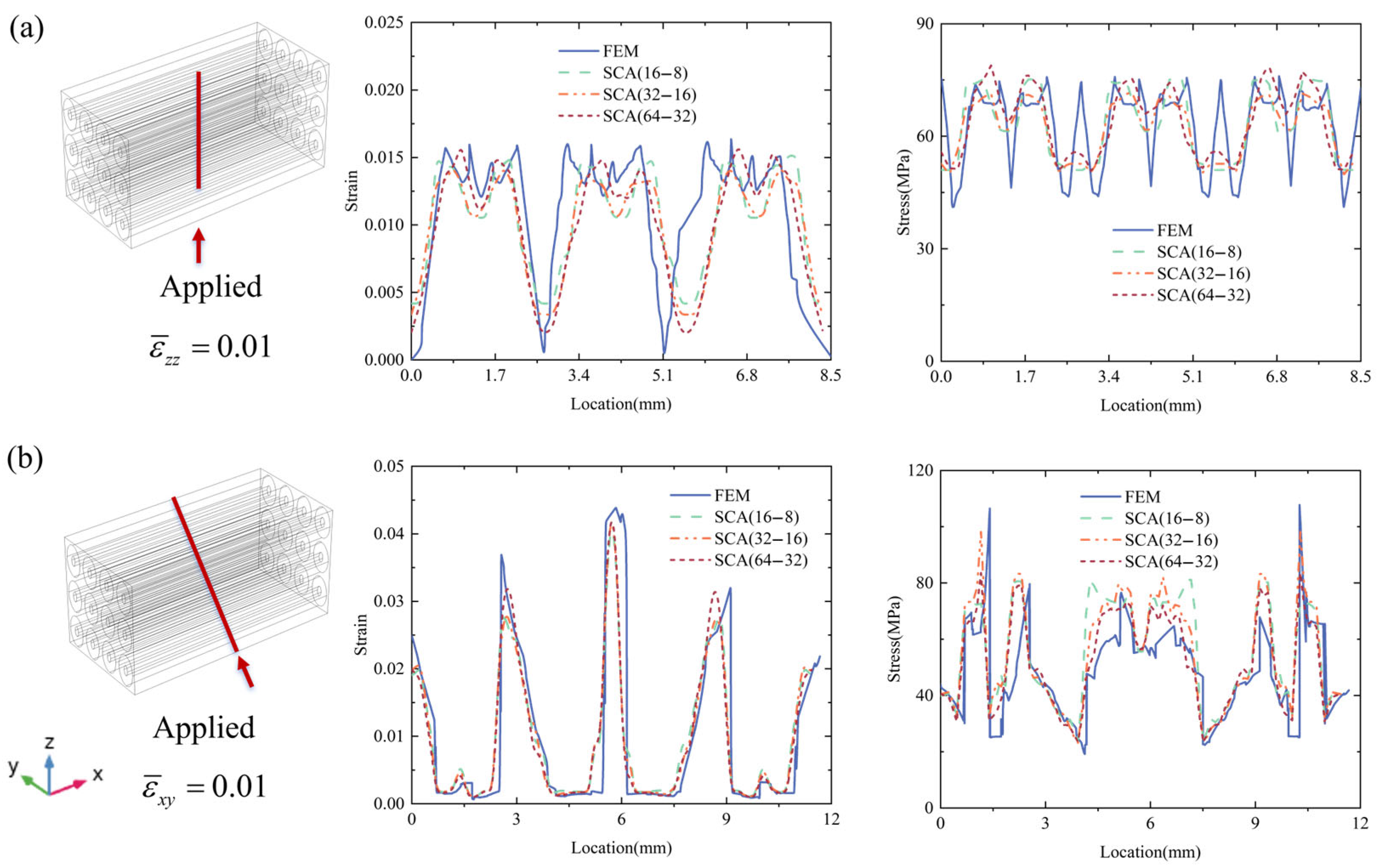
3. Numerical Validation of the Microscale Model
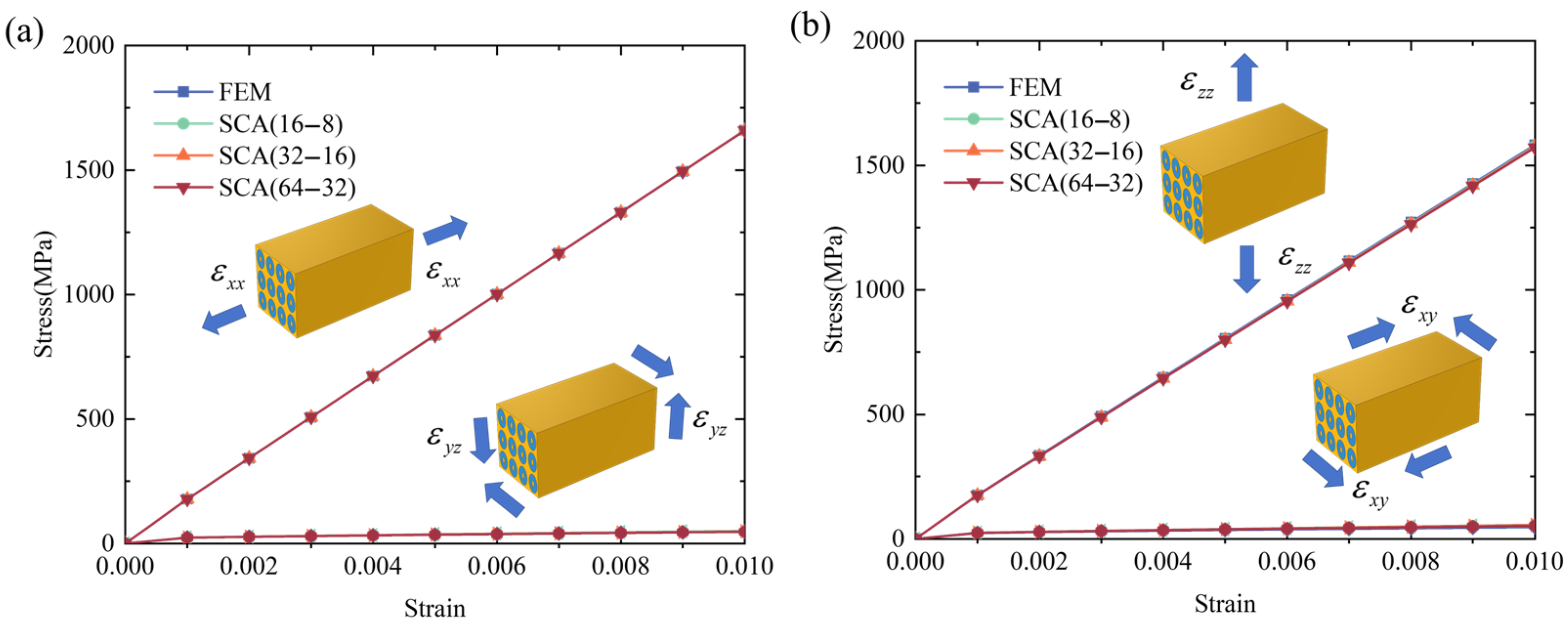
3.1. The Overall Responses Comparisons
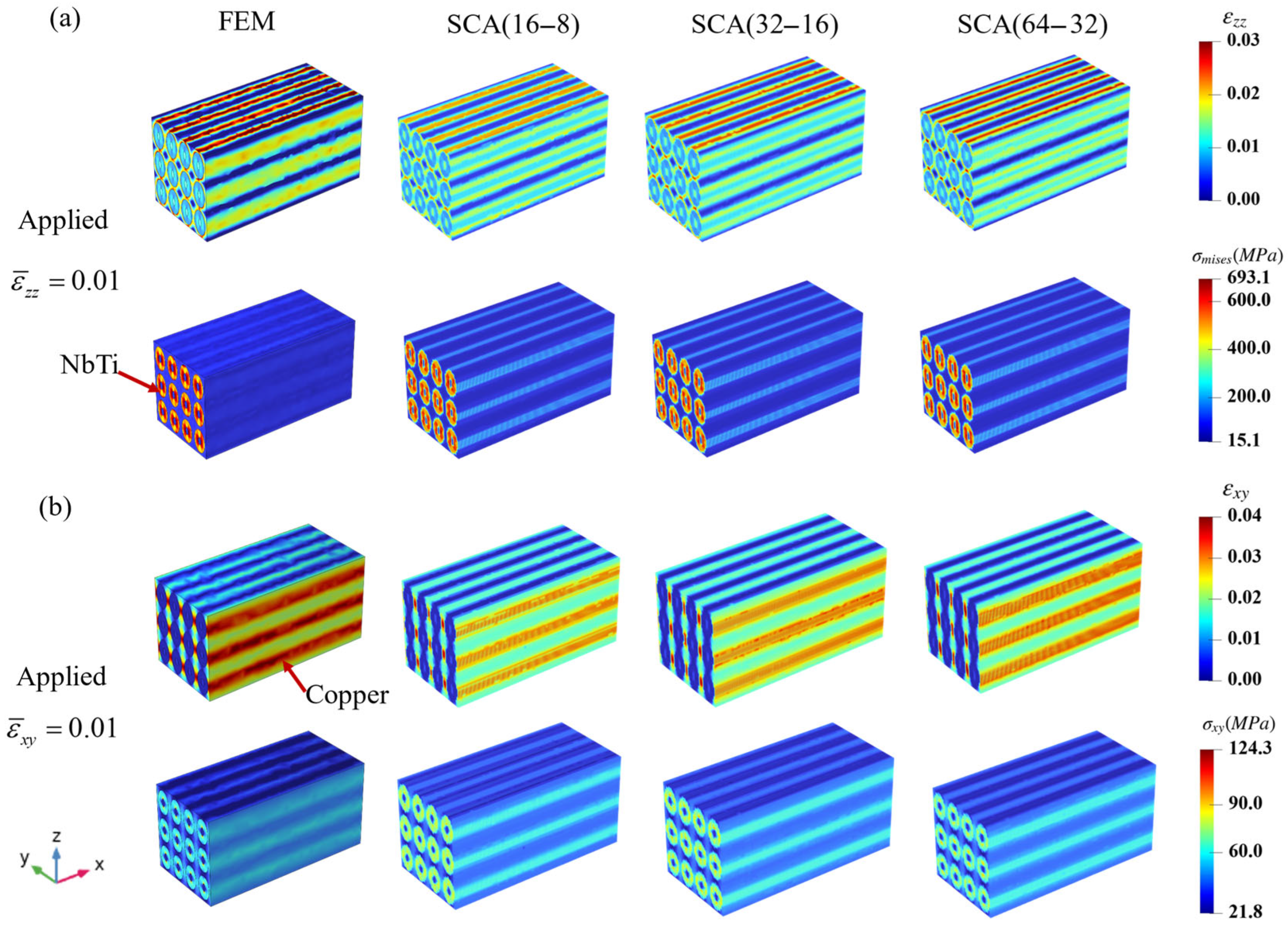
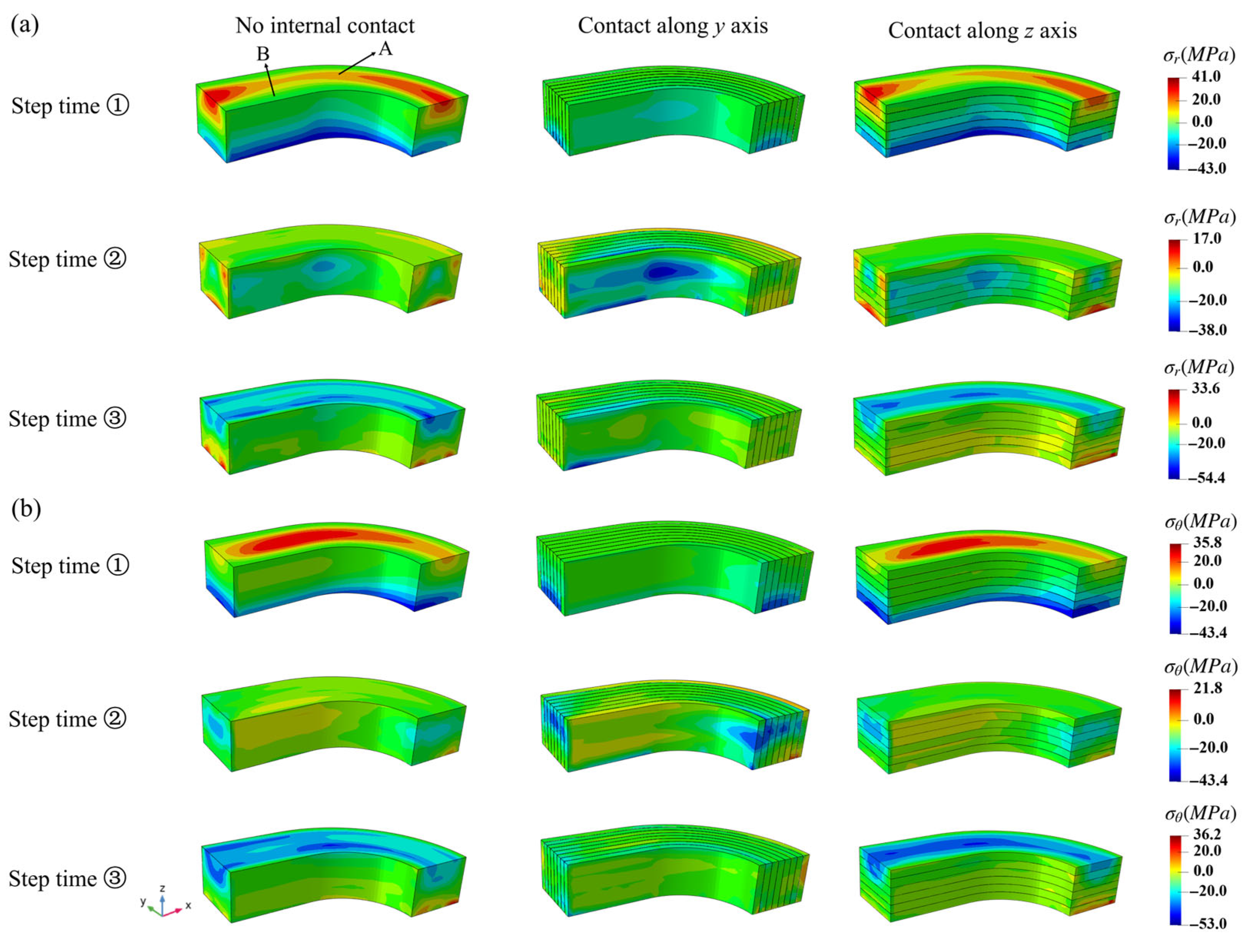
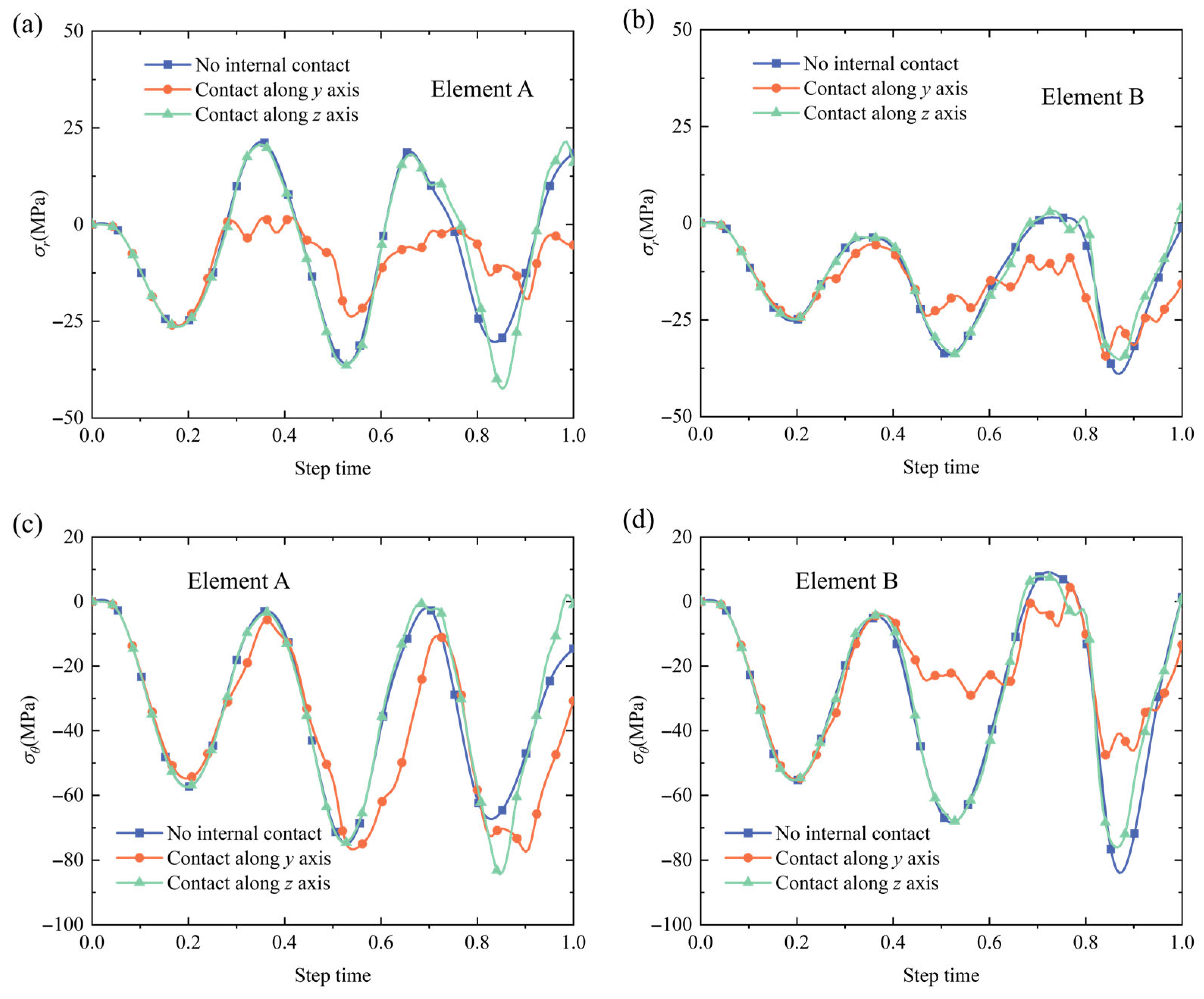
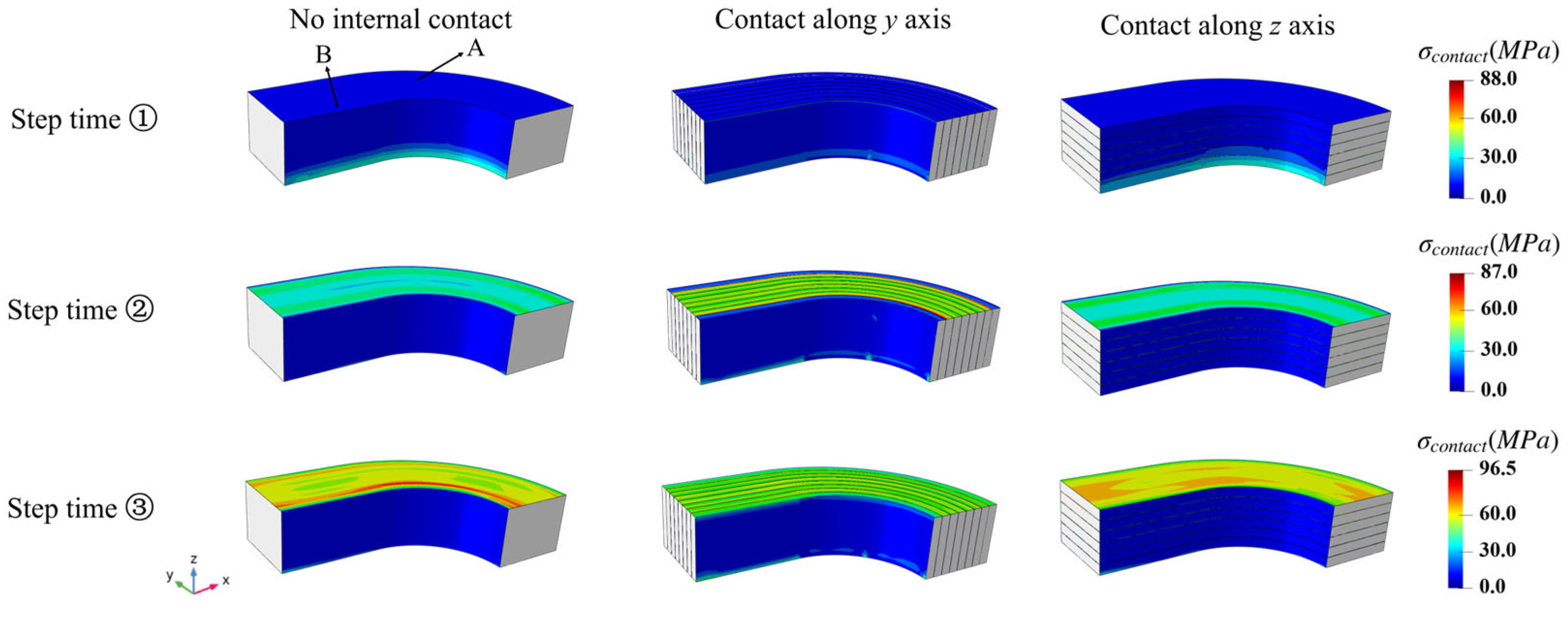
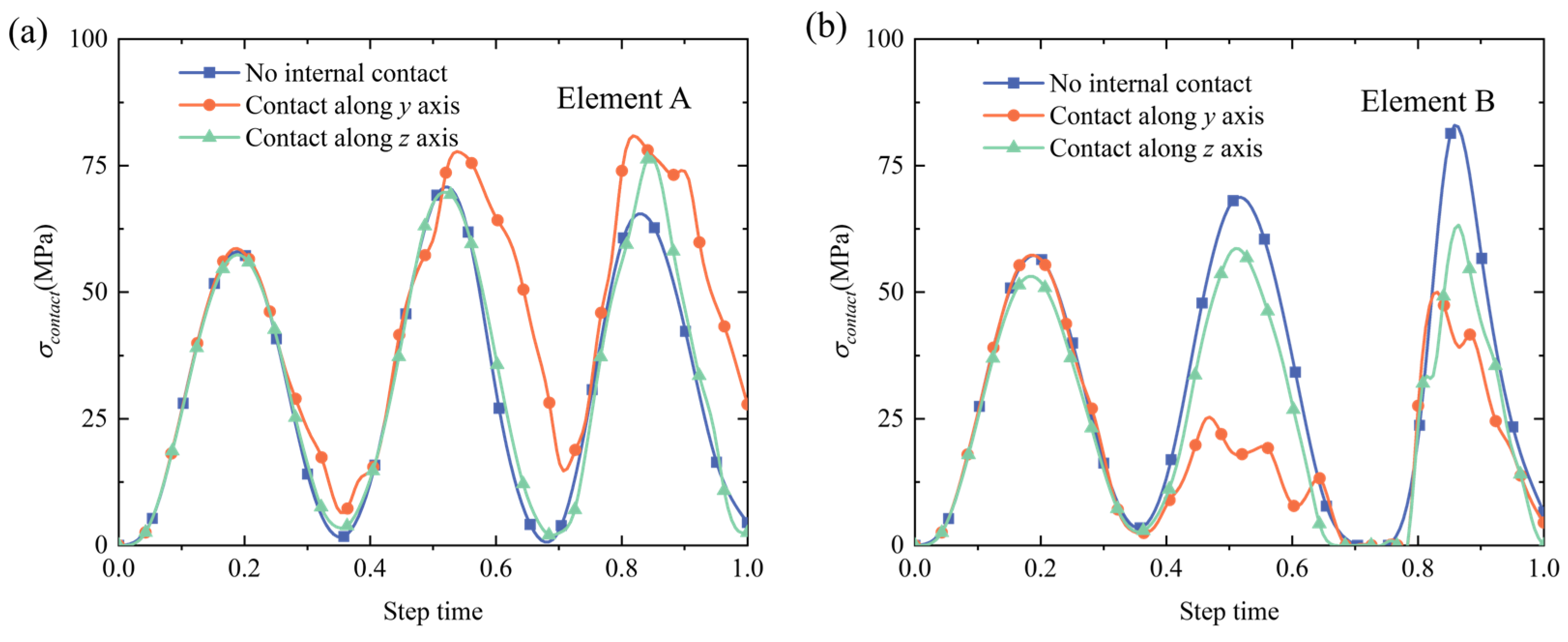
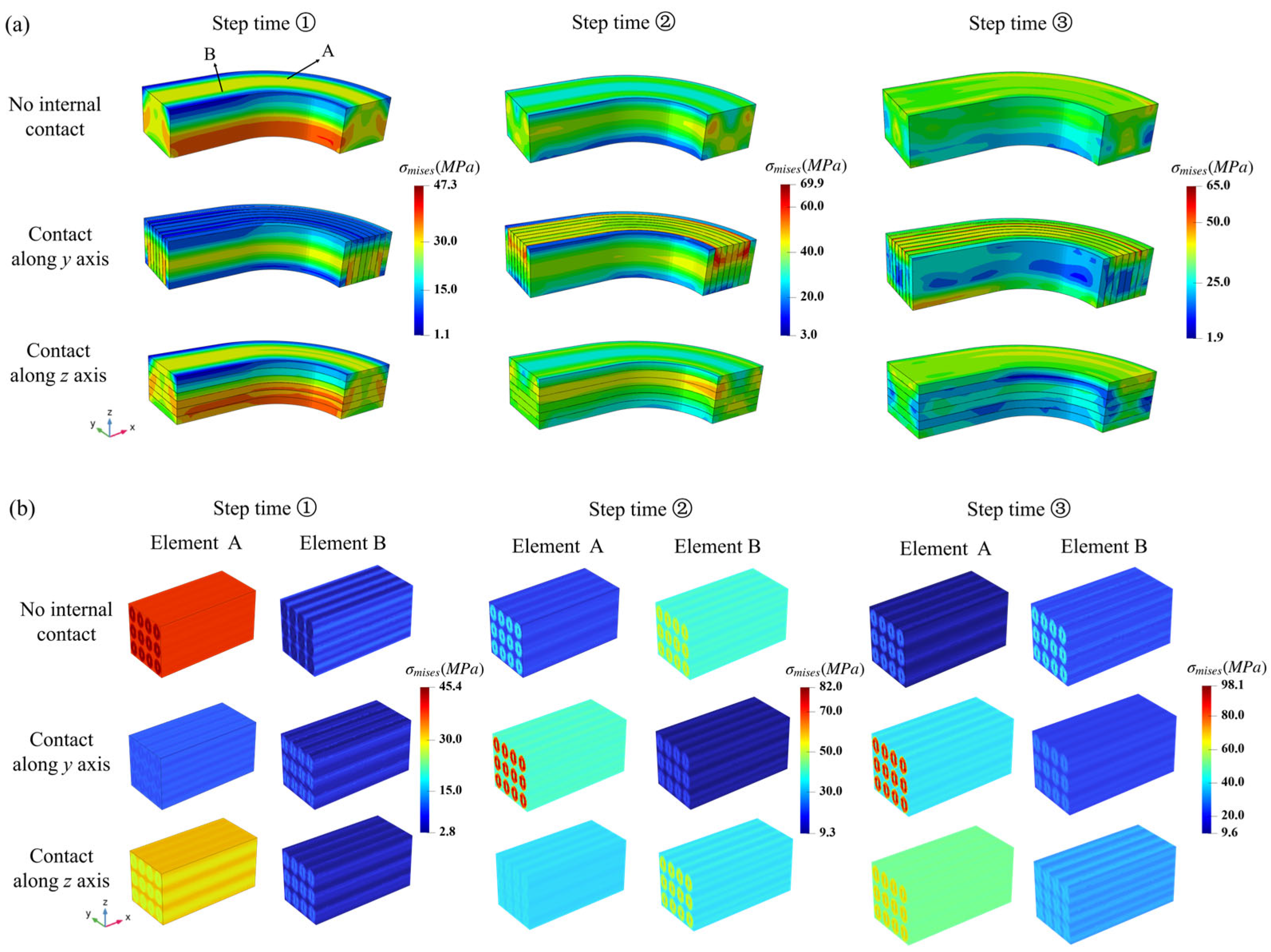
3.2. The Local Response Comparisons
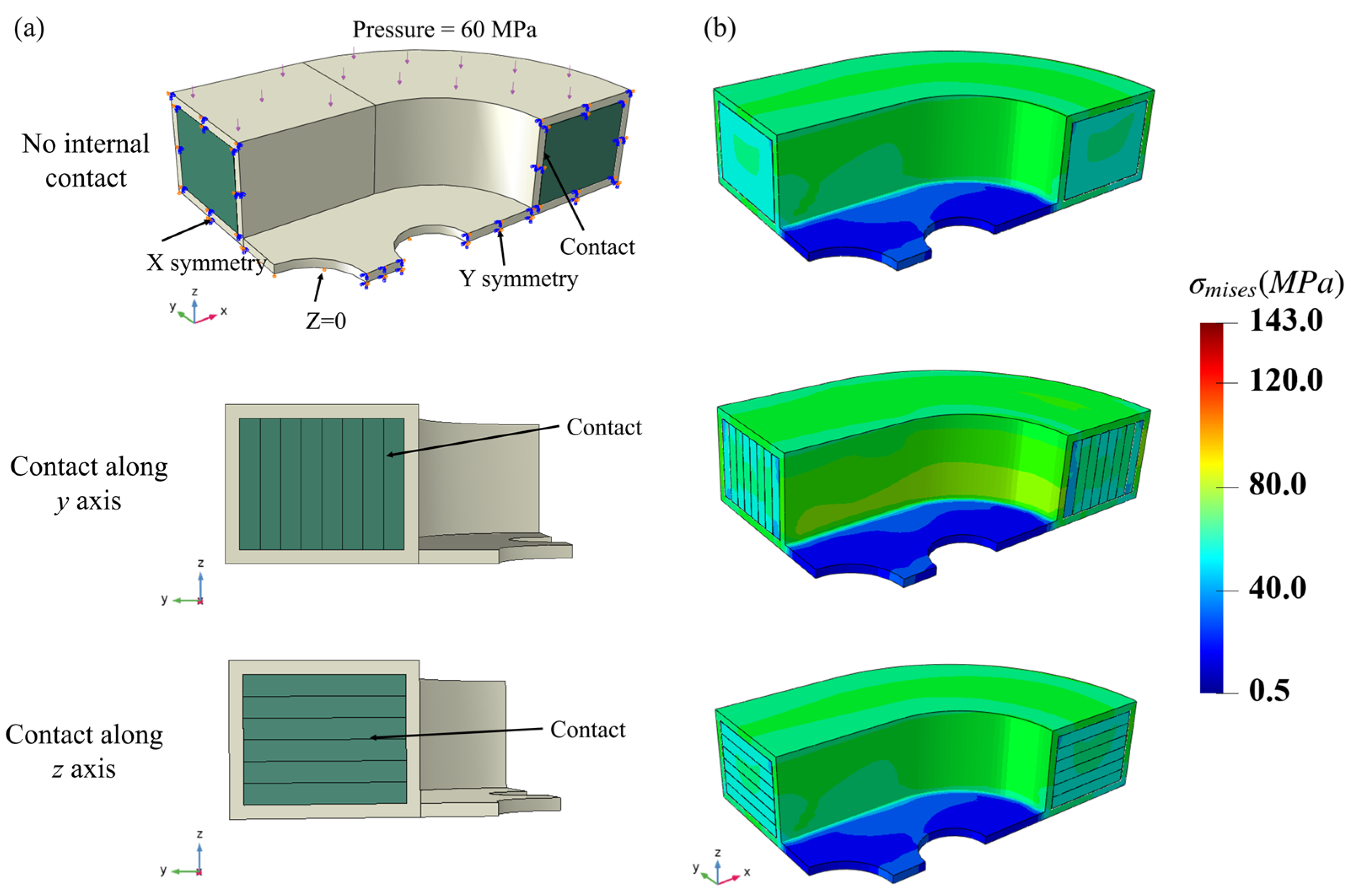
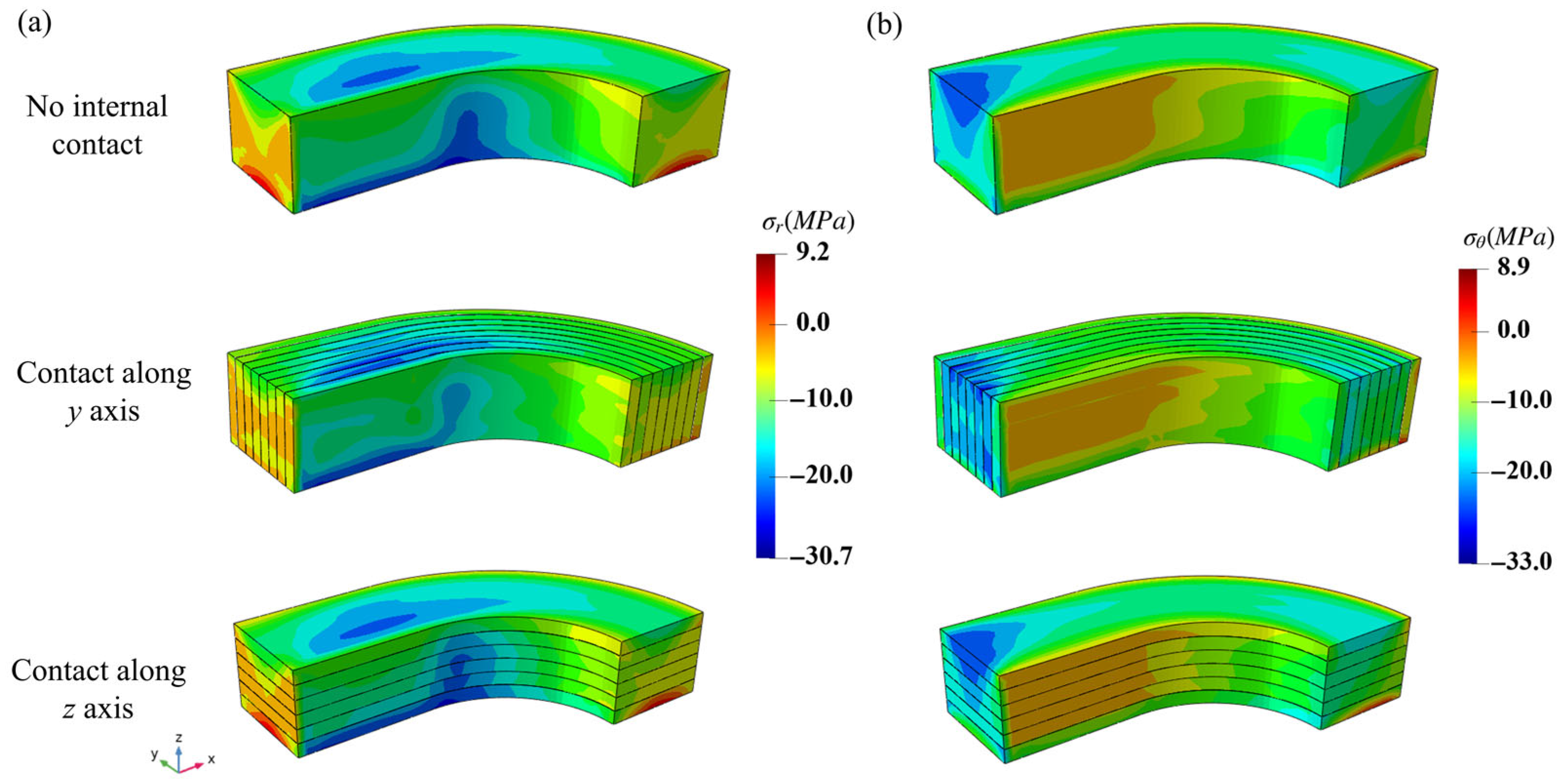
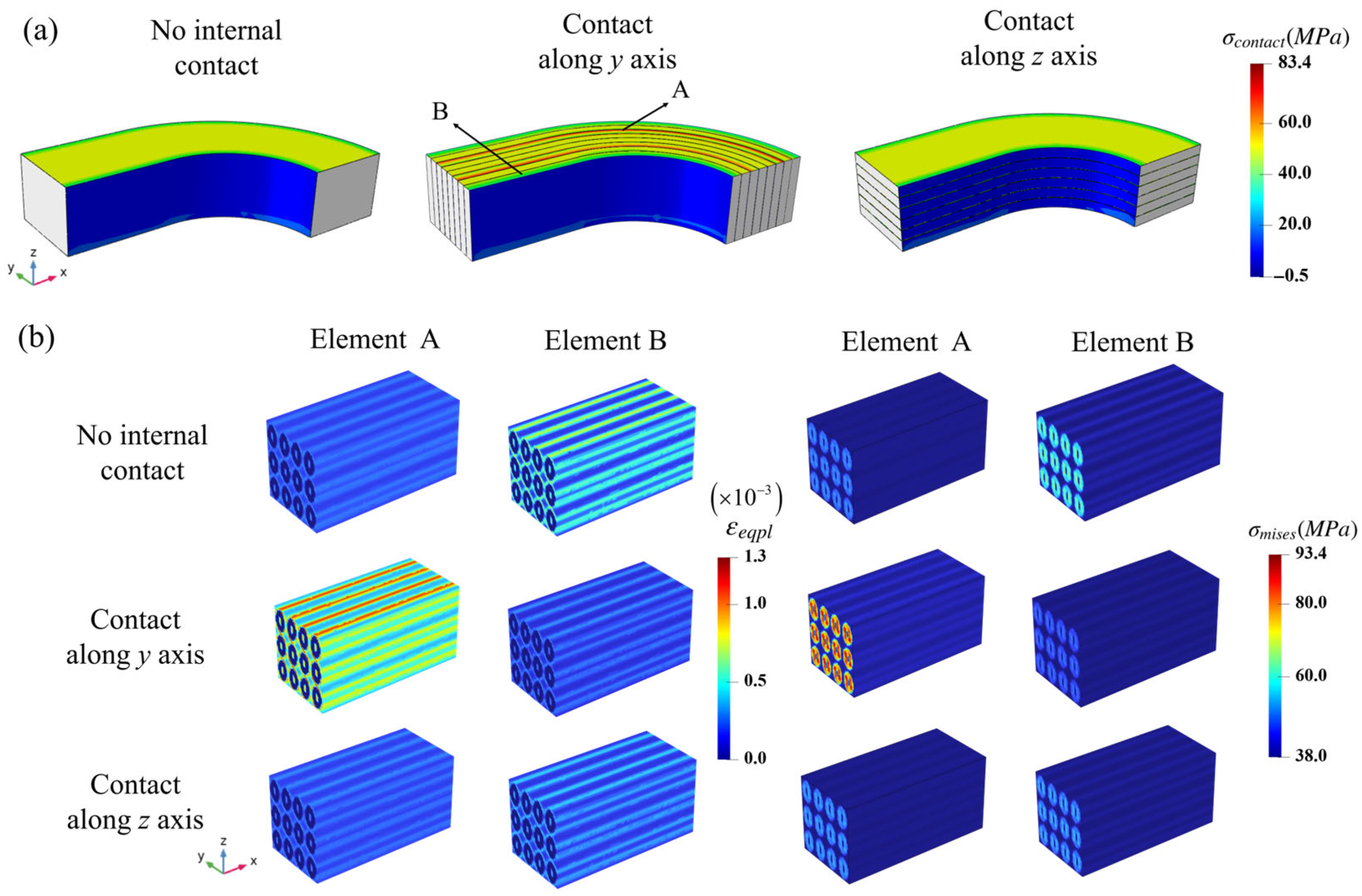
4. Two-Scale Analysis for the Racetrack NbTi Superconducting Coil
4.1. The Two-Scale Analysis Under Monotone Increasing Pressure
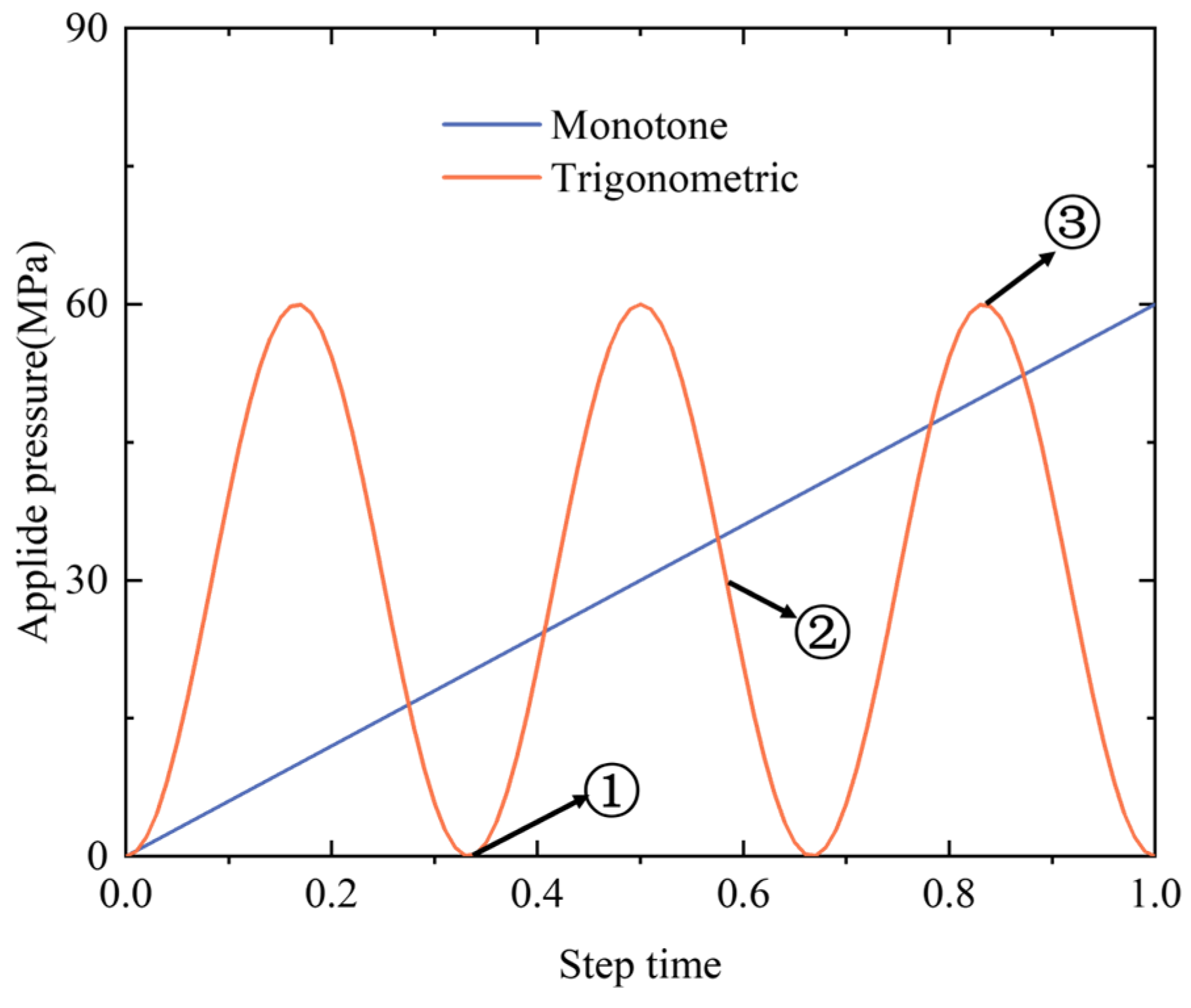
4.2. The Two-Scale Analysis Under Periodic Pressure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| strain concentration tensor | |
| body force | |
| homogeneous reference stiffness | |
| algorithm stiffness tensor of the Ith cluster domain | |
| averaged effective tangential stiffness | |
| volume fraction of the Ith cluster domain | |
| cluster-wise interaction tensors | |
| E | Young’s modulus |
| local displacement | |
| the prescribed displacements on the boundaries | |
| the prescribed traction forces on the boundaries | |
| Green’s function | |
| applied macroscopic incremental strain | |
| incremental strain of the Ith cluster domain | |
| incremental stress of the Ith cluster domain | |
| local total strain | |
| local strain in the offline stage | |
| macroscopic strain in the offline stage | |
| Poisson’s ratio | |
| local stress | |
| yield stress | |
| characteristic function |
Abbreviations
| DOF | Degree of freedom |
| FEM | Finite element method |
| FFT | Fast Fourier transform |
| L–S | Lippmann–Schwinger |
| RVE | Representative volume element |
| SCA | Self-consistent clustering analysis |
References
- Guan, M.; Wang, X.; Zhou, Y. Effects of cold-treatment and strain-rate on mechanical properties of NbTi/Cu superconducting composite wires. SpringerPlus 2015, 4, 81. [Google Scholar] [CrossRef]
- Zheng, J.; Zou, C.; Liu, X.; Dong, Y.; Zhu, L.; Ni, X.; Yu, X. Development of high current density, compactness NbTi superconducting coil for the maglev system. IEEE Trans. Appl. Supercond. 2022, 33, 4900205. [Google Scholar] [CrossRef]
- Flükiger, R. Overview of superconductivity and challenges in applications. Rev. Accel. Sci. Technol. 2012, 5, 1–23. [Google Scholar] [CrossRef]
- Parizh, M.; Lvovsky, Y.; Sumption, M. Conductors for commercial MRI magnets beyond NbTi: Requirements and challenges. Supercond. Sci. Technol. 2016, 30, 014007. [Google Scholar] [CrossRef] [PubMed]
- Wilson, M.N. NbTi superconductors with low ac loss: A review. Cryogenics 2008, 48, 381–395. [Google Scholar] [CrossRef]
- Hong, Z.; Yuan, W.; Ainslie, M.; Yan, Y.; Pei, R.; Coombs, T. AC losses of superconducting racetrack coil in various magnetic conditions. IEEE Trans. Appl. Supercond. 2010, 21, 2466–2469. [Google Scholar] [CrossRef]
- Han, S.; Zhang, J.; Xiong, X.; Ji, P.; Zhang, L.; Sheridan, J.; Gao, G. Influence of high-speed maglev train speed on tunnel aerodynamic effects. Build. Environ. 2022, 223, 109460. [Google Scholar] [CrossRef]
- Yonezu, T.; Watanabe, K.; Suzuki, E.; Sasakawa, T. Study on electromagnetic force characteristics acting on levitation/guidance coils of a superconducting maglev vehicle system. IEEE Trans. Magn. 2017, 53, 8300605. [Google Scholar] [CrossRef]
- Haack, J. Superconductivity for nuclear fusion: Past, present, and future. Arab. J. Sci. Eng. 2024, 50, 3233–3237. [Google Scholar] [CrossRef]
- Zhu, B.; Chen, Z.; Cao, Y.; Liu, Y.; Kang, X.; Chen, Y.; Liu, H.; Fu, P.; Luan, Y.; Li, D. Characteristics, mechanism and criterion of channel segregation in NbTi alloy via numerical simulations and experimental characterizations. Materials 2021, 14, 796. [Google Scholar] [CrossRef]
- Kanouté, P.; Boso, D.; Chaboche, J.-L.; Schrefler, B. Multiscale methods for composites: A review. Arch. Comput. Methods Eng. 2009, 16, 31–75. [Google Scholar] [CrossRef]
- Fish, J.; Wagner, G.J.; Keten, S. Mesoscopic and multiscale modelling in materials. Nat. Mater. 2021, 20, 774–786. [Google Scholar] [CrossRef]
- He, C.; Gao, J.; Li, H.; Ge, J.; Chen, Y.; Liu, J.; Fang, D. A data-driven self-consistent clustering analysis for the progressive damage behavior of 3D braided composites. Compos. Struct. 2020, 249, 112471. [Google Scholar] [CrossRef]
- He, C.; Ge, J.; Gao, J.; Liu, J.; Chen, H.; Liu, W.K.; Fang, D. From microscale to mesoscale: The non-linear behavior prediction of 3D braided composites based on the SCA2 concurrent multiscale simulation. Compos. Sci. Technol. 2021, 213, 108947. [Google Scholar] [CrossRef]
- Kochmann, J.; Wulfinghoff, S.; Reese, S.; Mianroodi, J.R.; Svendsen, B. Two-scale FE–FFT-and phase-field-based computational modeling of bulk microstructural evolution and macroscopic material behavior. Comput. Methods Appl. Mech. Eng. 2016, 305, 89–110. [Google Scholar] [CrossRef]
- Li, X.; Xiong, H.; Li, X.; Wu, X.; Zhang, X.; Liu, J.; Bian, J.; Dou, D. Interpretable deep learning: Interpretation, interpretability, trustworthiness, and beyond. Knowl. Inf. Syst. 2022, 64, 3197–3234. [Google Scholar] [CrossRef]
- Doshi-Velez, F.; Kim, B. Towards a rigorous science of interpretable machine learning. arXiv 2017, arXiv:1702.08608. [Google Scholar] [CrossRef]
- Sun, E.Q. Multi-scale nonlinear stress analysis of Nb3Sn superconducting accelerator magnets. Supercond. Sci. Technol. 2022, 35, 045019. [Google Scholar] [CrossRef]
- Zlobin, A.V.; Novitski, I.; Barzi, E.; Kashikhin, V.V.; Carmichael, J.; Caspi, S.; Chlachidze, G.; Krave, S.; Orozco, C.; Schoerling, D. Development and first test of the 15 T Nb3Sn dipole demonstrator MDPCT1. IEEE Trans. Appl. Supercond. 2020, 30, 4000805. [Google Scholar] [CrossRef]
- Gao, J.; Mojumder, S.; Zhang, W.; Li, H.; Suarez, D.; He, C.; Cao, J.; Liu, W.K. Concurrent n-scale modeling for non-orthogonal woven composite. Comput. Mech. 2022, 70, 853–866. [Google Scholar] [CrossRef]
- Yu, C.; Kafka, O.L.; Liu, W.K. Self-consistent clustering analysis for multiscale modeling at finite strains. Comput. Methods Appl. Mech. Eng. 2019, 349, 339–359. [Google Scholar] [CrossRef]
- Sumption, M.; Collings, E.; Scanlan, R.; Nijhuis, A.; ten Kate, H.H.; Kim, S.; Wake, M.; Shintomi, T. Influence of strand surface condition on interstrand contact resistance and coupling loss in NbTi-wound Rutherford cables. Cryogenics 1999, 39, 197–208. [Google Scholar] [CrossRef]
- Seino, H. Method for controlling frictional heat inside superconducting coils. Q. Rep. RTRI 2007, 48, 115–120. [Google Scholar] [CrossRef]
- Wang, D.; Ren, Y.; Zhang, M.; Gao, X. Design and analysis of the 16T superconducting magnet for CFETR strand test facilities. Fusion Eng. Des. 2021, 162, 112097. [Google Scholar] [CrossRef]
- Moulinec, H.; Suquet, P. A numerical method for computing the overall response of nonlinear composites with complex microstructure. Comput. Methods Appl. Mech. Eng. 1998, 157, 69–94. [Google Scholar] [CrossRef]
- Fang, G.; Wang, B.; Liang, J. A coupled FE-FFT multiscale method for progressive damage analysis of 3D braided composite beam under bending load. Compos. Sci. Technol. 2019, 181, 107691. [Google Scholar] [CrossRef]
- Liu, Z.; Bessa, M.; Liu, W.K. Self-consistent clustering analysis: An efficient multi-scale scheme for inelastic heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2016, 306, 319–341. [Google Scholar] [CrossRef]
- Liu, Z.; Fleming, M.; Liu, W.K. Microstructural material database for self-consistent clustering analysis of elastoplastic strain softening materials. Comput. Methods Appl. Mech. Eng. 2018, 330, 547–577. [Google Scholar] [CrossRef]
- Pan, Y.; He, X.; Zhou, B.; Strong, D.; Zhang, J.; Yu, H.-B.; Tan, Y.; Cava, R.J.; Luo, Y. Elastic properties of a Sc–Zr–Nb–Ta–Rh–Pd high-entropy alloy superconductor. Mater. Today Commun. 2022, 33, 104265. [Google Scholar] [CrossRef]
- Ando, R.; Fujimoto, R.; Nakayama, T.; Abe, M. Development of a design method for superconducting electromagnets using racetrack coils. IEEE Trans. Appl. Supercond. 2008, 18, 1525–1528. [Google Scholar] [CrossRef]


| Material | E (GPa) | v | ρ (kg/m3) |
|---|---|---|---|
| NbTi filament | 111.7 | 0.36 | 6535 |
| Copper matrix | 139.6 | 0.34 | 8920 |
| Stainless steel | 210 | 0.28 | 7850 |
| Offline | Uniaxial Tension | Pure Shearing | |
|---|---|---|---|
| Online (Averaged) | Online (Averaged) | ||
| FEM (130,294 elements) | / | 508 | 654 |
| SCA(16–8) | 7.07 | 0.18 | 0.14 |
| SCA(32–16) | 11.42 | 0.24 | 0.20 |
| SCA(64–32) | 57.75 | 0.59 | 0.69 |
| Elements/Clusters | DOFs | Computational Time | ||
|---|---|---|---|---|
| Offline | Online | |||
| FEM2 | 1.23109 | 7.35109 | 6.09104 h (estimated) | |
| FEM-SCA | 4.54105 | 2.73106 | 11.42 s | 20.95 h |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Wang, L.; Ma, P.; Li, Y.; Zhang, W.; Yu, P.; Chen, Q.; Wang, Y.; Zhang, W. Multiscale Mechanical Responses of the Racetrack NbTi Superconducting Coil Under Dynamic Pressures. Materials 2025, 18, 4072. https://doi.org/10.3390/ma18174072
Liu W, Wang L, Ma P, Li Y, Zhang W, Yu P, Chen Q, Wang Y, Zhang W. Multiscale Mechanical Responses of the Racetrack NbTi Superconducting Coil Under Dynamic Pressures. Materials. 2025; 18(17):4072. https://doi.org/10.3390/ma18174072
Chicago/Turabian StyleLiu, Wei, Lianchun Wang, Peng Ma, Yong Li, Wentao Zhang, Peichang Yu, Qiang Chen, Yongbin Wang, and Weiwei Zhang. 2025. "Multiscale Mechanical Responses of the Racetrack NbTi Superconducting Coil Under Dynamic Pressures" Materials 18, no. 17: 4072. https://doi.org/10.3390/ma18174072
APA StyleLiu, W., Wang, L., Ma, P., Li, Y., Zhang, W., Yu, P., Chen, Q., Wang, Y., & Zhang, W. (2025). Multiscale Mechanical Responses of the Racetrack NbTi Superconducting Coil Under Dynamic Pressures. Materials, 18(17), 4072. https://doi.org/10.3390/ma18174072






