Canvas-Ground Interaction: A New Approach to Quantifying Ground Mechanical Degradation
Abstract
1. Introduction
2. Materials and Methods
- Comparison of canvas types: the primary criterion was to obtain samples that allow for comparison between the same type of canvas—one without any preparatory layer and one with a commercial preparation layer applied;
- Representation of market varieties: the secondary criterion was to represent a range of canvases currently available on the market, reflecting different qualities used for painting and sold regularly over the years. Therefore, two polycotton canvases and two traditional linen canvases were chosen, to represent both contemporary and classic materials.
2.1. Textile Identification and Characterization
2.2. Ground Identification and Characterization
2.3. Aging Procedure
- Polyester fibers in canvas samples:
- Linen canvas samples:
- Primed samples with ground layers:
2.4. Mechanical Tests
2.5. Method for Calculating the Degradation Attributable to the Ground Layer in Polycotton- and Linen-Primed Canvases
- Total ground degradation compares the energy absorbed by the ground layer during the second cycle versus the one in the first cycle, both up to the end of the elastic phase in the primed samples. The resulting degradation is expressed as a percentage of energy loss (Ground Degradation%). Since energy is measured in Joules (N·m), and all samples have the same length and width, we compare the energy values using the energy area ratio in (N%) instead of (N·m).
- 2.
- Bedding-down degradation assesses degradation at the end of the first phase, capturing the ‘bedding-down’ effect. The ground degradation at the bedding down (Ground bed Degr%) can be calculated as
3. Results and Discussion
3.1. Textile Identification and Characterization
3.2. Ground Characterization and Identification
3.3. Dynamometric Tests and Phases Analysis
3.3.1. General Evolution of the Samples
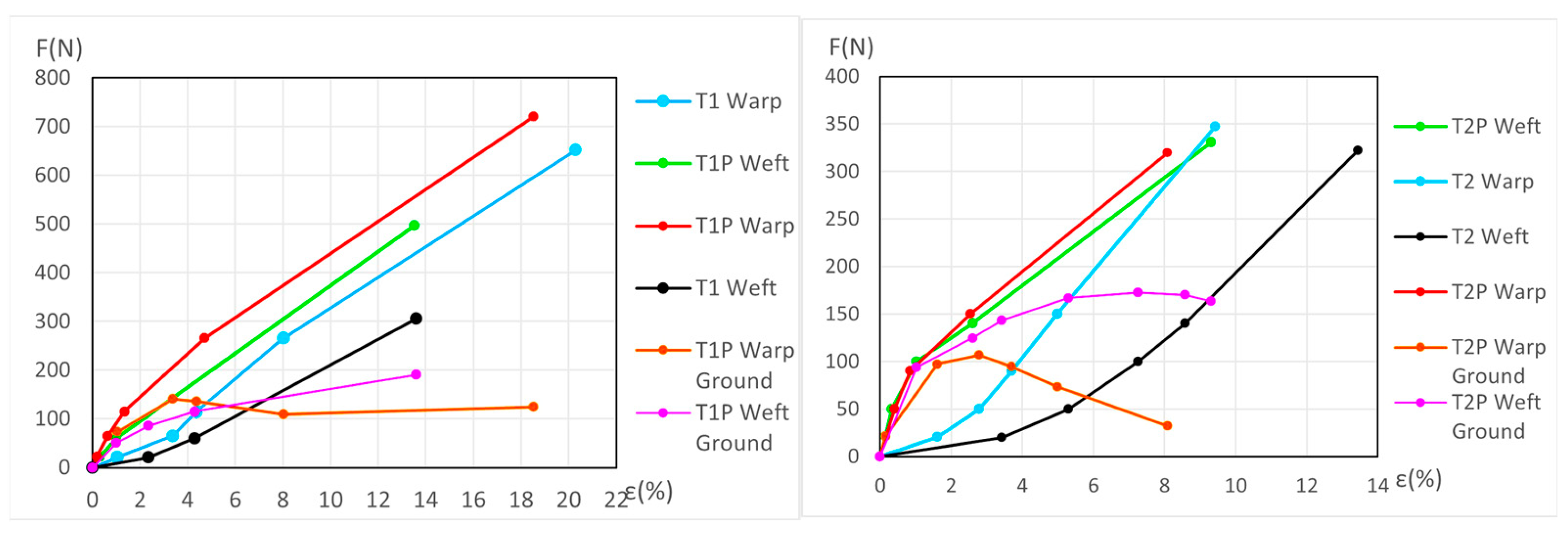
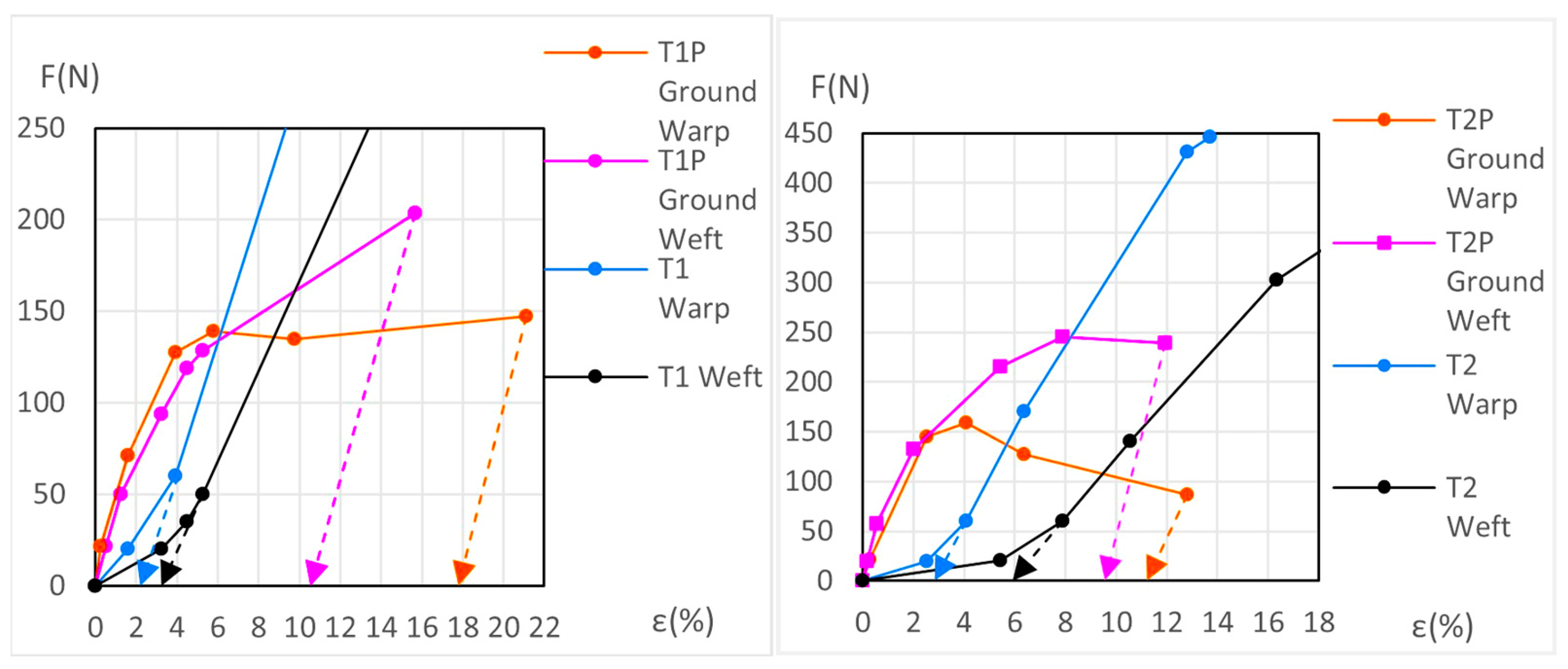
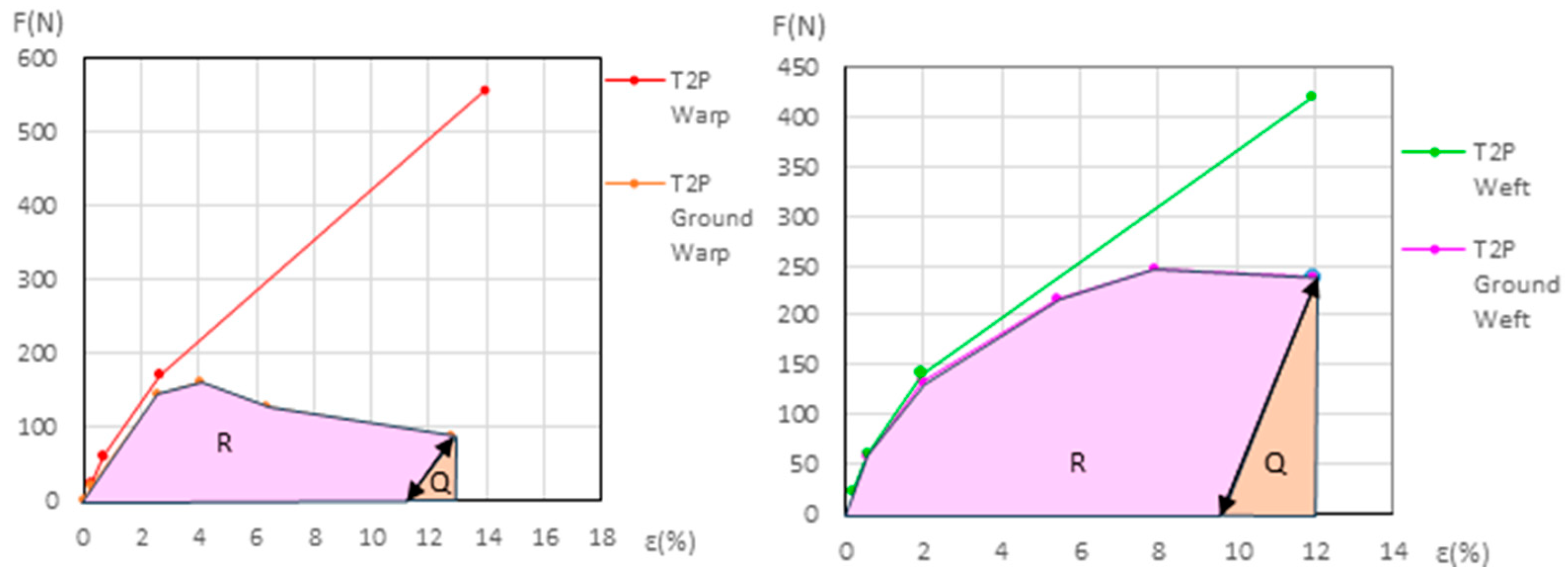
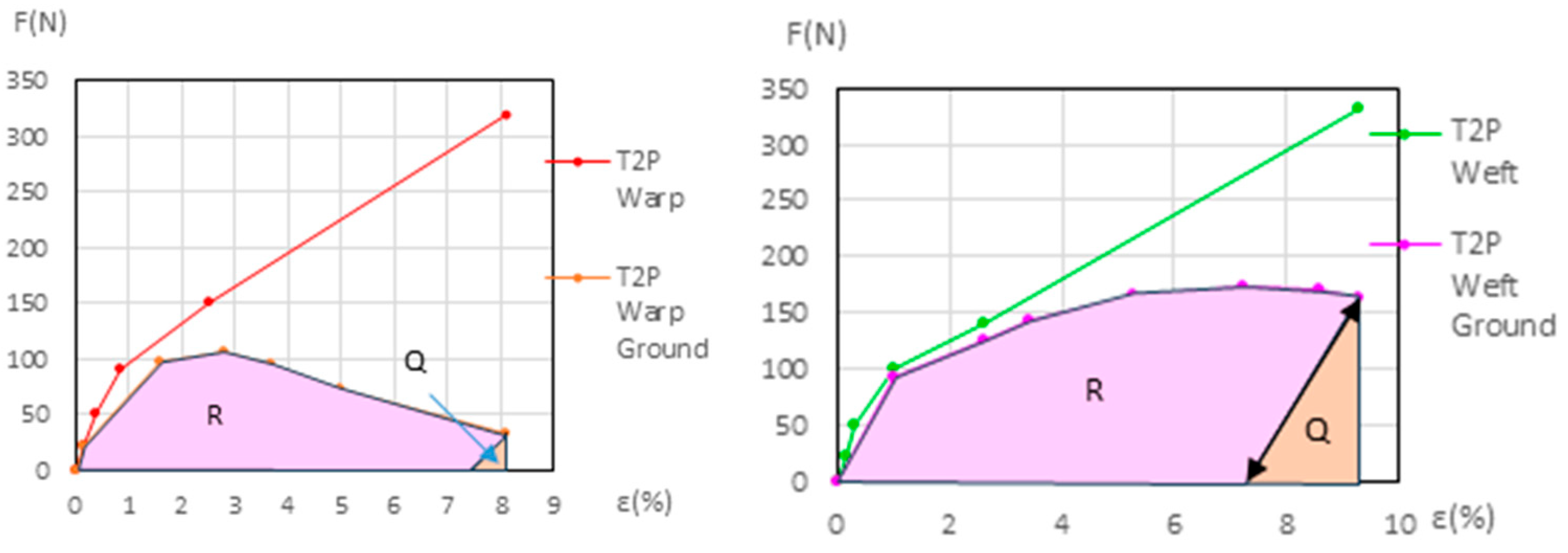
3.3.2. Detailed Evolution of New Polycotton Samples T1P and T2P
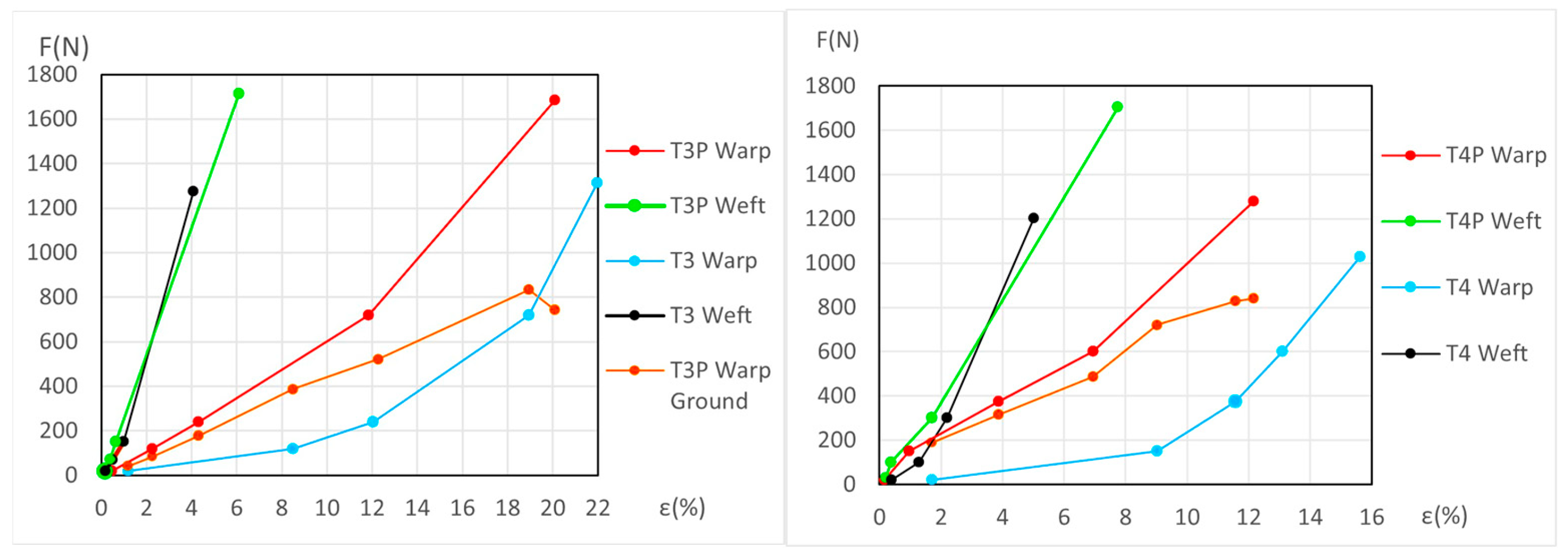
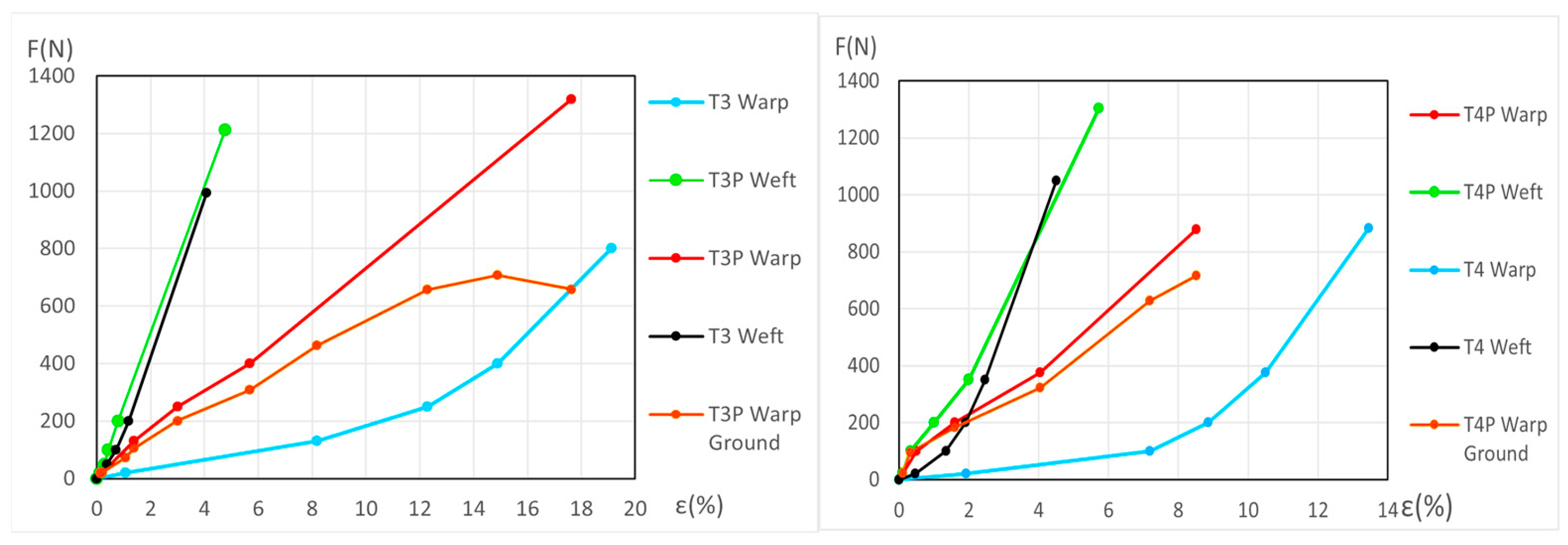
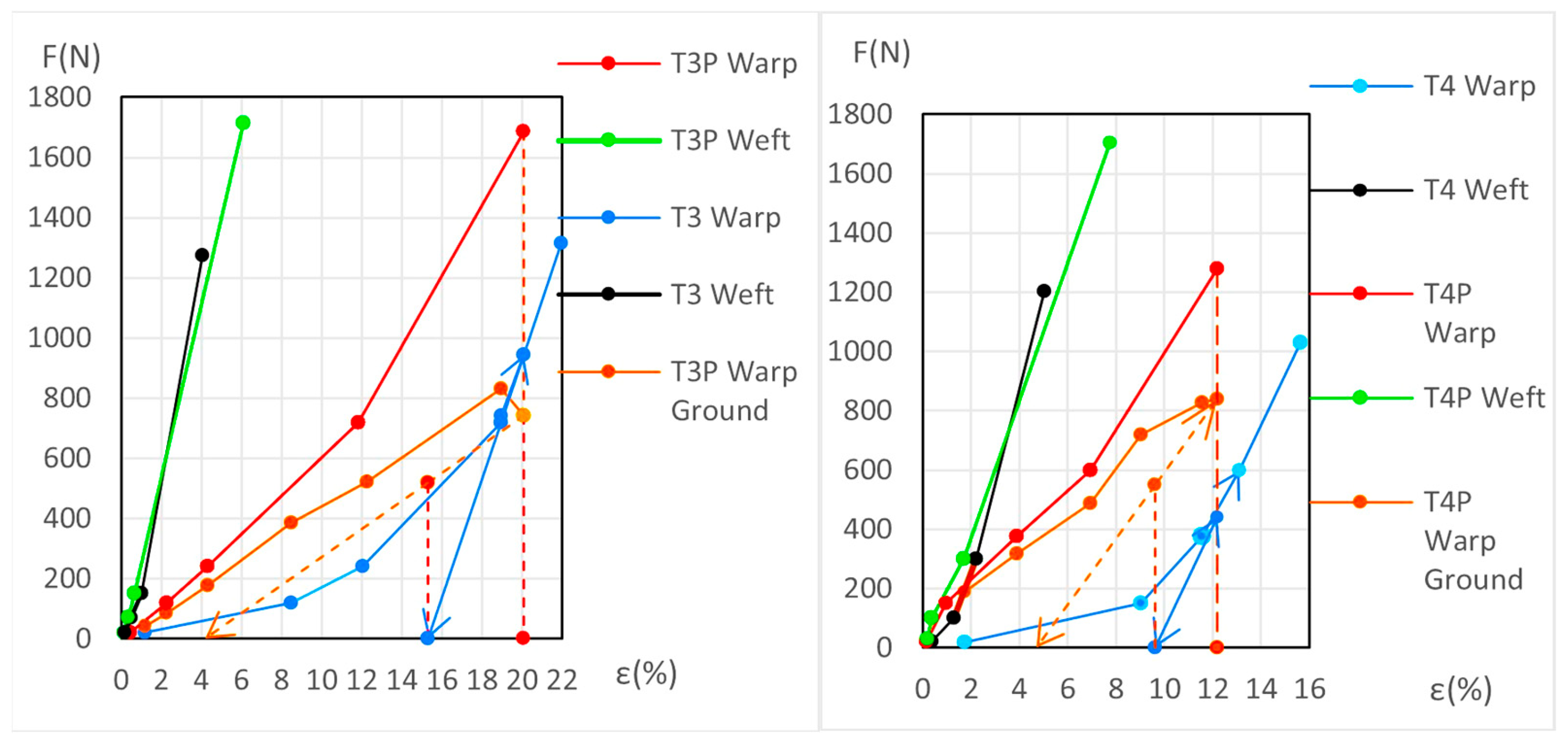
3.3.3. Detailed Evolution of New Samples T3P Warp (Linen)
3.3.4. Detailed Evolution of New Samples T4P Warp (Linen)
3.3.5. Detailed Evolution of New Linen Samples T3P and T4P Weft
3.3.6. Detailed Evolution of Aged Samples T1P and T2P (Primed Polycotton)
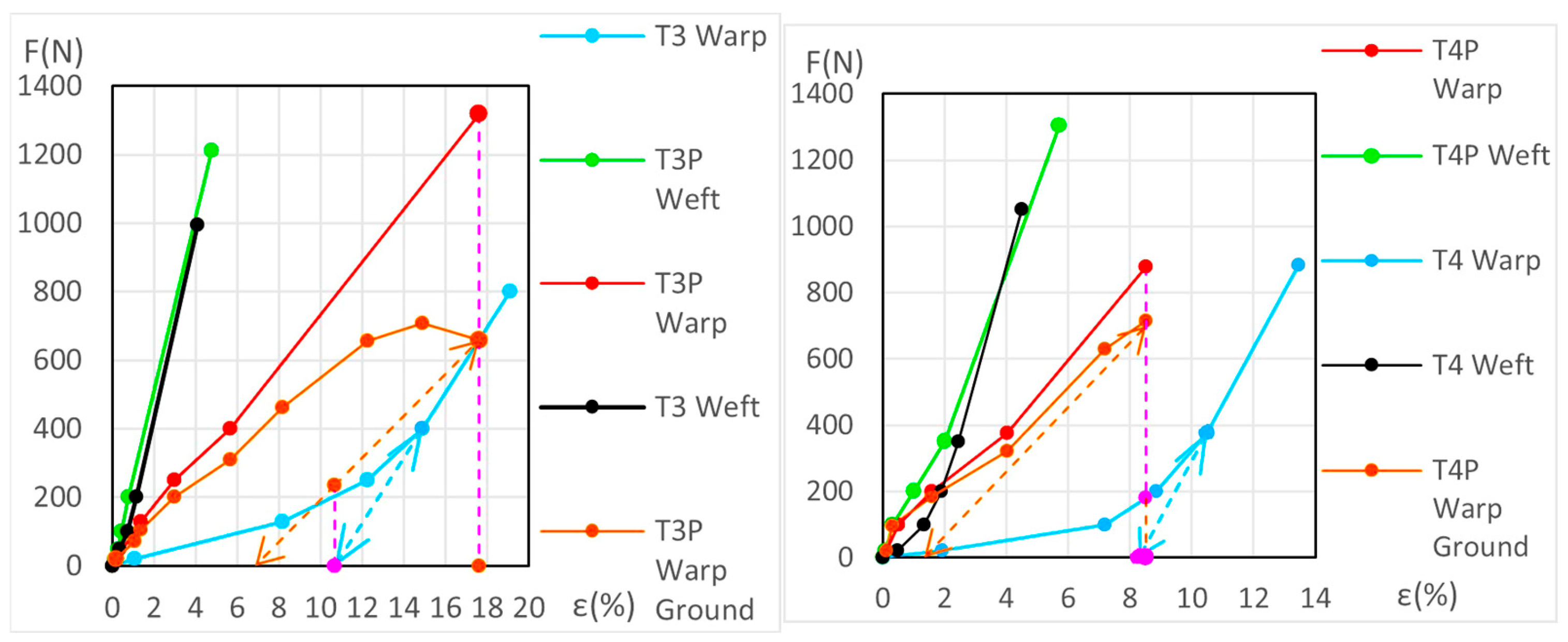
3.3.7. Detailed Evolution of Aged Samples T3P Warp (Primed Linen)
3.3.8. Detailed Evolution of Aged Samples T4P Warp (Primed Linen)
3.3.9. Detailed Evolution of Aged Samples T3P andT4P Weft (Primed Linen)
3.4. Ground Degradation
3.4.1. Ground Degradation in Primed Linen
3.4.2. Ground Degradation in Primed Polycottons
3.4.3. Ground Degradation at the Bedding Down
3.5. Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hedley, G. Some empirical determinations of the strain distribution of stretched canvases. In Proceedings of the ICOM-CC Preprints 4th Triennial Meeting, Venice, Italy, 13–18 October 1975. paper 75/11/4. [Google Scholar]
- Russell, W.H.; Berger, G.A. The behaviour of canvas as a structural support for painting. Stud. Conserv. 1982, 27, 139–145. [Google Scholar] [CrossRef]
- Berger, G.A.; Russell, W.H. An evaluation of canvas paintings using stress measurements. Stud. Conserv. 1988, 33, 187–204. [Google Scholar] [CrossRef]
- Campo-Frances, G.; Cayuela, D.; Carrera-Gallissà, E.; Ferrer, S.; Viladrich, N. Polycotton Canvases. Characterisation, and Mechanical Behaviour Before and After Artificial Ageing. Stud. Conserv. 2024, 70, 89–105. [Google Scholar] [CrossRef]
- Young, C.R.T. Measurement of the Biaxial Tensile Properties of Paintings on Canvas. Ph.D. Thesis, University of London, London, UK, 1996; pp. 151–154. [Google Scholar]
- Young, C.R.T. Biaxial Properties of Sized Cotton-Duck. In Proceedings of the 11th Triennial Meeting, ICOM Committee for Conservation, Edinburgh, UK, 1–6 September 1996; pp. 322–331, ISBN 9781873936504. [Google Scholar]
- Young, C.R.T.; Hibberd, R.D. Biaxial Tensile Testing of Paintings on Canvas. Stud. Conserv. 1999, 44, 129–141. [Google Scholar] [CrossRef]
- Penava, Ž.; Simic Penava, D.; Knezic, Ž. Determination of the Elastic Constants of Plain Woven Fabrics by a Tensile Test in Various Directions. Fibres Text. East. Eur. 2014, 22, 57–63. [Google Scholar]
- Penava, Ž.; Simic Penava, D.; Tkalec, M. Experimental Analysis of the Tensile Properties of Painting Canvas. AUTEX Res. J. 2016, 16, 182–195. [Google Scholar] [CrossRef]
- Stols-Wiltox, M. Grounds 1400–1900. In Conservation of Easel Paintings; Hill Stoner, J., Rushfield, R., Eds.; Routledge: Abingdon, UK, 2012; p. 183. [Google Scholar]
- Ormsby, B.; Gottsegen, M. Twentieth-Century Grounds. In Conservation of Easel Paintings; Hill Stoner, J., Rushfield, R., Eds.; Routledge: Abingdon, UK, 2012; p. 186. [Google Scholar]
- Mecklenburg, M.F.; Tumosa, C.S. An introduction into the mechanical behaviour of paintings under rapid loading conditions. In Art in Transit; Mecklenburg, M.F., Ed.; National Gallery of Art: Washington, DC, USA, 1991; pp. 137–172. [Google Scholar]
- Mecklenburg, M.F.; Tumosa, C.S. Mechanical behaviour of paintings subjected to changes in temperature and relative humidity. In Art in Transit: Studies in the Transport of Paintings; Mecklenburg, M.F., Ed.; National Gallery of Art: Washington, DC, USA, 1991; pp. 172–214. [Google Scholar]
- Mecklenburg, M.F.; Tumosa, C.S.; McCormick-Goodhart, M.H. A general method for determining the mechanical properties needed for the computer analysis of polymeric structures subjected to changes in temperature and relative humidity. In Materials Issues in Art and Archaeology III; Vandiver, P.B., Druzik, J.R., Wheeler, G.S., Freestone, I., Eds.; Materials Research Society: Pittsburgh, PA, USA, 1993; pp. 337–358. [Google Scholar]
- Hedley, G. Relative humidity and the stress/strain response of canvas paintings: Uniaxial measurements of naturally aged samples. Stud. Conserv. 1988, 33, 133–148. [Google Scholar] [CrossRef]
- Janas, A.; Fuster-López, L.; Andersen, C.K.; Escuder, A.V.; Kozłowski, R.; Poznańska, K.; Gajda, A.; Scharff, M.; Bratasz, L. Mechanical properties and moisture-related dimensional change of canvas paintings—Canvas and glue sizing. Herit. Sci. 2022, 10, 160. [Google Scholar] [CrossRef]
- De Polo, G.; Walton, M.; Keune, K.; Shull, K.R. After the paint has dried: A review of testing techniques for studying the mechanical properties of artists’ paint. Herit. Sci. 2021, 9, 68. [Google Scholar] [CrossRef]
- Bury, M.; Bratasz, L. Development of craquelure patterns in paintings on canvas. Herit. Sci. 2024, 12, 375. [Google Scholar] [CrossRef]
- Zhang, R.; Wood, J.D.; Young, C.R.T.; Taylor, A.C.; Balint, D.S.; Charalambides, M.N. A numerical investigation of interfacial and channelling crack growth rates under low-cycle fatigue in bi-layer materials relevant to cultural heritage. J. Cult. Herit. 2021, 49, 70–78. [Google Scholar] [CrossRef]
- Lee, D.S.-H.; Kim, N.S.; Scharff, M.; Nielsen, A.V.; Mecklenburg, M.F.; Fuster-López, L.; Bratasz, L.; Andersen, C.K. Numerical modelling of mechanical degradation of canvas paintings under desiccation. Herit. Sci. 2022, 10, 130. [Google Scholar] [CrossRef]
- Janas, A.; Mecklenburg, M.F.; Fuster-López, L.; Kozłowski, R.; Kékicheff, P.; Favier, D.; Anders, C.K.; Bratasz, Ł. Shrinkage and mechanical properties of drying oil paints. Herit. Sci. 2022, 10, 181. [Google Scholar] [CrossRef]
- Iaccarino, A.; Bergsma, O.; Groves, R. Methodology for measures od twist and crimp im canvas paintings supports and historical textiles. J. Cult. Herit. 2025, 71, 1–9. [Google Scholar] [CrossRef]
- Janas, A.; Avgerou, N.; Charalambides, M.N.; Fuster-López, L.; Bratasz, Ł. Fracture toughness of aged oil paints. Herit. Sci. 2024, 12, 103. [Google Scholar] [CrossRef]
- Young, C.R.T. Canvas Complexity: The Life of a Complex Composite. In Conserving Canvas; Schwarz, C., McClure, I., Coddington, J., Eds.; Getty Publications: Los Angeles, CA, USA, 2023; pp. 120–128. [Google Scholar]
- Braunig, T.; von Reden, A.; Lichtblau, D.A.; Herm, C. A Novel Technique to Determine the Strength of Canvas and Its Correlation with the Degree of Cellulose Polymerization. In Conserving Canvas; Schwarz, C., McClure, I., Coddington, J., Eds.; Getty Publications: Los Angeles, CA, USA, 2023; pp. 129–136. [Google Scholar]
- Hackney, S. Understanding Structure, Changing Practice. In Conserving Canvas; Schwarz, C., McClure, I., Coddington, J., Eds.; Getty Publications: Los Angeles, CA, USA, 2023; pp. 6–11. [Google Scholar]
- Carter, A.; Chua, L.; Amir, F.; Awburn, R.; Osmond, G.; Ng, J. Investigating Commercially Primed Contemporary Artist Canvases. In Conserving Canvas; Schwarz, C., McClure, I., Coddington, J., Eds.; Getty Publications: Los Angeles, CA, USA, 2023; pp. 449–453. [Google Scholar] [CrossRef]
- Osmond, G.; Chua, L.; Carter, A.; Awburn, R.; Mohd Amir, F. An FTIR survey of contemporary pre-primed artist canvases. In Proceedings of the 13th Infrared and Raman Users Group Symposium, Sydney, Australia, 5–7 December 2018. [Google Scholar]
- Young, R.T. Towards a better understanding of the physical properties of lining materials for paintings: Interim results. Conservator 1999, 23, 83–91. [Google Scholar] [CrossRef]
- Andersen, C.K. Lined Canvas Paintings. Mechanical Properties and Structural Response to Fluctuating Relative Humidity, Exemplified by the Collection of Danish Golden Age Paintings at Statens Museum for Kunst (SMK). Ph.D. Thesis, Royal Danish Academy of Fine Arts, Schools of Architecture, Design and Conservation, Copenhagen, Denmark, 2013; p. 77. [Google Scholar]
- Andersen, C.K.; Nielsen, I. Lining with fixed interleaf. A case study in the mechanical effects of paper interleaf and binder. In Adhesives & Consolidants in Paintings Conservation; Barros d’sa, A., Bone, L., Clarricoates, R., Gent, A., Eds.; Archetype Publications & ICON Paintings Group: London, UK, 2012; pp. 32–43. [Google Scholar]
- Hackney, S. On Canvas: Preserving the Structure of Paintings; Getty Publications: Los Angeles, CA, USA, 2020; 30p, ISBN 978-1-60606-626-3. [Google Scholar]
- Erhardt, D.; Mecklenburg, M. Accelerated vs Natural Aging: Effect of Aging Conditions on the Aging Process of Cellulose. In Materials Issues in Art and Archaeology IV; Vandiver, P.B., Druzik, J.R., Galvan Madrid, J.L., Wheeler, G.S., Freestone, I., Eds.; Materials Research Society Symposium Proceedings Series 352; Materials Research Society: Pittsburgh, PA, USA, 1995; pp. 247–270. [Google Scholar] [CrossRef]
- Zervos, S. Natural and Accelerated Ageing of Cellulose and Paper: A Literature Review. In Cellulose: Structure and Properties, Derivatives and Industrial Uses; Arnaud Lejeune, T.D., Ed.; Nova Science Publishers, Inc.: New York, NY, USA, 2010; pp. 155–204. [Google Scholar]
- Poggi, G.; Toccafondi, N.; Melita, L.N.; Knowles, J.C.; Bozec, L.; Giorgi, R.; Baglioni, P. Calcium hydroxide nanoparticles for the conservation of cultural heritage: New formulations for the deacidification of cellulose-based artifacts. Appl. Phys. A 2014, 114, 685–693. [Google Scholar] [CrossRef]
- Nechyporchuk, O.; Kolman, K.; Oriola, M.; Persson, M.; Holmberg, K.; Bordes, R. Accelerated ageing of cotton canvas as a model for further consolidation practices. J. Cult. Herit. 2017, 28, 183–187. [Google Scholar] [CrossRef]
- T1. Polycotton Ref: 3210022 and T1P. Primed Polycotton Ref: 3210026. Casa Piera. Available online: https://casapiera.com/es/telas/6998-110369-rollo-tela-cruda-algodon-y-poliester.html#/53001-6998talla-105_x_10_m/53002-6998color-grano_medio (accessed on 6 July 2025).
- T2. Polycotton Ref: 0062CR. and T2P. Primed Polycotton Ref: 0062CR Barna Art. Available online: https://www.barna-art.com/algodon/tela-algodon-2-10-x-10-metros-preparacion-oleoacrilico-grano-medio-139-grm2 (accessed on 6 July 2025).
- T3. Linen Ref: 066. Claessens and T3P. Primed Linen Ref: B166. Barna Art. Available online: https://www.barna-art.com/telas-belgas-claessens/tela-lino-belga-claessens-2-10-x-1-metro-preparacion-oleoacrilico-grano-medio (accessed on 6 July 2025).
- T4. Linen Ref.: T300S and T4P. Primed Linen. Ref.: T300S-P. Vicenç Piera. Available online: https://vpiera.com/es/tela-lino-preparada-a-mano-aprox-3-m-x-8-mts-imprimacion-universal (accessed on 6 July 2025).
- AATCC. Technical Manual; American Association of Textile Chemists and Colorists: Durham, NC, USA, 2006; Volume 81. [Google Scholar]
- Bergen, W.; von Krauss, W. Textile Fiber Atlas; American Wool Handbook, Co.: New York, NY, USA, 1942. [Google Scholar] [CrossRef]
- Catling, D.; Grayson, J. Identification of Vegetable Fibres; Springer: Dordrecht, The Netherlands, 1982. [Google Scholar] [CrossRef]
- Carrera-Gallissà, E. Manual Práctico de Indentificación de Fibras Textiles; Universitat Politècnica de Catalunya, Departament d’Enginyeria Textil i Paperera: Terrassa, Spain, 2017. [Google Scholar]
- Instituto de Investigación Textil y Cooperación Industrial de Terrassa. INTEXTER. Análisis Cualitativo de Fibras. MO 04020; Instituto de Investigación Textil y Cooperación Industrial de Terrassa: Terrassa, Spain, 2022; (Unpublished internal operating procedure). [Google Scholar]
- ISO 1833-1; Textiles. Quantitative Chemical Analysis. Part 1. General Principles of Testing. International Organization for Standardization: Geneva, Switzerland, 2020.
- ISO 1833-11; Textiles. Quantitative Chemical Analysis. Part 11: Mixtures of Certain Cellulose Fibres with Certain Other Fibres (Method Using Sulfuric acid). International Organization for Standardization: Geneva, Switzerland, 2017.
- ISO 1833-6; Textiles. Quantitative Chemical Analysis. Part 6 Mixtures of Viscose, Certain Types of Cupro, Modal or Lyocell with Certain Other Fibres (Method Using Formic Acid and Zinc Chloride). International Organization for Standardization: Geneva, Switzerland, 2018.
- Mark, J.E. Polymer Data Handbook, 2nd ed.; Oxford University Press: New York, NY, USA, 1999. [Google Scholar] [CrossRef]
- Feller, R.L. Thoughts About Crosslinking. In WAAC Newsletter; Western Association for Art Conservation: Los Angeles, CA, USA, 2008; Volume 30, pp. 16–17. [Google Scholar]
- Betz, J. The Influence of Glass Transition Temperatures on The Performance of Acrylic Thermoplastic Adhesives. Master’s Thesis, Columbia University, New York, NY, USA, 2017. [Google Scholar]
- Farmakalidis, H.V.; Douvas, A.M.; Sotiropoulou, S.; Boyatzis, S. Accelerated Thermal Ageing of Acrylic Copolymers, Cyclohexanone-Based and Urea-Aldehyde Resins Used in Paintings Conservation. Mediterr. Archaeol. Archaeom. 2016, 16, 213–228. [Google Scholar]
- ISO-5630-1; Paper and Board—Accelerated Ageing—Part 1: Dry Heat Treatment at 105 Degrees C. International Organization for Standardization: Geneva, Switzerland, 1991.
- ISO-5630-3; Paper and Board—Accelerated Ageing—Part 3: Moist Heat Treatment at 80 Degrees C and 65% Relative Humidity. International Organization for Standardization: Geneva, Switzerland, 1996.
- ISO-139; Standard Atmospheres for Conditioning and Testing. International Organization for Standardization: Geneva, Switzerland, 2005.
- Dowling, N.E. Mechanical Behaviour of Materials: Engineering Methods for Deformation, Fracture and Fatigue, 4th ed.; Pearson Education: London, UK, 2012; Chapter 12; pp. 638–671. ISBN 978-0-13-139506-0. [Google Scholar]
- Bresee, R.R. General Effects of Ageing on Textiles. J. Am. Inst. Conserv. 1986, 25, 39–48. [Google Scholar] [CrossRef]











| Sample | Fiber Type Warp Threads | Fiber Type Weft Threads | Whole Canvas Composition | Canvas Weight g/m2 | Threads/cm | Yarn Spinning System |
|---|---|---|---|---|---|---|
| T1 | Polyester 66% Viscose 34% | Cotton 50.5% Polyester 35.5% Viscose 16% | Cotton 25%; Polyester 50%; Viscose 25% | 168.20 | Warp 18 Weft 11 | open-end spinning |
| T2 | Polyester 52.5% Viscose 47.5% | Cotton 71% Polyester 29% (Flax traces) | Cotton 60%; Polyester 40%; | 157.99 | Warp 13 Weft 13 | open-end spinning |
| T3 | Flax 100% | Flax 100% | Linen 100% | 286.99 | Warp 16.8 Weft 13.9 | ring spinning |
| T4 | Flax 100% | Flax 100% | Linen 100% | 213.62 | Warp 12.6 Weft 12.6 | ring spinning |
| Sample | Layer Number | Thickness (μ) | Pigments and Fillers | Optical Microscope Image. Cross Section (Objective MPlan10X/0.25) | Optical Microscope Image. Cross Section. UV Light (Objective MPlan10X/0.25) | SEM Image with Backscattered Electron Detector (BSE) Cross Section |
|---|---|---|---|---|---|---|
| T1P | 4 | 30 | Calcite, titanium white (rutile) | 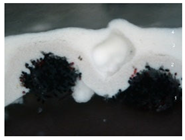 |  | 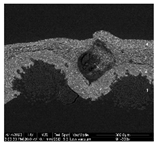 |
| 3 | 45 | Titanium white (rutile), calcite | ||||
| 2 | 35 | Titanium white (rutile), calcite | ||||
| T2P | 3 | 25 | Dolomite, talc, titanium white (rutile) (l.p.), barium white (e.l.p.), calcium phosphate (e.l.p.) | 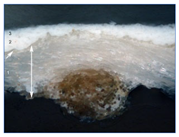 | 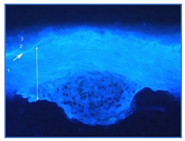 |  |
| 2 | 30–65 | Dolomite, talc, titanium white (rutile) (l.p.), barium white (e.l.p.) | ||||
| T3P | 2 | 50–70 | Calcite, titanium white (rutile) (l.p.) |  |  |  |
| T4P | 2 | 60–110 | Dolomite, calcite (l.p.), titanium white (rutile) (l.p.), talc (v.l.p.) |  | 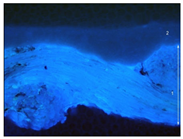 |  |
| T1P | T2P | T3P | T4P |
|---|---|---|---|
| CaCO3 Calcite, syn (2.000) 55.8% TiO2 Rutile, syn (3.400) 44.2% | TiO2 Rutile syn (3.400) 14.7% CaMg(CO3)2 dolomite 53.7% Mg3Si4O10(OH)2 talc 31.6% BaSO4 baryte traces Calcium phosphate traces | CaCO3 calcite (3.150) 59.7% TiO2 rutile, syn (3.200) 40.3% | CaMg(CO3)2 dolomite ((1)) 80.4% TiO2 Rutile syn (3.400) 6.1% Mg3Si4O10(OH)2 talc 2M ((1)) 11.7% CaCO3 calcite, syn (2.000) 1.7% |
| PHASES | 1st PHASE | 2nd PHASE | 3rd PHASE | 4th PHASE |
|---|---|---|---|---|
| BEHAVIOUR | ELASTIC Force/ elongation li-neal | VISCOELASTIC Force/ elongation not lineal | ELASTIC Force/ elongation lineal | PLASTIC Permanent deformation |
| PHENOMENA | Slack + Bedding Down | Crimp removal | Erratic/sample break | |
| MATERIAL AFFECTED | Canvas Unprimed | Canvas Unprimed | Canvas Unprimed (at big ε) | Canvas Unprimed |
| MATERIAL AFFECTED | Canvas Primed | Canvas Primed | Canvas Primed (at big ε) | Canvas Primed |
| MATERIAL AFFECTED | Ground | Ground (at small ε) | Ground |
| New (Not Aged) Samples Averaged Values F, F/L, ε, and ε/εbed Ratio at the Different Phases | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Samples | 1st Phase Up to the Bedding | 1st Phase End | 2nd Phase End | 3rd Phase End | 4th Phase Max F | Break Values | |||||||
| F | F/L | εbed | ε | ε/εbed | F | ε | F | ε | F | ε | F | ε | |
| N | N/m | % | % | N | % | N | % | N | % | N | % | ||
| T1 Warp | 20 | 377 | 1.556 | 1.598 | 1.027 | 265 | 9.76 | 642 | 21.1 | 677 | 23.1 | 550 | 26.0 |
| T2 Warp | 20.0 | 377 | 2.520 | 2.540 | 1.008 | 170 | 6.36 | 431 | 12.8 | 447 | 13.7 | 262 | 14.7 |
| T3 Warp | 20.4 | 385 | 1.144 | 1.192 | 1.042 | 720 | 18.96 | 1314 | 22.0 | 1391 | 27.0 | 379 | 37.3 |
| T4 Warp | 20.1 | 379 | 1.672 | 1.716 | 1.026 | 375 | 11.57 | 1030 | 15.6 | 1124 | 16.3 | 290 | 22.2 |
| T1 Weft | 20.3 | 383 | 3.206 | 3.254 | 1.015 | 50 | 5.28 | 374 | 18.4 | 380 | 18.6 | 253 | 17.5 |
| T2 Weft | 20.4 | 385 | 5.400 | 5.424 | 1.004 | 140 | 10.56 | 303 | 16.3 | 363 | 19.9 | 77 | 23.9 |
| T3 Weft | 20.4 | 385 | 0.152 | 0.178 | 1.171 | 150 | 1.00 | 1276 | 4.08 | 1322 | 4.08 | 294 | 36.1 |
| T4 Weft | 22.0 | 415 | 0.308 | 0.382 | 1.240 | 300 | 2.20 | 1202 | 5.02 | 1277 | 5.50 | 284 | 17.0 |
| T1P Warp | 21.6 | 408 | 0.212 | 0.274 | 1.292 | 265 | 5.80 | 806 | 21.4 | 812 | 21.5 | 810 | 21.5 |
| T2P Warp | 24 | 453 | 0.230 | 0.28 | 1.217 | 170 | 2.64 | 557 | 13.9 | 557 | 13.9 | 538 | 14.1 |
| T3P Warp | 21 | 396 | 0.452 | 0.472 | 1.044 | 720 | 11.84 | 1686 | 20.1 | 1686 | 20.1 | 1608 | 20.2 |
| T4P Warp | 20.6 | 390 | 0.114 | 0.152 | 1.333 | 600 | 6.90 | 1280 | 12.2 | 1294 | 12.4 | 931 | 13.6 |
| T1P Weft | 21.4 | 404 | 0.460 | 0.522 | 1.135 | 50 | 1.24 | 509 | 15.7 | 509 | 15.7 | 501 | 15.7 |
| T2P Weft | 22 | 415 | 0.150 | 0.180 | 1.200 | 140 | 2.000 | 419 | 11.9 | 421 | 12.0 | 95 | 25.5 |
| T3P Weft | 21 | 396 | 0.152 | 0.166 | 1.092 | 150 | 0.66 | 1714 | 6.10 | 2007 | 7.43 | 1989 | 7.4 |
| T4P Weft | 29.0 | 547 | 0.170 | 0.203 | 1.191 | 300 | 1.70 | 1703 | 7.75 | 1703 | 7.75 | 1637 | 7.9 |
| Aged Samples Averaged Values F, F/L, ε, and ε/εbed Ratio at the Different Phases | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Samples | 1st Phase Up to the Bedding | 1st PHASE END | 2nd Phase End | 3rd Phase End | 4th Phase Max F | Break Values | |||||||
| F | F/L | εbed | ε | ε/εbed | F | ε | F | ε | F | ε | F | ε | |
| N | N/m | % | % | - | N | % | N | % | N | % | N | % | |
| T1 Warp | 20.4 | 385 | 1.002 | 1.046 | 1.044 | 265 | 8.02 | 651 | 20.3 | 654 | 20.5 | 543 | 21.0 |
| T2 Warp | 20.8 | 392 | 1.452 | 1.614 | 1.112 | 150 | 4.98 | 347 | 9.42 | 402 | 11.4 | 209 | 12.8 |
| T3 Warp | 19.3 | 363 | 0.988 | 1.057 | 1.070 | 400 | 14.90 | 801 | 19.1 | 976 | 26.8 | 725 | 37.3 |
| T4 Warp | 21.0 | 396 | 1.828 | 1.912 | 1.046 | 375 | 10.50 | 882 | 13.5 | 943 | 14.1 | 212 | 23.1 |
| T1 Weft | 21.0 | 396 | 2.300 | 2.350 | 1.022 | 60 | 4.30 | 306 | 13.6 | 312 | 14.0 | 214 | 15.5 |
| T2 Weft | 20.1 | 379 | 3.370 | 3.420 | 1.015 | 140 | 8.58 | 322 | 13.4 | 363 | 15.2 | 142 | 17.6 |
| T3 Weft | 20.0 | 377 | 0.148 | 0.172 | 1.162 | 200 | 1.18 | 994 | 4.08 | 1270 | 9.4 | 279 | 19.0 |
| T4 Weft | 21.0 | 396 | 0.424 | 0.468 | 1.104 | 350 | 2.46 | 1050 | 4.50 | 1147 | 4.9 | 386 | 11.4 |
| T1P Warp | 22.5 | 425 | 0.160 | 0.200 | 1.250 | 265 | 4.70 | 720 | 18.5 | 720 | 18.5 | 720 | 18.5 |
| T2P Warp | 21.5 | 406 | 0.122 | 0.158 | 1.295 | 150 | 2.54 | 320 | 8.08 | 320 | 8.08 | 370 | 12.8 |
| T3P Warp | 20.3 | 383 | 0.158 | 0.174 | 1.101 | 400 | 5.68 | 1318 | 17.6 | 1482 | 20.3 | 1477 | 20.5 |
| T4P Warp | 22.4 | 423 | 0.072 | 0.106 | 1.472 | 375 | 4.04 | 879 | 8.52 | 879 | 8.52 | 840 | 9.7 |
| T1P Weft | 22.0 | 415 | 0.270 | 0.310 | 1.148 | 60 | 1.00 | 497 | 13.5 | 497 | 13.5 | 496 | 13.6 |
| T2P Weft | 21.1 | 398 | 0.100 | 0.144 | 1.440 | 140 | 2.60 | 331 | 9.3 | 331 | 9.3 | 172 | 2.2 |
| T3P Weft | 18.2 | 343 | 0.090 | 0.104 | 1.156 | 200 | 0.79 | 1212 | 4.76 | 1728 | 8.5 | 1717 | 8.6 |
| T4P Weft | 22.4 | 423 | 0.068 | 0.090 | 1.324 | 350 | 2.00 | 1304 | 5.73 | 1304 | 5.73 | 1333 | 5.9 |
| Samples | Ground Degr % in Linen Warp | ||
|---|---|---|---|
| New | Aged | ∆% Aging | |
| T3P warp | 32 | 59.0 | 27 |
| T4P warp | 44.8 | 55.8 | 11 |
| Samples | Total Ground Degr% in Polycottons | ||
|---|---|---|---|
| New | Aged | ∆% Aging | |
| T1P Warp | 90.9 | 95.6 | 4.7 |
| T1P Weft | 75.5 | 79.7 | 4.2 |
| T2P Warp | 95.2 | 99.3 | 4.1 |
| T2P Weft | 87.5 | 93 | 5.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campo-Frances, G.; Ferrer, S.; Cayuela, D.; Carrera-Gallisà, E. Canvas-Ground Interaction: A New Approach to Quantifying Ground Mechanical Degradation. Materials 2025, 18, 4041. https://doi.org/10.3390/ma18174041
Campo-Frances G, Ferrer S, Cayuela D, Carrera-Gallisà E. Canvas-Ground Interaction: A New Approach to Quantifying Ground Mechanical Degradation. Materials. 2025; 18(17):4041. https://doi.org/10.3390/ma18174041
Chicago/Turabian StyleCampo-Frances, Gema, Santi Ferrer, Diana Cayuela, and Enric Carrera-Gallisà. 2025. "Canvas-Ground Interaction: A New Approach to Quantifying Ground Mechanical Degradation" Materials 18, no. 17: 4041. https://doi.org/10.3390/ma18174041
APA StyleCampo-Frances, G., Ferrer, S., Cayuela, D., & Carrera-Gallisà, E. (2025). Canvas-Ground Interaction: A New Approach to Quantifying Ground Mechanical Degradation. Materials, 18(17), 4041. https://doi.org/10.3390/ma18174041








