Engineering Metamaterials for Civil Infrastructure: From Acoustic Performance to Programmable Mechanical Responses
Abstract
1. Introduction
2. Properties of Metamaterials
| Dimensionality | Traditional | Metamaterial |
|---|---|---|
| Design objective | Static strength, stability, economy | Dynamic response [64], multifunctional integration [65], extreme environmental adaptability [38] |
| Freedom to innovate | Limited by inherent properties of materials | Defining new properties from microstructure and material combinations |
| Environmental interaction | Passively endure | Active sensing and adaptation [38] |
| Material system | Single homogeneous material or simple composite | Heterogeneous composite of multi-materials [66] |
| Upper limit of performance | Limited by material intrinsic properties | Defined by structural design |
| Environmental adaptability | Dependence on external protection | Intrinsic adaptation [67] |
| Function expandability | Low (external equipment required) | High (structure intrinsic multifunction) |
| Energy dependence | High (external power required) | Low (self-powered potential) |
3. Metamaterials in Vibration Control
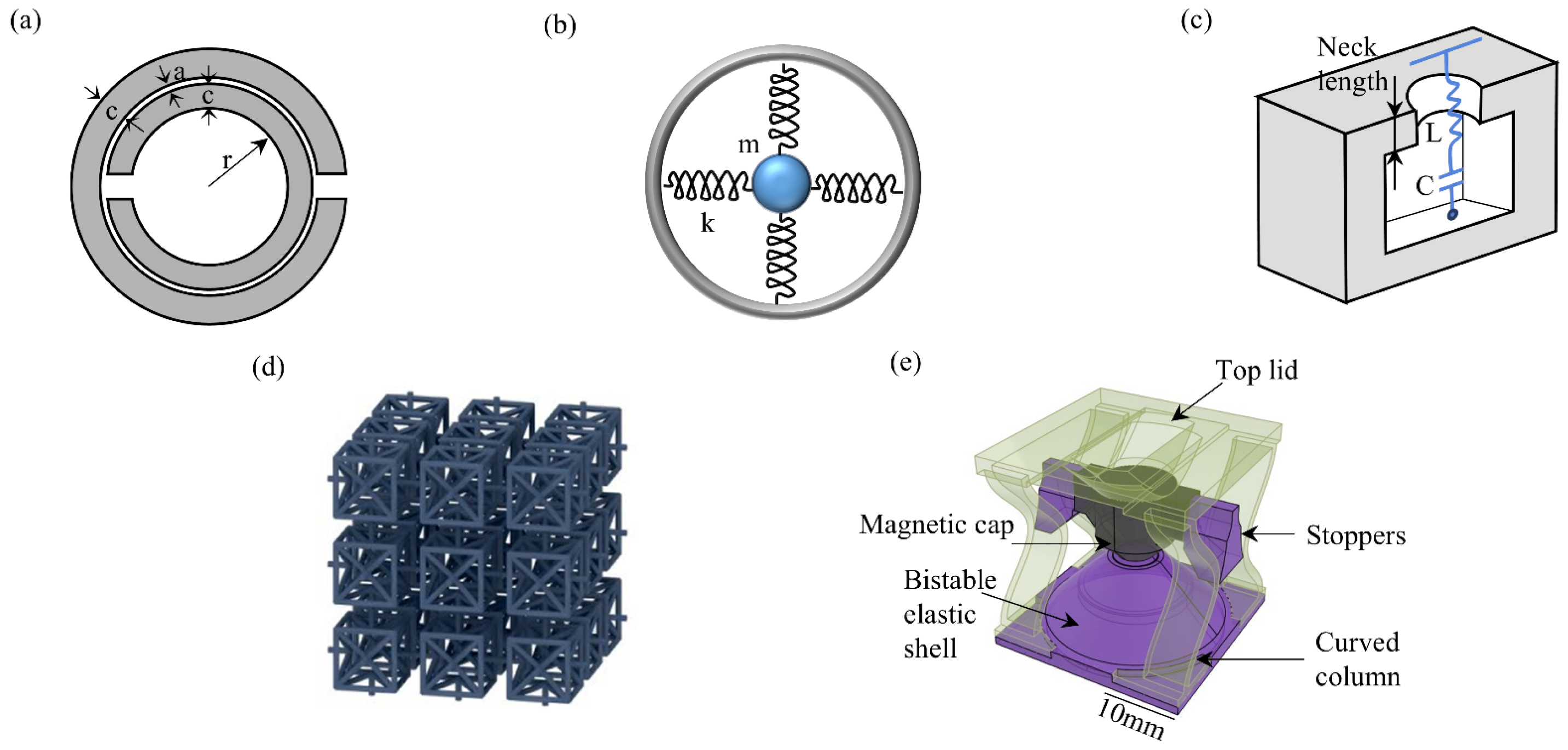
3.1. Vibration Control Using Cavity Resonators
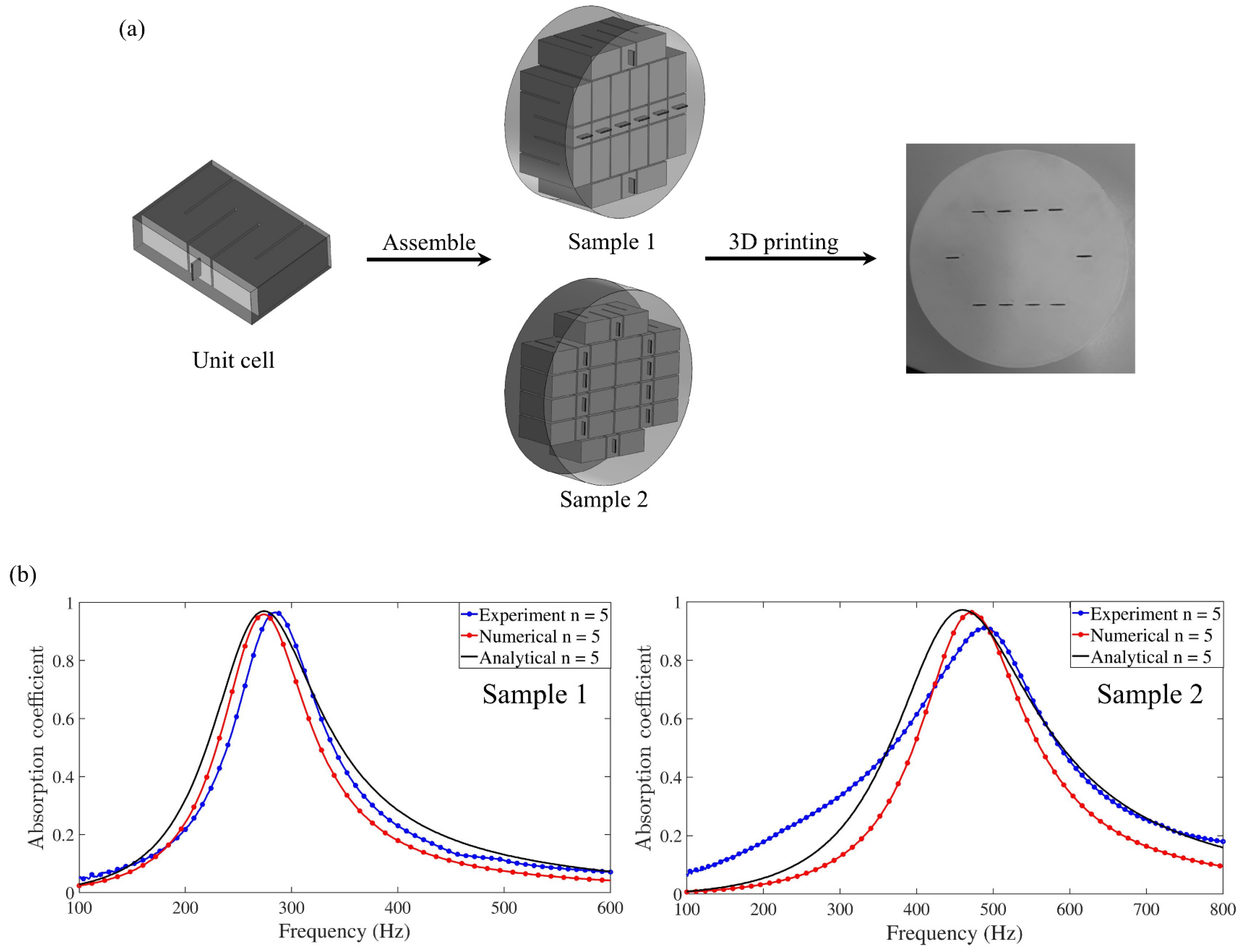
3.2. Vibration Control Using External Cavity Resonators
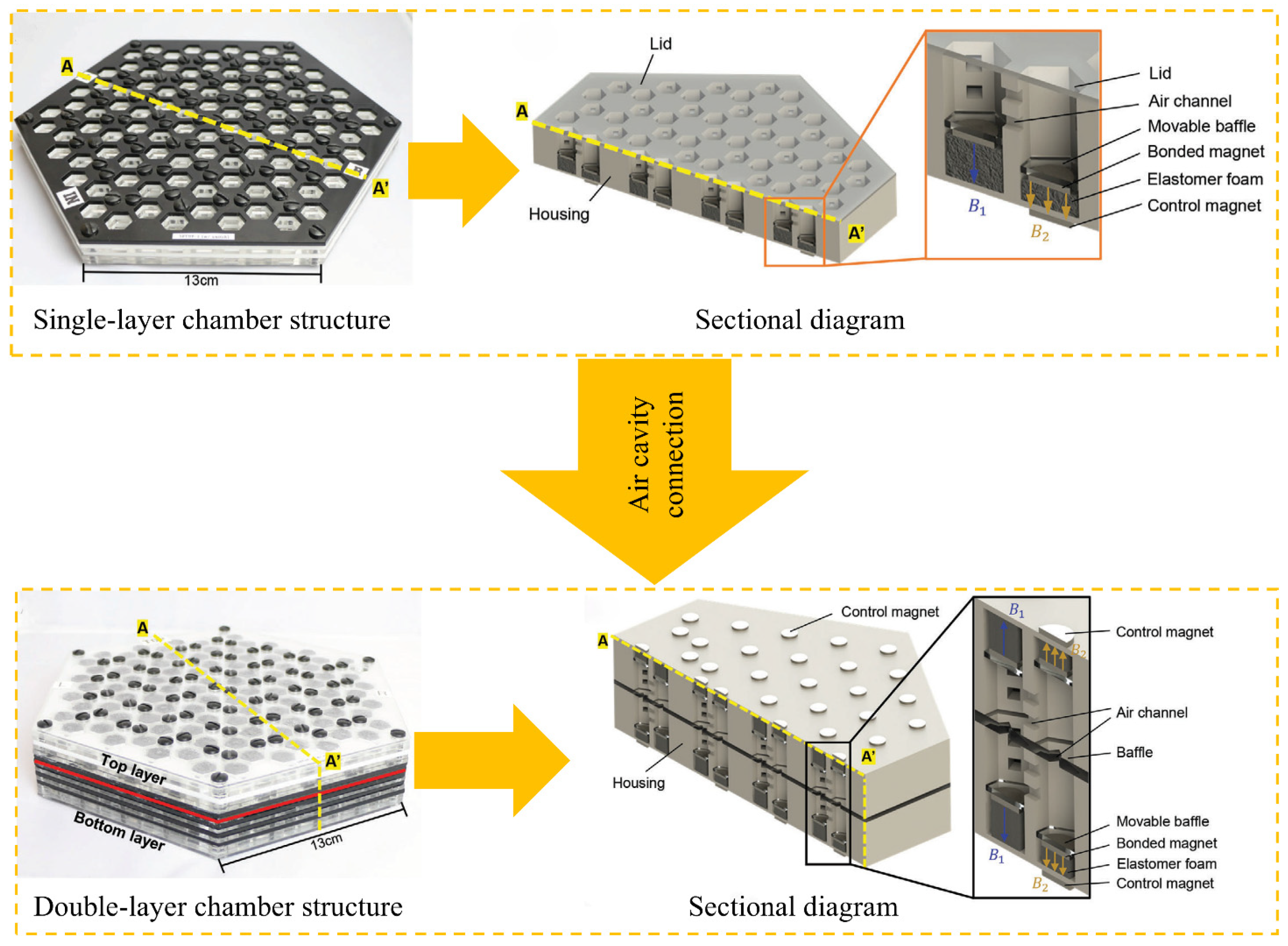
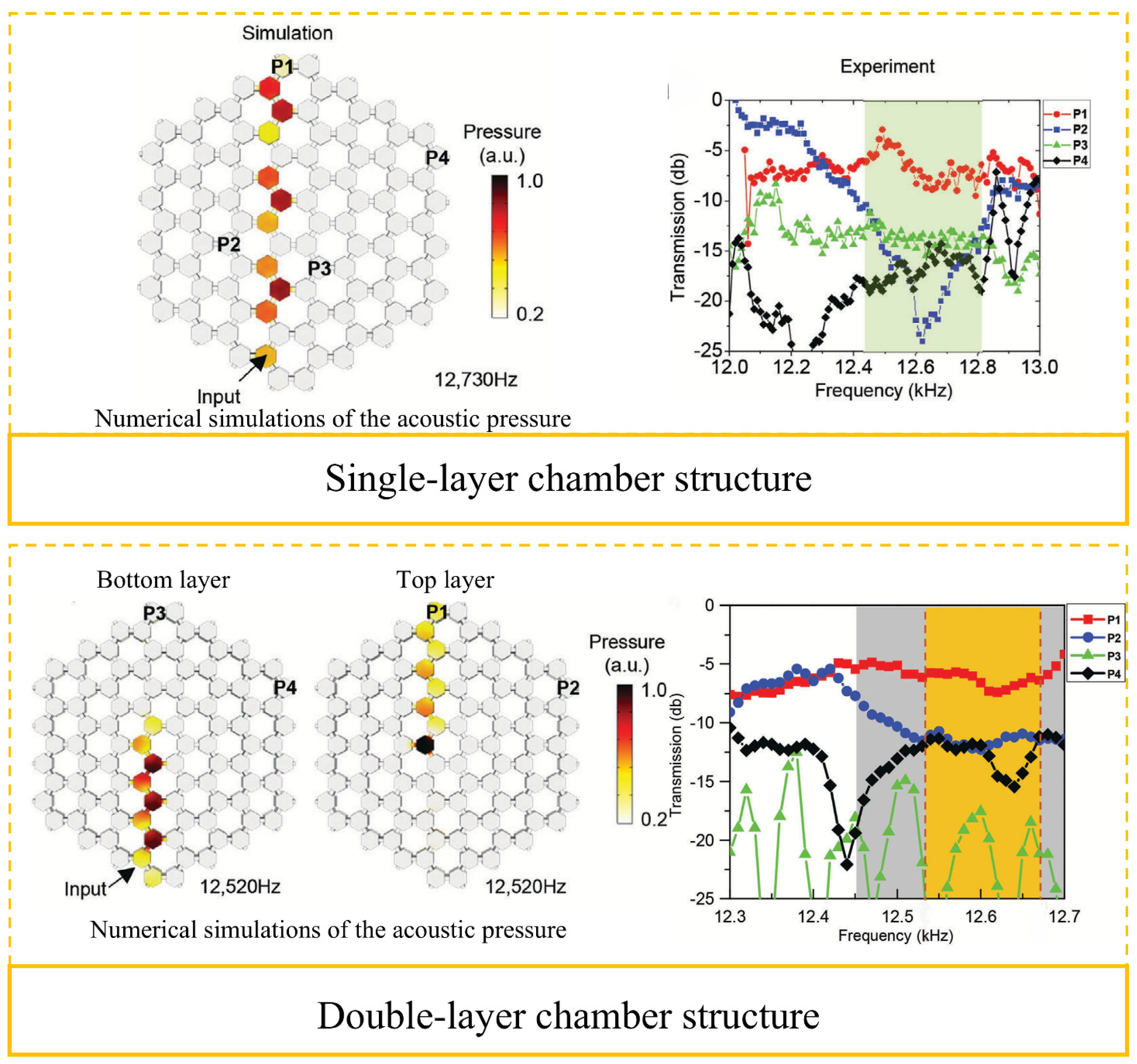
4. Metamaterials in Acoustic Performance
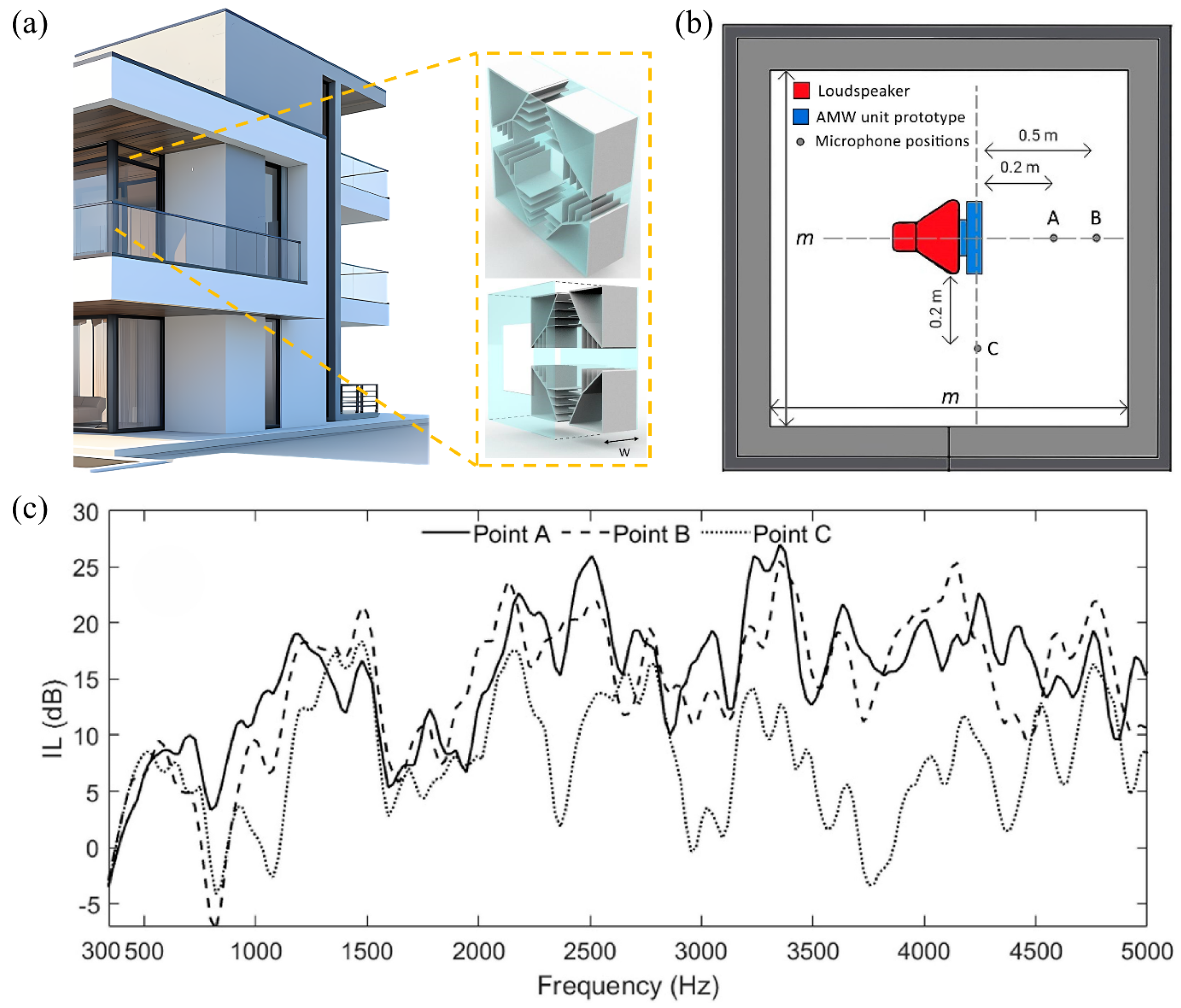
4.1. High-Rise Building Application
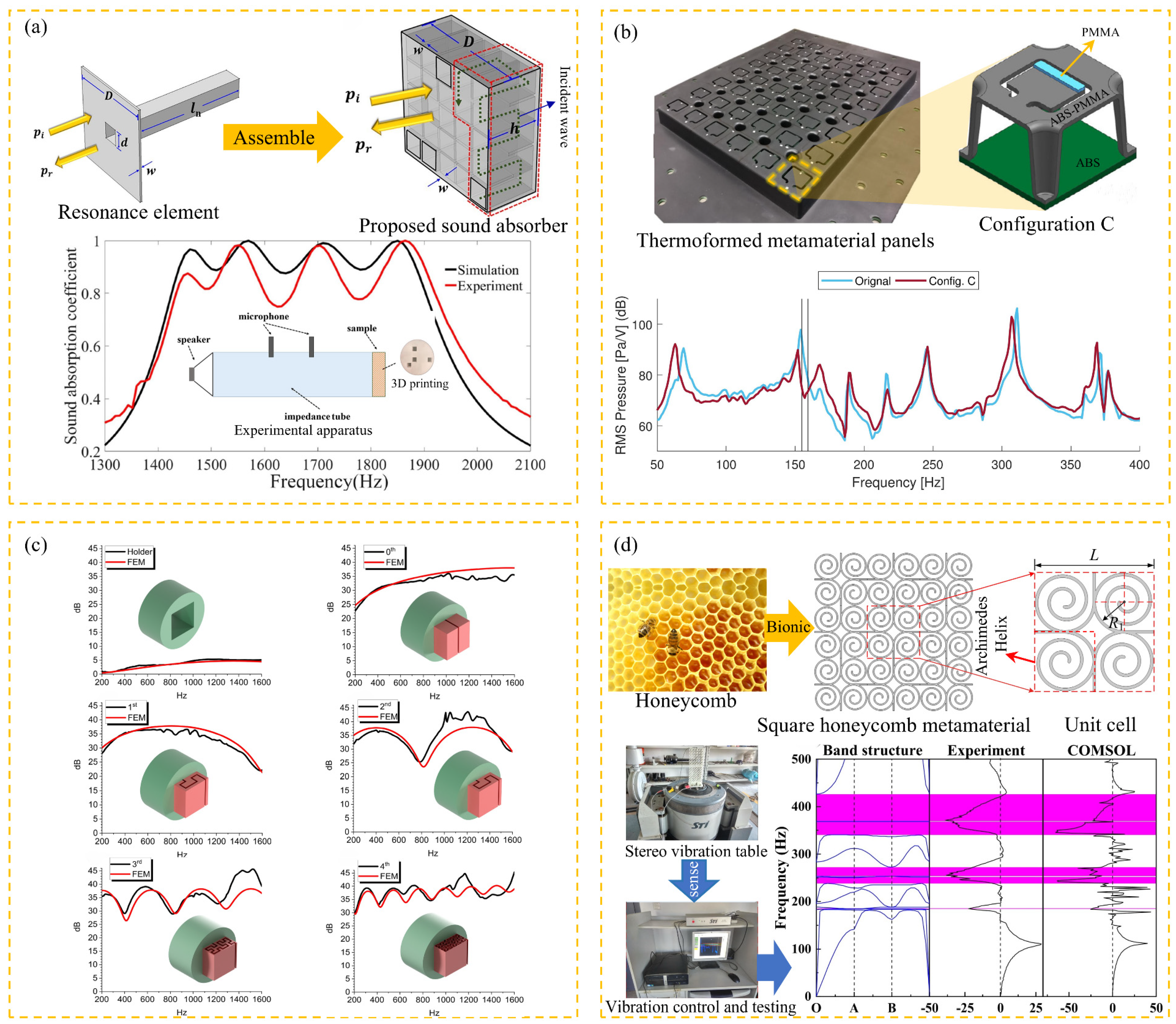
4.2. Public Place Application
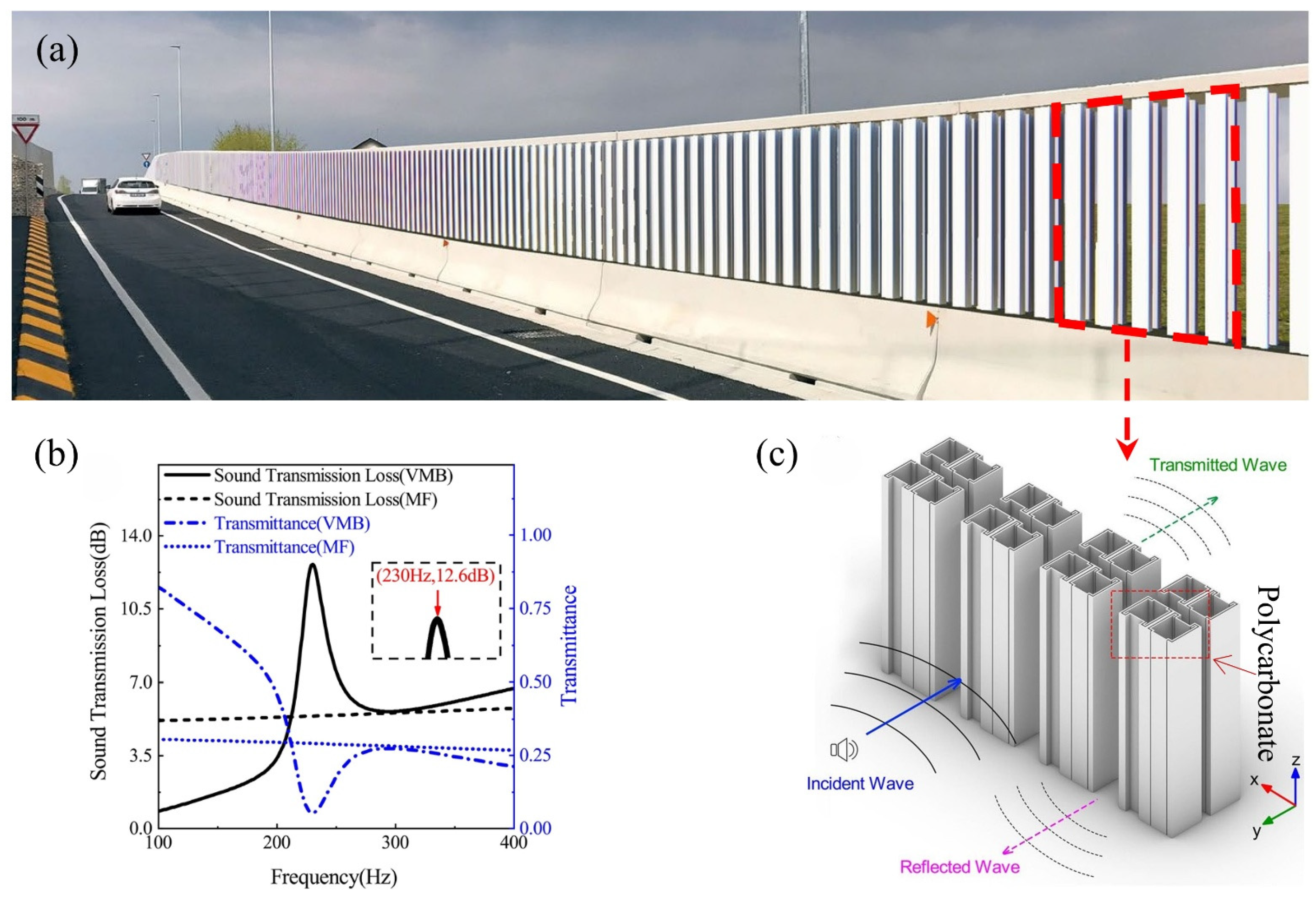
4.3. Road Traffic Application
4.4. Tunnel Engineering Application
4.5. Other Engineering Applications
5. Metamaterials in Mechanical Responses
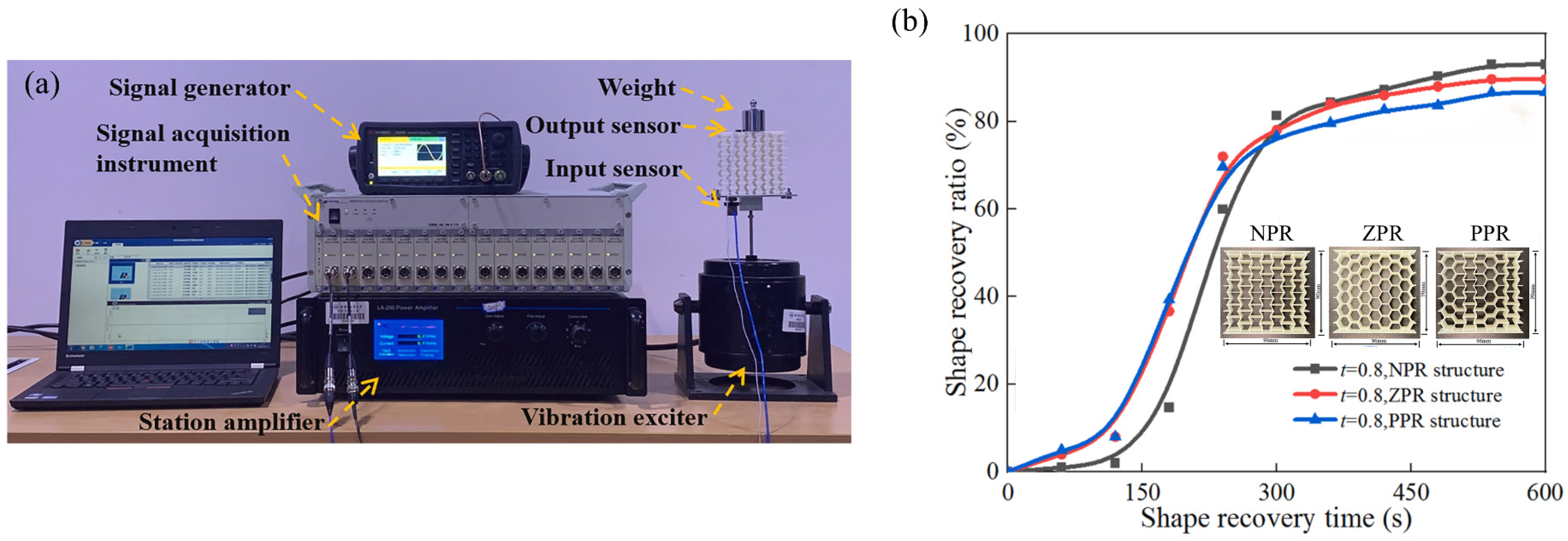
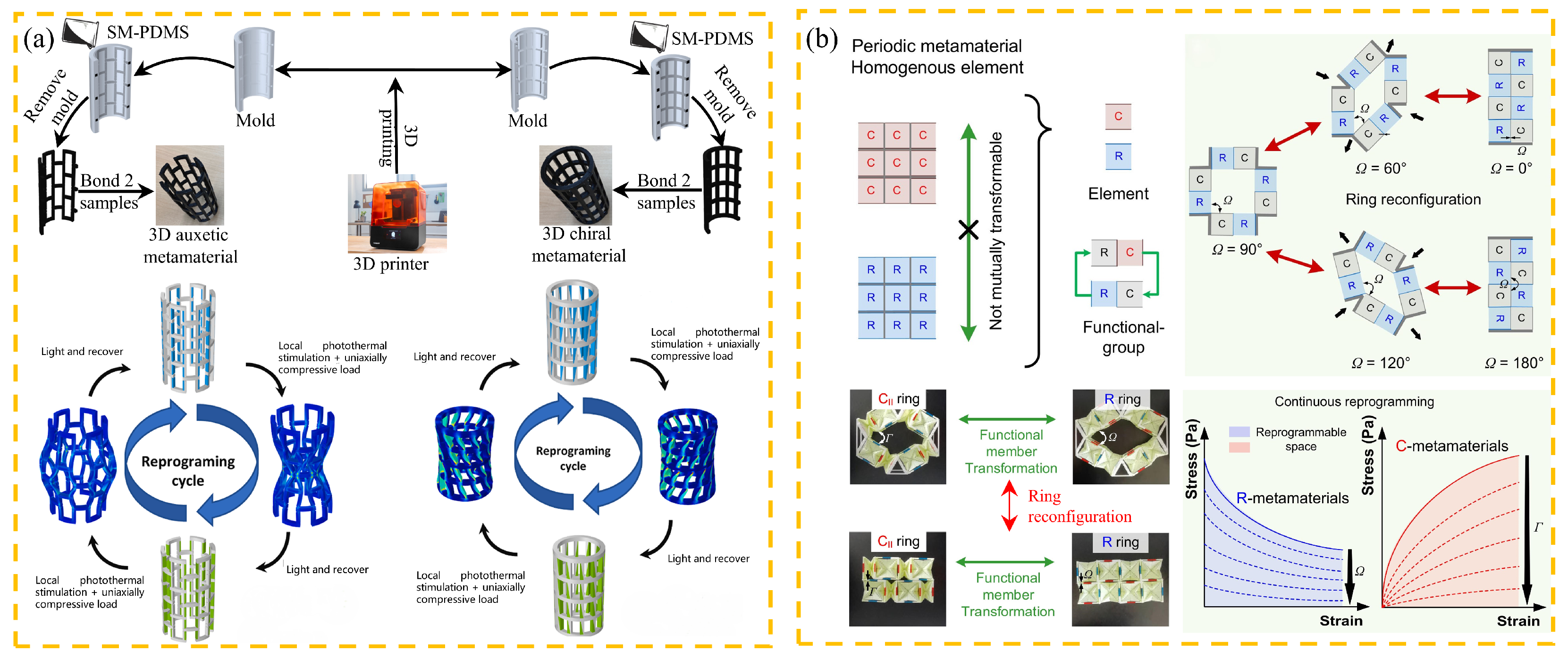
5.1. Shape Memory
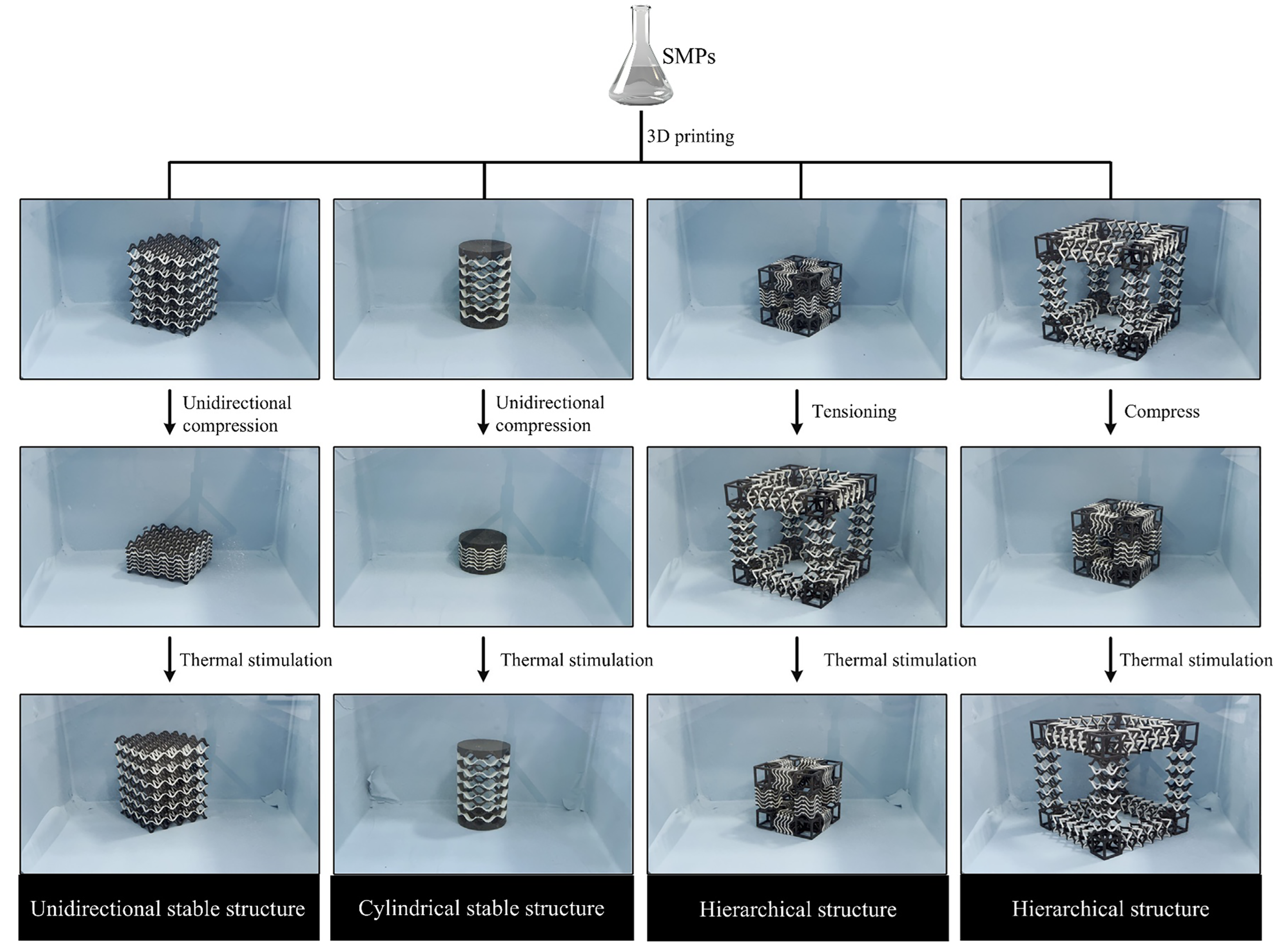
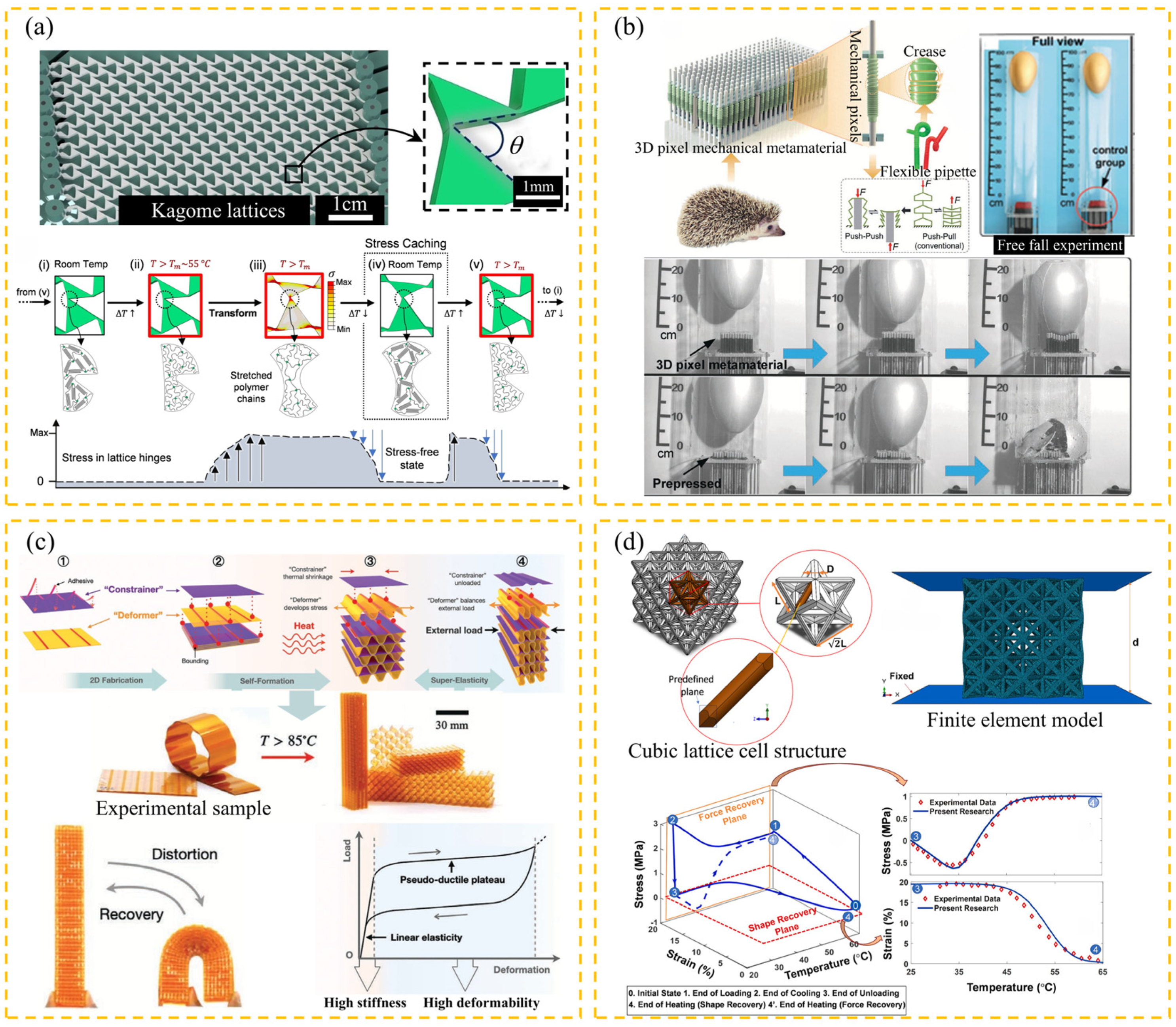
5.2. Extraordinary Stiffness and Toughness
| Test Type | Test Condition | Test Method | Assessment Criteria |
|---|---|---|---|
| Cycle fatigue | Pressure level 0.5 fc | Three-point bending or axial compression loading was applied at a frequency of 1 Hz until the specimen broke. | Stress–life curve, residual strength, stiffness degradation |
| Creep | Constant load 0.3 fc, 1000 days at 20 °C | A cylindrical specimen (Φ150 × 300 mm) was subjected to constant stress, and strain was continuously measured for 1000 days. | Creep coefficient |
| Cycle of freezing and thawing | 300 freeze–thaw cycles | After immersion, the specimen was subjected to freezing and thawing cycles between −18 °C and 4 °C, and the mass loss and dynamic elastic modulus were tested every 50 cycles. | Mass loss and dynamic elastic modulus |
| Chloride ion penetration | 90-day salt spray test | Immerse in 3% NaCl solution and periodically sample for chloride ion concentration profile. | Diffusion coefficient of chloride ion |
| Carbonization | CO2 concentration 20%, humidity 60%, 1 year | Under the condition of accelerated reaction test, carbonization was detected by phenolphthalein reagent. | Carbonation depth |
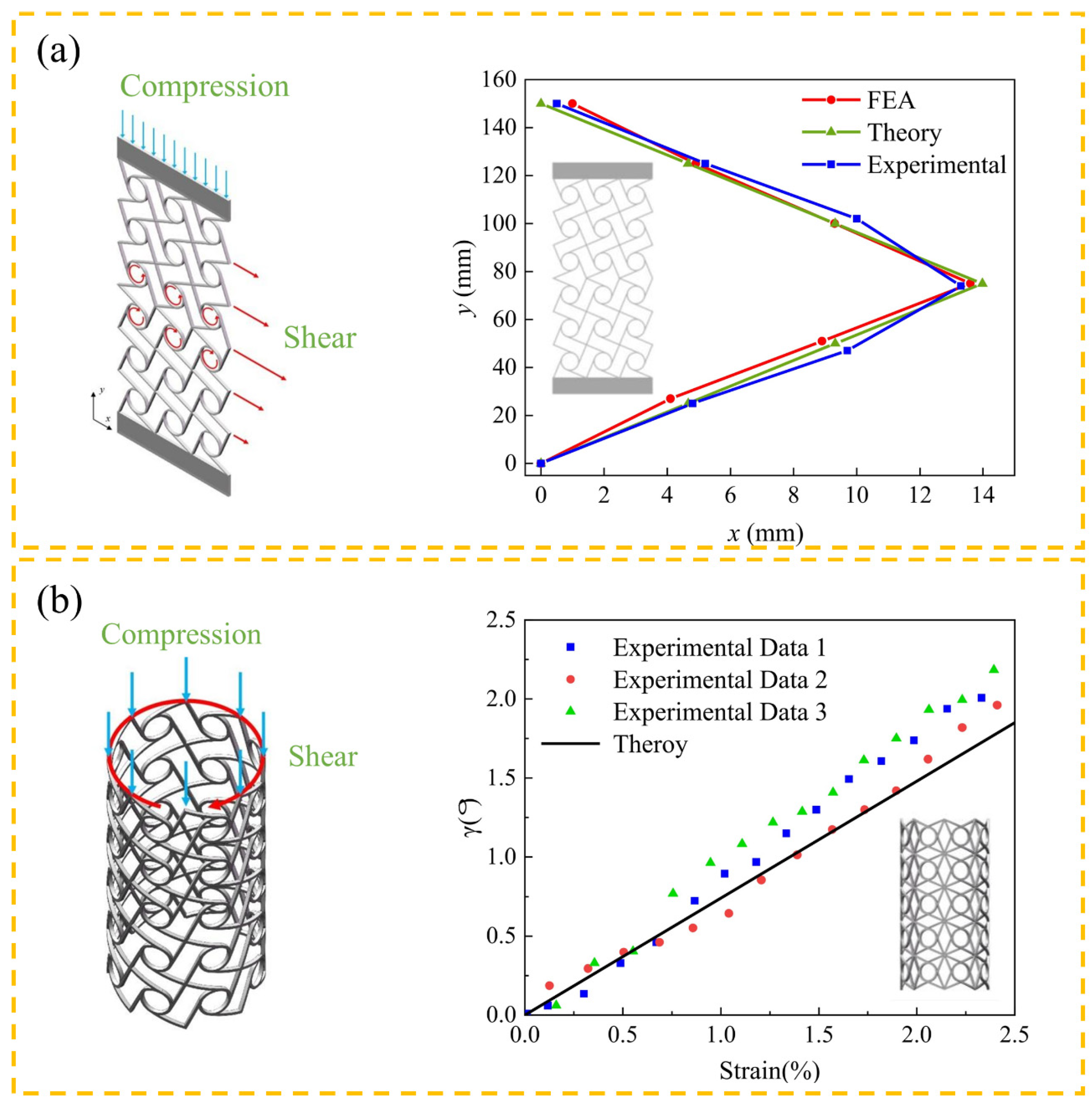
5.3. Mechanical Response
6. Conclusions and Prospects
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, K.; Fan, R.; Zhang, X.; Zhang, Z.; Shi, Z.; Wang, N.; Xie, P.; Wang, Z.; Fan, G.; Liu, H.; et al. Correction: An Overview of Metamaterials and Their Achievements in Wireless Power Transfer. J. Mater. Chem. C 2018, 6, 4328. [Google Scholar] [CrossRef]
- Engheta, N.; Ziolkowski, R.W. (Eds.) Metamaterials: Physics and Engineering Explorations, 1st ed.; Wiley-IEEE Press: Hoboken, NJ, USA, 2006; ISBN 978-0-471-76102-0. [Google Scholar]
- Pendry, J.B.; Holden, A.J.; Robbins, D.J.; Stewart, W.J. Magnetism from Conductors and Enhanced Nonlinear Phenomena. IEEE Trans. Microw. Theory Tech. 1999, 47, 2075–2084. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling Sound with Acoustic Metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Li, N.; Ren, J.; Wang, L.; Zhang, G.; Hänggi, P.; Li, B. Colloquium: Phononics: Manipulating Heat Flow with Electronic Analogs and Beyond. Rev. Mod. Phys. 2012, 84, 1045–1066. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef]
- Gliozzi, A.S.; Miniaci, M.; Krushynska, A.O.; Morvan, B.; Scalerandi, M.; Pugno, N.M.; Bosia, F. Proof of Concept of a Frequency-Preserving and Time-Invariant Metamaterial-Based Nonlinear Acoustic Diode. Sci. Rep. 2019, 9, 9560. [Google Scholar] [CrossRef]
- Kumar, S.; Lee, H. The Present and Future Role of Acoustic Metamaterials for Architectural and Urban Noise Mitigations. Acoustics 2019, 1, 590–607. [Google Scholar] [CrossRef]
- Huang, Z.; Zhao, Z.; Zhao, S.; Cai, X.; Zhang, Y.; Cai, Z.; Li, H.; Li, Z.; Su, M.; Zhang, C.; et al. Lotus Metasurface for Wide-Angle Intermediate-Frequency Water-Air Acoustic Transmission. ACS Appl. Mater. Interfaces 2021, 13, 53242–53251. [Google Scholar] [CrossRef]
- Badino, E.; Shtrepi, L.; Astolfi, A. Acoustic Performance-Based Design: A Brief Overview of the Opportunities and Limits in Current Practice. Acoustics 2020, 2, 246–278. [Google Scholar] [CrossRef]
- Lee, K.H.; Yu, K.; Al Ba’ba’a, H.; Xin, A.; Feng, Z.; Wang, Q. Sharkskin-Inspired Magnetoactive Reconfigurable Acoustic Metamaterials. Research 2020, 2020, 4825185. [Google Scholar] [CrossRef]
- Qi, Y.; Zhang, Y.; Liu, C.; Zhang, T.; Zhang, B.; Wang, L.; Deng, X.; Wang, X.; Yu, Y. A Tunable Terahertz Metamaterial Absorber Composed of Hourglass-Shaped Graphene Arrays. Nanomaterials 2020, 10, 533. [Google Scholar] [CrossRef]
- Yi, Z.; Liang, C.; Chen, X.; Zhou, Z.; Tang, Y.; Ye, X.; Yi, Y.; Wang, J.; Wu, P. Dual-Band Plasmonic Perfect Absorber Based on Graphene Metamaterials for Refractive Index Sensing Application. Micromachines 2019, 10, 443. [Google Scholar] [CrossRef]
- Mirabolghasemi, A.; Akbarzadeh, A.H.; Rodrigue, D.; Therriault, D. Thermal Conductivity of Architected Cellular Metamaterials. Acta Mater. 2019, 174, 61–80. [Google Scholar] [CrossRef]
- Mahani, R.B.; Mohammed, H.I.; Mahdi, J.M.; Alamshahi, F.; Ghalambaz, M.; Talebizadehsardari, P.; Yaïci, W. Phase Change Process in a Zigzag Plate Latent Heat Storage System during Melting and Solidification. Molecules 2020, 25, 4643. [Google Scholar] [CrossRef]
- Chen, T.; Lin, J.H. Novel Connections and Physical Implications of Thermal Metamaterials with Imperfect Interfaces. Sci. Rep. 2022, 12, 2734. [Google Scholar] [CrossRef]
- So, S.; Mun, J.; Rho, J. Simultaneous Inverse Design of Materials and Structures via Deep Learning: Demonstration of Dipole Resonance Engineering Using Core-Shell Nanoparticles. ACS Appl. Mater. Interfaces 2019, 11, 24264–24268. [Google Scholar] [CrossRef]
- Bilal, O.R.; Foehr, A.; Daraio, C. Bistable Metamaterial for Switching and Cascading Elastic Vibrations. Proc. Natl. Acad. Sci. USA 2017, 114, 4603–4606. [Google Scholar] [CrossRef] [PubMed]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, Ultrastiff Mechanical Metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef] [PubMed]
- Al Sabouni-Zawadzka, A. Extreme Mechanical Properties of Regular Tensegrity Unit Cells in 3D Lattice Metamaterials. Materials 2020, 13, 4845. [Google Scholar] [CrossRef] [PubMed]
- Xue, T.; Beatson, A.; Chiaramonte, M.; Roeder, G.; Ash, J.T.; Menguc, Y.; Adriaenssens, S.; Adams, R.P.; Mao, S. A Data-Driven Computational Scheme for the Nonlinear Mechanical Properties of Cellular Mechanical Metamaterials under Large Deformation. Soft Matter 2020, 16, 7524–7534. [Google Scholar] [CrossRef]
- Dalela, S.; Balaji, P.S.; Jena, D.P. A Review on Application of Mechanical Metamaterials for Vibration Control. Mech. Adv. Mater. Struct. 2022, 29, 3237–3262. [Google Scholar] [CrossRef]
- Barri, K.; Jiao, P.; Zhang, Q.; Chen, J.; Lin Wang, Z.; Alavi, A.H. Multifunctional Meta-Tribomaterial Nanogenerators for Energy Harvesting and Active Sensing. Nano Energy 2021, 86, 106074. [Google Scholar] [CrossRef]
- Jiao, P.; Hong, L.; Wang, J.; Yang, J.; Zhu, R.; Lajnef, N.; Zhu, Z. Self-Triggered Thermomechanical Metamaterials with Asymmetric Structures for Programmable Response under Thermal Excitations. Materials 2021, 14, 2177. [Google Scholar] [CrossRef]
- Zhang, S.; Yin, L.; Fang, N. Focusing Ultrasound with an Acoustic Metamaterial Network. Phys. Rev. Lett. 2009, 102, 194301. [Google Scholar] [CrossRef]
- Fusaro, G.; Yu, X.; Lu, Z.; Cui, F.; Kang, J. A Metawindow with Optimised Acoustic and Ventilation Performance. Appl. Sci. 2021, 11, 3168. [Google Scholar] [CrossRef]
- Bertoldi, K.; Vitelli, V.; Christensen, J.; Van Hecke, M. Flexible Mechanical Metamaterials. Nat. Rev. Mater. 2017, 2, 17066. [Google Scholar] [CrossRef]
- Lee, J.; Singer, J.P.; Thomas, E.L. Micro-/Nanostructured Mechanical Metamaterials. Adv. Mater. 2012, 24, 4782–4810. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Inda, M.E.; Lai, Y.; Lu, T.K.; Zhao, X. Engineered Living Hydrogels. Adv. Mater. 2022, 34, 2201326. [Google Scholar] [CrossRef]
- Yao, H.; Wang, Y.; Liu, J.; Xu, M.; Ma, P.; Ji, J.; You, Z. Review on Applications of Lignin in Pavement Engineering: A Recent Survey. Front. Mater. 2022, 8, 803524. [Google Scholar] [CrossRef]
- Zhong, H.; Zhang, M. Engineered Geopolymer Composites: A State-of-the-Art Review. Cem. Concr. Compos. 2023, 135, 104850. [Google Scholar] [CrossRef]
- He, P.; Du, T.; Zhao, K.; Dong, J.; Liang, Y.; Zhang, Q. Lightweight 3D Graphene Metamaterials with Tunable Negative Thermal Expansion. Adv. Mater. 2023, 35, e2208562. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Roberts, P.C.E.; Lyu, S.; Zheng, F.; Soutis, C.; Diver, C.; Zhou, D.; Li, L.; Deng, Z. Lightweight Self-Forming Super-Elastic Mechanical Metamaterials with Adaptive Stiffness. Adv. Funct. Mater. 2021, 31, 2008252. [Google Scholar] [CrossRef]
- Appusamy, S.; Krishnan, S.; Gopikrishna, M.; Raman, S. Bio-Based Materials for Microwave Devices: A Review. J. Electron. Mater. 2021, 50, 1893–1921. [Google Scholar] [CrossRef]
- Barbaros, I.; Yang, Y.; Safaei, B.; Yang, Z.; Qin, Z.; Asmael, M. State-of-the-Art Review of Fabrication, Application, and Mechanical Properties of Functionally Graded Porous Nanocomposite Materials. Nanotechnol. Rev. 2022, 11, 321–371. [Google Scholar] [CrossRef]
- Xu, P.; Lan, X.; Zeng, C.; Zhang, X.; Zhao, H.; Leng, J.; Liu, Y. Compression Behavior of 4D Printed Metamaterials with Various Poisson’s Ratios. Int. J. Mech. Sci. 2024, 264, 108819. [Google Scholar] [CrossRef]
- Jolly, J.C.; Jin, B.; Jin, L.; Lee, Y.; Xie, T.; Gonella, S.; Sun, K.; Mao, X.; Yang, S. Soft Mechanical Metamaterials with Transformable Topology Protected by Stress Caching. Adv. Sci. 2023, 10, e2302475. [Google Scholar] [CrossRef]
- Jiao, P.; Mueller, J.; Raney, J.R.; Zheng, X.R.; Alavi, A.H. Mechanical Metamaterials and Beyond. Nat. Commun. 2023, 14, 6004. [Google Scholar] [CrossRef]
- Hu, X.; Tan, T.; Wang, B.; Yan, Z. A Reprogrammable Mechanical Metamaterial with Origami Functional-Group Transformation and Ring Reconfiguration. Nat. Commun. 2023, 14, 6709. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.; Chen, W.W.; Wang, L.; Chan, Y.C.; Chen, W. Data-Driven Design for Metamaterials and Multiscale Systems: A Review. Adv. Mater. 2024, 36, e2305254. [Google Scholar] [CrossRef]
- Liu, H.; Li, L.; Wei, Z.; Smedskjaer, M.M.; Zheng, X.R.; Bauchy, M. De Novo Atomistic Discovery of Disordered Mechanical Metamaterials by Machine Learning. Adv. Sci. 2024, 11, e2304834. [Google Scholar] [CrossRef]
- Sun, C.; Liu, H.; Yang, B.; Zhang, K.; Zhang, B.; Wu, X. An Ultra-Broadband and Wide-Angle Absorber Based on a TiN Metamaterial for Solar Harvesting. Phys. Chem. Chem. Phys. 2023, 25, 806–812. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, Y.; Feng, Y.; Yi, Z.; Liu, H.; Wu, X. Efficient Solar Energy Absorber Based on Titanium Nitride Metamaterial. Plasmonics 2023, 18, 2187–2194. [Google Scholar] [CrossRef]
- Barri, K.; Zhang, Q.; Kline, J.; Lu, W.; Luo, J.; Sun, Z.; Taylor, B.E.; Sachs, S.G.; Khazanovich, L.; Wang, Z.L.; et al. Multifunctional Nanogenerator-Integrated Metamaterial Concrete Systems for Smart Civil Infrastructure. Adv. Mater. 2023, 35, e2211027. [Google Scholar] [CrossRef] [PubMed]
- Gulia, P.; Gupta, A. Traffic Noise Control by Periodically Arranged Trees. Res. J. 2016, 2, 10–14. [Google Scholar]
- Fan, W.; Cheng, Z.; Xu, S.; Dou, Y. A Novel Ventilated Metamaterial Barrier (VMB) for Traffic Noise Reduction. J. Vib. Eng. Technol. 2023, 12, 4495–4510. [Google Scholar] [CrossRef]
- Schwarz, A.; Lichti, T.; Wenz, F.; Scheuring, B.M.; Hübner, C.; Eberl, C.; Elsner, P. Development of a Scalable Fabrication Concept for Sustainable, Programmable Shape-Morphing Metamaterials. Adv. Eng. Mater. 2022, 24, 2200386. [Google Scholar] [CrossRef]
- Chui, S.; Hu, L. Theoretical Investigation on the Possibility of Preparing Left-Handed Materials in Metallic Magnetic Granular Composites. Phys. Rev. B 2002, 65, 144407. [Google Scholar] [CrossRef]
- Sun, K.; Zhang, Z.; Fan, R.; Chen, M.; Cheng, C.; Hou, Q.; Zhang, X.; Liu, Y. Random Copper/Yttrium Iron Garnet Composites with Tunable Negative Electromagnetic Parameters Prepared by in Situ Synthesis. RSC Adv. 2015, 5, 61155–61160. [Google Scholar] [CrossRef]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental Verification of a Negative Index of Refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef]
- Yang, Z.; Mei, J.; Yang, M.; Chan, N.H.; Sheng, P. Membrane-Type Acoustic Metamaterial with Negative Dynamic Mass. Phys. Rev. Lett. 2008, 101, 204301. [Google Scholar] [CrossRef]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic Metamaterials with Negative Modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef]
- Zhai, S.; Chen, H.; Ding, C.; Zhao, X. Double-Negative Acoustic Metamaterial Based on Meta-Molecule. J. Phys. D Appl. Phys. 2013, 46, 475105. [Google Scholar] [CrossRef]
- Ding, C.L.; Dong, Y.B.; Zhao, X.-P. Research advances in acoustic metamaterials and metasurface. Acta Phys. Sin. 2018, 67, 194301. [Google Scholar] [CrossRef]
- Lu, M.H.; Feng, L.; Chen, Y.F. Phononic Crystals and Acoustic Metamaterials. Mater. Today 2009, 12, 34–42. [Google Scholar] [CrossRef]
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired Structural Materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Feng, Z.; Hao, L.; Huang, L.; Xin, C.; Wang, Y.; Bilotti, E.; Essa, K.; Zhang, H.; Li, Z.; et al. A Review on Functionally Graded Materials and Structures via Additive Manufacturing: From Multi-Scale Design to Versatile Functional Properties. Adv. Mater. Technol. 2020, 5, 1900981. [Google Scholar] [CrossRef]
- Greer, J.R.; De Hosson, J.T.M. Plasticity in Small-Sized Metallic Systems: Intrinsic versus Extrinsic Size Effect. Prog. Mater. Sci. 2011, 56, 654–724. [Google Scholar] [CrossRef]
- Gu, X.W.; Loynachan, C.N.; Wu, Z.; Zhang, Y.W.; Srolovitz, D.J.; Greer, J.R. Size-Dependent Deformation of Nanocrystalline Pt Nanopillars. Nano Lett. 2012, 12, 6385–6392. [Google Scholar] [CrossRef]
- Gao, H.J.; Ji, B.H.; Jäger, I.L.; Arzt, E.; Fratzl, P. Materials Become Insensitive to Flaws at Nanoscale:: Lessons from Nature. Proc. Natl. Acad. Sci. USA 2003, 100, 5597–5600. [Google Scholar] [CrossRef]
- Chen, T.; Pauly, M.; Reis, P.M. A Reprogrammable Mechanical Metamaterial with Stable Memory. Nature 2021, 589, 386–390. [Google Scholar] [CrossRef]
- Smith, D.R.; Padilla, W.J.; Vier, D.C.; Nemat-Nasser, S.C.; Schultz, S. Composite Medium with Simultaneously Negative Permeability and Permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.Y.; Shen, C.; Jing, Y. Membrane- and Plate-Type Acoustic Metamaterials. J. Acoust. Soc. Am. 2016, 139, 3240–3250. [Google Scholar] [CrossRef] [PubMed]
- Schwartz, M.; Lagerwall, J.P.F. Embedding Intelligence in Materials for Responsive Built Environment: A Topical Review on Liquid Crystal Elastomer Actuators and Sensors. Build. Environ. 2022, 226, 109714. [Google Scholar] [CrossRef]
- Yuan, X.; Chen, M.; Yao, Y.; Guo, X.; Huang, Y.; Peng, Z.; Xu, B.; Lv, B.; Tao, R.; Duan, S.; et al. Recent Progress in the Design and Fabrication of Multifunctional Structures Based on Metamaterials. Curr. Opin. Solid. State Mat. Sci. 2021, 25, 100883. [Google Scholar] [CrossRef]
- Singh, R.; Kumar, R.; Farina, I.; Colangelo, F.; Feo, L.; Fraternali, F. Multi-Material Additive Manufacturing of Sustainable Innovative Materials and Structures. Polymers 2019, 11, 62. [Google Scholar] [CrossRef]
- Ding, X.H.; Luo, B.; Zhou, H.T.; Chen, Y.H. Generalized Solutions for Advection–Dispersion Transport Equations Subject to Time- and Space-Dependent Internal and Boundary Sources. Comput. Geotech. 2025, 178, 106944. [Google Scholar] [CrossRef]
- Liu, S.; Chen, H.; Liu, Y.; He, H.; An, X.; Jin, F.; Fan, H. Vibration Attenuation of Meta-Mortar with Spring-Mass Resonators. Def. Technol. 2023, 20, 11–23. [Google Scholar] [CrossRef]
- Chen, H.; Li, X.P.; Chen, Y.Y.; Huang, G.L. Wave Propagation and Absorption of Sandwich Beams Containing Interior Dissipative Multi-Resonators. Ultrasonics 2017, 76, 99–108. [Google Scholar] [CrossRef]
- Vo, N.H.; Pham, T.M.; Hao, H.; Bi, K.; Chen, W. Experimental and Numerical Validation of Impact Mitigation Capability of Meta-Panels. Int. J. Mech. Sci. 2022, 231, 107591. [Google Scholar] [CrossRef]
- Manimala, J.M.; Huang, H.H.; Sun, C.T.; Snyder, R.; Bland, S. Dynamic Load Mitigation Using Negative Effective Mass Structures. Eng. Struct. 2014, 80, 458–468. [Google Scholar] [CrossRef]
- Ma, G.; Fu, C.; Wang, G.; del Hougne, P.; Christensen, J.; Lai, Y.; Sheng, P. Polarization Bandgaps and Fluid-like Elasticity in Fully Solid Elastic Metamaterials. Nat. Commun. 2016, 7, 13536. [Google Scholar] [CrossRef]
- Mitchell, S.J.; Pandolfi, A.; Ortiz, M. Metaconcrete: Designed Aggregates to Enhance Dynamic Performance. J. Mech. Phys. Solids 2014, 65, 69–81. [Google Scholar] [CrossRef]
- Quinteros, L.; Meruane, V.; Lenz Cardoso, E.; Ruiz, R.O. Phononic Bandgap Optimization in Sandwich Panels Using Cellular Truss Cores. Materials 2021, 14, 5236. [Google Scholar] [CrossRef] [PubMed]
- Su, Y.C.; Wang, S.S. Gradient V-Shaped and N-Shaped Seismic Metamaterials. Materials 2023, 16, 3074. [Google Scholar] [CrossRef]
- Osman, M.M.; Shazly, M.; El-Danaf, E.A.; Jamshidi, P.; Attallah, M.M. Compressive Behavior of Stretched and Composite Microlattice Metamaterial for Energy Absorption Applications. Compos. Part B Eng. 2020, 184, 107715. [Google Scholar] [CrossRef]
- Vo, N.H.; Pham, T.M.; Hao, H.; Bi, K.; Chen, W.; Ngoc, S.H. Blast Resistant Enhancement of Meta-Panels Using Multiple Types of Resonators. Int. J. Mech. Sci. 2022, 215, 106965. [Google Scholar] [CrossRef]
- Yu, D.; Liu, Y.; Zhao, H.; Wang, G.; Qiu, J. Flexural Vibration Band Gaps in Euler-Bernoulli Beams with Locally Resonant Structures with Two Degrees of Freedom. Phys. Rev. B 2006, 73, 064301. [Google Scholar] [CrossRef]
- Kim, S.H.; Das, M.P. Artificial Seismic Shadow Zone by Acoustic Metamaterials. Mod. Phys. Lett. B 2013, 27, 1350140. [Google Scholar] [CrossRef]
- Colombi, A.; Roux, P.; Guenneau, S.; Gueguen, P.; Craster, R.V. Forests as a Natural Seismic Metamaterial: Rayleigh Wave Bandgaps Induced by Local Resonances. Sci. Rep. 2016, 6, 19238. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Y.; Peng, P.; Du, Q.-J.; Wang, Y.S.; Assouar, B. Subwavelength Seismic Metamaterial with an Ultra-Low Frequency Bandgap. J. Appl. Phys. 2020, 128, 014901. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, Y.; Yang, H.; Muzamil, M.; Xu, R.; Deng, K.; Peng, P.; Du, Q. A Matryoshka-like Seismic Metamaterial with Wide Band-Gap Characteristics. Int. J. Solids Struct. 2020, 185, 334–341. [Google Scholar] [CrossRef]
- Lou, J.; Fang, X.; Fan, H.; Du, J. A Nonlinear Seismic Metamaterial Lying on Layered Soils. Eng. Struct. 2022, 272, 115032. [Google Scholar] [CrossRef]
- Wang, X.; Wan, S.; Nian, Y.; Zhou, P.; Zhu, Y. Periodic In-Filled Pipes Embedded in Semi-Infinite Space as Seismic Metamaterials for Filtering Ultra-Low-Frequency Surface Waves. Constr. Build. Mater. 2021, 313, 125498. [Google Scholar] [CrossRef]
- Shi, Z.; Cheng, Z.; Xiang, H. Seismic Isolation Foundations with Effective Attenuation Zones. Soil. Dyn. Earthq. Eng. 2014, 57, 143–151. [Google Scholar] [CrossRef]
- La Salandra, V.; Wenzel, M.; Bursi, O.S.; Carta, G.; Movchan, A.B. Conception of a 3D Metamaterial-Based Foundation for Static and Seismic Protection of Fuel Storage Tanks. Front. Mater. 2017, 4, 30. [Google Scholar] [CrossRef]
- Achaoui, Y.; Ungureanu, B.; Enoch, S.; Brule, S.; Guenneau, S. Seismic Waves Damping with Arrays of Inertial Resonators. Extrem. Mech. Lett. 2016, 8, 30–37. [Google Scholar] [CrossRef]
- Xiang, H.J.; Shi, Z.F.; Wang, S.J.; Mo, Y.L. Periodic Materials-Based Vibration Attenuation in Layered Foundations: Experimental Validation. Smart Mater. Struct. 2012, 21, 112003. [Google Scholar] [CrossRef]
- Witarto, W.; Wang, S.J.; Yang, C.Y.; Nie, X.; Mo, Y.L.; Chang, K.C.; Tang, Y.; Kassawara, R. Seismic Isolation of Small Modular Reactors Using Metamaterials. AIP Adv. 2018, 8, 045307. [Google Scholar] [CrossRef]
- Yu, D.; Wen, J.; Zhao, H.; Liu, Y.; Wen, X. Vibration Reduction by Using the Idea of Phononic Crystals in a Pipe-Conveying Fluid. J. Sound Vib. 2008, 318, 193–205. [Google Scholar] [CrossRef]
- Asiri, S.A.; AL-Zahrani, Y.Z. Theoretical Analysis of Mechanical Vibration for Offshore Platform Structures. World J. Mech. 2014, 4, 1–11. [Google Scholar] [CrossRef]
- Huang, T.T.; Ren, X.; Zeng, Y.; Zhang, Y.; Luo, C.; Zhang, X.Y.; Xie, Y.M. Based on Auxetic Foam: A Novel Type of Seismic Metamaterial for Lamb Waves. Eng. Struct. 2021, 246, 112976. [Google Scholar] [CrossRef]
- Mohamed, A.M.O.; Paleologos, E.K.; Howari, F.M. Noise Pollution and Its Impact on Human Health and the Environment. In Pollution Assessment for Sustainable Practices in Applied Sciences and Engineering; Elsevier: Amsterdam, The Netherlands, 2021; pp. 975–1026. ISBN 978-0-12-809582-9. [Google Scholar]
- Yamamoto, T. Acoustic Metamaterial Plate Embedded with Helmholtz Resonators for Extraordinary Sound Transmission Loss. J. Appl. Phys. 2018, 123, 215110. [Google Scholar] [CrossRef]
- Guo, H.; Wang, Y.; Wang, X.; Xu, C. Investigation on Acoustic Energy Harvesting Based on Quarter-Wavelength Resonator Phononic Crystals. Adv. Mech. Eng. 2018, 10, 1687814017748077. [Google Scholar] [CrossRef]
- Li, Y.; Liang, B.; Zou, X.; Cheng, J. Extraordinary Acoustic Transmission through Ultrathin Acoustic Metamaterials by Coiling up Space. Appl. Phys. Lett. 2013, 103, 063509. [Google Scholar] [CrossRef]
- Ma, G.; Sheng, P. Acoustic Metamaterials: From Local Resonances to Broad Horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef] [PubMed]
- Fusaro, G.; Barbaresi, L.; Guidorzi, P.; Garai, M. Investigation of the Sound Insulation and Natural Ventilation Performance of a Metamaterial-Based Open Window. Build. Environ. 2024, 266, 112140. [Google Scholar] [CrossRef]
- Gao, Y.; Lin, Y.; Zhu, Y.; Liang, B.; Yang, J.; Yang, J.; Cheng, J. Broadband Thin Sound Absorber Based on Hybrid Labyrinthine Metastructures with Optimally Designed Parameters. Sci. Rep. 2020, 10, 10705. [Google Scholar] [CrossRef]
- Almeida, G.D.N.; Vergara, E.F.; Barbosa, L.R.; Brum, R. Low-Frequency Sound Absorption of a Metamaterial with Symmetrical-Coiled-up Spaces. Appl. Acoust. 2021, 172, 107593. [Google Scholar] [CrossRef]
- Comandini, G.; Ouisse, M.; Ting, V.P.; Scarpa, F. Acoustic Transmission Loss in Hilbert Fractal Metamaterials. Sci. Rep. 2023, 13, 19058. [Google Scholar] [CrossRef]
- Xia, B.; Li, L.; Liu, J.; Yu, D. Acoustic Metamaterial With Fractal Coiling Up Space for Sound Blocking in a Deep Subwavelength Scale. J. Vib. Acoust. 2018, 140, 011011. [Google Scholar] [CrossRef]
- Gao, H.; Yan, Q.; Liu, X.; Zhang, Y.; Sun, Y.; Ding, Q.; Wang, L.; Xu, J.; Yan, H. Low-Frequency Bandgaps of the Lightweight Single-Phase Acoustic Metamaterials with Locally Resonant Archimedean Spirals. Materials 2022, 15, 373. [Google Scholar] [CrossRef]
- De Melo Filho, N.G.R.; Claeys, C.; Deckers, E.; Desmet, W. Realisation of a Thermoformed Vibro-Acoustic Metamaterial for Increased STL in Acoustic Resonance Driven Environments. Appl. Acoust. 2019, 156, 78–82. [Google Scholar] [CrossRef]
- Lee, K.H.; Al Ba’ba’a, H.; Yu, K.; Li, K.; Zhang, Y.; Du, H.; Masri, S.F.; Wang, Q. Magnetoactive Acoustic Topological Transistors. Adv. Sci. 2022, 9, e2201204. [Google Scholar] [CrossRef] [PubMed]
- Martins, M.; Godinho, L.; Picado-Santos, L. Numerical Evaluation of Sound Attenuation Provided by Periodic Structures. Arch. Acoust. 2013, 38, 503–516. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, C.; Yu, Q.; Yi, Q.; Lu, T.; Wang, P.; Chen, R. Reverse Optimization Design of OAM Sound Barrier Based on Acoustic Metamaterials. Constr. Build. Mater. 2024, 432, 136600. [Google Scholar] [CrossRef]
- He, C.; Zhou, S.; Li, X.; Di, H.; Zhang, X. Forest Trees as a Natural Metamaterial for Surface Wave Attenuation in Stratified Soils. Constr. Build. Mater. 2023, 363, 129769. [Google Scholar] [CrossRef]
- Xia, J.; Sun, Y.Y.; Guan, Y.J.; Wang, Y.; Lu, Y.J.; Hu, H.G.; Ge, Y.; Sun, H.X.; Yuan, S.Q.; Lai, Y.; et al. Broadband Low-Frequency Sound Absorption in Open Tunnels with Deep Sub-Wavelength Mie Resonators. Front. Phys. 2022, 10, 1047892. [Google Scholar] [CrossRef]
- Dal Poggetto, V.F.; Pugno, N.M.; Arruda, J.R. de F. Bioinspired Periodic Panels Optimized for Acoustic Insulation. Philos. Trans. A Math. Phys. Eng. Sci. 2022, 380, 20210389. [Google Scholar] [CrossRef]
- Papathanasiou, T.K.; Tsolakis, E.; Spitas, V.; Movchan, A.B. The Herschel-Quincke Tube with Modulated Branches. Philos. Trans. A Math. Phys. Eng. Sci. 2022, 380, 20220074. [Google Scholar] [CrossRef]
- Kim, D.Y.; Ih, J.G.; Åbom, M. Virtual Herschel-Quincke Tube Using the Multiple Small Resonators and Acoustic Metamaterials. J. Sound. Vib. 2020, 466, 115045. [Google Scholar] [CrossRef]
- Pan, F.; Li, Y.; Li, Z.; Yang, J.; Liu, B.; Chen, Y. 3D Pixel Mechanical Metamaterials. Adv. Mater. 2019, 31, e1900548. [Google Scholar] [CrossRef]
- Pirhaji, A.; Jebellat, E.; Roudbarian, N.; Mohammadi, K.; Movahhedy, M.R.; Asle Zaeem, M. Large Deformation of Shape-Memory Polymer-Based Lattice Metamaterials. Int. J. Mech. Sci. 2022, 232, 107593. [Google Scholar] [CrossRef]
- Bauer, J.; Kraus, J.A.; Crook, C.; Rimoli, J.J.; Valdevit, L. Tensegrity Metamaterials: Toward Failure-Resistant Engineering Systems through Delocalized Deformation. Adv. Mater. 2021, 33, e2005647. [Google Scholar] [CrossRef]
- Tao, R.; Ji, L.; Li, Y.; Wan, Z.; Hu, W.; Wu, W.; Liao, B.; Ma, L.; Fang, D. 4D Printed Origami Metamaterials with Tunable Compression Twist Behavior and Stress-Strain Curves. Compos. Part B Eng. 2020, 201, 108344. [Google Scholar] [CrossRef]
- Kang, S.W.; Mueller, J. Multiscale 3D Printing via Active Nozzle Size and Shape Control. Sci. Adv. 2024, 10, eadn7772. [Google Scholar] [CrossRef]
- Gardiner, A.; Daly, P.; Domingo-Roca, R.; Windmill, J.F.C.; Feeney, A.; Jackson-Camargo, J.C. Additive Manufacture of Small-Scale Metamaterial Structures for Acoustic and Ultrasonic Applications. Micromachines 2021, 12, 634. [Google Scholar] [CrossRef]
- Nemani, S.K.; Annavarapu, R.K.; Mohammadian, B.; Raiyan, A.; Heil, J.; Haque, M.A.; Abdelaal, A.; Sojoudi, H. Surface Modification of Polymers: Methods and Applications. Adv. Mater. Inter. 2018, 5, 1801247. [Google Scholar] [CrossRef]
- Yang, H.; D’Ambrosio, N.; Liu, P.; Pasini, D.; Ma, L. Shape Memory Mechanical Metamaterials. Mater. Today 2023, 66, 36–49. [Google Scholar] [CrossRef]
- Al Sabouni-Zawadzka, A.; Gilewski, W. Soft and Stiff Simplex Tensegrity Lattices as Extreme Smart Metamaterials. Materials 2019, 12, 187. [Google Scholar] [CrossRef]
- Vangelatos, Z.; Micheletti, A.; P Grigoropoulos, C.; Fraternali, F. Design and Testing of Bistable Lattices with Tensegrity Architecture and Nanoscale Features Fabricated by Multiphoton Lithography. Nanomaterials 2020, 10, 652. [Google Scholar] [CrossRef] [PubMed]
- Talebizadehsardari, P.; Eyvazian, A.; Musharavati, F.; Mahani, R.B.; Sebaey, T.A. Elastic Wave Characteristics of Graphene Reinforced Polymer Nanocomposite Curved Beams Including Thickness Stretching Effect. Polymers 2020, 12, 2194. [Google Scholar] [CrossRef] [PubMed]
- Buccino, F.; Martinoia, G.; Vergani, L.M. Torsion-Resistant Structures: A Nature Addressed Solution. Materials 2021, 14, 5368. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Li, Y. Mechanical Behaviors of Three-Dimensional Chiral Mechanical Metamaterials. Compos. Part B Eng. 2024, 270, 111141. [Google Scholar] [CrossRef]
- Zheng, X.; Uto, K.; Hu, W.-H.; Chen, T.T.; Naito, M.; Watanabe, I. Reprogrammable Flexible Mechanical Metamaterials. Appl. Mater. Today 2022, 29, 101662. [Google Scholar] [CrossRef]
- Bekele, A.; Wadee, M.A.; Phillips, A.T.M. Enhancing Energy Absorption through Sequential Instabilities in Mechanical Metamaterials. R. Soc. Open Sci. 2023, 10, 230762. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, Y.; Li, K.; Su, L. Origami-Inspired Metamaterials Hierarchical Structure with Tailorable Crushing Behavior. Constr. Build. Mater. 2022, 345, 128328. [Google Scholar] [CrossRef]
- Morales Ferrer, J.M.; Sánchez Cruz, R.E.; Caplan, S.; van Rees, W.M.; Boley, J.W. Multiscale Heterogeneous Polymer Composites for High Stiffness 4D Printed Electrically Controllable Multifunctional Structures. Adv. Mater. 2024, 36, e2307858. [Google Scholar] [CrossRef]
- Zhou, X.; Liang, X.; Liu, Z.; Tao, C.; Li, H. Compression Deformation Prediction of Chiral Metamaterials: A Compression-Shear Coupling Model. Materials 2022, 15, 5180. [Google Scholar] [CrossRef]
- Chen, H.; Shi, J.; Yan, L.; Akbarzadeh, A. Multifunctional Triboelectric Metamaterials with Unidirectional Charge Transfer Channels for Linear Mechanical Motion Energy Harvesting. Adv. Funct. Mater. 2025, 35, 2416749. [Google Scholar] [CrossRef]
- Lee, G.; Lee, D.; Park, J.; Jang, Y.; Kim, M.; Rho, J. Piezoelectric Energy Harvesting Using Mechanical Metamaterials and Phononic Crystals. Commun. Phys. 2022, 5, 94. [Google Scholar] [CrossRef]
- Kubo, W. Metamaterial Thermoelectric Conversion. In Thermal Plasmonics and Metamaterials for a Low-Carbon Society; CRC Press: Boca Raton, FL, USA, 2024; pp. 104–116. ISBN 978-1-00-340909-0. [Google Scholar]
- Jiao, P.; Zhang, H.; Li, W. Origami Tribo-Metamaterials with Mechanoelectrical Multistability. ACS Appl. Mater. Interfaces 2023, 15, 2873–2880. [Google Scholar] [CrossRef] [PubMed]
- Shufrin, I.; Pasternak, E.; Dyskin, A.V. Planar Isotropic Structures with Negative Poisson’s Ratio. Int. J. Solids Struct. 2012, 49, 2239–2253. [Google Scholar] [CrossRef]
- Lira, C.; Scarpa, F. Transverse Shear Stiffness of Thickness Gradient Honeycombs. Compos. Sci. Technol. 2010, 70, 930–936. [Google Scholar] [CrossRef]
- Ha, C.S.; Yao, D.; Xu, Z.; Liu, C.; Liu, H.; Elkins, D.; Kile, M.; Deshpande, V.; Kong, Z.; Bauchy, M.; et al. Rapid Inverse Design of Metamaterials Based on Prescribed Mechanical Behavior through Machine Learning. Nat. Commun. 2023, 14, 5765. [Google Scholar] [CrossRef]
- Lin, Z.; Dong, J.; Wang, X.; Huang, Q.; Shen, X.; Yang, M.; Sun, X.; Yuan, Y.; Wang, S.; Ning, Y.; et al. Twin-Structured Graphene Metamaterials with Anomalous Mechanical Properties. Adv. Mater. 2022, 34, e2200444. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Wang, Y.; Chen, T.; Zhang, X.S. Algorithmic Encoding of Adaptive Responses in Temperature-Sensing Multimaterial Architectures. Sci. Adv. 2023, 9, eadk0620. [Google Scholar] [CrossRef]
- Tian, J.; Tang, K.; Chen, X.; Wang, X. Machine Learning-Based Prediction and Inverse Design of 2D Metamaterial Structures with Tunable Deformation-Dependent Poisson’s Ratio. Nanoscale 2022, 14, 12677–12691. [Google Scholar] [CrossRef]
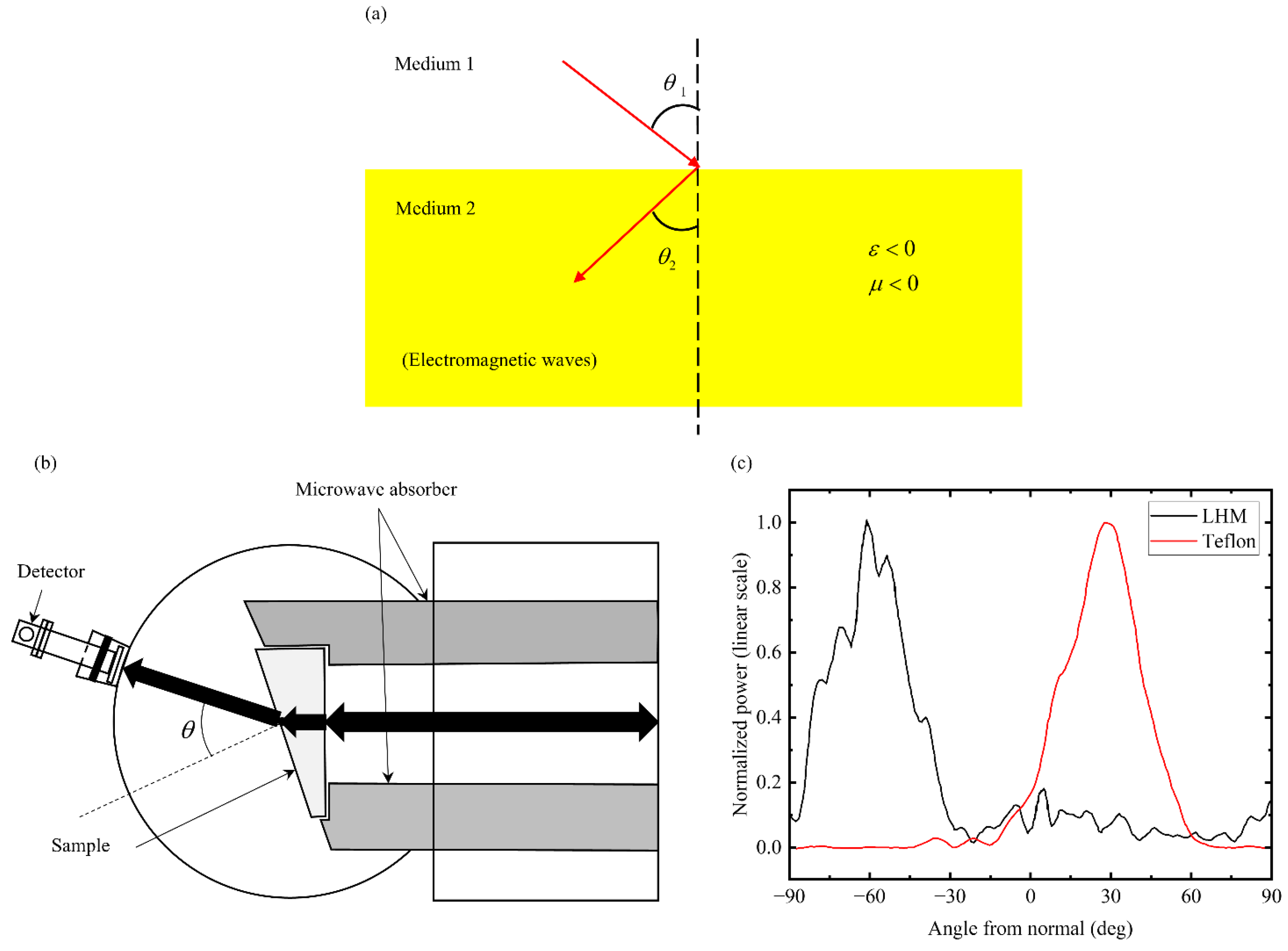
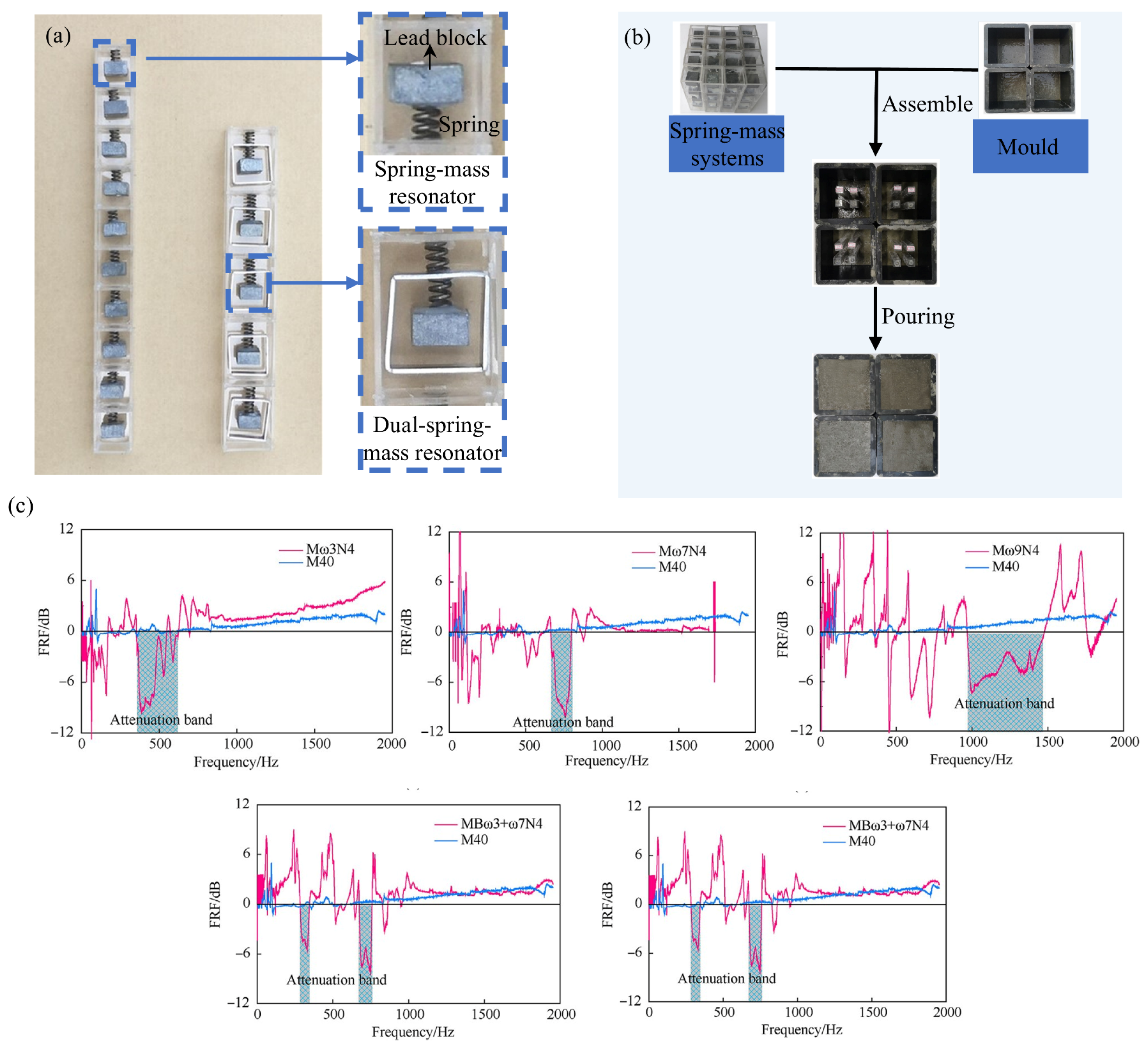
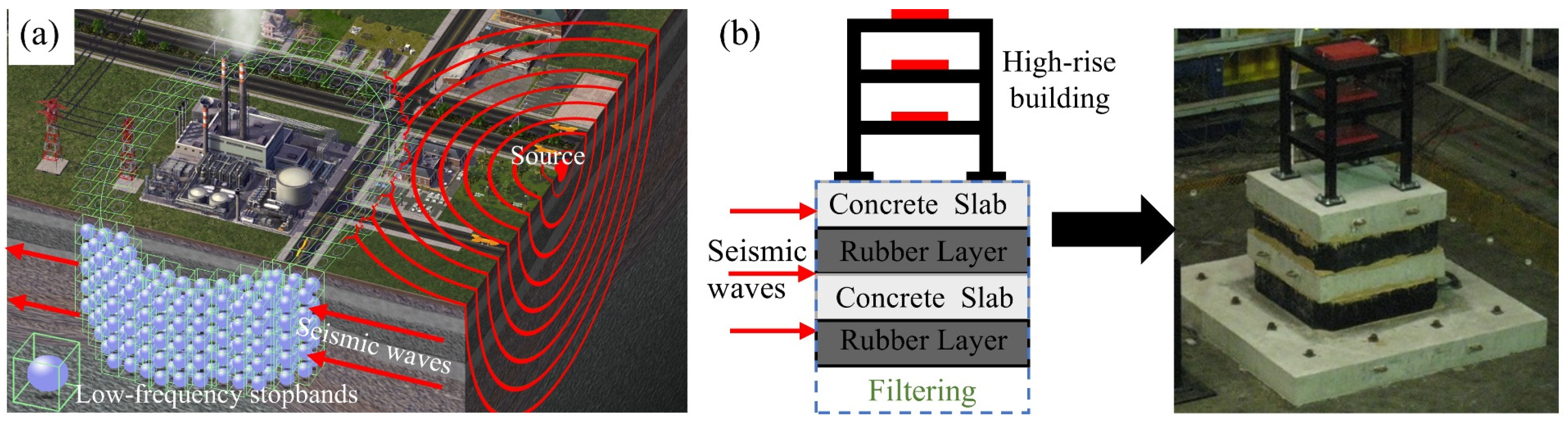
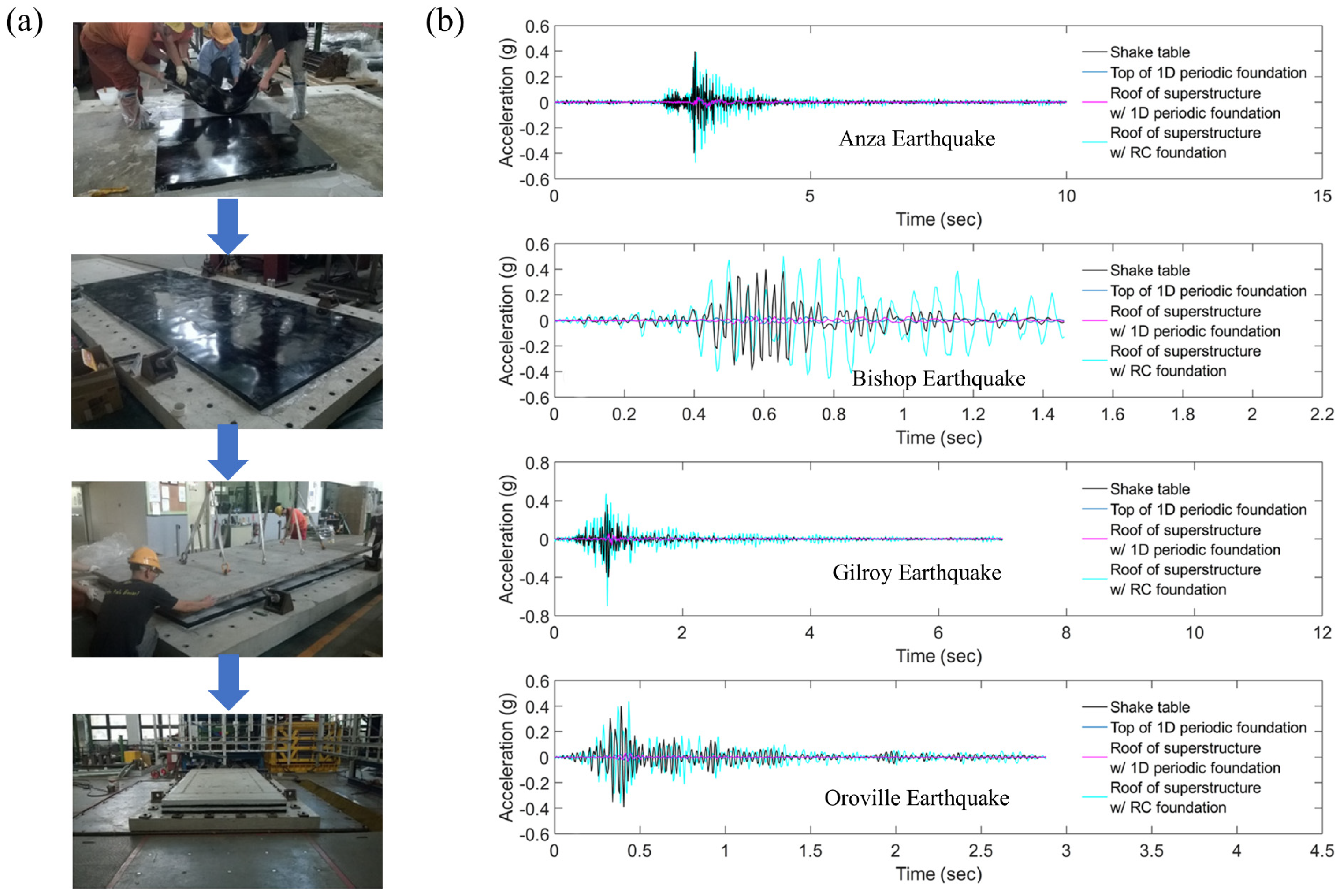
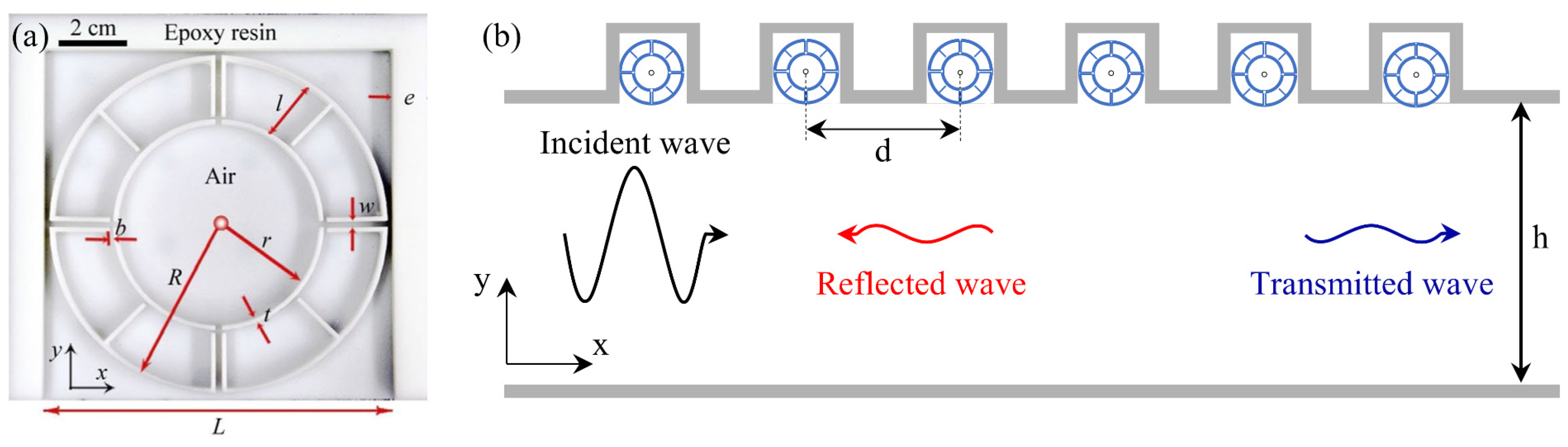
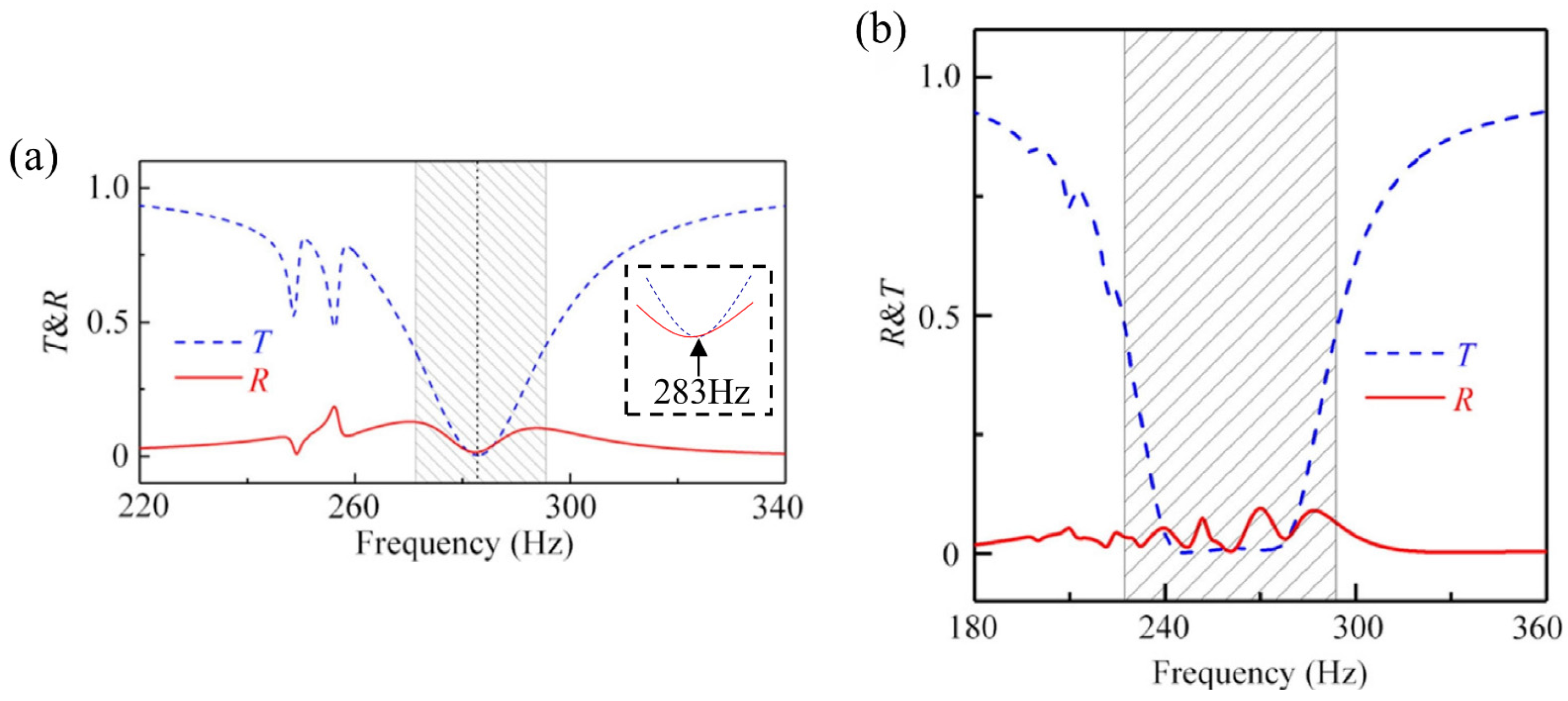
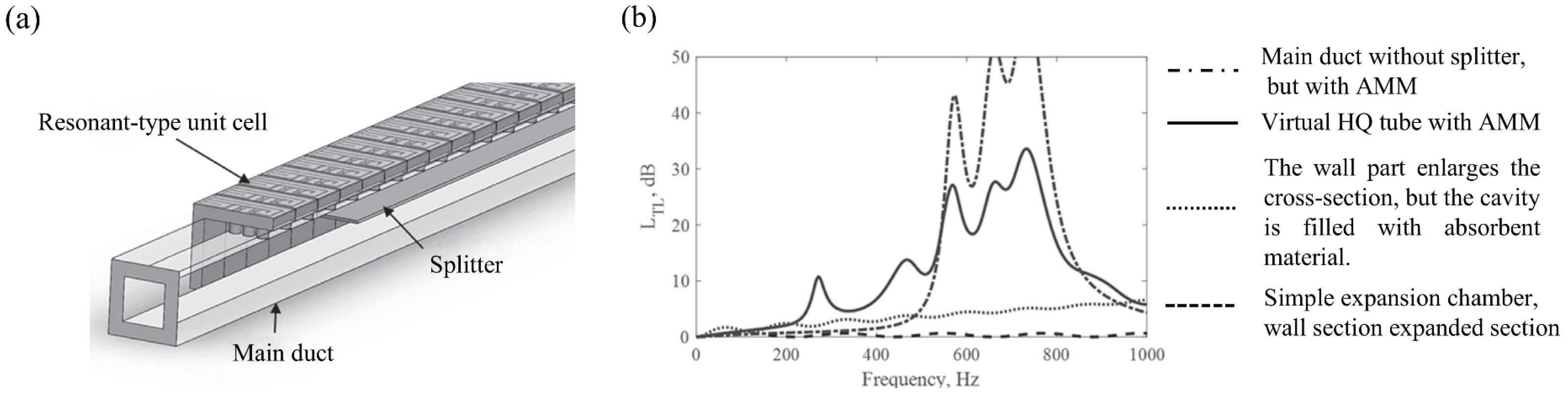
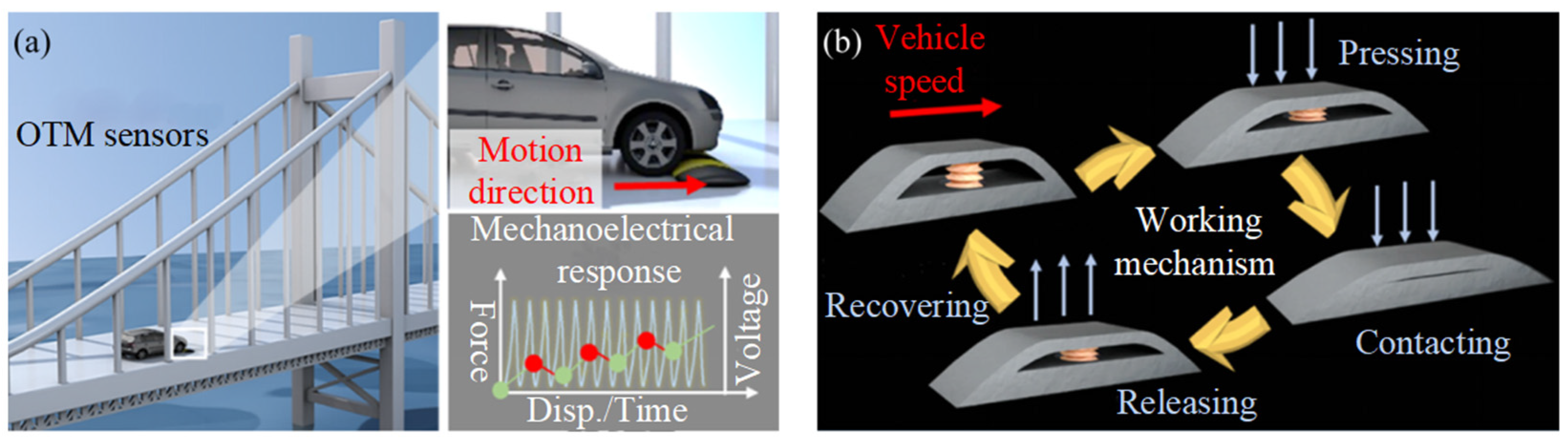
| Property | Traditional Materials | Metamaterials |
|---|---|---|
| Noise reduction | Wide-band sound insulation (depends on the density and structure of the material) | Sound insulation in specific frequency bands and even the “stealth” of sound waves can be realized [8,10]. |
| Heat insulation | Thermal conductivity is fixed (depends on the thickness and type of material). | Modulation of thermal conductivity for special effects of thermal insulation or heat absorption (e.g., thermal “stealth”) [14,16,32] |
| Lightweight and high-strength | There is a trade-off between strength and weight. | Balance of high strength and low density (depending on nanoscale structure design) [33] |
| Corrosion resistance | Embalming is required. | Resist corrosion and aging (design-dependent) [34,35] |
| Self-healing | Manual repair is required. | Self-healing properties (depending on material properties) [22,36,37] |
| Durability | The technology is mature and dominant. | Exploratory phase (innovative) |
| Programmability | - | High programmability (depending on the precise design of the microstructure) [38,39,40,41] |
| Energy harvesting and response | - | Active and efficient energy harvesting and conversion and fast and flexible energy response [12,38,42,43,44] |
| Environmental impact | The environmental impact is more obvious. | Low energy consumption and environmentally friendly [45,46,47] |
| Sustainability | Poor sustainability (high consumption in the production process and difficulty in recycling) | Sustainable (great potential and more opportunities for innovation) [47] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhao, S.; Xu, C.; Sun, K.; Fan, R. Engineering Metamaterials for Civil Infrastructure: From Acoustic Performance to Programmable Mechanical Responses. Materials 2025, 18, 4032. https://doi.org/10.3390/ma18174032
Wang H, Zhao S, Xu C, Sun K, Fan R. Engineering Metamaterials for Civil Infrastructure: From Acoustic Performance to Programmable Mechanical Responses. Materials. 2025; 18(17):4032. https://doi.org/10.3390/ma18174032
Chicago/Turabian StyleWang, Hao, Shan Zhao, Chen Xu, Kai Sun, and Runhua Fan. 2025. "Engineering Metamaterials for Civil Infrastructure: From Acoustic Performance to Programmable Mechanical Responses" Materials 18, no. 17: 4032. https://doi.org/10.3390/ma18174032
APA StyleWang, H., Zhao, S., Xu, C., Sun, K., & Fan, R. (2025). Engineering Metamaterials for Civil Infrastructure: From Acoustic Performance to Programmable Mechanical Responses. Materials, 18(17), 4032. https://doi.org/10.3390/ma18174032








