A Novel Test Set-Up for Direct Evaluation of Impact and Energy Absorption for Lattices
Highlights
- Direct measurement of both energy and impact absorptions of lattices.
- New lattice specimen configuration based on the required functionality, densification, and compatibility to machine components.
- Modification in the structure and components of commercially available Charpy pendulum impact tester.
- Equipping the Charpy machine with suitable accelerometer as the instrument to measure the impact.
- Data collection and analysis procedure for sensor signal and smoothing procedure for recorded signal.
- Comprehensive post-processing of data and possible errors are eliminated by direct measurement.
Abstract
1. Introduction
2. Theory/Calculation
2.1. High-Strain-Rate Testing Methods
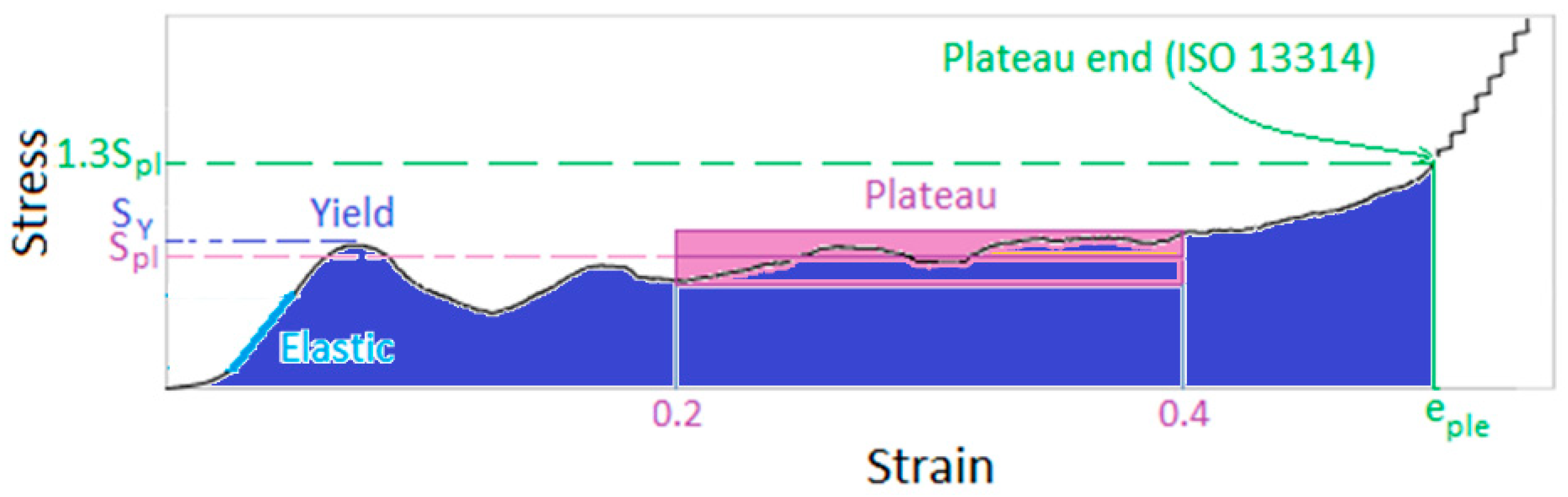
2.2. Calculation of Absorbed Energy
2.3. Calculation of Impact
2.4. Development of Energy-Impact Diagram
3. Material and Methods
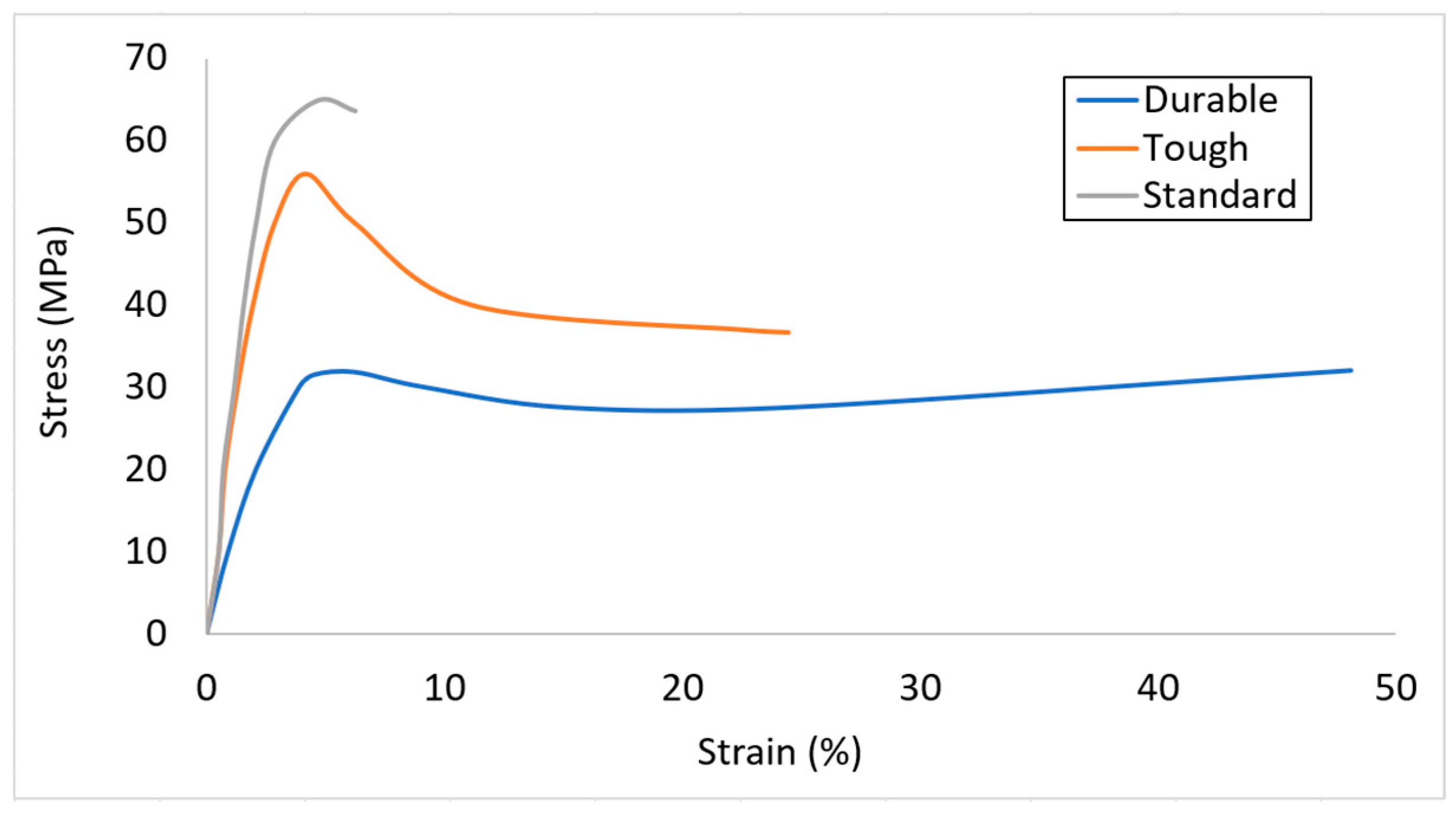
3.1. Selection of Material
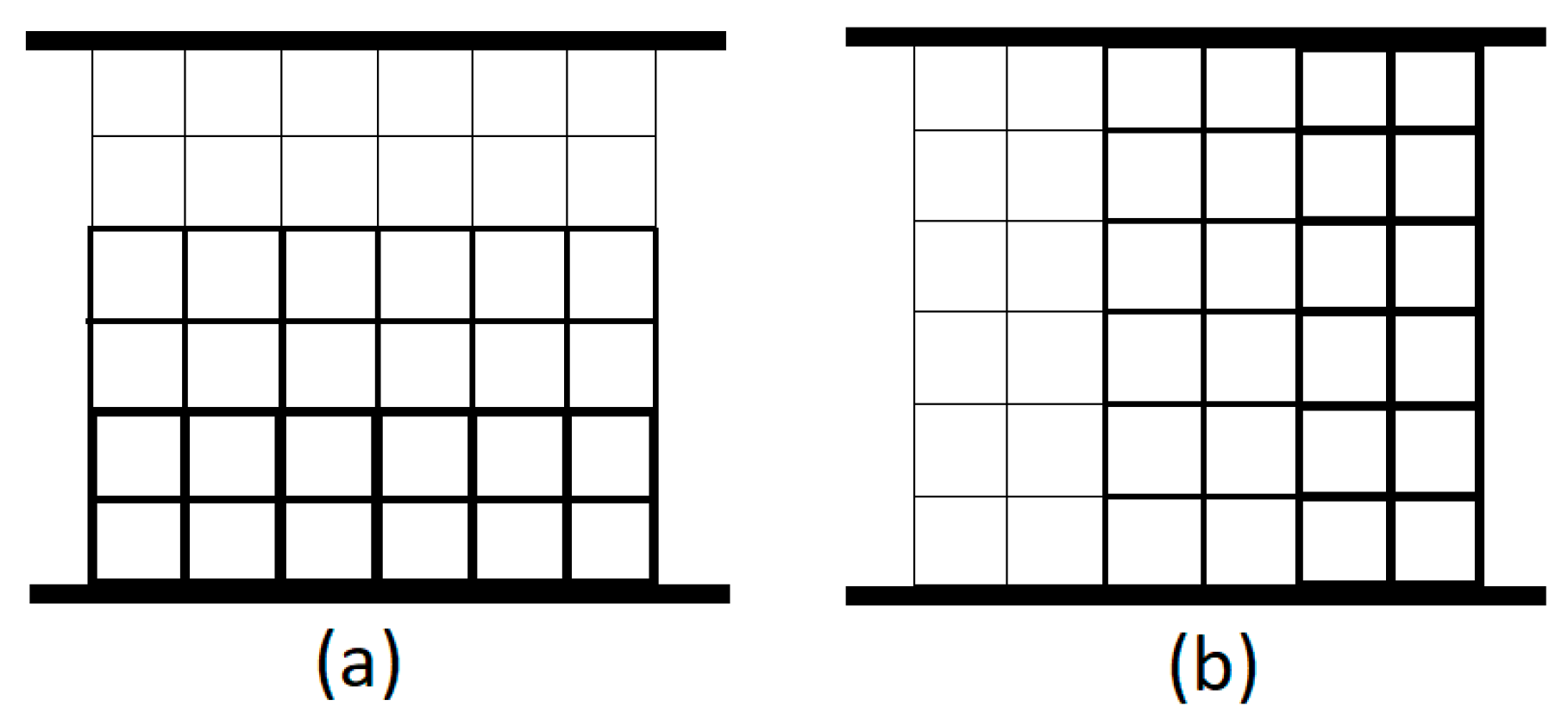
3.2. Sample Preparation
- Maximum unsupported overhang length is 3.0 mm.
- Minimum unsupported overhang angle is 19° from level.
- Minimum vertical-wire diameter for a 7 mm-tall wire is 0.4 mm and for a 30 mm-tall wire is 1.5 mm
3.3. Sensors and Instrumentation
4. Results and Discussion
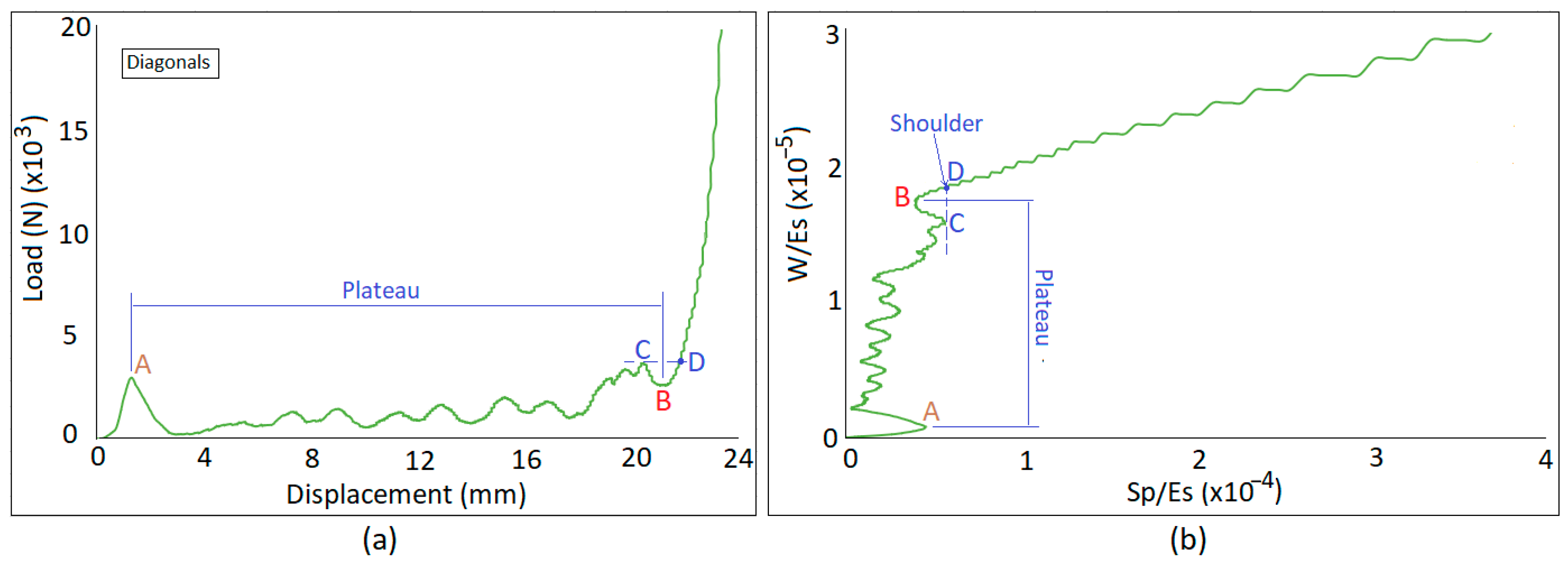
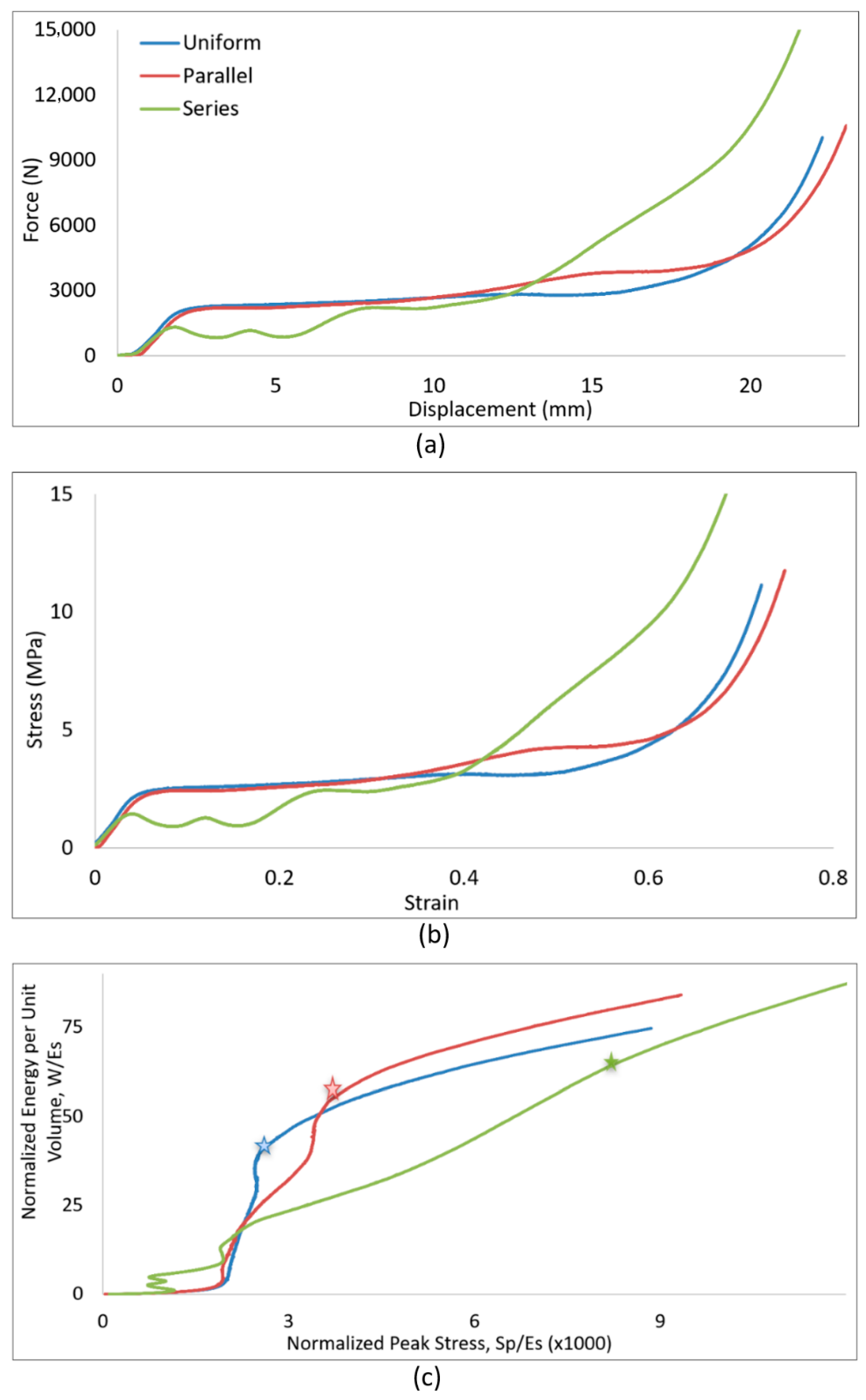
4.1. Energy-Impact Diagrams
4.2. Direct Measurement of Energy and Impact
4.2.1. Test Set-Up
4.2.2. Data Collection and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Korkmaz, M.E.; Gupta, M.K.; Robak, G.; Moj, K.; Krolczyk, G.M.; Kuntoğlu, M. Development of lattice structure with selective laser melting process: A state of the art on properties, future trends and challenges. J. Manuf. Process. 2022, 81, 1040–1063. [Google Scholar] [CrossRef]
- Ramasamy, A.; Masouros, S.D.; Newell, N.; Hill, A.M.; Proud, W.G.; Brown, K.A.; Bull, A.M.J.; Clasper, J.C. In-vehicle extremity injuries from improvised explosive devices: Current and future foci. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2011, 366, 160–170. [Google Scholar] [CrossRef] [PubMed]
- Rigby, S.E.; Fay, S.D.; Clarke, S.D.; Tyas, A.; Reay, J.J.; Warren, J.A.; Gant, M.; Elgy, I. Measuring spatial pressure distribution from explosives buried in dry Leighton Buzzard sand. Int. J. Impact Eng. 2016, 96, 89–104. [Google Scholar] [CrossRef]
- Santosa, S.P.; Arifurrahaman, F.; Izzudin, M.H.; Widagdo, D.; Gunawan, L. Response analysis of blast impact loading of metal-foam sandwich panels. Procedia Eng. 2017, 173, 495–502. [Google Scholar] [CrossRef]
- Vaziri Sereshk, M.R.; Faierson, E.J. Development of characteristic diagram for optimum energy and impact absorption of lattices. Int. J. Adv. Manuf. Technol. 2024, 132, 4663–4676. [Google Scholar] [CrossRef]
- Farajzadeh Khosroshahi, S.; Duckworth, H.; Galvanetto, U.; Ghajari, M. The effects of topology and relative density of lattice liners on traumatic brain injury mitigation. J. Biomech. 2019, 97, 109376. [Google Scholar] [CrossRef] [PubMed]
- Gibson, L.; Ashby, M. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- McKown, S.; Shen, Y.; Brookes, W.K.; Sutcliffe, C.J.; Cantwell, W.J.; Langdon, G.S.; Nurick, G.N.; Theobald, M.D. The quasi-static and blast loading response of lattice structures. Int. J. Impact Eng. 2008, 35, 795–810. [Google Scholar] [CrossRef]
- Vaziri Sereshk, M.R.; Faierson, E.J. Concept development for innovative functionally graded lattice structures to absorb desired energy and impact. Adv. Manuf. 2025. [Google Scholar] [CrossRef]
- Vrana, R.; Koutny, D.; Palousek, D. Impact resistance of different types of lattice structures manufactured by SLM. MM Sci. J. 2016, 2016, 1579–1585. [Google Scholar] [CrossRef]
- Chiacchiarelli, L.M.; Cerrutti, P.; Flores-Johnson, E.A. Compressive behavior of rigid polyurethane foams nanostructured with bacterial nanocellulose at low and intermediate strain rates. J. Appl. Polym. Sci. 2020, 137, 48701. [Google Scholar] [CrossRef]
- Hussain, N.N.; Regalla, S.P.; Daseswara Rao, Y.V.; Dirgantara, T.; Gunawan, L.; Jusuf, A. Drop-weight impact testing for the study of energy absorption in automobile crash boxes made of composite material. Proc. IMechE Part L J. Mater. Des. Appl. 2021, 235, 114–130. [Google Scholar] [CrossRef]
- Al Rifaie, M.; Mian, A.; Katiyar, P.; Majumdar, P.; Srinivasan, R. Drop-weight impact behavior of three-dimensional printed polymer lattice structures with spatially distributed vertical struts. J. Dyn. Behav. Mater. 2019, 5, 387–395. [Google Scholar] [CrossRef]
- Atrash Mohsin, M.A.; Iannucci, L.; Greenhalgh, E.S. Experimental and numerical analysis of low-velocity impact of carbon fibre-based non-crimp fabric reinforced thermoplastic composites. Polymers 2021, 13, 3642. [Google Scholar] [CrossRef] [PubMed]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar]
- Callister, W.D.; Rethwisch, D.G. Materials Science and Engineering: An Introduction, 10th ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Gray, G.T., III. Classic Split Hopkinson Bar Testing. ASM Handb. Mech. Test. Evaluat. 2000, 8, 462–476. [Google Scholar]
- Meyers, M.A. Dynamic Behavior of Materials; Wiley: Hoboken, NJ, USA, 1994. [Google Scholar]
- ISO 13314; Mechanical Testing of Metals—Ductility Testing—Compression Testing for Porous and Cellular Metals. ISO: Geneva, Switzerland, 2011. Available online: https://www.iso.org/standard/53669.html (accessed on 1 May 2025).
- Cui, X.; Zhao, L.; Wang, Z.; Zhao, H.; Fang, D. Dynamic response of metallic lattice sandwich structures to impulsive loading. Int. J. Impact. Eng. 2012, 43, 1–5. [Google Scholar] [CrossRef]
- Ozdemir, Z.; Hernandez-Nava, E.; Tyas, A.; Warren, J.A.; Fay, S.D.; Goodall, R.; Todd, I.; Askes, H. Energy absorption in lattice structures in dynamics: Experiments. Int. J. Impact Eng. 2016, 89, 49–61. [Google Scholar] [CrossRef]
- Karagiozova, D.; Nurick, G.N.; Langdon, G.S.; Yuen, S.C.K.; Chi, Y.; Bartle, S. Response of flexible sandwich-type panels to blast loading. Compos. Sci. Technol. 2009, 69, 754–763. [Google Scholar] [CrossRef]
- Dharmasena, K.P.; Wadley, H.N.G.; Williams, K.; Xue, Z.; Hutchinson, J.W. Response of metallic pyramidal lattice core sandwich panels to high intensity impulsive loading in air. Int. J. Impact Eng. 2011, 38, 275–289. [Google Scholar] [CrossRef]
- Available online: https://www.faa.gov/regulations_policies/advisory_circulars/index.cfm/go/document.information/documentid/22249 (accessed on 1 March 2025).
- Available online: https://formlabs.com/blog/choosing-prototyping-material-mechanical-properties/ (accessed on 1 March 2025).
- Available online: https://support.formlabs.com/s/article/Design-Specs?language=en_US (accessed on 1 March 2025).
- Vaziri Sereshk, M.R.; Faierson, E.J.; Nelson, B.D. Design of experiment and analysis of deformation for compression test of lattices using digital image correlation. Int. J. Adv. Manuf. Technol. 2025, 136, 1131–1147. [Google Scholar] [CrossRef]
- Available online: https://www.pcb.com/contentstore/MktgContent/Linkeddocuments/Technotes/TN-24_MechShock.pdf (accessed on 1 April 2025).
- Available online: https://www.pcb.com/products?m=352C23 (accessed on 1 April 2025).
- Available online: https://www.pcb.com/products?m=485B39 (accessed on 1 April 2025).
- Available online: https://www.spectraplus.com/ (accessed on 1 May 2025).
- ASTM D7136/D7136M-20; Standard Test Method for Measuring the Damage Resistance of a Fiber-Reinforced Polymer Matrix Composite to a Drop-Weight Impact Event. ISO: Geneva, Switzerland, 2020. Available online: https://www.astm.org/d7136_d7136m-20.html (accessed on 1 May 2025).





| Method | Purpose | Strain Rate Range | Sample Size | Data Output | Advantages | Limitations |
|---|---|---|---|---|---|---|
| Charpy Impact Test | Measures material toughness (energy absorption in fracture) | ~102 s−1 (low strain rate) | Standardized notched specimens (ISO/ASTM) | Impact energy, fracture appearance | Simple, fast, low cost, standardized | Limited to brittle/ductile transition; not true stress–strain; low strain rate |
| Drop Weight Test | Fracture behavior, toughness, or energy absorption under impact | ~102–103 s−1 | Varies (larger than Charpy) | Force, energy absorbed | Customizable loading rate; useful for large/complex specimens | Less standardized; can be noisy; strain data limited |
| Split-Hopkinson Pressure Bar (SHPB) | High-strain-rate stress–strain behavior | ~103–104 s−1 | Small cylindrical/dogbone samples | True stress–strain, strain rate, modulus | Accurate strain rate control; dynamic behavior | Complex setup; requires strain gauges, assumptions (1D wave propagation) |
| Taylor Impact Test | Study dynamic deformation & failure; validate simulations | ~104 s−1 | Cylindrical rods | Deformed profile, high-speed imaging, sometimes strain | Visualizes failure modes; simple in concept | Limited quantification; post-mortem analysis |
| Izod Impact Test | Similar to Charpy, for plastics/metals | ~102 s−1 | Notched specimens | Energy absorbed | Easy, standardized for plastics | Similar limitations to Charpy |
| Gas Gun/Projectile Impact | Penetration, ballistic performance, high-energy impacts | ~104–106 s−1 | Varies, often large or armor samples | High-speed imaging, strain fields, damage | Simulates real impacts; extreme conditions | Expensive, complex setup, safety concerns |
| Property | Standard | Tough | Durable |
|---|---|---|---|
| IZOD impact strength (J/m) | 25 | 38 | 109 |
| Elongation at break (%) | 6.2 | 24 | 49 |
| Tensile strength (MPa) | 65.0 | 55.7 | 31.8 |
| Tensile modulus (GPa) | 2.80 | 2.80 | 1.26 |
| Flexural modulus (GPa) | 2.2 | 1.6 | 0.82 |
| Topology | Strut Diameter (mm) | Volume Fraction | |
|---|---|---|---|
| Gradient | Uniform | ||
| FCC | 0.8, 1, 1.3 | 1.04 | 0.277 |
| Sensitivity (±20%) | 5 mV/g |
|---|---|
| Measurement Range | ±1000 g pk |
| Frequency Range (±5%) | 2.0 to 10,000 Hz |
| Frequency Range (±10%) | 1.5 to 15,000 Hz |
| Frequency Range (±3 dB) | 0.7 to 25,000 Hz |
| Resonant Frequency | ≥70 kHz |
| Broadband Resolution (1) | 0.003 g rms |
| Non-Linearity | ≤1% |
| Transverse Sensitivity | ≤5% |
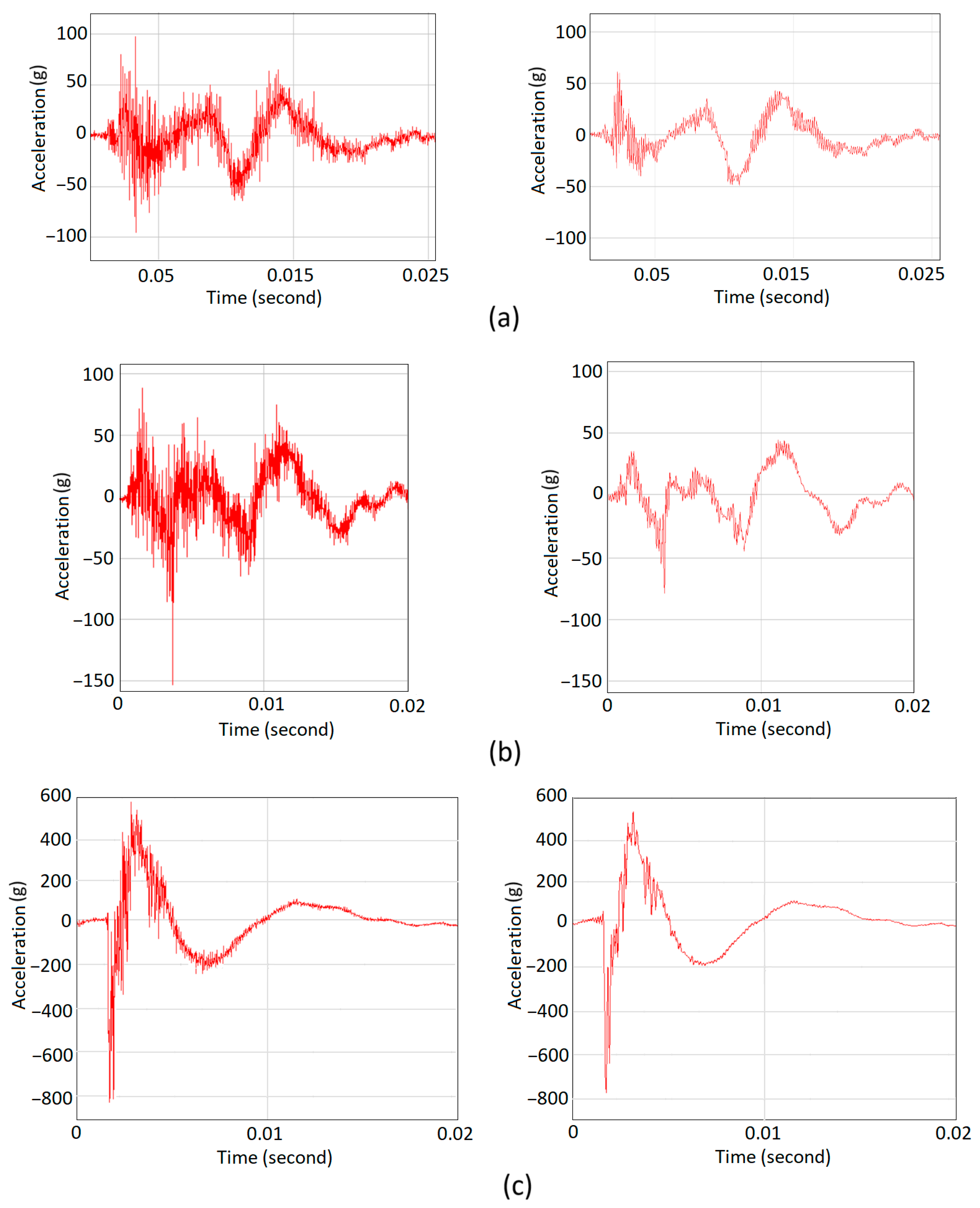
| Sample | Absorbed Energy (J) | Maximum Acceleration (Original) | Maximum Acceleration (Filtered) |
|---|---|---|---|
| FCC-Parallel | 291 | −95 g | −50 g |
| FCC-Uniform | 341 | −155 g | −75 g |
| FCC-Series | 347 | −820 g | −770 g |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaziri Sereshk, M.R.; Kwiecien, K.L.; Lodhi, A.T.; Mahjoob, M. A Novel Test Set-Up for Direct Evaluation of Impact and Energy Absorption for Lattices. Materials 2025, 18, 3938. https://doi.org/10.3390/ma18173938
Vaziri Sereshk MR, Kwiecien KL, Lodhi AT, Mahjoob M. A Novel Test Set-Up for Direct Evaluation of Impact and Energy Absorption for Lattices. Materials. 2025; 18(17):3938. https://doi.org/10.3390/ma18173938
Chicago/Turabian StyleVaziri Sereshk, Mohammad Reza, Kamil L. Kwiecien, Akib T. Lodhi, and Mohammad Mahjoob. 2025. "A Novel Test Set-Up for Direct Evaluation of Impact and Energy Absorption for Lattices" Materials 18, no. 17: 3938. https://doi.org/10.3390/ma18173938
APA StyleVaziri Sereshk, M. R., Kwiecien, K. L., Lodhi, A. T., & Mahjoob, M. (2025). A Novel Test Set-Up for Direct Evaluation of Impact and Energy Absorption for Lattices. Materials, 18(17), 3938. https://doi.org/10.3390/ma18173938






