Role of Structural Changes at Vitrification and Glass–Liquid Transition
Abstract
1. Introduction
2. Structural Differences Between Glasses and Melts
3. Role of Configurons in the Phase Transformation
- Universality—All disordered systems should exhibit percolation-type transformations from solid-like at higher degrees of connectivity (e.g., at lower temperatures) to fluid-like (plastic) at lower degrees of connectivity (e.g., at higher temperatures or intensity of irradiation).
- Singularities for derivative parameters—Thermal expansion, heat capacity, shear modulus, and other properties of glasses show a relatively sudden change at the glass transition temperature. Derivative parameters of amorphous materials thus show typical features of second-order phase transformations, e.g., theoretically, they diverge at Tg.
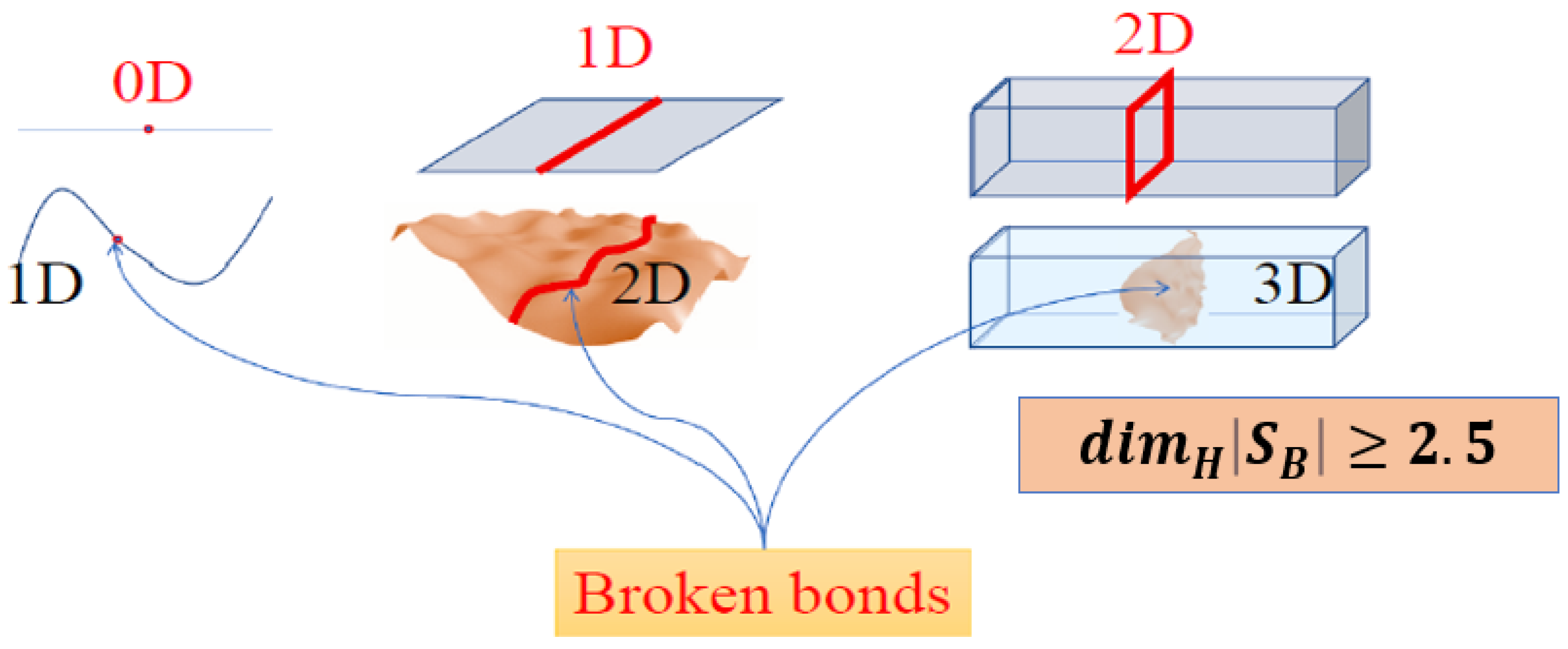
- Dynamic (twinkling) fractals—The glass–liquid transition is accompanied by the formation of a percolation macroscopic cluster made up of broken chemical bonds—configurons. This cluster is similar to Wool’s twinkling fractals [70,71,72]. The percolation cluster is dynamic and changes with time due to configuron migration controlled by diffusion. Nonetheless, at any moment of time there is a percolating cluster made of configurons above the Tg, whereas such macroscopic clusters do not exist in the glassy state (below the Tg). The characteristic linear scale that describes the branch sizes of dynamic clusters formed by configurons is the correlation length ξ(T);
- Fractal medium-range order—The higher the cooling rate, the larger are the remnant fractal clusters frozen at liquid–glass transition. The correlation length gives the average size of clusters made out of broken bonds at T < Tg. At T > Tg, the correlation length gives the average size of atomic clusters formed. Second-order phase transitions in ordered substances are typically associated with a change in the crystal lattice symmetry, and the symmetry is lower in the ordered phase than in the less ordered phase. In the spirit of Landau’s ideas, the transition from a glass to a liquid spontaneously breaks the symmetry of bonds that is of the system of configurons. At the glass–liquid transition the amorphous material changes the group of isometries from the Euclidean to the fractal space group of isometries at length scales smaller than ξ(T).
- Two activation energies of viscosity—The viscous flow has a variable activation energy above the glass transition temperature Q(T), which becomes lower at higher temperatures (Table 3).
4. The Jump of Heat Capacity
5. Melting Criteria
6. Importance of Bond Breakage
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CET | Coefficient of thermal expansion |
| CPT | Configuron percolation theory |
| DSC | Differential scanning calorimetry |
| HB | Hausdorff–Besicovitch dimensionality |
| MRO | Medium-range order |
| SRO | Short-range order |
References
- Musgraves, J.D.; Hu, J.; Calvez, L. (Eds.) Springer Handbook of Glass; Springer Handbooks; Springer Nature: Cham, Switzerland, 2019; p. 1851. [Google Scholar] [CrossRef]
- Sanditov, D.S.; Ojovan, M.I.; Darmaev, M.V. Glass transition criterion and plastic deformation of glass. Phys. B 2020, 582, 411914. [Google Scholar] [CrossRef]
- Schmelzer, J.W.P.; Tropin, T.V. Glass Transition, Crystallization of Glass-Forming Melts, and Entropy. Entropy 2018, 20, 103. [Google Scholar] [CrossRef] [PubMed]
- Angell, C.A. Oxide glasses in light of the ’Ideal glass’ concept. I. General aspects: Ideal and non-ideal transitions. J. Am. Ceram. Soc. 1968, 51, 117–124. [Google Scholar] [CrossRef]
- Angell, C.A.; Richards, B.E.; Velikov, V. Simple glass-forming liquids: Their definition, fragilities, and landscape excitation profiles. J. Phys. B Condens. Matter 1999, 11, A75–A94. [Google Scholar] [CrossRef]
- Angell, C.A.; Wong, J.J. Structure and glass transition thermodynamics of liquid zinc chloride from far-infrared, Raman, and probe ion electronic and vibrational spectra. Chem. Phys. 1970, 53, 2053–2066. [Google Scholar] [CrossRef]
- Angell, C.A.; Rao, K.J. Configurational excitations in condensed matter, and “bond lattice” model for the liquid-glass transition. J. Chem. Phys. 1972, 57, 470–481. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Tournier, R.F. On structural rearrangements near the glass transition temperature in amorphous silica. Materials 2021, 14, 5235. [Google Scholar] [CrossRef]
- Ojovan, M.I. The Flow of Glasses and Glass–Liquid Transition under Electron Irradiation. Int. J. Mol. Sci. 2023, 24, 12120. [Google Scholar] [CrossRef]
- Kantor, Y.; Webman, I. Elastic properties of random percolating systems. Phys. Rev. Lett. 1984, 52, 1891–1894. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Lee, W.E. Connectivity and glass transition in disordered oxide systems. J. Non Cryst. Solids 2010, 356, 2534–2540. [Google Scholar] [CrossRef]
- Vasin, M.G. Glass transition as a topological phase transition. Phys. Rev. E 2022, 106, 044124. [Google Scholar] [CrossRef]
- Gori, M.; Franzosi, R.; Pettini, G.; Pettini, M. Topological Theory of Phase Transitions. J. Phys. A Math. Theor. 2022, 55, 375002. [Google Scholar] [CrossRef]
- Vesperini, A.; Franzosi, R.; Pettini, M. The Glass Transition: A Topological Perspective. Entropy 2024, 27, 258. [Google Scholar] [CrossRef]
- Nussinov, Z.; Weingartner, N.B.; Nogueira, F.S. The “glass transition” as a topological defect driven transition in a distribution of crystals and a prediction of a universal viscosity collapse. In Topological Phase Transitions and New Developments; Brink, L., Gunn, M., José, J.V., Kosterlitz, J.M., Phua, K.K., Eds.; World Scientific: Singapore, 2018; pp. 61–79. [Google Scholar] [CrossRef]
- de Candia, A.; Fierro, A.; Coniglio, A. Scaling and universality in glass transition. Sci. Rep. 2016, 6, 26481. [Google Scholar] [CrossRef] [PubMed]
- Ojovan, M.I. Glass formation in amorphous SiO2 as a percolation phase transition in a system of network defects. J. Exp. Theor. Phys. Let. 2004, 79, 632–634. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Lee, W.E. Topologically disordered systems at the glass transition. J. Phys. Condens. Matter 2006, 18, 11507–11520. [Google Scholar] [CrossRef]
- Ozhovan, M.I. Topological characteristics of bonds in SiO2 and GeO2 oxide systems at glass-liquid transition. J. Exp. Theor. Phys. 2006, 103, 819–829. [Google Scholar] [CrossRef]
- Ojovan, M.I. Configurons: Thermodynamic parameters and symmetry changes at glass transition. Entropy 2008, 10, 334–364. [Google Scholar] [CrossRef]
- Ojovan, M. Glass formation. In Encyclopedia of Glass Science, Technology, History, and Culture; Richet, P., Conradt, R., Takada, A., Dyon, J., Eds.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; pp. 249–259. [Google Scholar] [CrossRef]
- Županović, V.; Žubrinić, D. Fractal Dimensions in Dynamics. In Encyclopedia of Mathematical Physics; Françoise, J.-P., Naber, G.L., Tsun, T.S., Eds.; Academic Press: Cambridge, MA, USA, 2006; pp. 394–402. ISBN 9780125126663. [Google Scholar] [CrossRef]
- Angell, C.A.; Sichina, W. Thermodynamics of the glass transition: Empirical aspects. Ann. N. Y. Acad. Sci. 1976, 279, 53–67. [Google Scholar] [CrossRef]
- Angell, C.A. Formation of glasses from liquids and biopolymers. Science 1995, 267, 1924–1935. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics; J. Wiley and Sons Inc.: New York, NY, USA, 1996. [Google Scholar]
- Richert, R. Heterogeneous dynamics in liquids: Fluctuations in space and time. J. Phys. Condens. Matter 2002, 14, R703–R738. [Google Scholar] [CrossRef]
- Holubova, J.; Černošek, Z.; Cernoskova, E.; Liska, M. Isothermal structural relaxation: Temperature and time dependencies of relaxation parameters. J. Non Cryst. Solids 2003, 326, 135–140. [Google Scholar] [CrossRef]
- Machacek, J.; Gedeon, O.; Liska, M. Group connectivity in binary silicate glasses. J. Non Cryst. Solids 2006, 352, 2173–2179. [Google Scholar] [CrossRef]
- Fluegel, A. Glass viscosity calculation based on a global statistical modelling approach. Glass Technol. 2007, 48, 13–30. [Google Scholar]
- Mauro, J.C.; Yue, Y.; Ellison, A.J.; Gupta, P.K.; Allan, D.C. Viscosity of glass-forming liquids. Proc. Natl. Acad. Sci. USA 2009, 106, 19780–19784. [Google Scholar] [CrossRef]
- Zheng, Q.; Mauro, J.C. Viscosity of glass forming systems. J. Am. Ceram. Soc. 2017, 100, 6–25. [Google Scholar] [CrossRef]
- Fotheringham, U. Viscosity of glass and glass-forming melts. In Springer Handbook of Glass; Musgraves, J.D., Hu, J., Calvez, L., Eds.; Springer Handbooks; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Richet, P.; Conradt, R.; Takada, A.; Dyon, J. Encyclopedia of Glass Science, Technology, History, and Culture; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2021; p. 1568. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9781118801017 (accessed on 5 May 2025).
- Louzguine-Luzgin, D.V.; Belosludov, R.; Saito, M.; Kawazoe, Y. Inoue. Glass-transition behavior of Ni: Calculation, prediction, and experiment. J. Appl. Phys. 2008, 104, 123529. [Google Scholar] [CrossRef]
- Dyre, J.C. Colloquium: The glass transition and elastic models of glass-forming liquids. Rev. Mod. Phys. 2006, 78, 953–972. [Google Scholar] [CrossRef]
- Tournier, R.F.; Ojovan, M.I. Undercooled phase behind the glass phase with superheated medium-range order above glass transition temperature. Phys. B Condens. Matter 2021, 602, 412542. [Google Scholar] [CrossRef]
- Ojovan, M.I. The Modified Random Network (MRN) Model within the Configuron Percolation Theory (CPT) of Glass Transition. Ceramics 2021, 4, 121–134. [Google Scholar] [CrossRef]
- Tournier, R.F.; Ojovan, M.I. Prediction of Second Melting Temperatures Already Observed in Pure Elements by Molecular Dynamics Simulations. Materials 2021, 14, 6509. [Google Scholar] [CrossRef] [PubMed]
- Tournier, R.F.; Ojovan, M.I. NiTi2, a New Liquid Glass. Materials 2023, 16, 6681. [Google Scholar] [CrossRef] [PubMed]
- Sanditov, D.S.; Ojovan, M.I. On relaxation nature of glass transition in amorphous materials. Phys. B 2017, 523, 96–113. [Google Scholar] [CrossRef]
- Sanditov, D.S.; Ojovan, M.I. Relaxation aspects of the liquid—Glass transition. Phys. Uspekhi 2019, 62, 111–130. [Google Scholar] [CrossRef]
- Ojovan, M.I. On Viscous Flow in Glass-Forming Organic Liquids. Molecules 2020, 25, 4029. [Google Scholar] [CrossRef]
- Bruns, S.; Durst, K. Local crack suppression and activation of plastic flow via electron irradiation in oxide glasses. Mater. Des. 2025, 251, 113726. [Google Scholar] [CrossRef]
- Bruns, S.; Kang, S.-G.; Choi, I.S.; Durst, K. The role of electron-beam irradiation on small-scale deformation: Challenges and benefits in in situ SEM indentation tests. MRS Bull. 2025, 50, 735–748. [Google Scholar] [CrossRef]
- Rusinowicz, M.; Sao-Joao, S.; Bourguignon, M.; Rosales-Sosa, G.; Kato, Y.; Volpi, F.; Barthel, E.; Kermouche, G. Electric charges as an apparent governing parameter for electron induced stress relaxation in amorphous silica micropillars. Scr. Mater. 2025, 261, 116628. [Google Scholar] [CrossRef]
- Huang, P.Y.; Kurasch, S.; Srivastava, A.; Skakalova, V.; Kotakoski, J.; Krasheninnikov, A.V.; Hovden, R.; Mao, Q.; Meyer, J.C.; Smet, J.; et al. Direct Imaging of a Two-Dimensional Silica Glass on Graphene. Nano Lett. 2012, 12, 1081–1086. [Google Scholar] [CrossRef]
- Khouchaf, L.; Boulahya, K.; Das, P.P.; Nicolopoulos, S.; Kis, V.K.; Lábár, J.L. Study of the Microstructure of Amorphous Silica Nanostructures Using High-Resolution Electron Microscopy, Electron Energy Loss Spectroscopy, X-ray Powder Diffraction, and Electron Pair Distribution Function. Materials 2020, 13, 4393. [Google Scholar] [CrossRef]
- Wendt, H.H.; Abraham, F.F. Empirical Criterion for the Glass Transition Region Based on Monte Carlo Simulations. Phys. Rev. Lett. 1978, 41, 1244–1246. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Louzguine-Luzgin, D.V. Revealing Structural Changes at Glass Transition via Radial Distribution Functions. J. Phys. Chem. B 2020, 124, 3186–3194. [Google Scholar] [CrossRef] [PubMed]
- Scher, H.; Zallen, R. Critical Density in Percolation Processes. J. Chem. Phys. 1970, 53, 3759. [Google Scholar] [CrossRef]
- Isichenko, M.B. Percolation, statistical topography, and transport in random media. Rev. Mod. Phys. 1992, 64, 961–1043. [Google Scholar] [CrossRef]
- Mattern, N.; Hermann, H.; Roth, S.; Sakowski, J.; Macht, M.-P.; Jovari, P.; Jiang, J. Structural behavior of Pd40Cu30Ni10P20 bulk metallic glass below and above the glass transition. Appl. Phys. Lett. 2003, 82, 2589–2591. [Google Scholar] [CrossRef]
- Egami, T.; Billinge, S.J.L. Underneath the Bragg Peaks: Structural Analysis of Complex Materials; Pergamon Materials Series; Elsevier: Amsterdam, The Netherlands, 2013; Volume 16, ISBN 978-0-08-097133-9. [Google Scholar]
- Egami, T.; Ryu, C.W. Origin of medium-range atomic correlation in simple liquids: Density wave theory. AIP Adv. 2023, 13, 085308. [Google Scholar] [CrossRef]
- Du, J. Molecular Dynamics Simulations of Oxide Glasses. In Springer Handbook of Glass; Musgraves, J.D., Hu, J., Calvez, L., Eds.; Springer Handbooks; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, J.; Zhu, F.; Yuan, Y.; Chang, D.J.; Kim, D.S.; Pham, M.; Rana, A.; Tian, X.; Yao, Y.; et al. Determining the three-dimensional atomic structure of an amorphous solid. Nature 2021, 592, 60. [Google Scholar] [CrossRef]
- Benigni, P. CALPHAD modeling of the glass transition for a pure substance, coupling thermodynamics and relaxation kinetics. CALPHAD Comput. Coupling Phase Diagr. Thermochem. 2012, 72, 102238. [Google Scholar] [CrossRef]
- Becker, C.A.; Ågren, J.; Baricco, M.; Chen, Q.; Decterov, S.A.; Kattner, U.R.; Perepezko, J.H.; Pottlacher, G.R.; Selleby, M. Thermodynamic modelling of liquids: CALPHAD approaches and contributions from statistical physics. Phys. Status Solidi 2014, 52, 33–52. [Google Scholar] [CrossRef]
- Ågren, J. Thermodynamics of supercooled liquids and their glass transition. Phys. Chem. Liq. 1988, 18, 123–139. [Google Scholar] [CrossRef]
- Macedo, P.B.; Capps, W.; Litovitz, T.A. Two-state model for the free volume of vitreous B2O3. J. Chem. Phys. 1966, 44, 3357–3364. [Google Scholar] [CrossRef]
- Langer, S.A.; Dorsey, A.T.; Sethna, J.P. Entropy distribution of a two-level system: An asymptotic analysis. Phys. Rev. B 1989, 40, 345–352. [Google Scholar] [CrossRef]
- Langer, S.A.; Sethna, J.P.; Grannan, E.R. Nonequilibrium entropy and entropy distributions. Phys. Rev. B 1990, 41, 2261–2278. [Google Scholar] [CrossRef]
- Halpern, V.; Bisquert, J. The effect of the cooling rate on the fictive temperature in some model glassy systems. J. Chem. Phys. 2001, 114, 9512–9517. [Google Scholar] [CrossRef]
- Bisquert, J. Master equation approach to the non-equilibrium negative specific heat at the glass transition. Am. J. Phys. 2005, 73, 735–741. [Google Scholar] [CrossRef]
- Bisquert, J.; Henn, F.; Giuntini, J.C. A simple model of entropy relaxation for explaining effective activation energy behavior below the glass transition temperature. J. Chem. Phys. 2005, 122, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Takada, A.; Conradt, R.; Richet, P. Residual entropy and structural disorder in glass: A two-level model and a review of spatial and ensemble vs. temporal sampling. J. Non-Cryst. Solids 2013, 360, 13–20. [Google Scholar] [CrossRef]
- Jabraoui, H.; Ouaskit, S.; Richard, J.; Garden, J.-L. Determination of the entropy production during glass transition: Theory and experiment. J. Non-Cryst. Solids 2020, 533, 119907. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef]
- Ojovan, M.I. Ordering and structural changes at the glass-liquid transition. J. Non-Cryst. Solids 2013, 382, 79–86. [Google Scholar] [CrossRef]
- Wool, R.P. Twinkling fractal theory of the glass transition. J. Polym. Sci. B Polym. Phys. 2008, 46, 2765–2778. [Google Scholar] [CrossRef]
- Wool, R.P.; Campanella, A. Twinkling fractal theory of the glass transition: Rate dependence and time–temperature superposition. J. Polym. Sci. B Polym. Phys. 2009, 47, 2578–2589. [Google Scholar] [CrossRef]
- Stanzione, J.F., III.; Strawhecker, K.E.; Wool, R.P. Observing the Twinkling Nature of the Glass Transition. J. Non-Cryst. Solids 2011, 357, 311–319. [Google Scholar] [CrossRef]
- Hrma, P.; Ferkl, P.; Kruger, A.A. Arrhenian to non-Arrhenian crossover in glass melt viscosity. J. Non-Cryst. Solids 2023, 619, 122556. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Louzguine-Luzgin, D.V. On Crossover Temperatures of Viscous Flow Related to Structural Rearrangements in Liquids. Materials 2024, 17, 1261. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Louzguine-Luzgin, D.V. The Minima of Viscosities. Materials 2024, 17, 1822. [Google Scholar] [CrossRef]
- Ludlam, J.J.; Taraskin, S.N.; Elliott, S.R.; Drabold, D.A. Universal features of localized eigenstates in disordered systems. J. Phys. Condens. Matter 2005, 17, L321–L327. [Google Scholar] [CrossRef]
- Lagendijk, A.; van Tiggelen, B.; Wiersma, D.S. Fifty years of Anderson localization. Phys. Today 2009, 62, 24–29. [Google Scholar] [CrossRef]
- Mirlin, A.D. Statistics of energy levels and eigenfunctions in disordered systems. Phys. Rep. 2000, 326, 259–382. [Google Scholar] [CrossRef]
- Anderson, P.W. Absence of Diffusion in Certain Random Lattices. Phys. Rev. 1958, 109, 1492–1505. [Google Scholar] [CrossRef]
- Dembovsky, S.A. Symmetry of a liquid and symmetry breaking at the glass transition. Phys. Lett. A 1998, 238, 315–321. [Google Scholar] [CrossRef]
- Salmon, P.S. Order within disorder. Nat. Mater. 2002, 1, 87–88. [Google Scholar] [CrossRef]
- Zhou, Y.; Xue, D.; Tian, Y.; Ding, X.; Guo, S.; Otsuka, K.; Sun, J.; Ren, X. Direct evidence for local symmetry breaking during a strain glass transition. Phys. Rev. Lett. 2014, 112, 025701. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S. New paradigm for configurational entropy in glass-forming systems. Sci. Rep. 2022, 12, 3058. [Google Scholar] [CrossRef]
- Albert, S.; Bauer, T.; Michl, M.; Biroli, G.; Bouchaud, J.-P.; Loidl, A.; Lunkenheimer, P.; Tourbot, R.; Wiertel-Gasquet, C.; Ladieu, F. Fifth-order Susceptibility Unveils Growth of Thermodynamic Amorphous Order in Glass-formers. Science 2016, 352, 1308–1311. [Google Scholar] [CrossRef]
- Sanditov, D.S. Model of Delocalized Atoms in the Physics of the Vitreous State. J. Exp. Theor. Phys. 2012, 115, 112–124. [Google Scholar] [CrossRef]
- IUPAC. Compendium of Chemical Terminology; Royal Society of Chemistry: Cambridge, UK, 1997; Volume 66, p. 583. [Google Scholar]
- Zheng, Q.; Zhang, Y.; Montazerian, M.; Gulbiten, O.; Mauro, J.C.; Zanotto, E.D.; Yue, Y. Understanding glass through differential scanning calorimetry. Chem. Rev. 2019, 119, 7848–7939. [Google Scholar] [CrossRef] [PubMed]
- Frenkel, J. Kinetic Theory of Liquids; Clarendon: Oxford, UK, 1946. [Google Scholar]
- Frenkel, J. Über die Wärmebewegung in festen und flüssigen Körpern. Z. Physik 1926, 35, 652–669. [Google Scholar] [CrossRef]
- Wallace, D.C. Statistical mechanics of monatomic liquids. Phys. Rev. E 1997, 56, 4179–4186. [Google Scholar] [CrossRef]
- Wallace, D.C. Liquid dynamics theory of high-temperature specific heat. Phys. Rev. E 1998, 57, 1717–1722. [Google Scholar] [CrossRef]
- Ke, H.B.; Wen, P.; Wang, W.H. The inquiry of liquids and glass transition by heat capacity. AIP Adv. 2012, 2, 041404. [Google Scholar] [CrossRef]
- Tang, M.B.; Wang, W.H.; Xia, L.; Zhao, J.T. Constant-volume heat capacity at glass transition. J. Alloys Compd. 2013, 577, 299–302. [Google Scholar] [CrossRef]
- Cockrell, C.; Grimes, R.W. Crossover in atomic mobility underlying the glass transition in inorganic glasses. J. Phys. Condens. Matter 2025, 37, 095402. [Google Scholar] [CrossRef]
- Shirai, K.; Watanabe, K.; Momida, H.; Hyun, S. First-principles study on the specific heat jump in the glass transition of silica glass and the Prigogine-Defay ratio. arXiv 2022, arXiv:2202.09088v1. [Google Scholar] [CrossRef]
- Conradt, R. Thermodynamics and Kinetics of Glass. In Springer Handbook of Glass; Musgraves, J.D., Calvez, Eds.; Springer Handbooks; Springer: Cham, Switzerland, 2019; pp. 51–77. [Google Scholar] [CrossRef]
- Konchakov, R.A.; Makarov, A.S.; Afonin, G.V.; Qiao, J.C.; Vasin, M.G.; Kobelev, N.P.; Khonik, V.A. Critical behavior of the fluctuation heat capacity near the glass transition of metallic glasses. J. Non-Cryst. Solids 2025, 619, 122555. [Google Scholar] [CrossRef]
- Klein, I.S.; Angell, C.A. Excess thermodynamic properties of glassforming liquids: The rational scaling of heat capacities, and the thermodynamic fragility dilemma resolved. J. Non-Cryst. Solids 2016, 451, 116–123. [Google Scholar] [CrossRef]
- Louzguine, D.V.; Sobu, S.; Inoue, A. The influence of scandium in effecting fragile to strong glass transition in aluminium-based alloys. Appl. Phys. Lett. 2004, 85, 3758–3759. [Google Scholar] [CrossRef]
- Hong, Q.-J.; Liu, Z.-K. Generalized approach for rapid entropy calculation of liquids and solids. Phys. Rev. Res. 2025, 7, L012030. [Google Scholar] [CrossRef]
- Wang, H.; Lu, G.; Tan, W.; Li, J.; Su, K.; Huang, S.; Yang, L.; Wang, H. Giant Negative Temperature Coefficient of Resistance and Magnetotransport in Antiferromagnetic CaMnO3. J. Low Temp. Phys. 2025. [Google Scholar] [CrossRef]
- Vopson, M.M.; Rogers, N.; Hepburn, I. The generalized Lindemann melting coefficient. Solid State Commun. 2020, 318, 113977. [Google Scholar] [CrossRef]
- Melting. Encyclopaedia Britanica. Available online: https://www.britannica.com/science/melting (accessed on 1 February 2025).
- Lindemann, F.A. Über die Berechnung molekularer Eigenfrequenzen. Phys. Z. 1910, 11, 609–614. [Google Scholar]
- Born, M. Thermodynamics of Crystals and Melting. J. Chem. Phys. 1939, 7, 591–603. [Google Scholar] [CrossRef]
- Born, M. Dynamical Theory of Crystal Lattices; Born, M., Huang, K., Eds.; Clarendon: Oxford, UK, 1956; p. 160. [Google Scholar]
- Lindemann, F.A. The calculation of molecular vibration frequencies. Phys. Z. 1910, 11, 609–614. [Google Scholar]
- Gilvarry, J.J. The Lindemann and grüneisen laws. Phys. Rev. 1956, 102, 308–316. [Google Scholar] [CrossRef]
- Guardiola, R.; Navarro, J. On the Lindemann criterion for quantum clusters at very low temperature. J. Phys. Chem. 2011, 115, 6843–6850. [Google Scholar] [CrossRef]
- Lubchenko, V. A Universal Criterion of Melting. J. Phys. Chem. B 2006, 110, 18779–18786. [Google Scholar] [CrossRef]
- Sanditov, D.S. A criterion for the glass–liquid transition. J. Non-Cryst. Solids 2014, 385, 148–152. [Google Scholar] [CrossRef]
- Tournier, R.F. Lindemann’s rule applied to the melting of crystals and ultra-stable glasses. Chem. Phys. Lett. 2016, 651, 198–202. [Google Scholar] [CrossRef]
- Tournier, R.F.; Ojovan, M.I. Multiple Melting Temperatures in Glass-Forming Melts. Sustainability 2022, 14, 2351. [Google Scholar] [CrossRef]
- Khrapak, S.A. Lindemann melting criterion in two dimensions. Phys. Rev. Res. 2020, 2, 012040(R). [Google Scholar] [CrossRef]
- Wang, J.; Li, J.; Yip, S.; Phillpot, S.; Wolf, D. Mechanical instabilities of homogeneous crystals. Phys. Rev. B 1995, 52, 12627–12635. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D.V.; Belosludov, R.V.; Ojovan, M.I. Room-temperature Pressure-induced Phase Separation in Glassy Alloys. Mater. Today Commun. 2024, 40, 109453. [Google Scholar] [CrossRef]
- Bunde, A.; Havlin, S. Fractals and Disordered Systems; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Stauffer, D.; Aharony, A. Introduction to Percolation Theory; Taylor & Francis: London, UK, 1994. [Google Scholar]
- Schrenk, K.J.; Posé, N.; Kranz, J.J.; van Kessenich, L.V.M.; Araújo, N.A.M.; Herrmann, H.J. Percolation with long-range correlated disorder. Phys. Rev. E 2013, 88, 052102. [Google Scholar] [CrossRef]
- Richet, P.; Bottinga, Y.; Denielou, L.; Petitet, J.P.; Tequi, C. Thermodynamic properties of quartz, cristobalite and amorphous SiO2: Drop calorimetry measurements between 1000 and 1800 K and a review from 0 to 2000 K. Geochim. Cosmochim. Acta 1982, 46, 2639–2658. [Google Scholar] [CrossRef]
- Afonin, G.V.; Qiao, J.C.; Makarov, A.S.; Konchakov, R.A.; Goncharova, E.V.; Kobelev, N.P. High entropy metallic glasses, what does it mean? Appl. Phys. Lett. 2024, 124, 151905. [Google Scholar] [CrossRef]
- Luan, H.; Li, K.; Shi, L.; Zhao, W.; Bu, H.; Gong, P.; Yao, K.-F. Recent progress in high-entropy metallic glasses. J. Mater. Sci. Technol. 2023, 161, 50–62. [Google Scholar] [CrossRef]
- Dienes, G.J. Frequency Factor and Activation Energy for the Volume Diffusion of Metals. J. Appl. Phys. 1950, 21, 1189–1192. [Google Scholar] [CrossRef]
- Almond, D.P.; West, A.R. The activation entropy for transport in ionic conductors. Solid State Ion. 1987, 23, 27–35. [Google Scholar] [CrossRef]
- Bolmatov, D.; Brazhkin, V.; Trachenko, K. The phonon theory of liquid thermodynamics. Sci. Rep. 2012, 2, 421. [Google Scholar] [CrossRef]
- Bolmatov, D. The Phonon Theory of Liquids and Biological Fluids: Developments and Applications. J. Phys. Chem. Lett. 2022, 13, 7121–7129. [Google Scholar] [CrossRef]
- Trachenko, K. Theory of Liquids: From Excitations to Thermodynamics; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
- Glova, A.; Karttunen, M. Learning glass transition temperatures via dimensionality reduction with data from computer simulations: Polymers as the pilot case. J. Chem. Phys. 2024, 161, 184902. [Google Scholar] [CrossRef] [PubMed]
- Noether, E. Invariante Variations probleme. In Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse; Weidmannsche Buchhandlung: Berlin, Germany, 1918; pp. 235–257. [Google Scholar]
- Feynman, R.P.; Weinberg, S. Elementary Particles and the Laws of Physics; University Press: Cambridge, UK, 1999; p. 73. ISBN 0521658624. [Google Scholar]
- Hanc, J.; Tuleja, S.; Hancova, M. Symmetries and Conservation Laws: Consequences of Noether’s Theorem. Am. J. Phys. 2004, 72, 428–435. [Google Scholar] [CrossRef]
- Louzguine-Luzgin, D.V. Structural Changes in Metallic Glass-Forming Liquids on Cooling and Subsequent Vitrification in Relationship with Their Properties. Materials 2022, 15, 7285. [Google Scholar] [CrossRef] [PubMed]
- Louzguine-Luzgin, D.V. Crystallization of Metallic Glasses and Supercooled Liquids. Materials 2024, 17, 3573. [Google Scholar] [CrossRef]
- Stoch, P.; Krakowiak, I. Thermal properties of Sr-containing iron-phosphate glasses experimental and theoretical approach. J. Therm. Anal. Calorim 2025. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics Volume 5: Statistical Physics Part 1; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Goldenfeld, N. Lectures on Phase Transitions and the Renormalization Group; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Henkel, M.; Pleimling, M. Non-Equilibrium Phase Transitions: Volume 2: Ageing and Dynamical Scaling Far from Equilibrium; Springer Science & Business Media: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Haken, H. Synergetics: An Introduction: Nonequilibrium Phase Transitions and Self-Organization in Physics; Chemistry and Biology; Springer: Berlin, Germany, 2004. [Google Scholar]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 851. [Google Scholar] [CrossRef]
- Wang, J.; Li, R. Effects, methods and limits of the cryopreservation on mesenchymal stem cells. Stem Cell Res. Ther. 2024, 15, 337. [Google Scholar] [CrossRef]
- Gallino, I.; Busch, R. Thermodynamic and Kinetic Aspects of the Glass Transition. In Physical Metallurgy of Bulk Metallic Glass-Forming Liquids; Springer Series in Materials Science; Springer: Cham, Switzerland, 2024; Volume 341. [Google Scholar] [CrossRef]
- Doremus, R.H. Viscosity of silica. J. Appl. Phys. 2002, 92, 7619. [Google Scholar] [CrossRef]
- Cohen, M.; Turnbull, D. Free-volume model of the amorphous phase: Glass transition. J. Chem. Phys. 1961, 34, 120–125. [Google Scholar] [CrossRef]
- Spaepen, F. A microscopic mechanism for steady state inhomogeneous flow in metallic glasses. Acta Metall. 1977, 25, 407–415. [Google Scholar] [CrossRef]
- Janssen, L.M.C. Mode-Coupling Theory of the Glass Transition: A Primer. Front. Phys. 2018, 6, 97. [Google Scholar] [CrossRef]
- Ojovan, M.I.; Lu, A.K.A.; Louzguine-Luzgin, D.V. Massive Fluctuations in the Derivatives of Pair Distribution Function Minima and Maxima During the Glass Transition. Metals 2025, 15, 869. [Google Scholar] [CrossRef]
- Zhang, H.R.; Yang, Q.; Fang, Z.L.; Zhang, W.X.; Yin, Z.; Zeng, M.H.; Yu, H.B. Size-dependent vitrification in hybrid glasses at micro-meter scale. Sci. China Phys. Mech. Astron. 2025, 68, 266103. [Google Scholar] [CrossRef]
- Stiehler, M.E.; Georgarakis, K. From metallic liquids to metallic glasses: In-situ monitoring the atomic structure evolution by synchrotron X-ray diffraction. Crit. Rev. Solid. State Mater. Sci. 2025. [Google Scholar] [CrossRef]
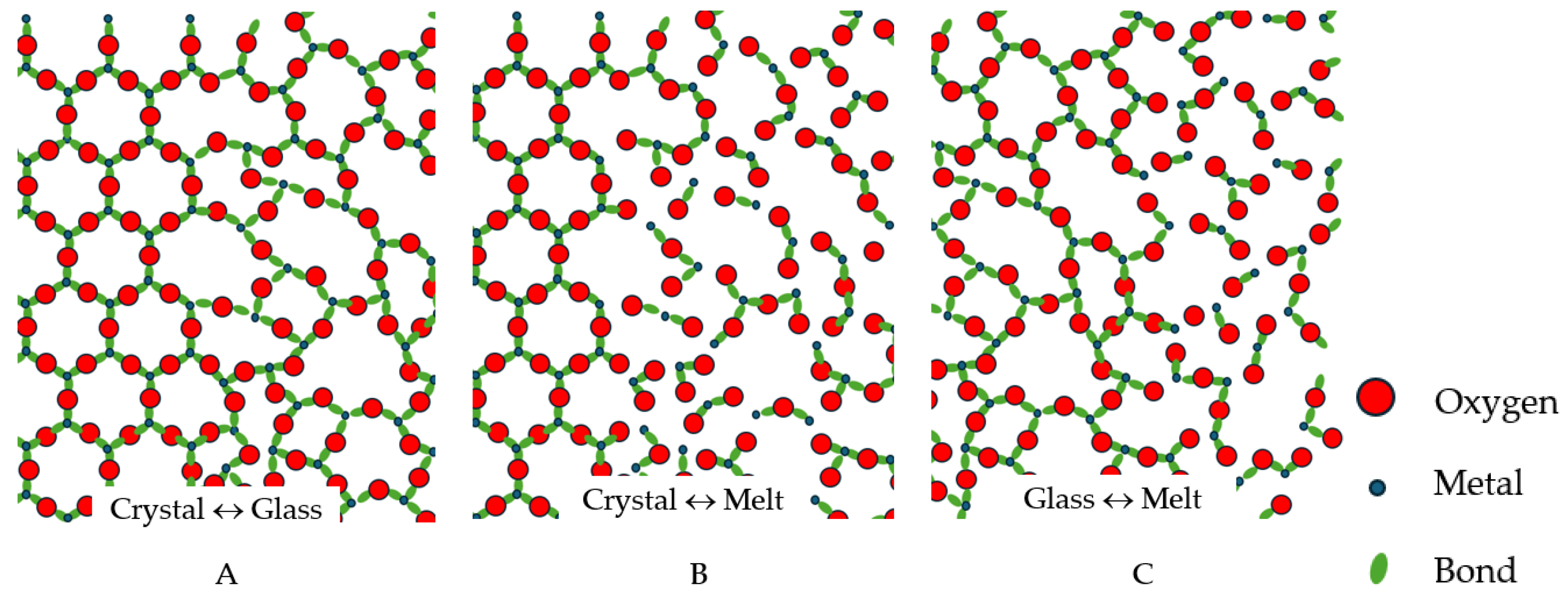

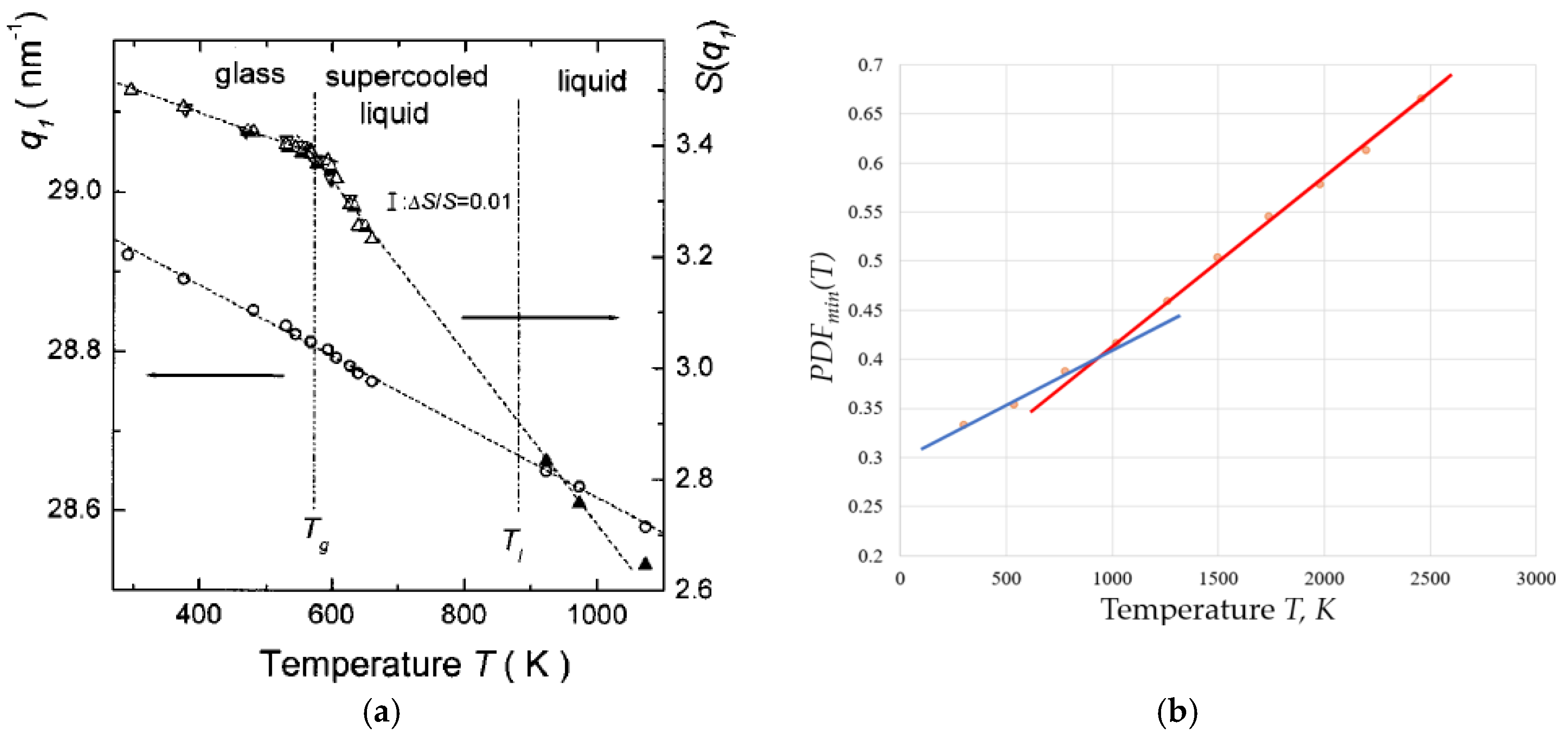
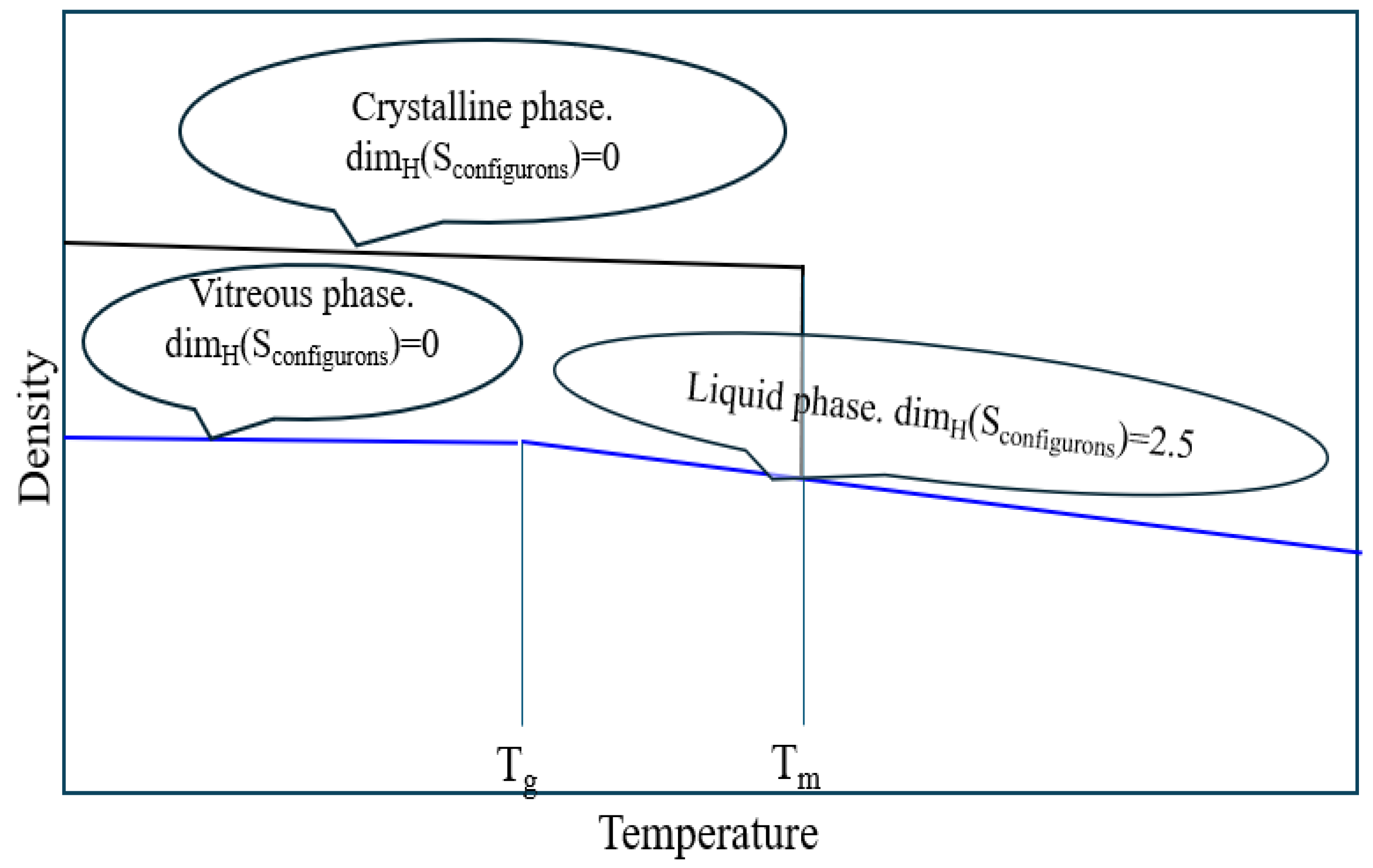
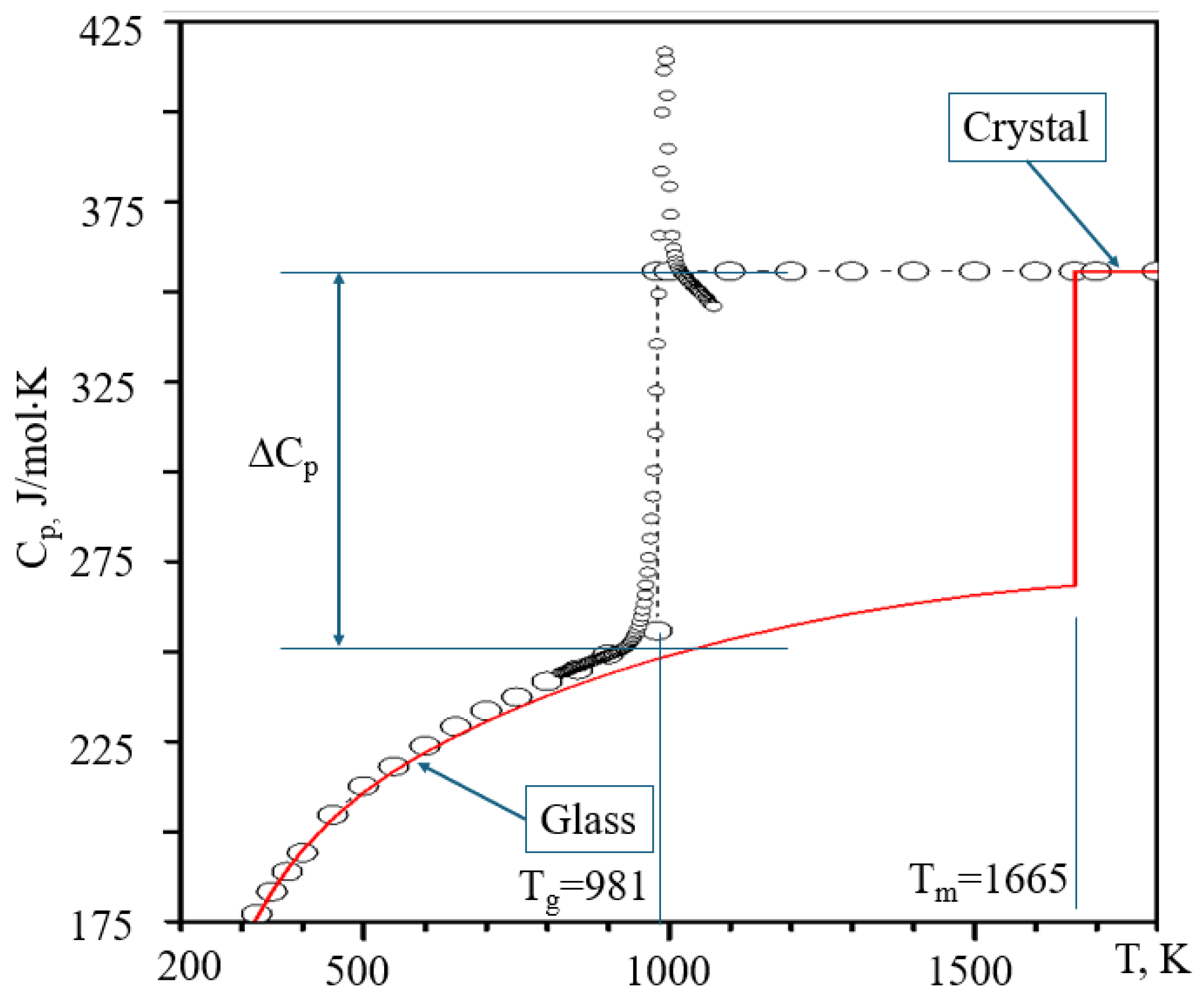
| Bond Type | Substance | Bond Energy (kJ/mol) | Configuron Description | Microscopic Result of Configuron Formation |
|---|---|---|---|---|
| Covalent | SiO2 | 443 | A Si–O broken bond with neighbouring adjustments | A shift by one or more atoms from the first coordination shell |
| Ionic | CuF2 | 2591 | A Cu–F broken bond with neighbouring adjustments | Same as above |
| Metallic | Fe | 407 | A displacement of an atom out of the first coordination shell with neighbouring adjustments | Same as above |
| Van der Waals | Ar | 7.6 | A broken Ar–Ar bond with neighbouring adjustments | Same as above |
| Hydrogen | H2O | 50 | A broken hydrogen bond with neighbouring adjustments | Same as above |
| Degree of Ordering | Degree of Connectivity | |
|---|---|---|
| Low | High | |
| High | Liquid crystals; Liquid quasi-crystals | Crystals; Quasi-crystals |
| Medium | Liquid glasses | Glass–crystalline materials |
| Low | Melts | Glass 1 |
| Table 1. | Low (in the Glass) T < Tg | Intermediate (in the Supercooled Melt) Tg < T < TA | High (in the Melt) T > TA = (1.10 ± 0.15) Tm | Extremely High |
|---|---|---|---|---|
| Viscous flow type | Arrhenian with high activation energy QH | Non-Arrhenian, apparent variable activation energy Q(T) | Arrhenian with low activation energy QL | Non-activated, growing with temperature rise |
| CPT universal viscosity equation 1 | ||||
| Alloy, Compound | Tg, K | ∆Cv, J/mol·K |
|---|---|---|
| La55Al25Ni20 | 465 | 12.31 |
| Zr65Al7.5Ni10Cu17.5 | 653 | 11.02 |
| Mg65Cu25Y10 | 380 | 10.06 |
| Zr41.2Ti13.8Cu12.5Ni10Be22.5 | 623 | 11.95 |
| Pd77.5Cu6Si16.5 | 625 | 10.33 |
| Pd40Cu30Ni10P20 | 525 | 10.89 |
| Pd40Ni40P20 | 551 | 11.02 |
| Zr55Al10Ni5Cu30 | 653 | 11.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ojovan, M.I.; Louzguine-Luzgin, D.V. Role of Structural Changes at Vitrification and Glass–Liquid Transition. Materials 2025, 18, 3886. https://doi.org/10.3390/ma18163886
Ojovan MI, Louzguine-Luzgin DV. Role of Structural Changes at Vitrification and Glass–Liquid Transition. Materials. 2025; 18(16):3886. https://doi.org/10.3390/ma18163886
Chicago/Turabian StyleOjovan, Michael I., and Dmitri V. Louzguine-Luzgin. 2025. "Role of Structural Changes at Vitrification and Glass–Liquid Transition" Materials 18, no. 16: 3886. https://doi.org/10.3390/ma18163886
APA StyleOjovan, M. I., & Louzguine-Luzgin, D. V. (2025). Role of Structural Changes at Vitrification and Glass–Liquid Transition. Materials, 18(16), 3886. https://doi.org/10.3390/ma18163886







