Dynamical Characterization of Plates Containing Plane Cracks with Functional Gradient Materials
Highlights
- The kinetic and potential energies of a cracked FGM plate are derived using thin plate theory, divided into four sub-zones.
- The influence of crack and gradient parameters on vibration in exponential FGM plates is studied.
- Longer planar cracks reduce natural frequencies and alter nodal lines and mode symmetry in FGM plates.
- The planar crack causes the FGM plate’s upper and lower surfaces to vibrate out of phase.
- Material gradients cause thickness-direction asymmetry with unequal upper/lower displacements in FGM plates.
Abstract
1. Introduction
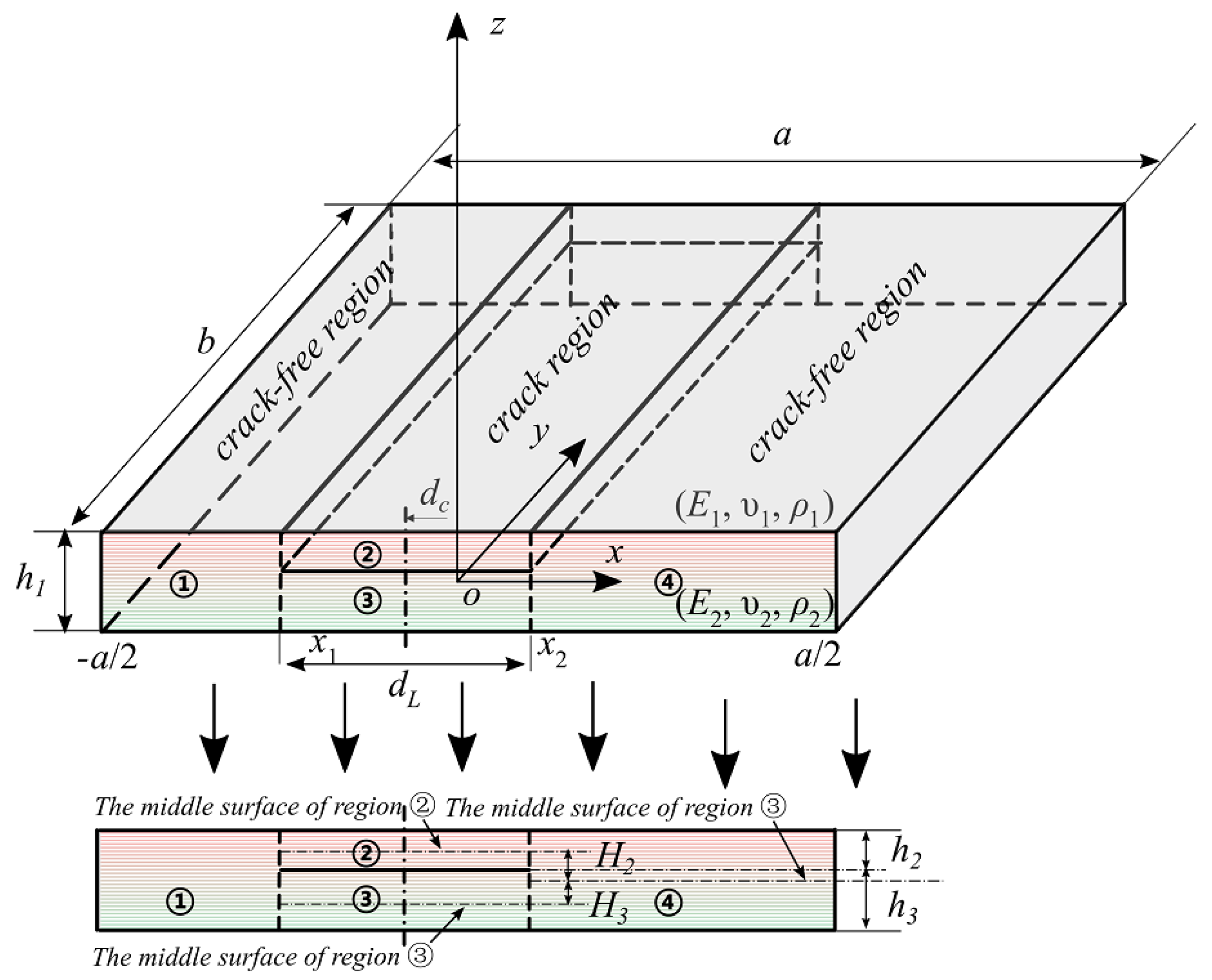
2. Modeling
3. Displacement Field of the Cracked Plate
4. Free Vibration
5. Natural Frequency and Modes
5.1. Convergence Analysis and Validation of Results
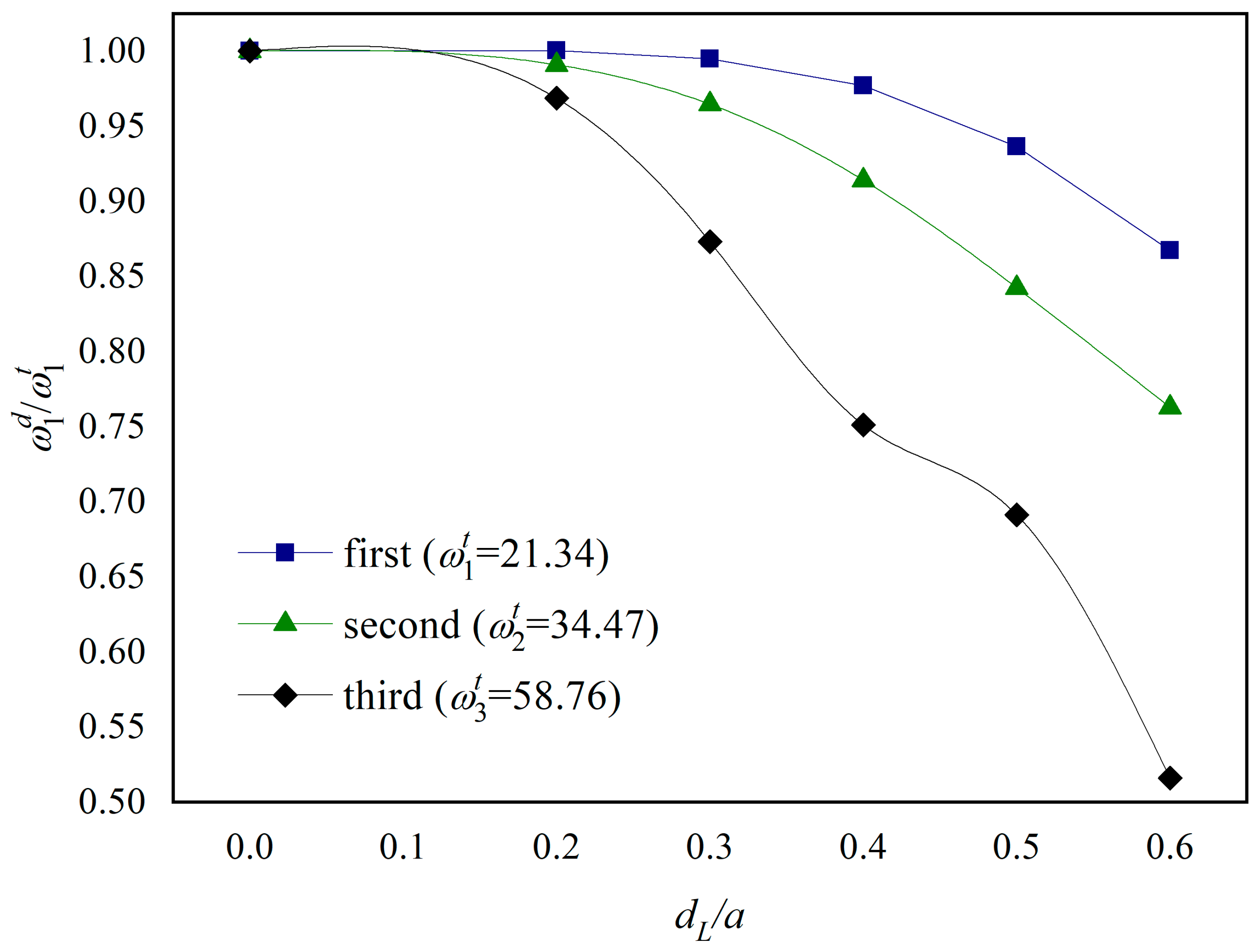
5.2. Effect of Crack Length on Vibration Characteristics of FGM Plates
5.3. Effect of Crack Location on Vibration Characteristics of FGM Plates
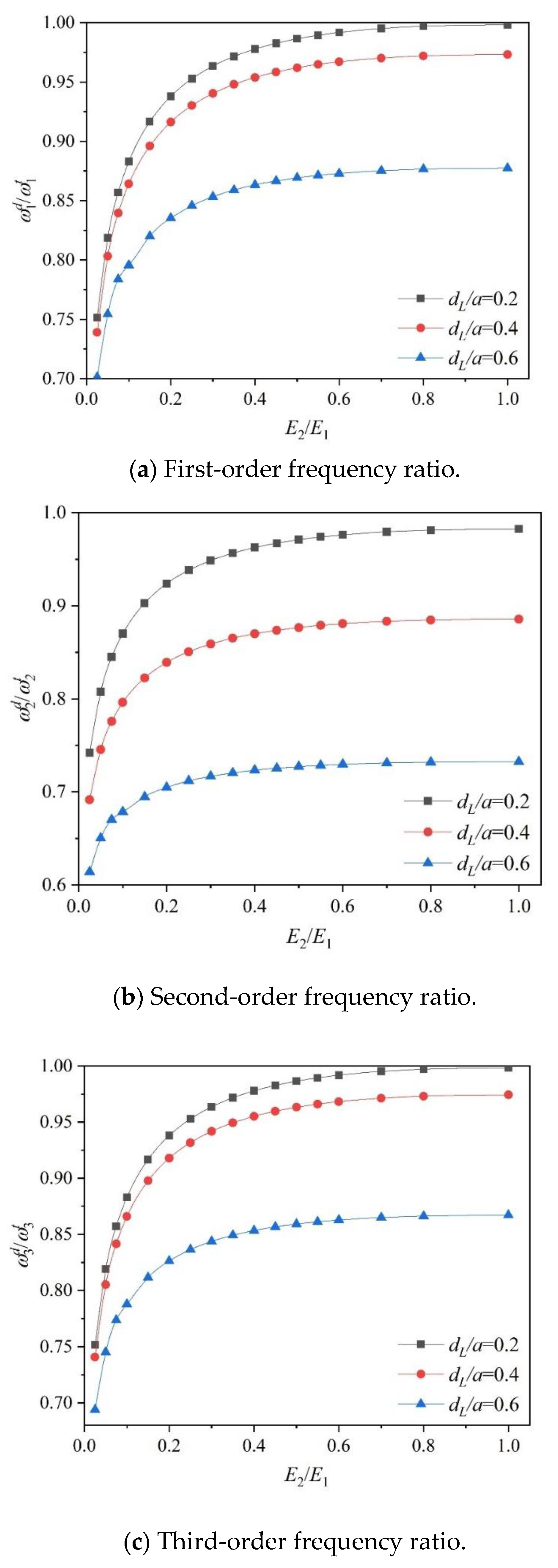
5.4. Natural Frequency Study of Cracked FGM Plates with Different Material Gradients
6. Conclusions
- (1)
- As the length of the plane crack increases, the influence of the gradient parameter on the natural frequency diminishes. Specifically, a longer crack reduces the sensitivity of the natural frequency to variations in the gradient parameter.
- (2)
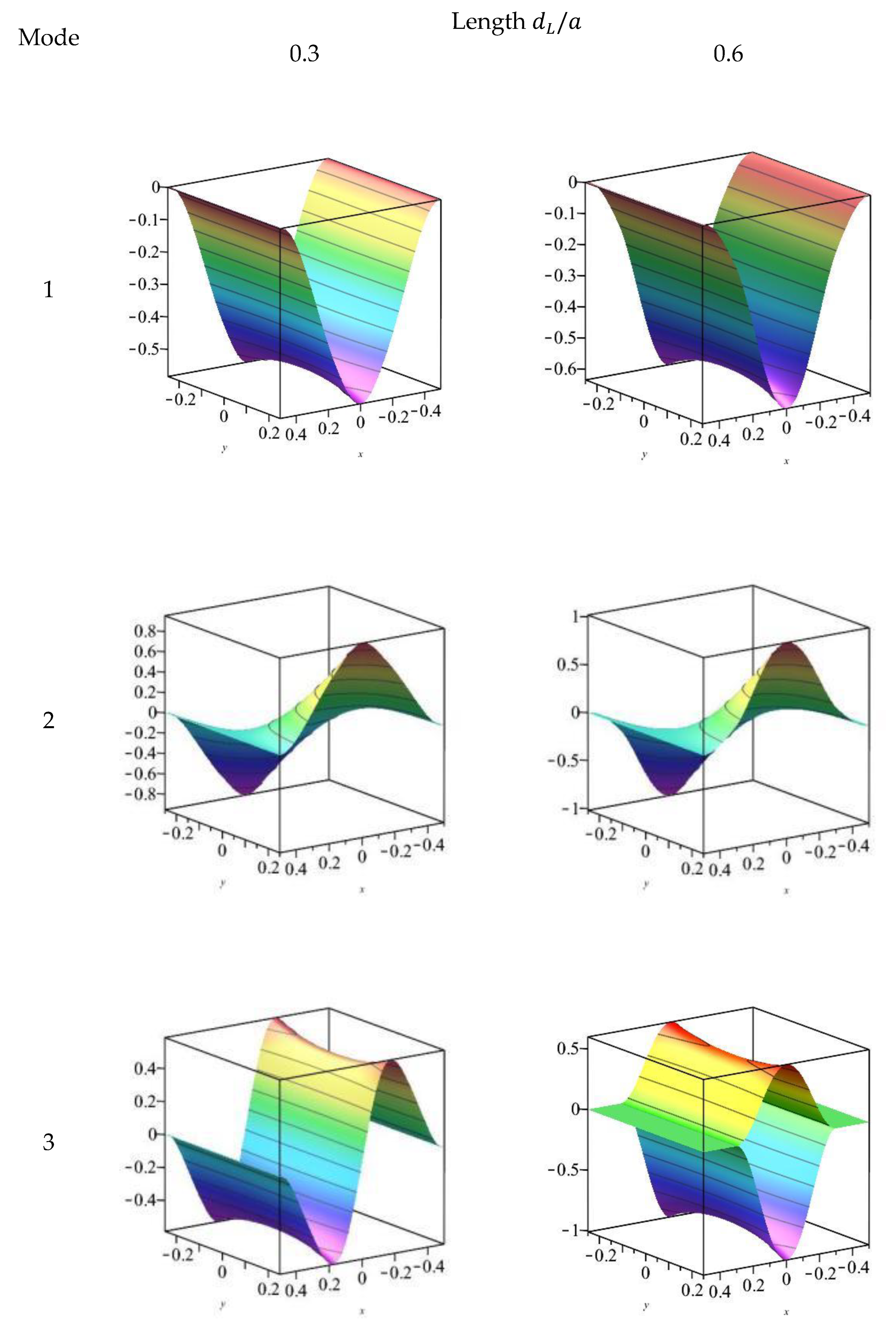
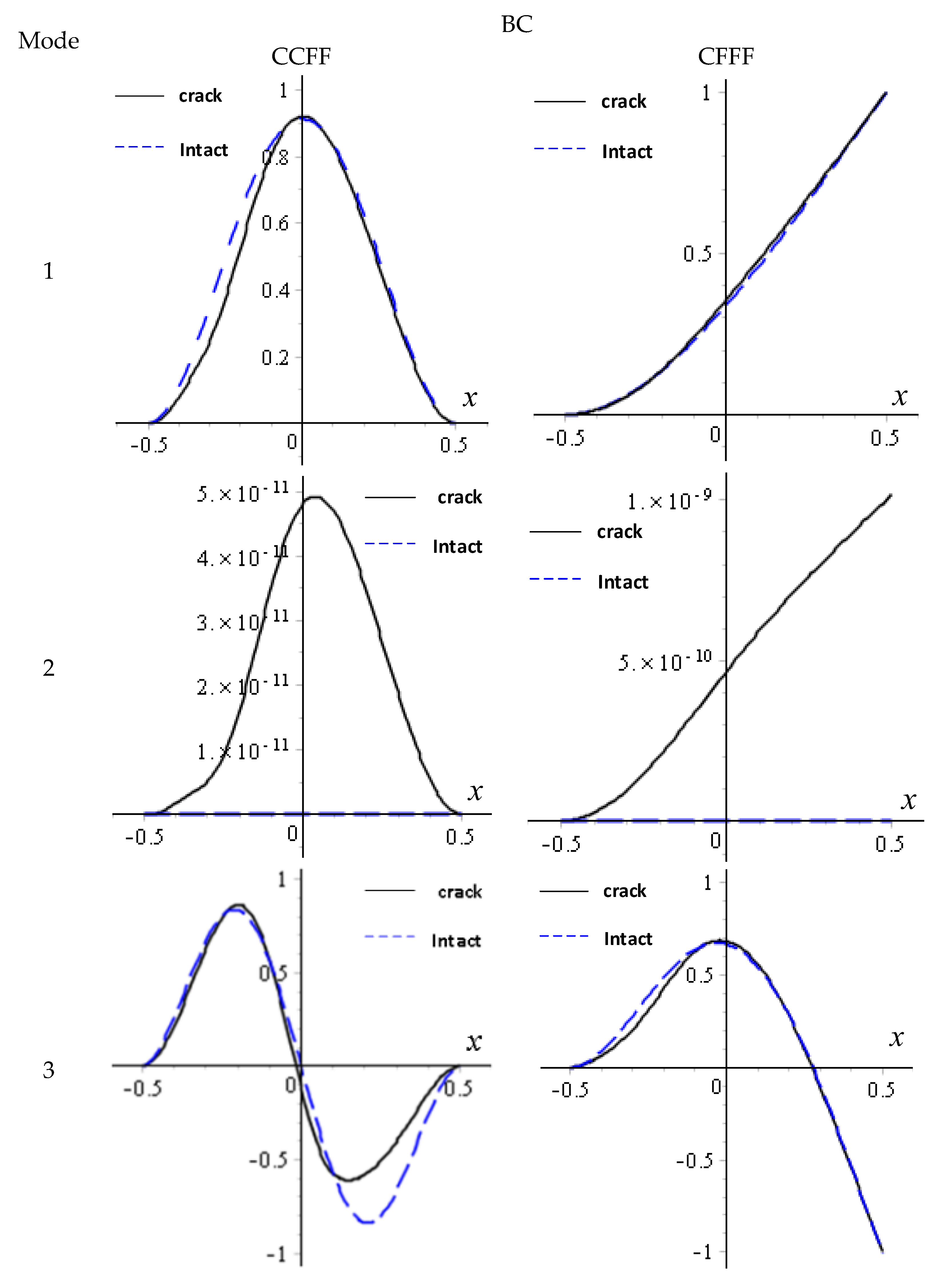
- The effect of crack location on the natural frequency is governed by both the boundary conditions of the FGM plate and the nodal lines of the mode shapes for each order. Moreover, the presence of a plane crack alters the nodal lines and symmetry of the mode shapes. This indicates that the crack location interacts with the boundary conditions and mode characteristics to influence the vibration behavior of the plate.
- (3)
- During free vibration, the upper and lower parts of the FGM plate in the plane crack region exhibit a deviation from each other, resulting in an opening behavior. This deviation is further influenced by the material gradient, causing the upper and lower parts of the opening region to have different displacements and exhibit asymmetry in the thickness direction. This phenomenon highlights the significant impact of material gradient on the vibration response of a cracked FGM plate.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| symbol | description |
| the length of the plate | |
| the width of the plate | |
| the length of the crack | |
| the distance between the mid-point of the planar crack and the mid-point of the plate | |
| modulus of elasticity of the FGM plate | |
| density of the FGM plate | |
| the gradient parameter of the material | |
| modulus of elasticity, Poisson’s ratio, and density at the upper surfaces of the plate | |
| modulus of elasticity, Poisson’s ratio, and density at the lower surfaces of the plate | |
| FGM | functionally graded material |
| CFFF | For a plate solidly supported at with other sides free |
| CCFF | are fixed and the other two sides are free |
References
- Minh, P.P.; Duc, N.D. The effect of cracks and thermal environment on free vibration of FGM plates. Thin-Walled Struct. 2021, 159, 107291. [Google Scholar] [CrossRef]
- Burlayenko, V.N.; Sadowski, T.; Dimitrova, S. Three-dimensional free vibration analysis of thermally loaded FGM sandwich plates. Materials 2019, 12, 2377. [Google Scholar] [CrossRef] [PubMed]
- Obalareddy, B.; Sathujoda, P.; Citarella, R. Dynamic stiffness matrix approach to free vibration analysis of functionally graded rotor bearing system subjected to thermal gradients. Materials 2022, 15, 1540. [Google Scholar] [CrossRef]
- Gupta, A.; Soni, S.; Jain, N.K. A Non-classical analytical approach for vibration analysis of isotropic and Fgm plate containing a star shaped crack. J. Mech. 2020, 36, 465–484. [Google Scholar] [CrossRef]
- Safaeifar, H. Vibration Analysis of FGM Plate Under the Effect of Axial and Lateral Loading Using VIM. J. Vib. Eng. Technol. 2022, 10, 1917–1930. [Google Scholar] [CrossRef]
- Wang, J.F.; Cao, G.; Song, Z.W.; Lai, S.K. Dynamic analysis of FGM plates with variable delamination parameters by the Chebyshev–Ritz method. Int. J. Struct. Stab. Dyn. 2023, 23, 2340013. [Google Scholar] [CrossRef]
- Mishra, P.K.; Panda, S.K.; Pati, S.N.; Kumar, E.K.; Panda, S.K. Minimization of delamination effect on laminated composite plates using functional materials (piezoelectric and magnetostrictive). Mech. Based Des. Struct. Mach. 2024, 52, 5849–5870. [Google Scholar] [CrossRef]
- Li, D.H.; Yang, X.; Qian, R.L.; Xu, D. Static and dynamic response analysis of functionally graded material plates with damage. Mech. Adv. Mater. Struct. 2020, 27, 94–107. [Google Scholar] [CrossRef]
- Sahoo, S.S.; Panda, S.K.; Sen, D. Effect of delamination on static and dynamic behavior of laminated composite plate. AIAA J. 2016, 54, 2530–2544. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J.; Guo, Y. Investigation of delamination effect on nonlinear vibration behaviors of a composite plate resting on nonlinear elastic foundation. Compos. Struct. 2022, 280, 114897. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Doan, D.H. Buckling of cracked FG plate resting on elastic foundation considering the effect of delamination phenomenon. Compos. Struct. 2021, 273, 114278. [Google Scholar] [CrossRef]
- Taheri, M.H.; Memarzadeh, P. Effect of crack on shear buckling of CNTRC plates. Int. J. Mech. Sci. 2022, 229, 107519. [Google Scholar] [CrossRef]
- Zhong, J.R. Analytical solution for buckling behavior of FGM plate considering surface effect based on general third-order plate theory and non-local theory. Int. J. Struct. Stab. Dyn. 2020, 20, 2050125. [Google Scholar] [CrossRef]
- Karataş, E.E. Buckling delamination of a rectangular orthotropic thick plate with an embedded rectangular crack subjected to an axial compressive force. Mech. Compos. Mater. 2019, 55, 643–654. [Google Scholar] [CrossRef]
- Ertenli, M.F.; Esen, İ. The effect of the various porous layers on thermomechanical buckling of FGM sandwich plates. Mech. Adv. Mater. Struct. 2024, 31, 10935–10961. [Google Scholar] [CrossRef]
- Kim, I.B.; Song-Hak, U.; Sin, S.H. Global stiffness determination of a cross-ply laminated composite plate with distributed delaminations and matrix cracks and its application. Compos. Struct. 2020, 233, 111586. [Google Scholar] [CrossRef]
- Juhász, Z.; Szekrényes, A. The effect of delamination on the critical buckling force of composite plates: Experiment and simulation. Compos. Struct. 2017, 168, 456–464. [Google Scholar] [CrossRef]
- Kiani, Y. Axisymmetric static and dynamics snap-through phenomena in a thermally postbuckled temperature-dependent FGM circular plate. Int. J. Non-Linear Mech. 2017, 89, 1–13. [Google Scholar] [CrossRef]
- Li, D.H. Delamination and transverse crack growth prediction for laminated composite plates and shells. Comput. Struct. 2016, 177, 39–55. [Google Scholar] [CrossRef]
- Li, D.H.; Zhang, X.; Sze, K.Y.; Liu, Y. Extended layerwise method for laminated composite plates with multiple delaminations and transverse cracks. Comput. Mech. 2016, 58, 657–679. [Google Scholar] [CrossRef]
- Nabil, B.; Abdelkader, B.; Miloud, A.; Noureddine, B. On the mixed-mode crack propagation in FGMs plates: Comparison of different criteria. Struct. Eng. Mech. Int. J. 2017, 61, 371–379. [Google Scholar] [CrossRef]
- Pokrovskii, A.M.; Chermoshentseva, A.S.; Bokhoeva, L.A. Evaluation of crack resistance of a compressed composite plate with initial delamination. J. Mach. Manuf. Reliab. 2021, 50, 446–454. [Google Scholar] [CrossRef]
- McElroy, M.; Jackson, W.; Olsson, R.; Hellström, P.; Tsampas, S.; Pankow, M. Interaction of delaminations and matrix cracks in a CFRP plate, Part I: A test method for model validation. Compos. Part A Appl. Sci. Manuf. 2017, 103, 314–326. [Google Scholar] [CrossRef]
- Zheng, H.; Sladek, J.; Sladek, V.; Wang, S.; Wen, P. Hybrid meshless/displacement discontinuity method for FGM Reissner’s plate with cracks. Appl. Math. Model. 2021, 90, 1226–1244. [Google Scholar] [CrossRef]
- Tran, M.T.; Tran, Q.S.; Suzuki, T.; Cuong-Le, T.; Luong, V.H. Dynamic analysis of FGM plate under moving load considering effect of temperature. Int. J. Struct. Stab. Dyn. 2022, 22, 2250130. [Google Scholar] [CrossRef]
- Kim, I.B.; Song-Hak, U.; Ji, T.H. Determination of local stiffness of a cross-ply composite plate with delaminations and matrix cracks. Compos. Struct. 2018, 196, 127–134. [Google Scholar] [CrossRef]
- Lu, X.; Yang, J.Y.; Wu, Y.G.; Zhang, F.; Li, D.H. An extended layerwise/solid-element method of stiffened composite plates with delaminations and transverse crack. Int. J. Mech. Mater. Des. 2018, 14, 345–358. [Google Scholar] [CrossRef]
- Xu, J.X.; Xiao, Z.G.; Wu, Y.G.; Li, D.H. Extended layerwise method for laminated piezoelectric and composite plates with delaminations, cracks or debonding of a piezoelectric patch. Compos. Struct. 2020, 234, 111692. [Google Scholar] [CrossRef]
- Wu, Y.; Xiao, Z.; Li, D.; Xu, J. On numerical static analysis of stiffened laminated composite plates with delaminations, cracks, or debonding of a piezoelectric patch. Mech. Adv. Mater. Struct. 2022, 29, 89–103. [Google Scholar] [CrossRef]
- Wu, Y.; Xiao, Z.; Liu, K.; Li, D. A three-dimensional numerical model for delaminations, transverse crack or debonding in composite sandwich plates with piezoelectric sensors. J. Intell. Mater. Syst. Struct. 2022, 33, 883–900. [Google Scholar] [CrossRef]
- Ghazali, M.; Karamooz Mahdiabadi, M. Delamination and crack detection and localization of a laminated composite plate structure using regression and regression-based neural network methods. Mech. Based Des. Struct. Mach. 2024, 52, 9479–9503. [Google Scholar] [CrossRef]
- Wang, Z.; Zhong, X.; Jiang, L.; Qi, F.; Ouyang, X.; Wang, J.; Liao, B.; Luo, J. Effect of interfacial delamination on coating crack in thick diamond-like carbon coatings under indentation. Acta Mech. Sin. 2020, 36, 524–535. [Google Scholar] [CrossRef]
- Aylikci, F.; Akbarov, S.D.; Yahnioglu, N. Buckling delamination of a PZT/Metal/PZT sandwich rectangular thick plate containing interface inner band cracks. Compos. Struct. 2018, 202, 9–16. [Google Scholar] [CrossRef]
- Cui, J.; Li, P.; Yin, H.; Zhang, D.; Yang, Y. Towards the effect of cracks on the instability of a plate loaded by low-speed axial flow. Thin-Walled Struct. 2024, 198, 111685. [Google Scholar] [CrossRef]
- Khoram-Nejad, E.S.; Moradi, S.; Shishehsaz, M. Effect of crack characteristics on the vibration behavior of post-buckled functionally graded plates. In Structures; Elsevier: Amsterdam, The Netherlands, 2023; Volume 50, pp. 181–199. [Google Scholar]
- Dong, H.; Xu, L.; Zhou, P.-H.; Yang, G.-J.; Wang, L.-S.; Yao, J.-T. Coupling effect of delamination cracks and vertical cracks on local phase transition of ceramic topcoat in thermal barrier coatings. Ceram. Int. 2023, 49, 13176–13184. [Google Scholar] [CrossRef]
- Salunkhe, S.B.; Singh, C.V.; Guruprasad, P.J. Effect of matrix cracks and delamination on extension-twist coupling of thin pretwisted composite strips. Compos. Struct. 2017, 180, 234–250. [Google Scholar] [CrossRef]
- Xue, J.; Zhang, W.; Wu, J.; Wang, C.; Ma, H. A semi-analytical method for vibration localization of plates integrated with low-frequency plate-type resonators. Thin-Walled Struct. 2024, 194, 111332. [Google Scholar] [CrossRef]
- Xue, J.; Chen, L.Q. A semi-analytical model for dynamic analysis of thin plates with plate-type resonators. Acta Mech. 2023, 234, 2315–2329. [Google Scholar] [CrossRef]
- Xue, J.; Ma, H.W.; Chen, L.Q. Vibration localization and reduction of double-plate structures. Aerosp. Sci. Technol. 2024, 152, 109340. [Google Scholar] [CrossRef]
- Liu, G.; Chen, G.F.; Cui, F.; Xi, A. Nonlinear vibration analysis of composite blade with variable rotating speed using Chebyshev polynomials. Eur. J. Mech./A Solids 2020, 82, 103976. [Google Scholar] [CrossRef]
- Yang, J.; Chen, Y. Free vibration and buckling analyses of functionally graded beams with edge cracks. Compos. Struct. 2008, 83, 48–60. [Google Scholar] [CrossRef]


| Mode | I × J | Yang [40] | Relative Error | ||||
|---|---|---|---|---|---|---|---|
| 5 × 5 | 6 × 6 | 7 × 7 | 8 × 8 | ||||
| 0.2 | 1 | 3.224 | 3.220 | 3.217 | 3.216 | 3.30 | 2.5% |
| 3 | 20.04 | 20.03 | 20.02 | 20.02 | 20.70 | 3.3% | |
| 1 | 1 | 3.431 | 3.427 | 3.424 | 3.423 | 3.52 | 2.8% |
| 3 | 21.33 | 21.32 | 21.31 | 21.31 | 22.03 | 3.3% | |
| Method | Frequency (Hz) | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| This paper | 84.45 | 122.40 | 170.39 |
| ABAQUS | 84.20 | 123.46 | 168.65 |
| relative error | 0.30% | 0.87% | 1.0% |
| BC | Mode | |||||
|---|---|---|---|---|---|---|
| −0.1 | −0.05 | 0 | 0.05 | 0.1 | ||
| CCFF | 3 | 48.79 | 46.22 | 44.60 | 46.22 | 48.79 |
| 2 | 31.21 | 31.69 | 31.84 | 31.69 | 31.21 | |
| 1 | 20.04 | 20.79 | 21.07 | 20.79 | 20.04 | |
| CFFF | 3 | 19.37 | 20.00 | 20.45 | 20.60 | 20.47 |
| 2 | 12.49 | 12.62 | 12.70 | 12.93 | 13.12 | |
| 1 | 3.274 | 3.278 | 3.279 | 3.294 | 3.305 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Xi, A.; Qi, Y.; Han, W. Dynamical Characterization of Plates Containing Plane Cracks with Functional Gradient Materials. Materials 2025, 18, 3868. https://doi.org/10.3390/ma18163868
Liu G, Xi A, Qi Y, Han W. Dynamical Characterization of Plates Containing Plane Cracks with Functional Gradient Materials. Materials. 2025; 18(16):3868. https://doi.org/10.3390/ma18163868
Chicago/Turabian StyleLiu, Gen, An Xi, Yunchao Qi, and Wenju Han. 2025. "Dynamical Characterization of Plates Containing Plane Cracks with Functional Gradient Materials" Materials 18, no. 16: 3868. https://doi.org/10.3390/ma18163868
APA StyleLiu, G., Xi, A., Qi, Y., & Han, W. (2025). Dynamical Characterization of Plates Containing Plane Cracks with Functional Gradient Materials. Materials, 18(16), 3868. https://doi.org/10.3390/ma18163868





