Descriptors for Predicting Single- and Multi-Phase Formation in High-Entropy Oxides: A Unified Framework Approach
Abstract
1. Introduction
2. Structures and Compositions
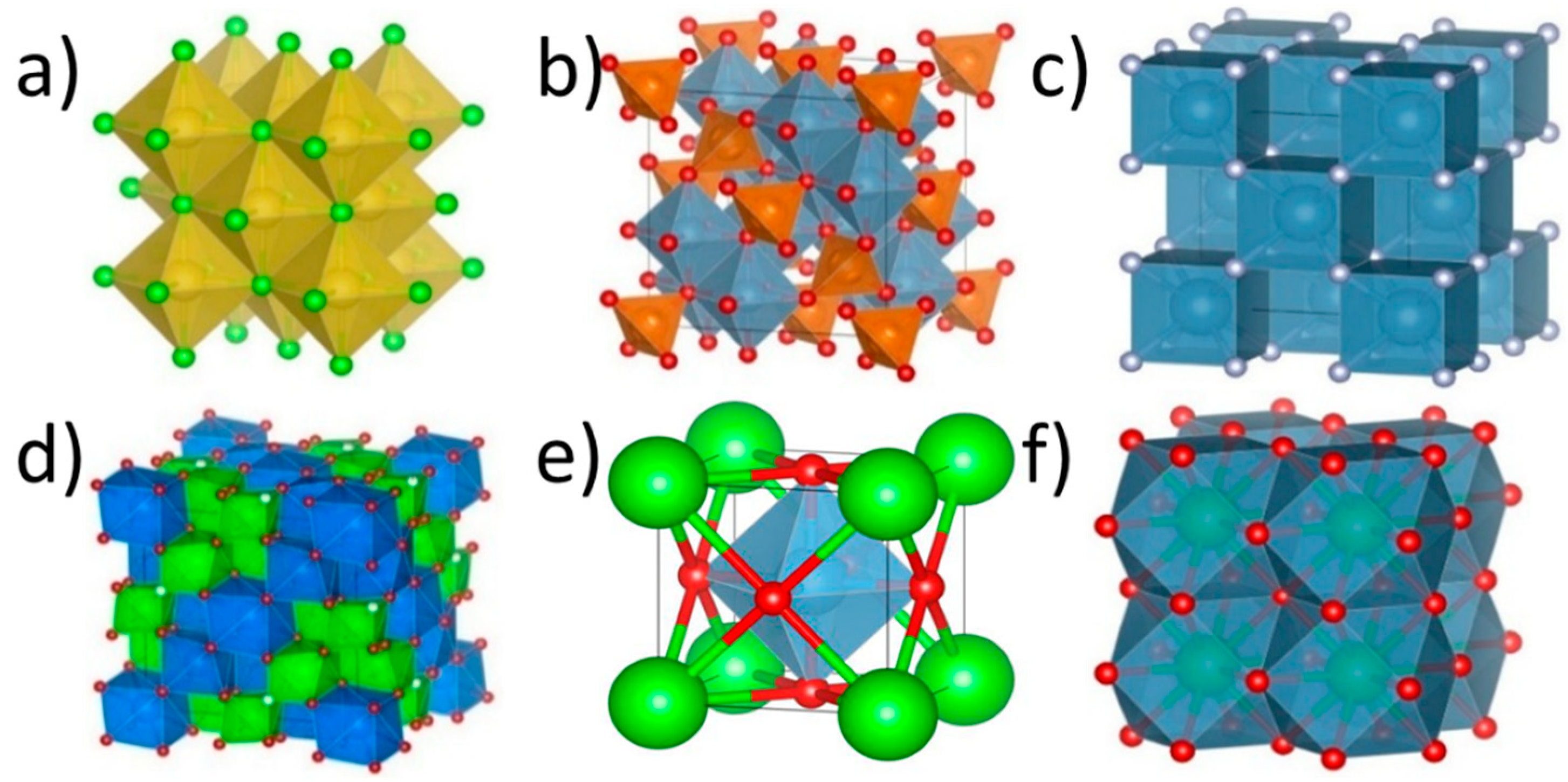
2.1. High-Entropy Oxides with the Rock Salt Structure, R-HEOs
2.2. High-Entropy Oxides with the Spinel Structure, S-HEOs
2.3. High-Entropy Oxides with the Perovskite Structure, P-HEOs
2.4. High-Entropy Oxides with Pyrochlore, Py-HEO, and Fluorite, F-HEO, Structures
3. Descriptors
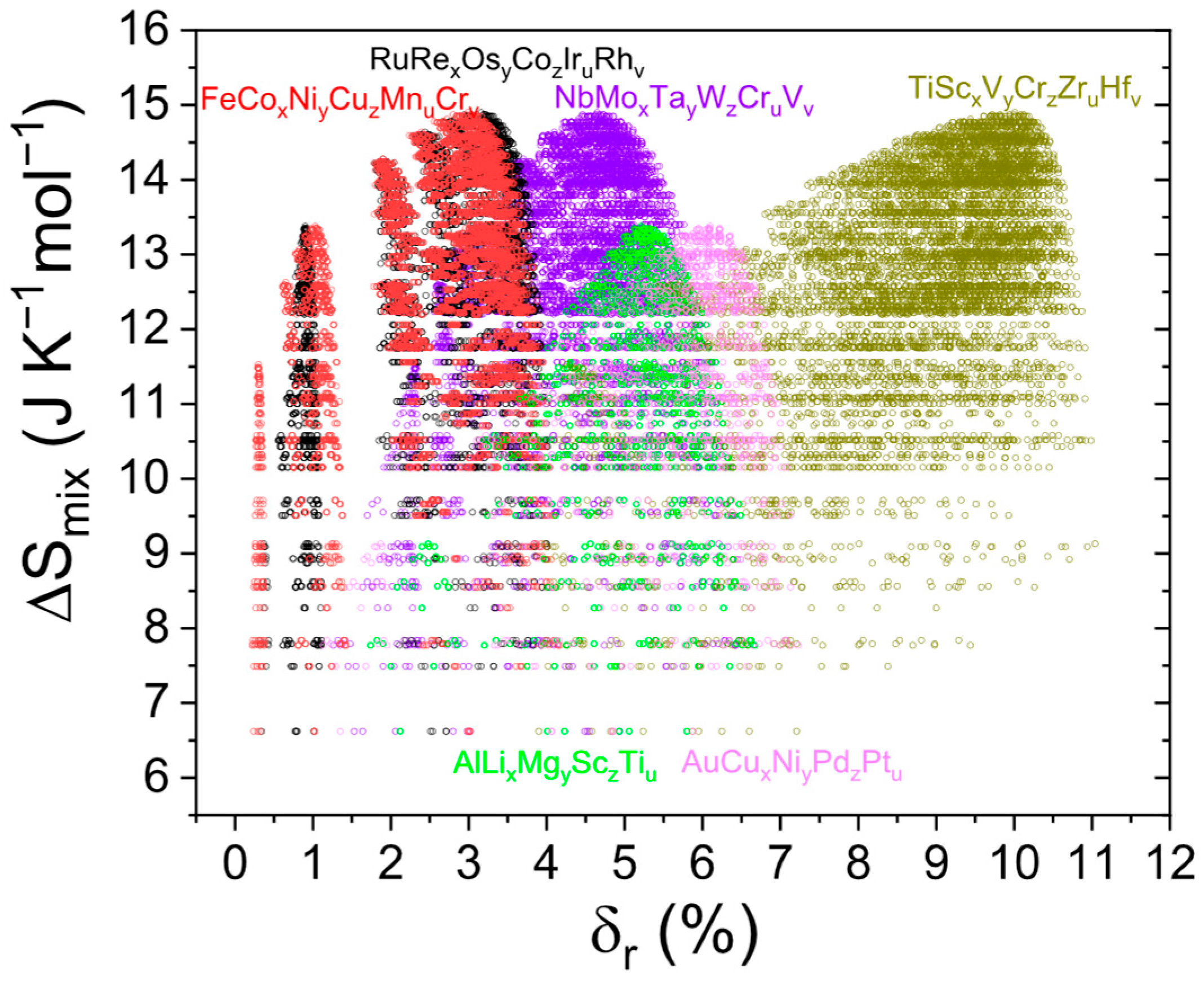
3.1. Descriptors Based on Entropy and Enthalpy
3.2. Disorder Factor for Different Structures
3.3. Classical Structure Descriptor for Different Structures
4. Unified Descriptors
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cantor, B.; Chang, I.T.H.; Knight, P.; Vincent, A.J.B. Microstructural development in equiatomic multicomponent alloys. Mater. Sci. Eng. A 2004, 375–377, 213–218. [Google Scholar] [CrossRef]
- Yu, B.; Ren, Y.; Zeng, Y.; Ma, W.; Morita, K.; Zhan, S.; Lei, Y.; Lv, G.; Li, S.; Wu, J. Recent progress in high-entropy alloys: A focused review of preparation processes and properties. J. Mater. Res. Technol. 2024, 29, 2689–2719. [Google Scholar] [CrossRef]
- Rost, C.M.; Sachet, E.; Borman, T.; Moballegh, A.; Dickey, E.C.; Hou, D.; Jones, J.L.; Curtarolo, S.; Maria, J.-P. Entropy-stabilized oxides. Nat. Commun. 2015, 6, 8485. [Google Scholar] [CrossRef]
- Anandkumar, M.; Trofimov, E. Synthesis, properties, and applications of high-entropy oxide ceramics: Current progress and future perspectives. J. Alloys Compd. 2023, 960, 170690. [Google Scholar] [CrossRef]
- Qiu, N.; Chen, H.; Yang, Z.; Sun, S.; Wang, Y.; Cui, Y. A high entropy oxide (Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O) with superior lithium storage performance. J. Alloys Compd. 2019, 777, 767–774. [Google Scholar] [CrossRef]
- Bérardan, D.; Franger, S.; Meena, A.K.; Dragoe, N. Room temperature lithium superionic conductivity in high entropy oxides. J. Mater. Chem. A 2016, 4, 9536–9541. [Google Scholar] [CrossRef]
- Fracchia, M.; Ghigna, P.; Pozzi, T.; Tamburini, U.A.; Colombo, V.; Braglia, L.; Torelli, P. Stabilization by Configurational Entropy of the Cu(II) Active Site during CO Oxidation on Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O. J. Phys. Chem. Lett. 2020, 11, 3589–3593. [Google Scholar] [CrossRef]
- Aamlid, S.S.; Oudah, M.; Rottler, J.; Hallas, A.M. Understanding the Role of Entropy in High Entropy Oxides. J. Am. Chem. Soc. 2023, 145, 5991–6006. [Google Scholar] [CrossRef]
- Fracchia, M.; Coduri, M.; Manzoli, M.; Ghigna, P.; Tamburini, U.A. Is configurational entropy the main stabilizing term in rock-salt Mg0.2Co0.2Ni0.2Cu0.2Zn0.2O high entropy oxide? Nat. Commun. 2022, 13, 2977. [Google Scholar] [CrossRef]
- Fracchia, M.; Coduri, M.; Ghigna, P.; Anselmi-Tamburini, U. Phase stability of high entropy oxides: A critical review. J. Eur. Ceram. Soc. 2024, 44, 585–594. [Google Scholar] [CrossRef]
- Liu, C.; Li, S.; Zheng, Y.; Xu, M.; Su, H.; Miao, X.; Liu, Y.; Zhou, Z.; Qi, J.; Yang, B.; et al. Advances in high entropy oxides: Synthesis, structure, properties and beyond. Prog. Mater. Sci. 2025, 148, 101385. [Google Scholar] [CrossRef]
- Jiang, B.; Bridges, C.A.; Unocic, R.R.; Pitike, K.C.; Cooper, V.R.; Zhang, Y.; Lin, D.-Y.; Page, K. Probing the Local Site Disorder and Distortion in Pyrochlore High-Entropy Oxides. J. Am. Chem. Soc. 2020, 143, 4193–4204. [Google Scholar] [CrossRef] [PubMed]
- Aamlid, S.S.; Mugiraneza, S.; González-Rivas, M.U.; King, G.; Hallas, A.M.; Rottler, J. Short-Range Order and Local Distortions in Entropy Stabilized Oxides. Chem. Mater. 2024, 36, 9636–9645. [Google Scholar] [CrossRef]
- Mansley, Z.R.; Millares, M.F.; Kazanjian, O.; Luo, J.; Takeuchi, E.S.; Marschilok, A.C.; Bai, J.; Yan, S.; Takeuchi, K.J.; Zhu, Y. Understanding the Role of Short-Range Order in High-Entropy Layered Oxides for Energy Storage. Nano Lett. 2025, 25, 11594–11600. [Google Scholar] [CrossRef]
- Sarker, P.; Harrington, T.; Toher, C.; Oses, C.; Samiee, M.; Maria, J.-P.; Brenner, D.W.; Vecchio, K.S.; Curtarolo, S. High-entropy high-hardness metal carbides discovered by entropy descriptors. Nat. Commun. 2018, 9, 4980. [Google Scholar] [CrossRef]
- Liu, J.; Wang, A.; Gao, P.; Bai, R.; Liu, J.; Du, B.; Fang, C. Machine learning-based crystal structure prediction for high-entropy oxide ceramics. J. Am. Ceram. Soc. 2024, 107, 1361–1371. [Google Scholar] [CrossRef]
- Kaufmann, K.; Maryanovsky, D.; Mellor, W.M.; Zhu, C.; Rosengarten, A.S.; Harrington, T.J.; Oses, C.; Toher, C.; Curtarolo, S.; Vecchio, K.S. Discovery of high-entropy ceramics via machine learning. Npj Comput. Mater. 2020, 6, 42. [Google Scholar] [CrossRef]
- Mitra, R.; Bajpai, A.; Biswas, K. Machine learning based approach for phase prediction in high entropy borides. Ceram. Int. 2022, 48, 16695–16706. [Google Scholar] [CrossRef]
- Wan, X.; Li, Z.; Yu, W.; Wang, A.; Ke, X.; Guo, H.; Su, J.; Li, L.; Gui, Q.; Zhao, S.; et al. Machine Learning Paves the Way for High Entropy Compounds Exploration: Challenges, Progress, and Outlook. Adv. Mater. 2023, 37, 2305192. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, Y. Artificial intelligence in high-entropy materials. Next Mater. 2025, 9, 100993. [Google Scholar] [CrossRef]
- Pitike, K.C.; Kc, S.; Eisenbach, M.; Bridges, C.A.; Cooper, V.R. Predicting the phase stability of multicomponent high-entropy compounds. Chem. Mater. 2020, 32, 7507–7515. [Google Scholar] [CrossRef]
- Pu, Y.; Moseley, D.; He, Z.; Pitike, K.C.; Manley, M.E.; Yan, J.; Cooper, V.R.; Mitchell, V.; Peterson, V.K.; Johannessen, B.; et al. (Mg,Mn,Fe,Co,Ni)O: A rocksalt high-entropy oxide containing divalent Mn and Fe. Sci. Adv. 2023, 9, eadi8809. [Google Scholar] [CrossRef] [PubMed]
- Bérardan, D.; Franger, S.; Dragoe, D.; Meena, A.K.; Dragoe, N. Colossal dielectric constant in high entropy oxides. Phys. Status Solidi (RRL)–Rapid Res. Lett. 2016, 10, 328–333. [Google Scholar] [CrossRef]
- Usharani, N.J.; Bhandarkar, A.; Subramanian, S.; Bhattacharya, S.S. Antiferromagnetism in a nanocrystalline high entropy oxide (Co,Cu,Mg,Ni,Zn)O: Magnetic constituents and surface anisotropy leading to lattice distortion. Acta Mater. 2020, 200, 526–536. [Google Scholar] [CrossRef]
- Manchón-Gordón, A.F.; Lobo-Llamas, C.; Molina-Molina, S.; Perejón, A.; Sánchez-Jiménez, P.E.; Pérez-Maqueda, L.A. Influence of the atmosphere on the formation of high-entropy oxides within the Co–Cu–Fe–Mg–Mn–Ni–O system via reactive flash sintering. Ceram. Int. 2024, 50, 42276–42285. [Google Scholar] [CrossRef]
- Wang, J.; Stenzel, D.; Azmi, R.; Najib, S.; Wang, K.; Jeong, J.; Sarkar, A.; Wang, Q.; Sukkurji, P.A.; Bergfeldt, T.; et al. Spinel to Rock-Salt Transformation in High Entropy Oxides with Li Incorporation. Electrochem 2020, 1, 60–74. [Google Scholar] [CrossRef]
- Monteverde, F.; Gaboardi, M. Entropy-driven expansion of the thermodynamic stability of compositionally complex spinel oxides. J. Eur. Ceram. Soc. 2024, 44, 7704–7715. [Google Scholar] [CrossRef]
- Fracchia, M.; Coduri, M.; Bonati, S.; Dejoie, C.; Ghigna, P.; Anselmi-Tamburini, U. Beyond configurational entropy: The role of solubility equilibria in the stability of the system (Co,Cu,Mg,Ni,Zn)O. J. Eur. Ceram. Soc. 2025, 45, 117237. [Google Scholar] [CrossRef]
- Dąbrowa, J.; Stygar, M.; Mikuła, A.; Knapik, A.; Mroczka, K.; Tejchman, W.; Danielewski, M.; Martin, M. Synthesis and microstructure of the (Co,Cr,Fe,Mn,Ni)3O4 high entropy oxide characterized by spinel structure. Mater. Lett. 2018, 216, 32–36. [Google Scholar] [CrossRef]
- Musicó, B.; Wright, Q.; Ward, T.Z.; Grutter, A.; Arenholz, E.; Gilbert, D.; Mandrus, D.; Keppens, V. Tunable magnetic ordering through cation selection in entropic spinel oxides. Phys. Rev. Mater. 2019, 3, 104416. [Google Scholar] [CrossRef]
- Katzbaer, R.R.; Vieira, F.M.D.S.; Dabo, I.; Mao, Z.; Schaak, R.E. Band Gap Narrowing in a High-Entropy Spinel Oxide Semiconductor for Enhanced Oxygen Evolution Catalysis. J. Am. Chem. Soc. 2023, 145, 6753–6761. [Google Scholar] [CrossRef]
- Stygar, M.; Dąbrowa, J.; Moździerz, M.; Zajusz, M.; Skubida, W.; Mroczka, K.; Berent, K.; Świerczek, K.; Danielewski, M. Formation and properties of high entropy oxides in Co-Cr-Fe-Mg-Mn-Ni-O system: Novel (Cr,Fe,Mg,Mn,Ni)3O4 and (Co,Cr,Fe,Mg,Mn)3O4 high entropy spinels. J. Eur. Ceram. Soc. 2020, 40, 1644–1650. [Google Scholar] [CrossRef]
- Shaw, S.K.; Gangwar, A.; Sharma, A.; Alla, S.K.; Kavita, S.; Vasundhara, M.; Meena, S.S.; Maiti, P.; Prasad, N.K. Structural and magnetic properties of nanocrystalline equi-atomic spinel high-entropy oxide (AlCoFeMnNi)3O4synthesised by microwave assisted co-precipitation technique. J. Alloys Compd. 2021, 878, 160269. [Google Scholar] [CrossRef]
- Zhu, H.; Xie, H.; Zhao, Y.; Dai, S.; Li, M.; Wang, X. Structure and magnetic properties of a class of spinel high-entropy oxides. J. Magn. Magn. Mater. 2021, 535, 168063. [Google Scholar] [CrossRef]
- Mallesh, S.; Noh, J.-S.; Nam, Y.-W. Structure and magnetic properties of (Mg1/6Zn1/6Mn1/6Co1/6Ni1/6Fe1/6)3O4 nanocrystalline high-entropy oxide synthesized using a sol-gel auto combustion approach. J. Magn. Magn. Mater. 2022, 564, 170108. [Google Scholar] [CrossRef]
- Gupta, A.K.; Kumari, P.; Prakash, A.; Giri, N.K.; Shahi, R.R. Synthesis; characterizations, and magnetic behavior of novel (CuNiTiZnFe)3O4 high entropy spinel oxide. Ceram. Int. 2022, 48, 36258–36263. [Google Scholar] [CrossRef]
- Coduri, M.; Fracchia, M.; Guerrini, M.; Dejoie, C.; Ghigna, P.; Tamburini, U.A. Novel In-based high entropy spinel oxides with tunable lattice parameter. J. Eur. Ceram. Soc. 2023, 43, 2728–2739. [Google Scholar] [CrossRef]
- Manchón-Gordón, A.F.; Almanza-Vergara, G.E.; Molina-Molina, S.; Perejón, A.; Blázquez, J.S.; Sánchez-Jiménez, P.E.; Pérez-Maqueda, L.A. Structural, Mössbauer and magnetic study of (Mn0.2Co0.2Ni0.2Cu0.2X0.2)Fe2O4 (X=Fe, Mg) spinel high-entropy oxides fabricated via reactive flash sintering. J. Eur. Ceram. Soc. 2024, 44, 116686. [Google Scholar] [CrossRef]
- Sarkar, A.; Eggert, B.; Witte, R.; Lill, J.; Velasco, L.; Wang, Q.; Sonar, J.; Ollefs, K.; Bhattacharya, S.S.; Brand, R.A.; et al. Comprehensive investigation of crystallographic, spin-electronic and magnetic structure of (Co0.2Cr0.2Fe0.2Mn0.2Ni0.2)3O4: Unraveling the suppression of configuration entropy in high entropy oxides. Acta Mater. 2022, 226, 117581. [Google Scholar] [CrossRef]
- Navrotsky, A.; Kleppa, O.J. The thermodynamics of cation distributions in simple spinels. J. Inorg. Nucl. Chem. 1967, 29, 2701–2714. [Google Scholar] [CrossRef]
- Navrotsky, A.; Kleppa, O.J. Thermodynamics of formation of simple spinels. J. Inorg. Nucl. Chem. 1968, 30, 479–498. [Google Scholar] [CrossRef]
- Navrotsky, A. Thermodynamics of A3O4-B3O4 spinel solid solutions. J. Inorg. Nucl. Chem. 1969, 31, 59–72. [Google Scholar] [CrossRef]
- Jiang, S.; Hu, T.; Gild, J.; Zhou, N.; Nie, J.; Qin, M.; Harrington, T.; Vecchio, K.; Luo, J. A new class of high-entropy perovskite oxides. Scr. Mater. 2018, 142, 116–120. [Google Scholar] [CrossRef]
- Beskow, G.V.M. Goldschmidt: Geochemische Verteilungsgesetze der Elemente. Geol. Föreningen Stockh. Förhandlingar 1924, 46, 738–743. [Google Scholar] [CrossRef]
- Li, Z.; Yang, M.; Park, J.-S.; Wei, S.-H.; Berry, J.J.; Zhu, K. Stabilizing perovskite structures by tuning tolerance factor: Formation of formamidinium and cesium lead iodide solid-state alloys. Chem. Mater. 2016, 28, 284–292. [Google Scholar] [CrossRef]
- Bartel, C.J.; Sutton, C.; Goldsmith, B.R.; Ouyang, R.; Musgrave, C.B.; Ghiringhelli, L.M.; Scheffler, M. New tolerance factor to predict the stability of perovskite oxides and halides. Sci. Adv. 2019, 5, eaav0693. [Google Scholar] [CrossRef]
- Banerjee, R.; Chatterjee, S.; Ranjan, M.; Bhattacharya, T.; Mukherjee, S.; Jana, S.S.; Dwivedi, A.; Maiti, T. High-entropy perovskites: An emergent class of oxide thermoelectrics with ultralow thermal conductivity. ACS Sustain. Chem. Eng. 2020, 8, 17022–17032. [Google Scholar] [CrossRef]
- Sarkar, A.; Djenadic, R.; Wang, D.; Hein, C.; Kautenburger, R.; Clemens, O.; Hahn, H. Rare earth and transition metal based entropy stabilised perovskite type oxides. J. Eur. Ceram. Soc. 2018, 38, 2318–2327. [Google Scholar] [CrossRef]
- Tang, L.; Li, Z.; Chen, K.; Li, C.; Zhang, X.; An, L. High-entropy oxides based on valence combinations: Design and practice. J. Am. Ceram. Soc. 2021, 104, 1953–1958. [Google Scholar] [CrossRef]
- Ma, J.; Chen, K.; Li, C.; Zhang, X.; An, L. High-entropy stoichiometric perovskite oxides based on valence combinations. Ceram. Int. 2021, 47, 24348–24352. [Google Scholar] [CrossRef]
- Cheng, F.; Meng, Z.; Cheng, C.; Hou, J.; Liu, Y.; Ren, B.; Hu, H.; Gao, F.; Miao, Y.; Wang, X. Fluorite-pyrochlore structured high-entropy oxides: Tuning the ratio of B-site cations for resistance to CMAS corrosion. Corros. Sci. 2023, 218, 111199. [Google Scholar] [CrossRef]
- Trofimov, E.; Moghaddam, A.O.; Litvinyuk, K.; Anandkumar, M.; Efimova, M.; Mikhailov, D.; Zaitseva, O. Synthesis and characterization of the RE2A2O7 oxides with an ultrahigh-entropy sublattice occupied by rare-earth elements. Mater. Lett. 2025, 379, 137668. [Google Scholar] [CrossRef]
- Pitike, K.C.; Macias, A.; Eisenbach, M.; Bridges, C.A.; Cooper, V.R. Computationally accelerated discovery of high entropy pyrochlore oxides. Chem. Mater. 2022, 34, 1459–1472. [Google Scholar] [CrossRef]
- Wright, A.J.; Wang, Q.; Hu, C.; Yeh, Y.-T.; Chen, R.; Luo, J. Single-phase duodenary high-entropy fluorite/pyrochlore oxides with an order-disorder transition. Acta Mater. 2021, 211, 116858. [Google Scholar] [CrossRef]
- Subramanian, M.; Aravamudan, G.; Rao, G.S. Oxide pyrochlores—A review. Prog. Solid State Chem. 1983, 15, 55–143. [Google Scholar] [CrossRef]
- Zhao, Z.; Xiang, H.; Dai, F.-Z.; Peng, Z.; Zhou, Y. (La0.2Ce0.2Nd0.2Sm0.2Eu0.2)2Zr2O7: A novel high-entropy ceramic with low thermal conductivity and sluggish grain growth rate. J. Mater. Sci. Technol. 2019, 35, 2647–2651. [Google Scholar] [CrossRef]
- Li, F.; Zhou, L.; Liu, J.-X.; Liang, Y.; Zhang, G.-J. High-entropy pyrochlores with low thermal conductivity for thermal barrier coating materials. J. Adv. Ceram. 2019, 8, 576–582. [Google Scholar] [CrossRef]
- Wright, A.J.; Wang, Q.; Ko, S.-T.; Chung, K.M.; Chen, R.; Luo, J. Size disorder as a descriptor for predicting reduced thermal conductivity in medium-and high-entropy pyrochlore oxides. Scr. Mater. 2020, 181, 76–81. [Google Scholar] [CrossRef]
- Djenadic, R.; Sarkar, A.; Clemens, O.; Loho, C.; Botros, M.; Chakravadhanula, V.S.; Kübel, C.; Bhattacharya, S.S.; Gandhi, A.S.; Hahn, H. Multicomponent equiatomic rare earth oxides. Mater. Res. Lett. 2017, 5, 102–109. [Google Scholar] [CrossRef]
- Gild, J.; Samiee, M.; Braun, J.L.; Harrington, T.; Vega, H.; Hopkins, P.E.; Vecchio, K.; Luo, J. High-entropy fluorite oxides. J. Eur. Ceram. Soc. 2018, 38, 3578–3584. [Google Scholar] [CrossRef]
- Chen, K.; Pei, X.; Tang, L.; Cheng, H.; Li, Z.; Li, C.; Zhang, X.; An, L. A five-component entropy-stabilized fluorite oxide. J. Eur. Ceram. Soc. 2018, 38, 4161–4164. [Google Scholar] [CrossRef]
- Velasco, L.; Castillo, J.S.; Kante, M.V.; Olaya, J.J.; Friederich, P.; Hahn, H. Phase–property diagrams for multicomponent oxide systems toward materials libraries. Adv. Mater. 2021, 33, 2102301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.-Z.; Reece, M.J. Review of high entropy ceramics: Design, synthesis, structure and properties. J. Mater. Chem. A 2019, 7, 22148–22162. [Google Scholar] [CrossRef]
- Sarkar, A.; Wang, Q.; Schiele, A.; Chellali, M.R.; Bhattacharya, S.S.; Wang, D.; Brezesinski, T.; Hahn, H.; Velasco, L.; Breitung, B. High-entropy oxides: Fundamental aspects and electrochemical properties. Adv. Mater. 2019, 31, 1806236. [Google Scholar] [CrossRef]
- Divilov, S.; Eckert, H.; Hicks, D.; Oses, C.; Toher, C.; Friedrich, R.; Esters, M.; Mehl, M.J.; Zettel, A.C.; Lederer, Y. Disordered enthalpy–entropy descriptor for high-entropy ceramics discovery. Nature 2024, 625, 66–73. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, Y.J.; Lin, J.P.; Chen, G.L.; Liaw, P.K. Solid-Solution Phase Formation Rules for Multi-component Alloys. Adv. Eng. Mater. 2008, 10, 534–538. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Ning, Y.; Pu, Y.; Wu, C.; Zhou, S.; Zhang, L.; Zhang, J.; Zhang, X.; Shang, Y. Enhanced capacitive energy storage and dielectric temperature stability of A-site disordered high-entropy perovskite oxides. J. Mater. Sci. Technol. 2023, 145, 66–73. [Google Scholar] [CrossRef]
- Zhao, Z.; Rehder, L.; Steinbach, F.; Feldhoff, A. High-Entropy Perovskites Pr1−xSrx(Cr,Mn,Fe,Co,Ni)O3−δ (x = 0–0.5): Synthesis and Oxygen Permeation Properties. Membranes 2022, 12, 1123. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, S.; Tian, Z.; Zhang, Y.; Shi, Z. The Formation and Phase Stability of A-Site High-Entropy Perovskite Oxides. Materials 2023, 16, 2214. [Google Scholar] [CrossRef]
- Shi, Y.; Ni, N.; Ding, Q.; Zhao, X. Tailoring high-temperature stability and electrical conductivity of high entropy lanthanum manganite for solid oxide fuel cell cathodes. J. Mater. Chem. A 2022, 10, 2256–2270. [Google Scholar] [CrossRef]
- Wang, J.; Cao, Z.; Zhu, X.; Yang, W. Improving intermediate-temperature stability of BSCF by constructing high entropy perovskites. J. Membr. Sci. Lett. 2022, 2, 100026. [Google Scholar] [CrossRef]
- Yu, Y.; Liu, S.; Wang, H.; Zhang, S.; Wang, N.; Jiang, W.; Liu, C.; Ding, W.; Zhang, Z.; Dong, C. Design, synthesis and photocatalytic performance of A32Ti8Sn8Nb4Ta4Me8O96 (A=Ba, Sr; Me=Fe, Ga) perovskite structure high entropy oxides. J. Solid State Chem. 2023, 317, 123694. [Google Scholar] [CrossRef]
- Yang, Y.; Bao, H.; Ni, H.; Ou, X.; Wang, S.; Lin, B.; Feng, P.; Ling, Y. A novel facile strategy to suppress Sr segregation for high-entropy stabilized La0·8Sr0·2MnO3-δ cathode. J. Power Sources 2021, 482, 228959. [Google Scholar] [CrossRef]
- Zhang, P.; Lou, Z.; Gong, L.; Xu, J.; Chen, Q.; Reece, M.J.; Yan, H.; Dashevsky, Z.; Gao, F. High-entropy MTiO3 perovskite oxides with glass-like thermal conductivity for thermoelectric applications. J. Alloys Compd. 2023, 937, 168366. [Google Scholar] [CrossRef]
- Shishkin, R.; Zhuravlev, V. Thermodynamic analysis and phase characterization of high-entropy oxide Sr(Ce0.05Sn0.08Zr0.2Ti0.16Y0.3Nb0.11Al0.1)O2.9: Insights into stability, microstructure, and mechanical properties. Ceram. Int. 2024, 50, 15348–15355. [Google Scholar] [CrossRef]
- Chen, Y.; Li, R.; Zhang, Y.; Long, Y.; Liu, N.; Xia, H.; Luo, X.; Meng, B. Preparation and dielectric properties of lead-free perovskite-structured high-entropy ceramics of (La0.25Sr0.25Ba0.25Na0.25)(Ti0.5Me0.5) O3-δ (Me= Sn, Zr, Hf) via doping at both A and B sites. Ceram. Int. 2023, 49, 1038–1047. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, S.; Li, T.; Xie, B.; Guo, K.; Lu, J. Microstructure and ferroelectric properties of high-entropy perovskite oxides with A-site disorder. Ceram. Int. 2021, 47, 33039–33046. [Google Scholar] [CrossRef]
- Han, X.; Yang, Y.; Fan, Y.; Ni, H.; Guo, Y.; Chen, Y.; Ou, X.; Ling, Y. New approach to enhance Sr-free cathode performance by high-entropy multi-component transition metal coupling. Ceram. Int. 2021, 47, 17383–17390. [Google Scholar] [CrossRef]
- Zhou, S.; Pu, Y.; Zhang, Q.; Shi, R.; Guo, X.; Wang, W.; Ji, J.; Wei, T.; Ouyang, T. Microstructure and dielectric properties of high entropy Ba(Zr0.2Ti0.2Sn0.2Hf0.2Me0.2)O3 perovskite oxides. Ceram. Int. 2020, 46, 7430–7437. [Google Scholar] [CrossRef]
- Xu, Z.; Du, Z.; Zhang, R.; Zeng, F.; Meng, Z.; Hu, X.; Tian, H. Regulating the lattice strain field by high-entropy strategy to realize the conformal growth of perovskites for efficient oxygen evolution. Appl. Catal. B Environ. Energy 2024, 344, 123668. [Google Scholar] [CrossRef]
- Teng, Z.; Tan, Y.; Zeng, S.; Meng, Y.; Chen, C.; Han, X.; Zhang, H. Preparation and phase evolution of high-entropy oxides A2B2O7 with multiple elements at A and B sites. J. Eur. Ceram. Soc. 2021, 41, 3614–3620. [Google Scholar] [CrossRef]
- Zhang, K.; Li, W.; Zeng, J.; Deng, T.; Luo, B.; Zhang, H.; Huang, X. Preparation of (La0.2Nd0.2Sm0.2Gd0.2Yb0.2)2Zr2O7 high-entropy transparent ceramic using combustion synthesized nanopowder. J. Alloys Compd. 2020, 817, 153328. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, H.; Xiang, H.; Dai, F.-Z.; Wang, X.; Xu, W.; Sun, K.; Peng, Z.; Zhou, Y. (Y0. 25Yb0. 25Er0. 25Lu0. 25)2(Zr0.5Hf0.5)2O7: A defective fluorite structured high entropy ceramic with low thermal conductivity and close thermal expansion coefficient to Al2O3. J. Mater. Sci. Technol. 2020, 39, 167. [Google Scholar]
- Zhou, L.; Li, F.; Liu, J.-X.; Hu, Q.; Bao, W.; Wu, Y.; Cao, X.; Xu, F.; Zhang, G.-J. High-entropy thermal barrier coating of rare-earth zirconate: A case study on (La0.2Nd0.2Sm0.2Eu0.2Gd0.2)2Zr2O7 prepared by atmospheric plasma spraying. J. Eur. Ceram. Soc. 2020, 40, 5731–5739. [Google Scholar] [CrossRef]
- Ren, K.; Wang, Q.; Shao, G.; Zhao, X.; Wang, Y. Multicomponent high-entropy zirconates with comprehensive properties for advanced thermal barrier coating. Scr. Mater. 2020, 178, 382–386. [Google Scholar] [CrossRef]
- Fan, W.; Bai, Y.; Liu, Y.; Li, T.; Li, B.; Zhang, L.; Gao, C.; Shan, S.; Han, H. Principal element design of pyrochlore-fluorite dual-phase medium- and high-entropy ceramics. J. Mater. Sci. Technol. 2022, 107, 149–154. [Google Scholar] [CrossRef]
- Zhu, J.; Meng, X.; Zhang, P.; Li, Z.; Xu, J.; Reece, M.J.; Gao, F. Dual-phase rare-earth-zirconate high-entropy ceramics with glass-like thermal conductivity. J. Eur. Ceram. Soc. 2021, 41, 2861–2869. [Google Scholar] [CrossRef]
- Teng, Z.; Zhu, L.; Tan, Y.; Zeng, S.; Xia, Y.; Wang, Y.; Zhang, H. Synthesis and structures of high-entropy pyrochlore oxides. J. Eur. Ceram. Soc. 2020, 40, 1639–1643. [Google Scholar] [CrossRef]
- Lowry, D.R.; Boro, J.R.; Blea-Kirby, M.; Valdez, N.R.; Bishop, S.R. Site Disorder as a Predictor for Compositionally Complex 5RE2Zr2O7 Ceramic Phase Stability. J. Am. Ceram. Soc. 2023, 106, 7078–7087. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, Y.-J.; Wei, T.; Wang, Z.-G.; Cao, G.; Ding, Z.-Y.; Liu, Z.-G.; Ouyang, J.-H.; Wang, Y.-J.; Wang, Y.-M. Size disorder: A descriptor for predicting the single- or dual-phase formation in multi-component rare earth zirconates. J. Alloys Compd. 2022, 918, 165636. [Google Scholar] [CrossRef]
- Liu, D.; Wang, Y.; Zhou, F.; Xu, B.; Lv, B. A novel high-entropy (Sm0.2Eu0.2Tb0.2Dy0.2Lu0.2)2Zr2O7 ceramic aerogel with ultralow thermal conductivity. Ceram. Int. 2021, 47, 29960–29968. [Google Scholar] [CrossRef]
- Lin, L.; Wang, K.; Azmi, R.; Wang, J.; Sarkar, A.; Botros, M.; Najib, S.; Cui, Y.; Stenzel, D.; Sukkurji, P.A.; et al. Mechanochemical synthesis: Route to novel rock-salt-structured high-entropy oxides and oxyfluorides. J. Mater. Sci. 2020, 55, 16879–16889. [Google Scholar] [CrossRef]
- Nie, S.; Wu, L.; Zhao, L.; Zheng, X.; Yang, S.; Zhang, P. Entropy-driven chemistry reveals highly stable denary MgAl2O4-type catalysts. Chem Catal. 2021, 1, 648–662. [Google Scholar] [CrossRef]
- Chen, G.; Li, C.; Jia, H.; Li, H.; Li, S.; Gong, B.; An, L.; Chen, K. Formation and properties of Ca2+ substituted (Ce0.2Zr0.2Ti0.2Sn0.2Hf0.2)O2 high-entropy ceramics. J. Eur. Ceram. Soc. 2023, 43, 2586–2592. [Google Scholar] [CrossRef]
- Cieslak, J.; Reissner, M.; Berent, K.; Dabrowa, J.; Stygar, M.; Mozdzierz, M.; Zajusz, M. Magnetic properties and ionic distribution in high entropy spinels studied by Mössbauer and ab initio methods. Acta Mater. 2021, 206, 116600. [Google Scholar] [CrossRef]
- Dąbrowa, J.; Szymczak, M.; Zajusz, M.; Mikuła, A.; Moździerz, M.; Berent, K.; Wytrwal-Sarna, M.; Bernasik, A.; Stygar, M.; Świerczek, K. Stabilizing fluorite structure in ceria-based high-entropy oxides: Influence of Mo addition on crystal structure and transport properties. J. Eur. Ceram. Soc. 2020, 40, 5870–5881. [Google Scholar] [CrossRef]
- Sun, J.; Guo, L.; Zhang, Y.; Wang, Y.; Fan, K.; Tang, Y. Superior phase stability of high entropy oxide ceramic in a wide temperature range. J. Eur. Ceram. Soc. 2022, 42, 5053–5064. [Google Scholar] [CrossRef]
- Spiridigliozzi, L.; Ferone, C.; Cioffi, R.; Dell, G. A simple and effective predictor to design novel fluorite-structured High Entropy Oxides (HEOs). Acta Mater. 2021, 202, 181–189. [Google Scholar] [CrossRef]
- Schweidler, S.; Tang, Y.; Lin, L.; Karkera, G.; Alsawaf, A.; Bernadet, L.; Breitung, B.; Hahn, H.; Fichtner, M.; Tarancón, A.; et al. Synthesis of perovskite-type high-entropy oxides as potential candidates for oxygen evolution. Front. Energy Res. 2022, 10, 983979. [Google Scholar] [CrossRef]
- Vayer, F.; Decorse, C.; Bérardan, D.; Dragoe, N. New entropy-stabilized oxide with pyrochlore structure: Dy2(Ti0.2Zr0.2Hf0.2Ge0.2Sn0.2)2O7. J. Alloys Compd. 2021, 883, 160773. [Google Scholar] [CrossRef]



| Structure | ||
|---|---|---|
| Rock salt | 1 | - |
| Fluorite | 1/2 | - |
| Spinel (normal) | 1/24 | 1/2 |
| Perovskite | 1/6 | 5/6 |
| Pyrochlore | 1/4 | /12 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manchón-Gordón, A.F.; Panadero-Medianero, P.; Blázquez, J.S. Descriptors for Predicting Single- and Multi-Phase Formation in High-Entropy Oxides: A Unified Framework Approach. Materials 2025, 18, 3862. https://doi.org/10.3390/ma18163862
Manchón-Gordón AF, Panadero-Medianero P, Blázquez JS. Descriptors for Predicting Single- and Multi-Phase Formation in High-Entropy Oxides: A Unified Framework Approach. Materials. 2025; 18(16):3862. https://doi.org/10.3390/ma18163862
Chicago/Turabian StyleManchón-Gordón, Alejandro F., Paula Panadero-Medianero, and Javier S. Blázquez. 2025. "Descriptors for Predicting Single- and Multi-Phase Formation in High-Entropy Oxides: A Unified Framework Approach" Materials 18, no. 16: 3862. https://doi.org/10.3390/ma18163862
APA StyleManchón-Gordón, A. F., Panadero-Medianero, P., & Blázquez, J. S. (2025). Descriptors for Predicting Single- and Multi-Phase Formation in High-Entropy Oxides: A Unified Framework Approach. Materials, 18(16), 3862. https://doi.org/10.3390/ma18163862






