Research on Laser Cladding Single-Pass Continuous Carbon Fiber-Reinforced Aluminum Matrix Composite Process Based on Abaqus
Abstract
1. Introduction
2. Finite Element Simulation
2.1. Heat Source Model
- af, ar, b, c—shape parameters of the heat source model;
- q1, q2—the laser input power;
- f1, f2—the energy distribution coefficients before and after the heat source.
2.2. Finite Element Geometry Model Design and Main Material Parameters
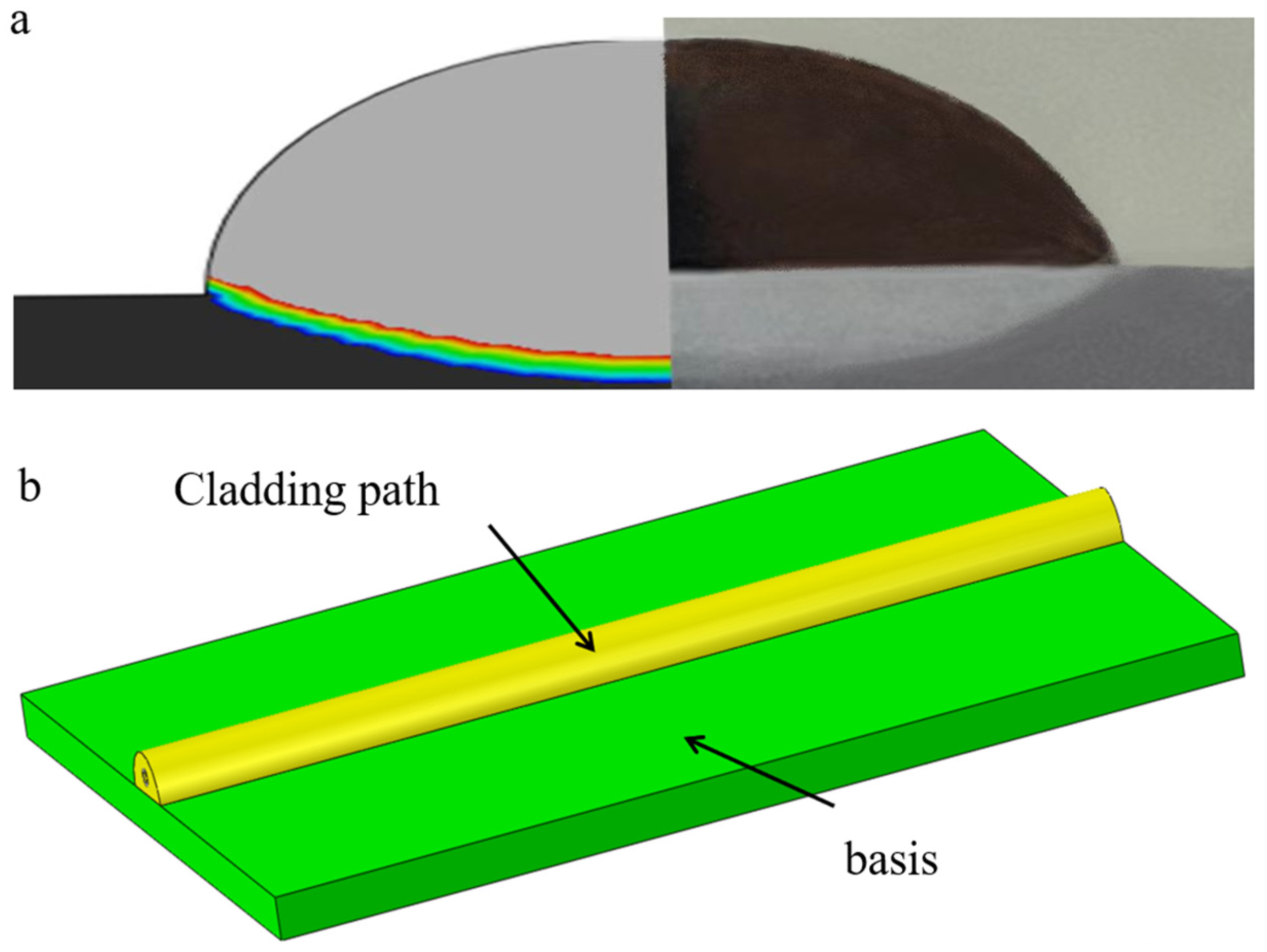
2.2.1. Finite Element Geometry Model Design
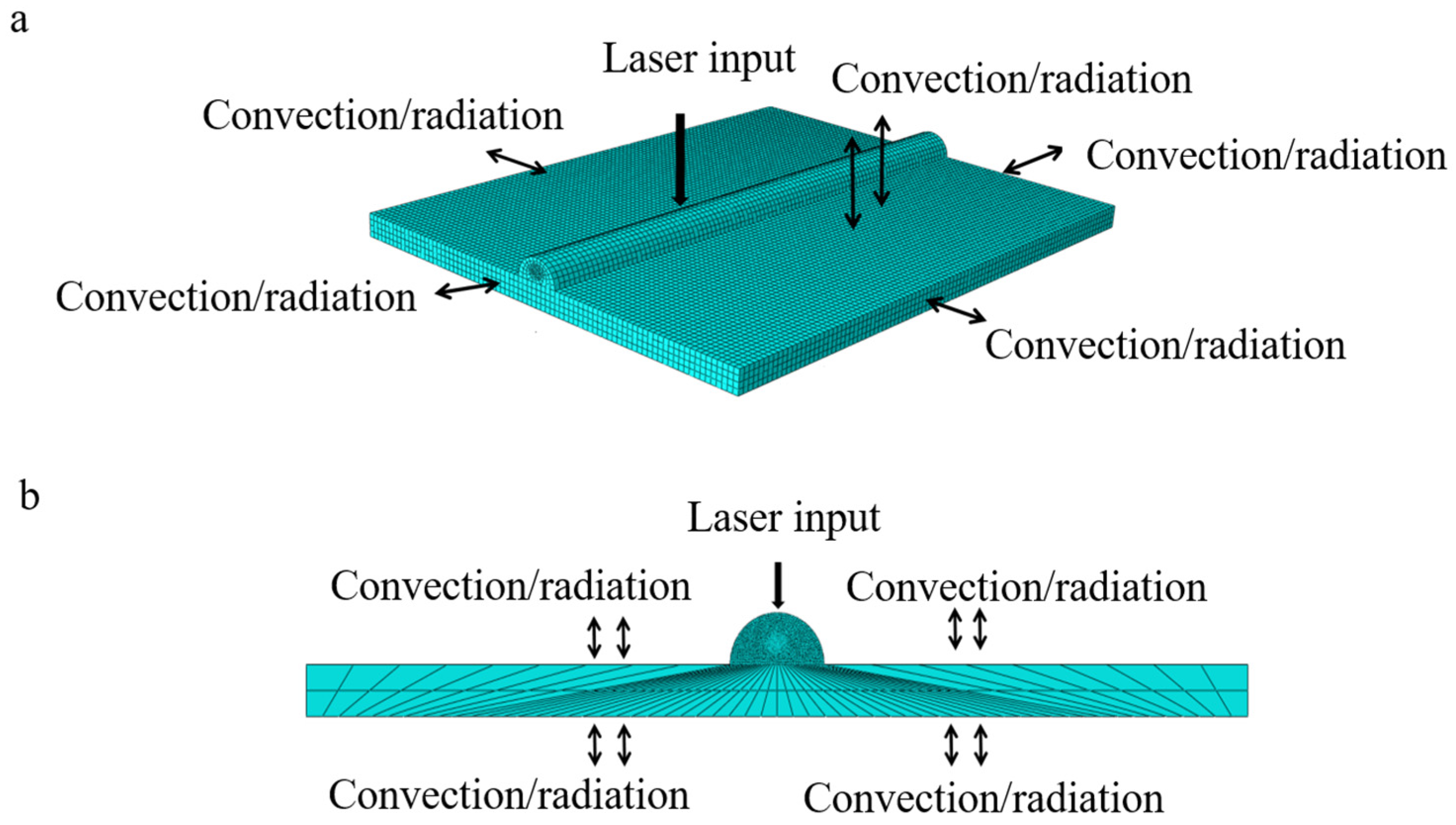
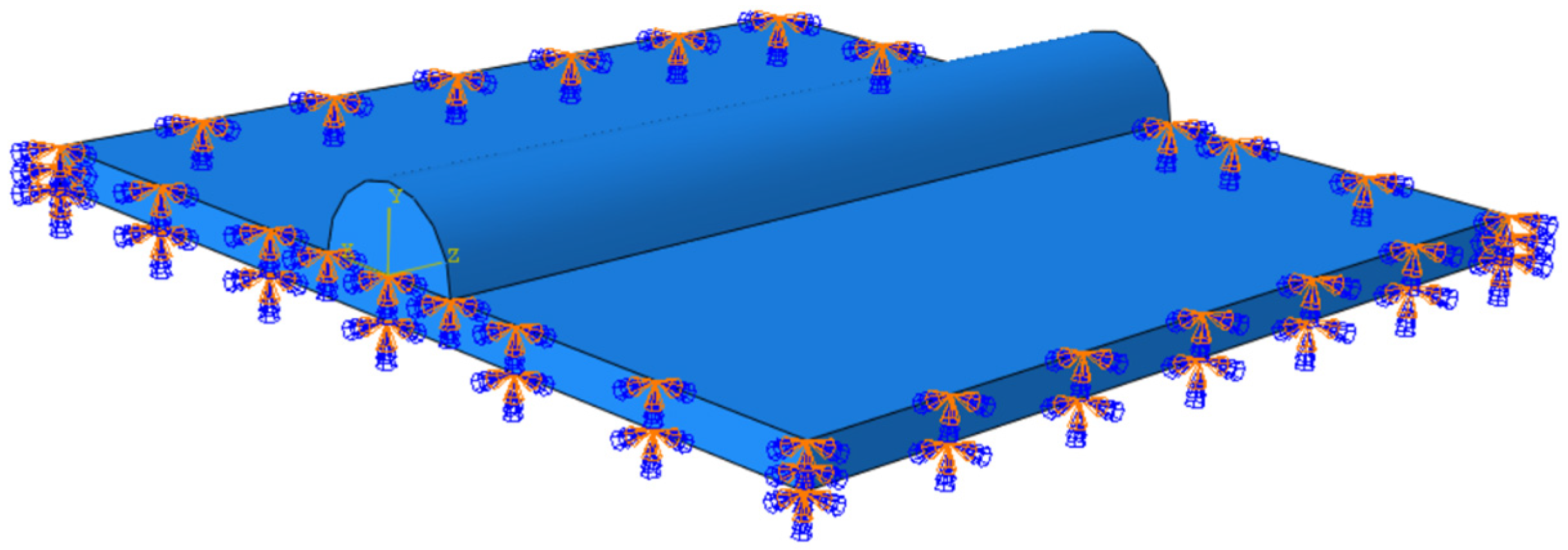
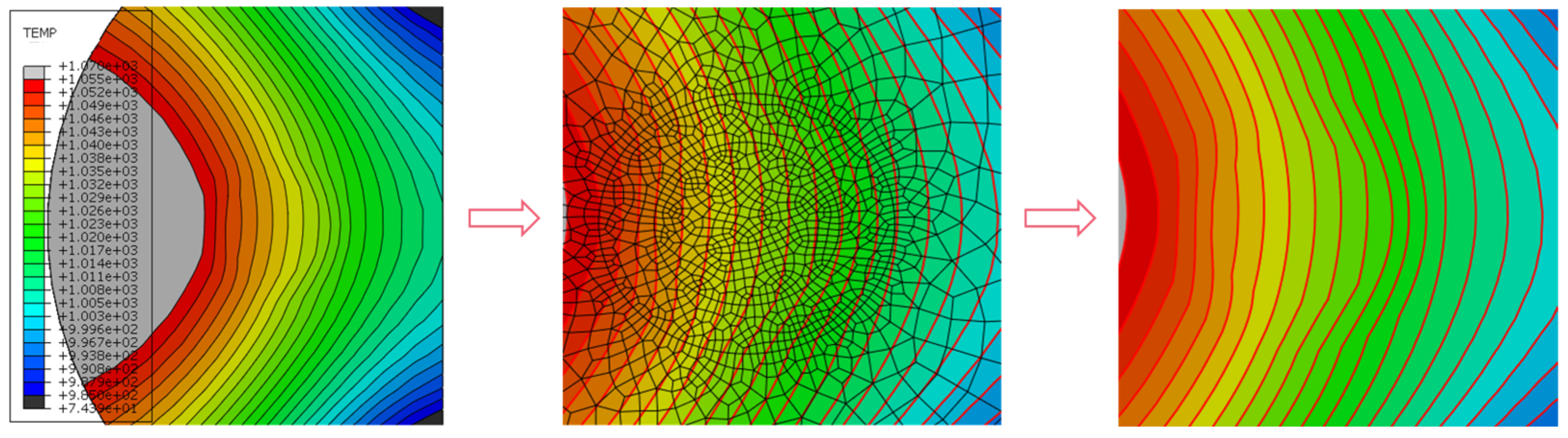
2.2.2. Geometric Model Boundary Condition Design and Meshing
2.2.3. Finite Element Simulation Parameters and Methods
2.3. Temperature Field Calculation
- qv—laser heat energy density, (W·mm−3);
- k—heat transfer coefficient, (W·m−1·K−1);
- T—temperature field, (K);
- —density, (kg·m−3);
- c—specific heat capacity, (J·kg−1·K−1).
- —convective heat transfer between substrate and environment;
- —radiative heat flux between substrate and ambient environment;
- —Stefan–Boltzman constant;
- —surface radiation coefficient;
- —outside ambient temperature;
- —convective heat transfer coefficient of the substrate.
2.4. Stress Field Calculation
3. Simulation Results and Analysis
3.1. Temperature Field Analysis
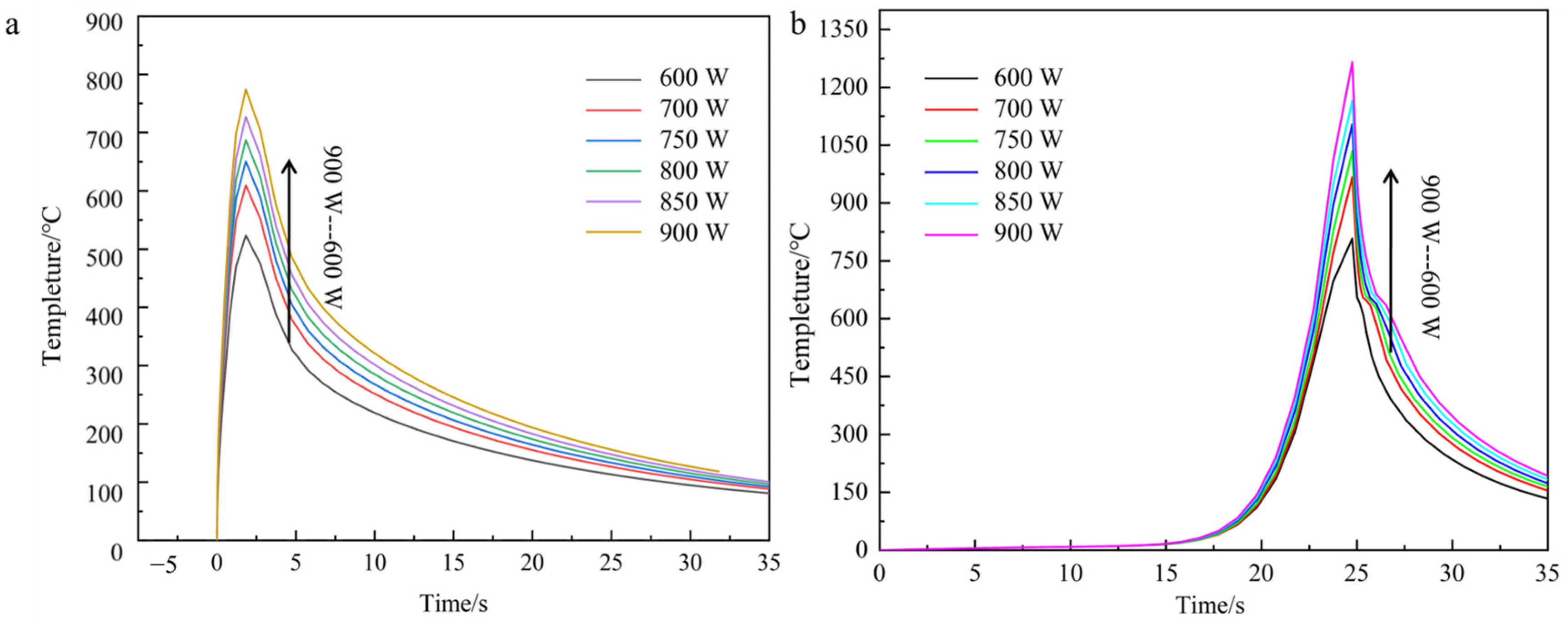
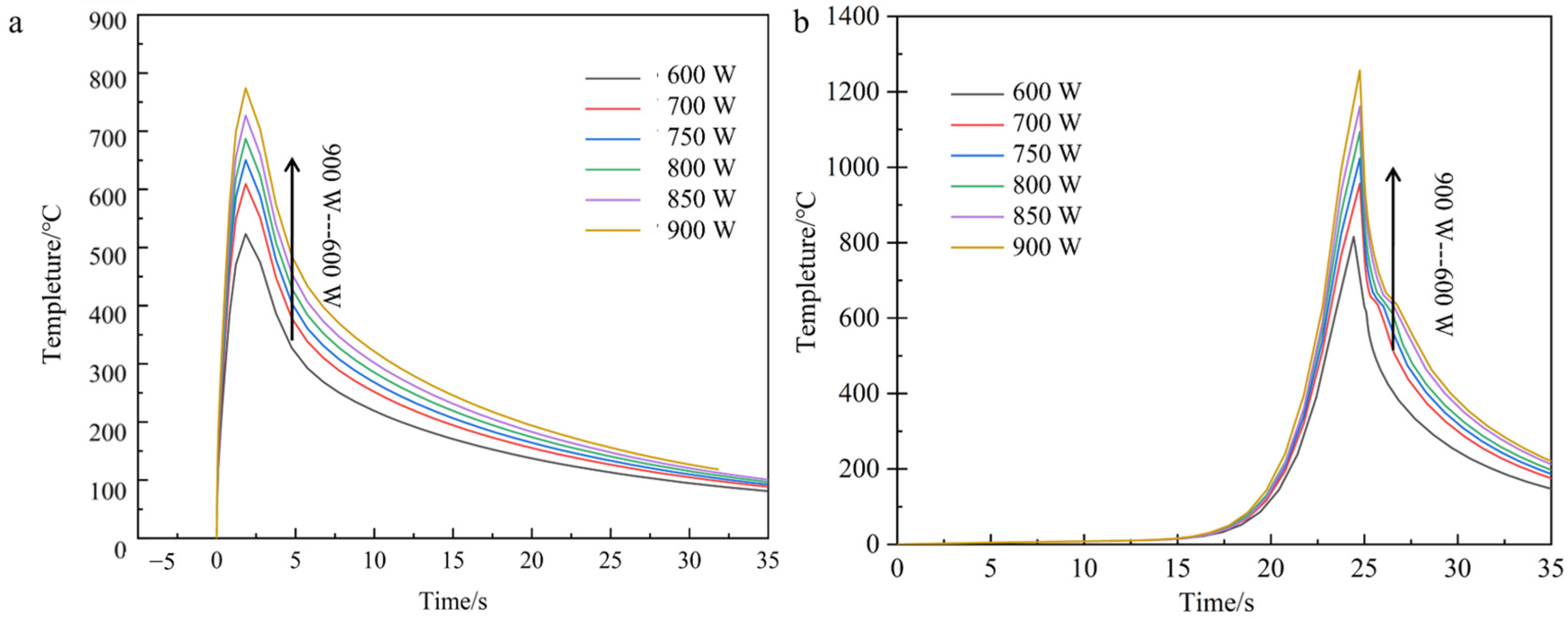
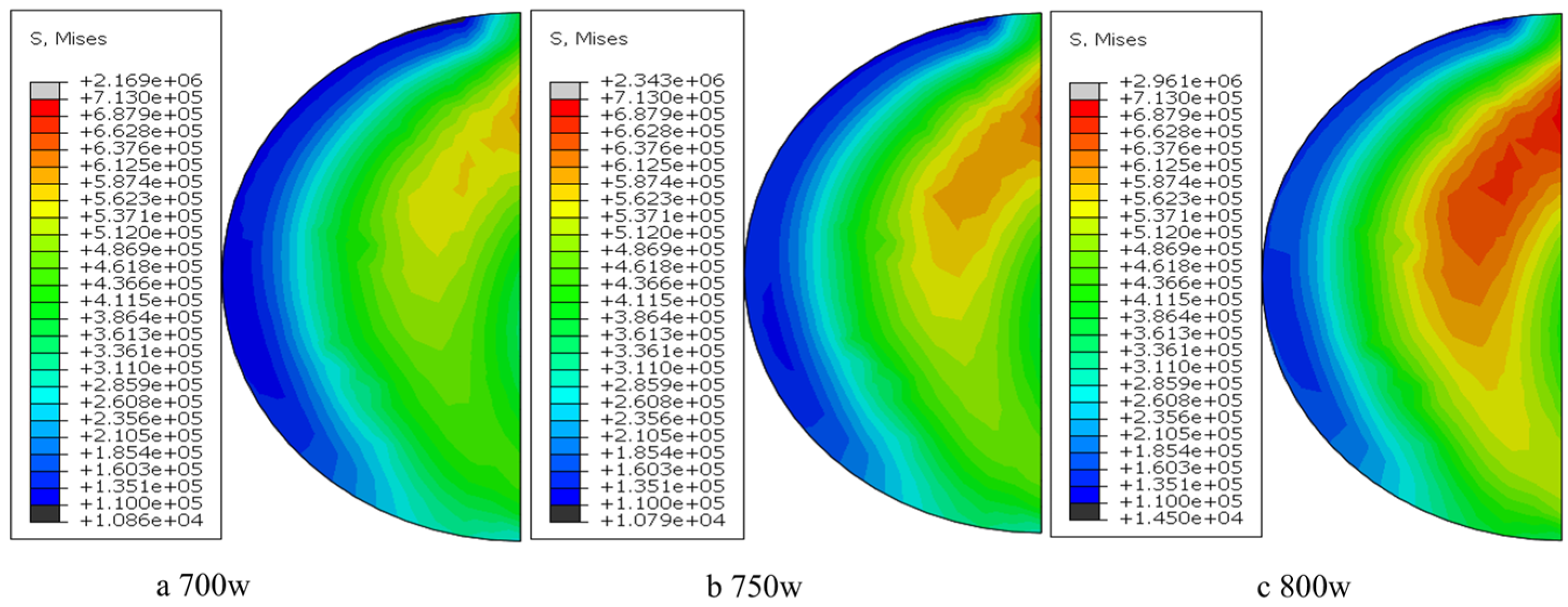
3.1.1. Effect of Laser Power on the Melting Temperature
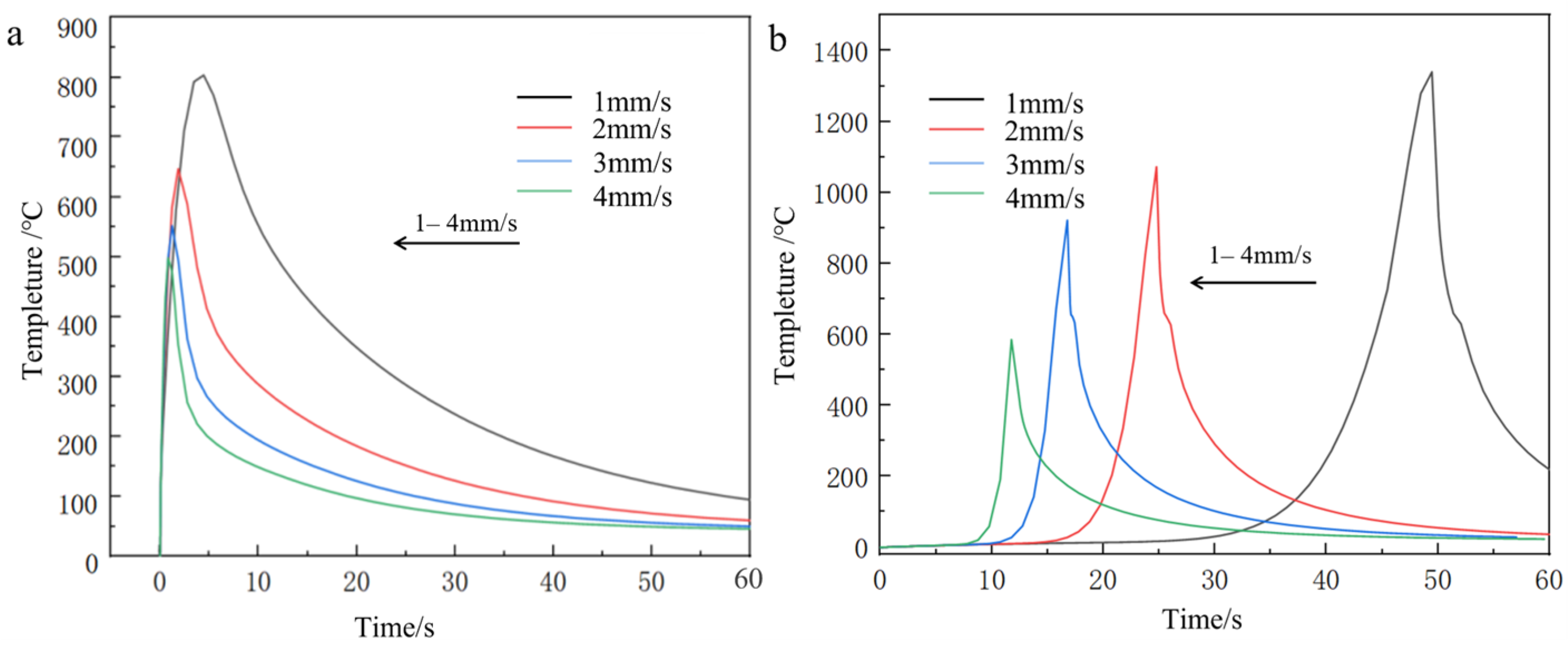
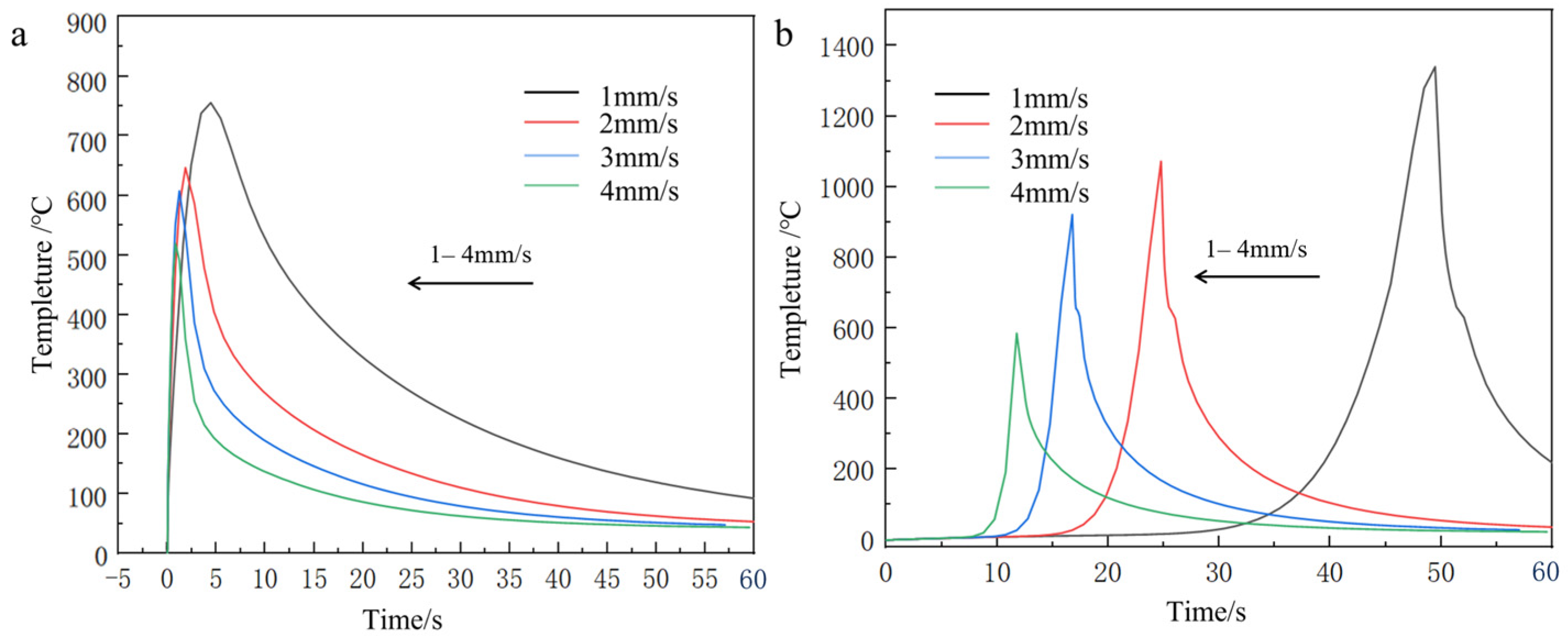
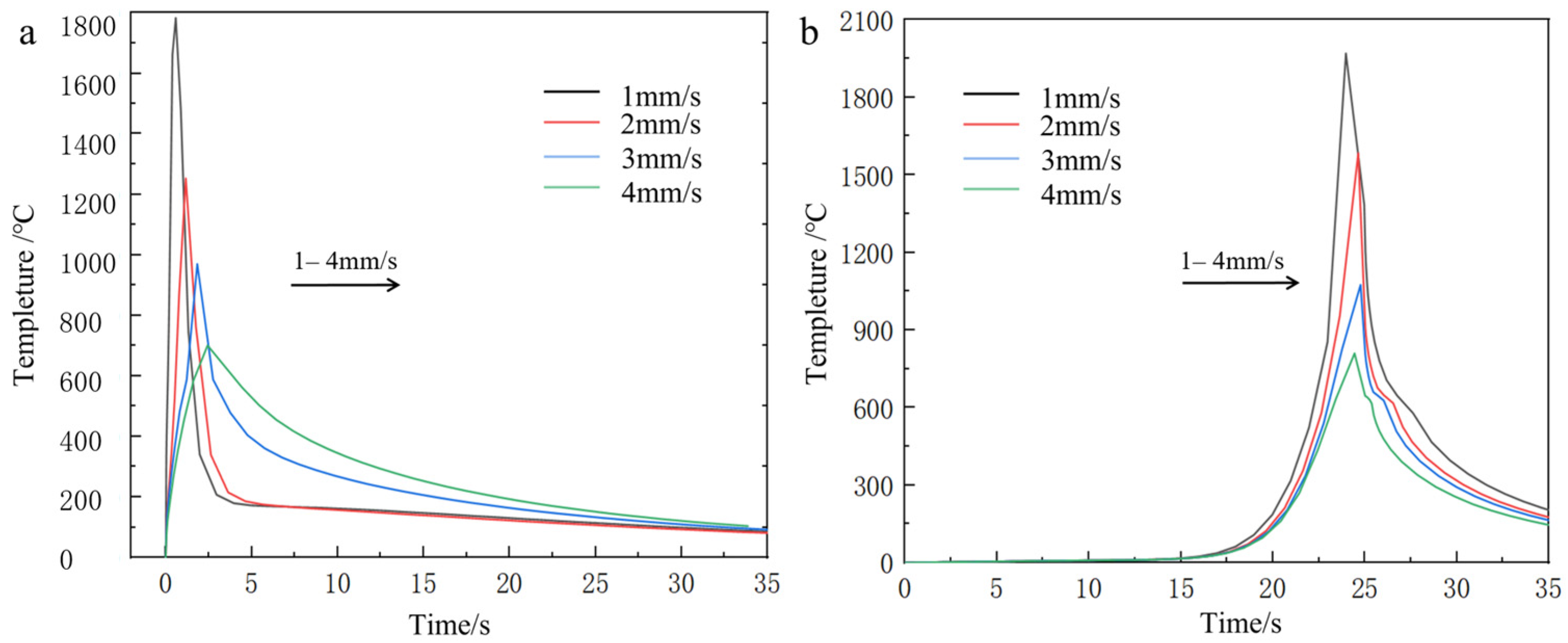
3.1.2. Effect of Scanning Speed on Cladding Temperature
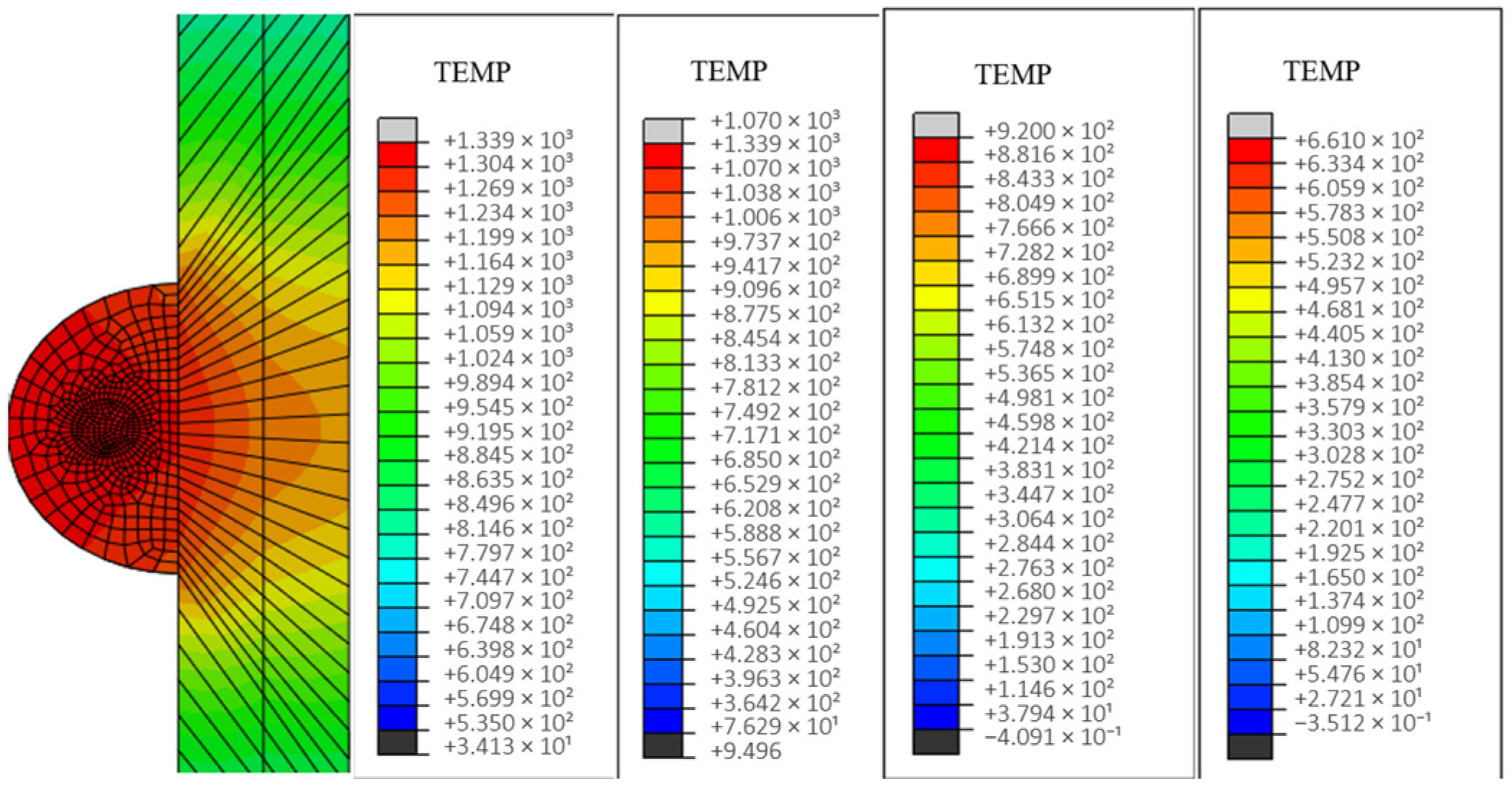
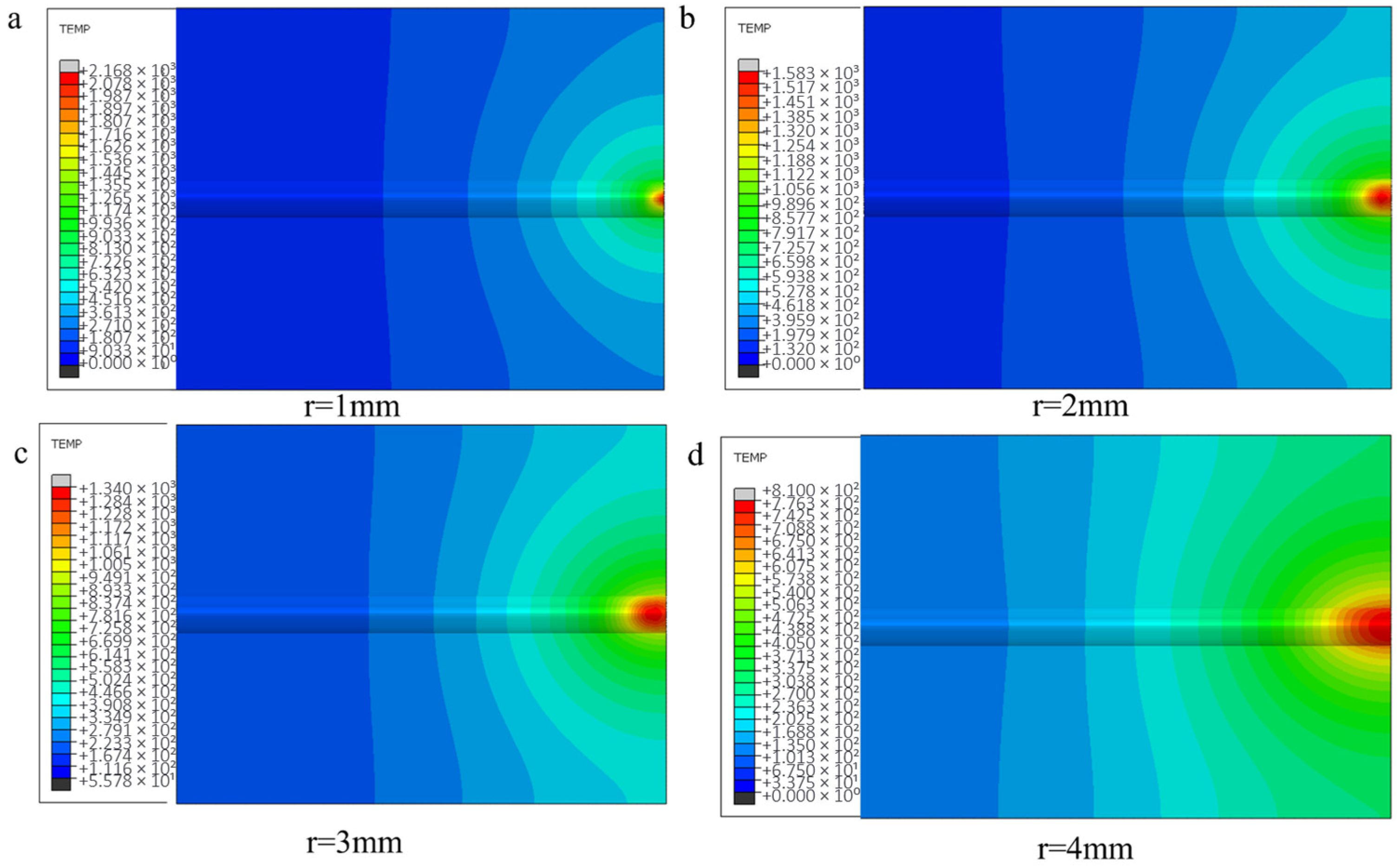
3.1.3. Influence of Spot Radius on Melting Temperature
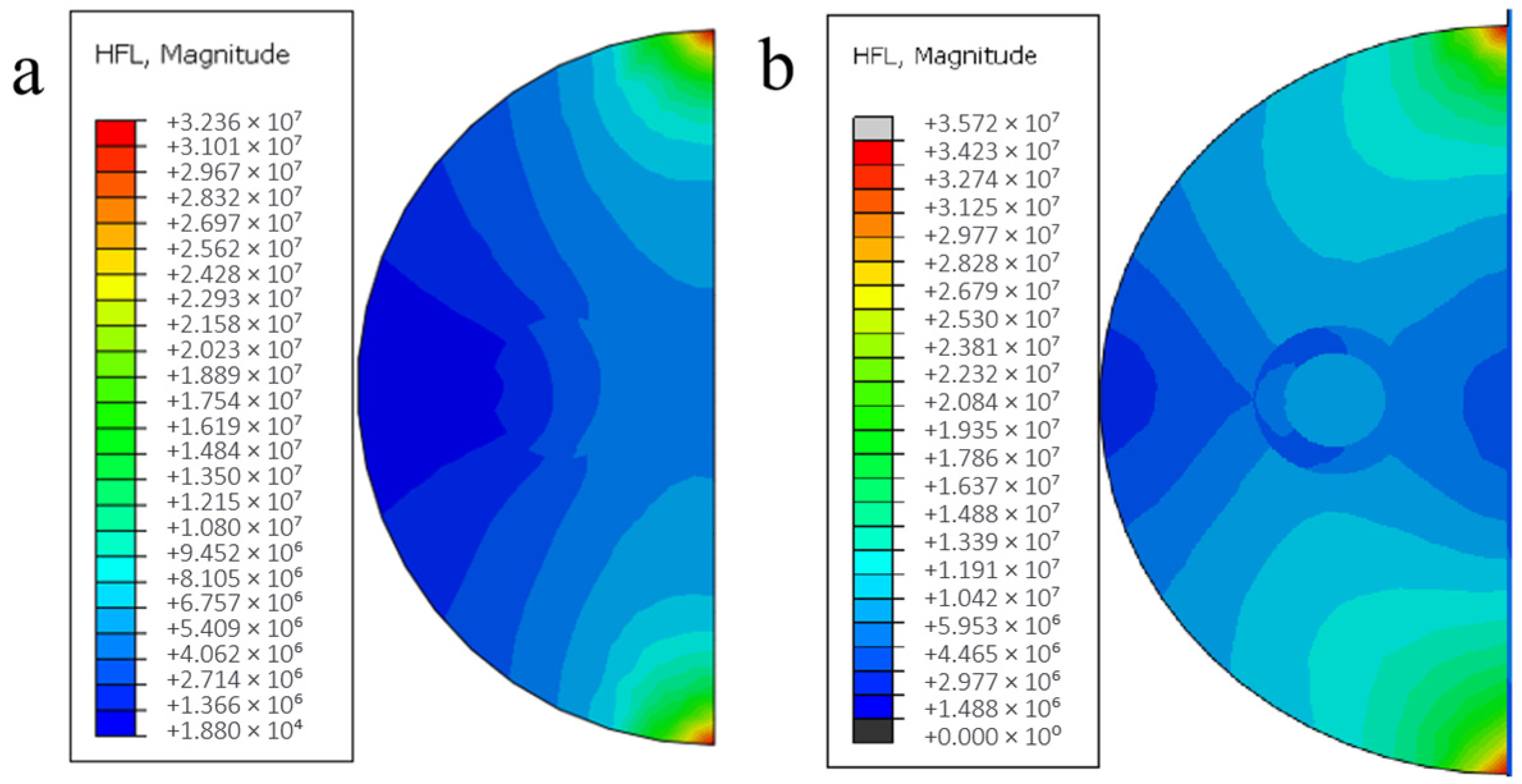
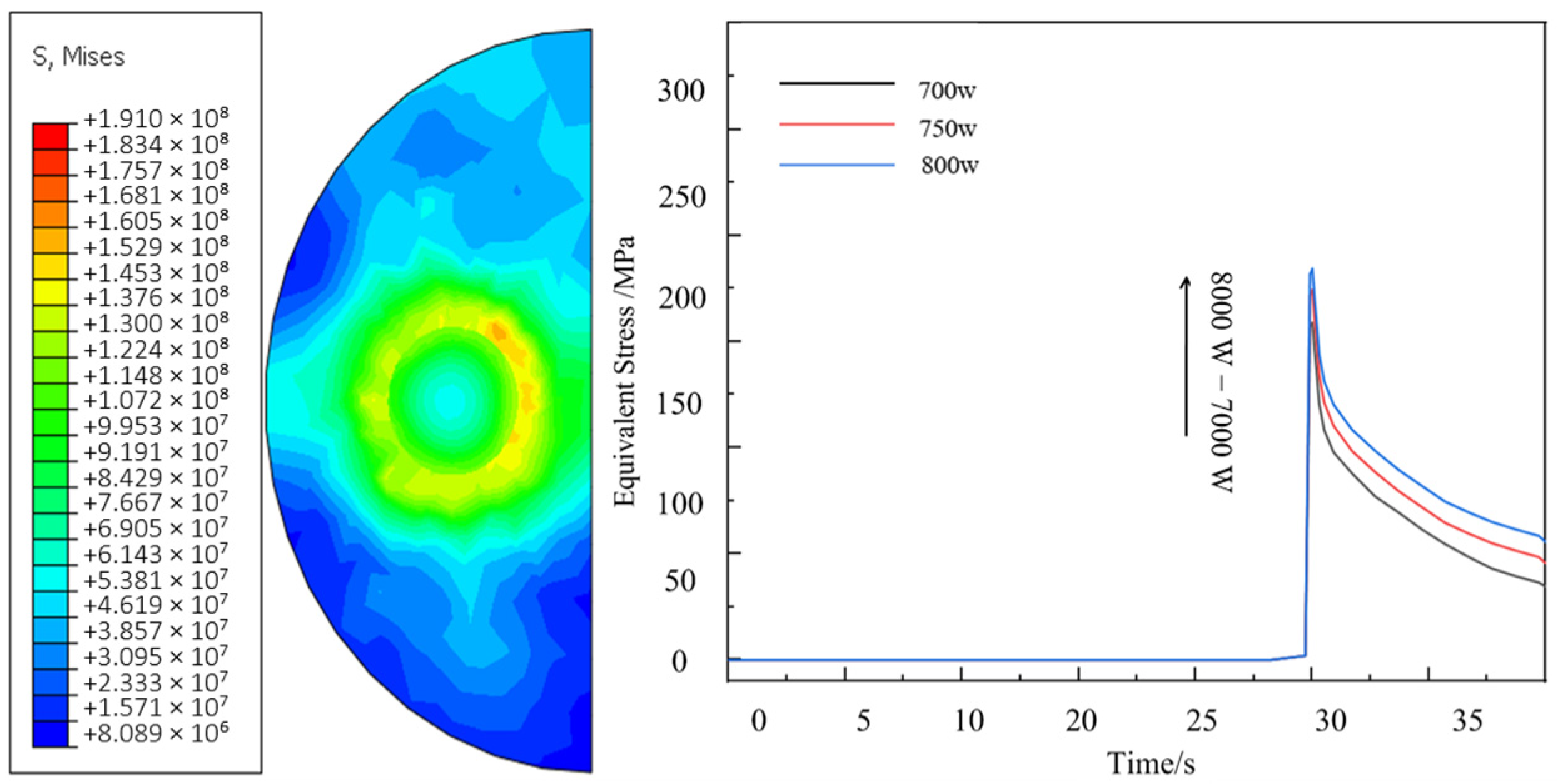
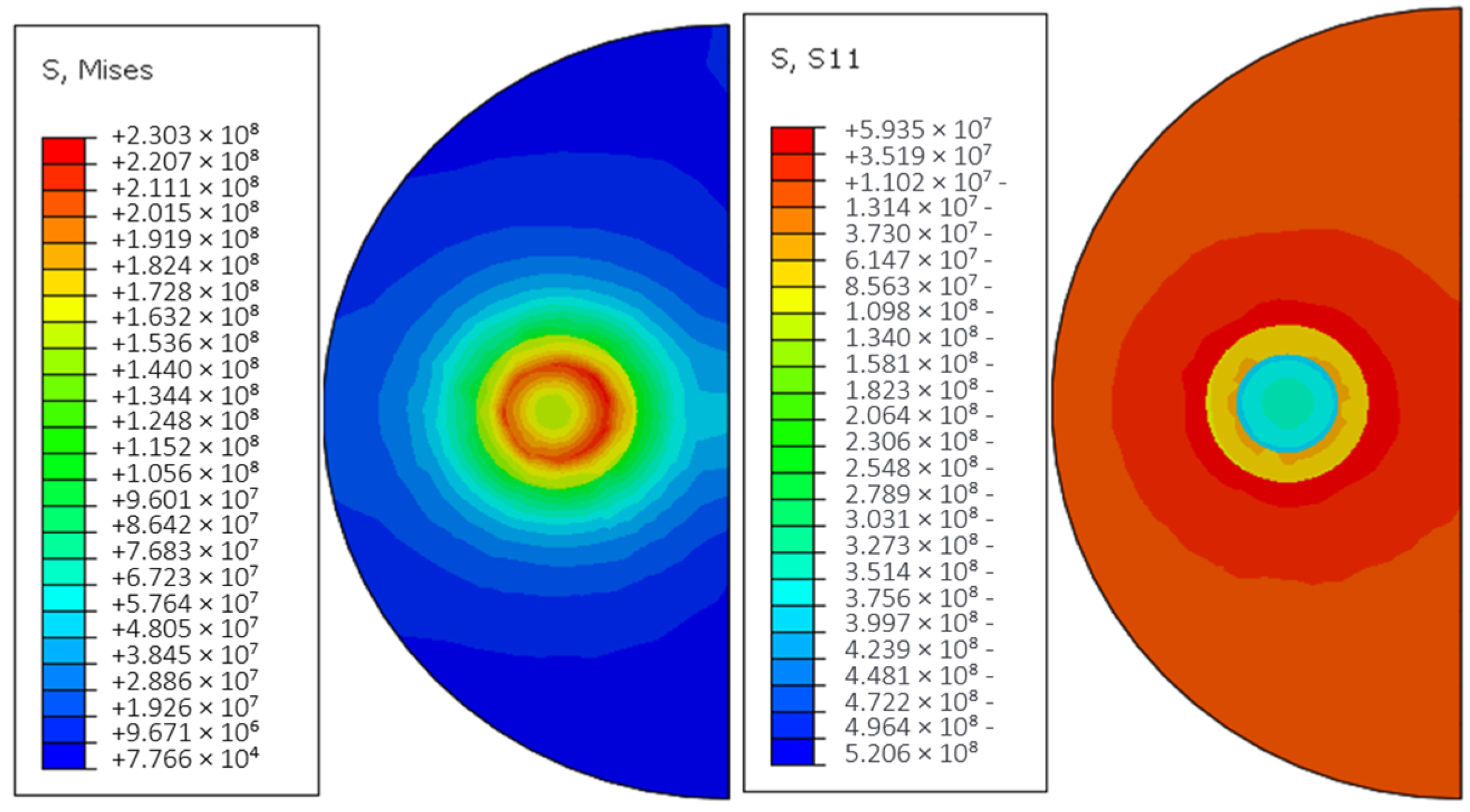
3.2. Stress Field Analysis
3.3. Experimental Validation
4. Conclusions
- (1)
- Laser power exhibited a positive correlation with material temperature, while scanning speed showed an inverse relationship. Spot radius negatively influenced both temperature distribution and melt pool geometry, with a 3 mm radius minimizing thermal gradients. The optimal combination of 2 mm/s scanning speed, 700–800 W laser power, and 3 mm spot radius produced interfacial temperatures reaching a peak of 1048 °C, corresponding to well-formed cladding specimens with favorable metallurgical integrity.
- (2)
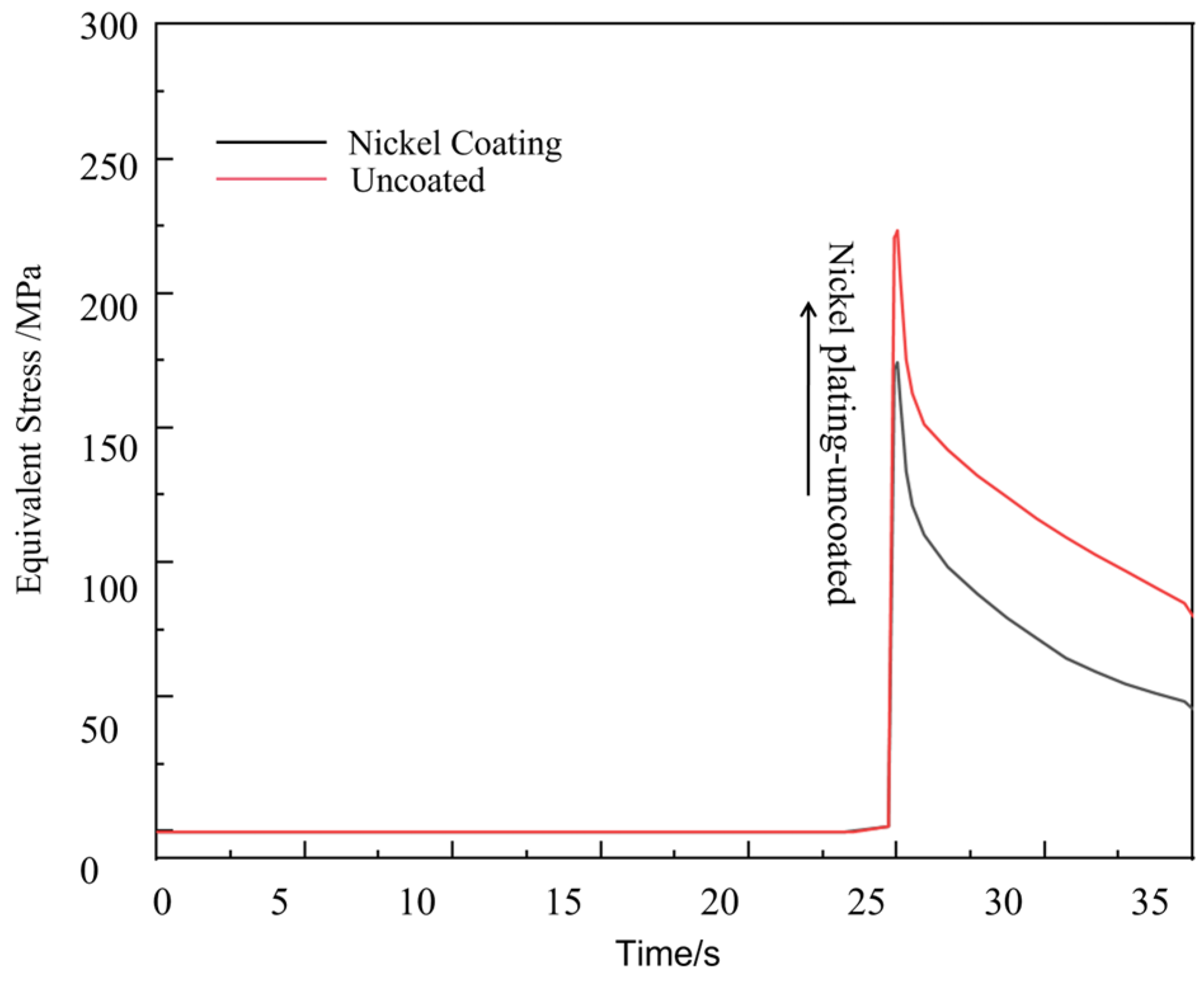
- The process induced steep thermal gradients exceeding 800 °C between front and back surfaces, generating tensile-dominated interfacial stresses. Maximum stress concentration reached 223.47 MPa at fiber/matrix interfaces in nickel-coated models, exceeding the 174.2 MPa stress reduction observed in aluminized layer configurations.
- (3)
- Nickel coating implementation reduced aluminum substrate interfacial stress by 174.2 MPa compared to non-coated counterparts, demonstrating a stress reduction rate of approximately 44%. The coating simultaneously localized peak stress at the fiber/coating interface while achieving thermal protection efficiency over 78% against direct laser oxidation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shirvanimoghaddam, K.; Hamim, S.U.; Akbari, M.K.; Fakhrhoseini, S.M.; Khayyam, H.; Pakseresht, A.H.; Ghasali, E.; Zabet, M.; Munir, K.S.; Jia, S.; et al. Carbon fiber reinforced metal matrix composites: Fabrication processes and properties. Compos. Part A Appl. Sci. Manuf. 2017, 92, 70–96. [Google Scholar] [CrossRef]
- Wang, X.; Tian, X.; Lian, Q.; Li, D. Fiber traction printing: A 3D printing method of continuous fiber reinforced metal matrix composite. Chin. J. Mech. Eng. 2020, 33, 31. [Google Scholar] [CrossRef]
- Ríos, A.; Martín-Meizoso, A. Micromechanical model of interface between fibre and matrix of metal matrix composite reinforced with continuous fibre. Adv. Mater. Res. 2009, 59, 158–163. [Google Scholar] [CrossRef]
- Wang, L.; Yan, W. Thermoelectric magnetohydrodynamic model for laser-based metal additive manufacturing. Phys. Rev. Appl. 2021, 15, 064051. [Google Scholar] [CrossRef]
- Paul, C.P.; Jinoop, A.N.; Kumar, A.; Bindra, K.S. Laser-Based Metal Additive Manufacturing: Technology, Global Scenario and Our Experiences. Trans. Indian Natl. Acad. Eng. 2021, 6, 895–908. [Google Scholar] [CrossRef]
- Lubin, Q. Static Behaviour of Laser-Welded Sandwich Beams with Corrugated-Strip-Core Connectors. Master’s Thesis, National University of Singapore, Singapore, 2017. [Google Scholar]
- Zhao, P.; Zhang, X.; Bian, S.; Zhang, W.; Cao, Z. Effect of pulse shaping on coupling efficiency of laser spot welding in AZ31 magnesium alloy. Int. J. Adv. Manuf. Technol. 2024, 132, 1753–1767. [Google Scholar] [CrossRef]
- Lian, G.; Yao, M.; Zhang, Y.; Chen, C. Analysis and prediction on geometric characteristics of multi-track overlapping laser cladding. Int. J. Adv. Manuf. Technol. 2018, 97, 2397–2407. [Google Scholar] [CrossRef]
- Farahmand, P.; Kovacevic, R. An experimental–Numerical investigation of heat distribution and stress field in single-and multi-track laser cladding by a high-power direct diode laser. Opt. Laser Technol. 2014, 63, 154–168. [Google Scholar] [CrossRef]
- Bjelić, M.B.; Radičević, B.S.; Kovanda, K.; Kolařík, L.; Petrović, A.V. Multi-objective calibration of the double-ellipsoid heat source model for GMAW process simulation. Therm. Sci. 2022, 26, 2081–2092. [Google Scholar] [CrossRef]
- Jafarzadegan, M.; Taghiabadi, R.; Mofid, M.A. Using double ellipsoid heat source model for prediction of HAZ grain growth in GTAW of stainless steel 304. Mater. Today Commun. 2022, 31, 103411. [Google Scholar] [CrossRef]
- Hao, L.; Wang, Y.; Shi, Z.; Xu, S.; Xiao, Y.; Wang, T. Simulation of laser cladding temperature field and flow field based on ellipse heat source model. Appl. Laser 2017, 37, 218–222. [Google Scholar]
- Scapin, M.; Manes, A. Behaviour of Al6061-T6 alloy at different temperatures and strain-rates: Experimental characterization and material modelling. Mater. Sci. Eng. A 2018, 734, 318–328. [Google Scholar] [CrossRef]
- Luksch, J.; Niegisch, J.; Jordt, M.; Weissenberger, M.; Pauly, C.; Schaefer, F.; Motz, C. Tailored Nickel Base Multilayer Systems with Adjusted Grain Size and Chemical Composition. Adv. Eng. Mater. 2025, 27, 2402331. [Google Scholar] [CrossRef]
- Lu, J.; Zheng, C.; Wang, L.; Dai, Y.; Wang, Z.; Song, Z. T700 Carbon Fiber/Epoxy Resin Composite Material Hygrothermal Aging Model. Materials 2025, 18, 369. [Google Scholar] [CrossRef] [PubMed]
- Man, X.; Peng, C.; Liao, Z.; Zong, J.; Wang, H.; Liu, H. Experimental study of heat transfer in aerogel-coated insulated walls. J. Eng. Appl. Sci. 2025, 72, 1–13. [Google Scholar] [CrossRef]
- Zhao, P.; Li, X.; Zhang, D.; Xu, W.; Liu, J.; Wu, W.; Deng, L. A simplified method to determine the comprehensive heat transfer quantity in subway tunnels. Energy Build. 2021, 247, 111090. [Google Scholar] [CrossRef]
- Trupiano, S.; Belardi, V.G.; Fanelli, P.; Gaetani, L.; Vivio, F. A semi-analytical method for the calculation of double-ellipsoidal heat source parameters in welding simulation. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2022; Volume 1214, p. 012023. [Google Scholar]
- Han, L.; Song, Y. Analysis on Welding Temperature Field and Stress Field of Boring Bar of New Boring Machine. In Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2022; Volume 2280, p. 012037. [Google Scholar]
- Wang, C.; Deng, C.; Wu, Y.; Chai, L.; Xiang, K.; Huang, Y. Temperature and stress field analysis for pulsed laser-cladding of pure titanium on Ti-6Al-4V. JOM 2022, 74, 755–763. [Google Scholar] [CrossRef]
- Wang, Z.; Song, H. Study on heat transfer of molten pool in laser cladding of titanium alloy TC4. Mach. Des. Manuf. 2018, 10, 85–88. [Google Scholar]
- Vundru, C.; Paul, S.; Singh, R.; Yan, W. Numerical analysis of multi-layered laser cladding for die repair applications to determine residual stresses and hardness. Procedia Manuf. 2018, 26, 952–961. [Google Scholar] [CrossRef]
- Liu, H.; Li, M.; Qin, X.; Huang, S.; Hong, F. Numerical simulation and experimental analysis of wide-beam laser cladding. Int. J. Adv. Manuf. Technol. 2019, 100, 237–249. [Google Scholar] [CrossRef]
- Le, T.N.; Lo, Y.L. Effects of sulfur concentration and Marangoni convection on melt-pool formation in transition mode of selective laser melting process. Mater. Des. 2019, 179, 107866. [Google Scholar] [CrossRef]
- Ji, D.; Zhang, B.; Liu, Y.; Lv, H.; Su, K.; Zhang, J. Microstructure Evolution and Temperature/Stress Field Simulation of Laser Cladded EA4T Axle Steel with Inconel 625 Alloy. Met. Mater. Int. 2024, 31, 1691–1707. [Google Scholar] [CrossRef]
- Azar, A.S.; Ås, S.K.; Akselsen, O.M. Determination of welding heat source parameters from actual bead shape. Comput. Mater. Sci. 2012, 54, 176–182. [Google Scholar] [CrossRef]
- Shao, Z.; Guo, J.; Liu, P. Preparation and research of electroless nickel on carbon fiber surfaces. Anti-Corros. Methods Mater. 2016, 63, 256–261. [Google Scholar] [CrossRef]











| Temperature T/(°C) | 20 | 100 | 200 | 300 | 500 |
|---|---|---|---|---|---|
| Density Kg/m3 | 2700 | 2689 | 2678 | 2667 | 2656 |
| Thermal conductivity K/(W·m−1*°C−1) | 119 | 121 | 126 | 130 | 140 |
| Specific heat capacity C/(J·kg−1*°C−1) | 880 | 900 | 920 | 940 | 970 |
| Modulus of elasticity Pa | 6.67 × 1011 | 6.08 × 1011 | 5.44 × 1011 | 4.31 × 1011 | 3.00 × 1011 |
| Coefficient of linear expansion | 2.23 × 10−5 | 2.28 × 10−5 | 2.47 × 10−5 | 2.55 × 10−5 | 2.70 × 10−5 |
| Poisson ratio | 0.30 | 0.31 | 0.32 | 0.33 | 0.35 |
| Yield strength | 2.5 × 108 | 2.25 × 108 | 1.9 × 108 | 1.33 × 108 | 8.60 × 107 |
| Temperature T/(°C) | 20 | 250 | 500 | 750 | 1000 |
|---|---|---|---|---|---|
| Density Kg/m3 | 7528 | 7489 | 7357 | 7293 | 7116 |
| Thermal conductivity K/(W·m−1*°C−1) | 90 | 91 | 92 | 93 | 95 |
| Specific heat capacity C/(J·kg−1*°C−1) | 440 | 451 | 460 | 490 | 510 |
| Modulus of elasticity Pa | 2.84 × 1011 | 2.65 × 1011 | 2.33 × 1011 | 1.38 × 1011 | 1.01 × 1011 |
| Coefficient of linear expansion | 11 × 10−6 | 12.2 × 10−6 | 13.1 × 10−6 | 13.6 × 10−6 | 13.8 × 10−6 |
| Poisson ratio | 0.30 | 0.31 | 0.34 | 0.36 | 0.37 |
| Name | Density/(g/cm3) | Tensile Strength/MPa | Modulus/GPa | Thermal Conductivity W/mK | Coefficient of Thermal Expansion mm/K | Fiber Diameter/μm | Tow Width/mm | Areal Weight/(g/m2) |
|---|---|---|---|---|---|---|---|---|
| T700 Carbon Fiber | 1.8 | 4950 | 230 | 155 | −1.10 × 10−6 | 7 | 3.2 | 200 |
| Laser Power (P/W) | Scan Speed (V/mm) | Spot Radius (r/mm) |
|---|---|---|
| 600 | 2 | 3 |
| 700 | 2 | 3 |
| 750 | 2 | 3 |
| 800 | 2 | 3 |
| 850 | 2 | 3 |
| 900 | 2 | 3 |
| Laser Power (P/W) | Scan Speed (V/mm) | Spot Radius (r/mm) |
|---|---|---|
| 750 | 1 | 3 |
| 750 | 2 | 3 |
| 750 | 3 | 3 |
| 750 | 4 | 3 |
| Laser Power (P/W) | Scan Speed (V/mm) | Spot Radius (r/mm) |
|---|---|---|
| 750 | 2 | 1 |
| 750 | 2 | 2 |
| 750 | 2 | 3 |
| 750 | 2 | 4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, P.; Cheng, X.; Deng, Y.; Peng, Y.; Qu, M.; Ren, P.; Wang, T. Research on Laser Cladding Single-Pass Continuous Carbon Fiber-Reinforced Aluminum Matrix Composite Process Based on Abaqus. Materials 2025, 18, 3859. https://doi.org/10.3390/ma18163859
Zhang P, Cheng X, Deng Y, Peng Y, Qu M, Ren P, Wang T. Research on Laser Cladding Single-Pass Continuous Carbon Fiber-Reinforced Aluminum Matrix Composite Process Based on Abaqus. Materials. 2025; 18(16):3859. https://doi.org/10.3390/ma18163859
Chicago/Turabian StyleZhang, Pengtao, Xiaole Cheng, Yuanyuan Deng, Yao Peng, Meijiao Qu, Peng Ren, and Teng Wang. 2025. "Research on Laser Cladding Single-Pass Continuous Carbon Fiber-Reinforced Aluminum Matrix Composite Process Based on Abaqus" Materials 18, no. 16: 3859. https://doi.org/10.3390/ma18163859
APA StyleZhang, P., Cheng, X., Deng, Y., Peng, Y., Qu, M., Ren, P., & Wang, T. (2025). Research on Laser Cladding Single-Pass Continuous Carbon Fiber-Reinforced Aluminum Matrix Composite Process Based on Abaqus. Materials, 18(16), 3859. https://doi.org/10.3390/ma18163859






