1. Introduction
Determining the processing–microstructure–property (PMP) linkage plays a vital role in material design. In particular, the size, shape, and spatial distribution of microstructural features are known to affect material properties [
1]. For example, in the case of metals and alloys, formation and subsequent growth of precipitates are known to affect the strength of a material. Phase field (PF) modeling based on fundamental principles of thermodynamics and kinetics has been successfully applied to provide insight into the evolution of precipitates in alloys [
2] and link them to the mechanical strength of the alloys [
3]. PF simulation provides microstructure evolution in alloys [
4] by solving differential equations, but such calculations are often computationally expensive, particularly in 3D. More recently, it has been observed that machine learning (ML) tools, when trained on phase field simulated microstructures, can significantly accelerate the prediction of microstructure evolution at a fraction of the computational cost [
5].
In this work, we focus on nickel–aluminum (Ni-Al) alloys, which are important high-temperature structural materials due to their low density, high strength, and excellent oxidation resistance [
6]. Their microstructure consists of ordered L1
2 Ni
3Al (γ′) precipitates coherently embedded in a disordered FCC Ni-rich (γ) matrix [
4]. The morphology, size, and distribution of these γ′ precipitates are the primary factors governing the strength, particularly under high-temperature loading. The microstructure–property relationships of these alloys can be determined using machine learning, which can play a critical role in optimizing alloy performance for aerospace and turbine applications.
There are two common approaches to predicting material properties with machine learning: The first is to use explicitly defined or extracted dataset features [
7], like elemental properties and electronic and ionic attributes, to predict material properties like band gap energy. This typically involves ML tools like linear regression (LR), extra trees (ET) [
8], and many others [
9]. The second approach is to use high-dimensional data like 2D or 3D images, or continuous spectral measurements [
10], which often require the use of deep learning (DL) tools like convolutional neural networks (CNNs). This approach has commonly been used to predict the material properties of simulated microstructures and experimental micrographs [
11]. The primary difference between these two approaches is that the former feature-statistics-based method has simpler, but more interpretable, models, while deeper layers in DL models are much more complex and less interpretable. For example, a CNN, which is often thought of as a ‘black box,’ can achieve very high accuracy but has difficulty explaining its predictions [
12]. In contrast, for feature statistics methods, while domain knowledge is required to know which features to extract, the model can be explained more intuitively in terms of those features. For example, feature importance studies can be performed with models like support vector machines (SVMs) and neural networks (NNs) [
13]. Overall, choosing an approach depends on the complexity of the data and the accuracy desired; therefore, an ML model that can make predictions of high-dimensional data with high accuracy, as well as effectively explain such predictions, is necessary.
There is currently a significant effort to reduce the computational requirements of CNNs and expedite the training process [
14,
15]. Instead of using such high-dimensional networks like a CNN, there is a need for an alternate neural network that is less computationally expensive and does not require high-end GPUs. This would provide a pathway to the scientific community in the ML field to better process their data and develop high-fidelity models from it.
In this research, we demonstrate the utility of a graph neural network (GNN) as an alternate explainable approach that requires significantly reduced GPU resources in comparison to CNNs. GNNs process graphs, which are data structures made of individual nodes with different features, and edges representing the relationships between nodes [
16]. GNNs have been successfully used in several material applications [
17], such as coarse graining molecular systems to expedite molecular dynamics simulations [
18]. GNNs have also been used to effectively predict the mechanical properties of polycrystalline materials where each grain is represented by a node and graph edges connecting nodes represent the grain boundaries [
19]. Polycrystalline microstructures can also be converted into graphs and were previously used by a GNN to predict the magnetostriction of the material with about 10% error [
20]. Additionally, integrated gradient analysis was used to determine the features in the microstructure that were most important in predicting magnetostriction. In this study, we used a GNN to predict the strengthening due to precipitate coarsening for phase field generated microstructures of Ni-Al alloys by representing high-dimensional microstructure as graphs with interpretable features.
In this work, we created a graph dataset from PF-generated microstructures of Ni-Al alloys by assigning a node to each precipitate in the microstructure and trained a GNN to predict the change in strength due to precipitate coarsening. We will demonstrate the equivalent/superior accuracy of the GNN compared to feature-statistics-based models and a high-dimensional-based CNN. Further, we will demonstrate superior generalizability with the GNN using train and test datasets comprising of microstructures of different sizes and dimensions. Later, we will also show the reduced computational resources required to train and test the GNN compared to the CNN.
Saliency analysis (SA), an explainable AI feature importance method, has been previously used in combination with CNNs to show the regions that have the most influence on the neural network prediction [
21]. In this work, we have shown that when using SA in combination with a GNN, it is possible to find the importance of each node feature on predicted strengthening, which can help us understand the underlying physics governing material evolution. Unlike previously published research [
22], in this work, we have also validated our results with a known equation for strengthening of alloys [
23] and demonstrated that using feature importance with a GNN yields more interpretable results than when feature importance is used with a CNN.
Lastly, we used BI to determine the coefficients of the power law equation [
24] that governs the growth of precipitates as a function of time. BI uses Bayes’ theory to estimate the coefficients of terms in an equation and their uncertainties [
25] and has been previously used in parameter estimation for physics models [
26]. Agreement between the BI-calculated coefficients with the known values of the coefficients confirms the accuracy of our PF data.
Overall, we demonstrate superior accuracy and generalizability while enabling unique insights with explainable AI using GNN. In addition, our proposed GNN-based approach uses fewer resources and can be run without access to expensive GPUs. This can make it easier to develop property prediction models of material microstructures with readily available CPUs.
2. Materials and Methods
In this work, we utilize a GNN with a PF-generated dataset of Ni-Al alloy microstructures converted into a graph dataset to predict the change in strength of the alloys from precipitate coarsening. Also, we use feature importance to find the most important features in the strengthening and BI to fit the precipitate growth to a power law equation. Finally, we compare the performance and speed of the GNN to other state-of-the-art feature-based ML tools and a comparable CNN. These methods are conducted to showcase the benefits of using GNN for materials microstructure over other ML tools.
2.1. Phase-Field Generation of Ni-Al Alloys
Microstructures of Ni-Al were generated with a phase field model governed by Cahn–Hilliard kinetic Equations (1) and (2) [
4,
27,
28]:
where
c is concentration of Al,
is the order parameter,
F is the total free energy,
f is the free energy density,
t is time,
M is diffusion mobility, and
L is a kinetic coefficient for order parameter relaxation. Further details regarding this model can be found elsewhere [
4]. PF simulations were performed at a temperature of 1273 K and an Al concentration of 17.7%. Five image sequences with different random initializations were generated. Each sequence comprised of 21 images, with a time step of 0.8 s during coarsening of precipitates in Ni-Al alloys.
Figure 1 shows microstructures at four different timesteps from one representative sequence obtained from phase field simulations.
2.2. Graph Construction
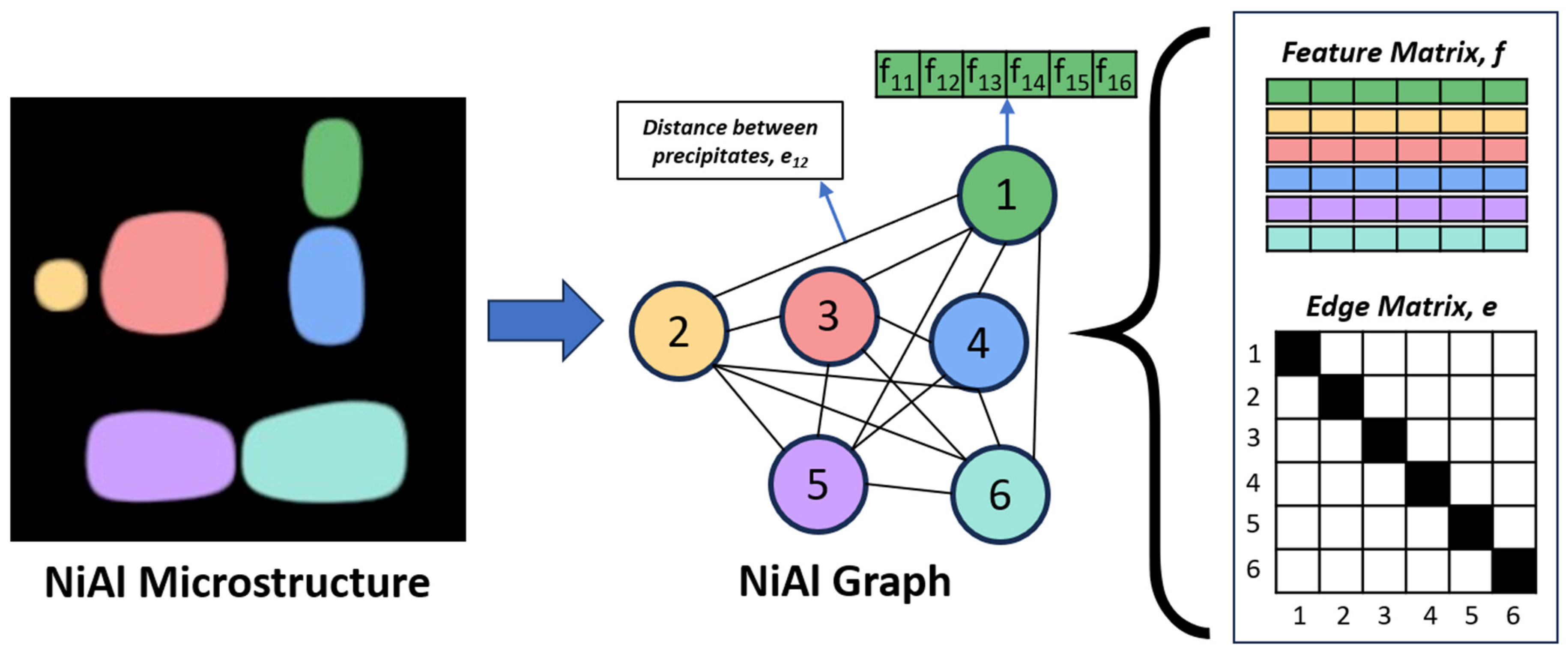
A microstructure is converted into a graph by assigning each precipitate to a node. Each node has features that describe a precipitate, and this collection of node features is called the feature matrix, f. Additionally, interactions or relationships between nodes are represented by edges and are stored in the edge/adjacency matrix, e. In this study, we define 6 features for each precipitate: size, x, y, and z position of centroid, equivalent cube length, and extent. The size is equal to the area of precipitates for the 2D microstructure and the volume of precipitates for the 3D microstructure. The x, y, and z centroid positions are normalized by dividing them by the total number of pixels within the microstructure in that direction. The equivalent cube length is calculated by taking the square root of the size (for 2D microstructures) or the cubic root of the size (for 3D microstructures), and the extent is calculated by dividing the size either by the area or volume of the bounding box of the precipitate. We also define the edges between two nodes as the reciprocal of the distance between the centroid of the two corresponding precipitates. Only precipitates whose centroids are within 62 pixels of each other are given an edge value, which may include non-immediate neighbors. We tested distances of 42, 62, and 82 pixels and found no significant difference in the test mean absolute error (
MAE = (1/
n) ∗ Σ|
yᵢ −
ŷᵢ|, where
n is the number of predictions,
yᵢ is the true value, and
ŷᵢ is the predicted value) of the GNN based on the distance used.
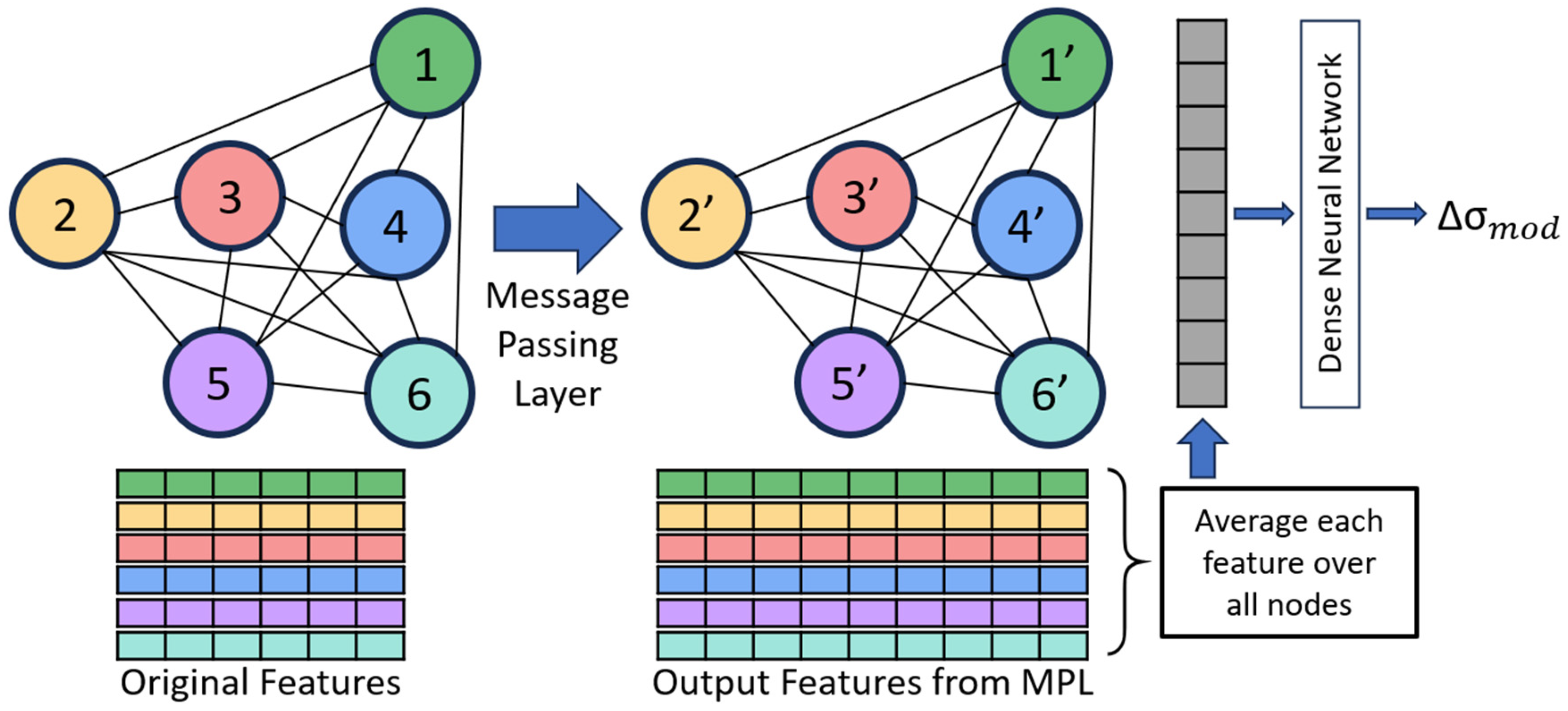
Figure 2 shows a summary of the image-to-graph conversion. We used Python 3.8 with the StellarGraph 1.2.1 package for building the graphs and the GNN operations, and we used TensorFlow 2.8 for the rest of the operations.
2.3. Dataset Generation
A dataset of 2D and 3D Ni-Al microstructures of different sizes is created from PF simulations. Later, each microstructure is converted into a graph. We build 5 graph datasets (3 in 2D and 2 in 3D), each with 105 graphs constructed from five 21-microstructure sequences of Ni-Al alloys. Three graph datasets are made using 2D microstructures with sizes of 128 × 128, 256 × 256, and 512 × 512, and these microstructure datasets will be referred to in this paper as 2D-128, 2D-256, and 2D-512, respectively. The other two graph datasets are made using 3D microstructures with sizes of 64 × 64 × 64 and 128 × 128 × 128 and will be referred to in this paper as 3D-64 and 3D-128, respectively.
For each microstructure in these datasets, we calculate the strengthening of the alloy using Equation (3) [
23]:
where
is the shear modulus difference between the matrix and precipitate (42.8 GPa),
= 0.85,
= 3.06, G is the shear modulus of Al (26.2 GPa), and
is the interatomic distance in slip direction of Al, which is 2.863 Å [
23].
is the area fraction, and
is the average cube length; both are calculated using a python script.
After calculating the strengthening of the alloy in the dataset, we sort them in order of increasing strengthening and then put every fifth microstructure in the test set while keeping the rest within the training set. We did this five times, each time offsetting the test data by one, resulting in five folds, each with an evenly distributed training set of 84 microstructures and a test set of 21 microstructures, allowing us to make consistent comparisons of model performances.
2.4. Graph Neural Network (GNN)
We built a commonly used regression graph neural network that implements message-passing layers (MPLs), averages the features over all nodes, and then uses a dense neural network to predict the strengthening as shown in
Figure 3 (additional description of GNN in
Appendix A). In the MPL, information from features is passed between connected nodes and later aggregated, which allows information from neighboring nodes to be included in the updated features [
29]. The next step returns the average value of each feature over all nodes, and the average feature values are used as input into the dense neural network. This contrasts with recent GNNs for predicting properties from microstructures, which concatenate the features of each node after the last MPL before being fed into the dense neural network [
20], restricting all the graph datasets to have the same number of nodes. By taking the average feature values over all nodes, our GNN architecture makes it possible to train and test on graphs with any possible number of nodes. This means the graphs in the dataset can be constructed from microstructures of any size or dimension and can predict the properties of alloys with other microstructure sizes and/or dimensions, thus making this GNN significantly more generalizable than previous models.
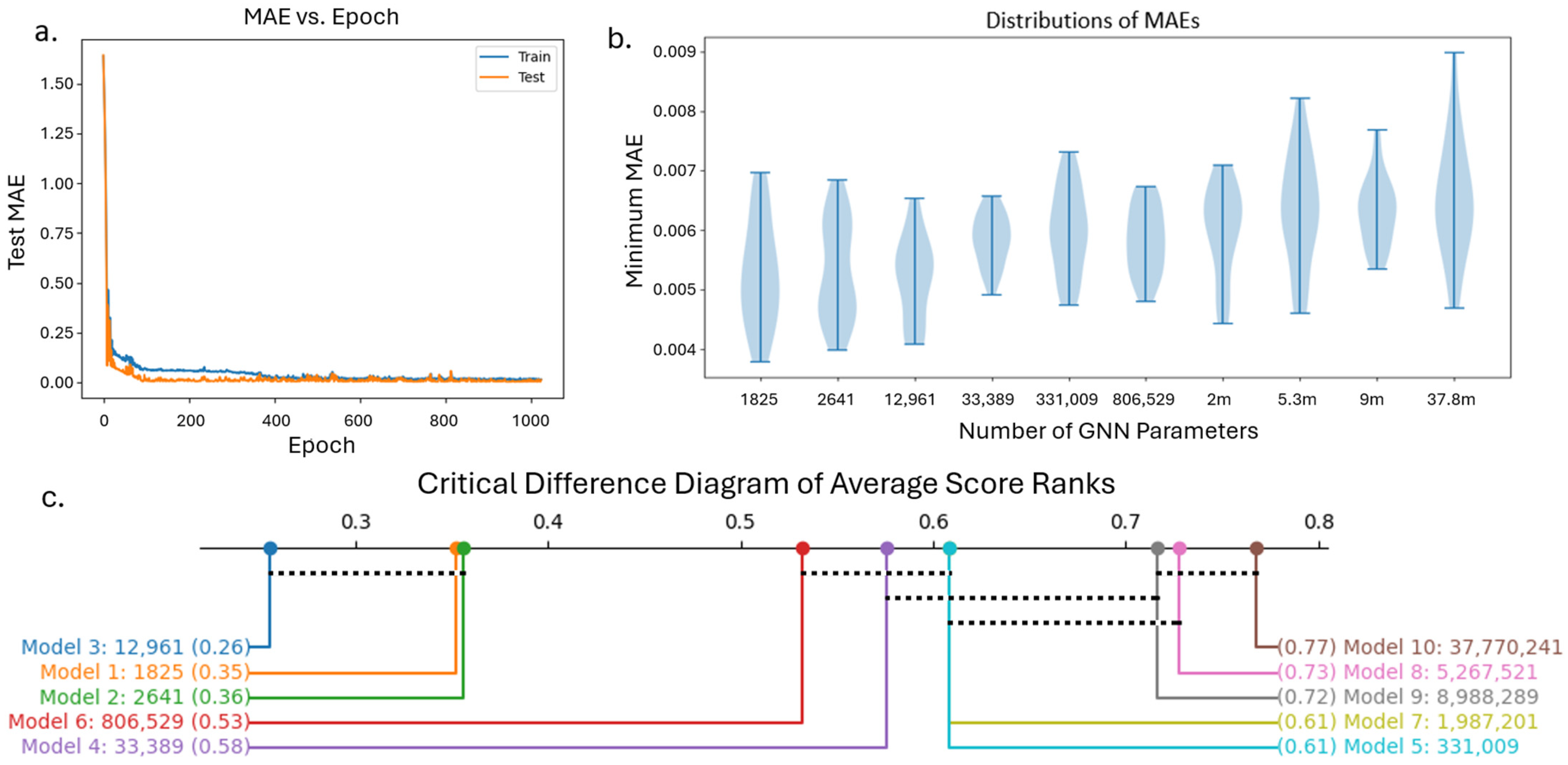
GNN Parameters and Architecture Optimization
In this study, we investigated ten GNN architectures with varying complexity to determine the most appropriate model for our dataset. The size of each MPL and dense neural network layer in these GNNs is listed in
Table 1. In this study, we use a dropout of 0.2 in each MPL and ReLU activation in each MPL and dense layer. Further, a learning rate of 0.001 with the Adam optimizer was used. We observed that the learning rate and dropout had little impact on GNN performance. ReLU activation function was used for its computational efficiency. We initialized the model weights with random Xavier distributions and used the MAE loss function between the true and predicted strengthening. Each model in
Table 1 is trained until the test MAE does not improve for 150 epochs and is relatively close to the train MAE to ensure there is no overfitting. Using the 2D-256 dataset with the 80–20 train–test split described in
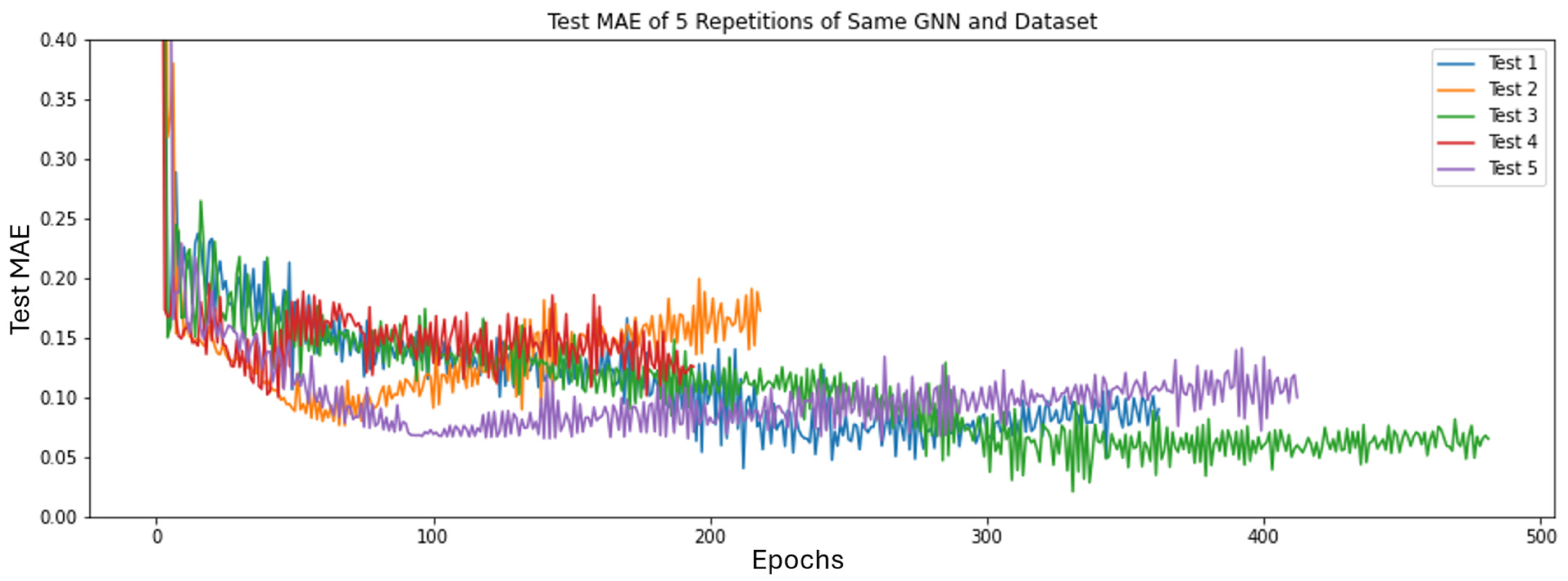
Section 2.3, we repeat 5-fold cross validation 5 times for a total of 25 comparisons for all GNN architectures. We determined the ranks of each GNN’s minimum test MAE over all 25 tests and used the architecture that achieves the best average rank for the remainder of the study.
2.5. Feature Importance
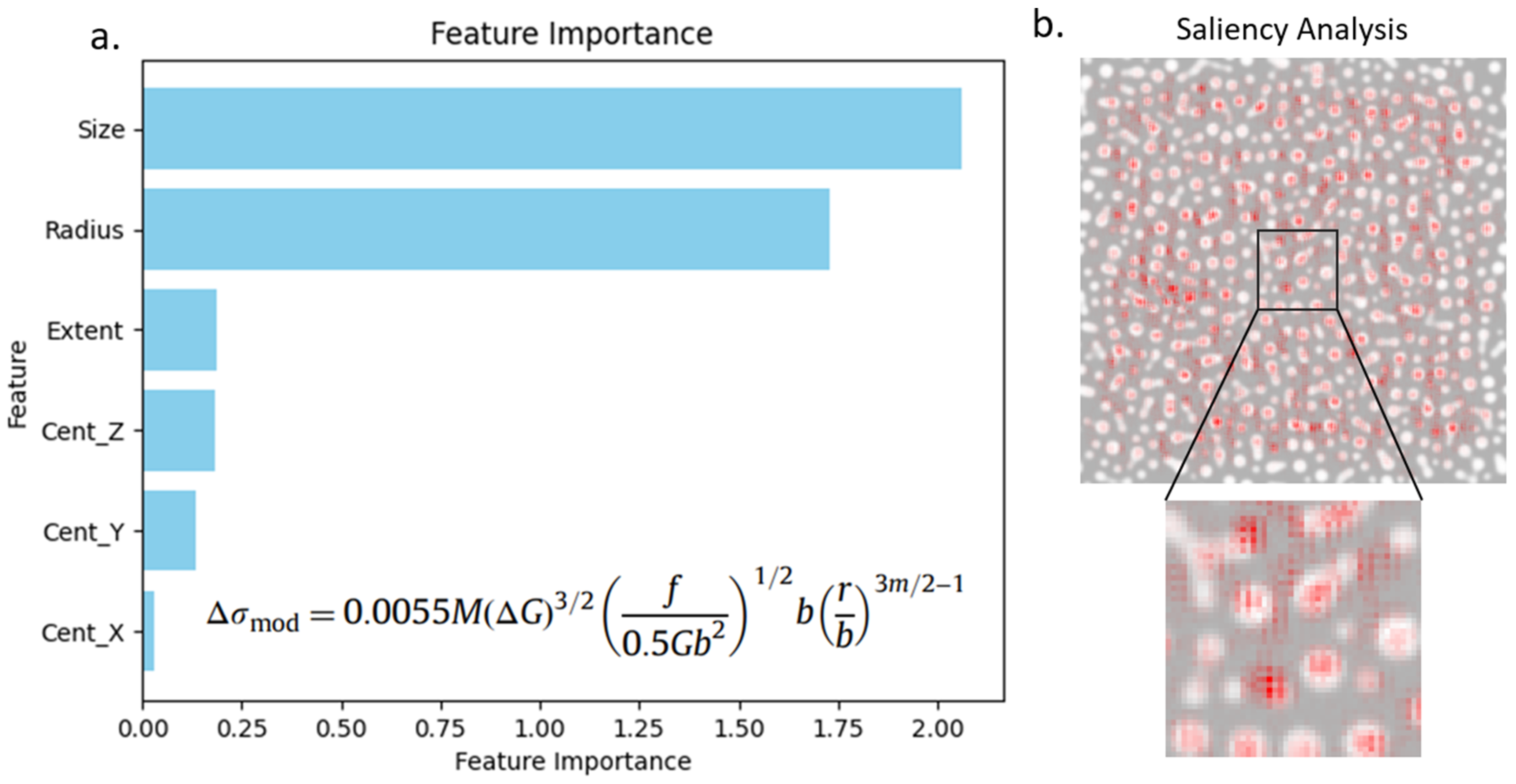
Using the optimized graph construction method and the GNN, we perform feature importance to determine which of the 6 manually defined features (size, x, y, and z position of centroid, equivalent cube length, and extent) are most important for predicting strengthening. The feature importance was performed by taking the gradient of the GNN strengthening prediction with respect to each feature in each node to obtain the importance score of each feature at each node. Then, we added all the individual feature importance scores for each feature across all nodes to determine a cumulative importance score of each feature. By comparing the cumulative score of each feature to the variables present in commonly used strengthening equation (Equation (3)), it is possible to determine if the GNN can extract important features linked to strengthening.
2.6. GNN Performance
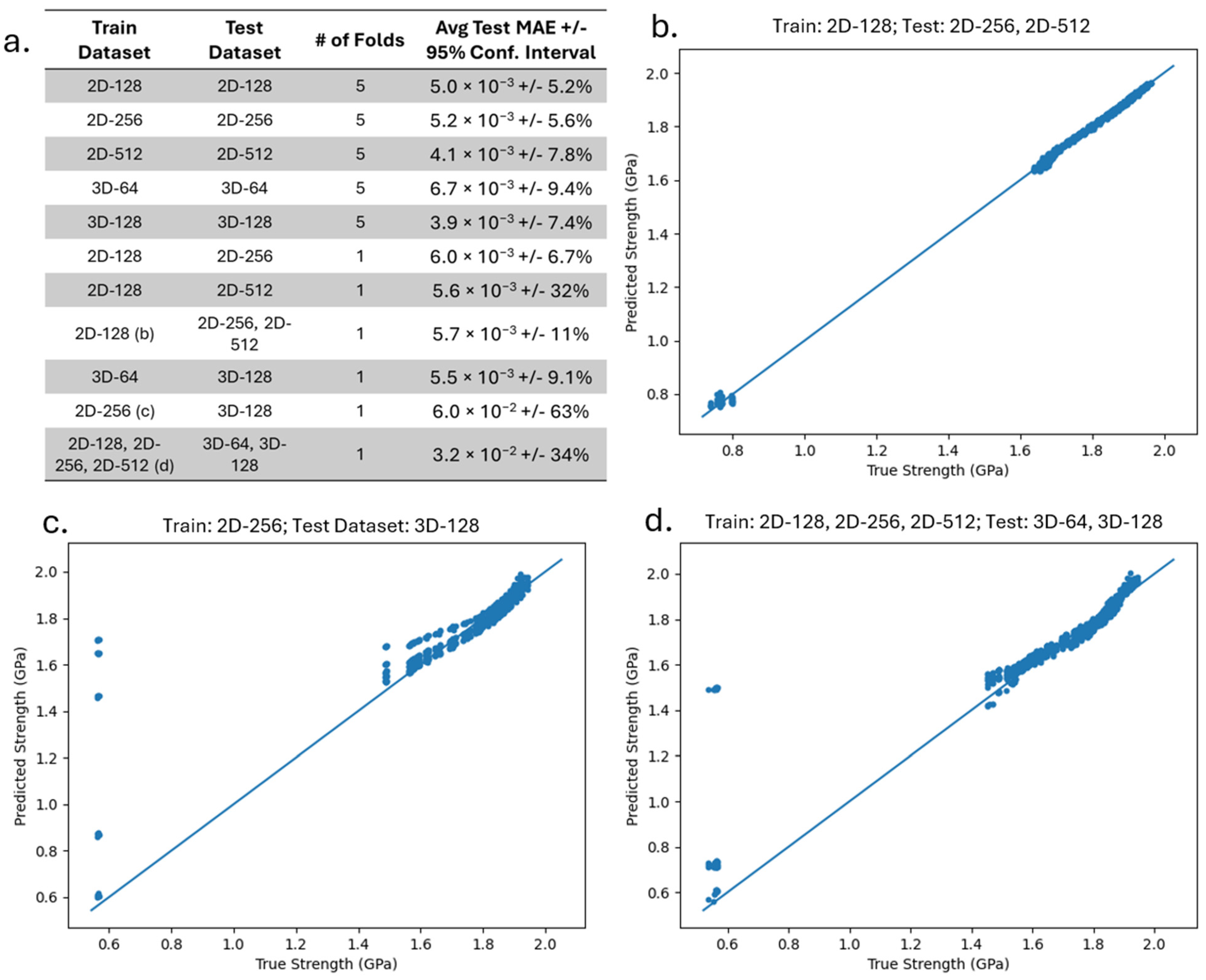
To demonstrate the robustness of the GNN, we analyze the ability of the GNN to make predictions on graph datasets that are created from microstructures of different dimensions and sizes. We train and test our GNN on the 2D-128, 2D-256, 2D-512, 3D-64, and 3D-128 datasets, using the train–test approach presented in
Section 2.3, and report the average test MAE of all 25 runs. We also investigate cases where we train on one or more dataset and test on separate dataset(s), and we measure the average test MAE. In these cases, there is only one train–test fold, but we still train and test on this fold with 5 different random weight initializations and take the average MAE from the 5 runs. These results will demonstrate the accuracy in predicting the strengthening when the training is performed on one dataset, while the testing is conducted on a different graph dataset comprising of microstructures of different dimensions and/or sizes.
2.7. Comparison of GNN to Other Machine Learning Models
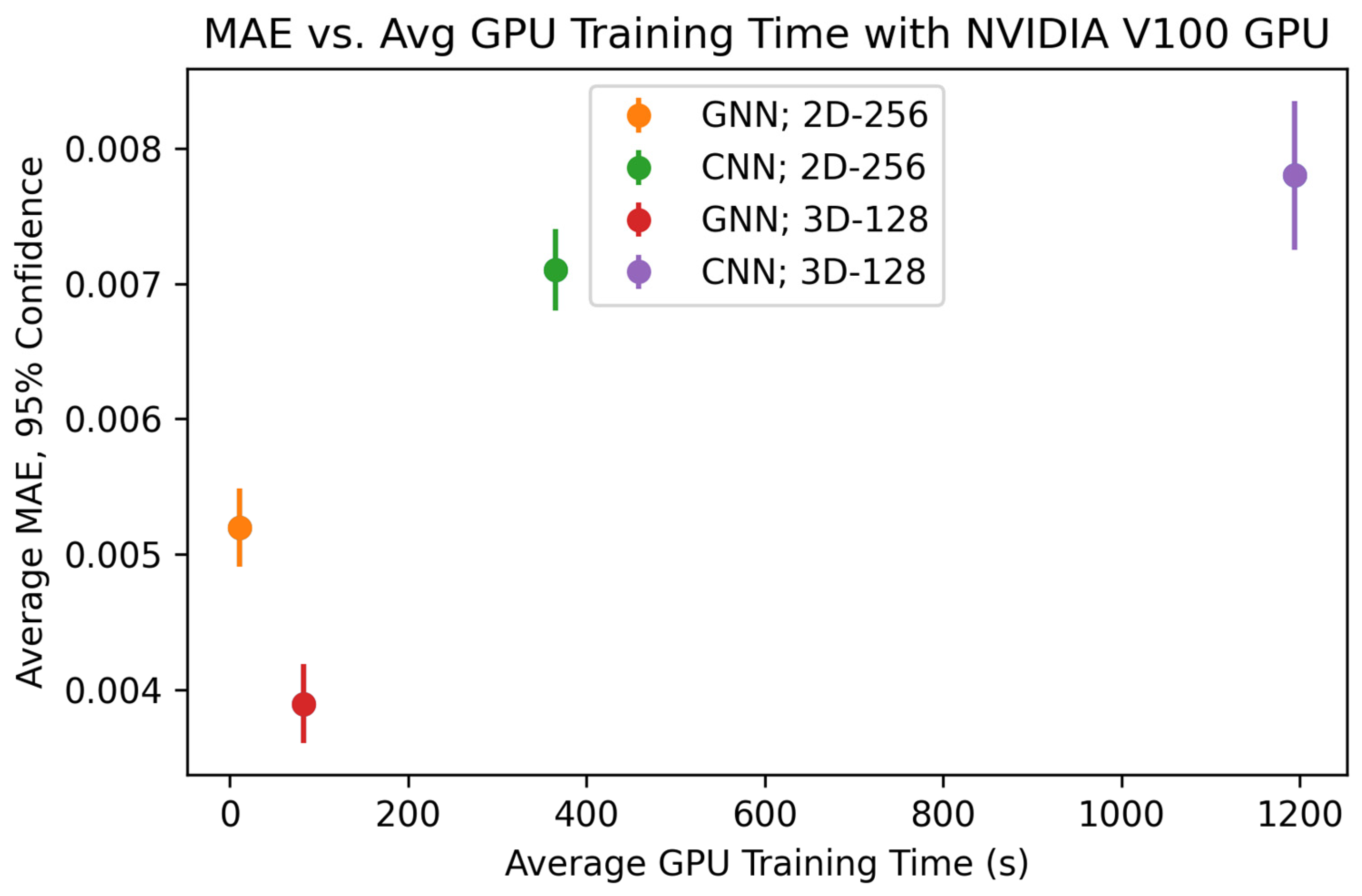
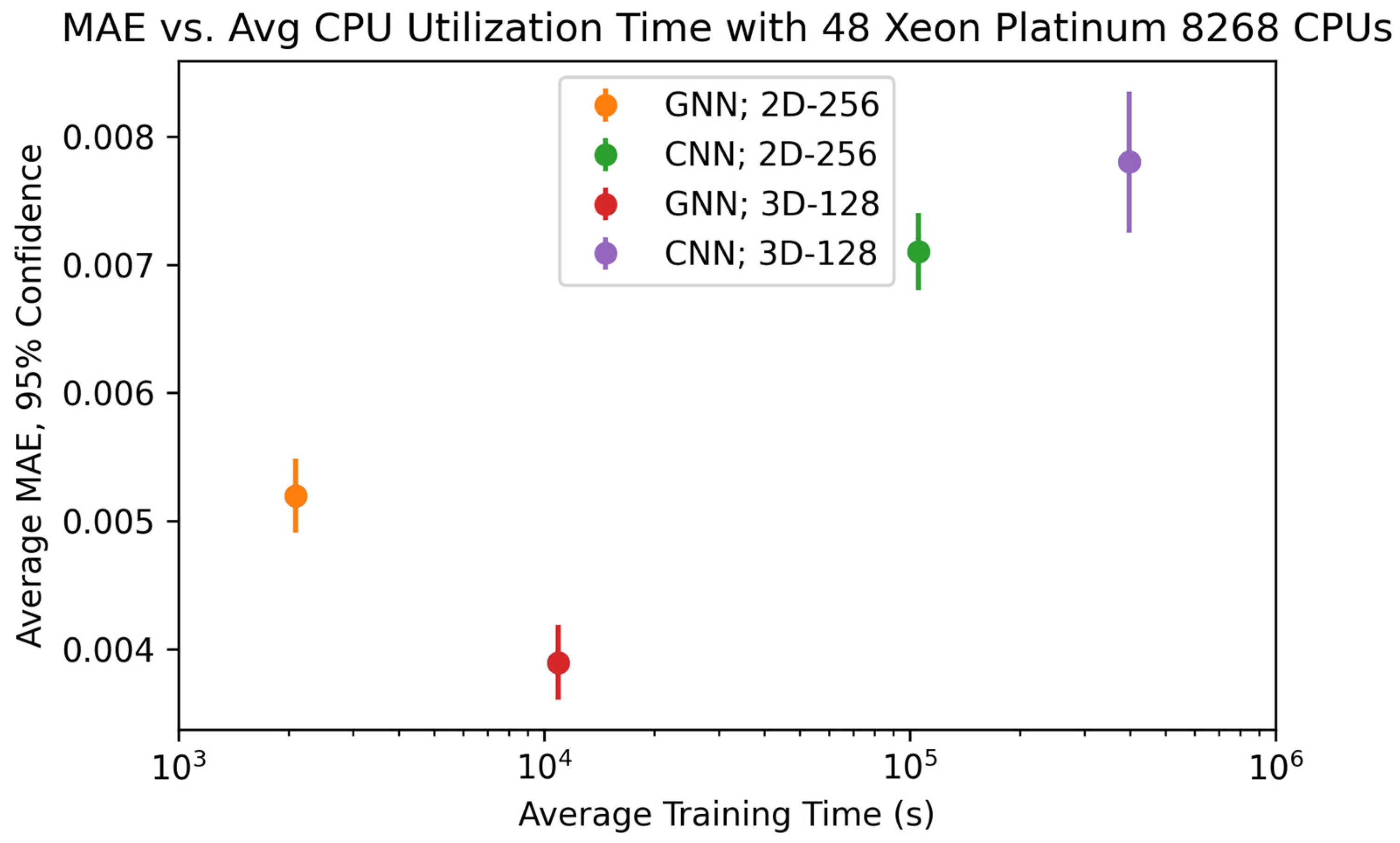
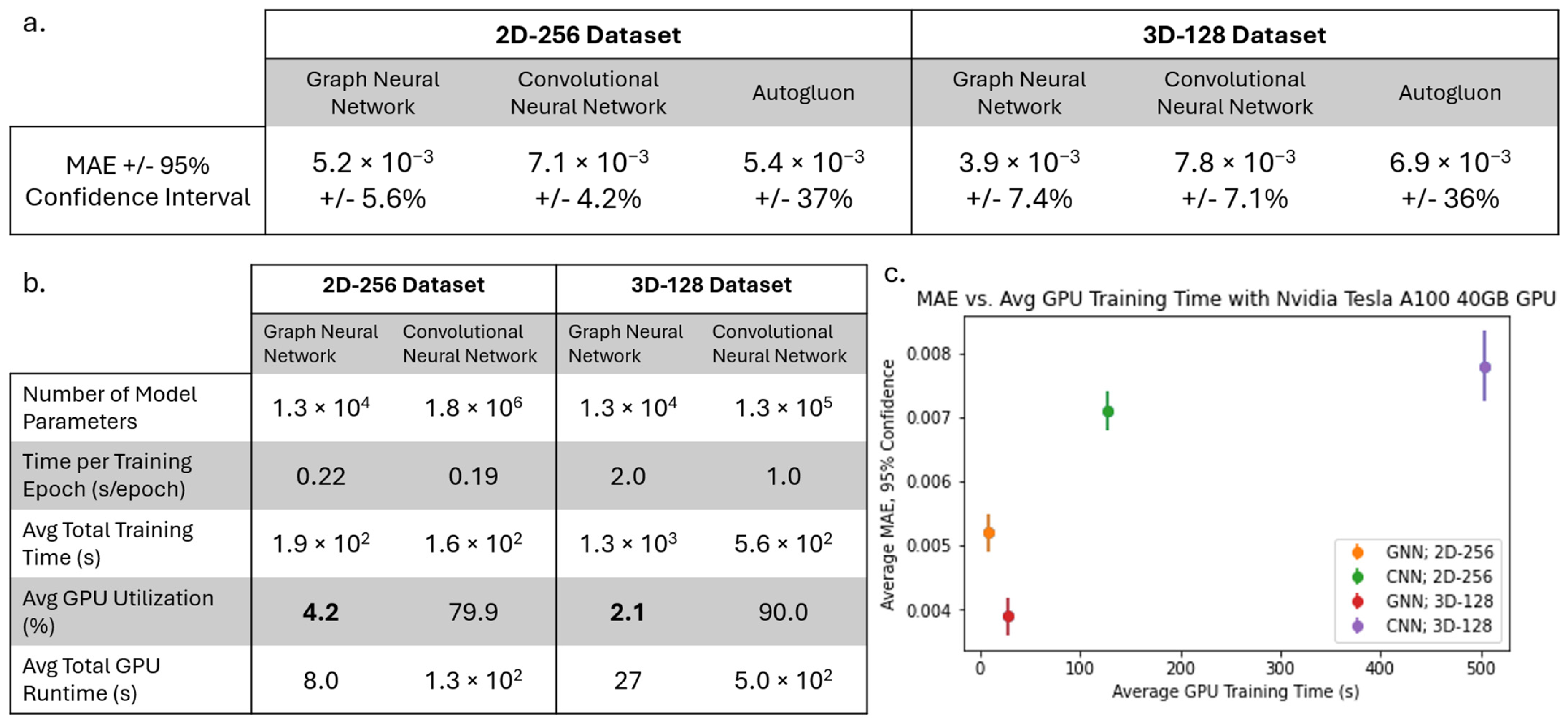
Later, we compared the performance of our GNN to other state-of-the-art ML tools to identify the types of applications for which GNNs are the most optimal ML tool choice. To determine the performance of the state-of-the-art ML tools, we first extract the average equivalent cube length, area fraction, and average extent from our 2D-256 and 3D-128 datasets and predict the strengthening using AutoGluon 1.4 [
30]. AutoGluon is a tool for training a variety of ML models on tabular data with minimal python code. In this study, we recorded the model used by Autogluon with the lowest test MAE as the baseline. We also trained a 2D and 3D CNN to predict strengthening with the images from 2D-256 and 3D-128 datasets, respectively. Each CNN uses 3 × 3 convolution kernels with stride 1 and ReLU activation, followed by max pooling layers of size 2. After the final convolution layer, the output is flattened and passed through dense layers. All models were trained until the MAE failed to improve for 150 consecutive epochs. We increased the complexity of the 3D CNN architecture until the memory of our Nvidia Tesla A100 40GB GPU was completely utilized during model training and/or testing. This ensures our GNN and CNN models have similar memory requirements. We determine the optimum CNN architecture based on the lowest error listed in
Table 2. All MAEs reported are the average minimum MAE of 25 total runs obtained by repeating 5-fold cross-validation 5 times.
Unlike CNNs where dimensionality is related to the number of pixels, the number of node features governs the dimensions of a GNN. Hence, in the case of GNN, we significantly reduce the dimensionality of the data when we construct graphs from images. Compared to GNN, the complexity of the data used with AutoGluon is further reduced as we only utilize extracted average equivalent cube length, area fraction, and average extent. Therefore, the comparison of the various models used in this study can also provide insight regarding how the dimensionality of the data can influence the error in the predictive models utilized.
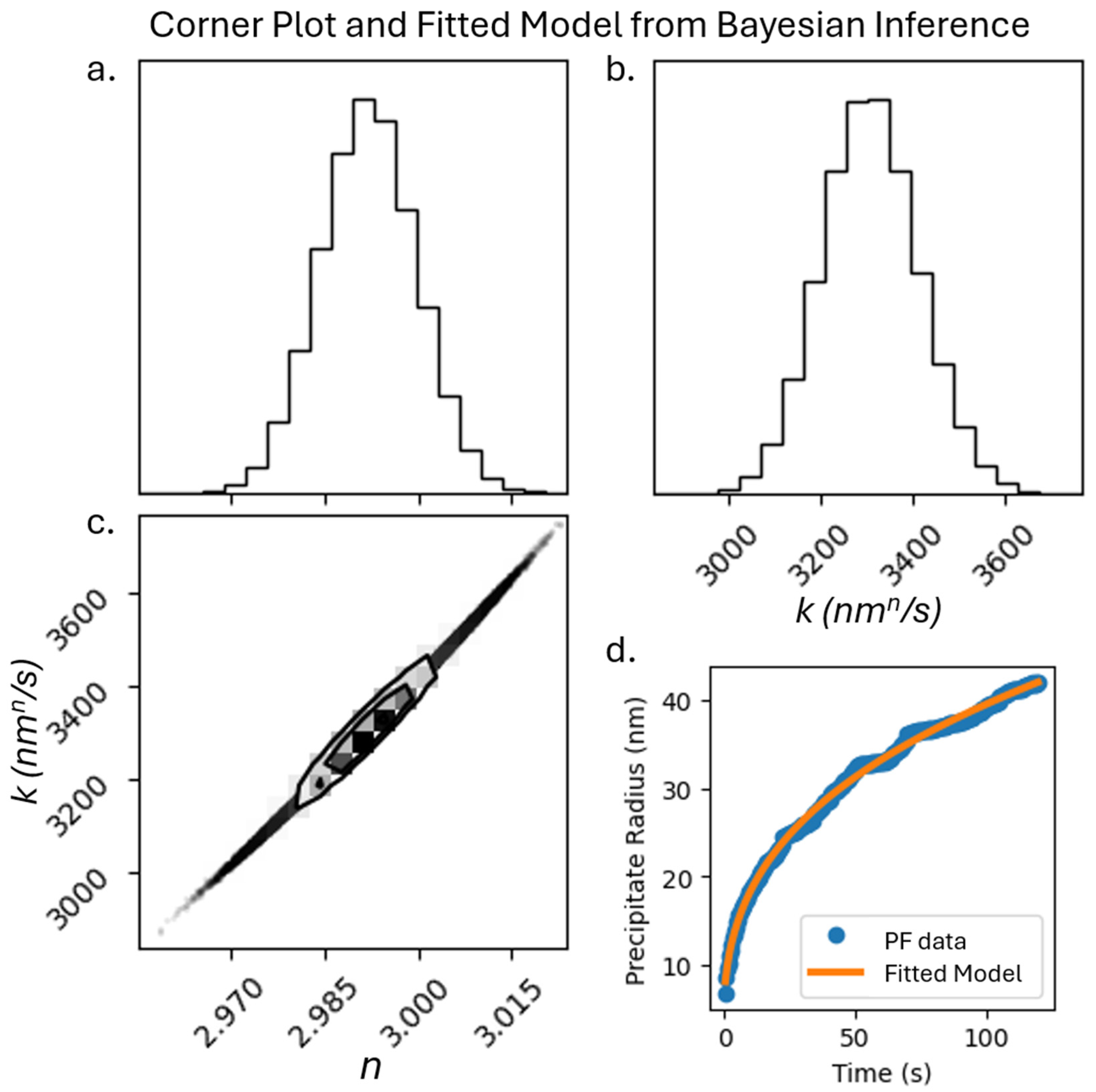
2.8. Bayesian Inference for Power Law Equation
The final component of this study will be to extract the coefficients of the power law equation governing precipitate growth during coarsening in alloys [
24]
where
is the equivalent cube length at time
,
is the equivalent cube length when coarsening starts,
is the coarsening rate constant, and
n~3. We utilize BI, which uses Bayes’ theorem to update prior distributions for given coefficients to find the most likely values of coefficients [
31]. Using BI, we determine the most likely values of
and
for a microstructure dataset generated from our phase field simulations. For this data, we use Ni-Al microstructures generated with the same phase field parameters as before but extend the real simulation time to 120 s and record the average equivalent cube length every 0.4 s.
4. Discussion
The results from this study have several promising implications in materials science. While recent studies apply GNNs to inherently graph-structured data such as atomic or molecular systems [
18,
33], our approach demonstrates that high-dimensional image-based microstructures can be effectively converted into graphs and that GNNs can still achieve high prediction accuracy on these derived graph representations. Additionally, we show the importance of node features to predict strengthening, which was confirmed by parameters in a typically used strengthening equation. Feature importance was also applied to find the importance of the individual precipitates and the edges between them. While no clear trend is observed for the case of individual precipitates and the edges between them, it is possible to use the same tool with other microstructure graph datasets to determine the features, nodes, and interactions between nodes that govern the prediction of material properties. For example, in grain growth [
34], the evolution of grains depends on nearby features, like neighboring grains or different types of grain boundaries. Other machine learning tools including physics-regularized interpretable machine learning microstructure evolution (PRIMME) [
35], as well as using feature importance with a CNN, can provide heat maps showing the importance of pixels within microstructures. However, using feature importance with a GNN can provide more specific importance scores of microstructure components (graph nodes), their features, and the interactions between components (graph edges). Another promising method is to embed physics components in the graph structure, like energy components and stress fields, which may help provide more scientific insights using explainable artificial intelligence methods. Therefore, usage of feature importance with GNNs has potential to increase our understanding of the underlying physics principles governing the properties and evolution of microstructures.
Another observation we made in this study was the difference in computational resources during training, which is a function of the complexity of the GNN compared to the CNN as well as the efficiency of each model on a GPU. Because the Ni-Al microstructures had very simple precipitates, there was a relatively small amount of data needed to fully describe each microstructure with a graph. Because of this, the optimized GNN architecture only had 12,961 trainable parameters, a fraction of the parameters needed in the 2D and 3D CNNs. However, for a more complicated microstructure with several microstructural features (grains, precipitates, domains, etc.), we expect that both the complexity of the graph and the GNN will increase. This may lead the computational requirements of the GNN to approach and possibly surpass that of the image data and CNN. Conversely, for even simpler microstructures compared to the microstructures presented in the work, we expect the graph to be less complex. This idea can be further studied to understand the degree to which GNN and graph complexity is dependent on microstructure complexity and can be a major factor in determining whether GNN is the best option for a given microstructure-based property prediction.
The final benefit of using the GNN with microstructure data is the ability to extrapolate the dimensions and sizes of the microstructures used to construct the graph dataset. This shows that a single GNN model can learn the necessary physics for predicting the strengthening, regardless of the size or dimension of the microstructure the graph is trained on. This suggests that GNNs can be a more efficient and generalizable material characterization tool or surrogate model for physics simulations, whereas other deep-learning-based models are restricted to predictions that have only a single dimension and size [
5]. Therefore, while it can take days to months to generate large 3D microstructures with PF, and then additional days to train a DL model on the data, a GNN can be trained in much less time on data generated in a fraction of the time (e.g., smaller size in 2D) and can make predictions for any other dimension or size. Additionally, the phase field generated microstructures used in this study were previously validated with TEM dark-field electron micrographs at various times during evolution by comparing the same morphological patterns in both simulation and experiment [
4,
24]. Based on this validation of the data used in this study, we expect a similar GNN can be trained on experimental micrographs if the dataset is of similar quantity and quality. These benefits of GNN can significantly expedite the material design and optimization process, allowing for rapid exploration of the microstructure–property relationship in materials.