Research on the Macroscopic Mechanical Property Continuum of Square Lattices Composed of Piezoelectric Laminated Zigzag Beams
Abstract
1. Introduction
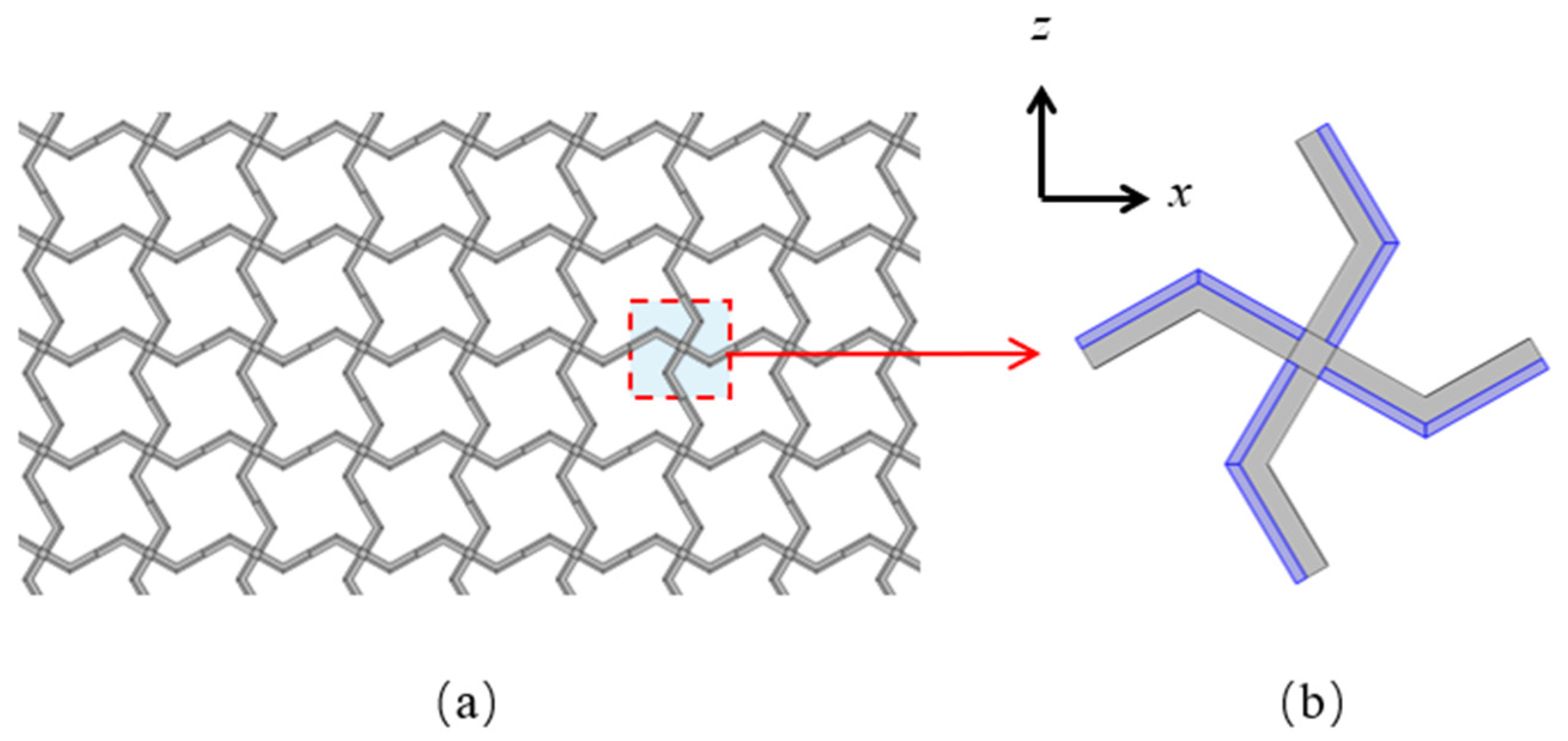
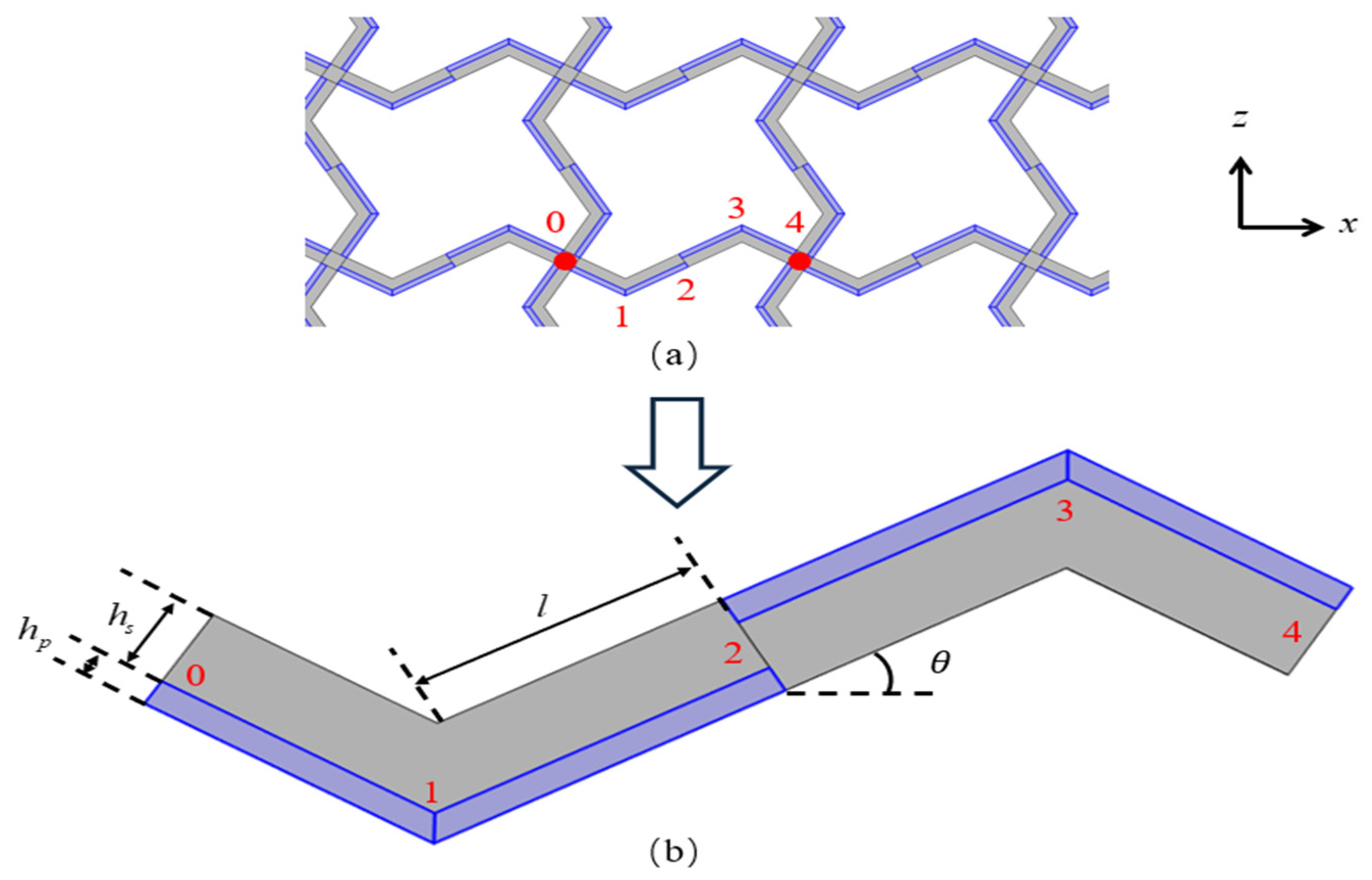
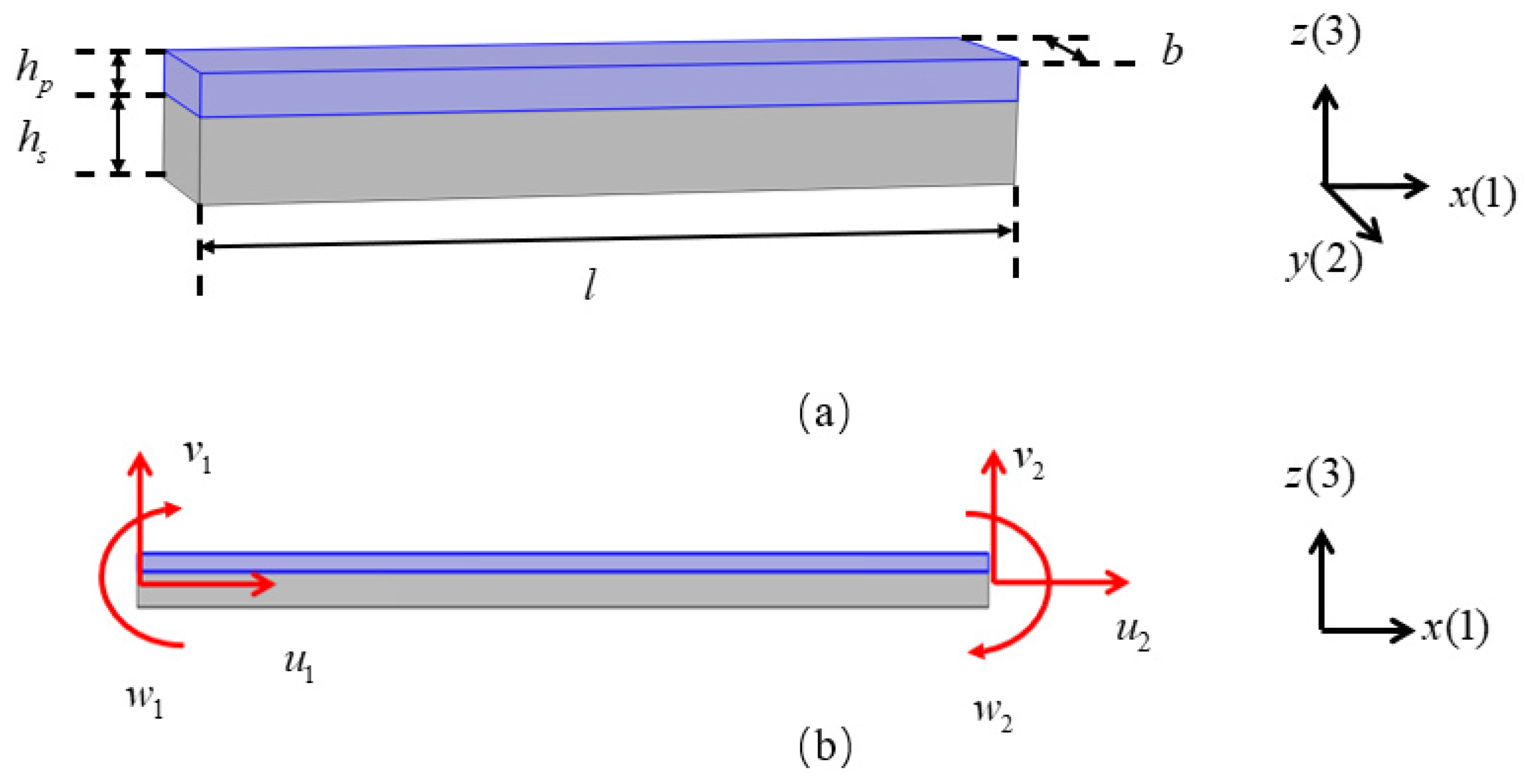
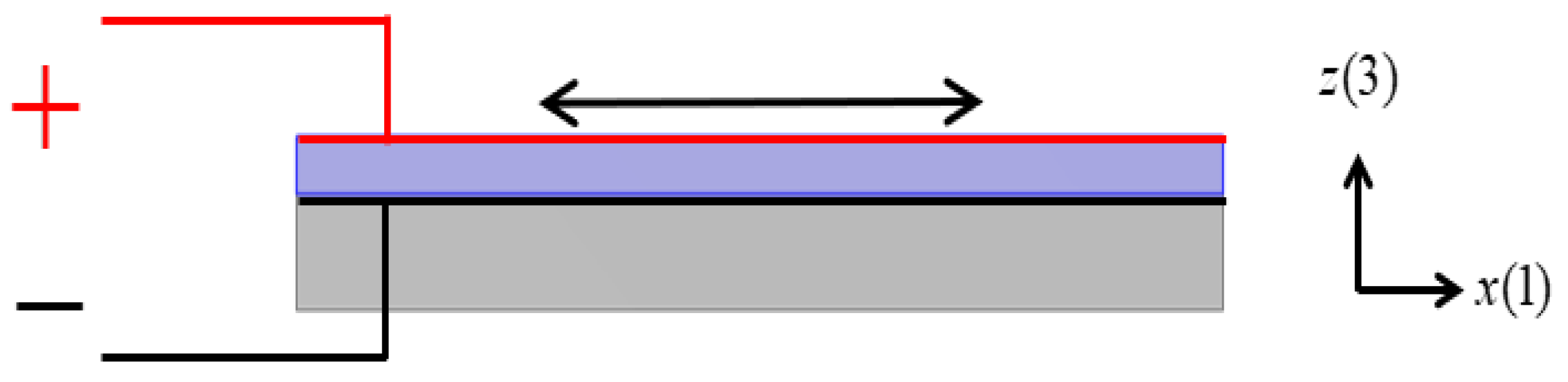
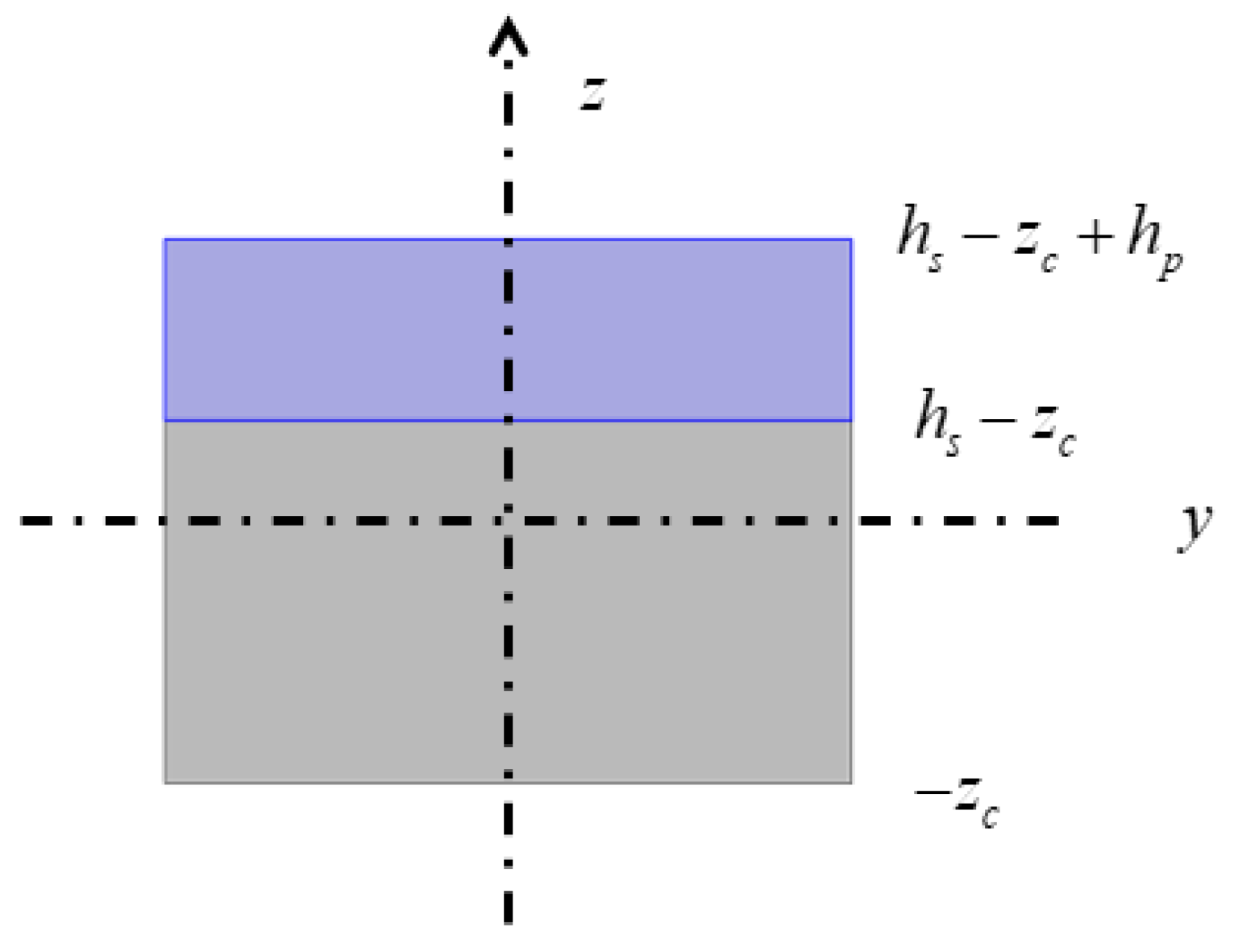
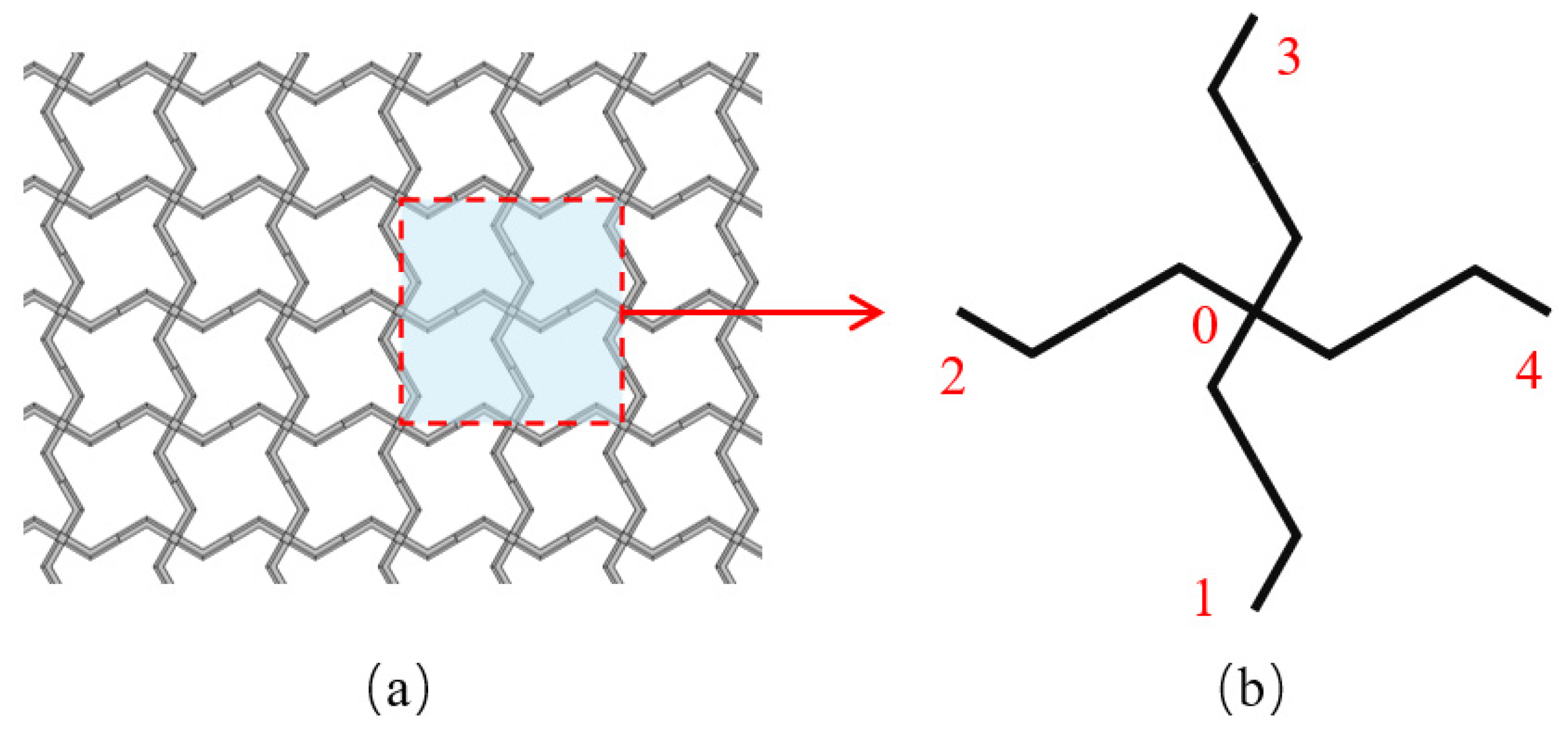
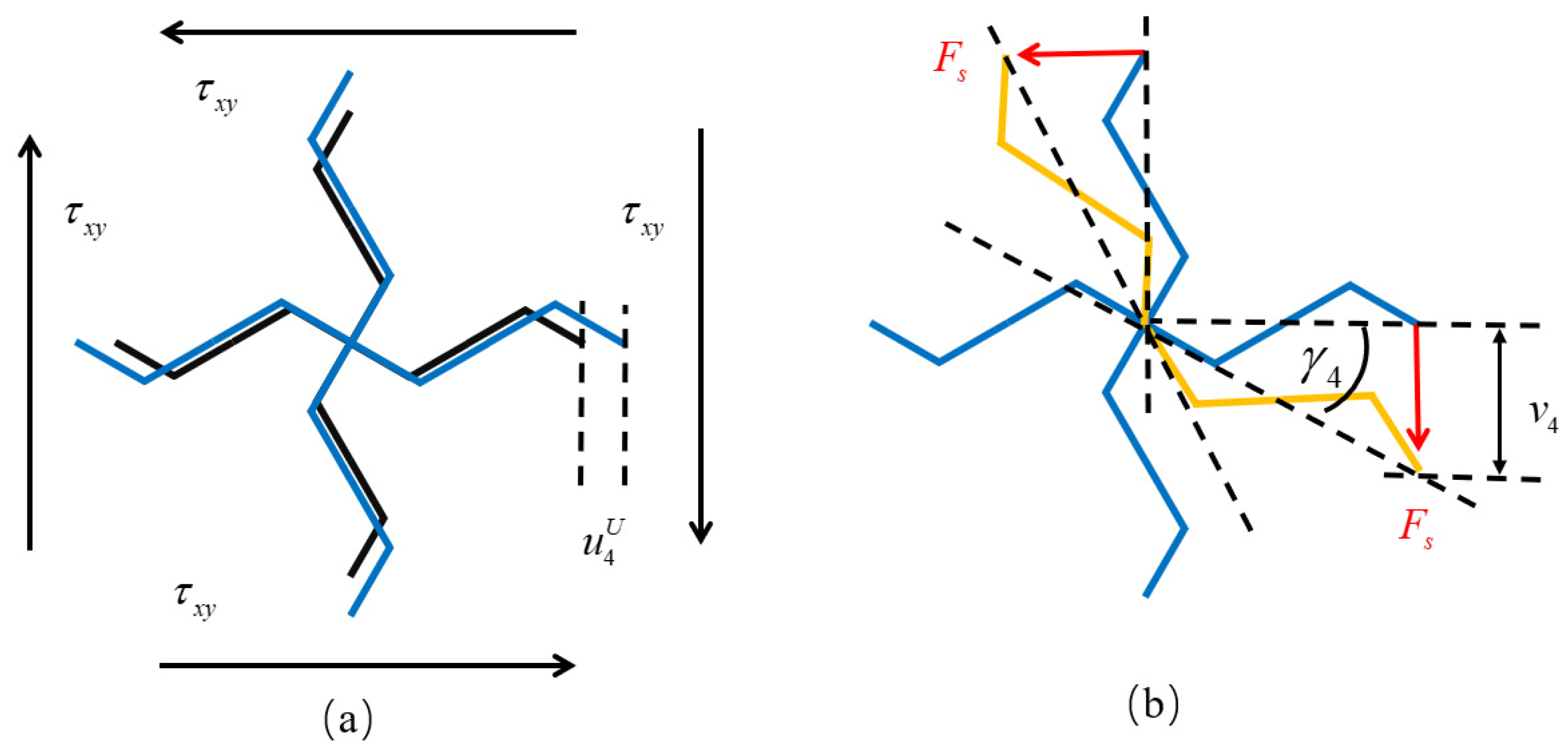
2. Square Lattices Composed of Piezoelectric Laminated Zigzag Beams
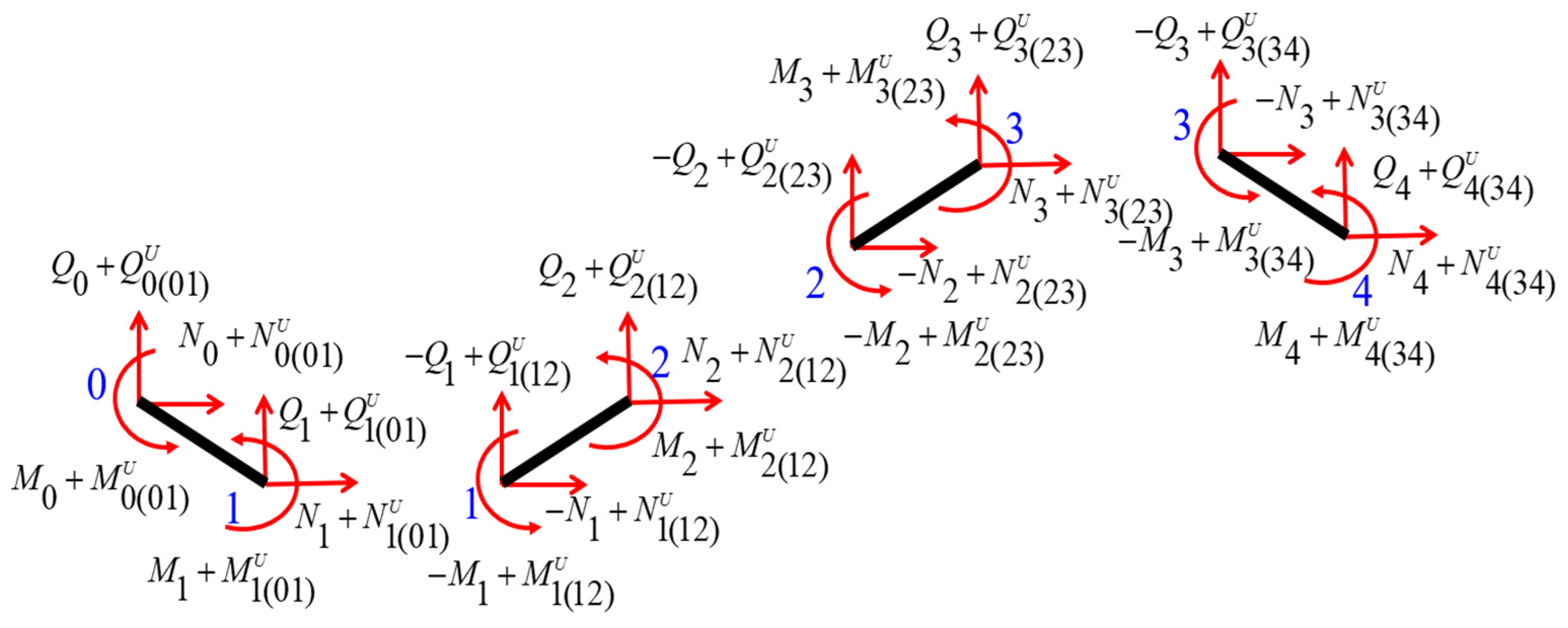
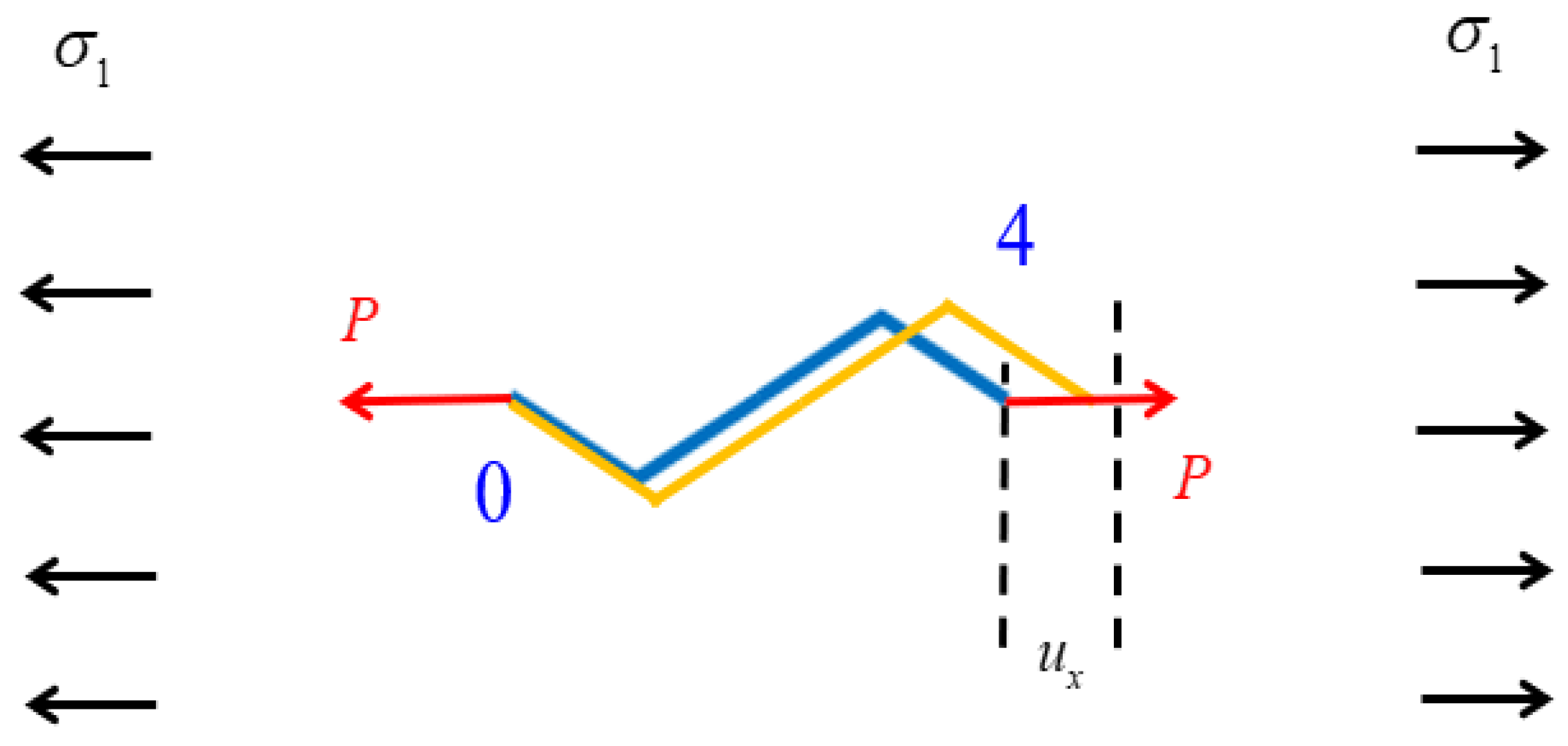
3. Macroscopic Mechanical Properties of the Lattices
3.1. Young’s Modulus
3.2. Poisson’s Ratio
3.3. Shear Modulus
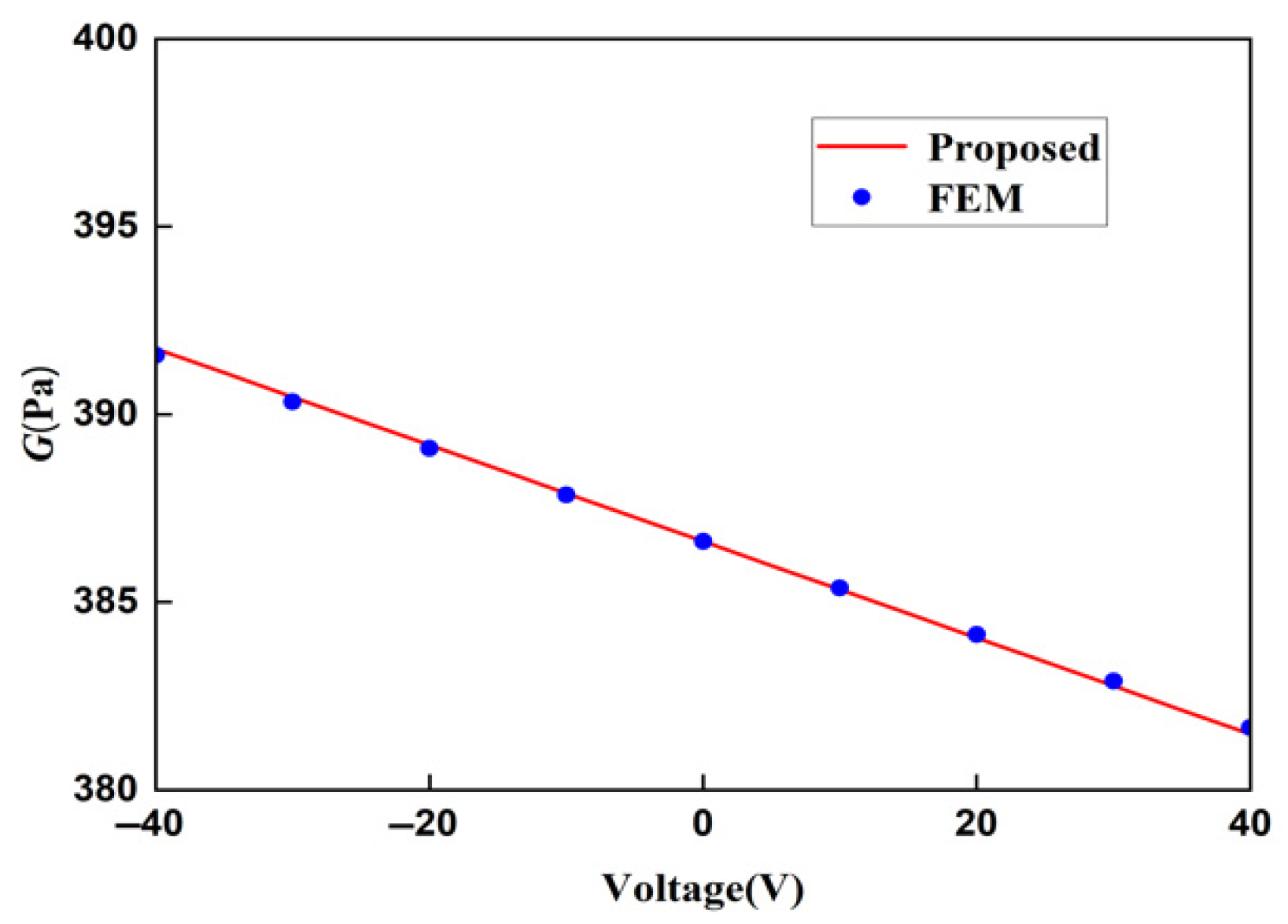
4. Comparative Verification of the Finite Element Method
5. Numerical Results and Analyses
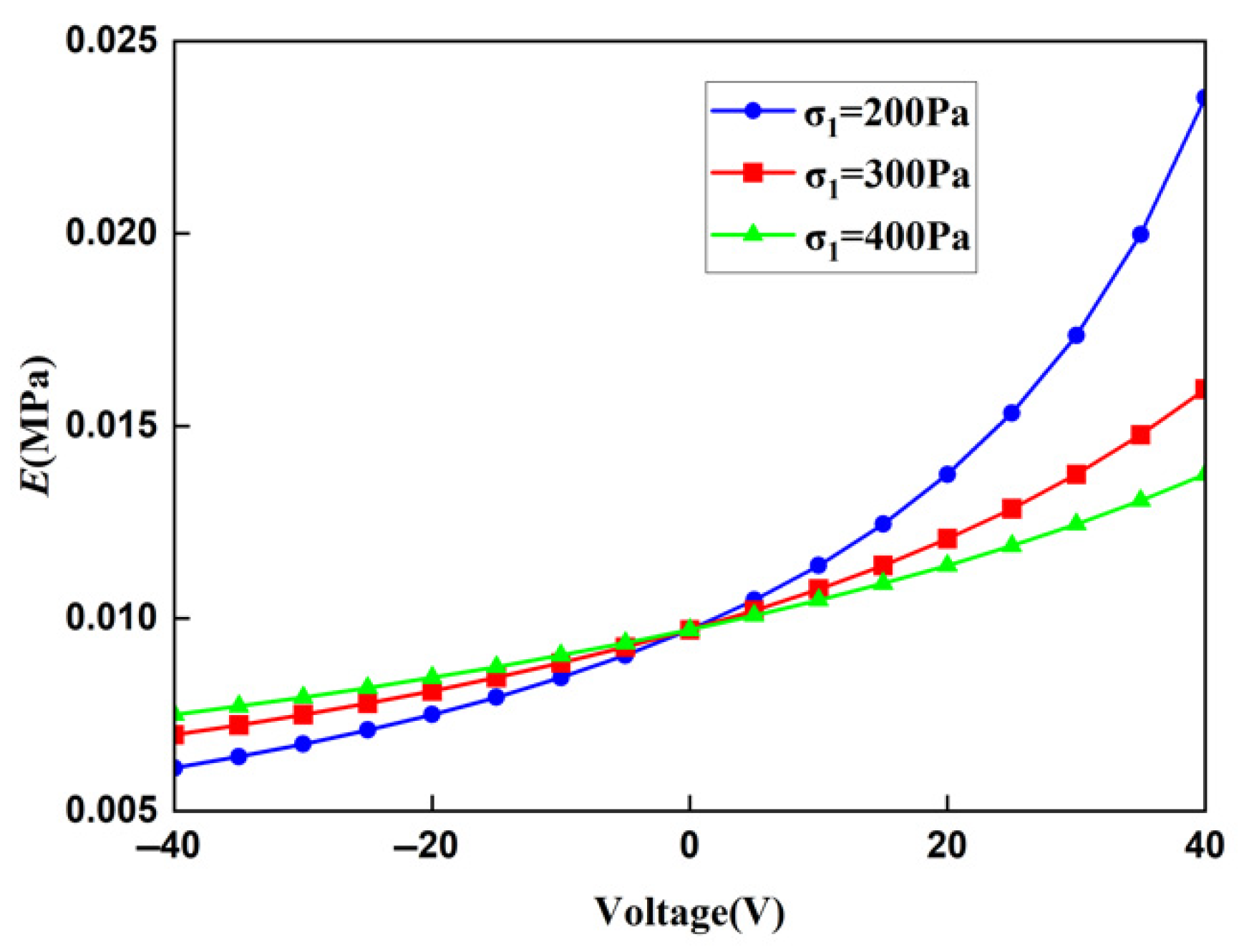
5.1. Young’s Modulus
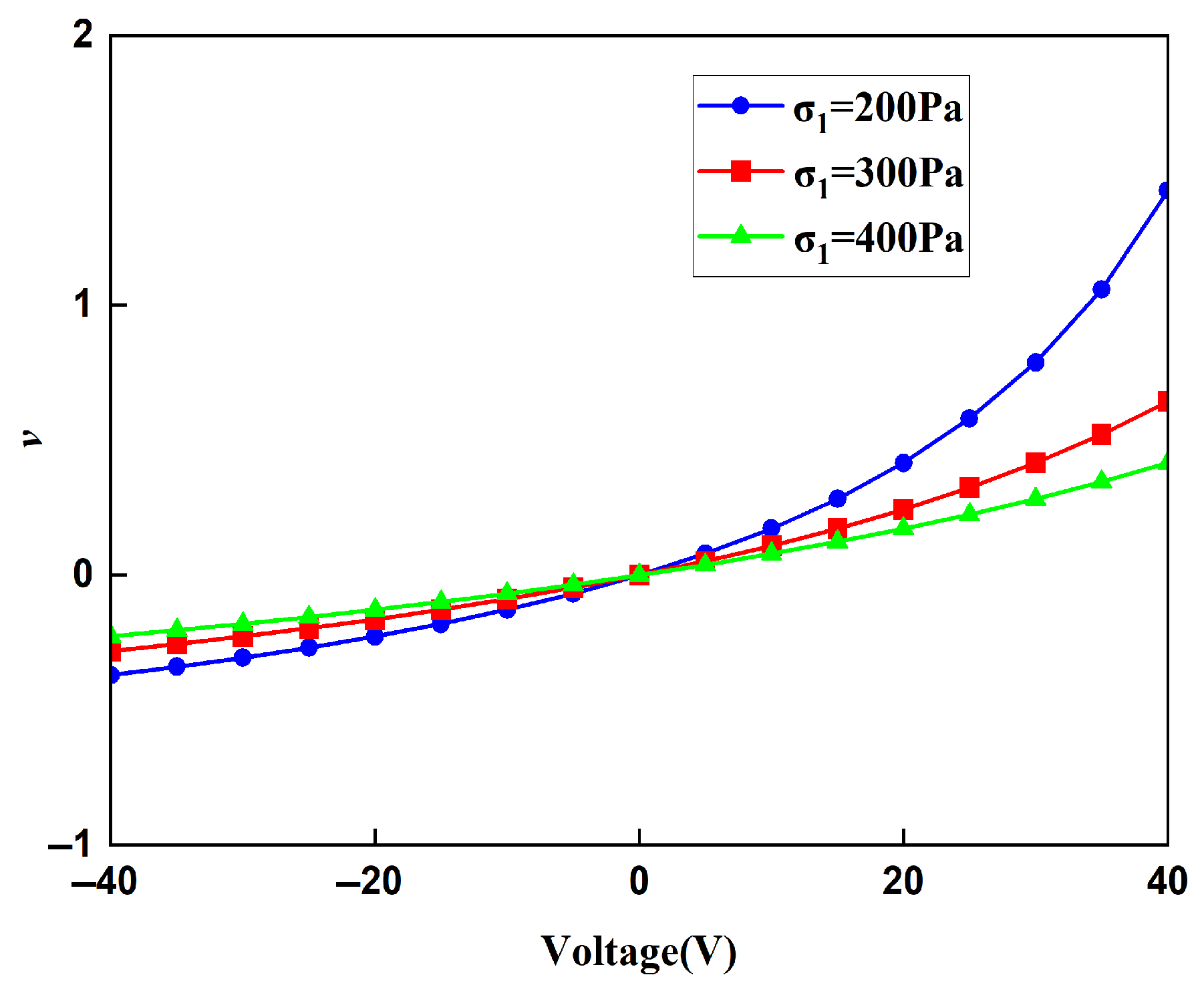
5.2. Poisson’s Ratio
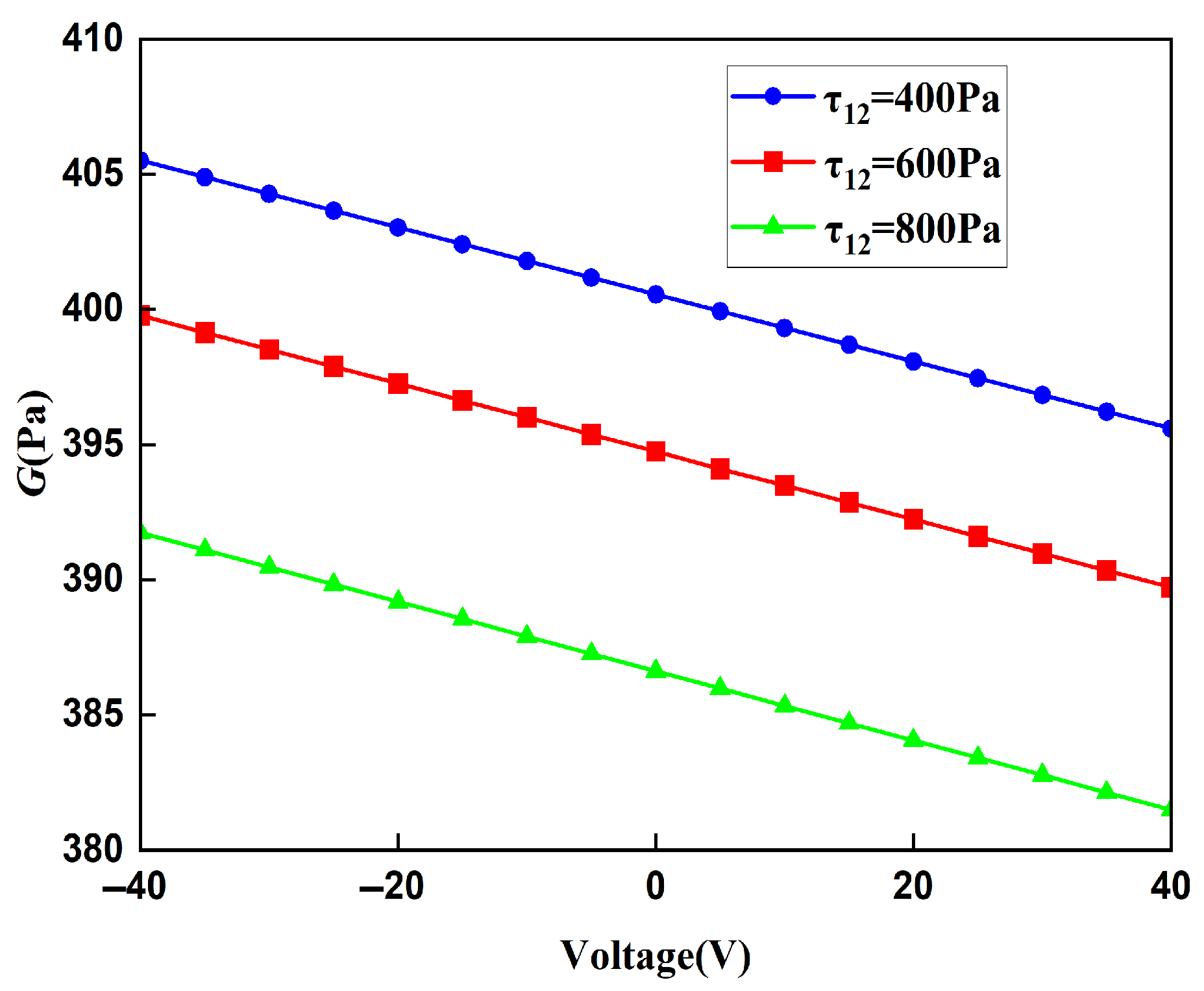
5.3. Shear Modulus
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Uspekhi 1968, 92, 517–526. [Google Scholar] [CrossRef]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef]
- Tancogne Dejean, T.; Spierings, A.B.; Mohr, D. Additively-manufactured metallic micro-lattice materials for high specific energy absorption under static and dynamic loading. Acta Mater. 2016, 116, 14–28. [Google Scholar] [CrossRef]
- Jin, Q.Y.; Yu, J.H.; Ha, K.S.; Lee, W.J.; Park, S.H. Multi-dimensional lattices design for ultrahigh specific strength metallic structure in additive manufacturing. Mater. Sci. Eng. 2021, 201, 109479. [Google Scholar]
- Li, T.T.; Jarrar, F.; Al Rub, R.A.; Cantwell, W. Additive manufactured semi-plate lattice materials with high stiffness, strength and toughness. Int. J. Solids 2021, 230, 111153. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Li, T.T.; Scarpa, F.; Wang, L.F. Lattice metamaterials with mechanically tunable Poisson’s ratio for vibration control. Phys. Rev. Appl. 2017, 7, 024012. [Google Scholar] [CrossRef]
- Liu, J.; Nie, Y.H.; Tong, H.; Xu, N. Realizing negative Poisson’s ratio in spring networks with close-packed lattice geometries. Phys. Rev. Mater. 2019, 3, 055607. [Google Scholar] [CrossRef]
- Hewage, T.A.M.; Alderson, K.L.; Alderson, A.; Scarpa, F. Double-negative mechanical metamaterials displaying simultaneous negative stiffness and negative Poisson’s ratio properties. Adv. Mater. 2016, 28, 10323–10332. [Google Scholar] [CrossRef]
- Adhikari, S.; Mukhopadhyay, T.; Shaw, A.; Lavery, N.P. Apparent negative values of Young’s moduli of lattice materials under dynamic conditions. Int. J. Eng. Sci. 2020, 150, 103231. [Google Scholar] [CrossRef]
- Fang, Z.Z.; Song, H.J.; Zhang, Y.; Jin, B.J.; Wu, J.J.; Zhao, Q.; Xie, T. Modular 4D Printing via Interfacial Welding of Digital Light-Controllable Dynamic Covalent Polymer Networks. Matter 2020, 2, 1187–1197. [Google Scholar] [CrossRef]
- Tao, R.; Ji, L.T.; Li, Y.; Wan, Z.S.; Hu, W.X.; Wu, W.W.; Liao, B.B.; Ma, L.H.; Fang, D.N. 4D printed origami metamaterials with tunable compression twist behavior and stress-strain curves. Compos. Part B Eng. 2020, 201, 108344. [Google Scholar] [CrossRef]
- Messner, M.C. Optimal lattice-structured materials. J. Mech. Phys. Solids 2016, 96, 162–183. [Google Scholar] [CrossRef]
- Wang, F.W. Systematic design of 3D auxetic lattice materials with programmable Poisson’s ratio for finite strains. J. Mech. Phys. Solids 2018, 114, 303–318. [Google Scholar] [CrossRef]
- Chen, D.; Zheng, X.Y. Multi-material additive manufacturing of metamaterials with giant, tailorable negative Poisson’s ratios. Sci. Rep. 2018, 8, 9139. [Google Scholar] [CrossRef]
- Kazemi, H.; Vaziri, A.; Norato, J.A. Multi-material topology optimization of lattice structures using geometry projection. Comput. Methods Appl. Mech. Eng. 2020, 363, 112895. [Google Scholar] [CrossRef]
- Prajapati, M.J.; Kumar, A.; Lin, S.C.; Jeng, J.Y. Multi-material additive manufacturing with lightweight closed-cell foam-filled lattice structures for enhanced mechanical and functional properties. Addit. Manuf. 2022, 54, 102766. [Google Scholar] [CrossRef]
- Liu, J.X.; Deng, S.C.; Zhang, J.; Liang, N.G. Lattice type of fracture model for concrete. Theor. Appl. Fract. Mech. 2007, 48, 269–284. [Google Scholar] [CrossRef]
- Chi, Z.Y.; Liu, J.X.; Soh, A.K. Micropolar modeling of a typical bending-dominant lattice comprising zigzag beams. Mech. Mater. 2021, 160, 103922. [Google Scholar] [CrossRef]
- Gasparetto, V.E.; ElSayed, M.S. Shape transformers for phononic band gaps tuning in two-dimensional Bloch-periodic lattice structures. Eur. J. Mech. -A/Solids 2021, 89, 104278. [Google Scholar] [CrossRef]
- An, X.Y.; Yuan, X.F.; Fan, H.L. Meta-Kagome lattice structures for broadband vibration isolation. Eng. Struct. 2023, 277, 115403. [Google Scholar] [CrossRef]
- Frenzel, T.; Kadic, M.; Wegener, M. Three-dimensional mechanical metamaterials with a twist. Science 2017, 358, 1072–1074. [Google Scholar] [CrossRef]
- Duan, S.; Wen, W.; Fang, D. A predictive micropolar continuum model for a novel three-dimensional chiral lattice with size effect and tension-twist coupling behavior. J. Mech. Phys. Solids 2018, 121, 23–46. [Google Scholar] [CrossRef]
- Meng, L.; Shi, J.; Yang, C.; Gao, T.; Hou, Y.; Song, L.; Gu, D.; Zhu, J.; Breitkopf, P.; Zhang, W. An emerging class of hyperbolic lattice exhibiting tunable elastic properties and impact absorption through chiral twisting. Extrem. Mech. Lett. 2020, 40, 100869. [Google Scholar] [CrossRef]
- Wu, Z.J.; Li, F.M.; Zhang, C.Z. Vibration properties of piezoelectric square lattice structures. Mech. Res. Commun. 2014, 62, 123–131. [Google Scholar] [CrossRef]
- Fey, T.; Eichhorn, F.; Han, G.F.; Ebert, K.; Wegener, M.; Roosen, A.; Kakimoto, K.-i.; Greil, P.J. Mechanical and electrical strain response of a piezoelectric auxetic PZT lattice structure. Smart Mater. Struct. 2015, 25, 015017. [Google Scholar] [CrossRef]
- Toledo, R.; Eisenträger, S.; Orszulik, R. Finite element analysis of thermopiezoelectric bimorph actuators considering temperature-dependent piezoelectric strain coefficients. Acta Mech. 2024, 235, 7199–7222. [Google Scholar] [CrossRef]
- Cevallos, F.A.; Stolze, K.; Kong, T.; Cava, R. Anisotropic magnetic properties of the triangular plane lattice material TmMgGaO4. Mater. Res. Bull. 2018, 105, 154–158. [Google Scholar] [CrossRef]
- Ye, H.L.; Li, Y.; Zhang, T. Magttice: A lattice model for hard-magnetic soft materials. Soft Matter 2021, 17, 3560–3568. [Google Scholar] [CrossRef]
- Singh, A.; Mukhopadhyay, T.; Adhikari, S.; Bhattacharya, B. Extreme on-demand contactless modulation of elastic properties in magnetostrictive lattices. Smart Mater. Struct. 2022, 31, 125005. [Google Scholar] [CrossRef]
- Du Pasquier, C.; Shea, K. Actuator placement optimization in an active lattice structure using generalized pattern search and verification. Smart Mater. Struct. 2021, 30, 115007. [Google Scholar] [CrossRef]
- Du Pasquier, C.; Shea, K. A nonlinear optimization method for large shape morphing in 3D printed pneumatic lattice structures. Smart Mater. Struct. 2022, 31, 065016. [Google Scholar] [CrossRef]
- Guo, J.M.; Zhang, Z.X.; Wang, C.G. Vibrational frequencies and modes of a kinked inflatable beam. Thin-Walled Struct. 2022, 179, 109628. [Google Scholar] [CrossRef]
- Sinha, P.; Mukhopadhyay, T. Pneumatic elastostatics of multi-functional inflatable lattices: Realization of extreme specific stiffness with active modulation and deployability. R. Soc. Open Sci. 2024, 11, 231272. [Google Scholar] [CrossRef]
- Singh, A.; Mukhopadhyay, T.; Adhikari, S.; Bhattacharya, B. Voltage-dependent modulation of elastic moduli in lattice metamaterials: Emergence of a programmable state-transition capability. Int. J. Solids Struct. 2021, 208, 31–48. [Google Scholar] [CrossRef]
- Wang, P.H.; Liu, H.T. Voltage-dependent modulation of effective young’s modulus and shape in piezoelectric composite metamaterials. Compos. Struct. 2023, 306, 116583. [Google Scholar] [CrossRef]
- Singh, A.; Mukhopadhyay, T.; Adhikari, S.; Bhattacharya, B. Active multi-physical modulation of Poisson’s ratios in composite piezoelectric lattices: On-demand sign reversal. Compos. Struct. 2022, 280, 114857. [Google Scholar] [CrossRef]
- Liu, H.T.; Wang, P.H.; Wu, W.J.; Li, J.Q. 3D piezoelectric composite honeycombs with alternating bi-material beam: An active control method for elastic properties. Mater. Today Commun. 2024, 38, 108191. [Google Scholar] [CrossRef]
- Chen, N.; Tian, C. Design, modeling and testing of a 3-DOF flexible piezoelectric thin sheet nanopositioner. Sens. Actuators A Phys. 2021, 323, 112660. [Google Scholar] [CrossRef]
- Sun, Y.; Han, Q.; Jiang, T.J.; Li, C.L. Coupled bandgap properties and wave attenuation in the piezoelectric metamaterial beam on periodic elastic foundation. Appl. Math. Model. 2024, 125, 293–310. [Google Scholar] [CrossRef]
- Fu, M.H.; Chen, Y.; Hu, L.L. Bilinear elastic characteristic of enhanced auxetic honeycombs. Compos. Struct. 2017, 175, 101–110. [Google Scholar] [CrossRef]
- Li, X.; Lu, Z.X.; Yang, Z.Y.; Wang, Q.S.; Zhang, Y. Yield surfaces of periodic honeycombs with tunable Poisson’s ratio. Int. J. Mech. Sci. 2018, 141, 290–302. [Google Scholar] [CrossRef]
- Qi, C.; Jiang, F.; Yang, S. Advanced honeycomb designs for improving mechanical properties: A review. Compos. Part B Eng. 2021, 227, 109393. [Google Scholar] [CrossRef]
- Gad, A.I.; Gao, X.L.; Li, K. A strain energy-based homogenization method for 2-D and 3-D cellular materials using the micropolar elasticity theory. Compos. Struct. 2021, 265, 113594. [Google Scholar] [CrossRef]
- Eringen, A.C. Linear theory of micropolar elasticity. J. Math. Mech. 1966, 15, 909–923. [Google Scholar]
- Yuan, X.; Tomita, Y.; Andou, T. A micromechanical approach of nonlocal modeling for media with periodic microstructures. Mech. Res. Commun. 2008, 35, 126–133. [Google Scholar] [CrossRef]
- Laganà, F.; Pellicanò, D.; Arruzzo, M.; Pratticò, D.; Pullano, S.A.; Fiorillo, A.S. FEM-Based Modelling and AI-Enhanced Monitoring System for Upper Limb Rehabilitation. Electronics 2025, 14, 2268. [Google Scholar] [CrossRef]
- Pratticò, D.; Laganà, F.; Oliva, G.; Fiorillo, A.S.; Pullano, S.A.; Calcagno, S.; De Carlo, D.; La Foresta, F. Integration of LSTM and U-Net Models for Monitoring Electrical Absorption With a System of Sensors and Electronic Circuits. IEEE Trans. Instrum. Meas. 2025, 74, 3573363. [Google Scholar] [CrossRef]
- Alper, E.; Daniel, J.I. Piezoelectric Energy Harvesting; John Wiley & Sons Ltd.: New York, NY, USA, 2011; pp. 151–197. [Google Scholar]
- Dieter, S.; Alan, P.; Tom, D. Self-expanding nitinol stents: Material and design considerations. Eur. Radiol. 2004, 14, 292–301. [Google Scholar]
- Lin, C.; Lv, J.X.; Li, Y.S.; Zhang, F.H.; Li, J.R.; Liu, Y.J.; Liu, L.W.; Leng, J.S. 4D-Printed Biodegradable and Remotely Controllable Shape Memory Occlusion Devices. Adv. Funct. Mater. 2019, 29, 1906569. [Google Scholar] [CrossRef]
- Gong, Y.H.; Liu, J.X.; Liang, N.G. On effective moduli of defective beam lattices via the lattice green’s functions. Int. J. Damage Mech. 2025, 34, 1182–1214. [Google Scholar] [CrossRef]


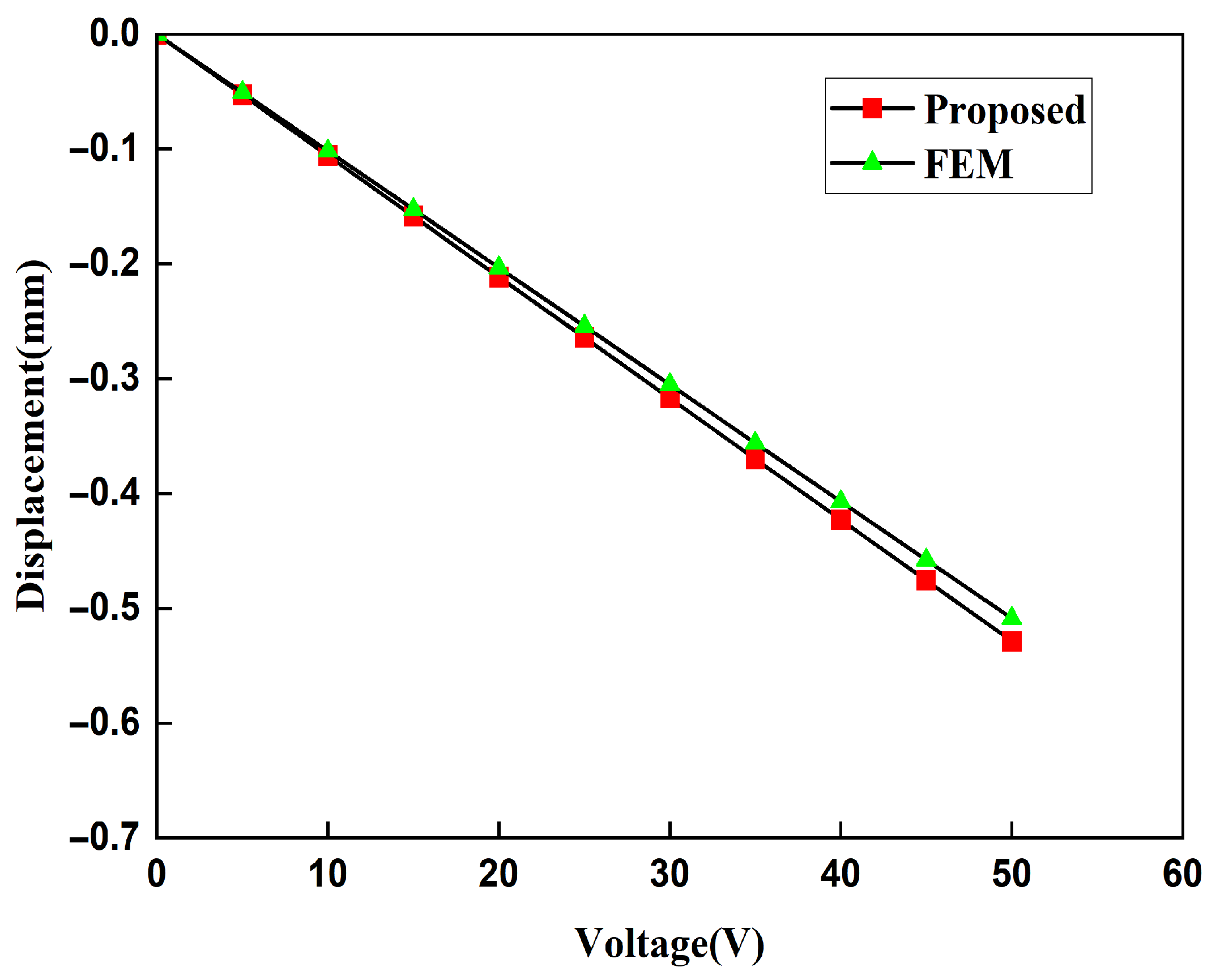
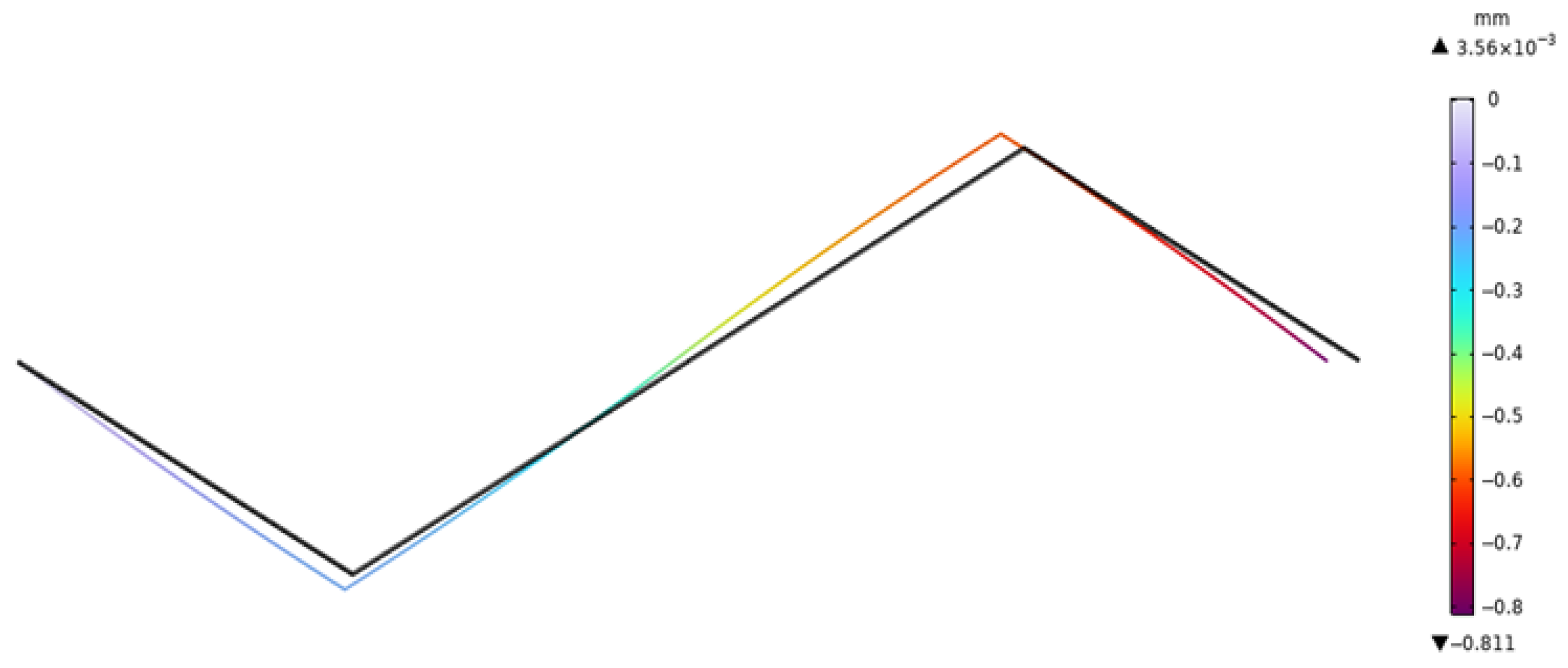
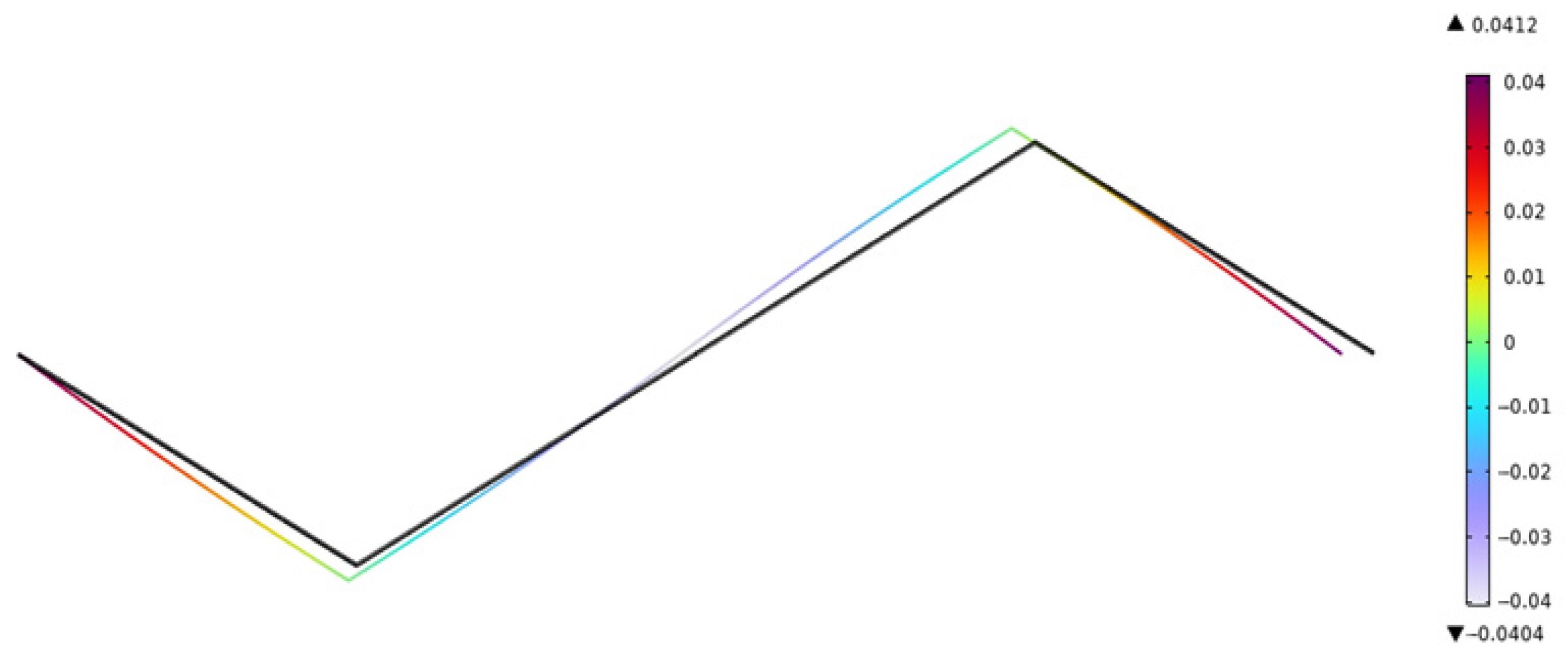
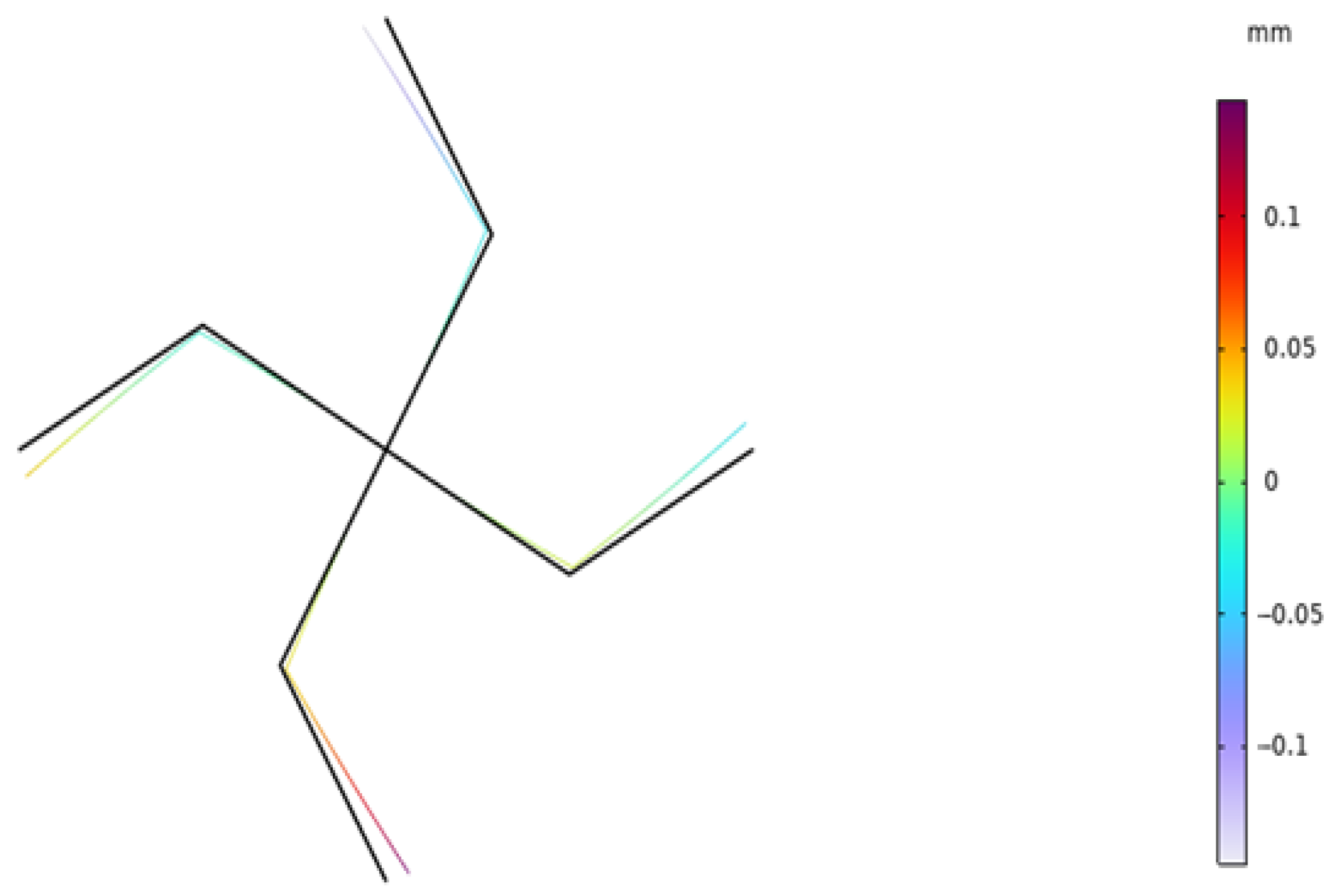

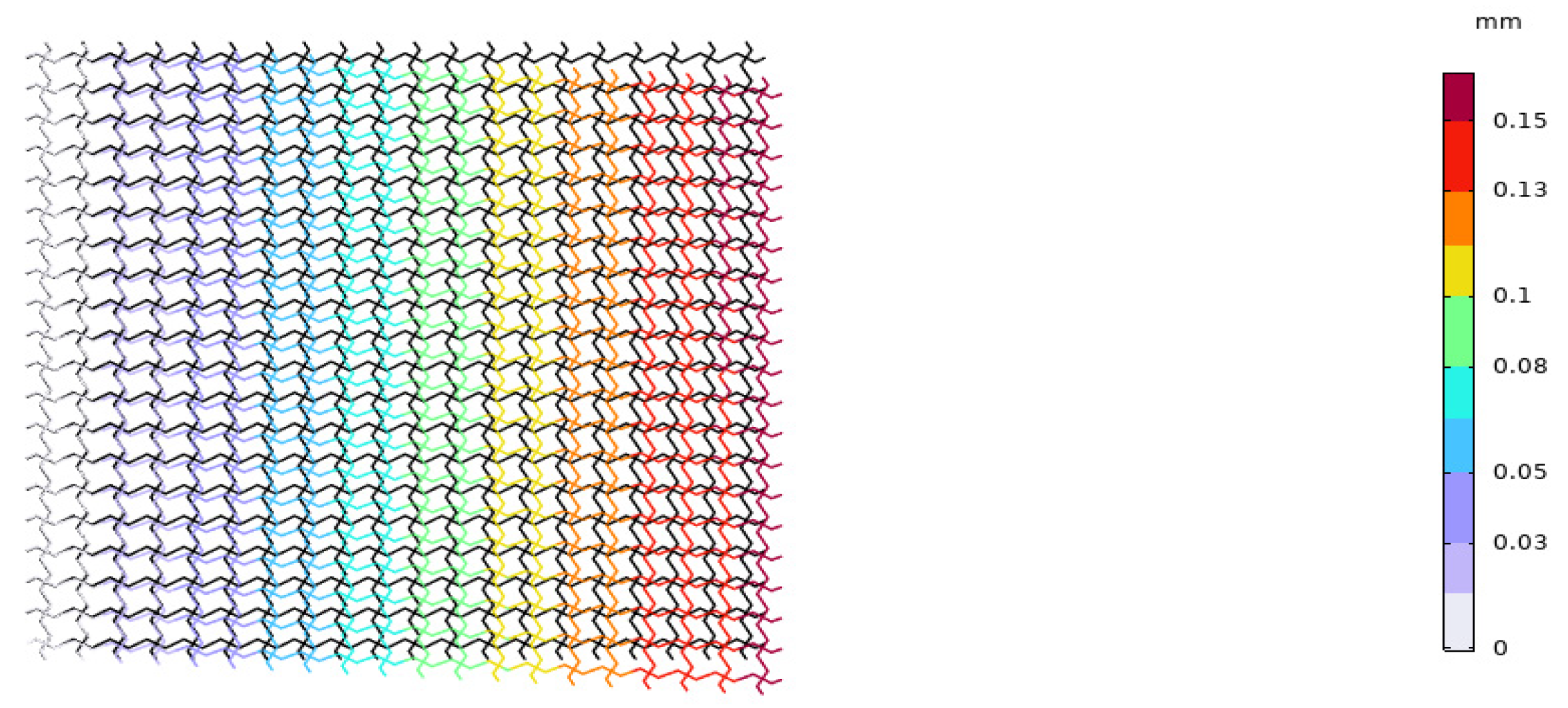
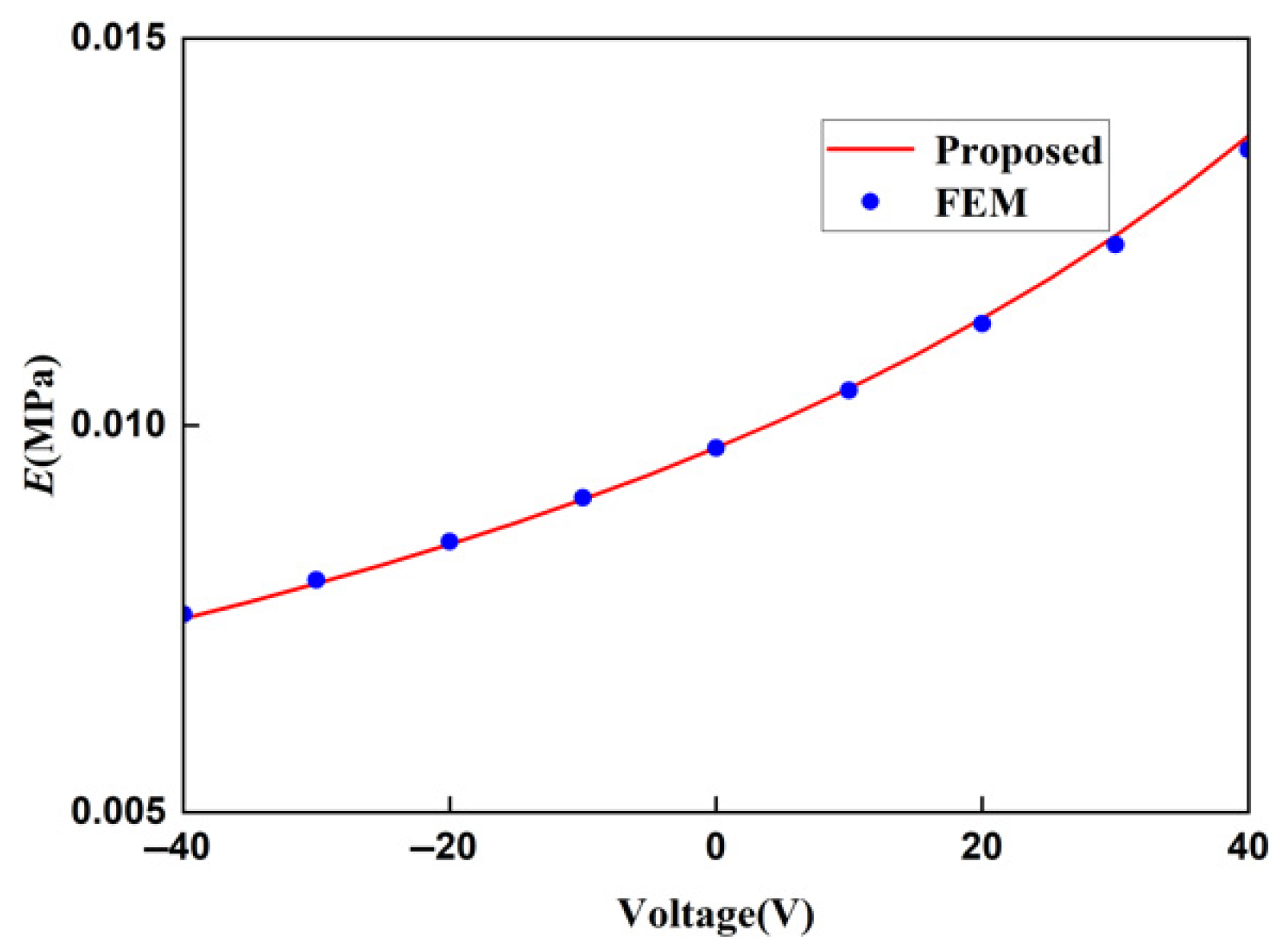
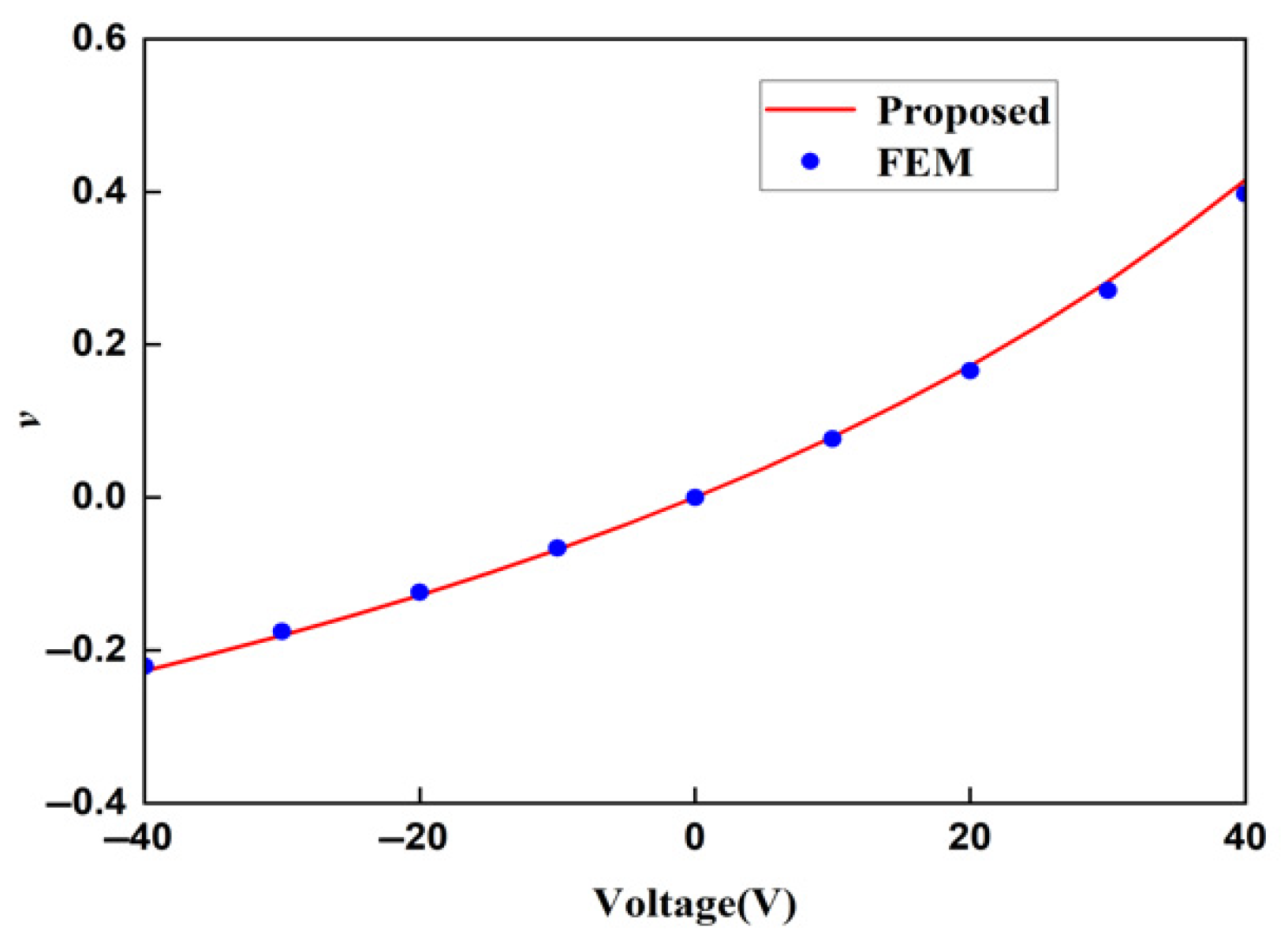
| () | FEM Displacement (mm) | Proposed Displacement (mm) |
|---|---|---|
| 0 | 0.008615 | 0.008532 |
| 10 | 0.1074 | 0.1062 |
| 20 | 0.897 | 0.8789 |
| 30 | 2.044 | 2.016 |
| 40 | 3.128 | 3.093 |
| 50 | 3.726 | 3.683 |
| Parameter | Value |
|---|---|
| Length of piezoelectric layer l (mm) | 20 |
| Width of piezoelectric layer b (mm) | 0.2 |
| Thickness of piezoelectric layer hp (mm) | 0.05 |
| Young’s modulus of piezoelectric layer Ep (N/m2) | |
| Piezoelectric constant d31 | |
| Relative permittivity | 1433.6 |
| Length of substrate layer l (mm) | 20 |
| Width of piezoelectric layer b (mm) | 0.2 |
| Thickness of piezoelectric layer hs (mm) | 0.1 |
| Young’s modulus of piezoelectric layer Es (N/m2) | |
| Angle of the zigzag beam (rad) |
| Voltage (V) | Displacement (mm) | Displacement (mm) | Rotation Angle (Rad) | Rotation Angle (Rad) |
|---|---|---|---|---|
| FEM | Proposed | FEM | Proposed | |
| −40 | 0.8113 | 0.8386 | 0.0403 | 0.0423 |
| −30 | 0.6085 | 0.629 | 0.0308 | 0.0317 |
| −20 | 0.4057 | 0.4193 | 0.0205 | 0.0211 |
| −10 | 0.2029 | 0.2097 | 0.0103 | 0.0106 |
| 0 | 0 | 0 | 0 | 0 |
| 10 | −0.2029 | −0.2097 | −0.0103 | −0.0106 |
| 20 | −0.4057 | −0.4193 | −0.0205 | −0.0211 |
| 30 | −0.6085 | −0.6290 | −0.0308 | −0.0317 |
| 40 | −0.8113 | −0.8386 | −0.0403 | −0.0423 |
| Mesh Precisions | Young’s Modulus (MPa) |
|---|---|
| Coarse | |
| Normal | |
| Fine | |
| Finer | |
| Extra fine |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Liu, J. Research on the Macroscopic Mechanical Property Continuum of Square Lattices Composed of Piezoelectric Laminated Zigzag Beams. Materials 2025, 18, 3499. https://doi.org/10.3390/ma18153499
Zhang Z, Liu J. Research on the Macroscopic Mechanical Property Continuum of Square Lattices Composed of Piezoelectric Laminated Zigzag Beams. Materials. 2025; 18(15):3499. https://doi.org/10.3390/ma18153499
Chicago/Turabian StyleZhang, Zengshuo, and Jinxing Liu. 2025. "Research on the Macroscopic Mechanical Property Continuum of Square Lattices Composed of Piezoelectric Laminated Zigzag Beams" Materials 18, no. 15: 3499. https://doi.org/10.3390/ma18153499
APA StyleZhang, Z., & Liu, J. (2025). Research on the Macroscopic Mechanical Property Continuum of Square Lattices Composed of Piezoelectric Laminated Zigzag Beams. Materials, 18(15), 3499. https://doi.org/10.3390/ma18153499





