Structural Mechanics Calculations of SiC/Mo-Re Composites with Improved High Temperature Creep Properties
Abstract
1. Introduction
2. Methodology
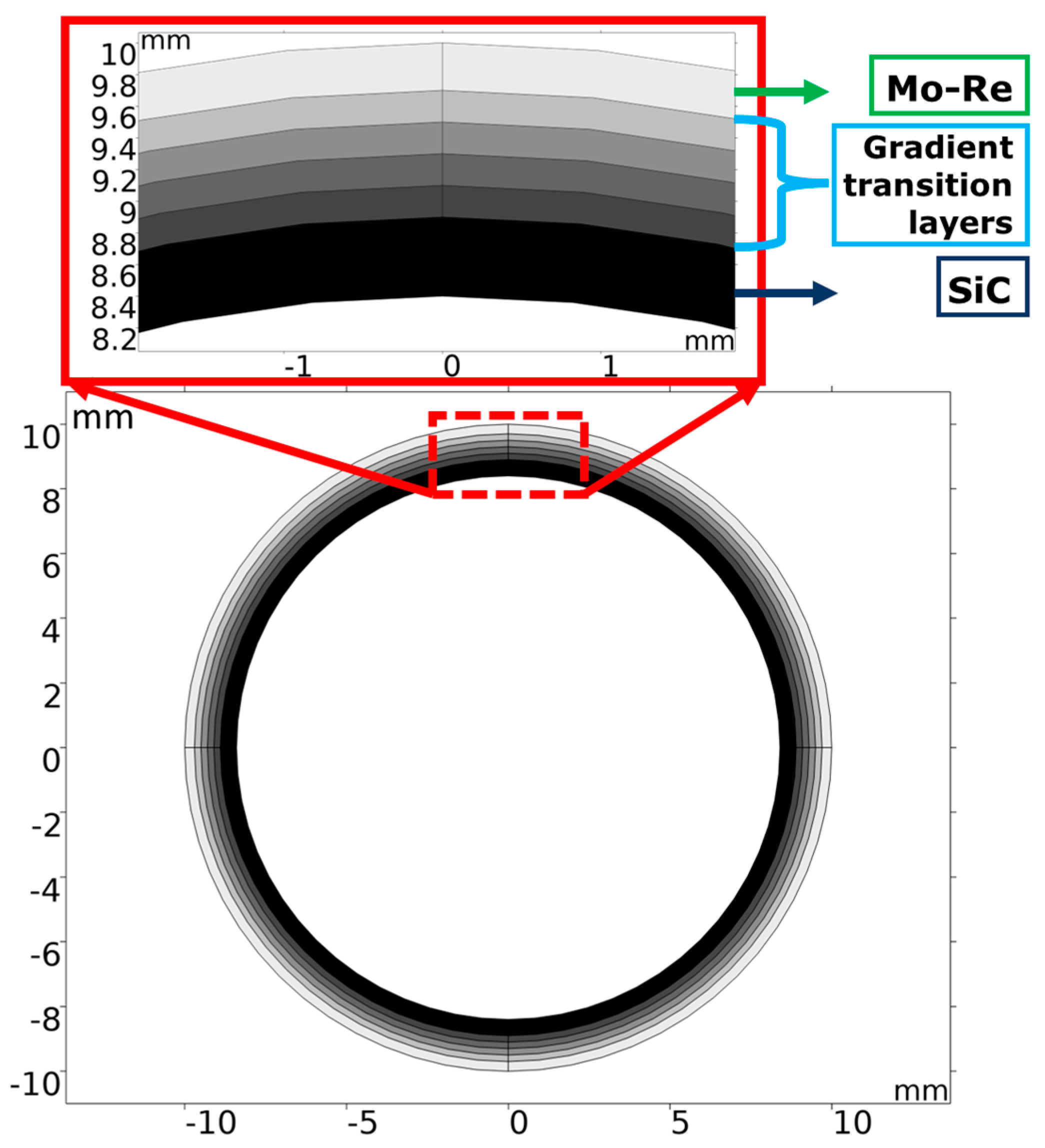
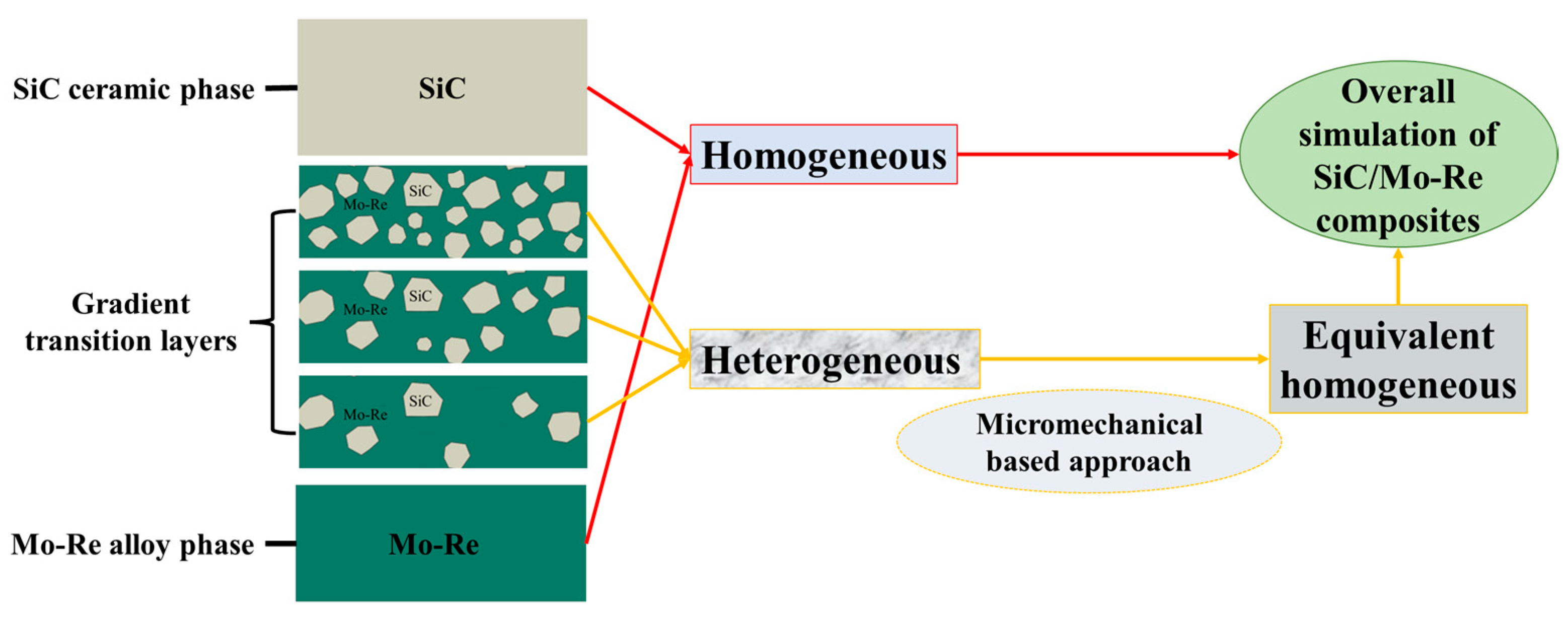
2.1. Design of Molybdenum-Based Silicon Carbide Composites
2.2. Calculations on Structural Mechanics by FES
3. Results and Discussion
3.1. Intrinsic Properties of Gradient Transition Layers
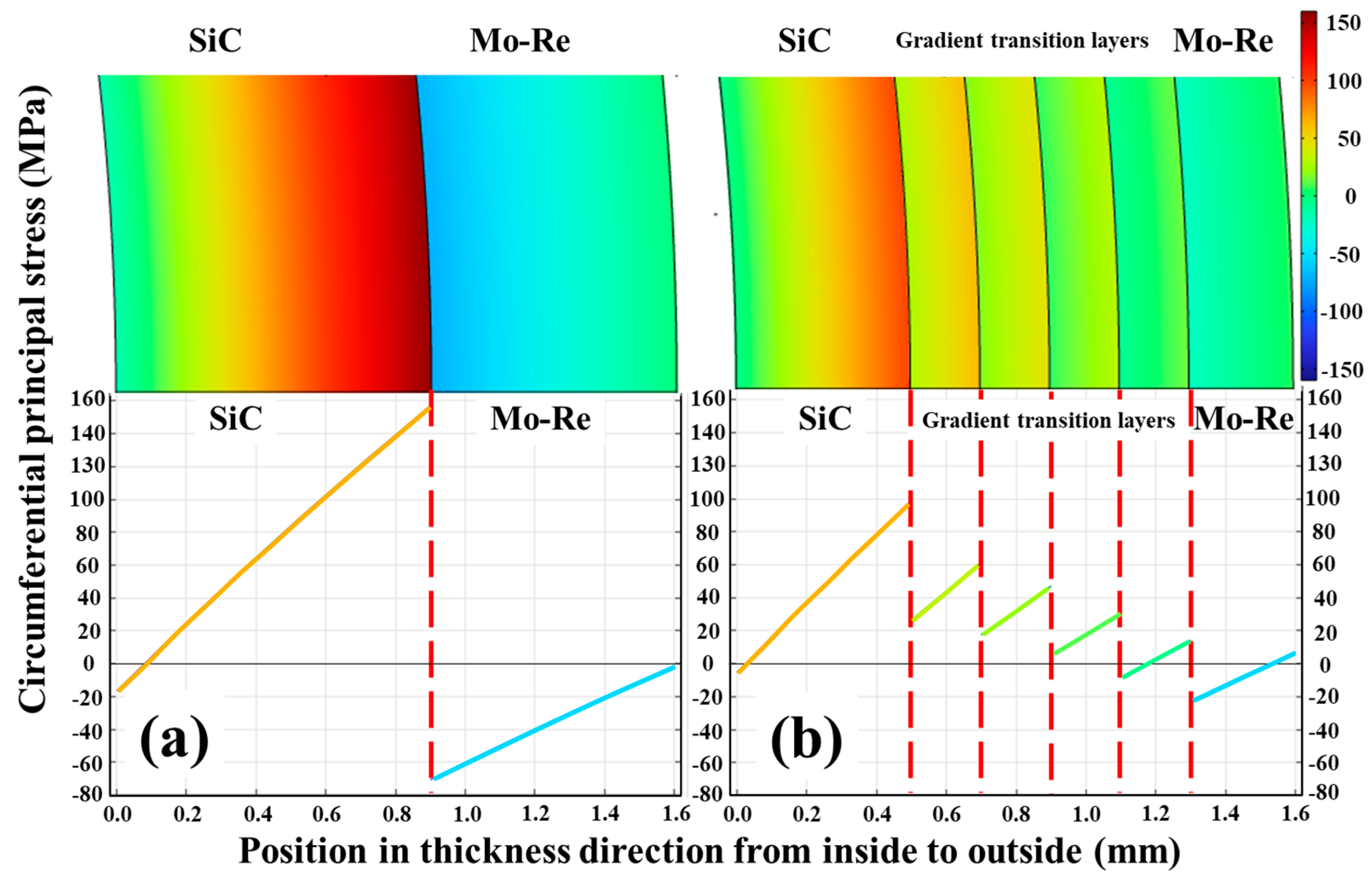
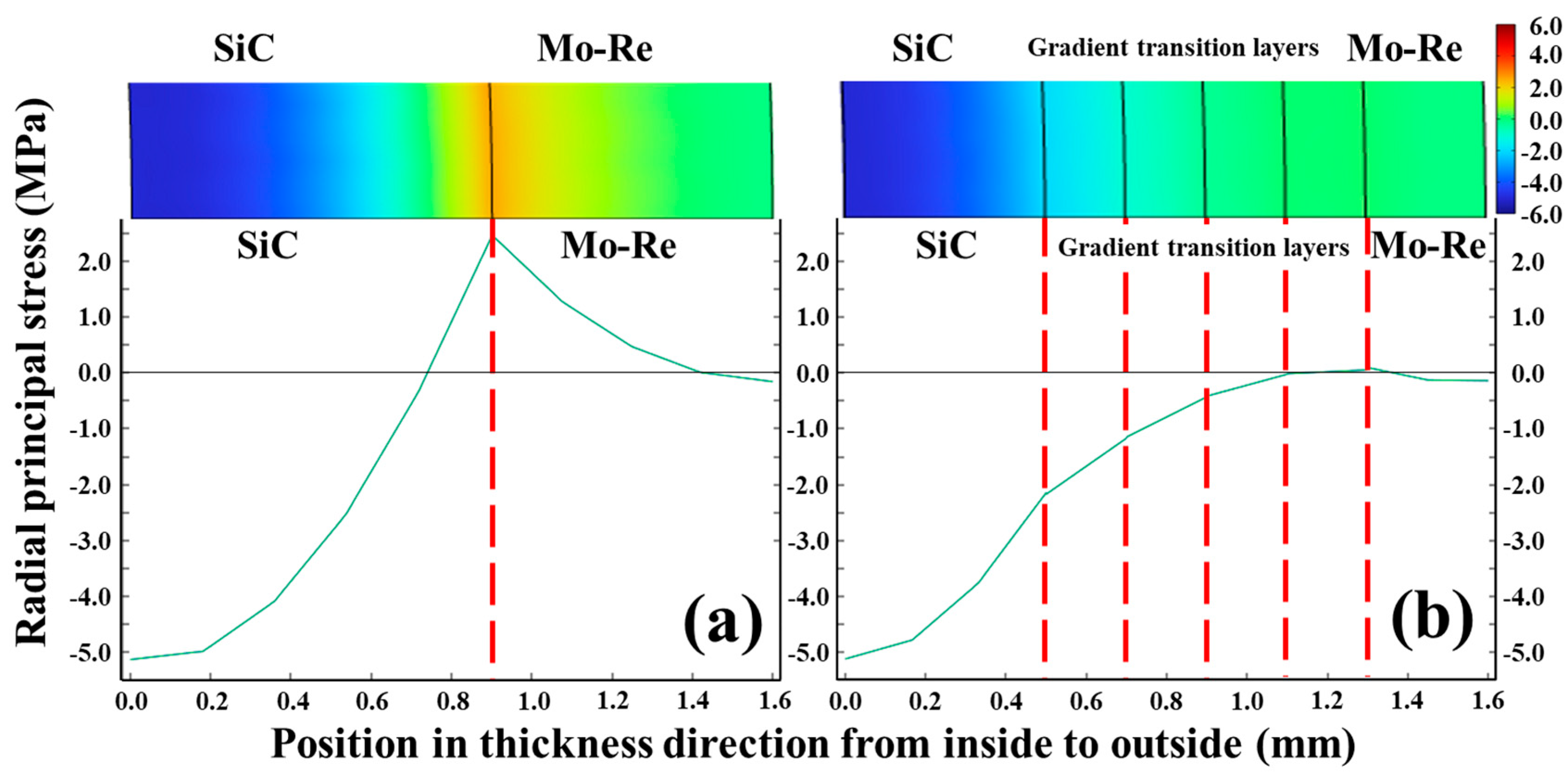
3.2. Intrinsic Properties of SiC/Mo-Re Laminated Composites
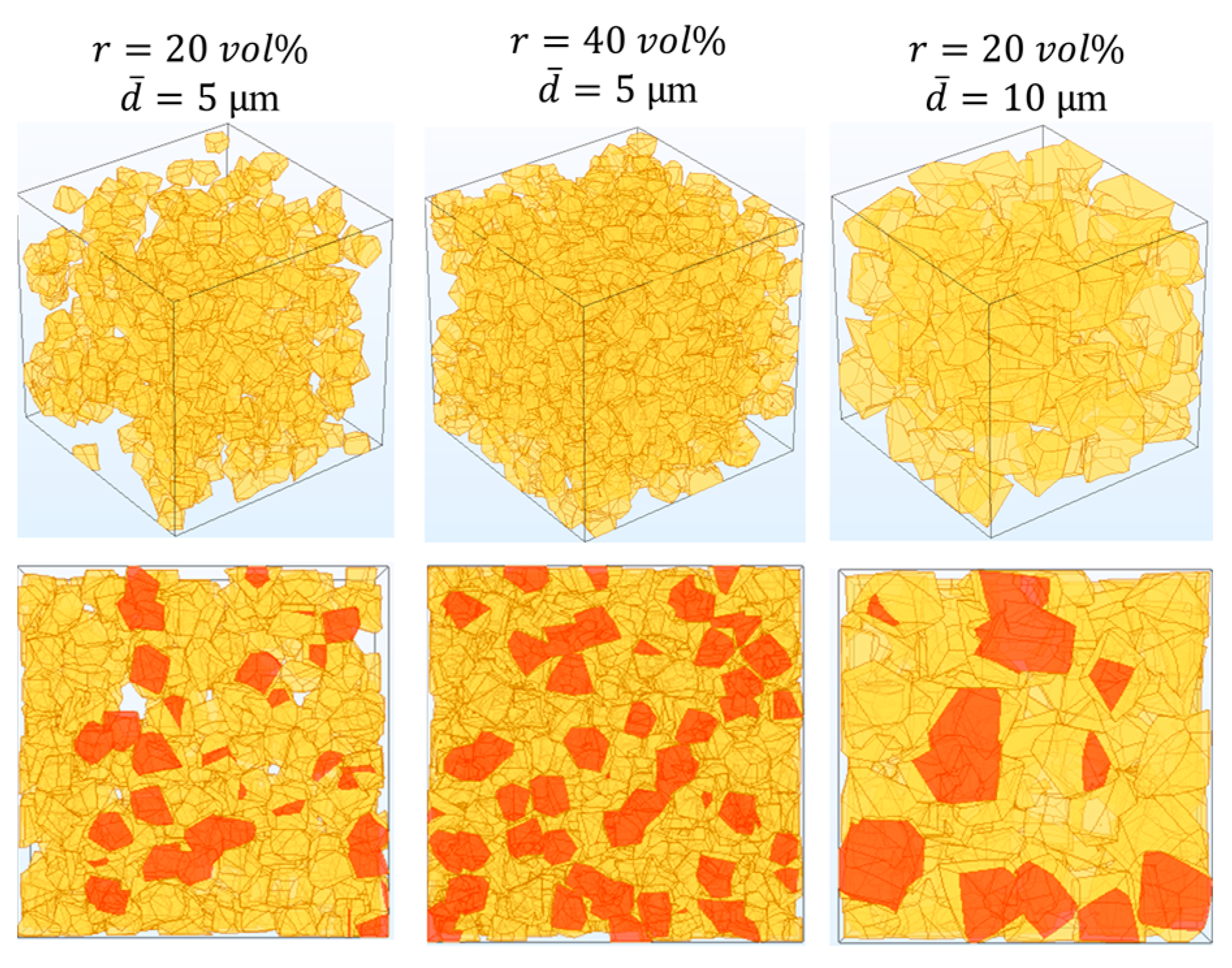
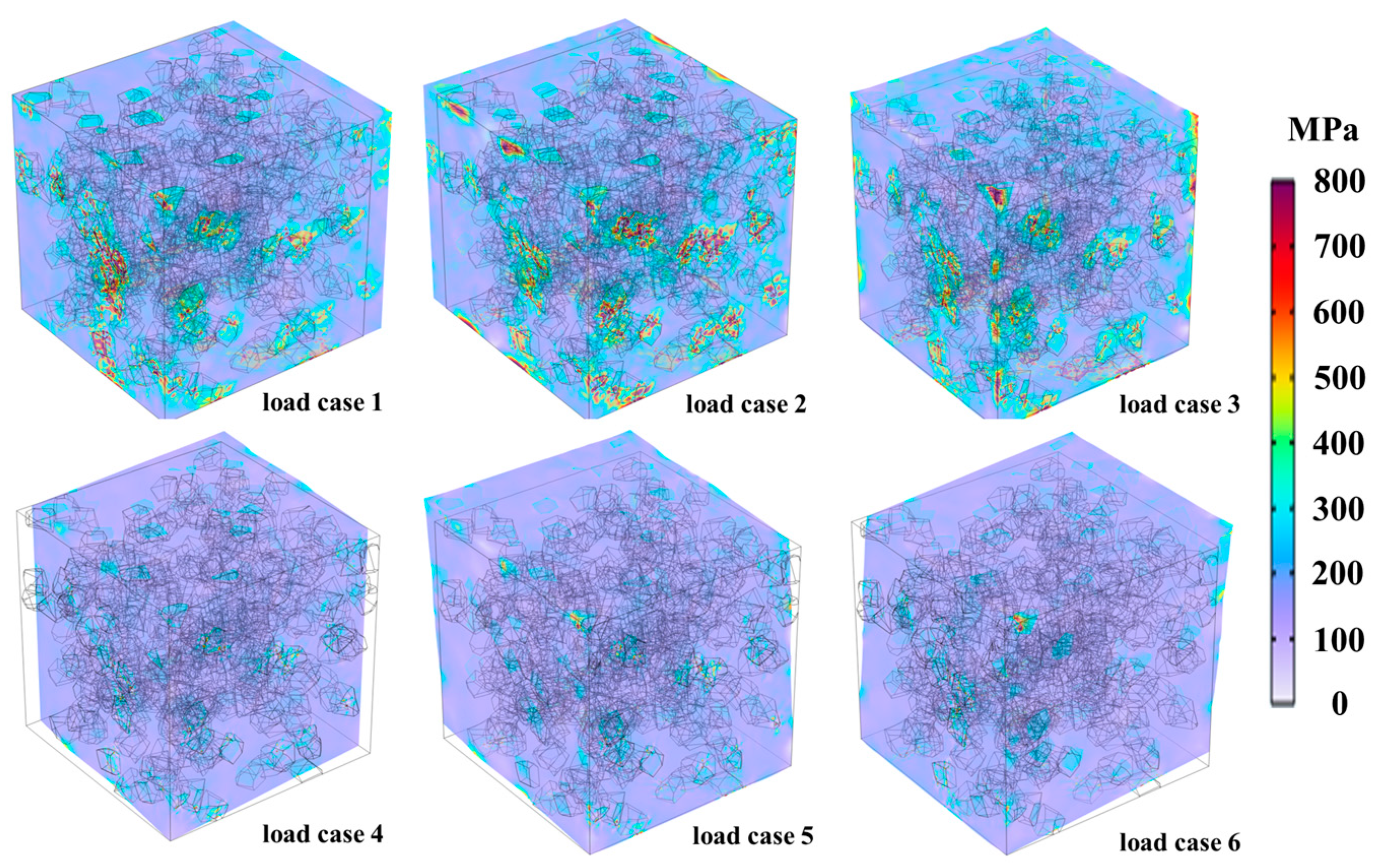
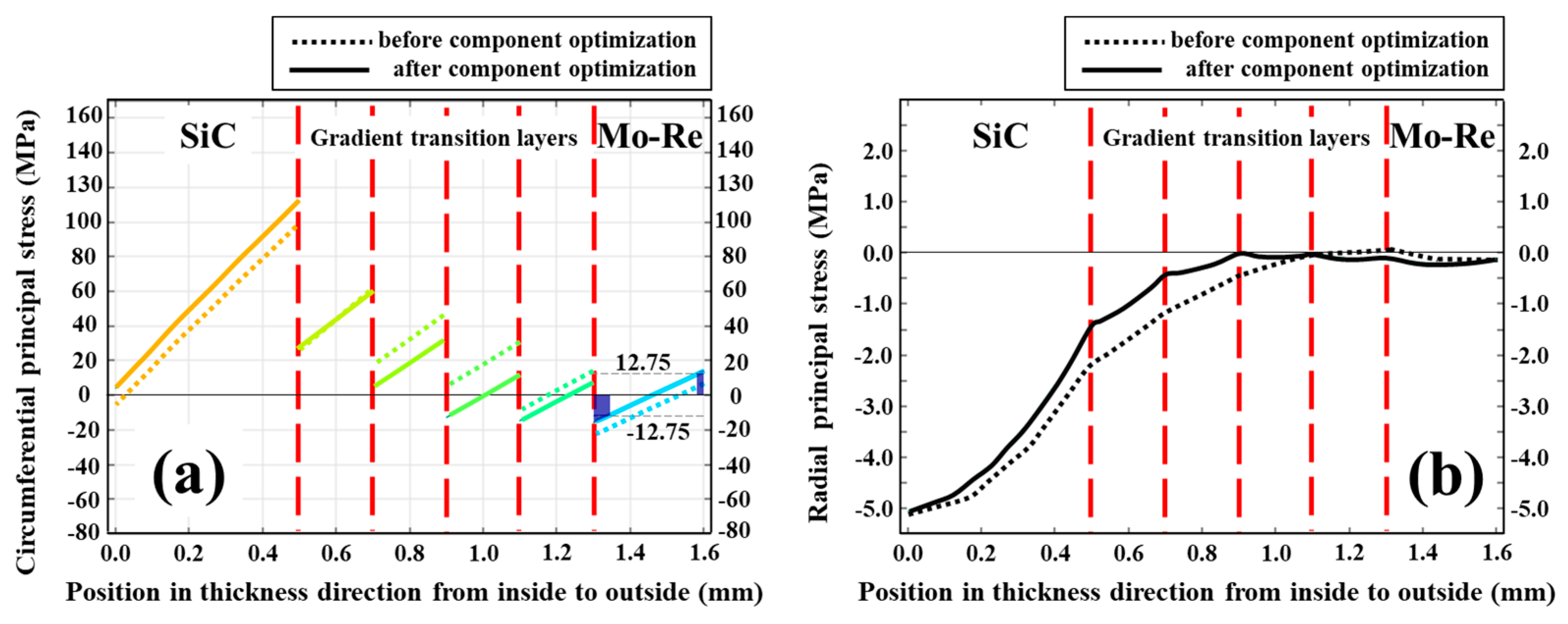
3.3. Optimization of Microstructure
4. Conclusions
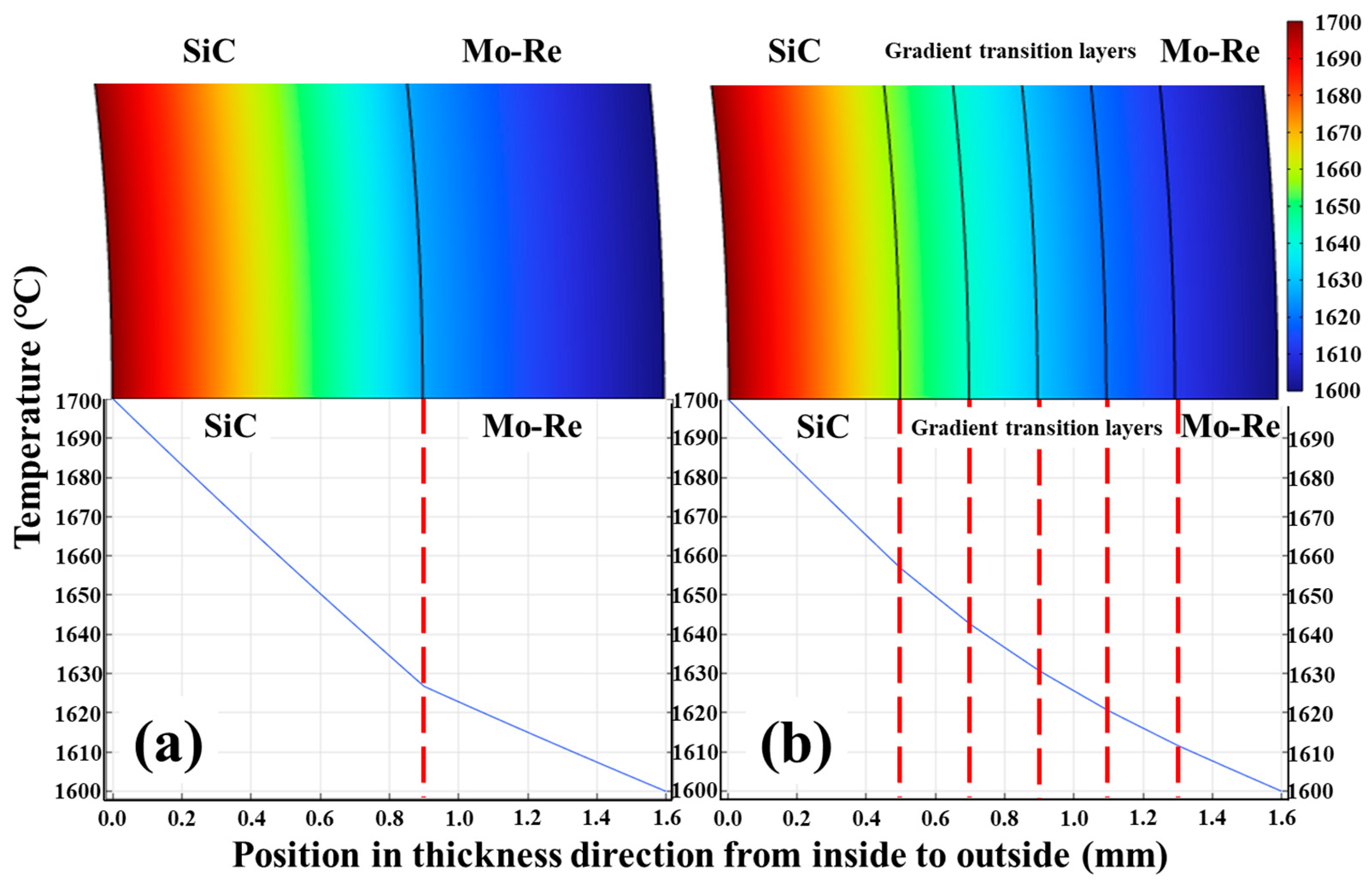
- Adding the gradient transition layers between the metallic and ceramic phases reduces the thermally induced local stresses caused by CTE mismatch of various phases inside the composites.
- The Young’s modulus and Poisson’s ratio of the gradient transition layers are insensitive to differences in the SiC particle size when the shapes, sizes, and positions are randomly distributed.
- By adjusting the components of various gradient transition layers, the stress distribution in various phases of the composite under operation conditions can be optimized to further reduce the stress in the Mo-Re alloy component.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Peakman, A.; Lindley, B. A review of nuclear electric fission space reactor technologies for achieving high-power output and operating with HALEU fuel. Prog. Nucl. Energy 2023, 163, 104815. [Google Scholar] [CrossRef]
- El-Genk, M.S.; Tournier, J.-M. A review of refractory metal alloys and mechanically alloyed-oxide dispersion strengthened steels for space nuclear power systems. J. Nucl. Mater. 2005, 340, 93–112. [Google Scholar] [CrossRef]
- Li, N.; Gao, J.; Wang, W.; Chen, S.; Wang, K.; Song, S.; Wen, C.; Sun, H. Effect of TiAlN diffusion barrier at MoSi2-SiO2 composite coating/Mo alloy interface. Surf. Interfaces 2024, 45, 103902. [Google Scholar] [CrossRef]
- Xing, H.; Hu, P.; He, C.; Zhang, X.; Han, J.; Yang, F.; Bai, R.; Zhang, W.; Wang, K.; Volinsky, A.A. Design of high-performance molybdenum alloys via doping metal oxide and carbide strengthening: A review. J. Mater. Sci. Technol. 2023, 160, 161–180. [Google Scholar] [CrossRef]
- Kurishita, H.; Kitsunai, Y.; Shibayama, T.; Kayano, H.; Hiraoka, Y. Development of Mo alloys with improved resistance to embrittlement by recrystallization and irradiation. J. Nucl. Mater. 1996, 233–237, 557–564. [Google Scholar] [CrossRef]
- Lundberg, L.B. A Critical Evaluation of Molybdenum and Its Alloys for Use in Space Reactor Core HEAT Pipes; Los Alamos Scientific Laboratory Report 1981, LA-8685-MS; Los Alamos Scientific Lab: Los Alamos, NM, USA, 1981.
- Knight, T.; Kaoumi, D.; Anghaie, S. Rhenium compatibility with uranium dioxide at elevated temperatures. AIP Conf. Proc. 2001, 552, 865–868. [Google Scholar] [CrossRef]
- King, J.C. Spectral shift absorbers for fast spectrum space nuclear reactors. In Proceedings of the Space Technology and Applications International Forum (STAIF 2005), Albuquerque, NM, USA, 13–17 February 2005; Volume 746, pp. 673–684. [Google Scholar] [CrossRef]
- Mueller, A.; Bianco, R.; Buckman, R. Evaluation of oxide dispersion strengthened (ODS) molybdenum and molybdenum–rhenium alloys. Int. J. Refract. Met. Hard Mater. 2000, 18, 205–211. [Google Scholar] [CrossRef]
- Samoilov, S. Creep and long-term strength of molybdenum alloy. Mater. Sci. Forum 2016, 843, 28–33. [Google Scholar] [CrossRef]
- Lim, K.-Y.; Kim, Y.-W.; Nishimura, T.; Seo, W.-S. High temperature strength of silicon carbide sintered with 1 wt.% aluminum nitride and lutetium oxide. J. Eur. Ceram. Soc. 2013, 33, 345–350. [Google Scholar] [CrossRef]
- Davidson, D.L. Transition metal alloys: Elastic properties and Peierls–Nabarro stress. Mater. Eng. 2000, 293, 281–291. [Google Scholar] [CrossRef]
- Shrivastava, S.; Rajak, D.K.; Joshi, T.; Singh, D.K.; Mondal, D.P. Ceramic Matrix Composites: Classifications, Manufacturing, Properties, and Applications. Ceramics 2024, 7, 652–679. [Google Scholar] [CrossRef]
- Radhika, N.; Sathish, M. A Review on Si-Based Ceramic Matrix Composites and their Infiltration Based Techniques. Silicon 2022, 14, 10141–10171. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Xiong, X.; Ye, Z.; Long, Q.; Wang, J.; Li, T.; Liu, C. Microstructure and Ablation Behavior of C/C-SiC-(ZrxHf1−x)C Composites Prepared by Reactive Melt Infiltration Method. Materials 2023, 16, 2120. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Kashkarov, E.; Syrtanov, M.; Sedanova, E.; Ivashutenko, S.; Lider, A.; Fan, P.; Yuan, D.; Travitzky, N. Preceramic Paper-Derived SiCf/SiCp Composites Obtained by Spark Plasma Sintering: Processing, Microstructure and Mechanical Properties. Materials 2020, 13, 607. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Kashkarov, E.; Ma, H.; Fan, P.; Zhang, Q.; Zhang, P.; Zhang, J.; Wu, Z.; Wahl, L.; Laptev, R.; et al. Microstructural Analysis of Novel Preceramic Paper-Derived SiCf/SiC Composites. Materials 2021, 14, 6737. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Kashkarov, E.; Ma, H.; Fan, P.; Zhang, Q.; Zhang, P.; Cao, X.; Zhang, J.; Wu, Z.; Lider, A.; et al. Irradiation resistance of preceramic paper-derived SiCf/SiC laminated composites. J. Mater. Sci. 2022, 57, 10153–10166. [Google Scholar] [CrossRef]
- Zhang, S.; Qin, H.; Li, Z.; Wei, C.; Zhang, C.; Li, X. In-situ observation of damage evolution in Mo-SiCf/SiC heterogeneous composite. Compos. Part B Eng. 2023, 264, 110901. [Google Scholar] [CrossRef]
- Grzesik, Z.; Kulikowski, K.; Kłys, A.; Krawczyk, M.; Wusatowska-Sarnek, A. Characterization of the gradient (Mo, Re)Si2/Mo-Re coatings deposited in the hybrid process. J. Therm. Spray Technol. 2019, 28, 855–868. [Google Scholar] [CrossRef]
- Roger, J.; Audubert, F.; Le Petitcorps, Y. Thermal reaction of SiC films with Mo, Re and Mo-Re alloy. J. Alloys Compd. 2009, 475, 635–642. [Google Scholar] [CrossRef]
- Abe, F. Creep ductility and modified Monkman–Grant equation for Gr.92 by incorporating total strain. Mater. High Temp. 2023, 40, 192–200. [Google Scholar] [CrossRef]
- Ghatak, A.K.; Robi, P.S. Analysis of Monkman–Grant relationships and damage tolerance factor for creep of 25Cr35NiNb micro-alloyed steel. Mater. Sci. Eng. A 2022, 845, 143027. [Google Scholar] [CrossRef]
- Farhat, H. Lifetime extension: Assessment and considerations. In Operation, Maintenance, and Repair of Land-Based Gas Turbines; Elsevier: Amsterdam, The Netherlands, 2021; pp. 175–196. [Google Scholar] [CrossRef]
- Evans, R.W.; Wilshire, B. Constitutive laws for high-temperature creep and creep fracture. In Unified Constitutive Laws of Plastic Deformation; Elsevier: Amsterdam, The Netherlands, 1996; pp. 107–152. [Google Scholar] [CrossRef]
- Rest, J.; Cooper, M.W.D.; Spino, J.; Turnbull, J.A.; Van Uffelen, P.; Walker, C.T. Fission gas release from UO2 nuclear fuel: A review. J. Nucl. Mater. 2019, 513, 310–345. [Google Scholar] [CrossRef]
- Qi, F.; Liu, Z.; Li, Q.; Yu, H.; Chen, P.; Li, Y.; Lu, H. Pellet-cladding mechanical interaction analysis of Cr-coated Zircaloy cladding. Nucl. Eng. Des. 2020, 367, 110792. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, B.; Li, J.; Shan, J. Development of mechanistic cladding rupture model for severe accident analysis and application in PHEBUS FPT3 experiment. Nucl. Eng. Technol. 2022, 54, 138–151. [Google Scholar] [CrossRef]
- Müzel, S.D.; Bonhin, E.P.; Guimarães, N.M.; Guidi, E.S. Application of the finite element method in the analysis of composite materials: A review. Polymers 2020, 12, 818. [Google Scholar] [CrossRef] [PubMed]
- Wan, L.; Ismail, Y.; Sheng, Y.; Ye, J.; Yang, D. A review on micromechanical modelling of progressive failure in unidirectional fibre-reinforced composites. Compos. Part C Open Access 2023, 10, 100348. [Google Scholar] [CrossRef]
- Mital, S.K.; Arnold, S.M.; Bednarcyk, B.A.; Pineda, E.J. Micromechanics-based modeling of SiC/SiC ceramic matrix composites and structures. Recent Prog. Mater. 2023, 5, 025. [Google Scholar] [CrossRef]
- Bednarcyk, B.A.; Aboudi, J.; Arnold, S.M. Micromechanics modeling of composites subjected to multiaxial progressive damage in the constituents. AIAA J. 2009, 47, 2603–2615. [Google Scholar] [CrossRef]
- Wang, Z.; Li, X.; Zhang, Y.; Chen, W. High-Temperature Mechanical Properties and Influence Mechanisms of ZrC-Modified C-SiC Ceramic Matrix Composites up to 1600 °C. Materials 2022, 13, 1581. [Google Scholar] [CrossRef]
- Almansour, A.S.; Morscher, G.N. Tensile Creep Behavior of SiCf/SiC Ceramic Matrix Minicomposites. J. Eur. Ceram. Soc. 2020, 40, 5132–5146. [Google Scholar] [CrossRef]
- Wan, L.; Ismail, Y.; Zhu, C.; Zhu, P.; Sheng, Y.; Liu, J.; Yang, D. Computational micromechanics-based prediction of the failure of unidirectional composite lamina subjected to transverse and in-plane shear stress states. J. Strain Anal. Eng. Des. 2020, 55, 728–744. [Google Scholar] [CrossRef]
- Gonabadi, H.; Chen, Y.; Bull, S. Investigation of the effects of volume fraction, aspect ratio and type of fibres on the mechanical properties of short fibre reinforced 3D printed composite materials. Prog. Addit. Manuf. 2025, 10, 261–277. [Google Scholar] [CrossRef]
- Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
- Tian, W.; Qi, L.; Zhou, J.; Liang, J.; Ma, Y. Representative volume element for composites reinforced by spatially randomly distributed discontinuous fibers and its applications. Compos. Struct. 2015, 131, 366–373. [Google Scholar] [CrossRef]
- Lu, S.; Li, Z.; Zhang, J.; Zhang, J.; Wang, X.; Yan, Y.; Sun, T. Finite element investigation of the influence of SiC particle distribution on diamond cutting of SiCP/Al composite. Nanomanuf. Metrol. 2020, 3, 251–259. [Google Scholar] [CrossRef]
- Khalil, N.Z.; Vajpai, S.K.; Ota, M.; Ameyama, K. Effect of Particle Size Distribution on SiC Ceramic Sinterability. J. Jpn. Soc. Powder Powder Metall. 2017, 64, 281–287. [Google Scholar] [CrossRef]
- Aßmus, M.; Glüge, R.; Altenbach, H. On the Analytical Estimation for Isotropic Approximation of Elastic Properties applied to Polycrystalline Cubic Silicon used at Solar Cells. Tech. Mech. 2020, 40, 120–133. [Google Scholar] [CrossRef]
- Evans, J.A.; Sturtevant, B.T.; Clausen, B.; Vogel, S.C.; Balakirev, F.F.; Betts, J.B.; Capolungo, L.; Lebensohn, R.A.; Maiorov, B. Determining elastic anisotropy of textured polycrystals using resonant ultrasound spectroscopy. J. Mater. Sci. 2021, 56, 10053–10073. [Google Scholar] [CrossRef]
- Kampouroglou, A.; Sideridis, E.P. Influence of particle contiguity and interphase on the stiffness of particulate epoxy composites. Polym. Bull. 2017, 74, 4619–4644. [Google Scholar] [CrossRef]
- Cui, Y.; Li, Y.; Zhang, L. Effect of SiC particle shape on mechanical properties of high volume fraction SiC particle reinforced aluminum matrix composites. J. Mater. Sci. Technol. 2019, 35, 2859–2868. [Google Scholar] [CrossRef]
- Cho, J.; Joshi, M.S.; Sun, C.T. Effect of inclusion size on mechanical properties of polymeric composites with micro and nano particles. Compos. Sci. Technol. 2006, 66, 1941–1952. [Google Scholar] [CrossRef]
- Kontou, E.; Christopoulos, A.; Koralli, P.; Mouzakis, D.E. The effect of silica particle size on the mechanical enhancement of polymer nanocomposites. Nanomaterials 2023, 13, 1095. [Google Scholar] [CrossRef] [PubMed]
- Karch, C. Micromechanical analysis of thermal expansion coefficients. Model. Numer. Simul. Mater. Sci. 2014, 4, 104–118. [Google Scholar] [CrossRef][Green Version]
- Kundalwal, S.I. Review on modeling of mechanical and thermal properties of nano- and micro-composites. arXiv 2017, arXiv:1708.00764. [Google Scholar] [CrossRef]
- Kundalwal, S.I.; Meguid, S.A. Micromechanics modelling of the effective thermoelastic response of nano-tailored composites. Eur. J. Mech. A Solids 2015, 53, 241–253. [Google Scholar] [CrossRef]
- Hsu, H.-C.; Yeh, C.-T.; Tuan, W.-H. Heat capacity of Al2O3–NiAl composites, a key parameter for thermal management. Ceram. Int. 2017, 43, S705–S709. [Google Scholar] [CrossRef]
- Li, J.; Li, M.; Guan, B.; Xin, Y.; Wu, Y.; Liu, X.; Chen, G. Uncovering the hydride orientation-mediated hoop fatigue mechanism in a zirconium alloy cladding tube. Int. J. Plast. 2022, 159, 103440. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, Y.; Saucedo-Mora, L.; Connolley, T.; Marrow, T.J. Hoop Strain Measurement During a SiC/SiC Ceramic Composite Tube Burst Test by Digital Volume Correlation of X-Ray Computed Tomographs. Exp. Mech. 2023, 63, 275–287. [Google Scholar] [CrossRef]
- Klopp, W.D.; Witzke, W.R. Mechanical properties of electron beam melted molybdenum and dilute Mo–Re alloys. Metall. Trans. 1973, 4, 2006–2008. [Google Scholar] [CrossRef]
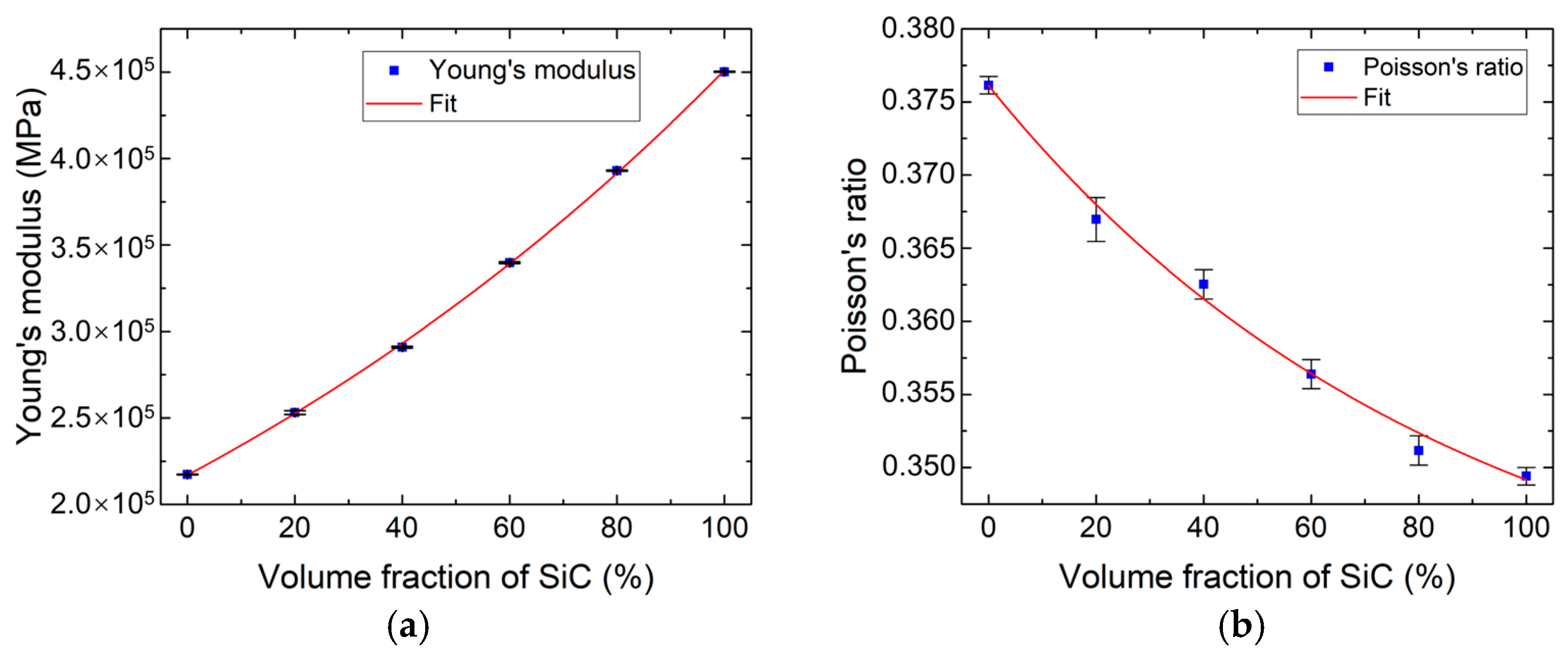
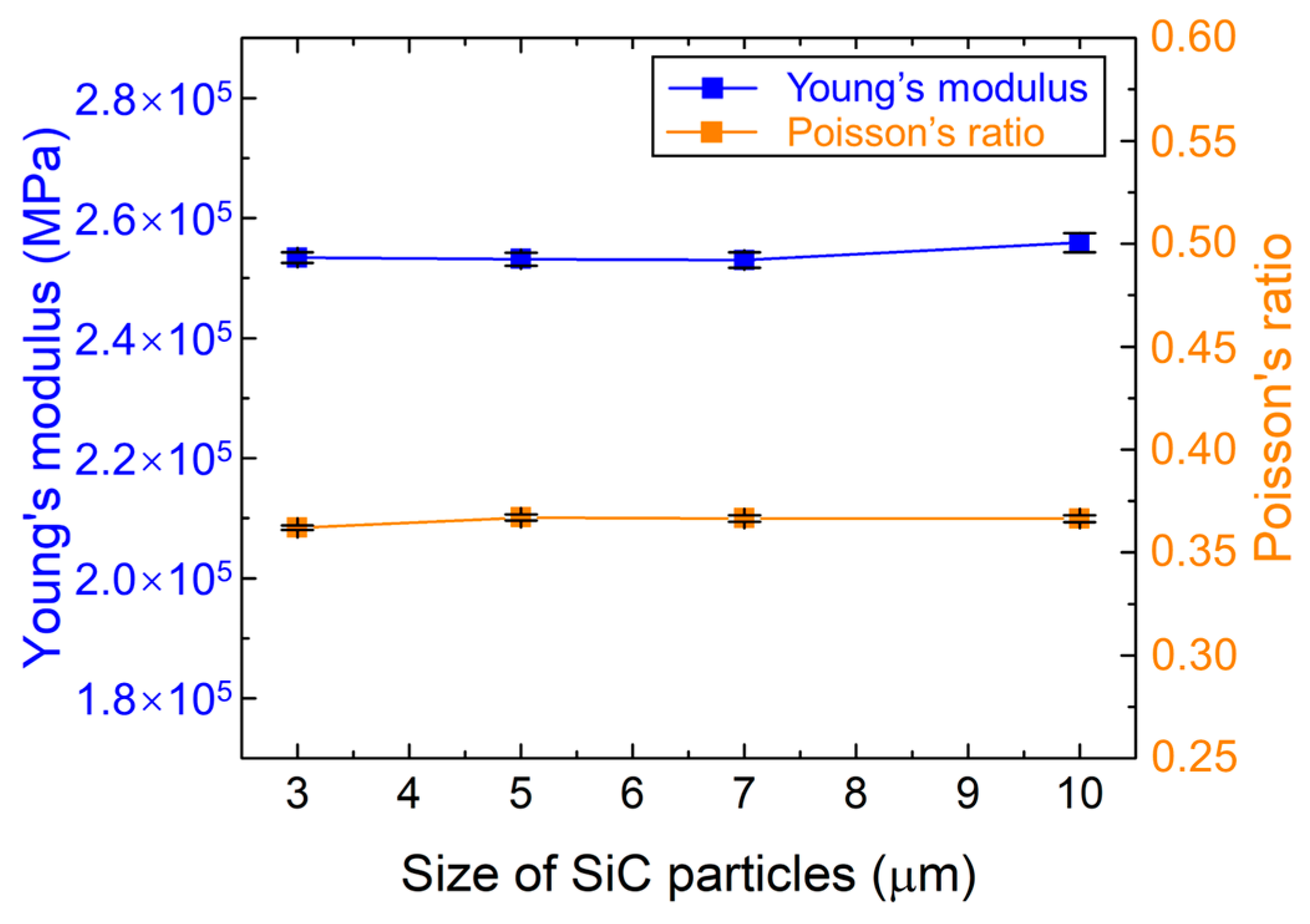
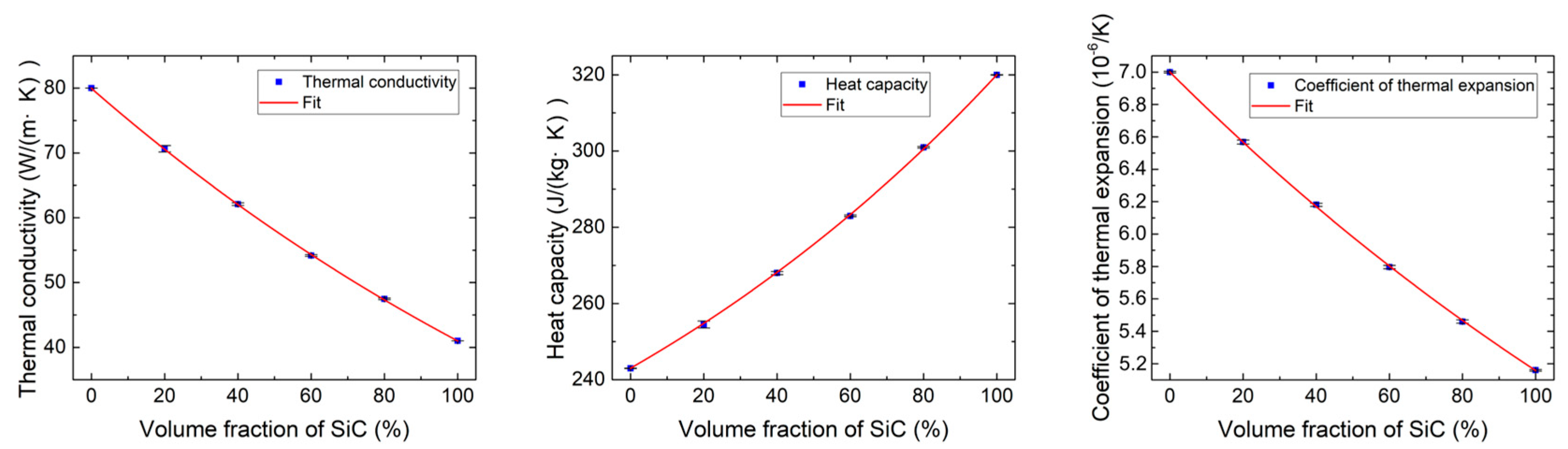
| Layers | Young’s Modulus (GPa) | Poisson’s Ratio | Volume Fraction of SiC Particle (vol %) | |||
|---|---|---|---|---|---|---|
| 1 | 445 | 0.355 | 51.73 | 289.2 | 5.68 | 67.2 |
| 2 | 390 | 0.360 | 60.41 | 271.1 | 6.09 | 44.1 |
| 3 | 348 | 0.367 | 68.90 | 257.2 | 6.49 | 23.8 |
| 4 | 325 | 0.371 | 74.47 | 249.6 | 6.75 | 11.5 |
| Layers | Young’s Modulus (GPa) | Poisson’s Ratio | Volume Fraction of SiC Particle (vol%) | ||
|---|---|---|---|---|---|
| Fitting Results | Simulation Results | Fitting Results | Simulation Results | ||
| 1 | 445 | 445 | 0.355 | 0.354 | 67.2 |
| 2 | 390 | 391 | 0.360 | 0.360 | 44.1 |
| 3 | 348 | 347 | 0.367 | 0.365 | 23.8 |
| 4 | 325 | 322 | 0.371 | 0.374 | 11.5 |
| Layers | ||||||
|---|---|---|---|---|---|---|
| Fitting Results | Simulation Results | Fitting Results | Simulation Results | Fitting Results | Simulation Results | |
| 1 | 51.73 | 51.81 | 289.2 | 288.9 | 5.68 | 5.66 |
| 2 | 60.41 | 60.49 | 271.1 | 270.8 | 6.09 | 6.12 |
| 3 | 68.90 | 69.03 | 257.2 | 256.5 | 6.49 | 6.54 |
| 4 | 74.47 | 74.71 | 249.6 | 250.3 | 6.75 | 6.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, K.; Kashkarov, E.; Ma, H.; Fan, P.; Zhang, Q.; Lider, A.; Yuan, D. Structural Mechanics Calculations of SiC/Mo-Re Composites with Improved High Temperature Creep Properties. Materials 2025, 18, 3459. https://doi.org/10.3390/ma18153459
Li K, Kashkarov E, Ma H, Fan P, Zhang Q, Lider A, Yuan D. Structural Mechanics Calculations of SiC/Mo-Re Composites with Improved High Temperature Creep Properties. Materials. 2025; 18(15):3459. https://doi.org/10.3390/ma18153459
Chicago/Turabian StyleLi, Ke, Egor Kashkarov, Hailiang Ma, Ping Fan, Qiaoli Zhang, Andrey Lider, and Daqing Yuan. 2025. "Structural Mechanics Calculations of SiC/Mo-Re Composites with Improved High Temperature Creep Properties" Materials 18, no. 15: 3459. https://doi.org/10.3390/ma18153459
APA StyleLi, K., Kashkarov, E., Ma, H., Fan, P., Zhang, Q., Lider, A., & Yuan, D. (2025). Structural Mechanics Calculations of SiC/Mo-Re Composites with Improved High Temperature Creep Properties. Materials, 18(15), 3459. https://doi.org/10.3390/ma18153459







