Experimental Investigation of Delayed Fracture Initiation in Advanced High-Strength Steel Under Accelerated Bending
Abstract
1. Introduction
2. Methods for Bending and Crack Measurement
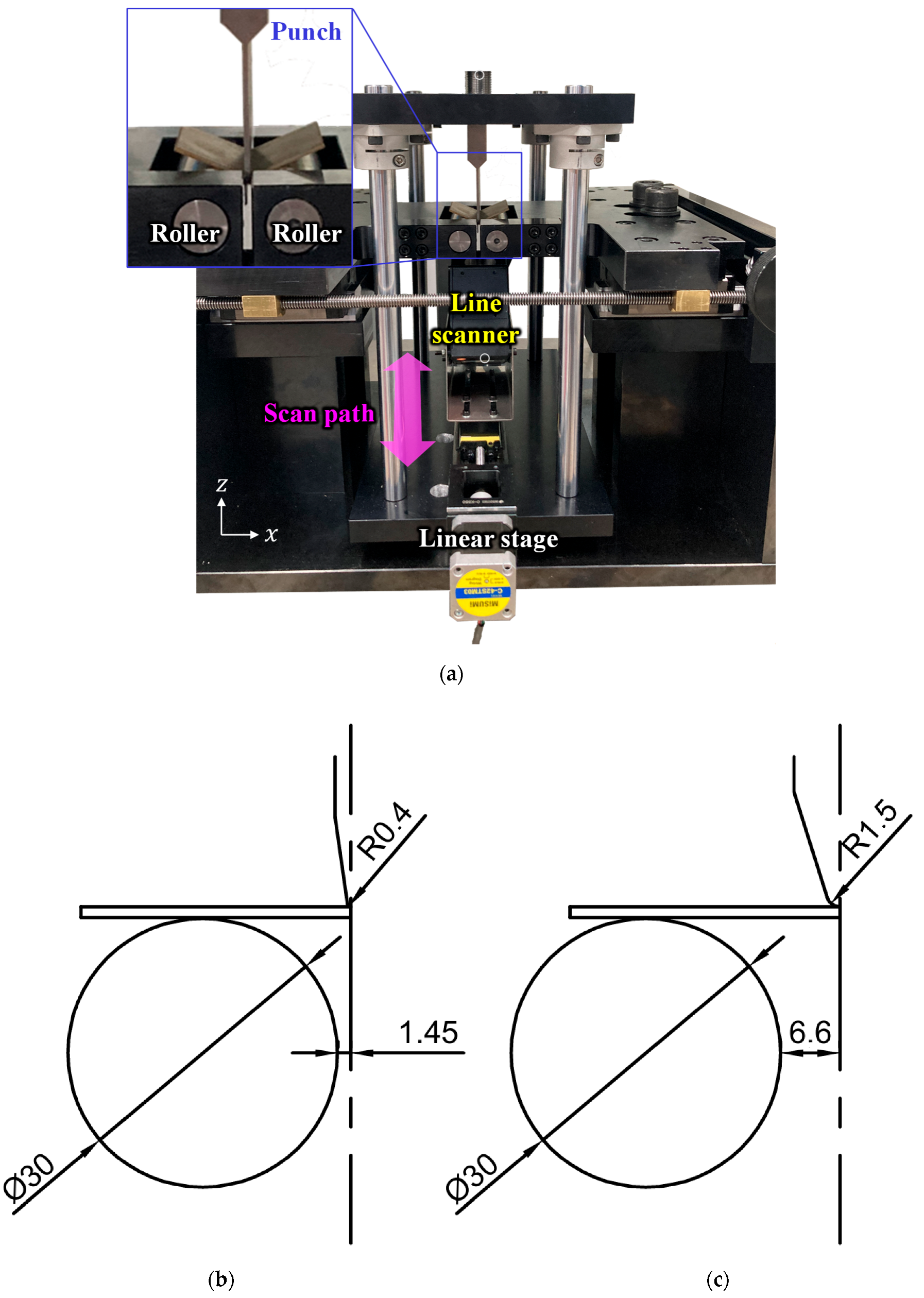
2.1. Bending Test at Different Speeds and Radii
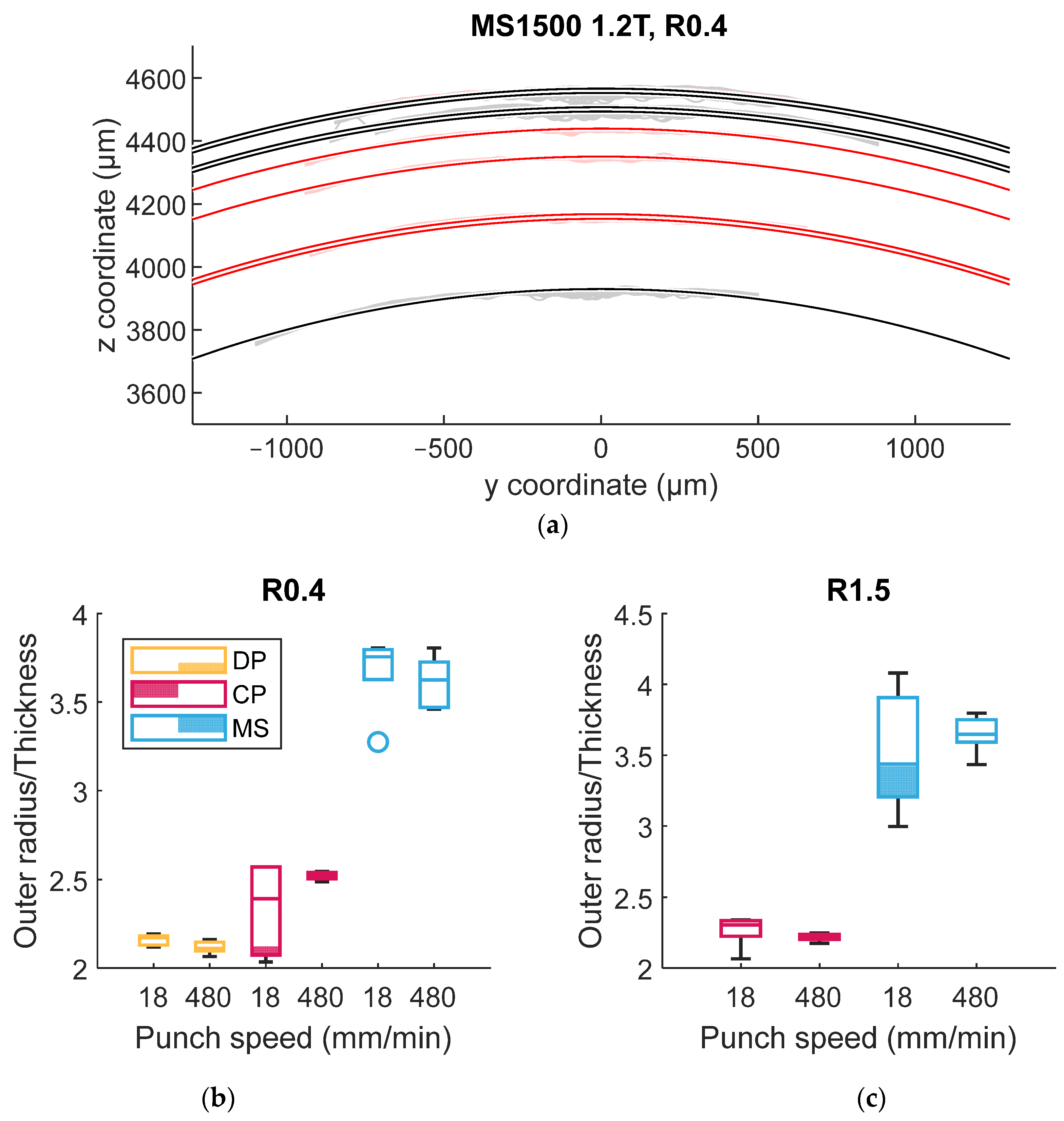
2.2. Surface Measurements for Outer Radii and Cracks
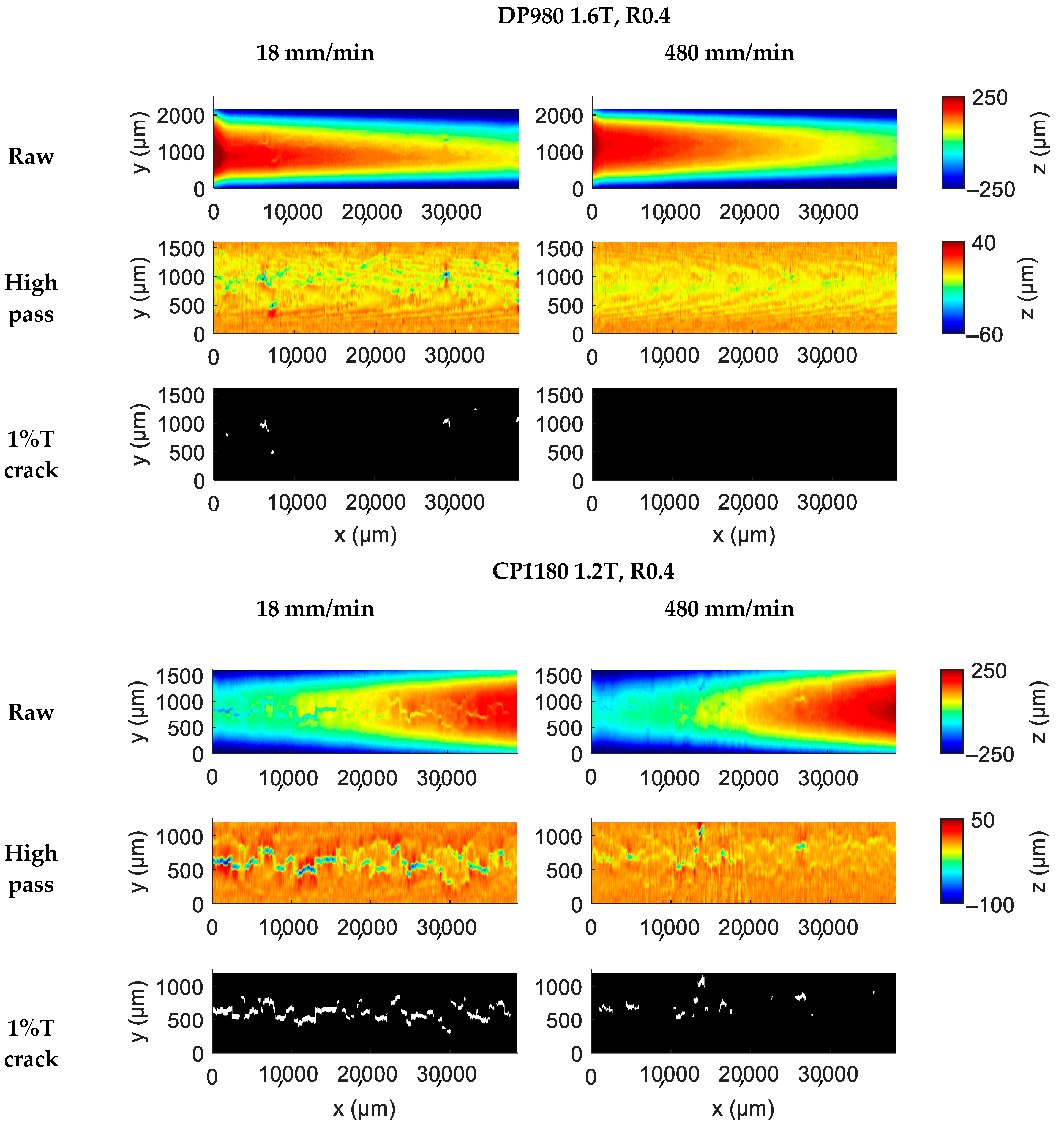
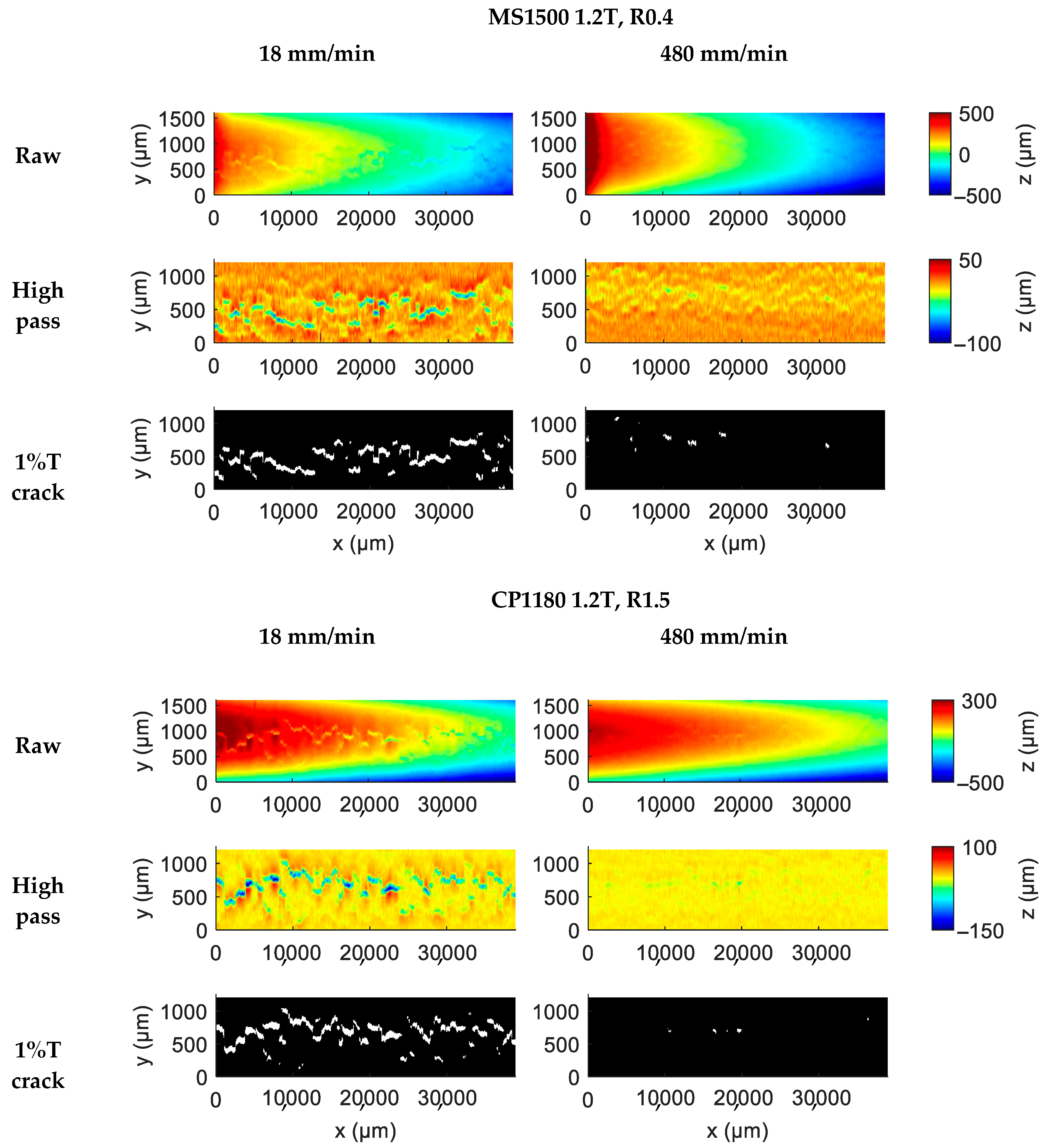
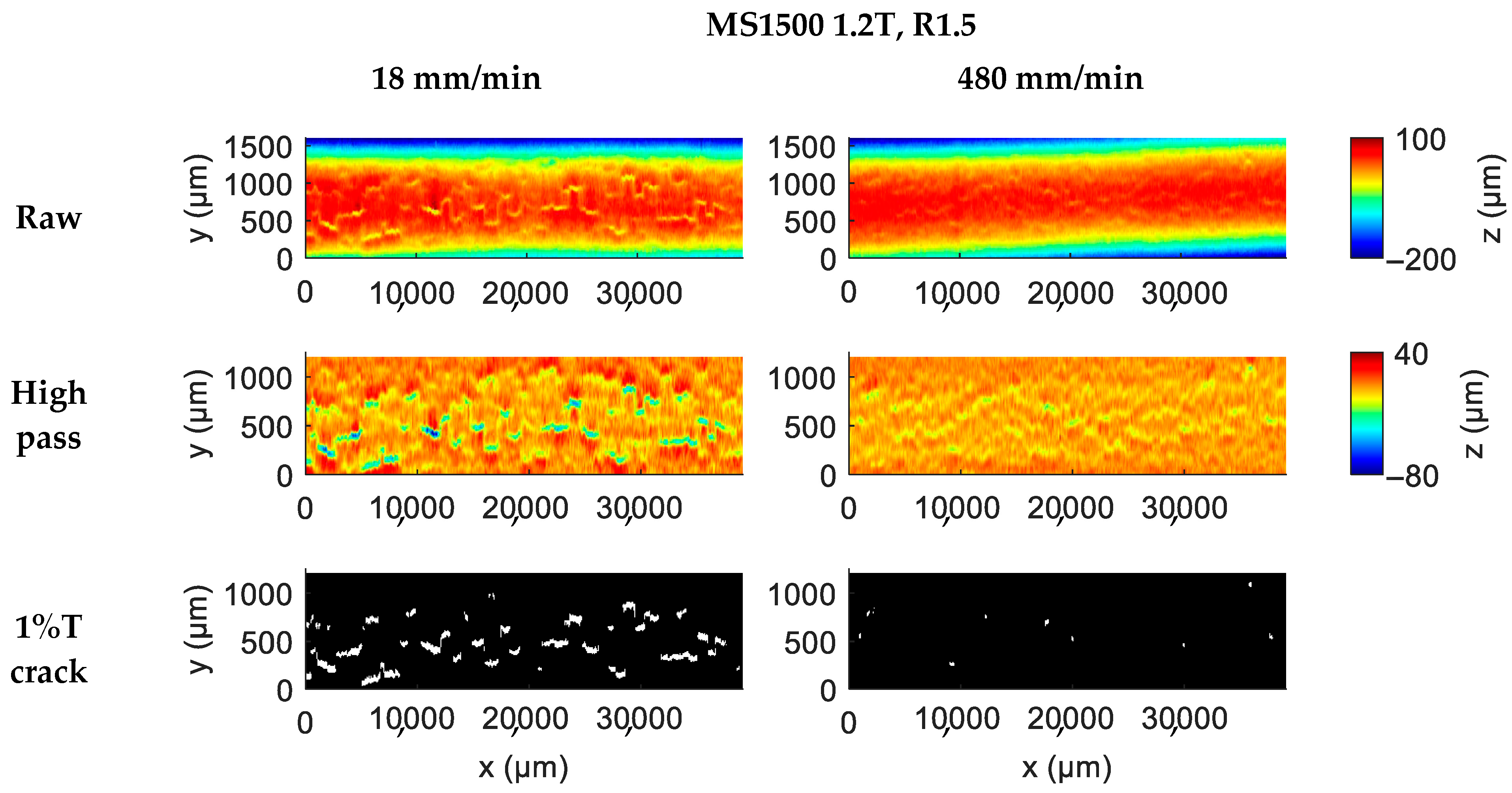
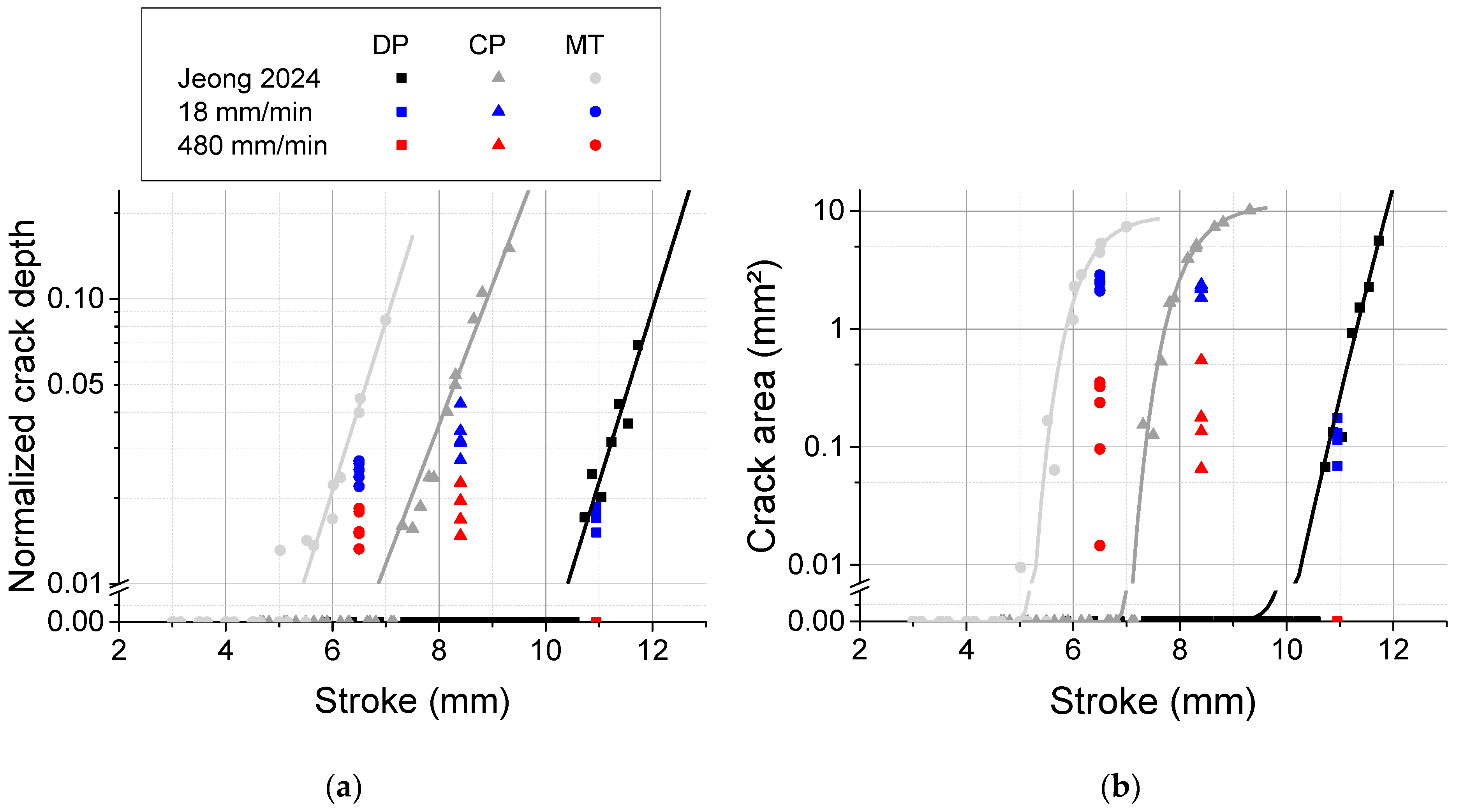
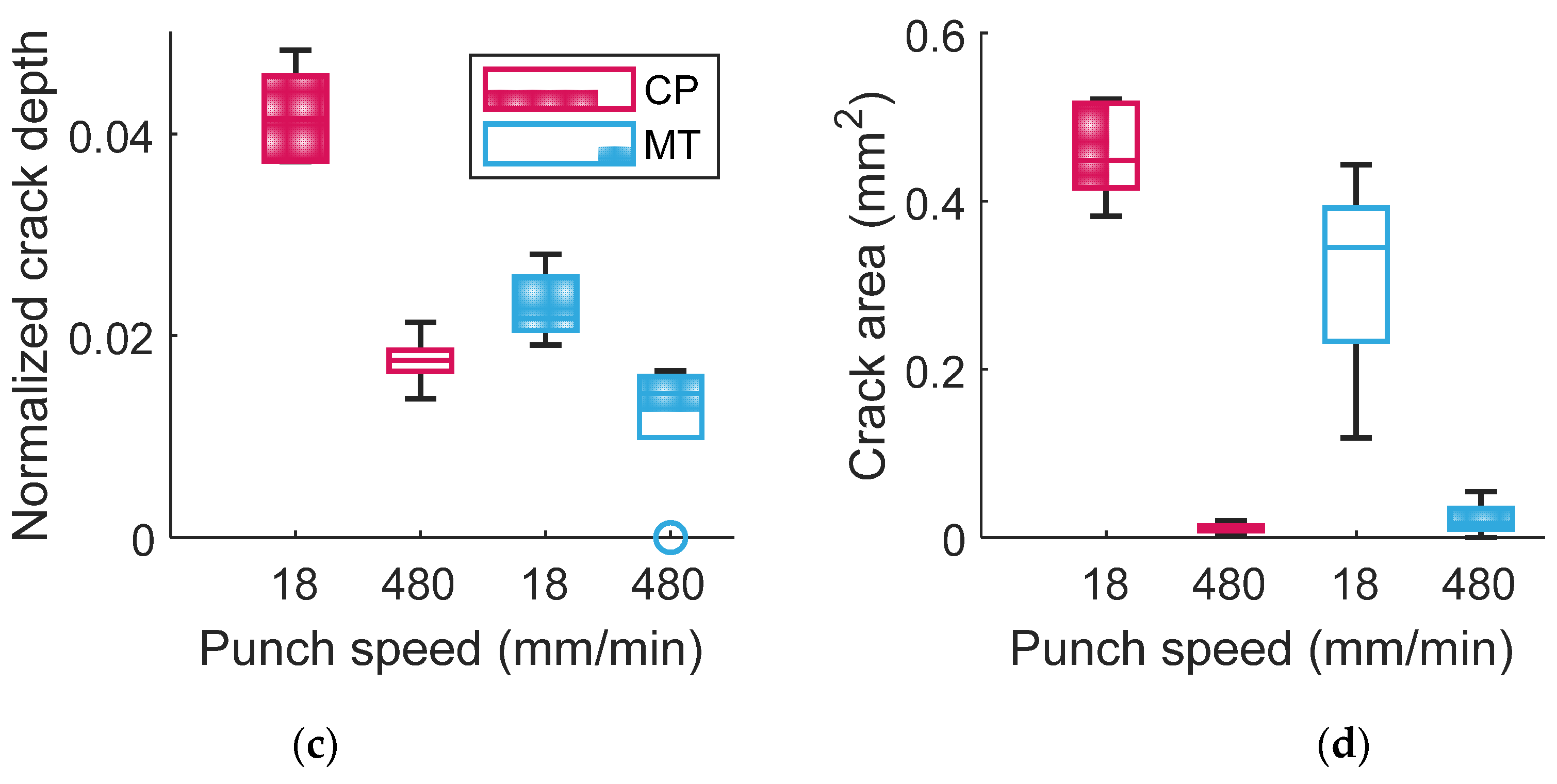
3. Results
4. Conclusions
- Accelerating the bending process delays the measured evolution of surface cracks. This trend was observed in DP, CP, and MS steels for both small-radius and large-radius bending.
- Unlike tension-based tests, bending tests allow the failure limit to be addressed without necking or flow instability. The enhanced bendability is attributed to an increase in failure strain rather than depending on the rate hardening (such as lift-off) since the bending radii were similar between the two speeds for DP and MS steel.
- For CP steel in tight-radius bending, accelerated bending produced larger bending radii, implying a significant effect of rate hardening. This indicates that accurate modeling of CP steel bending requires incorporating both rate hardening and rate-dependent fracture strain.
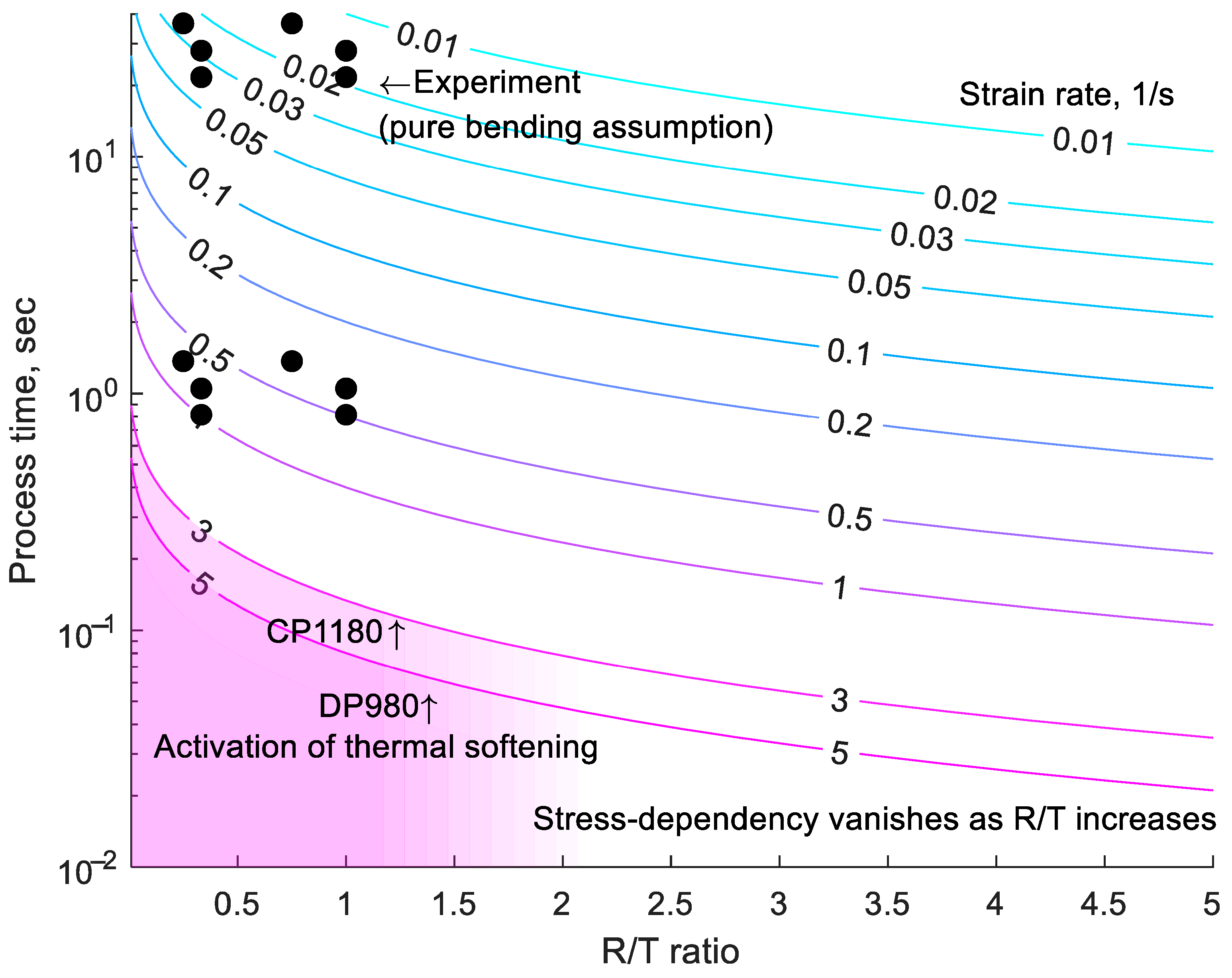
- Using pure bending theory, the process time limit beyond which bendability improvements are no longer guaranteed can be estimated. As discussed in Section 3, this limit is assumed to correspond to the strain rate at which thermal activation begins.
- Furthermore, our results suggest that the benefits of stepwise bending observed in industrial practice are due to relaxation or heat dissipation, rather than a direct strain rate effect itself. This distinction is important for interpreting the mechanism behind improved bendability in slow, incremental forming operations. However, additional experiments are needed to isolate and quantify the influence of relaxation effects.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Andersen, R.; Londono, J.; Woelke, P.; Nielsen, K. Fundamental Differences between Plane Strain Bending and Far-Field Plane Strain Tension in Ductile Plate Failure. J. Mech. Phys. Solids 2020, 141, 103960. [Google Scholar] [CrossRef]
- Kim, H.; Bandar, A.R.; Yang, Y.P.; Sung, J.H.; Wagoner, R.H. Failure Analysis of Advanced High Strength Steels (AHSS) during Draw Bending. In Proceedings of the International Deep Drawing Research Group Annual Conference (IDDRG 2009), Golden, CO, USA, 1–3 June 2009. [Google Scholar]
- Kaupper, M.; Merklein, M. Bendability of Advanced High Strength Steels—A New Evaluation Procedure. CIRP Ann. 2013, 62, 247–250. [Google Scholar] [CrossRef]
- Jeong, K.; Jeong, Y.; Lee, J.; Chung, G.; Kim, G.-H.; Yoon, J. Experimental Correlation between Bending Crack Evolution and Load-Drop Criterion in Tight-Radius Three-Point Bending Test with GPa-Grade Steels. Int. J. Solids Struct. 2024, 301, 112949. [Google Scholar] [CrossRef]
- Rèche, D.; Sturel, T.; Bouaziz, O.; Col, A.; Gourgues-Lorenzon, A. Damage Development in Low Alloy TRIP-Aided Steels During Air-Bending. Mater. Sci. Eng. A 2011, 528, 5241–5250. [Google Scholar] [CrossRef]
- Yamazaki, K.; Oka, M.; Yasuda, H.; Mizuyama, Y.; Tsuchiya, H. Recent Advances in Ultrahigh-Strength Sheet Steels for Automotive Structural Use; Nippon Steel Technical Report; Nippon Steel Corporation: Osaka, Japan, 1995. [Google Scholar]
- Hudgins, A.; Matlock, D. The Effects of Property Differences in Multiphase Sheet Steels on Local Formability. Mater. Sci. Eng. A 2016, 654, 169–176. [Google Scholar] [CrossRef]
- Barnwal, V.K.; Lee, S.-Y.; Choi, J.; Kim, J.-H.; Barlat, F. Performance Review of Various Uncoupled Fracture Criteria for TRIP Steel Sheet. Int. J. Mech. Sci. 2021, 195, 106269. [Google Scholar] [CrossRef]
- VDA-238-100; Plate Bending Test for Metallic Materials. Verband der Automobilindustrie: Berlin, Germany, 2020.
- Demeri, M.Y.; Lampman, S. Forming of Carbon Steels. In Metalworking: Sheet Forming; ASM International: Materials Park, OH, USA, 2006; pp. 495–529. [Google Scholar]
- Daehn, G.S. High-Velocity Metal Forming. In Metalworking: Sheet Forming; ASM International: Materials Park, OH, USA, 2006; pp. 405–418. [Google Scholar]
- ISO-7438; Metallic Materials—Bend Test. International Organization for Standardization: Geneva, Switzerland, 2016.
- ASTM-E290; Standard Test Methods for Bend Testing of Material for Ductility. ASTM International: West Conshohocken, PA, USA, 2009.
- Sato, K.; Yu, Q.; Hiramoto, J.; Urabe, T.; Yoshitake, A. A Method to Investigate Strain Rate Effects on Necking and Fracture Behaviors of Advanced High-Strength Steels Using Digital Imaging Strain Analysis. Int. J. Impact Eng. 2015, 75, 11–26. [Google Scholar] [CrossRef]
- Kim, J.-H.; Kim, D.; Han, H.N.; Barlat, F.; Lee, M.-G. Strain Rate Dependent Tensile Behavior of Advanced High Strength Steels: Experiment and Constitutive Modeling. Mater. Sci. Eng. A 2013, 559, 222–231. [Google Scholar] [CrossRef]
- Gronostajski, Z.; Niechajowicz, A.; Kuziak, R.; Krawczyk, J.; Polak, S. The Effect of the Strain Rate on the Stress-Strain Curve and Microstructure of AHSS. J. Mech. Work. Technol. 2017, 242, 246–259. [Google Scholar] [CrossRef]
- Roth, C.C.; Mohr, D. Effect of Strain Rate on Ductile Fracture Initiation in Advanced High Strength Steel Sheets: Experiments and Modeling. Int. J. Plast. 2014, 56, 19–44. [Google Scholar] [CrossRef]
- Erice, B.; Roth, C.C.; Mohr, D. Stress-State and Strain-Rate Dependent Ductile Fracture of Dual and Complex Phase Steel. Mech. Mater. 2018, 116, 11–32. [Google Scholar] [CrossRef]
- Johnson, G.R.; Cook, W.H. A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, The Netherlands, 19–21 April 1983. [Google Scholar]
- Kim, J.H.; Sung, J.H.; Wagoner, R.H. Thermo-Mechanical Modeling of Draw-Bend Formability Tests. In Proceedings of the International Deep Drawing Research Group Annual Conference (IDDRG 2009), Golden, CO, USA, 1–3 June 2009. [Google Scholar]
- Lee, J.; Kim, J.; Lee, M.; Barlat, F.; Zhou, C.; Chen, Z.; Wagoner, R. Properties Controlling the Bend-Assisted Fracture of AHSS. Int. J. Plast. 2015, 75, 100–120. [Google Scholar] [CrossRef]
- Hariharan, K.; Majidi, O.; Kim, C.; Lee, M.; Barlat, F. Stress Relaxation and Its Effect on Tensile Deformation of Steels. Mater. Des. 2013, 52, 284–288. [Google Scholar] [CrossRef]
- Majidi, O.; Barlat, F.; Lee, M.; Kim, D. Formability of AHSS under an Attach–Detach Forming Mode. Steel Res. Int. 2014, 86, 98–109. [Google Scholar] [CrossRef]
- Badr, O.M.; Rolfe, B.; Hodgson, P.; Weiss, M. Experimental Study into the Correlation Between the Incremental Forming and the Nature of Springback in Automotive Steels. Int. J. Mater. Prod. Technol. 2013, 47, 150–161. [Google Scholar] [CrossRef]
- Wagner, L.; Larour, P.; Dolzer, D.; Leomann, F.; Suppan, C. Experimental Issues in the Instrumented 3 Point Bending Vda238-100 Test. In Proceedings of the International Deep-Drawing Research Group (IDDRG 2020), Seoul, Republic of Korea, 26–30 October 2020. [Google Scholar]
- POSCO. 2022 Automotive Steel Catalog (Data Book); POSCO: Incheon, Republic of Korea, 2022. [Google Scholar]
- Barnwal, V.K.; Lee, S.-Y.; Choi, J.; Kim, J.-H.; Barlat, F. Fracture Assessment in Dual Phase and Transformation-Induced Plasticity Steels during 3-Point Bending. Theor. Appl. Fract. Mech. 2020, 110, 102834. [Google Scholar] [CrossRef]
- Lai, Q.; Bouaziz, O.; Gouné, M.; Brassart, L.; Verdier, M.; Parry, G.; Perlade, A.; Bréchet, Y.; Pardoen, T. Damage and Fracture of Dual-Phase Steels: Influence of Martensite Volume Fraction. Mater. Sci. Eng. A 2015, 646, 322–331. [Google Scholar] [CrossRef]
- Larour, P.; Hackl, B.; Leomann, F.; Benedyk, K. Bending Angle Calculation in the Instrumented Three-Point Bending Test. In Proceedings of the International Deep Drawing Research Group (IDDRG) Conference, Mumbai, India, 25–29 November 2012. [Google Scholar]
- Roth, C.C.; Mohr, D. Ductile Fracture Experiments with Locally Proportional Loading Histories. Int. J. Plast. 2016, 79, 328–354. [Google Scholar] [CrossRef]
- Pack, K.; Tancogne-Dejean, T.; Gorji, M.B.; Mohr, D. Hosford-Coulomb Ductile Failure Model for Shell Elements: Experimental Identification and Validation for DP980 Steel and Aluminum 6016-T4. Int. J. Solids Struct. 2018, 151, 214–232. [Google Scholar] [CrossRef]
- Meyers, M.A. Dynamic Behavior of Materials; John Wiley & Sons: Hoboken, NJ, USA, 1994. [Google Scholar]
- Meyers, M.A.; Krishan, K.C. Mechanical Behavior of Materials; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Pratt, V. Direct Least-Squares Fitting of Algebraic Surfaces. ACM SIGGRAPH Comput. Graph. 1987, 21, 145–152. [Google Scholar] [CrossRef]
- ASTM-E8; Standard Test Methods for Tension Testing of Metallic Materials. ASTM International: West Conshohocken, PA, USA, 2008.
- Cai, H.L.; Wang, J.F.; Wu, D.; Yi, H.L. A Simple Methodology to Determine Fracture Strain of Press-Hardened Steels Under Plane Strain Bending. Met. Mater. Trans. A 2021, 52, 644–654. [Google Scholar] [CrossRef]
- Cheong, K.; Omer, K.; Butcher, C.; George, R.; Dykeman, J. Evaluation of the Vda 238-100 Tight Radius Bending Test Using Digital Image Correlation Strain Measurement. J. Phys. Conf. Ser. 2017, 896, 012075. [Google Scholar] [CrossRef]


| DP980 1.6T | CP1180 1.2T | MS1500 1.2T | |
|---|---|---|---|
| 18 mm/min | 0.0224 | 0.0104 | 0.0095 |
| 480 mm/min | 0.5968 | 0.2773 | 0.2543 |
| Punch radius (mm) | 0.4 | 1.5 | ||||||||
| Material | DP980 | CP1180 | MS1500 | CP1180 | MS1500 | |||||
| Punch speed (mm/min) | 18 | 480 | 18 | 480 | 18 | 480 | 18 | 480 | 18 | 480 |
| Angle (degree) | 79.5524 | 79.3609 | 75.8111 | 76.0552 | 52.0668 | 50.603 | 89.1062 | 89.9101 | 59.02 | 56.9368 |
| 79.7246 | 79.8324 | 75.9962 | 75.5896 | 50.7595 | 51.0451 | 89.1015 | 89.2225 | 58.8665 | 57.0554 | |
| 79.04 | 79.359 | 75.9236 | 74.801 | 50.0062 | 50.7889 | 89.8222 | 89.8353 | 56.8551 | 57.2111 | |
| 79.0214 | 79.6706 | 75.1943 | 75.8007 | 50.8385 | 49.7906 | 89.1646 | 89.1777 | 56.9284 | 57.0547 | |
| 80.1123 | 79.9465 | 74.2204 | 74.9536 | 51.7876 | 50.8063 | - | 89.7726 | 56.8024 | 55.9274 | |
| Mean | 79.4901 | 79.6339 | 75.4291 | 75.4400 | 51.0917 | 50.6068 | 89.2986 | 89.5836 | 57.6945 | 56.8371 |
| Standard deviation | 0.4659 | 0.2686 | 0.7463 | 0.5422 | 0.8348 | 0.4825 | 0.3502 | 0.3538 | 1.1421 | 0.5178 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeong, K.; Lee, J.; Yoon, J. Experimental Investigation of Delayed Fracture Initiation in Advanced High-Strength Steel Under Accelerated Bending. Materials 2025, 18, 3415. https://doi.org/10.3390/ma18143415
Jeong K, Lee J, Yoon J. Experimental Investigation of Delayed Fracture Initiation in Advanced High-Strength Steel Under Accelerated Bending. Materials. 2025; 18(14):3415. https://doi.org/10.3390/ma18143415
Chicago/Turabian StyleJeong, Kyucheol, Jaewook Lee, and Jonghun Yoon. 2025. "Experimental Investigation of Delayed Fracture Initiation in Advanced High-Strength Steel Under Accelerated Bending" Materials 18, no. 14: 3415. https://doi.org/10.3390/ma18143415
APA StyleJeong, K., Lee, J., & Yoon, J. (2025). Experimental Investigation of Delayed Fracture Initiation in Advanced High-Strength Steel Under Accelerated Bending. Materials, 18(14), 3415. https://doi.org/10.3390/ma18143415





