Streamlining First-Order Reversal Curves Analysis of Molecular Magnetism Bistability Using a Calorimetric Approach
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Magnetometric Measurements
3.2. Calorimetric Measurements
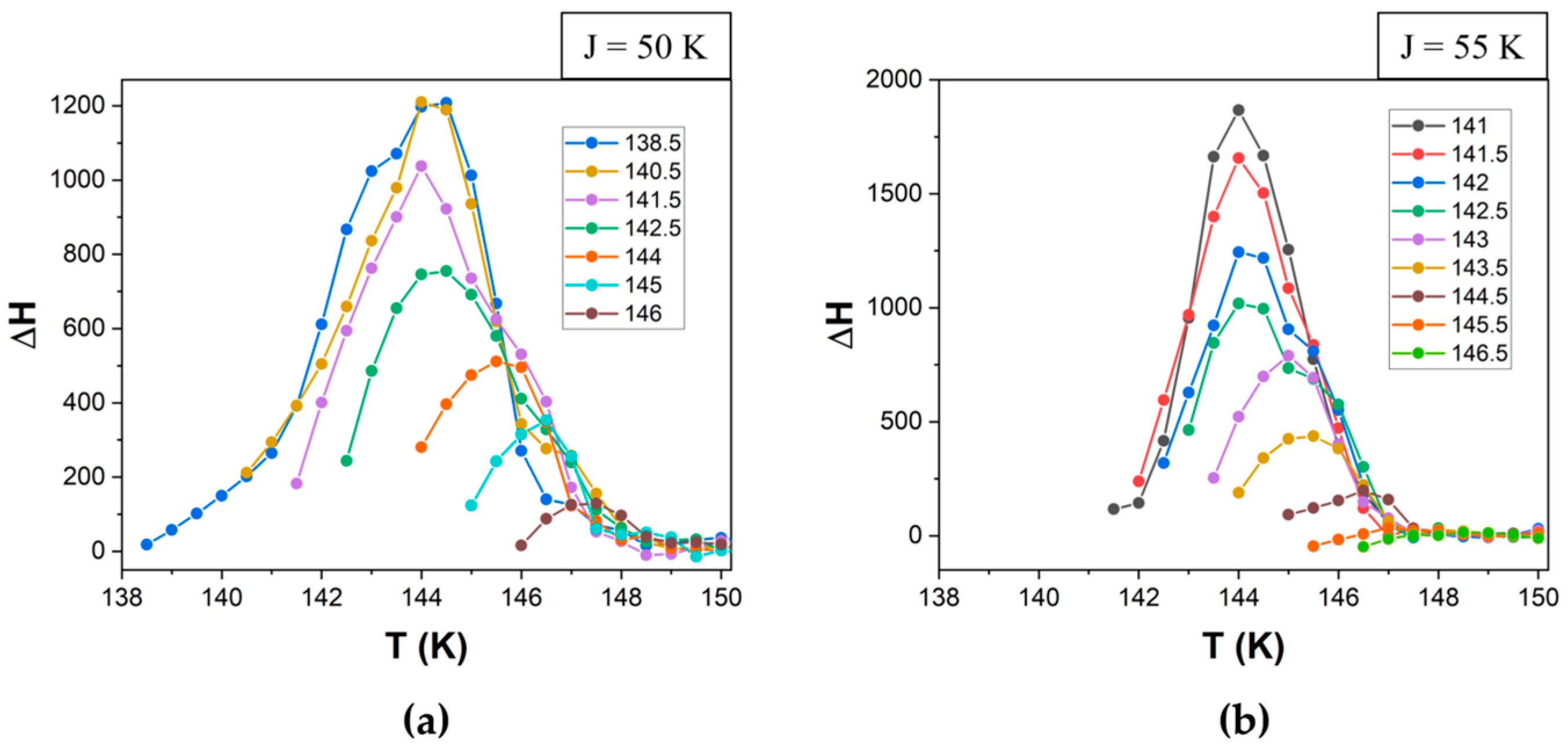
3.3. Simulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FORC | First-Order Reversal Curve |
| SQUID | Superconducting Quantum Interference Device |
| DSC | Differential Scanning Calorimetry |
| SCO | Spin Crossover |
| HS | High Spin |
| LS | Low Spin |
Appendix A
Appendix A.1. Calorimetric Measurements
Appendix A.2. Magnetometric Measurements
References
- Gütlich, P.; Goodwin, A. Spin Crossover in Transition Metal Compounds; Springer: Heidelberg, Germany, 2004; Volume I–III. [Google Scholar]
- Halcrow, M.A. Spin-Crossover Materials—Properties and Applications; John Wiley & Sons: Chichester, UK, 2013. [Google Scholar]
- Xu, F.-X.; Zhang, X.-Y.; Wei, H.-Y.; Wang, X.-Y. Hysteretic spin crossover in a Hofmann-type metal–organic framework constructed from a [MoIII(CN)7]4− unit. Inorg. Chem. Front. 2024, 11, 5546–5556. [Google Scholar] [CrossRef]
- Zhao, X.-H.; Deng, Y.-F.; Xi, J.; Huang, J.-Q.; Zhang, Y.-Z. Supramolecular Spring-Like Fe(II) Spin-Crossover Complexes Experiencing Giant and Anisotropic Thermal Expansion Across Two Distinct Temperature Regimes. Angew. Chem.-Int. Edit. 2025, 64, e202414826. [Google Scholar] [CrossRef] [PubMed]
- Linares, J.; Codjovi, E.; Garcia, Y. Pressure and Temperature Spin Crossover Sensors with Optical Detection. Sensors 2012, 12, 4479–4492. [Google Scholar] [CrossRef] [PubMed]
- Raza, Y.; Volatron, F.; Moldovan, S.; Ersen, O.; Huc, V.; Martini, C.; Brisset, F.; Gloter, A.; Stephan, O.; Bousseksou, A.; et al. Matrix-dependent cooperativity in spin crossover Fe(pyrazine)Pt(CN)4 nanoparticles. Chem. Commun. 2011, 47, 11501–11503. [Google Scholar] [CrossRef] [PubMed]
- Tokarev, A.; Long, J.; Guari, Y.; Larionova, J.; Quignard, F.; Agulhon, P.; Robitzer, M.; Molnár, G.; Salmon, L.; Bousseksou, A. Spin crossover polysaccharide nanocomposites. New J. Chem. 2013, 37, 3420–3432. [Google Scholar] [CrossRef]
- Salmon, L.; Catala, L. Spin-crossover nanoparticles and nanocomposite materials. Comptes Rendus Chim. 2018, 21, 1230–1269. [Google Scholar] [CrossRef]
- Manrique-Juárez, M.D.; Suleimanov, I.; Hernández, E.M.; Salmon, L.; Molnár, G.; Bousseksou, A. In Situ AFM Imaging of Microstructural Changes Associated with The Spin Transition in [Fe(Htrz)2(Trz)](Bf4) Nanoparticles. Materials 2016, 9, 537. [Google Scholar] [CrossRef] [PubMed]
- Sy, M.; Traiche, R.; Fourati, H.; Singh, Y.; Varret, F.; Boukheddaden, K. Spatiotemporal Investigations on Light-Driven High-Spin-Low-Spin Interface Dynamics in the Thermal Hysteresis Region of a Spin-Crossover Single Crystal. J. Phys. Chem. C 2018, 122, 20952–20962. [Google Scholar] [CrossRef]
- Tanasa, R.; Stancu, A.; Codjovi, E.; Linares, J.; Varret, F.; Létard, J.-F. A first order reversal curve investigation of pressure hysteresis in multiferroics spin transition compound. J. Appl. Phys. 2008, 103, 07B905. [Google Scholar] [CrossRef]
- Béron, F.; Novak, M.A.; Vaz, M.G.F.; Guedes, G.P.; Knobel, M.; Caldeira, A.; Pirota, K.R. Macroscopic quantum tunneling of magnetization explored by quantum-first-order reversal curves. Appl. Phys. Lett. 2013, 103, 052407. [Google Scholar] [CrossRef]
- Franco, V.; Gottschall, T.; Skokov, K.P.; Gutfleisch, O. First-Order Reversal Curve (FORC) Analysis of Magnetocaloric Heusler-Type Alloys. IEEE Magn. Lett. 2016, 7, 1–4. [Google Scholar] [CrossRef]
- Belyaev, V.K.; Murzin, D.; Martínez-García, J.C.; Rivas, M.; Andreev, N.V.; Kozlov, A.G.; Samardak, A.Y.; Ognev, A.V.; Samardak, A.S.; Rodionova, V. FORC-Diagram Analysis for a Step-like Magnetization Reversal in Nanopatterned Stripe Array. Materials 2021, 14, 7523. [Google Scholar] [CrossRef] [PubMed]
- Arzuza, L.C.; Beron, F.; Pirota, K.R. High-frequency GMI hysteresis effect analysis by first-order reversal curve (FORC) method. J. Magn. Magn. Mater. 2021, 534, 168008. [Google Scholar] [CrossRef]
- Cabanas, A.M.; Pérez del Real, R.; Laroze, D.; Vázquez, M. First-Order Reversal Curves of Sets of Bistable Magnetostrictive Microwires. Materials 2023, 16, 2131. [Google Scholar] [CrossRef] [PubMed]
- Tanasa, R.; Enachescu, C.; Stancu, A.; Linares, J.; Codjovi, E.; Varret, F.; Haasnoot, J.G. First-order reversal curve analysis of spin-transition thermal hysteresis in terms of physical-parameter distributions and their correlations. Phys. Rev. B 2005, 71, 014431. [Google Scholar] [CrossRef]
- Tanasa, R.; Enachescu, C.; Laisney, J.; Morineau, D.; Stancu, A.; Boillot, M.L. Unraveling the Environment Influence in Bistable Spin-Crossover Particles Using Magnetometric and Calorimetric First-Order Reverse Curves. J. Phys. Chem. C 2019, 123, 10120–10129. [Google Scholar] [CrossRef]
- Tanasa, R.; Enachescu, C.; Stancu, A.; Varret, F.; Linares, J.; Codjovi, E. Study of impurities effect in spin crossover compounds using first order reversal curves (FORC) method. Polyhedron 2007, 26, 1820–1824. [Google Scholar] [CrossRef]
- Boukheddaden, K.; Ritti, M.H.; Bouchez, G.; Sy, M.; Dirtu, M.M.; Parlier, M.; Linares, J.; Garcia, Y. Quantitative Contact Pressure Sensor Based on Spin Crossover Mechanism for Civil Security Applications. J. Phys. Chem. C 2018, 122, 7597–7604. [Google Scholar] [CrossRef]
- Tanasa, R.; Stancu, A.; Létard, J.F.; Codjovi, E.; Linares, J.; Varret, F. Piezo- and thermo-switch investigation of the spin-crossover compound [Fe(PM-BiA)2(NCS)2]. Chem. Phys. Lett. 2007, 443, 435–438. [Google Scholar] [CrossRef]
- Rat, S.; Piedrahita-Bello, M.; Salmon, L.; Molnár, G.; Demont, P.; Bousseksou, A. Coupling Mechanical and Electrical Properties in Spin Crossover Polymer Composites. Adv. Mater. 2018, 30, 1705275. [Google Scholar] [CrossRef] [PubMed]
- Piedrahita-Bello, M.; Angulo-Cervera, J.E.; Enriquez-Cabrera, A.; Molnár, G.; Tondu, B.; Salmon, L.; Bousseksou, A. Colossal expansion and fast motion in spin-crossover@polymer actuators. Mater. Horiz. 2021, 8, 3055–3062. [Google Scholar] [CrossRef] [PubMed]
- Glazyrin, K.; Khandarkhaeva, S.; Dubrovinsky, L.; Sprung, M. Revisiting spin-state crossover in (MgFe)O by means of high-resolution x-ray diffraction from a single crystal. Phys. Rev. B 2020, 101, 184203. [Google Scholar] [CrossRef]
- Sorai, M.; Burriel, R.; Westrum, E.F., Jr.; Hendrickson, D.N. Mechanochemical effect in the iron(III) spin crossover complex [Fe(3-MeO-salenEt2]PF6 as studied by heat capacity calorimetry. J. Phys. Chem. B 2008, 112, 4344–4350. [Google Scholar] [CrossRef] [PubMed]
- Benmansour, S.; Triki, S.; Gómez-García, C.J. A Spin Crossover Transition in a Mn(II) Chain Compound. Magnetochemistry 2016, 2, 1. [Google Scholar] [CrossRef]
- Laisney, J.; Morineau, D.; Enachescu, C.; Tanasa, R.; Riviere, E.; Guillot, R.; Boillot, M.L. Mechanical-tuning of the cooperativity of SC particles via the matrix crystallization and related size effects. J. Mater. Chem. C 2020, 8, 7067–7078. [Google Scholar] [CrossRef]
- Sorai, M.; Nakano, M.; Miyazaki, Y. Calorimetric investigation of phase transitions occurring in molecule-based magnets. Chem. Rev. 2006, 106, 976–1031. [Google Scholar] [CrossRef] [PubMed]
- Vreugdenhil, W.; Van Diemen, J.H.; De Graaff, R.A.G.; Haasnoot, J.G.; Reedijk, J.; Van Der Kraan, A.M.; Kahn, O.; Zarembowitch, J. High-spin α low-spin transition in [Fe(NCS)2(4,4′-bis-1,2,4-triazole)2](H2O). X-ray crystal structure and magnetic, mössbauer and EPR properties. Polyhedron 1990, 9, 2971–2979. [Google Scholar] [CrossRef]
- Martin, J.P.; Zarembowitch, J.; Dworkin, A.; Haasnoot, J.G.; Codjovi, E. Solid-State Effects in Spin Transitions: Influence of Iron(II) Dilution on the Magnetic and Calorimetric Properties of the Series [FexNi1-x(4,4′-bis(1,2,4-triazole))2(NCS)2].cntdot.H2O. Inorg. Chem. 1994, 33, 2617–2623. [Google Scholar] [CrossRef]
- Vreugdenhil, W.; Gorter, S.; Haasnoot, J.G.; Reedijk, J. Spectroscopic and magnetic properties of a new class of two-dimensional bitriazole compounds: The X-ray structure of poly-bis (thiocyanato-N)-bis-μ-(4,4′-bis-1,2,4-triazole-N1,N1′)-cobalt (II) monohydrate. Polyhedron 1985, 4, 1769–1775. [Google Scholar] [CrossRef]
- Legrand, V.; Pillet, S.; Carbonera, C.; Souhassou, M.; Létard, J.-F.; Guionneau, P.; Lecomte, C. Optical, Magnetic and Structural Properties of the Spin-Crossover Complex [Fe(btr)2(NCS)2]·H2O in the Light-Induced and Thermally Quenched Metastable States. Eur. J. Inorg. Chem. 2007, 2007, 5693–5706. [Google Scholar] [CrossRef]
- Plesca, D.; Railean, A.; Tanasa, R.; Stancu, A.; Laisney, J.; Boillot, M.L.; Enachescu, C. Unexpected Light-Induced Thermal Hysteresis in Matrix Embedded Low Cooperative Spin Crossover Microparticles. Magnetochemistry 2021, 7, 59. [Google Scholar] [CrossRef]
- Pike, C.R.; Roberts, A.P.; Verosub, K.L. Characterizing interactions in fine magnetic particle systems using first order reversal curves. J. Appl. Phys. 1999, 85, 6660–6667. [Google Scholar] [CrossRef]
- Pike, C.R.; Roberts, A.P.; Verosub, K.L. First-order reversal curve diagrams and thermal relaxation effects in magnetic particles. Geophys. J. Int. 2001, 145, 721–730. [Google Scholar] [CrossRef]
- Palacios, E.; Burriel, R.; Zhang, C.L. Calorimetric study of the giant magnetocaloric effect in (MnNiSi)_(0.56)(FeNiGe)_(0.44). Phys. Rev. B 2021, 103, 104402. [Google Scholar] [CrossRef]
- Law, J.Y.; Moreno-Ramírez, L.M.; Díaz-García, Á.; Franco, V. Current perspective in magnetocaloric materials research. J. Appl. Phys. 2023, 133, 040903. [Google Scholar] [CrossRef]










Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plesca, D.; Enachescu, C.; Tanasa, R.; Stancu, A.; Morineau, D.; Boillot, M.-L. Streamlining First-Order Reversal Curves Analysis of Molecular Magnetism Bistability Using a Calorimetric Approach. Materials 2025, 18, 3413. https://doi.org/10.3390/ma18143413
Plesca D, Enachescu C, Tanasa R, Stancu A, Morineau D, Boillot M-L. Streamlining First-Order Reversal Curves Analysis of Molecular Magnetism Bistability Using a Calorimetric Approach. Materials. 2025; 18(14):3413. https://doi.org/10.3390/ma18143413
Chicago/Turabian StylePlesca, Diana, Cristian Enachescu, Radu Tanasa, Alexandru Stancu, Denis Morineau, and Marie-Laure Boillot. 2025. "Streamlining First-Order Reversal Curves Analysis of Molecular Magnetism Bistability Using a Calorimetric Approach" Materials 18, no. 14: 3413. https://doi.org/10.3390/ma18143413
APA StylePlesca, D., Enachescu, C., Tanasa, R., Stancu, A., Morineau, D., & Boillot, M.-L. (2025). Streamlining First-Order Reversal Curves Analysis of Molecular Magnetism Bistability Using a Calorimetric Approach. Materials, 18(14), 3413. https://doi.org/10.3390/ma18143413






