Buckling Performance of Prefabricated Light-Gauge Steel Frame Materials Under Combined Random Defects During Construction: A CRITIC-Based Analysis
Abstract
1. Introduction
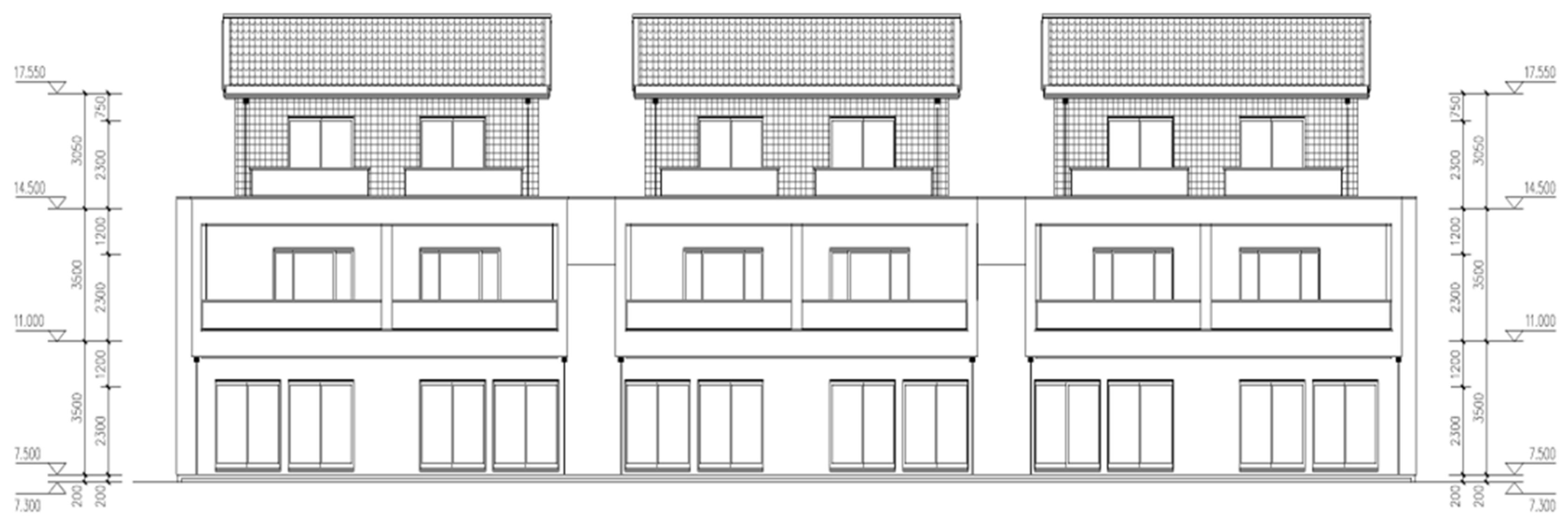
2. Finite Element Model of LGSF
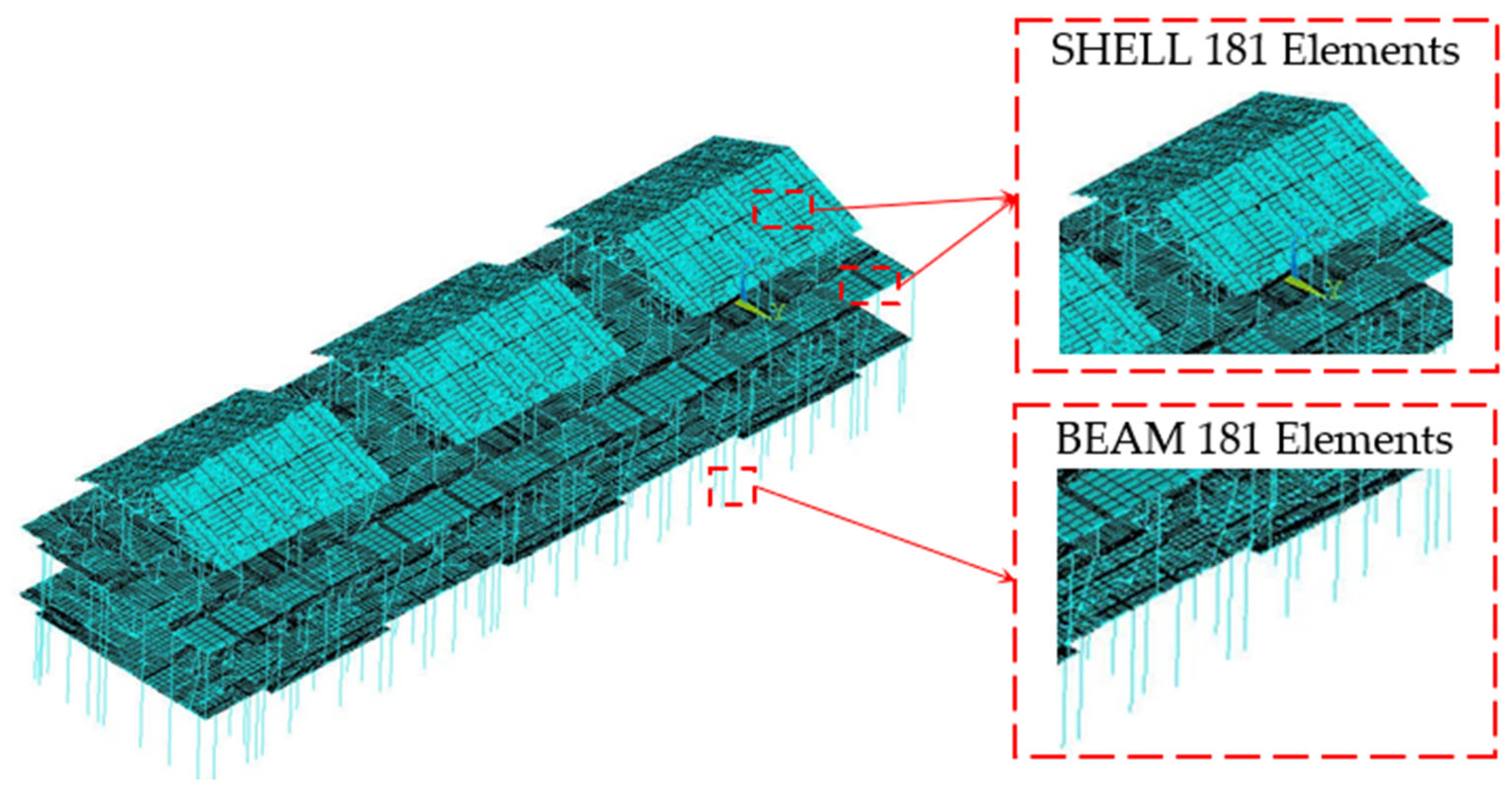
2.1. Finite Element Model Development and Validation
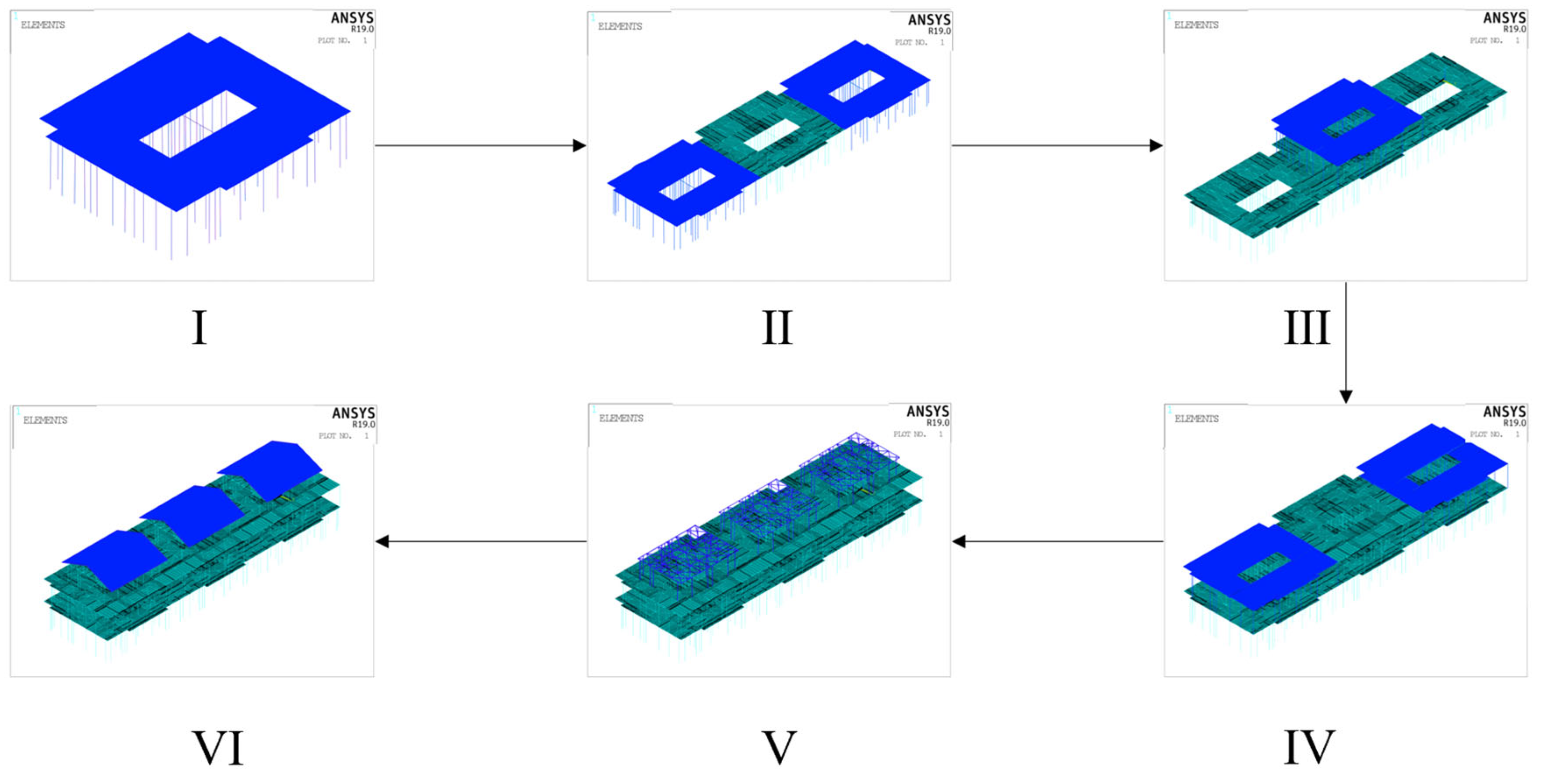
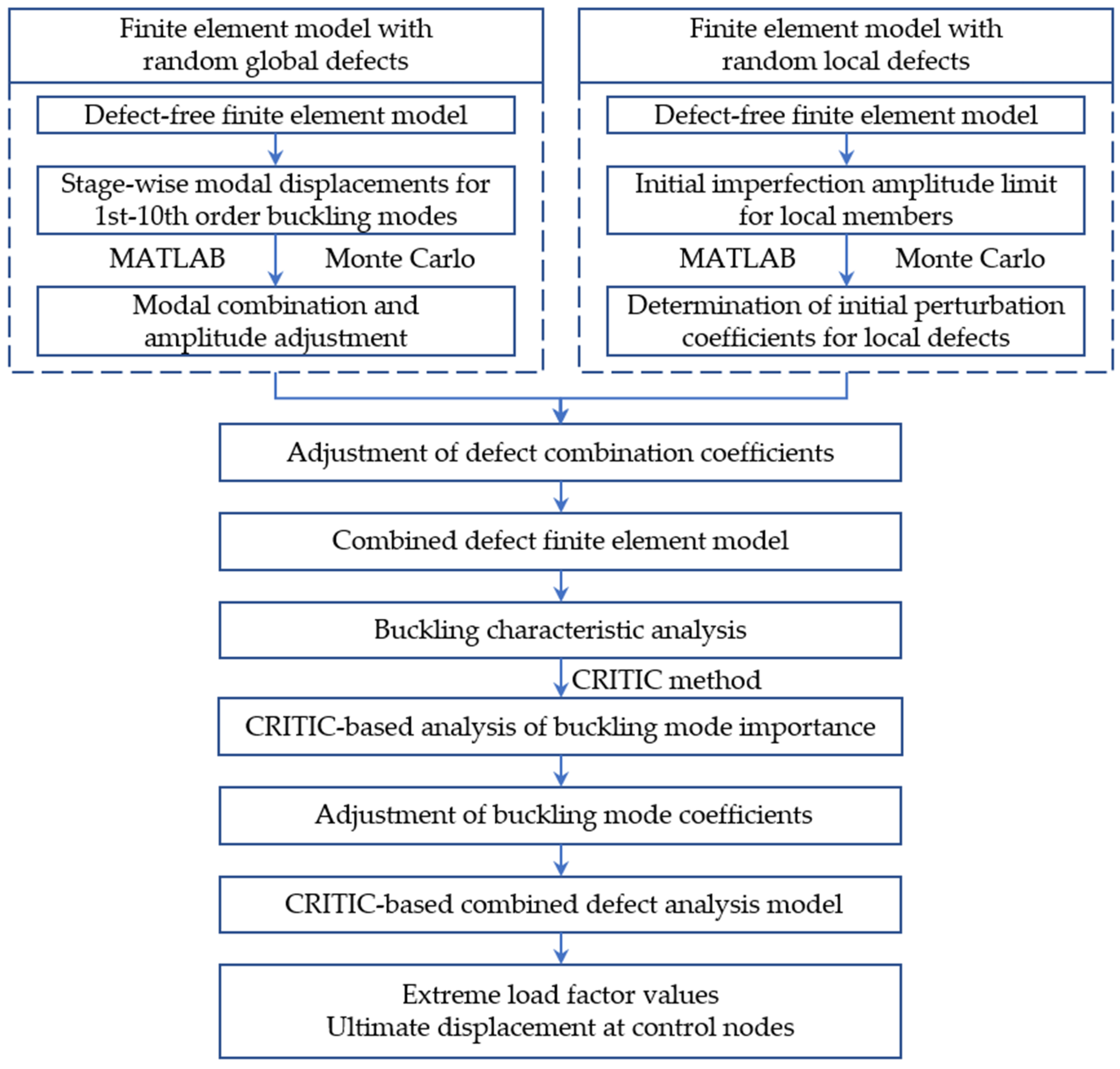
2.2. Combined Defect Application Method
3. CRITIC-Based Combined Defect Analysis Model
3.1. CRITIC Method
3.2. Data Preprocessing
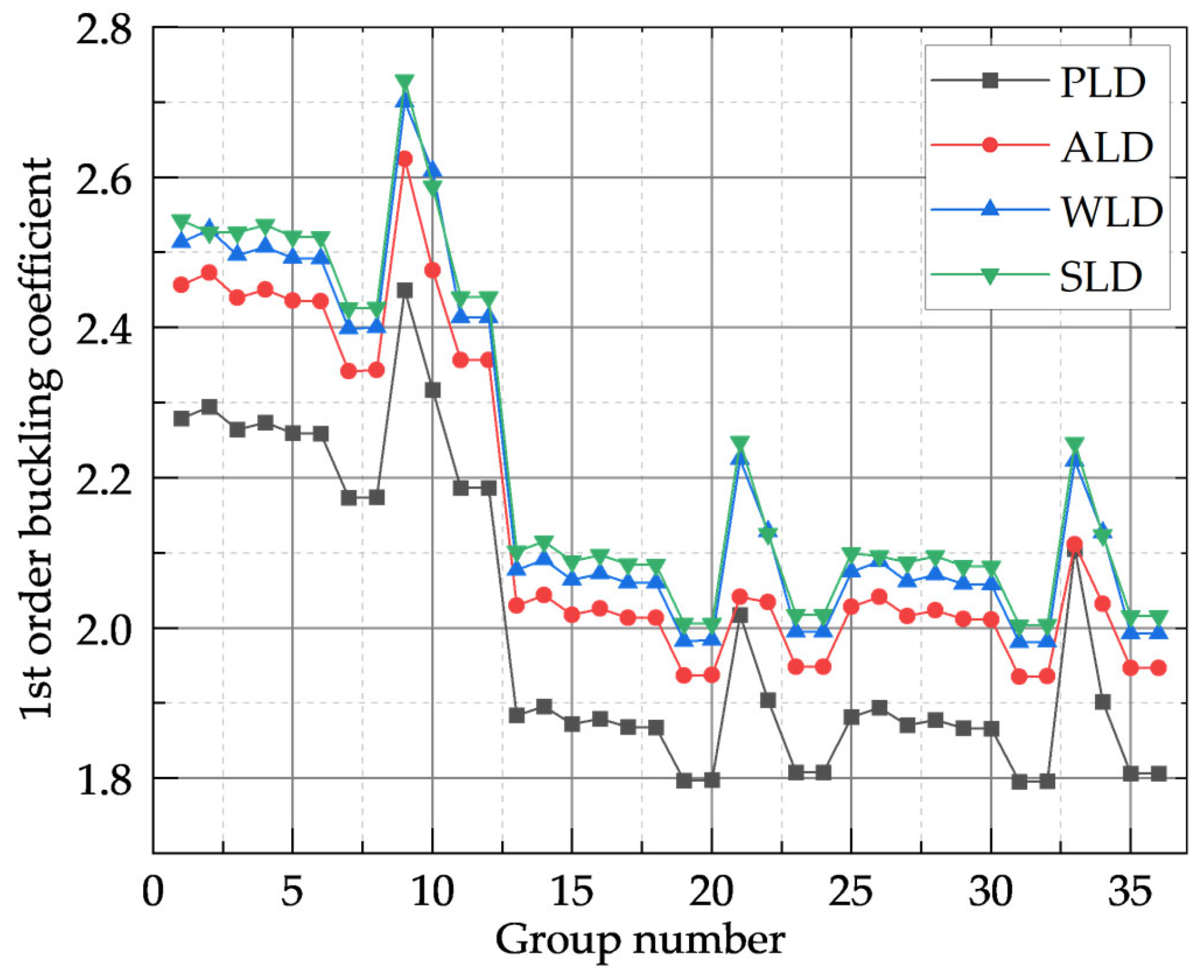
3.3. Method Comparison
3.3.1. Preprocessing
3.3.2. Comparison of Trial Results
3.4. The Proposed CRITIC-Based Combined Defect Analysis Model
4. Experiments and Results
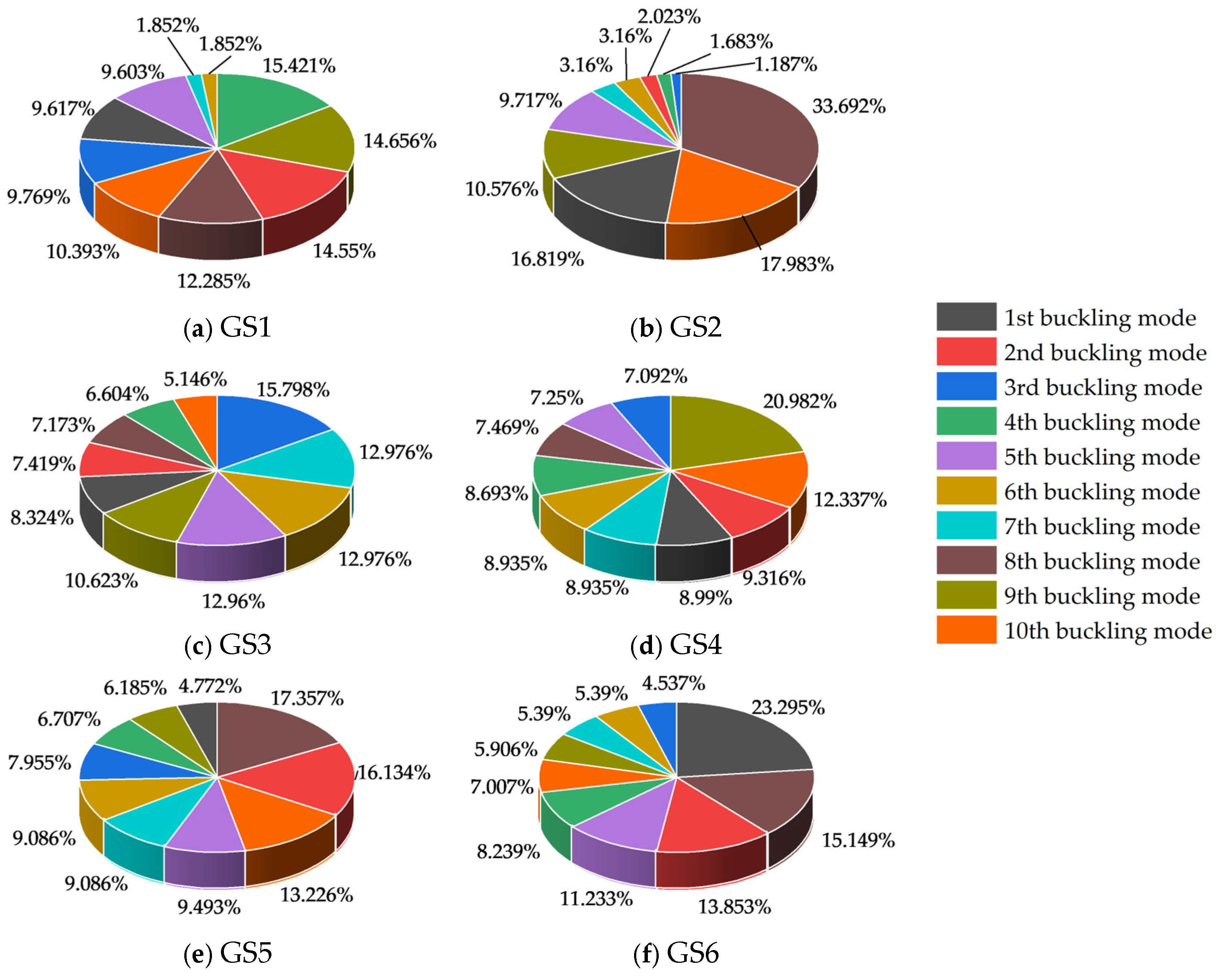
4.1. Buckling Mode Importance Analysis
4.1.1. Buckling Mode Importance Analysis Under Dominant Random Global Defects
4.1.2. Buckling Mode Importance Analysis Under Dominant Random Local Defects
4.2. CRITIC-Based Analysis of Buckling Characteristics Under Combined Defects
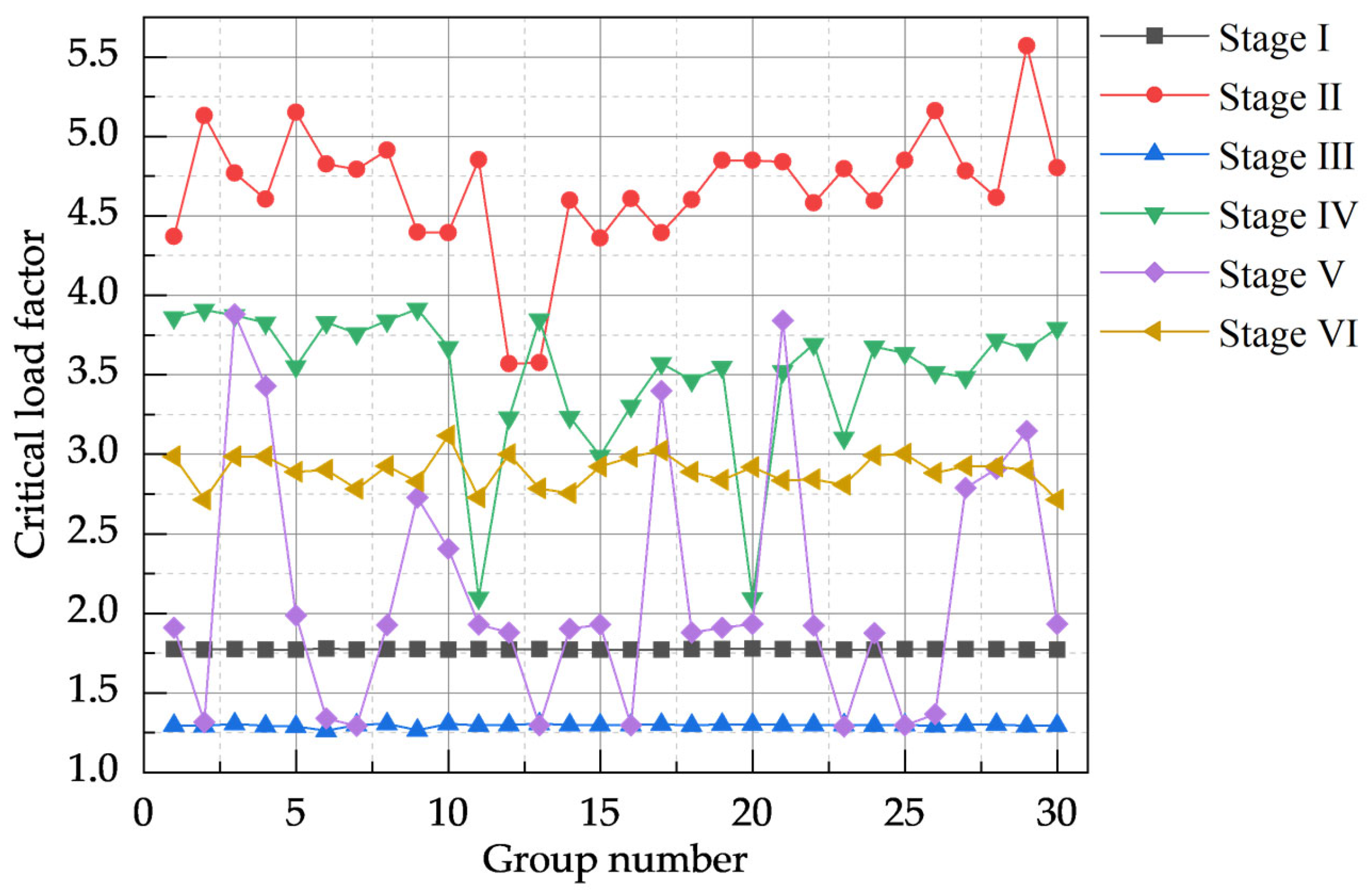
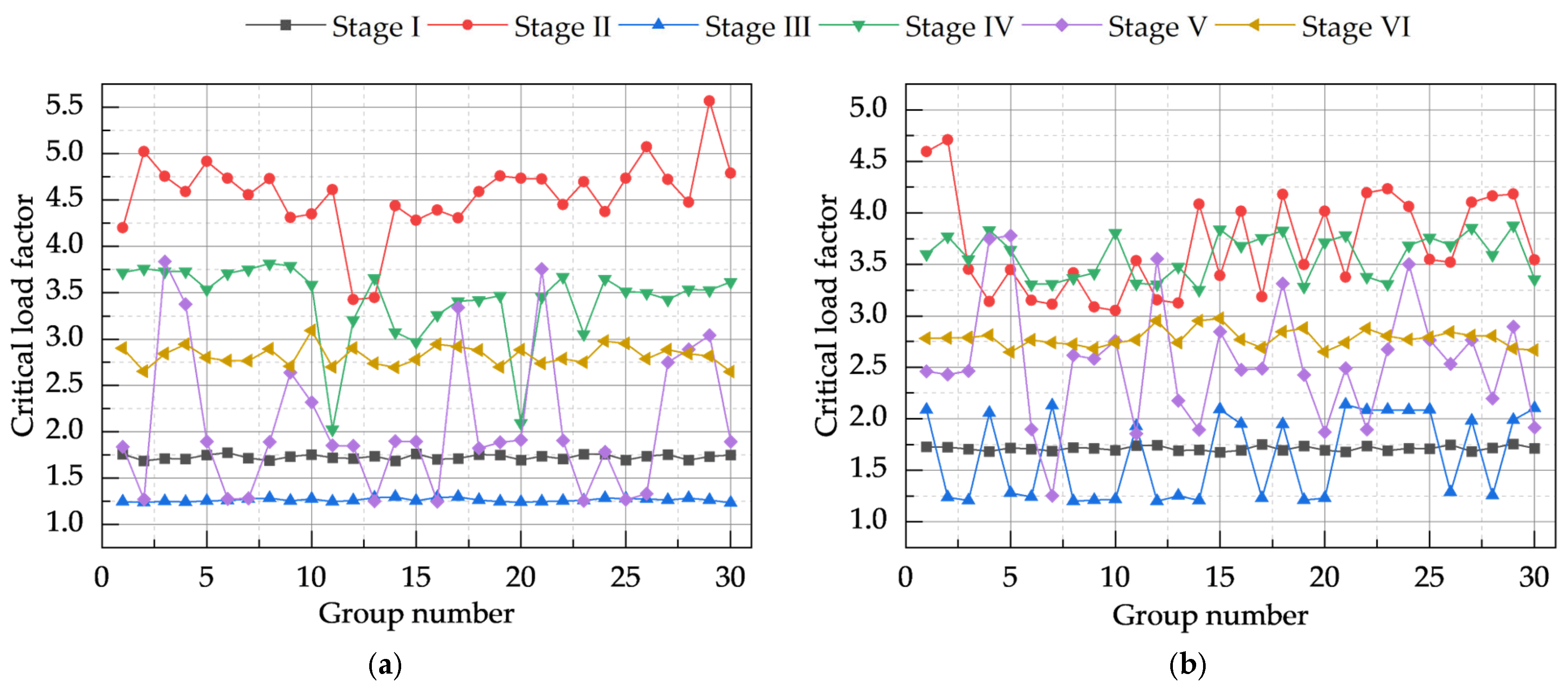
4.2.1. Critical Load Factor Analysis
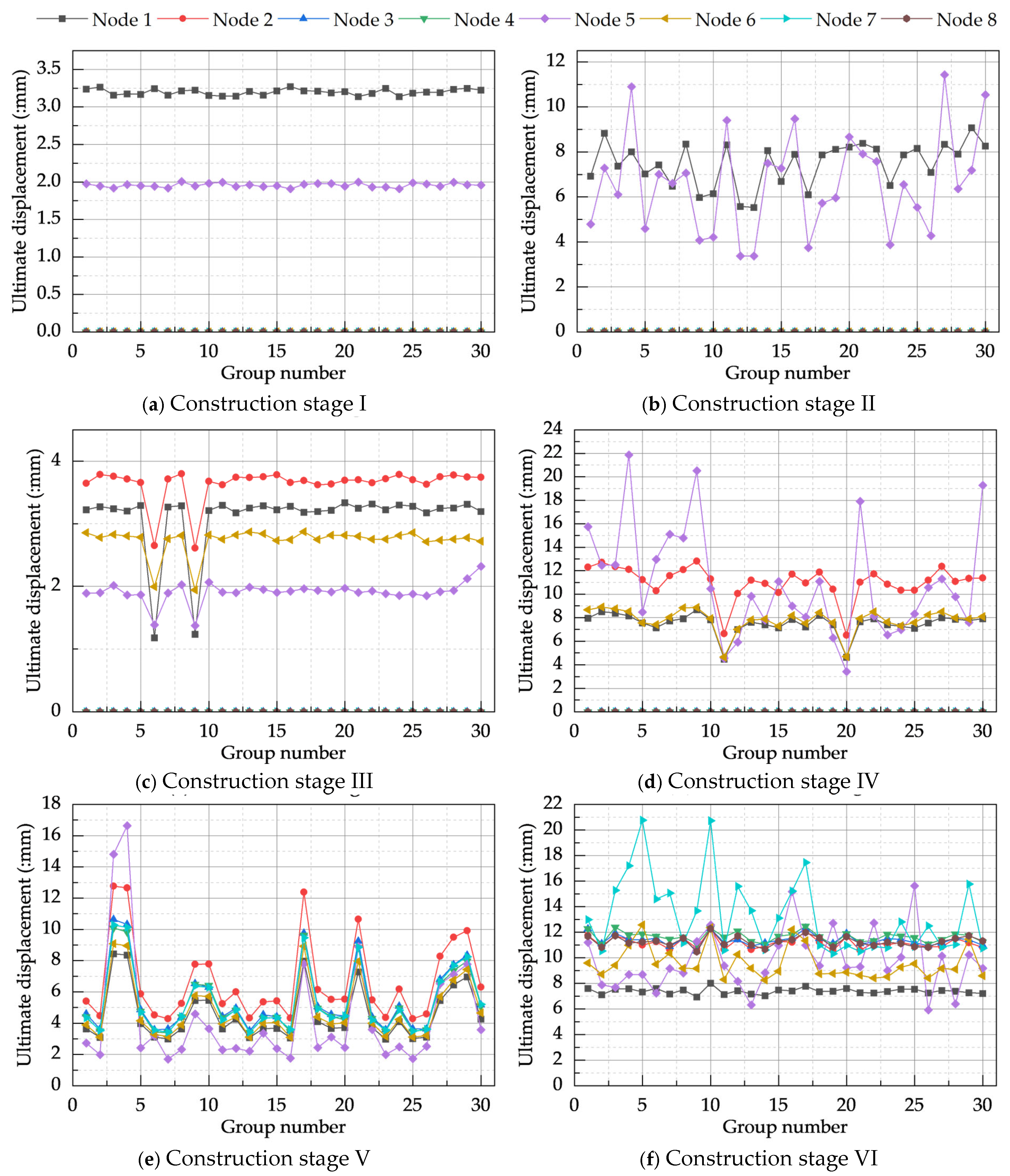
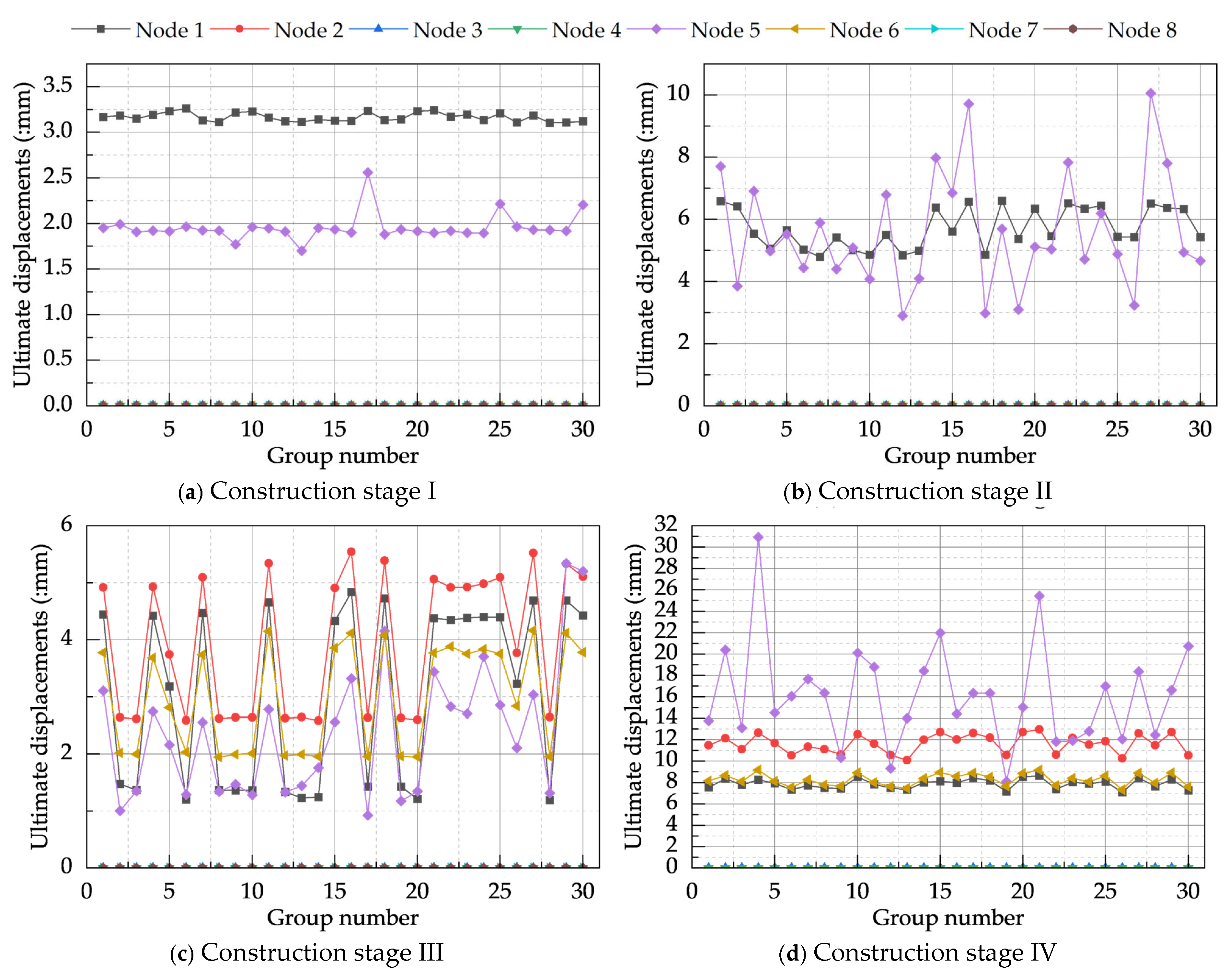
4.2.2. Control Node Ultimate Displacement Analysis
- (1)
- Global defect-dominated model
- (2)
- Local defect-dominated model
5. Conclusions
- (1)
- Compared to PCA, MLR, and SR algorithms, the CRITIC method is more conducive in quantitatively analyzing the importance of the buckling modes in LGSF models. It was found that under combined random defects, the influence of these buckling modes on the model’s buckling characteristics varies across different construction stages. Buckling mode weights typically fluctuated between 5% and 20%. This demonstrates that for LGSF materials, the traditional assumption that the first-order buckling mode is the most unfavorable is inaccurate; analyses simulating model defects based solely on the first-order buckling mode yield unconservative results.
- (2)
- Compared to random defect models established using a modified Monte Carlo-based random defect analysis method, defect models developed using the CRITIC method exhibited lower critical load factors and correspondingly higher ultimate displacements at control nodes. For combined defects under different dominant defect types, the reduction in critical load factors ranged from 0 to 5%, while the increase in ultimate displacement at control nodes ranged from 1 to 3%. This indicates that the combined defect model established using the CRITIC method represents the most unfavorable conditions.
- (3)
- For the engineering case study herein, under combined defects dominated by global defects, the most unfavorable buckling modes during construction stages I–VI were the 4th-, 8th-, 3rd-, 9th-, 8th-, and 1st-order modes, respectively. Under combined defects dominated by local defects, the most unfavorable buckling modes for these stages were the 9th-, 5th-, 1st-, 9th-, 2nd-, and, jointly, the 6th- and 7th-order modes, respectively.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, H.; Chen, Z.; Zhao, M.; Wang, B.; Ye, Y. Seismic Performance of Frame with Middle Partially Encased Composite Brace and Steel-Hollow Core Partially Encased Composite Spliced Frame Beam. J. Build. Eng. 2024, 95, 110226. [Google Scholar] [CrossRef]
- Zhou, T.; Sun, K.; Chen, Z.; Yang, Z.; Liu, H. Automated Optimum Design of Light Steel Frame Structures in Chinese Rural Areas Using Building Information Modeling and Simulated Annealing Algorithm. Sustainability 2023, 15, 9000. [Google Scholar] [CrossRef]
- Morales-Beltran, M.; Engür, P.; Şişman, Ö.A.; Aykar, G.N. Redesigning for Disassembly and Carbon Footprint Reduction: Shifting from Reinforced Concrete to Hybrid Timber–Steel Multi-Story Building. Sustainability 2023, 15, 7273. [Google Scholar] [CrossRef]
- Wu, H.; Tu, T.; Sui, L.; Yan, F.; Zhou, T. A Novel Modular CFS Composite Frame-Wall Structure: Experimental Investigation and Numerical Analysis. J. Constr. Steel Res. 2024, 218, 108702. [Google Scholar] [CrossRef]
- Olawumi, T.O.; Chan, D.W.M.; Ojo, S.; Yam, M.C.H. Automating the Modular Construction Process: A Review of Digital Technologies and Future Directions with Blockchain Technology. J. Build. Eng. 2022, 46, 103720. [Google Scholar] [CrossRef]
- Zhao, B.; Wu, D.; Zhu, H. New Modular Precast Composite Shear Wall Structural System and Experimental Study on Its Seismic Performance. Eng. Struct. 2022, 264, 114381. [Google Scholar] [CrossRef]
- Yao, G.; Chen, Y.; Yang, Y.; Ma, X.; Men, W. Investigation on Buckling Performance of Prefabricated Light Steel Frame Materials under the Action of Random Defects during Construction. Materials 2023, 16, 5666. [Google Scholar] [CrossRef]
- Feng, S.; Liu, Z.; Zhou, X.; Guo, Z. Seismic Performance of Curved Haunched Connections in Modularized Prefabricated Steel Structures. J. Constr. Steel Res. 2020, 172, 106188. [Google Scholar] [CrossRef]
- Skiadopoulos, A.; de Castro e Sousa, A.; Lignos, D.G. Experiments and Proposed Model for Residual Stresses in Hot-Rolled Wide Flange Shapes. J. Constr. Steel Res. 2023, 210, 108069. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, L.; Yao, G. Post-Processing of High Formwork Monitoring Data Based on the Back Propagation Neural Networks Model and the Autoregressive—Moving-Average Model. Symmetry 2021, 13, 1543. [Google Scholar] [CrossRef]
- Sun, J.; Dilger, K. Influence of Initial Residual Stresses on Welding Residual Stresses in Ultra-High Strength Steel S960. J. Manuf. Process. 2023, 101, 259–268. [Google Scholar] [CrossRef]
- GB50755-2012; Code for Construction of Steel Structures. China Building Industry Press: Beijing, China, 2012.
- Kepple, J.; Herath, M.; Pearce, G.; Prusty, G.; Thomson, R.; Degenhardt, R. Improved Stochastic Methods for Modelling Imperfections for Buckling Analysis of Composite Cylindrical Shells. Eng. Struct. 2015, 100, 385–398. [Google Scholar] [CrossRef]
- Arrayago, I.; Rasmussen, K.J.R.; Real, E. Statistical Analysis of the Material, Geometrical and Imperfection Characteristics of Structural Stainless Steels and Members. J. Constr. Steel Res. 2020, 175, 106378. [Google Scholar] [CrossRef]
- Bielewicz, E.; Górski, J. Shells with Random Geometric Imperfections Simulation—Based Approach. Int. J. Non Linear Mech. 2002, 37, 777–784. [Google Scholar] [CrossRef]
- Sobczyk, K.; Trębicki, J. Fatigue Crack Growth in Random Residual Stresses. Int. J. Fatigue 2004, 26, 1179–1187. [Google Scholar] [CrossRef]
- Cui, X.Z.; Li, Y.G.; Hong, H.P. Effect of Spatially Correlated Initial Geometric Imperfection on Reliability of Spherical Latticed Shell Considering Global Instability. Struct. Saf. 2020, 82, 101895. [Google Scholar] [CrossRef]
- Kala, Z.; Valeš, J. Imperfection Sensitivity Analysis of Steel Columns at Ultimate Limit State. Arch. Civ. Mech. Eng. 2018, 18, 1207–1218. [Google Scholar] [CrossRef]
- Zabojszcza, P.; Radoń, U. The Impact of Node Location Imperfections on the Reliability of Single-Layer Steel Domes. Appl. Sci. 2019, 9, 2742. [Google Scholar] [CrossRef]
- Valeš, J.; Kala, Z. Mesh Convergence Study of Solid FE Model for Buckling Analysis. AIP Conf. Proc. 2018, 1978, 150005. [Google Scholar] [CrossRef]
- Patton, M.L.; Singh, K.D. Buckling of Fixed-Ended Concrete-Filled Steel Columns under Axial Compression. Int. J. Steel Struct. 2017, 17, 1059–1071. [Google Scholar] [CrossRef]
- Lauterbach, S.; Fina, M.; Wagner, W. Influence of Stochastic Geometric Imperfections on the Load-Carrying Behaviour of Thin-Walled Structures Using Constrained Random Fields. Comput. Mech. 2018, 62, 1107–1125. [Google Scholar] [CrossRef]
- De Domenico, D.; Falsone, G.; Settineri, D. Probabilistic Buckling Analysis of Beam-Column Elements with Geometric Imperfections and Various Boundary Conditions. Meccanica 2018, 53, 1001–1013. [Google Scholar] [CrossRef]
- Fina, M.; Weber, P.; Wagner, W. Polymorphic Uncertainty Modeling for the Simulation of Geometric Imperfections in Probabilistic Design of Cylindrical Shells. Struct. Saf. 2020, 82, 101894. [Google Scholar] [CrossRef]
- Mirzaie, F.; Myers, A.T.; Jay, A.; Mahmoud, A.; Smith, E.; Schafer, B.W. Analysis of Geometric Imperfections of Spirally Welded Slender Steel Tubes. Thin Walled Struct. 2020, 146, 106447. [Google Scholar] [CrossRef]
- Fonseca, E.M.M. Steel Columns under Compression with Different Sizes of Square Hollow Cross-Sections, Lengths, and End Constraints. Appl. Sci. 2024, 14, 8668. [Google Scholar] [CrossRef]
- Kamari, A.; Peter Leslie Schultz, C. A Combined Principal Component Analysis and Clustering Approach for Exploring Enormous Renovation Design Spaces. J. Build. Eng. 2022, 48, 103971. [Google Scholar] [CrossRef]
- Sah, A.K.; Hong, Y.-M. Performance Comparison of Machine Learning Models for Concrete Compressive Strength Prediction. Materials 2024, 17, 2075. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Chen, H.; Guo, H.; Zhou, M.; Huang, J. Development of a Prior Model to Predict the Cracking Performance of Asphalt Mixture in General for Asphalt Material Selection and Mix Design. Int. J. Pavement Eng. 2023, 24, 2251080. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L.; Gu, T.; Yin, J.; Hao, E. CRITIC-TOPSIS-Based Evaluation of Smart Community Safety: A Case Study of Shenzhen, China. Buildings 2023, 13, 476. [Google Scholar] [CrossRef]
- Hassani, S.; Martens, H.; Qannari, E.M.; Kohler, A. Degrees of Freedom Estimation in Principal Component Analysis and Consensus Principal Component Analysis. Chemom. Intell. Lab. Syst. 2012, 118, 246–259. [Google Scholar] [CrossRef]
- Wang, X.; Yu, H.; Lv, P.; Wang, C.; Zhang, J.; Yu, J. Seepage Safety Assessment of Concrete Gravity Dam Based on Matter-Element Extension Model and FDA. Energies 2019, 12, 502. [Google Scholar] [CrossRef]
- Diakoulaki, D.; Mavrotas, G.; Papayannakis, L. Determining Objective Weights in Multiple Criteria Problems: The Critic Method. Comput. Oper. Res. 1995, 22, 763–770. [Google Scholar] [CrossRef]
- Ding, T.; Li, G.; Liu, Z.; Wang, Y. Cross-Scale Edge Purification Network for Salient Object Detection of Steel Defect Images. Measurement 2022, 199, 111429. [Google Scholar] [CrossRef]
- Mordia, R.; Kumar Verma, A. Visual Techniques for Defects Detection in Steel Products: A Comparative Study. Eng. Fail. Anal. 2022, 134, 106047. [Google Scholar] [CrossRef]
- GB50009-2012; Load Code for the Design of Building Structures. China Building Industry Press: Beijing, China, 2012.





| Load Case | Permanent Load | Variable Load | Wind Load | Snow Load |
|---|---|---|---|---|
| PLD (Permanent load design) | 1.35 | 0.7 | 0.6 | 0.7 |
| VLD (Variable load design) | 1.2 | 1.4 | 0.6 | 0.7 |
| WLD (Wind load design) | 1.2 | 0.7 | 1.4 | 0.7 |
| SLD (Snow load design) | 1.2 | 0.7 | 0.6 | 1.4 |
| Category | Section Size (mm) | Load Value | ||
|---|---|---|---|---|
| Standard Value | Service Stage | Construction Stage | ||
| I-section column (Z1) | 259 × 107 × 6 × 9 | 78.5 kN/m3 | - | - |
| Square hollow section column (Z2) | 75 × 75 × 4.5 | 78.5 kN/m3 | - | - |
| Square hollow section truss column (Z3) | 60 × 60 × 2.5 | 78.5 kN/m3 | - | - |
| I-section beam(B1) | 250 × 125 × 6 × 9 | 78.5 kN/m3 | - | - |
| I-section beam(B2) | 250 × 125 × 6 × 9 | 78.5 kN/m3 | - | - |
| I-section beam(B3) | 250 × 125 × 3.2 × 4.5 | 78.5 kN/m3 | - | - |
| C-section beam(B4) | 150 × 50 × 50 × 4.0 | 78.5 kN/m3 | - | - |
| Double C-section truss beam(B5) | 100 × 500 × 20 × 2.5 | 78.5 kN/m3 | - | - |
| Exterior wall | - | 9.6 kN/m3 | - | - |
| Interior partition wall | - | 0.54 kN/m3 | - | - |
| Floor grid | - | 0.4 kN/m3 | - | - |
| Roof | - | 0.55 kN/m3 | - | - |
| Roof live load | - | - | 0.5 kN/m2 | 0.5 kN/m2 |
| Floor live load | - | - | 2.0 kN/m2 | 0.6 kN/m2 |
| Wind load | - | - | 0.3 kN/m2 | 0.3 kN/m2 |
| Snow load | - | - | 0.25 kN/m2 | 0.25 kN/m2 |
| Group Number | Beam Mesh Division | Column Mesh Division | Floor Y-Direction Mesh Division | Floor X-Direction Mesh Division | Maximum Displacement | First-Order Buckling Coefficient |
|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 0.5 | 0.5 | 6.27452 | 2.27920 |
| 2 | 2 | 1 | 0.5 | 1 | 6.22487 | 2.29427 |
| 3 | 2 | 1 | 1 | 0.5 | 4.19172 | 2.26424 |
| 4 | 2 | 1 | 1 | 1 | 4.17472 | 2.27343 |
| 5 | 4 | 1 | 0.5 | 0.5 | 6.70931 | 2.25983 |
| 6 | 4 | 1 | 0.5 | 1 | 6.53670 | 2.25899 |
| 7 | 4 | 1 | 1 | 0.5 | 4.22604 | 2.17359 |
| 8 | 4 | 1 | 1 | 1 | 4.19341 | 2.17453 |
| 9 | 6 | 1 | 0.5 | 0.5 | 6.70584 | 2.44998 |
| 10 | 6 | 1 | 0.5 | 1 | 6.55545 | 2.31677 |
| 11 | 6 | 1 | 1 | 0.5 | 4.09863 | 2.18687 |
| 12 | 6 | 1 | 1 | 1 | 4.14017 | 2.18703 |
| 13 | 2 | 4 | 0.5 | 0.5 | 6.28060 | 1.88360 |
| 14 | 2 | 4 | 0.5 | 1 | 6.23104 | 1.89587 |
| 15 | 2 | 4 | 1 | 0.5 | 4.19643 | 1.87219 |
| 16 | 2 | 4 | 1 | 1 | 4.17950 | 1.87965 |
| 17 | 4 | 4 | 0.5 | 0.5 | 6.71548 | 1.86849 |
| 18 | 4 | 4 | 0.5 | 1 | 6.54293 | 1.86768 |
| 19 | 4 | 4 | 1 | 0.5 | 4.23088 | 1.79814 |
| 20 | 4 | 4 | 1 | 1 | 4.19821 | 1.79765 |
| 21 | 6 | 4 | 0.5 | 0.5 | 6.71209 | 2.01752 |
| 22 | 6 | 4 | 0.5 | 1 | 6.56184 | 1.90396 |
| 23 | 6 | 4 | 1 | 0.5 | 4.10337 | 1.80803 |
| 24 | 6 | 4 | 1 | 1 | 4.14500 | 1.80791 |
| 25 | 2 | 8 | 0.5 | 0.5 | 6.28062 | 1.88183 |
| 26 | 2 | 8 | 0.5 | 1 | 6.23106 | 1.89409 |
| 27 | 2 | 8 | 1 | 0.5 | 4.19645 | 1.87043 |
| 28 | 2 | 8 | 1 | 1 | 4.17952 | 1.87789 |
| 29 | 4 | 8 | 0.5 | 0.5 | 6.71550 | 1.86674 |
| 30 | 4 | 8 | 0.5 | 1 | 6.54295 | 1.86593 |
| 31 | 4 | 8 | 1 | 0.5 | 4.23090 | 1.79545 |
| 32 | 4 | 8 | 1 | 1 | 4.19822 | 1.79596 |
| 33 | 6 | 8 | 0.5 | 0.5 | 6.71211 | 2.10549 |
| 34 | 6 | 8 | 0.5 | 1 | 6.56186 | 1.90214 |
| 35 | 6 | 8 | 1 | 0.5 | 4.10338 | 1.80634 |
| 36 | 6 | 8 | 1 | 1 | 4.14501 | 1.80621 |
| Load Case | First-Order Buckling Coefficient | Extreme Displacement | ||
|---|---|---|---|---|
| Maximum | Minimum | Maximum | Minimum | |
| PLD | 2.44998 | 1.795451 | 6.71550 | 4.09863 |
| VLD | 2.62473 | 1.93496 | 6.69296 | 3.93503 |
| WLD | 2.70053 | 1.98086 | 8.63738 | 6.13039 |
| SLD | 2.72941 | 2.00359 | 6.68101 | 3.87817 |
| Model Designation | Defect Type | Reduction Factor |
|---|---|---|
| D20_G | Global defect | |
| Local defect | ||
| D20_L | Global defect | |
| Local defect |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1.7758 | 0.0377 | 0.1288 | 0.1586 | 0.0605 | 0.0224 | 0.0918 | 0.0304 | 0.0241 | 0.2512 | 0.1944 | |
| 1.7739 | 0.1282 | 0.2881 | 0.0689 | 0.0060 | 0.0679 | 0.0195 | 0.0118 | 0.1414 | 0.1338 | 0.1345 | |
| 1.7768 | 0.0854 | 0.1536 | 0.0912 | 0.2074 | 0.0622 | 0.1316 | 0.0925 | 0.0386 | 0.0374 | 0.1001 | |
| 1.7744 | 0.0713 | 0.0921 | 0.0858 | 0.0650 | 0.2363 | 0.1155 | 0.0261 | 0.0606 | 0.1100 | 0.1374 | |
| 1.7716 | 0.0210 | 0.0496 | 0.0656 | 0.0643 | 0.1777 | 0.0062 | 0.0339 | 0.1290 | 0.2247 | 0.2280 | |
| 1.7810 | 0.1184 | 0.0106 | 0.1665 | 0.1527 | 0.0009 | 0.2102 | 0.1055 | 0.0509 | 0.0309 | 0.1532 | |
| 1.7743 | 0.1084 | 0.0032 | 0.0550 | 0.1095 | 0.1536 | 0.0085 | 0.1484 | 0.0739 | 0.1056 | 0.2339 | |
| 1.7779 | 0.0893 | 0.1085 | 0.0279 | 0.1289 | 0.1109 | 0.2034 | 0.2063 | 0.0708 | 0.0257 | 0.0284 | |
| 1.7772 | 0.1903 | 0.0391 | 0.0265 | 0.2129 | 0.1079 | 0.0934 | 0.1120 | 0.0327 | 0.0289 | 0.1563 | |
| 1.7754 | 0.1188 | 0.0109 | 0.0747 | 0.2675 | 0.0690 | 0.0194 | 0.0085 | 0.2000 | 0.0454 | 0.1857 | |
| 1.7754 | 0.1311 | 0.1385 | 0.0156 | 0.0849 | 0.0473 | 0.0936 | 0.0764 | 0.1153 | 0.2670 | 0.0303 | |
| 1.7754 | 0.1894 | 0.0743 | 0.1200 | 0.0949 | 0.0851 | 0.0110 | 0.1272 | 0.1736 | 0.0175 | 0.1070 | |
| 1.7770 | 0.2634 | 0.0747 | 0.1249 | 0.0958 | 0.0424 | 0.0247 | 0.0995 | 0.0252 | 0.0635 | 0.1858 | |
| 1.7744 | 0.0529 | 0.1231 | 0.2358 | 0.0759 | 0.0422 | 0.0050 | 0.1994 | 0.1686 | 0.0524 | 0.0447 | |
| 1.7754 | 0.0026 | 0.0298 | 0.1992 | 0.0325 | 0.0946 | 0.1114 | 0.1316 | 0.0607 | 0.2279 | 0.1097 | |
| 1.7737 | 0.0962 | 0.0037 | 0.0064 | 0.1477 | 0.1885 | 0.0246 | 0.1322 | 0.2500 | 0.0416 | 0.1090 | |
| 1.7739 | 0.0298 | 0.0862 | 0.1138 | 0.2567 | 0.1682 | 0.0312 | 0.1277 | 0.0879 | 0.0179 | 0.0804 | |
| 1.7751 | 0.1678 | 0.2934 | 0.1825 | 0.0420 | 0.0493 | 0.0569 | 0.0164 | 0.0231 | 0.0600 | 0.1086 | |
| 1.7775 | 0.1769 | 0.0591 | 0.1102 | 0.0435 | 0.0718 | 0.1350 | 0.1452 | 0.1638 | 0.0857 | 0.0088 | |
| 1.7805 | 0.0439 | 0.0490 | 0.0682 | 0.0052 | 0.0115 | 0.1858 | 0.3435 | 0.1050 | 0.0472 | 0.1406 | |
| 1.7756 | 0.0396 | 0.2224 | 0.2050 | 0.0663 | 0.0292 | 0.1113 | 0.0564 | 0.2033 | 0.0351 | 0.0315 | |
| 1.7752 | 0.0690 | 0.2183 | 0.1137 | 0.0628 | 0.0924 | 0.1524 | 0.0249 | 0.0356 | 0.1986 | 0.0323 | |
| 1.7741 | 0.1474 | 0.2221 | 0.1710 | 0.0318 | 0.2086 | 0.0616 | 0.0216 | 0.0382 | 0.0362 | 0.0614 | |
| 1.7737 | 0.0440 | 0.1405 | 0.1065 | 0.0833 | 0.0571 | 0.0360 | 0.0014 | 0.3403 | 0.0513 | 0.1396 | |
| 1.7754 | 0.1791 | 0.1568 | 0.0588 | 0.0049 | 0.0306 | 0.2628 | 0.0142 | 0.2693 | 0.0165 | 0.0069 | |
| 1.7747 | 0.0827 | 0.0035 | 0.0262 | 0.0480 | 0.0420 | 0.0266 | 0.2278 | 0.2543 | 0.2510 | 0.0380 | |
| 1.7771 | 0.1246 | 0.2073 | 0.0735 | 0.0346 | 0.0527 | 0.2080 | 0.0587 | 0.1511 | 0.0082 | 0.0813 | |
| 1.7772 | 0.0498 | 0.1648 | 0.1531 | 0.0991 | 0.0391 | 0.1437 | 0.2012 | 0.1408 | 0.0000 | 0.0084 | |
| 1.7746 | 0.1082 | 0.0706 | 0.0416 | 0.1485 | 0.1104 | 0.0285 | 0.0820 | 0.0774 | 0.1416 | 0.1914 | |
| 1.7743 | 0.0021 | 0.1694 | 0.0887 | 0.0749 | 0.0001 | 0.0062 | 0.2161 | 0.0505 | 0.1905 | 0.2016 | |
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| j | |||||||||||
| 1 | 0.0399 | 0.1884 | 0.2214 | 0.0090 | 0.3699 | 0.2039 | 0.2039 | 0.2499 | 0.0632 | 0.0798 | |
| 2 | 0.4678 | 1.0413 | 0.0143 | 0.2546 | 0.4798 | 0.0580 | 0.0580 | 0.0543 | 0.3969 | 0.4079 | |
| 3 | 0.1227 | 0.1981 | 0.0488 | 0.2725 | 0.2201 | 0.2389 | 0.2389 | 0.1722 | 0.3568 | 0.2435 | |
| 4 | 0.1783 | 0.1505 | 0.0716 | 0.0024 | 0.2077 | 0.3875 | 0.3875 | 0.2425 | 0.4067 | 0.3212 | |
| 5 | 0.1030 | 0.0412 | 0.1067 | 0.0935 | 0.1869 | 0.2157 | 0.2157 | 0.0825 | 0.2048 | 0.0790 | |
| 6 | 0.3258 | 0.1730 | 0.0397 | 0.1687 | 0.0899 | 0.0089 | 0.0089 | 0.2057 | 0.4442 | 0.0220 | |
| 7 | 0.1087 | 0.0938 | 0.0600 | 0.1028 | 0.1065 | 0.3141 | 0.3141 | 0.0927 | 0.3169 | 0.3178 | |
| 8 | 0.3035 | 0.0189 | 0.0700 | 0.2663 | 0.1252 | 0.1564 | 0.1564 | 0.1727 | 0.3509 | 0.1284 | |
| 9 | 0.2550 | 0.1011 | 0.0238 | 0.5300 | 0.2836 | 0.0344 | 0.0344 | 0.1852 | 0.4675 | 0.1102 | |
| 10 | 0.2887 | 0.2332 | 0.1312 | 0.0541 | 0.3422 | 0.2294 | 0.2294 | 0.0359 | 0.1110 | 0.5187 | |
| 11 | 0.4380 | 0.0643 | 0.1414 | 0.0797 | 0.2411 | 0.0125 | 0.0125 | 0.1161 | 0.5391 | 0.3149 | |
| 12 | 0.4494 | 0.0466 | 0.1099 | 0.0585 | 0.2509 | 0.0343 | 0.0343 | 0.1925 | 0.2988 | 0.0781 | |
| 13 | 0.1117 | 0.2574 | 0.5959 | 0.0408 | 0.4747 | 0.0041 | 0.0041 | 0.1385 | 0.6033 | 0.6416 | |
| 14 | 0.0482 | 0.0518 | 0.3495 | 0.0832 | 0.2176 | 0.2754 | 0.2754 | 0.1787 | 0.0084 | 0.3095 | |
| 15 | 0.3589 | 0.2191 | 0.2824 | 0.3979 | 0.0512 | 0.0882 | 0.0882 | 0.5776 | 0.8738 | 0.5678 | |
| 16 | 0.0376 | 0.1555 | 0.2052 | 0.8188 | 0.0406 | 0.1067 | 0.1067 | 0.1748 | 0.8800 | 0.6281 | |
| 17 | 0.4136 | 0.6872 | 0.3295 | 0.0628 | 0.3620 | 0.1429 | 0.1429 | 0.2984 | 0.4642 | 0.3365 | |
| 18 | 0.2637 | 0.0160 | 0.0755 | 0.0352 | 0.1792 | 0.2179 | 0.2179 | 0.0588 | 0.2351 | 0.3708 | |
| 19 | 0.0258 | 0.0008 | 0.0029 | 0.0666 | 0.1873 | 0.2025 | 0.2025 | 0.0270 | 0.2000 | 0.0984 | |
| 20 | 0.0462 | 0.4304 | 0.3472 | 0.0050 | 0.3701 | 0.2618 | 0.2618 | 0.1851 | 0.4724 | 0.4894 | |
| 21 | 0.1328 | 0.4665 | 0.1329 | 0.0042 | 0.2360 | 0.4043 | 0.4043 | 0.2584 | 0.0722 | 0.5411 | |
| 22 | 0.5137 | 0.7009 | 0.4284 | 0.1320 | 0.1255 | 0.2252 | 0.2252 | 0.3688 | 0.7660 | 0.6768 | |
| 23 | 0.1116 | 0.4409 | 0.1984 | 0.0920 | 0.5855 | 0.1447 | 0.1447 | 1.0250 | 0.8408 | 0.4288 | |
| 24 | 0.4109 | 0.2785 | 0.0176 | 0.1544 | 0.3823 | 0.6669 | 0.6669 | 0.3647 | 0.5410 | 0.5744 | |
| 25 | 0.2007 | 0.1503 | 0.1284 | 0.0530 | 0.4420 | 0.0666 | 0.0666 | 0.4078 | 0.0857 | 0.6185 | |
| 26 | 0.1891 | 0.2880 | 0.0144 | 0.0542 | 0.2285 | 0.3687 | 0.3687 | 0.0403 | 0.3953 | 0.2680 | |
| 27 | 0.0509 | 0.2039 | 0.1550 | 0.0616 | 0.2454 | 0.2436 | 0.2436 | 0.0208 | 0.3978 | 0.3888 | |
| 28 | 0.2925 | 0.0704 | 0.0806 | 0.2824 | 0.2260 | 0.0748 | 0.0748 | 0.1733 | 0.2789 | 0.1227 | |
| 29 | 0.0698 | 0.4427 | 0.0853 | 0.0392 | 0.6567 | 0.0001 | 0.0001 | 0.2902 | 0.1262 | 0.0976 | |
| 30 | 0.0399 | 0.1884 | 0.2214 | 0.0090 | 0.3699 | 0.2039 | 0.2039 | 0.2499 | 0.0632 | 0.0798 | |
| KMO Test and Bartlett’s Test of Sphericity | ||
|---|---|---|
| KMO value | 0.518 | |
| Bartlett’s test of sphericity | 947.578 | |
| df | 45 | |
| p | 0.000 *** | |
| Independent Variable | Regression Coefficient | p | t | F | VIF | R2 |
|---|---|---|---|---|---|---|
| Constant | 1.614 | 0.000 *** | 11,290.908 | 19.438 (p = 0.000 ***) | - | 0.897 |
| 1st-order buckling | 0.167 | 0.000 *** | 76.696 | - | ||
| 2nd-order buckling | 0.155 | 0.000 *** | 79.882 | - | ||
| 3rd-order buckling | 0.164 | 0.000 *** | 69.766 | - | ||
| 4th-order buckling | 0.163 | 0.000 *** | 74.58 | - | ||
| 5th-order buckling | 0.149 | 0.000 *** | 67.702 | - | ||
| 6th-order buckling | 0.176 | 0.000 *** | 90.733 | - | ||
| 7th-order buckling | 0.167 | 0.000 *** | 97.711 | - | ||
| 8th-order buckling | 0.155 | 0.000 *** | 100.848 | - | ||
| 9th-order buckling | 0.156 | 0.000 *** | 90.985 | - | ||
| 10th-order buckling | 0.163 | 0.000 *** | 71.408 | - |
| Independent Variable | Regression Coefficient | p | t | F | VIF | R2 |
|---|---|---|---|---|---|---|
| 6th-order buckling | 0.02 | 0.001 ** | 9.254 | 26.887 p = 0.000 ** | 1.433 | 0.895 |
| 7th-order buckling | 0.011 | 0.001 ** | 6.165 | 1.23 | ||
| 1st-order buckling | 0.011 | 0.001 ** | 4.712 | 1.158 | ||
| 10th-order buckling | 0.008 | 0.002 ** | 3.422 | 1.407 | ||
| 3rd-order buckling | 0.008 | 0.005 ** | 3.129 | 1.255 | ||
| 4th-order buckling | 0.007 | 0.003 ** | 3.274 | 1.129 | ||
| 5th-order buckling | −0.007 | 0.014 ** | −2.673 | 1.292 |
| Number | Retained Variable | Regression Coefficient | p | t | F | VIF | R2 |
|---|---|---|---|---|---|---|---|
| S1 | 6th-order buckling | 0.02 | 0.000 ** | 9.254 | 26.887 (p = 0.000 **) | 1.433 | 0.895 |
| 7th-order buckling | 0.011 | 0.000 ** | 6.165 | 1.23 | |||
| 1st-order buckling | 0.011 | 0.000 ** | 4.712 | 1.158 | |||
| 10th-order buckling | 0.008 | 0.002 ** | 3.422 | 1.407 | |||
| 3rd-order buckling | 0.008 | 0.005 ** | 3.129 | 1.255 | |||
| 4th-order buckling | 0.007 | 0.003 ** | 3.274 | 1.129 | |||
| 5th-order buckling | −0.007 | 0.014 ** | −2.673 | 1.292 | |||
| S2 | 4th-order buckling | −3.518 | 0.001 *** | −3.939 | 8.353 (p = 0.006 **) | 1.045 | 0.432 |
| 1st-order buckling | −2.952 | 0.006 *** | −3.005 | 1.035 | |||
| 3rd-order buckling | −2.282 | 0.038 ** | −2.185 | 1.08 | |||
| S3 | 3rd-order buckling | 0.041 | 0.038 ** | 1.804 | 2.813 (p = 0.012 **) | 2.082 | 0.262 |
| 6th-order buckling | 0.022 | 0.024 ** | 1.203 | 2.003 | |||
| 7th-order buckling | 0.018 | 0.03 ** | 1.063 | 1.931 | |||
| S4 | 9th-order buckling | −2.752 | 0.008 ** | −2.875 | 6.142 (p = 0.026 **) | 1.003 | 0.713 |
| 7th-order buckling | −2.115 | 0.040 ** | −2.162 | 1.003 | |||
| S5 | 1st-order buckling | 5.501 | 0.036 ** | 2.198 | 4.829 (p = 0.036 **) | 1 | 0.117 |
| S6 | 10th-order buckling | 0.684 | 0.008 *** | 2.851 | 8.894 (p = 0.009 **) | 1.073 | 0.506 |
| 7th-order buckling | −0.514 | 0.014 ** | −2.632 | 1.014 | |||
| 4th-order buckling | 0.548 | 0.029 ** | 2.314 | 1.059 |
| Buckling Mode | Contrast Intensity | Conflict Measure | Information Content | Weight (%) |
|---|---|---|---|---|
| 1st-order buckling | 0.153 | 8.565 | 1.311 | 9.08 |
| 2nd-order buckling | 0.241 | 7.204 | 1.737 | 12.031 |
| 3rd-order buckling | 0.143 | 8.111 | 1.156 | 8.007 |
| 4th-order buckling | 0.18 | 9.384 | 1.691 | 11.707 |
| 5th-order buckling | 0.152 | 8.975 | 1.368 | 9.47 |
| 6th-order buckling | 0.15 | 8.627 | 1.298 | 8.985 |
| 7th-order buckling | 0.15 | 8.627 | 1.298 | 8.985 |
| 8th-order buckling | 0.201 | 7.433 | 1.494 | 10.345 |
| 9th-order buckling | 0.243 | 7.162 | 1.737 | 12.029 |
| 10th-order buckling | 0.204 | 6.623 | 1.352 | 9.36 |
| Stage | Minimum | Maximum | ||||
|---|---|---|---|---|---|---|
| Traditional | CRITIC | Traditional | CRITIC | |||
| I | 1.77006 | 1.685551 | (−4.77%) | 1.77787 | 1.769057 | (−0.50%) |
| II | 3.56872 | 3.40220 | (−4.67%) | 5.57023 | 5.366507 | (−3.66%) |
| III | 1.26132 | 1.222039 | (−3.11%) | 1.30647 | 1.303577 | (−0.22%) |
| IV | 2.09414 | 1.998511 | (−4.57%) | 3.91295 | 3.866979 | (−1.17%) |
| V | 1.28968 | 1.240389 | (−3.82%) | 3.87876 | 3.771617 | (−2.76%) |
| VI | 2.71184 | 2.603972 | (−3.98%) | 3.11541 | 2.995883 | (−3.84%) |
| Stage | Minimum | Maximum | ||||
|---|---|---|---|---|---|---|
| Traditional | CRITIC | Traditional | CRITIC | |||
| I | 1.7546 | 1.6737 | (−4.61%) | 1.7665 | 1.7654 | (−0.06%) |
| II | 3.1764 | 3.0308 | (−4.58%) | 4.7847 | 4.6524 | (−2.77%) |
| III | 1.2559 | 1.2012 | (−4.36%) | 2.1522 | 2.1193 | (−1.53%) |
| IV | 3.3555 | 3.2552 | (−2.99%) | 3.9517 | 3.8765 | (−1.90%) |
| V | 1.3135 | 1.2918 | (−1.65%) | 3.9529 | 3.7797 | (−4.38%) |
| VI | 2.6889 | 2.5943 | (−3.52%) | 2.9859 | 2.9569 | (−0.97%) |
| Node | I | II | III | IV | V | VI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditional | CRITIC | Traditional | CRITIC | Traditional | CRITIC | Traditional | CRITIC | Traditional | CRITIC | Traditional | CRITIC | |
| 1 | 3.125 | 3.198 | 7.315 | 7.493 | 3.037 | 3.114 | 7.286 | 7.506 | 4.451 | 4.547 | 7.216 | 7.395 |
| 2 | - | - | - | 3.541 | 3.638 | 10.737 | 11.024 | 6.518 | 6.687 | 10.903 | 11.172 | |
| 3 | - | - | - | - | - | - | - | 5.363 | 5.508 | 11.104 | 11.389 | |
| 4 | - | - | - | - | - | - | - | 5.212 | 5.345 | 11.383 | 11.642 | |
| 5 | 1.914 | 1.956 | 6.427 | 6.612 | 1.856 | 1.906 | 10.673 | 10.937 | 4.248 | 4.345 | 9.501 | 9.761 |
| 6 | - | - | - | 2.667 | 2.735 | 7.605 | 7.797 | 4.687 | 4.836 | 9.354 | 9.589 | |
| 7 | - | - | - | - | - | - | - | 5.249 | 5.378 | 12.865 | 13.236 | |
| 8 | - | - | - | - | - | - | - | - | - | 11.015 | 11.276 | |
| Node | I | II | III | IV | V | VI | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Traditional | CRITIC | Traditional | CRITIC | Traditional | CRITIC | Traditional | CRITIC | Traditional | CRITIC | Traditional | CRITIC | |
| 1 | 3.101 | 3.167 | 5.614 | 5.725 | 2.981 | 3.041 | 7.687 | 7.879 | 5.527 | 5.655 | 7.091 | 7.316 |
| 2 | - | - | - | - | 3.860 | 3.958 | 11.355 | 11.645 | 8.138 | 8.249 | 10.679 | 10.972 |
| 3 | - | - | - | - | - | - | - | - | 6.642 | 6.804 | 10.991 | 11.282 |
| 4 | - | - | - | - | - | - | - | - | 6.417 | 6.566 | 11.110 | 11.363 |
| 5 | 1.913 | 1.955 | 5.444 | 5.583 | 2.326 | 2.388 | 15.846 | 16.176 | 8.376 | 8.500 | 13.392 | 13.705 |
| 6 | - | - | - | - | 2.920 | 2.996 | 8.098 | 8.275 | 5.794 | 5.968 | 8.804 | 9.009 |
| 7 | - | - | - | - | - | - | - | - | 6.447 | 6.607 | 11.227 | 11.507 |
| 8 | - | - | - | - | - | - | - | - | - | - | 10.753 | 11.038 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, G.; Lei, T.; Yang, Y.; Zhu, M. Buckling Performance of Prefabricated Light-Gauge Steel Frame Materials Under Combined Random Defects During Construction: A CRITIC-Based Analysis. Materials 2025, 18, 3406. https://doi.org/10.3390/ma18143406
Yao G, Lei T, Yang Y, Zhu M. Buckling Performance of Prefabricated Light-Gauge Steel Frame Materials Under Combined Random Defects During Construction: A CRITIC-Based Analysis. Materials. 2025; 18(14):3406. https://doi.org/10.3390/ma18143406
Chicago/Turabian StyleYao, Gang, Ting Lei, Yang Yang, and Mingtao Zhu. 2025. "Buckling Performance of Prefabricated Light-Gauge Steel Frame Materials Under Combined Random Defects During Construction: A CRITIC-Based Analysis" Materials 18, no. 14: 3406. https://doi.org/10.3390/ma18143406
APA StyleYao, G., Lei, T., Yang, Y., & Zhu, M. (2025). Buckling Performance of Prefabricated Light-Gauge Steel Frame Materials Under Combined Random Defects During Construction: A CRITIC-Based Analysis. Materials, 18(14), 3406. https://doi.org/10.3390/ma18143406








