Four-Dimensional-Printed Woven Metamaterials for Vibration Reduction and Energy Absorption in Aircraft Landing Gear
Abstract
1. Introduction
2. Design and Fabrication of the Metamaterials
3. Mechanical Properties of SMP-PLA
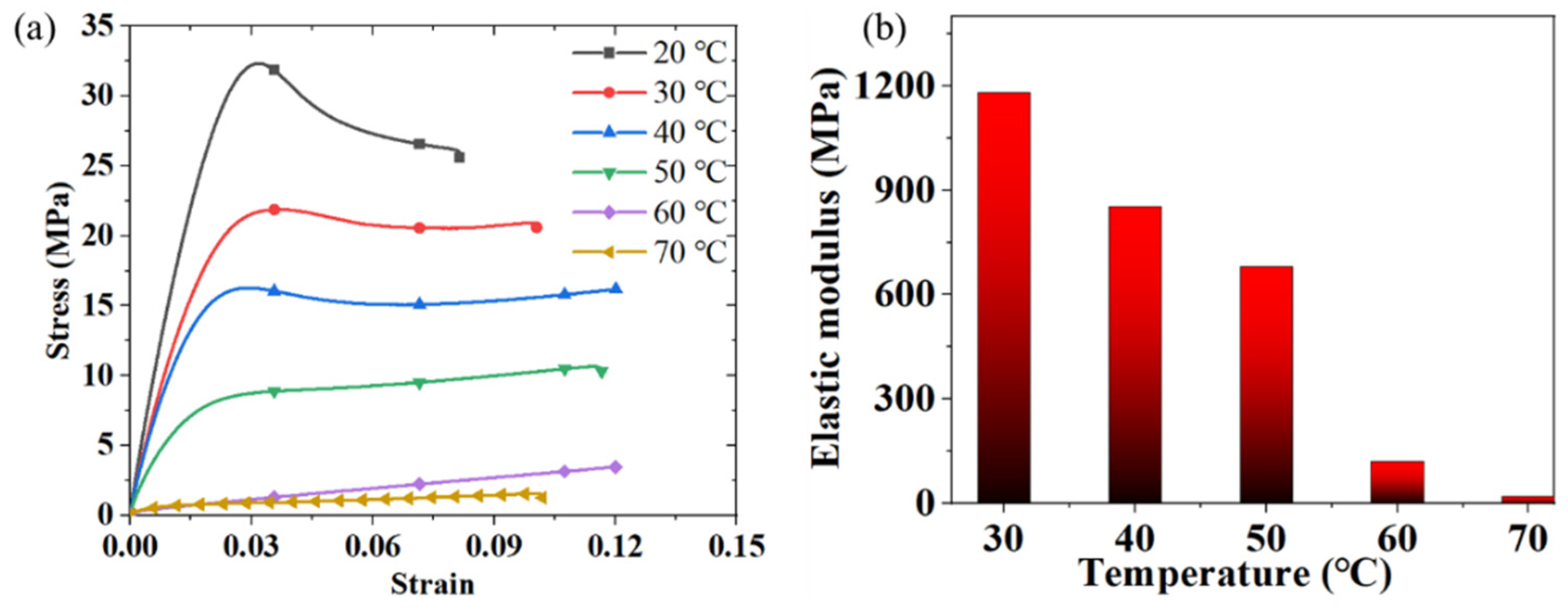
3.1. Uniaxial Tensile Test of Shape Memory Materials
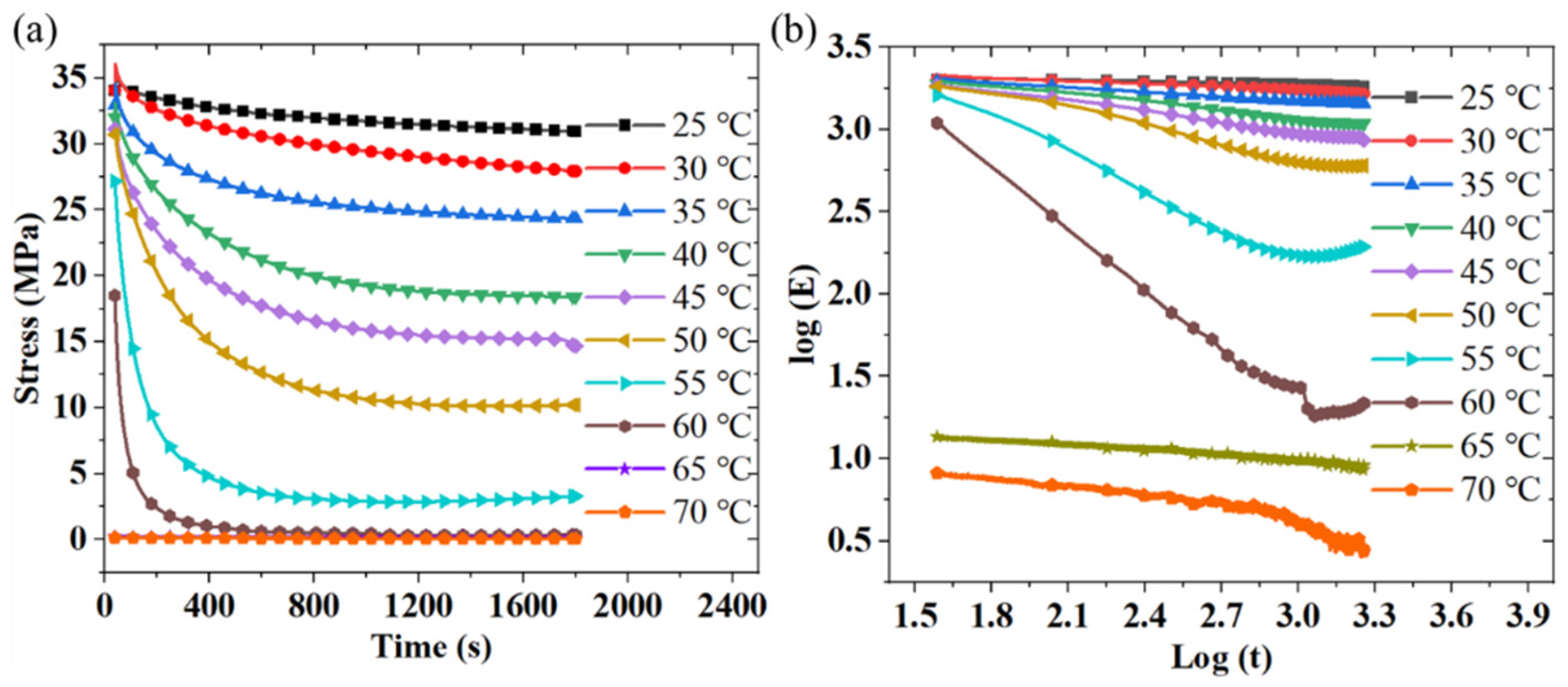
3.2. Relaxation Test of Shape Memory Materials
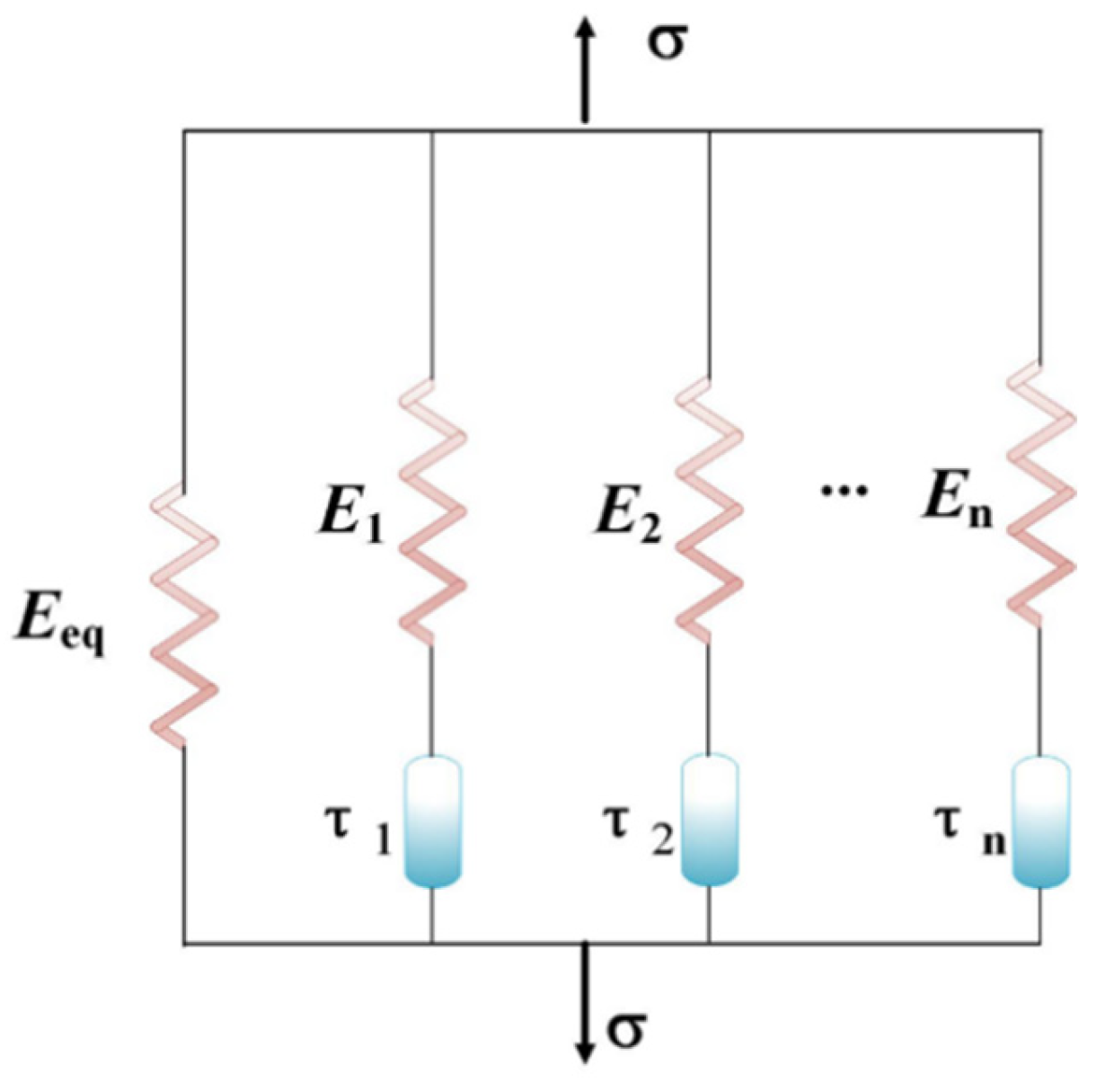
3.3. Constitutive Theory
4. Mechanical Properties of Metamaterials
4.1. Compressive Test
4.2. Three-Point Bending Test
4.3. Energy Absorption Performance Characterization
4.4. Reconfigurable Performance Characterization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chin, S.C.; Tee, K.F.; Tong, F.S.; Ong, H.R.; Gimbun, J. Thermal and Mechanical Properties of Bamboo Fiber Reinforced Composites. Mater. Today Commun. 2020, 23, 100876. [Google Scholar] [CrossRef]
- Maiti, S.; Islam, M.R.; Uddin, M.A.; Afroj, S.; Eichhorn, S.J.; Karim, N. Sustainable Fiber-Reinforced Composites: A Review. Adv. Sustain. Syst. 2022, 6, 2200258. [Google Scholar] [CrossRef]
- Zheng, H.; Zhang, W.; Li, B.; Zhu, J.; Wang, C.; Song, G.; Wu, G.; Yang, X.; Huang, Y.; Ma, L. Recent Advances of Interphases in Carbon Fiber-Reinforced Polymer Composites: A Review. Compos. Part B Eng. 2022, 233, 109639. [Google Scholar] [CrossRef]
- Li, M.; Pu, Y.; Thomas, V.M.; Yoo, C.G.; Ozcan, S.; Deng, Y.; Nelson, K.; Ragauskas, A.J. Recent Advancements of Plant-Based Natural Fiber–Reinforced Composites and Their Applications. Compos. Part B Eng. 2020, 200, 108254. [Google Scholar] [CrossRef]
- Khalid, M.Y.; Al Rashid, A.; Arif, Z.U.; Ahmed, W.; Arshad, H.; Zaidi, A.A. Natural Fiber Reinforced Composites: Sustainable Materials for Emerging Applications. Results Eng. 2021, 11, 100263. [Google Scholar] [CrossRef]
- Rangappa, S.M.; Siengchin, S.; Parameswaranpillai, J.; Jawaid, M.; Ozbakkaloglu, T. Lignocellulosic Fiber Reinforced Composites: Progress, Performance, Properties, Applications, and Future Perspectives. Polym. Compos. 2022, 43, 645–691. [Google Scholar] [CrossRef]
- Akil, H.M.; Omar, M.F.; Mazuki, A.A.M.; Safiee, S.; Ishak, Z.A.M.; Abu Bakar, A. Kenaf Fiber Reinforced Composites: A Review. Mater. Des. 2011, 32, 4107–4121. [Google Scholar] [CrossRef]
- Carey, J.P.; Melenka, G.W.; Hunt, A.J.; Batten, E.J.; Lepp, E.; Munro, M.; Pastore, C.M.; Ko, F.K.; van Ravenhorst, J.H.; Akkerman, R. 3-Manufacturing Processes for Braided Composite Materials. In Handbook of Advances in Braided Composite Materials, 2nd ed.; Carey, J.P., Ed.; Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing: Cambridge, UK, 2024; pp. 47–160. ISBN 978-0-443-18602-8. [Google Scholar]
- Li, Y.; Meng, Q.; Chen, S.; Ling, P.; Kuss, M.A.; Duan, B.; Wu, S. Advances, Challenges, and Prospects for Surgical Suture Materials. Acta Biomater. 2023, 168, 78–112. [Google Scholar] [CrossRef]
- Melenka, G.W.; Pastore, C.M.; Ko, F.K.; Batten, E.J.; Carey, J.P. 10-Advances in 2D and 3D Braided Composite Materials Modeling. In Handbook of Advances in Braided Composite Materials, 2nd ed.; Carey, J.P., Ed.; Woodhead Publishing Series in Composites Science and Engineering; Woodhead Publishing: Cambridge, UK, 2024; pp. 359–406. ISBN 978-0-443-18602-8. [Google Scholar]
- Rashid, M.B.; Habib, M.A. Channel Bar Development, Braiding and Bankline Migration of the Brahmaputra-Jamuna River, Bangladesh through RS and GIS Techniques. Int. J. River Basin Manag. 2024, 22, 203–215. [Google Scholar] [CrossRef]
- Peng, Z.; Niu, Z.; Zeng, C.; Zhao, W.; Leng, J.; Liu, Y. Design and Functional Verification of a Flexible Wireless Spinal Cord Stimulator with Spinal Motion Monitoring Function. Nano Energy 2025, 139, 110895. [Google Scholar] [CrossRef]
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber-Reinforced Polymer Composites: Manufacturing, Properties, and Applications. Polymers 2019, 11, 1667. [Google Scholar] [CrossRef]
- Karthi, N.; Kumaresan, K.; Sathish, S.; Gokulkumar, S.; Prabhu, L.; Vigneshkumar, N. An Overview: Natural Fiber Reinforced Hybrid Composites, Chemical Treatments and Application Areas. Mater. Today Proc. 2020, 27, 2828–2834. [Google Scholar] [CrossRef]
- Ku, H.; Wang, H.; Pattarachaiyakoop, N.; Trada, M. A Review on the Tensile Properties of Natural Fiber Reinforced Polymer Composites. Compos. Part B Eng. 2011, 42, 856–873. [Google Scholar] [CrossRef]
- Dhand, V.; Mittal, G.; Rhee, K.Y.; Park, S.-J.; Hui, D. A Short Review on Basalt Fiber Reinforced Polymer Composites. Compos. Part B Eng. 2015, 73, 166–180. [Google Scholar] [CrossRef]
- Mohammed, L.; Ansari, M.N.M.; Pua, G.; Jawaid, M.; Islam, M.S. A Review on Natural Fiber Reinforced Polymer Composite and Its Applications. Int. J. Polym. Sci. 2015, 2015, 243947. [Google Scholar] [CrossRef]
- Wu, Z.; Qin, S.; Zhang, P.; Pan, Z.; Hu, X.; Shi, L. Damage Evolution in Braided Composite Tubes under Axial Compression Studied by Combining Infrared Thermography and X-Ray Computed Tomography. Compos. Struct. 2023, 307, 116634. [Google Scholar] [CrossRef]
- Jiang, L.; Xiao, S.; Dong, D.; Yang, B.; Chen, D.; Yang, G.; Zhu, T.; Wang, M. Experimental Study of Bonded, Bolted, and Hybrid Braided CFRP Joints with Different Stacking Sequences and Lapping Patterns. Thin-Walled Struct. 2022, 177, 109408. [Google Scholar] [CrossRef]
- Qiu, H.; Zhang, Q.; Liu, T.; Fan, X.; Zhang, F.; Qiu, C. Minimal Non-Abelian Nodal Braiding in Ideal Metamaterials. Nat. Commun. 2023, 14, 1261. [Google Scholar] [CrossRef]
- Peng, B.; Bouhon, A.; Monserrat, B.; Slager, R.-J. Phonons as a Platform for Non-Abelian Braiding and Its Manifestation in Layered Silicates. Nat. Commun. 2022, 13, 423. [Google Scholar] [CrossRef]
- Yang, H.; Ren, Y. Stacking Design of Uniaxial/Biaxial Braided Composite Tube under Low-Velocity Impact Load. Mech. Adv. Mater. Struct. 2024, 31, 2901–2914. [Google Scholar] [CrossRef]
- Xia, F.; Durandet, Y.; Tan, P.J.; Ruan, D. Three-Point Bending Performance of Sandwich Panels with Various Types of Cores. Thin-Walled Struct. 2022, 179, 109723. [Google Scholar] [CrossRef]
- Kabir, S.M.F.; Mathur, K.; Seyam, A.-F.M. A Critical Review on 3D Printed Continuous Fiber-Reinforced Composites: History, Mechanism, Materials and Properties. Compos. Struct. 2020, 232, 111476. [Google Scholar] [CrossRef]
- Tian, X.; Todoroki, A.; Liu, T.; Wu, L.; Hou, Z.; Ueda, M.; Hirano, Y.; Matsuzaki, R.; Mizukami, K.; Iizuka, K.; et al. 3D Printing of Continuous Fiber Reinforced Polymer Composites: Development, Application, and Prospective. Chin. J. Mech. Eng. Addit. Manuf. Front. 2022, 1, 100016. [Google Scholar] [CrossRef]
- Cheng, P.; Peng, Y.; Li, S.; Rao, Y.; Le Duigou, A.; Wang, K.; Ahzi, S. 3D Printed Continuous Fiber Reinforced Composite Lightweight Structures: A Review and Outlook. Compos. Part B Eng. 2023, 250, 110450. [Google Scholar] [CrossRef]
- Quan, C.; Han, B.; Hou, Z.; Zhang, Q.; Tian, X.; Lu, T.J. 3d Printed Continuous Fiber Reinforced Composite Auxetic Honeycomb Structures. Compos. Part B Eng. 2020, 187, 107858. [Google Scholar] [CrossRef]
- Raouf, I.; Kumar, P.; Cheon, Y.; Tanveer, M.; Jo, S.-H.; Kim, H.S. Advances in Prognostics and Health Management for Aircraft Landing Gear—Progress, Challenges, and Future Possibilities. Int. J. Precis. Eng. Manuf.-Green Tech. 2025, 12, 301–320. [Google Scholar] [CrossRef]
- Wibawa, L.A.N. Effect of Fillet Radius of UAV Main Landing Gear on Static Stress and Fatigue Life Using Finite Element Method. J. Phys. Conf. Ser. 2021, 1811, 012082. [Google Scholar] [CrossRef]
- Al-Haddad, L.A.; Mahdi, N.M. Efficient Multidisciplinary Modeling of Aircraft Undercarriage Landing Gear Using Data-Driven Naïve Bayes and Finite Element Analysis. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 3187–3199. [Google Scholar] [CrossRef]
- Hameed, A.; Zubair, O.; Shams, T.A.; Mehmood, Z.; Javed, A.; Mehmood, Z. Failure Analysis of a Broken Support Strut of an Aircraft Landing Gear. Eng. Fail. Anal. 2020, 117, 104847. [Google Scholar] [CrossRef]
- Luong, Q.V.; Jang, D.-S.; Hwang, J.-H. Robust Adaptive Control for an Aircraft Landing Gear Equipped with a Magnetorheological Damper. Appl. Sci. 2020, 10, 1459. [Google Scholar] [CrossRef]
- Au, J.; Reid, D.; Bill, A. Challenges and Opportunities of Computer Vision Applications in Aircraft Landing Gear. In Proceedings of the 2022 IEEE Aerospace Conference (AERO), Big Sky, MT, USA, 5–12 March 2022; pp. 1–10. [Google Scholar]
- Han, C.; Kang, B.-H.; Choi, S.-B.; Tak, J.M.; Hwang, J.-H. Control of Landing Efficiency of an Aircraft Landing Gear System With Magnetorheological Dampers. J. Aircr. 2019, 56, 1980–1986. [Google Scholar] [CrossRef]
- Wong, J.; Ryan, L.; Kim, I.Y. Design Optimization of Aircraft Landing Gear Assembly under Dynamic Loading. Struct. Multidisc Optim. 2018, 57, 1357–1375. [Google Scholar] [CrossRef]
- Karpenko, M. Landing Gear Failures Connected with High-Pressure Hoses and Analysis of Trends in Aircraft Technical Problems. Aviation 2022, 26, 145–152. [Google Scholar] [CrossRef]
- Aftab, S.G.; Sirajuddin; Sreedhara, B.; Ganesh, E.; Babu, N.R.; Aithal, S.K. Finite Element Analysis of a Passenger Aircraft Landing Gear for Structural and Fatigue Safety. Mater. Today Proc. 2022, 54, 152–158. [Google Scholar] [CrossRef]
- Zhang, Y.; Tong, J.; Guo, Q.; Guo, J.; Liu, X.; Chen, L. Hierarchical Multiscale Analysis for 3D Woven Composite Leaf Spring Landing Gear. Thin-Walled Struct. 2023, 189, 110913. [Google Scholar] [CrossRef]
- Delprete, C.; Dagna, A.; Brusa, E. Model-Based Design of Aircraft Landing Gear System. Appl. Sci. 2023, 13, 11465. [Google Scholar] [CrossRef]
- Hsu, T.-H.; Chang, Y.-J.; Hsu, H.-K.; Chen, T.-T.; Hwang, P.-W. Predicting the Remaining Useful Life of Landing Gear with Prognostics and Health Management (PHM). Aerospace 2022, 9, 462. [Google Scholar] [CrossRef]
- Bale, H.A.; Haboub, A.; MacDowell, A.A.; Nasiatka, J.R.; Parkinson, D.Y.; Cox, B.N.; Marshall, D.B.; Ritchie, R.O. Real-Time Quantitative Imaging of Failure Events in Materials under Load at Temperatures above 1600 °C. Nat. Mater. 2013, 12, 40–46. [Google Scholar] [CrossRef]
- Mishra, R.R.; Sharma, A.K. Microwave–Material Interaction Phenomena: Heating Mechanisms, Challenges and Opportunities in Material Processing. Compos. Part A Appl. Sci. Manuf. 2016, 81, 78–97. [Google Scholar] [CrossRef]
- Dang, Z.-M.; Yuan, J.-K.; Zha, J.-W.; Zhou, T.; Li, S.-T.; Hu, G.-H. Fundamentals, Processes and Applications of High-Permittivity Polymer–Matrix Composites. Prog. Mater. Sci. 2012, 57, 660–723. [Google Scholar] [CrossRef]
- Garg, P.; Jamwal, A.; Kumar, D.; Sadasivuni, K.K.; Hussain, C.M.; Gupta, P. Advance Research Progresses in Aluminium Matrix Composites: Manufacturing & Applications. J. Mater. Res. Technol. 2019, 8, 4924–4939. [Google Scholar] [CrossRef]
- Cheng, L.; Cao, H.; Zhang, L. Two-Parameter Bifurcation Analysis of an Aircraft Nose Landing Gear Model. Nonlinear Dyn. 2021, 103, 367–381. [Google Scholar] [CrossRef]
- Arunagiri, P.; Vijayakumar; Ayesha Khan, M.; Jani, S.P. Structural Analysis and Materials Deformations of Landing Gear. Mater. Today Proc. 2022, 60, 2240–2244. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, T.; Yin, Y.; Wei, X. Reducing Shimmy Oscillation of a Dual-Wheel Nose Landing Gear Based on Torsional Nonlinear Energy Sink. Nonlinear Dyn. 2024, 112, 4027–4062. [Google Scholar] [CrossRef]
- Bodaghi, M.; Wang, L.; Zhang, F.; Liu, Y.; Leng, J.; Xing, R.; Dickey, M.D.; Vanaei, S.; Elahinia, M.; Hoa, S.V.; et al. 4D Printing Roadmap. Smart Mater. Struct. 2024, 33, 113501. [Google Scholar] [CrossRef]
- Ahmed, A.; Arya, S.; Gupta, V.; Furukawa, H.; Khosla, A. 4D Printing: Fundamentals, Materials, Applications and Challenges. Polymer 2021, 228, 123926. [Google Scholar] [CrossRef]
- Zhou, X.; Ren, L.; Song, Z.; Li, G.; Zhang, J.; Li, B.; Wu, Q.; Ren, L.; Liu, Q. Advances in 3D/4D Printing of Mechanical Metamaterials: From Manufacturing to Applications. Compos. Part B Eng. 2023, 254, 110585. [Google Scholar] [CrossRef]
- Abdullah, M.R.; Peng, Z.; Rajendren, V.b.; Ahmad, F.; Shah, S.S.A.; Zia, A.W.; Ali, A.; Qiao, G.; Shehzad, K. Comprehensive Review of 3D/4D Printing of Soft Materials, Methods and Applications. Appl. Mater. Today 2025, 43, 102667. [Google Scholar] [CrossRef]
- Nian, Y.; Wan, S.; Avcar, M.; Yue, R.; Li, M. 3D Printing Functionally Graded Metamaterial Structure: Design, Fabrication, Reinforcement, Optimization. Int. J. Mech. Sci. 2023, 258, 108580. [Google Scholar] [CrossRef]
- Zeng, Q.; Zhao, Z.; Lei, H.; Wang, P. A Deep Learning Approach for Inverse Design of Gradient Mechanical Metamaterials. Int. J. Mech. Sci. 2023, 240, 107920. [Google Scholar] [CrossRef]
- Surjadi, J.U.; Gao, L.; Du, H.; Li, X.; Xiong, X.; Fang, N.X.; Lu, Y. Mechanical Metamaterials and Their Engineering Applications. Adv. Eng. Mater. 2019, 21, 1800864. [Google Scholar] [CrossRef]
- Parandoush, P.; Zhou, C.; Lin, D. 3D Printing of Ultrahigh Strength Continuous Carbon Fiber Composites. Adv. Eng. Mater. 2019, 21, 1800622. [Google Scholar] [CrossRef]
- Lu, X.; Ambulo, C.P.; Wang, S.; Rivera-Tarazona, L.K.; Kim, H.; Searles, K.; Ware, T.H. 4D-Printing of Photoswitchable Actuators. Angew. Chem. Int. Ed. 2021, 60, 5536–5543. [Google Scholar] [CrossRef] [PubMed]
- Sarath Kumar, P.; Jayanarayanan, K.; Balachandran, M. Performance Comparison of Carbon Fiber Reinforced Polyaryletherketone and Epoxy Composites: Mechanical Properties, Failure Modes, Cryo-Thermal Behavior, and Finite Element Analysis. J. Appl. Polym. Sci. 2022, 139, e52494. [Google Scholar] [CrossRef]
- Rahmatabadi, D.; Soleyman, E.; Fallah Min Bashi, M.; Aberoumand, M.; Soltanmohammadi, K.; Ghasemi, I.; Baniassadi, M.; Abrinia, K.; Bodaghi, M.; Baghani, M. 4D Printing and Annealing of PETG Composites Reinforced with Short Carbon Fibers. Phys. Scr. 2024, 99, 055957. [Google Scholar] [CrossRef]
- Baniasadi, H.; Äkräs, L.; Madani, Z.; Silvenius, F.; Fazeli, M.; Lipponen, S.; Vapaavuori, J.; Seppälä, J. Development and Characterization of Polylactic Acid/Starch Biocomposites—From Melt Blending to Preliminary Life Cycle Assessment. Int. J. Biol. Macromol. 2024, 279, 135173. [Google Scholar] [CrossRef]
- Fazeli, M.; Islam, S.; Baniasadi, H.; Abidnejad, R.; Schlapp-Hackl, I.; Hummel, M.; Lipponen, J. Exploring the Potential of Regenerated Ioncell Fiber Composites: A Sustainable Alternative for High-Strength Applications. Green Chem. 2024, 26, 6822–6835. [Google Scholar] [CrossRef]
- Kamarudin, S.H.; Mohd Basri, M.S.; Rayung, M.; Abu, F.; Ahmad, S.; Norizan, M.N.; Osman, S.; Sarifuddin, N.; Desa, M.S.Z.M.; Abdullah, U.H.; et al. A Review on Natural Fiber Reinforced Polymer Composites (NFRPC) for Sustainable Industrial Applications. Polymers 2022, 14, 3698. [Google Scholar] [CrossRef]
- Zhang, P.; Hu, X.; Bui, T.Q.; Yao, W. Phase Field Modeling of Fracture in Fiber Reinforced Composite Laminate. Int. J. Mech. Sci. 2019, 161–162, 105008. [Google Scholar] [CrossRef]
- Morampudi, P.; Namala, K.K.; Gajjela, Y.K.; Barath, M.; Prudhvi, G. Review on Glass Fiber Reinforced Polymer Composites. Mater. Today Proc. 2021, 43, 314–319. [Google Scholar] [CrossRef]
- Wang, B.; Ma, S.; Yan, S.; Zhu, J. Readily Recyclable Carbon Fiber Reinforced Composites Based on Degradable Thermosets: A Review. Green Chem. 2019, 21, 5781–5796. [Google Scholar] [CrossRef]
- Chandramohan, D.; Sathish, T.; Kumar, S.D.; Sudhakar, M. Mechanical and Thermal Properties of Jute/Aloevera Hybrid Natural Fiber Reinforced Composites. AIP Conf. Proc. 2020, 2283, 020084. [Google Scholar] [CrossRef]
- Papon, E.A.; Haque, A. Fracture Toughness of Additively Manufactured Carbon Fiber Reinforced Composites. Addit. Manuf. 2019, 26, 41–52. [Google Scholar] [CrossRef]
- Han, D.; Morde, R.S.; Mariani, S.; La Mattina, A.A.; Vignali, E.; Yang, C.; Barillaro, G.; Lee, H. 4D Printing of a Bioinspired Microneedle Array with Backward-Facing Barbs for Enhanced Tissue Adhesion. Adv. Funct. Mater. 2020, 30, 1909197. [Google Scholar] [CrossRef]
- Sanei, S.H.R.; Popescu, D. 3D-Printed Carbon Fiber Reinforced Polymer Composites: A Systematic Review. J. Compos. Sci. 2020, 4, 98. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, F.; Leng, J.; Liu, Y. Personalized 4D Printing of Bioinspired Tracheal Scaffold Concept Based on Magnetic Stimulated Shape Memory Composites. Compos. Sci. Technol. 2019, 184, 107866. [Google Scholar] [CrossRef]
- ASTM D638; Standard Test Method for Tensile Properties of Plastics. ASTM: West Conshohocken, PA, USA, 2022.
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-Forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- ASTM D7264/D7264M-21; Standard Test Method for Flexural Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2021.


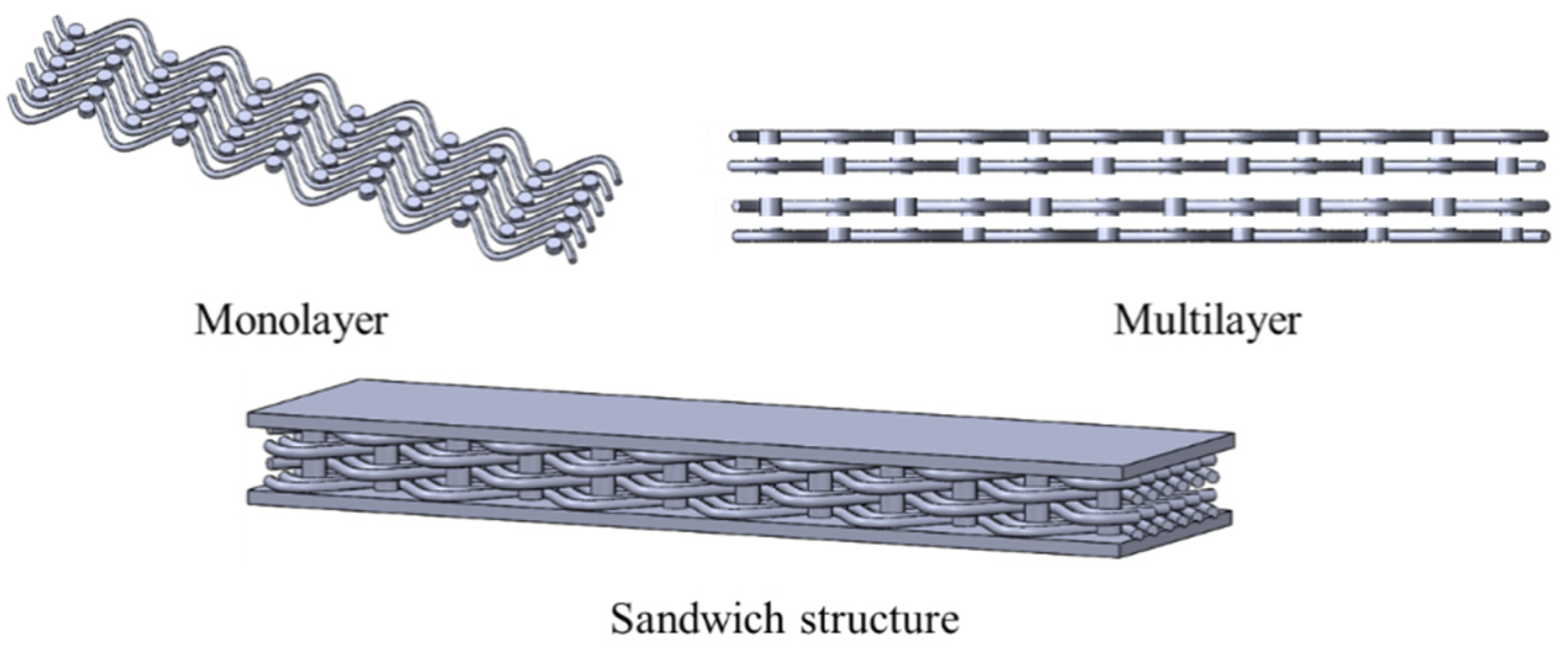

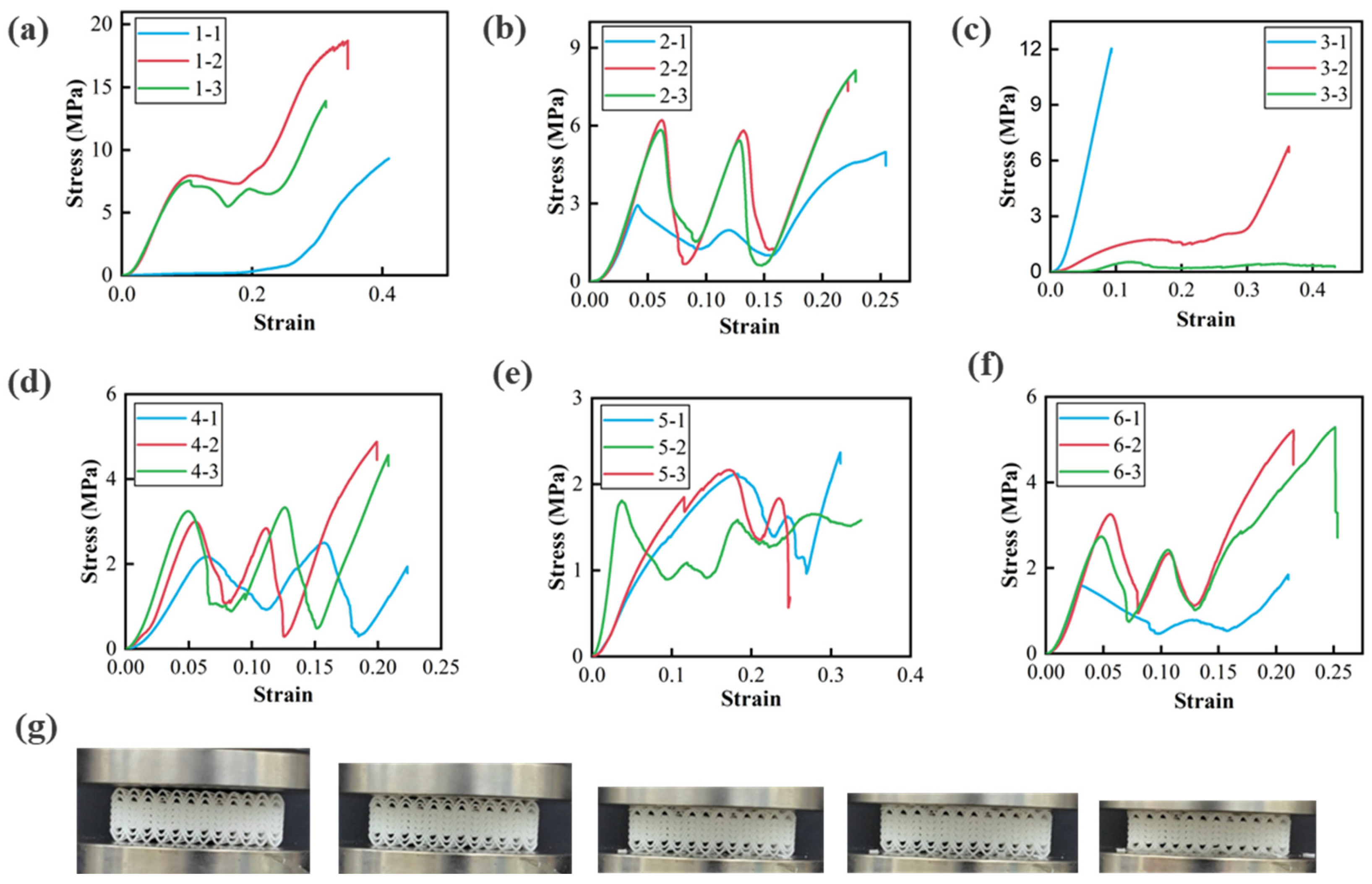
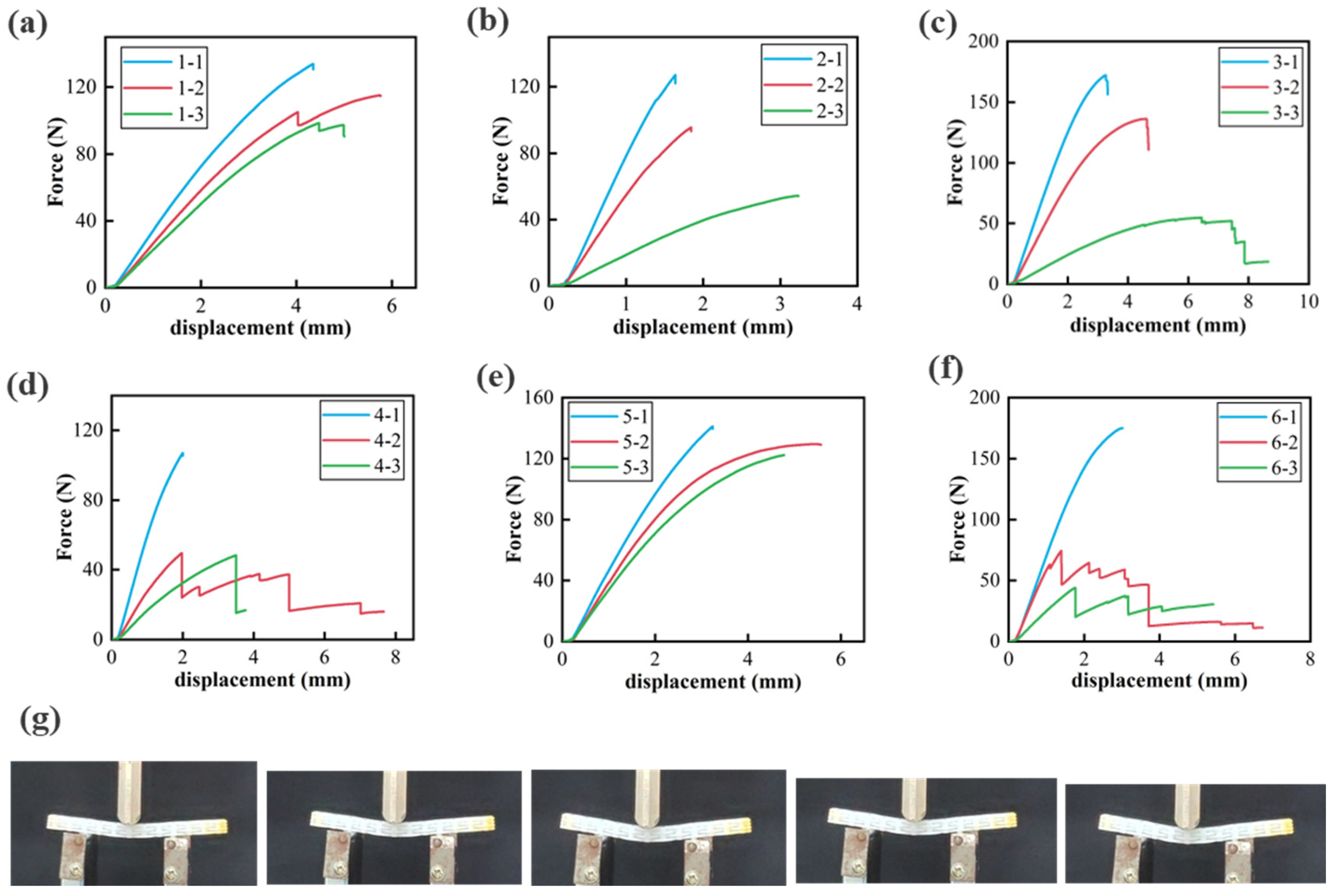
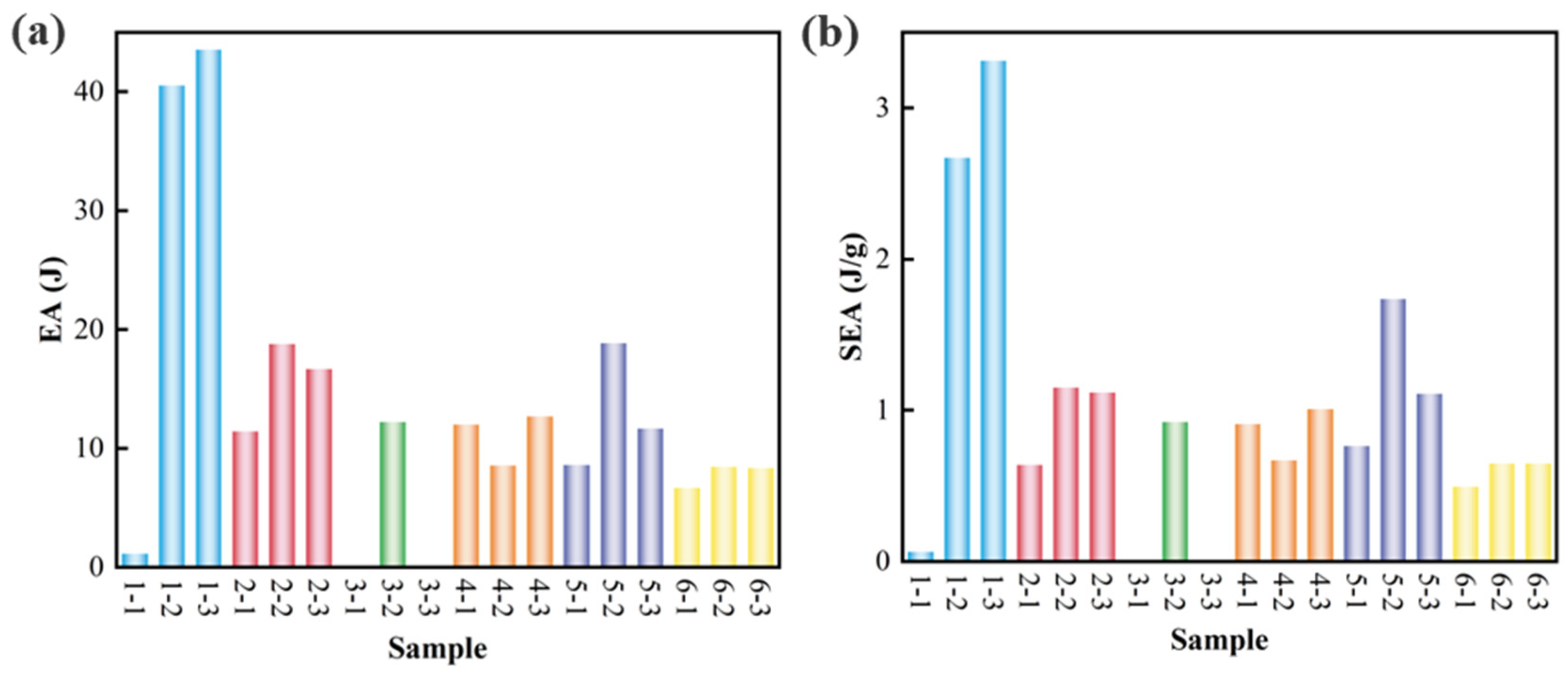
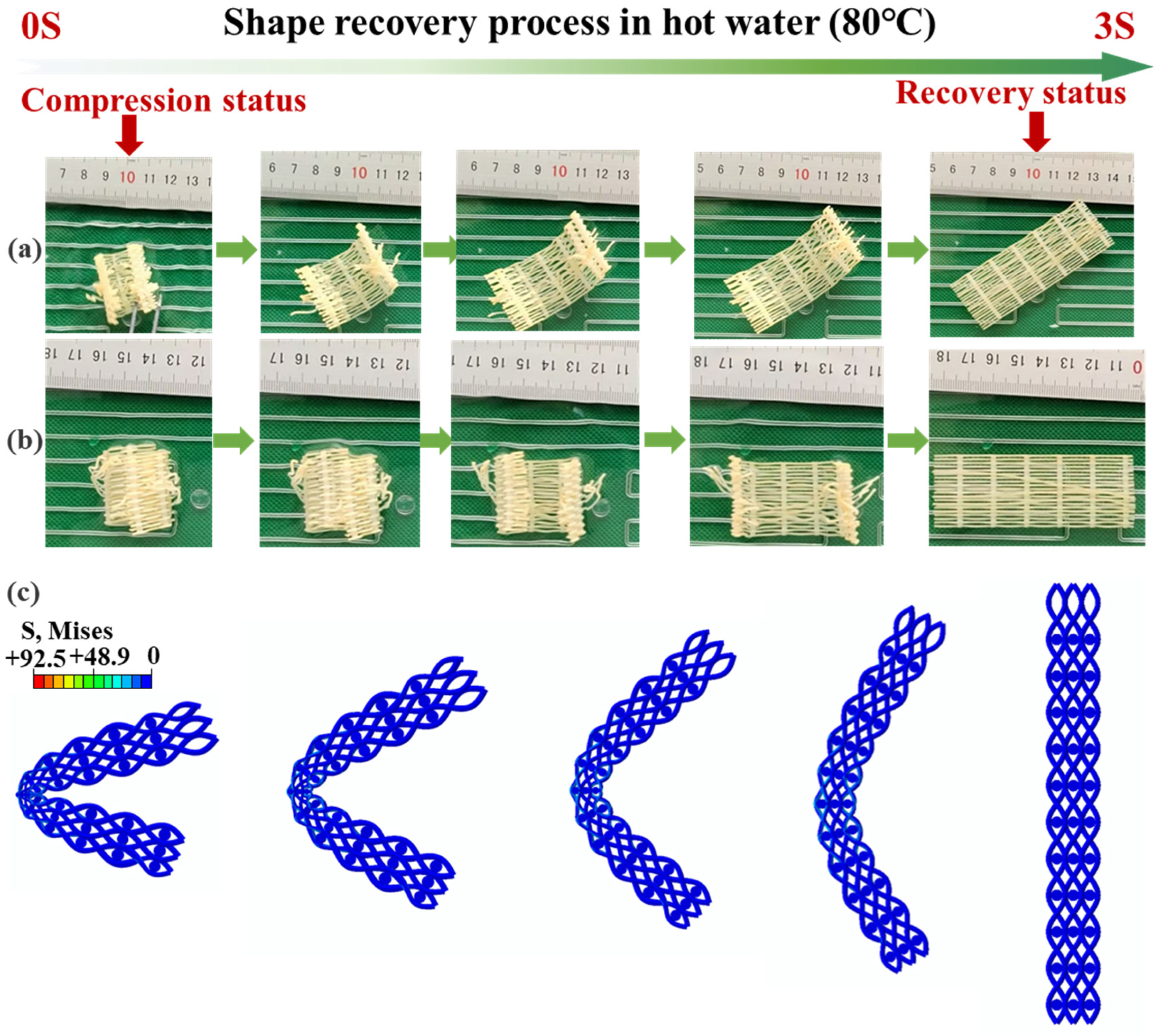
| Type | Yarn 1 | Yarn 2 | Diameter of the Bar (mm) | Overall Size (mm) |
|---|---|---|---|---|
| 1 | 3 | 3 | 2.1 | 80 × 29.5 × 22 |
| 2 | 4.5 | 4.5 | 2.1 | 80 × 29.5 × 25 |
| 3 | 1.5 | 1.5 | 2.1 | 80 × 29.5 × 18 |
| 4 | 3.2 | 4.5 | 0.8 | 80 × 29.5 × 25 |
| 5 | 3.2 | 1.5 | 0.8 | 80 × 29.5 × 21 |
| 6 | 5 | 2.6 | 0.8 | 80 × 29.5 × 24 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Lin, C.; Li, L.; Lu, Y.; Zhu, X.; Wang, W. Four-Dimensional-Printed Woven Metamaterials for Vibration Reduction and Energy Absorption in Aircraft Landing Gear. Materials 2025, 18, 3371. https://doi.org/10.3390/ma18143371
Wang X, Lin C, Li L, Lu Y, Zhu X, Wang W. Four-Dimensional-Printed Woven Metamaterials for Vibration Reduction and Energy Absorption in Aircraft Landing Gear. Materials. 2025; 18(14):3371. https://doi.org/10.3390/ma18143371
Chicago/Turabian StyleWang, Xiong, Changliang Lin, Liang Li, Yang Lu, Xizhe Zhu, and Wenjie Wang. 2025. "Four-Dimensional-Printed Woven Metamaterials for Vibration Reduction and Energy Absorption in Aircraft Landing Gear" Materials 18, no. 14: 3371. https://doi.org/10.3390/ma18143371
APA StyleWang, X., Lin, C., Li, L., Lu, Y., Zhu, X., & Wang, W. (2025). Four-Dimensional-Printed Woven Metamaterials for Vibration Reduction and Energy Absorption in Aircraft Landing Gear. Materials, 18(14), 3371. https://doi.org/10.3390/ma18143371







