Effect of Mass Reduction of 3D-Printed PLA on Load Transfer Capacity—A Circular Economy Perspective
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Mechanical Tests
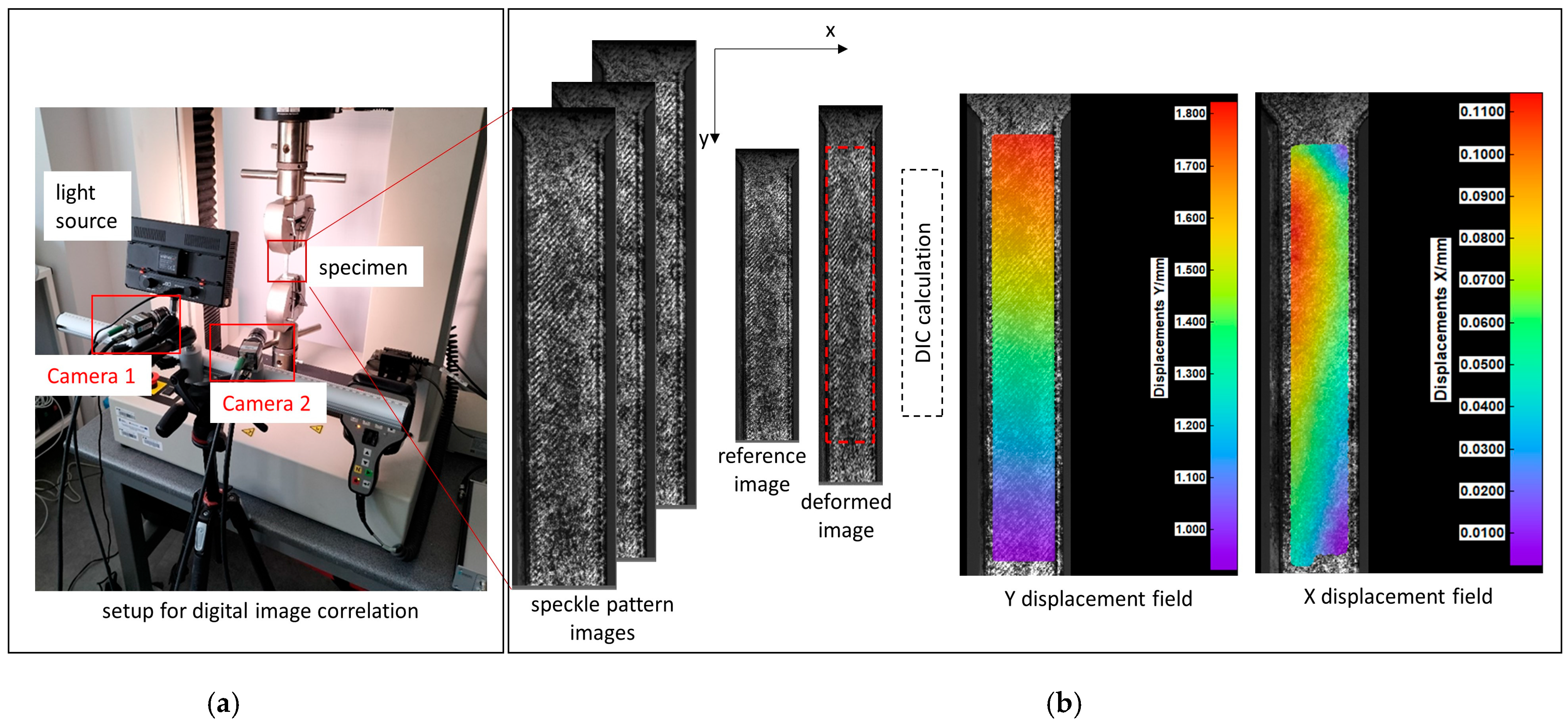
2.2.2. Digital Image Correlation (DIC)
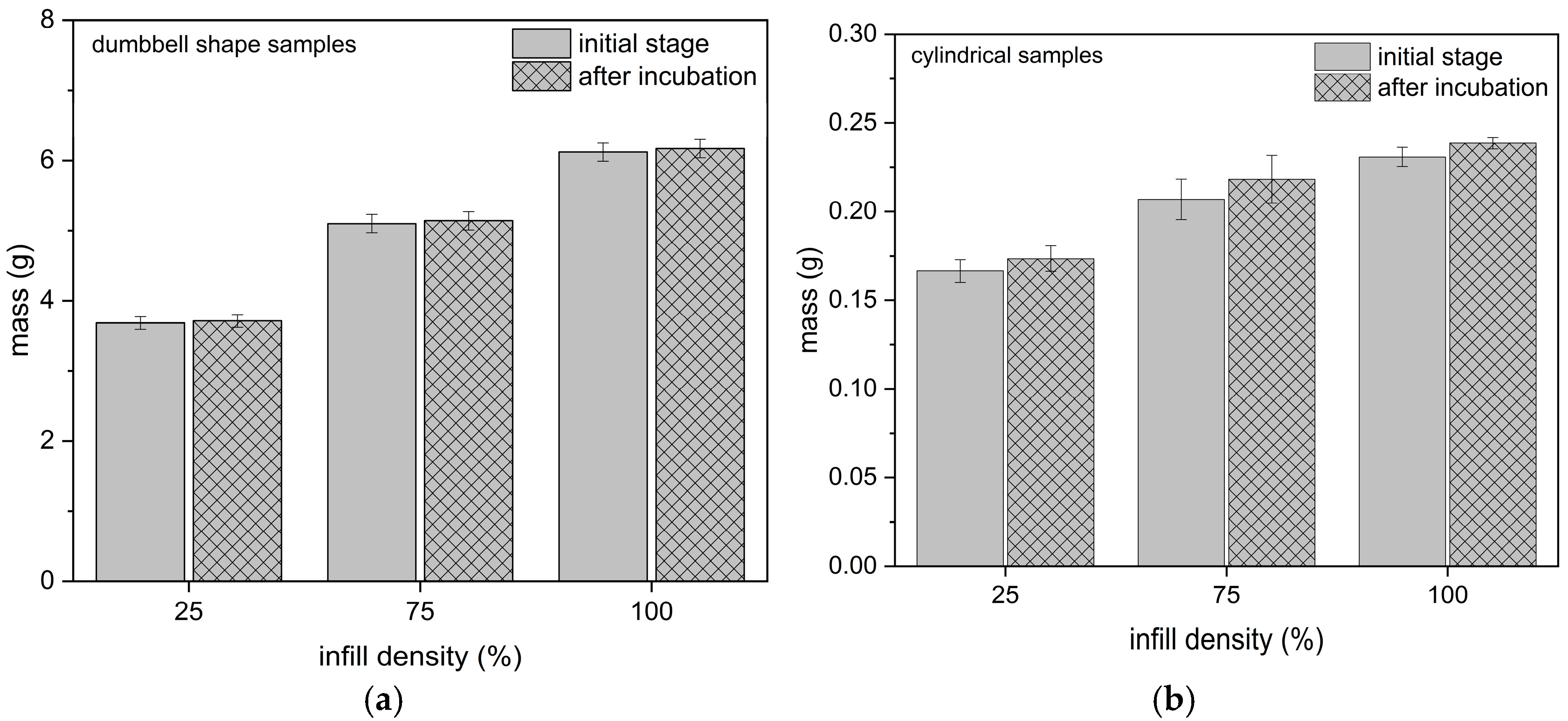
2.2.3. Hydration Test
2.2.4. Statistical Analysis
3. Results
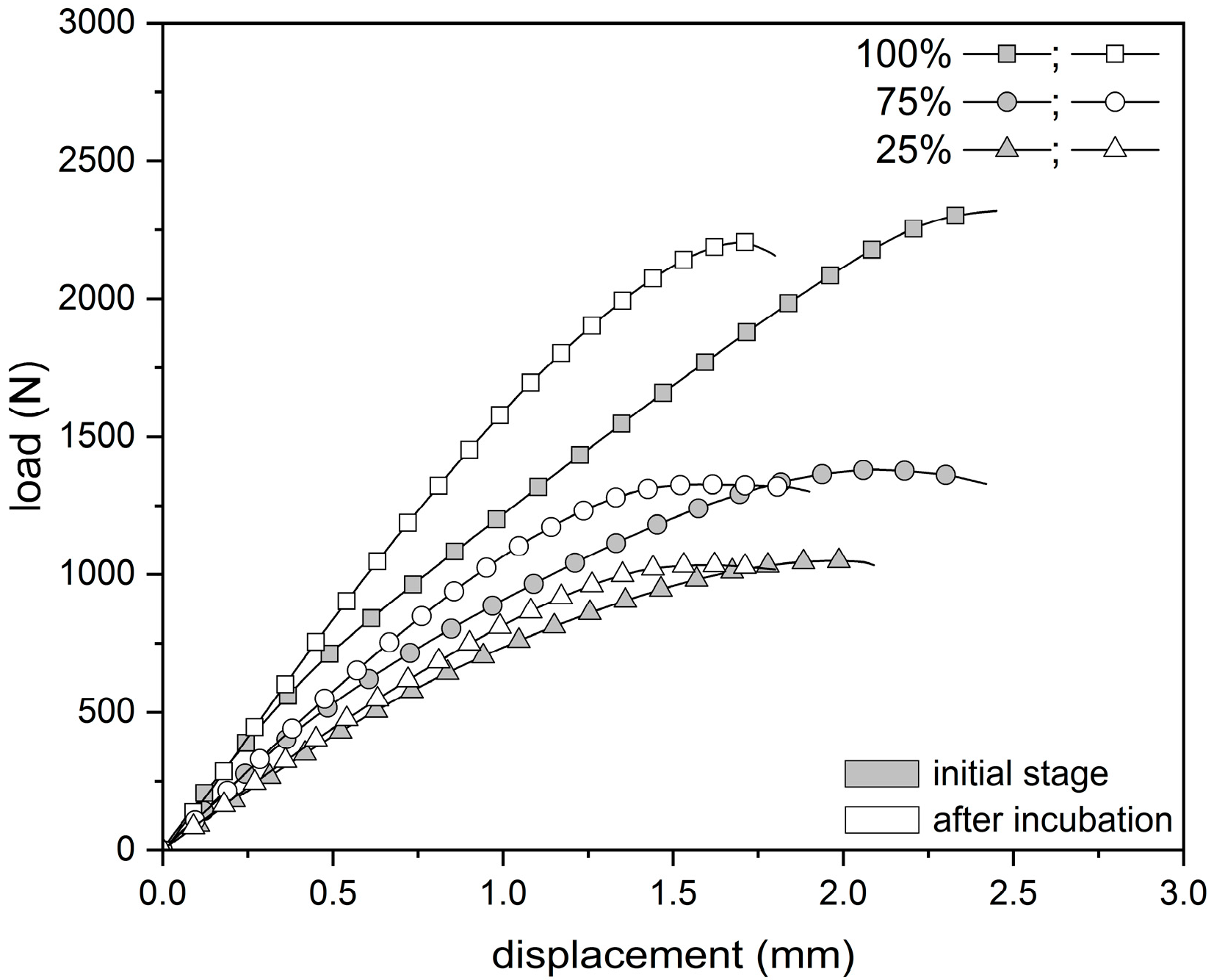
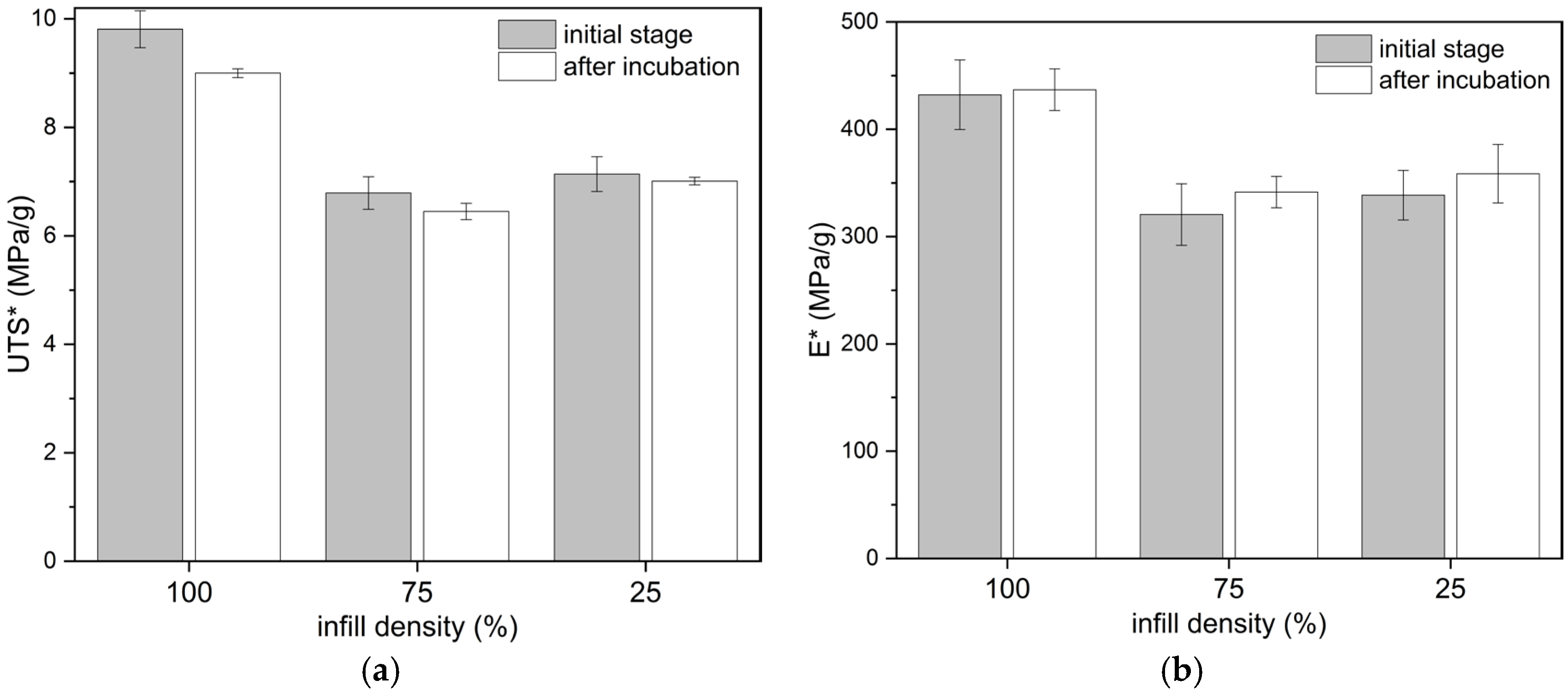
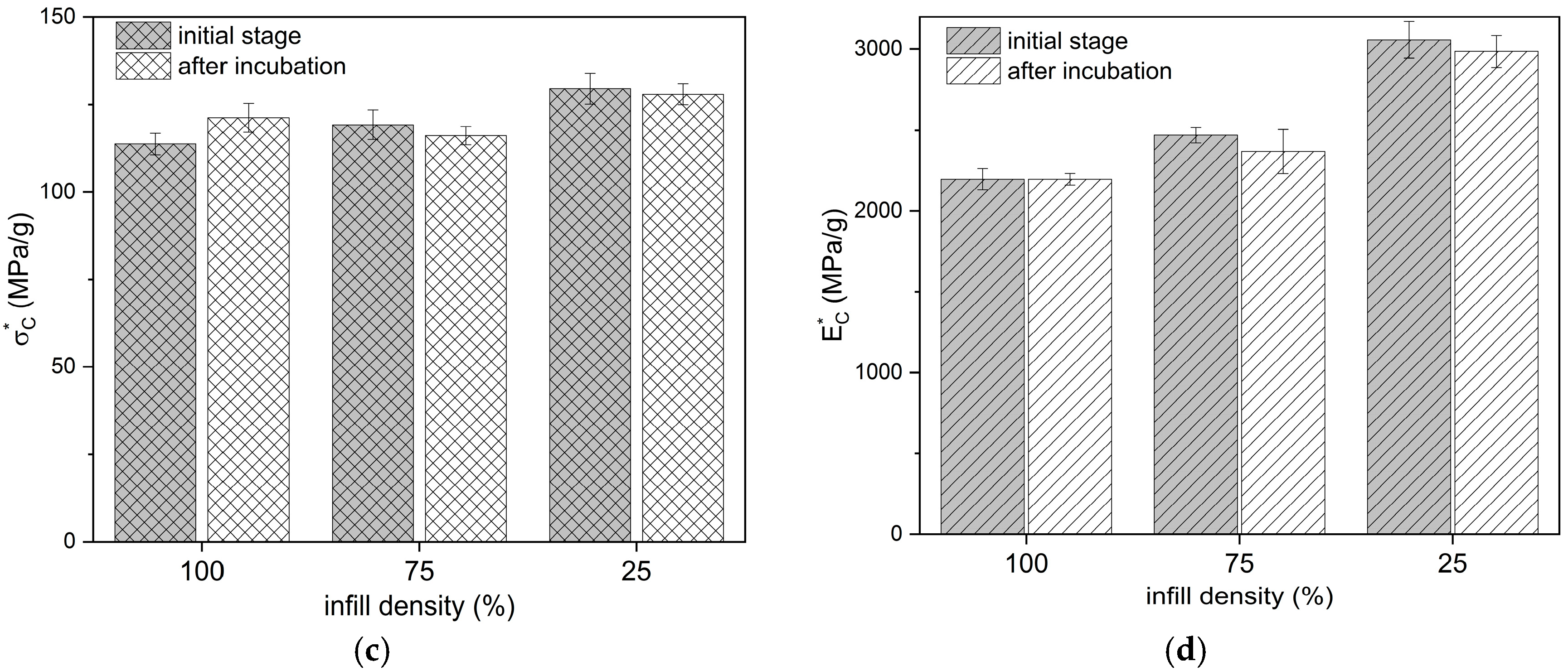
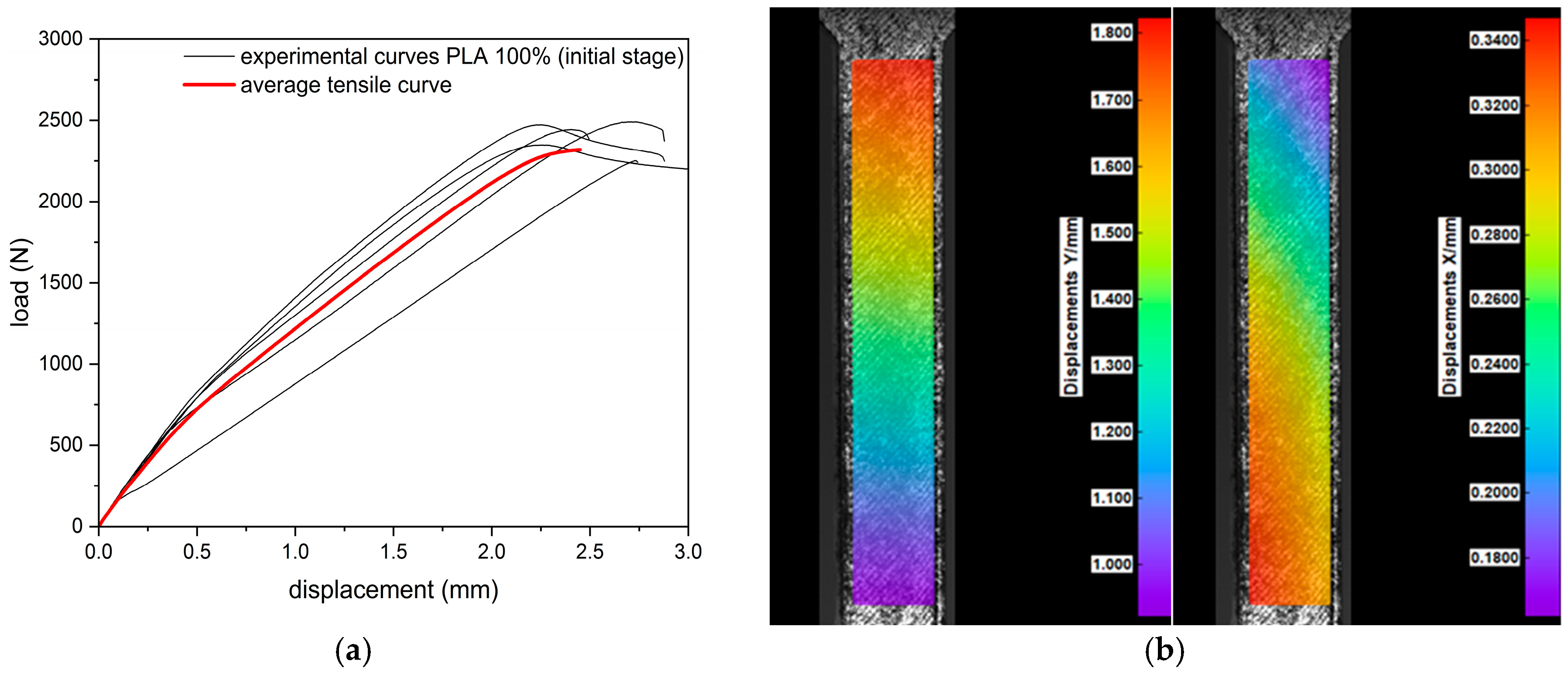
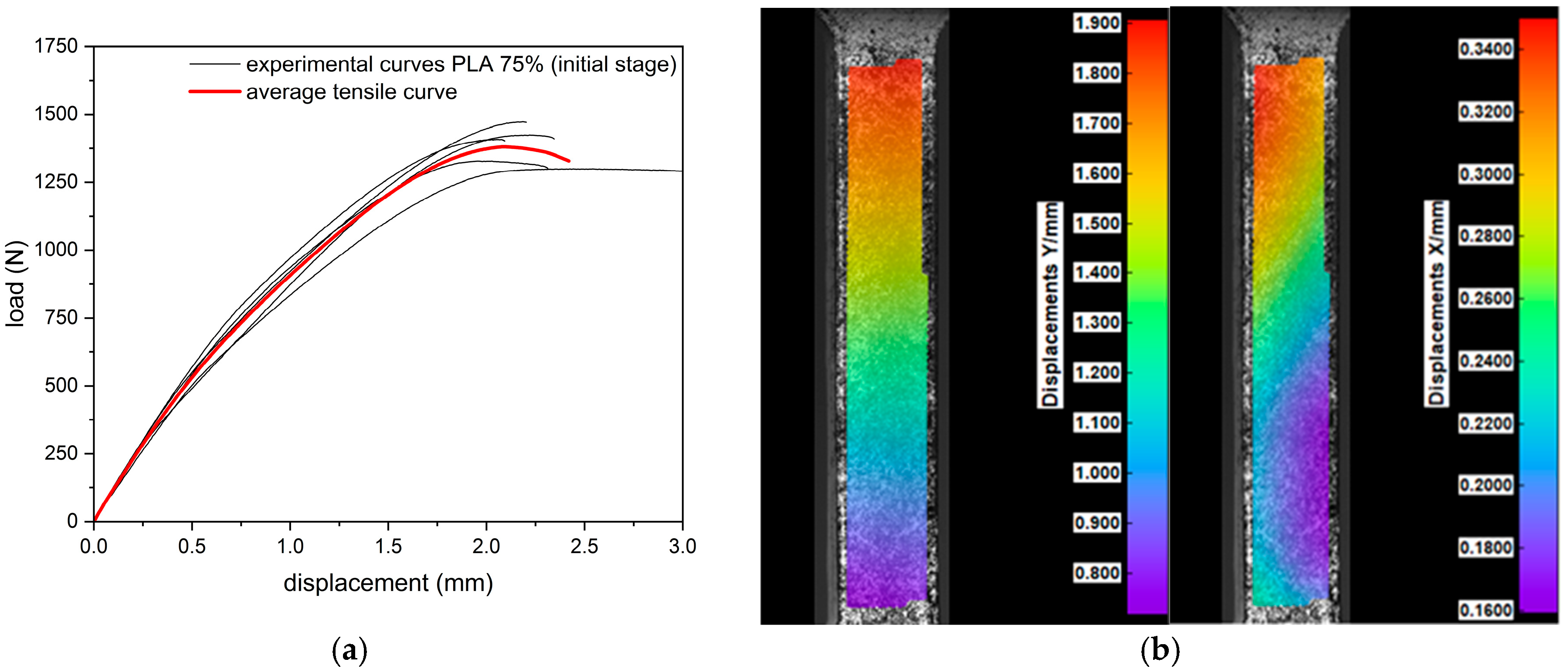
3.1. Tensile and Compression Tests
3.2. Digital Image Correlation (DIC)
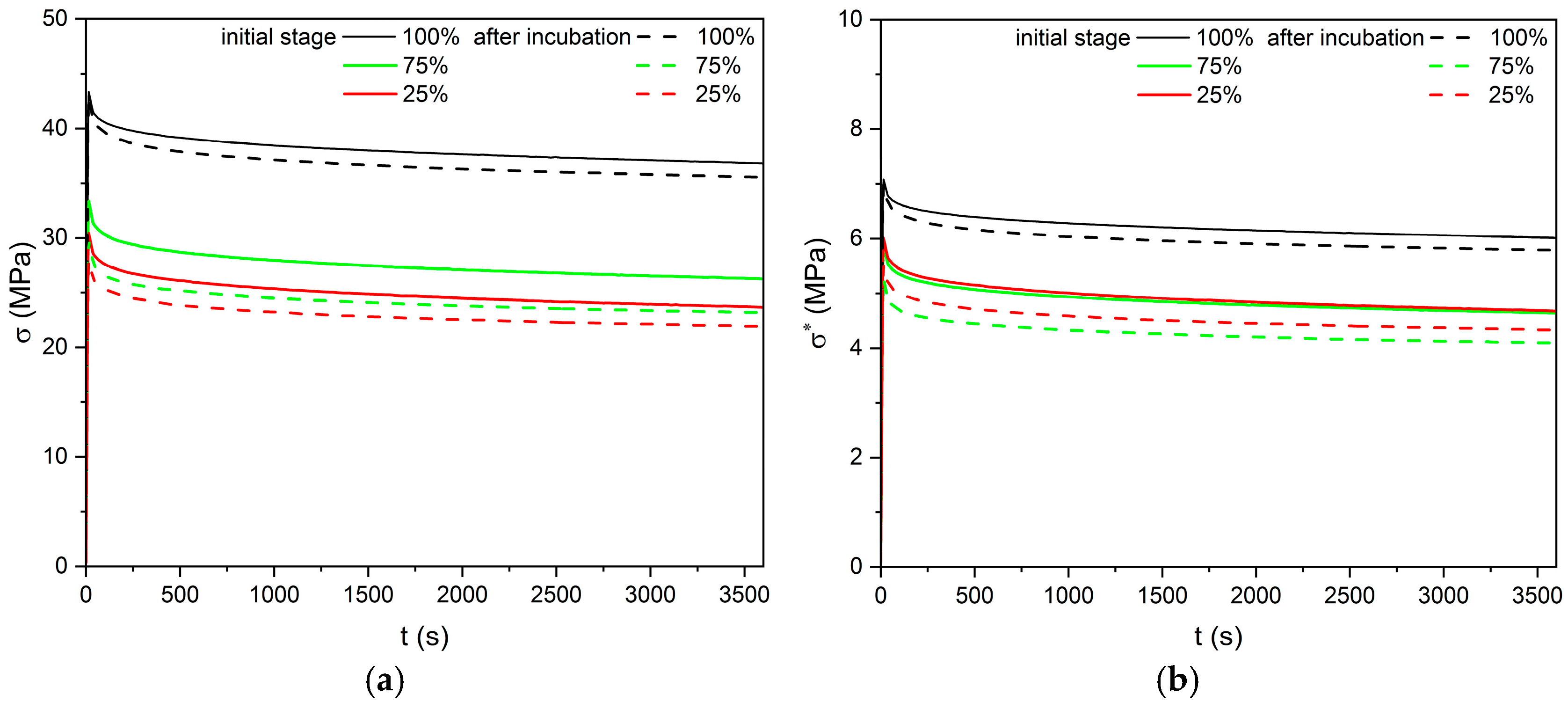
3.3. Stress Relaxation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Global Plastic Production 1950–2023, Published by Statista Research Department. Available online: https://www.statista.com/ (accessed on 8 May 2025).
- Plastic Waste Worldwide—Statistics & Facts, Published by Bruna Alves. Available online: https://www.statista.com/ (accessed on 8 May 2025).
- King, S.; Locock, K.E.S. A circular economy framework for plastics: A semi-systematic review. J. Clean. Prod. 2022, 364, 132503. [Google Scholar] [CrossRef]
- Kuclourya, T.; Monroy, R.; Ahmad, R. Design of experiments to compare the reprocessing effect with Fused Deposition Modeling printing parameters on mechanical properties of polylactic acid specimens towards circular economy. Prog. Rubber Plast. Recycl. Technol. 2023, 39, 111–140. [Google Scholar] [CrossRef]
- Sheldon, R.; Norton, M. Green chemistry and the plastic pollution challenge: Towards a circular economy. Green Chem. 2020, 22, 6310–6322. [Google Scholar] [CrossRef]
- Karan, H.; Funk, C.; Grabert, M.; Oey, M.; Hankamer, B. Green bioplastics as part of a circular bioeconomy. Plant Sci. J. 2019, 24, 237–249. [Google Scholar] [CrossRef]
- ISO 17088:2021; Plastics—Organic Recycling—Specifications for Compostable Plastics. ISO: Geneva, Switzerland, 2021.
- Mosomi, E.K.; Olanrewaju, O.A.; Adeosun, S.O. Pivotal role of polylactide in carbon emission reduction: A comprehensive review. Eng. Rep. 2024, 6, e12909. [Google Scholar] [CrossRef]
- Yu, J.; Xu, S.; Liu, B.; Wang, H.; Qiao, F.; Ren, X.; Wei, Q. PLA bioplastic production: From monomer to the polymer. Eur. Polym. J. 2023, 193, 112076. [Google Scholar] [CrossRef]
- Castro-Aguirre, E.; Iñiguez-Franco, F.; Samsudin, H.; Fang, X.; Auras, R. Poly(lactic acid)—Mass production, processing, industrial applications, and end of life. Adv. Drug Deliv. Rev. 2016, 107, 333–366. [Google Scholar] [CrossRef]
- Rossi, V.; Cleeve Edwards, N.; Lundquist, L.; Schenker, U.; Dubois, C.; Humbert, S.; Jolliet, O. Life cycle assessment of end-of-life options for two biodegradable packaging materials: Sound application of the European waste hierarchy. J. Clean. Prod. 2015, 86, 132–145. [Google Scholar] [CrossRef]
- Shamsuyeva, M.; Endres, H.-J. Plastics in the context of the circular economy and sustainable plastics recycling: Comprehensive review on research development, standardization and market. Compos. Part C 2021, 6, 100168. [Google Scholar] [CrossRef]
- Swetha, T.A.; Bora, A.; Mohanrasu, K.; Balaji, P.; Raja, R.; Ponnuchamy, K.; Muthusamy, G.; Arun, A. A comprehensive review on polylactic acid (PLA)—Synthesis, processing and application in food packaging. Int. J. Biol. Macromol. 2023, 234, 123715. [Google Scholar] [CrossRef]
- Giammaria, V.; Capretti, M.; Del Bianco, G.; Boria, S.; Santulli, C. Application of poly(lactic acid) composites in the automotive sector: A critical review. Polymers 2024, 16, 3059. [Google Scholar] [CrossRef] [PubMed]
- Khouri, N.G.; Bahú, J.O.; Blanco-Llamero, C.; Severino, P.; Concha, V.O.C.; Souto, E.B. Polylactic acid (PLA): Properties, synthesis, and biomedical applications—A review of the literature. J. Mol. Struct. 2024, 1309, 138243. [Google Scholar] [CrossRef]
- DeStefano, V.; Khan, S.; Tabada, A. Applications of PLA in modern medicine. Eng. Regen. 2020, 1, 76–87. [Google Scholar] [CrossRef] [PubMed]
- Al-Shalawi, F.D.; Hanim, M.A.; Ariffin, M.K.A.; Kim, C.L.S.; Brabazon, D.; Calin, R.; Al-Osaimi, M.O. Biodegradable synthetic polymer in orthopaedic application: A review. Mater. Today Proc. 2023, 74, 540–546. [Google Scholar] [CrossRef]
- Kharmanda, G. Challenges and Future Perspectives for Additively Manufactured Polylactic Acid Using Fused Filament Fabrication in Dentistry. J. Funct. Biomater. 2023, 14, 334. [Google Scholar] [CrossRef]
- Charasseangpaisarn, T.; Wiwatwarrapan, C.; Thunyakitpisal, P.; Srimaneepong, V. Development of poly(methyl methacrylate)/poly(lactic acid) blend as sustainable biomaterial for dental applications. Sci. Rep. 2023, 13, 16904. [Google Scholar] [CrossRef]
- Tsui, J.K.S.; Bell, S.; da Cruz, L.; Dick, A.D.; Sagoo, M.S. Applications of three-dimensional printing in ophthalmology. Surv. Ophthalmol. 2022, 67, 1287–1310. [Google Scholar] [CrossRef]
- Zimina, A.; Senatov, F.; Choudhary, R.; Kolesnikov, E.; Anisimova, N.; Kiselevskiy, M.; Orlova, P.; Strukova, N.; Generalova, M.; Manskikh, V.; et al. Biocompatibility and physico-chemical properties of highly porous PLA/HA scaffolds for bone reconstruction. Polymers 2020, 12, 2938. [Google Scholar] [CrossRef]
- Stodolak-Zych, E.; Ficek, K.; Wieczorek, J.; Kajor, M.; Gryń, K.; Rapacz-Kmita, A.; Rajca, J.; Kosenyuk, Y.; Stolarz, M.; Błażewicz, S. Assessment of sheep knee joint after ACL replacement with Achilles tendon autograft and PLA-based implant. J. Mech. Behav. Biomed. Mater. 2022, 125, 104923. [Google Scholar] [CrossRef]
- Guerra, A.J.; Cano, P.; Rabionet, M.; Puig, T.; Ciurana, J. 3D-Printed PCL/PLA Composite Stents: Towards a New Solution to Cardiovascular Problems. Materials 2018, 11, 1679. [Google Scholar] [CrossRef]
- Alhulaybi, Z.A. Fabrication and characterization of poly(lactic acid)-based biopolymer for surgical sutures. ChemEngineering 2023, 7, 98. [Google Scholar] [CrossRef]
- Paz-González, J.A.; Velasco-Santos, C.; Villarreal-Gómez, L.J.; Alcudia-Zacarias, E.; Olivas-Sarabia, A.; Cota-Leal, M.A.; Flores-López, L.Z.; Gochi-Ponce, Y. Structural composite based on 3D printing polylactic acid/carbon fiber laminates (PLA/CFRC) as an alternative material for femoral stem prosthesis. J. Mech. Behav. Biomed. Mater. 2023, 138, 105632. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.-A.; Plott, J.; Chen, R.; Wensman, J.; Shih, A. Additive Manufacturing of Custom Orthoses and Prostheses—A Review. Proc. CIRP 2015, 36, 199–204. [Google Scholar] [CrossRef]
- Morimoto, S.Y.U.; Cabral, A.K.P.S.; Sanguinetti, D.C.M.; Freitas, E.S.R.; Merino, G.S.A.D.; Costa, J.Â.P.; Coelho, W.K.; Amaral, D.S. Upper limbs orthesis and prostheses printed in 3D: An integrative review. Cad. Bras. Ter. Ocup. 2021, 29, e2078. [Google Scholar] [CrossRef]
- Tábi, T.; Ageyeva, T.; Kovács, J.G. Improving the ductility and heat deflection temperature of injection molded Poly(lactic acid) products: A comprehensive review. Polym. Test. 2021, 101, 107282. [Google Scholar] [CrossRef]
- Freeland, B.; McCarthy, E.; Balakrishnan, R.; Fahy, S.; Boland, A.; Rochfort, K.D.; Dabros, M.; Marti, R.; Kelleher, S.M.; Gaughran, J. A review of polylactic acid as a replacement material for single-use laboratory components. Materials 2022, 15, 2989. [Google Scholar] [CrossRef]
- RameshKumar, S.; Shaiju, P.; O’Connor, K.E.; Ramesh Babu, P. Bio-based and biodegradable polymers—State-of-the-art, challenges and emerging trends. Curr. Opin. Green Sustain. Chem. 2020, 21, 75–81. [Google Scholar] [CrossRef]
- Mikula, K.; Skrzypczak, D.; Izydorczyk, G.; Warchoł, J.; Moustakas, K.; Chojnacka, K.; Witek-Krowiak, A. 3D printing filament as a second life of waste plastics—A review. Environ. Sci. Pollut. Res. 2021, 28, 12321–12333. [Google Scholar] [CrossRef]
- DePalma, K.; Walluk, M.R.; Murtaugh, A.; Hilton, J.; McConky, S.; Hilton, B. Assessment of 3D printing using fused deposition modeling and selective laser sintering for a circular economy. J. Clean. Prod. 2020, 264, 121567. [Google Scholar] [CrossRef]
- Rodríguez-Panes, A.; Claver, J.; Camacho, A.M. The influence of manufacturing parameters on the mechanical behaviour of PLA and ABS pieces manufactured by FDM: A comparative analysis. Materials 2018, 11, 1333. [Google Scholar] [CrossRef]
- Alhazmi, M.W.; Backar, A.H. Influence of infill density and orientation on the mechanical response of PLA specimens produced using FDM 3D printing. Int. J. Adv. Sci. Technol. 2020, 29, 3362–3371. [Google Scholar]
- Albadrani, M.A. Effects of raster angle on the elasticity of 3D-printed polylactic acid and polyethylene terephthalate glycol. Designs 2023, 7, 112. [Google Scholar] [CrossRef]
- Zaneldin, E.; Ahmed, W.; Mansour, A.; Hassan, A.E. Dimensional stability of 3D printed objects made from plastic waste using FDM: Potential construction applications. Buildings 2021, 11, 516. [Google Scholar] [CrossRef]
- ISO 527:2019; Plastics—Determination of Tensile Properties—Part 1: General Principles. ISO: Geneva, Switzerland, 2019.
- Maszybrocka, J.; Dworak, M.; Nowakowska, G.; Osak, P.; Łosiewicz, B. The influence of the gradient infill of PLA samples produced with the FDM technique on their mechanical properties. Materials 2022, 15, 1304. [Google Scholar] [CrossRef]
- Dave, H.K.; Rajpurohit, S.R.; Patadiya, N.H.; Dave, S.J.; Sharma, K.S.; Thambad, S.S.; Srinivasn, V.P.; Sheth, K.V. Compressive strength of PLA based scaffolds: Effect of layer height, infill density and print speed. Int. J. Mod. Manuf. Technol. 2019, 11, 21–27. [Google Scholar]
- Hodzic, D.; Pandzic, A. Influence of infill design on compressive and flexural mechanical properties of FDM printed PLA material. Ann. DAAAM Proc. 2021, 32, 0191–0199. [Google Scholar]
- Pandzic, A.; Hodzic, D. Mechanical properties comparison of PLA, tough PLA and PC 3D printed materials with infill structure—Influence of infill pattern on tensile mechanical properties. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1208, 012019. [Google Scholar] [CrossRef]
- Eryildiz, M. The effects of infill patterns on the mechanical properties of 3D printed PLA parts fabricated by FDM. Ukr. J. Mech. Eng. Mater. Sci. 2021, 7, 1–8. [Google Scholar] [CrossRef]
- Torrente-Prato, G.; Sosa-Vivas, L.; Gonzalez-Delgado, J.; Hernandez-Silva, H.; León-Molina, H. Experimental and numerical study of the orthotropic behavior of 3D printed polylactic acid by material extrusion: Part two: An analysis about Poisson’s ratios. Prog. Addit. Manuf. 2025, 10, 2335–2350. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, L.; Fuh, J.Y.H.; Lee, H.P. Effect of porosity on mechanical properties of 3D printed polymers: Experiments and micromechanical modeling based on X-ray computed tomography analysis. Polymers 2019, 11, 1154. [Google Scholar] [CrossRef]
- Ferreira, R.T.L.; Amatte, I.C.; Dutra, T.A.; Bürger, D. Experimental characterization and micrography of 3D printed PLA and PLA reinforced with short carbon fibers. Compos. Part B Eng. 2017, 124, 88–100. [Google Scholar] [CrossRef]
- Tüfekci, K.; Çakan, B.G.; Küçükakarsu, V.M. Stress relaxation of 3D printed PLA of various infill orientations under tensile and bending loadings. J. Appl. Polym. Sci. 2023, 140, e54463. [Google Scholar] [CrossRef]
- Bertocco, A.; Bruno, M.; Armentani, E.; Esposito, L.; Perrella, M. Stress relaxation behavior of additively manufactured polylactic acid (PLA). Materials 2022, 15, 3509. [Google Scholar] [CrossRef] [PubMed]
- Vanaei, S.; Rastak, M.; Vanaei, H.; Magri, E.; Tcharkhtchi, A.; Raissi, K. Orientation-dependent mechanical behavior of 3D printed polylactic acid parts: An experimental-numerical study. Machines 2023, 10, 2335–2350. [Google Scholar] [CrossRef]
- Aly, R.; Olalere, O.; Ryder, A.; Alyammahi, M.; Samad, W.A. Mechanical property characterization of virgin and recycled PLA blends in single-screw filament extrusion for 3D printing. Polymers 2024, 16, 3569. [Google Scholar] [CrossRef]
- Bergaliyeva, S.; Sales, D.L.; Delgado, F.J.; Bolegenova, S.; Molina, S.I. Manufacture and characterization of polylactic acid filaments recycled from real waste for 3D printing. Polymers 2023, 15, 2165. [Google Scholar] [CrossRef]
- Gaweł, A.; Kuciel, S.; Liber-Kneć, A.; Mierzwiński, D. Examination of low-cyclic fatigue tests and Poisson’s ratio depending on the different infill density of polylactide (PLA) produced by the fused deposition modeling method. Polymers 2023, 15, 1651. [Google Scholar] [CrossRef]
- Gunasekaran, K.N.; Aravinth, V.; Kumaran, C.B.M.; Madhankumar, K.; Kumar, S.P. Investigation of mechanical properties of PLA printed materials under varying infill density. Mater. Today Proc. 2021, 45, 1849–1856. [Google Scholar] [CrossRef]
- Ali, S.; Abdallah, S.; Devjani, D.; John, J.; Samad, W.; Pervaiz, S. Effect of build parameters and strain rate on mechanical properties of 3D printed PLA using DIC and desirability function analysis. Rapid Prototyp. J. 2022, 29, 92–111. [Google Scholar] [CrossRef]






| Printing Parameters | Value |
|---|---|
| speed of monolithic layers, mm/s | 35 |
| speed of non-monolithic layers, mm/s | 50 |
| working table temperature, °C | 50 |
| speed of extruder travel over areas where material was not applied, mm/s | 80 |
| thickness of the invisible layers of the upper part of the sample, mm | 0.36 |
| thickness of the outer top layer, mm | 0.72 |
| filament withdrawal distance, mm | 5 |
| printing temperature (print head), °C | 220 |
| infill type | Diamond Fill Fast |
| layer height, mm | 0.2 |
| number of contours | 2 |
| raster angle, ° | 0/90 |
| density of infill, % | 100, 75, 25 |
| UTS [MPa] | E [MPa] | |
|---|---|---|
| PLA_100 | 60.04 ± 2.24 a,b | 2645.05 ± 204.15 a |
| PLA_100i | 55.50 ± 1.16 b | 2693.63 ± 123.01 |
| PLA_75 | 34.66 ± 1.59 a | 1635.93 ± 149.27 a |
| PLA_75i | 33.17 ± 1.20 | 1756.61 ± 87.87 |
| PLA_25 | 26.24 ± 0.77 a | 1245.41 ± 83.79 a |
| PLA_25i | 25.98 ± 0.47 | 1329.15 ± 97.23 |
| σc [MPa] | Ec [MPa] | |
|---|---|---|
| 1.5_PLA_100 | 36.24 ± 3.32 a,d | 504.60 ± 9.20 |
| 1.5_PLA_75 | 25.94 ± 1.82 a | 513.60 ± 11.91 |
| 1.5_PLA_25 | 19.42 ± 0.44 a,e | 516.60 ± 7.12 |
| 3_PLA_100 | 26.59 ± 0.80 b,c,d | 513.2 ± 9.68 |
| 3_PLA_100i | 28.92 ± 0.96 c | 513.2 ± 4.87 |
| 3_PLA_75 | 24.89 ± 0.88 b | 515.00 ± 7.01 |
| 3_PLA_75i | 25.32 ± 1.62 | 515.00 ± 8.74 |
| 3_PLA_25 | 21.83 ± 1.01 b,e | 514.60 ± 3.61 |
| 3_PLA_25i | 22.22 ± 1.24 | 517.40 ± 3.14 |
| Poisson’s Ratio [-] | |
|---|---|
| PLA_100 | 0.32 ± 0.01 a,b |
| PLA_75 | 0.30 ± 0.01 a |
| PLA_25 | 0.30 ± 0.01 b |
| [MPa] | [MPa] | [MPa/g] | [MPa/g] | [-] | |
|---|---|---|---|---|---|
| PLA_100 | 43.53 ± 1.54 a,b | 36.80 ± 3.33 a,b | 7.11 ± 0.25 | 6.02 ± 0.28 | 0.85 ± 0.01 |
| PLA_100i | 43.16 ± 0.40 | 35.55 ± 0.29 | 7.03 ± 0.03 | 5.79 ± 0.02 | 0.82 ± 0.00 |
| PLA_75 | 33.60 ± 1.31 a | 26.26 ± 1.10 a | 5.93 ± 0.23 | 4.64 ± 0.20 | 0.78 ± 0.00 |
| PLA_75i | 30.09 ± 1.16 | 23.20 ± 1.32 | 5.32 ± 0.21 | 4.10 ± 0.24 | 0.78 ± 0.08 |
| PLA_25 | 30.62 ± 0.76 b | 23.72 ± 1.02 b | 6.04 ± 0.15 | 4.83 ± 0.05 | 0.78 ± 0.02 |
| PLA_25i | 28.11 ± 0.90 | 21.94 ± 0.04 | 5.55 ± 0.18 | 4.33 ± 0.01 | 0.79 ± 0.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liber-Kneć, A.; Łagan, S. Effect of Mass Reduction of 3D-Printed PLA on Load Transfer Capacity—A Circular Economy Perspective. Materials 2025, 18, 3262. https://doi.org/10.3390/ma18143262
Liber-Kneć A, Łagan S. Effect of Mass Reduction of 3D-Printed PLA on Load Transfer Capacity—A Circular Economy Perspective. Materials. 2025; 18(14):3262. https://doi.org/10.3390/ma18143262
Chicago/Turabian StyleLiber-Kneć, Aneta, and Sylwia Łagan. 2025. "Effect of Mass Reduction of 3D-Printed PLA on Load Transfer Capacity—A Circular Economy Perspective" Materials 18, no. 14: 3262. https://doi.org/10.3390/ma18143262
APA StyleLiber-Kneć, A., & Łagan, S. (2025). Effect of Mass Reduction of 3D-Printed PLA on Load Transfer Capacity—A Circular Economy Perspective. Materials, 18(14), 3262. https://doi.org/10.3390/ma18143262






